Formation Enthalpies of C₃ and C₄ Brominated Hydrocarbons: Bringing Together Classical Thermodynamics, Modern Mass Spectrometry, and High-Level Ab Initio Calculations

Abstract

The enthalpies of formation of brominated C₃-C₄ hydrocarbons were critically evaluated using experimental data sources ranging from classical thermodynamics methods to modern high-precision mass spectrometry and reported in a time span of over a century. The experimental data were used in conjunction with the results of modern high-level ab initio calculations. To facilitate quantitative analysis, a recently developed local coupled cluster-based computational protocol was extended to organic compounds containing univalent Br. Several erroneous data sources were identified in a course of the study. Possible reasons of the inconsistency between the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values recommended by CODATA and Active Termochemical Tables for HBr in the gas and aqueous solution were discussed. The most up-to-date recommendations based on the comprehensive analysis of collected information are provided for 23 brominated hydrocarbons. For several compounds under consideration, the recommended values were previously lacking, while improved values and uncertainties were obtained for those with existing recommendations.

Graphical Absract

Introduction

Bromine-containing organic compounds have a wide range of practical applications. They are used as fire retardants, fumigants and biocides, dyes, pharmaceuticals, and intermediates in organic synthesis,^1,2 although some of these uses are being phased out due to environmental and health concerns. Knowledge of accurate thermochemical data, especially the enthalpies of formation, are important to facilitate the informed process design and practical applications.

The experimental enthalpies of formation for CHON molecules are normally determined from combustion experiments in a static bomb.³ Extension to bromine-containing compounds requires a rotating-bomb calorimeter and addition of a reducing agent $\left({\mathrm{A}\mathrm{s}}_2{\mathrm{O}}_3\right)$ to quantitatively transform ${\mathrm{B}\mathrm{r}}_2$ into ${\mathrm{B}\mathrm{r}}^{-}$.⁴ For relatively small brominated molecules, other techniques have also been widely used. They include reaction (hydrogenation, hydrobromination, bromination, etc.) calorimetry, chemical equilibrium studies in the liquid and gas phases, and mass-spectrometric methods. Overall, the experimental ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values are available for slightly over 100 compounds.

Kolesov and Papina reviewed the experimental enthalpies of formation of halogenated methanes⁵ and ethanes.⁶ Brominated compounds were also critically evaluated in general compilations such as those of Cox and Pilcher ⁷ and Pedley.⁸ These sources primarily considered the experimental data, although group-contribution estimates were used in some of them. The enthalpies of formation of brominated ${\mathrm{C}}_1$ and ${\mathrm{C}}_2$ compounds have also been reviewed using high-level ab initio computations.^9–12 Introduction of high-level computations to the data analysis and evaluation is beneficial for organoelement compounds because of experimental challenges in the associated thermochemical experiments. However, we are not aware of any high-level ab initio studies involving larger molecules as they were historically hindered by high computational costs.

In this work, the ab initio protocol proposed by us earlier^13,14 and used to compute ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ for about 400 CHON-containing species¹⁵ is parameterized for brominated compounds and its uncertainty is estimated. The experimental data for the enthalpies of formation and vaporization for ${\mathrm{C}}_3$ and ${\mathrm{C}}_4$ brominated compounds are collected. The data are evaluated using the ab initio protocol and the best estimates of these quantities are recommended. Finally, the experimental challenges are discussed and the erroneous data in the literature are identified.

Computations

The computations were performed according to the aLL5 protocol described in Ref. 14. The vibrational frequencies were calculated with the hybrid density-functional theory, B3LYP-D3(BJ)/def2-TZVP. Separate scaling factors were used for calculation of zero-point vibrational energies (ZPVE) and thermal correction to the enthalpy ${\mathrm{\Delta }}_0^{T}H$. For the former, the scaling factor was 0.990. For the latter, they were 0.960 for hydrogen stretches, and 0.985 for all other frequencies. The statistical thermodynamic calculations followed the rigid-rotor/harmonic oscillator approximation. The geometries for the coupled-cluster calculations were optimized with the density-fitted (resolution-of-identity) second-order Møller-Plesset perturbation theory (DF-MP2). The single-point energy calculations were performed with the 2016 version of local $\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)\left(\mathrm{L}\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\right(\mathrm{T}\left)\right)$ of Kállay et al.^16,17 In both calculations, aug-cc-pVQZ basis set was used. More details regarding the protocol can be found in the original publication.¹⁴ DFT calculations were performed with the Gaussian 16 software,¹⁸ DF-MP2 was done with the Psi4 package (version 1.5),^19,20 and $\mathrm{L}\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)$ was carried out with the MRCC suite (release of February 9, 2019).^21,22 All correlated calculations used the frozen-core approximation.

For the molecules exhibiting multiple conformations, the conformational search was performed using the procedure adopted from our previous studies (e.g., Refs 14,23–25). In this study, it was updated to include, in addition to the MMFF94²⁶ force field-based generators, the CREST framework²⁷ that uses the recent semi-empirical tight-binding model.²⁸

The standard entropy was found for each conformer using the rigid rotor/harmonic oscillator model described above. Enthalpy of formation for a given compound was computed as the Gibbs-energy average over the conformer population. The difference between this model and the one with hindered tops is discussed in the Supporting Information. For the brominated compounds considered in this work, the potential error introduced by this model is significantly lower than the expected uncertainty of the predicted ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values.

The enthalpies of formation at $T=298.15\mathrm{K}$ were obtained using the equation:^13,14,24

$${\Delta }_{\text{f}}{H}^{\circ }=E+\text{ZPVE}+{\Delta }_0^{T}H-\sum _{\text{types}}{n}_i{h}_i,$$ (1)

where $E$ is the total electronic energy, ZPVE is the zero-point vibrational energy, and ${\mathrm{\Delta }}_0^{T}H$ is the thermal correction from $T=\left(0\mathrm{to}298.15\right)\mathrm{K}$. The summation in the last term of Eq. 1 is performed over all atomic types present in the compound; $n_i$ is the ith type count, and $h_i$ is the type-specific constant. The following values, obtained previously,^14,24 were used: $h(\mathrm{C}$, saturated or aromatic $)=-99910.32\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},h(\mathrm{C}$, unsaturated $)=-99909.44\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},h(\mathrm{H})=-1524.23\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},h(\mathrm{O})=-197138.05\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, and $h\left(\mathrm{F}\right)=-261711.75\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$.

The expanded uncertainties (0.95 level of confidence) of the ab initio values were found as

$$U\left({\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\right)={\left[U^2(\text{CHON})+{(U(h(\text{F}))n(\text{F}))}^2+{(U(h(\text{Br}))n(\text{Br}))}^2\right]}^{1/2}$$ (2)

The procedure to calculate $U\left(\mathrm{C}\mathrm{H}\mathrm{O}\mathrm{N}\right)$ have been described previously,¹⁴ $U\left(h\left(\mathrm{F}\right)\right)=0.35\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$,²⁴ and $U\left(h\right(\mathrm{B}\mathrm{r}\left)\right)$ was determined in this study as described below.

The above protocol has been shown to be accurate and efficient for numerous neutral molecules.^14,24,29,30 In this work, analysis of mass spectrometry data also necessitates predictions for hydrocarbon ions. Tests for the methylium ion indicated that, in its original form, Eq. 1 does not predict the experimental ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ within the expected uncertainty of about $2.5\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. To improve the accuracy for ions, the complete-basis-set (CBS) version of the protocol²⁵ was used and the core-valence (CV) correlation was explicitly considered. The CBS extrapolation was based on the computations with aug-cc-pVNZ $(\mathrm{N}=\mathrm{Q},5)$ basis sets. For the Self-Consistent Field (SCF) contribution, the Karton-Martin modification³¹ of Jensen’s extrapolation formula³² was used:

$$E_{\infty }^{\text{SCF}}=E^{\text{SCF}}(L)+\frac{E^{\text{SCF}}(L)-E^{\text{SCF}}(L-1)}{c_1-1}$$ (3)

Where

$$c_1=\frac{L}{L+1}\text{exp}\left(9\right(\sqrt{L}-\sqrt{L-1}\left)\right)$$ (4)

and $L=5$.

The LCCSD$\left(\mathrm{T}\right)$ correlation contribution was extrapolated using

$$E_{\infty }^{\text{corr}}=E^{\text{corr}}(L)+\frac{E^{\text{corr}}(L)-E^{\text{corr}}(L-1)}{{\left(\frac{L}{L-1}\right)}^3-1}$$ (5)

which, to a large extent, is based on empirical observations (see, e.g., Ref. 33). For the CBS version of the protocol, $h(\mathrm{C}$, saturated or aromatic $)=-99924.23\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},h(\mathrm{C}$, unsaturated $)=-99923.22\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},h(\mathrm{H})=-1525.10\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}.$.²⁵

CV correlation energies were obtained as a difference between the all-electron and frozen-core results using the regular $\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)/\mathrm{c}\mathrm{c}-\mathrm{p}\mathrm{w}\mathrm{C}\mathrm{V}\mathrm{N}\mathrm{Z}(\mathrm{N}=\mathrm{T},\mathrm{Q})$ calculations carried out with CFOUR v2.1.³⁴ The total energies were extrapolated to the CBS limit using Eqs. (3) and (5) with $L=4$. For a set of neutral molecules including saturated, unsaturated, and aromatic hydrocarbons (Table 1), the CV correlation energy per carbon was found to be nearly constant, $⟨\mathrm{\Delta }{E}_{\mathrm{C}\mathrm{V}}/n_{\mathrm{C}}⟩={\epsilon }_{\mathrm{C}\mathrm{V}}=-(157.16\pm 0.12)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. This result is consistent with the additivity approximation for the contributions not explicitly included in Eq. 1, as implied in the original protocol.¹⁴ In other words, this contribution is already included in the effective enthalpies of the carbon atoms derived from the data for neutral compounds. When evaluating the enthalpy of formation for an ion with Eq. 1, the estimated CV contribution for a neutral compound, ${\epsilon }_{\mathrm{C}\mathrm{V}}\times n_{\mathrm{C}}$, was subtracted from the result and the explicitly computed $\mathrm{\Delta }{E}_{\mathrm{C}\mathrm{V}}$ was added instead.

Table 1:

Core-valence correlation energies for hydrocarbons calculated by the CBS extrapolation of the CCSD(T)/cc-pwCVNZ ($\mathrm{N}=\mathrm{T},\mathrm{Q}$) energies

Name	$\frac{-\Delta E_{\mathrm{CV}}}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{-\Delta E_{\mathrm{CV}}/n_{\text{C}}}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$
ethane	314.42	157.21
propane	471.46	157.15
butane	628.52	157.13
2-methylpropane	628.55	157.14
cyclohexane	942.38	157.06
ethylene	314.21	157.11
propene	471.49	157.16
2-methylpropene	628.68	157.17
acetylene	314.55	157.28
benzene	943.15	157.19
Average:		157.16 ± 0.12

Experimental data

In this section, a general characterization of the experimental techniques is provided. Details on particular measurements and the corresponding references are discussed in the subsequent sections. Typically, the main source of the formation enthalpies for brominated organic compounds in the condensed state is a rotating-bomb combustion calorimetry.⁴ However, this is not the case for the group considered here: three other techniques provided the largest fraction of thermochemical data. Reaction calorimetry has been used to obtain the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values in the gas and liquid phases. Typically, the molar enthalpies of the studied reactions (e.g., hydrogenation, bromination, hydrobromination) are at least an order of magnitude lower than the combustion energies of the corresponding brominated derivatives. The repeatability-based uncertainty close to $1\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ (comparable to that of combustion calorimetry) is often obtained with the instrument not as sophisticated as a rotating-bomb calorimeter (see, e.g., Refs. 7,35). As demonstrated below for 1- and 2-bromopropanes, these uncertainty estimates are not always adequate.

Temperature-dependent equilibrium constants can be used to derive the reaction enthalpies. This is accomplished by fitting the data in $\mathrm{l}\mathrm{n}K$ vs. $T^{-1}$ coordinates (the Second-Law method⁷). A more sophisticated form such as the Clarke-Glew equation can also be used.³⁶ Alternatively, if the standard entropies or Gibbs energy functions of the reaction participants are known, the reaction enthalpies can be found using the Third-Law method. The equilibrium data are considered here if they can be used to derive ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ for a brominated compound, i.e. when the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for all other reaction participants are available. Chemical equilibria have been studied for multiple brominated compounds both in the liquid and gas phases, mainly for isomerization. The uncertainties reported in the original publications were found to be acceptable for most systems analyzed in this work.

Thermochemical information for small molecules can also be obtained from high-precision mass spectrometry, particularly the variations of the Threshold PhotoElectron PhotoIon COincidence (TPEPICO) spectroscopy (see, e.g., Ref. 37). In this approach, an RBr molecule is ionized by monochromatic light and the ${\mathrm{R}\mathrm{B}\mathrm{r}}^{+}$ ion is formed; in this context, R is the Markush-style notation for a generic functional group. Next, the dissociation limit at $T=0\mathrm{K}$ leading to ${\mathrm{R}}^{+}$ and Br is determined relative to the energy of the initial molecule. ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left(\mathrm{B}\mathrm{r}\right)$ is well-established.^38,39 If ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left({\mathrm{R}}^{+}\right)$ is available, the enthalpy of formation of RBr can be derived. The resulting value is typically accurate within several $\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The uncertainty is often not rigorously defined in the studies of this type. We assume the reported uncertainties to be a reasonable estimate of the expanded uncertainties for 0.95 level of confidence.

The enthalpies of vaporization can be determined either calorimetrically or from the temperature-dependent vapor pressures $P_{\mathrm{s}}\left(T\right)$. If the vapor-pressure data are used, the quantity $\mathrm{\Delta }{H}_{\mathrm{m}}^{\prime }$ is derived first:

$$\Delta H_{\text{m}}^{\prime }=R{T}^2\frac{d\text{ln}{P}_{\text{s}}}{dT}.$$ (6)

This quantity is proportional to the enthalpy of vaporization to the saturated vapor:

$${\Delta }_{\text{l}}^{\text{g}}{H}_{\text{m}}=\Delta H_{\text{m}}^{\prime }\Delta Z,$$ (7)

where $\mathrm{\Delta }Z$ is the compressibility factor change in the process. At low pressures, $\mathrm{\Delta }Z$ is close to unity. At ambient pressures, this quantiy can be approximated with the following equation:

$$\Delta Z\approx 1+\frac{P_{\text{s}}}{RT}\left(B_{2,\text{m}}-V_{\text{m}}(\mathrm{l})\right),$$ (8)

where $B_{2,\mathrm{m}}$ is the second virial coefficient and $V_{\mathrm{m}}\left(\mathrm{l}\right)$ is the molar volume of the liquid. If this correction is required, the second virial coefficients are found using either the available experimental data evaluated by the NIST ThermoData Engine (TDE)⁴⁰ or the estimates by the Pitzer-Curl method⁴¹. The density of the condensed phase is also evaluated by TDE.

To find the standard enthalpy of vaporization, ${\mathrm{\Delta }}_{\text{vap}}{H}_{\mathrm{m}}^{\circ }$, a correction for the gas non-ideality should be applied:

$${\Delta }_{\text{vap}}{H}_{\text{m}}^{\circ }={\Delta }_{\text{l}}^{\text{s}}{H}_{\text{m}}-P_{\text{s}}(B_{2,\text{m}}-T\frac{d{B}_{2,\text{m}}}{dT}).$$ (9)

Equations (6) to (9) were derived and discussed in detail by Majer et al.⁴² Deviations of the non-ideality corrections at $T=298.15\mathrm{K}$ used in this work from those reported in the compilation of Majer and Svoboda⁴³ do not exceed $0.09\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ (Table S3 of Supporting Information).

To reduce the standard enthalpies of vaporization from the average temperature of the measurements $⟨T⟩$ to the reference temperature $T_{\text{ref}}=298.15\mathrm{K}$, three levels of approximation are possible.

(i) If the experimental heat capacities are available from $T_{\text{ref}}$ to $⟨T⟩$, the following equation is used:

$${\Delta }_1^{\text{g}}H(298.15\text{K})={\Delta }_1^{\text{g}}H(\langle T\rangle )+{\Delta }_1^{\text{g}}(H(298.15\text{K})-H(\langle T\rangle )).$$ (10)

For all compounds considered in this work, the computed ideal-gas heat capacities can be calculated at any temperature of practical interest using the statistical thermodynamic model described above.

(ii) If the liquid-phase heat capacity is only available at a single temperature (typically, $T=298.15\mathrm{K}$), then Eq. (10) transforms into

$${\Delta }_1^{\text{g}}H(298.15\text{K})={\Delta }_1^{\text{g}}H(\langle T\rangle )+{\Delta }_1^{\text{g}}{C}_p(298.15-\langle T\rangle /\text{K}).$$ (11)

(iii) If no liquid-phase heat capacities can be found in the literature, the correlation by Chickos et al.⁴⁴ is used in the form

$${\Delta }_{\text{l}}^{\text{g}}{C}_{p,\text{m}}(298.15\text{K})/\left(\text{J}\cdot {\text{K}}^{-1}\cdot {\text{mol}}^{-1}\right)=-14.30-0.35C_{p,\text{m}}(\text{g},298.15\text{K})/\left(\text{J}\cdot {\text{K}}^{-1}\cdot {\text{mol}}^{-1}\right).$$ (12)

The expanded uncertainty (0.95 level of confidence) for Eq. (12) has been estimated to be $30\mathrm{J}\cdot {\mathrm{K}}^{-1}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$.⁴⁴

Results and discussion

Discrepancy analysis for the reference enthalpies of formation of $\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{g}\right)\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{a}\mathrm{q}\right)$

Before proceeding any further, the discrepancy between the existing recommendations for the standard enthalpies of formation of $\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{g}\right)$ and $\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{a}\mathrm{q}\right)$ needs to be addressed because these values affect most of evaluation results in this work. The present values from CODATA³⁸ and $\mathrm{A}\mathrm{T}\mathrm{c}\mathrm{T}$³⁹ differ by $0.60\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for both, which substantially exceeds their stated uncertainties of $0.16\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and $0.13\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, respectively. Thermochemical networks were used in both cases. ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ for the dissociated hydrogen bromide HBr(aq, diss.) which is equivalent to ${\mathrm{B}\mathrm{r}}^{-}$ (aq) recommended by CODATA was derived by simultaneous regression of data for multiple aqueous ions. The gas-phase value was then obtained primarily using the enthalpy of the HBr dissolution in water reported by Vanderzee and Nutter.⁴⁵ In the ATcT network, the gas-phase ionization energies were introduced but some enthalpies considered by CODATA were omitted. The critical quantity here is the enthalpy of the gas-phase reaction ${\mathrm{H}\mathrm{B}\mathrm{r}}^{+}\to \mathrm{H}+{\mathrm{B}\mathrm{r}}^{+}$ at $T=0\mathrm{K}$ derived using the spectroscopic data from Refs. 46–48. Also, the standard Gibbs energies and enthalpies for the ammonium bromide decomposition ${\mathrm{N}\mathrm{H}}_4\mathrm{B}\mathrm{r}\left(\mathrm{c}\mathrm{r}\right)\to {\mathrm{N}\mathrm{H}}_3\left(\mathrm{g}\right)+\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{g}\right)$ considered in the NIST-JANAF Tables⁴⁹ were added. The data from both compilations with the highest impact on the resulting enthalpies of formation were analyzed to find a possible cause of the noted inconsistency. The processes involving bromine species considered by CODATA and their enthalpies are listed in Table 2; the results were verified against the original publications. Some of them are used in ATcT as well. Among listed, the processes 71, 75, 78, 81, and 82 require no further comments.

Table 2:

Experimental standard enthalpies of processes involving ${\mathrm{B}\mathrm{r}}_2$ and HBr at the reference temperature $T=298.15\mathrm{K}$ considered by CODATA^a,b

Eq. No.38	Process	$-\frac{{\Delta }_{\text{r}}{H}_{\text{m}}^{\circ }}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	Reference
71	$0.5{\mathrm{H}}_2\left(\mathrm{g}\right)+0.5{\mathrm{B}\mathrm{r}}_2\left(\mathrm{g}\right)=\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{g}\right)$	51.92 ± 0.45	50
72	${\mathrm{C}\mathrm{l}}_2\left(\mathrm{g}\right)+2\mathrm{H}\mathrm{B}\mathrm{r}(\mathrm{a}\mathrm{q}$, diss. $)={\mathrm{B}\mathrm{r}}_2(\mathrm{l})+2\mathrm{H}\mathrm{C}\mathrm{l}(\mathrm{a}\mathrm{q}$, diss. $)$	See text	51,52
73	${\mathrm{C}\mathrm{l}}_2\left(\mathrm{g}\right)+2\mathrm{H}\mathrm{B}\mathrm{r}(\mathrm{a}\mathrm{q}$, diss. $)={\mathrm{B}\mathrm{r}}_2(\mathrm{l})+2\mathrm{H}\mathrm{C}\mathrm{l}(\mathrm{a}\mathrm{q}$, diss. $)$	91.54 ± 0.64	53,54
75	$\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{g}\right)=\mathrm{H}\mathrm{B}\mathrm{r}(\mathrm{a}\mathrm{q}$, diss. $)$	85.144 ± 0.060	45
78	$0.5{\mathrm{H}}_2\left(\mathrm{g}\right)+0.5{\mathrm{B}\mathrm{r}}_2\left(\mathrm{l}\right)=\mathrm{H}\mathrm{B}\mathrm{r}(\mathrm{a}\mathrm{q}$, diss. $)$	120.37 ± 0.80c	55,56
79	${\mathrm{B}\mathrm{r}}_2\left(\mathrm{l}\right)={\mathrm{B}\mathrm{r}}_2\left(\mathrm{a}\mathrm{q}\right)$	0.83 ± 0.20	57
80	${\mathrm{B}\mathrm{r}}_2\left(\mathrm{l}\right)={\mathrm{B}\mathrm{r}}_2\left(\mathrm{a}\mathrm{q}\right)$	2.17 ± 0.20d	58
81	$\mathrm{H}\mathrm{B}\mathrm{r}\left(\mathrm{g}\right)=\mathrm{H}\mathrm{B}\mathrm{r}(\mathrm{a}\mathrm{q}$, diss. $)$	86.01 ± 1.00c	59
82	${\mathrm{B}\mathrm{r}}_2\left(\mathrm{a}\mathrm{q}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)=2\mathrm{H}\mathrm{B}\mathrm{r}($ aq,diss. $)$	240.94 ± 0.15	56,60

^aThe following reference values at $T=298.15\mathrm{K}$ recommended by CODATA³⁸ were used in the regression: ${\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{Br}}_2(\text{g})\right)=30.91\text{kJ}\cdot {\text{mol}}^{-1}$, ${\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }(\text{HCl}(\text{aq},\text{diss}.))={\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{Cl}}^{-}(\text{aq}.)\right)=-167.08\text{kJ}\cdot {\text{mol}}^{-1}$, $S_{\text{m}}^{\circ }\left({\text{H}}_2(\text{g})\right)=130.68\text{J}\cdot {\text{K}}^{-1}\cdot {\text{mol}}^{-1}$, $S_{\text{m}}^{\circ }\left({\mathrm{Br}}_2(1)\right)=152.51\text{J}\cdot {\text{K}}^{-1}\cdot {\text{mol}}^{-1}$, $S_{\text{m}}^{\circ }\left({\text{Br}}^{-}(\text{aq})\right)=82.55\text{J}\cdot {\text{K}}^{-1}\cdot {\text{mol}}^{-1}$, and $S_{\text{m}}^{\circ }(\text{HBr}(\text{g}))=198.70\text{J}\cdot {\text{K}}^{-1}\cdot {\text{mol}}^{-1}$

^bValues obtained by the weighted least-squares regression: ${\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{Br}}_2(\text{aq})\right)=-(0.97\pm 0.40)\text{kJ}\cdot {\text{mol}}^{-1}$, ${\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }(\mathrm{HBr}(\text{g}))=-(35.85\pm 0.28)\text{kJ}\cdot {\text{mol}}^{-1}$, and ${\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }(\mathrm{HBr}(\text{aq},\text{diss}.))={\text{Δ}}_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{Br}}^{-}(\text{aq})\right)=-(120.98\pm 0.24)\text{kJ}\cdot {\text{mol}}^{-1}$

^cObtained from the standard Gibbs energy using the reference values from footnote $a$

^dassumed incorrect in this work

The enthalpy of reaction 72 was obtained from a thermodynamic cycle involving ${\mathrm{S}\mathrm{O}}_2$ oxidation with ${\mathrm{C}\mathrm{l}}_2\left(\mathrm{g}\right)$ and ${\mathrm{B}\mathrm{r}}_2\left(\mathrm{l}\right)$.^51,52 To close the cycle, the corrections up to $14\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ had to be applied to the measured enthalpies. Using the enthalpies of dilution from the NBS Tables,⁶¹ the reaction enthalpy of $-94.0\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ can be obtained instead of the original value of $-91.3\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The differences are mainly caused by changes in the values for the concentrated $\left(\mathrm{H}\mathrm{C}\mathrm{l}\cdot 6.708{\mathrm{H}}_2\mathrm{O}\right.$ and $\left.\mathrm{H}\mathrm{B}\mathrm{r}\cdot 5.59{\mathrm{H}}_2\mathrm{O}\right)$ acid solutions used in the cycle. The NBS table on bromine was prepared in 1964. If the dilution enthalpies of HBr recommended by Vanderzee et al.⁶² in 1974 are used instead, the enthalpy becomes $-93.2\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The other problem is that a degree of dissociation of weak acids ${\mathrm{H}}_2{\mathrm{S}\mathrm{O}}_3$ and ${{\text{HSO}}_4}^{-}$ decreases if a strong acid is present. The enthalpies of dissociation of these acids are close to $-20\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and, therefore, this factor, ignored in the original publications, is expected to introduce an additional uncertainty. Because of the described issues, the enthalpy of reaction 72 should not be used as a reference value.

The enthalpy of reaction 73 is derived from a thermodynamic cycle involving ${\mathrm{A}\mathrm{s}}_2{\mathrm{O}}_3\left(\mathrm{a}\mathrm{q}\right)$ oxidation with ${\mathrm{C}\mathrm{l}}_2\left(\mathrm{g}\right)$ and ${\mathrm{B}\mathrm{r}}_2\left(\mathrm{l}\right).$^53,54 Unlike reaction 72, the calorimetric measurements were conducted with dilute solutions. The authors of the original works applied both the dilution and dissociation corrections. The revised enthalpy of reaction 73 is $0.3\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ more negative than the CODATA value. The updated enthalpies of dilution of the acids were taken from the NBS Tables.⁶¹ For the dissociation correction, $\mathrm{p}{K}_{\mathrm{a}}=2.31$ of ${\mathrm{H}}_3{\mathrm{A}\mathrm{s}\mathrm{O}}_4$ ⁶³ was used and the ionic activity coefficients were assumed to be equal to those of the aqueous HCl and $\mathrm{H}\mathrm{B}\mathrm{r}$⁶⁴ at the same ionic strength. Also, the correction to infinite dilution was applied.

The enthalpies of chemically identical processes 79 and 80 differ by $1.3\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ while their uncertainties are $0.2\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. To make these results consistent, either the uncertainties should be increased or one of the values should be rejected. If the uncertainties of these values are both increased to $0.65\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, the weighted least-square fit of the data in Table 2 leads to ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left(\mathrm{H}\mathrm{B}\mathrm{r}(\mathrm{a}\mathrm{q}\right.,\mathrm{diss}.)=-(121.26\pm 0.28)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, which does not help resolving the discrepancy. In the calorimetric measurements for both processes, liquid bromine was dissolved in dilute ${\mathrm{H}\mathrm{C}\mathrm{l}\mathrm{O}}_4\left(\mathrm{a}\mathrm{q}\right)$. The temperature rise was relatively small, (1 to 10) mK, in both works. Despite differences in the calorimeter design and materials, there is no obvious reason to reject either of these results.

On the other hand, the authors of Ref. 58 used the same instrument and technique to measure the enthalpies of solution of bromine in $\left[\left(0.95\mathrm{t}\mathrm{o}3.95\right)\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{d}\mathrm{m}}^{-3}\mathrm{K}\mathrm{B}\mathrm{r}+0.05\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{d}\mathrm{m}}^{-3}\right.\mathrm{H}\mathrm{B}\mathrm{r}]$ and $\left[(1\right.\mathrm{to}4\left.)\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{d}\mathrm{m}}^{-3}\mathrm{N}\mathrm{a}\mathrm{B}\mathrm{r}+0.05\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{d}\mathrm{m}}^{-3}{\mathrm{H}\mathrm{C}\mathrm{l}\mathrm{O}}_4\right]\cdot$.⁶⁵ The final molality of ${\mathrm{B}\mathrm{r}}_2$ was between $\left(0.009\mathrm{to}0.39\right)\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{k}\mathrm{g}}^{-1}$. The experimental data vary within $4.6\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and exhibit irregular changes with the solvent compositions and bromine molality. To check validity of the reported dependences, modeling of the equilibria between ${\mathrm{B}\mathrm{r}}_2\left(\mathrm{a}\mathrm{q}\right),{\mathrm{B}\mathrm{r}}^{-},{{\text{Br}}_3}^{-}$, and ${{\text{Br}}_5}^{-}$ using the equilibrium constants from the NBS Tables⁶¹ was performed in this work. The activity coefficients of the anions were cancelled in the equilibrium constants, and the activity coefficient of ${\mathrm{B}\mathrm{r}}_2\left(\mathrm{a}\mathrm{q}\right)$ was assumed to be equal to unity. For a given ${\mathrm{B}\mathrm{r}}_2$ molality, the predicted dissolution enthalpies change by less than $0.5\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ between different solvent compositions. For a given solvent composition, it varies with the amount of ${\mathrm{B}\mathrm{r}}_2$ by less than $0.1\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. These inconsistencies suggest that potential problems may also exist with the enthalpy of process 80. Considering the above, the value of Wu et al. (process 79) appears more credible.

If entry 80 is rejected, ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ (HBr(aq, diss.) becomes $-(120.99\pm 0.24)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, close to the ATcT value of $-(120.84\pm 0.14)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. Therefore, for the purposes of this work, we adopt the current ATcT recommendations for the species in question. However, future work on further refinement of the current recommendations and analysis of the available data is likley to be needed. For example, the enthalpy of reaction 82 obtained⁶⁶ with an alternative treatment of the electrochemical data from Ref. 60 differed from that in the original publication by $2\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, which an order of magnitude higher than its uncertainty.

Determination of the effective enthalpy of a bromine atom

The recent study of Bross et al.¹² focused on determination of the enthalpies of formation via total atomization energies suggested increased importance of contributions beyond $\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)$ for small bromine- and iodine-containing hydrocarbons. In particular, the second-order spin-orbit coupling, normally ignored for the first- and second-row species, was found to be important for the accurate description of total atomization energies. In our case, Eq. 1 implies that the combined contributions beyond $\mathrm{L}\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)$ as well as the core-valence correlation, spin-orbit, and relativistic contributions to the atomization energies can be reasonably described as a sum of atomic contributions. To verify this assumption, we used the results of Bross et al. for $\mathrm{H}\mathrm{B}\mathrm{r},{\mathrm{B}\mathrm{r}}_2$, and bromo derivatives of methane, ethene, and ethyne.¹² The additive (i.e., linear with respect to atomic counts) equation

$$\Delta E/\left(\text{kJ}\cdot {\text{mol}}^{-1}\right)=3.85n_{\text{C}}+0.15n_{\text{H}}-12.41n_{\text{Br}}$$ (13)

was found to closely approximate the sum of these contributions (Table 3) with the largest absolute deviation of $0.6\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and the standard error of $0.33\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. As seen, the results of Bross et al.¹² are indeed consistent with the additivity assumption¹⁴ for the contributions beyond $\mathrm{L}\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)$ for compounds containing univalent Br, and we proceed to extending this protocol to brominated organic compounds.

Table 3:

Contributions beyond $\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)$ to the atomization energy of brominated compounds $\left(\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}\right)$^a,b

Compound	CASRN	HOC	CV	DBOC	PP	SO	$\Sigma$	$\Delta$
bromomethane	74-83-9	0.0	6.4	0.2	−0.5	−14.5	−8.4	0.2
dibromomethane	74-95-3	−0.3	8.1	0.2	−0.3	−28.6	−20.9	0.2
tribromomethane	75-25-2	−0.8	9.9	0.2	−0.1	−42.5	−33.4	0.1
tetrabromomethane	558-13-4	−1.6	11.9	0.1	0.0	−56.1	−45.7	−0.1
bromoethyne	593-61-3	−0.1	11.8	0.3	−1.0	−14.9	−4.0	−0.6
dibromoethyne	624-61-3	−0.5	13.0	0.2	−0.9	−29.0	−17.2	0.0
bromoethene	593-60-2	−0.1	11.6	0.3	−1.1	−14.9	−4.2	0.0
(Z)-1,2-dibromoethene	590-11-4	−0.5	13.3	0.3	−0.9	−29.0	−16.8	0.0
1,1-dibromoethene	593-92-0	−0.5	13.3	0.3	−0.9	−28.9	−16.7	−0.2
tribromoethene	598-16-3	−1.0	14.8	0.3	−0.7	−43.0	−29.6	0.2
tetrabromoethene	79-28-7	−1.8	16.8	0.2	−0.6	−56.9	−42.3	0.3
hydrogen bromide	10035-10-6	0.1	2.0	0.1	0.3	−14.2	−11.7	−0.6
dibromine	7726-95-6	1.7	1.5	0.0	0.2	−27.7	−24.3	−0.5
methane	74-82-8	0.1	5.3	0.3	−0.8	−0.4	4.5	0.0
dihydrogen	1333-74-0	0.0	0.0	0.2	0.0	0.0	0.2	0.1

^aAll computed results are taken from Ref. 12;

^bHOC, higher-order correlation beyond CCSD(T); CV, core-valence correlation; DBOC, diagonal Born-Oppenheimer correction; PP, difference in energy between the ECP results with the awCVQZ-PP basis and the DK results with the awCVQZ basis set with all outer-core electrons correlated; SO, spin-orbit interaction; $\mathrm{\Sigma }$, sum of all contributions; $\mathrm{\Delta }$, deviation of Eq. 13 from $\mathrm{\Sigma }$.

The data for the auxiliary compounds used in the following sections are compiled in Table 4.

Table 4:

Standard enthalpies of formation for the liquid phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left(\mathrm{l}\right)$ and the ideal gas ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left(\mathrm{g}\right)$ for auxiliary compounds at the reference temperature $T=298.15K$^a

Compound	CASRN	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{l}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{g}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	Referencea
hydrogen atom	12385-13-6		217.998 ± 0.006	38
water	7732-18-5	−(285.83 ± 0.04)	−(241.83 ± 0.04)	38
carbon dioxide	124-38-9		−(393.51 ± 0.13)	38
bromine atom	10097-32-2		111.85 ± 0.06	39
hydrogen bromide	10035-10-6		−(35.69 ± 0.13)	39
$\mathrm{H}\mathrm{B}\mathrm{r}\left(\cdot x{\mathrm{H}}_2\mathrm{O}\right)$	10035-10-6			39,61
dibromine	7726-95-6	0	30.91 ± 0.11	38
hydrogen iodide	10034-85-2		26.47 ± 0.04	39
iodine bromide	7789-33-5		40.80 ± 0.14	67
ethane	74-98-6	−(93.6 ± 2.5)		8
propane	74-98-6	−(120.9 ± 2.5)		8
butane	106-97-8	−(147.3 ± 2.5)		8
2-methylpropane	75-28-5	−(154.2 ± 1.2)		8
2-methylbut-2-ene	75-28-5		−(41.7 ± 1.0)	8
propene	115-07-1	4.0 ± 2.5	20.02 ± 0.18	8; 39
but-1-ene	106-98-9	−20.8 ± 1.0	0.19 ± 0.34	8; 39
Compound	CASRN	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{l}\right)}{\mathrm{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{g}\right)}{\mathrm{kJ}\cdot {\text{mol}}^{-1}}$	Referenceb
propan-1-ol	71-23-8		−(255.11 ± 0.24)	39
allyl alcohol	107-18-6	−(169.5 ± 1.6)	−(124.5 ± 1.3)	40; 68
difluoromethane	75-10-5		−(452.3 ± 1.0)	69
trifluoromethane	75-46-7		−(696.6 ± 2.8)	69
tetrafluoroethylene	116-14-3		−(673.2 ± 3.0)	24
trichloromethane	67-66-3		−(134.1 ± 2.5)	70
2-chloropropane	75-29-6		−(144.9 ± 1.3)	8

^aFor hydrocarbons, only the sources different from ATcT v.1.130³⁹ are listed.

^bSources of ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }$ for the liquid and gas phases (if different) are separated by semicolon.

To use the ab initio protocol described above, the effective enthalpy of a bromine atom, $h\left(\mathrm{B}\mathrm{r}\right)$, needs to be quantified. Ideally, the compounds included in the training set should have the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values based on multiple consistent results from independent sources, which is not possible in the case of brominated compounds. Thus, a different approach was taken, as follows.

We were able to derive the gas-phase enthalpies of formation for about 80 molecular compounds containing $\mathrm{C},\mathrm{H},\mathrm{O}$, or F atoms in addition to univalent Br. All available experimental results were evaluated without the use of ab initio results to obtain a single value for each compound. Out of all data, the values with repeatability-based expanded uncertainties under $2.5\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ per bromine atom were selected. Uncertainties of this type represent the lower limit of this quantity. Potential data problems were detected using the ab initio results at the next step. The compounds with inconsistent data from different laboratories as well as with significant conformational ambiguity were excluded. These selection criteria decreased the number of candidates to 37.

The $h\left(\mathrm{B}\mathrm{r}\right)$ values were found for each of the remaining compounds using Eq. 1. Since the $h\left(\mathrm{B}\mathrm{r}\right)$ distribution was found to significantly deviate from the normal one (Fig. 1), its median value $h\left(\mathrm{B}\mathrm{r}\right)=-6754538.65\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ was used as a preliminary estimate of the effective enthalpy. The observed distribution, 27 out of 37 values lie within (−2.0 to $+2.0)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ of the median value. This domain was selected for further use. For the considered dataset, this is similar to the using of data between the fifteenth and eighty-fifth percentiles. Detailed discussion of the outliers and the entire dataset of brominated compounds is a subject of future work and is not covered here. The obtained dataset (Table 5) contained three inorganic, fifteen aliphatic, and nine aromatic compounds. The production effective enthalpy $h\left(\mathrm{B}\mathrm{r}\right)=-(6754538.55\pm 0.43)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ was found by averaging their effective enthalpies.

Figure 1:

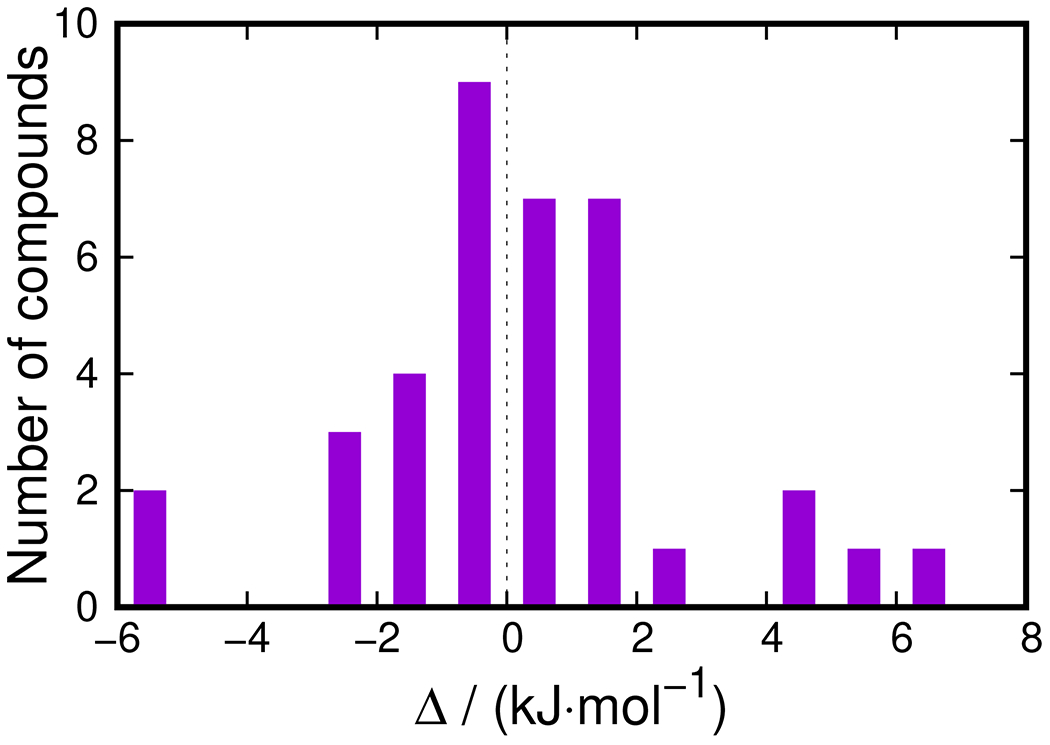
Distribution of compounds with respect to the deviation of the effective enthalpy of $\mathrm{B}\mathrm{r},h\left(\mathrm{B}\mathrm{r}\right)$, calculated from their experimental gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ from the median value for the preliminary set of compounds.

Table 5:

Experimental standard enthalpies of formation for the ideal gas ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{g}\right)$ for the training set at the reference temperature $T=298.15\text{K}$ and deviation of the effective enthalpies $h\left(\mathrm{Br}\right)$ calculated for each compound from the average value $⟨h\left(\mathrm{Br}\right)⟩=-6754538.55\mathrm{kJ}\cdot {\text{mol}}^{-1}$

Compound	CASRN	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{g}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	Referencea	$\frac{h\left(\text{Br}\right)-⟨h\left(\text{Br}\right)⟩}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$
Inorganic compounds
hydrogen bromide	10035-10-6	−35.7 ± 0.1	39	−0.4
bromine fluoride	13863-59-7	−58.85 ± 1.0	67	−0.9
dibromine	7726-95-6	30.9 ± 0.1	38	1.9
Aliphatic compounds
bromotrifluoromethane	75-63-8	−648.4 ± 1.9	7,72–74	−1.0
bromodifluoromethane	1511-62-2	−425.6 ± 1.2	75	1.6
tribromomethane	75-25-2	57.0 ± 3.1	76,77b; 78	0.1
bromomethane	74-83-9	−36.4 ± 0.2	7,79–81; 82	0.4
1,2-dibromotetrafluoroethane	124-73-2	−803.2 ± 4.1	50	−0.6
1,2-dibromoethane	106-93-4	−38.4 ± 1.3	7,83	−0.3
bromoethane	74-96-4	−62.0 ± 0.7	7,79,84–87; 88–90	−0.3
3-bromopropene	106-95-6	46.1 ± 2.3	91,92; 90	−1.9
1,2-dibromopropane	78-75-1	−(72.1 ± 0.9)	83	−0.3
1,3-dibromopropane	109-64-8	−61.6 ± 0.9)	93; 94–96	−1.2
1-bromobutane	109-65-9	−105.8 ± 1.0	7,97,98; 90,94,99,100	−0.4
2-bromobutane	78-76-2	−119.2 ± 0.3	7,101–103; 94,100	1.3
1-bromo-2-methylpropane	78-77-3	−113.5 ± 1.3	92,104; 90,94	−0.8
2-bromo-2-methylpropane	507-19-7	−131.7 ± 1.1	7,105,106	0.0
2,3-dibromo-2-methylbutane	594-51-4	−138.4 ± 2.0	7,83	1.8
Aromatic compounds
2-bromophenol	95-56-7	−77.5 ± 2.0	107; 107	1.4
4-bromophenol	106-41-2	−67.7 ± 1.5	107; 107,108: 109	0.1
2,6-dibromophenol	608-33-3	−48.0 ± 2.2	110; 110	1.0
4-bromobenzoic acid	586-76-5	−271.8 ± 2.0	evaluated in Ref. 71c	0.3
2-bromomethoxybenzene	578-57-4	−39.1 ± 2.1	111; 111	−1.9
3-bromomethoxybenzene	2398-37-0	−47.9 ± 2.1	111; 111	−0.1
4-bromomethoxybenzene	104-92-7	−47.8 ± 2.2	111; 111	1.5
4’-bromoacetophenone	99-90-1	−59.6 ± 1.3	112; 112,113	−0.5
2-bromofluorene	1133-80-8	208.7 ± 2.3	114; 114,115	0.5

^aSources of combustion or reaction energies used to derive the condensed-phase ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }$ and sources of enthalpies of sublimation or vaporization are separated by semicolon.

^bGas-phase value

^cCould not be corrected with respect to the updated ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{HBr}\right(aq\left)\right)$ because of insufficient information in some original publications noted by Chirico et al. ⁷¹

The experimental enthalpies of vaporization of brominated compounds are collected in Table 6. The experimental and computed enthalpies of formation are given in Table 7.

Table 6:

Experimental enthalpies of vaporization ${\Delta }_1^{\text{g}}{H}_{\text{m}}(⟨T⟩)$ and derived standard enthalpies of vaporization ${\Delta }_{\text{l}}^{\text{g}}{H}_{\text{m}}^{\circ }\left(T_{\text{ref}}\right)$ at the reference temperature $T=298.15\text{K}$ for brominated hydrocarbons^a

$T$ range $/\text{K}$	$⟨T⟩/\text{K}$	$\frac{{\Delta }_{\text{l}}^{\text{g}}{H}_{\text{m}}(⟨T⟩)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	Methodb	$\frac{{\Delta }_{\text{l}}^{\text{g}}{H}_{\text{m}}^{\circ }\left(298.15\text{K}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	Eq.	$\frac{-{\Delta }_{\text{l}}^{\text{g}}{C}_{P,\text{m}}}{\text{J}\cdot {\text{K}}^{-1}\cdot {\mathrm{mol}}^{-1}}$	Year	Reference
Propane and propene derivatives
1-bromopropane (106-94-5)
342.0	342.0	29.9 ± 0.3	C	32.3 ± 0.3	11	48 ± 2116	1931	Mathews and Fehlandt40,90,99
298.2	298.2		C	32.0 ± 0.2			1966	Wadsö40,90,100
322.3 to 352.4			C	32.4 ± 0.1	11	48 ± 2116	1977	Svoboda et al.40,90
302.1 to 343.5			E	32.1 ± 0.1			1977	Svoboda et al.40,90
N/A			E	32.2			1985	Radnai et al.40,117
				32.2 ± 0.1
2-bromopropane (75-26-3)
331.8	331.8	28.4 ± 0.3	C	30.4 ± 0.3	11	50 ± 2118	1931	Mathews and Fehlandt40,90,99
298.2	298.2		C	30.3 ± 0.2			1966	Wadsö40,90,100
297.4 to 333.1			E	30.7 ± 0.9			1974	van Diemen et al.40,119
304.6 to 337.7			C	30.3 ± 0.1	11	50 ± 2118	1977	Svoboda et al.40,90
299.7 to 331.4			E	30.3 ± 0.1			1977	Svoboda et al.40,90
				30.3 ± 0.1
1,2-dibromopropane (78-75-1)
312.8 to 402.4			E	42.5 ± 0.8			1975	Pisarev et al. 120–122
298.2	298.2	41.7 ± 0.1	C	41.7 ± 0.1			1980	Varushchenko et al. 123
				41.7 ± 0.1
1,3-dibromopropane (109-64-8)
298.2	298.2	47.5 ± 0.1	C	47.5 ± 0.1			1968	Wadsö94
N/A	N/A	47.2 ± 1.0	E	47.2 ± 1.0			1978	Varushchenko et al.95
308.2 to 338.2		48.1 ± 0.5	C	48.1 ± 0.5124			1992	Svoboda et al.96
				47.5 ± 0.1
3-bromopropene (106-95-6)
297.7 to 343.0	318.3		E	32.2 ± 0.3			1977	Svoboda et al. 40,90
318.0 to 340.7	329.5		C	32.6 ± 0.6	11	41 ± 30	1977	Svoboda et al. 40,90
				32.3 ± 0.3
Monobromobutanes
1-bromobutane (109-65-9)
372.6	372.6	32.5 ± 0.3	C	37.0 ± 0.3	11	54 ± 1125	1931	Mathews and Fehlandt 40,99
298.2	298.2		C	36.7 ± 0.3			1966	Wadsö 40,100
298.2	298.2		C	36.7 ± 0.1			1968	Wadsö 40,94
322.3 to 366.4			C	37.0 ± 0.1			1977	Svoboda et al. 40,90
				36.9 ± 0.1
2-bromobutane (78-76-2)
298.2	298.2	34.4 ± 0.2	C	34.4 ± 0.2			1966	Wadsö 40,100
298.2	298.2	34.5 ± 0.1	C	34.5 ± 0.1			1968	Wadsö 40,94
				34.5 ± 0.1
1-bromo-2-methylpropane (78-77-3)
298.2	298.2	34.9 ± 0.1	C	35.0 ± 0.1			1968	Wadsö 40,94
329.8 to 365.5			C	34.8 ± 0.1	11	54 ± 2118	1977	Svoboda et al. 40,90
305.8 to 363.0			E	34.3 ± 0.4			1977	Svoboda et al. 40,90
				34.9 ± 0.1
2-bromo-2-methylpropane (507-19-7)
see text			S	30.9 ± 0.3			1951	Bryce-Smith and Howlett 40,126
298.2	298.2	31.8 ± 0.1	C	31.9 ± 0.1			1968	Wadsö 40,94
295.2 to 323.2	308.7	31.4 ± 0.5	S	32.1 ± 0.5	11	51 ± 2118	1969	Chóliz Calero et al. 40,127
				31.9 ± 0.1
				Dibromobutanes
1,2-dibromobutane (533-98-2)
273.2 to 333.0	301.3	45.7 ± 2.5	S	45.9 ± 2.5	11	56 ± 30	1941	Lister 128
331.32 to 426.0			E	46.0 ± 0.7			1975	Pisarev et al. 120,122
				46.0 ± 0.6
1,3-dibromobutane (107-80-2)
354.8 to 466.2			E	49.4 ± 0.9			1980	Varushchenko et al. 123
1,4-dibromobutane (110-52-1)
305.2 to 470.7	see text			51.7 ± 1.5	12	55 ± 30	1947	Stull 129
298.2	298.2	53.1 ± 0.1	C	53.1 ± 0.1			1968	Wadsö 94
				53.1 ± 0.1
1,2-dibromo-2-methylpropane (594-34-3)
327 to 422	378.5	29 ± 1	M	32 ± 2	12	58 ± 30	1927	Coffin and Maass 130
298.2	298.2	43.3 ± 0.1	C	43.3 ± 0.1			1974	Sunner and Wulff 131
				43.3 ± 0.1
1,3-dibromo-2-methylpropane (28148-04-1)
287.2 to 447.8	see text			46.4 ± 1.5	12	58 ± 30	1947	Stull 129

^aThe excluded data are italicized, the evaluation results are in bold

^bC, calorimetry; E, ebulliometry; S, static method; M, manometric measurements

Table 7:

Experimental standard enthalpies of formation for the liquid phase ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{l}\right)$ and the ideal gas ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{g}\right)$, experimental standard enthalpies of vaporization or sublimation ${\Delta }_1^{\text{g}}{H}_{\text{m}}^{\circ }\left(\text{l}\right)$, and the computed enthalpies of formation for the ideal gas ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }(\text{g}$; calc) for brominated hydrocarbons at the reference temperature $T=298.15$^a

Method	$T$ range $/\text{K}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{l}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{{\Delta }_{\text{l}}^{\text{g}}{H}_{\text{m}}^{\circ }}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{g}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	Year	Reference	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }(\text{g};\mathrm{calc})}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$
Bromo- and dibromopropanes
1-bromopropane (106-94-5)
R	367			−76.8 ± 0.7	1950	Lacher et al. 132
R	401			−89.9 ± 1.4	1957	Lacher et al. 133
C	298.2	−(123.5 ± 1.4)			1961	Bjellerup 7,102
E	423.9 to 514.0			−(83.6 ± 1.2)	1964	Rozhnov and Andreevskii 134
R	523			−(83.8 ± 0.6)	1965	Davies et al. 135
E	273.2 to 303.2			−(84.0 ± 1.6)	1974	Alenin et al. 136,137
		−(116.0 ± 0.5)	32.2 ± 0.1	−(83.8 ± 0.5)			−(85.6 ± 2.6)
2-bromopropane (75-26-3)
R	367			−(99.7 ± 1.0)	1950	Lacher et al. 132
R	401			−(100.7 ± 0.7)	1957	Lacher et al. 133
C	298.2	−(128.2 ± 1.8)			1961	Bjellerup 7,102
E	393.8 to 447.5			−(97.7 ± 3.4)	1963	Rozhnov and Andreevskii 138
R	523			−(95.6 ± 1.0)	1965	Davies et al. 135
MS	0			−(95.9 ± 0.8)	2010	Stevens et al. 139
MS	0			−(94.9 ± 1.5)	2010	Stevens et al. 139
		−(126.3 ± 0.7)	30.3 ± 0.1	−(95.9 ± 0.7)			−(96.6 ± 2.6)
1,1-dibromopropane (598-17-4)
E	373 to 543	−(93.9 ± 1.0)			1974	Izmailov et al. 140,141
		−(93.9 ± 1.0)					−(53.9 ± 2.7)
1,2-dibromopropane (78-75-1)
R	355			−(72.1 ± 0.9)	1938	Conn et al. 7,83
		−(113.8 ± 0.9)	41.7 ± 0.1	−(72.1 ± 0.9)			−(72.7 ± 2.7)
1,3-dibromopropane (109-64-8)
E	273 to 403	−(109.1 ± 0.9)			1971	Sharonov and Rozhnov 93
		−(109.1 ± 0.9)	47.5 ± 0.1	−(61.6 ± 0.9)			−(64.0 ± 2.7)
2,2-dibromopropane (594-16-1)
E	397.7 to 446.2			−(70.4 ± 3.0)	1971	Sharonov and Rozhnov 142
				−(70.4 ± 3.0)			−(68.3 ± 2.7)
C3H5Br compounds
(Z)-1-bromopropene (590-13-6)
MS	0			38.4 ± 2.7	2012	Borkar et al. 143
				38.4 ± 2.7			39.1 ± 2.6
(E)-1-bromopropene (590-15-8)
MS	0			40.4 ± 2.6	2012	Borkar et al. 143
				40.4 ± 2.6			41.1 ± 2.6
2-bromopropene (557-93-7)
MS	0			34.5 ± 2.7	2012	Borkar et al. 143
				34.5 ± 2.7			32.9 ± 2.6
3-bromopropene (106-95-6)
R	298.2	15.0 ± 2.6			1949	Gellner and Skinner 91
R	308.2	10.6 ± 4.4			1981	Holm 92 b
		13.8 ± 2.3	32.3 ± 0.3	46.1 ± 2.3			44.2 ± 2.6
bromocyclopropane (4333-56-6)
R	308.2	See text			1981	Holm 92,144 b
MS	0			See text	2012	Borkar et al. 143
							79.6 ± 2.6
Bromobutanes
1-bromobutane (109-65-9)
C	298.2	−(143.1 ± 1.3)			1961	Bjellerup 7,97
E	298.2 to 513.7			−(105.2 ± 1.4)	1968	Peshchenko and Andreevskii 98
		−(142.6 ± 1.0)	36.9 ± 0.1	−(105.8 ± 1.0)			−(106.2 ± 2.6)
2-bromobutane (78-76-2)
R	367			−(119.3 ± 0.6)	1952	Lacher et al. 7,101
R	373			−(119.7 ± 0.5)	1952	Lacher et al. 7,101
R	373			−(119.0 ± 0.6)	1952	Lacher et al. 7,101
C	298.2	−(154.4 ± 1.3)			1961	Bjellerup 7,97
E	405.2 to 433.0			−(118.5 ± 0.6)	1968	Peshchenko and Andreevskii 103
		−(153.7 ± 0.3)	34.5 ± 0.1	−(119.2 ± 0.3)			−(117.9 ± 2.6)
1-bromo-2-methylpropane (78-77-3)
R	308.2	−(151.6 ± 4.4)			1981	Holm 92 b
E	273.2 to 526.2	−(148.1 ± 1.3)			1974	Nesterova and Rozhnov 104
		−(148.4 ± 1.3)	34.9 ± 0.1	−(113.5 ± 1.3)			−(114.3 ± 2.6)
2-bromo-2-methylpropane (507-19-7)
E	375.0 to 531.7			−(131.9 ± 2.1)	1937	Kistiakowsky and Stauffer 7,105
E	372.9 to 483.6			−(131.7 ± 1.3)	1957	Howlett 7,106
		−(163.7 ± 1.1)	31.9 ± 0.1	−(131.7 ± 1.1)			−(131.7 ± 2.6)
bromocyclobutane (4399-47-7)
R	308.2	−(7.9 ± 4.4)			1981	Holm 92 b
		−(7.9 ± 4.4)					32.7 ± 2.6
1,2-dibromobutane (533-98-2)
R	355			−(93.5 ± 1.7)	1938	Conn et al. 7,83
R	300	−(133.4 ± 2.7)			1941	Lister 128
C	298.2	−(146.2 ± 2.3)			1961	Bjellerup 7,97
		−(142.9 ± 4.5)	46.0 ± 0.6	−(96.9 ± 3.3)			−(94.6 ± 2.7)
1,3-dibromobutane (107-80-2)
E	275.2 to 553.2	−(149.2 ± 3.4)			1972	Nesterova et al. 145
		−(149.2 ± 3.4)	49.4 ± 0.9	−(99.8 ± 3.5)			−(97.7 ± 2.7)
1,4-dibromobutane (110-52-1)
E	275.2 to 553.2	−(141.3 ± 3.4)			1972	Rozhnov et al. 146
		−(141.3 ± 3.4)	53.1 ± 0.1	−(88.2 ± 3.4)			−(86.2 ± 2.7)
meso-2,3-dibromobutane (5780-13-2)
E	275.2 to 553.2	−(150.2 ± 3.4)			1972	Nesterova et al. 145
							−(102.5 ± 2.7)
dl-2,3-dibromobutane (598-71-0)
E	275.2 to 553.2	−(151.9 ± 3.4)			1972	Nesterova et al. 145
							−(103.3 ± 2.7)
1,2-dibromo-2-methylpropane (594-34-3)
R	298.2	−(156.6 ± 0.6)			1974	Sunner and Wulff 131
		−(156.6 ± 0.6)	43.3 ± 0.1	−(113.3 ± 0.6)			−(107.8 ± 2.7)
1,3-dibromo-2-methylpropane (28148-04-1)
E	273.2 to 553.2	−(147.8 ± 0.6)			1975	Rozhnov et al. 147
		−(147.8 ± 0.6)	46.4 ± 1.5	−(101.4 ± 1.6)			−(93.0 ± 2.7)

^aThe excluded outliers are italicized, the evaluated experimental results are in bold

^bSee Table 8

Reaction calorimetry through organic magnesium bromides

The majority of data sources considered here have measurements of the enthalpy-related properties for the target compounds as their main objectives. In some cases, however, additional useful information can be obtained as a by-product of seemingly unrelated data such as reaction calorimetry for inorganic or organometallic systems.^125,148

Holm^92,144 reported the enthalpies of two reactions involving organic magnesium bromides RMgBr in diethyl ether ${\mathrm{E}\mathrm{t}}_2\mathrm{O}$, which he described as

$$\text{RBr}(\text{l})+\text{Mg}(\text{s})=\text{RMgBr}\left({\text{soln in Et}}_2\text{O}\right)$$ (14)

$$\text{RMgBr}\left({\text{soln in Et}}_2\text{O}\right)+\text{HBr}(\text{g})=\text{RH}\left({\text{soln in Et}}_2\text{O}\right)+{\text{MgBr}}_2\left({\text{soln in Et}}_2\text{O}\right)$$ (15)

The experiments were carried out at $T=308.15\mathrm{K}$. The concentration of RMgBr was between (0.3 and 0.6) $\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{d}\mathrm{m}}^{-3}$. A sum of reactions 14 and 15,

$$\text{RBr}(\text{l})+\text{Mg}(\text{s})+\text{HBr}(\text{g})=\text{RH}\left({\text{soln in Et}}_2\text{O}\right)+{\text{MgBr}}_2\left({\text{soln in Et}}_2\text{O}\right)$$ (16)

can be used to obtain the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ value for RBr, if ${\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2\left({\text{soln in Et}}_2\text{O}\right)$ and ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }(\mathrm{R}\mathrm{H}\left({\text{soln in Et}}_2\text{O}\right)$) are known. Normally, the latter value is not available, and it is reasonably assumed that ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\mathrm{R}\mathrm{H}\left({\text{soln in Et}}_2\text{O}\right)\approx {\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left(\mathrm{R}\mathrm{H}\right(\mathrm{l}\left)\right)$. Also, the heat-capacity change in reaction 16 cannot be reliably estimated and is ignored.

We found ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left({\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2\left(\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{n}\right.\right.$ in $\left.\left.{\mathrm{E}\mathrm{t}}_2\mathrm{O}\right)\right)$ at $T=298.15\mathrm{K}$ using the available experimental data for five organic bromides (Table 8) to be $-(560.1\pm 2.1)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. Deviations of the individual values from the average did not exceed $\pm 2.9\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The values for 2-bromopropane and isomeric bromobutanes were derived from independent sources, as described below. The references for bromoethane are given in Table 5.

Table 8:

Enthalpies of reactions 14 and $15,$,^92,144 standard enthalpies of formation in the liquid phase ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }$ at $T=298.15\text{K}$ of brominated compounds RBr and the corresponding hydrocarbons $RH$⁸ as well as derived enthalpies of formation of ${\text{MgBr}}_2\left({\text{soln in Et}}_2\text{O}\right)$

RBr	CASRN(RBr)	$\frac{{\Delta }_{\text{r}14}{H}_{\text{m}}^{\circ }}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{r}15}{H}_{\text{m}}^{\circ }}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{RH}\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(\text{RBr}\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{MgBr}}_2\right({\text{soln in Et}}_2\text{O}\left)\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$
Reference compoundsa
bromoethane	74-96-4	−231.0	−299.2	−(93.6 ± 2.5)	−(90.1 ± 0.7)	−563.0
2-bromopropane	75-26-3	−210.0	−305.9	−(120.9 ± 2.5)	−(126.3 ± 0.7)	−557.6
1-bromobutane	109-65-9	−233.9	−292.5	−(147.3 ± 2.5)	−(142.6 ± 1.0)	−558.0
2-bromobutane	78-76-2	−211.7	−305.9	−(147.3 ± 2.5)	−(153.7 ± 0.3)	−560.3
2-bromo-2-methylpropane	507-19-7	−209.2	−306.7	−(154.2 ± 1.2)	−(163.7 ± 1.1)	−561.7
Average						−(560.1 ± 2.1)
Compounds with derived ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }$
1-bromo-2-methylpropane	78-77-3	−237.3	−289.1	−(154.2 ± 1.2)	−(151.6 ± 4.4)
bromocyclopropane	4333-56-6	−281.6	−282.8	35.8 ± 0.5b	$76.4\pm 4.4$ c
bromocyclobutane	4399-47-7	−223.4	−289.1	3.9 ± 0.4b	−(7.4 ± 4.4)
3-bromopropene	106-95-6	−271.0	−259.4	4.0 ± 2.5	10.6 ± 4.4

^aThe data for RBr were evaluated in this work from independent sources, see Tables 5 and 7

^bRef. 39

^cIncorrect, as discussed in the text

Solid-liquid equilibrium with the equilibrium solid phase ${\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2\cdot {\mathrm{E}\mathrm{t}}_2\mathrm{O}$ and metastable liquid-liquid equilibrium have been reported for $\left({\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2+{\mathrm{E}\mathrm{t}}_2\mathrm{O}\right)$^149–151 at $=308.15\mathrm{K}$. If SLE was reached in the considered experiments, ${\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2$ should be present in both phases. According to the reported solubilities,^149,151 about a half of the formed bromide would precipitate in the experiments with the lower RMgBr concentration of $0.3\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{d}\mathrm{m}}^{-3}$. The final solution also contained non-polar hydrocarbons that are anticipated to decrease the salt solubility. Therefore, ${\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2({\mathrm{soln\; in\; Et}}_2\mathrm{O})$ is expected to be primarily composed of solid ${\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2\cdot {\mathrm{E}\mathrm{t}}_2\mathrm{O}$. This suggestion is consistent with the fact that, as mentioned above, the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left({\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2\left({\text{soln in Et}}_2\text{O}\right))\right.$ values obtained with different reactants agree within $\pm 2.9\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The uncertainty of $4.4\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ reported by Holm appears to be a reasonable estimate for the expanded uncertainty of the enthalpies of formation obtained using this procedure.

Using the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left({\mathrm{M}\mathrm{g}\mathrm{B}\mathrm{r}}_2\left({\text{soln in Et}}_2\text{O}\right))\right.$ value obtained as described above, the enthalpies of formation were derived for four organic bromides (Table 8). For bromocyclopropane, the enthalpy of reaction 14 reported in the earlier paper¹⁴⁴ is missing in the author’s thesis¹⁵² and a more recent paper.⁹² ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }\left({\mathrm{C}}_3{\mathrm{H}}_5\mathrm{B}\mathrm{r}\left(\mathrm{l}\right)\right)=27.6\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ reported in the 1981 paper⁹² significantly deviates from the value of $75.9\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ obtained here using the published reaction enthalpies. The latter, in turn, is inconsistent with the ab initio results. Therefore, the enthalpy of formation of bromocyclopropane is excluded from further analysis.

Brominated Propanes

1- and 2-bromopropanes are liquids readily available at high purity. Despite that, it took significant efforts to obtain a consistent set of thermochemical data for these compounds. They were studied by combustion calorimetry by Bjellerup.¹⁰² The enthalpies of vaporization required to obtain the gas-phase values are primarily based on the calorimetric and ebulliometric results.^90,100 The gas-phase enthalpies of hydrobromination of cyclopropane and propene resulting in 1- and 2-bromopropanes, respectively, were reported by Lacher et al.¹³² Later, they repeated the measurements to improve the former value.¹³³ The enthalpies of hydrogenation of both bromopropanes in the gas phase were also determined at the same laboratory.¹³⁵ For both compounds, the enthalpies of formation derived from the hydrogenation study deviate from the earlier results by several $\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, which exceeds their combined uncertainty. The equilibrium of the 2-bromopropane dehydrobromination in the temperature range of (394 to 447) K was studied by Rozhnov and Andreevskii.¹³⁸ The resulting gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for 2-bromopropane vary within a reasonable range, $-\left(95.6\mathrm{to}100.7\right))\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The results can be further refined, as demonstrated below.

The enthalpy of formation of 2-bromopropane can also be derived from photoionization studies. In these experiments, the 2-propylium ion is formed. Since 2000, the enthalpy of formation of this ion has been determined using different variations of the PEPICO technique.^139,153,154 As demonstrated by Bodi et al.,¹⁵⁵ the experiments of Baer et al. ¹⁵³ were affected by formation of an adduct with argon and should not be used. Stevens et al. ¹³⁹ suggested that the 2-chloropropane ionization energy reported by Brooks et al. ¹⁵⁴ was too low by $30\mathrm{m}\mathrm{e}\mathrm{V}\left(2.9\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}\right)$ because of improper calibration.

In Table 9, the experimental enthalpies of formation of carbocations are compared with their ab initio counterparts. The ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values of some ions have been obtained from the photoionization studies for appropriate hydrocarbons. The values for 1-propylium and propen-2-ylium cations are based on the ones for 2-propylium and allylium, respectively, and should not be treated as independent entries in this context.

Table 9:

Standard enthalpies of formation in the ideal-gas state of ions ${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }$ at $T=298.15\text{K}$ and $0\text{K}$ calculated in this work and reported in the literature and thermal enthalpy of these ions ${\Delta }_0^{T}H$^a

Ion	CASRN	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(298\text{K}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{\mathrm{ZPVE}}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{{\Delta }_0^{T}H}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{{\Delta }_{\mathrm{CV}}E}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left(0\text{K}\right)}{\mathrm{kJ}\cdot {\mathrm{mol}}^{-1}}$		Reference compound	Ref.
						Calc.	Exp.
hydronium	12408-02-5	1531.3	0	6.20	0.0	1529.3	1528.1		39
methylium	14531-53-4	1093.8	81.2	9.98	2.68	1100.3	1099.35 ± 0.05	${\mathrm{CH}}_4$	156
ethylium (ethenium)	14936-94-8	903.5	158.1	11.00	1.25	917.0	915.5 ± 1.3	${\text{C}}_2{{\text{H}}_5}^{·}$	87 b
1-propylium (cyclopropanium)	19252-52-9	838.5	236.4	14.49	1.36	858.1	856.8 ± 0.8	${\text{C}}_3{\text{H}}_8$	39 b
2-propylium	19252-53-0	806.9	228.7	15.32	0.62	825.0	822.8 ± 0.3	${\text{C}}_3{\text{H}}_8$	139
							823.8 ± 1.4	${\text{CH}}_3{\text{CH}}_2{\text{ClCH}}_3$	139
vinylium (ethynium)	14604-48-9	1114.2	89.3c	11.28d	0.89	1119.3	1120.4 ± 1.9	${\text{C}}_2{\text{H}}_4$	157
							1119.7	${{\text{CH}}_3}^{+},{\text{CH}}_4,{\text{C}}_2{\text{H}}_4$	158 b
propen-2-ylium	50457-57-3	985.6	164.5	14.67	0.31	995.5	997	${\text{C}}_3{\text{H}}_6$	159 b
allylium (propen-3-ylium)	1724-44-3	951.8	177.5	14.67	2.26	965.8	966.8 ± 2.4	${\text{C}}_3{\text{H}}_6$	159
			176.8				964.6e		160

^aEnthalpies of formation are based on the ion (stationary electron) convention

^bDerived using experimental and ab initio results

^vTo improve quality of the computations, ZPVE was calculated using the unscaled harmonic frequencies and anharmonic constant matrix found using the CCSD(T)-based composite method as described in Ref. 161

^dUsing unscaled VPT2 frequencies reported in Ref. 161

^eCalculated using the HEAT-345(Q) protocol

The deviation of the computed value for 2-propylium from the experimental result obtained by propane ionization is larger than those of the hydronium, methylium, and ethylium cations. The enthalpy of formation of 2-propylium can also be obtained from the dissociation onset energies of 2-haloalkanes, particularly the chloro or iodo derivatives. To find ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }(2-$ propylium), accurate enthalpies of formation of the halogenated compounds are required. The uncertainty of ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ (2-iodopropane), $3.8\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},$⁸ is too large for this purpose. The enthalpy of formation of 2-chloropropane,⁸ ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }=-(144.9\pm 1.3)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $T=298.15\mathrm{K}$ corresponding to $-(124.2\pm 1.3)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $=0\mathrm{K}$, is based on multiple consistent experimental values. The ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ (2-propylium) values obtained from the dissociation onset energies of 2-chloropropane^139,154 are also shown in Table 9. These values are closer to the ab initio result.

Ionization of 2-bromopropane was studied in Ref. 139. We obtained its enthalpy of formation using the results both for propane and 2-chloropropane. Once the ionization results are added to the thermochemical data (Table 7), it becomes clear that both hydrobromination studies of Lacher et al. ^132,133 yield ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values which are too negative and should be excluded. The recommended gas-phase value is obtained by weight-averaging of the remaining data. The only liquid-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ was converted to the gas-phase value using the vaporization enthalpy derived in Table 6.

For 1-bromopropane, the variation of the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values, $-\left(76.8\mathrm{to}91.2\right))\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, is significantly worse than that for the 2-bromo isomer. The equilibrium data for the reaction 1-bromopropane $=2$-bromopropane^134,136,163 are available. Mayo and Dolnick¹⁶³ reported the liquid-phase equilibrium compositions at T = (299, 343, and 523) K. However, the latter temperature is above the estimated critical temperature of 517 K for 2-bromopropane.²³ Uncertainty of the enthalpy derived from the remaining two data points would be significant and these results are not considered in the further discussion.

The gas-phase equilbrium was studied in the temperature range of (423.9 to 514.0) K.¹³⁴ The reaction enthalpy was found by the least-squares fit of the $\mathrm{l}\mathrm{n}K$ vs. $T^{-1}$ data to be $\mathrm{\Delta }{H}_{\mathrm{m}}=-(12.0\pm 1.0)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $⟨T⟩=464.7\mathrm{K}$. This value is reduced to $T=298.15\mathrm{K}$ using the thermal enthalpies from the ideal-gas model of this work to be $\mathrm{\Delta }H=-(12.4\pm$ 1.0) $\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The equilibrium in the liquid phase was stated to be studied at T = (273.2, 303.2, 333.2, 533.2, and 583.2) K. ¹³⁶ As discussed above, the latter two temperatures are too high for the liquid phase and only three points at the lower temperatures are used here. The value $\mathrm{\Delta }{H}_{\mathrm{m}}=-(10.3\pm 1.5)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $T=301.2\mathrm{K}$ is derived from these data. The temperature correction to $T=298.15\mathrm{K}$ is estimated to be negligible. The corresponding gas-phase value, $\mathrm{\Delta }{H}_{\mathrm{m}}=-(12.0\pm 1.5)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, can be found using Table 6. These two isomerization enthalpies are combined with ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ of 2-bromopropane selected as described above to obtain two additional experimental ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for the 1-bromo isomer. As in the case of 1-bromopropane, the hydrobromination results of Lacher et al.^132,133 are found to be outliers. Unexpectedly, the value based on the combustion calorimetry study¹⁰² also appears anomalous. The other experimental values are weight-averaged to obtain the best estimate of ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ for 1-bromopropane. The enthalpies of formation derived from the experimental data and their computational counterparts for both bromopropanes differ by less than $2\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$.

The gas-phase enthalpy of formation of 1,2-dibromopropane is based on the enthalpy of the gas-phase bromination of propene reduced to $T=298.15\mathrm{K}$. The enthalpy of vaporization is mainly based on the calorimetric value reported by Varushchenko et al. ¹²³

For 1,3-dibromopropane, two calorimetric^94,96 and one ebulliometric⁹⁵ values of the vaporization enthalpy are available. Svoboda et al.⁹⁶ reported the values in the temperature range of (308 to 338) K. The heat-capacity change at vaporization of$-80\mathrm{J}\cdot {\mathrm{K}}^{-1}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ follows from the linear fit of the ${\mathrm{\Delta }}_{\mathrm{l}}^{\mathrm{g}}H\left(T\right)$ dependence. However, the ${\mathrm{\Delta }}_{\mathrm{l}}^{\mathrm{g}}{C}_{P,\mathrm{m}}=-60\mathrm{J}\cdot {\mathrm{K}}^{-1}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $T=298.15\mathrm{K}$ can be obtained from the statistical thermodynamic calculations for the gas phase and the experimental liquid heat capacity.¹²⁴ Therefore, the uncertainty of the ${\mathrm{\Delta }}_1^{\mathrm{g}}H$ value of Svoboda et al. is larger than the reported expanded uncertainty of $0.003{\mathrm{\Delta }}_1^{\mathrm{g}}H$. It was estimated to be $0.01{\mathrm{\Delta }}_1^{\mathrm{g}}H$. The recommended enthalpy of vaporization is primarily based on the calorimetric value of Wadsö.⁹⁴

The liquid-phase equilibria of 1,2-dibromopropane with the 1,1- and 1,3-isomers was studied by Rozhnov et al.^93,140,141 The eqilibrium with the 1,1-isomer was studied in the temperature range of (373 to 543) K. The enthalpy of this isomer was found to be (19.9 $\pm 0.4)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ higher than that of the 1,2-derivative. We are not aware of any heat-capacity data for 1,1-dibromopropane, but the heat capacities at $T=298.15\mathrm{K}$ of the other two isomers of dibromopropane are indistinguishable within their uncertainty.^118,124 Therefore, the enthalpy difference between 1,1- and 1,2-dibromopropanes is expected to insignificantly change with temperature. The enthalpy of formation of 1,1-dibromopropane is found as a sum of that for 1,2-dibromopropane and the above isomerization enthalpy. No vaporization enthalpy data is available for the 1,1-isomer. The use of $ab$ initio value for the gas phase yields a reasonable value of about $40\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for its enthalpy of vaporization.

The 1,3-dibromopropane $=\mathrm{1,2}$-dibromopropane equilibrium in the liquid phase was studied at $T=\left(273\mathrm{to}403\right))\mathrm{K}$. The enthalpy change was found to be ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}=(4.7\pm 0.1)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. As mentioned above, it is nearly independent of temperature. The enthalpy of formation of the 1,3-isomer in the liquid phase is found here using this value and the enthalpy of formation of 1,2-dibromopropane. The same authors¹⁴² also studied the equilibrium of the 2,2-dibromopropane dehydrobromination into 2-bromopropene in the gas phase. The obtained ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}=(69.6\pm 1.1)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $⟨T⟩=416.1\mathrm{K}$ becomes $(69.3\pm 1.1)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $=298.15\mathrm{K}$. The gas-phase enthalpy of formation of this compound was found using ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }(2$-bromopropene $)$ derived below. The results for bromocyclopropane are discussed in the next section.

The computed ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ of 1,2-dibromopropane is $0.6\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ more negative than the experimental one. This difference increases to $2.4\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for 1,3-dibromopropane and becomes negative $\left(-2.0\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}\right)$ for the 2,2-dibromo isomer.

Brominated Propenes and Cyclopropane

Gellner and Skinner ⁹¹ found the enthalpy of the 3-bromopropene hydrolysis reaction

$${\text{CH}}_2{\text{CHCH}}_2\text{Br}(\text{l})+{\text{H}}_2\text{O}(\text{EtOH soln}.)={\text{CH}}_2{\text{CHCH}}_2\text{OH}(\text{aq}.\text{EtOH soln}.)+\text{HBr}\left(\cdot 11{\text{H}}_2\text{O}\right)$$ (17)

to be ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}^{\circ }=-15.4\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ (presumably) at room temperature close to $T=298.15\mathrm{K}$. The enthalpy of formation is derived in this work assuming the excess enthalpies of the aqueous ethanol solutions and allyl alcohol in (ethanol + water) are small relative to the resulting uncertainty. The gas-phase enthalpy of formation of allyl alcohol is found from its enthalpy of hydrogenation⁶⁸ reduced to $T=298.15\mathrm{K}$ and ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ (propan-1-ol(g)). To obtain the liquid-phase value, the critically evaluated vaporization enthalpy,⁴⁰ ${\mathrm{\Delta }}_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\circ }=(45.0\pm 0.9)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, is used. The ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for ethanol and allyl alcohol (prop-2-en-1-ol) are listed in Table 4.

The liquid-phase enthalpy of formation of 3-bromopropene can also be derived from the calorimetric data of Holm⁹² as described above. The best estimate of this quantity is obtained by weight-averaging of these two values. The standard enthalpy of vaporization of 3-bromopropene is determined from the calorimetric and ebulliometric measurements by Svoboda et al.⁹⁰ The calculated gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ deviates from its experimental counterpart by $-1.9\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$.

Borkar et al.¹⁴³ studied ionization of five ${\mathrm{C}}_3{\mathrm{H}}_5\mathrm{B}\mathrm{r}$ compounds using the imaging PEPICO spectroscopy. Four of these compounds, $\left(E\right)-1-,\left(Z\right)-1$-, and 3-bromopropenes and bromocyclopropane, ultimately dissociated into the allylium cation. 2-bromopropene was found to form propen-2-ylium. The reported enthalpies of formation of all these compounds were based on ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ of the allylium cation determined by Shuman et al. ¹⁵⁹ The $ab$ initio values for the vinylium and allylium cations are about $1\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ lower than the experimental counterparts (Table 9). Our value for the allylium cation is also in a good agreement $\left(1.2\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}\right.$ difference) with the HEAT-345(Q) value reported recently.¹⁶⁰ About half of the difference is due to ZPVE, which was supposedly found at the $\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)/\mathrm{c}\mathrm{c}-\mathrm{p}\mathrm{V}\mathrm{Q}\mathrm{Z}$ theory level in the cited paper. Both computed values agree with the experimental enthalpy of formation within its uncertainty.

To derive the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for the neutral species, Borkar et al. ¹⁴³ generated a thermochemical network containing two domains tied by the PEPICO data. The first domain included the brominated neutral species and the second one consisted of the allylium and propen-2-ylium cations. The enthalpies of formation were found by minimizing the error function, which contained the differences squared with respect to isomerization energies computed with $ab$ initio methods and the experimental dissociation onset energies. To derive the absolute enthalpies of formation, the network was anchored to the ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for allyl cation ¹⁵⁹ and bromine atom.⁴⁹ Based on the subsequent analysis, the experimental value for bromocyclopropane was shown to be an outlier. The observed appearance energy was assumed to correspond to the overall barrier to its dissociation.

In this work, the gas-phase enthalpies of formation were first obtained using the experimental dissociation energy onsets, ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ (allyllium) from Ref. 159, and the statistical thermodynamic model adopted here. ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ of gaseous 3-bromopropene at $T=298.15\mathrm{K}$ derived above using the thermochemical results^91,92 is lower than the spectroscopic one, $(48.8\pm 2.5)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, by $2.7\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The computed ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for other bromopropenes are also systematically lower than the spectroscopic results by (4 to 6) $\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. On the other hand, our calculations support the spectroscopic enthalpies of the isomerization of bromopropenes (i.e., relative enthalpies). This discrepancy slightly exceeds the combined uncertainties of the spectroscopic and computed values. The distribution of the deviations, however, suggests a possible systematic error in the ionization data.

To circumvent the suspected systematic error, we chose to use 3-bromopropene as a reference compound with the difference between the enthalpies of formation of the 2-propenyl and allyl cations at $T=0\mathrm{K},29.8\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, taken from the results reported in Table 9. The enthalpies of formation of the ${\mathrm{C}}_3{\mathrm{H}}_5\mathrm{B}\mathrm{r}$ isomers at $T=298.15\mathrm{K}$ were found using the equation:

$${\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{C}}_3{\text{H}}_5\text{Br}\right)=-E_0\left({\text{C}}_3{\text{H}}_5\text{Br}\right)+E_0\left({\text{CH}}_2{\text{BrCHCH}}_2\right)+{\Delta }_0^T{H}_{\text{m}}\left({\text{C}}_3{\text{H}}_5\text{Br}\right)-{\Delta }_0^T{H}_{\text{m}}\left({\text{CH}}_2{\text{BrCHCH}}_2\right)+{\Delta }_{\text{f}}{H}_{\text{m}}^{\circ }\left({\text{CH}}_2{\text{BrCHCH}}_2\right)+X$$ (18)

where $E_0$ is the dissociation onset energy, ${\mathrm{\Delta }}_0^T{H}_{\mathrm{m}}$ is the thermal correction to enthalpy, and $X$ is equal to $29.8\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for 2-bromopropene and $0\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ otherwise. For 2-bromo- and both 1-bromopropenes, the resulting difference between the computed and experimental ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values does not exceed $\pm 1.7\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. For bromocyclopropane, the computed value is more credible.

Further verification of the chosen evaluation can be derived from the available equilibrium studies in the liquid¹⁶⁴ and gas¹⁶⁵ phases. For the isomerization reaction of $\left(E\right)-1$ and $\left(Z\right)$-1-bromopropenes in the liquid phase, ¹⁶⁴ ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}=-(1.88\pm 0.07)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and ${\mathrm{\Delta }}_{\mathrm{r}}{S}_{\mathrm{m}}^{\circ }=(2.77\pm 0.21)\mathrm{J}\cdot {\mathrm{K}}^{-1}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $⟨T⟩=354.7\mathrm{K}$ are consistent with $-2.0\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and $2.6\mathrm{J}\cdot {\mathrm{K}}^{-1}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, respectively, calculated in this work for the ideal gas. Abell and Adolf¹⁶⁵ determined the equilibrium constant of the 3-bromopropene isomerization into a mixture of the 1-bromopropene isomers as well as the one for the reaction between $\left(E\right)$-1- and $\left(Z\right)$-1-bromopropenes. The data provided in tables and graphs in the original source are not fully identical and we use the tabulated values for further analysis. The enthalpy difference between $\left(E\right)$-1- and $\left(Z\right)$-1-bromopropenes is found from the $\mathrm{l}\mathrm{n}K$ vs. $T^{-1}$ dependence to be ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}=-(3.1\pm 0.5)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $⟨T⟩=470.5\mathrm{K}$, compared to the mass-spectrometric, $-(2.1\pm 1.8)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, and ab initio, $-2.0\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, values. The fractions of each bromopropene isomer in the equilibrum mixture can also be found using the reported constants. The equilibrium constants for the 3-bromopropene isomerization into each 1-bromopropene determined from these compositions are used to calculate the corresponding enthalpy changes. The (E)-1-bromopropene enthalpy is found to be lower than that of 3-bromopropene by $-(1.0\pm 1.5)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at the same temperature. This enthalpy difference at $T=298.15\mathrm{K}$ is $-(3.5\pm 1.8)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ from the mass-spectrometric results¹⁴³ and $-3.1\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ from the ab initio calculations.

Monobromobutanes

The enthalpies of formation of 1- and 2-bromobutanes in the liquid phase were determined by combustion calorimetry.⁹⁷ Their enthalpies of vaporization have been reported by multiple authors. Because of the very large number of publications for vapor pressure and enthalpy of vaporization of 1-bromobutane, only the calorimetric works were considered here. The gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for 2-bromobutane derived from the hydrobromination enthalpies of butene isomers,¹⁰¹ the equilibrium of the 2-bromobutane decomposition to but-1-ene,¹⁰³ and the combustion data lie within $-\left(119.9\mathrm{to}118.5\right))\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. This is a remarkable result for an equilibrium study considering its relatively narrow temperature range of 28 K. The recommended value was obtained by weight-averaging of these results.

Alenin et al.^136,137 reported the constants of the 1-bromobutane $=2$-bromobutane equilibrium in the liquid phase at $T=(553$ and 583$)\mathrm{K}$. These temperatures are close to the estimated critical temperature of 1-bromobutane, $T_{\mathrm{c}}=564\mathrm{K}.$.²³ Therefore, these results are not used here. Peshchenko and Andreevskii⁹⁸ reported the constants of this equilibrium in the liquid phase at $T=298.2\mathrm{K}$ and in the gas phase in a range of temperatures of $\left(468.7\mathrm{to}513.7\right))\mathrm{K}$. At the average temperature, $T=490.7\mathrm{K},{\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}^{\circ }=-(12.8\pm 1.3)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. It becomes ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}^{\circ }=-(13.3\pm 1.3)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $T=298.15\mathrm{K}$ if one uses the ideal-gas model of Paulechka et al.¹²⁵ for both isomers. The derived gas-phase enthalpy of formation of 2-bromobutane was combined with the isomerization enthalpy to obtain an additional experimental ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ (1-bromobutane) in the gas phase. The recommended value for 1-bromobutane in the gas phase was obtained as the weight-average of this result and the one from combustion calorimetry adjusted for vaporization.

The gas-phase enthalpies of formation of 2-bromo-2-methylpropane were obtained from two consistent works on the equilibrium hydrobromination of 2-methylpropene.^105,106 The vaporization enthalpy of 2-bromo-2-methylpropane can be obtained from the results of two tensimetric works^126,127 and a calorimetric one.⁹⁴ Bryce-Smith and Howlett reported the vapor pressures at $T=\left(273.2\mathrm{to}346.0\right))\mathrm{K}$. We fit these results with a Clarke-Glew-type equation using three adjustable parameters. The data at $T=\left(280.0\mathrm{to}322.5\right))\mathrm{K}$ were found to deviate from the smooting curve by $<\pm 0.8\mathrm{\%}$. Outside this interval, the deviations were systematically positive and reached $3.4\mathrm{\%}$. Therefore, the results in the shorter interval were used to derive the tabulated enthalpy of vaporization. The recommended ${\mathrm{\Delta }}_1^{\mathrm{g}}{H}_{\mathrm{m}}$ value is based on two consistent experimental results.^94,127

For the fourth bromobutane isomer, 1-bromo-2-methylpropane, two data sources are available. Nesterova and Rozhnov¹⁰⁴ reported the liquid-phase constants for the equilibrium between 1- and 2-bromo-2-methylpropanes over a wide temperature range. The enthalpy of the former isomer relative to the latter was found to be $(15.4\pm 0.7)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at the average temperature of the measurements of 366.8 K. With the use of their heat capacities in the liquid phase at $T=298.15\mathrm{K},$,¹¹⁸ this difference became $(15.5\pm 0.7)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ at $=298.15\mathrm{K}$. A sum of the liquid-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ for 2-bromo-2-methylbutane and this difference gives ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ of the 1-bromo isomer. The other value was found from the reaction calorimetry with alkylmagnesium bromides of Holm,⁹² as described above. The results from both sources agree within their uncertainties. Therefore, the final value for the liquid phase was set to be their weighted average.

The computed gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values for monobromobutanes show excellent agreement with the experimental data (within $\pm 1.3\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$).

For bromocyclobutane, the experimental liquid-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ is the only available data point,⁹² and there is no vaporization data for the quantitative comparison with the ideal-gas ab intio value.

Dibromobutanes

For this group, there are two key compounds whose enthalpies can be derived from calorimetric measurements, 1,2-dibromobutane^83,97,128 and 1,2-dibromo-2-methylpropane.¹³¹ The liquid-phase isomerization data of Nesterova et al.^{145–147,166,167} is the only available source of information that can be used to derive the enthalpies of formation of other isomers. The equlibrium constants $K$ were reported in the temperature range of (275 to 553) K. The isomerization enthalpies were found from the slope of the experimental $\mathrm{l}\mathrm{n}K$ vs. $T^{-1}$ dependences and were assumed to be independent of temperature.

Bjellerup studied 1,2-dibromobutane by combustion calorimetry.⁹⁷ The enthalpy of the liquid-phase bromination of but-1-ene in which this dibromobutane was formed was measured by Lister.¹²⁸ Conn et al.⁸³ determined the enthalpies of the gas-phase bromination of but-1-ene as well as $\left(E\right)$- and $\left(Z\right)$-but-2-enes. In the case of but-1-ene, 1,2-dibromobutane is expected to be a product. For the but-2-enes, a mixture of meso- and $dl$-2,3-dibromobutanes of an unknown composition should be formed. The authors of the original publication incorrectly stated that these reactions are stereospecific and reported the reaction enthalpies for the specific 2,3-dibromobutane isomers.

The enthalpies of vaporization of 1,2-dibromobutane determined from the tensimetric¹²⁸ and ebulliometric^120,121 measurements are in good agreement. The gas-phase enthalpies of formation derived from the above data are inconsistent and vary from $-100\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ to $-87\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. The result of Lister, $-(87.4\pm 2.8)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ deviates from the ab initio value by $8.6\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. Considering the demonstrated performance of the computational method, the value of Lister ¹²⁸ was rejected. Two other gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ values are $-(93.5\pm 1.7)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-183}$ and $-\left(100.2\pm 2.3\right)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1},$.¹⁰² There is no obvious reason to give a preference to either of them. At the same time, the uncertainty for at least one of the results is far too low. The best estimate of the experimental gas-phase ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ was made by averaging these two values. The uncertainty was estimated as half of their difference. This result also agrees well with the corresponding $ab$ initio value.

To our knowledge, the only source of vaporization data for 1,3-dibromobutane is an ebulliometric study by Varushchenko et al. ¹²³ The enthalpy of vaporization was derived by the authors from their unpublished vapor-pressure data. This involved a long-range ($\mathrm{\Delta }T\approx 57\mathrm{K})$ extrapolation based exclusively on these results. Therefore, the real uncertainty of this ${\mathrm{\Delta }}_1^{\mathrm{g}}H$ value can be substantially higher. The vaporization enthalpy of 1,4-dibromobutane was determined in a calorimeter by Wadsö.⁹⁴ This quantity can also be derived from the smoothed vapor pressures reported by Stull. ¹²⁹ The value tabulated in this work is estimated from two lowest data points at $T=\left(\mathrm{305.2,332.0}\right)\mathrm{K}$. Deviation of this value from the calorimetric one allows one to estimate its uncertainty to be about $1.5\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$. We are not aware of any experimental vaporization data for 2,3-dibromobutanes.

The computed enthalpies of formation of dibromobutanes of normal structure are in good agreement with the experimental values.

Sunner and Wulff ¹³¹ determined the enthalpy of formation of 1,2-dibromo-2-methylpropane from the thermochemistry of the addition of bromine to 2-methylpropene in ${\mathrm{C}\mathrm{C}\mathrm{l}}_4$ and the vaporization enthalpy of the dibromide. Coffin and Maass¹³⁰ reported the temperature-dependent vapor pressures of this compound. The vaporization enthalpy found from these results is about $10\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ lower than the calorimetric value and too low relative to the results for similar compounds. The enthalpy of formation of liquid 1,3-dibromo-2-methylpropane is found as a sum of ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ of 1,2-dibromo-2-methylpropane discussed above and the enthalpy difference between the isomers, ${\mathrm{\Delta }}_{\mathrm{r}}{H}_{\mathrm{m}}^{\circ }=-(8.8\pm 0.3)\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}.$¹⁴⁷ The vaporization enthalpy of this compound is derived from the smoothed vapor-pressure data tabulated by Stull¹²⁹ at $T=(287.2$ and 313.2) K. Its uncertainty is taken to be the same as for $\mathrm{1,4}-$-dibromobutane. For both dibromo-2-methylpropanes, the computed ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\mathrm{m}}^{\circ }$ are significantly less negative than the experimental values. The differences are $5.5\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and $8.5\mathrm{k}\mathrm{J}\cdot {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for the 1,2-dibromo and 1,3-dibromo isomers, respectively. The reason for these deviations cannot be determined given the available information and further experimental investigations would be beneficial.

For the isomeric dibromobutanes, the differences between the experimental and computed values are unexpectedly large considering the demonstrated performance of the ab initio procedure for the other brominated compounds. Therefore, one can suggest that the real uncertainties of these experimental results are higher than those reported by the authors. Uncertainties of the experimental enthalpies of formation for normal dibromobutanes are larger than those of the computed values because of the large uncertainty for 1,2-dibromobutane. Therefore, we recommend using the computed gas-phase enthalpies of formation for all dibromobutanes.

Finally, based on the discussion above, the recommended thermochemical properties of the considered brominated hydrocarbons are compiled in Table 10.

Table 10:

Experimental standard enthalpies of formation for the liquid phase ${\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(\text{l}\right)$ and the ideal gas ${\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(\text{g}\right)$, the computed enthalpies of formation for the ideal gas ${\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }$ (g; calc) and corresponding recommended values for brominated hydrocarbons at the reference temperature $T=298.15\text{K}$

Compound (CASRN)	$\frac{{\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(1\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(\text{g}\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(\text{g}\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(\text{l}\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$	$\frac{{\Delta }_{\text{f}}{\text{H}}_{\text{m}}^{\circ }\left(\text{g}\right)}{\text{kJ}\cdot {\text{mol}}^{-1}}$
	Experimental		ab initio	Recommended
Bromo- and dibromopropanes
1-bromopropane (106-94-5)	−(116.0 ± 0.5)	−(83.8 ± 0.5)	−(85.6 ± 2.6)	−(116.0 ± 0.5)	−(83.8 ± 0.5)
2-bromopropane (75-26-3)	−(126.3 ± 0.7)	−(95.9 ± 0.7)	−(96.6 ± 2.6)	−(126.3 ± 0.7)	−(95.9 ± 0.7)
1,1-dibromopropane (598-17-4)	−(93.9 ± 1.0)		−(53.9 ± 2.7)	−(93.9 ± 1.0)	−(53.9 ± 2.7)
1,2-dibromopropane (78-75-1)	−(113.8 ± 0.9)	−(72.1 ± 0.9)	−(72.7 ± 2.7)	−(113.8 ± 0.9)	−(72.1 ± 0.9)
1,3-dibromopropane (109-64-8)	−(109.1 ± 0.9)	−(61.6 ± 0.9)	−(64.0 ± 2.7)	−(109.1 ± 0.9)	−(61.6 ± 0.9)
2,2-dibromopropane (594-16-1)		−(70.4 ± 3.0)	−(68.3 ± 2.7)		−(68.3 ± 2.7)
C3H5Br compounds
(Z)-1-bromopropene (590-13-6)		38.4 ± 2.7	39.1 ± 2.6		38.4 ± 2.7
(E)-1-bromopropene (590-15-8)		40.4 ± 2.6	41.1 ± 2.6		40.4 ± 2.6
bromopropene (557-93-7)		34.5 ± 2.7	32.9 ± 2.6		34.5 ± 3.8
3-bromopropene (106-95-6)	13.8 ± 2.3	46.1 ± 2.3	44.2 ± 2.6	13.8 ± 2.3	46.1 ± 2.3
bromocyclopropane (4333-56-6)			79.6 ± 2.6		79.6 ± 2.6
Bromobutanes
1-bromobutane (109-65-9)	−(142.6 ± 1.0)	−(105.8 ± 1.0)	−(106.2 ± 2.6)	−(142.6 ± 1.0)	−(105.8 ± 1.0)
2-bromobutane (78-76-2)	−(153.7 ± 0.3)	−(119.2 ± 0.3)	−(117.9 ± 2.6)	−(153.7 ± 0.3)	−(119.2 ± 0.3)
1-bromo-2-methylpropane (78-77-3)	−(148.4 ± 1.3)	−(113.5 ± 1.3)	−(114.3 ± 2.6)	−(148.4 ± 1.3)	−(113.5 ± 1.3)
2-bromo-2-methylpropane (507-19-7)	−(163.7 ± 1.1)	−(131.7 ± 1.1)	−(131.7 ± 2.6)	−(163.7 ± 1.1)	−(131.7 ± 1.1)
bromocyclobutane (4399-47-7)	−(7.4 ± 4.4)		32.7 ± 2.6	−(7.4 ± 4.4)	32.7 ± 2.6
1,2-dibromobutane (533-98-2)	−(142.9 ± 3.4)	−(96.9 ± 3.3)	−(94.6 ± 2.7)	−(140.6 ± 2.8)	−(94.6 ± 2.7)
1,3-dibromobutane (107-80-2)	−(149.2 ± 3.4)	−(99.8 ± 3.5)	−(97.7 ± 2.7)	−(147.0 ± 2.9)	−(97.7 ± 2.7)
1,4-dibromobutane (110-52-1)	−(141.3 ± 3.4)	−(88.2 ± 3.4)	−(86.2 ± 2.7)	−(139.3 ± 2.7)	−(86.2 ± 2.7)
meso-2,3-dibromobutane (5780-13-2)	−(150.2 ± 3.4)		−(102.5 ± 2.7)	−(150.2 ± 3.4)	−(102.5 ± 2.7)
dl-2,3-dibromobutane (598-71-0)	−(151.9 ± 3.4)		−(103.3 ± 2.7)	−(151.9 ± 3.4)	−(103.3 ± 2.7)
1,2-dibromo-2-methylpropane (594-34-3)	−(156.6 ± 0.6)	−(113.3 ± 0.6)	−(107.8 ± 2.7)	−(151.1 ± 2.7)	−(107.8 ± 2.7)
1,3-dibromo-2-methylpropane (28148-04-1)	−(147.8 ± 0.6)	−(101.4 ± 1.6)	−(93.0 ± 2.7)	−(139.3 ± 3.1)	−(93.0 ± 2.7)

Summary

A comprehensive investigation of the enthalpies of formation for $C_3$ and $C_4$ brominated hydrocarbons was conducted. Thorough review of available experimental data was combined with the computational results of the efficient high-level ab initio protocol developed previously and extended to Br-containing organic compounds in this work. As a part of this evaluation, an extensive analysis of the experimental enthalpies of vaporization was also carried out. Overall, the presented evaluation allowed establishing a consensus between the experimental results collected using different methods during the period of over a century as well as the modern computational chemistry methods. Availability of an accurate computational method capable of efficient treatment of moderate-sized molecules was shown to be essential for data evaluation: given a quite common lack of multiple independent experimental measurements, the computations provide the only means for data validation.

As a result of the present efforts, we have produced recommendations for the enthalpies of formation, in the liquid and gas phases, for 23 brominated compounds containing 3 or 4 carbon atoms. The recommendations substantially improve upon the existing values appearing in the reference literature^7,8 as well as cover new cases for which no values were recommended previously. The analysis also revealed a number of likely-erroneous measurements that should be treated with caution in the future studies. Finally, further experimental investigations are recommended for dibromobutanes and bromocycloalkanes $\left({\mathrm{C}}_3{\mathrm{H}}_5\mathrm{B}\mathrm{r}\right.$ and $\left.{\mathrm{C}}_4{\mathrm{H}}_7\mathrm{B}\mathrm{r}\right)$ for which the presently available data are not sufficient to yield unambiguous recommendations.