3D ED studies of synthetic rhabdophane allow single-crystal structure solution from individual nanocrystals and provides insight into the disordered water arrangment in the material. This highlights the usefulness of this technique to study order/disorder at nanoscale and its potential in exploring the effects of irradiation-induced structural and phase changes at such scales in the near future.
Keywords: crystal structure, 3DED, electron diffraction, rhabdophane, nanocrystal, superstructure, dysprosium phosphate
Abstract
In this study, we report the results of continuous rotation electron diffraction studies of single DyPO4·nH2O (rhabdophane) nanocrystals. The diffraction patterns can be fit to a trigonal lattice (P3121) with lattice parameters a = 7.019 (5) and c = 6.417 (5) Å. However, there is also a set of diffuse background scattering features present that are associated with a disordered superstructure that is double these lattice parameters and fits with an arrangement of water molecules present in the structure pore. Pair distribution function (PDF) maps based on the diffuse background allowed the extent of the water correlation to be estimated, with 2–3 nm correlation along the c axis and ∼5 nm along the a/b axis.
Introduction
Some of the naturally occurring monazite minerals (e.g. Monazite-Ce, CePO4) contain significant amounts of radioactive Th (>20 wt% ThO2) and U (up to 10 wt% UO2), and yet, these minerals are never found in the metamict (i.e. amorphous) state despite being exposed to self-irradiation damage (Nasdala et al., 2020 ▸). Due to their excellent radiation damage tolerance and chemical durability, monazite (REPO4, with RE = La–Gd; space group P21/n) based waste forms are proposed as potential candidates for managing long-lived radionuclides (Terra et al., 2003 ▸; Dacheux et al., 2013 ▸). Several studies have been carried out in the literature investigating the effects of radiation damage and corrosion on the structure of synthetic monazites and it was shown that in aggressive corrosive media, a secondary phase called rhabdophane (REPO4·nH2O, with RE = La–Gd) precipitates on the surface of the monazite ceramic (Arinicheva et al., 2018 ▸; Zhao et al., 2020 ▸). Rhabdophane has a low solubility constant and, as a result, possess good actinide retention properties which can help limit the release of actinides (including Th and U) into the biosphere (Du Fou de Kerdaniel et al., 2007 ▸). Therefore, understanding its structure and properties is important for assessing the long-term performance of actinide-rich monazite waste forms.
The crystal structural determination of rhabdophane poses an interesting scientific problem and in the literature, efforts have been made to solve the crystal structure via powder X-ray diffraction (PXRD, laboratory- and synchrotron-based) and, more recently, via three-dimensional electron diffraction (3DED) tomography (Mayence et al., 2014 ▸). It is important to note that the structure of rhabdophane has never been solved using single-crystal XRD due to the practical difficulties of growing a larger diffraction-quality crystal. In the late 1940s, using PXRD, Mooney (1948 ▸, 1950 ▸) first reported the crystal structure of rhabdophane (REPO4·nH2O, with RE = Ce, La, Pr and Nd) and concluded that it (CePO4·nH2O) crystallizes in the hexagonal structure with open channels running along the hexagonal axis. In that study, Mooney assigned two possible space groups (P3121 or P6222) to account for the systematic absence (i.e. it was reported in that study that the 00l planes were absent unless l = 3n) in the diffraction pattern of CePO4·nH2O. Mooney suggested that the water molecules could occupy the open channels in the structure; however, no attempt was made in that study to identify the location of the water molecules.
The precise arrangement of water in the hydrated structure was not determined until high-resolution synchrotron-based X-ray diffraction (HRXRD) and thermogravimetric analysis (TGA) by Mesbah et al. (2014 ▸). This work proposed a significant reduction in the symmetry of the structure to monoclinic (C2) with a structure analogous to partially hydrated calcium sulfate (this will be referred to as the monoclinic I structure). The relaxation of the structure was needed to accommodate several weak scattering features that could not be fit to the higher symmetry of the Mooney structure. Importantly, the study validated the hydration level of RePO4·0.667H2O as the stable room-temperature composition and proposed a configuration of the water molecules in the structure pore. Further studies of dehydration of the material (Mesbah et al., 2017 ▸) have also revealed changes in the material to a partially dehydrated monoclinic structure, RePO4·0.5H20 (monoclinic II), and finally a fully dehydrated structure that fits the original trigonal form proposed by Mooney. There are excellent overviews of the structural and chemical variations of the monazite–rhabdophane–xenotime–churchite system (Rafiuddin et al., 2022a ▸) that will not be repeated here, instead this report will focus on the hydrated rhabdophane structure only.
There has recently been a growth in the use of electron diffraction for structural studies of this kind, particularly where the high spatial resolution of electron microscopes allows individual nanocrystals to be studied within a powder sample (Kolb et al., 2007 ▸, 2011 ▸), removing the need for large single-crystal samples and so providing an opportunity to study materials where growth of large crystals is either difficult or not possible. The expansion of this methodology in recent years (Gemmi et al., 2019 ▸; Gruene et al., 2018 ▸) is also of value for studying systems exhibiting complex structural variations, since the coexistence of phases or the presence of microstructural features (Krysiak et al., 2018 ▸; Hua et al., 2021 ▸) can introduce artefacts into ensemble approaches, such as powder analysis. Electron diffraction can, therefore, provide useful complimentary evidence for such materials. Moreover, it is especially useful in determining the position of water and even hydrogen in the lattice (because of the strong Coulombic interaction), something that can be very difficult with X-rays. The focus of this study is to revisit the structure of hydrated rhabdophane through the study of hydrated dysprosium phosphate.
Experimental methods
The synthesis and structural characterization of the materials used in this work is covered in our earlier article (Rafiuddin et al., 2022b ▸), but the synthesis protocol is nevertheless briefly described here. Rhabdophane-type DyPO4·H2O was synthesized via the precipitation method. The following precursors were used to synthesize DyPO4·H2O: Dy2O3 (Alfa Aesar Chemicals, 99.9%), H3PO4 (Alfa Aesar Chemicals, 85%), HNO3 (Acros Organics, 70%) and NaOH (Fischer Chemicals, analytical reagent grade, pearls). Prior to the synthesis, 100 ml of a 0.05 M solution of Dy(NO3)3 were prepared by dissolving 0.94 g of Dy2O3 in 10 ml concentrated nitric acid solution, followed by dilution of the clear solution to a 100 ml volume in a volumetric flask using deionized water. 1 M H3PO4 and 8 M NaOH solutions were also prepared prior to the synthesis. 30 ml of 0.05 M Dy(NO3)3 were added to a vessel containing 6 ml of 1 M H3PO4 solution under continuous stirring and the pH of the solution was raised to ∼1.5 using 8 M NaOH and was left stirring for 1 h. After 1 h, the pH was increased to 1.5 and then heated to 45 °C in an oven for 1 d (without any further stirring) and the resulting fine precipitates were washed with deionized water and dried in air at 40 °C for 2 d.
A small fraction of the precipitate was dispersed in ethanol to obtain isolated single-crystal nanorods and then dispersed on to a standard TEM (transmission electron microscopy) carbon grid by pipetting a small drop of the liquid on to the grid.
Electron diffraction experiments were performed on a ThermoFisher Talos 200X TEM operated at 200 kV. Parallel beam illumination was used and a 10 µm C2 aperture inserted to minimize the beam size to approximately 800 nm diameter. The rotation range was limited by the overlap of the copper TEM grid at higher tilts and the usable range of +45 to −55° was achieved. The goniometer was rotated at approximately 1.12° s−1 and the diffraction patterns from individual crystals were recorded on a Quantum Detectors Merlin Quad hybrid pixel detector using continuous acquisition at 12-bit depth and 100 ms frame exposure.
Data was reconstructed and sectioned using the PETS software package (Palatinus et al., 2019 ▸). The structure solution was performed using charge-flipping (implemented as SUPERFLIP) in JANA (Petricek et al., 2014 ▸, 2023 ▸). Further diffraction pattern analysis was also performed using the Nanomegas ‘Automated crystal orientation mapping’ (ACOM) software (Rauch et al., 2010 ▸) and through Python routines developed within the electron microscopy group at the University of Manchester. PDF analysis was performed using the ‘numpy’ Python library for array manipulation and Fourier transforms.
Results
The rhabdophane sample comprised rod-like crystals with a typical width of 50–100 nm and lengths in the range 800–1500 nm. This allowed a single rhabdophane nanocrystal of width 80 nm to be identified and isolated in the electron beam. The nanocrystal was favourably oriented with its long axis lying approximately along the tilt axis of the goniometer. This meant that the effective sample thickness did not vary significantly during the tilt experiment (though there was increased thickness of the supporting carbon film at high tilts). Alignment of the sample height and the sample position to the tilt axis was performed to minimize sample movement; however, the crystal moved partially out of the illumination for the final 1.6° of the tilt range. Despite this, a very high level of completeness was achieved with 91% of the unique reflections with d-spacing greater than 0.7 Å was possible.
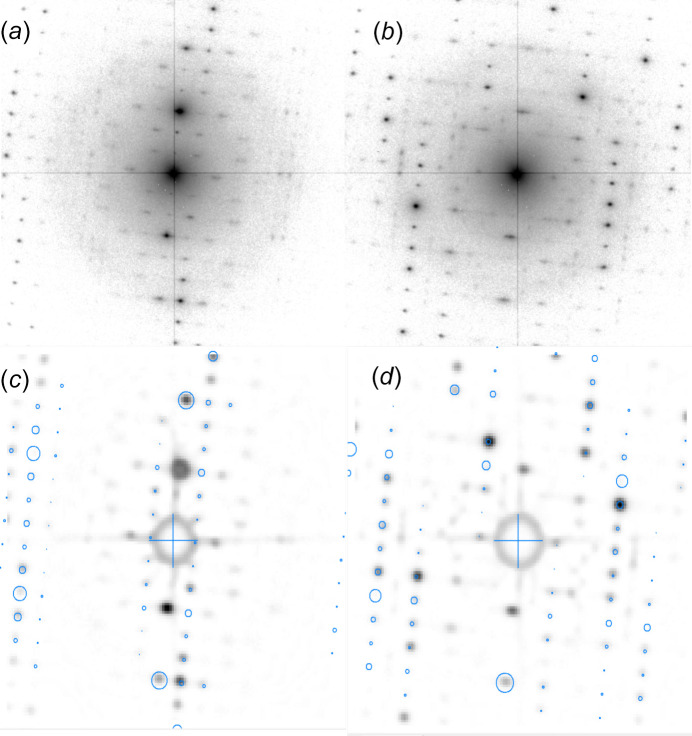
Figs. 1 ▸(a) and 1(b) show representative patterns extracted from a continuous diffraction acquisition modified to show log(Intensity) to enhance structured diffuse scattering present in the patterns. These patterns lie close to the <740> and <860> crystal directions of the trigonal structure model of rhabdophane, respectively, determined by template matching using the automated crystal orientation mapping (ACOM) software (Rauch et al., 2010 ▸). The patterns matching ACOM outputs are shown in Figs. 1 ▸(c) and 1(d), with blue circles overlaid to show the positions of the reflections in the kinematical template pattern. These orientations were chosen to lie relatively close (∼6° mis-orientation) to the [100] and [110] zone-axis orientations for the trigonal description of the rhabdophane crystal to provide clear matches to the simulated patterns but to be tilted far enough from the zone-axis orientation to show the reciprocal space between the zeroth and first Laue zones. What is notable is that beyond the clearly defined Bragg peaks indicated in Figs. 1 ▸(c) and 1(d), there is a clear structured diffuse background in the patterns (for comparison, examples of the natural intensity patterns are shown in Fig. S1 in the supporting information).
Figure 1.
Example electron diffraction patterns [reproduced with log(Intensity)] from the rhabdophane sample. Parts (a) and (b) show patterns recorded close to the <100> and <110> crystal orientations, respectively [note the halo arising from the amorphous carbon support films is more pronounced because of the log(Intensity) display]. Parts (c) and (d) show ACOM orientation matches to the <740> and <860> template libraries, respectively.
The natural intensity patterns were then processed using the PETS software (Palatinus et al., 2019 ▸) to analyse reciprocal space and reconstruct the reciprocal lattice. Automatic peak finding was performed at an intensity threshold (I/σ) of 5. The relative strength of the Bragg reflections (and the relative weakness of the structured background) is highlighted by the fact that, of the recovered reflections, 92% (1283/1381) fit a trigonal cell with the lattice parameters given in Table 1 ▸ that agrees well with the rhabdophane structure from Mooney (1948 ▸).
Table 1. Recovered lattice parameters from 3D ED of rhabdophane crystals.
| Parameter | Value |
|---|---|
| Formula | DyPO4·0.667H2O |
| System | trigonal |
| Space group | P3121 |
| a | 7.019 ± 0.05 Å |
| c | 6.417 ± 0.05 Å |
| Volume | 273.78 ± 0.01 Å3 |
| Wavelength | 0.0251 Å |
| R 2 | 0.239 |
| Completeness | 91% at 0.7 Å |
This indexing only fits the stronger reflections found in the experimental data. The weak background could not be isolated using a conventional peak-finding method and attempts to do so introduced artefacts from the background scattering around the direct beam, as well as from the amorphous carbon support film visible in the patterns.
To extract the weak background features from the diffraction data, reciprocal space sections equivalent to 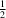 kl and hk
kl and hk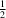 of the original trigonal cell were extracted (these can be thought of as the 1kl and hk1 sections of a 2a × 2b × 2c supercell). The effective increase in dimensions of the cell implied by this goes some way towards the increased size of the monoclinic superstructures proposed by Mesbah et al. (2014 ▸, 2017 ▸), though without any reduction in the symmetry of the cell. Other fractional reciprocal space sections were also tested to see if there was any additional higher-order diffuse scattering present, but no structured scattering was found beyond that found in the two sections mentioned previously.
of the original trigonal cell were extracted (these can be thought of as the 1kl and hk1 sections of a 2a × 2b × 2c supercell). The effective increase in dimensions of the cell implied by this goes some way towards the increased size of the monoclinic superstructures proposed by Mesbah et al. (2014 ▸, 2017 ▸), though without any reduction in the symmetry of the cell. Other fractional reciprocal space sections were also tested to see if there was any additional higher-order diffuse scattering present, but no structured scattering was found beyond that found in the two sections mentioned previously.
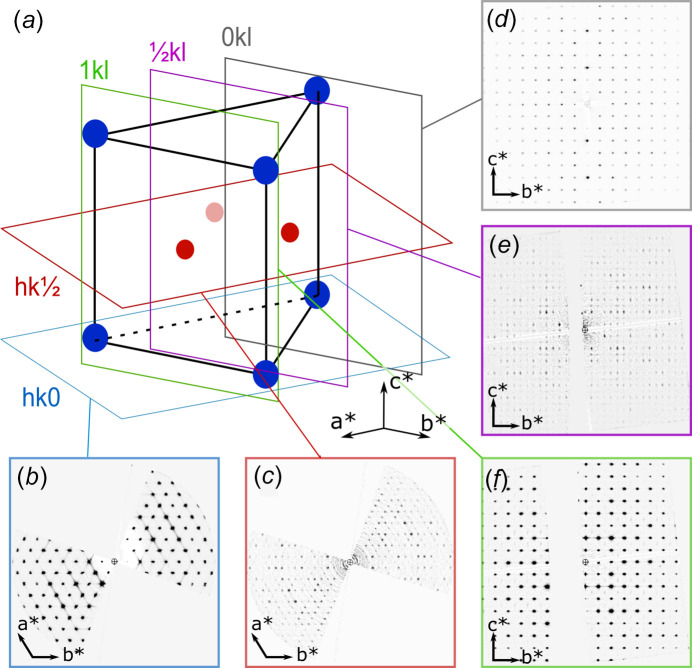
These sections, along with those containing the 0kl, 1kl and hk0 scattering vectors, are shown in Fig. 2 ▸. It should be noted that, since the tilt axis was aligned almost along the crystal c axis, the ‘missing wedge’ (arising from the finite tilt range in the TEM) is highly evident in the hk0 and hk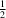 reciprocal space sections, with some portion of this manifesting as the empty bands in the
reciprocal space sections, with some portion of this manifesting as the empty bands in the 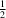 kl and 1kl sections. Fig. 2 ▸(b) shows the expected hexagonal arrangement of reflections; however, there are some weak diffuse streaks visible in the background of the section, suggesting at least one other additional type of disorder in the structure. These reinforce the threefold symmetry of pattern, even though much of the streaking is absent because of the missing wedge region of the slice. The ‘hk
kl and 1kl sections. Fig. 2 ▸(b) shows the expected hexagonal arrangement of reflections; however, there are some weak diffuse streaks visible in the background of the section, suggesting at least one other additional type of disorder in the structure. These reinforce the threefold symmetry of pattern, even though much of the streaking is absent because of the missing wedge region of the slice. The ‘hk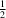 ’ section in Fig. 2 ▸(c) shows a set of scattering features lying at the midpoint between the Bragg peak positions in the ‘hk0’ section. Importantly, there are three of these arranged as a triangle in each reciprocal space subunit and so these also maintain the threefold rotation symmetry along this axis, rather than supporting a reduction to a lower symmetry.
’ section in Fig. 2 ▸(c) shows a set of scattering features lying at the midpoint between the Bragg peak positions in the ‘hk0’ section. Importantly, there are three of these arranged as a triangle in each reciprocal space subunit and so these also maintain the threefold rotation symmetry along this axis, rather than supporting a reduction to a lower symmetry.
Figure 2.
Reciprocal space sections from rhabdophane electron diffraction data. (a) A schematic of a partial unit of the reciprocal lattice with the trigonal reciprocal lattice indicated by blue circles and the disordered features marked by red circles. Individual reciprocal space sections corresponding to (b) hk0, (c) hk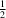 , (d) 0kl, (e)
, (d) 0kl, (e) 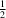 kl and (f) 1kl are indicated by planes in part (a).
kl and (f) 1kl are indicated by planes in part (a).
The ‘0kl’ section in Fig. 2 ▸(d) shows the expected rectangular arrangement of Bragg peaks. The 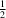 kl section in Fig. 2 ▸(e) confirms the position of the additional background peaks having basis vectors half the length of both a and c (but with alternating systematic rows along c), hence the general hkl indices are of the type
kl section in Fig. 2 ▸(e) confirms the position of the additional background peaks having basis vectors half the length of both a and c (but with alternating systematic rows along c), hence the general hkl indices are of the type 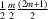 (where m is an integer). For the 1kl section, the diffuse streaking seen in the hk0 section is evident and the additional scattering features are located at the centres of the rectangles of Bragg reflections, meaning the background scattering has hkl indices of type
(where m is an integer). For the 1kl section, the diffuse streaking seen in the hk0 section is evident and the additional scattering features are located at the centres of the rectangles of Bragg reflections, meaning the background scattering has hkl indices of type 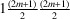 , which matches that expected from Fig. 2 ▸(c). The same centring is seen in the 0kl section, but the visibility of the background features is extremely low, making it almost impossible to visualize in this figure.
, which matches that expected from Fig. 2 ▸(c). The same centring is seen in the 0kl section, but the visibility of the background features is extremely low, making it almost impossible to visualize in this figure.
These are summarized in the schematic reciprocal lattice representation in Fig. 2 ▸(a). Here the trigonal substructure is indicated by the blue positions at the corners of the cell, while the background features are indicated by the red positions at the prismatic face centres. The position of each reciprocal space section is shown by the coloured planes. The suggestion here is that the doubling of all three unit-cell parameters within the trigonal space group is the most accurate description of the material being studied, though the superstructure is not fully correlated, as will be described in the next section.
Inspection of the reciprocal space sections showing background features, suggests that the additional scattering is not as sharp as that seen in the 0kl section, attributed only to Bragg scattering. Instead, these are considerably elongated along the c* direction, suggesting that they are arising from or affected by a breakdown of long-range order in the structure.
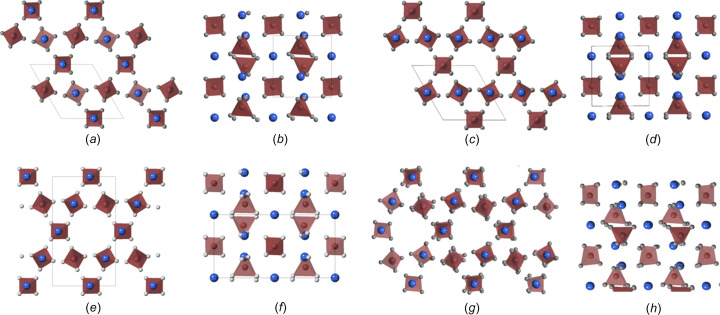
Finally, structure solution of the tilt-series data (only including the strong Bragg scattering and not the weak background) was performed in JANA (Petricek et al., 2014 ▸, 2023 ▸) using the ‘SUPERFLIP’ charge-flipping algorithm. The solution was made in the trigonal space group P3121, with the unit-cell parameters given in Table 1 ▸. The [001] and [100] projections of the solved structure are shown in Figs. 3 ▸(a) and 3(a), respectively, with the Dy ion and PO4 tetrahedron positions indicated. For comparison, the equivalent projections of the trigonal (Mooney, 1948 ▸), monoclinic II (Mesbah et al., 2017 ▸) and monoclinic I (Mesbah et al., 2014 ▸) structures are included in Figs. 3 ▸(c)–3(h), respectively.
Figure 3.
Structure projections of rhabdophane. Parts (a) and (b) are the solutions for the experimental data viewed along [001] and [100], respectively. Parts (c) and (d) are the same projections for the trigonal structure, parts (e) and (f) for the monoclinic II structure, and parts (g) and (h) for the monoclinic I structure (note the monoclinic I cell is larger than the others, so only a part of it is included for comparison). Blue refers to the Dy ion, grey to the O ion and brown to the PO4 tetrahedron.
Discussion
The solved structure [Figs. 3 ▸(c) and 3(b)] incorporates the symmetry of the original trigonal structure from Mooney (1948 ▸, 1950 ▸), but exhibits similar displacements of the cations from the monoclinic structures of Mesbah et al. (2014 ▸). Importantly, the structure, when viewed along the trigonal [100] direction [Fig. 3 ▸(b)], shows the clear zigzag of the cation positions (resulting from rotations of the PO4 tetrahedra) that was determined for the monoclinic I structure [Fig. 3 ▸(h)]. The distortion of the hexagonal channel at the centre of Fig. 3 ▸(a) is therefore similar to that seen in the monoclinic I structure [Fig. 3 ▸(g)], tending towards a triangular pore, rather than the hexagonal pores seen in the trigonal and monoclinic II [Figs. 3 ▸(c) and 3(e), respectively]. It is worth reiterating that the displacements of the cations shown in Figs. 3 ▸(a) and 3(b) occur within the symmetry of the trigonal structure, they do not require the reduction of symmetry of the crystal. It should be noted that the solution did not return positions for the oxygen or hydrogen in the water molecules.
Given the difference in the presented structures, the monoclinic II [Figs. 3 ▸(e)–3(f)] structure variant will no longer be considered for comparison. The evidence against the monoclinic transformation is strengthened if simulated electron diffraction patterns for this structure are considered. In the case of the reduction in symmetry, there would be a large number of (relatively weak) reflections introduced into the major zone axes.
The kinematical simulated [100] diffraction pattern is shown in Fig. 4 ▸(a), outlining the expected location of any additional scattering attributed to the monoclinic distortions. The highest gain example of the equivalent zone-axis diffraction from the experimental acquisition is shown in Fig. 4 ▸(b). The experimental pattern is clearly not kinematical as there is evidence of dynamical scattering (such as the relatively strong 001 and 002 reflections); however, there is no trace of the superstructure reflections that would be expected from the monoclinic structure. The only additional scattering is the faint presence of the 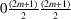 -type reflections (particularly
-type reflections (particularly 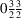 and
and 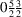 ).
).
Figure 4.
Electron diffraction patterns (a) simulated from the monoclinic crystal structure and (b) experimental data [log(Intensity)].
The diffuse features in the experimental data help to develop the description of the material. In Mesbah et al. (2014 ▸), the move to monoclinic symmetry is partly driven by weak reflections that could not be fit to the rhombic symmetry proposed by Mooney. However, these weak peaks can be indexed using the background scattering seen in the experimental data (particularly Figs. 2 ▸(c) and 2(e). Specifically, scattering to 2θ angles of 15.4 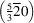 , 16.2
, 16.2 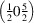 , 16.3
, 16.3 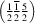 , 16.5
, 16.5 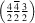 and 16.8°
and 16.8° 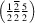 are all consistent with the experimental data presented. Furthermore, that study also reported changes in the lineshapes of the Bragg reflections, that can be explained by the superposition of both the Bragg and the diffuse scattering features seen in the electron diffraction data that have nearly identical scattering angles.
are all consistent with the experimental data presented. Furthermore, that study also reported changes in the lineshapes of the Bragg reflections, that can be explained by the superposition of both the Bragg and the diffuse scattering features seen in the electron diffraction data that have nearly identical scattering angles.
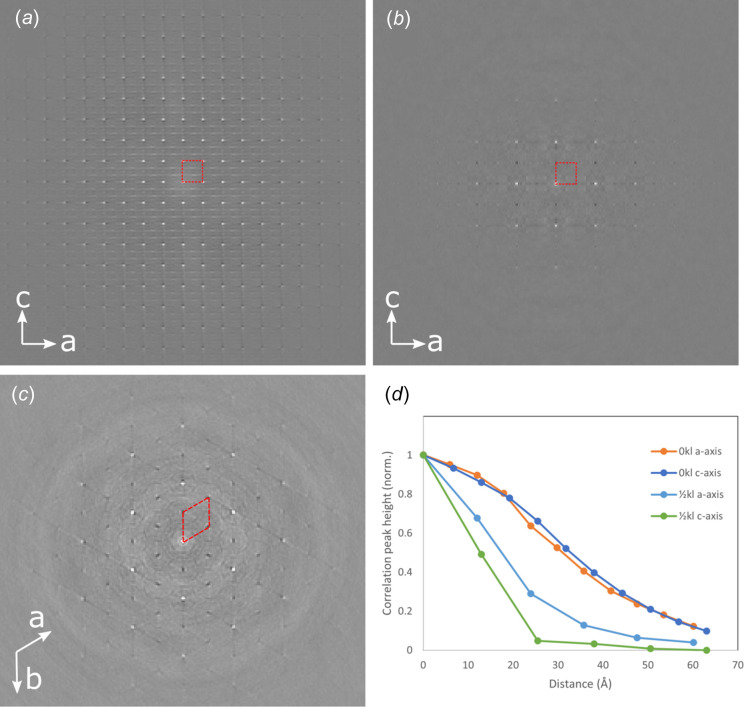
To study the diffuse character of the background scattering in more detail, a pair distribution function (PDF) analysis of the reciprocal space sections was performed, and the results shown in Fig. 5 ▸. Fig. 5 ▸(a) shows a PDF map produced from the 0kl reciprocal space section. This is almost entirely comprised of Bragg reflections and so strong positive correlation peaks are seen to extend across the map. The correlation of each atom with its equivalent site in adjacent cells gives rise to the approximately square arrangement of strong peaks in this map, corresponding to the unit-cell projection (this is indicated in all of the PDF maps by a red dotted line). The fact that each sublattice (both Dy and P) has cations with c coordinates separated by approximately  explains the strong bands of correlated vectors at c/3 and 2c/3 through the cell. Given the much higher atomic number of the cations, it is almost impossible to determine correlations involving the O atoms in the structure.
explains the strong bands of correlated vectors at c/3 and 2c/3 through the cell. Given the much higher atomic number of the cations, it is almost impossible to determine correlations involving the O atoms in the structure.
Figure 5.
PDF analysis of reciprocal space sections corresponding to (a) 0kl, (b) 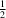 kl and (c) hk
kl and (c) hk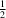 . Part (d) shows the normalized correlation peak intensity along the a and c directions in the 0kl and
. Part (d) shows the normalized correlation peak intensity along the a and c directions in the 0kl and 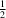 kl maps. Overlaid in red is the projection of the rhabdophane unit cell in all cases.
kl maps. Overlaid in red is the projection of the rhabdophane unit cell in all cases.
By contrast, the PDF of the 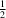 kl appears quite different and since this map excludes any long-range order (Bragg reflections) it can be interpreted as a Δ-PDF map (Weber & Simonov, 2012 ▸). In these maps, the white contrast indicates enhancements in the correlation (increased numbers of interatomic vectors above the average), while the dark contrast is decreased correlation (or fewer interatomic vectors). In general, there is little or no correlation related to the heavy ion (rare-earth or phosphorus) positions within the projected cell; instead all of the correlation peaks are at multiples of the projected cell dimensions. Along both a and c, there is a negative correlation peak at the first projected cell length and a strong enhancement of the vectors at twice the projected cell length (12.2 and 12.97 Å).
kl appears quite different and since this map excludes any long-range order (Bragg reflections) it can be interpreted as a Δ-PDF map (Weber & Simonov, 2012 ▸). In these maps, the white contrast indicates enhancements in the correlation (increased numbers of interatomic vectors above the average), while the dark contrast is decreased correlation (or fewer interatomic vectors). In general, there is little or no correlation related to the heavy ion (rare-earth or phosphorus) positions within the projected cell; instead all of the correlation peaks are at multiples of the projected cell dimensions. Along both a and c, there is a negative correlation peak at the first projected cell length and a strong enhancement of the vectors at twice the projected cell length (12.2 and 12.97 Å).
The positive peak at 2c suggests that there is a general ordering of atoms in alternating unit cells along the c axis. A similar behaviour is seen along a, particularly when the PDF of the hk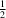 section [Fig. 5 ▸(c)] is considered. Here the vectors corresponding to the first neighbour cells (along all vectors equivalent to a) are negatively correlated, but there is a strong positive correlation in all of the second neighbour cells.
section [Fig. 5 ▸(c)] is considered. Here the vectors corresponding to the first neighbour cells (along all vectors equivalent to a) are negatively correlated, but there is a strong positive correlation in all of the second neighbour cells.
These observations fit a model where the background arises from the water molecules in the pore running through the structure. The monoclinic I structure describes the water arrangement in the hydrated structure. Here the water molecules within the central pore were reported to form hydrogen bonds with two of the six DyO8–PO4 polyhedra chains bounding the pore, creating a zigzag arrangement of water molecules that repeats over four unit cells of the fundamental trigonal structure. From the results reported here, we suggest that a similar zigzag arrangement of water molecules appears to repeat only every two cells (hence the background features describe the negative correlation at a distance of c and a positive correlation at a distance of 2c). The possibility of this type of diffuse scattering arising from other atomic displacements seems unlikely. The DyO8 and PO4 coordination polyhedra are all edge sharing, making a simple rigid unit displacements or rotations less likely, or subject to the same symmetry operations as the overall crystal. An independent distortion of one polyhedron would likely alter many of the heavy ion coordinates and so, in turn, would likely affect multiple heavy ion-ion vectors that lie within the projected cell [as seen in Fig. 5 ▸(a)], leading to additional changes in correlations within the individual unit cells, and these simply do not appear in the diffuse PDF maps [Figs. 5 ▸(b) and 5(c)].
The negative correlation along a, seen in both Figs. 5 ▸(b) and 5(c), suggests that the water molecules in adjacent pores form hydrogen bonds with a different subset of DyO8–PO4 polyhedra chains to those in the first pore, and only in the second neighbour shell does the water bonding revert to the original configuration (possible configurations of ordered water fitting hexagonal/trigonal symmetry and anti-phase boundaries between ordered domains are presented in Fig. S2 of the supporting information). This fits with the crystal exhibiting hexagonal/trigonal symmetry rather than the monoclinic symmetry where all of the water chains bond to the equivalent DyO8–PO4 polyhedra chain in each pore. The structure is also in good agreement with the water arrangement seen in the partially hydrated calcium sulfate structure (Schmidt et al., 2012 ▸) used to develop the original monoclinic model.
The disordered character of this behaviour is seen in more detail in Fig. 5 ▸(d), which shows linetraces taken along the a and c directions in Figs. 5 ▸(a) and 5(b). For the Bragg peaks (0kl section), the PDF shows strong correlation (that extends over many tens of Ångström), but which gradually decreases at higher distances as thermal displacements and finite beam-convergence effects lead to a breakdown in correlations. By contrast, the diffuse scattering in the 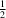 kl section data shows a far more rapid breakdown in the periodic order in the water substructure. It appears that, on average, the ordering of water in the c axis is highly disordered with the correlation falling to almost zero after only two of the water ‘zigzag’ arrangements (2–3 nm). Given there are three equivalent sets of DyO8–PO4 polyhedra chains that the water can hydrogen bond to, and two possible arrangements within each set of chains, there are a large number of possible ways to achieve the water arrangement in the structure. Domains of the order of a few nanometres that can randomly fit these different arrangements would explain the disorder reported in this study.
kl section data shows a far more rapid breakdown in the periodic order in the water substructure. It appears that, on average, the ordering of water in the c axis is highly disordered with the correlation falling to almost zero after only two of the water ‘zigzag’ arrangements (2–3 nm). Given there are three equivalent sets of DyO8–PO4 polyhedra chains that the water can hydrogen bond to, and two possible arrangements within each set of chains, there are a large number of possible ways to achieve the water arrangement in the structure. Domains of the order of a few nanometres that can randomly fit these different arrangements would explain the disorder reported in this study.
Along a, the ordering of hydrogen bonding in the second neighbour pores extends to around twice this distance (∼5 nm), suggesting that the domain size is somewhat larger in these directions.
The limited correlation along c explains why the background features are so extended in this direction [cf Figs. 2 ▸(e) and 2(f)]. Likewise, the general disorder in the water molecules helps to explain why the trigonal space group appears to fit the presented data. The experiments presented here were performed in TEM mode with a (quasi-)parallel electron beam, hence even with a small condenser aperture, the illumination area still covered approximately tens of nanometres of sample. If the domains of water arrangement are limited to a few nanometres in any direction, then the measurement will sample multiple different water configurations (ordered domains). Averaging across these will likely return the higher symmetry, as all the possible hydrogen-bonding configurations will be included. This suggests that were the water to arrange perfectly within the field of view, then the diffuse scattering features would no longer be elongated and the increased correlation would make them into stronger superlattice peaks, confirming a potential larger unit-cell size (2a × 2b × 2c) over the original trigonal cell.
Conclusions
Single-crystal electron diffraction data indicates that the general structure of hydrated rhabdophane can be described using the highest symmetry trigonal settings, albeit with an effective doubling of the cell compared to the original description by Mooney (1948 ▸, 1950 ▸) and considerable displacement of the ion positions within the unit cell that agrees with many of the features of the lower-symmetry monoclinic structure proposed for this material (Mesbah et al., 2014 ▸). This arises from disorder in the arrangement of the water molecules found in the pores of the structure, that give rise to weak scattering features that could easily be misinterpreted as evidence of more significant symmetry breaking. Instead, the arrangement of water molecules can initiate randomly at multiple equivalent sites in the structural pore, and when averaged by the relatively large electron beam, this leads to diffuse streaking of the equivalent features in reciprocal space. One future study is to examine the samples at cryogenic temperatures to see if removing thermal energy allows the water arrangement to become more regular. Furthermore, there is also likely to be a considerable inelastic scattering arising from the light elements (oxygen and hydrogen) in this structure. The exact difference that this will make to the quality of structure solution is uncertain but with the increasing use of electron-diffraction-based methods, there is a need to better quantify these effects and to utilize energy filtering to minimize them in future experiments.
In this study, it was possible to extract the diffuse scattering from within the overall ordered structure to allow PDF analysis of only the disordered sections of the structure to be examined. This allowed the disorder to be attributed solely to positions in the structure describing the network of water occurring in the pores of the mains structure. The ability to perform such single-crystal analysis on nanoscale crystals shows how electron diffraction is an important complimentary process to more well-established X-ray and neutron methods. This is particularly relevant when it comes to understanding not only the crystal structure but also the variations within complex nanostructured materials.
The results highlight the usefulness of this technique to study order/disorder at nanoscale and therefore its potential in exploring the effects of irradiation-induced structural and phase changes at such scales in the near future.
Supplementary Material
Crystal structure: contains datablock(s) I, I. DOI: 10.1107/S2053229624007885/eq3020sup1.cif
Unmodified versions of diffraction patterns and schematic diagrams of water ordering. DOI: 10.1107/S2053229624007885/eq3020sup2.pdf
Acknowledgments
This work was supported by the Henry Royce Institute for Advanced Materials, funded through EPSRC grants. A. Eggeman and E. Duran acknowledge the financial support provided by the Royal Society. M. R. Rafiuddin and A. H. Mir acknowledge the financial support provided by the EPSRC through an EPSRC Early Career Fellowship Grant. S. Hunt acknowledges support from NERC.
Funding Statement
This work was funded by Engineering and Physical Sciences Research Council grant EP/R00661X/1; Engineering and Physical Sciences Research Council grant EP/S019367/1; Engineering and Physical Sciences Research Council grant EP/S021531/1; Engineering and Physical Sciences Research Council grant EP/P025498/1; Engineering and Physical Sciences Research Council grant EP/T012811/1 to Anamul Haq Mir; Natural Environment Research Council grant NE/P017525 to Simon Hunt; Royal Society grant URF\R\191017 to Alexander Eggeman.
References
- Arinicheva, Y., Gausse, C., Neumeier, S., Brandt, F., Rozov, K., Szenknect, S., Dacheux, N., Bosbach, D. & Deissmann, G. (2018). J. Nucl. Mater.509, 488–495.
- Dacheux, N., Clavier, N. & Podor, R. (2013). Am. Mineral.98, 833–847.
- Du Fou de Kerdaniel, E., Clavier, N., Dacheux, N., Terra, O. & Podor, R. (2007). J. Nucl. Mater.362, 451–458.
- Gemmi, M., Mugnaioli, E., Gorelik, T. E., Kolb, U., Palatinus, L., Boullay, P., Hovmöller, S. & Abrahams, J. P. (2019). ACS Cent. Sci.5, 1315–1329. [DOI] [PMC free article] [PubMed]
- Gruene, T., Wennmacher, J. T. C., Zaubitzer, C., Holstein, J. J., Heidler, J., Fecteau–Lefebvre, A., De Carlo, S., Müller, E., Goldie, K. N., Regeni, I., Li, T., Santiso–Quinones, G., Steinfeld, G., Handschin, S., van Genderen, E., van Bokhoven, J. A., Clever, G. H. & Pantelic, R. (2018). Angew. Chem. Int. Ed.57, 16313–16317. [DOI] [PMC free article] [PubMed]
- Hua, X., Eggeman, A. S., Castillo-Martínez, E., Robert, R., Geddes, H. S., Lu, Z., Pickard, C. J., Meng, W., Wiaderek, K. M., Pereira, N., Amatucci, G. G., Midgley, P. A., Chapman, K. W., Steiner, U., Goodwin, A. L. & Grey, C. P. (2021). Nat. Mater.20, 841–850. [DOI] [PubMed]
- Kolb, U., Gorelik, T., Kübel, C., Otten, M. T. & Hubert, D. (2007). Ultramicroscopy, 107, 507–513. [DOI] [PubMed]
- Kolb, U., Mugnaioli, E. & Gorelik, T. E. (2011). Cryst. Res. Technol.46, 542–554.
- Krysiak, Y., Barton, B., Marler, B., Neder, R. B. & Kolb, U. (2018). Acta Cryst. A74, 93–101. [DOI] [PubMed]
- Mayence, A., Navarro, J. R. G., Ma, Y., Terasaki, O., Bergström, L. & Oleynikov, P. (2014). Inorg. Chem.53, 5067–5072. [DOI] [PubMed]
- Mesbah, A., Clavier, N., Elkaim, E., Gausse, C., Kacem, I. B., Szenknect, S. & Dacheux, N. (2014). Cryst. Growth Des.14, 5090–5098.
- Mesbah, A., Clavier, N., Elkaim, E., Szenknect, S. & Dacheux, N. (2017). J. Solid State Chem.249, 221–227.
- Mooney, R. C. L. (1948). J. Chem. Phys.16, 1003.
- Mooney, R. C. L. (1950). Acta Cryst.3, 337–340.
- Nasdala, L., Akhmadaliev, S., Burakov, B. E., Chanmuang, N. C. & Škoda, R. (2020). Sci. Rep.10, 14676. [DOI] [PMC free article] [PubMed]
- Palatinus, L., Brázda, P., Jelínek, M., Hrdá, J., Steciuk, G. & Klementová, M. (2019). Acta Cryst. B75, 512–522. [DOI] [PubMed]
- Petricek, V., Dusek, M. & Palatinus, L. (2014). Z. Kristallogr.229, 345–352.
- Petricek, V., Palatinus, L., Plasil, J. & Dusek, M. (2023). Z. Kristallogr.238, 271–282.
- Rafiuddin, M. R., Donato, G., McCaugherty, S., Mesbah, A. & Grosvenor, A. P. (2022a). ACS Omega, 7, 39482–39490. [DOI] [PMC free article] [PubMed]
- Rafiuddin, M. R., Tyagi, C. & Haq, M. A. (2022b). J. Solid State Chem.311, 123150.
- Rauch, E. F., Portillo, J., Nicolopoulos, S., Bultreys, D., Rouvimov, S. & Moeck, P. (2010). Z. Kristallogr.225, 103–109.
- Schmidt, H., Paschke, I., Freyer, D. & Voigt, W. (2012). Acta Cryst. B68, 92. [DOI] [PubMed]
- Terra, O., Clavier, N., Dacheux, N. & Podor, R. (2003). New J. Chem.27, 957–967.
- Weber, T. & Simonov, A. (2012). Z. Kristallogr.227, 238–247.
- Zhao, X., Yang, X., Li, Y. & Ahuja, R. (2020). J. Phys. Chem. C, 124, 22173–22184.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Crystal structure: contains datablock(s) I, I. DOI: 10.1107/S2053229624007885/eq3020sup1.cif
Unmodified versions of diffraction patterns and schematic diagrams of water ordering. DOI: 10.1107/S2053229624007885/eq3020sup2.pdf