Abstract
Background and aim
China has used traditional Chinese medicine (TCM) to treat diseases for more than 2000 years. Traditionally, TCMs in medicine cabinets are arranged alphabetically or on the basis of experience, but this arrangement greatly affects dispensing efficiency. However, owing to the unique properties and qualities of TCM, very few automatic approaches or systems have specifically addressed TCM dispensing problems. Therefore, it is necessary to establish a method of optimizing the traditional Chinese medicine placement scheme (TCMPS) via computer algorithms to improve the work efficiency of pharmacists.
Methods
A prescription dataset from a hospital in 2022 was obtained, and the association rule algorithm (ARA) was used to calculate the frequency of use for each type of TCM and the associations between different types of TCMs. On the basis of these association and frequency data, the optimal TCMPS was calculated using the simulated annealing algorithm (SAA) and then verified using the prescription dataset from 2023.
Results
A total of 10,601 prescriptions were collected in 2022, involving 360 different TCMs, and each prescription contained an average of 9.485 TCMs, with Danggui (3628) being the most frequently used. When the threshold of support was set to 0.05 and the confidence was set to 0.8, 78 couplet medicines used in orthopedics clinics were found through ARA. When the threshold value of support was set to 0, the confidence was set to 0, and the rule length was 2, a total of 129,240 rules were obtained, indicating support between all pairwise TCMs. The TCMPS, calculated using SAA, had a correlation sum of 14.183 and a distance sum of 3.292. The TCMPS was verified using a prescription dataset from 2023 and theoretically improved the dispensing efficiency of pharmacists by approximately 50%.
Conclusions
In this study, the ARA and SAA were successfully applied to pharmacies for the first time, and the optimal TCMPS was calculated. This approach not only significantly improves the dispensing efficiency of pharmacists and reduces patient waiting time but also enhances the quality of medical services and patient satisfaction, and provides a valuable reference for the development of smart medicine.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12913-024-11687-5.
Keywords: Association rule, Simulated annealing algorithms, Traditional Chinese medicine, Medicine cabinet
Introduction
Natural medicines have been extensively used for thousands of years in many regions of the world, including China, India, Sumer, Egypt, and Greece [1–4]. China, in particular, has a history of more than 2000 years of utilizing TCM to treat diseases and has developed a comprehensive theory of Chinese medicine. In recent years, TCM has played a significant role in the treatment of various challenging diseases, such as COVID-19, Ebola virus, and malaria, making it widely used in clinical treatment and drug health care in many regions of the world [5, 6].
In TCM clinics/hospitals, pharmacists are responsible for dispensing TCMs for each patient’s prescription. Traditionally, the various TCMs in the medicine cabinet are arranged in alphabetical order or are based on experience. However, this arrangement often leads to problems. For example, when frequently used TCMs are far from each other in the medicine cabinet, they not only lengthen the dispensing process but also place a greater burden on the mental and physical health of pharmacists [7]. According to the latest report, 36.8% of pharmacists’ negligence involves dispensing the wrong drug, whereas 15.3% involves dispensing the wrong dosage [8]. The most common reasons for dispensing errors include excessive work volume (21%), insufficient pharmacy staff (12%), time restrictions (11%), overwork (11%), and interruptions during the dispensing process (9.4%) [9].
In the field of Western medicine or concentrated extracts of TCM, numerous automated systems have been developed to reduce prescription error rates and improve the efficiency of pharmacists [10, 11]. However, owing to the unique properties and qualities of TCM, very few automatic approaches or systems have specifically addressed TCM dispensing problems [9], which has become a significant concern in TCM pharmacies and drug stores. Some researchers have introduced radio frequency identification technology in TCM dispensing systems to double-check prescriptions and pharmacy dispensing procedures to reduce the possibility of human error while ensuring the quality of dispensing [12, 13]. This technology does not alleviate the workload of pharmacists; additionally, for many small- and medium-sized TCM clinics/hospitals, the initial investment cost of developing such a system is high.
Therefore, this study aims to introduce ARA and SAA to improve the efficiency of drug dispensing. The ARA, which was the earliest association rule mining algorithm [14], can generate rules from a given dataset to describe specific relationships between variables. This algorithm was originally proposed for Market Basket Analysis, which was used to analyze the correlation between different products [15]. Owing to the natural correlation and frequent itemset characteristics of traditional Chinese medicine prescription data, different traditional Chinese medicines are often combined for the treatment of similar diseases. ARA excels at mining frequent patterns and association rules between itemsets from large amounts of data, which is crucial for understanding the compatibility rules between traditional Chinese medicines. Moreover, ARA can provide intuitive and easy-to-understand rules, such as “if the prescription includes drug A, it is likely to also include drug B”. These rules not only help understand the compatibility logic of traditional Chinese medicine but also provide important input data for subsequent optimization algorithms. By adjusting the support and confidence thresholds, ARA can flexibly control the quantity and quality of rule generation, making it easier for researchers to make adjustments according to actual needs. In addition, this algorithm has been applied to the TCM field. For example, Dong et al. utilized ARA to explore the medication patterns of TCM in the treatment of aplastic anemia and identified core components such as Danggui, Huangqi, Shudihuang, and Fuling [16].
The optimization problem of TCMPS involves multiple variables and complex constraints (such as the compatibility between traditional Chinese medicines and the frequency of their use), which makes it difficult to directly apply traditional optimization methods (such as linear programming and dynamic programming). SAA is a thermodynamic simulation annealing process that accepts solutions that are worse than the current solution with a certain probability, thus having the opportunity to escape from the trap of local optimal solutions and approach the global optimal solution. Random iterative heuristic algorithms can be divided into three parts: the objective function, the initial solution, and the solution space [17]. This characteristic is particularly important for solving TCMPS optimization problems with multiple local optima. The SAA algorithm does not depend on the specific form of the problem and has strong generality, which can be applied to various types of optimization problems. Moreover, its robustness enables the algorithm to maintain good performance in the face of data noise or uncertainty. The SAA has asymptotic convergence and has been theoretically proven to be a global optimization algorithm that converges to the global optimal solution with probability. Therefore, the SAA is very suitable for solving such complex optimization problems. Zhao et al. implemented the SAA to reconstruct the position of aircraft within the airport, reducing the distance traveled by passengers by a total of 4512 steps and saving one stand, and the efficiency of stand use increased by 31% [18].
In summary, the selection of ARA and SAA as the main algorithms for this study is based on a comprehensive consideration of their good matching of traditional Chinese medicine prescription data characteristics, ability to solve complex optimization problems, and the generality and robustness of the algorithms themselves. By combining the association rule mining ability of ARA with the optimization ability of SAA, the associations between traditional Chinese medicines can be first revealed through ARA, after which the optimal TCMPS can be more efficiently calculated through SAA. This combination strategy fully utilizes the advantages of both algorithms, improving the effectiveness and practicality of the entire solution. This optimization enables pharmacists to dispense drugs more efficiently and accurately, ultimately reducing the pharmacist workload and minimizing patient waiting time, and it significantly improves patient satisfaction.
Materials and methods
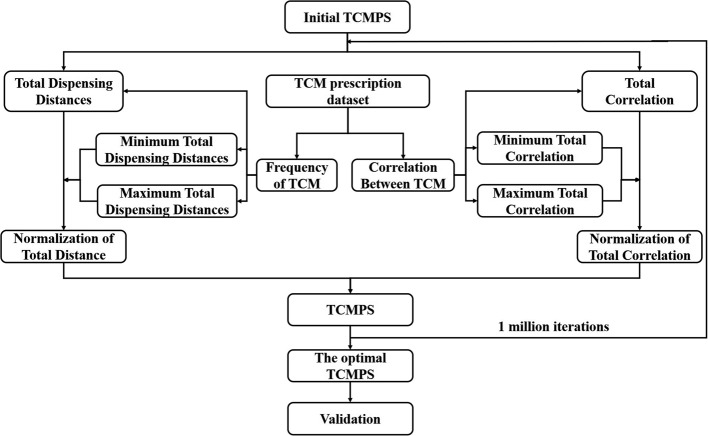
In this study, we propose a method for calculating the optimal TCMPS. This method uses the ARA to calculate the frequency and correlation between different TCMs in a dataset of TCM prescriptions. The TCMPS is optimized by the SAA, which considers the total dispensing distance and total correlation degree, resulting in the determination of the best TCMPS. Finally, we verify the validity of the optimal TCMPS using a new dataset.
The overall framework of this study is illustrated in Fig. 1:
Collection of TCM prescription data and analysis of the frequency and correlation of each TCM via the ARA.
Calculation of the maximum and minimum total dispensing distances on the basis of the frequency of each TCM.
Calculation of the maximum and minimum total correlations via the SAA on the basis of the correlations between different TCMs.
Utilizing the SAA, the optimal TCMPS is determined by considering both the total dispensing distance and the total correlation.
Verification of the optimal TCMPS using a new prescription dataset.
Fig. 1.
The overall framework of the study
The dataset of TCM prescriptions
The dataset was collected from a tertiary TCM orthopedics specialized hospital and included all TCM prescriptions from January 2020 to July 2023. Given the objectives of this study, each data sample consisted solely of the prescription’s identity number and the TCMs in each prescription. No patient-related information was included. All the data were summarized in Microsoft Excel, and a TCM prescription database was established. The statistical analysis of the data in this study was conducted using Microsoft Excel, VOSviewer, and RStudio.
Visualization analysis
VOSviewer is a scientific cartographic tool that was developed by Prof. Van Eck and Prof. Waltman from the Centre for Scientific and Technological Research of Leiden University for visual bibliometric analysis, which is mainly used to analyze details such as coauthors, countries, and keywords [19]. In our study, we employed VOSviewer to analyze and visualize the TCMs in prescriptions. The TCMs in the prescriptions can be considered equivalent to keywords in an article when the prescription is treated as an article.
Association analysis
To analyze the association rules of TCMs in the prescription, the Arules package in RStudio software was loaded, and ARA was used. The resulting association rules are expressed in the form of an implied expression X⇒Y, where X represents the antecedent item on the left-hand side (LHS) and Y represents the consequent item on the right-hand side (RHS). Each association rule was evaluated using support and confidence.
Support, confidence, and lift are three standard metrics used to measure the association between TCMs in the ARA. The support represents the proportion of the associated data (LHS and RHS) that appears in the total dataset (N). The confidence is the conditional probability of data, that is, the probability of RHS appearing in a prescription when LHS is present. The lift value indicates the probability of the simultaneous occurrence of RHS with LHS as a ratio of the probability of the overall occurrence of LHS. These three parameters statistically reflect TCM compatibility.
To obtain the core TCMs, we set the threshold of the support to 0.05 and the confidence to 0.8. When we set the threshold of the support and confidence to 0 and the length of the association rule to 2, we can obtain the correlation between all pairwise TCMs. The support, confidence, and lift are used to evaluate each association rule and can be calculated as follows:
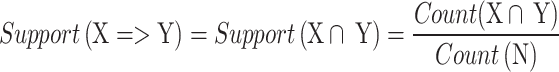 |
1 |
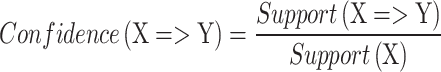 |
2 |
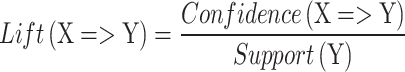 |
3 |
Establishment of the SAA model
Initial parameter setting
Medicine Cabinet Size: The medicine cabinet is typically a rectangular cabinet containing several compartments, each of which usually stores two types of TCMs, as shown in Fig. 2. Calculation of the Dispensing Distance for TCM: Pharmacists usually stand in the middle of the medicine cabinet to dispense medication, removing one TCM at a time and placing it on the front countertop. Therefore, the distance from each compartment to the center of the medicine cabinet represents the dispensing distance of each TCM in that compartment. Assuming that the coordinates of the center point of the medicine cabinet are K (a, b) and that the coordinates of a certain compartment are H (r, l), the distance from the TCM in the compartment to the center point is calculated as follows:
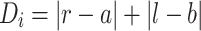 |
4 |
Fig. 2.
Schematic diagram of the medicine cabinet and weighing TCM operation
Average distance dor each TCM dispensing
Suppose there is a TCMPS, where Di represents the distance from the TCM to the center point; Ni represents the number of occurrences of the TCM in the prescription dataset; Pi represents the frequency of the occurrence of the TCM; and n represents the number of types of TCMs. The average distance for each TCM dispensing (Dave) is then calculated as follows:
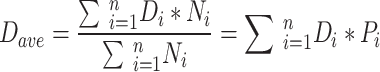 |
5 |
When the prescription dataset remains unchanged, the frequency of each TCM is also fixed; that is, Pi is a constant value. When the maximum Pi corresponds to the maximum Di, Formula (5) yields the maximum value of Dave, represented by Dmax. Conversely, when the maximum Pi corresponds to the minimum Di, the resulting Dave is the minimum value, represented by Dmin. The average distance is then normalized as follows:
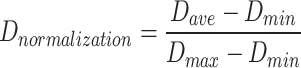 |
6 |
It is evident that the value of Dnormalization falls between [0, 1]. During the prescription dispensing process, it is usually expected that TCM can be dispensed as quickly as possible. Therefore, a smaller value of Dnormalization is preferred.
Total correlation between all tcms
According to the association rules in section “2.3”, each type of TCM has support, which represents the correlation between different TCMs. Suppose that there is a TCMPS, and the total correlation between each TCM and its adjacent TCMs is calculated and denoted by Csum. The SAA is used to randomly exchange the positions of any two TCMs in the TCMPS, and this process is repeated for 1 million iterations with the objective of determining the maximum and minimum Csum. Finally, the maximum Csum is represented by Cmax, and the minimum Csum is represented by Cmin. The correlation sum of any TCMPS is normalized using the following formula:
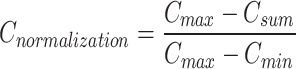 |
7 |
The value of Cnormalization falls between [0,1]. During the prescription dispensing process, it is usually expected that highly correlated TCMs are positioned adjacent to each other. Consequently, a smaller value of Cnormalization would result in a better outcome.
Objective function
Our objective for the TCMPS is twofold: to dispense the TCMs as quickly as possible and to ensure that some couplet medicinals are positioned adjacent to each other. To achieve this goal, the weights assigned to Dnormalization and Cnormalization are set at 50% each. Thus, the objective function is formulated as follows:
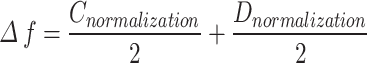 |
8 |
The value of Δf clearly lies within the range of [0, 1], with smaller values indicating a better outcome.
Steps of SAA
The following steps are executed using RStudio software. The relevant codes can be downloaded from https://github.com/github9852/TCMPS.
Step 1: Generate the initial position randomly and set the initial temperature T and temperature attenuation coefficient α. Then, calculate the initial value of Δf.
Step 2: Generate a new TCMPS by randomly exchanging the positions of two TCMs. Recalculate Δf and denote it as Δfnew.
Step 3: Judgment criteria. If Δfnew is smaller than Δf, replace the old TCMPS with the new one. Otherwise, accept the new TCMPS with a probability of exp((Δf-Δfnew)/T) > Random (1).
Step 4: Calculate the new temperature T = T*α and repeat steps 2 and 3 for 1 million iterations.
Step 5: Conclude the iteration and output the TCMPS corresponding to the minimum value of Δf as the optimal TCMPS.
Analysis process and data validation
To verify the performance of the optimal TCMPS, we compared the Dave and Csum values of the optimal TCMPS and real-world TCMPS in the 2022 and 2023 prescription datasets.
Results and discussion
Analysis of TCM prescriptions
The dataset of TCM prescriptions was collected from a tertiary TCM orthopedic hospital in Fujian Province. It contains 10,601 TCM prescriptions in 2022 and 7,207 TCM prescriptions in 2023. A total of 360 different TCMs were used in this dataset.
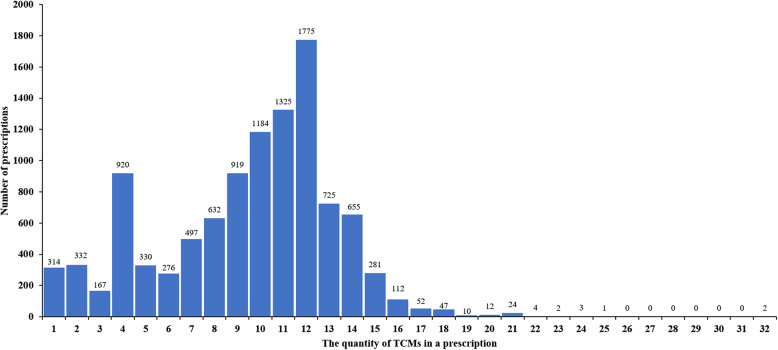
The 2023 prescription dataset was used to verify the optimal TCMPS. Further analysis of the prescription dataset from 2022 revealed that each prescription contained at least one kind of TCM and at most 32 kinds, with an average of 9.49 kinds. 80% of the prescriptions contained 4 ~ 14 kinds of TCMs, as shown in Fig. 3. Li et al. analyzed 84,418 prescriptions in ancient Chinese classics and reported that each prescription contained an average of 7.67 kinds of TCMs [20], which was significantly less than the number of TCMs in the prescriptions issued by modern TCM practitioners (P < 0.01). This difference may be attributed to the fact that the prescriptions issued by orthopedic hospitals contain more tonifying and replenishing medications, which are usually prescribed more frequently than other types of TCMs.
Fig. 3.
Distribution of prescriptions containing different quantities of TCMs
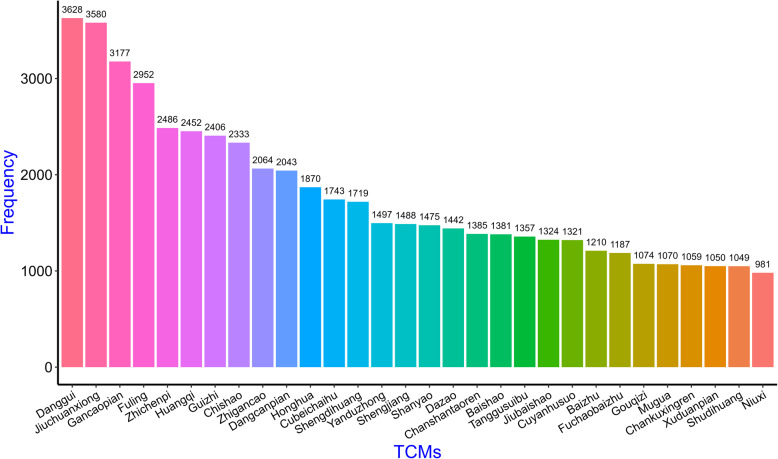
Through the analysis of each type of TCM, the top 10 most frequently used were Danggui, Jiuchuanxiong, Gancaopian, Fuling, Zhichenpi, Huangqi, Guizhi, Chishao, Zhigancao, and Dangshenpian. Among these, Danggui, Jiuchuanxiong, and Gancaopian were used more than 3000 times, accounting for more than 1/3 of the prescriptions. Eighty-one types of TCMs were used more than 300 times. Additionally, 148 kinds of TCMs are used fewer than 50 times, as shown in Fig. 4 and Table S1.
Fig. 4.
Top 30 TCMs in terms of their usage frequency
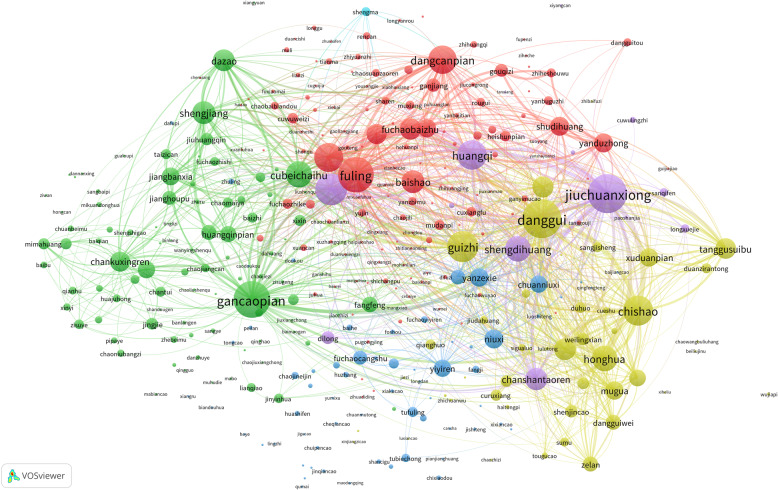
An analysis of the dataset using VOSviewer software revealed that the 360 kinds of TCMs could be grouped into 6 main categories (Fig. 5).
Category 1: This group consists of 137 kinds of TCMs, including Fuling, Zhigancao, Dangshenpian, Yanduzhong, Shanyao, Baizhu, Fuchaobaizhu, Gouqizi, and Shudihuang. These TCMs have functions such as tonifying the spleen and replenishing qi, tonifying the kidney and replenishing essence. They are used to treat patients with syndrome/pattern of the spleen and kidney insufficiency, and the representative prescription is Yuqin Decoction.
Category 2: This group consists of 93 kinds of TCMs, including Gancaopian, Cubeichaihu, Shengjiang, Dazao, Chankuxingren, Jiangbanxia, Jugeng, Huangqinpian, Fangfeng and Fabanxia. These TCMs mainly tonify the stomach and harmonize the middle. They are used to treat patients with a syndrome/pattern of stomach qi deficiency, and the representative prescription is Gancao Xiexin Decoction.
Category 3: This group consists of 64 kinds of TCMs, including Niuxi, Yiyiren, Yanzexie, Chuanniuxi, Jiudanseng, Fuchaocangzhu, Tufuling, Yanhuangbai, Tubiechong, and Yancheqianzi. These TCMs mainly have the effect of drying dampness because of their bitter taste and cold nature. They are used to treat patients with a syndrome/pattern of dampness and heat pouring downward, and the representative prescription is Simiao Pill.
Category 4: This group consists of 45 kinds of TCMs, including Danggui, Guizhi, Chishao, Honghua, Tanggusuibu, Jiubaishao, Cuyanhusuo, Mugua, and Xuduanpian. These TCMs mainly activate the blood and dispel stasis, and they are used to treat various pains caused by the syndrome/pattern of qi stagnation and blood stasis. The representative prescription is Huoxue Siwu Decoction.
Category 5: This group consists of 16 kinds of TCMs, including Jiuchuanxiong, Zhichenpi, Huangqi, Shengdihuang, Dilong, Sanqifen, and Longxuejie. These TCMs often appear in prescriptions, with the frequency of use of Jiuchuanxiong, Zhichenpi, Huangqi, and Shengdihuang ranking 2nd, 5th, 6th, and 13th, respectively, as shown in Fig. 4. In addition, Jiuchuanxiong, Dilong, Sanqifen, and Longxuejie all have the effect of tonifying and regulating qi and activating the blood, and they are often used in combination with each other, such as in the classic Chinese formula Huangqi Siwu Decoction, which is used to treat syndrome/pattern of qi and blood depletion.
Category 6: This group consists of 5 kinds of TCMs: Shengma, Gaobenpian, Manjingzi, Lingyangjiaofen, and Shengheshouwu. These types of TCMs have the characteristic of low frequency of use, which may be attributed to the following three reasons. Firstly, concerns over the safety of the medication. While Shengheshouwu has significant therapeutic effects in some traditional prescriptions, modern research suggests that it may contain harmful ingredients that are detrimental to human health. This has led doctors to exercise caution when prescribing it. Secondly, the economic cost. Lingyangjiaofen is expensive in the market due to scarce resources. In a healthcare system where medical resources are allocated tightly, doctors may prefer recommending drugs that offer better cost-effectiveness, thus limiting the use of these expensive TCMs. Thirdly, the characteristics of hospital specialties. Medicinal herbs such as Shengma, Gaobenpian, and Manjingzi are traditionally used to treat symptoms such as colds and headaches. However, as a specialized orthopedic hospital, there are fewer patients seeking treatment for colds and headaches, which directly leads to a lower frequency of use of these medications.
Fig. 5.
Classification of TCMs based on VOSviewer software
An analysis of the efficacy of the above TCMs revealed that most of them are related to tonifying the spleen, stomach, liver, and kidney or activating blood and removing stagnation.
According to TCM theory, there is a close relationship between bone and the kidney. The Great Simplicity of Huangdi’s Internal Classic Record explains that the kidney is connected to the bones and is responsible for generating bone marrow. If the kidney does not grow, the bone marrow cannot be filled. Kidney yang deficiency inhibits warming yang to activate qi flow, which leads to qi and blood impediment and obstruction, sinew and bone wilting, soreness and weakness of the waist and knees, unfavorable flexion and extension of the limbs and joints, slow fracture healing, and osteoporosis. The liver dominates the tendon and stores blood. When the blood stored in the liver is depleted, the muscles and bones cannot be nourished. Therefore, orthopedic diseases are closely related to the liver, kidney qi, and blood. Supplementing (and boosting) TCMs and blood-activating TCMs are two types of TCMs that are commonly used to treat orthopedic diseases [21].
Correlation between tcms
Using the ARA, we generated 78 rules when the threshold of support was set to 0.05, the confidence was set to 0.8, and the rule length was 10. Among these rules, the TCM combinations with a frequency ≥ 1000 were {Chanshantaoren} => {Honghua} and {Danggui, Honghua} => {Jiuchuanxiong}. The confidence of the couplet medicines {Shanyao, Yanduzhong, Zhiheshouwu}=>{Gouqizi} was 1, indicating that when Shanyao, Yanduzhong, Zhiheshouwu appeared simultaneously in a prescription, the probability of Gouqizi being included was 100%, and the frequency of the couplet medicines was 716. Additionally, {Gouqizi, Yanduzhong, Zhiheshouwu} => {Shanyao}, {Yanduzhong, Zhiheshouwu} => {Gouqizi} and {Yanduzhong, Zhiheshouwu} => {Shanyao} had high confidence and frequency (Table 1 and Table S2).
Table 1.
Top 20 rules for support ranking
| Rules | Support | Confidence | Coverage | Lift | Count |
|---|---|---|---|---|---|
| {Chanshantaoren} => {Honghua} | 0.106 | 0.813 | 0.131 | 4.609 | 1126 |
| {Danggui, Honghua} => {Jiuchuanxiong} | 0.098 | 0.860 | 0.114 | 2.547 | 1039 |
| {Chanshantaoren, Honghua} => {Jiuchuanxiong} | 0.089 | 0.839 | 0.106 | 2.485 | 945 |
| {Chanshantaoren, Jiuchuanxiong} => {Honghua} | 0.089 | 0.874 | 0.102 | 4.956 | 945 |
| {Chishao, Shengdihuang} => {Jiuchuanxiong} | 0.089 | 0.896 | 0.099 | 2.655 | 944 |
| {Chishao, Honghua} => {Jiuchuanxiong} | 0.086 | 0.910 | 0.095 | 2.694 | 916 |
| {Chanshantaoren, Chishao} => {Honghua} | 0.081 | 0.911 | 0.089 | 5.162 | 855 |
| {Chishao, Honghua} => {Chanshantaoren} | 0.081 | 0.849 | 0.095 | 6.499 | 855 |
| {Chanshantaoren, Chishao} => {Jiuchuanxiong} | 0.079 | 0.888 | 0.089 | 2.630 | 834 |
| {Chanshantaoren, Danggui} => {Honghua} | 0.073 | 0.871 | 0.084 | 4.939 | 778 |
| {Chanshantaoren, Chishao, Honghua} => {Jiuchuanxiong} | 0.073 | 0.905 | 0.081 | 2.681 | 774 |
| {Chanshantaoren, Honghua, Jiuchuanxiong} => {Chishao} | 0.073 | 0.819 | 0.089 | 3.722 | 774 |
| {Chanshantaoren, Chishao, Jiuchuanxiong} => {Honghua} | 0.073 | 0.928 | 0.079 | 5.261 | 774 |
| {Chishao, Honghua, Jiuchuanxiong} => {Chanshantaoren} | 0.073 | 0.845 | 0.086 | 6.468 | 774 |
| {Jiuchuanxiong, Tanggusuibu} => {Danggui} | 0.071 | 0.822 | 0.087 | 2.401 | 756 |
| {Chanshantaoren, Danggui} => {Jiuchuanxiong} | 0.071 | 0.838 | 0.084 | 2.480 | 748 |
| {Zhiheshouwu} => {Gouqizi} | 0.069 | 0.936 | 0.074 | 9.242 | 735 |
| {Gouqizi, Shanyao} => {Yanduzhong} | 0.069 | 0.896 | 0.077 | 6.346 | 733 |
| {Gouqizi, Yanduzhong} => {Shanyao} | 0.069 | 0.939 | 0.074 | 6.745 | 733 |
| {Shanyao, Yanduzhong} => {Gouqizi} | 0.069 | 0.927 | 0.075 | 9.147 | 733 |
The aforementioned couplet medicines are commonly found in various classic famous prescriptions, such as the Siwu Decoction and Liuwei Dihuang Pills, which have synergistic effects when used together. Furthermore, modern pharmacological research has confirmed the theory that the couplet medicines Chanshantaoren-Honghua can promote blood circulation, dissipate blood stasis, and significantly decrease whole blood viscosity, plasma viscosity, and packed cell volume [22]. Additionally, the couplet medicines Danggui-Jiuchuanxiong (DC) are frequently used as nourishing and blood-activating medicines in many gynecological prescriptions and modern Chinese medicine to prevent vascular diseases and alleviate pain. The results of animal experiments have shown that DC has antithrombotic, anti-inflammatory, antioxidant [23], and vasculogenesis activities. It can also prevent the development of liver fibrosis by inhibiting collagen deposition, decreasing inflammatory reactions, and reducing bile acid accumulation [24].
When the threshold value of support was set to 0, the confidence was set to 0, and the rule length was 2, a total of 129,240 rules were obtained, indicating support between all pairwise TCMs. The combination of Danggui and Jiuchuanxiong had the highest support (0.2032), indicating that 20.32% of prescriptions contained both Danggui and Jiuchuanxiong. Additionally, the confidence between Danggui and Jiuchuanxiong was 0.6017, suggesting that when one of the two TCMs appeared in a prescription, there was a probability of approximately 60% that the other TCM was also present. The support, confidence, and frequency data for the top 30 pairs of medicines are shown in Table 2 and Table S3, and they were used for the subsequent TCMPS analysis.
Table 2.
Top 30 couplet medicines
| Rules | support | confidence | coverage | lift | count |
|---|---|---|---|---|---|
| {Jiuchuanxiong} => {Danggui} | 0.203 | 0.602 | 0.338 | 1.758 | 2154 |
| {Danggui} => {Jiuchuanxiong} | 0.203 | 0.594 | 0.342 | 1.758 | 2154 |
| {Chishao} => {Jiuchuanxiong} | 0.162 | 0.738 | 0.220 | 2.184 | 1721 |
| {Jiuchuanxiong} => {Chishao} | 0.162 | 0.481 | 0.338 | 2.184 | 1721 |
| {Chishao} => {Danggui} | 0.143 | 0.651 | 0.220 | 1.901 | 1518 |
| {Danggui} => {Chishao} | 0.143 | 0.418 | 0.342 | 1.901 | 1518 |
| {Honghua} => {Jiuchuanxiong} | 0.131 | 0.745 | 0.176 | 2.206 | 1393 |
| {Jiuchuanxiong} => {Honghua} | 0.131 | 0.389 | 0.338 | 2.206 | 1393 |
| {Zhichenpi} => {Fuling} | 0.121 | 0.515 | 0.235 | 1.849 | 1280 |
| {Fuling} => {Zhichenpi} | 0.121 | 0.434 | 0.278 | 1.849 | 1280 |
| {Shengdihuang} => {Jiuchuanxiong} | 0.114 | 0.704 | 0.162 | 2.084 | 1210 |
| {Jiuchuanxiong} => {Shengdihuang} | 0.114 | 0.338 | 0.338 | 2.084 | 1210 |
| {Huangqi} => {Danggui} | 0.114 | 0.493 | 0.231 | 1.441 | 1209 |
| {Danggui} => {Huangqi} | 0.114 | 0.333 | 0.342 | 1.441 | 1209 |
| {Honghua} => {Danggui} | 0.114 | 0.646 | 0.176 | 1.888 | 1208 |
| {Danggui} => {Honghua} | 0.114 | 0.333 | 0.342 | 1.888 | 1208 |
| {Shengdihuang} => {Danggui} | 0.114 | 0.703 | 0.162 | 2.053 | 1208 |
| {Danggui} => {Shengdihuang} | 0.114 | 0.333 | 0.342 | 2.053 | 1208 |
| {Fuling} => {Danggui} | 0.109 | 0.390 | 0.278 | 1.140 | 1152 |
| {Danggui} => {Fuling} | 0.109 | 0.318 | 0.342 | 1.140 | 1152 |
| {Gancaopian} => {Danggui} | 0.109 | 0.363 | 0.300 | 1.060 | 1152 |
| {Danggui} => {Gancaopian} | 0.109 | 0.318 | 0.342 | 1.060 | 1152 |
| {Fuling} => {Jiuchuanxiong} | 0.108 | 0.389 | 0.278 | 1.152 | 1148 |
| {Jiuchuanxiong} => {Fuling} | 0.108 | 0.321 | 0.338 | 1.152 | 1148 |
| {Chanshantaoren} => {Honghua} | 0.106 | 0.813 | 0.131 | 4.609 | 1126 |
| {Honghua} => {Chanshantaoren} | 0.106 | 0.602 | 0.176 | 4.609 | 1126 |
| {Gancaopian} => {Jiuchuanxiong} | 0.106 | 0.353 | 0.300 | 1.045 | 1121 |
| {Jiuchuanxiong} => {Gancaopian} | 0.106 | 0.313 | 0.338 | 1.045 | 1121 |
| {Huangqi} => {Jiuchuanxiong} | 0.105 | 0.454 | 0.231 | 1.343 | 1112 |
| {Jiuchuanxiong} => {Huangqi} | 0.105 | 0.311 | 0.338 | 1.343 | 1112 |
The optimal TCMPS
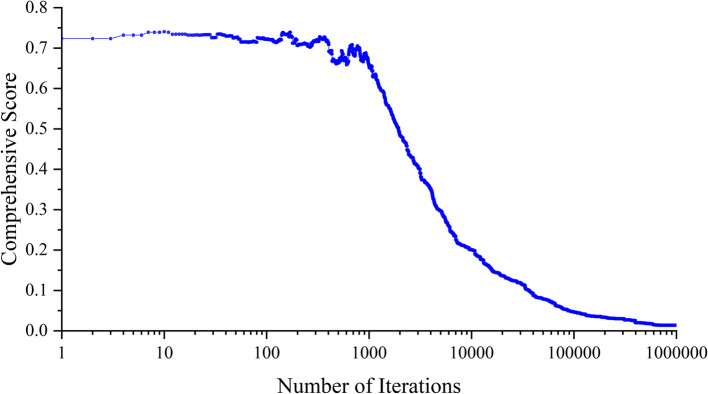
The medicine cabinet in our hospital consists of 10 rows and 18 columns, totaling 180 compartments, with each compartment storing two kinds of TCMs. On the basis of the frequency and support data of the TCMs obtained from the prescription dataset in 2022, the SAA was used for the calculations. First, we calculated the values of Dmax and Dmin of the TCMPS, which were 10.912 and 3.088, respectively. Next, by performing SAA iteration 1 million times, we obtained Cmax and Cmin values of 14.210 and 0.066, respectively. Then, with an initial temperature T of 100 and an annealing rate α of 0.99, we performed SAA iteration calculations another 1 million times to obtain the optimal TCMPS (Table S4). Finally, the minimum Δf was found to be 0.014, as shown in Fig. 6, and the corresponding values for Dsum and Csum were 3.292 and 14.183, respectively. According to the TCMPS corresponding to Dmax and Dmin, we calculated their respective Csum. Similarly, we calculated their corresponding Dave based on the TCMPS corresponding to Cmax and Cmin. Additionally, we calculated Csum and Dave for the current TCMPS in reality. The results are shown in Table 3. The Dave corresponding to Cmax was not the smallest, and the Csum corresponding to Dmin was not the largest. Furthermore, when the score of the optimal TCMPS was compared with that of the current TCMPS, the total correlation increased by 200.8%, whereas the total distance decreased by 51.5%. This improvement is expected to greatly increase the dispensing efficiency of pharmacists.
Fig. 6.
Changes in Δf under iterative calculation
Table 3.
Csum, Dave, and Δf corresponding to various placement schemes
| TCMPS | Csum | Dave | Δf |
|---|---|---|---|
| TCMPS corresponding to Cmax | 14.210 | 3.312 | 0.029 |
| TCMPS corresponding to Cmin | 0.066 | 7.414 | 1.553 |
| TCMPS corresponding to Dmax | 4.932 | 10.91 | 1.656 |
| TCMPS corresponding to Dmin | 8.209 | 3.088 | 0.424 |
| Optimal TCMPS | 14.183 | 3.292 | 0.028 |
| Current TCMPS in reality | 4.714 | 6.781 | 1.143 |
In the optimal TCMPS, the top 20 TCMs with the highest frequency of use are all located in the middle area of the medicine cabinet. This arrangement provides convenience and helps reduce the time needed for dispensing by pharmacists. Danggui is the most frequently used TCM, among others. Among the top 20 TCMs related to Danggui, 15 kinds of TCMs are adjacent to it, including Jiuchuanxiong, Chishao, Huangqi, Honghua, Shengdihuang, Gancaopian, Fuling, Tanggusuibu, Chanshantaoren, Dangshenpian, Zhichenpi, Guizhi, Zhigancao, Shudihuang and Xuduanpian.
The optimal TCMPS obtained through the aforementioned method appears to be ideal. This study further calculated the Dsum of the prescription datasets in 2022 and 2023 using the current TCMPS in reality and the optimal TCMPS. The results are shown in Table 4. When the optimal TCMPS was applied to the prescription dataset in 2023, Dave still decreased by 49.1%, which was basically consistent with the results in 2022. Therefore, by rearranging the position of TCMs, the work efficiency of pharmacists’ dispensing can be theoretically improved by approximately 50%.
Table 4.
Dave of the 2022 and 2023 TCM prescription datasets under the optimal TCMPS
| 2022 | 2023 | |
|---|---|---|
| Current TCMPS in reality | 6.781 | 6.724 |
| Optimal TCMPS | 3.292 | 3.424 |
| Reduce Dave’s percentage | 51.5% | 49.1% |
Conclusion
Starting from the practical perspective of pharmacy work, this study explores in depth the frequency of TCM use and the complex correlations between TCMs. Through the innovative application of ARA and SAA, the optimal TCMPS was successfully constructed for the first time in a TCM pharmacy. This achievement not only significantly improves the dispensing efficiency of pharmacists and reduces patient waiting time but also enhances the quality of medical services and patient satisfaction. In the current context of tight medical resources and increasing patient demand, this optimization plan is highly important for alleviating pharmacy work pressure and optimizing medical resource allocation. Second, this study has opened a new path for the development of smart health care. The successful integration of computer science, data science, and TCM has solved a practical problem in the field of TCM. This achievement not only promotes the modernization and intelligence of TCM but also provides a useful reference and guidance for the integration of other traditional medicines and modern technology. This interdisciplinary collaboration model also promotes communication and integration between disciplines and provides new perspectives and tools for solving more complex problems.
Supplementary Information
Acknowledgements
The authors would like to express gratitude to E Liu, a pharmacist from the Second Affiliated Hospital of Fujian Medical University, for demonstrating the weighing operation for traditional Chinese medicine.
Abbreviations
- TCM
Traditional Chinese medicine
- TCMPS
Traditional Chinese medicine placement scheme
- ARA
Association rule algorithm
- SAA
Simulated annealing algorithm
Authors’ contributions
Fu-Xian Zou: Investigation, methodology, software, writing – original draft, writing – review & editing. Jian-Xiang Huang: Formal analysis, methodology, software, writing – original draft. Shu-Ming Lin: Data curation, investigation, resources. Dong-Hong Wang: Data curation, investigation, validation, and visualization. Xiao-Lan Zhou: Data curation, project administration. Qiu-Ping Huang: Project administration. Jian-Feng Cai: Conceptualization, supervision. All the authors have read and approved the final manuscript.
Funding
Not applicable.
Open access funding was provided by Quanzhou Orthopedic Traumatological Hospital.
Availability of data and materials
The datasets generated for this study are available upon request to the corresponding authors.
Declarations
Ethics approval and consent to participate
This study was approved by the ethics committee of Quanzhou Orthopedic Hospital, and there is no need for ethical review. According to the measures for ethical review of life sciences and medical research involving human beings issued by the China Health Commission, because the data evaluated in this study do not involve any patient’s personal privacy information and will not cause damage to everyone, there is no need for ethical review.
Consent for publication
Written informed consent for publication of the ink line diagram (Fig. 2) was obtained from the pharmacist to better demonstrate the weighing operation of traditional Chinese medicine.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Fu-Xian Zou and Jian-Xiang Huang contributed equally to this work.
Contributor Information
Qiu-Ping Huang, Email: 1449972964@qq.com.
Jian-Feng Cai, Email: Caijianfeng666@126.com.
References
- 1.Ravi S, Bharadvaja N. Market Analysis of Medicinal Plants in India. Curr Pharm Biotechnol. 2019;20(14):1172–80. [DOI] [PubMed] [Google Scholar]
- 2.Bekele M, Woldeyes F, Lulekal E, Bekele T, Demissew S. Ethnobotanical investigation of medicinal plants in Buska Mountain range, Hamar district, Southwestern Ethiopia. J Ethnobiol Ethnomed. 2022;18(1):60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chebii WK, Muthee JK, Kiemo JK. Traditional medicine trade and uses in the surveyed medicine markets of Western Kenya. Afr Health Sci. 2022;22(4):695–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang B, Pei W, Cai P, Wang Z, Qi F. Recent advances in Chinese patent medicines entering the international market. Drug Discov Ther. 2022;16(6):258–72. [DOI] [PubMed] [Google Scholar]
- 5.Li Q, Wang H, Li X, Zheng Y, Wei Y, Zhang P, Ding Q, Lin J, Tang S, Zhao Y, et al. The role played by traditional Chinese medicine in preventing and treating COVID-19 in China. Front Med. 2020;14(5):681–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zheng S, Baak JP, Li S, Xiao W, Ren H, Yang H, Gan Y, Wen C. Network pharmacology analysis of the therapeutic mechanisms of the traditional Chinese herbal formula Lian Hua Qing Wen in Corona virus disease 2019 (COVID-19), gives fundamental support to the clinical use of LHQW. Phytomedicine. 2020;79:153336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen CW, Tsai CF, Tsai YH, Wu YC, Chang FR. Association rule mining for the ordered placement of traditional Chinese medicine containers: an experimental study. Med (Baltim). 2020;99(18):e20090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Reiner G, Pierce SL, Flynn J. Wrong drug and wrong dose dispensing errors identified in pharmacist professional liability claims. J Am Pharm Assoc (2003). 2020;60(5):e50–6. [DOI] [PubMed] [Google Scholar]
- 9.Lin CY, Hsieh PJ. Development of an Automatic Dispensing System for Traditional Chinese Herbs. J Healthc Eng. 2017;2017:9013508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chalmeta R, Navarro-Ruiz A, Soriano-Irigaray L. A computer architecture based on disruptive information technologies for drug management in hospitals. PeerJ Comput Sci. 2023;9:e1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang TY, Huang WT, Lin YC, Hung HH, Ou SC, Chang CW, Lin HE, Lin TY, Chang CW, Hung HC, et al. Chinese intelligence prescription system improves prescription accuracy while decreasing labor and drug costs. BMC Health Serv Res. 2023;23(1):514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chou SY, Hwang KY, Shieh SC. Design of an intelligent system to improve traditional Chinese medicine distributing practice. In: Stjepandić J, Rock G, Bil C. (eds) Concurrent Engineering Approaches for Sustainable Product Development in a Multi Disciplinary Environment. London: Springer; 2013. p. 657–66. https://link.springer.com/chapter/10.1007/978-1-4471-4426-7_56
- 13.Liu X, Liu H, Liu Y. Research on contactless intelligent medication pickup mode selection based on a hospital in China under COVID-19. Technol Health Care; 2023. [DOI] [PubMed] [Google Scholar]
- 14.Chen Y, Dou H, Chang Q, Fan C. PRIAS: An Intelligent Analysis System for Pesticide Residue Detection Data and Its Application in Food Safety Supervision. Foods. 2022;11(6):780. [DOI] [PMC free article] [PubMed]
- 15.Tai CJ, El-Shazly M, Tsai YH, Csupor D, Hohmann J, Wu YC, Tseng TG, Chang FR, Wang HC. Uncovering modern clinical applications of Fuzi and Fuzi-based formulas: a Nationwide Descriptive Study with Market Basket Analysis. Front Pharmacol. 2021;12:641530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dong N, Zhang X, Wu D, Hu Z, Liu W, Deng S, Ye B. Medication Regularity of Traditional Chinese Medicine in the Treatment of Aplastic Anemia Based on Data Mining. Evid Based Complement Alternat Med. 2022;2022:1605359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wan S, Zhang J, Hou R, Zheng M, Liu L, Zhang M, Li Z, Huang X. A strategy for component-based Chinese medicines design approach of Polygonum orientale L. against hypoxia/reoxygenation based on uniform design-stepwise regression-simulated annealing. BIOMED PHARMACOTHER. 2021;135:111177. [DOI] [PubMed] [Google Scholar]
- 18.Zhao N, Duan M. Research on airport multi-objective optimization of stand allocation based on simulated annealing algorithm. Math Biosci Eng. 2021;18(6):8314–30. [DOI] [PubMed] [Google Scholar]
- 19.Van Eck NJ, Waltman L. Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics. 2010;84(2):523–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li YB, Du Y, Liu FZ, Zhang YY, Li M, Wang J, Li YH, Yang Y. Applicability of Zipf’s Law in Traditional Chinese Medicine prescriptions. Chin Med Sci J. 2022;37(3):195–200. [DOI] [PubMed] [Google Scholar]
- 21.HU H, Fanxiang F, Xiaoyong L, Zujian X. Analysis of drugs commonly used in TCM therapy for treatment of osteonecrosis of the femoral head. J Trad Chin Orthop Trauma. 2016;28(08):24–6. [Google Scholar]
- 22.Liu L, Duan JA, Tang Y, Guo J, Yang N, Ma H, Shi X. Taoren-Honghua herb pair and its main components promoting blood circulation through influencing on hemorheology, plasma coagulation and platelet aggregation. J Ethnopharmacol. 2012;139(2):381–7. [DOI] [PubMed] [Google Scholar]
- 23.Zhang M, Li P, Zhang S, Zhang X, Wang L, Zhang Y, Li X, Liu K. Study on the mechanism of the Danggui-Chuanxiong Herb Pair on treating Thrombus through network pharmacology and zebrafish models. ACS Omega. 2021;6(22):14677–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wu JZ, Li YJ, Huang GR, Xu B, Zhou F, Liu RP, Gao F, Ge JD, Cai YJ, Zheng Q, et al. Mechanisms exploration of Angelicae Sinensis Radix and Ligusticum Chuanxiong Rhizoma herb-pair for liver fibrosis prevention based on network pharmacology and experimental pharmacologylogy. Chin J Nat Med. 2021;19(4):241–54. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated for this study are available upon request to the corresponding authors.