Recurrent stroke prediction by applying a stroke polygenic risk score in the Japanese population

Abstract

Background

Recently, various polygenic risk score (PRS)-based methods were developed to improve stroke prediction. However, current PRSs (including cross-ancestry PRS) poorly predict recurrent stroke. Here, we aimed to determine whether the best PRS for Japanese individuals can also predict stroke recurrence in this population by extensively comparing the methods and maximizing the predictive performance for stroke onset.

Methods

We used data from the BioBank Japan (BBJ) 1^st cohort (n=179,938) to derive and optimize the PRSs using a 10-fold cross-validation. We integrated the optimized PRSs for multiple traits, such as vascular risk factors and stroke subtypes to generate a single PRS using the meta-scoring approach (metaGRS). We used an independent BBJ 2^nd cohort (n=41,929) as a test sample to evaluate the association of the metaGRS with stroke and recurrent stroke.

Results

We analyzed recurrent stroke cases (n=174) and non-recurrent stroke controls (n=1,153) among subjects within the BBJ 2^nd cohort. After adjusting for known risk factors, metaGRS was associated with stroke recurrence (adjusted OR per SD 1.18 [95% CI: 1.00–1.39, p=0.044]), although no significant correlation was observed with the published PRSs. We administered three distinct tests to consider the potential index event bias; however, the outcomes derived from these examinations did not provide any significant indication of the influence of index event bias. The high metaGRS group without a history of hypertension had a higher risk of stroke recurrence than that of the low metaGRS group (adjusted OR 2.24 [95% CI: 1.07–4.66, p=0.032]). However, this association was weak in the hypertension group (adjusted OR 1.21 [95% CI: 0.69–2.13, p=0.50]).

Conclusions

The metaGRS developed in a Japanese cohort predicted stroke recurrence in an independent cohort of patients. In particular, it predicted an increased risk of recurrence among stroke patients without hypertension. These findings provide clues for additional genetic risk stratification and help in developing personalized strategies for stroke recurrence prevention.

Introduction

Stroke is a major cause of mortality in Japan, with 56,000 deaths reported in 2020.¹ The conventional risk factors for stroke include hypertension, high waist-to-hip ratio, smoking, cardiac causes, dyslipidemia, and diabetes mellitus.² In Japan, the stroke recurrence rate is up to 30–50% during 5–10 years of follow-up after the first stroke.^3,4 Accordingly, it will be medically beneficial to stratify high-risk groups for recurrent stroke among those who have experienced a stroke to potentially generate more intensive secondary prevention strategies than current recommendations.

Genome-wide association studies (GWAS) have identified many disease-susceptibility variants associated with complex traits.⁵ A polygenic risk score (PRS) is the weighted summation of the individual genetic effects of these variants. Its weighting strategy varies depending on the construction method; traditionally, only significant variants are used in developing this score. The recently developed PRS methods involve non-significant variants and updated effect weights and consider the linkage disequilibrium (LD) structure. The development of PRS methods has helped stratify high-risk groups for complex traits,^6–11 including stroke.¹²

Polygenic risk scores developed using the 32 genome-wide significant (p< 5.0×10⁻⁸) variants or 90 marginally associated (p<1.0×10⁻⁵) variants (PRS₉₀) from the MEGASTROKE study¹² are associated with stroke onset in subjects of European ancestry.^12,13 The meta-scoring PRS approach (metaGRS) includes 3.2 million variants by combining PRSs for stroke subtypes, risk factors, and comorbidities by adjusting the effect weight via elastic-net logistic regression; this approach has an improved predictive performance for stroke compared to that of PRS₉₀.¹⁴ MetaGRS can predict stroke incidence independent of environmental factors and could help motivate individuals with high genetic risk to make lifestyle changes for stroke prevention (although not yet implemented in clinical practice outside a research setting).¹⁵ The PRS shows reduced transferability between populations. Additionally, a PRS developed using various variants derived from Japanese GWAS successfully predicted stroke onset in the Japanese population.^16,17 Most recently, the GIGASTROKE study proposed an integrated PRS approach among PRSs derived from populations of multiple ancestries using the metaGRS framework (iPGS), which showed a better predictive ability than the MEGASTROKE European or East Asian PRS.¹⁸ However, the PRS did not successfully predict stroke recurrence; for example, PRS₃₂ and iPGS did not significantly predict stroke recurrence after adjusting for clinical comorbidities, with notably smaller effect sizes than for non-recurrent stroke.^12,18 Furthermore, the potential effect of index event (also known as “collider”) bias that may distort the association of PRS was suspected.^19,20

The optimal method to improve the predictive accuracy of PRS depends on the population- and trait-specific genetic architecture.^21–30 Therefore, we compared different PRS methods and determined whether the best PRS can predict the onset of recurrent stroke in a Japanese population.

Methods

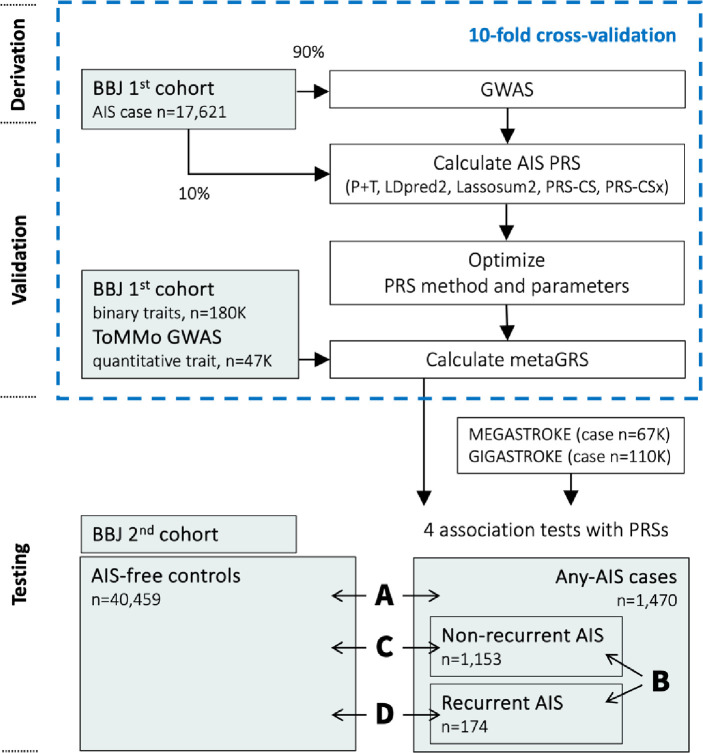
The workflow of this study is shown in Figure 1. This article follows the TRIPOD (Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis) reporting guidelines.

Figure 1. Workflow.

MEGASTROKE AIS summary statistics of European (EUR) studies were only used for PRS-CSx. 1000 Genomes Project super population samples (EAS or EUR) were used for the LD reference panel. Abbreviations: GWAS = genome-wide association study, PRS = polygenic risk score, P+T = pruning and thresholding, OR = odds ratio, AIS = all ischemic stroke, ToMMo = Tohoku Medical Megabank; LD, linkage disequilibrium.

We used a logistic regression model to assess the association of the PRS using the two case-control settings for AIS (A: any-AIS vs. AIS-free controls) and AIS recurrence (B: recurrent AIS vs. non-recurrent AIS). We also applied two other combinations of case-controls (C: recurrent versus AIS-free controls and D: non-recurrent versus AIS-free controls).

Study subjects and quality control

BioBank Japan (BBJ) involves physicians diagnosing all ischemic stroke (AIS) cases at the collaborating hospitals. BBJ was established in 2003 and recruited 267,000 patients from 12 medical institutions (66 hospitals) in two phases.^31–33 The recruited patients had at least one of the 51 primarily multifactorial (common) diseases, which accounted for 440,000 cases. We used BBJ 1^st cohort (BBJ1) data to derive PRSs and available independent BBJ 2^nd cohort (BBJ2) data to evaluate the performance of PRSs in predicting AIS and recurrent AIS. Recurrent AIS information was unavailable for the BBJ1 data. In BBJ2, any AIS cases (n=1,470), AIS-free controls (n=40,459), recurrent AIS cases (n=174), and non-recurrent AIS controls (n=1,153) were available. The mean duration from the first episode of AIS onset to recurrent AIS onset was 4.88 years. Detailed sample characteristics are listed in Supplementary Methods and Table 1.

Table 1.

Characteristic of the testing sample (BBJ2)

	Any-AIS versus AIS-free controls				Recurrent AIS versus non-recurrent AIS
	N sample (%, SD)	OR	95% CI	p-value	N sample (%, SD)	OR	95% CI	p-value
Total participants	41,929 (100%)	-	-	-	1,327 (100%)	-	-	-
AIS / AIS recurrent	1,470 (3.5%)	-	-	-	174 (13.1%)	-	-	-
Age (SD)*	70.0 (SD=12.6)	1.18	[1.06–1.31]	0.002	64.1 (SD=11.5)	0.83	[0.59–1.16]	0.256
Female sex	19,407 (46.3%)	0.48	[0.43–0.54]	<0.001	383 (28.9%)	0.63	[0.42–0.93]	0.019
Hypertension	17,710 (42.2%)	2.27	[2.04–2.53]	<0.001	838 (63.1%)	0.92	[0.66–1.3]	0.673
Hyperlipidemia	11,604 (27.7%)	2.17	[1.95–2.41]	<0.001	603 (45.4%)	0.92	[0.66–1.29]	0.625
Diabetes	3,622 (8.6%)	1.16	[0.97–1.39]	0.089	125 (9.4%)	0.97	[0.52–1.7]	1.000
Smoking**	21,570 (51.9%)	1.43	[1.28–1.59]	<0.001	795 (60.5%)	1.28	[0.90–1.82]	0.179
Vascular disease	3,136 (7.5%)	1.31	[1.08–1.56]	0.005	122 (9.2%)	1.08	[0.59–1.87]	0.778
Heart failure	1,329 (3.2%)	1.27	[0.95–1.66]	0.095	48 (3.6%)	1.79	[0.78–3.75]	0.124
Atrial fibrillation	1,004 (2.4%)	2.22	[1.71–2.84]	<0.001	65 (4.9%)	1.07	[0.46–2.23]	0.850

All risk factor characteristics were derived from history and not at the time of registration. Odds ratio (OR), 95% CI (95% confidence intervals, and p-values were calculated using logistic regression for onset and AIS recurrence (unadjusted for other factors).

^*Age at AIS case-control was that at recruitment, while age at recurrent AIS case-control was that at first incidence. The numbers indicate the median threshold age.

^**The total number of missing values of smoking was 389 for all case-control and 12 for recurrent AIS case-control samples.

Abbreviations: BBJ2, BioBank 2^nd cohort; AIS, all ischemic stroke; SD = standard deviation

This study was approved by the ethics committee of the Institute of Medical Science, the University of Tokyo, Japan. Quality control, pre-phasing, and genotype imputation were conducted using PLINK(v2.0),^34–37 Eagle (v2.4.1), and Minimac4 (v1.0.2), respectively. The detailed processes are presented in the Supplementary Methods.

Constructing PRSs for AIS

Unbiased PRSs were obtained by applying a 10-fold cross-validation to select the model and optimize the parameters.^26,38 Briefly, BBJ1 samples were randomly split into ten equal-sized subsamples. We retained one subsample for validation and the others for training. We repeated this process 10 times, with each of the ten subsamples used exactly once for validation. A GWAS was conducted on the training set in each iteration, adjusted for age, sex, and the first 10 principal components (PCs) via Firth logistic regression using PLINK (v.2.0).³⁴

We obtained the weights of variants for PRS from the GWAS summary statistics of the training set using five PRS methods—P+T (PLINK (v.1.9)³⁵ for clumping), LDpred2,³⁹ Lassosum2,⁴⁰ (LDpred2 and Lassosum2 by bigsnpr package (v.1.7.2) in R (v.3.5.0)), PRS-CS (v.1.0.0),⁴¹ and PRS-CSx (v.1.0.0).⁴² The PRS-CSx integrated BBJ1 with the European stroke GWAS summary statistics (MEGASTROKE; the largest study available at this study design)⁴³ by learning an optimal linear combination. We used combinations of parameters for P+T (1,224 parameters), LDpred2 (126 parameters), Lassosum2 (200 parameters), PRS-CS (9 parameters), and PRS-CSx (9 parameters), as described in the Supplementary Methods. Subsequently, the PRSs for the validation sample were calculated using the weights obtained from the training samples. The accuracy for predicting AIS cases was evaluated from Nagelkerke’s R² (simply “R²” from this point onwards)^29,44 after adjusting for age, sex, and the first 10 PCs. We calculated the mean R² over 10 cross-validation results for each method with each parameter after a 10-fold cross-validation. We chose the method and parameters that maximized incremental R² (PRS_AIS) among these PRSs.

We further integrated the PRS_AIS with PRSs of vascular risk factors, such as stroke subtypes and comorbid diseases presence, using the elastic net framework to construct a metaGRS using the glmnet package (v.4.1.3) in R (v.4.1.0). Nine binary traits and eight quantitative traits of vascular risk factors reported in a previous study¹⁴ are described in the Supplementary Methods. Binary traits were determined by conducting GWAS and attempting to obtain unbiased weights using cross-validations. The effect weights from the derivation sample every 17 traits were calculated using PRS-CS-auto since it did not require an independent validation sample set for parameter optimization and performed well for various traits.^{21,26,39,41,45} Subsequently, we used a validation sample to calculate the weight of AIS and the 17-trait PRSs to predict AIS using elastic-net logistic regression. We conducted a 10-fold cross-validation and used the mean weight for testing.

We used PLINK (v2.0)³⁴ to calculate the individual PRS by aggregating the effect estimates multiplied by each imputed dosage into a single score per person.

Risk factors

The following seven risk factors that were previously utilized as covariates¹² were used as covariates for testing: hypertension (systolic blood pressure>140 mmHg, diastolic blood pressure>90 mmHg, or hypertension history), hyperlipidemia, diabetes (all types), smoking (current smoker), vascular disease (myocardial infarction, peripheral artery disease, stable angina pectoris, and unstable angina pectoris), congestive heart failure, and atrial fibrillation (including atrial flutter). A sample was considered to have a risk factor status if it had that status at enrollment or from historical records (Tables 1 and S1).

Assessment of the association of PRS with AIS and AIS recurrence

We used a single selected method with optimized parameters and calculated the metaGRS in independent testing sample sets. We used a logistic regression model to assess the association of the PRS using the two case-control settings for AIS (any-AIS versus AIS-free controls) and AIS recurrence (recurrent AIS versus non-recurrent AIS). We also applied two other combinations of case-controls: recurrent AIS versus AIS-free controls and non-recurrent AIS versus AIS-free controls (Figure 1). Furthermore, we examined additional PRS contributions of the seven risk factors to predictive accuracy and discriminative performance using the values of R² and area under the curve (AUC), according to our previous studies.^14,46

Additionally, we evaluated the performance of the following PRSs derived from other milestone studies for stroke prediction: 32 genome-wide significant variants (for any stroke, ischemic stroke, or ischemic stroke subtypes) from the MEGASTROKE cross-ancestry study of 524,354 individuals (PRS₃₂),⁴³ 89 genome-wide significant variants of 1,614,080 multi-population individuals (PRS₈₉), and 6,010,730 variants of the East Asian PRS developed from 9,809 individuals (iPGS_EAS),¹⁸ both from the GIGASTROKE study. The PRS calculation process is described in the Supplementary Methods.

Considering potential index event bias

An index event bias may be induced when the samples are only selected from cases.⁴⁷ We evaluated the extent to which the index event bias affected our results since we used case-only samples in this study. The association of PRSs with recurrent AIS was evaluated after adjusting for seven risk factors, in addition to age, sex, and the first 10 PCs. Adjusting for such confounding bias will not be enough to eliminate bias for a recurrence association study.⁴⁸ Therefore, we sought to mitigate a potential index event bias by applying three distinct methodologies.^48,49 First, we utilized linear and logistic regression models to assess the relationships between metaGRS and covariates within the any-AIS case (n=1,327) and AIS-free control groups (n=40,459). Initially, we did not adjust for age, sex, the seven risk factors, or the first 10 PCs. Subsequently, we observed the distributions of covariate values across the metaGRS quintiles. We performed statistical tests to detect heterogeneity in the estimates between the prevalent case and control groups, following the methodology of a prior study.^19,50 Second, we refined our analysis by adjusting for associations between metaGRS and AIS recurrence while considering the differential effects of covariates, according to a previous method.¹⁹ Finally, we applied the inverse probability weighted (IPW) approach⁴⁷ to comprehensively account for index event bias. Collectively, these analytical approaches were adopted to enhance the validity of our findings.

Association of metaGRS and AIS recurrence in patients with/without hypertension

Logistic regression was conducted in subgroups with and without hypertension and metaGRS tertiles among recurrent AIS cases (with hypertension n=107, without hypertension n=67) and non-recurrent AIS controls (with hypertension n=731, without hypertension n=422) to assess the relationship between the PRS and the risk of AIS recurrence. The low metaGRS tertile was set as the reference group and adjusted for age, sex, and the first 10 PCs.

Statistical analysis

The mean with standard deviation (SD) or proportion of factors was reported for the baseline characteristics of testing samples. The incremental value (R² or AUC) was estimated from the differences between patients with and without PRSs of the fitted values of age, sex, first 10 PCs, and seven risk factors^48,57,58 and calculated as the 95% confidence interval. The pROC package (v.1.18.0) in R was used to determine the discriminative ability of the AUC. The IPW package (v.1.2) in R was used for the IPW approach. R (v. 3.5.0) was used to perform logistic regression to calculate R², Pearson’s correlation coefficient, and linear regression. All statistical tests were two-sided. The significance level was set at p = 0.05.

Results

Derivation of effect weight

The imputed genotype data of 17,621 AIS cases and 162,317 controls without an AIS diagnosis were used for 9,622,629 autosomal variants after implementing quality control of the BBJ1 dataset (Tables S2–S4).

We conducted a 10-fold cross-validation to adjust the parameters and select the best PRS associated with AIS. We performed GWAS 10 times on 90% of the randomly selected BBJ1 dataset (training data). We successfully detected previously reported^43,51 signals in each dataset (p<5×10⁻⁸), including SH3PXD2A, CCDC63 (eight times), CUX2, and LINC02356 (every time) (Figure S1, Table S5).

We confirmed some expected characteristics of each PRS method (such as low accuracy) using only genome-wide significant variants (Tables S6–10 and Supplementary Notes). The mean incremental R² values of each scoring method with the best-performed parameters were 0.0038 (95% CI: 0.0030–0.0046), 0.00443 (95% CI: 0.0035–0.0054), 0.0039 (95% CI: 0.0030–0.0048), 0.00441 (95% CI: 0.0036–0.0053), and 0.0037 (95% CI: 0.0031–0.0042) for P+T, LDpred2, Lassosum2, PRS-CS, and PRS-CSx, respectively (Table 2). We chose LDpred2 with the parameter set of ^ρ-value = 0.0056, a heritability-value = 1.0×h²_LDSC, where h²_LDSC is the heritability estimate from the constrained LD score regression⁵², and a no-sparse model for subsequent analyses, since it showed the best mean incremental R² value among the five methods.

Table 2.

Polygenic risk score performance at validation

Method	Best parameters	Mean number of variants	Best mean incremental Nagelkerke R2	Standard deviation	95% confidence interval
P+T	Clumping R2=0.95, Clumping kb=526, Imputation R2=0.8, p-value threshold=1	3,144,737	0.0038	0.0012	0.0030–0.0046
LDpred2	p value=0.0056, heritability value × 1.0, no sparse	898,456	0.00443	0.0013	0.0035–0.0054
Lassosum2	S=0.9, lambda=0.00388	282,520	0.0039	0.0013	0.0030–0.0048
PRS-CS	Phi=1.00E-04	985,439	0.00441	0.0012	0.0036–0.0053
PRS-CSx	Phi=1.00E-05	1,016,745	0.0037	0.0008	0.0031–0.0042

We observed an average number of nonzero weights for 8.4 traits after computing the metaGRS via elastic net regularization 10 times (10-fold). The metaGRS weight of AIS was highest (mean=0.123, SD=0.026), followed by diastolic blood pressure (mean=0.039, SD=0.039), atrial fibrillation (mean=0.023, SD=0.024), and myocardial infarction (mean=0.018, SD=0.025) (Figure S2 and Table S11). Only the triglyceride weights were zero at all 10 measurements among the 18 traits included in the metaGRS calculation. The number of variants used for metaGRS was 1,014,026; a total of 1,011,847 variants (99.8%) remained after matching with the BBJ2 dataset.

Association of metaGRS with AIS cases and recurrent AIS

We used the imputed genotype data of 1,470 AIS cases and 40,459 controls without a diagnosis of AIS for 59,387,070 variants from the BBJ2 dataset to test the association of metaGRS with AIS and AIS recurrence. The AIS case-only sample of the BBJ2 was used to analyze AIS recurrence. Table 1 presents the characteristics of the test samples.

MetaGRS was associated with AIS diagnosis after adjusting for age, sex, first 10 PCs, and seven risk factors (adjusted OR, 1.21 [95% CI: 1.15–1.27, p=2.89×10⁻¹²]), as previously reported.^14,18 MetaGRS was also associated with AIS recurrence compared with recurrence-free AIS (adjusted OR 1.18 [95% CI: 1.00–1.39, p=0.044]; Table 3 and Figure S3). MetaGRS showed stronger association when comparing recurrent AIS with AIS-free controls (adjusted OR 1.37 [95% CI: 1.18–1.59, p=5.35×10⁻⁵]; Table S12).

Table 3.

Polygenic risk score performance at testing

PRS Method	Association tests	OR per SD [95% CI]	p-value	Incremental AUC	Incremental Nagelkerke R2
MetaGRS	AIS	1.21[1.15–1.27]	2.89E-12	0.0087	0.0044
	Recurrence	1.18[1.00–1.39]	0.044	0.0123	0.0057
MEGASTROKE 27 SNVs	AIS	1.11[1.06–1.17]	4.23E-05	0.0033	0.0015
	Recurrence	1.07[0.91–1.25]	0.41	0.0032	0.0009
GIGASTROKE 84 SNVs	AIS	1.08[1.03–1.14]	2.96E-03	0.0022	0.0008
	Recurrence	1.17[1.00–1.38]	0.054	0.0125	0.0052
GIGASTROKE iPGS	AIS	1.26[1.20–1.33]	1.24E-17	0.0130	0.0066
	Recurrence	1.08[0.91–1.27]	0.37	0.0044	0.0011

Polygenic risk score performance was evaluated using an independent testing set for AIS and recurrent AIS. We showed two main association tests; AIS (any-AIS cases vs. AIS-free controls) and AIS recurrence (recurrent AIS vs. non-recurrent AIS). Incremental AUC and R² are the differences in the values when fitting with/without PRS, along with age, sex, the first 10 PCs, and seven risk factors. Abbreviations: AIS, all ischemic strokes; OR, odds ratio; AUC, area under the curve; PC, principal components; PRS, polygenic risk score; SD = standard deviation

The contribution of the metaGRS and traditional risk factors showed an AIS prediction accuracy with an R² value of 0.06 and an AUC of 0.689 after constructing the baseline model using age, sex, the first 10 PCs, and seven risk factors. The incremental AUCs were 0.0087 and 0.0123 for AIS and AIS recurrence, respectively when metaGRS was added to the baseline model (Table 3). In our dataset, clinical risk factors (including hypertension) were related to AIS diagnosis but were insignificantly associated with AIS recurrence (Table S1). We assessed the prediction performance of previously developed PRSs for AIS and AIS recurrence in our dataset. After matching with the BBJ2 dataset (Supplementary Methods), 27, 84, and 5,756,652 variants remained in PRS₃₂, PRS₈₉, and iPGS, respectively. We confirmed their association with AIS diagnosis; adjusted ORs were 1.11 [95% CI: 1.06–1.17, p=4.23×10⁻⁵], 1.08 [95% CI: 1.03–1.14, p=2.96×10⁻³], and 1.26 [95% CI: 1.20–1.33, p=1.24×10⁻¹⁷] for PRS₃₂, PRS₈₉, and iPGS, respectively (Table 3, Figure S3); however, a significant association was not observed between PRSs and AIS recurrence (p-values of 0.41, 0.054, and 0.37, respectively; Table 3 and Figure S3). Our Japanese optimized metaGRS was the only PRS significantly associated with AIS recurrence in this study.

Analyzing for potential index event bias

We observed the values of covariates at the AIS-free control group and any-AIS case group in each quintile. We did not find any significant heterogeneous relationships between the covariates and the metaGRS in terms of regression estimates in the prevalent case and control samples (p>0.05, Table S13).

We used three different variable models—i) age and sex; ii) age, sex, and seven risk factors; and iii) age, sex, the first 10 PCs, and seven risk factors—to determine the association between metaGRS and recurrent AIS; none of these confounders significantly influenced our results (Figure S4).

We compared the association results of IPW adjusted (accounting for index event bias) with those of non-adjusted IPW (accounting for confounding bias). The results remained almost unchanged, but the 95% confidence intervals overlapped (Figure S5). A comparison of the three distinct models did not indicate an effect of index event bias.

Association of metaGRS and AIS recurrence in patients with/without hypertension

We divided the test sample into subgroups according to the presence or absence of a history of hypertension and evaluated the risk effect of the metaGRS tertile. The high metaGRS group without a history of hypertension showed a higher risk effect for AIS recurrence compared to the low metaGRS group (OR of the high metaGRS group compared to that of the low metaGRS group was 2.24 [95% CI: 1.07–4.66, p=0.032], Figure 2 and Table S14). However, no significant association was observed between the metaGRS and AIS recurrence in the group with a history of hypertension (the OR of the high metaGRS group compared to that of the low metaGRS group was 1.21 [95% CI: 0.69–2.13, p=0.50] (Figure 2 and Table S14).

Figure 2. Odds ratio of metaGRS tertiles with/without a history of hypertension.

Association of AIS recurrence and meta-GRS tertiles with or without a history of hypertension (HT) in the testing sample, with reference to the low metaGRS tertiles.

Discussion

We successfully examined the association between recurrent AIS and our best model PRS (metaGRS using LDpred2); the adjusted OR was 1.18 for each unit of SD increase in PRS. Our metaGRS showed stronger (adjusted OR per SD=1.37) association when comparing recurrent AIS with AIS-free controls. Furthermore, a high PRS was associated with AIS recurrence particularly in groups without a history of hypertension (OR of the top vs. bottom metaGRS tertile=2.24). These results are consistent with the result of a previous study wherein the stroke prediction accuracy of the PRS was high in the group with low CHA2DS2-VASc scores.¹² These results indicate the utility of the PRS in developing more precise strategies to prevent AIS recurrence in individuals with a high PRS who do not have high profiles based on clinical risk factors.

We attempted to mitigate potential index event bias since our purpose was to specifically determine the efficacy of PRS among AIS patients. It is difficult to predict and provide an accurate assessment of recurrent AIS based on genetic predisposition owing to the possible effect of index event bias leading to a distorted association in studies on recurrent stroke.^19,20,53 This study found no evidence of heterogeneous associations between covariates and the metaGRS; we did not find any evidence of a solid collider bias of known variables. By applying IPW, we confirmed that our results support the association between metaGRS and recurrent AIS.

There are three putative reasons our metaGRS could predict AIS recurrence. First, the metaGRS algorithm combines the genetic profiles of related traits and slightly improves the performance, reaching the level of significance. Second, the performances of PRS-CS (incremental R²=0.00441) and LDpred2 (incremental R²=0.00443) in our validation analysis were better than those of other traditional PRS methods, such as P+T (incremental R²=0.0038). This demonstrated the importance of using shrinkage estimation methods that consider LD to predict AIS and AIS recurrence. Third, we restricted to use only single matched ancestry throughout.

Nevertheless, our study had several limitations. First, the sample size for recurrent AIS needs to be increased (n=174 at testing), even in the largest hospital-based biobank in Japan. Compared to our metaGRS, iPGS constructed in GIGASTROKE showed a stronger association for AIS and weaker association for AIS recurrence. Although potential discrepancies exist, both PRSs (metaGRS and iPGS) exhibit the same direction of effects and have overlapping confidence intervals (Table 3, Figure S3). Second, despite using as many covariates (age, sex, the first 10 PCs, and seven risk factors (hypertension, hyperlipidemia, diabetes mellitus, smoking, vascular disease, congestive heart failure, and atrial fibrillation)) as possible based on a previous study,¹² other confounders might have affected our results. Finally, there may have been an index event bias that was not fully detected by each method that we implemented; however this risk was minimized using multiple approaches. Further studies using different sample sets (including other ancestry groups) are warranted to confirm the prediction of recurrent stroke using the PRS.

In conclusion, our study indicated that PRS can be applied to predict AIS recurrence in addition to traditional clinical risk factors. This shows the potential utility of PRS in population-based screening and in the clinical setting. Overall, our results indicate that stratifying high-risk groups for recurrent stroke among those who have experienced a stroke could be medically beneficial and help in developing personalized strategies for recurrence prevention. Our results suggest that it might be particularly useful in patients with AIS without hypertension, although this requires confirmation in independent datasets.

Non-standard abbreviations and acronyms

PRS

polygenic risk score

P+T

pruning and thresholding

BBJ

BioBank Japan

BBJ1

BBJ 1^st cohort

BBJ2

BBJ 2^nd cohort

ToMMo

Tohoku Medical Megabank

AIS

all ischemic stroke

IPW

inverse probability weighting

LD

linkage disequilibrium

GWAS

genome-wide association study

PC

principal component

IPW

inverse probability weight

AUC

area under the curve

LAS

large artery stroke

SVS

small vessel stroke

CES

cardioembolic stroke

TIS

transient ischemic attack

HWE

Hardy-Weinberg equilibrium

WGS

whole genome sequencing

MI

myocardial infarction

SAP

stable angina pectoris

AP

unstable angina pectoris

AF

atrial fibrillation

DM

diabetes mellitus

SM

smoking

BMI

body mass index

HE

height

SBP

systolic blood pressure

DBP

diastolic blood pressure

TC

total cholesterol

TG

triglyceride

HDL

high-density lipoprotein

LDL

low-density lipoprotein

Data availability

The weights of metaGRS derived in this study will be publicly available after acceptance. Genotype datasets were deposited in the National Bioscience Database Center Human Database (BBJ1, Research ID: hum0014; BBJ2, Research ID: hum0311).