Hypoxia Regulated Gene Network in Glioblastoma Has Special Algebraic Topology Structures and Revealed Communications Involving Warburg Effect and Immune Regulation

Abstract

Hypoxia regulated genes (HRGs) formed a complex molecular interaction network (MINW), contributing to many aspects of glioblastoma (GBM) tumor biology. However, little is known about the intrinsic structures of the HRGs–MINW, mainly due to a lack of analysis tools to decipher MINWs. By introducing general hyper-geometric distribution, we obtained a statistically reliable gene set of HRGs (SR-HRGs) from several datasets. Next, MINWs were reconstructed from several independent GBM expression datasets. Algebraic topological analysis was performed to quantitatively analyze the amount of equivalence classes of cycles in various dimensions by calculating the Betti numbers. Persistent homology analysis of a filtration of growing networks was further performed to examine robust topological structures in the network by investigating the Betti curves, life length of the cycles. Random networks with the same number of node and edge and degree distribution were produced as controls. As a result, GBM–HRGs–MINWs reconstructed from different datasets exhibited great consistent Betti curves to each other, which were significantly different from that of random networks. Furthermore, HRGs–MINWs reconstructed from normal brain expression datasets exhibited topological structures significantly different from that of GBM–HRGs–MINWs. Analysis of cycles in GBM–HRGs–MINWs revealed genes that had clinical implications, and key parts of the cycles were also identified in reconstructed protein–protein interaction networks. In addition, the cycles are composed by genes involved in the Warburg effect, immune regulation, and angiogenesis. In summary, GBM–HRGs–MINWs contained abundant molecular interacting cycles in different dimensions, which are composed by genes involved in multiple programs essential for the tumorigenesis of GBM, revealing novel interaction diagrams in GBM and providing novel potential therapeutic targets.

Electronic supplementary material

The online version of this article (10.1007/s10571-019-00704-5) contains supplementary material, which is available to authorized users.

Introduction

Glioblastoma (GBM), the most lethal primary malignant brain tumor in adult, still lacks ideal treatment, and patients with GBM only have a median survival of about 14.6 months after combined treatment including surgery resection and adjuvant chemo- and radiotherapies (Stupp et al. 2005). A lot of potential molecule targets have been proposed, while effective treatment strategies are not available. The recently approved anti-VEGF mono-antibody bevacizumab has limited effect which would result in drug resistance and ultimately recurrence of the tumor (Mahase et al. 2017; Michaelsen et al. 2018; Tamura et al. 2017). Therefore, efforts were made to find more promising therapeutic targets. However, given the fact that cancers including GBM are diseases driven by multiple genetic and epigenetic alterations, single or few molecule targets may not be sufficient to cure this kind of tumor (Brennan et al. 2013; TCGA 2008). Based on this assumption, and along with the progress in high-throughput data acquisition technologies, it is reasonable that a cohort of genes, and more precisely, a molecular interacting network may fundamentally drive the disease (Chen et al. 2014; Plaisier et al. 2016). For example, the existence of drug resistance when targeting certain key genes implied a hidden unknown molecular network with ingenious organizational structures developed by the tumor (Piao et al. 2013; Rizzolio et al. 2018; Tamura et al. 2017; Urup et al. 2017), which have great adaptability to compensate the missing of certain key genes. Therefore, great efforts have been made to reconstruct the molecular interaction network (MINW) for cancers (Carro et al. 2010; Kim et al. 2010; Kleaveland et al. 2018; Li and Izpisua Belmonte 2018; Nakagawa et al. 2018; Shi et al. 2018). The reconstruction and investigation of the structure and function of the MINW not only revealed the intrinsic nature of the tumor biology, but also provide potential therapeutic avenues to change or even reverse the global biological features of the tumorigenic potential of the cancer. A lot of experimental and theoretical approaches have been developed to reconstruct the network (Markmiller et al. 2018; Shi et al. 2018), and some achieved excellent results (Wang et al. 2009). As has been reported previously, hypoxia is a critical factor promoting the tumorigenesis of GBM (Li et al. 2009; Man et al. 2018; Wang et al. 2018), and is involved in many biological processes, including tumorigenic potential, cancer stem cell (CSC) maintenance (Li et al. 2009), invasion (Du et al. 2008; Joseph et al. 2015), angiogenesis or vascular mimicry (Joseph et al. 2015; Mao et al. 2013c), and anti-VEGF therapy resistance (Mahase et al. 2017; Mao et al. 2016; Tamura et al. 2017; Xu et al. 2015), et al.

However, little is known about the global characteristics of the MINW, especially in the high dimensional space containing thousands of genes, given that each gene represents a dimension. Obviously, the MINW is a network defined by the relationships between each gene, and is metric independent. As has been described and developed in mathematics, topology studied the integral features of the geometric space without consideration of the measures such as length and angle quantity (Giusti et al. 2015, 2016; Sizemore et al. 2018). To more rigorously describe the characteristics of different geometric objects, especially the more complicated cases such as molecular networks, algebraic topology was established and homology group analysis was used to quantitatively describe different topological objects (Adams et al. 2014; Giusti et al. 2016; Sizemore et al. 2018). Although traditional graph analysis provides certain information, little, if any, is reported to deeply decipher the integral structures of MINW quantitatively, especially the loop structures, by algebraic topology analysis. In this study, we reconstructed the MINW of hypoxia regulated genes (HRGs) in GBM, and analyzed its algebraic topology features by calculating the number of simplexes, Betti numbers, and Betti curves by persistent homology (PH) analysis. Our results first implied that GBM–HRGs–MIWN had special robust intrinsic topological structures, which are statistically different from that of random networks, and importantly, different from that of normal brains.

Materials and Methods

Identification of Hypoxia Regulated Genes (HRGs)

To get a reliable HRGs set, we searched and screened high-throughput datasets of hypoxia regulated genes in GBM from Pubmed Dataset website by searching the item “(glioblastoma or glioma) and (hypoxia or oxygen)”. At last, HRGs were identified from 5 cell results, including two U87 cells data [GSE32100 (Nissou et al. 2013) and GSE45301 (Kucharzewska et al. 2013)], one GSC cell data [GSE32100 (Nissou et al. 2013)], one serum cultured GSC cell data [GSE32100 (Nissou et al. 2013)], and one LN229 cell line data [GSE27523 (Koh et al. 2011)]. The genes which are statistically significantly up-regulated or down-regulated (p < 0.05) are chosen as candidate HRGs in GBM. Given the relatively great variation of high-throughput data, we selected overlapped genes in the 5 datasets to get most reliable HRGs by taking advantages of the general hyper-geometric distribution (GHG) (Mao and Xue 2018). The GHG was used because if we use the genes overlapped in at least 5 or 4 datasets, then we only get a few genes and would lose too many HRGs, while if we use genes overlapped in too few sets then the result HRGs would contain too many false positive genes. By using the formulas of mathematical expectations and variances of the GHG (Mao and Xue 2018), the 95% confidential interval (CI) of the GHG can be estimated with Chebyshev’s inequality, which give an upper bound of number of randomly overlapped genes (random_Up_NOGs). Then the number of statistically significant overlapped genes (sig_NOGs) can be deduced by sig_NOGs = observed_NOGs − random_Up_NOGs (Mao and Xue 2018). Then total number of sig_NOGs genes ranked by change folds will be taken as statistically reliable HRGs (SR-HRGs).

Reconstruction of MINW with ARACNe Based on Information Theory

To reconstruct a MINW, the first step is to get the interactome of each gene in the HRGs. We also used several datasets (Mao et al. 2013a, b, 2016) to reconstruct the HRGs–MINW (GBM–HRGs–MINWs), by using Algorithm for the Reconstruction of Accurate Cellular Networks (ARACNe), an information-theoretic algorithm for inferring transcriptional interactions (Margolin et al. 2006a), to identify a repertoire of candidate transcriptional regulators of interesting genes. First, candidate interactions between a transcription factor (TF, x) and its potential target (y) are identified by computing pairwise mutual information, MI[x; y], using a Gaussian kernel estimator and by thresholding the mutual information based on the null hypothesis of statistical independence (p < 0.05, Bonferroni corrected for the number of tested pairs). Here mutual information (MI) is a concept in information theory which measures the degree of statistical dependency between two variables (Margolin et al. 2006a; Shi et al. 2018), like the commonly used Pearson correlation. However, correlation coefficients are not feasible to deal with nonlinear associations, and may be zero even for manifestly dependent variables. MI is reparameterization invariant and is nonzero if and only if any kind of statistical dependence exists (Margolin et al. 2006a). Then, indirect interactions are removed using the data processing inequality (DPI), a well-known property of the mutual information. The DPI states that if genes g1 and g3 interact only through a third gene g2, then MI(g1, g3) ≤ min [MI(g1, g2); MI(g2, g3)] (Cover and Thomas 1991; Margolin et al. 2006a). To remove potential indirect interactions, during DPI process, in each gene triplet for which all three MIs are greater than the MI threshold, the edge with the smallest value would be removed. Therefore, the networks identified with DPI (DPI-MINWs) do not contain simplexes with a dimension higher than 1, because the DPI process removed potential 2-simplexes. The DPI-MINWs contained more reliable direct interactions and was used to analyze 1-cycles, while the NoDPI-MINWs were used to find higher-dimensional cycles of the networks.

Calculation of Homology Group and Betti Numbers

Here a simplicial complex K was made up of vertices and simplexes (Giusti et al. 2016). A p-dimensional simplex (p-simplex) is defined in terms of collections of (p + 1) full connected vertices. For example, a point is a 0-dimensional simplex, an object of two points with a connection in a network is a 1-dimensional simplex, and an object of three points which are connected to each other is a 2-dimensional simplex, et al. It should be noted that a p-simplex is not simply the collection of its verities and edges, it is actually a p-dimension object, and therefore the edges are actually its “sub-simplex”, which is called a “face” of the simplex. Actually, any subset of the vertices of one simplex is a face of the simplex. For all p-simplexes, assign a value (or an element) in a group for each of the p-simplex (coefficient group; here group is a conception in algebra, which is defined as follows. A group is an algebraic structure consisting of a set of elements equipped with a binary operation which combines any two elements to form a third element. To be a group, this operation must satisfy four conditions called the group axioms, namely closure, associativity, identity and invertibility). An operation for the p-simplex was defined as the same operation of its corresponding element in the group. Therefore, a finite number of p-simplex with the above defined operation formed a chain with p-dimension (p-chain). For example, for a set of p-simplexes, s₁, s₂, …, s_l, each s_i can be represented by its vertices: ${\sigma }_k=\sigma \left[v_{i_1},v_{i_2},\dots ,v_{i_p}\right]$, and the p-chain is:

$$C_p\left(K\right)=\sum _{i=0}^l\sigma \left[v_{i_1},v_{i_2}\dots v_{i_p}\right]$$

Therefore, each p-chain has a value belonging to the group. All of the p-chains with the above defined operation forms a group $C_p\left(K\right).$

The simplex can be oriented according to the order of the vertices. Next define the boundary map for each simplex $C_p\left(K\right)\to C_{p-1}\left(K\right)$ ($\widehat{v_{i_j}}$ indicates omission of the vertex $v_{i_j}$):

$$\partial \sigma \left[v_{i_1},v_{i_2},\dots ,v_{i_k}\right]=\sum _{j=0}^k{\left(-1\right)}^j\sigma \left[v_{i_1},v_{i_2}\dots \widehat{v_{i_j}}\dots v_{i_k}\right]$$

It is clear that the boundary map $\partial$ transforma a p-simplex to a series of (p −1)-simplexes, and the result (p − 1)-simplexes, which form a (p −1)-chian, are denoted as a boundary for the p-simplex. For a given p, the image from a upper dimension ${\partial }_{p+1}\left(C_{p+1}\left(K\right)\right)$ ($\text{im}{\partial }_{p+1},$ that is boundaries of the p + 1 chains) is a subgroup of the $C_p\left(K\right),$, and the kernal of the ${\partial }_p\left(C_p\left(K\right)\right)$ ($ker{\partial }_p,$ closed chains in the $C_p(K)$, which are termed as cycles) is also a subgroup of $C_p\left(K\right).$ Here a p-dimensional cycle (p-cycle) is a “closed p-chain”, that is, all the p-simplexes constituting the p-cycle have a 0 value in the above defined operation. In addition, considering that ${\partial }_{p+1}{\partial }_p=0$, any boundary from an upper dimension is a cycle, and therefore the $\text{im}{\partial }_{p+1}$ is a subgroup of $ker{\partial }_p$. Based on these definitions, the homology group for dimension q H_q(K) is defined as the quotient group:

$$H_p\left(K\right)=ker{\partial }_p/\text{im}{\partial }_{p+1}$$

Behind the highly abstract definition process of the homology group, the $H_p\left(K\right)$ have special geometric meanings. For finite simplicial complexes, which is the main topic for gene networks, the $H_p\left(K\right)$ is a finitely generated Abel group, and the rank of the group is called Betti number Betti_q. Intuitively, betti₀ indicates the number of connected graphs, betti₁ indicates the number of 1-dimensional cycles, while betti₂ indicates the number of 2-dimensional cycles (geometrical structures similar to the surface of a ball, but not containing the inside). In the present study, the Z/Z2 group (a 2-order cyclic group; here Z is an abelian group consisted of all integers in the operation addition “ + ”; Z2 is the group consisted of all even integers; Z/Z2 is the quotient group of Z and Z2, which is a 2-order cyclic group containing two elements) was used as the coefficients group. Calculation of Betti numbers were performed by using the JPlex program (Adams et al. 2014).

Persistence Homology Analysis of the MINWs

Given the great fluctuations of biological data, especially high-throughput data, the MINWs reconstrued with the static data would not reflect their intrinsic structures. Therefore, persistent homology (PH) analysis was introduced to examine the stable intrinsic algebraic topological structures (Giusti et al. 2015; Sizemore et al. 2018). PH was performed on a series of simplicial complex, which is called a filtration. A filtration is formed by a growing simplicial complex, that is, simplexes are gradually added to the complex, and therefore cycles are formed and diminished. During the process, a filtration value was assigned for each step, and the length between the values of appear and disappear of a cycle was defined as the life for that cycle. For example, as shown in Fig. S1, the filtration started in value 1 and ended in value 5. At value 1, there are five 0-simplexes (points) [1], [2], [3], [4], [5] and four 1-simplexes [1,2], [2,3], [4,5], [1,5]. At value 2, one more 1-simplex [3,4] was added into the complex and thus a 1-cycle (cycle 1) was formed, hence the life of the 1-cycle started at value 2. At value 3, two more 0-simplexes [6], [7] and three more 1-simplex [2,6], [3,7], [6,7] were added and another 1-cycle (cycle 2) was formed whose life started as value 3. At value 4, a 2-simplex δ1 [3,6,7] was added, and the two 1-cycles were persisted. At value 5, another 2-simplex δ2 [2,3,6] was added and thus cycle 2 was disappeared whose life ended at value 5, while cycle 1 still persisted. Therefore, there are totally two 1-cycles, and the life length of cycle 1 was infinite − 2 (here infinite indicates the cycle persists longer than the observed filtration values), while that of cycle 2 was 5 − 3 = 2.

In the present MINW, for PH analysis, at value 0, all of the 0-simplex were added to the MINW complex. Then the mutual information MI[x; y] for each paired genes were ranked in descending order, and the edges formed by these two genes [x,y] were added gradually to the complex according to their order. For each step, the value of rank order for the edge was assigned as filtration value. Therefore, any high-order simplexes (interconnected nodes) formed due to the addition of the edge were also added into the complex in this step. When all of the edges in the above reconstructed MINW were added, a filtration formed and PH analysis was performed by using the JPlex program (Adams et al. 2014).

Construction of Random Networks

To get topological features of random networks (Random-MINWs), networks with the defined nodes and edges were constructed. For PH analysis, the filtration began at value 0 with all of the nodes in the complex, and edges were randomly added to the simplicial complex (SC). One edge was added in each step, until the total number of edges reached to the defined amount. For DPI-networks which did not contain 2 or greater-dimension simplexes, edges were randomly added only when it did not form 2 or greater-dimension simplexes with other edges. When the number of edges reached to the defined amount, a random filtration with defined nodes and edges was produced. Then the above algebraic topological and PH analysis were performed to get betti number in each dimension. To get the distribution properties of the topological features of Random-MINWs, 1000 filtrations were produced, and the betti number, life lengths, et al. were calculated with the above process, and the statistical distribution of these parameters were established. In our practice, only 100 or fewer random filtrations would produce quite consistent distribution curves of the Betti numbers, life lengths, et al.

To produce Random-MINWs with same degree distribution (DD) (RandomSameDD–MINWs) of the GBM–HRGs–MINWs, during the Random-MINWs production, a random edge was evaluated before adding to the network. Only the edge meeting the following criteria would be added to the network: the network with the added edge have a DD that is not larger than that of the GBM–HRGs–MINWs. The definition of comparison between two DDs (for example DD1 and DD2) are defined as follows: the two networks should have same number of nodes (N_node), let the degrees for all nodes are D_nodes (here D_nodes is a integer array with N_node elements; let the two D_nodes are D1_nodes and D2_nodes), sort the both D_node descending, if each value in D1_node is not larger than the corresponding value in D2_node then DD1 is not larger than DD2. For example, let D1_nodes = {5,4,4,3,1,1}, D2_nodes = {4,3,4,3,1,1}, D3_nodes = {5,5,3,3,1,1}, then DD1 is not larger then DD2, while DD2 and DD3 can not be compared. Because each GBM–HRGs–MINWs reconstructed from the 5 GBM datasets has its own DD, corresponding RandomSameDD–MINWs were produced. Totally 100 RandomSameDD–MINWs for each DD were produced for statistical analysis.

Ranking Values of the Cycles

First, all of the cycles during PH analysis were listed. Then, the degree of each node (gene; here degree indicate the number of edges containing the node) in the MINW were calculated, which is denoted as degree of the gene’s (D_gene). The number of q-cycles containing the node was defined as number of q-cycles involved a gene (q-NC_gene), and the q-NC_gene for each gene was calculated by examining all of the q-cycles during PH analysis. Next, a rank value for a q-cycle representing its importance was defined as the average value of all q-NC_gene for each gene in the q-cycle. Then the cycles can be ordered by their rank values and cycles in the top rank represent relatively more important ones for the network.

Culture of Primary GSCs and NSCs

Isolation and culture of cells, including GSCs, NSCs, U87, and U251 cells, were performed as described in our previous papers (Mao et al. 2009a, Mao et al. 2010, 2011, 2013a, b). Briefly, for primary GSC culturing, GBM samples were dissociated to a single cell suspension using a fire-polished Pasteur pipette and cultured in serum-free medium (SFM) consisting of DMEM-F12 medium, EGF (20 ng/mL; Invitrogen, Carlsbad, CA), bFGF (20 ng/mL; Invitrogen, Carlsbad, CA) and B27 (1:50; Invitrogen, Carlsbad, CA). Human glioblastoma U251MG and U87MG cells (U87 and U251) were purchased from GENECHEM Company (Shanghai, China) and cultured in DMEM medium supplemented with 10% newborn calf serum (GIBCO BRL, Invitrogen). U87 and U251 cell lines were authenticated with short tandem repeat in 2018. Two human fetal cortical NSCs were isolated from spontaneous aborted fetuses (8–12 weeks), which were dissociated into single cells as described above and then cultured in SFM. Primary human astrocytes (Life Technologies, Carlsbad, CA, USA; lot number 802268) were cultured in DMEM medium supplemented with 10% newborn calf serum, 1% N-2 Supplement (Life Technologies), and EEF (20 ng/mL). The study protocol was approved by the institutional review board of Xijing Hospital of the Fourth Military Medical University, and written informed consent was obtained from patients.

qPCR

RNA was extracted from cultured cells and brain tumor tissues using Trizol Reagent (Invitrogen). The extracted RNA was then reverse transcribed into cDNA using Superscript II RT (Gibco-BRL, Gaithersburg, Maryland) and a mixture of oligo dT primers and random hexamers, according to the manufacturers’ instructions. qPCR analysis was performed on an ABI7700 using SYBR Green PCR Core Reagents in 20 μL volume (Applied Biosystems, Warrington, UK). qPCR using water instead of template was used as negative controls. All samples were assayed in triplicate and the relative amount of target transcripts normalized to the number of human β-actin transcripts found in the same sample. Specificity was verified by melting curve analysis and agarose gel electrophoresis. Relative fold changes were calculated using the ΔΔC_t method by using the threshold cycle values of each sample.

Results

Definition of Statistically Reliable Hypoxia Regulated Genes (SR-HRGs)

To reconstruct the HRGs–MINW, the first step is to identify a gene set of SR-HRGs. We screened the up-regulated and down-regulated HRGs (Up-HRGs and Down-HRGs) under hypoxia conditions, by using five cell datasets. The genes which are statistically up-regulated or down-regulated (p < 0.05) are chosen as candidate HRGs in GBM. Next, we used the general hyper-geometric distribution (GHG) (Mao and Xue 2018) to get genes that are overlapped in the five lists of HRGs with statistically significance as the bona fide SR-HRGs. The GHG distribution is used because we are going to find a set of genes, where “all of the genes” rather than “existence of genes” are HRGs with statistical significance (Mao and Xue 2018). Therefore, to quantitatively determine how reliability of these genes can be used as SR-HRGs, we should examine the statistical distribution of the “number of genes overlapped in at least t times” (N_OL≥t, and the corresponding genes were denoted as G_OL≥t, here 1 < t ≤ 5). By taking advantage of the GHG, the 95% confidential interval (CI) of N_OL≥t are calculated, and the HRG set with statistical significance can be deduced (Mao and Xue 2018) (Fig. 1, Table 1, and Supplementary Table S1).

Fig. 1.

Procedures of obtaining reliable HRGs and reconstruction of the HRG-MINWs. Hypoxia regulated genes were identified from five datasets, resulting in five HRG lists. The significance of genes overlapped in these five lists (G_OL≥t, 5 ≥ t ≥ 1) were examined with GHG distribution, and at last G_OL≥3 excluding the potential random ones were chosen as reliable HRGs, which were used to reconstruct the MINW with or without DPI

Table 1.

Statistical analysis of the overlapped Up-SR-HRGs derived from the five datasets according to the GHG distribution

Random variable	Mean	Variance	95% CIa	Observed values	N of observed values with significance	% (observed values with significance)
N OL≥5	0.00212	0.0022	[0, 0.2]	42	42	100%
N OL≥4	0.29	0.29	[0, 2.7]	108	106	98.15%
N OL≥3	15.15	14.71	[0, 32.3]	276	244	88.41%
N OL≥2	361.74	254.04	[290.4, 433.0]	780	347	44.49%
N OL≥1	4162.80	286.46	[4087.1, 4238.5]	3334	–	–

^aThe 95% CI was estimated by using the Chebyshev’s inequality

As a result, we got 1424, 545, 986, 1205, 380 genes that are significantly up-regulated in the five datasets respectively, and there are 42, 108, 276 genes that are overlapped at least 5, 4, and 3 times (N_OL≥5=42, N_OL≥4 = 108, N_OL≥3 = 276). According to the GHG analysis, all of the G_OL≥5 are statistically significant, while for the G_OL≥4 and G_OL≥3, there are at most 2 and 32 false positive genes that may be caused by random, respectively. At last, we used the G_OL≥3 as the SR-HRGs by excluding bottom 32 genes ranked by their change folds, resulting in 244 (= 276 − 32) Up-SR-HRGs (Table 1). Similarly, 208 Down-HRGs were identified with the same procedure (Supplementary Table S1). We would focus on the Up-SR-HRGs, which would be simplified as HRGs thereafter, if not confused.

Reconstruction of Hypoxia Regulated Gene Networks

Next, the 244 HRGs were used to reconstruct the HRGs–MINWs. To reconstruct a network, we used the mutual information (MI) based dependency to define the relationships between paired genes. By using the MI based ARACNe algorithm (Margolin et al. 2006a), the HRGs–MINWs were reconstructed from five different GBM sample expression datasets (GBM–HRGs–MINWs): a unified GBM data from TCGA (Verhaak et al. 2010), a validation GBM data from Verhaak et al. (2010), the GBM data from Rembrendt (GSE68848) (Madhavan et al. 2009), a GBM dataset from Lee et al. (2008) (GSE13041), and a GBM data from Gravendeel et al. (2009) (GSE16011), which contained 197, 260, 228, 191, and 159 samples, respectively. A threshold of 10⁻⁸ was used to obtain candidate genes that interacted with each gene in the 244 HRGs with or without a DPI process to remove potential indirectly interacting genes. It should be noted that there is still no ideal approach to reconstruct the MINW exactly, either by experimental or theoretical approaches, and any reconstructed network is an approximation of the realistic one with certain deviation. In recent years, information-theoretic approaches were more and more widely recognized as powerfully tools to reconstruct the MINW (Shi et al. 2018). There has been several MI based approaches to reconstruct a MINW based on gene chip data, and some achieved excellent results with recall comparable to that of high-throughput assays from protein–protein interactions (Basso et al. 2005; Margolin et al. 2006a, b, Shi et al. 2018; Wang et al. 2009).

Algebraic Topology Features of the Reconstructed GBM–HRGs–MINWs

For each reconstructed network, denote the number of nodes as N_node and the number of edges as N_edge. To analyze the algebraic topological features of the HRGs–MINWs, we first introduced the concept of algebraic topology (Giusti et al. 2016; Sizemore et al. 2018). Traditional graph theory normally deals with partial or local parameters of the network structure, such as degree of vertices, simplex distribution, maximal simplex distribution, efficiency, and path length, et al. Unlike the graph theory approach, algebraic topology further seeks the intrinsic property of the global structure of the graph quantitatively (Curto 2016; Giusti et al. 2016). The most important and commonly used measurement is the homology group $H_q\left(K\right)$ (here q is the dimension of simplex) of the simplicial complex, for which the Betti numbers is the most important feature of the group (detailed information about the definition of homology group and Betti numbers is provided in methods). Simplified, the homology group quantitatively describes the integral structure of a geometric object, and the Betti numbers specifying the amount of “holes” or “cycles” in each dimension. Intuitively, the betti₁ represents the number of 1-dimensional cycles in a graph, while betti₂ represents the number of 2-dimensional cycle (similar to a hollow spherical structure). Similarly, for q > 2, the Betti_q reflects the number of high-dimension holes. It should be noted that Betti numbers represent the amount of equiveillance classes of cycles, implying that for a same “hole”, there would be more than one “cycles” surrounding it. For a class of k-cycles surrounding a same (k + 1)-dim hole, they are equivalent but differ from one to another by the boundaries of some (k + 1)-cliques.

For algebraic topological analysis, a network is considered as a simplicial complex, that is, a set of (q + 1) fully connected nodes (each pair in the (q + 1) nodes are connected) is considered as a q-simplex. By using a Z/Z2 group as coefficients group, we calculated the Betti numbers of the network with the JPlex algorithm (Adams et al. 2014; Lockwood and Krishnamoorthy 2015). By mapping the q-simplex to the coefficients group, finite number of q-simplexes formed a chain (q-chain) with the operation in the coefficients group. Closed chains are called cycles (q-cycle, see detail for the definition of chains and cycles in methods).

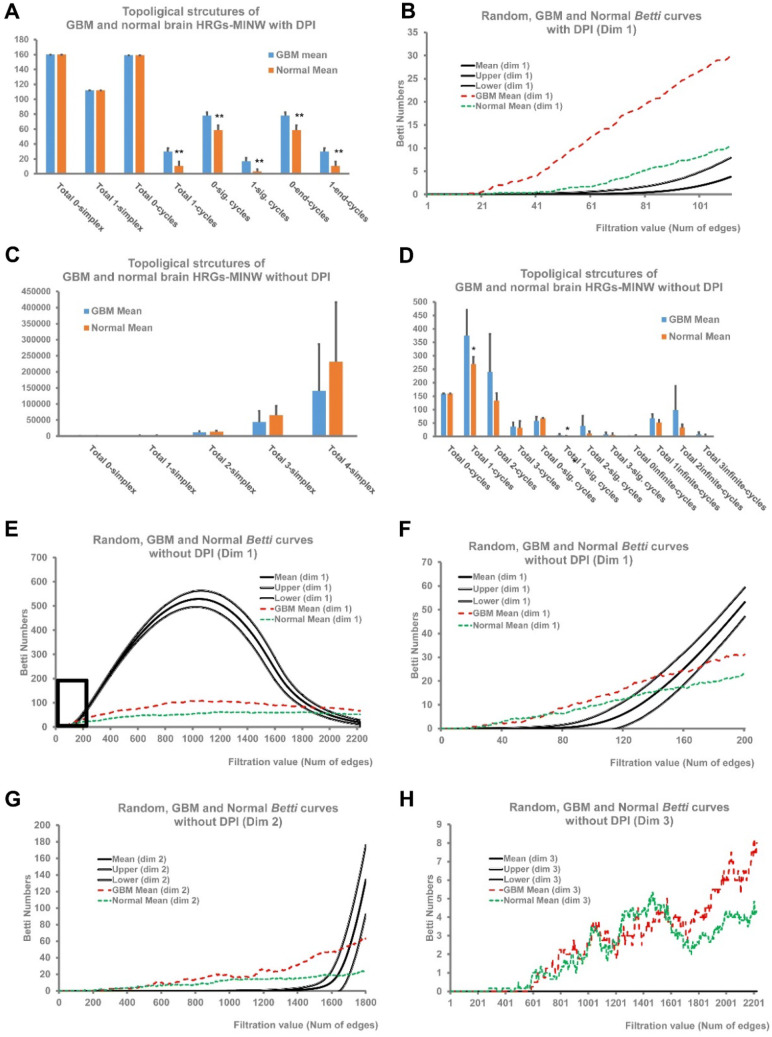
We then analyzed the algebraic topological features of the GBM–HRGs–MINW. Because during DPI process the simplexes with dimension q ≥ 2 are removed, the MINWs reconstructed with DPI only have 0- and 1-simplexes. We first investigated the $H_0\left(K\right)$ and $H_1\left(K\right)$ of the reconstructed networks. Take the Rembrandt GBM data set as a representative in the 5 datasets. There are totally 244 nodes (genes) and 406 edges (gene–gene interactions) in the HRGs–MINW. Algebraic topological analysis demonstrated that Betti₀ = 19 and Betti₁ = 181. Because Betti₀ reflects the number of connected graphs, there are totally 19 connected graphs which are not connected together. Betti₁ = 181, indicating there are 181 loops in the HRGs–MINW (Table S2). The Betti numbers were similarly calculated in the other GBM–HRGs–MINWs.

Any network has its own topological structure. Therefore, it should be stringently examine that the topological features observed in the GBM–HRGs–MINW have significance rather than just random structures. To this end, Betti numbers in the random networks were investigated as controls (Giusti et al. 2015). Random networks with the same N_node and N_edge were constructed and their Betti numbers were calculated. A total of 1000 random networks (Random-MINWs) were produced and the distribution of Betti numbers was calculated. As a result, the 95% CI were obtained by examining the Betti number distribution (Table S2). According to the null hypothesis, betti₁ (= 181) in the Rembrandt HRGs–MINW is beyond the range of 95% CI (162.99–174.91) in Random-MINWs, indicating the observed structures had statistical significance and are not randomly produced ones. Similarly, although with different nodes and edges, most of the five databases had similar statistical results for Betti₁ results (Table S2).

Persistence Homolog Analysis Revealed Robust Algebraic Topological Structures of the GBM–HRGs–MINWs

Given the relatively large variances in biological data, the fluctuations of the MI values may apparently influence the network structure. To get more robust intrinsic topological structure of the network, we further performed persistence homology (PH) analysis by constructing filtrations of simplicial complexes (Curto 2016; Giusti et al. 2016; Sizemore et al. 2018). A filtration is defined by a growing network along with gradually addition of more simplexes to the simplicial complex (See detail in methods, Supplementary Fig. S1). As indicated by the name, “persistent” revealed the length of the cycles’ life, and, reasonably, cycles with longer life would reflect more robust features of the network structure.

For the reconstructed GBM–HRGs–MINW, filtrations were built by adding edges according to their indexes ranked by MI values. Similarly, to rule out that the simplexes and cycles appeared in the GBM–HRGs–MINW are random structures, 1000 Random-MINWs with the same N_node and N_edge were analyzed as controls.

Take the Rembrandt dataset as a representative. During the PH analysis, Betti numbers for each step (or filtration value) were obtained, and at last curves of Betti number versus the filtration values were plotted (Betti curves, Fig. 2). In addition, the statistical distribution of Betti numbers and the corresponding 95% CI in the random networks in each step were also calculated and shown as Betti curves with upper and bottom bounds defined by the 95% CI (Fig. 2a). It was clearly that, the GBM–HRGs–MINW had Betti curves significantly different from that of random networks, as revealed by the fact they were deviated from the upper bounds of the curves from random networks (Fig. 2b). Analysis of other GBM databases exhibited similar results (Fig. 2b, Table 2; Supplementary Fig. S2). Strikingly, although with different N_node and N_edge, the Betti curves derived from the five independent GBM datasets showed great consistence to each other, implying this topological feature is intrinsic for GBM–HRGs–MINWs. The datasets used different gene ID list according to their gene Chip platform, resulting in different N_node and N_edge values in the datasets. To reduce the impact of different N_node values for the results and compare their Betti curves together, we used the common Up-HRGs in the five datasets to re-perform the analysis, and, as a result, the Betti curves of the five GBM datasets still exhibited great consistence to each other (Fig. 2c). All of these data implied that the GBM–HRGs–MINW have intrinsic rather than random algebraic topological structures.

Fig. 2.

Betti curves and life length distribution of the random network and GBM–HRG–MINWs reconstructed with DPI. a Betti₁ curves with different N_node values in the random networks. b Betti₁ curves of the GBM–HRG–MINWs reconstructed from Rembrandt GBM expression datasets. c All of the Betti₁ curves of GBM–HRG–MINW adjusted to have same N_node values exhibited great consistence to each other. d, e Probability density curve (d) and cumulative probability distribution (e) of life lengths for 1-cycles in random networks. f Betti curve of the HRGs–MINW derived from the random-expression data exhibited high consistence to that of random network, which is located exactly in the 95% CI range of the Betti curve from random network. The vertical red lines indicate the end point of the Betti curves

Table 2.

Number of simplexes, cycles, and Sig.-cycles during the filtration process revealed persistently robust topological structures of the Up-HRGs–MINWs in GBM

Database	0-simplex	1-simplex	0-cycles	1-cycles	0-sig. cycles	1-sig. cycles	95% threshold of life length for 0 cycles	95% threshold of life length for 1 cycles
GBM_GSE13041	178	282	177	116	15	38	275	153
GBM_GSE16011	212	425	211	217	21	54	329	260
GBM_Rembrandt	244	406	243	181	28	65	375	226
GBM_Unified	174	285	173	120	12	27	274	157
GBM_Validation	174	285	173	127	19	38	268	158

PH Analysis Revealed Cycles with Significantly Long Life in the GBM–HRGs–MINWs

PH analysis revealed robust topological features of HRGs–MINW intrinsic for GBM. Next, we explored how to find cycles with statistical significance. To this end, the life lengths of all cycles produced in the filtration process were calculated, and the statistical distribution of life length in the Random-MINWs were analyzed as controls (Fig. 2d). Similarly, the distribution and 95% CI of cycle life lengths in the Random-MINWs were obtained. As revealed by the density curve of life length distribution (Fig. 2d), most of the cycles have very short life, and therefore the 95% bound in the accumulated distribution was used as thresholds for significantly long life cycles (Sig.-cycles, Table 2, Fig. 2e) in the GBM–HRGs–MINW. Taking the results from Rembrandt data as representative (Table 2), the 95% bound value is 226 in the Random-MINWs, and thus cycles with a life ≥ 226 were considered as Sig.-cycles. As a result, there are totally 65 Sig.-1-cycles (life ≥ 226), which would be potential molecular cycles contributing to the hypoxia regulated biological in GBM. Similarly, the number of simplexes, total Betti numbers and number of Sig.-cycles were also investigated in all of the five databases (Table 2). Although with different N_node and N_edge values, the five GBM datasets resulted in relatively comparable results, indicating the topological structures uncovered by our PH analysis reflected stable intrinsic features of the GBM–HRGs–MINW. For example, the numbers of Sig.-1-cycles (N_{Sig.-1-cycles}) in all of the datasets ranged from 27 to 65, while their normalized values to the N_node (N_{Sig.-1-cycles}/N_node) ranged from 0.16 to 0.25, exhibiting a great consistence with each other.

Adjusted GBM–HRGs–MINWs Have Consistent Algebraic Topological Structures

Different genome genes, N_node and N_edge values would have impacts in the topological structures of reconstructed HRGs–MINW. To reduce the variances introduced by these differences, we next re-performed the analysis by using the adjusted datasets which contained the common genome set in all databases. The adjusted networks have about 228–341 1-simplexes and 26–37 1-cycles. To further reduce the influence of different N_edge values in the network topology, we used the same number of top edges ranked by their MI values to construct the filtration. As a result, all of the networks have quite consistent parameters of topological structures, such as total number of 1-simplex, 1-cycles, and Sig.-cycles (Table S3), further validating the results that the topological structures uncovered here are intrinsic features of the GBM–HRGs–MINW.

Topological Structures in the GBM–HRGs–MINWs are Not Caused by Algorithm Biases and Specific Degree Distributions (DD)

To further examine whether the consistent topological features of all the GBM–HRGs–MINW would be caused by biases originated from the algorithm, we generated random gene expression datasets (RandomExp), and reconstructed their HRGs–MINW (RandomExp-HRGs–MINWs) with the same procedure. As a result, the Betti curves of the RandomExp-HRGs–MINWs are located almost exactly in the range of the 95% CI of Random-MINWs (Fig. 2f), indicating the reconstruction algorithm did not bring perceptual biases to the topological structures.

In addition, to further examine whether the GBM–HRGs–MINWs have significant rather than random produced structures, we studied the Random-MINWs with the same degree distribution (DD) to the GBM–HRGs–MINWs (RandomSameDD–MINWs) with DPI. First, the DD of all the GBM–HRGs–MINWs with DPI exhibited consistency to each other (Supplementary Fig. S4A). Totally five kinds of RandomSameDD–MINWs were produced with identical DD to each of the five GBM–HRGs–MINWs with DPI. As a result, strikingly, the Betti₁ curves of the RandomSameDD–MINWs with DPI are almost completely overlapped with that of Random-MINWs (Fig. S4B-C). Together, these results indicated that the observed topological structures in GBM–HRGs–MINWs are not produced by Random-MINWs with specific DDs, and these data further strengthened the conclusion that GBM–HRGs–MINW had its own intrinsic topological structures.

Higher Dimension Topological Structures of the GBM–HRGs–MINWs Reconstructed Without DPI

To investigate higher dimension topological structures in the GBM–HRGs–MINW, we used the network reconstructed by ARACNe without DPI (GBM–HRGs–MINW-NoDPI). In this scenario, the network described a relationship of the genes where the gene–gene interactions can be direct or indirect. The networks were constructed from the adjusted expression data, and 1000 random networks were produced as controls to get statistical distributions of the parameters of random network (Fig. 3a, b).

Fig. 3.

Betti curves and life length distribution of the random network and GBM–HRG–MINWs reconstructed without DPI. a Betti₁ and Betti₂ curves (N_node = 161) in the random networks. b Probability density curves for 0, 1, and 2-cycles in random networks (N_node = 161). c–f Representative Betti₁, Betti₂ and Betti₃ curves for GBM–HRG–MINWs reconstructed from the Unified TCGA dataset without DPI. Image in (d) showed the detailed information of the boxed part in the curve in (c). g, h Betti₁ curve of HRG-MINW reconstructed from random-expression dataset, and image in (h) showed detailed information of the boxed part in the curve in (g)

First, the GBM–HRGs–MINW-NoDPI showed much richer structures, and the highest dimension of cycles are 3 (Supplementary Table S4). In this situation, the Betti curves are apparently deviated from the 95% CI of the Random-MINWs (Fig. 3c–f). The Betti₁ curve in the Random-MINWs had an apparent peak along with the increase of edge numbers, while that from the GBM network exhibited relatively gentle curves with small amount of Betti numbers. When investigating the Betti₁ curves in detail, at the beginning of the filtration process (edges < 150, Fig. 3c), the Betti numbers of the GBM–HRGs–MINW-NoDPI are larger than that of the Random-MINWs, but it kept relative stable values across the whole filtration process (Fig. 3c, d).

The Betti₂ curves of GBM–HRGs–MINW-NoDPI exhibited more apparent differences from that of Random-MINWs (Fig. 3e). Similar to the situation of Betti₁ curves, ahead the ascending section of the curve, the Betti₂ curve in the GBM–HRGs–MINW-NoDPI are significantly larger than that of Random-MINWs (Fig. 3e). Similar situation was observed in the Betti₃, with no 3-cycles observed in the Random-MINWs until the observed edge numbers (Fig. 3f), demonstrating the GBM–HRGs–MINW-NoDPI also have significant high-dimension topological structures.

Next, further investigation of Betti curves derived from RandomExp-MINWs showed that they are located exactly in the 95% CI range of Betti curves of the Random-MINWs (Fig. 3g, h), ruling out the possibility that the observed topological structures are biases caused by the algorithm. Furthermore, the Betti₁ curves of RandomSameDD–MINWs exhibited only slight deviation from that of Random-MINWs after the peak of the curves (Fig. S4D), implying the observed topological structures in GBM–HRGs–MINW-NoDPI are not produced by specific DDs.

The Topological Structures of GBM–HRGs–MINW are Significantly Different from that Derived from Normal Brains

A further question is, whether the GBM–HRGs–MINWs have structures specific for the GBM disease. To this end, we analyzed the HRGs–MINW reconstructed by genome expression data derived from normal brains (Normal-HRGs–MINWs), by using six datasets [one from GSE11882 (Berchtold et al. 2008), one from GSE8919 (Myers et al. 2007), and four datasets of different brain regions (including cerebellar, frontal cortex, ponts, and temporal cortex) from GSE15745 (Gibbs et al. 2010)]. By analyzing the topological structures of the Normal-HRGs–MINWs, we found they had topological structures significantly different from that of GBM–HRGs–MINWs.

Similar to the above analysis, we first analyzed the network reconstructed with DPI. Interestingly, although with the same value of N_node, Normal-HRGs–MINWs had less amount of 1-simplexes, total cycles and Sig.-cycles, and cycles in the simplicial complex at the endpoint of filtration (end-cycles) (Supplementary Table S5).

Next, we adjusted all of the GBM and normal brain MINWs to have the same N_edge value, by taking the same number of topped edges ranked by their MI values. As a result, the GBM–HRGs–MINWs and Normal-HRGs–MINWs showed significantly different topological structures, such as number of cycles, Sig.-cycles, and end-cycles (p < 0.05, Table S6). It should be noted that Normal-HRGs–MINWs derived from different datasets also exhibited consistent results to each other. Interestingly, GBM had significantly more 0-cycles and 1-cycles than normal brains (Table S5, Fig. 4a, b).

Fig. 4.

GBM derived HRGs–MINW had algebraic topological structures significantly different from that of normal brains. a, b For the MINW reconstructed with DPI, GBM–HRGs–MINW had more total cycles, Sig-cycles and end-cycles than that of normal brains (a). PH analysis revealed that the averaged Betti₁ curve of GBM–HRGs–MINW was apparently different from that of normal brains (b). c, d For the MINW reconstructed without DPI, GBM–HRGs–MINW had a smaller number of simplexes, but more cycles in dimensions 1–3, compared to that of normal brains. e–h Averaged Betti₁, Betti₂, and Betti₃ curves for GBM and normal brain-HRG-MINWs. The image f showed the detailed information in the boxed part in (E)

At last, we further analyzed networks reconstructed without DPI (Normal-HRGs–MINW-NoDPI) to investigate high dimensional structures. Normal-HRGs–MINW-NoDPI tend to have more simplexes in all dimensions (although not statistically significant, p = 0.22–0.44, Fig. 4c), while, like the situation in the DPI results, they had less cycles than the GBM–HRGs–MINW-NoDPI, especially in dimension-1 (Fig. 4d). Investigation of the averaged Betti curves for GBM and normal brain demonstrated that GBM- HRGs–MINW-NoDPI have more cycles than Normal-HRGs–MINW-NoDPI in dimension 1 and 2, and slightly in dimension 3 (Fig. 4e–h). Quite interestingly, when examining the Betti curves in detail (Fig. 4f), Betti curves of normal brain showed larger values at beginning and kept more stable values which are gradually become smaller than that of GBM–HRGs–MINWs (Fig. 4e, f), indicating that Betti curves of normal brains more deviated from Betti curves of Random-MINWs than GBMs did.

Algebraic Topological Analysis Revealed Richer Information About the GBM–HRGs–MINW Structures and Identified Key Cycles for GBM Tumorigenesis

Different from results obtained by traditional graph analysis, algebraic topological analysis revealed much richer information about the integral features of network. As a representative result, we investigated the number of cycles involved for a gene (NC_gene), and the connectivity degree of the gene (D_gene). Genes with high values of D_gene did not necessarily had high value of NC_gene. Interestingly, some genes had very low D_gene but are involved in large number of cycles (Supplementary Table S7), and there are also genes exhibiting opposite feature. Nevertheless, the topology analysis identified potential novel targets that are more frequently involved in loops of cell signal transmission, rather than those that only have more interactions. For example, some hypoxia responsive genes contributing to the tumorigenesis of GBM are identified, including ADM, VEGFA, EPAS1, PGK1, et al. In addition, a cohort of novel potential targets for hypoxia in GBM were identified, such as PLOD1, PLOD2, GPRC5A, LDHA, GBE1, SPAG4, et al. Because one gene can be viewed as 0-clique, we can also investigate the NC_clique of 1- or higher dimension cliques. For example, the NC_1-clique were identified and revealed the most frequently appeared paired gene interactions (Supplementary Table S8), containing many unreported potential interactions, such as ADM-SPAG4, GBE1-PLOD2, et al.

To quantitatively evaluate the importance of the cycles, we assigned a rank value to each cycle, by calculating the average values of the NC_gene of all the nodes in the cycle. Analysis of the distribution of 1-cycle lengths revealed that the cycle lengths are ranged from 4 to 10 and peaked at 5 (Fig. 5a). For higher topological structures, the 2-cycles in the GBM–HRGs–MINW-NoDPI were studied (Fig. 5b). The 1-cycles, such as the representative ones in the top rank (ADM–SLC2A1–PGK1–SPAG4–ADM) and (GBE1–HK2–LDHA–VEGFA–PLOD2–PGK1–GBE1) (Fig. 5c), can be viewed as loops. The 2-cycles can be viewed as spherical structures, where signals can transfer in any directions along the surface but not inside of them (Fig. 5d, e), reflecting certain rules controlling the information flow. Differentially, Normal-HRGs–MINWs not only have different topological structures, but also have different gene compositions of the top ranked cycles (Supplementary Table S9).

Fig. 5.

Representative 1- and 2-cycles (1- and 2-dimension cycles) in the reconstructed GBM–HRGs–MINWs and PPI-HRGs–MINWs. a 1-Cycles length distribution in the GBM–HRGs–MINWs reconstructed with DPI. b 2-Cycles length distribution in the GBM–HRGs–MINWs reconstructed without DPI. c Representative 1-cycles, which can be viewed as traditional loops. d, e Representative 2-cycles (d), which can be considered as extensions of 1-dimenional loops and viewed as 2-dimensional sphere surfaces (e). f, g The PPI-HRGs–MINWs contained sub-cycles-3genes [HK2, LDHA, VEGFA] (f) and [GBE1-PLOD2-VEGFA] that are identified in the GBM–HRGs–MINWs 1-cycles

Topologically Identified Cycles Have Biological and Clinical Indications

What are the biological or clinical implications of the topological structures identified above? An apparent significance is that the topological structures revealed novel interactions between genes or, more interestingly, biological modules. Firstly, we observed the clinical significance of the above representative 1-cycles. These genes are poor prognostic factors for the patient’s survival (Fig. S5, A–D). In addition, to investigate the influence of cycles for survival, the sum of the rank values ordered by expression levels for each gene (SRExp) were defined as the expression index for the cycle. Analysis of the survival of patients with high and low SRexp revealed that high level of SRExp of the 1-cycles were significantly predictors for poor survival (Fig. 6a, b). By interrogating the Rembrandt database, almost all of the genes were significantly highly expressed in gliomas than in normal brain, and especially more highly expressed in GBMs (Fig. S6). In addition, all of the genes in the representative 1-cycles exhibited positive correlation to each other (Fig. S7, Table S10), implying potential interactions among these genes.

Fig. 6.

a, b The expression index of a cycle is defined as the sum of the rank values ordered by expression levels for each gene (SRExp) in the cycle. For the two 1-cycles indicated in Fig. 5c, GBM patients with high SRExp values had a significantly poor prognosis. c, d Genes in the 1-cycles, such as HK2 and LDHA are specifically expressed in certain cell types in both normal brain cells (c) and GBM cells (d). e Genes in the 1-cycles such as LDHA, PLOD2 and GBE1 are more highly expressed in GBM cells than in normal NSCs. f Treatment of microglial cells with GBM cell culture medium resulted in significant up-regulation of HK2 expressions

To further validate the biological indications of our identified cycles, we reconstructed protein–protein interaction (PPI) MINW (PPI-MINW) of the HRGs (PPI-HRGs–MINW) by using the STRING database (Szklarczyk et al. 2015) (Fig. S8). Next, algebraic topological analysis were performed to identify 1-cycles and 2-cycles of the PPI-HRGs–MINW. Then we examined the overlaps between the cycles of the PPI-HRGs–MINW and our identified GBM–HRGs–MINWs. As a result, we totally identified 48 sub-cycles containing 3 genes (sub-cycles-3genes, Figs. 5c, f, g, S9) and 129 sub-cycles-2genes that were presented in both of the MINWs. As representatives, the sub-cycles-3genes included [HK2, LDHA, VEGFA] (Fig. 5c, f, Tables S11, S12), [GBE1–PLOD2–VEGFA] (Fig. 5c, g, Tables S11, S12), which are key parts of the identified representative 1-cycles (GBE1–HK2–LDHA–VEGFA–PLOD2–PGK1–GBE1) (Figs. 5c, S9). It should be noted that, the PPI-HRGs–MINW is not disease specific and may missing other kinds of direct interactions, such as protein or RNA binding to promoters or in other DNA/RNA regions. Nevertheless, the identified sub-cycles in the PPI-HRGs–MINW provided biological evidences that the cycles in the GBM-GRGs-MINWs identified by PH analysis would played certain biological roles for the GBM.

GBM–HRGs–MINW Contained Novel Loops Implying Interplays Between Warburg Effect, Immune Regulation, and Angiogenesis

We further analyzed the potential functions of the genes in the loops. Interestingly, these genes exhibited different biological modules and/or features. For example, the top ranked representative loop (GBE1–HK2–LDHA–VEGFA–PLOD2–PGK1–GBE1) contained key genes for the Warburg effect, including LDHA (Liu et al. 2018; Pathria et al. 2018; Valvona et al. 2016), PGK1 (Li et al. 2016), HK2 (Lis et al. 2016), and gene GBE1, which has not been investigated in GBM. In addition, there are also potential genes that are involved in the immune response of GBM, such as HK2 (Li et al. 2018). By examining the expression profile of HK2 in different cell types in normal (GSE52564) (Zhang et al. 2014) and GBM datasets (GSE84465) (Darmanis et al. 2017), we found that HK2 was almost exclusively highly expressed in microglial cells in normal brain and immune cells in GBM (Fig. 6c, d). Interestingly, the genes involved in the Warburg effect also showed specific expression in certain cell types: for example, LDHA was enriched in both microglial and vascular cells (Fig. 6c, d). In addition, some of the genes (including LDHA, PLOD2, GBE1) were highly expressed in GBM cell lines, including U87, U251, and glioblastoma stem like cells (GSCs), than in normal neural stem cells (NSCs) (Fig. 6e), indicating specific roles of these genes for GBM cells. Furthermore, by examining a database investigating the glioma-induced polarization of microglia (Walentynowicz et al. 2018), HK2 was significantly up-regulated in microglial cells after treatment with GBM cell culture medium (Fig. 6f). Another loop (ADM–SLC2A1–PGK1–SPAG4–ADM) revealed similar multi-components interplays in GBM: ADM and SLC2A1 were both specifically highly expressed in vascular cells, while SPAG4 was enriched in neuronal, vascular and immune cells (Supplementary Figs. S6 and S10), and they are all involved in Warburg effect or aerobic glycolysis by interacting with PGK1. These identified loops revealed intrinsic complicated cycled communications among multiple cell components (including tumor cells, vascular cells, immune cells, neuronal cells, et al.) and with Warburg effect. All of the cells together with Warburg effect are essential cell types or programs for the tumorigenesis of GBM, while the detailed interplays have not been well understood. There are still a lot of potential loops identified, which give clues to further decipher the complicated interplays of multiple programs in GBM.

Discussion

A considerable number of potential targets and results about gene interactions in GBM have been obtained by experimental research. However, it is more and more widely recognized that gliomas are caused by multiple genetic or epigenetic changes (Brennan et al. 2013; Chen et al. 2014; Mao et al. 2009b; TCGA 2008). Therefore, targeting several key genes may not be sufficient to reverse the disease. In addition, acquisition of resistance to anti-angiogenesis treatment indicates that the MINW in GBM have much great elastic adaptability to the therapeutic interventions. For example, anti-VEGF monoclonal antibody Bevacizumab only have limited effect on GBM patients and caused drug resistance rapidly (Piao et al. 2013). In addition, anti-Notch therapy with a gamma-secretase inhibitor can lead to therapy resistance by suppressing Hedgehog via Hes1 mediated inhibition of Gli1 transcription (Schreck et al. 2010), disclosing an ingenious adaptability of the molecular network. Therefore, there are increasing requirements to study the global gene interaction network in tumors, especially with the rapid advancement of high-throughput data acquisition technologies. However, although a lot of research revealed gene to gene interactions and the significance of certain genes for tumors, little is known about the global structures of the MINW of GBM.

There are two major obstacles to study the global structures of gene interaction networks. First, ideal approach to get exact gene interaction networks is lacking, especially the MINW in special contexts (Kleaveland et al. 2018; Markmiller et al. 2018; Shi et al. 2018). Progressions are made in recent years in experimental and theoretical approaches (Kermany et al. 2018; Kleaveland et al. 2018; Li and Izpisua Belmonte 2018; Markmiller et al. 2018; Shi et al. 2018). Given the large number of genes in a network, it is not feasible to get the exact interactions between all paired genes or molecules experimentally, and theoretical methods are especially important for the reconstruction of MINW (Plaisier et al. 2016; Shi et al. 2018). Information theory based analysis is proved to have important roles in MINW reconstruction in recent years (Plaisier et al. 2016; Shi et al. 2018; Wang et al. 2009). Actually, in some studies, information theory based analysis can get results comparable to that from high-throughput experiments (Basso et al. 2005; Wang et al. 2009). In addition, besides paired gene interactions, there are still triplet and multiple gene interactions in the MINW, which are more difficult to get the interaction patterns by pure biological experiments.

Another difficult is the analysis of the reconstructed MINW. For a given reconstructed network, how to decipher its structure and its relevance to tumor biological is also a, probably more, difficult task (Bullmore and Sporns 2009; Sporns and Betzel 2016). A direct difficult issue is how to describe the structure of MINW, especially when it contains thousands of genes. The similar problem is encountered in mathematics about 100 years ago, when the algebraic geometry is established to quantitatively study the integral structure of a geometry independent of metric features such as length, angle et al. The precise mathematical language to study the structure of geometries is based on the abstract algebraic concept—group, an essential tool in modern mathematics and physics. Interestingly, MINWs are geometries that are determined by the structures rather than their measures. Therefore, they are useful tools to study the intrinsic features of MINW in depth. For example, algebraic topological studies have been performed in neuronal activity correlation networks in the brain (Giusti et al. 2015), and intrinsic organization patterns of the network were detected. Nevertheless, little, if any, is known about the geometric organization of the MINWs in tumor.

Given the huge amount of computation for a network consisted of thousands of genes, a prominent problem for the MINW study at first is how to determine a gene set responsible for certain functions, such as hypoxia regulated genes. Because of the great variance in biological study, we introduced GHG to get a significant gene set from several independent datasets. The particular advantage of the GHG is that it can quantitatively tell about exactly how many genes with certain overlapping criteria can reach the statistical significance (Mao and Xue 2018). Based on the GHG, we got more than 200 genes that are up-regulated or down-regulated under hypoxia, which is then used for further study.

To get intrinsic topological structures of the HRGs–MINW in GBM, one fundamental issue is how to distinguish special topological structures in the network from nonspecific noise. To this end, we studied random networks with the same N_node and N_edge parameters of the GBM–HRG–MINW, and even RandomSameDD–MINWs with the same DD of the GBM–HRG–MINW. Strikingly, both the Random-MINWs and the RandomSameDD-MINWs generated structures with quite stable Betti curves, while, in contrast, GBM–HRGs–MINWs had significantly different Betti curves which kept stable Betti values across the filtration process. Importantly, by examining five independent GBM datasets, the HRGs–MINW in all of the datasets exhibited great consistent Betti curves and Sig.-cycles. Therefore, the topological structures represented by Betti numbers and Sig.-cycles reflected invariant intrinsic features of the GBM–HRGs–MINW. Next, to exclude the possibility that the algorithms used to reconstruct the network would generate biases, we further investigated a randomly expressed gene dataset. Interestingly, the RandomExp-MINWs exhibited high consistent topological features to the Random-MINWs, confirming the unbiasedness of the algorithm, and further validated that the detected topological structures are intrinsic for GBM. In addition, analysis of the MINWs reconstructed with Down-HRGs (GBM-Down-HRGs–MINWs) also revealed that the Betti curves of these MINWs exhibited high consistency to each other and are significantly different from that of Random-MINWs (Fig. S11A). Furthermore, GBM-Down-HRGs–MINWs and GBM-Up-HRGs–MINWs had different Betti curves (Fig. S11B), indicating that PH analysis also revealed function (or gene set) specific structures.

To further explore whether the HRGs–MINW have topological structures specific for the disease, we next studied the Normal-HRGs–MINW. Similarly, several independent datasets were used to reconstruct the Normal-HRGs–MINWs. First of all, all of the Normal-HRGs–MINW also have consistent topological structures to each other. An apparent characteristic of the Normal-HRGs–MINW compared to that of GBM–HRGs–MINWs is that they have much less number of simplexes and cycles in dimension 1 or higher, indicating less loops in the Normal-HRGs–MINWs. To get comparable results to GBM, we used adjusted networks by using top edges ranked by the MI values to make all GBM- and Normal-HRGs–MINW to have same N_node and N_edge. As a result, GBM–HRGs–MINWs have more cycles than that of Normal-HRGs–MINW, indicating GBM changed their MINW organization pattern during progression into malignant tumors. Besides altered expression levels of tumorigenic genes or tumor-suppressor genes as has been widely studied, the GBM also exhibited apparent changes of the organization of gene information flow. However, as discussed above, some key genes can be compensated by redundant loops in the gene network (Rizzolio et al. 2018; Schreck et al. 2010; Tamura et al. 2017). It is possible that the topological nature of MINW in GBM is the more essential and invariant feature of the disease, and interventions to change the topological structure may reverse its tumorigenic behavior.

Different from traditional graph analysis, algebraic topological analysis revealed more abundant and intrinsic characteristics of the network (Curto, 2016; Giusti et al. 2015, 2016). Higher dimension cycles can be viewed as extensions of traditional loops. For example, a 2-cycle reflects gene information flow in a 2-dimensional closed manifold (Fig. 5d, e), where genes can propagate their information flow in all directions in the surface but not inside of the sphere, uncovering a more flexible but controlled gene interaction pattern that can’t be described by traditional 1-dimension loops. In the present study, the HRGs–MINW reconstructed without DPI exhibited apparent two and higher dimension persistent cycles.

It should be noted that algebraic topology used in the present work identified equivalence classes of cycles in various dimensions, different from traditional loop-finding algorithms which extract all loops (Sizemore et al. 2018; Tiernan 1970). Considering the high variability of biological data, it would be questioned that small changes of the edge weights or their ordering would change the results. It has been demonstrated that persistent homology is quite robust to noise, as small changes in the order of the edges will results in small changes in the persistence diagram (Cohen-Steiner et al. 2007; Sizemore et al. 2018). These results, together with that our results were based on several independent datasets, heavily confirmed the validation of the present data, revealing intrinsic structures of the GBM–HRGs–MINW.

Limitations of the Present Results and Future Perspectives

First, as discussed above, reconstruction of MINW is still a main obstacle for network analysis. Any network, no matter how precise the method is used, is an approximation of the real one. The methods used in the present study have been proven to be useful to reconstruct networks (Basso et al. 2005; Margolin et al. 2006a, b; Wang et al. 2009). More accurate approaches, including experimental and theoretical methods to detect direct physical interactions between genes or molecules, would provide more accurate MINW, and analysis based on these networks would reveal more intrinsic topological features of the GBM–HRGs–MINW. Notably, our PPI analysis provided important biological basis that the identified cycles would have functional roles in tumor (Figs. 5f, g, S8, S9). Therefore, based on the methods adopted here, we have first clearly addressed that GBM have a HRGs–MINW with significant typological structures different from that of random networks and normal brains.

Second, given the importance of hypoxia for the tumorigenicity of GBM, the current study investigated the HRGs–MINW containing more than 200 genes, while it would be constructive to study bigger networks, and ultimately, the whole genome network. Nevertheless, because our gene set is derived from stringent procedure, and the gene interaction relationship is calculated from whole genome dataset, we firstly uncovered intrinsic topological features of the hypoxia driven program in GBM.

Third, how to validate the biological relevance of the topological structures of the HRG-MINW and, more interestingly, how to target it to reverse the disease into a normal pattern as a therapeutic strategy are all open questions for future research. Possible perspectives include: by changing the global gene interaction pattern, or by targeting novel genes which are essential for topological structure of the MINW in GBM, the GBM can be reprogramed into normal cells.

For the many novel potential loops identified in our analysis, we have examined the biological significance of a few representative ones in clinical samples and GBM cell lines. There are still a lot of loops providing clues of novel gene interactions in GBM, and future studies based on these results would be useful to fundamentally decipher the tumorigenic mechanisms of GBM.

Conclusion

As a conclusion, by stringently select a set of HRGs in GBM, we reconstructed the HRGs–MINW in GBM and normal brains. Algebraic topological analysis showed that GBM-MINW had special topological structures, significantly different from random networks and networks reconstructed from random gene expressions. PH analysis further revealed Sig-cycles in the GBM-MINW. In addition, GBM–HRGs–MINW have more simplexes and cycles compared to that of Normal-HRGs–MINW, indicating GBM changed the network organization significantly after malignant transformation. A lot of potential interactions between different cell types or programs in GBM are uncovered and some of them were validated by PPI analysis. In summary, GBM–HRG–MINWs have significantly special topological structures, revealing intrinsic natures of the disease.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Abbreviations

ARACNe

Algorithm for the reconstruction of accurate cellular networks

CI

Confidential interval

CSC

Cancer stem cell

DD

Degree distribution

DPI

Data processing inequality

D_gene

Connectivity degree of the gene

GBM

Glioblastoma

GBM–HRGs–MINWs

Molecular interaction network of hypoxia regulated gene reconstructed from GBM expression datasets

GSCs

Glioblastoma stem like cells

HRGs

Hypoxia regulated genes

MI

Mutual information

MINW

Molecular interaction network

N_edge

Number of edges

N_node

Number of nodes

NC_gene

Number of cycles involved for a gene

NC_q-clique

Number of cycles involved for a q dimensional clique (or simplex)

Normal-HRGs–MINWs

Molecular interaction network of hypoxia regulated gene reconstructed from normal brain expression datasets

NSC

Neural stem cells

PH

Persistent homology

PPI

Protein–protein interaction

PPI–MINWs

Protein–protein interaction MINWs

PPI–HRGs–MINWs

PPI–MINWs reconstructed with the HRGs

q-simplex

q dimensional simplex (fully connected (q + 1) nodes)

q-cycle

q dimensional cycle

q-sig-cycle

q dimensional cycle whose life is statistically long (longer than the 95% bound of q-cycle life in random-MINWs)

q-end-cycles

q dimensional cycle in the end point of filtration

RandomExp

Random gene expression datasets

RandomSameDD-MINWs

Random-MINWs with the same degree distribution (DD) to the corresponding MINWs

SR-HRGs

Statistically reliable gene set of HRGs

SRExp

Rank values ordered by expression levels for each gene

sub-cycles-3genes

Sub-cycles containing three genes that are presented in both GBM–HRG–MINWs and PPI–HRGs–MINW

TF

Transcription factor

Up-HRGs

Up-regulated HRGs

Funding

This study was funded by National Natural Science Foundation of China (Grant Numbers: 81502143, 51675411, 81671302) and foundation of fourth military medical university (2018JSTS05).

Compliance with Ethical Standards

Conflicts of interest

All authors declare that they have no conflicts of interest.

Ethical Approval

The study protocol was approved by the institutional review board of Xijing Hospital of the Fourth Military Medical University. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

Research Involving Human Participants and/or Animals

This article does not contain any studies with animals performed by any of the authors.

Informed Consent

Informed consent was obtained from all individual participants included in the study.