Research on the mechanism and measures of riding comfort deterioration in a low floor tram

Abstract

With the global widespread preference for low-floor trams, the expectation for tram riding comfort has been increasingly heightened. This paper identifies an abnormal riding comfort problem (ARCP, characterized by an excessive and W-shaped distribution of riding comfort) during dynamic field tests on a low-floor tram. To address ARCP, a multi-body dynamics model of the tram was constructed and validated its accuracy through dynamic field tests. By integrating track irregularities and wheel-rail contact analysis, the riding comfort index was assessed and reproduced the ARCP phenomenon. Linearization and time-domain integration studies were conducted on the mechanisms and measures to resolve the ARCP. The research findings reveal that the primary cause of the deterioration in the mean comfort index is the large amplitude of the track irregularity and the low equivalent conicity of the wheel-rail contact relationship. The main reason for the W-shaped distribution of riding comfort is the weaker inter-vehicle constraints and the lack of lateral energy-absorbing devices. Finally, optimization measures were proposed, including reducing the lateral stiffness of the second suspension, altering the carbody structural parameters, and modifying the inter-vehicle connection devices. This research enriches the study of tram dynamic performance and offers insights that may contribute to the resolution of ARCP.

Introduction

Urban trains offer notable advantages such as low cost, low running resistance and exceptional curve negotiating performance, particularly low-floor trams, which are superior to buses in terms of passenger capacity, comfort, stability and noise. Consequently, low-floor trams are widely favored around the world. However, as trams become increasingly prevalent in cities and passengers’ expectations for riding comfort escalate, there is a heightened emphasis on improving this aspect. The riding comfort of a tram is a crucial indicator for evaluating its dynamic performance, as it comprehensively reflects the overall experience of passengers. Sun et al¹. introduced the Sperling method, Mean Comfort standard method and Continuous Comfort method, and compared them with specific experimental data. Sadeghi et al^2–4. conducted an in-depth examination of rail vehicles riding comfort through a combination of line tests and simulations, proposing tangible optimization solutions for the identified issues.

In recent years, there has been an increasing interest in improving the dynamics performance of trams to meet the increasing demand of passengers for riding comfort. Focusing on minimizing wear between the rail and wheel in urban rail systems, Licciardello et al⁵. and Łuczak et al⁶. conducted studies on methods for predicting wheel wear. Yu et al⁷. established a passenger-train-track vertical coupling dynamic model, and applied Hertz nonlinear elastic contact theory to the wheel-rail coupling relationship. Bruner and Rizzetto⁸compared the dynamic performance of trams equipped with the tram-train wheel profile KVV and the ORE S1002, the difference in wheel-rail contact relationship led to the difference in its dynamic performance. Suarez et al⁹. assess the efficacy of three types of resilient wheels in mitigating railway noise and vibrations, employing finite element method for vibratory characteristics and spectral analysis with actual measurement track irregularities. The derived results, combined with estimations of emitted sound power, demonstrate the effectiveness of resilient wheel designs in both reducing environmental noise and controlling structural vibrations. Han¹⁰established a low-floor tram model composed of three modules and observed that as the wheel-rail adhesion coefficient increases, the critical speed decreases and the dynamic performance deteriorates. Li¹¹proposed optimization measures to increase the equivalent conicity and dynamic damping of the yaw damper, which were put forward and verified by on-track tests. Tian et al¹². provide new insights into the effect of wheel elasticity on vibration characteristics, and thereby provides directions to improve riding quality and passenger comfort.

To improve the dynamic performance of the tram, in addition to designing an appropriate wheel profile, optimization can also be performed on the structural parameters and suspension parameters. Sun et al¹³. proposed two objective functions related to the minimum damping ratio, and optimized suspension parameters using sensitivity analysis and vector evaluated genetic algorithm. After 20 generations of evolution, the optimal solution for suspension parameters was obtained, thus effectively improving the vehicle’s dynamic performance. To study the riding comfort of high-speed train passengers, Xu et al¹⁴. developed a detailed human body-seat-vehicle-track coupled model. When the train is loaded, the effect of passengers on the car body is similar to that of a damper or mass element, which can reduce the car-body vibration and enhance riding comfort. Li et al¹⁵. developed a dynamic model for a 70% low-floor tram and conducted a dynamic analysis by analyzing the articulated structure between the carbodies. Sun et al¹⁶. developed a second quasi-zero-stiffness suspension system, which can be applied to low-floor trams and exhibit superior vibration isolation qualities and running stability when compared to equivalent linear suspension. Jeong et al¹⁷. used the Design of Experiments (DOE) method to optimize the parameters of the tram model, and the optimized tram showed a better dynamic performance in terms of test response (including riding safety, riding comfort and critical speed). Liu¹⁸constructed a dynamic simulation model for a 100% low-floor tram consisting of five modules. The main parameters of the primary and second suspensions have been optimized and the proper combination of suspension parameters has been selected. The research found that modifications in the lateral stiffness of the second suspension exert a significant influence on the tram’s riding quality. In view of improvement in the riding quality and comfort of the rail vehicle, Sharma and Kumar¹⁹integrated a magnetorheological damper in the secondary vertical suspension system. Wen et al²⁰. and Jiang et al²¹. performed multi-objective analyses of a monorail vehicle suspension system using a GA and obtained satisfactory results.

The diversity of inter-vehicle connection devices also exerts a considerable impact on the dynamic performance characteristics of the tram. Kuba and Lugner²²used SIMPACK to model bogies with independently rotating wheels and bogies with wheelsets, and analyzed their respective advantages and drawbacks in dynamic performance. They suggested further research on the impact of inter-vehicle connections and bogie construction parameters on dynamic performance. Xue et al²³. found that the coupling devices between carbodies in articulated and non-articulated trams influenced their impact stability. Non-articulated vehicles exhibited more unpredictable behavior due to their flexible connections, whereas articulated vehicles maintained high stiffness and effective inter-vehicle coupling alignment through rigid connections. Jiang et al²⁴. compared the curve negotiation properties of two distinct articulated monorails and a traditional monorail. They found that the comprehensive riding comfort for the lead and the tail vehicle of the ‘’bolster type’’ monorail is better than that of the inner vehicles. Despite these findings, further research into the underlying causes remains unexplored.

This research reveals, through dynamic field testing, that the riding comfort of low-floor trams not only exceeds standard limit but also displaying a W-shaped distribution, a phenomenon we term ARCP. While extant literature on low-floor trams is limited, with few researchers investigating the overall distribution of riding comfort within the tram, especially the W-shaped distribution. To address the ARCP, this study established a multibody system dynamics model for the tram, and the accuracy of the model was verified by comparing simulation results with field tests’ results. Subsequent linear analysis techniques and time-domain integration methods were employed to explore the mechanism of ARCP, focusing on wheel-rail equivalent conicity and track irregularities. Additionally, drawing from vehicle parameters, which include structural and suspension system parameters, along with inter-vehicle connection devices, solutions for ARCP were proposed. The implementation of these strategies effectively resolved the ARCP.

Field test and result analysis

Tram type

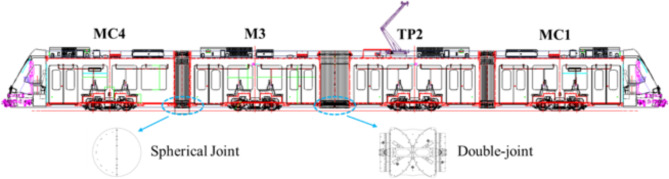
The focus of this paper is to analyze the dynamic performance of a low-floor tram, comprising three power cars and one non-power car. The tram is in the form of single-module, with four distinct modules. Each module contains a bogie at the center (refer to Fig. 1). MC (the lead or tail vehicle) represents the power car module for installing a motor bogie and a cab. The presence of the cab results in a centroid shift in the carbody towards the cab’s direction. TP2 (the second vehicle) is a trailer module with a trailer bogie. M3 (the third vehicle), similar to MC, contains a motor bogie but has no cab, leading to the center of gravity of the carbody is basically located directly above the center of the bogie.

Fig. 1.

Structural diagram of low-floor tram.

Two connection methods are employed between each module: spherical joints and double joints, as illustrated in Fig. 1. The MC1 and TP2 are interconnected through a spherical joint mechanism, restricting their relative translational motion in three directions while releasing the degrees of freedom in three rotational directions. A similar connection is established between M3 and MC4, thus we can consider MC1 and TP2 as a marshaling unit, while the M3 and MC4 as another marshaling unit. The two marshaling units (i.e., TP2 and M3) are connected by a double-joint mechanism, which only constrains their longitudinal translational freedom. Similar to a two-force connecting rod, this mechanism solely transmits longitudinal forces, either in traction or braking.

Riding comfort analysis.

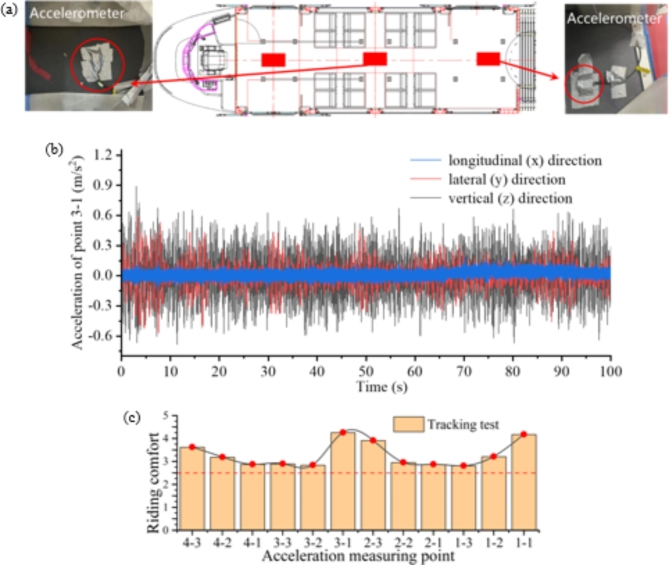
During the dynamic field test, accelerometers were placed on the front, middle, and rear of carbody as illustrated in Fig. 2. These points were respectively located on the floor surface at the end of the carbody and the floor surface above the center of the bogie corresponding to the carbody. The three-dimensional acceleration time-domain data measured by the accelerometers served as input for subsequent riding comfort calculations.

Fig. 2.

Acceleration measurement point.

The mean comfort standard method was proposed in the EN-12,299 standards²⁵ and has been widely adopted by the majority of countries for evaluating riding comfort. In general, the level of the tram’s riding comfort aims to achieve comfortable, utilizing 2.5 as the standard limit value. The mean comfort index (N_MV) is defined as the 95th percentile of the five-minute frequency-weighted root-mean-square (r.m.s) values of the accelerations, which are measured in the longitudinal (x), lateral (y), and vertical (z) directions. Subsequently, the sixty continuous five-second weighted r.m.s values are computed for each direction along the entire tested track. From these sixty r.m.s values, the 95th percentiles of the weighted accelerations in the three directions are ultimately chosen and combined using a root-sum-square calculation, as depicted in Eq. (1).

1

where a_XP95, a_YP95 and a_ZP95 are the weighted r.m.s values of the accelerations with respect to X(longitudinal), Y(lateral) and Z(vertical) directions respectively. The subscripts XP95, YP95 and ZP95 denote that RMS values of the accelerations regarding X, Y and Z directions are contained in a 95% confidence interval. Wd and Wb denote that the frequencies are weighted according to the corresponding weighting curves. The frequency weighting r.m.s accelerations in three directions are expressed as follow.

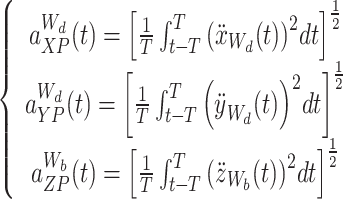2

The dynamic field test of the tram was carried out on an experimental track, referred to as Track-I, which features a straight line. During the test, the low-floor tram appeared the phenomenon of ARCP when it was running on the Track-I with a speed of 80 km/h. The specific test was subsequently carried out by researchers. The on-boarded data acquisition system was used to continuously record the accelerations via accelerometers, which were installed on the middle and the end of the carbody floor, as shown in Fig. 3(a). The model of the accelerometers is LC0709-18, with a measuring range of 18 g, capable of accurately recording the vibration accelerations of the carbody.

Fig. 3.

Field test: (a) accelerometer mounted on the middle and the end of the carbody floor; (b) acceleration of point 3 − 1; (c) dynamic field test riding comfort.

The acceleration time-domain data in the longitudinal, lateral, and vertical directions can be measured at each measuring point by the accelerometer. The three-directional acceleration of point 3 − 1 is shown in Fig. 3(b). The acceleration time-domain data of each measuring point are calculated for comfort, and the N_MV values of each measuring point are shown in Fig. 3(c). Results indicate that the N_MV at certain measurement points exceeds the standard limit value, and riding comfort of the tram exhibits a W-shaped distribution, also known as ARCP. This means that the riding comfort indexes of the front and rear ends (MC1-1, MC4-3) and the middle (TP2-3, M3-1) of the tram are higher than those of other measuring points, with the peak N_MV appearing at the measurement point (M3-1) near the double-joint of the M3. This abnormal phenomenon made the driver feel uncomfortable and drew the attention of the railway department.

Dynamic modelling for the low-floor tram

Utilizing advanced multi-body dynamics simulation (MBS) software, the research integrates principles from rigid mechanics, analytical mechanics, and computer technology. This approach enables the unveiling of kinematic patterns and the acquisition of dynamic responses under specific operational conditions.

Tram modelling and modal analysis

The dynamics of multibody systems serve as the theoretical basis for the dynamic simulation of railway vehicles. The Multi-body tool SIMPACK is adopted for the simulation work. The Tram Model is composed of four cars (MC1, TP2, M3, and MC4), where each car comprising a carbody, a bogie, two wheelsets, and four axle boxes, as shown in Fig. 4. Furthermore, the power car also contains two motors and two gearboxes, and the MC also includes a cab. The inter-vehicle connections are composed of a spherical joint with an additional rotational damper, and the connection between the TP2 and the M3 is replaced with a double joint.

Fig. 4.

Multibody system dynamics model of low-floor tram.

Compared to the multibody system dynamics model of traditional railway vehicles, there are significant differences in the modeling approach for the inter-vehicle connection device of low-floor tram. The mathematical expression of the spherical joint can be described as:

3

where c and d represent the stiffness and damping of the spherical joint, respectively, and F_nom represents the initial nominal force, which is the magnitude of the joint force when the system is in equilibrium. The mathematical expression of the double-joint can be described as:

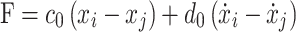4

where c₀ and d₀ respectively represent the stiffness and damping between the two joints of the double-joint, i and j represent the two joints’ connection points.

In multibody system modeling, to prevent excessive computation, the dynamics model was simplified by reducing certain degrees of freedom. The vehicle carbody, bogie, and motor have six degrees each, which include longitudinal movement(x), lateral movement(y), vertical movement(z), roll(α), pitch(β), and yaw(γ). The gearbox and axle box are respectively assigned one rotational pitch freedom, while the roll of the wheelset is a non-independent degree of freedom, thus only five degrees of freedom are assigned. The tramway dynamics model consists of 44 rigid bodies and has a total of 146 degrees of freedom.

The primary suspensions consist mainly of springs, which act between the axle box and the bogie frame with two springs at each wheel. Secondary suspensions between the bogie frame and carbody include two rubber springs, a lateral damper, two vertical dampers, and an anti-rolling torsion bar. Furthermore, the traction rod connects the bogie frame to the carbody. Two traction motors are installed on both sides of the bogie frame for MC1, M3, and MC4, respectively. The structure of the trailer bogie closely resembles that of the motor bogie but without traction motors. Consequently, the masses of the frames are different, and further details can be found in Table 1.

Table 1.

Main technical data of the low-floor tram.

Parameters	Values
Tram length (m)	38.34
Power car length (m)	7.395
Trailer car length (m)	7.800
Weight of motor bogie (kg)	4580
Weight of trailer bogie (kg)	3200
Floor surface to rail surface height(mm)	350
Vehicle distance (MC1-TP2) (mm)	8,720
Vehicle distance (TP2-M3) (mm)	9,500
Fixed axle base (mm)	1850
Nominal wheel diameter (mm)	600
Primary suspension cross span (mm)	1160
Horizontal stiffness of primary suspension (MN/m)	4.60
Vertical stiffness of primary suspension (MN/m)	1.70
Horizontal stiffness of second suspension (MN/m)	0.45
Vertical stiffness of second suspension (MN/m)	0.90
Weight of MC1 (kg)	9000
Weight of M3 (kg)	7000
Longitudinal position of the center of gravity relative to the bogie center in MC1/TP2/M3/MC4 (mm)	643/0/79/643
Longitudinal and lateral stiffness of spherical joint (MN/m)	200/33
Longitudinal stiffness of double-joint (MN/m)	50

Modal analysis based on complex mode analysis is an effective and efficient method for exploring the deterioration of riding comfort caused by modal coupling resonance. This method can formulate the linear differential equations of motion for the tram as.

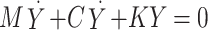5

where M, C, and K are the mass, damping, and stiffness matrices, respectively; Y is the generalized coordinate column vector with an order of n corresponding to the DOF number.

Sun²⁶ reduced the second-order differential equations to first-order equations by substituting the physical coordinate Eq. (5) into the spatial domain, as follows.

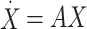6

where , .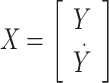

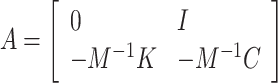The particular solution for the first-order differential equations is expressed in the form X = X₀e^τt, which is represented as follows

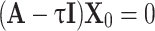7

where τ and X₀ are the eigenvalues and eigenvectors, respectively. The railway vehicle system, as per principles of matrix theory and linear algebra, is characterized by 2×n distinct complex characteristic roots in the form of conjugate pairs

8

where α_k and β_k are the real part and imaginary part of τ_k, and they are related to the modal frequency f_k and modal damping ratio η_k as

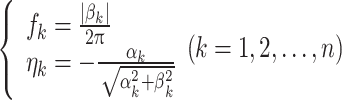9

By substituting the conjugate eigenvalues into Eq. (7), The conjugate eigenvectors can be obtained as follow:

10

where and 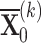are the kth diverse complex modal shapes, 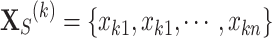is the n-dimensional modal shape vector.

Wheel-rail boundary conditions

In railway vehicle simulations, accurate modeling of the nonlinear wheel-rail contact is crucial. Throughout the field test, this study used a wear-resistant tread CB10, designed for low-floor trams, and the Chinese standard 60 kg rail CH60²⁷. Figure 5(a) shows the potential contact area between the CB10 and CH60 when matched together under different lateral wheelset displacements. Within the frequent wheel-rail contact area, which typically occur during minor lateral wheelset displacement, the wheel tread design encompassed both a curve with a radius of 350 mm and a straight line with an incline ratio of 1:40. For significant displacements, the linear section of wheel flange (having an incline ratio of 1:3) came into contact with the rail. Thus, throughout the tram operation, the wheel-rail contact relationship manifested a striking nonlinearity. Furthermore, the friction coefficient between the wheel and the rail is designated as µ = 0.4 to represent an ideal, dry wheel-rail contact scenario.

Fig. 5.

Wheel-rail boundary conditions: (a) wheel-rail profile and pair of contact points; (b)Track-I irregularity; (c) PSD of Track-I.

Track geometry irregularities generally refer to deviations in the actual rail geometry from its ideal state, including height, alignment, cross-level, and gauge irregularities²⁸. In this section, Track-I, the spatial domain and power spectral density (PSD) of which are depicted in Fig. 5(b, c), is used as the input for the simulation model. Among the four types of irregularities, height irregularity exhibits the most significant amplitude fluctuation with a maximum amplitude of 16.7 mm. Its PSD is greater than the other three irregularities, indicating a larger impact on tram operations.

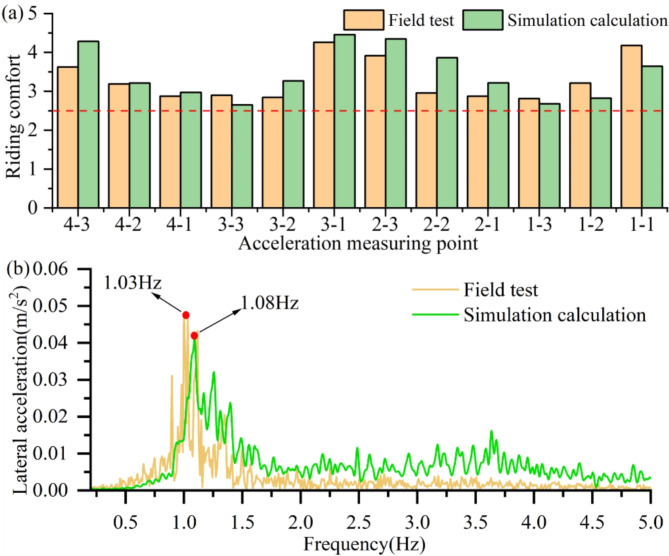
Model validation

The dynamic model, operating at a speed of 80 km/h to match field tests, produced N_MV calculations that closely aligned with field test results. As depicted in Fig. 6(a), the overall error between simulation and field test results was 3.17%, demonstrating a good agreement and displaying a characteristic W-shaped distribution. Furthermore, the time domain data of the lateral acceleration at the measurement point (3 − 1) were analyzed using spectrum analysis as shown in Fig. 6(b). The field test results show a peak value of 1.03 Hz, and the simulation results have a peak value of 1.08 Hz. In summary, the simulation results align with the field test results, proving the model’s accuracy for ARCP cause analysis.

Fig. 6.

Comparison between the field test and the simulation calculation: (a) N_MV of each measuring point, (b) spectrum analysis of the lateral acceleration at the point 3 − 1.

Analysis on mechanism and measures of ARCP

Preliminary analysis with linear method

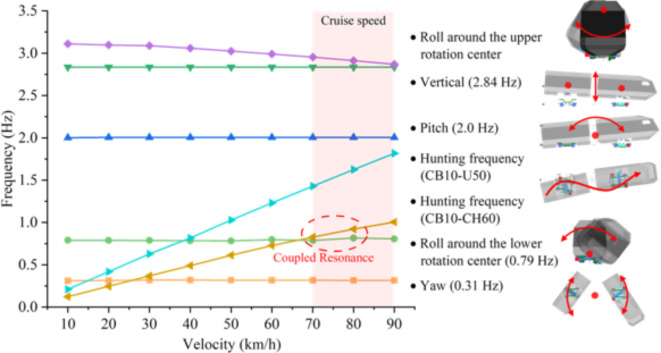
To address the issue of ARCP, the initial step is to clearly understand which parameters require optimization. The linearized calculations²⁹, which are ideal for preliminary analysis, facilitate the selection of specific parameters with potential efficacy. Carbody motion is evaluated through the determination of eigenvalues and eigenvectors for the tram system’s linearization matrix. The stability and frequency of each mode are signified by the real and imaginary components of the eigenvalues, respectively, while the mode shape for each eigenvalue is reflected by the eigenvectors. Root locus analysis³⁰ is used to calculate the eigenvalues and eigenvectors of the linearized tram system equations. All nonlinearities in the model are eliminated or linearized. Dampers on the tram consist of linear stiffness with linear damping. The secondary lateral stoppers are removed. Harmonic linearization is used to linearize the wheel-rail contact, while Kalker’s linear theory is implemented to calculate the creep forces.

Figure 7 depicts the modal frequencies and shapes of trams, with corresponding yaw, roll around the lower rotation center, pitch, and vertical motion frequencies of 0.31 Hz, 0.79 Hz, 2.0 Hz, and 2.84 Hz respectively. The frequency of rolling around the upper rotation center decreases slightly with increasing speed, settling around 3 Hz. Figure 8 depicts the root locus, where enlarging circles signify increasing speed. With the tram’s velocity increment, a rise in the hunting frequency is observed when operating on both rail types, simultaneously resulting in a reduction in the damping ratio of the hunting mode.”

Fig. 7.

Modal frequency and modal shape of trams.

Fig. 8.

Root locus diagram.

On the CH60 rail at a cruising speed of 70–90 km/h, the tram’s hunting frequency (0.8–1.0 Hz) approaches the mode of roll around the lower rotation center, resulting in a coupling resonance between them. Moreover, when the vehicle speed exceeds 70 km/h, the hunting motion damping ratio falls below zero, causing the tram’s hunting motion to be uninhibited and instead amplified. In this situation, the tram may experience increasingly severe oscillations, which is one of the causes of ARCP. In contrast, when the tram operates on the U50 rail at the same speed, its hunting frequency (1.4–1.8 Hz) is nearer to the pitch mode, and its damping ratio remains above zero. Since hunting motion primarily contributes to lateral vibration, it does not readily provoke a coupling resonance phenomenon, thereby inducing ARCP. Although the tram’s hunting frequency still couples with the tram’s mode in the lateral direction when operating at low speeds (20–40 km/h) on both rail types, the speed is low and not the tram’s typical operating velocity. Consequently, the energy input of the tram system is insufficient to generate coupling vibration. Therefore, by optimizing the wheel-rail matching relationship, the hunting frequency of the tram at operating speed can be shifted away from the tram’s natural mode, particularly in the lateral direction. This can effectively reduce the tram’s lateral vibration and improve riding comfort.

Equivalent conicity serves as a crucial parameter in the wheel-rail contact relationship, which is closely related to the hunting motion of a tram. Moreover, it is one of the essential requirements for the design of railway vehicle wheel profiles. According to the UIC519 standard of the International Union of Railways³¹, the motion of a wheelset on a track satisfies the following equation:

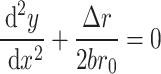11

where y is the lateral displacement of the wheelset, x is the distance traveled by the wheelset along the track, Δr is the difference in the radii of the left and right wheel rolling circles, 2b is the distance between the left and right wheel-rail contact points, and r₀ is the nominal rolling radius.

The initial conditions for Eq. (11) are:

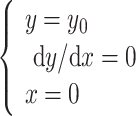12

where y₀ is the given initial lateral displacement amplitude. The solution to Eq. (11) is a sine wave with a wavelength of L_w. Thus, the equivalent conicity is given by:

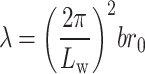13

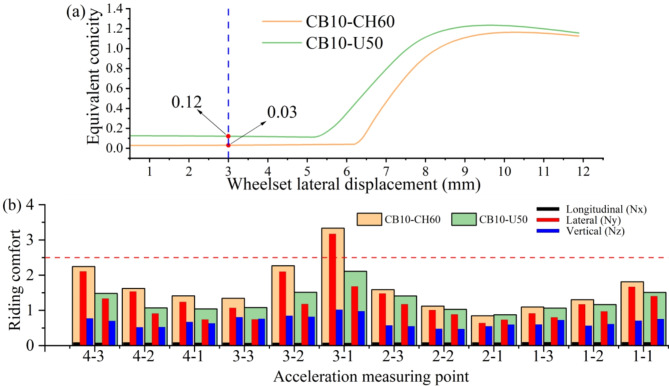
This equivalent conicity corresponds to the lateral displacement of y₀. The nominal equivalent conicity is defined as the position where the hunting motion amplitude of the wheelset is 3 mm. Should the equivalent conicity be excessively small, hunting instability may arise in the tram at low speeds, leading to passenger discomfort. Conversely, if the equivalent conicity is overly large, the wheelset might become unstable, resulting in safety concerns. As shown in Fig. 9(a), the equivalent conicity for CB10 matched with CH60 and U50³² is 0.03 and 0.12 respectively. The riding comfort of the tram operating on two different types of rails is shown in Fig. 9(b). The comprehensive comfort for CB10-U50 demonstrates a significant improvement in comparison to CB10-CH60, primarily due to the reduction in the Ny. In addition, the W-shaped distribution of riding comfort has also been improved, and N_MV at point 3 − 1 has been reduced to below the limit of 2.5.

Fig. 9.

Comparison of different rails: (a) equivalent conicity; (b) riding comfort.

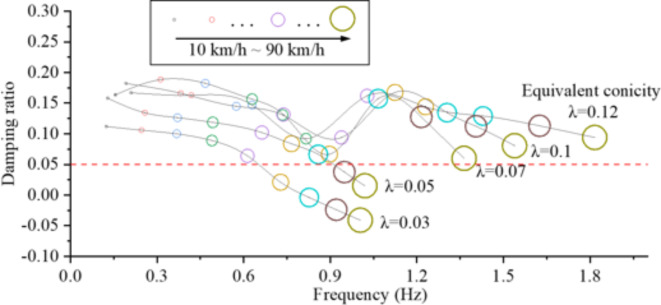
In conjunction with the aforementioned analysis, one of the causes for ARCP in field testing is due to the lower equivalent conicity of wheel-rail matching, which induces a coupling effect between the tram’s hunting motion and the mode of roll around the lower rotation center. Consequently, by linearizing the wheel tread to match the rail, the equivalent conicity remains constant under a certain amount of wheel lateral displacement. The root locus for the tram’s hunting motion was calculated with equivalent conicities of 0.03, 0.05, 0.07, 0.1, and 0.12, as shown in Fig. 10. When the damping ratio of a root locus falls below 0, the tram system becomes unstable. Typically, a damping ratio of 0.05 is considered a safety margin. At speeds above 70 km/h and with λ < 0.07, the damping ratio drops below 0.05, leading to instability and excessive lateral vibration, thus causing the ARCP phenomenon. Conversely, when λ exceeds 0.07, the hunting frequency increases with speed, and at around 0.8 Hz, coupling resonance occurs between the hunting motion and the mode of roll around the lower rotation center, reducing the damping ratio of the hunting motion. However, within the cruising speed range, the damping ratio remains above 0.05, ensuring stability. Therefore, in designing the wheel and rail profiles, the equivalent conicity should be maintained above 0.07.

Fig. 10.

Root locus of tram’s hunting motion under different equivalent conicity.

Analysis of ARCP caused by track irregularities

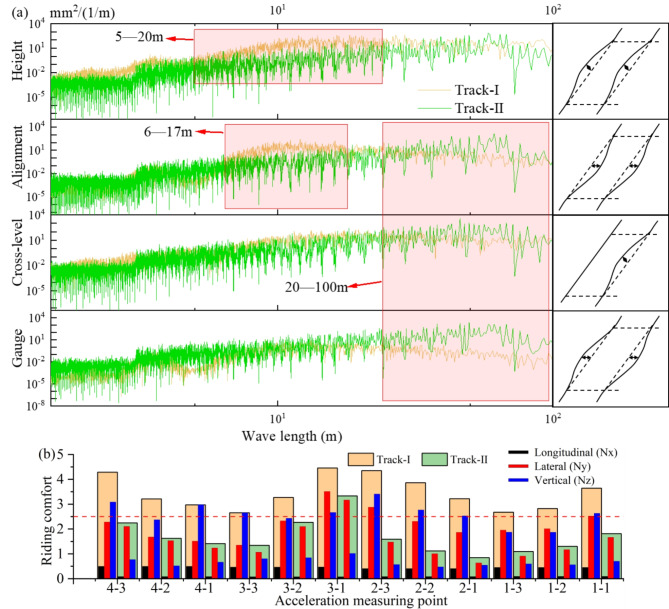
Track irregularity is the primary cause of increased tram vibration, which considerably influences the riding comfort. Therefore, considering the disparity in track conditions, the measured operating-track (Track-II) irregularity was selected for comparison and analysis with the Track-I. Track-II that has been measured is an existing track with a history of successful tram operations. Figure 11(a) depicts the comparison of the PSD between these two types of track irregularity. The four categories of track irregularity, namely height, alignment, cross-level, and gauge, have been compared. The Track-I exhibits an elevated PSD for the height irregularity within the wavelength range of 5–20 m, compared to the Track-II. Additionally, the PSD for the alignment irregularity is also higher within the wavelength range of 6–17 m. In contrast, for the wavelength range exceeding 50 m, the overall PSD of the Track-II surpasses that of the Track-I, especially for the cross-level and gauge irregularity. When the tram operates at a speed of 80 km/h on the Track-I, it exhibits a higher probability of inducing vertical vibration at 1.1–4.4 Hz and lateral vibration within the range of 1.3–3.7 Hz. Conversely, the Track-II is more likely to excite vibration below 1.1 Hz. Based on the spatial domain analysis of the track irregularity, the difference in RMS between the two tracks is not significant. However, the amplitude of the height irregularity of the Track-I is approximately three times larger than that of the Track-II.

Fig. 11.

Comparison of different tracks: (a) PSD; (b) riding comfort.

The comparison of the tram’s riding comfort when operating on the Track-I and the Track-II is shown in Fig. 11(b). The comprehensive riding comfort N_MV can be decomposed into three directions: longitudinal (Nx), lateral (Ny), and vertical (Nz) comfort. The calculation results show that: (a)In comparison to the Track-I, the comprehensive riding comfort of the tram is considerably improved when operating on the Track-II. Riding comfort in three directions is reduced, and Nz is the most increased due to the larger amplitude of height in the Track-I. (b)Upon running on the Track-I, height disturbances excite pitch (2.02 Hz) and vertical (3.08 Hz) modes in the tram. Vertical vibration exerts the greatest impact on comprehensive riding comfort as it dominates other vibrations. The so-called ‘snake motion’ or hunting mode, is a unique characteristic of railway vehicles, which is positively correlated with tram’s speed. At 80 km/h, the hunting frequency is 0.78 Hz, while other natural modes of the vehicle are independent of speed. Consequently, Ny at point 3 − 1 exceeds Nz due to the coupling of the M3’s hunting frequency and the yaw (0.82 Hz) mode, as hunting motion chiefly induces lateral vibrations in the tram. (c) When the tram operates on the Track-II, it exhibits a higher propensity for inducing vibrations below 1.1 Hz, which are closer to the hunting frequency and yaw frequency of a tram. As a result, Ny exerts the greatest impact on comprehensive riding comfort.

In conclusion, the large amplitude of the Track-I in terms of height leads to the pitch and vertical motion of the tram, which is the primary factors contributing to excessive comprehensive riding comfort. Controlling the amplitude of track irregularities at wavelengths ranging from 5 to 20 m in height is advisable.

Further measures for ARCP

The rubber spring, as a vital constituent of the secondary suspension system of the bogie, exerts a definite influence on the lateral dynamic performance of the tram. The lateral stiffness of the second suspension (Ksy) has a particularly significant effect on the riding comfort of the tram, especially on the transmission of lateral vibrations. Figure 12(a) illustrates the influence of variations in the Ksy, ranging from 0.3 MN/m to 0.5 MN/m, on the tram’s riding comfort. A decrease in the lateral stiffness of the secondary suspension leads to improved riding comfort, with each vehicle experiencing greater comfort. However, there are limitations in the manufacturing process, preventing the lateral stiffness from becoming too low. Therefore, it is advisable to maintain the lateral stiffness at an optimal value of 0.4 MN/m.

Fig. 12.

Comparing the effects of various measures on ARCP: (a) the lateral stiffness of the second suspension; (b) the structural parameters; (c) the inter-vehicle connection devices.

The main differences between M3 and MC1 are reflected in the vehicle’s center of gravity location and mass. However, there are significant differences in riding comfort between these two vehicles. To explore the causes of W-shaped distribution, the riding comfort was calculated using a low-floor tram dynamic model for the following two measures: (A)augmenting the mass of M3 from its original 7 t to the same as MC1’s 9 t; (B)based on measure A, shifting the center of gravity of M3 by 0.5 m towards the direction of double-joint. The influence of tram structure parameters on riding comfort is shown in Fig. 12(b). The results indicate that both measures can significantly improve the riding comfort of M3. Employing the first measure reduces the N_MV at point 3 − 1 from 2.1 to 1.8, a decrease of 14.3%. Meanwhile, the implementation of the second measure decreases the N_MV at point 3 − 1 to 1.6, a 23.8% reduction. Therefore, by increasing the mass of M3 or shifting the center of gravity towards the direction of the double-joint, the phenomenon of W-shaped distribution of riding comfort can be effectively improved.

In the original tram design, a spherical joint is employed for the strongly constrained connection between MC1 and TP2, as well as M3 and MC4. Additionally, a double-joint connection with comparatively less constraints is used between the middle two vehicles (TP2 and M3). The influence of two distinct inter-vehicle connection devices on the tram’s riding comfort, as shown in Fig. 12(c): (A)A spherical joint is used between TP2 and M3; (B)In the case of a double-joint established between TP2 and M3, an inter-vehicle lateral damper with a damping coefficient of 50 kNs/m is added between the two vehicles. In the case of Device-A, the N_MV in the M3 is significantly improved from 2.1 to 1.25 due to the strengthened constraint between TP2 and M3, which changes the M3’s lateral natural mode and enhances the transfer of lateral vibration from M3 to TP2. Additionally, the phenomenon of the tram’s riding comfort distribution taking on a W-shaped is resolved. As for Device-B, the inter-vehicle lateral damper can absorb the lateral vibration energy. Consequently, the N_MV at point 3 − 1 is reduced from 2.1 to 1.23, effectively addressing the W-shaped comfort distribution of the tram. In summary, the primary factors inducing the W-shaped distribution of the tram’s comfort are the weak inter-vehicle constraints and an absence of lateral energy-absorbing devices. It is recommended to substitute the connection device between TP2 and M3 with a spherical joint or introduce an inter-vehicle lateral damper with a damping coefficient of 50 kNs/m.

Experimental validation

Based on preliminary field test results conducted on Track-I, dynamic simulation analysis reveals that the differences in track irregularity and the low equivalent conicity are the main reasons for the high riding comfort. To validate the reliability of the simulation analysis conclusions, tracking tests were performed on trams operating on an actual operating-track (Track-III), constructed according to the same standards as Track-II. During tracking testing, the Track-III is the measured operating-track irregularity, with CB10 selected as the wheel tread and U50 as the measured profile of the rail. Therefore, the equivalent conicity for wheel-rail matching is 0.12, and other vehicle parameters are consistent with the field test. It is important to note that, unlike the accelerometer measurement points during the field test, they are only installed at the front and rear of each carbody, while there are no accelerometer measurement points in the middle of the carbody.

The comparison of riding comfort between the tram running on Track-I and Track-III at each measurement point is shown in Fig. 13. When operating on Track-III, the riding comfort of the tram has significantly improved, meeting the requirements of standard limits. From this observation, it is evident that reducing the amplitude of track irregularity and replacing the rail profile can effectively address the issue of excessive riding comfort for trams. However, the overall riding comfort of the tram still presents a W-shaped distribution, which is mainly attributed to the lack of constraints and energy absorption devices between the middle carbodies. Unfortunately, this experiment did not delve into verifying measures to improve the W-shaped distribution of riding comfort.

Fig. 13.

Comparing Riding Comfort of Trams on Track-I and Track-III.

Conclusion

The purpose of this paper is to investigate the causes of the ARCP of a low-floor tram during the dynamic field test, and propose corresponding countermeasures for addressing abnormal dynamic behavior, as well as the riding comfort of the W-shaped distribution. By conducting a thorough analysis of experimental data and dynamic simulation calculations, the following conclusions are drawn:

1. The lower equivalent conicity, which induces a coupling effect between the tram’s hunting motion and the mode of roll around the lower rotation center, is one of the reasons for the ARCP. The employment of U50 rails, exhibiting higher equivalent conicity, is recommended to enable the tram’s hunting frequency to deviate from the natural mode during operational speed.

2. The primary reason underlying the excessive riding comfort is the large amplitude of the Track-I. It is advisable to grind the rail to improve the track irregularity and prevent pitch and vertical oscillation.

3. Improving lateral riding comfort can be achieved by reducing the Ksy to a recommended value of 0.4 MN/m. Addressing the ARCP issue may be realized by increasing the mass of M3 or shifting the center of gravity towards the double-joint direction. The primary causes of the W-shaped distribution of riding comfort from inadequate inter-vehicle constraints and a lack of lateral energy-absorbing devices. Introducing a spherical joint between the middle two vehicles or an inter-vehicle lateral damper with a 50 kN/m damping coefficient can effectively solve the issue of the W-shaped distribution.

From the test results of tram operation on the Track-III, it is evident that the overall riding comfort has improved, which also confirms some conclusions from previous simulation. However, there is still a slight W-shaped distribution of the riding comfort. Regrettably, the current tracking test has not yet applied the parameter optimization measures proposed in simulation studies to improve the W-shaped distribution of riding comfort. Future research will investigate and resolve this issue.

Author contributions

We would like to acknowledge the valuable contributions made by each author to this article. As the lead author, HS.W. has taken primary responsibility for conceptualizing the article, developing the structure, and writing the majority of the content. His expertise in the field and dedication to the project have been instrumental in shaping the final version.Professor MR.C., WB. C. and JF. S., as the senior authors, have provided invaluable guidance and supervision throughout the writing process. Their rich experience and insights have significantly enhanced the quality and depth of the article. Dr. YC. X. Significant contributions have been made in literature review and analysis, with in-depth examination of relevant research and theories. Simultaneously shooting and providing Fig. 3aa and 3bProfessor LC.D., who provided financial support for the research in this article, is the funder.All authors have contributed to the revision and refinement of the article, ensuring its clarity, coherence, and accuracy. We would like to express our gratitude to each author for their dedication, hard work, and invaluable contributions to this article.

Funding

This research has been supported by the National Key R&D Program of China (grant number 2022YFB4301202), and by the National Key R&D Program of China (grant number 2022YFB4301303).

Data availability

The datasets used during the current study are available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.