Unsupervised few shot learning architecture for diagnosis of periodontal disease in dental panoramic radiographs

Abstract

In the domain of medical imaging, the advent of deep learning has marked a significant progression, particularly in the nuanced area of periodontal disease diagnosis. This study specifically targets the prevalent issue of scarce labeled data in medical imaging. We introduce a novel unsupervised few-shot learning algorithm, meticulously crafted for classifying periodontal diseases using a limited collection of dental panoramic radiographs. Our method leverages UNet architecture for generating regions of interest (RoI) from radiographs, which are then processed through a Convolutional Variational Autoencoder (CVAE). This approach is pivotal in extracting critical latent features, subsequently clustered using an advanced algorithm. This clustering is key in our methodology, enabling the assignment of labels to images indicative of periodontal diseases, thus circumventing the challenges posed by limited datasets. Our validation process, involving a comparative analysis with traditional supervised learning and standard autoencoder-based clustering, demonstrates a marked improvement in both diagnostic accuracy and efficiency. For three real-world validation datasets, our UNet-CVAE architecture achieved up to average 14% higher accuracy compared to state-of-the-art supervised models including the vision transformer model when trained with 100 labeled images. This study not only highlights the capability of unsupervised learning in overcoming data limitations but also sets a new benchmark for diagnostic methodologies in medical AI, potentially transforming practices in data-constrained scenarios.

Introduction

As classification and clustering methods, machine learning algorithms have been extensively adopted to a variety of applications including medical studies. In particular, deep learning algorithms are now recognized as a dominant method in the field of medicine, from drug discovery to clinical decision-making. The success of deep learning algorithms is mainly come from the digitalization of medical records with expert-level accuracy in radiopathologic categorization tasks. The accuracies clearly demonstrate the capability of deep learning algorithms in predictive modeling, reliable diagnosis, classifying of diseases, and precisely annotating anatomical characteristics.

In dentistry, as a degenerative disorder caused by inflammation of periodontal tissues, periodontal disease requires sophisticated diagnostic techniques for its accurate detection and resulting treatements. Periodontal disease may even cause serious consequences such as alveolar bone loss, tooth loss, and impaired masticatory function, which can greatly impact the quality of life and self-esteem. To effectively diagnose periodontal disease, loss images of clinical attachments for teeth has been widely used. Recently, more attentions have been paid to radiographic assessment of bone level (RBL)¹ as an improved diagnostic tool by adopting deep learning algorithms². In particular, convolutional neural networks (CNNs) have made significant improvements in detecting caries and other dental disorders by resolving the difficulties in dental panoramic radiograph interpretation^3–8. For instance, providing automated staging of periodontal disease, innovative hybrid deep learning architectures such as DeNTNet were employed for lesion detection and tooth numbering in dentistry^9–13. However, the application of fully supervised state-of-the-art algorithms has been a challenging issue in medical fields due to higher costs and impracticality in collecting large annotated datasets, where patient privacy concerns are of the utmost importance¹⁴. The introduction of a few-shot learning concept, which aims to accurately classify various images using a few sets of labeled data^15–17, is making a new leap forward in medical image analysis. Its extensive applications to image data analysis have been aided by generative adversarial networks (GANs)¹⁸ for enhancing training datasets, CNNs and Autoencoders (AEs) for strong feature representation conjoined with clustering algorithms¹⁹, and transfer learning²⁰. However, such techniques still depend on feature extractions from overall images with large size of base dataset, which may not suitable for dental diagnostics that pose intricate nature of periodontal disorders under limited availability of labeled data.

In this study, to make up for the shortcomings of existing deep learning methods, we propose a robust few-shot learning architecture; that is, UNet-CVAE (convolutional variational autoencoder) to accurately diagnose and classify periodontal disease using a small number of labeled dental panoramic radiographs. The proposed framework employs the UNet architecture to extract regions of interest (RoIs) of anatomic structures and the CVAE to generate efficient representations from sparse data by restricting latent space into statistical distributions, then clustering algorithms (e.g., k-means algorithm, density-based spatial clustering of applications with noise (DBSCAN), Gaussian mixture model (GMM)) to accurately classify features obtained from the UNet-CVAE procedure. The proposed few-shot learning architecture mainly aims to diagnose periodontal disease with limited amount of image data by adopting UNet’s capability in medical picture segmentation and CVAE’s efficiency to handle such sparse data. Main contributions of our work are summarized at the following:

• We propose an efficient automatic process of feature extraction for accurately identifying RoIs in dental panoramic radiographs instead of conventional manual feature extractions.

• We enhance the identification of dental tissues using CVAE by effectively extracting underlying features from small datasets for the purpose of capturing subtle symptoms of periodontal disease.

• The proposed UNet-CVAE framework adopts unsupervised learning concept against state-of-the-art fully-supervised approach to alleviate the reliance on large labeled dataset in dental diagnostics, efficiently tackling data scarcity and decreasing the laborious task of data labeling in dental diagnostics.

Methods

This study proposes an unsupervised learning framework that integrates the few-shot learning for analyzing dental panoramic radiographs. The framework is specifically designed to address the issue of sparse labeled medical image data for diagnosing periodontal disease. The proposed framework combines UNet architecture with CVAE in a way that is suitable under limited available data. The method begins with the UNet model in detecting probable RoIs within dental panoramic radiographs. The expertise of UNet in medical picture segmentation aids in accurate identification and extraction of regions indicating the presence of periodontal disease. In a sequence, extracted RoIs are fed into the CVAE module in our proposed architecture. CVAE plays a crucial role in extracting important latent features from these regions to reduce the dimensionality of the data, while maintaining key diagnostic information using small size of base training data. The combined UNet-CVAE architecture is specially designed to handle limited size of image data commonly encountered under few-shot learning scenarios.

After feature extraction, our method employs various unsupervised clustering algorithms for classifying dental imaging data into separate clusters to lessen the need for a substantial collection of labeled data. To enhance the accuracy of the diagnostic process, we integrate a specific collection of annotated photos to assign diagnostic labels to clustered images only during validation phase, connecting unsupervised clustering with practical needs of medical diagnostics. The proposed architecture shows a potential in adopting advanced artificial intelligence (AI) methodologies, namely few-shot learning, in transforming medical images particularly under resource-constrained environments. Operational flow and components of our framework are depicted in Fig. 1.

Fig. 1.

Proposed integrated framework for diagnosing periodontal disease in dental panoramic radiographs.

UNet

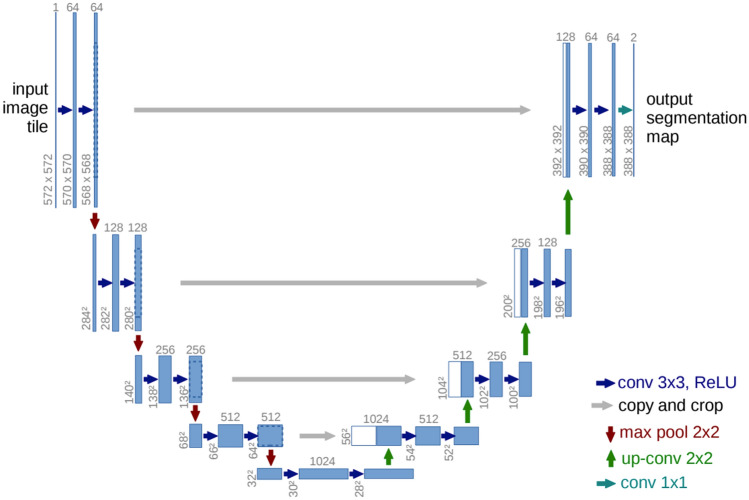
UNet architecture, which was initially designed to segment biological images, serves as a crucial component of our framework for diagnosing periodontal disease. UNets have been widely adopted due to its exceptional capability in localizing visual objects. We introduce the UNet architecture to handle subtle characteristics that are inherent in dental panoramic radiographs^21,22, since dental caries, peridontal disease, and perapical lesions are lurking in and around teeth, requiring tooth segmentation to highlight surrounding areas as an important basis for automatically diagnosing tooth-related diseases²³.

UNet architecture is an end-to-end fully CNN and consists of two paths: contraction path (left side) and expansion path (right side), which looks like ‘U’ shaped structure as in Fig. 2. Each blue box corresponds to a multi-channel feature map, where the number of channels is listed on top of the box. The x–y sizes are provided at the lower left edge of the box. White boxes represent copied feature maps and the arrows denote different operations. For more details on the UNet architecture, refer to Ronneberger et al.²¹. In contraction path, the UNet architectural design uses a series of two successive $(3\times 3)$ convolutions, where each convolution is immediately followed by a Rectified Linear Unit (ReLU) activation. This path enables the retrieval of multi-resolution characteristics that is essential for detecting subtle dental structure. After the convolution process, a $(2\times 2)$ maximum pooling operation is performed with the stride of 2. This procedure is designed to serve two functions: downsampling the image and doubling the number of feature channels. The downsampling procedure D at layer l can be mathematically represented as

$$\begin{array}{c}\hfill x^{l+1}=D(x^l)=\underset{2\times 2}{\mathit{max}}(\text{ReLU}(Con{v}_{3\times 3}(x^l))),\end{array}$$ 1

for the convolution layer $Con{v}_{3\times 3}(x^l)$.

Fig. 2.

UNet architecture.

On the contrary, the expanding path uses $(2\times 2)$ transposed convolutions to increase the size of feature map for accurately identifying the location of tooth and surrounding structures. Skip connections S from the contracting path are incorporated, merging low-level feature maps with upsampled outputs, denoted as U to maintain spatial information, which is crucial for precise RoI extraction. The upsampling process at next $(l+1)$ layer can be defined as

$$\begin{array}{c}\hfill x^{l+1}=U\left(x^l\right)\oplus S\left(x^{l_{\mathit{down}}}\right),\end{array}$$ 2

where the symbol $\oplus$ represents concatenation and $l_{\mathit{down}}$ denotes the layer in the contracting path. The use of ReLU activation in UNet effectively addresses the issue of vanishing gradients, hence enabling accelerated training. The network’s schematic provides a clear representation of its organization and showcases the presence of multiple channels and spatial dimensions, which are clearly labeled for better understanding. In our application, we adopt He initialization²⁴ for convolutional layers to avoid activation saturation. This method is mainly represented by normally distributed weights, that is, $W\sim \mathcal{N}\left(0,,,\sqrt{\frac{2}{n_l}}\right)$ and well suited for layers that arise after ReLU activation. Here, $n_l$ is the number of inputs to a layer. It considers nonlinear characteristics of the ReLU function, guaranteeing efficient distribution of weights at the beginning of the training process.

Within our proposed few-shot learning architecture, UNet plays a multifaceted role that goes beyond simple image segmentation. It is extensively integrated into our few-shot learning architecture, smoothly connecting with CVAE component. This integration aids in effectively retrieving and analyzing diagnostic features from limited data to overcome the difficulties in the diagnosis of periodontal disease.

CVAE

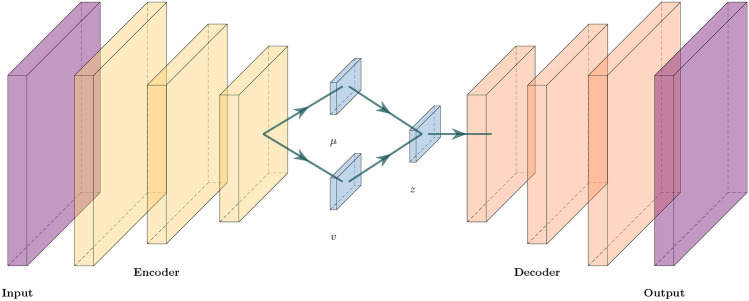
Convolutional variational autoencoder (CVAE) serves as a fundamental element in our framework for diagnosing sparse periodontal imaging data. CVAE is an advanced version of the conventional autoencoder (AE) that has been used to reconstruct input signals by using deep neural networks. The basic structure of CVAE is given in Fig. 3. CVAE is specifically designed to acquire efficient representations of input data under a primary purpose of reducing dimensionality²⁵. In contrast to conventional AEs, CVAE incorporates a probabilistic methodology for encoding. The encoder, also known as the inference network $q_{\varphi }\left(\mathbf{z},\mid ,{\mathbf{x}}_i\right)$, generates a probability distribution for each latent variable $\mathbf{z}$. Each of latent variable has been commonly modeled by the normal distribution, $z\sim \mathcal{N}(\mu ,{\sigma }^2)$, where $\mu$ and ${\sigma }^2$ are the mean and the variance of the normal distribution, respectively. The re-parameterization method includes the equation of a vector form: $\mathbf{z}=\mathit{\mu }+\sigma \odot \mathit{ϵ}$, where $\mathit{ϵ}$ follows a multivariate normal distribution with the mean vector of zeros and identity covariance matrix. This procedure guarantees that the latent space retains a certain level of randomness for securing the robustness of the model.

Fig. 3.

Structure of the convolutional variational autoencoder (CVAE).

The decoder, also known as the generative network $p_{\theta }\left({\mathbf{x}}_i,\mid ,\mathbf{z}\right)$, is responsible for reconstructing the ith input data ${\mathbf{x}}_i$ using latent variables $\mathbf{z}$. Training of CVAE entails the task of maximizing the evidence lower bound (ELBO), which is mathematically described as

$$\begin{array}{c}\hfill \mathcal{L}\left(\varphi ,,,\theta ,;,{\mathbf{x}}_i\right)=-D_{\mathit{KL}}\left(q_{\varphi },\left(\mathbf{z},\mid ,{\mathbf{x}}_i\right),\Vert ,p_{\theta },(\mathbf{z})\right)+{\mathbb{E}}_{q_{\varphi }\left(\mathbf{z},\mid ,{\mathbf{x}}_i\right)}\left[log,p_{\theta },\left({\mathbf{x}}_i,\mid ,\mathbf{z}\right)\right],\end{array}$$ 3

where $\varphi$ and $\theta$ are the variational parameter and generative parameter, respectively. Here ${\mathbb{E}}_{q_{\varphi }\left(\mathbf{z},\mid ,{\mathbf{x}}_i\right)}[·]$ denote the expectation in term of $q_{\varphi }\left(\mathbf{z},\mid ,{\mathbf{x}}_i\right)$. In this context, ELBO maintains a trade-off between the precision of reconstructed data and the smoothness of latent space, which is quantified by Kullback–Leibler divergence $D_{\mathit{KL}}(·)$. By incorporating convolutional layers into variational autoencoder (VAE), it becomes possible to capture spatial hierarchies present in dental image data. This is particularly important in medical imaging applications such as the diagnosis of periodontal disease²⁶. CVAE’s encoder compresses the input image into feature maps, then they are used to calculate the parameters of the latent space distribution. In contrast to the encoder, the decoder employs deconvolutional layers to rebuild the images based on sampled latent variables.

In our proposed architecture, UNet effectively extracts RoIs from dental panoramic radiographs, and CVAE then analyzes these RoIs to extract essential latent properties. This hybrid technique is essential in effectively managing the scarcity of data under few-shot learning paradigm. Latent vectors created by CVAE contain unique characteristics in dental radiographs that are used at the unsupervised clustering stage of our methodology. This enables the categorization of imaging data with subtle distinctions to accurately identify periodontal disease using small size of dental panoramic radiographs.

This study was conducted according to the principles of the Declaration of Helsinki and was approved by the Institutional Review Board (IRB) of the Hanyang University Seoul Hospital (IRB number 2019-01-007-026). The requirement for informed consent was waived by the IRB because of the retrospective nature of the study.

Unsupervised clustering

Our dental panoramic radiograph classification framework introduces unsupervised clustering methods to support few-shot learning scheme. The methods are based on latent variables derived from CVAE, which encompass condensed information vital for detecting the patterns that are indicative of periodontal disease.

k-means clustering

k-means clustering is a popular technique for dividing data into several groups with similar characteristics²⁷. The process entails dividing a set of n samples into k groups, where each group is characterized by its centroid. The algorithm proceeds by performing two main steps: firstly, it assigns each data point to the centroid that is closest to it, and secondly, it updates the positions of the centroids based on the points that have been assigned to the centroids. This process continues until convergence, usually when the centroids reach a state of stability. Within our framework, the use of k-means clustering algorithm assists in categorizing radiograph images into separate clusters according to the characteristics presented in the latent space produced by CVAE. This process facilitates the recognition of various phases or types of periodontal disease.

DBSCAN

Density-based spatial clustering of applications with noise (DBSCAN) is a kind of clustering technique developed by Ester et al.²⁸. It features several clusters by evaluating the density of data points. The characteristics of the clusters are determined by two parameters: the parameter specifying the size of a neighborhood around a point and the parameter representing the minimal number of points needed to create a dense region. DBSCAN distinguishes core points, border points, and noises, making it effective in handling outliers and identifying clusters of various forms. In our study, DBSCAN is employed to identify intricate patterns in dental radiographs that may not take a spherical shape, allowing for a more sophisticated clustering that is well-suited for various presentations of periodontal disease.

GMM

Gaussian mixture model (GMM) is a statistical model under the postulation that data is derived from a number of Gaussian distributions with unspecified characteristics²⁹. It is especially efficient in the situations where the clusters exhibit different variations. GMM employs an expectation-maximization (EM) technique to progressively estimate the parameters of the Gaussian distributions, allowing the model to handle overlapped clusters with different sizes. The GMM is used in this work since radiographic features may overlap or change greatly from feature to feature. Along with the distribution of latent features recovered by CVAE, the GMM helps us detect minor variations in radiographic images that indicate different stages of periodontal disease.

The efficacy of these clustering algorithms is evaluated by their abilities to accurately classify radiographs into several groups that indicate the presence or absence of periodontal disease; that is, the precision and the extent to which detected clusters align with clinical diagnoses. The selected algorithms are then incorporated into our few-shot learning architecture to improve the diagnostic process by offering an automated and resource-efficient way for classifying dental panoramic radiographs. Note that the clustering is a critical stage in the early identification and treatment of periodontal disease.

Bayesian optimization for hyperparameter tuning in few-shot learning

We introduce the Bayesian optimization method to decide hyper-parameter values in our integrated framework. The procedure operates in the context of few-shot learning strategy for diagnosing periodontal conditions since the hyper-parameters in both UNet-CVAE and clustering algorithms affect accurate and quick detection of periodontal disease. Bayesian optimization aims to fast converge to the optimal solution with respect to a computationally intensive objective function, such as the framework proposed by Wu et al.³⁰. Bayesian optimization operates under the principle of Bayes’ rule as

$$\begin{array}{c}\hfill p(w|D)=\frac{p(D|w)p(w)}{p(D)}.\end{array}$$ 4

Here, p(w) is the prior distribution of an unobserved quantity w, p(D|w) is the likelihood, and p(w|D) is the posterior distribution of the data D. This optimization method updates the results of previous iterations to select appropriate values via the acquisition function $\mathbf{u}$ for identifying next observations that could potentially maximize the objective function. Popular acquisition functions include the probability of improvement (PI), expected improvement (EI), and upper confidence bound (UCB)³¹. The optimal hyper-parameters, ${\mathit{\lambda }}^{\ast }$, are determined such that ${\mathit{\lambda }}^{\ast }=\text{arg}{min}_{\mathbf{x}\in A}f(\mathit{\lambda })$, with $\mathbf{x}(\in A:A\to \mathbb{R})$ representing evaluation points in the search space. Here, $f(·)$ denotes a surrogate model. Typically, it employs the Gaussian process regression (GPR) that estimates the target function iteratively as

$$\begin{array}{c}\hfill f(\mathbf{x})\approx GP(m(\mathbf{x}),k(\mathbf{x},{\mathbf{x}}^{\prime })),\end{array}$$ 5

where $m(·)$ and $k(·)$ represent the mean and covariance function of GPR, respectively. A commonly used covariance function is the squared exponential function: $k({\mathbf{x}}_i,{\mathbf{x}}_j)=exp\left(-,\frac{1}{2},{|{\mathbf{x}}_i-{\mathbf{x}}_j|}^2\right)$. Along with its efficiency in fast convergence compared to random sampling methods, Bayesian optimization is implemented through a sequence of updating the posterior distribution and maximizing the acquisition function in the proposed integrated architecture. The Bayesian optimization algorithm is given in Algorithm 1. Note that $D_{1:t-1}={\{x_n,y_n\}}_{n=1}^{t-1}$ is the training dataset for the surrogate model f.

Algorithm 1.

Bayesian optimization with prior and posterior updating.

Description of the data

Tufts dental database

Tufts dental database (TDD)³² is a collection of one thousand digital panoramic radiographs that have not been completely supervised. The data was collected with the agreement of the Tufts University Institutional Research Board (IRB ID MODCR-01-12631, authorized on 7/14/2017). The images during the period spanning from January 1, 2014, to December 31, 2016 were carefully selected based on their diagnostic accuracies, along with a focus of minimizing technical faults. The radiographs were converted to a standard picture format (TIFF/JPEG) and were annotated by both a dental specialist and a student using the Labelbox program. The annotations specifically targeted dental masks and maxillomandibular RoIs, which were used as the reference data for training UNet model that learns to recognize important structural components for automated detection of periodontal disorders. Figure 4 presents sample panoramic radiographs of normal (left panel) and periodontal disease (right panel) in the TDD.

Fig. 4.

Sample panoramic radiographs from tufts dental database.

Hanyang university seoul hospital dental database

The second dataset consists of 256 photos in HUSHDD (Hanyang University Seoul Hospital Dental Database), following Hanyang university’s ethical requirements (IRB 2019-01-007-026). Out of them, 138 photos illustrate different phases of periodontal disease, whereas 118 photos portray healthy dental conditions from patients aged over 20 years. Figure 5 presents sample panoramic radiographs of normal (left panel) and periodontal disease (right panel) in HUSHDD.

Fig. 5.

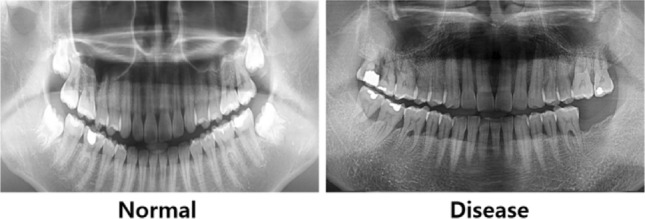
Sample panoramic radiographs from Hanyang University Seoul Hospital Dental Database.

Noor medical imaging center dental database

NMICDD (Noor medical imaging center dental database) is comprised of 116 panoramic dental X-rays collected at the Noor Medical Imaging Center in Qom, Iran, anonymized to protect patient confidentiality³³. The dataset reflects a broad spectrum of dental conditions, encompassing healthy individuals, partially edentulous, and completely edentulous patients. Labeling process of the data was performed to align with the principles applied in HUSHDD, where 70 images capture various stages of periodontal disease and 18 images depict healthy dental states. Exclusions were made for images lacking teeth, patients under 20 years of age, and duplicated records (Fig. 6).

Fig. 6.

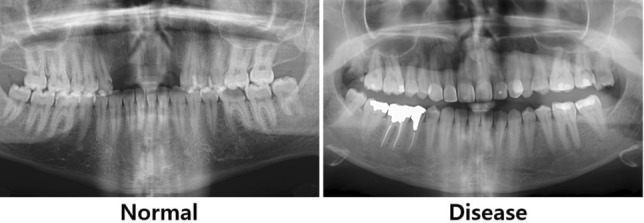
Sample Panoramic Radiographs from Noor Medical Imaging Center Dental Database.

Data pre-processing

The collected dental radiographic images were carefully reviewed by a dental professional, adhering to the classification standards established by the 2017 World Workshop. The images were categorized into control and chronic periodontal disease groups based on observed alveolar bone resorption patterns. Periodontal disease was diagnosed when generalized alveolar bone resorption exceeded 3 mm from the cementoenamel junction (CEJ) in the radiographs. To ensure data quality, images that meet following exclusion criteria were removed from the dataset: mixed dentition (coexistence of primary and permanent teeth), pathologic lesions (e.g., tumors, osteomyelitis, cysts), localized periodontitis affecting one or two teeth, partial or complete edentulous alveolar ridges due to multiple missing teeth, sequelae and metal plates from maxillofacial trauma, and supernumerary teeth in the alveolar bone region. In medical imaging, exposures play a crucial role in radiograph interpretation. However, each radiograph imaging equipment manufacturer has developed its own controlling mechanisms for exposures, resulting in different exposure results and potentially affecting automated image classification tasks³⁴. To mitigate unintentional effects of EIs, we performed picture standardization as a vital pre-requisite for effective application of the UNet-CVAE framework in our few-shot learning architecture. Histogram standardization was employed to improve the uniformity of three image datasets for analysis: TDD, HUSHDD, and NMICDD. The standardization process involved in calculating a global histogram representing the entirety of the image collection by transforming and combining individual image histograms into a uniform format. The global histogram data was then normalized by dividing it by the total number of images in the dataset. Subsequently, histogram equalization³⁵ was implemented on each image to ensure uniformity in contrast and brightness across all the radiographs. This approach utilizes a cumulative distribution function obtained from the global histogram to adjust pixel values of each image to match the standardized distribution. The radiographs were then normalized to guarantee consistent scaling of pixel values within a pre-defined range. Histogram equalization was particularly important for the HUSHDD, as the image data exhibited significant differences in pixel values between normal and periodontal disease data, which could unintentionally affect classification performance. After the global histogram equalization, the exposure of the HUSHDD showed consistency among images. To evaluate the performance of histogram equalization, the standard deviation of average information content (entropy) was employed as an image quality measure. The entropy is defined as

$$\begin{array}{c}\hfill H=-\sum _{i=0}^{L-1}P(i){log}_{2}P(i),\end{array}$$ 6

where P(i) is the probability density function at intensity level i, measuring the richness of image details. Here, L is the total number of grey levels. The standard deviation of average information of radiographs before normalization was 0.2025 and it was reduced to 0.1013 after normalization, effectively mitigating potential biases in model evaluation resulting from these differences.

Analytical results

This section presents the assessment of our proposed few-shot learning framework for identifying periodontal disease via sparse dental panoramic radiographs. Our primary objective is to evaluate the precision and the accuracy of the proposed framework by comparing its effectiveness with traditional deep learning models based on supervised learning concept. In this comparative study of medical imaging diagnostics, accuracy and precision metrics were calculated along with sensitivity and specificity. As the most instinctive performance measure, the accuracy is a ratio of correctly predicted observations to the total observations, and precision is the ratio of correctly predicted positive observations to the total predicted positive observations, while sensitivity and specificity are the ability of the model to correctly identify positive cases (true positive rate) and the ability of the model to correctly identify negative cases (true negative rate), respectively.

Experimental setup

We evaluated the performance of the proposed few-shot learning framework by comparing it with the baseline CNN networks with four convolutional layers, the widely used VGG16 model, the state-of-the-art vision transformer model³⁶, and a UNet-CAE model that uses simple convolutional AE (CAE) instead of CVAE adopted in our proposed framework. For the three datasets, each models underwent same training phases to simulate a few-shot scenario with a restricted number of training data, using periodontal disease photos in sets of 10, 50, and 100 images. The performance of the vision transformer model was assessed by fine-tuning all layers with weights pre-trained with ImageNet. The experimental setups are described in Table 1. Each subset of images was augmented using horizontal mirroring. This approach mirrors real-world scenarios in medical diagnostic enviroments, where large volume of data is limited or sometimes are not available. The experiments were performed on a high-performance workstation with an Intel Xeon Gold 6234 processor, 512 GB of RAM, and an NVIDIA RTX 3090 GPU. This setup used Python 3.10 and Tensorflow 2.12 to facilitate the best utilization of the latest software capabilities and GPU acceleration. The hyper-parameters for each model were optimized using the Bayesian optimization, where the optimization proceeded with three starting points and five iterations. The hyper-parameters for Bayesian optimization include learning rate, the number of layers, filter sizes, and regularization terms, as shown in Table 2. We compared the performance metrics across all the models with same training phases. To ensure the consistency of the modeling, the training process was conducted throughout 100 epochs with a batch size of 16. In order to validate the reliability of the models, we used the fivefold cross-validation. This approach involved in partitioning our dataset into five equal segments. Each subset was used as the test set in a sequential manner, while remaining segments consisted of training data. Upon finishing five iterations, we calculated average performance metrics from each fold to evaluate the efficiency of medical imaging models, specifically when dealing with sparse training data under few-shot learning paradigm.

Table 1.

Training scenarios and model setup in the experiment.

Method type	Training scenarios	Model	Clustering method
Supervised	Training using 10/20/100 images	Baseline CNN/VGG16/Vision transformer
Unsupervised		UNet-CAE/UNet-CVAE	DBSCAN/GMM/k-Means

Table 2.

Search ranges for hyper-parameters in Bayesian optimization.

Parameter	Range	Description
The number of layers	[5, 10]	Adjusting the complexity of the mode
Bottleneck layer size	[5, 50]	Latent dimension size
Learning rate	[0.0001, 0.1]	Used when the optimizer updates weights
The number of clusters	[2, 20]	Used when the optimizer updates weights
Eps	[0.0001, 1.5]	Neighborhood inclusion distance
Min-points	[2, 20]	The minimum number of data points required to form a cluster
KL term weight	[0.001, 10]	Constraining the latent space to regulate the quality of model generation

Comparative performance analysis

To validate the performance of the proposed few-shot learning architecture for sparse dental image classification, we analyzed three sets of dental panoramic radiographs: TDD, HUSHDD, and NMICDD. For performance evaluation, the precision and the accuracy in classifying periodontal disease were calculated.

Tuffs dental database

We first evaluated the performance of our proposed framework on the TDD. The proposed approach was firstly compared with popular supervised models; the baseline CNN, the VGG16 model, and the vision transformer model, under training scenarios of 10, 20, and 100 radiograph images. Table 3 presents the accuracy and precision results for our proposed framework and the supervised models. The results show that our proposed framework achieves comparable performance to the state-of-the-art supervised models, even without training with labeled data. This highlights the potential of our approach in scenarios where annotated data is scarce, which is often the case in medical image analysis. Notably, the vision transformer model structure experienced significant overfitting problems, showing zero specificity when trained with 10 images. This suggests that deeper models like the vision transformer are prone to overfitting to specific data when trained on very limited datasets. Additionally, we compared our proposed framework with an unsupervised framework using a standard CAE with UNet. The results indicate that our proposed model outperforms the CAE-based model. This performance improvement is mainly attributed to the ability of CVAE to capture more informative latent representations by assuming a probabilistic distribution in the latent space.

Table 3.

Performance comparison of models using TDD.

Method type	Model	Training scenarios	Clustering methods	Accuracy	Precision	Sensitivity	Specificity
Supervised	Baseline CNN	Training using 10 images		0.513	0.554	0.546	0.474
		Training using 20 images		0.610	0.636	0.559	0.663
		Training using 100 images		0.827	0.696	0.794	0.842
	VGG16	Training using 10 images		0.566	0.636	0.426	0.723
		Training using 20 images		0.718	0.732	0.619	0.803
		Training using 100 images		0.754	0.798	0.639	0.856
	Vision transformer	Training using 10 images		0.510	0.510	1.000	0.000
		Training using 20 images		0.610	0.607	0.667	0.551
		Training using 100 images		0.710	0.704	0.745	0.673
Unsupervised	UNet-CAE		DBSCAN	0.804	0.851	0.698	0.895
			GMM	0.751	0.758	0.661	0.825
			k-Means	0.703	0.688	0.624	0.768
	UNet-CVAE (proposed)		DBSCAN	0.854	0.852	0.840	0.867
			GMM	0.676	0.708	0.646	0.708
			k-Means	0.640	0.703	0.588	0.703

In particular, an important observation involved in the investigation of instances where detections of periodontal disease are not properly performed. Our framework sometimes fails to successfully identify periodontal diseases in photos that have only a small portion of affected areas. For example, our method identified several cases as normal that were ambiguously borderline cases, especially in young ages who present earlier signs of periodontal disease. The change of accuracy in detecting the disease according to age addresses the importance of adopting customized diagnostic techniques taking individual characteristics, e.g., age, sex, medical history, into account.

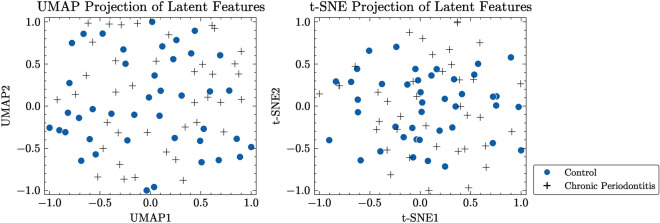
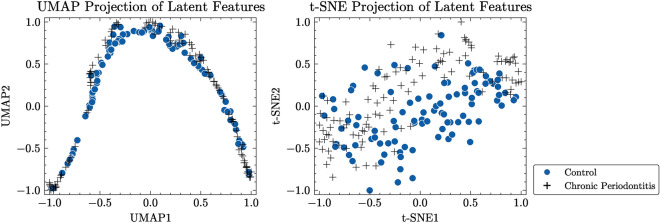
To better illustrate the efficacy of our proposed method in capturing underlying structures of dental radiography data, we created two-dimensional maps utilizing the latent variables derived from both the CAE-embedded method and our approach. We employed two commonly used methods for reducing dimensionality and visualizing data: Uniform Manifold Approximation and Projection (UMAP)³⁷ and t-Distributed Stochastic Neighbor Embedding (t-SNE)³⁸. These techniques allowed us to map high-dimensional latent variables onto a two-dimensional space. UMAP is effective in learning the structure of data in a lower-dimensional representation while maintaining both local and global characteristics of the original data. Conversely, t-SNE prioritizes maintaining the nearby arrangement of data points by reducing the Kullback–Leibler divergence between the probabilities of original high-dimensional data and transformed low-dimensional embeddings.

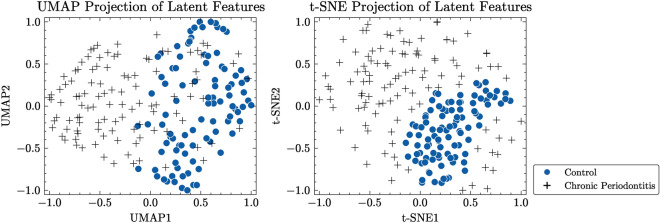
Figure 7 displays normalized visualizations of latent features obtained by the CAE model, while Fig. 8 presents normalized visualizations of latent features generated with our proposed approach. In the CAE model’s visualization, there is a noticeable overlap between control and periodontitis groups, indicating less effective discrimination between these classes. Conversely, our proposed model demonstrates a clear distinction between the two groups, particularly in the UMAP visualization. This distinction is crucial, as it highlights the ability of our model to better separate different conditions. The latent space acquired by our model shows a dense, non-spherical structure for instances of periodontal disease, which enables DBSCAN to outperform k-means and GMM, both of which rely on the assumption that data points are grouped within connected, spherical or ellipsoidal shapes. The reduced overlap and enhanced separation capability observed in our model suggest that it provides better discrimination among the classes compared to the CAE model.

Fig. 7.

Visualization of latent features from CAE model for TDD.

Fig. 8.

Visualization of latent features from the proposed model for TDD.

Hanyang university seoul hospital dental database

Our proposed framework was also applied to the HUSHDD. Similar to the TDD performance comparison, we compared our method with supervised models, as well as an unsupervised framework. It is noted from Table 4 that our unsupervised framework without training labels shows comparable precision and accuracy performance over supervised models with labeled training images. In addition, the comparison results with the other unsupervised model indicate that our proposed framework shows superior precision and accuracy performance, across various clustering methods, in dealing with a variety of subtleties in dental panoramic radiographs. The vision transformer model suffers from overfitting, particularly when trained with a smaller number of images, which affected its overall performance. In particular, HUSHDD only include two categories of normal and periodontal disease unlike TDD that contains another medical conditions, as well as normal and periodontal disease. As a result, classification performance is significantly improved by only classifying succinct status of periodontal disease in HUSHDD.

Table 4.

Performance comparison of models using HUSHDD.

Method type	Model	Training scenarios	Clustering methods	Accuracy	Precision	Sensitivity	Specificity
Supervised	Baseline CNN	Training using 10 images		0.602	0.659	0.570	0.641
		Training using 20 images		0.679	0.716	0.653	0.708
		Training using 100 images		0.717	0.735	0.676	0.758
	VGG16	Training using 10 images		0.591	0.604	0.668	0.505
		Training using 20 images		0.670	0.672	0.685	0.655
		Training using 100 images		0.696	0.710	0.594	0.786
	Vision transformer	Training using 10 images		0.539	0.539	1.000	0.000
		Training using 20 images		0.539	0.539	1.000	0.000
		Training using 100 images		0.805	0.824	0.812	0.797
Unsupervised	UNet-CAE		DBSCAN	0.743	0.791	0.625	0.850
			GMM	0.789	0.807	0.829	0.736
			k-Means	0.657	0.669	0.551	0.752
	UNet-CVAE (proposed)		DBSCAN	0.949	0.974	0.921	0.976
			GMM	0.919	0.916	0.908	0.928
			k-Means	0.879	0.909	0.885	0.870

To further investigate the effectiveness of our proposed method in capturing the latent structure of the HUSHDD, we generated 2-dimensional visualizations using the latent variables obtained from the CAE-based method and our proposed approach. Similar to the TDD analysis, we employed UMAP and t-SNE techniques to project high-dimensional latent variables onto a 2D space.

Figure 9 displays normalized visualizations of latent features recovered by the CAE model, whereas Fig. 10 presents normalized visualizations of latent features constructed with our proposed approach. By comparing these representations, it is noticeable that our method achieves a more pronounced differentiation between the normal and periodontal disease instances in the HUSHDD dataset, unlike the CAE-embedding method, which makes it difficult to identify the difference between control and chronic periodontitis groups. The clusters formed by our method are tighter and more cohesive compared to the TDD cases. As a result, both clustering methods perform similarly. These visualizations address the need for additional verification to support the efficacy of our proposed UNet-CVAE framework in accurately representing underlying structure of dental panoramic radiographs.

Fig. 9.

Visualization of latent features from CAE model for HUSHDD.

Fig. 10.

Visualization of latent features from the proposed model for HUSHDD.

Noor medical imaging center dental database

To further assess the efficacy of our proposed framework, we applied the proposed framework to NMICDD. Similar to the evaluations conducted on the TDD and HUSHDD datasets, we compared the performance of our method against both supervised models, including the baseline CNN, VGG16, Vision Transformer, and an unsupervised framework utilizing a UNet-based Convolutional Autoencoder (CAE). The training scenarios were adjusted according to the size of the dataset, trained under training scanarios of 10, 20, and 45 radiograph images.

As detailed in Table 5, our framework demonstrates superior accuracy and precision in classifying periodontal disease, even when trained with the minimal number of labeled images. As observed in previous cases, deeper models like VGG16 and vision transformer suffer from significant overfitting, particularly due to imbalanced nature of the data. In contrast, the baseline CNN do not suffer from overfitting as heavily, addressing significant effects of model depth on overfitting in these scenarios. The results underscore the robustness of our method, particularly in scenarios where labeled data is sparse, a common challenge in medical image analysis. Notably, our approach outperforms the CAE-based model across various clustering methods, validating its ability to capture intricate latent structures within dental radiographs.

Table 5.

Performance comparison of models using NMICDD.

Method type	Model	Training scenarios	Clustering methods	Accuracy	Precision	Sensitivity	Specificity
Supervised	Baseline CNN	Training using 10 images		0.791	0.791	0.480	0.918
		Training using 20 images		0.721	0.514	0.720	0.721
		Training using 45 images		0.861	0.760	0.760	0.902
	VGG16	Training using 10 images		0.791	0.000	0.000	1.000
		Training using 20 images		0.791	0.000	0.000	1.000
		Training using 45 images		0.791	0.000	0.000	1.000
	Vision transformer	Training using 10 images		0.791	0.000	0.000	1.000
		Training using 20 images		0.535	0.347	0.680	0.475
		Training using 45 images		0.686	0.400	0.160	0.902
Unsupervised	UNet-CAE		DBSCAN	0.802	0.833	0.400	0.967
			GMM	0.686	0.469	0.600	0.721
			k-Means	0.674	0.462	0.720	0.656
	UNet-CVAE (proposed)		DBSCAN	0.884	0.941	0.640	0.984
			GMM	0.814	1.000	0.360	1.000
			k-Means	0.709	0.500	0.760	0.689

A noteworthy observation during our analysis is the ability of our model to handle diverse range of dental conditions present in the NMICDD, including the cases of partial edentulism. However, similar to the results seen with TDD, our framework occasionally struggles with borderline cases of periodontal disease, particularly in younger patients or those with minimally affected areas. This suggests the potential need for age-specific or condition-specific tuning of the model to improve diagnostic accuracy.

To further explore latent structures captured by our proposed model within the NMICDD dataset, we employed UMAP and t-SNE techniques to project high-dimensional latent variables onto a two-dimensional space, as depicted in Figs. 11 and 12. Figure 11 illustrates normalized visualizations of latent features recovered by the CAE model, while Fig. 12 presents those generated by our proposed method. These visualizations reveal that our approach achieves a more distinct separation between different dental conditions present in NMICDD, compared to the CAE model. The clustering formed by our method is more cohesive and distinct, particularly in distinguishing between healthy and edentulous patients, affirming the strength of our UNet-CVAE framework in effectively modeling underlying structures in dental panoramic radiographs.

Fig. 11.

Visualization of latent features from CAE model for NMICDD.

Fig. 12.

Visualization of latent features from the proposed model for NMICDD.

In summary, comparative analyses on TDD, HUSHDD, and NMICDD demonstrate the effectiveness of our proposed few-shot learning architecture in diagnosing periodontal disease with sparse labeled radiographs. The architecture achieves comparable performance to state-of-the-art supervised models with labeled radiographs and outperforms the popular unsupervised method of CAE. The visualization results of latent features address the need for incorporating distributional assumptions for latent features, as shown in the comparison with the CAE-embedded method that does not consider distributional assumptions for latent features.

Conclusions and discussion

The primary objective of this study is to provide an efficient method for diagnosing periodontal disease from sparse panoramic radiograph images using a few-shot learning architecture. This framework aims to overcome the issues of limited data availability commonly observed in medical image processing. The effectiveness of our UNet-CVAE model was demonstrated by using two real dental image datasets, highlighting the potential in accurate diagnosing periodontal disease without a large amount of training data. The combined architecture of UNet for RoI detection and CVAE network for feature extraction is a notable contribution in few-shot learning, which showcases the ability to achieve higher diagnostic accuracy even with a small amount of image data. Our comparative analyses demonstrate that our unsupervised learning-based framework achieves the higher level of performance over supervised learning models such as baseline CNN, VGG16, and even with pre-trained vision transformer model fine-tuned with large amount of data. Our comparative analyses further reveal that deeper models, such as VGG16 and the vision transformer, are prone to significant overfitting, particularly when faced with imbalanced and limited datasets.

An essential aspect of our study includes pre-processing procedure such as histogram equalization to rectify the wide-spread imbalance problems in pixel values in panoramic radiographs. The disparity, particularly evident in the dataset obtained from Hanyang university Seoul hospital, was successfully alleviated such that model performance and dependability were greatly improved by grouping various progressions of periodontal diseases a priori.

Significant advancements in deep learning methods have shown promising results in the automated detection and classification of periodontal diseases from dental radiographs. Kim et al.¹⁰ introduced a deep neural transfer network (DeNTNet) that was specifically designed to detect periodontal bone losses in panoramic dental radiographs. By leveraging transfer learning and incorporating clinical prior knowledge, DeNTNet effectively handles morphological variations and imbalanced datasets. The model was evaluated on a large dataset consisting of 12,179 radiographs, demonstrating superior performance with an F1 score of 0.75, surpassing average performance of dental clinicians, who achieved an F1 score of 0.69. In another study, Chang et al.⁹ proposed a computer-aided diagnosis (CAD) method based on Mask R-CNN for automatic diagnosis of periodontal bone losses and the stage of periodontitis on dental panoramic radiographs. This approach combines a deep learning architecture for detection with conventional CAD processing for classification, resulting in high accuracy and reliability, as evidenced by a Pearson correlation coefficient of 0.73 and an intraclass correlation coefficient of 0.91. Although such approaches as DeNTNet and Mask R-CNN have shown the efficacy in tooth segmentation and classification tasks, their performances are dependent highly on the availability of large training datasets. In contrast, our current research focuses mainly on developing an unsupervised few-shot learning framework for the diagnosis of periodontal disease even with small size of data. By employing a small amount of labeled data, this framework aims to address the limitations encountered in previous studies and provide a more efficient and practical solution for clinical applications.

Although our study demonstrated promising results, there are limitations to be addressed in future research. To further validate the robustness and effectiveness of our proposed framework, it is essential to test the proposed model across a broader range of medical images under more varied conditions with multi-center study. This would provide deeper insights into its generalizability to handle diverse clinical scenarios. While our study employed a UNet-CVAE structure to fully leverage the convolutional architecture and enable seamless integration between models, future work could explore the incorporation of our ROI extraction framework with other advanced techniques such as vision transformers, potentially leading to further improvements in diagnostic accuracy. Additionally, incorporating additional data attributes could further enhance the robustness and effectiveness of our proposed framework.

Author contributions

M.J.K.: investigation, methodology, validation, writing-original draft. S.G.C.: formal analysis, investigation, methodology, validation, writing-original draft. S.J.B.: conceptualization, supervision, funding acquisition, writing-review & editing. K.G.H.: supervision, funding acquisition, resources, data curation.

Funding

This work was supported by “Human Resources Program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP), granted financial resources from the Ministry of Trade, Industry & Energy, Republic of Korea (No. 20204010600090) and supported by a grant from the Korea Health Technology R & D Project through the Korea Health Industry Development Institute, funded by the Ministry of Health & Welfare, Republic of Korea (Grant Number: HI20C0013).

Data availability

The Tufts dental database and Noor Medical Imaging Center dental database used in this article are available online at https://tdd.ece.tufts.edu/ and https://data.mendeley.com/datasets/hxt48yk462/2, respectively. The HUSHDD dataset generated during and analysed during the current study are available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.