Enhancing source apportionment of carbon, nitrogen, and phosphorus through integrating PMF and observed source profiles in a subtropical river

Abstract

Apportioning pollution sources under compound pollution conditions is challenging in river pollution source analysis. The positive matrix factorization (PMF) model is widely used to analyze river pollution sources. However, the identification of pollutants in this model relies primarily on the subjective experience of the researchers, leading to ineffective identification of different contaminants from similar sources. In this study, we propose a comprehensive deviation index (CDI) to quantitatively identify pollution source types based on the PMF and observed source profiles. Taking the subtropical Xizhijiang River Basin as a case study, we quantitatively identified the pollution sources and their contributions to dissolved organic carbon (DOC), total nitrogen (TN), and total phosphorus (TP) using observed water quality and pollution sources data. The results showed that the eight major pollutants in the study region exhibited significant positive correlations, indicating the similarity of pollutant sources in the watershed. The PMF model identified three primary pollution sources with coefficients of determination for observed versus predicted concentrations ranging from 0.60 to 0.98. The CDI unveiled that the watershed's three pollution sources were farmland, rural, and wastewater treatment plants (WTPs). Farmland emerges as the predominant contributor to DOC (68.04 %), TC (63.29 %), and TDP (44.51 %). Rural notably contributes to NH₃-N, PO₄³⁻, TDP, and TN, with percentages of 86.37 %, 57.65 %, 41.40 %, and 30.45 %, respectively. WTPs significantly contribute to NO₂⁻, NO₃⁻, and TN, accounting for 71.81 %, 57.39 %, and 37.26 %, respectively. Incorporating source fingerprints into the PMF model, the CDI can accurately identify pollution sources, improve the interpretability of source identification, and mitigate uncertainty in the multiple-source unknown receptor model. These findings have immediate and practical implications for river ecosystem management and pollution control, providing a more effective method for identifying and addressing pollution sources.

1. Introduction

As climate change and human activities intensify, environmental pollutants' diversity and migration patterns are becoming increasingly complex, posing significant challenges in identifying their sources and contributions [1,2]. Source apportionment is a vital method for determining the origins and contributions of environmental pollutants and is essential for effective pollution control. Enhancing water quality hinges on the precise identification of pollution sources. Objective identification and quantitative evaluation of these sources are prerequisites for implementing refined water management strategies and devising effective watershed pollution control measures [3]. Methods for identifying water environment pollution sources can be categorized into source inventory methods, dispersion models, and receptor models. The source inventory method involves quantifying the emissions of major pollutants within a basin to identify the primary pollution sources in the environment. Dispersion models are predictive tools that effectively forecast the spatial and temporal distribution of input pollutants [4]. However, the source inventory method and dispersion model method have practical limitations, such as being labor-intensive, requiring numerous parameters, and demanding high data volume and accuracy [5]. Receptor models are methods used to identify pollution sources and their contributions based on environmental pollutants' characteristics. These models are among the mainstream source apportionment methods, including source-known and source-unknown receptor models [6]. Source-unknown receptor models, which require less information about the types and quantities of pollution sources, have become essential for apportioning sources in complex environmental pollution scenarios. However, the current methods for determining pollution source types in source-unknown receptor models are primarily qualitative and semi-quantitative, significantly contributing to uncertainty in source apportionment. Therefore, our research objective is to optimize the PMF model for quantitatively identifying pollution sources in receptor models, a critical challenge that must be resolved in source apportionment.

Source apportionment was initially applied to study atmospheric pollutants [[7], [8], [9]]. It has gradually been extended to water bodies and soils [10,11]. A typical method within source-known receptor models is the chemical mass balance (CMB) method, which is suitable for calculating source contributions when the source composition profiles are known. However, due to the complexity of pollution sources in the natural environment, obtaining comprehensive source composition profiles is often not feasible, thus limiting its application in natural water environments [12]. Source-unknown receptor models can calculate characteristic information representing pollution source compositions, making them commonly used for water pollution source apportionment. Models such as UNMIX, principal components analysis (PCA), and positive matrix factorization (PMF) have been widely applied to identify the sources and distribution of pollutants in the environment [[13], [14], [15]]. In recent years, the UNMIX model has been frequently used abroad for source apportionment of PM_2.5 and PM₁₀, while domestically, it has been applied more to the source apportionment of organic compounds. The approach employed by the UNMIX model to mitigate outliers in the dataset is relatively coarse, consequently leading to challenges in finely distinguishing sources with limited distinctiveness [16]. Although PCA yields reliable source identification results and is relatively straightforward, it cannot quantitatively provide source contributions [17], thus necessitating further combination with other methods, such as multiple linear regression [18]. The PMF model is a multivariate factor analysis tool that decomposes the sample concentration data matrix input into two matrices: factor contributions (G) and factor profiles (F) using a multilinear iterative algorithm [19]. Supported by the U.S. EPA, the PMF model has evolved to version 5.0, which includes three error assessment methods: Bootstrap (BS), Displacement (DISP), and Bootstrap-Displacement (BS-DISP), reducing the uncertainty in the number of identified factors [20]. Thus, the PMF model not only provides the number of pollution sources but also outputs the source profiles and contributions, making it widely used in the source apportionment of various environmental pollutants [[21], [22], [23]]. Zanotti et al. (2019) [24] demonstrated that the PMF model could effectively identify pollutant sources in surface water. By incorporating an uncertainty data matrix and a non-negative constraint solution, the PMF model addresses the limitations of PCA [19]. The PMF model excels in handling missing data and interpreting data accurately, resulting in more accurate calculations of source contributions without relying on previously observed or emission inventory source information [25,26]. In receptor models, PMF applies non-negative constraints to the factor decomposition matrix, ensuring that the resulting source profiles and source contribution rates do not have negative values, making the results more reasonable [19].

Despite the widespread application of the PMF model in apportioning the sources of air, water, and soil pollutants, the model can only produce the calculated source profiles without specifying the exact types of pollution sources. Currently, the identification of pollution source types in the PMF model relies heavily on researchers' subjective judgment, leading to significant biases and reducing the objectivity of source identification. The primary methods for PMF source identification are the empirical method and the characteristic pollutant ratio method. The empirical method involves identifying the pollution sources of major pollutants based on the source apportionment factors from the PMF model, using experience or pollution source characteristics summarized in other literature. After running the PMF model, this method allows experts to quickly and easily identify pollution sources based on their experience, making it more aligned with real-world conditions [27]. A drawback is that, due to changes in geographical environment and climate, there can be significant differences in pollutant characteristics between different studies. This introduces uncertainty and subjectivity in source identification [28]. The characteristic pollutant ratio method involves comparing the ratios of characteristic pollutants with the ratios of the same pollutants in the measured sources. This method allows for a preliminary determination of the pollution sources and the relative contributions of the associated species [29]. However, when the characteristic pollutant ratios in different source apportionment factors are similar to those in the measured pollution sources, it increases the difficulty of identifying the pollution sources. To mitigate this subjectivity, Soonthornnonda and Christensen et al. (2008) [30] combined PMF and CMB models to identify the sources of pollutants in sewer wastewater. Comero et al. (2012) [22] used the PMF model to analyze soil samples from abandoned mines in Italy and employed geographical information systems (GIS) to interpret the sources of pollutants. Zhang et al. (2020) [31] explored the applicability and effectiveness of the PMF model and absolute principal component score-multiple linear regression (APCS-MLR) in identifying groundwater pollution sources. Zhang et al. (2022) [32] utilized the PMF model and machine learning to reveal the synergistic effects of pollution sources and meteorological factors on PM_2.5. Although previous studies have used various model combinations for comparative analysis to interpret pollutant sources, identifying pollution source types still largely depends on researchers' judgment, and the issue of subjectivity remains unresolved.

To address the subjectivity in pollution source identification, this study proposes a source identification method based on the deviation of source profiles in calculated and observed source profiles. This method quantitatively identifies pollution source types by comparing the CDI between the resolved source profiles of the PMF model and observed source profiles, thereby reducing the uncertainty in source identification factors in the PMF model and enhancing the objectivity of pollution source apportionment. A case study was conducted using the Xizhijiang River Basin (XRB), characterized by multiple pollution sources. In December 2023, samples were collected from 38 sites along the mainstream and primary tributaries of the XRB. Using the EPA PMF5.0 model results and error analysis, the number of pollution sources in the XRB was identified, and their contributions were quantitatively analyzed. By comparing the PMF model source apportionment factors with observed pollutant concentrations and using a CDI, the pollution sources in the XRB were identified with limited pollution source information and multiple indicator comparisons. The objectives of this study include: 1) analyzing the characteristics of water quality in the XRB; 2) quantitatively identifying the number and contributions of pollution sources in the XRB using the PMF model; 3) constructing a comprehensive deviation index calculation model to identify pollution sources.

2. Materials and methods

2.1. Study area

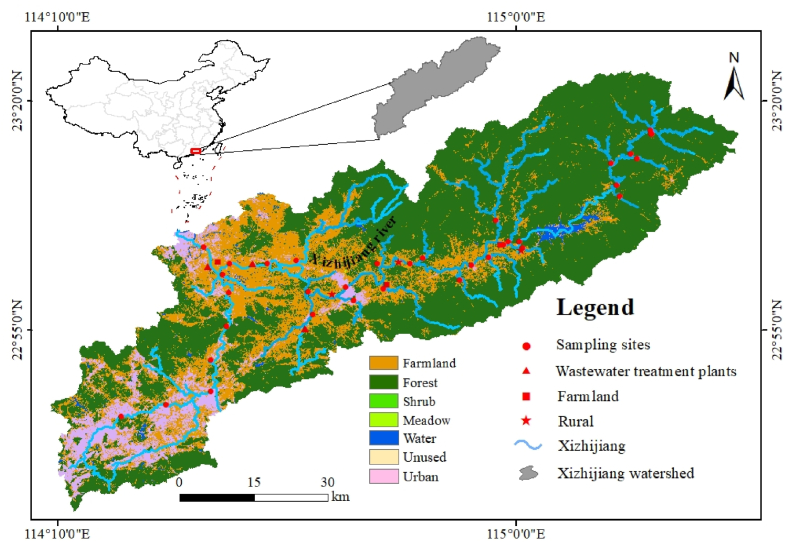
The Xizhijiang River, the second largest tributary of the Dongjiang River in the Pearl River Basin, is one of the most important rivers in Huizhou City, with a length of 176 km and a basin area of 4120 km². Located in the subtropical marine monsoon climate zone, the Xizhijiang River Basin has an average annual precipitation of 1900 mm and an average annual temperature of 22 °C. The river flows roughly from northeast to southwest, with steep terrain in the middle and upper reaches and flat terrain in the lower reaches (Fig. 1). The XRB flows to the Dongjiang River in the Dongxin District of Huizhou City, significantly impacting the water quality of the Dongjiang River. Since the 1980s, the basin has undergone rapid economic and social development, accelerated urbanization, escalating water demand, and relatively delayed endeavors in water pollution control [33]. Some sections of the river had water quality that falls into Class V, according to the Chinese Environmental Quality Standards for Surface Water (GB3838-2002), which indicates that it has lost most environmental functions, such as drinking. According to the Ecological Environment Bulletin of Huizhou City recently, all four water quality monitoring sections of the XRB were rated as Class V in 2010, with ammonia nitrogen (NH₃-N) and total phosphorus (TP) being the primary pollutants. The water quality in the upper and middle reaches of the XRB is good. Still, the lower reaches are mildly polluted due to the influence of the Danshui River, with dissolved oxygen (DO), NH₃-N, and fecal coliforms exceeding Class III standards, indicating Class IV water quality. In 2019, the water quality of the Danshui River was severely polluted, mainly exceeding the standard for NH₃-N; in 2020, it was mildly polluted, and there was a slight improvement in water quality in 2022. Overall, from 2019 to 2022, the water quality of the XRB remained excellent.

Fig. 1.

Geographic location and sampling points of water quality and pollution sources in the Xizhijiang River Basin.

2.2. Positive matrix factorization

The positive matrix factorization model (PMF), introduced by Paatero and Tapper, is a bilinear model incorporating non-negativity constraints based on the least squares method [19]. As one of the source apportionment models recommended by the United States Environmental Protection Agency (EPA), EPA PMF5.0 has evolved into a robust and comprehensive tool for source apportionment factor analysis [34,35]. The fundamental principle of the PMF model is to decompose the input matrix of sample paraments concentration data into two matrices: factor contributions (G) and factor profiles (F) [36]. Analyzing the factor profiles can determine the types and contributions of various pollution sources. This can be mathematically represented as Eq. (1):

$$\begin{array}{c}X=GF+E\end{array}$$ (1)

where X is an n × m matrix representing the concentrations of m species in n samples. G is an n × p matrix representing the contributions of p sources to the samples. F is a p × m matrix representing the composition profiles of the p sources, with p being the number of identified pollution sources and E being the residual matrix.

Its component form is expressed as Eq. (2):

$$\begin{array}{c}{x}_{ij}=\sum _{k=1}^p{g}_{ik}{f}_{kj}+e_{ij}=c_{ij}+e_{ij}\end{array}$$ (2)

where p represents the number of factors, x_ij is the concentration of species j in sample i, g_ik denotes the contribution of source k to sample i, f_kj is the concentration of species j in source k, and e_ij represents the error for species j in sample i in the PMF model.

The solution of the PMF model is determined through iterative calculations that minimize the objective function Q (Eq. (3)) based on uncertainties. The optimal number of factors is initially identified by evaluating the Q value, and the stability of the solution is assessed by examining the distribution of each parameter [37]. The definition of Q is:

$$\begin{array}{c}\mathrm{Q}={\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\sum }_{\mathrm{j}=1}^{\mathrm{m}}{\left[\frac{{\mathrm{x}}_{\text{ij}}‐\sum _{\mathrm{k}=1}^{\mathrm{p}}{\mathrm{g}}_{\text{ik}}{\mathrm{f}}_{\text{kj}}}{{\mathrm{U}}_{\text{ij}}}\right]}^2\end{array}$$ (3)

where U_ij represents the uncertainty of species j in sample i, which includes both sampling and analytical errors [38].

The PMF model provides two Q values: Q_true and Q_robust. These values are crucial in the PMF model, as they measure the model's goodness of fit. Q_true is the goodness-of-fit parameter calculated using all data points. Q_robust, on the other hand, is the goodness-of-fit parameter calculated excluding points not fit by the model, defined as samples for which the uncertainty-scaled residual is greater than 4. Typically, Q_robust serves as the basis for iterative calculations.

The input files for the PMF model include matrices of sample species concentrations and their uncertainties. Sample concentration data collected are utilized to form the species concentration matrix. When the sample concentration is less than or equal to the MDL, the species concentration was replaced with the half of the MDL [39]. In case of missing values, the absent points should be substituted with the median of the contaminant concentration series. The computation of species uncertainties is a critical step in the PMF model, as it involves the range of species concentration data [38]. Following the guidelines provided in the user manual [38] and methods outlined by Reff et al. (2007) [39], the formulas for determining species uncertainties (U_ij) are given in Eq. (4), Eq. (5) and Eq. (6):

$$\begin{array}{c}{U}_{ij}=4\times {Median}_j\left({\mathrm{x}}_{ij}\text{is}\text{missing}\right)\end{array}$$ (4)

$$\begin{array}{c}{U}_{ij}=\frac{5}{6}\times {MDL}_j\left({\mathrm{x}}_{ij}\le {\mathrm{M}\text{DL}}_j\right)\end{array}$$ (5)

$$\begin{array}{c}{U}_{ij}=0.05\ast x_{ij}+MDL\left({\mathrm{x}}_{ij}>{\mathrm{M}\text{DL}}_j\right)\end{array}$$ (6)

where "Median" signifies the median concentration of pollutant j, "MDL" refers to the method detection limit of pollutant j, and x_ij represents the concentration of pollutant j in sample i.

To further refine the determination of the optimal number of factors, the PMF model's fundamental computations are subjected to error assessments, including Bootstrap (BS), Displacement (DISP), and Bootstrap-Displacement (BS-DISP) analyses. These error assessment procedures elucidate the uncertainty associated with the model's source profiles and facilitate the identification of overfitted factors [40]. Through iterative adjustments of the F-matrix peak model rotation, a dQ value lower than 5 % of the baseline Q_Robust value is considered acceptable. Subsequently, the appropriate F_peak result is selected based on the G-space map to characterize the stability of the PMF model's source apportionment [38]. We used the ggcor package in R to perform a Spearman correlation test on the pollutants in the PMF source apportionment results.

2.3. Comprehensive deviation index model

The pollution source profile serves as the primary indicator of pollution source characteristics, typically reflected by the concentrations or relative percentages of various monitored pollutants in the source. In models like PMF, which handle unknown sources, the model can derive analytical pollution source profiles. By comparing the calculated source profiles with the observed pollution source profiles, the type of the resolved pollution source types can be determined, constituting a source matching process. However, current comparison methods often rely on partial elemental ratios or subjective experience, lacking quantitative identification methods. This study proposes a pollution source Comprehensive Deviation Index Model (CDI) to enhance the objectivity of pollution source identification. By calculating the percentage concentrations of characteristic pollutants based on the values from PMF model source apportionment factors and observed pollution sources, the uncertainty in pollution source identification can be initially minimized. The deviation refers to the variance in the percentages of identical pollutant concentrations between the source apportionment factors and the observed pollution sources. A smaller deviation suggests a higher degree of consistency between the resolved source apportionment factors and the observed pollution sources. The calculation formula is shown in Eq. (7):

$$\begin{array}{c}{CRE}_{ijk}=\left|\frac{{CR}_{ijk}}{{AR}_{ijk}}-1\right|\times 100\%\end{array}$$ (7)

where CRE represents the deviation of the k-th characteristic pollutant concentration percentage between the resolved source apportionment factor i and the observed pollution source j. It assumes absolute non-negative values, where larger values indicate more significant disparities between the resolved and observed pollution sources. CR and AR denote the characteristic pollutant concentration percentages of the source apportionment factor and the observed pollution source, respectively. Subscripts i, j, and k represent the source apportionment factor, the observed pollution source, and the pollutant index, respectively.

However, the presence of multiple pollutants in pollution sources implies that relying solely on individual indicators may not sufficiently encapsulate the information of other factors. Therefore, it's necessary to compute CRE for various indicators and then integrate them. This entails calculating a CDI based on the deviation of each characteristic pollutant, thus leveraging the characteristics of pollutants to identify pollution sources accurately. The CDI assesses the overall deviation of multiple pollutant concentration percentages, which is determined using the arithmetic weighting method. The PMF model source apportionment factors are identified based on the results of the CDI. The observed pollution source corresponding to the minimum CDI of the PMF model source apportionment factors is considered the best match for source identification in the PMF model. The calculation method for CDI is shown in Eq. (8):

$$\begin{array}{c}{CE}_{ij}=\sum _k^K{IW}_k\times {CRE}_{ijk}\end{array}$$ (8)

where CE represents the CDI between the resolved source apportionment factor i and the observed pollution source j. IW_k denotes the relative weight of the k-th pollutant, with IW = 1/K when the weights of different pollutant indicators are equal, where K represents the number of pollutant indicators. The weights can also be determined using the Analytic Hierarchy Process (AHP) or the entropy weighting method [41]. In this study, we adopt the equal weighting method, assuming that all the species are equally important.

To enhance the objectivity of source identification in the PMF model, this study introduces a comprehensive deviation index. The source apportionment process based on the CDI in the PMF model consists of four steps. First, the concentration and uncertainty data matrices from the study area are imported into the PMF model, where parameters are adjusted, and the PMF model is run to obtain the concentration percentages of pollutants in each factor. Second, the average concentrations of characteristic pollutants are calculated using the measured pollution source concentration data from two periods. These averages are then used in place of the concentration values to calculate the concentration percentages of pollutants in the measured pollution sources. Third, based on the selected characteristic pollutants, the deviation of each source apportionment factor from the characteristic pollutants in the measured pollution sources is calculated using the concentration percentages and the deviation formula. Finally, on the basis of the arithmetic weighting method, the CDI for the measured pollution sources corresponding to each source apportionment factor is calculated by using the deviations of the characteristic pollutants. Source identification is then performed by comparing the CDI of each factor with those of the measured pollution sources.

2.4. Sample collection

The data used in the PMF model comprise monitored concentrations of pollutants in the environment. This study utilizes data collected from 38 samples at 34 river sampling points along the mainstream and primary tributaries of the XRB in December 2023. We used an upright water sampler to collect water samples and measure pollution sources during the flood season in August and the non-flood season in December in the Xizhijiang River. The samples were collected in polyethylene plastic bottles, sealed, and promptly transported to the laboratory for physicochemical analysis. Since the PMF is a receptor model, it only requires the physical and chemical properties of the receptor samples and pollution sources, without considering pollutant output or transformation processes [5,31]. To avoid the impact of hydrodynamic processes during the flood season on pollutant concentrations, only water quality data from December, the non-flood season, were used as input data for the PMF model. On-site pH and dissolved oxygen (DO) measurements were performed using handheld meters. Total nitrogen (TN), ammonia nitrogen (NH₃-N), nitrate (NO₃⁻), nitrite (NO₂⁻), total dissolved phosphorus (TDP), and orthophosphate (PO₄³⁻) were determined using a spectrophotometer (HACH DR1900). Total carbon (TC) and dissolved organic carbon (DOC) were observed by combustion oxidation-non-dispersive infrared absorption, with samples filtered through a 0.45 μm membrane using a Shimadzu TOC-L CPH analyzer.

In the PMF model, parameters must be expressed as concentrations. Therefore, typical surface water measurements like pH cannot be directly incorporated into the PMF model [24]. Certain elements, including TP, DO, and sulfides, were excluded from the PMF model operation due to their non-normal distributions in residual histograms or low goodness-of-fit between observed and predicted values in the PMF model results. To accurately identify pollution sources for PMF model source apportionment factors, samples were collected from three typical pollution sources within the watershed in August 2023 and December 2023 (Fig. 1). The sources were categorized as wastewater treatment plants (WTPs) source, farmland source, and rural source. For the WTPs source, we collected wastewater discharged from outside the treatment plant area. The farmland source was characterized by collecting wastewater from ditches or rivers near intensive farmland production areas. The rural source was identified by collecting untreated wastewater from areas surrounding rural residential zones, which was then discharged into rivers or channels. The pollutant concentrations of these sources were determined using the same methods mentioned above. The average values of the same pollutants observed during the two sampling periods were used as the final concentration data for the corresponding pollutants of the observed sources. This approach provides a comprehensive profile of the characteristics and concentrations of contaminants from natural sources over two periods and offers a solid basis for identifying the PMF model source apportionment factors.

3. Results

3.1. Basic water quality characteristics

After screening, eight water quality indicators were selected, with basic statistics presented in Table 1. The concentrations of N and P in the XRB are relatively high, with average values for TN, TP, and TDP being 3.4 mg/L, 1.38 mg/L, and 0.53 mg/L, respectively. Nearly 95 % of the sampling points exceeded the class III water standard limits for TN and TP, indicating a significant pressure of nutrient pollution in the XRB. Among the TN, nitrate nitrogen is predominant, with the average NO₃⁻ content being nearly three times that of NH₃-N. Other water quality indicators in the basin are relatively good. The pH ranges from 6.84 to 8.62, with an average value of 7.40, suggesting that the water quality of the XRB is generally neutral and complies with the class III water quality standard outlined. Additionally, NO₃⁻ concentrations are within the limits of the class III water standard. In 97.37 % of the sampling points, DO meets the class III water standard limits, and 92.11 % of the points have NH₃-N concentrations below the class III water standard limits. The average concentrations of TC and DOC are 13.15 mg/L and 9.67 mg/L, respectively, with DOC levels being relatively high, surpassing the global river average (5.75 mg/L) [42]. Although the standard deviation of NO₂⁻ is the smallest, there is significant variability among different observation points.

Table 1.

Basic statistical characteristics of water quality testing data for the Xizhijiang River Basin.

Index	Parameters	Unit	Mean±sda	Min	Max	Standard	Exceeding standard rate (%)c
pHc		–	7.40 ± 0.40	6.84	8.62	6∼9	0
DOc	Dissolved oxygen	mg/L	8.35 ± 1.58	1.27	10.92	5	2.63
TN	Total nitrogen	mg/L	3.40 ± 3.05	0.25	10.60	1.00	94.74
NH3-N	Ammonia nitrogen	mg/L	0.63 ± 1.49	0.01	9.00	1.00	7.89
NO3−	Nitrate	mg/L	1.75 ± 1.88	0.10	6.60	10	0
NO2−	Nitrite	mg/L	0.06 ± 0.08	0.002	0.24	–	–
TC	Total carbon	mg/L	13.15 ± 5.31	6.31	30.15	–	–
DOC	Dissolved organic carbon	mg/L	9.67 ± 3.36	4.80	22.33	–	–
TPc	Total phosphorus	mg/L	1.38 ± 2.06	0.25	9.45	0.2	100
TDP	Total dissolved phosphorus	mg/L	0.53 ± 0.34	0.03	1.94	0.2	–
PO43-	Orthophosphate	mg/L	0.26 ± 0.29	0.02	1.45	–	–

b The "Environmental Quality Standards for Surface Water" Class III water standard limits.

^asd: standard deviation.

^cExceeding standards rate is the number of exceeded samples to the total number of samples.

^cFiltered indicators.

3.2. Identification of the pollution sources number

Determining pollution source numbers in the PMF model involves factor identification, a critical step where a balance between too many factors leading to unclear distributions and too few factors complicating mixed source separation must be struck [43,44]. In EPA PMF5.0, sample concentrations and their corresponding uncertainty data are provided as inputs. Initially, the weighting of each pollutant in the input data is established. Subsequently, the PMF model determines the quantity of source apportionment factors using Q values alongside error assessments such as BS, DISP, and BS-DISP. Given the inadequacy of the signal-to-noise(S/N) ratio in this study for determining pollutant weights, emphasis is placed on assessing weights through residual histograms and the goodness-of-fit (R²) between observed and predicted values. Results from multiple experiments suggest that residuals for some elements like TP, DO, and sulfides lack apparent normal distributions, with copper and fluoride exhibiting relatively low R² values, indicating poor fit. Consequently, "Strong" weights are assigned to TN, NH₃-N, NO₃⁻, NO₂⁻, TC, DOC, TDP, and PO₄³⁻ (Table 2). PMF incorporates only these eight indicators in its calculations, yielding a satisfactory fit in residual histograms and R² values. Moreover, the model ensures robust computational accuracy with BS mapping results consistently above 85 %, indicating low uncertainty in pollutant operating outcomes.

Table 2.

Statistical evaluation of PMF model source apportionment factors.

Diagnostics	3 factor	4 factor	5 factor
Species	TN, NH3-N, NO3−, NO2−, TC, DOC, TDP, PO43-
Seed value	Random
QRobust	569.1	355.6	178.7
QTrue	793.5	368.7	178.7
QRobust/QTrue	0.72	0.96	1
N bootstraps in BS	100
DISP %dQ	<0.1 %	<0.1 %	<0.1 %
DISP swaps	2	14	52
Factors with BS mapping<100 %	Factor3: 95 %	Factor1: 94 %,	Factor1,2,4,5: 99 %,88 %,97 %,97 %
BS-DISP Displaced Species	TN, NH3-N, DOC, TDP
BS-DISP % of Cases Accepted	98 %	79 %	37 %

Under 20 base runs and random seed numbers, the optimal number of factors was determined based on Q values for 3 to 5 factors and error assessment results (Table 2). When representing the number of pollution sources in the PMF model as 3, 4, and 5, the Q_true and Q_robust values for different factor numbers showed negligible variation, indicating the model's robustness to dataset changes [45]. As the number of factors increased, Q_true and Q_robust values gradually decreased, with Q_robust/Q_true approaching 1. This proximity to 1 can suggest either a reasonable number of factors or the presence of very high uncertainties causing Q_true and Q_robust values to be close to 1 [38]. Under the conditions with 4 and 5 factors, the BS results showed good matching, but the DISP and BS-DISP results indicated extensive swapping, suggesting overfitting. When the number of pollution sources was set to 3, Factors 1 and 2 in the BS operation had a 100 % matching degree, and DISP had only two swaps. The TN, NH₃-N, DOC, and TDP pollutants were swapped in BS-DISP, with 98 % acceptable results. Furthermore, with three factors, the goodness-of-fit R² ranged from 0.60 to 0.98, indicating good consistency between observed and predicted values and reliable source apportionment results. To enhance the stability of the PMF model results, the F_peak model was rotated, and the F_peak of −0.25 result was selected as the final outcome based on the G-space plot. The goodness-of-fit R² also ranged from 0.60 to 0.98, specifically DOC (0.98) > TC (0.97) > NO₂⁻ (0.96) > TDP (0.86) > NH₃-N (0.83) > PO₄³⁻ (0.81) > TN (0.78) > NO₃⁻ (0.60). Consequently, the final number of factors was set to 3, indicating that the XRB has three primary pollution sources.

3.3. Pollution source identification

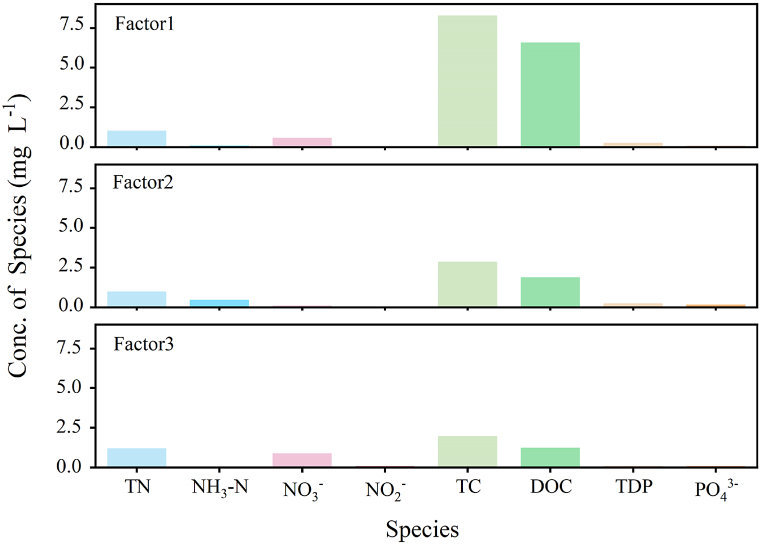
The PMF model weights the uncertainty of each data point and imposes non-negative constraints on the factor decomposition matrices to ensure that the resulting source profiles and source contributions are positive [19,36]. By selecting the F_peak of −0.25, the data points in the G-space distribution plot for each factor are closer to the axes, which enhances the stability of the PMF model's source apportionment results. In the source apportionment factors, the pollutant concentrations, denoted as f_kj in equation (2), indicate that pollutants with higher concentrations contribute more significantly to the factors. The species concentrations for each factor in the study area are shown in Fig. 2. Among the three factors, TC and DOC concentrations are the highest. Comparing the TC and DOC concentrations across the factors, Factor 1 has the highest, and Factor 3 has the lowest concentrations. Moreover, Factor 1 shows the most remarkable difference between TC and DOC, with a difference of 1.68 mg/L. Additionally, in Factor 1, TN and NO₃⁻ concentrations are relatively high, while NH₃-N and TDP concentrations are lower. In Factor 2, the pollutant concentrations in descending order are TN (0.96 mg/L), NH₃-N (0.44 mg/L), and TDP (0.21 mg/L), with NO₃⁻, NO₂⁻, and PO₄³⁻ all below 0.20 mg/L. In Factor 3, the pollutant concentration order is TN > NO₃⁻ > TDP > PO₄³⁻ > NO₂⁻ > NH₃-N. Among the three factors, TN concentration is highest in Factor 3, followed by Factor 1, and then Factor 2. The TDP concentrations in Factors 1 and 2 are similar, at 0.23 mg/L and 0.21 mg/L, respectively, whereas Factor 3 has a TDP concentration of 0.07 mg/L. Although the pollutant concentration contribution trends in Factors 1 and 2 are similar, there is a significant difference in the magnitude of their contributions.

Fig. 2.

Source apportionment factors profiles calculated from the PMF model.

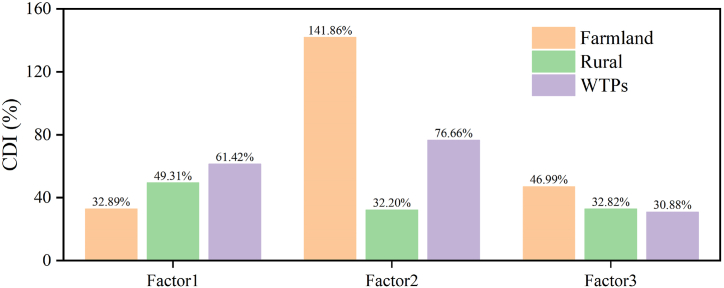
Based on the percentage of characteristic pollutant concentrations from the PMF model's source apportionment factors and observed pollution sources, the relative weights for deviations of characteristic pollutants were set consistently. Using deviation (Eq. (7)) and CDI (Eq. (8)), pollution source information and multi-indicator comparisons were conducted to identify the PMF model's source apportionment factors. By comparing the relationship between the CDI of the PMF model's source apportionment factors and the observed pollution sources (Fig. 3), the sources of pollutants in the XRB were determined. TC, TN, TDP, NH₃-N, and DOC were selected as characteristic pollutants for the watershed. Factor 1 has the smallest CDI from farmland sources, identifying Factor 1 as farmland. Factor 2 shows the smallest CDI from rural sources, identifying Factor 2 as the rural sources. For Factor 3, the CDI from farmland, rural sources, and wastewater treatment plants (WTPs) sources are 46.99 %, 32.82 %, and 30.88 %, respectively. Since the WTPs have the smallest CDI in Factor 3, Factor 3 is identified as the WTPs.

Fig. 3.

Relationship between observed pollution sources and source apportionment factors based on comprehensive deviation index.

3.4. Source contribution calculation

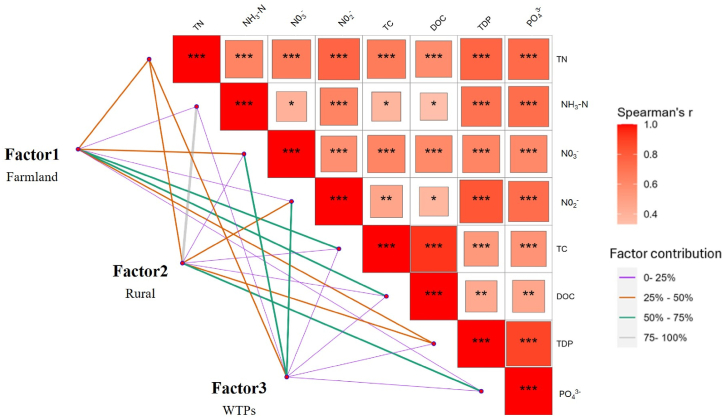
The PMF model output provides pollutant concentrations for each source apportionment factor, enabling the determination of each factor's contribution to each pollutant [46]. The quantitative contributions of the PMF model's identified different factors are illustrated in Fig. 4. Factor 1, recognized as the farmland source based on the CDI, contributes to pollutants in the following order: DOC (68.04 %) > TC (63.29 %) > TDP (44.51 %) > NO₃⁻ (36.64 %) > TN (32.29 %) > PO₄³⁻ (22.94 %) > NH₃-N (13.63 %). This suggests that effectively controlling pollution emissions from farmland sources can significantly reduce DOC and TDP levels in the XRB, thereby mitigating overall pollution. Factor 2, identified as the rural source, is mainly characterized by NH₃-N (86.37 %) and PO₄³⁻ (57.65 %), followed by TDP (41.40 %) and TN (30.45 %). This indicates that rural sources are the major contributors to NH₃-N pollution in the XRB. Factor 3, identified as the WTPs, mainly contributes to NO₂⁻ (71.81 %), NO₃⁻(57.39 %), and TN (37.26 %). This underscores that WTPs are the principal sources of N nutrients. Strict management of N treatment standards in WTPs can further reduce their impact on N levels in the XRB.

Fig. 4.

Source contributions and correlation heatmap of various pollutants.

This study utilized Spearman correlation analysis to explore the relationships among various pollutants in the XRB, as depicted in Fig. 4. Significant positive correlations were detected among all pairs of the eight pollutants in the basin, with correlation coefficients spanning from 0.33 to 0.93. TN displayed notably strong positive correlations with NH₃-N, NO₃⁻, NO₂⁻, TC, DOC, TDP, and PO₄³⁻, ranging from 0.56 to 0.76. Particularly robust correlations were evident between DOC, TN, and TDP, suggesting similarities in C, N, and P sources, further complicating the differentiation of pollution sources.

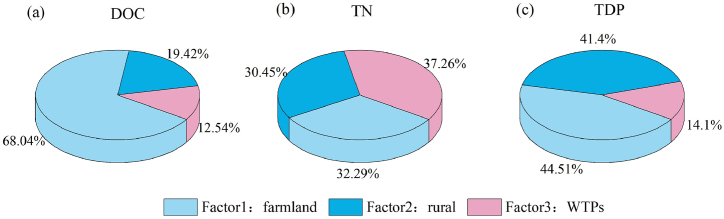
The concentration contributions of DOC, TN, and TDP from various pollution sources in the PMF model source apportionment are illustrated in Fig. 5. Farmland sources predominantly contribute to DOC (Fig. 5a), representing 68.04 % of the total pollution sources, followed by rural and WTPs sources at 19.42 % and 12.54 %, respectively. The contributions of different source apportionment factors to TN (Fig. 5b) are relatively similar, suggesting that farmland, rural, and WTPs sources are the primary contributors to TN in the XRB, with WTPs making the most considerable contribution at 37.26 %. Regarding TDP (Fig. 5c), the contributions from farmland and rural sources are comparable, at 44.51 % and 41.40 %, respectively, while WTPs sources contribute the least, at 14.10 %. This highlights that TDP in the XRB primarily stems from farmland and rural sources. Fig. 5a–c emphasizes that farmland sources are the primary drivers of C, N, and P pollution in the XRB, followed by rural sources. Except for TN, WTPs exhibit the lowest contribution, indicating their effective removal of C and P nutrients. Simultaneously, enhancing the treatment technology for N nutrients in WTPs can effectively mitigate total nitrogen pollution in the XRB.

Fig. 5.

Concentration ratios of characteristic pollutants, including (a) dissolved organic carbon (DOC), (b) total nitrogen (TN), and (c) total dissolved phosphorus (TDP), in different pollution sources.

4. Discussion

4.1. Comparison between CDI and existing source identification methods

The proportion of species concentrations in the factors of the PMF model is depicted in Fig. 6a. Among the three pollution sources identified by the PMF model, species with higher concentrations are predominantly TC > DOC > TN. This suggests that pollutants with higher concentrations across different source apportionment factors exhibit similarities, implying that relying solely on one or a few paraments may not effectively discern pollution sources in the factors. In numerous studies, identifying pollution sources with the PMF model often involves comparing characteristic pollutants of factor profiles with those from other investigations [10,31]. When identifying pollution sources in the XRB, the proportions of characteristic pollutants TC, DOC, and TN are relatively high and similar in both the source apportionment factors and observed pollution sources (Fig. 6). Conversely, other indicators such as TDP exhibit lower proportions and less discriminative power. This indicates that the characteristic pollutants TC, DOC, TN, and TDP in the XRB lack distinctiveness among different source apportionment factors and observed pollution sources. Consequently, the method of linking the factor profiles obtained by the PMF model to observed pollution sources is relatively subjective. Furthermore, the effectiveness of identifying pollution sources in the XRB through characteristic pollutant comparison is limited, leading to excessively subjective identification outcomes.

Fig. 6.

Comparison of source profiles of (a) PMF and (b) observed pollution source.

Characteristic pollutant ratios, or the stoichiometric ratios of characteristic pollutants, can provide insights into the characteristics of pollution sources. For example, Fu et al. (2020) [29] utilized the stoichiometric ratios of characteristic species in VOC components to preliminarily evaluate pollution sources and their contributions. Similarly, Calzolai et al. (2015) [47], when identifying pollution sources of PM₁₀ in the Mediterranean, integrated ratios of characteristic pollutants from prior studies with PMF model source apportionment results in pinpointing sea salt as one pollution source. To mitigate uncertainty stemming from the number of characteristic pollutants in identifying pollution sources based on stoichiometric ratios, five species in the XRB were designated as characteristic pollutants: TC, DOC, TN, NH₃-N, and TDP. The stoichiometric ratios of these characteristic pollutants in the source apportionment factors and observed pollution sources are presented in Table 3. However, the TN/TDP and DOC/TC ratios in Factors 1 and 2 exhibit similarities, posing challenges in distinguishing between different pollution sources solely based on these indicators. Despite this, when paired with pollution sources, the TC/TDP and NH₃-N/TN ratios in Factor 1 align closely with those of farmland sources, whereas the DOC/TC and TC/TN ratios in Factor 2 resemble those of farmland sources, complicating the determination of the pairing relationship between Factors 1 and 2 and farmland sources. Therefore, relying solely on characteristic pollutant stoichiometric ratios proves challenging in discerning similar sources, leading to lower objectivity in source identification results. Additionally, some stoichiometric ratios of characteristic pollutants lack practical significance, so this study uses the concentration percentages of characteristic pollutants from each pollution source. By leveraging characteristic pollutants within water bodies to enhance the representativeness of concentration percentages and deviations, the explanatory capacity of CDI in PMF model source identification is further bolstered, thus strengthening the discrimination between pollution sources.

Table 3.

Stoichiometric ratios of characteristic pollutants for observed and calculated pollution sources.

Source	Type	TN/TDP	DOC/TC	TC/TN	TC/TDP	NH3-N/TN
Observed	Farmland	11.45	0.67	3.57	40.90	0.08
	Rural	10.91	0.66	2.29	25.02	0.31
	WTPs	26.37	0.66	1.25	32.88	0.13
Calculated	Factor1	4.51	0.80	8.09	36.53	0.07
	Factor 2	4.58	0.66	2.95	13.51	0.45
	Factor3	16.45	0.62	1.66	27.23	0.00

With the continued economic development within the basin, the XRB is expected to face increasing pressure on water quality, aquatic ecosystems, and drinking water safety. However, there have been relatively few studies focused on pollution source apportionment in the XRB. Most research has been conducted on similar water bodies, such as the Dongjiang River, where studies have examined the aquatic environment and ecological conditions [48], as well as the impact of non-point source pollution in tributaries like the Danshui River [49]. Zhang et al. (2013) [50] identified five major environmental factors in both the main stream and tributaries of the XRB. Factor 1 was dominated by SiO₃ and water temperature, while Factor 5 was dominated by suspended solids. In contrast, this study primarily focused on C, N, and P indicators in the water body, and the PMF model did not include suspended solids and water temperature as input data.

Jiang et al. (2009) [33] reported that during the rainy season in the upper and middle reaches of the Dongjiang River, rainfall runoff processes such as leaching and scouring transport pesticides, fertilizers, plant and animal residues, and soil nutrients like N and P from agricultural fields into the river, leading to an increase in pollutant concentrations in the water. The Danshui River, a primary tributary of the XRB, is heavily polluted due to the direct discharge of untreated industrial and domestic wastewater from upstream areas in Shenzhen, which affects the water quality of the Xizhijiang River's lower reaches. The lower reaches are also influenced by pollution from the Danshui River and effluent discharges along the banks. Cheng et al. (2024) [51] demonstrated that non-point sources are the main contributors to nitrogen and phosphorus inputs in the Dongjiang River's main stream. The sources of organic matter in the Dongjiang River primarily include domestic and industrial waste, aquaculture, and agricultural surface runoff [48]. Previous studies on the Xizhijiang River and similar water bodies suggest that non-point sources are a major concern in the Xizhijiang River Basin. In this study, farmland and rural sources in the Xizhijiang River's source apportionment are both influenced by rainfall and can be considered as non-point sources.

4.2. The limitations of this study

The uncertainty matrix, as the primary data input for the PMF model, directly influences the Q values in Equation (3), thereby affecting the preliminary determination of the number of factors and the results of three error analyses [38]. Therefore, accurate calculation of uncertainty values is crucial for the computational results of the PMF model. For some datasets, uncertainty values corresponding to each concentration data provided by the laboratory can be analyzed. However, when uncertainty values are not provided, the reliability of the calculation results of the algorithm provided in the guidance manual is compromised, leading to bias in the preliminary determination of the number of factors due to the influence of uncertainty values. Therefore, in future studies on PMF model source apportionment, uncertainty results should first be determined based on various algorithms for uncertainty values of multiple PMF model inputs provided by Reff et al. (2007) [39] to reduce errors in uncertainty data input. To accurately identify the number of factors, three error analysis results should be run and analyzed to increase the understanding of uncertainty estimation for different source apportionment factors. Finally, the stability of the source apportionment factor results should be judged based on the G-space plot. The CDI model proposed in this study effectively integrates information from different pollution indicators, thereby enhancing the discrimination between pollution sources. However, in this study, there were significant differences in the deviation of individual pollution indicators, indicating that the selection of indicators has a significant impact on the final results. To further improve the accuracy of pollution source identification, future research should endeavor to include more characteristic pollutant indicators in the calculation of CDI.

The CDI was established based on the measured pollution sources and PMF results within the study area. However, the sampling points for the measured pollution sources were not unique. To reduce the uncertainty in the water quality results of these measurements and enhance the reliability of the source apportionment, this study selected three regions within the basin to sample three characteristic pollution sources. The choice of characteristic pollutants can lead to variability in the deviation results, which in turn affects the source apportionment outcomes. In this study, C, N, and P were selected as the characteristic pollutants. By using multiple characteristic pollutants and comparing the PMF model source apportionment results with the percentage of these pollutants in the measured sources, we preliminarily reduced the uncertainty associated with the number of characteristic pollutants and the deviation in source identification. Future research should further sample and analyze measured pollution sources within the study area, increasing the number of characteristic pollutants considered in the source apportionment process to reduce discrepancies caused by insufficient information from measured pollution sources.

5. Conclusions

In source-unknown apportionment models, accurately identifying pollution source types is a critical step. Current methods rely heavily on empirical and semi-quantitative approaches, leading to high uncertainties in source identification. This study utilizes the CDI to identify source factors in the PMF model, enhancing the scientific rigor of source apportionment and reducing uncertainties in factor identification. Results from the PMF model analysis of the XRB demonstrate that the CDI enables quantitative identification of pollution sources, facilitating the precise matching of simulated factors and observed pollution sources. The XRB exhibits high levels of C, N, and P, with TN and TP being the most severe pollutants, exceeding standards at rates of 94.74 % and 100 %, respectively. The PMF model identifies three pollution sources influencing eight water quality chemical parameters in the XRB. According to the CDI model, the three pollution sources in the XRB are identified as farmland, rural, and WTPs. Farmland sources are the primary contributors to DOC, TC, and TDP; rural sources are the main contributors to NH₃-N and PO₄³⁻; WTPs sources contribute the most to N indicators such as TN, NO₃⁻, and NO₂⁻. Traditional ratio methods demonstrate lower efficiency in identifying pollution sources in the study area, with significant challenges in distinguishing similar sources and lower objectivity in source identification. The CDI model proposed in this study considers the correlation between different source apportionment factors and observed pollution sources, using quantitative indicators to identify pollution source types and enhance the reliability of source apportionment. This method can be applied not only to source identification in the PMF model but also to other receptor-based source apportionment models, providing an objective basis for quantitatively identifying source types.

Date availability statement

Data will be made available on request.

CRediT authorship contribution statement

Yajing Sheng: Writing – original draft, Investigation, Formal analysis, Data curation. Wei Gao: Writing – review & editing, Methodology, Funding acquisition, Conceptualization. Min Cao: Investigation, Data curation. Hao Cheng: Investigation, Data curation. Yanpeng Cai: Supervision, Resources.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.