The Impact of Race, Ethnicity, and Sex on Fairness in Artificial Intelligence for Glaucoma Prediction Models

Abstract

Objective

Despite advances in artificial intelligence (AI) in glaucoma prediction, most works lack multicenter focus and do not consider fairness concerning sex, race, or ethnicity. This study aims to examine the impact of these sensitive attributes on developing fair AI models that predict glaucoma progression to necessitating incisional glaucoma surgery.

Design

Database study.

Participants

Thirty-nine thousand ninety patients with glaucoma, as identified by International Classification of Disease codes from 7 academic eye centers participating in the Sight OUtcomes Research Collaborative.

Methods

We developed XGBoost models using 3 approaches: (1) excluding sensitive attributes as input features, (2) including them explicitly as input features, and (3) training separate models for each group. Model input features included demographic details, diagnosis codes, medications, and clinical information (intraocular pressure, visual acuity, etc.), from electronic health records. The models were trained on patients from 5 sites (N = 27 999) and evaluated on a held-out internal test set (N = 3499) and 2 external test sets consisting of N = 1550 and N = 2542 patients.

Main Outcomes and Measures

Area under the receiver operating characteristic curve (AUROC) and equalized odds on the test set and external sites.

Results

Six thousand six hundred eighty-two (17.1%) of 39 090 patients underwent glaucoma surgery with a mean age of 70.1 (standard deviation 14.6) years, 54.5% female, 62.3% White, 22.1% Black, and 4.7% Latinx/Hispanic. We found that not including the sensitive attributes led to better classification performance (AUROC: 0.77–0.82) but worsened fairness when evaluated on the internal test set. However, on external test sites, the opposite was true: including sensitive attributes resulted in better classification performance (AUROC: external #1 - [0.73–0.81], external #2 - [0.67–0.70]), but varying degrees of fairness for sex and race as measured by equalized odds.

Conclusions

Artificial intelligence models predicting whether patients with glaucoma progress to surgery demonstrated bias with respect to sex, race, and ethnicity. The effect of sensitive attribute inclusion and exclusion on fairness and performance varied based on internal versus external test sets. Prior to deployment, AI models should be evaluated for fairness on the target population.

Financial Disclosures

Proprietary or commercial disclosure may be found in the Footnotes and Disclosures at the end of this article.

Recent years have seen a rapid proliferation of artificial intelligence (AI) algorithms in health care using data from electronic health records (EHRs) to predict a variety of outcomes.1, 2, 3, 4, 5 In the field of ophthalmology, these have included promising algorithms that can accurately predict which patients with glaucoma will progress to the point of requiring glaucoma surgery using structured^6,7 and unstructured (free-text) data8, 9, 10 from EHRs. The performance of some of these algorithms is superior to even a glaucoma specialist’s predictions.¹⁰ Prediction algorithms that can accurately identify those at high risk for disease progression might ultimately assist clinicians in personalizing glaucoma management plans, allowing for more aggressive interventions in high-risk patients before vision is irreversibly lost, or relaxing the burden of surveillance in patients who are likely to remain stable.

However, the potential for implementation of any AI prediction model depends on more than just the overall accuracy of its predictions. Unfortunately, some AI prediction algorithms in the field of health care have inadvertently demonstrated discrimination against minoritized groups, exacerbating existing disparities in care and outcomes.^11,12 For example, a widely used algorithm used to identify and help patients with complex health needs was shown to be biased, as Black patients were considerably sicker than White patients for a given risk score, reducing their chances of accessing special care programs.¹¹ Thus, whether an algorithm performs fairly or exhibits bias against particular demographic subgroups of a population should be an important component of its evaluation prior to implementation. The question of bias is especially important for glaucoma algorithms because of the wealth of prior research that has demonstrated that glaucoma disproportionately impacts Black^13,14 and Latinx/Hispanic patients.15, 16, 17 These patients are more likely to go blind from glaucoma and experience worse outcomes,^15,17 and yet are underrepresented in many landmark studies.¹⁸ Furthermore, studies have shown a sex-dependent susceptibility to developing some types of glaucoma, with women outnumbering men in total cases worldwide and having a higher risk for primary angle-closure glaucoma due to anatomical predisposition and other factors.19, 20, 21 Artificial intelligence algorithms can combat biases against marginalized groups through responsible development and deployment.²²

Some authorities have advocated for a "fairness through unawareness” approach toward developing models, arguing that race or ethnicity, as sociopolitical constructs without consistent biologic meaning, should not be included as input features in prediction algorithms.²³ However, others have suggested that training models that are “unaware” of race or other sensitive attributes can result in models that are optimized for the majority group and underperform in minority groups, which may actually harm minorities.^24,25 To the best of our knowledge, whether race, ethnicity, or other sensitive patient attributes should be included in EHR models for ophthalmology has not been previously explored. This question is especially important for glaucoma because of the potentially complex interplay of social, economic, and biologic factors that underpin the relationship between race/ethnicity and glaucoma.

The recent establishment of the Sight Outcomes Research Collaborative (SOURCE), a multicenter repository of EHR from academic ophthalmology departments across the United States, offers a promising opportunity for investigating fairness in AI algorithms for ophthalmology. The large and diverse population in SOURCE enables researchers to develop and evaluate the fairness of AI algorithms on racial and ethnic subgroups, an evaluation that is difficult to perform using data from a single center, especially if patients seen at that center are very homogenous in their sociodemographic characteristics. The objective of this study is to examine the impact of sensitive attributes (such as sex, race, and ethnicity) on developing and implementing fair and equitable EHR models that predict the progression of glaucoma to necessitating incisional glaucoma surgery. We evaluate both standard model performance metrics and model fairness criteria, under conditions when the model excludes sensitive characteristics as input features, includes them as input features, or when separate models are developed for each group. We evaluated a variety of fairness criteria, and we focused on the widely accepted equalized odds metric for fairness, which stipulates that comparison groups should have equal true positive rates (sensitivity) and equal false positive rates (FPRs). We also evaluated how model fairness generalizes when evaluated on patients from sites not included in the training data.

Methods

Data Source

The data for this study were obtained from the SOURCE Ophthalmology Data Repository (https://www.sourcecollaborative.org/). The repository collects EHR data of all patients who have received eye care at academic health systems participating in the consortium. The data spans a time frame from when a site implements the EHR up until the present. For this study, data were extracted from 7 active SOURCE sites, each contributing patient data spanning 7 to 14 years. The information captured by SOURCE includes patient demographics, diagnoses based on International Classification of Diseases (ICD) billing codes, eye examination findings from each clinic visit, and details about ocular and nonocular medications prescribed, laser treatments, and surgical interventions. All data in the repository have been deidentified to protect patient privacy. However, privacy-preserving software (Datavant Inc) permits researchers to follow patients longitudinally over time, while still protecting patients’ privacy. This study was approved by the University of Michigan and Stanford Institutional Review Boards and adhered to the tenets of the Declaration of Helsinki. As data were deidentified, informed consent was not obtained in this study.

Study Population

In the SOURCE database, we first selected all patients with ≥1 glaucoma-related billing code (codes starting with ICD 365.xx, H40.xx, Q15). We excluded patients with only glaucoma suspect codes (H40.0, and ICD 365.0 and their descendants). Within this group, we identified persons who underwent incisional glaucoma surgery, as determined by Current Procedural Terminology²⁶ billing codes, or had ≥2 distinct visits with a glaucoma diagnosis identified by ICD²⁷ coding (Table S1, available at www.ophthalmologyscience.org).

Our models sought to predict the likelihood that a patient with glaucoma will undergo incisional glaucoma surgery in either eye within 12 months of an index date, using data from the preceding 4 to 12 months and a cut-off threshold/score based on a validation dataset, similar to our previous work.²⁸ This approach predicts surgery at the patient level, and it allows for prediction at any time point during the patient’s time in the health system, as opposed to only at baseline (which would be the case for models using only baseline data). Briefly, for each patient, we established a prediction date (or index date) that divided their medical timeline into 2 periods: a look forward period during which the model would predict the likelihood of progression to surgery, and a lookback period of ≥4 months and up to 12 months, from which the model drew its input data. Patients with <4 months of lookback data were excluded from the analysis. For patients who underwent glaucoma surgery, we identified the date of their first surgery and defined the prediction date as either 12 months prior to the surgery date or after the initial 4 months of follow-up (whichever was later). The prediction date for nonsurgical patients was defined as 12 months before their last follow-up date. A summary of cohort construction timelines with examples is given in Fig S1 (available at www.ophthalmologyscience.org).

Feature Engineering

The feature engineering and cohort construction process have been previously described.²⁸ Briefly, the input features extracted from the EHRs included demographics (age at prediction date, sex, race, ethnicity, rural/urban [Rural-Urban Commuting Area] codes,²⁹ and distressed communities index score³⁰); clinical variables (logarithm of the minimum angle of resolution best recorded visual acuity, intraocular pressure, refraction spherical equivalent, and central corneal thickness for both eyes), ocular and systemic ICD diagnosis codes, and ocular and systemic medication prescriptions. Demographic information on race, ethnicity, and sex were as recorded in the EHR, which is likely to be self-reported, though collection methods at each participating SOURCE institution may vary. Continuous variables were scaled; categorical variables were dummy-encoded. Encounter-level ICD codes were aggregated to the first decimal level. Systemic and ocular outpatient medication data from the specified time period were aggregated based on their generic names. Patients with a particular ICD code or medication in the lookback period were assigned a "1" for that feature, "0" otherwise. International Classification of Diseases codes and medication with near-zero variance (<0.5% and <2%, respectively) were removed, resulting in a total of 92 ICD code-based features and 52 medication-based features. The total number of structured data input features was 179.

The data were split for model training, model validation, and evaluation. Data from 2 sites was reserved as an “External Site #1” (N = 1550) and “External Site #2” (N = 2542). The remaining 5 sites of SOURCE data were split by patient in an 80:10:10 ratio for training (N = 27 999), validation (N = 3500), and internal testing (N = 3499). The purpose of validation data is to fine-tune hyperparameters, like threshold cutoffs or scores, to enhance performance while guarding against overfitting to the training data. Internal test data evaluate the model's performance after hyperparameter tuning on the same data distribution as the training set. Conversely, external test data, drawn from a distinct data source, asses the model's performance and its ability to generalize beyond the training data's distribution.

Sensitive Attributes

We analyzed fairness and generalizability of fairness across 3 sensitive attributes. These attributes and the comparison groups for each were:

• •Race - White (G1) vs. non-White (G2)
• •Sex - Male (G1) vs. Female (G2)
• •Ethnicity - non-Latinx/Hispanic (G1) vs. Latinx/Hispanic (G2)

Decision Boundary Complexity

A classification decision boundary is a dividing line or surface in the feature space that separates different classes or categories in a classification problem. It represents the threshold at which a classifier assigns different labels or predictions to different regions of the feature space. We first investigated whether the complexity of the classification decision boundary differed between each subgroup, which would suggest that including sensitive attributes in modeling could be beneficial. For example, if White (G1) individuals can be adequately classified into those who will progress to glaucoma surgery and those who will not using a linear classifier, while non-White (G2) individuals require a complex nonlinear model for classification, this would imply that complexity of the classification problem differs between the 2 groups.

The N2 measure quantifies the geometric complexity of the classification problem by assessing the ratio between the average distance to the intraclass (i.e., within the same outcome) nearest neighbor and the average distance to the interclass nearest neighbor, for each individual.³¹ The minimum value for the N2 measure is 0. Smaller N2 values indicate that the classification problem is easier, and the classes can be separated more effectively using a smoother discriminant function. We tested the significance of the difference between the decision boundary complexity of the groups by first (1) selecting 500 subsets randomly from each group within the training set, (2) computing the mean and standard deviation of the N2 data complexity measure for each group, and (3) use a t test to analyze whether there is a significant difference between the mean complexity of G1 and G2 in each sensitive attribute.

Modeling

We developed XGBoost models using the Python xgboost 1.7.6 package using 3 approaches: (1) a model not using sensitive attributes (M1) as input features, (2) a model including sensitive attributes as explicit input features (M2), and (3) models which use the sensitive attributes to train separate models for each group (M3). Hyperparameters were tuned using random search and threefold cross-validation on the training set to optimize the area under the receiver operating characteristic curve (AUROC). Probability thresholds for classification were optimized for best F1 score on a validation set.

Evaluation

The primary outcome was model fairness as defined by the widely used equalized odds metric.³² In models which are fair with respect to equalized odds, the true positive and the FPRs are equalized across comparison groups of patients. For example, a model’s prediction of whether a glaucoma patient will progress to surgery performs with equal FPRs for White and non-White patients, and equal true positive rates for White and non-White patients. Secondary fairness metrics included independence (demographic parity),³² overall accuracy equality,³³ and sufficiency (calibration).³³ Table S2 (available at www.ophthalmologyscience.org) provides the definitions for each of the fairness metrics. We used equalized odds as the primary metric in this study over other metrics such as overall accuracy equality as it specifically assesses fairness in terms of predictive parity across different demographic groups, ensuring that predictive performance is similar for all groups regardless of their characteristics, thus providing a more comprehensive measure of fairness in predictive models. All fairness measures are reported as absolute value differences between subgroups (G1 and G2). Optimal fairness approaches a difference of 0, signaling minimal unfairness, while higher numbers denote increased disparity and unfairness between subgroups. In clinical settings, employing the absolute value difference provides a straightforward measure of disparity between groups, facilitating clear interpretation. By assessing the magnitude of unfairness regardless of its direction, stakeholders can effectively identify and address disparities, enhancing overall fairness in decision-making processes.

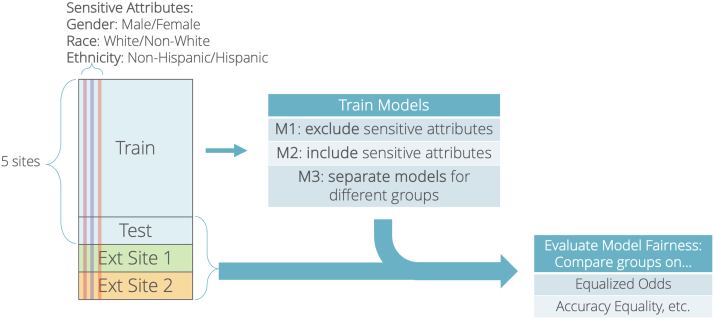
We also evaluated standard classification performance metrics including sensitivity (recall), specificity, positive predictive value (precision), FPR, false omission rate, AUROC, and accuracy. A bootstrap analysis with 1000 samples was conducted to generate 95% confidence intervals (CIs) for the AUROC. We also computed the proportion of data assigned to the positive class (i.e., support $[\frac{TP+FP}{TP+TN+FP+FN}$]). All metrics were evaluated on both the internal test set and the independent external site data. An overview of the entire study design is shown in Figure 1.

Figure 1.

Study design overview. Flowchart depicts the overall study design, including the training and evaluation set, the modeling approaches, and the fairness and classification evaluation metrics.

Results

Study Population

Table 3 summarizes the population characteristics for the study cohort of 39 090 patients with glaucoma, stratified by the internal training, validation, and testing groups, and external subgroups. Of 39 090 participants, the mean age of the population was 70.1 years (standard deviation 14.6). A majority (N = 21 312, 54.5%) were female. Most patients were White (N = 24 372, 62.3%). There were N = 8638 Black patients (22.1%) and 1832 Latinx/Hispanic patients (4.7%). Overall, 16.9% (N = 6019) of the patients progressed to undergo glaucoma surgery. The base rate of patients progressing to surgery was 17.6% for males and 16.6% for females. For White and non-White patients, the base rates of undergoing surgery were 16.0% and 18.8%, respectively. Finally, the base rates for Latinx/Hispanic and non-Latinx/Hispanic patients were 24.7% and 16.7%, respectively.

Table 3.

Population Characteristics

	Train		Val		Internal Test		External Test #1		External Test #2		Total
	N = 27 999		N = 3500		N = 3499		N = 1550		N = 2542		N = 39 090
	Mean	Std Dev.	Mean	Std Dev.	Mean	Std Dev.	Mean	Std Dev.	Mean	Std Dev.	Mean	Std Dev.
Age (yrs)	70.3	14.6	70.2	14.4	70.4	14.6	66.7	13.9	67.5	16.4	70.1	14.6
Best logMAR VA, OD	0.6	1.1	0.7	1.2	0.7	1.1	0.7	1.2	0.7	1.1	0.6	1.1
Best logMAR VA, OS	0.6	1.1	0.6	1.1	0.7	1.1	0.7	1.3	0.7	1.1	0.7	1.1
IOP max, OD (mmHg)	17.4	6.6	17.5	6.6	17.5	6.6	18.8	7	18	6.2	17.5	6.6
IOP max, OS (mmHg)	17.4	6.6	17.5	6.7	17.5	6.8	19.1	7	17.8	6	17.5	6.7
IOP max of either eye (mmHg)	19.2	7.5	19.3	7.8	19.3	7.6	20.7	8.1	19.6	6.9	19.3	7.6
Spherical equivalent, OD	−1.1	3.4	−1.2	3.6	−1	3.5	−1	3.8	−1.6	4.2	−1.1	3.5
Spherical equivalent, OS	−1.1	3.5	−1.3	3.5	−1	3.4	−0.8	3.2	−1.4	4.3	−1.1	3.5
CCT, OD (um)	550.5	52.5	551.2	52.6	551.9	54.2	546.8	47.4	554.1	65.7	550.5	52.4
CCT, OS (um)	551.0	53.9	551.5	53.7	553.5	56.6	547.4	47.6	555.7	67.2	551.1	53.8

	N	%	N	%	N	%	N	%	N	%	N	%
Surgery	4550	16.3%	612	17.49%	595	17.00%	262	16.90%	663	26.08%	6682	17.1%
Female	15 259	54.5%	1869	53.40%	1906	54.47%	919	59.29%	1359	53.46%	21 312	54.5%
Race
White	18 371	65.6%	2313	66.1%	2269	64.85%	249	16.06%	1170	46.03%	24 372	62.3%
Black	5788	20.7%	716	20.5%	730	20.86%	1183	76.32%	221	8.69%	8638	22.1%
Asian	1826	6.5%	225	6.4%	238	6.80%	39	2.52%	707	27.81%	3035	7.8%
American Indian or Hawaiian	94	0.3%	10	0.3%	10	0.29%	4	0.26%	46	1.81%	164	0.4%
Other	1575	5.6%	193	5.5%	209	5.97%	48	3.10%	339	13.34%	2364	6.0%
Unknown	345	1.2%	43	1.2%	43	1.23%	27	1.74%	59	2.32%	517	1.3%
Ethnicity
Hispanic	1193	4.26%	151	4.3%	146	4.17%	36	2.32%	306	12.04%	1832	4.7%
Non-Hispanic	25 776	92.1%	3229	92.3%	3237	92.51%	1444	93.16%	2219	87.29%	35 905	91.9%
Unknown	1030	3.7%	120	3.4%	116	3.32%	70	4.52%	17	0.67%	1353	3.5%
Rural/urban
Rural	878	3.1%	108	3.1%	108	3.09%	2	0.13%	43	1.69%	1139	2.9%
Urban	25 621	91.5%	3206	91.6%	3191	91.20%	474	30.58%	2497	98.23%	34 989	89.5%
Missing	1500	5.4%	186	5.3%	200	5.72%	1074	69.29%	2	0.08%	2962	7.6%

CCT = central corneal thickness; IOP = intraocular pressure; logMAR = logarithm of the minimum angle of resolution; OD = right eye; OS = left eye; VA = visual acuity.

Comparing Decision Boundaries for Subgroups in Sensitive Attributes

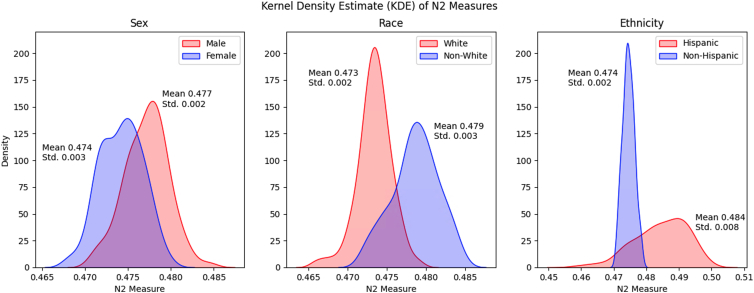
We investigated the complexity of the classification decision boundary for each demographic subgroup defined by the sensitive attributes, comparing the N2 measure between subgroups. Figure 2 visualizes the distribution of the N2 measure for each subgroup in each sensitive attribute. We found that the complexity of the classification problem was significantly different between the subgroups (t test, P < 0.001 for G1 vs. G2 for each sensitive attribute). The difference in N2 distribution curves was notably distinct compared between Latinx/Hispanic and non-Latinx/Hispanic subgroups, potentially suggesting the necessity of employing distinct models for each group to faithfully capture the decision boundaries.

Figure 2.

Kernel density estimate of N2 measures. Plots visualizing the distribution of nonparametric separability of classes (N2) for each group in each sensitive attribute. Each subplot showcases the difference in distribution of the N2 measure between the subgroups for each sensitive attribute, over 500 subsets randomly sampled in the training set. That the distributions of the N2 measure differ between subgroups of patients suggests that there are varying levels of complexity of the classification problem of distinguishing between patients who will progress to glaucoma surgery or not. Std = standard deviation.

Model Performance and Fairness

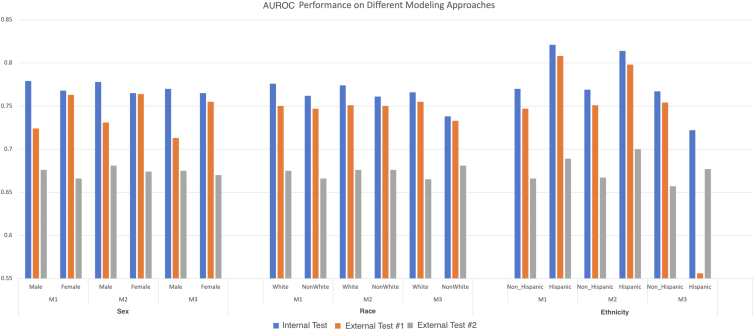
Area under the receiver operating characteristic curve scores are shown in Figure 3 for models which exclude (M1), include (M2), and stratify (M3, separate models for each group) on sensitive features. All standard classification performance metrics are reported in Table S4a and Table S4b (available at www.ophthalmologyscience.org). For sex, the model excluding sex as an input feature (M1) achieved the highest AUROCs on the internal testing set (0.779 [95% CI 0.779–0.780] male, 0.768 [95% CI 0.766–0.769] female), but the performance of the model including sex as an input feature (M2) achieved the highest AUROCs on external site #1 (0.731 [95% CI 0.730–0.734] male, 0.764 [95% CI 0.764–0.765] female) and external site #2 (0.681 [95% CI 0.679–0.682] male, 0.674 [95% CI 0.671–0.676] female). Similarly, for race the M1 AUROC was highest for the internal test set (0.776 [5% CI 0.775–0.775] White, 0.762 [95% CI 0.762–0.764] non-White), but for the external test sites the race-aware approaches (M2 and M3) had higher AUROCs. For ethnicity, M1 achieved the highest AUROC for the internal testing set and M2 achieved the highest AUROC on external site #2. For external site #1, the highest-performing modeling approach was different for Latinx/Hispanic and non-Latinx/Hispanic patients: M1 was best for Latinx/Hispanic patients in external site #1 but M3 was best for non-Latinx/Hispanic patients.

Figure 3.

Area under the receiver operating characteristic curve for different modeling approaches regarding sensitive attributes. Figure illustrates the AUROC for different modeling approaches which exclude (M1), include (M2), or stratify (M3) on the sensitive attributes of sex, race, and ethnicity. Area under the receiver operating characteristic curve is plotted separately for subgroups by sex (male and female), race (White and non-White), or ethnicity (non-Hispanic and Hispanic). Model performance is shown evaluated on an internal test set of patients from the same 5 sites used for model training (“Test”) and for patients from 2 different independent sites (“External #1” and “External #2”). AUROC = area under the receiver operating characteristic curve.

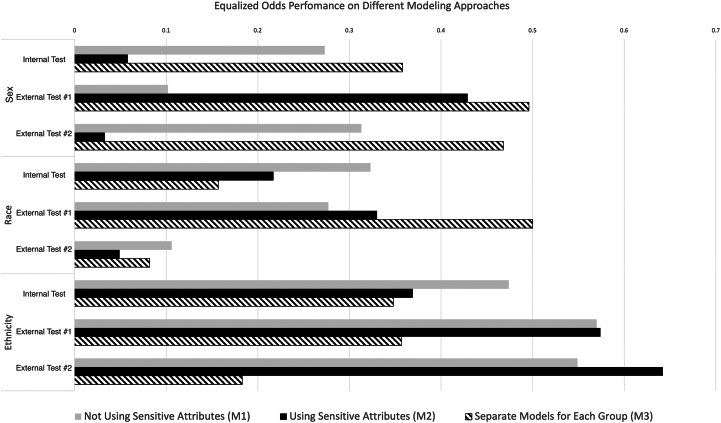
Figure 4 illustrates the fairness of each modeling approach with respect to sex, race, and ethnicity, as determined by equalized odds for the internal test set and external test sets. For fairness metrics, a difference between G1 and G2 which is closer to zero is more fair and less biased; for example, if model true positive and FPRs are the same for females as for males, then the difference is 0 and the model is perfectly fair with respect to sex as measured by equalized odds. We found that for sex, M2 was most fair on the internal test set and external test site #2 while M1 was most fair on the external test site #1. For race, models using sensitive attributes (M2 and M3) were fairer on the internal testing set and external test site #2, while M1 was most fair on external test site #1. For ethnicity, M3 was most fair for both the internal testing set and external test sites. For other fairness metrics such as overall accuracy equality and sufficiency, we also observed varying degrees of fairness across different modeling strategies for all sensitive attributes, which were not consistent between evaluation sites. Results for all evaluated fairness metrics are reported in Table S5 (available at www.ophthalmologyscience.org).

Figure 4.

Fairness as measured by equalized odds for different modeling approaches regarding sensitive attributes. Figure illustrates the fairness of different modeling approaches regarding sensitive attributes. Fairness is determined by equalized odds, defined as the gap between the demographic subgroups in true positive rates and false positive rates. The comparison subgroups are male and female for sex, White and non-White for race, and non-Hispanic and Hispanic for ethnicity. Fair models have an equalized odds measure near zero (short bars) indicating small or no gap in the true and false positive rates between demographic subgroups, whereas biased models have an equalized odds measure which is high (longer bars), indicating a large gap in true and false positive rates between demographic subgroups.

Discussion

In this multicenter study of nearly 40 000 patients across 7 large United States health systems, we evaluated the fairness and generalizability of AI algorithms that predict whether patients with glaucoma will progress to require surgery in the coming year. Such algorithms could eventually aid physicians in personalizing therapies for patients with high- and low-risk glaucoma. We found evidence of bias for sex, race, and ethnicity that was not wholly ameliorated by removing these sensitive attributes as inputs to the models. When we systematically evaluated the inclusion and exclusion of race, ethnicity, and sex in our models, we found that not including these sensitive attributes resulted in better classification performance but worse fairness when evaluated on an internal test set from the same distribution as the training data. However, these results did not generalize well, as we found that when we tested our models on data from external test site #1, the opposite was true: including sensitive attributes resulted in better classification performance, but worse fairness for sex and race as measured by equalized odds. For external test site #2, including sensitive attributes results in both better classification and fairness for all sensitive attributes. These results underscore the importance of external validation and subpopulation analyses for uncovering potential biases in AI models.

A key insight gleaned from the results of this study was that the modeling approach for sensitive attributes which achieved the best classification performance was not necessarily the fairest—similar to another study that analyzed the impact of race and ethnicity on diabetic screening.³⁴ On the internal test set of patients from the 5 sites used for model training, models that were ‘“blind” to the sensitive attribute, whether that was sex, race, or ethnicity, achieved higher AUROCs, but models that were “aware” of the attributes were considered fairer in terms of equalized odds. This is likely consistent with the trade-off between fairness and performance described in other contexts outside of medicine,35, 36, 37, 38 such as the loan eligibility problem where there is an apparent trade-off between fairness and accuracy among racial groups.³⁹ This trade-off between fairness and performance was also notable in external site #1, though the pattern was opposite: the models that were “blind” to race and sex were fairer, but had lower AUROCs. However, for external site #2 where models that were “aware” of attributes were both fairer and had better AUROCs. The difference in results between the 2 external sites may potentially be attributable to the large differences in population demographics between these sites. For example, there is a substantial demographic shift in regards to White (65.6% vs. 16.1% vs. 46.0%), Black (20.7% vs. 76.3% vs. 8.7%), and Hispanic (4.26% vs. 2.3% vs. 12.0%) patients between the training set, external site #1, and external site #2, respectively.

These results lead to a second key insight, which is that models that appear fairest when evaluated on a standard internal test set are not necessarily the fairest models for completely independent external sites. Some prior studies analyzing the generalizability of fairness using clinical risk prediction models across various medical domains indicate a consistent bias against minoritized groups when applied to new and unseen data.11, 40, 41, 42 For example, Singh et al explored generalizability challenges of mortality risk prediction models using multicenter EHR data.⁴² The study found that models vary considerably in fairness and calibration when trained and tested across different hospitals. The authors reported a median value of 0.16 (interquartile range 0.08–0.29) for sufficiency (i.e., calibration) across various hospitals. Our results show a median value of 0.10 (interquartile range 0.1–0.11) on external test site #1 and 0.06 (0.05–0.07) on external test site #2 for race—showcasing fairer results with lower variance.

The failure of modeling approaches to remain consistently fair when deployed to external validation sets could be considered as a specific case of the failure of model performance metrics to generalize in the face of dataset shifts,11, 40, 41, 42 which occur when data distributions differ between the training and testing/deployment environments. In this study, there were large demographic differences between the training/test sets and the external test sites: the internal train/test set was almost two-thirds White individuals, while external set #1 was over three-quarters Black patients and external set #2 was less than one-tenth Black patients. Differences in demographic populations have been shown to reduce model generalizability in various domains, most notably in the health care industry, such as in the aforementioned mortality prediction model.^41,42 These large demographic differences pose a useful and illustrative stress test for the performance of our models, highlighting how fairness could change under almost the most extreme circumstances for population changes. We found that models trained with sensitive attributes as input features (M2) or trained separately for different groups (M3) demonstrated much more bias for sex and race when evaluated on external test sites.

This study is subject to various limitations. Many standard fairness evaluation methods constrain analyses to a simplified, binary view of sensitive attributes: White vs. non-White, etc. In reality, sensitive attributes such as race contain numerous subgroups and there may be a spectrum of privilege. Individuals can have intersectional identities and belong to multiple groups (e.g., Hispanic Black male). Further investigation is required to examine systemic biases and develop models that produce fair predictions across multiple groups (>2) and for combinations of sensitive attributes.^32,43,44 Another limitation is in separating effects attributable to site-specific versus patient-group-specific care patterns. For instance, if site A’s population has a majority of Black patients and routinely performs surgery, while site B is more hesitant to recommend surgery and primarily serves a White population, this could potentially influence model outcomes and introduce biases for particular groups. Additional factors such as the number of glaucoma specialists at a given site, how they vary in being conservative or aggressive in their desire to operate, operating room availability, and others could also affect the decision to perform surgery. Finally, training models on real-world observational health data can potentially replicate the biases already embedded within the health care system. Access to health care affects health outcomes, and thus any model trained on data in the EHR is predicated on access to health care and has the potential to be biased in ways that are difficult to assess. Future studies could encompass developing different models that predict complementary outcomes that may be less (or differently) affected by existing health inequities, such as glaucoma progression to maximum medical therapy, elevated intraocular pressure, visual field progression, and optic nerve structural changes.

In conclusion, in this study of fairness and generalizability of an EHR algorithm predicting glaucoma patients’ progression to surgery, we found evidence of bias for sex, race, and ethnicity. Not including these sensitive attributes as input features produced better-performing but less fair algorithms for an internal test set, whereas on external test sets, using sensitive attributes resulted in better performance but worse fairness metrics for sex and race. Since removing sex, race, and ethnicity is not a comprehensive solution to eliminate bias in glaucoma algorithm predictions, it may be reasonable to include them if external validation and thorough subpopulation analyses are performed. Clinicians and researchers who seek to develop, deploy, or utilize clinical decision support systems based on AI algorithms should critically evaluate the potential biases in these algorithms and understand that even if an algorithm’s performance metrics have been evaluated in demographic subgroups, results may not generalize to the specific setting in which the algorithm will ultimately be used. Moreover, different fairness metrics target distinct fairness constraints, potentially leading to disparate conclusions. Models may need to be exclusively trained and deployed within a single hospital setting to optimize both fairness and performance or retrained for each specific site. Future studies developing and evaluating model training methods which specifically aim to mitigate bias and improve generalizability will be important for the future of AI in ophthalmology.

Manuscript no. XOPS-D-24-00136.