Abstract
The current study aims to evaluate the feasibility of creatine (Cr) chemical exchange saturation transfer (CEST)-weighted MRI at 7 T in the human brain by optimizing the saturation pulse parameters and computing contrast using a Z-spectral fitting approach. The Cr-weighted (Cr-w) CEST contrast was computed from phantoms data. Simulations were carried out to obtain the optimum saturation parameters for Cr-w CEST with lower contribution from other brain metabolites. CEST-w images were acquired from the brains of four human subjects at different saturation parameters. The Cr-w CEST contrast was computed using both asymmetry analysis and Z-spectra fitting approaches (models 1 and 2, respectively) based on Lorentzian functions. For broad magnetization transfer (MT) effect, Gaussian and Super-Lorentzian line shapes were also evaluated. In the phantom study, the Cr-w CEST contrast showed a linear dependence on concentration in physiological range and a nonlinear dependence on saturation parameters. The in vivo Cr-w CEST map generated using asymmetry analysis from the brain represents mixed contrast with contribution from other metabolites as well and relayed nuclear Overhauser effect (rNOE). Simulations provided an estimate for the optimum range of saturation parameters to be used for acquiring brain CEST data. The optimum saturation parameters for Cr-w CEST to be used for brain data were around B1rms = 1.45 μT and duration = 2 seconds. The Z-spectral fitting approach enabled computation of individual components. This also resulted in mitigating the contribution from MT and rNOE to Cr-w CEST contrast, which is a major source of underestimation in asymmetry analysis. The proposed modified z-spectra fitting approach (model 2) is more stable to noise compared with model 1. Cr-w CEST contrast obtained using fitting was 6.98 ± 0.31% in gray matter and 5.45 ± 0.16% in white matter. Optimal saturation parameters reduced the contribution from other CEST effects to Cr-w CEST contrast, and the proposed Z-spectral fitting approach enabled computation of individual components in Z-spectra of the brain. Therefore, it is feasible to compute Cr-w CEST contrast with a lower contribution from other CEST and rNOE.
Keywords: chemical exchange saturation transfer, creatine, creatine-weighted chemical exchange saturation transfer, Lorentzian, magnetic resonance imaging, Z-spectra
1 |. INTRODUCTION
The chemical-exchange-saturation-transfer (CEST) MRI technique is used for the high-resolution mapping of metabolites/molecules/macromolecules possessing protons exhibiting exchange phenomena with protons of bulk water.1,2 In a typical CEST experiment, exchangeable protons of the solute pool are saturated using a long radio-frequency (RF) pulse, which results in a reduction of bulk water proton signal due to the transfer of saturated magnetization from solute to bulk water. CEST-MRI techniques are being developed for in vivo mapping of labile molecules and metabolites.3–5
Creatine (Cr) is a significant metabolite in the brain and its alteration has been linked to various diseases.6–9 It has been shown that Cr concentration ([Cr]) in the brain decreases with aging as well as in diseases including Alzheimer's disease (AD) and Huntington disease, and in brain tumors.7,8,10 Using both invasive and noninvasive methods, the brain's Cr level is reported to be in the range of 6–14mM.11–16 Proton magnetic resonance spectroscopy (1H MRS) provides a noninvasive approach to detect the total Cr (tCr) (phosphocreatine [PCr] + Cr) level in the brain. In the brain, PCr concentration is smaller compared with Cr (the Cr/PCr ratio is ~ 2:1).12,17 However, using 1H MRS, the free Cr level in the brain cannot be quantified and, moreover, it is unable to provide higher resolution mapping of Cr. The CEST-based method has been recently developed to map the Cr at a higher resolution by exploiting the exchangeable amine protons resonating at a frequency offset of ~ 1.8 ppm downfield from water resonance.18,19 Cr-weighted (Cr-w) CEST imaging in human calf muscle has been used to probe the exercised induced changes in Cr level on 720 and 3 T human scanners.21 Further, Cr-w CEST mapping is used to detect the failing bioenergetics in the infarcted myocardium.22 Recently, Cr-w CEST imaging mapped the spatial distribution of Cr in rat brain on a 9.4 T animal scanner.23 Another study reported that the molecular origins of CEST signals at 2 ppm in rat brain is predominantly due to Cr.24
The exchange rate of amine protons of Cr has been reported in the range of 500–1190 Hz.4,19,25 The exchange rate of amine protons (1.8 ppm downfield from water resonance) and amide protons (2.5 ppm downfield from water resonance) of PCr were reported as ~ 120 and ~ 140 Hz, respectively, in a phantom study.19 Due to the intermediate exchange rate, the CEST effect from Cr is dominant over PCr.19 The CEST effect from PCr (for physiological range) for a particular saturation parameter was reported to be negligible in the phantom study at 3 T.19 However, by using low saturation power with a very long saturation duration, the CEST effect from PCr can be enhanced.
In vivo mapping of the CEST effect from amide proton transfer (APT-w CEST),3,26–29 myo-inositol (MI-w CEST),30 glutamate (Glu-w CEST)4,31,32 and glucose (Gluco-w CEST)33 has been performed in the human brain. Various clinical applications of these CEST techniques are emerging for investigating human brain diseases. As such, amide protons of APT resonate at 3.5 ppm, amine protons of glutamate at 3.0 ppm, and hydroxyl protons of MI at ~ 0.6 ppm downfield of the bulk water resonance; however, the line shapes of their CEST effect are usually broad, and therefore they may contribute to the CEST effect from Cr at 1.8 ppm. Therefore, it is imperative to evaluate the contribution from various metabolites/molecules to Cr-w CEST.
In general, computation of CEST contrast is challenging due to contribution from direct saturation (DS), magnetization transfer (MT) and other metabolites showing a broad CEST effect. Although the conventional CEST asymmetry (CESTasy) approach enables a substantial reduction of DS and MT effects, this approach is highly sensitive to static field (B0) inhomogeneity and requires accurate correction before interpretation of CEST contrast. CESTasy is also known as magnetization transfer ratio (MTRasy). Another issue with CESTasy analysis is the negative contribution to CEST contrast from relayed nuclear Overhauser effect (rNOE) (centered at 3.5 ppm upfield to the water resonance), which reduces the sensitivity of measurement of CESTasy contrast. Alternative approaches like Z-spectral fitting are used to mitigate these effects.23,24 Several studies have used a combination of Lorentzian functions22–24,34,35 for computing CEST contrast. Recently, superposition of Lorentzian function was used to calculate CEST contrast at 2 ppm in rat brain at 9.4 T23. Two studies36,37 have also used partial fitting of Z-spectra corresponding to wide-offset frequencies using a two-pool Henkelman's model for the computation of APT and rNOE at 3 and 4.7 T. It was reported that with steady state condition, super-Lorentzian line shapes performed better than Lorentzian and Gaussian in computing the broad MT effect from the Z-spectra of tissue.38 However, in another study, for nonsteady state saturation, Gaussian line shape was reported as better than super-Lorentzian.39,40 The choice of line shape for fitting MT component depends on several factors like shape of the saturation pulse, saturation parameters (amplitude and duration), and steady state versus nonsteady state conditions. Therefore, depending upon the type of Z-spectra data, an appropriate line shape should be used. Another study used an apparent exchange-dependent relaxation method (AREXfit)41 for computing the CEST effect at 2 ppm.24
The CEST effect is highly dependent on saturation parameters, field strength and tissue type. Therefore, a systematic study to investigate the feasibility of Cr-w CEST mapping of the human brain with optimal saturation pulse parameters and evaluation of possible contributions from different metabolites is required.
The objectives of the current study were to carry out optimization of saturation parameters using phantom and simulations; to evaluate contributions from other sources to Cr-w CEST contrast using simulations; and to propose an improved Z-spectral fitting approach for better computation of individual Z-spectral components for in vivo human brain data from 7 T. Reproducibility of Cr-w CEST contrast was also evaluated. The effect of Lorentzian, Gaussian and super-Lorentzian line shapes for a broad MT pool on Z-spectra fitting was also investigated.
2 |. MATERIALS AND METHODS
MR imaging of phantoms and healthy human brain was performed using a vendor-supplied 32-channel receive and single-channel transmit RF coil on a Siemens 7 T human research scanner (Siemens Medical Solutions, Malvern, PA, USA).
2.1 |. CEST MRI pulse sequence
The pulse sequence used in the current study consisted of a frequency selective saturation pulse train (user-selected saturation offset , saturation duration and saturation power) followed by a segmented RF-spoiled gradient echo (GRE) readout acquisition with centric phase encoding order.42 The saturation pulse train consisted of a series of Hanning-windowed rectangular pulses each of 100 ms duration separated by a 200 μs delay (duty cycle = 99.80%). The excitation bandwidth of this saturation pulse train was 5 Hz for a 1 second saturation duration with a 1% bandwidth of 20 Hz. At the end of the GRE acquisition segments, a variable delay was added to provide T1 recovery and to keep the sequence under the permitted RF safety limits on the scanner. This sequence was flexible enough to be used for water saturation shift referencing (WASSR)43 data acquisition and CEST imaging.
2.2 |. Phantom preparation
To study the dependence of CrCEST contrast on concentration, Cr solution phantoms with varying concentrations (0, 2, 4, 6, 8 and 10mM) (Sigma Aldrich, USA) at pH 7.0 were prepared in phosphate buffered saline (PBS). These samples were added to small test tubes (of 10 mm diameter) and immersed inside a large cylindrical container with PBS. This cylindrical container was placed inside a thermally isolated rectangular box for temperature maintenance. The temperature of PBS inside the container was maintained at 37 ± 1°C during the MRI experiment.
2.3 |. Acquisition protocol for phantom MR imaging
The MRI study protocol consisted of the following steps: a three-plane localizer, B0 map, B1 map, Z-spectra or CEST data, and a control image without saturation. The CEST MRI imaging parameters were: slice thickness = 10 mm, GRE flip angle (FA) = 10o, GRE readout repetition time (TR)/echo time (TE) = 5.6/2.7 ms, field of view (FOV) = 120 × 120 mm2, matrix size = 192 × 192, and a single shot acquired every 15 seconds. Z-spectrum data were acquired using a saturation pulse of a root mean square B1 (B1rms) of 2.2 μT and 1 second duration at frequencies offset ranging from −4 to +4 ppm in steps of 0.2 ppm. The total time for the Z-spectra data acquisition was 10.5 minutes. To evaluate the B1 dependence of Cr CEST, CEST-weighted images were acquired at varying B1rms (1.4, 2.1, 2.9 and 3.6 μT) with 1 second saturation duration over the limited offset frequency range (±1.4 to ±2.2 ppm with a step-size of 0.2 ppm). For studying the saturation duration dependence of Cr-w CEST, CEST-weighted images at B1rms of 2.2 μT and durations of 1, 2 and 3 seconds were acquired over the limited offset frequency range (±1.4 to ±2.2 ppm with a step-size of 0.2 ppm). Both saturation power and duration dependence data were acquired in 17.5 minutes.
Data for generating B0 and B1 maps from the same imaging slice were obtained for removing the B0 and B1 field inhomogeneities effect on CEST data. For the B0 field map, WASSR data were acquired using a B1rms of 0.4 μT with a duration of 200 ms and offset frequency range of (±0 to ±1) ppm with a step-size of 0.1 ppm. The total time for WASSR data acquisition was 2.2 minutes. Data for the B1 field map were obtained using a single slice fast spin echo readout sequence with TR/TE = 6 s/12 ms. Two images were obtained using preparation square pulses with FAs of 30o and 60o (pulse duration = 0.3 ms) followed by a spoiler gradient. It took 12 seconds to acquire B1 map data.
2.4 |. Bloch-McConnell numerical simulations
Bloch-McConnell equation solvers were written in in-house developed code using MATLAB R2014b-R2017a incorporating relaxation and chemical exchange for the experimental conditions used in the current study.4,44,45 We simulated the magnetization available at the end of the saturation pulse train and calculated Z-spectra, CESTasy plots and CESTasy values. Table 1 shows the details of parameters used for simulations, mimicking in vivo situations. Specifically, we used three sites (free and bound pools of water and CEST pool at 1.8 ppm) for optimizing B1rms (0.37 to 7.4 μT with a step-size of 0.37 μT) and a duration of 0.2 to 4 seconds (with a step-size of 0.2 seconds). Surface plots of CESTasy contrast with respect to B1rms and duration were generated.
TABLE 1.
Simulation results on potential contributions to in vivo human brain creatine-weighted chemical exchange saturation transfer contrast at 7 T
| Metabolites | T1 (s) | T2 (s) | ω (ppm) | Concentration (M) | Exchange rate (Hz) |
|---|---|---|---|---|---|
| Free watera | 2 | 0.115 | 0.0 | 81 | - |
| Bound waterb | 1 | 0.00001 | −2.4 | 7 | 10 |
| Amidec | 1 | 0.033 | 3.5 | 0.072 | 30 |
| Creatined | 1 | 0.010 | 1.8 | 0.010 | 500, 900, 1190 |
| Glutamatee | 1 | 0.010 | 3.0 | 0.011 | 2000 |
| Myo-inositolf | 1 | 0.010 | 0.6 | 0.006 | 600 |
For simulation, T1 and T2 for free water were taken from reference.4
For simulation, the bound water parameters were used from reference 51. This reflects MTR asymmetry contribution.
For simulation, all parameters were taken from reference.3
For simulation, the concentrations were taken from references 47,48, and exchange rates of 500, 900 and 1190 Hz were taken from references,4,19 and,25 respectively. Four amine protons were considered for each creatine molecule.
For simulation, the concentrations were taken from references 52,53, and exchange rate measured in vivo from rat brain.4 Three amine protons were considered for each glutamate molecule.
For simulation, the concentration and exchange rate were taken from reference30 and relaxation parameters for -OH were assumed to be the same as creatine. Six -OH protons were considered for each myo-inositol molecule.
A multi-pool exchange model mimicking in vivo brain simulations4 was considered to estimate the amount of overlap to Cr-w CEST contrast from other brain metabolites. The multi-pool model consists of DS pool (free pool of water) centered at 0 ppm, MT (bound pools of water) centered at −2.4 ppm, MI-w pool centered at 0.6 ppm, Glu-weighted pool centered at 3 ppm and APT-w pool centered at 3.5 ppm (Table 1). Simulations were carried out for different B1rms (0.37 to 7.4 μT with a step-size of 0.37 μT) and duration (0.2 to 4 seconds with a step-size of 0.2 seconds) values. The surface plot of CESTasy contrast from various metabolites (except Cr at 1.8 ppm) was generated for different B1rms and duration values.
Contribution from individual components to Cr-w CEST contrast was also estimated by simulating the CEST effect from the corresponding component. For obtaining estimates of bound water, which provide the MT effect, to Cr-w CEST contrast, the concentrations of amide protons, Cr, myo-inositol and glutamate metabolites were set to zero in simulations. For estimating the contribution of a specific metabolite to Cr-w CEST contrast, the concentrations of all other metabolites were set to zero keeping the bound water concentration fixed. The dependence of Cr-w CEST on exchange rate was also evaluated.
2.5 |. In vivo human brain MR imaging
All the human scans were performed according to the approved protocol of the Institutional Review Board committee of the University of Pennsylvania, USA. Four healthy volunteers aged 28–40 years were recruited, and informed consent was obtained from each volunteer after the study protocol had been explained to them.
The MRI study protocol consisted of the following steps: a localizer, T1-weighted anatomical three-dimensional (3D) magnetization-prepared rapid gradient echo (MPRAGE) data, B0/WASSR map data, B1 map data, CEST or Z-spectra data, and a control image without saturation. Whole-brain MPRAGE protocol consisted of 176 axial slices, TR/TE/inversion time (TI) = 2800/4.4/1500 ms, FA = 7°, resolution = 0.8 × 0.8 × 0.8 mm3, iPAT = 2. The scan time for MPRAGE was 4.4 minutes.
Image without saturation pulse (M0) was acquired using imaging readout parameters: FOV = 240 × 240 mm2, matrix = 192 × 192, slice thickness = 8 mm, FA = 10°, TR/TE = 5.4/2.6 ms and a single shot. For the same slice, CEST data were acquired at B1rms of 0.75, 1.1, 1.45, 2.2 and 2.9 μT and a duration of 2 seconds. Offset frequency range used in this protocol were ± 0 to ±3 ppm in steps of 0.3 ppm, ±3.5 to ±6 ppm in steps of 0.5 ppm, and ± 8 to ±20 ppm in steps of 4 ppm, ±40 and ± 100 ppm. Time per shot including delay and duration of CEST pulse was 8 seconds. The number of averages used for CEST data was one. The acquisition time for the entire CEST data (corresponding to five B1rms and 46 offset frequencies) was 31 minutes. For the same slice, WASSR data and B1 map data were also acquired using the parameters described in section 2.3. In the current study, a total of four subjects were scanned for CEST data. Two of these subjects were scanned twice to obtain data for reproducibility. Proper cushions and pads were used for minimizing head movement during MRI.
2.6 |. CEST contrast computation
CEST contrast computed using asymmetry analysis is given by:
| (1) |
where are the magnetizations obtained with saturation at ‘+’ and ‘−’ offset (= 1.8 ppm for Cr) of the water resonance and is the magnetization without saturation. Pixelwise Z-spectra were obtained from CEST-weighted images by plotting the normalized image intensity as a function of the frequency offset of the saturation pulse for each sample.
| (2) |
In this study, for fitting we have used scaled Z-spectra, which is also known as the magnetization transfer ratio (MTR), given by the following equation:
| (3) |
2.7 |. Z-spectra fitting methods
For estimating CEST effects from individual components, scaled Z-spectrum (Zsc) data were fitted using superposition of Lorentzian functions corresponding to multiple pools.23
| (4) |
where is the frequency offset from the water resonance, , and are the amplitude, frequency offset and line width of the nth proton pool, respectively. In this study, two Z-spectra fitting approaches (models 1 and 2) were used. In model 1, the scaled Z-spectra (Zsc) were fitted with the sum of five Lorentzian functions. For the in vivo brain data, the following five pools were considered: DS (at 0 ppm), MT (at −2.4 ppm), rNOE (at −3.5 ppm), Cr-w CEST (at 1.8 ppm) and CEST@3.5 ppm (at 3.5 ppm). In the current study, CEST@3.5 ppm corresponds to both APT-w and Glu-w contrasts. Resonances of these exchanging pools are well reported; therefore, in this study the position of exchanging pools was fixed with respect to the center of the DS component. This approach enabled reduction of fitting parameters. For MT effect, super-Lorentzian and Gaussian line shapes were also evaluated. Lorentzian function corresponding to MT line shape in Equation 4 was replaced by super-Lorentzian and Gaussian line shapes. Equations for these line shapes have been described previously.38
Model 2 is a modified version of model 1. In model 2, instead of fitting Zsc directly, we initially used limited data from ±12 to ±40 ppm to fit and compute the MT component. It was assumed that, in this range, there is only MT contribution and negligible contribution from DS, rNOE or any other CEST effect. In the current study, different line shapes, namely, Lorentzian, Gaussian and super-Lorentzian, were used to fit broad MT component. After fitting broad MT component, the MT spectrum was interpolated over the whole offset frequency range. This fitted MT component was removed from the Zsc and the remaining part was fitted (±0 to ±12 ppm) using superposition of 4-pool Lorentizian function corresponding to DS (at 0 ppm), rNOE (at −3.5 ppm), Cr-w CEST (at 1.8 ppm) and CEST@3.5 ppm (at 3.5 ppm).
2.8 |. Data analysis/postprocessing
All image processing and data analysis were performed using in-house developed programs written in MATLAB (R2009b to R2017a) (Natick, MA, USA). For motion correction, all images (WASSR data, B0 map, B1 map, Z-spectra or CEST) were registered to the control image without saturation using affine transformation followed by manual desculping. Pixelwise Z-spectra data were interpolated using inbuilt cubic spline function in MATLAB for generating an offset frequency range of ±0 to ±3 ppm in steps of 0.2 ppm, ±3.5 to ±6 ppm in steps of 0.5 ppm, ± 8 to ±20 ppm in steps of 1 ppm, and ± 25 to ±40 ppm in steps of 5 ppm.
Z-spectra fitting was performed using an in-house written program which used the inbuilt nonlinear fitting “lsqcurvefit” routine of MATLAB. Parameters used as initial guess and bound constraints are listed in the next paragraph. Before fitting Z-spectra, frequency offset corresponding to minimum intensity value was estimated and Z-spectra were automatically shifted accordingly for mitigating B0 field inhomogeneity. This shifting takes care of large drift in B0. Moreover, the resonance frequency of DS is one of the free parameters of the fitting model, which enable further improvement in the accuracy of automatic B0 correction. Therefore, B0 or WASSR map data are not required for computing the CEST contrast based on Z-spectra fitting approaches. This hypothesis was tested by simulating the effect of offset frequency shift on z-spectra fitting as well as by asymmetry analysis. In the current study, we only used the WASSR data-based B0 map for computation of conventional CESTasy.
Four circular regions of interest (ROIs) (~ 15 pixels) were drawn in gray matter (GM) and four in white matter (WM) tissues on the MTR map. The MTR map was computed as 100*(1-Msat [20 ppm]/M0). First of all, fitting was carried out for representative Z-spectra from ROIs in GM and WM tissues. Lower and upper bounds for the amplitude and width of each component were set based on physiological constraints and prior knowledge from simulation and reported literature. Lower bounds of 20, 0, 0, 0 and 0% and upper bounds of 100, 70, 20, 10 and 10% were set for amplitudes of DS, MT, rNOE, Cr-w CEST and CEST@3.5 ppm, respectively. Lower bounds of 0.1, 10, 0.5, 0.5 and 0.5 ppm and upper bounds of 5, 100, 10, 4 and 8 ppm were set for the width of DS, MT, rNOE, Cr-w CEST and CEST@3.5 ppm, respectively. The initial values for the amplitude and width of each component were taken as averages of the lower and upper bounds. The initial value for the center of DS was set as 0 ppm. Lower and upper bounds for the DS center were − 0.2 and + 0.2 ppm, respectively.
The average value of the fitted width parameter in representative GM and WM ROIs was taken as an initial guess for the pixelwise Z-spectra fitting. Lower and upper bounds for width were set as 50 and 150% of the average initial values, respectively. For the amplitude, the initial value and constraints were the same as those described in the previous section. For the center of DS, the initial guess and constraints were the same as those described in the previous section.
Residual errors and the difference between Z-spectra and fitted Z-spectra were calculated for evaluating the accuracy of fit. Average residual error (σ) was calculated using the following equation:
| (5) |
where represents Z-spectra data, represents fitted Z-spectra data and represents the number of data points in Z-spectra. The goodness-of-fit parameter (R2) was also calculated for each fitting.
Moreover, WM and GM masks were segmented using a MTR map followed by morphological operation erosion (kernel size: 3 × 3) to obtain pure normal appearing WM (NAWM) and normal appearing GM (NAGM) masks and to remove contribution from partial volume effects.
2.9 |. Monte-Carlo simulations
Z-spectra from the GM data obtained at a B1rms of 1.45 μT and duration of 2 seconds was subjected to Gaussian noise for testing the stability of models 1 and 2 for five pools. Different levels of noise, obtained by changing standard deviation (SD), were used for simulations. For each noise level, 500 noisy Z-spectra data were generated and were fitted using models 1 and 2. Original Z-spectra without additional added noise were also fitted using both models. Absolute relative percentage error (ARPE) between fitted parameters corresponding to noisy Z-spectra and fitted parameters corresponding to Z-spectra without additional noise were computed. Average and SD for each of the fitted parameters over 500 iterations were computed for both models.
Similarly, the noise stability of model 2 corresponding to six pools was evaluated. For the sixth pool, the following pools were considered, one by one: rNOE at −1.6 ppm (rNOE@2), CEST pool at 1 ppm (CEST@1 ppm) and CEST pool at 3 ppm (CEST@3 ppm).
2.10 |. B0 inhomogeneity correction for CESTasy contrast
Because calculation of CESTasy is highly sensitive to B0 inhomogeneity, it requires an accurate B0 map. An offset frequency map generated by finding a minimum of Z-spectra is less accurate and is not suitable for the CESTasy map. Therefore, a B0 map was generated from WASSR data followed by the correction of CEST data for B0 inhomogeneity using the previously described method.4,45 Briefly, CEST data were smoothed and interpolated using a cubic spline to generate data with a step-size of 0.01 ppm. For B0 inhomogeneity correction, each voxel data value at offset frequency ppm was replaced by the interpolated data value from ppm. B0 corrected CESTasy contrast maps were generated using Equation 1.
2.11 |. B1 inhomogeneity corrections
The transmit B1 field map (B1rel) was generated using the double angle method described previously.4 Amplitude and width of all the maps as well as the CESTasy map were corrected using the B1 calibration-based method described previously49 considering multiple ROIs (section 2.8).
2.12 |. Statistical analysis
Studenťs t-test with two tails was used to compare the contrast between GM and WM. The difference was significant if P < 0.05. For reproducibility, CEST maps of the same volunteers at two time points were used to measure the coefficient of variation (COV) in %. The COVs were computed for multiple ROIs (section 2.8) in GM and WM tissues as well as in NAWM and NAGM masks.
3 |. RESULTS
Z-spectra from Cr solution phantom (10mM) showed a clear dip at ~ 1.8 ppm downfield to the water resonance while no CEST effect was observed from PBS (Figure 1A). Figure 1B shows the plot of Cr-w CEST contrast as a function of Cr concentration. Cr-w CEST contrast linearly correlated with Cr concentration with a detection sensitivity of ~ 0.65% per mM Cr concentration for a B1rms of 2.2 μT and duration of 1 second. Cr-w CEST contrast showed a nonlinear dependence on B1rms (Figure 1C). For a fixed B1rms, Cr-w CEST contrast increased with increase in saturation duration (Figure 1D).
FIGURE 1.
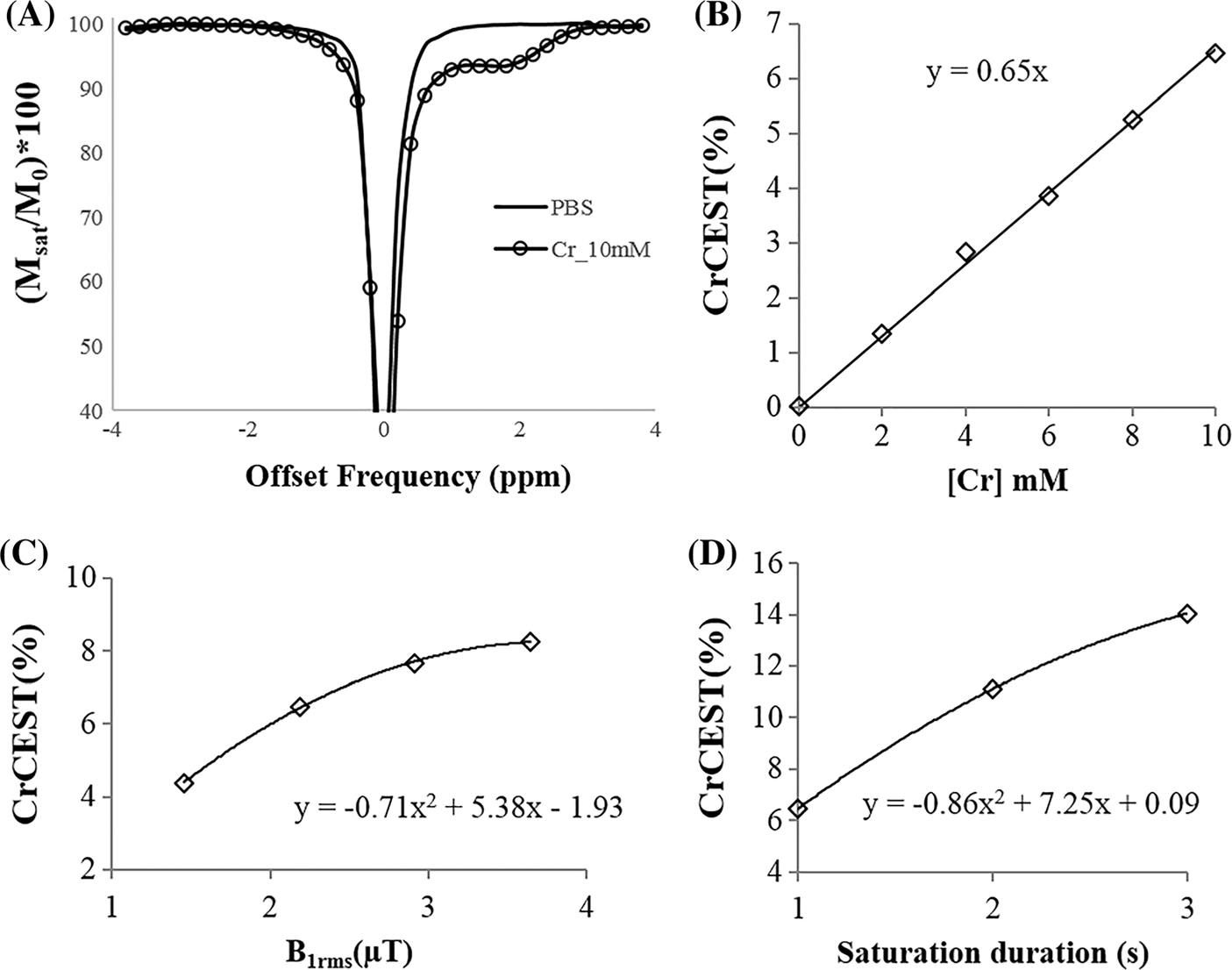
(A) Z-spectra of Cr (10 mM) and PBS using a saturation B1rms of 2.2 μT and duration of 1 second. (B) Dependence of Cr-w CEST as contrast on Cr concentration ([Cr]) using a B1rms of 2.2 μT and duration of 1 second. (C) Dependence of Cr-w CEST contrast on saturation power for a fixed duration of 1 second and (D) dependence on saturation duration for a fixed saturation B1rms of 2.2 μT. Phantom data was acquired at temperature of 37 ± 1°C and pH of 7.0. Here, y represents CrCEST (%) and x represents [Cr] in (B), B1rms in (C) and saturation duration in (D)
Figure 2 shows surface plots demonstrating the dependence of simulated Cr-w CEST contrast on B1rms and saturation duration corresponding to an exchange rate of 500 Hz. CEST contrast showed a nonlinear dependence on saturation parameters. The surface plot in Figure 2A shows that Cr-w CEST contrast peaks at long durations for low saturation B1rms. The peak value of Cr-w CEST contrast shifts towards short duration with further increase in B1rms. The optimum range of B1rms and saturation duration provide CEST contrast in the region highlighted in yellow-red color. For in vivo experiments, this optimum range is further limited by the hardware set limits and restrictions on scan time. The MR scanner used in the current study allowed a maximum B1rms of 2.9 μT at a duration of 2 seconds. For a 1 second saturation duration, the scanner was allowed to acquire data up to B1rms of 3.6 μT. Figure 2B shows the contribution from other brain metabolites to Cr-w CEST, illustrating the CEST effect from brain metabolites (myo-inositol, glutamate and amide protons) at 1.8 ppm as a function of the saturation parameters. The dotted ellipse on the surface plot (Figure 2A) highlights an optimum region for selection of saturation parameters for Cr-w CEST in terms of maximum Cr-w CEST contrast, less overlap from other brain metabolites, and hardware constraints. Simulations showed that an optimum B1rms of 1.45 μT and duration of 2 seconds resulted in small contribution (~ 30%) from other known metabolites to Cr-w CEST. Similar surface plots were obtained for Cr exchange rates of 900 and 1190 Hz (Figure S1). There was a small shift in the region of maximum CEST value compared with an exchange rate of 500 Hz.
FIGURE 2.
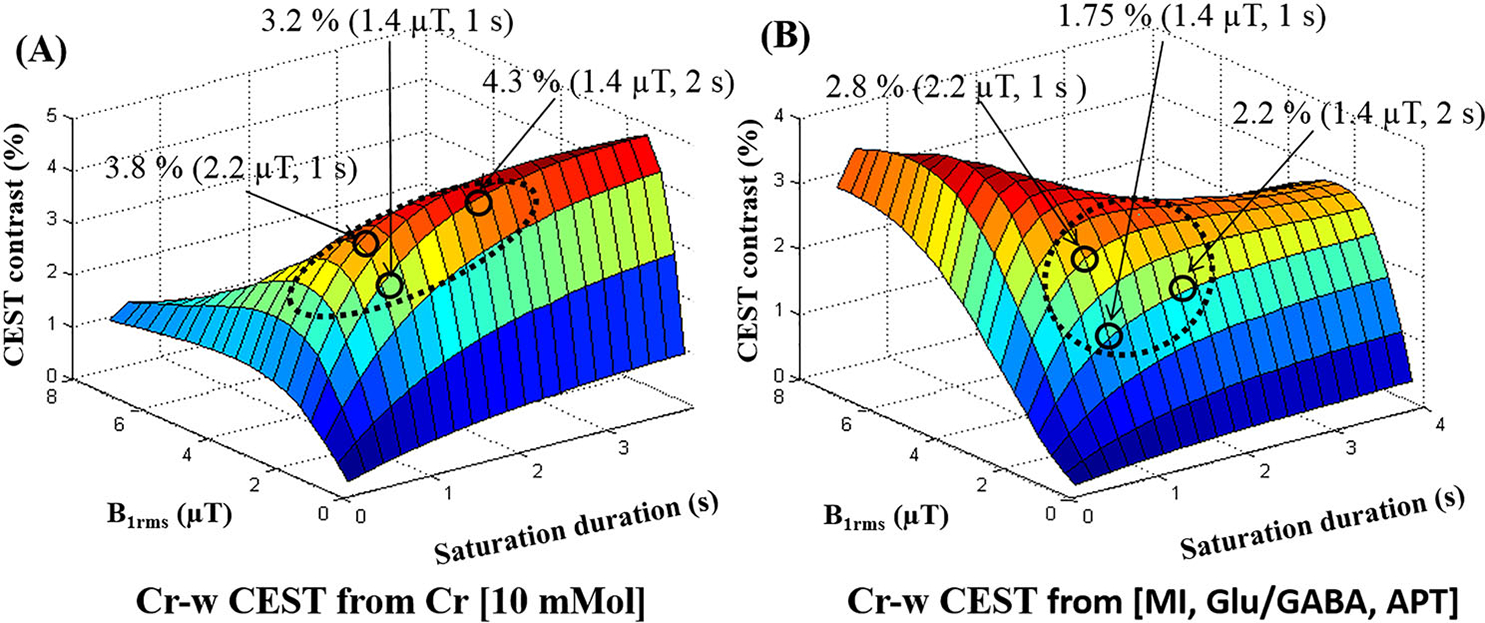
Surface plots demonstrating dependence of Cr-weighted (w) CEST contrast at 1.8 ppm on B1rms and saturation duration using numerical simulations at 7 T. (A) CEST contrast from Cr [10mM] only. (B) CEST effect from combined metabolites [MI, Glu/GABA, APT] except Cr at 1.8 ppm. Arrows point to the three different saturation values and corresponding contrast. Circles show regions corresponding to optimum range of saturation parameters. Dotted ellipse highlight the regions for optimal CrCEST contrast with less contamination. APT, amide proton transfer; Glu, glutamate; MI, myo-inositol
Figure 3 shows Z-spectra (Figure 3A) and asymmetry plots (Figure 3B) from an ROI in GM tissue of human brain at 7 T with B1rms of 0.7, 1.1, 1.45, 2.2 and 2.9 μT and duration of 2 seconds. At low B1rms, the dip around 3.5 ppm upfield to the water resonance corresponds mainly to rNOE, which overlaps with DS and MT effects with increase in B1rms. Similarly, at low B1rms, the dip at 3.5 ppm downfield to the water resonance corresponds to APT-w contrast. For other resonances, the CEST effect seems to be broad, overlapped, and is not clearly visible on the Z-spectra or MTRasy analysis for the saturation parameters and sampling used in the current study. Asymmetry plots shown in Figure 3b were normalized with M0 signal. Asymmetry plots show mixed contrast from CEST and rNOE. At low B1rms, contrast is negative due to high rNOE and MT effect compared with the CEST effect. Higher CEST contrast and lower rNOE were observed with increased B1rms (Figures 3).
FIGURE 3.
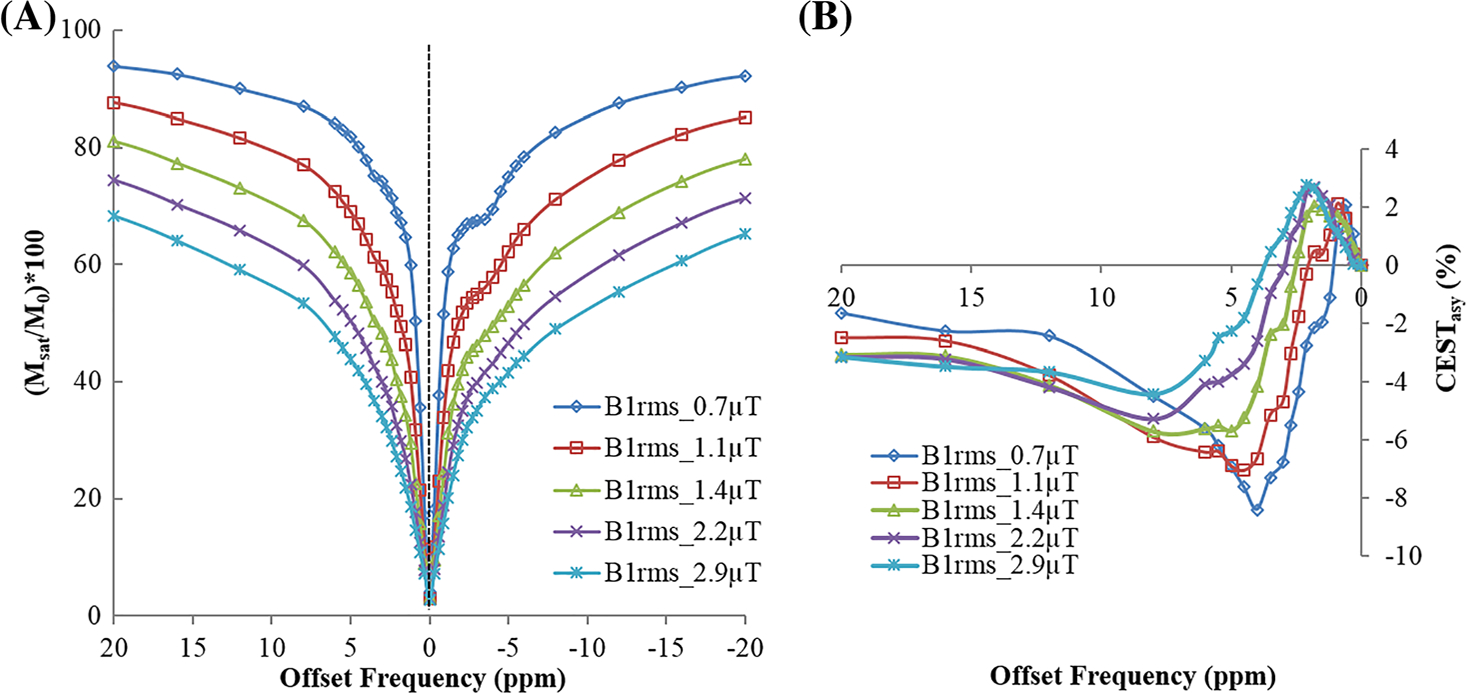
(A) Z-spectra and (B) asymmetry plot from a region of interest in gray matter tissue of human brain at 7 T with a saturation pulse B1rms of 0.7, 1.45, 2.2 and 2.9 μT and duration of 2 seconds. Asymmetry plots in (B) use normalization by signal without saturation (M0)
Figure S2 shows unsaturated image (a), CEST-weighted image at 1.8 ppm (b), B0 field map (c), relative B1 field map (d) and Cr-w CESTasy map (e). A substantial amount of inhomogeneity was present in the B0 and B1 field maps obtained from human brain at 7 T. Cr-w CESTasy maps obtained without correction of these field inhomogeneities were heterogeneous even in the same type of tissue. After correction for the field inhomogeneities, maps become uniform, particularly in the same type of tissues (e). For a B1rms of 1.45 μT and duration of 2 seconds, Cr-w CESTasy contrast in GM was 4.1 ± 0.91%, and in WM it was −0.31 ± 29%.
Plots in Figure 4 show an example of fitting in vivo Z-spectra from an ROI in GM tissue (B1rms = 1.45 μT, duration = 2 seconds) using model 1. The Z-spectra fitted well with R2 = 0.99 and σ = 0.055 (Figure 4C). The pointwise residual plot (Figure 4C) also shows that error was within ±2%, except at water resonance where it was ~ 3%. Individual fitted components are also shown (Figure 4D).
FIGURE 4.
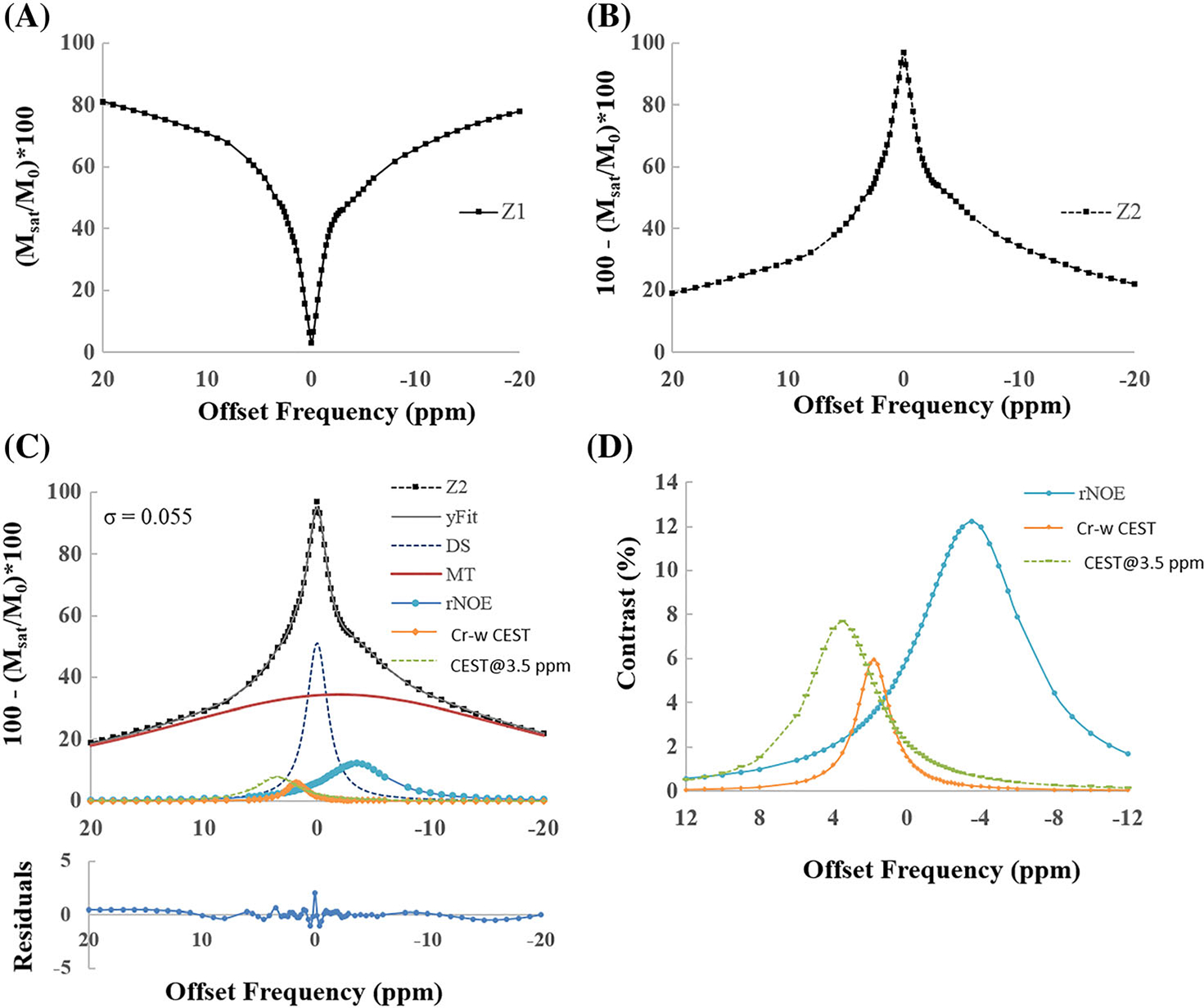
Plots show an example of fitting in vivo Z-spectra, from a region of interest in gray matter tissue, for a B1rms of 1.45 μT and duration of 2 seconds using model 1. (A) Original Z-spectra (Z1). (B) Scaled Z-spectra (Z2). (C) Five-pool fitting of scaled Z-spectra (Z2) along with various fitted components DS, MT, rNOE-w, Cr-w CEST and CEST@3.5 ppm contrast. R2 = 0.99 and residual errors are less than 2%. (D) Individual CEST and rNOE components. Fitting is performed over a range of −40 to +40 ppm and shown for a range of −20 to +20 ppm for better visualization. CEST@3.5 ppm, CEST contrast at 3.5 ppm; Cr-w CEST, CEST contrast at 1.8 ppm; DS, direct saturation; MT, magnetization transfer; rNOE, relayed nuclear Overhauser effect; σ, average residual error; R2, goodness of fit
Plots in Figure 5 show an example of fitting in vivo Z-spectra from ROIs in GM tissue (B1rms = 1.45 μT, duration = 2 seconds) using model 2. The Z-spectra fitted well with R2 = 0.99 and σ = 0.059. Figure 5A,B shows original Z-spectra (Z1) and scaled or inverted Z-spectra (Z2) along with the fitted MT component and Z-spectra after removal of MT (Z3). Figure 5C shows four-pool model fitting of Z3 along with various components like DS, rNOE, Cr-w CEST and CEST@3.5 ppm. This is due to the broad spectrum of Glu-w CEST, which overlaps with the APT-w effect and the use of suboptimial parameters for both of these effects. Individual CEST and rNOE components are also shown in the zoomed pan (Figure 5D). Widths of Cr-w, CEST@3.5 ppm and rNOE pools were small for model 2 compared with those obtained using model 1. The amplitude of the rNOE pool decreased in model 2. The amplitude of Cr-w CEST and CEST@3.5 ppm was similar in both models. Width and amplitude of DS and MT pools remained similar for both models.
FIGURE 5.
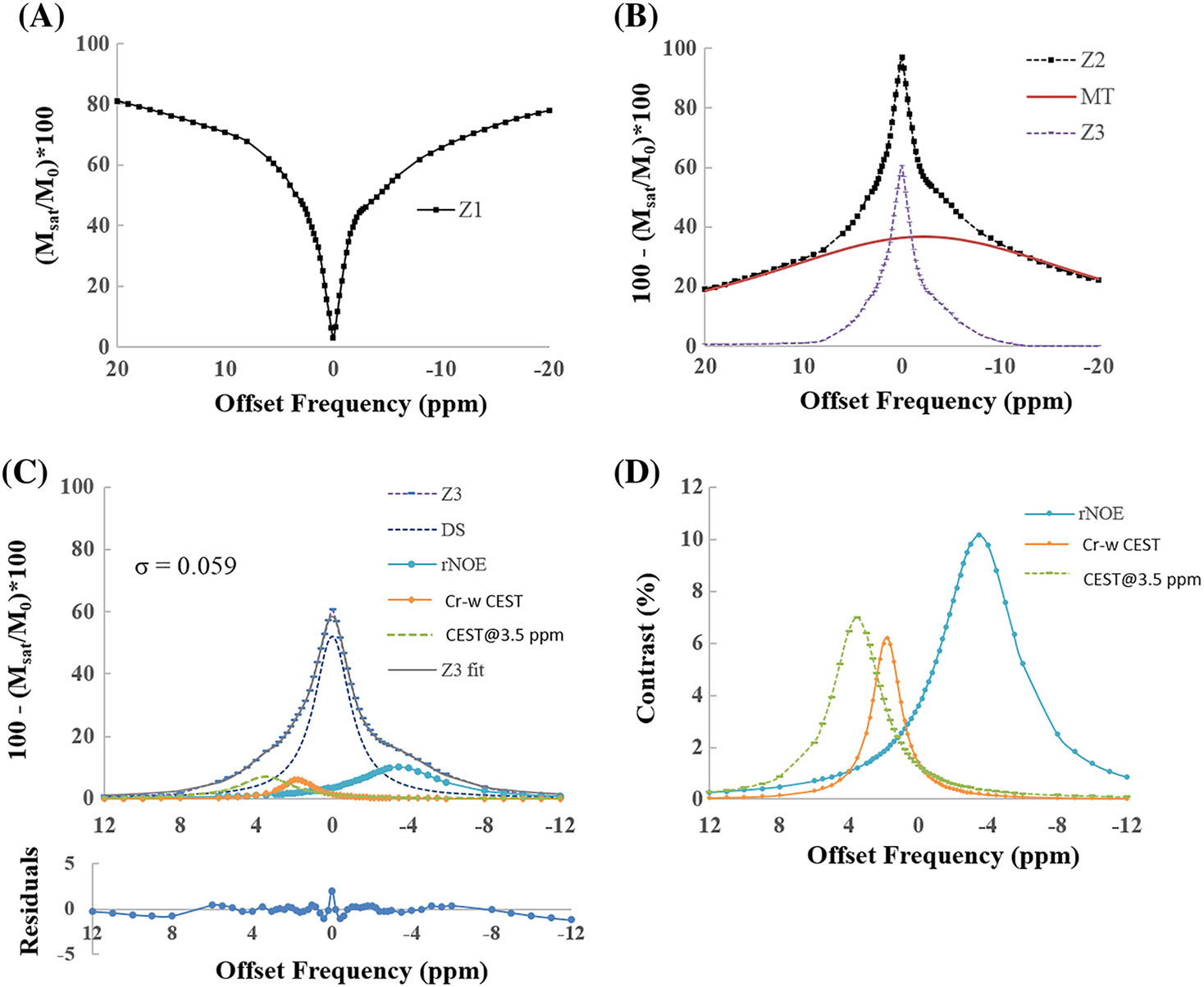
Plots show an example of fitting in vivo Z-spectra, from region of interests in gray matter tissue, for a B1rms of 1.45 μT and duration of 2 seconds using model 2. (A) Original Z-spectra (Z1). (B) Scaled Z-spectra (Z2) along with fitted MT component and Z-spectra after removal of MT component (Z3). (C) Four-pool fitting of Z3 along with various fitted components like DS, rNOE, Cr-w CEST and CEST@3.5 ppm contrast. R2 = 0.99 and residual errors are under 2%. (D) Individual CEST and rNOE components. Fitting of Z2 is performed over a range of −40 to +40 ppm and shown for a range of −20 to +20 ppm for better visualization. CEST@3.5 ppm, CEST contrast at 3.5 ppm; Cr-w CEST, CEST contrast at 1.8 ppm; DS, direct saturation; MT, magnetization transfer; rNOE, relayed nuclear Overhauser effect; σ, average residual error; R2, goodness of fit
Figure 6A–C shows fitting of Z-spectra using model 2 at B1rms of 0.7, 1.45 and 2.1 μT and duration of 2 seconds. For all of the cases, fitting was reasonable (σ ~ 0.06–0.07) and residual errors of fitting at all the offset frequencies remained within ±2%. Figure 6D–F shows the variation in amplitude of rNOE, Cr-w CEST and CEST@3.5 ppm pool with different B1rms. rNOE decreases with increase in B1rms. Cr-w CEST and CEST@3.5 ppm increase then decrease with increase in B1rms.
FIGURE 6.
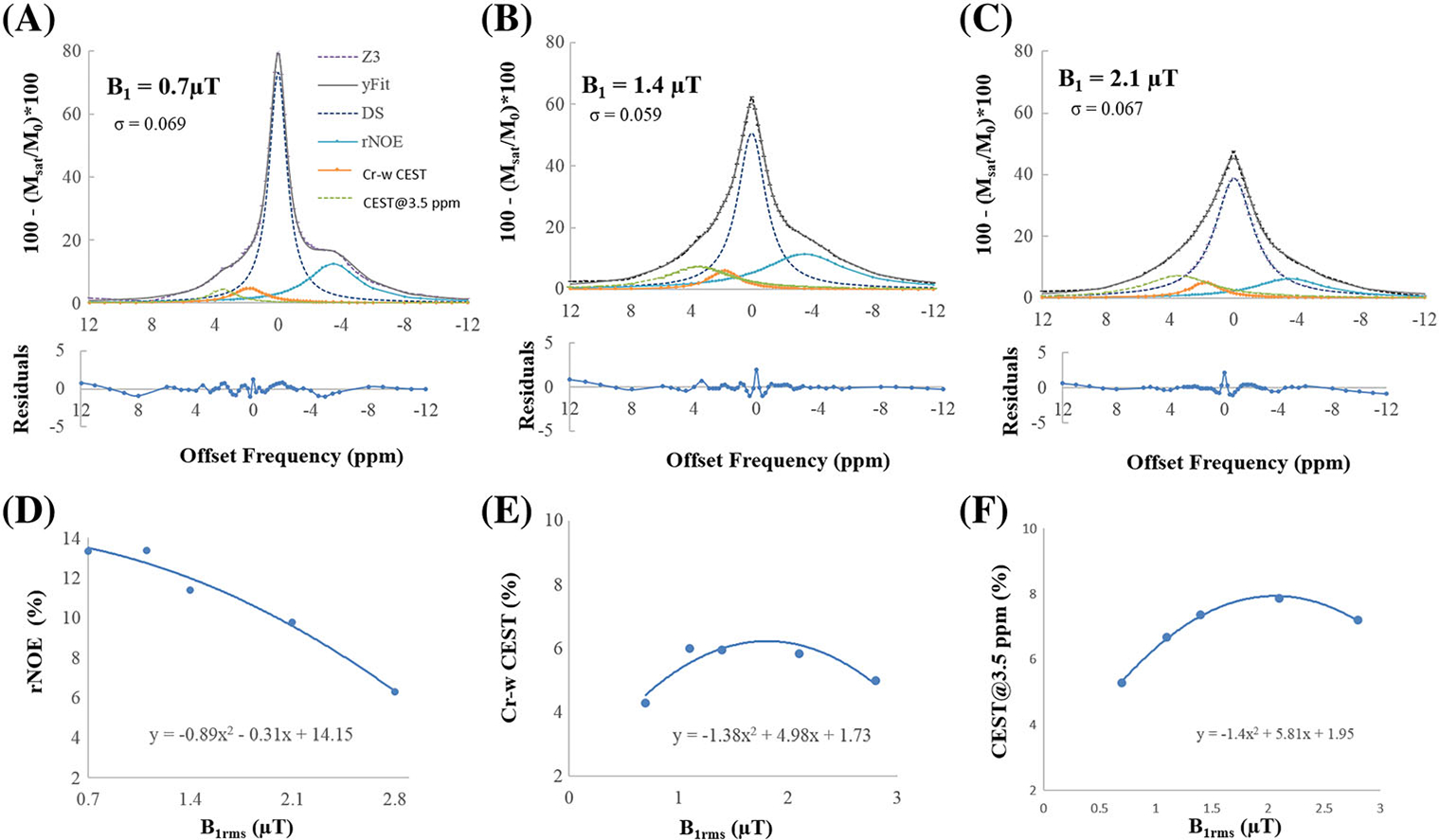
Fitting of in vivo Z-spectra from gray matter tissue using model 2 at durations of 2 seconds and B1rms of (A) 0.7, (B) 1.45 and (C) 2.2 μT. Residual errors of fitting are less than 2%. rNOE decreases with increase in B1rms. Cr-w CEST and CEST@3.5 ppm initially increase and then decrease with B1rms. CEST@3.5 ppm, CEST contrast at 3.5 ppm; Cr-w CEST, CEST contrast at 1.8 ppm; DS, direct saturation; MT, magnetization transfer; rNOE, relayed nuclear Overhauser effect; σ, average residual error; R2, goodness of fit
Figure 7 shows amplitude and width maps of DS, MT, rNOE, Cr-w CEST and CEST@3.5 ppm computed by pixelwise fitting of Z-spectra data from a representative healthy human brain using model 1 (rows 1 and 3) and model 2 (rows 2 and 4). Model 2 maps show a better distribution of rNOE, Cr-w CEST contrast and CEST@3.5 ppm contrast between GM and WM than model 1. DS and MT distributions are similar for both models in GM and WM. The Cr-w CEST contrast (Figure 7D,I) was higher in GM compared with WM and was significantly different (P < 0.01) for both models. The Cr-w CEST contrast ratio in GM/WM was 1.28 in model 2 and 1.43 in model 1. For width maps, the distribution of contrasts was similar in GM and WM. The white arrows in Figure 7S point to representative subarachnoid space of brain, which show high Cr width and low MT amplitude (Figure 7B,G) compared with other regions. Z-spectra of these regions showed some artifacts. Thus, Z-spectra fitting and fitted values of various parameters such as rNOE, Cr-w CEST and CEST@3.5 ppm are not reliable in these regions. Therefore, these voxels should be removed from final maps, otherwise this can lead to misinterpretation. Further studies should be carried out to obtain good quality Z-spectra in these regions for reliable parameter computation. Table 2 shows mean ± SD of individual components of Z-spectra using model 2 averaged over all healthy volunteers taken from multiple ROIs on GM and WM. Preliminary results on two subjects show that the maps obtained using the fitting approach are reproducible with COV < 5%.
FIGURE 7.
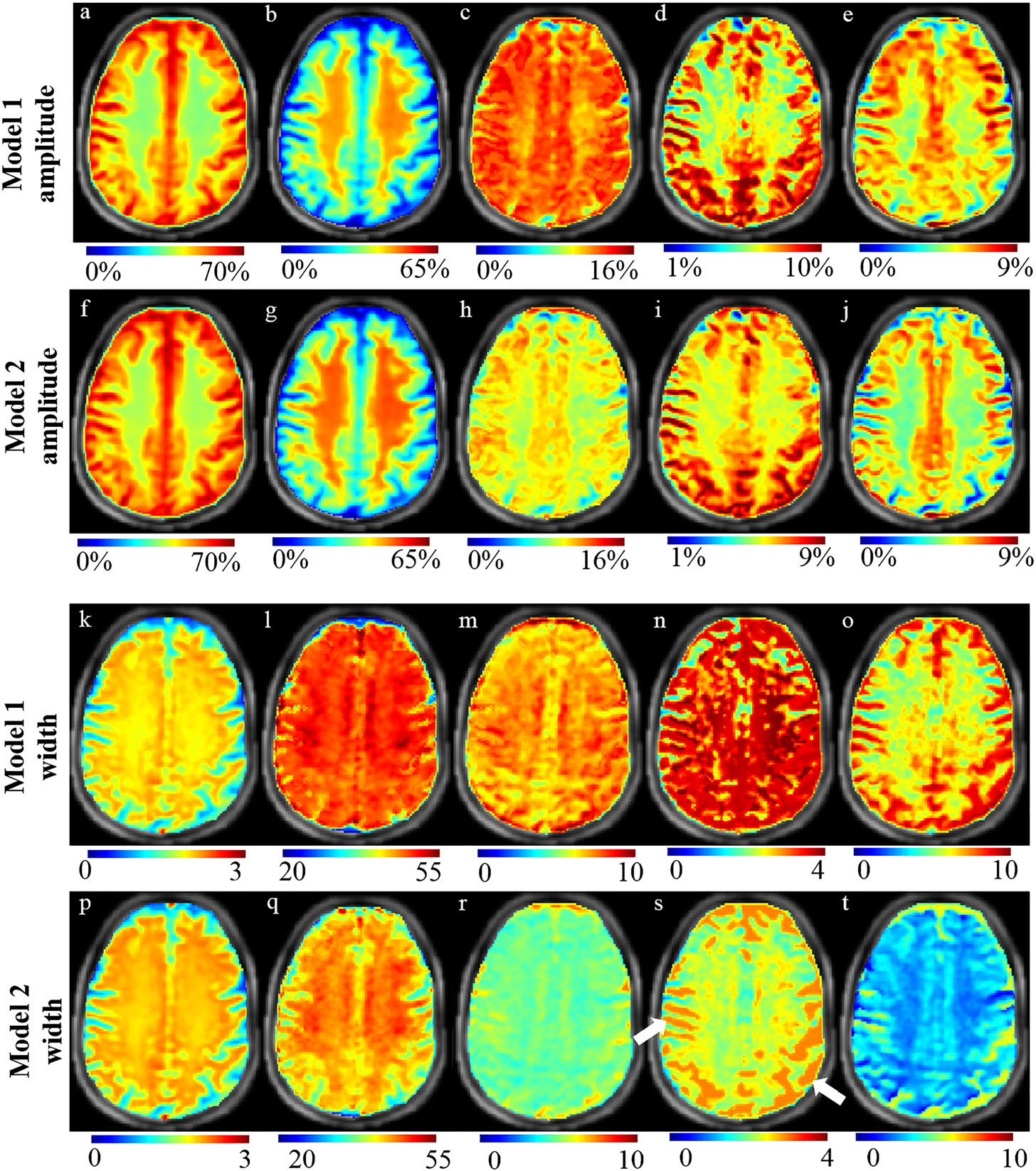
Amplitude and width maps of various components of Z-spectra from a representative healthy human brain using model 1 (rows 1 and 3) and model 2 (rows 2 and 4). Amplitude maps of DS (A, F), MT (B, G), rNOE (C, H), Cr-w CEST (D, I), CEST@3.5 ppm (E, J). Width maps of DS (K, P), MT (L, Q), rNOE (M, R), Cr-w CEST (N, S), CEST@3.5 ppm (O, T). The scales for width maps are in ppm. White arrows point to representative subarachnoid space of brain. Images are cropped and descalped
TABLE 2.
Fitted amplitude parameter obtained at B1rms of 1.4 μT and duration of 2 seconds using model 2 for multiple regions of interest on gray matter (GM) and white matter (WM) tissue averaged over all healthy human volunteers
| Amplitude (%) |
|||||
|---|---|---|---|---|---|
| DS | MT | rNOE | Cr-w CEST | CEST@3.5 ppm | |
| GM | 55.08 ± 0.52 | 32.77 ± 1.46 | 10.86 ± 0.67 | 6.98 ± 0.31 | 7.01 ± 0.31 |
| WM | 38.9 ± 0.8 | 50.51 ± 1.01 | 9.74 ± 0.25 | 5.45 ± 0.16 | 4.79 ± 0.28 |
Abbreviations: CEST@3.5 ppm, CEST contrast at 3.5 ppm; Cr‐w CEST, CEST contrast at 1.8 ppm; DS, direct saturation; MT, magnetization transfer; rNOE, relayed nuclear Overhauser effect.
The shift in resonance frequency based upon minimum of Z-spectra resulted in first order correction of Z-spectra data for B0 inhomogeneity. Automatic estimation of the position of DS using the Z-spectra fitting approach further improves its accuracy. Figure 8 shows the sensitivity of Cr-w CEST contrast computed using the fitting approach to shift in the resonance frequency. It was observed that the Cr-w CEST contrast map computed using the fitting approach is less sensitive to B0 inhomogeneity and does not require a separate B0 map. On the other hand, the Cr-w CESTasy contrast is highly sensitive to B0 inhomogeneity and even a small error in B0 estimation can affect the contrast value.
FIGURE 8.
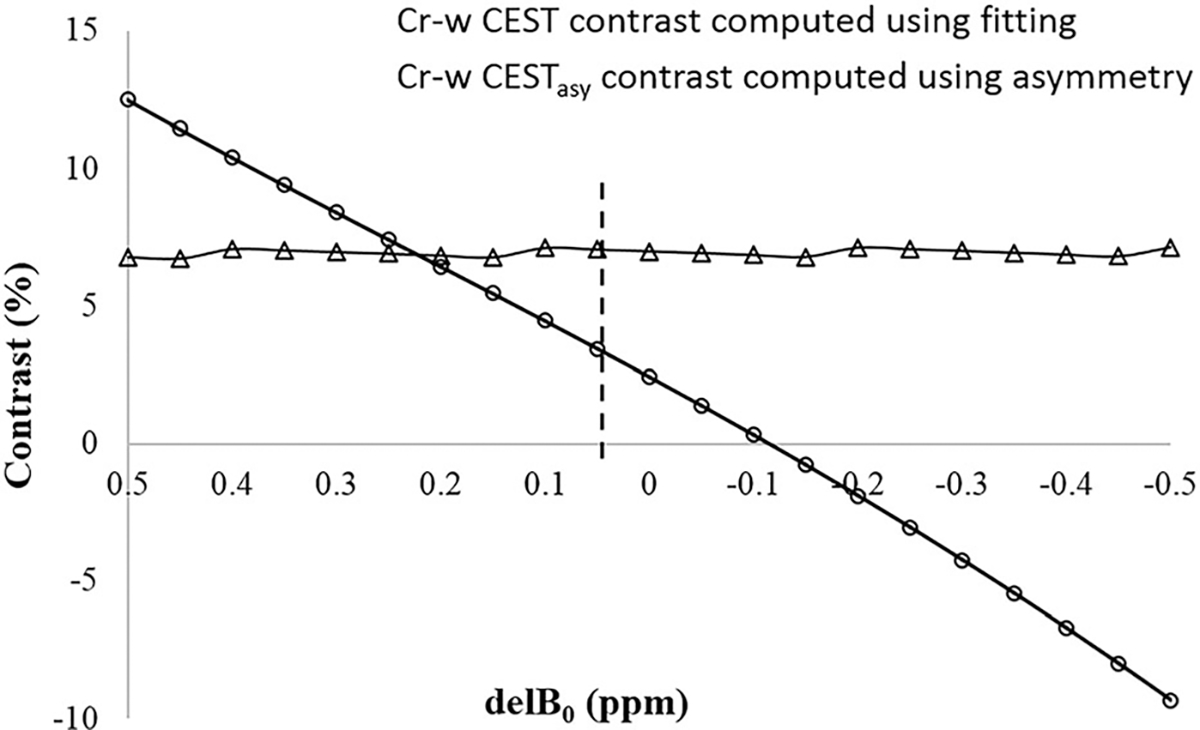
Plots show the sensitivity of Cr-w CEST contrast computed using fitting approach to shift in resonance frequency (delB0). Z-spectra from a region of interest in gray matter tissue was selected followed by fitting. Simulated Z-spectra were generated by varying the center, corresponding to direct saturation of free water obtained using fitting, from −0.5 to 0.5 ppm. These simulated Z-spectra were fitted using model 2 for computing Cr-w CEST as well as for computing asymmetry contrast
Table 3 shows the results of noise stability of model 2 versus model 1 for Z-spectral fitting. ARPE for all the fitted parameters (except amplitude of MT) were lower in model 2 compared with model 1. Simulation results showed that ARPE for amplitudes of DS, rNOE, Cr-w CEST and CEST@3.5 ppm were 26, 14, 12 and 4%, respectively, lower in model 2 compared with model 1. Similarly, ARPE for widths of DS, MT, rNOE, Cr-w CESTand CEST@3.5 ppm were 6, 25, 22, 7 and 17%, respectively, and found to be lower in model 2 compared with model 1. For an amplitude of MT both models showed a similar stability; however, for width, model 2 was more stable to noise compared with model 1.
TABLE 3.
Comparison of model 2 and model 1 fitting to Z‐spectra data obtained at B1rms of 1.4 μT and duration of 2 seconds from gray matter tissue of human brain using Monte‐Carlo simulations
| Amplitude (%) | Width (ppm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DS | MT | rNOE | Cr‐w CEST | CEST@3.5 ppm | DS | MT | rNOE | Cr‐w CEST | CEST@3.5 ppm | ||
| Model 2 | Par0 | 52.22 | 36.51 | 10.38 | 6.22 | 7.09 | 2.31 | 45.12 | 5.27 | 1.99 | 3.39 |
| mean ± SD | 51.96 ± 1.61 | 38.38 ± 2.01 | 11.12 ± 1.68 | 6.86 ± 1.89 | 7.19 ± 1.73 | 2.30 ± 0.12 | 50.12 ± 3.65 | 5.51 ± 1.14 | 2.25 ± 0.90 | 3.60 ± 1.29 | |
| ARPE | 2.46 | 6.18 | 14.68 | 25.96 | 19.92 | 4.27 | 12.12 | 17.60 | 38.74 | 31.70 | |
| Model 1 | Par0 | 51.07 | 33.99 | 12.55 | 5.96 | 7.79 | 2.27 | 46.72 | 6.96 | 2.19 | 4.58 |
| mean ± SD | 50.55 ± 2.02 | 34.90 ± 2.42 | 13.97 ± 2.15 | 6.64 ± 2.16 | 8.04 ± 2.00 | 2.25 ± 0.13 | 53.75 ± 5.64 | 7.65 ± 1.79 | 2.46 ± 1.01 | 5.41 ± 2.02 | |
| ARPE | 3.33 | 6.06 | 17.15 | 29.55 | 20.79 | 4.56 | 16.13 | 22.66 | 41.70 | 37.97 |
Abbreviations: ARPE, average absolute relative percentage error; CEST@3.5 ppm, CEST contrast at 3.5 ppm; Cr‐w CEST, CEST contrast at 1.8 ppm; DS, direct saturation; MT, magnetization transfer; rNOE, relayed nuclear Overhauser effect; Par0, parameters obtained from fitting of Z‐spectra without noise; SD, standard deviation.
Figure 9 shows fitting of Z-spectra using model 2 (B1rms = 1.45 μT, duration = 2 seconds) considering multi-pool models. Figure 9A shows fitting using a five-pool model (DS pool at 0 ppm, MT pool at −2.4 ppm, rNOE pool at −3.5 ppm, Cr-w CEST pool at 1.8 ppm and CEST@3.5 ppm). The reliability of fitting is tested by increasing the number of pools. Figure 9B shows fitting considering six pools, where the first five pools are similar to those of Figure 9A and the sixth pool (CEST@3 ppm) is considered at 3 ppm. In Figure 9C, the sixth pool (CEST@1 ppm) is considered at 1 ppm. In Figure 9D, the sixth pool (rNOE-2) is considered at −1.6 ppm. Residual errors of fittings were more than 2% and σ = ~ 0.05 for all cases. However, Monte-Carlo simulations showed that the stability and reliability of the fit decreases with increase in the number of pools. Figures S4 and S5 show the fitting of Z-spectra using model 2 for B1rms = 0.7 and 2.1 μT, respectively, at a duration of 2 seconds considering multipool models.
FIGURE 9.
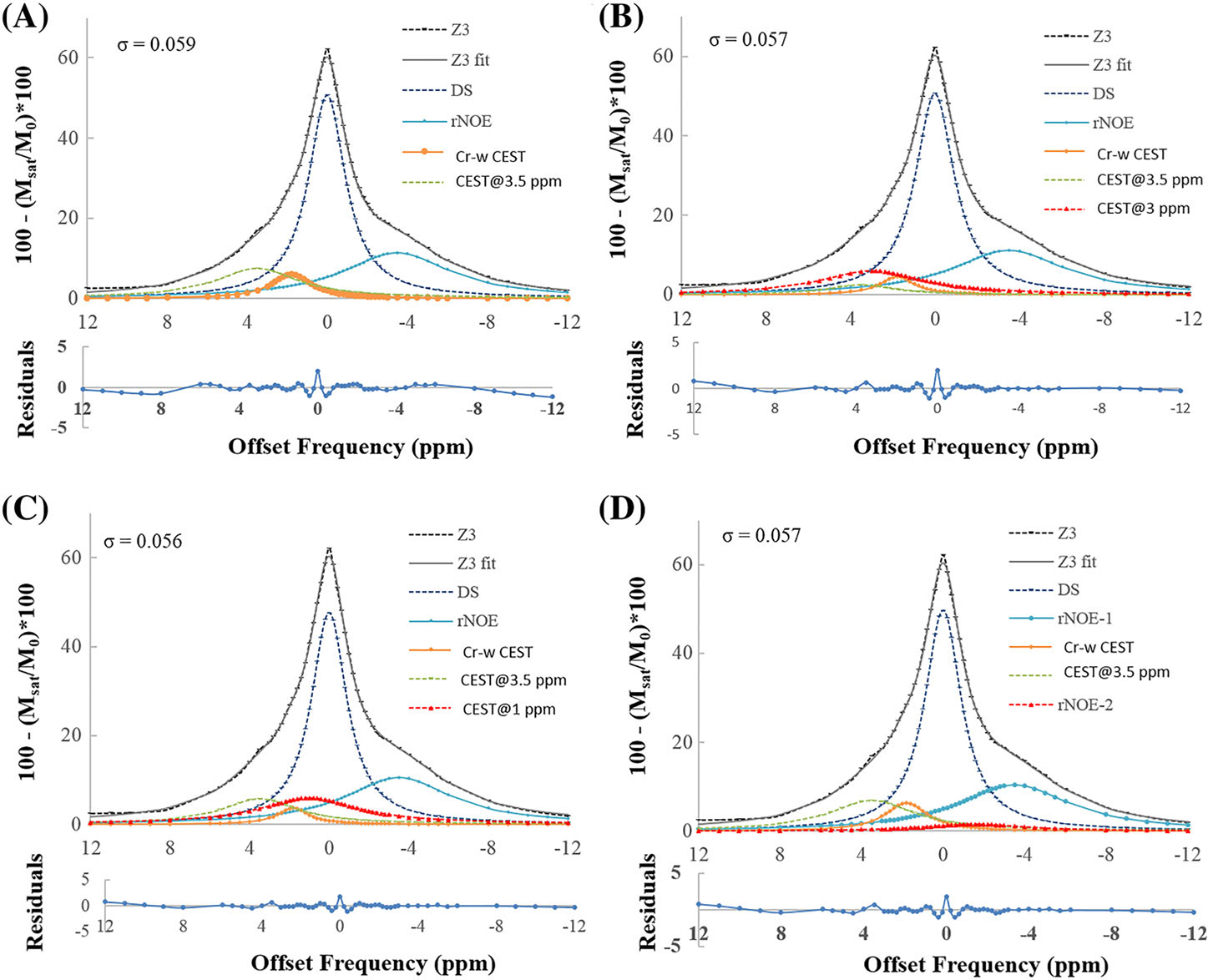
Fitting of Z-spectra using model 2 at a B1rms of 1.45 μT and duration of 2 seconds using multi-pool models. (A) Fitting using a five-pool model (DS pool at 0 ppm, MT pool at −2.4 ppm, rNOE pool at −3.5 ppm, Cr-w CEST pool at 1.8 ppm and CEST@3.5 ppm). (B) Fitting considering six pools, where the first five pools are similar to those of (A) and the sixth pool (CEST@3 ppm) is considered at 3 ppm. (C) Sixth pool (CEST@1 ppm) is considered at 1 ppm. (D) Sixth pool (rNOE-2) is considered at −1.6 ppm. Residual errors of fittings were less than 2% and σ = ~ 0.05 for all cases. CEST@3 ppm, CEST contrast at 3 ppm; CEST@3.5 ppm, CEST contrast at 3.5 ppm; Cr-w CEST, CEST contrast at 1.8 ppm; DS, direct saturation; MT, magnetization transfer; rNOE, relayed nuclear Overhauser effect; rNOE-2, rNOE pool at −1.6 ppm; σ, average residual error; R2, goodness of fit
Figure S3 shows a comparison of partial fitting of Z-spectra, at far-off resonance where MT effects dominate and other CEST and rNOE pools have a negligible effect, using Lorentzian, Gaussian and super-Lorentzian line shapes for B1rms of 0.7, 1.45 and 2.1 μT at a saturation duration of 2 seconds. For the current set of saturation parameters, the Lorentzian line shape fitted better to broad MT spectra with the lowest average residual error (σ = 0.0003 to 0.0012) compared with other line shapes for all B1rms. For the super-Lorentzian line shape, interpolated Z-spectra resulted in a pole at −2.4 ppm, which affected the accuracy of the entire Z-spectra fitting.
4 |. DISCUSSION
In the current study, we have used numerical simulations to obtain optimized saturation parameters for Cr-w CEST contrast with minimal overlap from known metabolites exhibiting CEST contrast. Optimized parameters were used to obtain in vivo Z-spectral data. The improved Z-spectral fitting approach resulted in an estimate of CEST contrast at 1.8 ppm with reduced overlap from other metabolites.
In phantom studies, a linear dependence of Cr-w CEST contrast on a physiological concentration range of Cr was observed. The Cr-w CEST contrast showed a nonlinear dependence on saturation duration and saturation B1rms. For in vivo data, the dependence of Cr-w CEST contrast on saturation parameters might be quite different compared with Cr solution phantom data due to substantial direct saturation of bulk water, MT effects from macromolecules, and overlap from other CEST and rNOE. Therefore, in this study, we have performed numerical simulations, mimicking the in vivo situation for DS and MT effects, exchange rates, relaxation times and different experimental conditions. Although it is not possible to completely simulate an in vivo environment, major contributors to in vivo Cr-w CEST contrast have been evaluated in this study. For optimization, we have not simulated contribution from rNOE to Cr-w CEST as we planned to separate out rNOE using a fitting-based approach. Based upon preliminary observations using simulations, it was possible to reduce overlap and obtain optimal Cr-w CEST contrast. However, it was difficult to find saturation parameters to completely remove the overlap from other metabolites. Simulation results show that 10mM of Cr provide ~ 4.3% of CEST effect at 1.8 ppm using a B1rms of 1.45 μT and duration of 2 seconds at 7 T. It was also observed that PCr exhibits a small CEST effect at 1.8 and 2.5 ppm.19 Due to a slow exchange rate compared with amine protons of Cr, the CEST effect from PCr is negligible (~ 0.2% per mM). Amine protons of GABA also exhibit the CEST effect at ~ 3 ppm, with an exchange rate similar to that of glutamate. The concentration of GABA in human brain is ~ 1–2mM. Therefore, in this study, GABA was considered a part of glutamate for the purposes of simulation.
The superposition of Lorentzian functions has been successfully used to fit in vivo Z-spectra data from rat brain at 9.4 T.23 In the reported studie,23 CEST peaks at 3.5 and 1.8 ppm were visible and fitted nicely to the superposition of Lorentzian functions. However, the in vivo Z-spectral data obtained at 7 T using saturation parameters (1.4 μT, 2 seconds) showed broad CEST effects, and because of this model 1 resulted in higher values of width compared with model 2. Model 2 fits a broad MT component using partial Z-spectra data with negligible contribution from other effects and removes this component from the Z-spectra before finer fitting. This approach results in lower values of the width of rNOE and CEST pools compared with model 1. The amplitude of rNOE showed a clear decrease for model 2. As such, both models fitted reasonably well to Z-spectra data and there were differences in the width and amplitude. However, it is difficult to compare these two models on the basis of only residual error, and change in width and amplitude. Thus, Monte-Carlo simulations were carried out to check the stability of both models and to determine which one works better. Monte-Carlo simulations showed that ARPE decreases for all of the parameters, except for MT in model 2 compared with model 1. Thus, it can be concluded that model 2 is less sensitive to noise than model 1.
A previous study50 at 9.4 T compared different fitting quantification methods such as Lorentzian difference, multiple-pool Lorentzian fitting or model 1 and three-point methods and reported that model 1 was better than the other methods. However, model 2 was not included in this study and the saturation parameters were quite different compared with the current study. The fitting model accuracy depends on saturation parameters and field strength, etc. Therefore, one should evaluate the accuracy of different models for their Z-spectra data. Our in vivo human study at 7 T showed that model 2 is slightly better than model 1.
In general, contrast computed using CEST asymmetry analysis is highly sensitive to B0 field inhomogeneity, and accurate B0 mapping and correction are required before interpretation of the results. On the other hand, CEST contrast computed using a fitting-based approach is less sensitive to B0 field inhomogeneity and there is no need to acquire separate WASSR/B0 map data. An estimate of DS offset frequency based upon the minimum value of Z-spectra followed by an improvement during fitting is good enough for automatic correction of B0 field inhomogeneity artifacts.
In this study, Cr-w CEST contrast in the GM and WM tissue was 6.98 ± 0.31% and 5.45 ± 0.16%, respectively. A spectroscopic studies have reported that the Cr ratio in GM/WM is in the range of 1.2 to 1.5.13 In the current study, the Cr-w CEST contrast ratio in GM/WM was 1.28 and 1.43 using models 2 and 1, respectively. Therefore, Cr-w CEST correlated with spectroscopy-based Cr measurements in GM and WM tissues.
For brain tissue, a ratio of 2:1 is reported for the Cr/PCr ratio. However, for the saturation parameter used in the current study, the PCr contribution is negligible in brain tissue. As such, although we have tried to mitigate overlap from different effects using optimized saturation parameters and a fitting-based approach, the Cr-w CEST contrast might still have some overlap. However, a major contribution from Cr to Cr-w CEST contrast cannot be ruled out. A recently published study24 on rat brain data has reported that amine protons from side chain proteins also exhibit the CEST effect at ~ 2 ppm, which can also overlap with Cr-w CEST contrast. Another study51 also showed that CEST effects from side chain protein amines are very broad and can contribute to the CEST signal at ~ 2 ppm. However, due to the use of low saturation power in the current study, contribution from these fast exchanging amine protons should be small. Further studies are required to estimate the overlap of such broad peaks to CrCEST.
The chemical shift of the exchangeable proton is proportional to field strength while the exchange rate is constant. In the current study, in which we performed the phantom experiments at 7 T, due to the slow intermediate exchange rates of Cr it is possible to observe the Cr-w CEST effect even with low field scanners such as 3 T.22 The feasibility of Cr-w CEST mapping for calf muscle and myocardium has been demonstrated previously at 3 T.21,22 The CEST effect is also highly dependent on saturation pulse parameters, field homogeneity and tissue type. Further studies to optimize the parameters for in vivo mapping of Cr-w CEST in human brain on a lower field scanner are required.
In this study, MT components of Z-spectra data were fitted using Lorentzian, Gaussian and super-Lorentzian line shapes. It was observed that all three line shapes fitted reasonably well to far-off resonance MT components of Z-spectra data, having negligible contribution from other effects. However, for model 1, super-Lorentzian line shape resulted in poor fitting close to water resonance due to the presence of a large hump at −2.4 ppm. Similarly, for model 2, the interpolation of fitted super-Lorentzian component created a large hump at −2.4 ppm and hence resulted in poor fitting of Z-spectra, particularly close to water resonance. Due to this pole of super-Lorentzian line shape, a recent study52 has used symmetric interpolation between ±20 ppm using a cubic-spline interpolation to remove the pole that occurs close to its resonance frequency. In the current study, Lorentzian line shape for MT provided the least residual error compared with other line shapes. Several other studies22,23,34 have also used either Lorentzian line shapes or polynomials. Computation of rNOE and CEST components using a multipool Z-spectra-fitting approach (models 1 and 2) with super-Lorentzian line shape for MT pool is not suitable for the data presented in the current study. It should be noted that when super-Lorentzian line shape for MT pool was proposed for Z-spectra fitting, CEST and rNOE were not considered and the main emphasis was on fitting Z-spectra over far-off resonance frequencies. The previously reported analytical model was valid for two-pool Z-spectra under steady state conditions. Z-spectra data acquired in the current study are nonsteady state, have multiple pools and were acquired using low saturation B1rms, and were optimized for Cr-w CEST contrast for a limited frequency range of −40 to 40 ppm. Due to the presence of multiple pool and nonsteady state conditions, the derivation of analytical models is not possible. Therefore, for such nonsteady state data, empirical models based upon combinations of different line shapes such as sum of Lorentzians can be used. Thus, for the set of saturation parameters used in this study, Lorentzian line shape is a better approximation to the MT component of Z-spectra and thus we used Lorentzian line shape for removal of the MT component.
In general, the CEST MRI signal depends upon direct saturation of free water pool, semi-solid macromolecular concentration (MT effect), solute pool concentration, exchange rate, pH, water longitudinal relaxation time (T1), saturation pulse parameters and field strength. Thus, CEST contrast is usually compared with similar saturation parameters and at the same field strength. CEST contrast computed using a conventional CESTasy analysis still has some tissue-specific bias due to differences in MT effect and T1. Different approaches have been adopted to mitigate these effects on computed CEST contrast. The AREX method41 and normalization by negative offset frequency4,49 are two such examples. In the current study, CrCEST contrast between GM and WM tissue also has some bias due to different MT effects and T1 in these tissues. CEST contrast computation using the proposed Z-spectra fitting using both models 1 and 2 mitigates the MT effect and is less sensitive to T1; however, complete removal of these effects from true CEST contrast has not been achieved to date. Another study53 reported that for nonsteady-state acquisition, the effect of T1 is substantially less. In this study, we have considered only two CEST pools and a single rNOE. For testing purposes, when additional CEST pools were included in the Z-spectra fitting then the stability of the model to noise was reduced. An additional rNOE pool centered at −1.6 ppm was also considered for the Z-spectra fitting, which resulted in negligible amplitude corresponding to B1rms of 1.4 μT. The same additional pool resulted in a broad line shape for B1rms of 0.7 μT and a narrow line shape for B1rms of 2.1 μT. These results show that the fitting of this additional rNOE pool is not reliable for the saturation parameters and models considered in the current study.
Limitations of the current study are stated below along with directions for future research. The acquisition of Z-spectra data over a wide range of offset frequencies increases the scan time, as do the extra data required for B1 inhomogeneity correction. We have tried to optimize the data acquisition strategy to minimize the number of data points required. Alternative approaches based upon machine learning can be considered in future studies to reduce the scan time. Cr-w CEST contrast in GM and WM was correlated with a reported spectroscopy-based ratio of [Cr]. In future study, MR spectroscopic data could be collected in representative GM and WM regions to evaluate subject-specific correlation between [Cr] and Cr-w CEST contrast.
5 |. CONCLUSION
It is feasible to perform Cr-w CEST mapping in human brain at 7 T using optimal saturation parameters and a Z-spectra fitting approach. In the limited, far-off resonance frequency range, the Lorentzian line shape provided a slightly better approximation for the broad MT component of Z-spectra compared with Gaussian and super-Lorentzian functions. Although goodness of fit and residual errors of fit were similar in both Z-spectra fitting models, Monte-Carlo simulations showed that model 2 is more stable to noise than model 1. Imaging protocol and the fitting approach proposed in the current study can be used for acquiring patient data and computing Cr-w CEST contrast.
Supplementary Material
ACKNOWLEDGEMENTS
The authors acknowledge an internal seed grant from the Indian Institute of Technology Delhi. This project was partially supported by MATRICS, SERB-DST, Grant Number MTR_2017_001021, and was also partially supported by the National Institute of Biomedical Imaging and Bioengineering of the NIH through grant number P41-EB015893, R21-EB023516, and the Centre for Magnetic Resonance and Optical Imaging (CMROI), University of Pennsylvania.
Abbreviations used:
- ARPE
absolute relative percentage error
- CEST
chemical exchange saturation transfer
- CEST@1 ppm
CEST pool centered at 1 ppm
- CEST@3.5 ppm
CEST pool centered at 3.5 ppm
- Cr-w
creatine-weighted
- GM
gray matter
- RF
radio frequency
- rNOE
relayed nuclear Overhauser effect
- WM
white matter
Footnotes
CONFLICTS OF INTEREST
The authors declare no financial interests.
SUPPORTING INFORMATION
Additional supporting information may be found online in the Supporting Information section at the end of the article.
REFERENCES
- 1.Ward K, Balaban R. Determination of pH using water protons and chemical exchange dependent saturation transfer (CEST). Magn Reson Med. 2000;44:799–802. [DOI] [PubMed] [Google Scholar]
- 2.Ward K, Aletras A, Balaban R. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST). J Magn Reson. 2000;143:79–87. [DOI] [PubMed] [Google Scholar]
- 3.Zhou J, Payen J-F, Wilson DA, Traystman RJ, van Zijl PCM. Using the amide proton signals of intracellular proteins and peptides to detect pH effects in MRI. Nat Med. 2003;9:1085–1090. [DOI] [PubMed] [Google Scholar]
- 4.Cai K, Haris M, Singh A, et al. Magnetic resonance imaging of glutamate. Nat Med. 2012;18:302–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ling W, Regatte RR, Navon G, Jerschow A. Assessment of glycosaminoglycan concentration in vivo by chemical exchange-dependent saturation transfer (gagCEST). Proc Natl Acad Sci. 2008;105:2266–2270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Adhihetty PJ, Beal MF. Creatine and its potential therapeutic value for targeting cellular energy impairment in neurodegenerative diseases. Neuromolecular Med. 2008;10:275–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tabrizi SJ, Blamire AM, Manners DN, et al. Creatine therapy for Huntington's disease: clinical and MRS findings in a 1-year pilot study. Neurology. 2003;61:141–142. [DOI] [PubMed] [Google Scholar]
- 8.Tong Z, Yamaki T, Harada K, Houkin K. In vivo quantification of the metabolites in normal brain and brain tumors by proton MR spectroscopy using water as an internal standard. Magn Reson Imaging. 2004;22:1017–1024. [DOI] [PubMed] [Google Scholar]
- 9.Renema WKJ, Schmidt A, Van Asten JJA, et al. MR Spectroscopy of muscle and brain in guanidinoacetate methyltransferase (GAMT)-deficient mice: validation of an animal model to study creatine deficiency. Magn Reson Med. 2003;50:936–943. [DOI] [PubMed] [Google Scholar]
- 10.Huang W, Alexander GE, Chang L, et al. Brain metabolite concentration and dementia severity in Alzheimer's disease: a 1H MRS study. Neurology. 2001;57:626–632. [DOI] [PubMed] [Google Scholar]
- 11.Minati L, Aquino D, Bruzzone M, Erbetta A. Quantitation of normal metabolite concentrations in six brain regions by in-vivo 1 H-MR spectroscopy. J Med Phys. 2010;35:154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Michaelis T, Merboldt KD, Bruhn H, Hänicke W, Frahm J. Absolute concentrations of metabolites in the adult human brain in vivo: quantification of localized proton MR spectra. Radiology. 1993;187:219–227. [DOI] [PubMed] [Google Scholar]
- 13.Pouwels PJ, Brockmann K, Kruse B, et al. Regional age dependence of human brain metabolites from infancy to adulthood as detected by quantitative localized proton MRS. Pediatr Res. 1999;46:474–485. [DOI] [PubMed] [Google Scholar]
- 14.Pouwels PJW, Frahm J. Regional metabolite concentrations in human brain as determined by quantitative localized proton MRS. Magn Reson Med. 1998;39:53–60. [DOI] [PubMed] [Google Scholar]
- 15.Soher BJ, Hurd RE, Sailasuta N, Barker PB. Quantitation of automated single-voxel proton MRS using cerebral water as an internal reference. Magn Reson Med. 1996;36:335–339. [DOI] [PubMed] [Google Scholar]
- 16.Petroff OAC, Pleban LA, Spencer DD. Symbiosis between in vivo and in vitro NMR spectroscopy: the creatine, N-acetylaspartate, glutamate, and GABA content of the epileptic human brain. Magn Reson Imaging. 1995;13:1197–1211. [DOI] [PubMed] [Google Scholar]
- 17.Miscevic F, Foong J, Schmitt B, Blaser S, Brudno M, Schulze A. An MRspec database query and visualization engine with applications as a clinical diagnostic and research tool. Mol Genet Metab. 2016;119:300–306. [DOI] [PubMed] [Google Scholar]
- 18.Zhou IY, Wang E, Cheung JS, Zhang X, Fulci G, Sun PZ. Quantitative chemical exchange saturation transfer (CEST) MRI of glioma using Image Downsampling Expedited Adaptive Least-squares (IDEAL) fitting. Sci Rep. 2017;7:84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Haris M, Nanga RPR, Singh A, et al. Exchange rates of creatine kinase metabolites: Feasibility of imaging creatine by chemical exchange saturation transfer MRI. NMR Biomed. 2012;25:1305–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kogan F, Haris M, Singh A, et al. Method for high-resolution imaging of creatine in vivo using chemical exchange saturation transfer. Magn Reson Med. 2014;71:164–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kogan F, Haris M, Debrosse C, et al. In vivo chemical exchange saturation transfer imaging of creatine (CrCEST) in skeletal muscle at 3T. J Magn Reson Imaging. 2014;40:596–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Haris M, Singh A, Cai K, et al. A technique for in vivo mapping of myocardial creatine kinase metabolism. Nat Med. 2014;20:209–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cai K, Singh A, Poptani H, et al. CEST signal at 2ppm (CEST at 2ppm) from Z-spectral fitting correlates with creatine distribution in brain tumor. NMR Biomed. 2015;28:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhang XY, Xie J, Wang F, et al. Assignment of the molecular origins of CEST signals at 2ppm in rat brain. Magn Reson Med. 2017;26:881–887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Goerke S, Zaiss M, Bachert P. Characterization of creatine guanidinium proton exchange by water-exchange (WEX) spectroscopy for absolute-pH CEST imaging in vitro. NMR Biomed. 2014;27:507–518. [DOI] [PubMed] [Google Scholar]
- 26.Zhou J, Lal B, Wilson DA, Laterra J, Van Zijl PCM. Amide proton transfer (APT) contrast for imaging of brain tumors. Magn Reson Med. 2003;50:1120–1126. [DOI] [PubMed] [Google Scholar]
- 27.Debnath A, Gupta RK, Singh A. Evaluating the role of amide proton transfer (APT)–weighted contrast, optimized for normalization and region of interest selection, in differentiation of neoplastic and infective mass lesions on 3T MRI. Mol Imaging Biol. 2019. 10.1007/s11307-019-01382-x. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhou J, Heo H-Y, Knutsson L, van Zijl PCM, Jiang S. APT-weighted MRI: techniques, current neuro applications, and challenging issues. J Magn Reson Imaging. 2019;50:347–364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bai Y, Zuo P, Schmitt B, Shi D, Zhou J, Wang M. Amide proton transfer MRI in patients with high-grade and low-grade gliomas. MAGNETOM Flash. 2014;3:39–41. [Google Scholar]
- 30.Haris M, Cai K, Singh A, Hariharan H, Reddy R. In vivo mapping of brain myo-inositol. Neuroimage. 2011;54:2079–2085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Davis KA, Nanga RPR, Das S, et al. Glutamate imaging (GluCEST) lateralizes epileptic foci in nonlesional temporal lobe epilepsy. Sci Transl Med. 2015;7:309ra161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nanga RPR, DeBrosse C, Kumar D, et al. Reproducibility of 2DGluCEST in healthy human volunteers at 7 T. Magn Reson Med. 2018;80:2033–2039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Walker-Samuel S, Ramasawmy R, Torrealdea F, et al. In vivo imaging of glucose uptake and metabolism in tumors. Nat Med. 2013;19:1067–1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu G, Song X, Chan KWY, Mcmahon MT. Nuts and bolts of chemical exchange saturation transfer MRI. NMR Biomed. 2013;26:810–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J Magn Reson. 2011;211:149–155. [DOI] [PubMed] [Google Scholar]
- 36.Heo HY, Zhang Y, Jiang S, Lee DH, Zhou J. Quantitative assessment of amide proton transfer (APT) and nuclear overhauser enhancement (NOE) imaging with extrapolated semisolid magnetization transfer reference (EMR) signals: II. Comparison of three EMR models and application to human brain glioma at. Magn Reson Med. 2016;75:1630–1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Heo H-Y, Zhang Y, Lee D-H, Hong X, Zhou J. Quantitative assessment of amide proton transfer (APT) and nuclear overhauser enhancement (NOE) imaging with extrapolated semi-solid magnetization transfer reference (EMR) signals: application to a rat glioma model at 4.7 Tesla. Magn Reson Med. 2016;75:137–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J Magn Reson Ser B. 1995;108:103–113. [DOI] [PubMed] [Google Scholar]
- 39.Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ. Precise estimate of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn Reson Imaging. 2002;20:721–731. [DOI] [PubMed] [Google Scholar]
- 40.Tozer D, Ramani A, Barker GJ, Davies GR, Miller DH, Tofts PS. Quantitative magnetization transfer mapping of bound protons in multiple sclerosis. Magn Reson Med. 2003;50:83–91. [DOI] [PubMed] [Google Scholar]
- 41.Zaiss M, Xu J, Goerke S, et al. Inverse Z-spectrum analysis for spillover-, MT-, and T1-corrected steady-state pulsed CEST-MRI - application to pH-weighted MRI of acute stroke. NMR Biomed. 2014;27:240–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kogan F, Singh A, Debrosse C, et al. Imaging of glutamate in the spinal cord using GluCEST. Neuroimage. 2013;77:262–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kim M, Gillen J, Landman BA, Zhou J, Van Zijl PCM. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn Reson Med. 2009;61:1441–1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.McConnell HM. Reaction rates by nuclear magnetic resonance. J Chem Phys. 1958;28:430–431. [Google Scholar]
- 45.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med. 2005;53:790–799. [DOI] [PubMed] [Google Scholar]
- 46.Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ. Precise estimate of fundamentalin-vivo MT parameters in human brain in clinically feasible times. MagnReson Imaging. 2002;20(10):721–731. [DOI] [PubMed] [Google Scholar]
- 47.Wijnen JP, VanAsten JJA, Klomp DWJ, et al. Short echo time 1H MRSI of the human brain at 3T with adiabatic slice-selective refocusing pulses; reproducibility and variancein a dual center setting. J Magn Reson Imaging. 2010;31(1):61–70. [DOI] [PubMed] [Google Scholar]
- 48.Dechent P, Pouwels PJ, Wilken B, Hanefeld F, Frahm J. Increase of total creatine in humanbrain after oral supplementation of creatine-monohydrate. Am J Physiol. 1999;277(3):R698–R704. [DOI] [PubMed] [Google Scholar]
- 49.Singh A, Cai K, Haris M, Hariharan H, Reddy R. On B1 inhomogeneity correction of in vivo human brain glutamate chemical exchange saturation transfer contrast at 7T. Magn Reson Med. 2013;69:818–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang XY, Wang F, Li H, et al. Accuracy in the quantification of chemical exchange saturation transfer (CEST) and relayed nuclear Overhauser enhancement (rNOE) saturation transfer effects. NMR Biomed. 2017;30:(7). 10.1002/nbm.3716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zong X, Wang P, Kim SG, Jin T. Sensitivity and source of amine-proton exchange and amide-proton transfer magnetic resonance imaging in cerebral ischemia. Magn Reson Med. 2014;71:118–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Stephen Evans V, Torrealdea F, Rega M, et al. Optimization and repeatability of multipool chemical exchange saturation transfer MRI of the prostate at 3.0 T. J Magn Reson Imaging. 2019. 10.1002/jmri.26690 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zu Z Towards the complex dependence of MTRasym on T1w in amide proton transfer (APT) imaging. NMR Biomed. 2018;31:e3934. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


