Universal quantum operations and ancilla-based read-out for tweezer clocks

Abstract

Enhancing the precision of measurements by harnessing entanglement is a long-sought goal in quantum metrology^1,2. Yet attaining the best sensitivity allowed by quantum theory in the presence of noise is an outstanding challenge, requiring optimal probe-state generation and read-out strategies^3–7. Neutral-atom optical clocks⁸, which are the leading systems for measuring time, have shown recent progress in terms of entanglement generation^9–11 but at present lack the control capabilities for realizing such schemes. Here we show universal quantum operations and ancilla-based read-out for ultranarrow optical transitions of neutral atoms. Our demonstration in a tweezer clock platform^9,12–16 enables a circuit-based approach to quantum metrology with neutral-atom optical clocks. To this end, we demonstrate two-qubit entangling gates with 99.62(3)% fidelity—averaged over symmetric input states—through Rydberg interactions^15,17,18 and dynamical connectivity¹⁹ for optical clock qubits, which we combine with local addressing¹⁶ to implement universally programmable quantum circuits. Using this approach, we generate a near-optimal entangled probe state^1,4, a cascade of Greenberger–Horne–Zeilinger states of different sizes, and perform a dual-quadrature⁵ Greenberger–Horne–Zeilinger read-out. We also show repeated fast phase detection with non-destructive conditional reset of clock qubits and minimal dead time between repetitions by implementing ancilla-based quantum logic spectroscopy²⁰ for neutral atoms. Finally, we extend this to multi-qubit parity checks and measurement-based, heralded, Bell-state preparation^21–24. Our work lays the foundation for hybrid processor–clock devices with neutral atoms and more generally points to a future of practical applications for quantum processors linked with quantum sensors²⁵.

We demonstrate high-fidelity entangling gates, universal quantum operations, and ancilla-based read-out for ultranarrow optical transitions of neutral atoms in a tweezer clock platform.

Main

The control of quantum systems is evolving rapidly on many fronts. On the one hand, quantum processors, which use quantum mechanics to perform calculations, have matured into intermediate-scale systems with high-fidelity entangling operations and universal control capabilities^19,26–33. On the other hand, quantum sensors²⁵ and, in particular, optical atomic clocks⁸, which use quantum mechanics to measure time, have become both more accurate and more precise, thus revealing new phenomena³⁴ and enabling the measurement of relativistic effects at a laboratory scale^35,36. Thus, a natural question and a long-sought goal is how to use quantum information processing tools and entanglement to improve quantum sensors.

Two main strategies are typically considered in this context¹: entangled state preparation and entanglement-assisted measurements. For the first, entanglement introduces correlations between probes, resulting in jointly enhanced sensitivity; unfortunately, this also entails jointly enhanced vulnerability to errors and reduced dynamic range, which often nullifies or strongly reduces any effective gains^3,4,37–39. Schemes to circumvent this apparent drawback use specific, finely tuned, entangled, probe-state preparation and read-out schemes^1,4,6. Although one such scheme has been recently realized with trapped ions⁷, so far there has been no demonstration in neutral-atom optical clocks, despite recent progress in generating entanglement^9–11.

Second, entanglement with an ancillary system can be harnessed in non-destructive read-out of a sensor to benefit metrology, for example, logic spectroscopy of inaccessible probes as demonstrated with ions²⁰, sequential multi-round phase estimation¹, fast mid-circuit detection for multi-ensemble metrology⁵, and shallow-circuit preparation of long-range entangled states^21–24. Only very recently, ancilla-based read-out for hyperfine qubits in neutral atoms has been shown^24,40, but a demonstration for ultranarrow optical transitions—as needed for optical atomic clocks—is outstanding. Further, it is critical that ancilla-based read-out can be performed repeatedly to fully realize its potential for metrology (and for quantum error correction⁴¹), which is an outstanding challenge for neutral atoms in general.

To demonstrate such complex entangled probe-state generation and repeated ancilla-based read-out, we realize a scalable universal quantum processor with neutral-atom qubits encoded in an ultranarrow optical transition (Fig. 1a). Importantly, the same experimental system can be used as a neutral-atom optical clock⁸, which is at present the most stable frequency reference^35,36. Specifically, our system is a tweezer optical clock^9,12–16 composed of neutral strontium-88 trapped in a tweezer array⁴² (Fig. 1b,c), which we now equip with universal quantum computing and repeated ancilla-based read-out capabilities.

Fig. 1. Universal quantum operations for tweezer clocks.

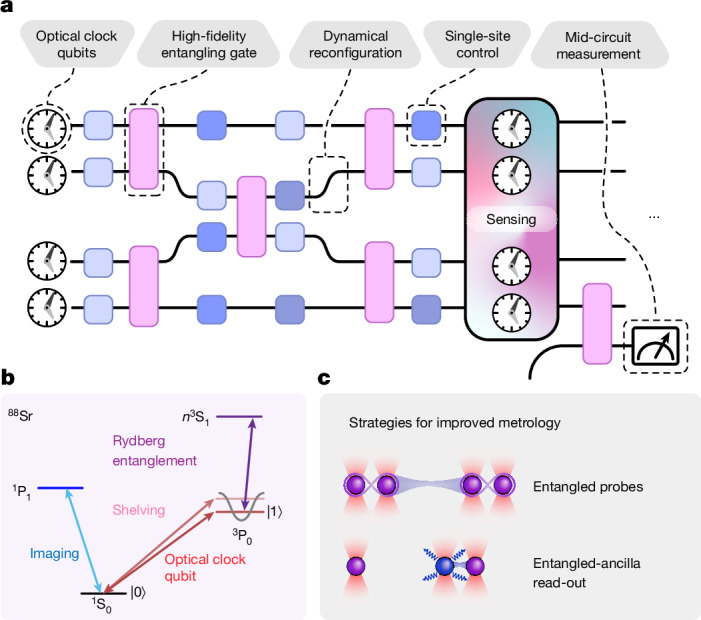
a, We demonstrate a universal quantum processor based on optical clock qubits. This processor is designed to perform any computational task and is also a highly sensitive clock. To realize this device, we demonstrate high-fidelity entangling gates between optical clock qubits and circuits with dynamical reconfiguration. We combine these with local single-qubit rotations through subwavelength atomic shifts and local MCR. b, We use tweezer-trapped ⁸⁸Sr atoms. Qubits are based on the ultranarrow optical clock transition ¹S₀ ↔ ³P₀, and entangling operations are realized through transient excitation to a Rydberg state n³S₁. We use coherent superpositions of quantized motional states in tweezers to shelve protected clock qubits for mid-circuit detection of ancilla qubits. c, We identify two instances where these universal quantum operations can be used in optimizing quantum metrology: entangled state preparation for near-optimal probes and entanglement-assisted read-out with ancilla qubits, thus realizing quantum logic spectroscopy for neutral atoms.

In particular, we demonstrate high-fidelity entangling gates^17,18,27 for optical clock qubits¹⁵, achieving a state-of-the-art controlled-Z (CZ) fidelity for neutral atoms of 0.9962(3) (averaged over symmetric two-qubit states). We generate an array of optical-clock-transition Bell pairs with a record fidelity. We further show that optical coherence is preserved during qubit transport in tweezers, which has previously been realized with hyperfine qubits^19,43, enabling dynamical circuit reconfiguration. Together with high-fidelity global single-qubit rotations, single-site control¹⁶, and mid-circuit read-out (MCR)⁴⁴, this allows us to take a circuit-based approach to realize strategies for entangled state preparation and read-out designed to improve metrology (Fig. 1c).

High-fidelity entangling gates for optical qubits

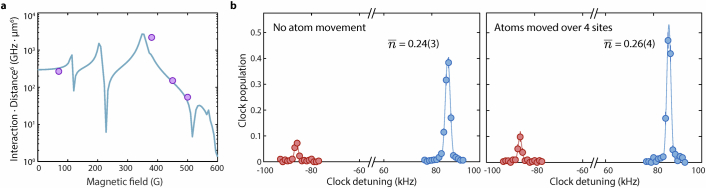
We begin by demonstrating high-fidelity entangling gates for the ultranarrow optical clock transition. The optical transition defines a qubit composed of the ground state of strontium-88 ¹S₀, denoted as $\mid 0⟩$, and the metastable state ³P₀, denoted as $\mid 1⟩$ (Fig. 1b). To realize a high-fidelity entangling operation, we apply a single phase-modulated Rydberg pulse for a CZ gate, which has been shown to be time-optimal^45,46 and has recently been implemented in hyperfine and nuclear atomic qubits^17,18. To simultaneously realize high-fidelity single-qubit rotations, we operate with a magnetic field of 450 G, which achieves a balance between a sufficiently high Rabi frequency on the clock transition (scaling linearly with the magnetic field) and sufficiently strong interactions (as the Rydberg interaction strength is magnetic field dependent; Methods and Extended Data Fig. 1). We prepare atoms in the $\mid 1⟩$ state and perform erasure-cooling⁴⁴, which prepares atoms close to the motional ground state.

Extended Data Fig. 1. Rydberg interaction strength and minimal heating due to dynamical reconfiguration.

a, Rydberg interaction strength at different magnetic fields. The solid line represents numerical calculations performed for a 7 μm spacing with the ‘PairInteraction’ package⁶¹. Markers represent interaction energy measured via a two-atom spin echo experiment at ≈ 7 μm spacing. b, No observable heating due to dynamical array reconfiguration. An array reconfiguration step consists of transporting the atoms over multiple inter-tweezer distances to desired positions. We use sideband spectroscopy to measure the average radial motional occupation $\overline{n}$ in the tweezers before and after such atom movements. We move the atoms over 13 μm in 160 μs, the typical distance and duration in all of the experiments presented in the main text. We perform this measurement at nominal temperature $\overline{n}=0.24\left(3\right)$ with no further erasure-cooling, as opposed to the temperature $\overline{n}=0.01$ with erasure-cooling⁴⁴. After performing dynamical reconfiguration, the measured $\overline{n}$ is 0.26(4), i.e. no significant heating (within error bars), an important feature for high-fidelity rotations of optical clock qubits.

We characterize the performance of such gates with a randomized circuit (Fig. 2a) designed to benchmark the CZ gate fidelity averaged over the two-qubit symmetric states (Methods and Extended Data Fig. 3). By varying the number of CZ gates N_CZ, we infer a CZ fidelity of 0.9962(3) by fitting the decay of the return probability as a function of N_CZ to an exponential trend (Fig. 2b). The quoted fidelity is corrected for the false contribution from leakage out of the qubit manifold during the gate (Methods). We numerically find this gate benchmark to be within 5% of the infidelity averaged over Haar random states for our gate parameters⁴⁷. Our result sets a new state-of-the-art fidelity in Rydberg-based two-qubit entangling gates for long-lived qubits^17,48.

Fig. 2. High-fidelity entangling gates for optical clock qubits.

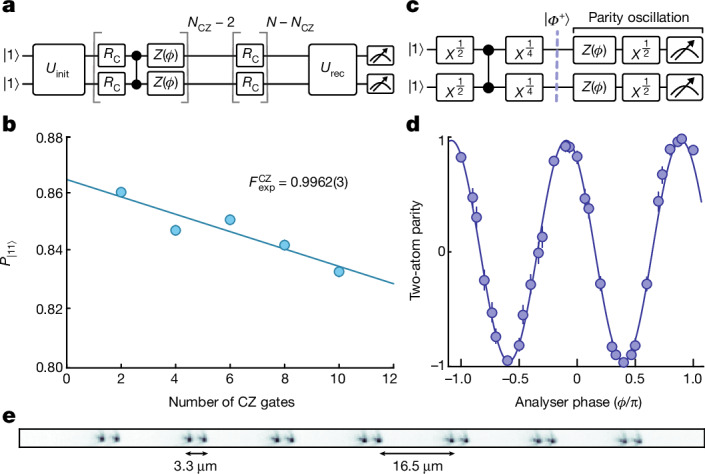
a, Randomized circuit characterization of CZ gate fidelity averaged over symmetric input states prepared by ${\widehat{U}}_{\mathrm{init}}$. The circuit includes a fixed number of random single-qubit gates R_C and a variable number N_CZ of CZ gates. The final unitary ${\widehat{U}}_{\mathrm{rec}}$ is precomputed to maximize the return probability $P_{\mid 11⟩}$ in the absence of errors. b, By fitting the return probability as a function of N_CZ, we infer a gate fidelity of 0.9962(3) after correcting for the false contribution from leakage errors (Methods). c, A circuit for creating and characterizing the Bell state $\mid {\Phi }^{+}⟩$. d, Parity oscillations with a measured bare parity contrast of $0.963_{-10}^{+7}$. Together with the population overlap (Methods), we obtain a Bell-state generation fidelity of $0.976_{-6}^{+4}$ ($0.989_{-6}^{+4}$ SPAM corrected). In b and d, the data are conditioned on atom pairs surviving erasure-cooling, which occurs at a rate of 51%. e, Array configuration depicted by the average atomic fluorescence image. The interatomic separation is chosen to induce strong Rydberg interactions within each pair and avoid unwanted interactions between pairs.

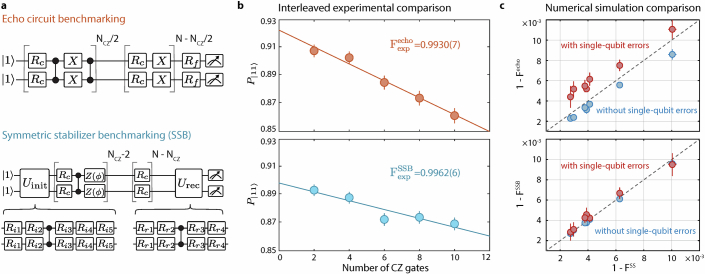
Extended Data Fig. 3. Comparison of benchmarking circuits.

a, Top: a randomized circuit where CZ gates are interleaved with global single-qubit π-pulses (echo pulses) and random π/2 rotations R_c (echo circuit). Bottom: a randomized circuit in which an initial unitary ${\widehat{U}}_{init}$ prepares one of the 12 two-qubit symmetric stabilizer states with a uniform probability via a series of single-qubit rotations R_i and a CZ gate. The circuit (SSB circuit) is then designed to maintain such uniform distribution, in order to reduce sensitivity to single-qubit gate errors (see Methods). Each Rydberg CZ gate is composed of a Rydberg pulse followed by a phase gate Z(ϕ) which we apply virtually by shifting the phase of the next global rotation. Z(ϕ) is separately calibrated to find the single-atom phase acquired during the Rydberg pulse. A final unitary ${\widehat{U}}_{rec}$ returns the atoms to the state $\mid 11⟩$ in the absence of errors. This unitary is also composed of single-qubit rotations R_r and a CZ gate. b, Interleaved experimental comparison of the two randomized circuits described in a. Using the same gate we find a difference of about 3 × 10⁻³ between benchmarking methods, stemming from the additional sensitivity of the echo circuit to single-qubit gate errors. This is consistent with the results of a full error model accounting for clock and Rydberg imperfections. c, We use a numerical simulation of the full error model to compare the true fidelity overlap averaged over the symmetric stabilizer states F^SS with the inferred fidelity from the echo circuit benchmarking F^echo (top) and with the inferred fidelity from the symmetric stabilizer circuit benchmarking F^SSB (bottom). By rescaling the magnitude of different error sources, we find the SSB circuit to be a good proxy of the CZ fidelity averaged over symmetric stabilizer states. We further find the sensitivity of this sequence to single-qubit gate errors to be significantly attenuated relative to the echo benchmarking circuit (Methods).

As an important application of the CZ gate, we generate an array of Bell pairs with optical clock qubits (Fig. 2c). After initializing atoms in superposition states and applying a CZ gate, a π/4 pulse rotates the state into the even-parity, metrologically relevant, Bell state $\mid {\Phi }^{+}⟩=\left(1/\sqrt{2}\right)\left(\mid 00⟩+\mid 11⟩\right)$. For the state obtained in the experiment, we measure the population overlap with the ideal Bell state and we drive parity oscillations (Fig. 2d) to infer the off-diagonal (coherence) terms⁴⁹. Overall, we obtain a Bell-state generation fidelity of $0.976_{-6}^{+4}$ ($0.989_{-6}^{+4}$ when corrected for state preparation and measurement errors (SPAM)) which is limited, beyond the CZ fidelity, by the finite fidelity of clock π/2 pulses and decoherence in the circuit (Methods).

Cascaded GHZ generation and dual-quadrature read-out

Having demonstrated high-fidelity gates on optical clock qubits, we next prepare larger entangled states and execute algorithms requiring more complex circuits. Specifically, we first prepare a complex quantum register with metrological significance based on a cascade of entangled Greenberger–Horne–Zeilinger (GHZ) states. Such GHZ states enable, in principle, the best sensitivity for linear observables allowed by quantum theory—the Heisenberg limit—with precision scaling as 1/N, where N is the number of atoms. However, for a single N-qubit GHZ state, although the sensitivity to phase variations is increased by a factor of N, the dynamic range of phases that can be unambiguously measured is likewise reduced by a factor of N (refs. ^3,4,37). A similar trade-off exists for spin-squeezed entangled states^38,39. Importantly, a smaller dynamic range means a shorter allowable interrogation time, resulting in precision loss.

A proposed scheme^1,4 for circumventing this trade-off between sensitivity and dynamic range requires the simultaneous preparation of a cascade of M different groups of GHZ-like states of the form $\mid {\psi }_j⟩\propto \left({\mid 0⟩}^{\otimes 2^j}+{\mid 1⟩}^{\otimes 2^j}\right)$ with j = 0, 1, …, M − 1. Such a probe state enables Heisenberg-limited sensitivity, up to logarithmic corrections, while preserving the dynamic range. It, thus, enables a viable path to quantum-enhanced metrology under realistic conditions in which local oscillator noise is the main limitation, as in current neutral-atom optical clocks³⁷. Note that these proposals are quantum-enhanced extensions of the classical optimal interrogation schemes^5,50 that have recently been experimentally shown^16,51.

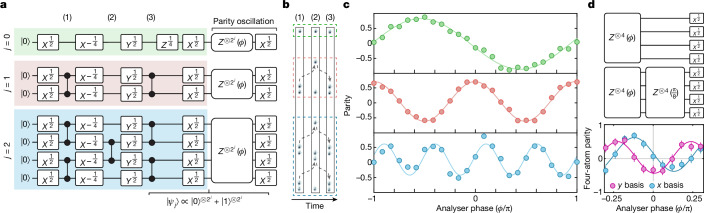
We consider different circuit realizations for generating the required simultaneous preparation of GHZ states with j = 0, 1, 2, using our universal quantum processor aided by dynamical array reconfiguration. Although large GHZ states can be prepared with circuits applying extensive local control (Extended Data Fig. 5), here we realize a circuit compiled with global control up to its final layer (Fig. 3a). This choice is guided by the need to minimize idle time added by local operations, during which laser–atom dephasing occurs. The local control for single-qubit rotations is achieved through local phase shifts imparted through subwavelength shifts in atomic position¹⁶. The connectivity for two-qubit gates is realized by a mid-circuit array reconfiguration (Fig. 3b). We verify the simultaneous preparation of increasingly phase-sensitive states by varying the phase of a final π/2 pulse and measuring the parity signal $\widehat{\mathcal{P}}=\prod _i{\widehat{Z}}_i$ for each GHZ state. Plotting this signal against phase in Fig. 3c gives a ratio in phase sensitivity of 1:1.96(6):3.9(1), which is consistent with the 1:2:4 ratio expected.

Extended Data Fig. 5. Quantum circuit for generating 8-qubit GHZ state.

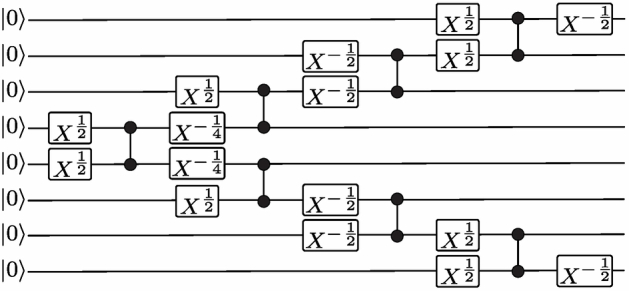
With the toolbox proposed in this work, one can in principle prepare arbitrary-size GHZ states, limited by the number of atoms. We give a circuit that generates an 8-qubit GHZ state while respecting the 1D array constraint in our current setup.

Fig. 3. Simultaneous generation of a cascade of GHZ states and GHZ dual-quadrature read-out.

a, Quantum circuit for the simultaneous preparation and characterization of GHZ states of the form $\mid {\psi }_j⟩\propto \left({\mid 0⟩}^{\otimes 2^j}+{\mid 1⟩}^{\otimes 2^j}\right)$, where j = 0, 1, 2. b, Array reconfiguration steps depicted by average atomic fluorescence images at each one-dimensional array configuration (1), (2) and (3), as marked in the circuit in a. Dashed arrows represent atom movements performed between two sequential array configurations. c, Simultaneous parity oscillations for j = 0, 1 and 2, from top to bottom, showing a 1:1.96(6):3.9(1) ratio in phase sensitivity. d, Simultaneous dual-quadrature parity read-out of two copies of a four-atom GHZ state realized through a π/8 phase shift on each atom in one copy, resulting in a collective π/2 phase shift before the final read-out pulse.

This demonstration measures only one quadrature of the optical phase signal. Importantly, the dynamic range can be doubled if both phase quadratures are probed simultaneously, the so-called dual-quadrature read-out^4,5,16,51. We demonstrate such a dual-quadrature read-out for entangled states (Fig. 3d) by preparing two four-atom GHZ states and then imparting a phase rotation to only one through local phase shifts. This enables the read-out in the $\widehat{Y}$-basis in parallel to the read-out in the $\widehat{X}$-basis. Here, a π/8 phase shift per atom (π/2 phase on the entangled four-atom register) is realized by moving¹⁶ all four atoms by λ/16 ≈ 44 nm. Note that such phase shifts could alternatively be realized by moving a single atom in the GHZ state by λ/4.

An important question concerns the limitations on the maximum attainable size of a GHZ state in terms of achievable fidelity. We hypothesize that the phase noise of our clock laser was the dominant error source, which we test with experimental and numerical investigations. In the simultaneous GHZ-state preparation scheme, we achieve a bare parity contrast of 0.52(3) for N = 4 (Fig. 3c). To reduce the impact of clock laser phase noise, we prepare N = 4 and N = 2 GHZ states using a circuit with a shorter idle time, which is the wait time during which operations are done on other registers (by removing the single-site operation ${\widehat{Z}}^{\frac{1}{4}}$ shown in Fig. 3a). With this sequence, we find an improved contrast of 0.68(3) and a fidelity of 0.71(2) (Extended Data Fig. 9). Note that the contrasts from both sequences are at or above the threshold of $1/\sqrt{N}=0.5$ required for a metrological gain^2,52 for a fixed, short interrogation time. However, they do not exceed the higher threshold for the cascaded-GHZ scheme (Methods).

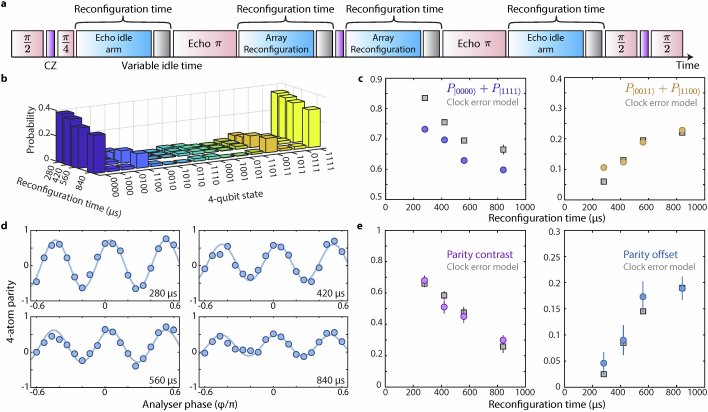
Extended Data Fig. 9. Atom-laser dephasing effect on 4-qubit GHZ state preparation.

a, Experimental pulse sequence for the circuit described in Fig. 3a. In the actual sequence, echo pulses are added during the array reconfiguration operation, which are not shown in the main text for simplicity. The relative sizes of the blocks represent the relative duration of each operation, except for the Rydberg CZ gate (which takes a much shorter time) and the variable idle time (grey blocks) which is adjusted to vary the array reconfiguration time (total idle time) to study the effect due to clock laser frequency noise, or equivalently atom-laser dephasing. In this sequence, π pulse takes ≈ 240 μs, and the CZ gates take ≈ 500 ns. The actual array reconfiguration (blue blocks) takes 280 μs. b, Experimental raw data of the population distribution as a function of total reconfiguration time. c, We plot the target state population overlap and the growth of dominant non-target states ($\mid 0011⟩$ and $\mid 1100⟩$) as a function of total reconfiguration time. Our error model predictions (grey squares) successfully verify the decreasing trend for target state population overlap and the non-target state population growth. d, Experimental raw data of the parity oscillation contrast for different total reconfiguration times. e, Decay of parity contrast and growth of parity offset. Our error model predictions (grey squares) are in good agreement with experimental results (see Methods for error model details).

Motivated by this, we study fidelity as a function of the circuit idle time. We measure the decay in fidelity and a modification of the bit-string distribution (Extended Data Fig. 9), which follows the prediction of our error model, consistent with our hypothesis that clock laser phase noise is the dominant error source. We then run a model using a frequency noise spectrum of a 26-mHz clock laser system⁵³, for which we predict a N = 4 GHZ-state fidelity of approximately 0.97 (Methods and Extended Data Fig. 6). Thus, we expect significantly improved results with an upgraded clock laser system, which would surpass the metrological gain threshold for the cascaded-GHZ scheme, even for larger N (Methods and Extended Data Fig. 7).

Extended Data Fig. 6. Effects of clock frequency noise on entangled state fidelity.

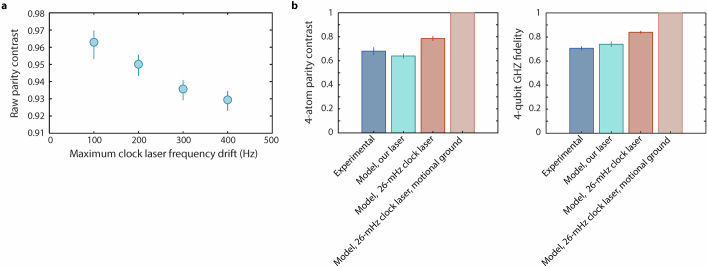
a, Experimental Bell state raw parity contrast as a function of maximum clock laser frequency drift, determined by clock laser feedback frequency (Methods). We analyse the Bell state parity experimental runs with associated clock feedback frequencies less than a certain maximum drift cutoff. The fitted raw parity contrast shows a clear decreasing trend as we increase the cutoff frequency. The parity contrast shown in Fig. 2d is taken with the cutoff frequency of 100 Hz. b, Experimental results and error model prediction for the 4-qubit GHZ state parity contrast (left) and fidelity (right). In our experimental sequence, the 4-qubit GHZ state generation fidelity is mainly limited by clock laser frequency noise and finite atomic temperature. We simulate the circuit with our error model including the clock laser frequency PSD and finite temperature of $\overline{n}=0.24$. We also assume perfect CZ gates. The error model predicts the parity oscillation contrast to be 0.66 and the state fidelity to be 0.75, which are consistent with our experimental realization (contrast being 0.68(3) and fidelity being 0.71(2)). We also simulate the same circuit with our clock error model with the frequency PSD of a 26-mHz laser⁵³. The model predicts a contrast of 0.79 and a fidelity of 0.84 for $\overline{n}=0.24$. With zero temperature ($\overline{n}=0$), the clock error model predicts near-unity state fidelity (>0.999). The limitation in this regime is the entangling gate fidelity. With the high-fidelity entangling gate presented in this work, we estimate a 4-qubit GHZ state generation fidelity of ≈ 0.97.

Extended Data Fig. 7. Projected metrological gain.

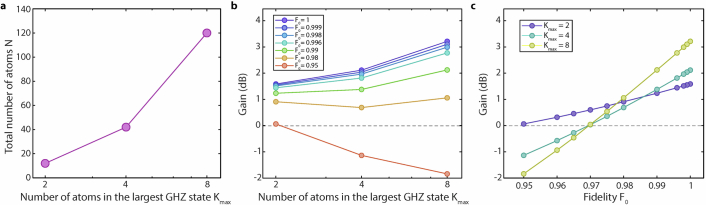
a, Total number of atoms N required as a function of the number of atoms in the largest GHZ state used in the protocol proposed in ref. ⁴. Efficient implementation requires n₀ copies of each GHZ state with 2^j atoms, j = 0, 1, …M − 1, where the largest GHZ state contains K_max = 2^M−1 atoms, and N = n₀(2^M − 1). The number of copies for K_max = 2, 4, 8 are n₀ = 6, 8, 9 respectively. b, Projected metrological gain for various effective fidelities per qubit F₀, as a function of the number of atoms in the largest GHZ state, K_max. We assume the contrast C of the parity oscillations for a K-atom GHZ state to scale as $C\left(K\right)=F_0^K$. c, Projected metrological gain as a function of effective fidelity per qubit F₀, for maximum GHZ size K_max = 2, 4, 8. We see that the effect of finite fidelity is more prominent for states with larger maximum GHZ sizes, causing the gain to decrease steeply with decreasing fidelity.

Ancilla-based quantum logic spectroscopy

Having used entanglement to prepare metrological probe states, we next use it to read out the resulting state. Specifically, we demonstrate a method based on mapping quantum information from a set of sensor qubits to a set of ancillary qubits, which are measured while the sensor qubits are quickly available for sensing once more. Such repeated, non-destructive, ancilla-based measurements are a central building block in quantum error detection and correction⁴¹. In a metrological context, repeated mid-evolution measurement and reset cycles are desirable for efficient multi-ensemble schemes⁵. These schemes enable extended dynamic range and effective coherence time, even in the absence of entangled probes. However, realizing fast mid-circuit measurement and the reset of atomic qubits is challenging due to the overhead in resetting both the motional state and the electronic state of a qubit after direct measurement.

To efficiently realize an ancilla-based read-out in atomic systems, information-carrying data qubits must first be protected from global imaging light and their coherence must be preserved during the MCR of ancilla qubits. Such protection can be realized by using dual-species arrays⁴⁰, cavity-assisted read-out⁵⁴, a separate read-out zone²⁴ or shelving to states that are dark to imaging light^55–57. For our system, we took the last approach and have recently realized MCR⁴⁴ by shelving optical qubits into superpositions of motional states that are long-lived and dark to imaging light.

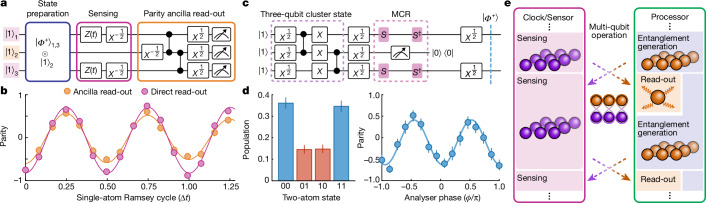
By performing high-fidelity entangling gates between information-carrying (clock) qubits and ancilla qubits before MCR (Fig. 4a), we realize a form of quantum logic spectroscopy with neutral-atom optical clock qubits, as originally introduced for mixed-species ion traps²⁰. In our case, we use local control to prepare certain atoms in superposition states sensitive to the clock laser detuning Δ, whereas ancilla atoms remained in the insensitive state $\mid 1⟩$. Clock qubits acquire a time-dependent phase Δ × t, which is mapped onto the population in a Ramsey sequence. A subsequent clock-ancilla CNOT gate (controlled on qubit state $\mid 0⟩$) then maps this signal onto the ancilla state (Fig. 4b). This sequence realizes an ancilla-based detection of $\widehat{X}$ of the clock qubit.

Fig. 4. Repeated ancilla-based quantum logic spectroscopy.

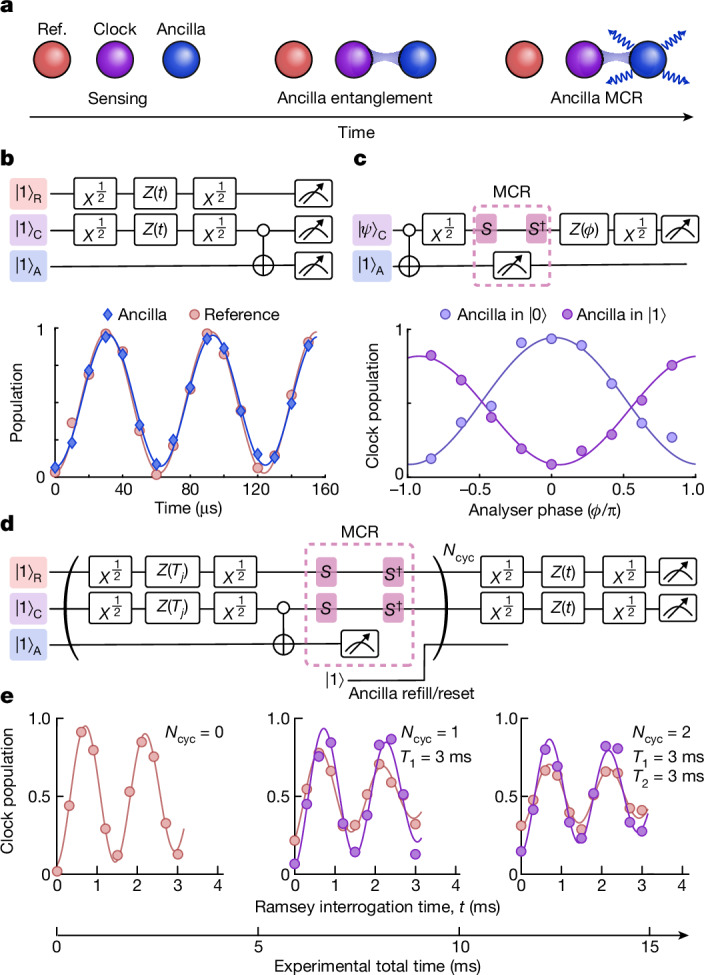
a, We consider three ensembles of atoms: reference (Ref.) atoms (R; red), clock atoms (C; purple) and ancillas (A; blue). An entangling gate maps the state of clock atoms to the state of ancilla atoms before the MCR of the ancilla state. b, Logic spectroscopy with ancilla atoms. A Ramsey interrogation is performed in parallel on reference atoms (R) and clock atoms (C). A clock-ancilla CNOT gate (controlled on qubit state $\mid 0⟩$) maps the state onto ancilla atoms (A) for read-out. c, Ancilla-based $\widehat{X}$ measurement. A non-destructive measurement of the state ${\mid \psi ⟩}_C$ is realized by shelving clock qubits ($\widehat{S}$ operation) followed by ancilla MCR. We show that following the unshelving (${\widehat{S}}^{†}$), the state of the clock qubit is projected to a well-defined state in the measurement basis, conditioned on the ancilla state. d, N_cyc repeated rounds of quantum logic spectroscopy with minimal dead time (2.9 ms), enabled by ancilla replacement through an array reconfiguration. Each round j consists of a fixed evolution time T_j followed by ancilla-based $\widehat{X}$ measurement before a final round where the clock qubit is directly measured in a Ramsey sequence with variable time t. e, We find improved contrast in the final measurement round when conditioned on ancilla results (see text) in all previous rounds (purple markers) compared to the reference clock atoms, which are protected during MCR but do not interact with the ancillas (red markers).

To realize a non-destructive ancilla-based $\widehat{X}$ measurement, we then shelve clock qubits and read out the ancilla state. Thus, we ramp up the depth of ancilla traps by a factor of 5 (leaving traps with clock atoms unchanged) such that they are not resonant with the global motional shelving drive. Following shelving of clock qubits, we perform ancilla MCR of the signal field Δ. Conditioned on the ancilla measurement result, the clock atom is projected to a known state in the measurement basis, which enables repeated interrogation. We verify this by measuring the clock qubit state in the $\widehat{X}$ basis through a π/2 pulse with a variable phase ϕ before detection (Fig. 4c). We find that the clock qubit is projected onto the $\mid +⟩$ ($\mid -⟩$) state conditioned on the ancilla measurement result $\mid 0⟩$ ($\mid 1⟩$) in the $\widehat{Z}$ basis, with a contrast of 0.84(4) (0.73(4)). These results were conditioned on successful one-way shelving^18,44 (Methods).

Ideally, a non-destructive read-out enables repetitive measurements of the same qubit or the same register. This can be achieved by resetting the ancilla qubit and repeating the read-out cycle. We use an 18 μs fast imaging method⁵⁸ that is much shorter than the qubit coherence time but results in a high probability of losing the ancilla atom during imaging. We, thus, realize repeated rounds of measurement and reset by replacing the ancilla atom with a reserve atom, which was shelved during ancilla MCR, using dynamical reconfiguration. This yields a dead time of only 2.9 ms, which is dominated by shelving and unshelving operations. Alternatively, we demonstrate the reuse of the same ancilla atom by applying a 10 ms low-loss imaging followed by recooling (Methods and Extended Data Fig. 10).

Extended Data Fig. 10. High-survival mid-circuit imaging with ancilla recool and reuse.

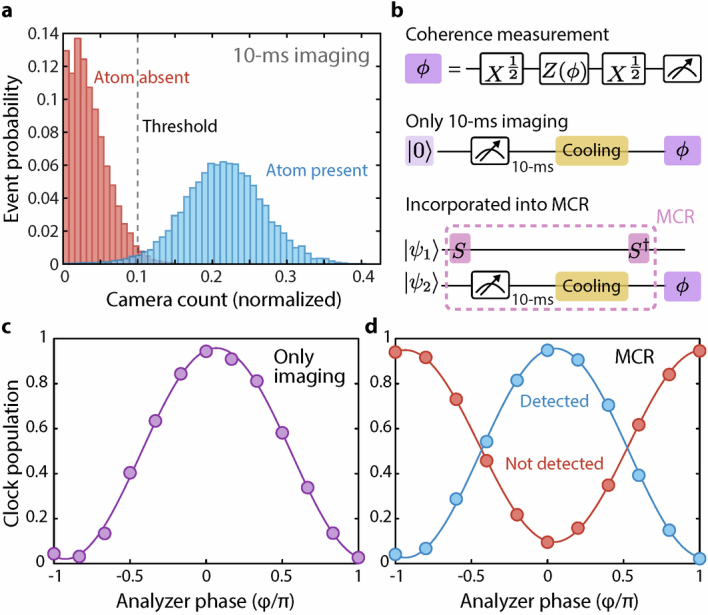
a, Histograms of the normalized camera count for 10-ms imaging. Using 120-ms standard imaging, we can detect if a tweezer is empty (red) or filled (blue) with ≈ 0.9999 fidelity prior to the 10-ms imaging. In this scheme, the typical detection fidelity which corresponds to equal error probability in detecting absence or presence of an atom is 0.98. Survival after imaging is 0.965(2), as opposed to the lossy 18 μs fast imaging employed in the main text (Fig. 5). b, We check if we can coherently apply single-qubit rotations by applying a π/2 pulse and a second π/2 pulse with a variable phase. We then extract the parity contrast as a way of coherence measurement. We first measure the coherence after this 10-ms imaging. Then we incorporate this into MCR and measure the coherence. c, The parity contrast of atoms after 10-ms imaging and cooling is measured to be 0.94(1). d, The parity contrast of atoms after being detected during the MCR reads 0.93(1) (blue) while that of the atoms not detected during the MCR reads 0.86(1) (red). The difference can be explained by the finite decay from $\mathrm{P}_0^3\left(\mid 1⟩\right)$ to $\mathrm{S}_0^1\left(\mid 0⟩\right)$ (see Methods).

We use ancilla-based read-out to perform fast and repeated phase detection ($\widehat{X}$ measurement) cycles with a clock qubit reset (Fig. 4d). In Fig. 4e, we plot the resulting Ramsey signal for up to three consecutive measurement rounds. We use information from ancilla detection in previous rounds to remove shots where the ancilla state was toggled from $\mid 1⟩$ to $\mid 0⟩$ (maintaining 78% of the experimental shots for a single round of ancilla detection), indicating a phase flip. We contrast this with reference qubits that did not interact with ancillas and find an improved contrast for the ancilla-based detection. For the latter, the contrast is limited by the fidelity of shelving and unshelving operations as part of the MCR.

Although we use ancillas to measure a single qubit, extending our demonstration to a larger ensemble of ancillas interacting with an ensemble of clock qubits would enable single-shot phase estimation of the global field Δ. Information on phase deviation outside the dynamic range could be used to correct the phase estimation of the longer evolving ensemble realized by the reference qubits in our demonstration⁵. Such fast detection and reset are further advantageous for low dead-time clock operation, as this would reduce the instability due to the Dick effect⁸. On the other hand, using ancillas in a single-species array comes at the expense of a reduced number of clock qubits, which would increase the quantum projection noise, so that the metrological gain depends on the balance of the two.

Multi-qubit parity checks

We next generalize our experimental demonstration of ancilla-based read-out to multi-qubit measurements. In a multi-qubit measurement, an ancilla is entangled with several qubits and then measured. The measurement projects the register qubits to a well-defined parity subspace. This may prove especially useful for preparing large-scale long-range entangled states, such as GHZ states, through ancilla measurements^21–24, for which we show a proof-of-principle for optical qubits. Note that multi-qubit measurements, which measure higher-weight observables, are also central to stabilizer-based quantum error correction⁴¹.

We demonstrate the lowest-order version of such schemes, a weight-2 parity measurement for which the ancilla is entangled with two different clock qubits before measurement. To do this, we prepare an input state composed of an ancilla atom in the clock state $\mid 1⟩$ and two atoms in a Bell state and perform a $\widehat{X}\widehat{X}$ parity measurement (Fig. 5a). Figure 5b compares the direct read-out of a parity signal from the Bell pair (pink) with the ancilla read-out (orange). We find that, indeed, the single ancilla atom observable now oscillates at a frequency of twice the single-atom detuning Δ. This frequency, as well as the phase of the signal, is consistent with a direct read-out of the Bell-pair parity (Methods).

Fig. 5. Ancilla parity read-out and measurement-based Bell-state generation.

a, An ancilla qubit (middle) is prepared in parallel with a Bell pair, which is then used in Ramsey interrogation. A parity signal is measured either directly on the Bell pair or through ancilla-based parity read-out. b, Direct read-out of the Bell-pair parity signal (pink) is compared with a single ancilla read-out (orange) yielding a weight-2 parity signal oscillating at the same frequency and phase within error bars (Methods). c, A circuit for the measurement-based preparation of a long-range Bell pair, composed of three-qubit cluster state generation followed by MCR on the middle ancilla qubit. Conditioning on the ancilla result $\mid 0⟩$ (approximately 45% of experimental shots) projects the two exterior atoms to the Bell state $\mid {\Phi }^{+}⟩$. d, Characterization of the resulting Bell state with population overlap of 0.71(2) in the even-parity subspace $\left\{\mid 00⟩,\mid 11⟩\right\}$. The parity oscillation of the resulting state yields a contrast of 0.52(3), resulting in an overall raw Bell-state fidelity of 0.61(2). Data were conditioned on the successful shelving of the two exterior qubits (approximately 82% of experimental shots). e, A proposal for a continuous clock based on a modular architecture (see ‘Outlook’ for details).

We next demonstrate another relevant application of the conditional parity projection in a weight-2 ancilla MCR: long-range entanglement induced by measurement^21–24. We first prepare a three-qubit cluster state and then perform MCR of the central qubit in the $\widehat{X}$ basis (Fig. 5c). As $\widehat{Z}\widehat{X}\widehat{Z}$ is a stabilizer of the cluster state, this measurement generates a Bell pair with a well-defined parity for the exterior atoms. Conditioning on the ancilla result $\mid 0⟩$, we find the Bell state $\mid {\Phi }^{+}⟩$ with population 0.71(2) in the even-parity subspace $\left\{\mid 00⟩,\mid 11⟩\right\}$ and a parity oscillation contrast of 0.52(3), yielding an overall raw fidelity of 0.61(2) (Fig. 5d). When, instead, we condition on the ancilla result $\mid 1⟩$, the state is projected to the odd-parity Bell state $\mid {\Psi }^{-}⟩=\left(1/\sqrt{2}\right)\left(\mid 01⟩-\mid 10⟩\right)$, which is not metrologically useful in our context, with 0.64(2) in the odd-parity subspace $\left\{\mid 01⟩,\mid 10⟩\right\}$. Alternatively, by performing an ancilla-based $\widehat{X}\widehat{X}$ measurement, one can prepare both metrologically relevant Bell states $\mid {\Phi }^{+}⟩,\mid {\Phi }^{-}⟩=\left(1/\sqrt{2}\right)\left(\mid 00⟩-\mid 11⟩\right)$. Such schemes can be considered a heralded preparation, which could be made deterministic by a feedback operation^21–24. Note that with improvements in fidelity and with sufficiently fast feedback, this could then be readily extended to the measurement-based preparation of large-scale GHZ states with only a constant-depth circuit^21–23. This is in contrast to linear or log-depth standard unitary circuits³¹ and could be instrumental for generating large-scale optical clock GHZ states in future devices.

Outlook

Our results demonstrate how universal quantum processing and ancilla-based read-out can be integrated with a neutral-atom optical clock. Extending such schemes to larger two-dimensional tweezer clock systems¹⁴ would enable the creation of several copies of GHZ states at a given size. Note that, in particular, the schemes demonstrated here could easily be generalized to two dimensions by performing all operations for a set of rows in parallel to generate several copies of GHZ states. We see this as a viable avenue towards the quantum-enhanced operation of neutral-atom clocks using cascades of GHZ states^1,4 combined with classically optimal interrogation schemes and quadrature read-out^5,16,50,51.

We have demonstrated a CZ fidelity of 0.9962(3), averaged over two-qubit symmetric states, providing state-of-the-art entangling gate fidelity, as well as the full toolbox needed to execute relevant algorithms for metrology and computation with optical clock qubits. The main limitation for current circuit fidelities is the clock laser phase noise, which results in dephasing during circuit idle times. The ancilla-based MCR is further limited by the fidelity of shelving qubits in motional states. Upgrading the clock laser system used in this work to match the current state of the art^14,35 would enable the generation of significantly larger GHZ states than demonstrated here (Extended Data Fig. 6 and Methods). We expect the maximum size of a GHZ state will eventually be limited by a combination of clock laser phase noise and CZ gate fidelity. In this context, note that the CZ gate fidelity is at present dominated by the phase noise of the Rydberg laser (Extended Data Fig. 4 and Methods), which could easily be improved by implementing cavity filtering techniques. Further, using native, multi-qubit gates^17,59 or effective all-to-all connectivity¹⁹ could reduce the required circuit depth. Ancilla-based MCR could also be improved with a higher stability clock laser and better control and homogenization of the trap waists⁴⁴. Finally, GHZ states can be prepared with constant-depth circuits through measurement-based schemes^21,22, for which we show the first steps with optical clock qubits in Fig. 5c,d.

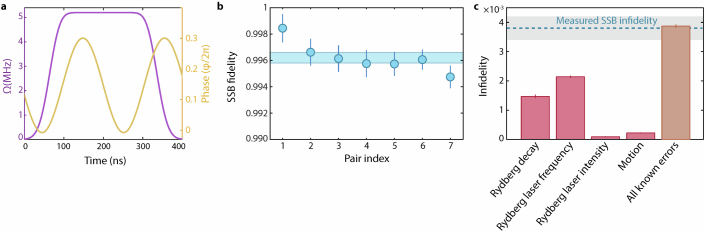
Extended Data Fig. 4. Controlled-Z gate via Rydberg interactions and associated error budget.

a, Rydberg pulse shape that realizes a CZ gate between two optical qubits. We adopt the time-optimal pulse^17,18,46 with a Rydberg Rabi frequency of 5.4 MHz. We optimize the parameters of the phase modulation function and the Rydberg detuning by varying each one in search of the maximal return probability as part of the randomized circuit used to benchmark the fidelity (Fig. 2a). b, Pair-resolved fidelity, inferred from the sequence in Fig. 2a. The blue shaded area represents the array-averaged fidelity 0.9962(3). c, Our error model predicts the infidelity to be 0.00387(5), consistent with the experimental result of 0.0038(3) (blue dashed line and shaded area).

Our results further point to a modular device with distinct quantum processing and sensing modules. This would realize a quantum computer connected to a high-precision sensor (Fig. 5e). The processing module could be used to prepare entangled probe states in parallel to sensing, followed by a state exchange operation between the sensor and the processor. Subsequently, read-out could be performed in the processing module in parallel to sensing, before preparing new entangled probe states, which would yield very low dead-time operation. Options for fully realizing this vision could be based on a multi-zone approach with a single species²⁴, a dual-species⁴⁰ device composed of alkaline-earth and alkali atoms (for example, strontium and rubidium), an optical-metastable-ground-state qubit architecture^56,60 or combinations thereof. Several of our results can be viewed as proof-of-principle demonstrations towards this modular vision, including state exchange operations (Extended Data Fig. 11) and higher-weight ancilla-based read-out. In the quest to push the limits of precision measurements, such a device could be part of next-generation quantum technologies from field-transportable sensors to state-of-the-art optical clocks³⁵.

Extended Data Fig. 11. State exchange operations of a Bell pair between two quantum registers.

a, As part of the ancilla-based parity readout (Fig. 5a,b), we employ a state exchange between two quantum registers. Shown is the generation and swap of a Bell pair from two inner atoms to two outer atoms which did not interact directly. b, c, Characterization of the resulting long-range Bell pair. We obtain a population overlap of 0.842(8) and a parity contrast of 0.71(2), yielding a raw fidelity of 0.78(1).

Methods

Experimental considerations and constraints

Our experimental set-up has been detailed in previous work^13,16,58. Here, we discuss the experimental requirements specific to executing quantum circuits on a quantum processor with optical clock qubits. In particular, several trade-offs need to be balanced in the choice of magnetic field, trap depth and interatomic spacing.

Due to laser frequency noise, high-fidelity single-qubit rotations benefit from a large Rabi frequency on the clock transition (¹S₀ ↔ ³P₀). The clock-transition Rabi frequency scales linearly with the magnetic field, and we achieved Ω = 2π × 2.1 kHz at 450 G. On the other hand, the Rydberg interaction strength varies with the magnetic field due to admixing with other Rydberg states⁶¹. Specifically, a numerical calculation (using the ‘Pairinteraction’ package⁶¹ and limiting the considered Rydberg states to n ± 5 for faster convergence) shows that the interaction energy peaked around 380 G and decreases for higher magnetic fields (Extended Data Fig. 1a). Our experimental measurements for several magnetic fields are consistent with this overall trend. Therefore, we operate at a magnetic field of 450 G, which provides a balance between a sufficiently high clock Rabi frequency and sufficiently strong Rydberg interactions.

Our nominal tweezer trap depth (U₀ ≈ 450 μK) is chosen to ensure efficient atom loading and high-survival, high-fidelity imaging⁶², as well as efficient driving of the carrier transition for clock qubits. However, we find that the Rydberg gate performs slightly better when the trap is turned off. In our case, this is predominantly due to beating between adjacent tweezers, which results in trap-depth fluctuations at a frequency of 650 kHz (equal to the tone separation on our tweezer-creating acousto-optic deflector). As the Rydberg transition (³P₀ ↔ 61³S₁) is not under magic trap conditions, this results in detuning noise for the gate operation. For an optimized CZ gate with traps kept on at 0.2U₀, we find that the two-qubit gate fidelity is lower by approximately 3 × 10⁻³ (not shown). By placing an acousto-optic modulator in the tweezer optical path, we implement a fast switch-off of the trapping light (rise/fall time of the order of 50 ns). At this timescale, we find that switching traps off from a shallower trap 0.2U₀ is preferable as this imparts minimal heating with no observed loss for clock qubits. Furthermore, in MCR, efficient motional shelving relies on strong sideband coupling⁴⁴, which becomes stronger as the Lamb–Dicke factor increases (trap depth decreases). On the other hand, array reconfiguration benefits from sufficiently deep traps.

The experimental sequence, thus, involves adiabatic ramps of trap depth as well as fast switch-off and -on. After loading the atoms into the tweezers at U₀, we lower the tweezer depth to 0.5U₀ to perform erasure-cooling⁴⁴. For gate operations, we drive coherent clock rotations at 0.2U₀ and switch the trap off for about 500 ns to perform the Rydberg entangling pulse. When selective local MCR is applied, we adiabatically ramp to deeper traps of U₀ for the ancilla qubits, while holding the clock qubits at fixed depth.

We now discuss how we perform the dynamical array reconfiguration, shown in Fig. 1 as part of a full quantum operation toolbox. We coherently transport an atom across several sites by performing a minimal-jerk trajectory that follows x(t) = 6t⁵ − 15t⁴ + 10t³ for t ∈ [0, 1]. For this trajectory, the acceleration is zero at the two end points, which avoids the sudden jump in the acceleration profile and minimizes the associated jerk. The aim is to achieve minimal heating, which is especially important for driving optical clock transitions in the sideband-resolved regime.

With this trajectory, we find no significant temperature increase for atoms transported over four sites (equivalent to 13.26 μm) in 160 μs at trap depth U₀ (Extended Data Fig. 1b). This is the typical distance applied in dynamical array reconfiguration. Another interatomic spacing choice is 13.26 μm ≈ 19 × 698 nm (corresponding to the clock-transition wavelength), which would ensure an effective zero displacement-induced phase shift¹⁶.

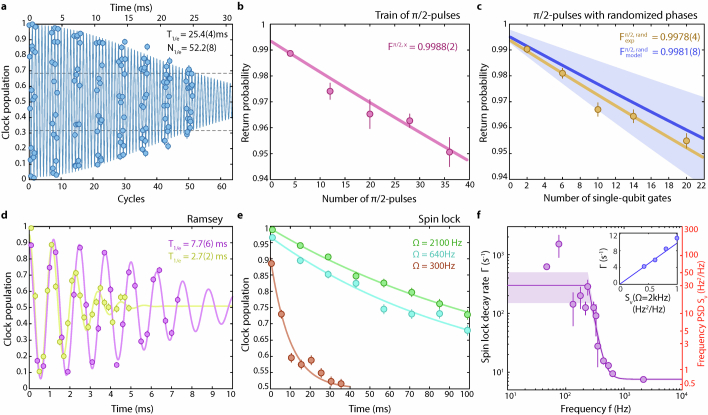
Single-qubit (clock) error model

We characterize our ability to perform coherent single-qubit rotations with a global addressing beam and test our error model by driving the clock transition on atoms with an average motional occupation of $\overline{n}\approx 0.01$, following erasure-cooling along the optical axis⁴⁴. We drive Rabi oscillations with a nominal Rabi frequency Ω = 2.1 kHz and observe 52.2(8) coherent cycles (Extended Data Fig. 2a). Applying a train of π/2 pulses along the X axis, we find a per-pulse fidelity of 0.9988(2). Note that in such sequences, the effect of slow frequency variations is suppressed. We, thus, characterize the π/2 pulse fidelity by applying a pulse train of π/2 pulses with random rotation axes ±X and ±Y (ref. ⁶³). The resulting π/2 pulse fidelity is measured to be 0.9978(4) (Extended Data Fig. 2c).

Extended Data Fig. 2. Verification of clock error model and clock laser frequency noise power spectral density (PSD).

a, Rabi oscillations between $\mid 0⟩$ and $\mid 1⟩$. When averaging over the entire array, the Rabi oscillation shows a coherence time of 25.4(4) ms and 52.2(8) coherent cycles (dashed lines represent 1/e oscillation amplitude). The long-term coherence is mainly limited by clock laser frequency noise and Rabi frequency inhomogeneity across the array. b, The return probability of driving a train of π/2 pulses with the same phase. We obtain a per-pulse fidelity of 0.9988(2) from this method. c, Random phase π/2 pulse benchmarking. We randomly draw N π/2 pulses from the set {R_X(π/2), R_−X(π/2), R_Y(π/2), R_−Y(π/2)} under the constraint that the final state returns to the initial state with perfect single-qubit operations. We obtain a single-qubit π/2 fidelity of 0.9978(4) (yellow) from this method. The described single-qubit (clock) error model (Methods) predicts the π/2 fidelity being 0.9981(8) (blue), the error bar of which indicates the model parameter uncertainty (shaded area). Note that all single-qubit operations are performed globally. d, Ramsey measurements taken on two different days, representing the typical fluctuations of the clock laser performance. We use these to estimate the low-frequency part of the clock laser frequency PSD. e, The spin-lock experiment at different Rabi frequencies. We fit the clock population as a function of time using an exponential function with time constant τ and determine the decay rate Γ = 1/τ at each frequency. f, Measured decay rates at different frequencies and the inferred laser frequency power spectral density. We find that the spin-lock decay rate is linearly proportional to the PSD at the corresponding Rabi frequency (Inset). We interpolate the PSD down to low frequencies (solid line). The shaded area represents the model uncertainty, considering the fitting model uncertainty and the observed Ramsey coherence time fluctuations as in d.

The dominant error source in the single-qubit operation is laser frequency noise, which is characterized by the frequency power spectral density (PSD) function S_ν(f). We characterize this with Ramsey and spin-lock⁶⁴ sequences.

Ramsey sequence

The Ramsey sequence is sensitive to the low-frequency component of the laser frequency PSD up to the inverse of the Ramsey interrogation time (approximately 100 Hz). In our experimental set-up, we observe day-to-day fluctuations in the Ramsey coherence time (Extended Data Fig. 2d). We use an effective model of the PSD at low frequencies (Extended Data Fig. 2f) to account for the fluctuations of the Ramsey coherence time. We set the PSD to be a constant H at low frequencies up to some frequency of interest (approximately 200 Hz) and find numerically that the Ramsey coherence time was inversely proportional to H.

Spin lock

To probe and quantify fast frequency noise up to our Rabi frequency, we perform a spin-lock sequence. We initialize all atoms in an eigenstate of $\widehat{X}$ and turn on a continuous drive along the X axis for a variable time. Then we apply a π/2 pulse along the Y axis, which transfers all atoms into state $\mid 1⟩$ in the absence of errors. The probability of returning to $\mid 1⟩$ decays over time (Extended Data Fig. 2e), and the decay rate is predominantly sensitive to frequency noise at this Rabi frequency⁶⁴. By varying the Rabi frequency of the continuous drive field and measuring the decay of the probability in $\mid 1⟩$, we determine the frequency PSD by using the linear relation between the decay rate and the frequency PSD S_ν(f) at the Rabi frequency (Extended Data Fig. 2f).

To account for both the fast frequency noise measured by the spin-lock experiment and the slow frequency noise that determines the Ramsey coherence time, we interpolate the laser frequency PSD with a power-law function $S_{\nu }\left(f\right)=h_0+{\left(h_{\alpha }/f\right)}^{\alpha }$ upper-bounded by H at low frequencies. The model parameters h₀, h_α and α are obtained by fitting the spin-lock data (Extended Data Fig. 2e,f). The upper bound H is flexible within a range (shown as the shaded area in Extended Data Fig. 2f) and can effectively describe the day-to-day fluctuations of the Ramsey coherence time. This range is reflected in the uncertainties of the error model predictions quoted throughout this work.

In addition to laser frequency noise, note that although the single-qubit operations are sensitive to the finite temperature, we perform erasure-cooling⁴⁴ to prepare atoms close to their motional ground state ($\overline{n}\approx 0.01$). This has a negligible impact (approximately 1 × 10⁻⁴) on the clock π/2 pulse fidelity, as predicted by our error model.

In addition to the error sources described above, we also include laser intensity noise, pulse shape imperfection, spatial Rabi frequency inhomogeneity and Raman scattering induced by the tweezer light. All these error sources result in an aggregate of approximately 1 × 10⁻⁴ infidelity for the clock π/2 pulse.

With all described error sources included, the error model predicts an average π/2 fidelity of 0.9981(8) (Extended Data Fig. 2c), which is in good agreement with the experimental value of 0.9978(4).

Two-qubit gate fidelity benchmarking

Here, we give more details about the randomized circuit (Fig. 2), which is used to benchmark the CZ gate fidelity. We first apply a randomized circuit like the one proposed and used in ref. ¹⁷, which includes echo pulses (π pulses along X) interleaved with random single-qubit rotations and CZ gates (Extended Data Fig. 3a). For this circuit, we observe that both two-qubit (Rydberg) errors and single-qubit (clock) errors contribute to the inferred infidelity (Extended Data Fig. 3b,c). That such a circuit is sensitive to single-qubit gate errors, although the number of single-qubit gates was kept fixed, is because the probability distribution of two-qubit states before each single-qubit gate changes as a function of the number of CZ gates applied. Note that as errors affect entangled states and non-entangled states differently, changing the probability distribution would result in a non-unity return probability, even if the fidelity of CZ gates were perfect, in the presence of single-qubit gate errors. In this context, the sequence used in Extended Data Fig. 6 of ref. ¹⁷ also showed sensitivity to single-qubit errors, as the probability distribution between entangled and non-entangled states was not fixed as a function of the number of CZ gates.

To mitigate this effect, we design a randomized circuit (Extended Data Fig. 3a) such that the probability of finding any one of the 12 two-qubit symmetric stabilizer states would be uniform, irrespective of the number of CZ gates, at each stage of the circuit⁴⁷. We term this circuit the symmetric stabilizer benchmarking (SSB) circuit. Specifically, the probabilities of finding an entangled or separable state are equal throughout the circuit.

Using an interleaved experimental comparison, we find a difference of about 3 × 10⁻³ between benchmarking methods in the fidelity directly inferred from the slope of the return probability (Extended Data Fig. 3b). This difference stems from the higher sensitivity of the echo circuit benchmarking to single-qubit gate errors. This observation is in good agreement with a full error model that accounts for both clock and Rydberg excitation imperfections (Extended Data Fig. 3c). This model confirms that the fidelity inferred from the symmetric stabilizer benchmarking circuit is an accurate proxy of the gate fidelity averaged over all two-qubit symmetric stabilizer states. We confirm that this observation holds over a wide range of error rates by rescaling the strength of individual error sources in the numerical model (Extended Data Fig. 3c). These include incoherent and coherent errors. However, note that coherent errors or gate miscalibration of larger magnitude would result in an increased error in estimating the gate fidelity, which is a common issue across various benchmarking techniques. Also note that the gate fidelity averaged over all two-qubit symmetric stabilizer states is equal to the gate fidelity averaged over two-qubit symmetric input states. This can be seen because these symmetric stabilizer states form a quantum state two-design on the symmetric subspace⁴⁷.

Correcting for the false contribution from leakage errors

We read out the return probability for the randomized circuit benchmarking by pushing out ground-state atoms and pumping clock-state atoms to the ground state for imaging. As part of this optical pumping, any population in the ³P₂ state would be pumped and identified as bright, which is the clock-state population. We, thus, correct for leakage from the Rydberg state into the state ³P₂ identified as bright. We separately measure the decay into ³P₂ per gate by repeating the benchmarking sequence, which is followed by pushing out the atoms in the qubit subspace and repumping the ³P₂ state for imaging. At a Rydberg Rabi frequency of 5.4 MHz, the false contribution to the CZ fidelity is measured to be 1.8(4) × 10⁻⁴ per gate, in good agreement with numerical predictions. The CZ fidelity quoted throughout this work has been corrected downwards for this effect.

Two-qubit gate (Rydberg) error model

Our model for the two-qubit gate accounting for Rydberg errors is based on previous modelling of errors during Rydberg entangling operations^58,65. We adapt it to model the dynamics of a three-level system with ground ($\mid 0⟩$), clock ($\mid 1⟩$), and Rydberg states ($\mid r⟩$). Following the optimization of the gate parameters for a time-optimal pulse^17,18 in the error-free case (Extended Data Fig. 4a), we fix these parameters and simulated noisy dynamics with the Monte Carlo wavefunction approach. The model includes Rydberg laser intensity noise, Rydberg laser frequency noise, Rydberg decay (quantum jumps) and atomic motion. The predicted contribution of each error source to the CZ gate infidelity is shown in Extended Data Fig. 4c. For the analysis shown in Extended Data Fig. 3c, we repeat the numerical simulation several times and change the magnitude of one of the error model parameters in each run. For example, we rescale the overall magnitude of the noise PSD for frequency or intensity noise or the Rydberg decay rate.

Data-taking and analysis

Data-taking and clock laser feedback

Here, we discuss the general data-taking procedure for all experiments described in the main text. Typically, each experimental repetition takes approximately 1 s. To collect enough statistics, we perform the same sequence for from several hours up to several days (for the randomized circuit two-qubit gate characterization). However, on this timescale, the clock laser reference cavity experiences environmental fluctuations, resulting in clock laser frequency drifts from approximately 10 to approximately 100 Hz over a timescale of approximately 10 min.

We, thus, interleave data-taking with calibration and feedback runs^16,65. To measure the clock laser detuning from atomic resonance, we perform Rabi spectroscopy with the same nominal power and π pulse time as used in the experiment. The laser frequency is then shifted accordingly by an acousto-optic modulator. Such feedback is performed every 5–10 min, depending on the details of the experimental sequence. We reccord the applied laser frequency shifts, which can serve as an indicator of the clock laser stability during the experimental runs. To compare the stability from experiment to experiment, we take the standard deviation of the feedback values. In the main text, the gate benchmarking (Fig. 2a,b) and the simultaneous preparation of a cascade of GHZ states (Fig. 3) have feedback standard deviations of 73 and 68 Hz, respectively. During the data-taking of the optical-clock-transition Bell-state generation experiment (Fig. 2c,d), the feedback standard deviation is 203 Hz, significantly higher than other experiments. To ensure the consistency of clock laser conditions among all experiments, we select the Bell-state generation experimental runs with associated clock laser feedbacks of less than 100 Hz. After applying this cutoff, the standard deviation of the feedback frequencies is 67 Hz, comparable with the other experiments.

To study the effects of the short-term clock stability, we analyse the Bell-state parity experimental runs with associated clock feedback frequencies less than a certain cutoff. With the cutoff frequency increasing from 100 Hz (results are presented in Fig. 2d) to 400 Hz (all data included), the parity contrast shows a clear decreasing trend (Extended Data Fig. 6a). This is consistent with our Bell-pair generation fidelity being limited by clock laser phase noise.

In contrast, note that using the randomized symmetric stabilizer benchmarking circuit to characterize the CZ gate itself, our results are consistent run to run and day to day within our experimental error bars. This further attests to the largely reduced sensitivity of this sequence to single-qubit gate errors stemming from clock laser drift and clock laser phase noise.

Error bars and fitting

Error bars on individual data points throughout this work represent 68% confidence intervals for the standard error of the mean. If not visible, error bars are smaller than the markers. The randomized circuit return probability shown in Fig. 2b and the parity signal shown in Fig. 2d are fitted using the maximum-likelihood method⁵⁸ (see details in the next section). Error bars on fitted parameters represent one standard deviation. Fitting for all other experimental data is done using the weighted least squares method.

Data analysis of Bell-state fidelity

We analyse the results of the Bell-state experiments as in our previous work⁵⁸. We use a beta distribution to assess the underlying probabilities. For the parity signal shown in Fig. 2d, we fit the data with a sine function with four free parameters: offset, contrast, phase and frequency. We find that using the maximum-likelihood method while taking the underlying beta distribution of each data point into account is necessary, as the standard Gaussian fit typically overestimate the contrast by approximately 0.015. This is because the beta distribution deviates from a Gaussian distribution when the two-atom parity is close to ±1, which breaks the underlying assumption of a Gaussian fit. From this, we obtain a parity contrast of $0.963_{-10}^{+7}$ ($0.983_{-10}^{+7}$ SPAM corrected). Together with the measured population overlap P₀₀ + P₁₁ = $0.988_{-7}^{+5}$ ($0.994_{-7}^{+5}$ SPAM corrected) (not shown), we obtain a Bell-state generation fidelity of $0.976_{-6}^{+4}$ ($0.989_{-6}^{+4}$ SPAM corrected). These results are obtained by analysing experimental runs with associated clock feedback frequencies of less than 100 Hz.

SPAM correction

The dominant measurement error stems from the long tails in a typical fluorescence imaging scheme. In our experiment, we infer the imaging true negative and true positive rates as F₀ = 0.99997 and F₁ = 0.99995, respectively, from experimental measurements through a model-free calculation (ref. ⁶⁶, section 2.6.7). Note that these are not state detection fidelities in a circuit, as state detection in a circuit would require a further push-out before imaging⁶². The probability of successfully expelling the ground-state atom from the trap for state discrimination is B = 0.9989(1). Taking these into account, the single-atom measurement-corrected values $P_0^{\mathrm{m}}$ and $P_1^{\mathrm{m}}$ have the following relation with the raw values $P_0^{\mathrm{r}}$ and $P_1^{\mathrm{r}}$:

$$\left[\begin{array}{c}\hfill P_0^{\mathrm{m}}\hfill \\ \hfill P_1^{\mathrm{m}}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1-C\hfill & \hfill 1-A-C\hfill \\ \hfill C\hfill & \hfill A+C\hfill \end{array}\right]\left[\begin{array}{c}\hfill P_0^{\mathrm{r}}\hfill \\ \hfill P_1^{\mathrm{r}}\hfill \end{array}\right],$$ 1

where $A={\left[B\left(F_0+F_1-1\right)\right]}^{-1}=1.0012$ and $C=1-F_1{\left[B\left(F_0+F_1-1\right)\right]}^{-1}=-0.0011$. By assuming that a measurement was independent among the atoms, we extend this correction to multi-qubit measurements by taking the Kronecker product of the above matrix.

After correcting the measurements, we then correct for state preparation errors for the Bell-pair generation circuit (Extended Data Fig. 8). At the circuit initialization (state preparation) stage, we implement an erasure-cooling scheme⁴⁴ and analysed the results conditioned on no erasure detected. We identify that the dominant imperfections in this state preparation stage are (1) atom loss (with probability ε_l = 0.0027 for a single atom) and (2) decay from $\mid 1⟩$ to $\mid 0⟩$ (with probability ε_d = 0.0037 for a single atom). We keep track of how all two-qubit initial states ($\mid 11⟩,\mid 10⟩,\mid 01⟩,\mid 1,\mathrm{lost}⟩,\mid \mathrm{lost},1⟩,$ …) contribute to the population distribution and the coherence at the measurement stage.

Extended Data Fig. 8. State-preparation correction for Bell state population.

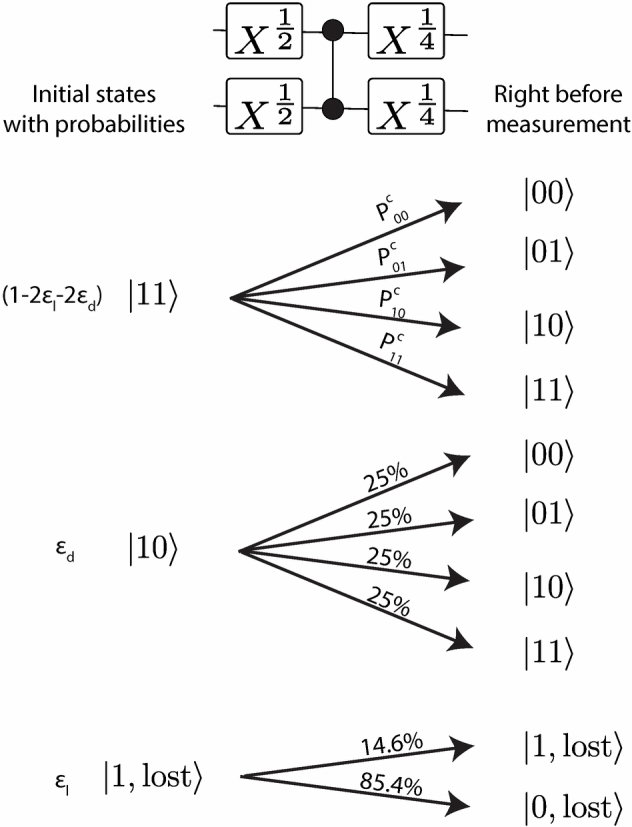
We draw the probability tree, starting from circuit initialization (state preparation), and track the evolution up to the measurement stage. From this, we can correct for state preparation errors. Following erasure-cooling as part of the state preparation, we have the ideal initial state and erroneous initial states with respective probabilities. We track their evolution under the Bell state generation circuit and see how each initial state contributes to the population distribution before the measurement. The SPAM corrected values, labelled by $P_b^c$, where b labels the different two-qubit bitstring, are the quantities that we want to evaluate. The pathway for $\mid \mathrm{lost},1⟩$ and $\mid 01⟩$ can be inferred easily from the clear symmetry with $\mid 1,\mathrm{lost}⟩$ and $\mid 10⟩$. For simplicity, $\mid 00⟩,\mid \mathrm{lost},\mathrm{lost}⟩,\mid 0,\mathrm{lost}⟩,\mid \mathrm{lost},0⟩$ are not shown due to their small probability on the order of ${\epsilon }_d^2,{\epsilon }_l^2\approx 10^{-5}$.

For the population distribution, apart from the ideal initial state $\mid 11⟩$, we keep track of how the erroneous initial states evolve under a perfect circuit execution and contribute to the final population distribution (Extended Data Fig. 8). We correct the bit-string populations to the first order of ε_d and ε_l. Following the probability tree, we can write:

$$\begin{array}{c}{P}_{00}^{\mathrm{m}}=\left(1-2{\epsilon }_{\mathrm{l}}-2{\epsilon }_{\mathrm{d}}\right)P_{00}^{\mathrm{c}}+\frac{1}{4}\times 2{\epsilon }_{\mathrm{d}}{+\cos }^2\frac{\mathrm{\pi }}{8}\times 2{\epsilon }_{\mathrm{l}},\hfill \\ P_{11}^{\mathrm{m}}=\left(1-2{\epsilon }_{\mathrm{l}}-2{\epsilon }_{\mathrm{d}}\right)P_{11}^{\mathrm{c}}+\frac{1}{4}\times 2{\epsilon }_{\mathrm{d}},\hfill \end{array}$$ 2

where the bit-string probabilities $P_{\mathrm{b}}^{\mathrm{m}}$ are measurement-corrected and $P_{\mathrm{b}}^{\mathrm{c}}$ (the SPAM-corrected population) are issued from perfect initial state preparation, inherent to the quantum circuit execution errors.

For the coherence measurement, we keep track of how the different erroneous initial states contribute to the observed parity contrast. The error channel with one lost atom (initial state being $\mid 1,\text{lost}⟩$ or $\mid \text{lost},1⟩$) does not affect the contrast due to having a different oscillation frequency. On the other hand, if an atom has decayed to the ground state ($\mid 01⟩$ or $\mid 10⟩$), its parity oscillation frequency remains the same but with a π phase shift and a contrast of 0.5. This contributes negatively to the observed parity contrast. Hence, the measured parity oscillation contrast C^m (after measurement correction), in terms of the SPAM-corrected contrast C^c, to the first order of error probabilities, is

$$C^{\mathrm{m}}=\left(1-2{\epsilon }_{\mathrm{l}}-2{\epsilon }_{\mathrm{d}}\right)C^{\mathrm{c}}-2{\epsilon }_{\mathrm{d}}\times \frac{1}{2}.$$ 3

Erasure conversion for motional qubit initialization

In the main text, there are several results where the analysis of a final image is conditioned on a preceding fast image that verified the state preparation (after erasure-cooling) or motional qubit initialization (after shelving). First, note that erasure-cooling is needed strictly only for the motional qubit initialization in mid-circuit measurements. Additionally, we find improved single-qubit (clock) gate fidelities following erasure-cooling, and this improvement becomes significant for shallow tweezers. In contrast, the improvement in CZ gate fidelity following erasure-cooling is insignificant. In the full error model, we find only a 2 × 10⁻⁵ increase when cooling the radial degree of freedom to its motional ground state.

For experiments in which MCR is applied (Figs. 4 and 5), we report the results conditioned on not detecting atoms in the ground state after a shelving pulse⁴⁴. We provide the results here with no conditioning for completeness. For measurement-based Bell-state generation (Fig. 5d), without erasure excision, the contrast is 0.39(3), and the population overlap would be 0.64(2), yielding a raw Bell-state fidelity of 0.52(2). For ancilla-based $\widehat{X}$ measurement (Fig. 4c), the contrast, conditioned on the ancilla result $\mid 0⟩$ ($\mid 1⟩$), is 0.60(3) (0.45(3)).

We attribute the limited shelving fidelity mostly to the limited Rabi frequency on the sideband transition, compared with typical frequency variations of the addressing laser or the trap frequency. Further limitations may arise from the uniformity of the trap waists (and depths) of different tweezers across the array. These limitations can be overcome with a more stable clock laser or by employing more advanced pulse sequences designed to be insensitive to such inhomogeneities⁶⁷.

Effects of clock error on four-qubit GHZ-state preparation

As discussed in the main text, during the preparation of the four-qubit GHZ state, the entangled state is vulnerable to finite atomic temperature and clock laser noise. Entangled states dephase during the array reconfiguration time, which is considered idle time in the quantum circuit, due to laser frequency noise. To quantitatively study the effect of laser frequency noise, we perform the experiment with different idle times. We then measure the parity oscillation contrast and the population overlap of the four-qubit GHZ state and compared with our error model predictions, assuming perfect CZ gates (Extended Data Fig. 9). The experimental pulse sequence is shown in Extended Data Fig. 9a. We increase the total idle time from 280 to 840 μs per arm and observe a decrease in both the overlap of the GHZ-state population and the parity oscillation contrast (Extended Data Fig. 9c,e). We also observe similar trends in a numerical simulation with our error model, which assumes perfect CZ gates, a finite temperature of $\overline{n}=0.24$ and the calibrated clock laser frequency PSD. With the actual reconfiguration time (280 μs), this error model predicts the parity oscillation contrast to be 0.66 and the state fidelity to be 0.75, consistent with our experimental realization (contrast being 0.68(3) and fidelity being 0.71(2)).

Error model with a 26-mHz clock laser system

The experimental results with the variable idle time show that the generation fidelity of four-qubit GHZ states is limited by the clock laser frequency noise. This motivates us to simulate this state generation circuit with our clock error model and the frequency PSD of a 26-mHz laser⁵³. Keeping a finite temperature of $\overline{n}=0.24$ and assuming perfect CZ gates, we find a contrast of 0.79 and a fidelity of 0.84 (Extended Data Fig. 6b). With this reduced frequency noise, we find the four-qubit GHZ generation fidelity less sensitive to the idle time. For the simultaneous generation of a cascade of GHZ states, we find that the four-qubit GHZ fidelity is consistent with the shorter idle time sequence. Furthermore, with zero temperature ($\overline{n}=0$), the clock error model predicts near-unity state fidelity (over 0.999). In this low-temperature and 26-mHz clock laser scenario, the state fidelity is limited by the entangling gate fidelity. With the high-fidelity entangling gate demonstrated in this work, we estimate the generation fidelity of four-qubit GHZ states to be approximately 0.97. This improvement of the atomic temperature could readily be achieved by erasure-cooling⁴⁴ or other methods⁶⁸. Note that erasure-cooling is not applied during this particular experiment to speed up the data-taking on a four-atom register.

Projected metrological gain

We analyse the experimental fidelities required to obtain a metrological gain in phase estimation. The metrological gain g is defined as the ratio of posterior variances². If we consider the gain of a protocol with N entangled atoms over the interrogation of N uncorrelated atoms, it can be written as $g={\left(\mathrm{\Delta }{\varphi }_{\mathrm{UC}}\right)}^2/{\left(\mathrm{\Delta }{\varphi }_{\mathrm{C}}\right)}^2$, where ${\left(\mathrm{\Delta }{\varphi }_{\mathrm{C}}\right)}^2$ and ${\left(\mathrm{\Delta }{\varphi }_{\mathrm{UC}}\right)}^2$ are the posterior variances for the entangled case and the uncorrelated case, respectively. For both cases, we assume a dual-quadrature read-out^5,16,51. We first describe the expected metrological gain with perfect state preparation and then consider the case of imperfect state preparation.

There are two distinct regimes for phase estimation. Local phase estimation corresponds to the limit of a vanishing prior phase width or equivalently to short interrogation times in atomic clocks. This limit holds only if the prior phase width is smaller than the dynamic range of the quantum state. In this limit, the optimal probe state is an N-atom GHZ state, and the gain is² g ≈ N.

For a large phase prior distribution width or equivalently for long interrogation times in atomic clocks, GHZ states do not provide a metrological gain due to their limited dynamic range, so that new protocols are needed. In the main text, we consider the protocol proposed in refs. ^1,4 and demonstrate a scheme to generate the required input state and read out the phase in both quadratures (Fig. 3). The protocol uses N atoms divided into M groups of GHZ states with K = 2^j atoms each, where j = 0, …, M − 1. The number of atoms in the largest GHZ state is, thus, $K_{\max }=2^{M-1}.$ The projected metrological gain with ideal state preparation was predicted to be $g\approx {\mathrm{\pi }}^{2}N/\left(64\log \left(N\right)\right)$ (ref. ⁴). The gain can be understood by considering phase estimation at the Heisenberg limit for the largest GHZ state, which contained N/2 atoms. To exponentially suppress rounding errors in phase estimation, one needs to use n₀ copies of each GHZ state with $n_0=\left(16/{\mathrm{\pi }}^2\right)\log \left(\mathrm{N}\right)$. Note that these expressions hold only in the limit of large N.

We now consider a limited number of atoms N and analyse the effect of finite state preparation fidelity on the projected metrological gain. We assume that the interrogation time is long and perform numerical Bayesian phase estimation. We use a Gaussian prior distribution to model the prior knowledge of the laser phase. For Bayesian phase estimation, the posterior variance of a given protocol depends on the variance of the prior distribution. The figure of merit of phase estimation is typically given by^6,37 R = Δϕ_C/δϕ, where δϕ is the prior phase distribution width. R quantifies how much information was obtained in the measurement compared to our initial knowledge of the parameter. It has been shown numerically that for relevant values of N (N ≈ 100), the optimal performance, quantified by R, is obtained for a phase prior width around δϕ = 0.7 rad for a large class of states^6,37. We, therefore, choose to work with this prior width. Experimentally, the prior width is set by the Ramsey interrogation time and can be tuned to this optimal value.

Using the protocol in ref. ⁴ for GHZ states with one, two or four atoms, the minimal number of copies per GHZ size is n₀ = 6, resulting in N = 42 atoms (Extended Data Fig. 7). Using optimal Bayesian estimators³⁷, we find numerically a metrological gain of 1.627 (2.114 dB) with perfect state preparation. Imperfect preparation fidelity results in a parity signal with limited contrast C(K) for a K-atom GHZ state. The probabilities for the outcome of a parity measurement are then modified to $P\left(\pm \right)=\left(1\pm C\left(K\right)\cos \left(K\varphi \right)\right)/2$, where {+, −} denote even and odd parity, respectively.

To estimate the effect of such limited contrast on the metrological gain, we consider two characteristic scenarios, motivated by our experimental results. First, we look at a case with perfect state preparation for the one-atom and two-atom GHZ states (C(1) = C(2) = 1), whereas the four-atom GHZ state has a finite parity signal contrast C(4). In this case, we find numerically that the minimal contrast to obtain a gain g ≥ 1 is C(4) = 0.656. This is higher than the threshold contrast for a narrow prior width given the same state, that is $C\ge 1/\sqrt{K_{\max }}=0.5$ (refs. ^2,52).

Second, we look at a case where the contrast of each GHZ state scales as $C\left(K\right)=F_0^K$, where F₀ is the effective fidelity per qubit. We repeat the calculation and find that the threshold fidelity to obtain a gain was F₀ = 0.969, or equivalently a contrast of C(4) = 0.969⁴ = 0.883 for the four-atom GHZ state. Numerically, this threshold seems to be robust to the introduction of more copies of the one-atom and two-atom GHZ states: if n₀ = 12 only for these states (keeping n₀ = 6 for the four-atom GHZ states), the threshold is only slightly reduced to F₀ ≳ 0.965. Finally, we show the projected metrological gain for various F₀ with respect to the number of atoms in the largest GHZ state used in the protocol of ref. ⁴ in Extended Data Fig. 7.

Our experimental values for C(K) from the simultaneous GHZ-state generation scheme (C(1) = 0.82, C(2) = 0.68 and C(4) = 0.52) fall between the two cases considered here: the best case scenario of C(K) = 1 for $K<K_{\max }$ and the worst case scenario of $C\left(K\right)=F_0^K$. Hence, we expect the threshold for metrological gain to lie between the values obtained from these two cases.

Note that the observed parity oscillation contrasts in our current experimental demonstration are below these thresholds. However, the contrast reduction is entirely dominated by clock laser noise (Extended Data Fig. 6). With the high-fidelity CZ gates obtained in this work, where F_CZ ≈ 0.996, combined with a reduced clock laser noise (achieved, for example, by a laser with frequency PSD as in ref. ⁵³ as discussed above), we numerically project a performance superior to the same number of uncorrelated atoms. Specifically, if we assume F₀ ≈ 0.996, the predicted metrological gain with six copies of GHZ states with one, two or four atoms each is calculated to be 1.519 (1.815 dB). If eight-atom GHZ states are included, the predicted metrological gain with eight copies of GHZ states with one, two, four or eight atoms each is calculated to be 1.893 (2.772 dB). Note that the above gain analysis assumes zero dead time. Introducing dead time would degrade the gain, and we defer the analysis of this effect to future work.

Repeated ancilla detection with ancilla reuse

For the MCR illustrated in Fig. 4, fast 18 μs imaging⁵⁸ is applied with a fidelity of approximately 0.96 at a tweezer spacing of 3.3 μm. The strong driving on the ¹S₀ ↔ ¹P₁ transition without cooling results in the low survival of detected atoms. Therefore, for experiments where repeated ancilla measurements are needed, we refill the original ancilla position with another atom through array reconfiguration. Alternatively, we recool and reuse the ancilla atoms instead of refilling them. In this section, we describe a proof-of-concept experiment with different imaging parameters for the ancilla atoms (Extended Data Fig. 10).

The new imaging scheme is based on the standard high-fidelity, high-survival imaging with cooling light (¹S₀ ↔ ³P₁ intercombination line)⁶². We increase the imaging power to collect more photons over 10 ms and apply the cooling light on one of the axes for another 10 ms, which is shorter than the motional shelving coherence time  of approximately 100 ms (ref. ⁴⁴). This imaging scheme allows us to obtain an imaging fidelity of 0.98 with 0.965(2) survival (Extended Data Fig. 10a).

We then check whether we could coherently apply single-qubit rotations after this 10 ms imaging by applying a π/2 pulse and a second π/2 pulse with a variable phase (Extended Data Fig. 10b). The measured coherence after imaging 0.94(1) (Extended Data Fig. 10c) is mainly limited by survival, which could readily be improved with further optimizations on cooling during the imaging. Once added to the complete MCR (Extended Data Fig. 10d), we see a similar coherence for the detected atoms in the ground state (blue) and a slightly lower coherence for the undetected atoms in the clock state (red), due to the decay (time constant approximately 300 ms) during the 10 ms cooling. These decayed atoms contribute doubly to the loss of coherence of approximately 0.07. With this coherent driving, we can see when the ancilla atoms are ready to be reused. In the same experiment, we also measure a coherence of approximately 0.73 on the shelved atoms after unshelving them (not shown), matching the numbers for motional coherence in our previous work⁴⁴.

Weight-2 ancilla-based parity read-out

Here, we give the fitted parameters of the plot presented in Fig. 5b. For the direct read-out on the Bell pair, we fit an oscillation of 16.5(1) kHz with a phase 3.16(7) rad and a contrast of 0.77(3). The ancilla read-out gives a Ramsey oscillation of 16.5(2) kHz with a phase of 3.19(9) rad and a contrast of 0.59(4). In a separate experiment interleaved with this experiment, we measure the single-atom detuning to be 8.26(5) kHz.

With perfect gates, the quantum circuit in Fig. 5a yields an oscillating state between $\mid {\Phi }^{+}⟩\otimes {\mid 0⟩}_{\mathrm{ancilla}}$ and $\mid {\Phi }^{-}⟩\otimes {\mid 1⟩}_{\mathrm{ancilla}}$. For either state, the pair would be measured in $\mid 00⟩$ or $\mid 11⟩$ in this ideal case. Given this information, one can post-select on the experimental repetitions where the pair is measured in the expected state, either $\mid 00⟩$ or $\mid 11⟩$. This post-selection could identify errors in the execution of the circuit. Looking at the oscillating state, this post-selection should not bias either of the ancilla measurement outcomes. Performing this post-selection analysis (not shown), we see a Ramsey oscillation of 16.5(3) kHz and a contrast of 0.71(8).

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-024-08005-8.

Author contributions

R.F., R.B.T. and X.S. performed the experiments, data analysis and numerical simulations. S.D., R.F. and T.G. performed the metrological gain calculation and analysis. R.F., R.B.T., X.S., P.S., J.C. and A.L.S. contributed to the experimental set-up. M.E. supervised this project. All authors contributed to writing the manuscript.

Peer review

Peer review information

Nature thanks Christian Marciniak and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Data availability

The data supporting this study’s findings are available from the corresponding author upon reasonable request.

Code availability

The codes supporting this study’s findings are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.

Extended data

is available for this paper at 10.1038/s41586-024-08005-8.