Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Sep 19;63(39):18251–18262. doi: 10.1021/acs.inorgchem.4c03139

From (Sub)Porphyrins to (Sub)Phthalocyanines: Aromaticity Signatures in the UV–Vis Absorption Spectra

Sílvia Escayola †,‡, Jorge Labella §, Dariusz W Szczepanik ∥, Albert Poater †, Tomas Torres §,⊥,#, Miquel Solà †,*, Eduard Matito ‡,∇,*
PMCID: PMC11465665  PMID: 39297344

Abstract

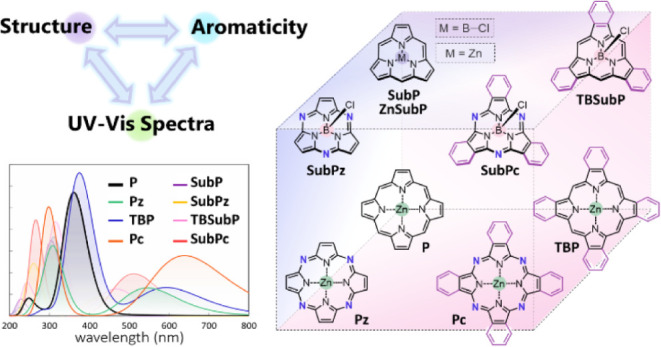
graphic file with name ic4c03139_0009.jpg

The development of novel synthetic methods has greatly expanded the toolbox available to chemists for engineering porphyrin and phthalocyanine derivatives with precise electronic and optical properties. In this study, we focus on the UV–vis absorption characteristics of substituted phthalocyanines and their contracted analogs, subphthalocyanines, which feature nonplanar, bowl-shaped geometries. These macrocycles, which are central to numerous applications in materials science and catalysis, possess extensive π-conjugated systems that drive their unique electronic properties. We explore how the change from a metalloid (B) to a metal (Zn) and the resulting coordination environments influence the aromaticity and, consequently, the spectroscopic features of these systems. A combined computational and experimental approach reveals a direct correlation between the aromaticity of the external conjugated pathways and the Q bands in the UV–vis spectra. Our findings highlight key structural modifications that can be leveraged to fine-tune the optical properties of porphyrinoid systems, offering new pathways for the design of advanced materials and catalysts with tailored functionalities.

Short abstract

Exploring structural variations in zinc and boron-hydride coordinated (sub)porphyrin and (sub)phthalocyanine systems while uncovering correlations between spectroscopic features and aromatic pathways.

Introduction

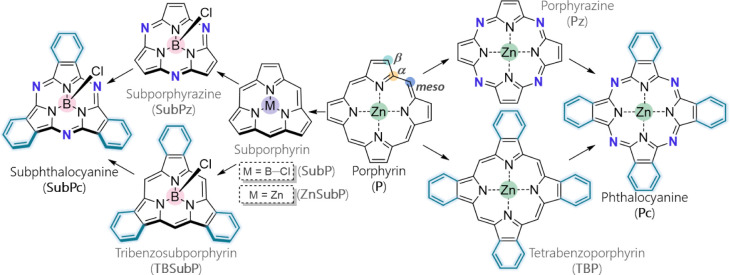
Over the last century, the continuous improvement of synthetic methodologies for generating porphyrin derivatives converged to the point where these can be obtained based on targeted properties.1 Among the wide variety of systems, some interesting examples are phthalocyanines (Pcs),2−4 porphyrazines (Pzs),5,6 tetrabenzoporphyrins (TBPs),7 and their respective ring-contracted versions, subporphyrins (SubPs),8 subphthalocyanines (SubPcs),8−10 subporphyrazines (SubPzs),9 and tribenzosubporphyrins (TBSubPs),11 see Scheme 1. The former are aromatic and composed of four isoindole units, interconnected via nitrogen (N) or methine (=CH−) bridges (at the meso positions, Scheme 1)12,13 and tend to be highly planar unless distortion is forced by the addition of bulky substituents or large metal ions, as observed in some metal-substituted Pcs and TBPs.14,15 The latter, also aromatic, only have three isoindole moieties and adopt nonplanar bowl-shaped geometries.16

Scheme 1. Metallo or B–X Coordinated (Sub)Porphyrins and (Sub)Phthalocyanines Included in This Study.

Scheme 1

Open in a new tab

The structural differences that relate porphyrin with phthalocyanine and subphthalocyanine are highlighted in dark blue (N–meso) and turquoise (fused 6-MR). In subporphyrin, we considered both central Zn and B–Cl coordination.

Key features of these macrocyclic compounds are their extended π-conjugated system and central coordination, which are responsible for their unique properties. Compared to porphyrin, (Sub)Pcs exhibit characteristic ultraviolet–visible (UV–vis) absorption spectra, with (blue)red-shifted Q bands and blue-shifted Soret, or B, bands. According to the Gouterman four-orbital model for porphyrins,17−19 Q and B bands arise from π–π* transitions and can be understood by considering the four frontier orbitals: a2u, a1u, and two eg (corresponding to HOMO – 1, HOMO, LUMO, and LUMO + 1, which will be referred to as H – 1, H, L, and L + 1, respectively), depicted in Figure 1. The different orbital mixing splits the resulting excited states into lower-energy, Q bands (S0 → S1), and higher-energy, Soret bands (S0 → S2).20 The central metal coordination affects these spectra by altering the overlap between the metal and ligand orbitals, leading to variations in their energy gaps and thus influencing the position of the absorption bands.21 For instance, nickel porphyrins have similar ring currents to their zinc analogs, but due to their vacant dx2–y2 orbitals they tend to have larger HOMO–LUMO gaps and lower HOMO levels, resulting in blue-shifted absorption spectra and lower chemical reactivity.22

Figure 1.

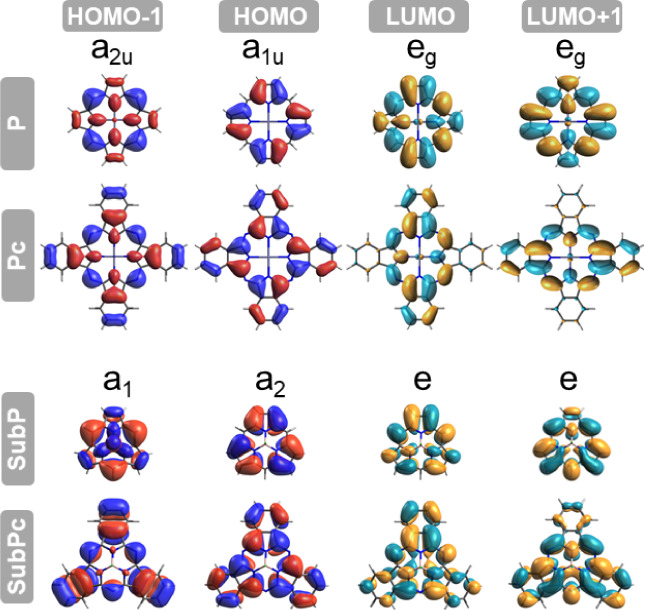
Figure 1

Open in a new tab

Spatial representation of frontier a2u, a1u, and eg (or a1, a2, and e in C3v) molecular orbitals, with an isocontour of 0.02 a.u., from top to bottom for P, Pc, SubP, and SubPc. In the case of SubPc, the a1 orbital corresponds to the HOMO – 3.

The typical absorption spectra of metalloporphyrins consist of two weak Q bands at 500–650 nm and a Soret intense band at 370–450 nm.20 In the case of metallophthalocyanines, Q and B bands lie around 600–800 and 300–400 nm, respectively, whereas in subphthalocyanines, Q and B bands appear at 460–560 and 260–370 nm regions.9 In Zn-phthalocyanine (Pc) and subphthalocyanine (SubPc), the relative intensity of Q and Soret bands is reversed compared to Zn-porphyrin (P). 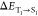This change has been primarily attributed to the N–meso substitution that breaks the a2u–a1u near-degeneracy, selectively stabilizing the a2u orbital, thereby increasing the intensity of the Q-band.23−25 Their characteristic UV–vis spectra, low-lying singlet (S1)–triplet (T1) energy gaps (Inline graphic), H–L gaps, and other properties (e.g., conductance)26 make them optimal candidates for solar cells,3,27−30 nonlinear optics,31 molecular electronics,32 and photonics.33,34 Furthermore, (sub)phthalocyanine derivatives are unique photoactive materials to prepare energy and electron donor–acceptor systems.35 In this regard, notable is the use of Pcs complexing heavy metals for triplet–triplet annihilation upconversion (TTA-UC),36−39 and the use of SubPcs and SubPzs for singlet-fission downconversion (SF-DC).40−42 Overall, these compounds are promising materials for a wide array of applications. However, a clear establishment of structure–property–and property–property relationships is crucial to fully exploiting their highly tunable potential and applications. Some examples along the lines of identifying these relationships are the independent studies of Zhang et al.,23 Belosludov et al.,43 Holst et al.,44 and Peterson et al.,45 where they found a correspondence between computed H–L gaps and spectroscopic properties or variations in S1 and T1 state energies. The mere calculation of H–L gaps might not be adequate to pinpoint these properties due to potential accuracy issues, as highlighted by Holst and co-workers.44 There is an ongoing need for streamlined methods that enable faster screening through alternative computational analyses. Several authors have unveiled connections between the (anti)aromaticity in diverse free-base or metal substituted porphyrinoids and their UV–vis or infrared spectra,46 with some focusing on nonlinear optical properties.47−53 Ke et al. recently introduced a way to regulate the properties of silicon(IV) phthalocyanines by switching their aromaticity.54 These discoveries hint at a potential interplay between the aromaticity and properties of porphyrinoids. 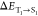Expanding upon this research, we propose the use of chemical bonding and aromaticity analyses as a systematic procedure to identify π-system–UV–vis absorption and Inline graphic correlations in porphyrin-related compounds, improving the understanding of physical properties and reactivity in these complexes.

Aromaticity is widely acknowledged as a pivotal concept in characterizing electronic structures,55−59 the Hückel rule (4N + 2)60−62 offering the most straightforward approach to predicting the aromatic nature of molecules. While the application of the Hückel rule is primarily focused on planar monocyclic molecules, such as annulenes and their analogues,63,64 its simplicity spurred researchers to modify it for intricate systems.65−68 Traditionally, the aromaticity of porphyrins and Pcs has been ascribed to an 18π-electron aromatic cycle (and a 14π-electron cycle in SubPs and SubPcs) akin to [18]annulene, adhering to the Hückel rule.69,70 Obviously, this rule cannot differentiate among molecules with an identical number of π-electrons, and falls short when accounting for the aromaticity of some nonplanar systems; other tools are becoming essential to comprehensively address aromaticity.47,48,50,51,71−73 Aromaticity investigations of Pcs and, especially, SubPcs are sparse and primarily restricted to nucleus-independent chemical shift (NICS) and the harmonic oscillator model of aromaticity (HOMA).74−78 Given the intricacy of these molecules—attributable to their size, topology, and the presence of multiple π-electron circuits—and the inherent limitations of NICS and HOMA as aromaticity gauges,79−81 there is a compelling case for using more reliable aromaticity descriptors. A more holistic method, integrating both global and local aromaticity metrics, remains desirable to unveil the most favorable pathways for electron delocalization in Pcs and SubPcs.

One of the main challenges in the description of aromaticity in porphyrinoids is the identification of the most conjugated pathway among the complex ring constructed of bridged rings (including but not limited to pyrrole, isoindole, and derivatives), a task that is not suited for some popular aromaticity indicators such as global NICS analysis. The molecule can be divided into different regions, including benzo (b), outer (o), and inner (i), as defined in Scheme 2. From these regions, potential circuits emerge. Determining the key pathways in such a complex system requires careful analysis and consideration of all possible routes. Over the past few years, significant efforts have been dedicated to the development and application of specific electronic indices to large rings.71−73,82,83 The latter need emerges from the inadequacy of the most reliable indices of aromaticity79 for their application to ring structures with more than 14 atoms.82

Scheme 2. Possible Routes to Follow, i Inner, o Outer, and b Benzo, at Each Pyrrole or Isoindole Moiety, Which Define the Closed Pathways along the Molecule.

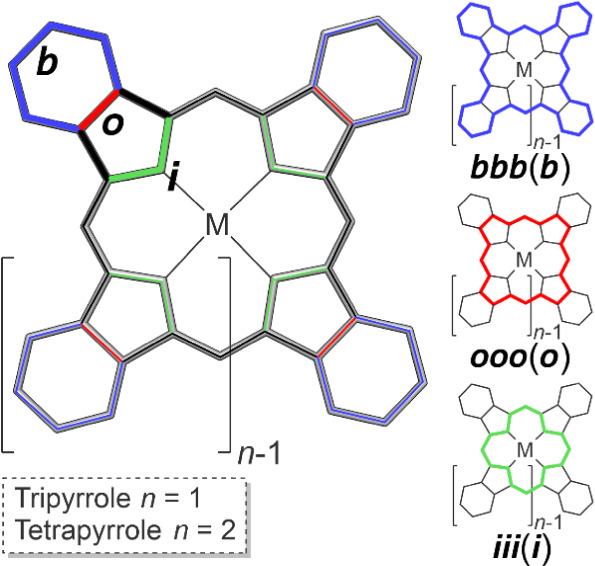
Scheme 2

Open in a new tab

Three examples are the bbb(b), ooo(o), and iii(i) pathways in blue, red, and green, respectively.

In this work, we employ aromaticity indices to identify the key conjugated pathways and discuss the similarities and differences between P and Pc or SubPc. Considering the intrinsic connection between UV–vis absorption spectrum and H–L gap in these molecules and the relationship this gap maintains with the aromaticity of π-conjugated systems,84,85 we will investigate a previously unexplored correlation between UV–vis absorbance and local pathways, which holds the promise to serve as a powerful tool for property-guided molecular design. 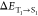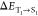Additionally, we also study the relationship between aromaticity in the singlet ground state and the excited-singlet–triplet gap, Inline graphic. The latter is particularly pertinent given the rising utility of this compound family in applications like triplet photosensitizers,86 optoelectronic components,77 and photodynamic therapy.87,88 Our final goal is to establish the connection between aromaticity and UV–vis absorption spectra or Inline graphic, and identify the molecular segments that are key for the control of electron delocalization, offering a promising avenue to suggest specific modifications, leveraging cost-efficient DFT over TDDFT or more accurate wave function methods that require a full study of the excited states.

Results

In the following, we present the results of our investigation, comparing the structural differences among P, Pc, and SubPc. These differences (shown in Scheme 1) include (i) the replacement of CH at the meso position by N, (ii) the inclusion of C4H4 fragments at the β positions to have isoindoles instead of pyrroles, (iii) the reduction in the number of pyrrole or isoindole units from four to three, and (iv) the replacement of the central Zn atom by the B–Cl moiety in SubPc compared to P and Pc. This study does not chiefly address the role of the central atom and its axial ligation or the effect of peripheral substitutions, which are other common structural changes that tune these molecules. While these modifications can also affect the molecular properties, their impact on the π-system is typically less pronounced compared with the modifications considered. We focused on Zn (d10) tetrapyrroles to avoid complications associated with axial ligation and the presence of π to d charge transfer and d-d excited states89,90 in open d-shell species. Apart from P, Pc, and SubPc, we also included other systems, presenting only one (or two, in the case of contracted systems) of the above-mentioned modifications with respect to P: porphyrazine (Pz), tetrabenzoporphyrin (TBP), Zn-subporphyrin (ZnSubP), subporphyrin (SubP), subporphyrazine (SubPz), and tribenzosubporphyrin (TBSubP). The study focuses on the changes (i)–(iii), mentioned above. However, for SubP, we also tested the role of the central coordination (iv), by considering the ZnSubP system, to assess whether the central element affects the aromaticity and whether the comparison between tri- and tetra-pyrrole/isoindoles is consistent. To determine structural changes in the physical properties, we compared the computational and experimental UV–vis spectra and analyzed the 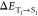Inline graphic, H–L gap, and aromaticity of the different molecules.

UV–Vis Absorption Spectra, H–L Gaps, and 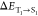Inline graphic

A detailed assignment of the Q and B bands has been done through TDDFT and UV–vis spectroscopy. Table 1 presents the vertical absorption energies, oscillator strengths, and TDDFT roots associated with Q and Soret (B) bands for the eight (sub)porphyrinoids under study. For the sake of simplicity, in the ensuing discussion, we will refer to the set of P, Pz, TBP, and Pc as phthalocyanines and ZnSubP, SubP, SubPz, TBSubP, and SubPc as subphthalocyanines. Computational absorption maxima (λmax, in nm) are slightly underestimated compared to those of the experimental counterpart. However, they follow the same trend, presenting excellent linear correlations with R2 = 0.98 and 0.94 for the Q and B bands, respectively (see Figure S3). While CAM-B3LYP may not reproduce the absolute experimental excitation energies to the highest accuracy, it exhibits consistency in predicting qualitative band shifts. Indeed, the relative band shifts, defined as Δλmax = λmax,X – λmax,P (where X represents any system but P), show a minimal discrepancy with the experimental values, with differences not exceeding 0.2 eV (26.6 nm). For this reason, further discussions will focus on CAM-B3LYP values.

Table 1. Comparison of Computational and Experimental Vertical Absorption Spectra for P, Pz, TBP, Pc, SubP, SubPz, TBSubP, and SubPca.

  Q-band
 Soret (B) band
  state λmax f λmax exp. state λmax f λmax exp.
P S1, S2 520.3 0.010 565b S3, S4 354.1 1.370 398b
Pz S1, S2 537.9 0.316 596c S6, S7 323.2 0.226 343c
TBP S1, S2 582.9 0.304 623b S3, S4 368.1 1.603 422b
Pc S1, S2 636.3 0.675 671c S12, S13 297.0 1.139 348c
SubP S1, S2 403.9 0.025 454d S3, S4 304.2 0.855 341d
SubPz S1, S2 425.7 0.221 497c S9, S10 262.7 0.458 290c
TBSubP S1, S2 461.0 0.308 514e S3, S4 312.4 1.055 355e
SubPc S1, S2 503.3 0.475 565c S10, S11 262.9 0.866 305c
Open in a new tab
a

TDDFT Q and Soret (B) bands, computed absorption maxima (λmax in nm), computed oscillator strengths (f), and experimental λmax. Computational results were obtained considering the same solvent as that used in experiments.

b

In ethanol from ref (129).

c

These results were generated by our own experimental setup in THF. In the case of SubPz, the spectrum corresponds to the β-substituted SubPz (see Figure S2a).

d

In dichloromethane (DCM) from ref (95).

e

In dichloromethane (DCM) from ref (128).

The Q and B band shifts of the substituted subphthalocyanines (SubPz, TBSubP, and SubPc) with respect to SubP exhibit the same behavior as the shifts observed in their phthalocyanine counterparts (Pz, TBP, and Pc) when compared to those of P. In fact, the magnitude of these band shifts is comparable between the analogs of both groups, indicating a consistent pattern in the response to substitution. The sole exception to this rule is TBP, where the B-band is slightly red-shifted owing to the destabilizing influence of the fused benzene in the a1u (H) orbital, coupled with the absence of stabilization in the a2u (H – 1) orbital due to the presence of CH–meso groups. The latter similarities between phthalocyanines and subphthalocyanines suggest the modifications in meso and β positions have a similar effect regardless of the molecule’s planarity and number of pyrrole or isoindole units. In general, the reduction in the number of pyrrole or isoindole units increases the band gap, as expected from the decrease of the π-conjugated units (the same happens with linear paraphenylenes, for instance).91

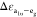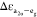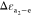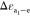The optical spectra of P and SubP are primarily influenced by frontier orbitals. In these molecules, the Q-band is associated with the a1u → eg (in P) and a2 → e (in SubP) transitions. For the B-band, a2u → eg (P) and a1 → e (SubP) transitions play a major role. In general, an increase in Inline graphic and Inline graphic (or Inline graphic and Inline graphic in C3v systems) leads to higher absorption energies in the Q and B bands, respectively. 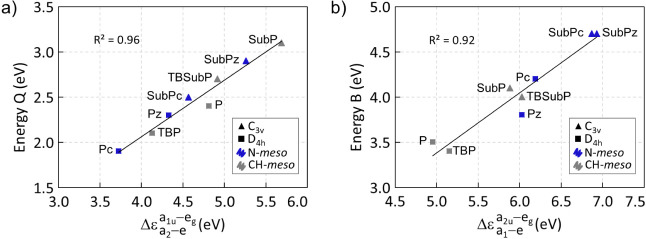This relationship between the frontier orbitals and the absorption spectra aligns with the Gouterman model and studies by Belosludov,43 Martynov and Mack,92,93 and Nemykin.94 There is a particularly good correlation between the Q-band and Inline graphic (Inline graphic), as displayed in Figure 3. 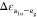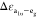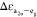It is worth noting that for SubP, the energy gap Inline graphic of 5.7 eV at the CAM-B3LYP/cc-pVTZ level should be compared with a value of 3.64 eV obtained using B3LYP/6-311G(d).95 Despite the correlation between the B-band and Inline graphic (Inline graphic), data points tend to cluster based on substitution at the meso positions and number of pyrrole and isoindole units, leading to a nonuniform distribution along the regression line. In the case of systems with CH–meso, the B and Q bands have contributions from only H – 1 (a2u), H (a1u), and L (eg). A similar pattern is observed for the Q-band in the N–meso systems. Yet the B-band in these systems not only has a significant contribution from a2u to eg but also incorporates transitions from b2u to eg, see Tables S9, S11, S14, and S16. Thus, in these cases, the Gouterman model is insufficient to explain the nature of the B-band. Given the involvement of additional transitions in the B-band, we expanded the Gouterman four-orbital model to consider other orbitals involved in the transitions and their influence on the excitation energy (Section S2.3). The resulting pondered Δε shows a more uniform distribution of the data, leaving Pz as the only outlier (the correlation coefficient R2 increases from 0.84 to 0.98 upon removing Pz; see Figure S4). In Pz, the Eu states associated with the B1 and B2 bands show a significant contribution (the weight is 0.49; see Table S9 and Figure S5) from the b2u–eg transition, in contrast to all other systems where the contributions come from the a1u and a2u to eg transitions.

Figure 3.

Figure 3

Open in a new tab

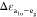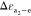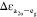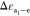Relationship between (a) Q-band energy and Inline graphic (Inline graphic) and (b) B-band energy and Inline graphic (Inline graphic).

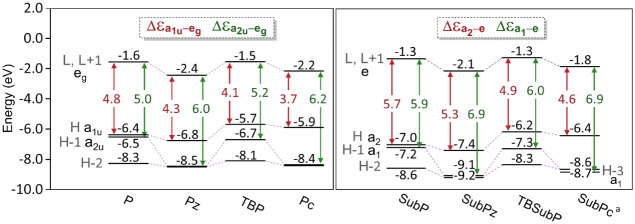
In P (SubP), the a1u and a2u (a2 and a1) orbitals correspond to H and H – 1, respectively. The latter orbitals are nearly degenerate (energy difference below 0.2 eV; see Figure 2), contributing to both the Q and B bands. Upon addition of the benzo substituents at the β-positions, the energy difference between a1u and a2u (a2 and a1) orbitals increases to approximately 1 eV, thus eliminating near degeneracy. The difference is further increased upon inclusion of the N–meso substituent, leading to a near degeneracy of H – 1 and H – 2 orbitals. The H–L gaps decrease with the inclusion of the benzo moieties, primarily due to the destabilization of the H upon addition of the substituents, which give antibonding character to this orbital around the β-position. Systems that also have N–meso (Pc and SubPc) exhibit further reduction of the H–L gap due to the stabilization of the LUMO orbital. This results in Pc having the smallest H–L gap among all the systems.

Figure 2.

Figure 2

Open in a new tab

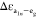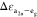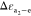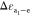Energy of the frontier orbitals (in eV), and Inline graphic and Inline graphic (or Inline graphic and Inline graphic) (in eV) at the CAM-B3LYP/cc-pVTZ level of theory for phthalocyanines (left) and subphthalocyanines (right). In the case of SubPc, the orbital with a1 symmetry is H – 3 instead of H – 1. Further details are given in Tables S17–S19.

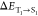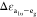Given the similarity between the orbital distribution of S1 and T1 states, in the following, we analyze whether the Gouterman model, which is only useful to predict the Q-band, can also be used to anticipate the behavior of T1 and its influence in the Inline graphic. To this end, we have computed the triplet vertical excited states at the TDDFT level of theory (see Table S21 and Figures S6 and S7a for a comparison with TDA, Supporting Information). In all cases, the first two roots correspond to two degenerate triplet states (T1) with a predominant H – 1, H → L (a2u, a1u to eg) transitions and energies 1.04–1.55 eV below the singlet excited states associated with the Q-band. In the case of P and SubP, two additional degenerate triplets (T2) exist, 0.23 and 0.44 eV beneath the first singlet excited state, respectively. For the remaining systems, T2 is above S1; however, there is an inverse relationship between the energies of T1 and T2 within each family, phthalocyanines and subphthalocyanines (when T1 increases, T2 decreases, and the other way around; see Figure S7c). T1 presents a positive correlation (see Figure S7b,d) with both the energy of S1 and Inline graphic (or Inline graphic). Thus, the observations made earlier in the paper regarding the role of frontier orbitals on the Q-band can be qualitatively extended to the T1 state.

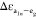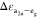Our analysis reveals that the evaluation of Inline graphic and Inline graphic do not comprehensively describe the absorption spectra, in particular the B-band for N–meso systems where the Gouterman model falls short. An extended Gouterman model provides a rationale for the trends observed in the B-band but lacks the simplicity of the original model. To provide a more chemically intuitive explanation, we resort to the study of the aromaticity of these compounds.

Aromaticity of Phthalocyanines and Subphthalocyanines

The aromatic stabilization energy (ASE) is known to diminish with an increase in the size of [n]annulenes, a trend that is accompanied by a marked decrease in electron conjugation. Notably, the ASE value for [18]annulene is as low as 2.6 kcal/mol,64 which stands in stark contrast to that of benzene, approximately 30 kcal/mol,96 depending on the homodesmotic reaction considered. The local aromaticity of the pyrrole rings is important to explain the overall ASE in porphyrinoids.97 In our case, systems containing benzo rings have a multicenter index (MCI) value close to 0.050, not far from the value obtained for benzene at the same level of theory (MCI = 0.071), while all the five-membered rings display MCI values about half the values of pyrrole or lower (benzo-substituted compounds) (see Table S32). Nevertheless, the global aromatic character of the molecule is influenced by the conjugated pathways along the whole molecule, which pass through these five- and six-membered rings. In simple neutral porphyrinoid systems, the aromatic character expected from straightforward π-electron counting rules is observed, whereas more intricate systems call for a more profound analysis. Hence, in this study, we opt for various electronic and magnetic aromaticity measures.51,71

Among the few aromaticity studies of (sub)phthalocyanines, the use of magnetic criteria, especially NICS, is prevalent.98 However, the utilization of global NICS measures for systems featuring fused rings has, until now, limited the ability to explore conjugated pathways individually. Additionally, previous studies have not delved into the effect of molecular substitutions. In this work, we embark on a comprehensive, two-pronged exploration of aromaticity. This entails an examination of intrinsic electronic aromaticity measures such as AV1245 (and AVmin)82 and electron density of delocalized bonds (EDDB),99,100 complemented by a comprehensive analysis of response aromaticity through the investigation of ring currents.

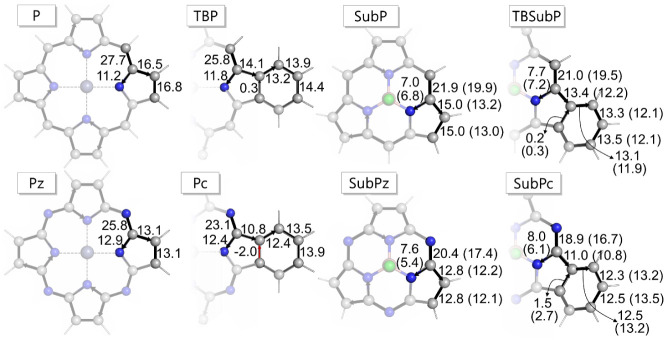
From the ring current perspective, all systems display diatropic currents with global current strengths exceeding 20 nA·T–1, a value larger than the 12 nA·T–1 found in benzene (see Figure S10). Hence, all investigated systems display conjugated pathways and can be considered magnetically global aromatic (Figure 3).

Although the current density maps show a global diatropic circulation, indicative of aromaticity, the global current is evenly split between the outer (o), inner (i), and benzo (b) pathways (see Scheme 2), as evidenced by examining the current strength in Figure 4. For instance, consider the case of Pc, where the total current of 23.1 nA·T–1 is broken down into two components: a 12.4 nA·T–1 current passing through the iii(i) pathway and a 10.8 nA·T–1 current passing through the ooo(o) pathway. This pattern is akin to what has been observed in free-base Pc and TBP. Both N–meso and benzo substitutions play a role in enhancing the intensity of the inner current, with the N–meso substitution exerting a particularly significant influence. This becomes apparent when examining the current strengths across different systems, such as the transition from P to Pz, where a clear outer pathway dominance over the inner one shifts to a similar preference upon N–meso substitution. Similarly, in the transition from Pz to Pc, the preference from the outer to inner pathway is entirely reversed upon benzo substitution. Similar trends are observed in the case of subphthalocyanines. However, due to the nonplanar nature of these molecules, defining an external magnetic field perpendicular to the system is not straightforward, and the results should be considered semiquantitative.

Figure 4.

Figure 4

Open in a new tab

Net current strengths (in nA·T–1) passing through selected bonds in the S0 state. In the case of subphthalocyanines, the values within parentheses represent the calculated current strengths when an external magnetic field is oriented perpendicular to the plane defined by the pyrrole or isoindole ring (refer to Section S4.1 for details).

In the following, we examine electronic aromaticity indices, specifically AV1245 (and AVmin), and EDDBP (and limit of EDDBP), which provide information about the electron delocalization in the conjugated pathways of the molecule in the absence of an external perturbation.47,48,51,63,68,71−73,101 Unlike the magnetic indices, the nonplanarity of subphthalocyanines does not represent a challenge for electronic indices, which can also be decomposed into contributions from individual groups or fragments. AV1245 is calculated as the average of multiple four-center MCI computed at positions 1, 2, 4, and 5 for each five-atom fragment along the conjugated pathway. In contrast, AVmin represents the smallest absolute value among these 4-center MCI values. The EDDB method involves the decomposition of the electron density into three components: electron density localized on the atoms (EDLA), electron density localized on the bonds (EDLB), and delocalized density, referred to as the electron density of delocalized bonds (EDDB). The latter quantity, when measured within a closed circuit, serves as an indicator of aromaticity. In our study, we focus on the EDDBP(r) function and electron populations (referred to as EDDBP), which specifically consider adjacent chemical bonds along the selected pathway. Additionally, similar to the AVmin index, we examine the limit of EDDBP (limitEDDB), which corresponds to the atom in the pathway with the smallest delocalized electron population. For all these indices, large values indicate aromaticity, while small values indicate nonaromaticity or antiaromaticity. AV1245 and EDDBP consider the average delocalization along the pathways and are expected to reflect features connected with the conjugated nature of these molecules, whereas AVmin and limEDDB indicate the least delocalized fragment/atom in the pathway, and this limiting value has been successfully connected to the aromaticity of the pathway in porphyrinoids.51,71,72 In practice, both values contribute to the overall assessment of the conjugated pathways. Finally, in the case of P, we have studied the effect of a coordinated solvent molecule to Zn(II) in the aromaticity of the macrocycle. Results show only minor changes in electronic indices (Figure S21 and Table S35).

The total number of nonequivalent conjugated pathways depends on the symmetry of the molecules. We identify 4 in SubP and SubPz, 6 in P and Pz, 10 in TBSubP and SubPc, and 21 in TBP and Pc, for which we have listed all electronic aromaticity indices in Tables S23–S31. However, in practice, the most important contributions are given by three conjugated pathways: inner iii(i), outer ooo(o), or benzo bbb (b) pathways, the results of which are summarized in Figure 5. AV1245 and AVmin show significantly reduced values for the most conjugated pathways in the molecules depicted in Scheme 1. Specifically, the AV1245 values are found to be below 3.0, and AVmin values are below 1.5 for all of the pathways. The latter figures are markedly lower than the values of 10.50 for both indices in benzene; however, they are in line with the values reported for other porphyrinoid systems.51,71 AV1245 and AVmin values do not agree on which pathway is the most conjugated, indicating that minimal and average multicenter delocalizations differ significantly. This difference is particularly evident for benzo-substituted molecules. As discussed in previous publications,83,102 AVmin is the index that better reflects aromatic character, whereas AV1245 provides an average delocalization value that can obscure weakly conjugated fragments.

Figure 5.

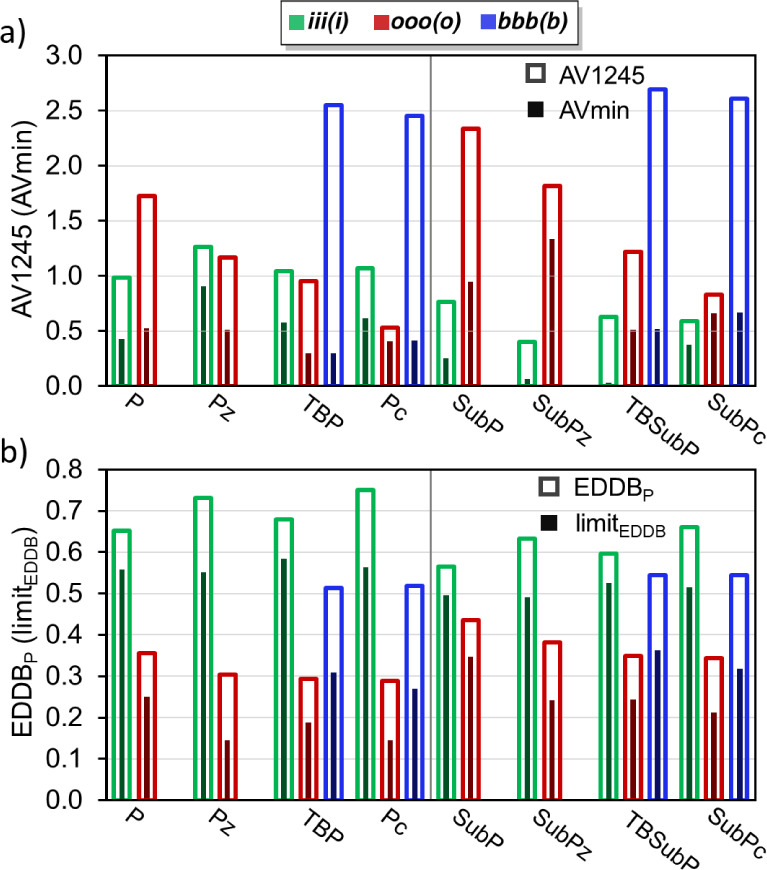
Figure 5

Open in a new tab

Aromaticity values of iii(i), ooo(o), and bbb(b) circuits in each system according to (a) AV1245 and (b) EDDBP (normalized according to the number of atoms in the circuit) aromaticity measures. The darker filled bars represent the (a) AVmin and (b) limit of EDDBP.

According to EDDBP and limitEDDB, iii(i) is always the most aromatic pathway with values lower than 0.75 and 0.59 electrons, respectively. In comparison, benzene demonstrates values of 0.92 electrons for both EDDBP and limitEDDB. Hence, there is a qualitative consensus regarding the most conjugated pathway in phthalocyanines, with AVmin, EDDBP, and limitEDDB consistently identifying the iii(i) pathway as the most conjugated. The sole exception is observed in Pz, where AVmin does not show a distinct preference between the ooo(o) and iii(i) pathways. Conversely, AVmin identifies the ooo(o) and bbb(b) as the most aromatic pathways in subphthalocyanines, whereas limitEDDB always identifies the iiii(i) pathway as the most aromatic. Nevertheless, in instances where the aromaticity of the ooo(o) and iii(i) pathways is ranked separately for each molecule using AV1245 and EDDBP, both indices consistently produce the same order, from the most aromatic to the least aromatic. The only deviation occurs in the ranking of the iii(i) circuit in subphthalocyanines, which is also observed with the electronic-based FLU and geometric-based HOMA indices (Tables S23–S31). In the case of the ooo(o) pathway, there is even a good linear correlation between AV1245 and EDDBP (see Figure S20). All in all, the most important difference between the electronic indices and magnetic ring currents is the magnitude of the aromaticity. According to the ring current strengths, all compounds are highly aromatic, while electronic indices indicate lower aromaticity.

The aromaticity of each pathway reflects the trends we observed in the UV–vis absorption energies (Figure 6). Both AV1245 and EDDBP show that the aromaticity of the ooo(o) circuit decreases along the P–Pz–TBP–Pc and SubP–SubPz–TBSubP–SubPc series, as occurred for the energy of the Q-band and Inline graphic. All aromaticity indices uniformly recognize the ooo(o) circuit in phthalocyanines as being less aromatic than the corresponding ooo(o) pathway in their contracted analogs, namely subphthalocyanines. This observation aligns with the higher excitation energies observed in the Q-band of these compounds.

Figure 6.

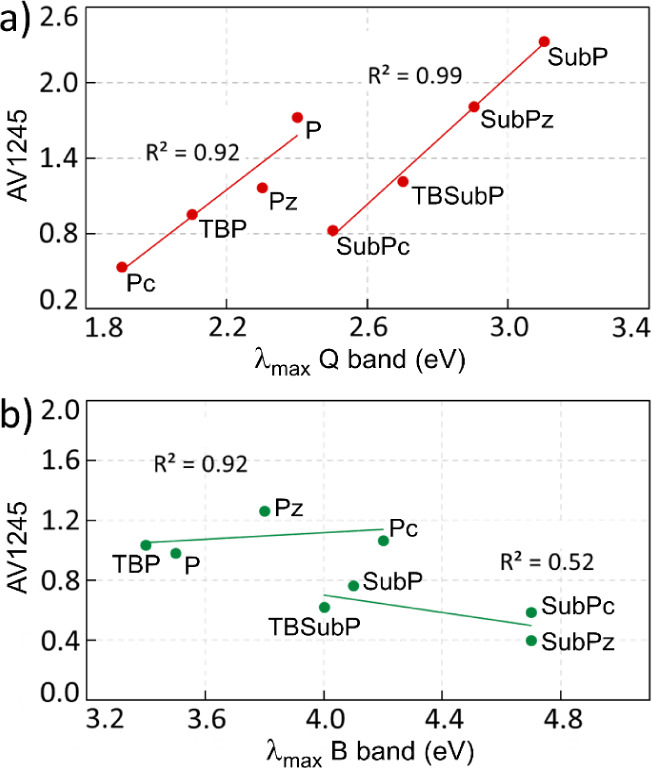
Figure 6

Open in a new tab

Relationship between (a) Q-band energy and AV1245 of the ooo(o) pathway and (b) B-band energy and AV1245 of the iii(i) pathway.

AVmin and limitEDDB, while they might reflect the limiting conjugated part of the pathway, do not show any evident connection with the Q and B bands. Instead, they can be used to identify the least conjugated fragment in the molecule and be instrumental in modifying the pathway’s aromaticity and, given their connection to the average counterparts, in the case of the ooo(o) pathway, tuning the Q-band. In Figures S16–S19, we split the information on AV1245 into five-atom fragments, in which we can easily recognize the fragment(s) giving rise to AVmin. Interestingly, the values of the fragments in the ooo(o) pathways follow the same distribution for a given phthalocyanine and its analog subphthalocyanine. The least (or second least) delocalized fragment of the ooo(o) pathways always corresponds to the fragment centered in the meso-position. This implies that meso-substitution influences the Q bands across all systems studied. To achieve a blue shift of the Q bands, a meso-substitution is necessary, but it must be distinct from the N–meso substitution. Indeed, the transition from P to Pz or Pc (N–meso substitution) results in a reduced AV1245 value, which in turn shifts the Q-band to the red. The addition of a benzo-group affects similarly, reducing the delocalization of other five-atom fragments and red-shifting the Q-band. The interplay of these effects results in a 3-fold reduction in delocalization for certain fragments in phthalocyanines and a 5-fold reduction in subphthalocyanines. This significant decrease in delocalization effectively eliminates any conjugated fragments within the ooo(o) pathway, consequently leading to a red shift in the Q bands. While the aforementioned analysis provides a reasonable understanding of the Q-band shifts, the correlation between the B-band and AV1245 values is less clear (see Figure 6b).

Conclusions

This study examines substituted phthalocyanines (P, TBP, Pc, and Pz) and their contracted analogs, subphthalocyanines (SubP, TBSubP, SubPc, and SubPz), which are characterized by nonplanar, bowl-shaped geometries. The methodology employed in this study, which includes CAM-B3LYP/cc-pVTZ calculations, is validated through the comparison of UV–vis computational and experimental studies. In addition, we rely on the Gouterman four-orbital model for porphyrinoids.

Our analysis reveals that evaluation of the four orbital energies is insufficient to describe the absorption spectra, particularly the B-band for N–meso systems, where deviations from the Gouterman model are apparent. An extension of the Gouterman model, including more orbitals, provides a rationale for the trends observed in the B-band, but it sacrifices the simplicity of the original model. Consequently, we turn to the examination of the aromaticity of these compounds, providing a more chemically intuitive explanation of their spectral features.

Magnetic response indices characterize all the molecules studied as aromatic, exhibiting important ring current strengths. Conversely, an analysis of electron delocalization and π-conjugation through AV1245, AVmin, and EDDB indices reveals that—despite the important response upon the application of an external magnetic field—the conjugated circuits are much less aromatic than those found in classical organic molecules like benzene, being closer to those already reported in other porphyrinoid systems.47,71 This evidence adds to the results already reported in the literature, where intrinsic (electronic) and response (magnetic) measures of aromaticity do not align.72,73,101,103−109 This divergence between intrinsic electronic and magnetic aromaticity measures adds a critical dimension to our understanding of these complexes, offering insights relevant to inorganic chemists focused on the interplay between electronic structure and reactivity in coordination compounds. In general, subphthalocyanines can be considered slightly more aromatic than phthalocyanines, according to the least delocalized fragment of the external-most circuit of these systems, and in agreement with the larger HOMO–LUMO gap observed in subphthalocyanines.

Interestingly, the electronic aromaticity indices help explain part of the UV–vis spectrum of (sub)phthalocyanines, giving a direct connection between the aromaticity of the external-most conjugated pathways and the Q bands. Particularly, the substitution at the meso position seems to have a large effect on the aromaticity and the position of the Q and B bands. This insight is pivotal for pinpointing modifications in porphyrinoid structures that lead to marked shifts in the UV–vis bands. Our findings offer a strategic framework for designing novel phthalocyanine derivatives, where the fine-tuning of electronic properties through structural modifications can lead to the development of advanced materials and catalysts.

Computational Details

The systems presented in Scheme 1 have been fully optimized and characterized as energy minima in the ground state using harmonic vibrational frequency calculations at the CAM-B3LYP/cc-pVTZ level of theory.110,111 The choice of the functional was based on the comparison between optimized Pc and SubPc using B3LYP, ωB97X, M062X, TPSSH, and LC-ωHPBE together with cc-pVTZ basis set and the X-ray structure (Tables S1–S4). Additionally, we examined the UV–vis spectra using different functionals: B3LYP, CAM-B3LYP, ωB97xD, M062X, and LC-BLYP and optimally tuned LC-BLYP functionals (Tables S5–S7) to assess the performance of each method. We computed in-solution optical spectra of all systems using CAM-B3LYP functional and cc-pVTZ basis set by means of TDDFT considering the first 20 singlet states solvated in THF, DCM, or ethanol, according to the experimental data available. The effect of the implicit solvent has been accounted with the polarizable continuum model (PCM)112 approach. For the calculation of the vertical triplet state, our choice was to employ time dependent and Tamm–Dancoff approximation (TD and TDA)-DFT (CAM-B3LYP/cc-pVTZ) to calculate the two degenerate triplets resulting from having degenerate L/L + 1 orbitals. All calculations have been done with the Gaussian 09 and 16 software packages.114 For the characterization of the aromaticity, we used a variety of measures, including geometrical, electronic, and magnetic indices, to determine local and global aromaticity. The 2- (delocalization indices (DIs)), 3-, and 4-center indices for each set of atoms in the system and the fluctuation index (FLU),113,115 bond order alternation (BOA),63 Iring,116 multicenter index (MCI),117 AV1245,82 and AVmin102 electronic indices were computed using AIMAll118 and ESI-3D113,119,120 (available upon request: ematito@gmail.com) programs. The harmonic oscillator measure of aromaticity (HOMA)121 and the bond length alternation (BLA) were calculated with ESI-3D using molecular geometries as input.64 Electron density of delocalized bond (EDDB)99,100 results were computed using NBO 6.0122 software to first obtain the natural atomic orbitals (NAO) and the 1-electron density matrix used as input for the RunEDDB (v20200925) program (available on www.aromaticity.eu). Finally, the magnetic current density and the current strengths were obtained using Gaussian 09 together with the GIMIC program.123,124 Further explanation regarding the calculation of aromaticity indices can be found, Sections S1 and S4.

Experimental Data

SubPc,125Pz,126 and SubPz(127) were synthesized following reported procedures. Pc was purchased from Aldrich and used without further purification. The UV–vis spectra of these compounds were recorded in THF (concentration = 2 × 10–5 M) employing a JASCO-V660 spectrophotometer. SubPz has to be prepared as β-substituted-SubPz with propyl groups for synthetic reasons.11 However, since there is no conjugation of the ethyl groups with the pyrroles, their influence on the absorption spectrum is expected to be minor (Q-band can be displaced 5–10 nm at most).11 The data for the remaining molecules have been sourced from the literature. The measured absorption spectra of SubP and TBSubP were obtained in DCM using derivatives bearing OMe and OH as axial ligands, respectively, in order to avoid hydrolysis.95,128 It is well-known that neither the shape nor displacement of the spectrum is highly affected by the axial ligand. In the case of P and TBP, presenting very poor solubility, the absorption spectra were obtained in ethanol.129

Acknowledgments

We thank Dr. Irene Casademont Reig and Dr. Eloy Ramos Cordoba for providing the algorithm for the optimization of ω parameter in OT-LC-BLYP and Dr. Pau Besalú Sala for helpful advice. We also thank Dr. Maria Dimitrova for the feedback on some GIMIC computations. S.E. is grateful to Universitat de Girona and DIPC for an IFUdG2019 PhD fellowship. E.M., A.P., and M.S. are grateful for financial support from Agencia Española de Investigación for projects: PID2022-140666NB-C21, PID2021-127423NB-I00, RED2022-134939-T, PID2020-113711GB-I00, and PID2023-147424NB-I00 funded by MCIN/AEI/10.13039/501100011033 and “FEDER Una manera de hacer Europa”. E.M. acknowledges the Gobierno Vasco grant PIBA_2023_1_0055 and IT588-22. A.P. and M.S. also acknowledge Generalitat de Catalunya for Project 2021SGR623 and ICREA Academia prize 2019 to A.P. A.P. is a Serra Húnter fellow. D.W.S. thanks the computer facilities provided by the Polish high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) within computational grant no. PLG/2022/015950. T.T. acknowledges financial support from the Spanish MCIN/AEI/10.13039/501100011033 and European Union NextGenerationEU/ PRTR (PID2020-116490GB-I00, TED2021-131255B-C43), MCIU /AEI /10.13039/501100011033 / FEDER, UE (PID2023-151167NB-I00), the Comunidad de Madrid and the Spanish State through the Recovery, Transformation and Resilience Plan [“Materiales Disruptivos Bidimensionales (2D)” (MAD2D-CM) (UAM1)-MRR Materiales Avanzados], and the European Union through the Next Generation EU funds. IMDEA Nanociencia acknowledges support from the “Severo Ochoa” Programme for Centres of Excellence in R&D (MINECO, Grant SEV2016-0686). T.T. also acknowledges the Alexander von Humboldt Foundation (Germany) for the A. v. Humboldt—J. C. Mutis Research Award 2023 (ref 3.3-1231125—ESP-GSA). J.L. acknowledges MECD, Spain, for an F.P.U. fellowship. Calculations were performed on the computing facilities provided by the IQCC.

Data Availability Statement

The inputs and outputs of the calculations, including Cartesian coordinates (CML), are available in ioChem-BD130 and can be accessed via https://doi.org/10.19061/iochem-bd-4-71.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.4c03139.

  • Detailed computational data including performance assessments of various functionals on geometry optimization, experimental and computational UV–vis absorption spectra, and electron delocalization and aromaticity analyses (PDF)

The authors declare no competing financial interest.

Supplementary Material

ic4c03139_si_001.pdf (10.2MB, pdf)

References

  1. Senge M. O.; Sergeeva N. N.; Hale K. J. Classic highlights in porphyrin and porphyrinoid total synthesis and biosynthesis. Chem. Soc. Rev. 2021, 50 (7), 4730–4789. 10.1039/C7CS00719A. [DOI] [PubMed] [Google Scholar]
  2. Claessens C. G.; Hahn U Fau - Torres U.; Torres T. Phthalocyanines: from outstanding electronic properties to emerging applications. Chem. Rec. 2008, 8 (2), 75–97. 10.1002/tcr.20139. [DOI] [PubMed] [Google Scholar]
  3. Urbani M.; Ragoussi M.-E.; Nazeeruddin M. K.; Torres T. Phthalocyanines for dye-sensitized solar cells. Coord. Chem. Rev. 2019, 381, 1–64. 10.1016/j.ccr.2018.10.007. [DOI] [Google Scholar]
  4. Leznoff C.; Lever A.. Phthalocyanines: properties and Applications; VCH: New York, 1989. [Google Scholar]
  5. Rodríguez-Morgade M. S.; Stuzhin P. A. The chemistry of porphyrazines: an overview. J. Porphyr. Phthalocya 2004, 8 (9), 1129–1165. 10.1142/S1088424604000490. [DOI] [Google Scholar]
  6. Kudrevich S. V.; van Lier J. E. Azaanalogs of phthalocyanine: syntheses and properties. Coord. Chem. Rev. 1996, 156, 163–182. 10.1016/S0010-8545(96)01251-9. [DOI] [Google Scholar]
  7. Finikova O. S.; Cheprakov A. V.; Vinogradov S. A. Synthesis and Luminescence of Soluble meso-Unsubstituted Tetrabenzo- and Tetranaphtho[2,3]porphyrins. J. Org. Chem. 2005, 70 (23), 9562–9572. 10.1021/jo051580r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Shimizu S. Recent Advances in Subporphyrins and Triphyrin Analogues: Contracted Porphyrins Comprising Three Pyrrole Rings. Chem. Rev. 2017, 117 (4), 2730–2784. 10.1021/acs.chemrev.6b00403. [DOI] [PubMed] [Google Scholar]
  9. Claessens C. G.; González-Rodríguez D.; Rodríguez-Morgade M. S.; Medina A.; Torres T. Subphthalocyanines, Subporphyrazines, and Subporphyrins: Singular Nonplanar Aromatic Systems. Chem. Rev. 2014, 114 (4), 2192–2277. 10.1021/cr400088w. [DOI] [PubMed] [Google Scholar]
  10. Labella J.; Torres T. Subphthalocyanines: contracted porphyrinoids with expanded applications. Trends Chem. 2023, 5 (5), 353–366. 10.1016/j.trechm.2023.02.003. [DOI] [Google Scholar]
  11. Lavarda G.; Labella J.; Martínez-Díaz M. V.; Rodríguez-Morgade M. S.; Osuka A.; Torres T. Recent advances in subphthalocyanines and related subporphyrinoids. Chem. Soc. Rev. 2022, 51 (23), 9482–9619. 10.1039/D2CS00280A. [DOI] [PubMed] [Google Scholar]
  12. Smith K. M.Porphyrins Corrins and Phthalocyanines. In Comprehensive Heterocyclic Chemistry, Katritzky A. R.; Rees C. W., Eds.; Pergamon: New York, 1984; pp. 377–442.. [Google Scholar]
  13. Robertson J. M.; Woodward I. 37 An X-ray study of the phthalocyanines. Part III. Quantitative structure determination of nickel phthalocyanine. J. Chem. Soc. 1937, 219–230. 10.1039/jr9370000219. [DOI] [Google Scholar]
  14. Kobayashi N.; Fukuda T.; Ueno K.; Ogino H. Extremely Non-Planar Phthalocyanines with Saddle or Helical Conformation: Synthesis and Structural Characterizations. J. Am. Chem. Soc. 2001, 123 (43), 10740–10741. 10.1021/ja0113753. [DOI] [PubMed] [Google Scholar]
  15. Kondou K.; Shiga M.; Sakamoto S.; Inuzuka H.; Nihonyanagi A.; Araoka F.; Kobayashi M.; Miwa S.; Miyajima D.; Otani Y. Chirality-Induced Magnetoresistance Due to Thermally Driven Spin Polarization. J. Am. Chem. Soc. 2022, 144 (16), 7302–7307. 10.1021/jacs.2c00496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Torres T. From Subphthalocyanines to Subporphyrins. Angew. Chem., Int. Ed. 2006, 45 (18), 2834–2837. 10.1002/anie.200504265. [DOI] [PubMed] [Google Scholar]
  17. Gouterman M. Spectra of porphyrins. J. Mol. Spectrosc. 1961, 6, 138–163. 10.1016/0022-2852(61)90236-3. [DOI] [Google Scholar]
  18. Gouterman M. Study of the Effects of Substitution on the Absorption Spectra of Porphin. J. Chem. Phys. 1959, 30 (5), 1139–1161. 10.1063/1.1730148. [DOI] [Google Scholar]
  19. Gouterman M.; Wagnière G. H.; Snyder L. C. Spectra of porphyrins: Part II. Four orbital model. J. Mol. Spectrosc. 1963, 11 (1), 108–127. 10.1016/0022-2852(63)90011-0. [DOI] [Google Scholar]
  20. Simpson M. C.; Novikova N. I.. Porphyrins: Electronic Structure and Ultraviolet/Visible Absorption Spectroscopy. In Fundamentals of Porphyrin Chemistry, Brothers P. J.; Senge M. O., Eds.; Wiley: Hoboken, 2022; pp. 505-586. [Google Scholar]
  21. Valicsek Z.; Horváth O. Application of the electronic spectra of porphyrins for analytical purposes: The effects of metal ions and structural distortions. Microchem. J. 2013, 107, 47–62. 10.1016/j.microc.2012.07.002. [DOI] [Google Scholar]
  22. Zhu H.; Chen Q.; Rončević I.; Christensen K. E.; Anderson H. L. Anthracene-Porphyrin Nanoribbons. Angew. Chem., Int. Ed. 2023, 62 (31), e202307035 10.1002/anie.202307035. [DOI] [PubMed] [Google Scholar]
  23. Zhang A.; Kwan L.; Stillman M. J. The spectroscopic impact of interactions with the four Gouterman orbitals from peripheral decoration of porphyrins with simple electron withdrawing and donating groups. Org. Biomol. Chem. 2017, 15 (43), 9081–9094. 10.1039/C7OB01960B. [DOI] [PubMed] [Google Scholar]
  24. Mack J.; Asano Y.; Kobayashi N.; Stillman M. J. Application of MCD Spectroscopy and TD–DFT to a Highly Non-Planar Porphyrinoid Ring System. New Insights on Red–Shifted Porphyrinoid Spectral Bands. J. Am. Chem. Soc. 2005, 127 (50), 17697–17711. 10.1021/ja0540728. [DOI] [PubMed] [Google Scholar]
  25. Mack J.; Stillman M. J. Assignment of the optical spectra of metal phthalocyanines through spectral band deconvolution analysis and ZINDO calculations. Coord. Chem. Rev. 2001, 219–221, 993–1032. 10.1016/S0010-8545(01)00394-0. [DOI] [Google Scholar]
  26. Breslow R.; Foss Jr F. W. Charge transport in nanoscale aromatic and antiaromatic systems. J. Phys.: Condens. Matter 2008, 20 (37), 374104. 10.1088/0953-8984/20/37/374104. [DOI] [Google Scholar]
  27. Molina D.; Follana-Berná J.; Sastre-Santos Á. Phthalocyanines, porphyrins and other porphyrinoids as components of perovskite solar cells. J. Mater. Chem. C 2023, 11 (24), 7885–7919. 10.1039/D2TC04441B. [DOI] [Google Scholar]
  28. Martín-Gomis L.; Fernández-Lázaro F.; Sastre-Santos Á. Advances in phthalocyanine-sensitized solar cells (PcSSCs). J. Mater. Chem. A 2014, 2 (38), 15672–15682. 10.1039/C4TA01894J. [DOI] [Google Scholar]
  29. Ikeuchi T.; Nomoto H.; Masaki N.; Griffith M. J.; Mori S.; Kimura M. Molecular engineering of zinc phthalocyanine sensitizers for efficient dye-sensitized solar cells. Chem. Commun. 2014, 50 (16), 1941–1943. 10.1039/c3cc47714b. [DOI] [PubMed] [Google Scholar]
  30. Urbani M.; de la Torre G.; Nazeeruddin M. K.; Torres T. Phthalocyanines and porphyrinoid analogues as hole- and electron-transporting materials for perovskite solar cells. Chem. Soc. Rev. 2019, 48 (10), 2738–2766. 10.1039/C9CS00059C. [DOI] [PubMed] [Google Scholar]
  31. Yahya M.; Nural Y.; Seferoğlu Z. Recent advances in the nonlinear optical (NLO) properties of phthalocyanines: A review. Dyes Pigm. 2022, 198, 109960. 10.1016/j.dyepig.2021.109960. [DOI] [Google Scholar]
  32. Cranston R. R.; King B.; Dindault C.; Grant T. M.; Rice N. A.; Tonnelé C.; Muccioli L.; Castet F.; Swaraj S.; Lessard B. H. Highlighting the processing versatility of a silicon phthalocyanine derivative for organic thin-film transistors. J. Mater. Chem. C 2022, 10 (2), 485–495. 10.1039/D1TC05238A. [DOI] [Google Scholar]
  33. Martínez-Díaz M. V.; de la Torre G.; Torres T. Lighting porphyrins and phthalocyanines for molecular photovoltaics. Chem. Commun. 2010, 46 (38), 7090–7108. 10.1039/c0cc02213f. [DOI] [PubMed] [Google Scholar]
  34. Adachi C. Third-generation organic electroluminescence materials. Jpn. J. Appl. Phys. 2014, 53 (6), 060101. 10.7567/JJAP.53.060101. [DOI] [Google Scholar]
  35. See section 2.6 of ref (11):; Lavarda G.; Labella J.; Martínez-Díaz M. V.; Rodríguez-Morgade M. S.; Osuka A.; Torres T. Recent advances in subphthalocyanines and related subporphyrinoids. Chem. Soc. Rev. 2022, 51 (23), 9482. 10.1039/D2CS00280A. [DOI] [PubMed] [Google Scholar]; and references therein.
  36. Bharmoria P.; Bildirir H.; Moth-Poulsen K. Triplet–triplet annihilation based near infrared to visible molecular photon upconversion. Chem. Soc. Rev. 2020, 49 (18), 6529–6554. 10.1039/D0CS00257G. [DOI] [PubMed] [Google Scholar]
  37. Radiunas E.; Raišys S.; Juršėnas S.; Jozeliu̅naitė A.; Javorskis T.; Šinkevičiu̅tė U.; Orentas E.; Kazlauskas K. Understanding the limitations of NIR-to-visible photon upconversion in phthalocyanine-sensitized rubrene systems. J. Mater. Chem. C 2020, 8 (16), 5525–5534. 10.1039/C9TC06031F. [DOI] [Google Scholar]
  38. Naimovičius L.; Bharmoria P.; Moth-Poulsen K. Triplet–triplet annihilation mediated photon upconversion solar energy systems. Mater. Chem. Front. 2023, 7 (12), 2297–2315. 10.1039/D3QM00069A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Can Karanlık C.; Aguilar-Galindo F.; Sobotta L.; Güzel E.; Erdoğmuş A. Combination of Light and Ultrasound: Exploring Sono–Photochemical Activities of Phthalocyanine-Based Sensitizers. J. Phys. Chem. C 2023, 127 (19), 9145–9153. 10.1021/acs.jpcc.3c01176. [DOI] [Google Scholar]
  40. Guzmán D.; Papadopoulos I.; Lavarda G.; Rami P. R.; Tykwinski R. R.; Rodríguez-Morgade M. S.; Guldi D. M.; Torres T. Controlling Intramolecular Förster Resonance Energy Transfer and Singlet Fission in a Subporphyrazine–Pentacene Conjugate by Solvent Polarity. Angew. Chem., Int. Ed. 2021, 60 (3), 1474–1481. 10.1002/anie.202011197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Gotfredsen H.; Thiel D.; Greißel P. M.; Chen L.; Krug M.; Papadopoulos I.; Ferguson M. J.; Nielsen M. B.; Torres T.; Clark T.; et al. Sensitized Singlet Fission in Rigidly Linked Axial and Peripheral Pentacene-Subphthalocyanine Conjugates. J. Am. Chem. Soc. 2023, 145 (17), 9548–9563. 10.1021/jacs.2c13353. [DOI] [PubMed] [Google Scholar]
  42. Lavarda G.; Zirzlmeier J.; Gruber M.; Rami P. R.; Tykwinski R. R.; Torres T.; Guldi D. M. Tuning Intramolecular Förster Resonance Energy Transfer and Activating Intramolecular Singlet Fission. Angew. Chem., Int. Ed. 2018, 57 (50), 16291–16295. 10.1002/anie.201808652. [DOI] [PubMed] [Google Scholar]
  43. Belosludov R. V.; Nevonen D.; Rhoda H. M.; Sabin J. R.; Nemykin V. N. Simultaneous Prediction of the Energies of Qx and Qy Bands and Intramolecular Charge-Transfer Transitions in Benzoannulated and Non-Peripherally Substituted Metal-Free Phthalocyanines and Their Analogues: No Standard TDDFT Silver Bullet Yet. J. Phys. Chem. A 2019, 123 (1), 132–152. 10.1021/acs.jpca.8b07647. [DOI] [PubMed] [Google Scholar]
  44. Holst D. P.; Friederich P.; Aspuru-Guzik A.; Bender T. P. Updated Calibrated Model for the Prediction of Molecular Frontier Orbital Energies and Its Application to Boron Subphthalocyanines. J. Chem. Inf. Model. 2022, 62 (4), 829–840. 10.1021/acs.jcim.1c01048. [DOI] [PubMed] [Google Scholar]
  45. Peterson E. J.; Rawson J.; Beratan D. N.; Zhang P.; Therien M. J. Regulating Singlet–Triplet Energy Gaps through Substituent-Driven Modulation of the Exchange and Coulomb Interactions. J. Am. Chem. Soc. 2022, 144 (34), 15457–15461. 10.1021/jacs.2c06713. [DOI] [PubMed] [Google Scholar]
  46. Bortolussi S. D. S.; Zhou C.; Lynch N. B.; Peeks M. D. Spectroscopic Manifestations of (Anti)Aromaticity in Oxidized and Reduced Porphyrin and Norcorrole. Chem.—Eur. J. 2024, 30 (46), e202401741 10.1002/chem.202401741. [DOI] [PubMed] [Google Scholar]
  47. Woller T.; Geerlings P.; De Proft F.; Champagne B.; Alonso M. Aromaticity as a Guiding Concept for Spectroscopic Features and Nonlinear Optical Properties of Porphyrinoids. Molecules 2018, 23 (6), 1333. 10.3390/molecules23061333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Woller T.; Geerlings P.; De Proft F.; Champagne B.; Alonso M. Fingerprint of Aromaticity and Molecular Topology on the Photophysical Properties of Octaphyrins. J. Phys. Chem. C 2019, 123 (12), 7318–7335. 10.1021/acs.jpcc.8b10908. [DOI] [Google Scholar]
  49. Torrent-Sucarrat M.; Anglada J. M.; Luis J. M. Evaluation of the nonlinear optical properties for an expanded porphyrin Hückel-Möbius aromaticity switch. J. Chem. Phys. 2012, 137 (18), 184306. 10.1063/1.4765667. [DOI] [PubMed] [Google Scholar]
  50. Torrent-Sucarrat M.; Navarro S.; Marcos E.; Anglada J. M.; Luis J. M. Design of Hückel–Möbius Topological Switches with High Nonlinear Optical Properties. J. Phys. Chem. C 2017, 121 (35), 19348–19357. 10.1021/acs.jpcc.7b05900. [DOI] [Google Scholar]
  51. Casademont-Reig I.; Woller T.; García V.; Contreras-García J.; Tiznado W.; Torrent-Sucarrat M.; Matito E.; Alonso M. Quest for the Most Aromatic Pathway in Charged Expanded Porphyrins. Chem.—Eur. J. 2023, 29 (6), e202202264 10.1002/chem.202202264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Ko M.-S.; Roh T.-H.; Desale P. P.; Choi S.-W.; Cho D.-G. Effects of Electron-Withdrawing and Electron-Donating Groups on Aromaticity in Cyclic Conjugated Polyenes. J. Am. Chem. Soc. 2024, 146 (9), 6266–6273. 10.1021/jacs.3c14390. [DOI] [PubMed] [Google Scholar]
  53. Desmedt E.; Casademont-Reig I.; Monreal-Corona R.; De Vleeschouwer F.; Alonso M. Aromaticity in the Spectroscopic Spotlight of Hexaphyrins. Chem.—Eur. J. 2024, e202401933 10.1002/chem.202401933. [DOI] [PubMed] [Google Scholar]
  54. Ke M.-R.; Chen Z.; Shi J.; Wei Y.; Liu H.; Huang S.; Li X.; Zheng B.-Y.; Huang J.-D. A smart and visible way to switch aromaticity of silicon(IV) phthalocyanines. Chem. Commun. 2023, 59, 9832–9835. 10.1039/D3CC02910G. [DOI] [PubMed] [Google Scholar]
  55. von Schleyer P. R.; Jiao H. What is aromaticity?. Pure Appl. Chem. 1996, 68 (2), 209–218. 10.1351/pac199668020209. [DOI] [Google Scholar]
  56. Solà M. Why Aromaticity Is a Suspicious Concept? Why?. Front. Chem. 2017, 5, 22. 10.3389/fchem.2017.00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Feixas F.; Matito E.; Poater J.; Solà M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015, 44 (18), 6434–6451. 10.1039/C5CS00066A. [DOI] [PubMed] [Google Scholar]
  58. Hoffmann R. The many guises of aromaticity. Am. Sci. 2015, 103 (1), 18. 10.1511/2015.112.18. [DOI] [Google Scholar]
  59. Stanger A. What is··· aromaticity: a critique of the concept of aromaticity—can it really be defined?. Chem. Commun. 2009, 15, 1939–1947. 10.1039/b816811c. [DOI] [PubMed] [Google Scholar]
  60. Hückel E. Quantentheoretische Beiträge zum Benzolproblem. Z. Phys. 1931, 70 (3), 204–286. 10.1007/BF01339530. [DOI] [Google Scholar]
  61. Hückel E. Quanstentheoretische Beiträge zum Benzolproblem. Z. Phys. 1931, 72 (5), 310–337. 10.1007/BF01341953. [DOI] [Google Scholar]
  62. Hückel E. Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. III. Z. Phys. 1932, 76 (9), 628–648. 10.1007/BF01341936. [DOI] [Google Scholar]
  63. Casademont-Reig I.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E. How do the Hückel and Baird Rules Fade away in Annulenes?. Molecules 2020, 25 (3), 711. 10.3390/molecules25030711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Jirásek M.; Rickhaus M.; Tejerina L.; Anderson H. L. Experimental and Theoretical Evidence for Aromatic Stabilization Energy in Large Macrocycles. J. Am. Chem. Soc. 2021, 143 (5), 2403–2412. 10.1021/jacs.0c12845. [DOI] [PubMed] [Google Scholar]
  65. Feixas F.; Matito E.; Solà M.; Poater J. Patterns of π-electron delocalization in aromatic and antiaromatic organic compounds in the light of Hückel’s 4n + 2 rule. Phys. Chem. Chem. Phys. 2010, 12 (26), 7126–7137. 10.1039/b924972a. [DOI] [PubMed] [Google Scholar]
  66. Solà M. Aromaticity rules. Nat. Chem. 2022, 14 (6), 585–590. 10.1038/s41557-022-00961-w. [DOI] [PubMed] [Google Scholar]
  67. Feixas F.; Matito E.; Poater J.; Solà M.. Rules of Aromaticity. In Applications of Topological Methods in Molecular Chemistry, Chauvin R.; Lepetit C.; Silvi B.; Alikhani E., Eds.; Springer International Publishing: Cham, 2016; pp. 321–335.. [Google Scholar]
  68. Escayola S.; Poater A.; Muñoz-Castro A.; Solà M. An unprecedented π-electronic circuit involving an odd number of carbon atoms in a grossly warped non-planar nanographene. Chem. Commun. 2021, 57 (25), 3087–3090. 10.1039/D1CC00593F. [DOI] [PubMed] [Google Scholar]
  69. Sondheimer F.; Wolovsky R.; Amiel Y. Unsaturated Macrocyclic Compounds. XXIII.1 The Synthesis of the Fully Conjugated Macrocyclic Polyenes Cycloöctadecanonaene ([18]Annulene),2 Cyclotetracosadodecaene ([24]Annulene), and Cyclotriacontapentadecaene ([30]Annulene). J. Am. Chem. Soc. 1962, 84 (2), 274–284. 10.1021/ja00861a030. [DOI] [Google Scholar]
  70. Vogel E. The porphyrins from the ’annulene chemist’s’ perspective. Pure Appl. Chem. 1993, 65 (1), 143–152. 10.1351/pac199365010143. [DOI] [Google Scholar]
  71. Casademont-Reig I.; Woller T.; Contreras-García J.; Alonso M.; Torrent-Sucarrat M.; Matito E. New electron delocalization tools to describe the aromaticity in porphyrinoids. Phys. Chem. Chem. Phys. 2018, 20 (4), 2787–2796. 10.1039/C7CP07581B. [DOI] [PubMed] [Google Scholar]
  72. Casademont-Reig I.; Guerrero-Avilés R.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E. How Aromatic Are Molecular Nanorings? The Case of a Six-Porphyrin Nanoring. Angew. Chem., Int. Ed. 2021, 133 (45), 24282–24290. 10.1002/ange.202108997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Casademont-Reig I.; Soriano-Agueda L.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E. Reply to the Correspondence on “How Aromatic Are Molecular Nanorings? The Case of a Six-Porphyrin Nanoring. Angew. Chem., Int. Ed. 2022, 61 (36), e202206836 10.1002/anie.202206836. [DOI] [PubMed] [Google Scholar]
  74. Kolomeychuk F. M.; Safonova E. A.; Polovkova M. A.; Sinelshchikova A. A.; Martynov A. G.; Shokurov A. V.; Kirakosyan G. A.; Efimov N. N.; Tsivadze A. Y.; Gorbunova Y. G. Switchable Aromaticity of Phthalocyanine via Reversible Nucleophilic Aromatic Addition to an Electron-Deficient Phosphorus(V) Complex. J. Am. Chem. Soc. 2021, 143 (35), 14053–14058. 10.1021/jacs.1c05831. [DOI] [PubMed] [Google Scholar]
  75. Yang Y. Hexacoordinate Bonding and Aromaticity in Silicon Phthalocyanine. J. Phys. Chem. A 2010, 114 (50), 13257–13267. 10.1021/jp109278v. [DOI] [PubMed] [Google Scholar]
  76. Yang Y. A theoretical study of experimentally unknown metallosubphthalocyanines. Chem. Phys. Lett. 2011, 511 (1), 51–56. 10.1016/j.cplett.2011.06.003. [DOI] [Google Scholar]
  77. Bartkowski K.; Pawlicki M. (Aza)Acenes Share the C2 Bridge with (Anti)Aromatic Macrocycles: Local vs. Global Delocalization Paths. Angew. Chem., Int. Ed. 2021, 60 (16), 9063–9070. 10.1002/anie.202011848. [DOI] [PubMed] [Google Scholar]
  78. Yanagi S.; Takayama O.; Toriumi N.; Muranaka A.; Hashizume D.; Uchiyama M. 20π-Electron Antiaromatic Benziphthalocyanines with Absorption Reaching the Near-Infrared-II Region. Chem.—Eur. J. 2024, 30 (29), e202400401 10.1002/chem.202400401. [DOI] [PubMed] [Google Scholar]
  79. Feixas F.; Matito E.; Poater J.; Solà M. On the performance of some aromaticity indices: a critical assessment using a test set. J. Comput. Chem. 2008, 29 (10), 1543–1554. 10.1002/jcc.20914. [DOI] [PubMed] [Google Scholar]
  80. Feixas F.; Jiménez-Halla J. O. C.; Matito E.; Poater J.; Solà M. A Test to Evaluate the Performance of Aromaticity Descriptors in All-Metal and Semimetal Clusters. An Appraisal of Electronic and Magnetic Indicators of Aromaticity. J. Chem. Theory Comput. 2010, 6 (4), 1118–1130. 10.1021/ct100034p. [DOI] [Google Scholar]
  81. Pelloni S.; Monaco G.; Lazzeretti P.; Zanasi R. Beyond NICS: estimation of the magnetotropicity of inorganic unsaturated planar rings. Phys. Chem. Chem. Phys. 2011, 13 (46), 20666–20672. 10.1039/c1cp21952a. [DOI] [PubMed] [Google Scholar]
  82. Matito E. An electronic aromaticity index for large rings. Phys. Chem. Chem. Phys. 2016, 18 (17), 11839–11846. 10.1039/C6CP00636A. [DOI] [PubMed] [Google Scholar]
  83. Casademont-Reig I.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E.. 7 - Aromaticity descriptors based on electron delocalization. Aromaticity, Fernández, I; Elsevier: Dordretch, 2021; pp. 235–259.. [Google Scholar]
  84. Zhou Z.; Parr R. G. New measures of aromaticity: absolute hardness and relative hardness. J. Am. Chem. Soc. 1989, 111 (19), 7371–7379. 10.1021/ja00201a014. [DOI] [Google Scholar]
  85. De Proft F.; Geerlings P. Relative hardness as a measure of aromaticity. Phys. Chem. Chem. Phys. 2004, 6 (2), 242–248. 10.1039/B312566C. [DOI] [Google Scholar]
  86. Kwak H. S.; David J. G.; Thomas F. H.; Alexander G.; Yixiang C.; Jacob G.; Steve D.; Mathew D. H. In silico evaluation of highly efficient organic light-emitting materials. SPIE Proc. 2016, 9941, 994119. 10.1117/12.2237951. [DOI] [Google Scholar]
  87. Abrahamse H.; Hamblin M. R. New photosensitizers for photodynamic therapy. Biochem. J. 2016, 473 (4), 347–364. 10.1042/bj20150942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  88. Huis in ‘t Veld R. V.; Heuts J.; Ma S.; Cruz L. J.; Ossendorp F. A.; Jager M. J. Current Challenges and Opportunities of Photodynamic Therapy against Cancer. Pharmaceutics 2023, 15 (2), 330. 10.3390/pharmaceutics15020330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. Sorgues S.; Poisson L.; Raffael K.; Krim L.; Soep B.; Shafizadeh N. Femtosecond electronic relaxation of excited metalloporphyrins in the gas phase. J. Chem. Phys. 2006, 124 (11), 114302. 10.1063/1.2176612. [DOI] [PubMed] [Google Scholar]
  90. Bhowmick R.; Roy Chowdhury S.; Vlaisavljevich B. Molecular Geometry and Electronic Structure of Copper Corroles. Inorg. Chem. 2023, 62 (34), 13877–13891. 10.1021/acs.inorgchem.3c01779. [DOI] [PubMed] [Google Scholar]
  91. Darzi E. R.; Jasti R. The dynamic, size-dependent properties of [5]–[12]cycloparaphenylenes. Chem. Soc. Rev 2015, 44 (18), 6401–6410. 10.1039/C5CS00143A. [DOI] [PubMed] [Google Scholar]
  92. Martynov A. G.; Mack J.; May A. K.; Nyokong T.; Gorbunova Y. G.; Tsivadze A. Y. Methodological Survey of Simplified TD-DFT Methods for Fast and Accurate Interpretation of UV–Vis–NIR Spectra of Phthalocyanines. ACS Omega 2019, 4 (4), 7265–7284. 10.1021/acsomega.8b03500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  93. Mack J.; Bunya M.; Shimizu Y.; Uoyama H.; Komobuchi N.; Okujima T.; Uno H.; Ito S.; Stillman M. J.; Ono N.; et al. Application of MCD Spectroscopy and TD-DFT to Nonplanar Core-Modified Tetrabenzoporphyrins: Effect of Reduced Symmetry on Nonplanar Porphyrinoids. Chem.—Eur. J. 2008, 14 (16), 5001–5020. 10.1002/chem.200701611. [DOI] [PubMed] [Google Scholar]
  94. Nemykin V. N.; Hadt R. G.; Belosludov R. V.; Mizuseki H.; Kawazoe Y. Influence of Molecular Geometry, Exchange-Correlation Functional, and Solvent Effects in the Modeling of Vertical Excitation Energies in Phthalocyanines Using Time-Dependent Density Functional Theory (TDDFT) and Polarized Continuum Model TDDFT Methods: Can Modern Computational Chemistry Methods Explain Experimental Controversies?. J. Phys. Chem. A 2007, 111 (50), 12901–12913. 10.1021/jp0759731. [DOI] [PubMed] [Google Scholar]
  95. Kise K.; Yoshida K.; Kotani R.; Shimizu D.; Osuka A. BIII 5-Arylsubporphyrins and BIII Subporphine. Chem.—Eur. J. 2018, 24 (72), 19136–19140. 10.1002/chem.201801491. [DOI] [PubMed] [Google Scholar]
  96. Cyrański M. K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105 (10), 3773–3811. 10.1021/cr0300845. [DOI] [PubMed] [Google Scholar]
  97. Pino-Rios R.; Cárdenas-Jirón G.; Tiznado W. Local and macrocyclic (anti)aromaticity of porphyrinoids revealed by the topology of the induced magnetic field. Phys. Chem. Chem. Phys. 2020, 22 (37), 21267–21274. 10.1039/D0CP03272G. [DOI] [PubMed] [Google Scholar]
  98. Kupka T.; Broda M. Aromaticity and planarity of zinc phthalocyanine (ZnPc) characterized by splitting of NICS (1) index. Turk. Comput. Theor. Chem. 2018, 2 (1), 23–30. [Google Scholar]
  99. Szczepanik D. W.; Andrzejak M.; Dominikowska J.; Pawełek B.; Krygowski T. M.; Szatylowicz H.; Solà M. The electron density of delocalized bonds (EDDB) applied for quantifying aromaticity. Phys. Chem. Chem. Phys. 2017, 19 (42), 28970–28981. 10.1039/C7CP06114E. [DOI] [PubMed] [Google Scholar]
  100. Szczepanik D. W.; Andrzejak M.; Dyduch K.; Żak E.; Makowski M.; Mazur G.; Mrozek J. A uniform approach to the description of multicenter bonding. Phys. Chem. Chem. Phys. 2014, 16 (38), 20514–20523. 10.1039/C4CP02932A. [DOI] [PubMed] [Google Scholar]
  101. Orozco-Ic M.; Soriano-Agueda L.; Escayola S.; Sundholm D.; Merino G.; Matito E. Understanding Aromaticity in [5]Helicene-Bridged Cyclophanes: A Comprehensive Study. J. Org. Chem. 2024, 89, 2459–2466. 10.1021/acs.joc.3c02485. [DOI] [PubMed] [Google Scholar]
  102. García-Fernández C.; Sierda E.; Abadía M.; Bugenhagen B.; Prosenc M. H.; Wiesendanger R.; Bazarnik M.; Ortega J. E.; Brede J.; Matito E.; et al. Exploring the Relation Between Intramolecular Conjugation and Band Dispersion in One-Dimensional Polymers. J. Phys. Chem. C 2017, 121 (48), 27118–27125. 10.1021/acs.jpcc.7b08668. [DOI] [Google Scholar]
  103. Zhao L.; Grande-Aztatzi R.; Foroutan-Nejad C.; Ugalde J. M.; Frenking G. Aromaticity the Hückel 4n+2 Rule and Magnetic Current. ChemistrySelect 2017, 2 (3), 863–870. 10.1002/slct.201602080. [DOI] [Google Scholar]
  104. Poater J.; Escayola S.; Poater A.; Teixidor F.; Ottosson H.; Viñas C.; Solà M. Single–Not Double–3D-Aromaticity in an Oxidized Closo Icosahedral Dodecaiodo-Dodecaborate Cluster. J. Am. Chem. Soc. 2023, 145 (41), 22527–22538. 10.1021/jacs.3c07335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  105. Ottosson H. A focus on aromaticity: fuzzier than ever before?. Chem. Sci. 2023, 14 (21), 5542–5544. 10.1039/D3SC90075D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  106. Islas R.; Martínez-Guajardo G.; Jiménez-Halla J. O. C.; Solà M.; Merino G. Not All That Has a Negative NICS Is Aromatic: The Case of the H-Bonded Cyclic Trimer of HF. J. Chem. Theory Comput. 2010, 6 (4), 1131–1135. 10.1021/ct100098c. [DOI] [Google Scholar]
  107. Foroutan-Nejad C. Magnetic Antiaromaticity–Paratropicity–Does Not Necessarily Imply Instability. J. Org. Chem. 2023, 88 (20), 14831–14835. 10.1021/acs.joc.3c01807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  108. Janda T.; Foroutan-Nejad C. Why is Benzene Unique? Screening Magnetic Properties of C6H6 Isomers. ChemPhyschem 2018, 19 (18), 2357–2363. 10.1002/cphc.201800364. [DOI] [PubMed] [Google Scholar]
  109. Foroutan-Nejad C. Interatomic Magnetizability: A QTAIM-Based Approach toward Deciphering Magnetic Aromaticity. J. Phys. Chem. A 2011, 115 (45), 12555–12560. 10.1021/jp202901f. [DOI] [PubMed] [Google Scholar]
  110. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393 (1), 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  111. Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90 (2), 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  112. Tomasi J.; Mennucci B.; Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105 (8), 2999–3094. 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  113. Matito E.; Duran M.; Solà M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem. Phys. 2005, 122 (1), 014109. 10.1063/1.1824895. [DOI] [PubMed] [Google Scholar]
  114. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H., et al. Gaussian 16, Revision C.01; Gaussian Inc: Wallingford, CT, 2016.
  115. Matito E.; Duran M.; Solà M. Erratum The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization” [J. Chem Phys. 122, 014109 (2005)]. J. Chem. Phys. 2006, 125 (5), 059901. 10.1063/1.2222352. [DOI] [PubMed] [Google Scholar]
  116. Giambiagi M.; de Giambiagi M. S.; dos Santos Silva C. D.; de Figueiredo A. P. Multicenter bond indices as a measure of aromaticity. Phys. Chem. Chem. Phys. 2000, 2 (15), 3381–3392. 10.1039/B002009P. [DOI] [Google Scholar]
  117. Bultinck P.; Ponec R.; Van Damme S. Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons. J. Phys. Org. Chem. 2005, 18 (8), 706–718. 10.1002/poc.922. [DOI] [Google Scholar]
  118. AIMAll (Version 19.10.12); TK Gristmill Software: Overland Park KS, USA, 2019. [Google Scholar]
  119. ESI-3D: Electron Sharing Indexes Program for 3D Molecular Space Partitioning; by Eduard Matito. Institute of Computational Chemistry and Catalysis; (IQCC), Girona, and Donostia International Physics Center (DIPC), Donostia, 2024. [Google Scholar]
  120. Matito E.; Solà M.; Salvador P.; Duran M. Electron sharing indexes at the correlated level. Application to aromaticity calculations. Faraday Discuss 2007, 135, 325–345. 10.1039/B605086G. [DOI] [PubMed] [Google Scholar]
  121. Kruszewski J.; Krygowski T. M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. 10.1016/S0040-4039(01)94175-9. [DOI] [Google Scholar]
  122. Glendening E. D.; Landis C. R.; Weinhold F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34 (16), 1429–1437. 10.1002/jcc.23266. [DOI] [PubMed] [Google Scholar]
  123. Fliegl H.; Taubert S.; Lehtonen O.; Sundholm D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 2011, 13 (46), 20500–20518. 10.1039/c1cp21812c. [DOI] [PubMed] [Google Scholar]
  124. Sundholm D.; Fliegl H.; Berger R. J. F. Calculations of magnetically induced current densities: theory and applications. WIREs Comput. Mol. Sci. 2016, 6 (6), 639–678. 10.1002/wcms.1270. [DOI] [Google Scholar]
  125. Claessens C. G.; González-Rodríguez D.; McCallum C. M.; Nohr R. S.; Schuchmann H.-P.; Torres T. On the mechanism of boron-subphthalocyanine chloride formation. J. Porphyrins Phthalocyanines 2007, 11 (3), 181–188. 10.1142/S1088424607000230. [DOI] [Google Scholar]
  126. Khelevina O.; Stuzhin P.; Berezin B. Influence of the Nature of Protonodonor Solvent on Solvoprotolytic Dissociation of the Zinc-Tetraazaporphine Complex. Koord. Khim. 1988, 14 (9), 1199–1203. [Google Scholar]
  127. Rodríguez-Morgade M. S.; Claessens C. G.; Medina A.; González-Rodríguez D.; Gutiérrez-Puebla E.; Monge A.; Alkorta I.; Elguero J.; Torres T. Synthesis, Characterization, Molecular Structure and Theoretical Studies of Axially Fluoro-Substituted Subazaporphyrins. Chem.—Eur. J. 2008, 14 (4), 1342–1350. 10.1002/chem.200701542. [DOI] [PubMed] [Google Scholar]
  128. Inokuma Y.; Kwon J. H.; Ahn T. K.; Yoo M.-C.; Kim D.; Osuka A. Tribenzosubporphines: Synthesis and Characterization. Angew. Chem., Int. Ed. 2006, 45 (6), 961–964. 10.1002/anie.200503426. [DOI] [PubMed] [Google Scholar]
  129. Liu X.; Yeow E. K. L.; Velate S.; Steer R. P. Photophysics and spectroscopy of the higher electronic states of zinc metalloporphyrins: a theoretical and experimental study. Phys. Chem. Chem. Phys. 2006, 8 (11), 1298–1309. 10.1039/b516042a. [DOI] [PubMed] [Google Scholar]
  130. Álvarez-Moreno M.; de Graaf C.; López N.; Maseras F.; Poblet J. M.; Bo C. Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform. J. Chem. Inf. Model. 2015, 55 (1), 95–103. 10.1021/ci500593j. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic4c03139_si_001.pdf (10.2MB, pdf)

Data Availability Statement

The inputs and outputs of the calculations, including Cartesian coordinates (CML), are available in ioChem-BD130 and can be accessed via https://doi.org/10.19061/iochem-bd-4-71.

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES