Crystallization by Amorphous Particle Attachment: On the Evolution of Texture

Abstract

Crystallization by particle attachment (CPA) is a gradual process where each step has its own thermodynamic and kinetic constrains defining a unique pathway of crystal growth. An important example is biomineralization of calcium carbonate through amorphous precursors that are morphed into shapes and textural patterns that cannot be envisioned by the classical monomer‐by‐monomer approach. Here, a mechanistic link between the collective kinetics of mineral deposition and the emergence of crystallographic texture is established. Using the prismatic ultrastructure in bivalve shells as a model, a fundamental leap is made in the ability to analytically describe the evolution of form and texture of biological mineralized tissues and to design the structure and crystallographic properties of synthetic materials formed by CPA.

Biogenic minerals are shown not only to provide key insight into material morphogenesis during crystallization by amorphous particle attachment but also to teach us fundamental new mechanisms that have a profound effect on textural evolution during non‐classical crystal growth. A link between the emergence of texture and amorphous particle accretion rate is established.

1. Introduction

Since the early 17th century, the human interest in geometric forms of crystals grew into one of the most impactful scientific domains aiming at understanding how crystals nucleate, grow and assemble into larger structures.^{[ 1} , ^{2 ]} From Kepler's interest in the symmetry of snowflakes in 1611 followed by Steno's fascination with rock‐crystals in 1669 and up until now, crystallization has been recognized as one of the most important physicochemical processes and crystal structure has been shown to define the physical properties of condensed matter.^{[ 3 ]} Classically, the origins of crystal habits and properties were understood based on the assumption that they grow by the addition of single lattice entities, monomer by monomer.^{[ 2} , ³ , ⁴ , ^{5 ]} Whereas this postulation is at the core of our interpretation of atomistic processes during crystal growth and numerous technological applications, its totality was significantly challenged in the course of the last two decades.^{[ 6 ]} Namely, abundant evidence from synthetic, geological and biological systems suggests that crystallization can proceed with the attachment of a wide range of higher order entities—particles.^{[ 7 ]} These include clustered ionic or molecular species, liquid droplets, and crystalline and amorphous particles.

Crystallization by particle attachment (CPA), a so called non‐classical crystallization mechanism, is known to form morphological and textural patterns that cannot be explained in the scope of classical nucleation and growth models.^{[ 8 ]} This is not surprising as CPA is a multi‐step process where every step has its own intricate interplay between thermodynamic and kinetic constrains defining a very unique crystal growth pathway. As an example, crystallization by amorphous particle attachment involves the formation and stabilization of amorphous particles, their accretion and, finally, transformation into the crystalline phase.^{[ 9} , ¹⁰ , ^{11 ]} Each step can be affected by a multitude of physicochemical factors. Recently, significant efforts have been directed into studying and modeling the different CPA pathways.^{[ 12} , ¹³ , ^{14 ]} A mechanistic understanding of each step has the potential to generate a comprehensive toolkit for the design and synthesis of novel materials systems liberated from the limitations of classical crystallization models. However, many knowledge gaps still remain.

Biogenic mineralized tissues are postulated to form by crystallization of amorphous precursors throughout the documented history of Animalia.^{[ 15 ]} These biological materials exhibit a variety of hierarchically structured mineral‐organic architectures that provide various functions to the organisms.^{[ 16 ]} Crystallization by amorphous particle attachment was selected through evolution to form unique structural motifs and distinctive textural patterns. Here, the individual mineral building blocks are morphed into shapes that cannot be explained by the classical monomer‐by‐monomer approach.^{[ 17 ]}

Molluscan shells are formed extracellularly in an extrapallial space between the outer organic skin covering the shell (periostracum) and the epithelial cells layer of the mantle.^{[ 18 ]} Thus, the growth of the shell in thickness proceeds unidirectionally, from the outer to the inner part of the mollusc. Every animal exhibits a species‐specific sequence of shell ultrastructures, each assembled from individual building blocks made of calcium carbonate (CaCO₃, calcite or aragonite) joined together by an organic phase.^{[ 19} , ^{20 ]} For example, one of the most studied shell ultrastructures is sheet nacre that is composed of aragonitic platelets connected by extremely thin organic membranes to form the so‐called brick‐and‐mortar architecture.^{[ 21 ]} Another well studied structural motif is the prismatic assembly made of calcitic columns aligned parallel to the growth direction of the shell.^{[ 22 ]} Grown by aggregation of amorphous calcium carbonate (ACC) particles, like all other mineral building units in molluscs, the prisms exhibit shapes that are far from the geometric forms predicted by classical crystallization models. Specifically, the most common geological calcite form is scalenohedron where facets from the $\{10\overline{1}4\}$ plane family in the hexagonal structural setting are cleaved.^{[ 23 ]} It is important to note that direct evidence of ACC precursors in molluscan shell mineralization was so far reported only in nacre.^{[ 24} , ^{25 ]}

In recent years, we used the prismatic ultrastructure to demonstrate that the formation of the various shell ultrastructures is a self‐assembly process that is governed by the chemical and physical thermodynamic boundary conditions set by the organisms.^{[ 26} , ^{27 ]} This allowed us to quantitatively describe the morphogenesis of mineralized biological tissues in time and in space. However, we still lack a fundamental understanding of how the collective kinetics of this spontaneous process is reflected in the evolution of the crystallographic properties of the mineral units. Kinetics and thermodynamics of ACC formation, aggregation and crystallization is probably one of the most studied CPA pathways leading to identification of many aspects affecting the steps of ACC nucleation, stabilization and transformation into a crystalline solid.^{[ 28} , ²⁹ , ³⁰ , ³¹ , ^{32 ]} However, so far, these were never linked to the emergence of texture of the formed biocomposites at the highest hierarchical level—the entire assembly on the macroscale.

2. Results and Discussion

In many bivalves having a bilaterally symmetrical shell, the calcitic prismatic architecture forms first and only later sheet nacre is deposited.^{[ 19 ]} As it is evident in the two species taken from two of the most investigated bivalve families: Pinna nobilis from the Pinnidae family (Figure  1A) and Pinctada nigra from Pteriidae (Figure 1D), the prismatic ultrastructure comprises the major portion of the shell (light and dark brown shell portions in both images). On the other hand, nacre is a thin shiny layer seen only in the inner part of the shell—the upper valve in Figure 1A,D. Despite the simplicity of this assembly, the prismatic mineral units exhibit a variety of morphologies and crystallographic properties between species. In P. nobilis, which has a thicker shell, the prisms exhibit a much larger aspect ratio and can reach the length of a few millimeters (Figure 1B). In comparison, while having a similar diameter of a few tens of microns, the length of the prisms in P. nigra is only few hundred microns (Figure 1E).

Figure 1.

Textural evolution of the prismatic ultrastructure in bivalve shells. A) The bivalve shell of P. nobilis. B) Fracture of the prismatic architecture in P. nobilis imaged parallel to the direction of growth. C) Electron backscatter diffraction (EBSD) map of the prismatic architecture in P. nobilis obtained parallel to the direction of growth. The corresponding color‐coded inverse pole figure of calcite, with the reference direction normal to the image plane, is depicted in (H). (0001)‐pole figures describe the overall texture of the entire assembly at the beginning and at the end of growth. D) The bivalve shell of P. nigra. E) Fracture of the prismatic architecture in P. nigra imaged parallel to the direction of growth. F) EBSD map of the prismatic architecture in P. nigra obtained parallel to the direction of growth. The corresponding color‐coded inverse pole figure of calcite, with the reference direction normal to the image plane, is depicted in (H). Prisms that have their crystallographic c‐axis of calcite parallel to the direction of growth and do not rotate are marked by black dots. (0001)‐pole figures describe the overall texture of the prismatic assembly at the beginning and at the end of growth. G) A 3D‐EBSD series of two prisms from P. nigra obtained perpendicular to the direction of growth taken with approximately 15 µm steps along the direction of growth. (0001)‐pole figures describe the overall texture of the prisms at different stages of formation. H) Color‐coded inverse pole figure of calcite, with the reference direction normal to the image plane.

However, a major difference is observed in the texture of these ultrastructures. In P. nobilis, the c‐axis of calcite is oriented parallel to the direction of growth throughout the entire thickness of the prismatic assembly. This is clearly evident in an electron backscattered diffraction (EBSD) map of a longitudinal section of the prisms and the corresponding (0001) pole‐figures taken in the beginning and the end of the prismatic tissue (Figure 1C). In P. nigra, EBSD maps show a completely different behavior (Figure 1F). Here, the starting crystallographic orientation of the nucleating prisms is sporadic with the c‐axis of calcite tilted by up to 30 degrees relative to the direction of growth. Immediately after nucleation, the lattice of most of the prisms starts to rotate until the prisms reach the length of ≈50 µm and the c‐axis of calcite becomes oriented perpendicular to the direction of growth. At this point, the prisms begin to split first forming low angle grain boundaries that with further growth divide the prisms into well‐defined crystallographic domains. This behavior does not include prisms that, like in P. nobilis, have their c‐axis of calcite aligned with the direction of growth (Figure 1F). During the entire process, the prisms in both cases maintain their columnar morphology.

Similar characteristics were demonstrated in many studied Pinnidae and Pteriidae species: lattice alignment versus lattice rotation and splitting, respectively.^{[ 22} , ³³ , ^{34 ]} In fact, lattice rotation of biogenic minerals was demonstrated in a number of other systems.^{[ 35} , ^{36 ]} Research into these traits tends to follow the adaptationist program,^{[ 37 ]} suggesting that the observed shapes and textures are “purposeful” and were evolved and optimized to comply with functional demands, such as superior mechanical performance.^{[ 38 ]} In the following, we demonstrate that these features do not arise from the omnipotent force of functional adaptation, but, as defined by Seilacher,^{[ 39 ]} are a result of architectural restrictions that are necessary consequences of the formation process. In this case, the kinetics of crystal growth by amorphous particle attachment.

To understand the textural evolution of the prismatic layer in P. nigra, we performed a 3D‐EBSD study by analyzing a sequence of sections prepared perpendicular to the direction of growth with a step size of ≈15 µm. The change in the crystallographic properties of two representative prisms is depicted in EBSD maps in Figure 1G, which also includes (0001) pole‐figures taken after formation (black color), after lattice rotation (red color) and at the end of their growth (green color). Just after nucleation, both prisms are coherent having a relatively narrow orientation distribution. With growth, EBSD maps gradually change their color—the lattice rotates; and striations depicting low angle grain boundaries oriented parallel to the c‐axis of calcite appear. These patterns become more pronounced until the prisms separate into sub‐prismatic domains with well‐defined grain boundaries. The pole‐figures not only illustrate the mosaicity of the prisms at the end of their growth, but also show that their rotation proceeds around an axis that lays on the basal plane of calcite, most probably around <$10\overline{1}0$> or <$1\overline{2}10$> axes (Figure  2G). Here, the c‐axis shifts on a straight line that connects the center of the pole‐figures and the point of initial orientation of the prisms until it is perpendicular to the direction of growth. This interpretation is supported by rotation axis analysis in Figure S1, Supporting Information.

Figure 2.

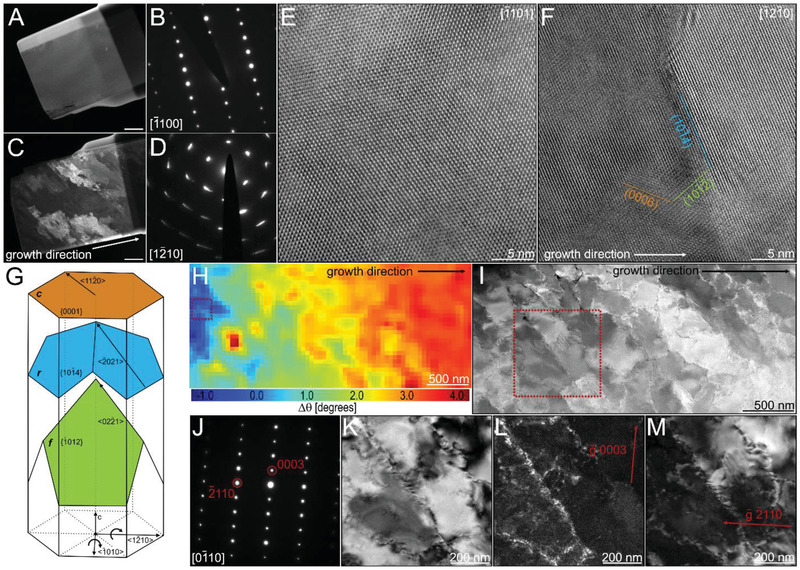
Dislocation analysis using a high resolution transmission electron microscopy (HRTEM). A,C) Dark‐field images of TEM lamella taken from the prisms of P. nobilis and P. nigra, respectively. Scale bars are 1 µm; and B,D) are the corresponding large area electron diffraction patterns, respectively. E,F) HRTEM images of P. nobilis and P. nigra using the samples in (A) and (C), respectively. Indicated crystal planes were extracted from the corresponding Fourier transforms. Zone axes are indicated in the upper right corner. G) Schematic representation of slip‐systems and basal lattice rotation axes in calcite. H) Misorientation map displaying the change in lattice orientation in P. nigra relative to the area marked by a red rectangle obtained using 4D scanning electron nano‐diffraction microscopy (4D‐STEM) analysis. I) Scanning transmission electron microscopy (STEM) image of the TEM lamella investigated with 4D‐STEM in (H). Red rectangle indicates the area further studied using the two‐beam condition. J) Electron diffraction pattern of the area indicated in (I). K) Bright field image with $\overline{g}=0003$. L) Dark field image with $\overline{g}=0003$. M) Dark field image with $\overline{g}=\overline{2}110$.

Remarkably, this behavior is a textbook description of generic crystalline materials that undergo plastic deformation as a result of an applied external force. Elastic energy in these materials is released through the formation and motion of dislocations, followed by their interaction that leads to the development of dislocation sub‐structures (dislocation tangles, walls and cells), then the generation of low angle grain boundaries and, finally, recrystallization into a new granular structure.^{[ 40 ]} A behavior that is well recorded in geological calcite.^{[ 41} , ^{42 ]} The main difference is that whereas in abiotic materials this phenomenon proceeds in bulk, in the prismatic structure of P. nigra the chronological record of events is embedded in the mineral building blocks along their direction of growth. This analogy suggests that in this species the prisms that do not have their c‐axis of calcite parallel to the direction of growth experience persistent influx of dislocations during formation.

We tested this hypothesis using transmission electron microscopy (TEM). Differences in crystallographic properties of TEM lamellae lifted from the prisms of the two studied species are already evident at low magnification dark‐field imaging conditions. Whereas the sample taken from P. nobilis is homogeneous (Figure 2A), the lamella extracted from P. nigra reveals approximately 250 nm thick elongated domains that run across the specimen (Figure 2C). The rotation of the crystal lattice in P. nigra compared to no rotation in P. nobilis is demonstrated by azimuthal arcs that characterize high index diffraction spots versus sharp electron diffraction pattern obtained from the lamellae, respectively (Figures 2D and 2B, respectively). At high magnification, calcite lattice in P. nobilis is homogeneous and practically defect free (Figure 2E). In comparison, in P. nigra, various defects seem to accumulate at the faceted interfaces between the observed domains (Figure 2F), which mainly follow the {$10\overline{1}4\}$ and the $\{\overline{1}012\}$ plane families of calcite (Figure 2G).

Lattice rotation and interface properties were further analyzed using a TEM sample that was prepared such that the observation direction could be aligned with the rotation axis [$0\overline{1}10$] (Figure 2G). 4D scanning electron nano‐diffraction (4D‐STEM) mapping of the sample confirms the presence of coherent domains that together exhibit a continuous rotation of the lattice by approximately 1.2 degree per micron (Figure 2H). A scanning transmission electron microscopy (STEM) image of the sample was used to find a region with a long straight interface for dislocations analysis using two‐beam conditions (Figure 2I), which is a well‐established method to localize and characterize dislocations in a material.^{[ 43 ]}

Dislocation‐induced plastic deformation of calcite is known to proceed by the activation of three main slip systems: $r\{10\overline{1}4\}\overline{2}021$, $f\{\overline{1}012\}02\overline{2}1$ and $c\{0001\}11\overline{2}0$.^{[ 44 ]} The former two being the dominant systems at moderate temperatures (Figure 2G). Two‐beam conditions with reflection vectors$\overline{g}=0003$ and $\overline{g}=\overline{2}110$ were used for dislocation characterization (Figure 2J). In this dark field imaging mode, the sample is tilted in such a way that only the incident beam and one plane with a reflection vector $\overline{g}$ provide strong signals and only the latter is admitted by an aperture. This way, the registered signal coming from the material is extremely weak—the image is dark, and only dislocations that comply with the $\overline{g}·\overline{b}\ne 0$ criterion provide a strong contrast, with $\overline{b}$ being the Burgers vector of the dislocation system. When $\overline{g}·\overline{b}=0$ the dislocation is invisible. Therefore, basal c‐slip dislocations with $b=1\mathrm{/}3(2\overline{1}\overline{1}0)$ should not be visible when $\overline{g}=0003$, but both r‐slip with $\overline{b}=1\mathrm{/}3(\overline{2}021)$) and f‐slip with $\overline{b}=1\mathrm{/}3(02\overline{2}1)$ should be visible. When $g=\overline{2}110$ f‐slip should be invisible. The region of the interface shows an accumulation of dislocations in the bright field image (Figure 2K) that are bright in the dark field mode with $\overline{g}=0003$ and $\overline{g}=\overline{2}110$ (Figures 2L and 2M, respectively). In agreement with facets observed using HRTEM (Figure 2F), this analysis suggests an accumulation of r‐slip and f‐slip dislocations at the interfaces. These data support the occurrence of an extensive plastic deformation.

Initially, in order to investigate a possible correlation between the location of intra‐domain interfaces and the distribution of the intracrystalline organic material, energy filtered TEM (EFTEM) analysis and synchrotron‐based scanning transmission X‐ray microscopy (STXM) of a P. nigra prism were performed (Figure S2, Supporting Information). Scanning a TEM lamella at the carbon K‐edge employing STXM demonstrated that the organic matter is distributed evenly throughout the prism. Both approaches showed that the organic inclusions are not concentrated at the interface between the domains and, most probably, are not responsible for the observed plastic behavior (Figure S2, Supporting Information). Further, Schmid's law analysis was performed in an attempt to describe the deformation of calcite during growth (Figure 1G).^{[ 45 ]} Knowing the orientation of a crystal in space and the active slip system, this analysis allows determining the stresses that lead to the observed deformation. However, considering that, at‐least two slip systems are active and that critical stresses for dislocation motion in both are unknown, we were unable to derive an external force that would drive the observed prism rotations, especially since some prisms do not rotate at all. This outcome raises the questions: lacking an obvious external force, what drives the continuous influx of new dislocations during prism formation? Can it be an internal phenomenon inherent to crystallization by amorphous particle attachment?

Formation of lattice defects, such as misfit dislocations, during amorphous‐to‐crystalline phase transformation was theoretically described and observed in a number of abiotic materials systems.^{[ 46} , ⁴⁷ , ⁴⁸ , ⁴⁹ , ^{50 ]} They form to compensate for the increase in density (reduction in volume) during the solid state transition from a disordered amorphous to an ordered crystalline state. Most interestingly, a recent study demonstrated that in the case of a unidirectional amorphous‐to‐crystalline phase transformation the generation of misfit dislocations can result in a gradual lattice rotation the magnitude of which is dependent on the initial orientation of the crystallizing solid.^{[ 51 ]} In particular, it was shown that for some starting crystal orientations the formation of dislocations will not be possible due to the symmetry of misfit induced stresses activating the corresponding slip systems.

The change in density during ACC crystallization in biogenic environments is especially significant as it is known to sometimes start from hydrous ACC species that have an even lower density than anhydrous ACC (density of calcite is 2.71 g cm⁻³, of hydrous ACC with 1.1:1 H₂O to CaCO₃ is 2.28 g cm⁻³ and of ACC with 0.5:1 H₂O to CaCO₃ is 2.42 g cm^{−3[ 52 ]}).^{[ 31 ]} It is reasonable to postulate that a substantial amount of misfit‐induced strain energy is generated during prisms’ crystallization. This energy is released by dislocation nucleation when the directional crystallization front proceeds through the amorphous phase. Indeed, extremely large residual stresses were reported in biogenic calcite with values exceeding 150 MPa^{[ 53 ]}—well above a critical stress that is required to activate a dislocation system.^{[ 44 ]} Hence, we conclude that the plastic deformation observed on the macro‐ and the nano‐scale (Figures 1 and 2, respectively) is not a result of an integral force applied to the growing system, but has an internal differential driving force which, due to the symmetry of available slip systems in calcite (Figure 2G), does not induce lattice rotation in prisms that have their c‐axis co‐aligned with the direction of growth. In fact, it implies that texture development in the prisms of molluscan shells is a spontaneous process dependent on the initial calcite lattice orientation of a prism with respect to the direction of growth. Therefore, it is a direct result of this unique crystallization pathway. However, this brings us to the question: what defines the initial crystallographic orientation of the growing prisms?

Specimens from the prismatic ultrastructures from the two studied shells were aggressively bleached to partially etch the shell and to reveal the nature of the particulate substructure formed during the initial stages of prism deposition (Figure  3 ). Looking at the cross section of the ultrastructure, in the case of P. nobilis, this treatment revealed a loose particle assembly forming a rough surface made of triangular pyramids as demonstrated by scanning electron microscopy (SEM) (Figure 3A,B) and by atomic force microscopy (AFM) (Figure 3C,D) at different magnifications. Each exposed pyramidal surface belongs to the $\{10\overline{1}4\}$ plane family, which are the preferred cleavage surfaces of calcite. Accordingly, the prisms have their c‐axis of calcite parallel to the long axis of the prisms.

Figure 3.

Crystal growth pathways by amorphous particles attachment. Bleached surface of the prisms in P. nobilis at the beginning of their formation imaged using: A,B) scanning electron microscopy (SEM); and C,D) atomic force microscopy (AFM). The pyramid in (B) reveals {101–4} planes of calcite. Bleached surface of the prisms in P. nigra at the beginning of their formation imaged using: E,F) SEM; and G,H) AFM. The lines in (F) designate the faceted circular patterns formed around what we assume to be the nucleus marked by an arrow and highlighted in the insert.

In contrast, the substructure of the prisms in P. nigra, is a compact array of nanoparticles assembled to form a smooth growth front lacking a specific crystallographic orientation. Each prism seems to have a single nucleation center^{[ 54 ]} surrounded by nanoparticles that, judging by the faceted circular patterns around the nucleus, are accreted by what appears to be a spiral or a 2D nucleation growth mode (Figure 3E–H). Astonishingly, the two biogenic model systems demonstrate two fundamentally different growth mechanisms that are described in full by classical crystal growth models.

A number of well‐established theories, starting with the classical analysis by Hartman and Perdok,^{[ 55 ]} distinguish between crystal morphologies and textures that are formed at low and high growth rates, which in the framework of classical crystallization can proceed at low and high levels of supersaturation, respectively.^{[ 2} , ³ , ⁴ , ^{5 ]} At a low driving force, the crystal will grow slowly with the assistance of either screw dislocations or critical‐sized 2D nuclei. These modes of growth form flat surfaces, they have no preferred orientation and the growth rate is significantly limited by the rate of molecule integration. At a higher driving force a “rough” growth mode is achieved. Here, the large amount of solute molecules can be immediately integrated regardless of their location due to the rough nature of the growing surface and the growth rate is limited only by molecule supply.

Consolidating the analogy, in P. nobilis, a high rate of amorphous particle deposition can be inferred. A large accretion rate on the growing front of the prisms requires a large surface that is readily provided by the thermodynamically preferred $\{10\overline{1}4\}$ planes forming a rough surface (Figure 3A). The prisms appear to grow in the [0001] direction when, in fact, in contrast to previous assumptions,^{[ 33 ]} the crystallographic alignment of the entire prismatic assembly is the result of fast growth on $\{10\overline{1}4\}$ planes (Figure  4A). Due to the symmetry of possible dislocation slip systems around the direction of growth (Figure 2G), these prisms exhibit no crystallographic rotation. The final product are coherent calcitic columns.

Figure 4.

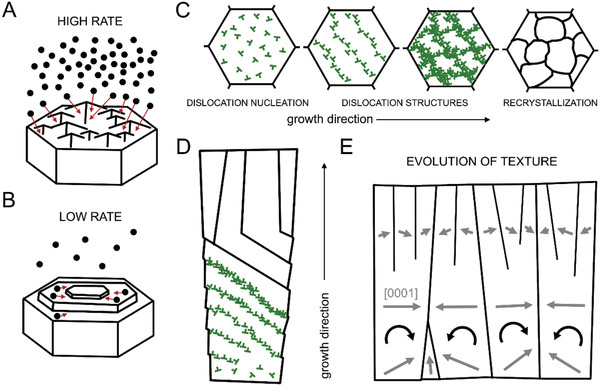
Schematic representation of the suggested mechanisms of textural evolution during prism biomineralization. A) High growth rate by amorphous particle attachment as observed in P. nobilis. The large influx of amorphous particles is accommodated by the rough surface of the growing prism. B) Low growth rate by amorphous particle attachment as observed in P. nigra. The ACC particles first arrive at the surface and then diffuse until integration. C,D) Cross‐sectional and longitudinal view of prism recrystallization process induced by dislocations formed during the amorphous‐to‐crystalline phase transformation in P. nigra, respectively. Initially, they form dislocation structures that rotate the prisms. When rotation is no longer possible the stored elastic energy is released by recrystallization. Each prism rotates following an activation of a specific slip‐system that depends on the initial orientation of the prism. Dislocations are marked in green. E) Longitudinal view on textural evolution of the entire prismatic assembly in P. nigra. Gray arrows indicate the [0001] direction of the lattice.

In P. nigra, a low deposition rate can be inferred. We hypothesize that the growth proceeds slowly by the diffusion and integration of amorphous particles on a small number of arbitrarily oriented nuclei (Figure 4B).^{[ 56} , ^{57 ]} Next, amorphous phase crystallization is accompanied by misfit‐induced plastic deformation realized by dislocation generation and motion (Figure 4C,D). During the initial stages of prism deposition they entangle to form dislocation walls (Figure 2C)—low angle grain boundaries—that gradually rotate the lattice of the calcitic columns. The activated dislocation slip system in every prism is directly dependent on its initial crystallographic orientation resulting in a very specific rotation (Figure 1G). Similarly to P. nobilis, prisms that initially have their c‐axis co‐aligned with the direction of growth cannot rotate. This deformation mode ends when the c‐axis of calcite in all other prisms is perpendicular to the direction of growth (Figure 1F). In accordance to the model (Figure 4E), any further attempt to rotate will induce plastic deformation that will bring the lattice back. From this point on, the stored elastic energy cannot be released by lattice rotation and the accumulated dislocations are not able to slip (Figure 4E). Therefore, recrystallization of the sub‐prismatic structure and the formation of high angle grain boundaries are induced to release the stored mechanical energy (Figure 1G). In contrast to P. nobilis, the final product are prisms that exhibit complex non‐coherent crystallographic properties. However, in both cases, while not addressing the physicochemical and genetic details of crystal growth in a biological setting, the evolution of texture is well‐described by adapting concepts from classical crystal nucleation and growth theories.

3. Conclusion

In this work, using the prismatic ultrastructure in molluscan shells as a model, we show that biogenic minerals not only provide key insight into material morphogenesis during crystallization by amorphous particle attachment but also teach us fundamental new mechanisms that have a profound effect on textural evolution during non‐classical crystal growth. Our analysis establishes a mechanistic link between the emergence of texture and the cumulative growth rate by amorphous particle accretion. We make a fundamental step towards our ability to quantitatively describe the evolution of form and texture of biological mineralized tissues and towards gaining the power to predict and design the structure and crystallographic properties of synthetic materials formed by CPA.

4. Experimental Section

Sample Preparation

Samples of the shells of P. nobilis and P. nigra were fractured parallel to the growth direction of the shell and coated with Pt/Pd for electron microscopy. For EBSD and TEM investigations, pieces of the shells were embedded in poly(methyl methacrylate), cut parallel or perpendicular to the direction of growth, polished with a diamond solution, and finally polished with a colloidal silica solution. Etched samples from both species were prepared by keeping fragments of the shells in sodium hypochlorite 5% Cl₂ aqueous solution for an hour.

Focused Ion Beam Sample Preparation

TEM lamellae were prepared at the National Center for Electron Microscopy (NCEM), Molecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA (USA), using a FEI Helios G4 UX dual beam Focused Ion Beam (FIB), utilizing a focused Ga+ ion beam for site‐selective material removal and a monochromated field emission scanning electron microscope (SEM) column for imaging. To avoid charging during FIB milling, an alcohol‐based graphite conductive adhesive was applied to the polished surface of samples preliminary analyzed with EBSD, sparing the region of interest, and subsequently a 5 nm thick chromium layer was deposited on the entire sample surface.

For milling, rectangular regions, covering an area of 15 × 2 µm² with the long‐axis parallel to the growth direction of the prisms were chosen close to the periostracum, where a 1.5 µm thick protective platinum layer was deposited, to protect the sample surface from damage by the ion beam during the FIB procedure. For P. nigra, EBSD data were utilized to choose an area where the calcite c‐axis is parallel to the mill direction which was normal to the sample surface. The milling depth was 10 µm, producing a rectangular FIB lift‐out lamella by exerting a standard u‐cut technique.

The lift‐out procedure was performed with an EasyLift rotatable needle. The accelerating voltage of the ion beam was kept at 30 kV, and the ion beam currents were in the range from 20 nA to 90 pA. The milled sample was then welded to an Omniprobe 4 Post Cu Lift‐out Grid. The lamella was thinned to a final thickness of 100 to 150 nm using decreasing ion beam accelerating voltages of 30, 5, and 2 kV and ion currents from 0.75 nA to 44 pA.

Scanning Electron Microscopy

Imaging of the fractured/bleached and Pt/Pd‐coated samples was performed using a Scios Dual Beam FIB/SEM (FEI/Thermo Fisher) in high‐vacuum conditions.

Electron Backscatter Diffraction

Electron Backscatter Diffraction (EBSD) data were collected using a Hikari Super EBSD (EDAX) system on a Scios Dual Beam FIB/SEM (FEI/Thermo Fisher). To minimize damage to the specimen surface by the electron beam, we used a low current of 1.6 nA and a voltage of 15 kV. Step sizes of 400 nm for longitudinal scans and 500 nm for transversal scans were used. EBSD patterns were processed using neighbor pattern averaging indexing. MTEX, a free crystallographic texture analysis software, was used for analysis.^{[ 58 ]}

Transmission Electron Microscopy

All transmission electron microscopy (TEM) investigations were performed at the National Center for Electron Microscopy (NCEM), Molecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA (USA). Low‐ and high‐resolution TEM images of P. nobilis and P. nigra lift‐out samples were acquired using a FEI F20 UT Tecnai transmission electron microscope operating at 200 kV accelerating voltage. Acquisition of confined area diffraction patterns, 4D‐STEM scans and two‐beam dislocation analysis were performed utilizing a FEI TitanX 60–300 microscope operating at 300 kV accelerating voltage.

Confined area diffraction patterns of P. nobilis and P. nigra lift‐out samples were acquired with an area of ≈4 µm in diameter. HRTEM images and diffraction patterns were analyzed with the Crystallographic Tool Box (CrysTBox).^{[ 59 ]}

4D‐STEM analysis was performed on a P. nigra TEM lamella. Converging beam electron diffraction patterns were recorded while scanning over a total area of 1.5 × 3 µm² in STEM mode with a step size of 30 nm and a frame time of 50 ms. The convergence half‐angle was 0.48 mrad resulting in a ≈2.2 nm probe. The beam current was 5 pA, which resulted in an average dose of 4E3 e^– A⁻² in an area defined by the 2.2 nm FWHM or 17 e^– A⁻² if calculated based on the 30 nm × 30 nm real space STEM pixel. This is considered a low‐dose for 4D‐STEM and was used to minimize radiation damage. The 4D‐STEM data were processed using the open‐source Python‐based py4DSTEM software^{[ 60 ]} and the relative lattice rotation was extracted.

Two‐beam dislocation analysis was performed on a pristine P. nigra TEM lamella. To reduce the radiation dose a STEM image of the sample was used to find a region with a long straight interface after rotating to zone axis $[0\overline{1}10]$. The reflection vectors g = 0003 and $g=\overline{2}110$ were used for dislocation analysis using a 10 µm objective aperture.

Atomic Force Microscopy

Atomic force microscopy (AFM) measurements were carried out using a JPK NanoWizard4 AFM (Bruker Nano GmbH, Germany) at the Molecular Imaging and Manipulation Facility, a core facility of the CMCB at Technische Universität Dresden. Images were acquired in intermittent contact mode (AC mode) using PPP‐NCH cantilevers (Nanosensors, NanoWorld AG, Switzerland) driven at just below their free‐space resonance frequency (typically between 280 and 300 kHz). The set‐point was chosen between 65 and 85% of their free‐space amplitude of 1 V. Tip velocities were set between 10 and 20 µm s⁻¹. The Gain parameter was set to values between 500 and 1500, depending on scanning area and tip velocity.

Scanning Transmission X‐Ray Microscopy

Scanning transmission X‐ray microscopy (STXM) measurements were performed at Beamline 5.3.2.2 at the Advanced Light Source. This microscope is equipped with a zone plate having 25 nm outer zones and a spherical‐grating monochromator with an energy resolution at the C K‐edge better than 0.1 eV. The data was taken with 50 nm pixels over a 10 µm × 5 µm field of view. The energy step in the detail region 282–291 eV was 0.11 eV. Calibration was done using the 3σ (ν = 0) peak of CO₂ gas at 292.74 eV. Data were analyzed using homebuilt software available at the beamline.

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Schoeppler V., Stier D., Best R. J., Song C., Turner J., Savitzky B. H., Ophus C., Marcus M. A., Zhao S., Bustillo K., Zlotnikov I., Crystallization by Amorphous Particle Attachment: On the Evolution of Texture. Adv. Mater. 2021, 33, 2101358. 10.1002/adma.202101358

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.