Simultaneously Toughening and Stiffening Elastomers with Octuple Hydrogen Bonding

Abstract

Current synthetic elastomers suffer from the well‐known trade‐off between toughness and stiffness. By a combination of multiscale experiments and atomistic simulations, a transparent unfilled elastomer with simultaneously enhanced toughness and stiffness is demonstrated. The designed elastomer comprises homogeneous networks with ultrastrong, reversible, and sacrificial octuple hydrogen bonding (HB), which evenly distribute the stress to each polymer chain during loading, thus enhancing stretchability and delaying fracture. Strong HBs and corresponding nanodomains enhance the stiffness by restricting the network mobility, and at the same time improve the toughness by dissipating energy during the transformation between different configurations. In addition, the stiffness mismatch between the hard HB domain and the soft poly(dimethylsiloxane)‐rich phase promotes crack deflection and branching, which can further dissipate energy and alleviate local stress. These cooperative mechanisms endow the elastomer with both high fracture toughness (17016 J m⁻²) and high Young's modulus (14.7 MPa), circumventing the trade‐off between toughness and stiffness. This work is expected to impact many fields of engineering requiring elastomers with unprecedented mechanical performance.

A bioinspired multifunctional elastomer with both high fracture toughness and high Young's modulus is designed, breaking through the current trade‐off present in the state‐of‐the‐art. The octuple hydrogen bonding promotes the formation of ultrastrong nanodomains, which, together with a soft poly(dimethylsiloxane)‐rich phase, form a bicontinuous network structure. Such hierarchical networks with ultrastrong nanodomains enhance the mechanical properties.

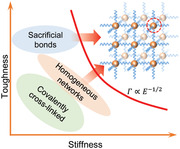
1. Introduction

Elastomers are indispensable both in classical fields of engineering and emerging research areas such as wearable devices, flexible electronics, and soft robotics.^{[ 1 ]} Despite the great versatility of synthetic unfilled elastomers, the combination of high stiffness and high toughness remains difficult to achieve (Figure 1a).^{[ 1} , ^{2 ]} For example, increasing the cross‐linking density of conventional covalently cross‐linked polymers yields high stiffness, but leads to a corresponding reduction in toughness (green ellipse, Figure 1a).^{[ 2b ]} As a means of strengthening and toughening unfilled elastomers, homogeneous networks and energy dissipative mechanisms have been adopted.^{[ 3 ]} Homogeneous networks possess similar polymer chain length between two adjacent crosslinks, thereby evenly distributing the external loading stress. Consequently, they can avoid stress concentration on shorter chains and subsequent nucleation of fracture, thus leading to a higher stretchability and strength.^{[ 2} , ^{4 ]} However, current homogeneous networks, built up by tetrahedron‐like macromonomers^{[ 3a ]} or sliding cross‐links,^{[ 5 ]} still exhibit limited toughness enhancement owing to the absence of molecular structure units for effective energy dissipation (orange ellipse, Figure 1a).^{[ 2a ]} Furthermore, the energy dissipative networks, like those with incorporated sacrificial bonds such as partially pre‐stretched chains,^{[ 6 ]} metal–ligand coordination,^{[ 2b ]} Coulombic interactions,^{[ 7 ]} and hydrogen bonding (HB),^{[ 3b ]} indeed exhibit high toughness, but at the same time suffer from low stiffness due to the inherent weak nature of these interactions (blue ellipse, Figure 1a). Clusters of multiple HB have been introduced into elastomers to address this weakness since they can allow for stronger interchain interactions and increase the energy dissipation.^{[ 3} , ^{8 ]} Given that high density of HBs can lead to poor solubility of polymers during synthesis,^{[ 9 ]} the current state‐of‐the‐art multiple HB for synthetic elastomer toughening is limited to triple, quadruple, and sextuple HB, all of which are not sufficiently strong.^{[ 3b ]} Strikingly, multiple HB motifs with varied sizes have also been observed in natural tough and stiff materials, such as octuple HB which has been identified in spider dragline silk as an optimal enhancer for the polymer networks.^{[ 10 ]} Hence, mimicking spider dragline silk (the toughest known natural fiber) to construct polymeric networks holds great promises to significantly improve the mechanical properties of elastomers.^{[ 8 ]} Spider silk contains two major types of components, namely, crystalline and amorphous segments.^{[ 11 ]} The crystalline segments of spider silk involve short peptides of 6–10 amino acids, which form antiparallel and parallel beta‐sheets via HB. Inspired by the structure of spider silk, finding a viable synthetic route to incorporating a higher number of HBs, for example, octuple HB, as stronger sacrificial bonds for energy dissipation into an amorphous matrix, should circumvent the trade‐off between stiffness and toughness in state‐of‐the‐art synthetic, unfilled elastomers.

Figure 1.

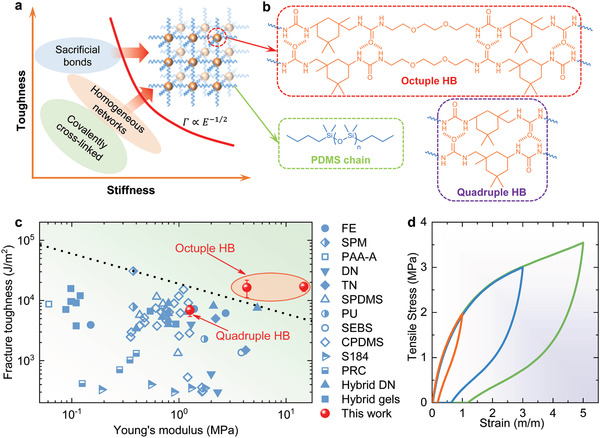
Schematic of the design strategy and mechanical properties of PDMS–urea containing octuple hydrogen bonding (PDUO) elastomers. a) The trade‐off between toughness and stiffness in common elastomers and the design principle of the PDUO. b) The molecular structure of PDUO consists of flexible PDMS chains (blue) and octuple HB motifs, forming a homogeneous network. A similar molecular architecture, namely PDU with quadruple HB, is prepared for comparison. c) Mechanical performance of PDUO and PDMS–urea containing quadruple hydrogen bonding (PDUQ) (red markers) in the state‐of‐the‐art toughness–modulus diagram together with reference results from previously reported elastomers (FE,^{[ 12f ]} SPM,^{[ 12e ]} PAA‐A,^{[ 12d ]} DN and TN,^{[ 6a ]} SPDMS and PU and SEBS,^{[ 12b ]} CPDMS and S184,^{[ 12g ]} PRC,^{[ 5 ]} hybrid DN,^{[ 12c ]} hybrid gels^{[ 12a ]}). Note: FE = filled elastomer, including physiotherapy rubber, natural rubber, and acrylic‐based material; SPM = supramolecular polymeric materials; PAA‐A = polyacrylamide–alginate hydrogels; DN = double‐network elastomer; TN = triple network elastomer; SPDMS = supramolecular PDMS; PU = polyurethane; SEBS = styrene–ethylene–butylene–styrene; CPDMS = composite PDMS; S184 = Sylgard 184; and PRC = polyrotaxane‐crosslinked elastomers. The black dashed line indicates the trade‐off between toughness and stiffness for the reference materials (Γ = 18 915 kN^3/2m⁻² × E ^−1/2). The values representing the elastomers in this work were obtained from the pure shear and uniaxial tensile tests reported in Figure S1, Supporting information. d) PDUO subjected to cyclic loading/unloading tests with different maximum tensile strains.

Herein, through a combination of multiscale experiments and atomistic simulations, we present, for the first time, a rational design strategy for the synthesis of a novel transparent unfilled elastomer with simultaneous high stiffness and toughness. By introducing strong, reversible, and sacrificial octuple HB into linear poly(dimethylsiloxane) (PDMS) via the chain extension reaction, we build both homogeneous and energy dissipative networks (Figure 1a,b). The designed homogeneous networks can evenly distribute the stress to each polymer chain during loading, thereby reducing the stress concentrations, consequently, enhancing the stretchability and delaying fracture. In addition, the synthesized elastomer exhibits distinct microphase separation, containing soft hydrophobic PDMS segments and hard hydrophilic HB nanodomains. These strong HB nanodomains serve to restrict the mobility of polymer chains and transform between different configurations to dissipate energy under stress, thus further enhancing both stiffness and toughness beyond the current state‐of‐the‐art (Figure 1c and Figure S1, Supporting Information).^{[ 5} , ⁶ , ^{12 ]} This work represents a significant leap in improving the mechanical durability of applied unfilled elastomers and demonstrates how smart materials design can be used to overcome existing trade‐offs in material properties. This next generation of bioinspired multifunctional elastomers is thus expected to be of practical relevance across the different fields of engineering.

2. Results and Discussion

In the preparation of homogeneous polymer networks with the local high number of HB crosslinks, it is crucial to avoid chain aggregation and precipitation due to the dense interacting HBs during synthesis. For such purpose, we use the chain extension reaction in this study. To ensure the final homogeneity of the formed network, aminopropyl‐terminated PDMS (NH₂‐PDMS‐NH₂) is chosen as macromonomers to react with isophorone diisocyanate (IDI) in a molar ratio of 1:2, yielding an intermediate product (PDUO‐m) with two ureido groups terminated with isocyanate groups (Figure S2, Supporting Information). Subsequently, a chain extender, 1,2‐bis(2‐aminoethyoxy)ethane), is added to elongate the polymer chains and generate two new ureido groups in the connecting section of two PDMS segments (Figure S2, Supporting Information). The synthesized polymer, named PDUO, thus contains long uniform PDMS segments, and short polyurea segments (Figure 1b) giving rise to interchain HB. Molecular structures of PDUO‐m and PDUO are confirmed by Fourier transform infrared (FTIR) spectroscopy and ¹H nuclear magnetic resonance (NMR) spectroscopy (Figures S3 and S4, Supporting Information). Unless stated otherwise, the molecular weight of NH₂‐PDMS‐NH₂ is 5000 Dalton, where the corresponding product is termed PDUO5000.

The fracture toughness (Γ) of PDUO is characterized by the widely adopted pure shear test proposed by Rivlin and Thomas^{[ 13 ]} for soft materials (Figure S1a, Supporting Information).^{[ 12} , ^{14 ]} The Young's modulus (E) of PDUO is used to evaluate the stiffness and is obtained from the initial parts of the stress–strain curves (i.e., slope of the fitting line, Figure S1b, Supporting Information) of the samples subjected to uniaxial tensile tests. Since elastomers often exhibit a trade‐off between stiffness and toughness (Γ ∝ E ^−1/2),^{[ 2a ]} there is a performance upper bound among the state‐of‐the‐art elastomers (red dashed line, Figure 1c).^{[ 5} , ⁶ , ^{12 ]} Remarkably, the prepared PDUO5000 presents a Young's modulus of 4.3 MPa combined with a fracture toughness of 16 434 J m⁻², circumventing the known trade‐off. PDUO is further subjected to cyclic loading/unloading tests with different maximum tensile strains to investigate the energy dissipation and shape recoverability, as shown in Figure 1d and Figure S5, Supporting Information. The energy dissipation and dissipation ratio increase with maximum strain, because more and more HBs are broken as the strain increases, providing the energy for high toughness.^{[ 15 ]} PDUO also exhibits excellent shape recoverability, with a shape recovery ratio always higher than 75% in the maximum strain range of 1–5.

The mechanism of the extraordinary mechanical performance of the PDUO samples is elucidated by the experimental investigation of the homogeneous network and strong HBs. The HB is confirmed by temperature‐dependent FTIR spectroscopy and X‐ray photoelectron spectroscopy (XPS). The FTIR spectra (Figure 2a and Figure S6, Supporting Information) from the PDUO samples are recorded under raising the temperature from 30 to 150 °C, in which no polymer degradation is confirmed by thermogravimetric analysis (Figure S7, Supporting Information). The evolution of the FTIR spectrum with increasing temperature indicates the dissociation of HBs and the generation of free C=O and N–H groups (Figure 2a and Figure S6, Supporting Information).^{[ 16 ]} Two‐peak components of narrow‐scan XPS spectra of the N 1s are identified (Figure 2b), reaffirming the presence of both bonded N–H and free N–H groups (bonded N–H groups lie in lower binding energy than free N–H groups).^{[ 17 ]} Because the PDMS segments are much more hydrophobic than the polyurea segments, they are more likely to self‐arrange on the surface, while ureido groups tend to bury themselves into the polymer matrix to lower the surface energy. As a result, the atomic percentage of N, solely provided by the ureido group, increases with the etching depth in the sample until reaching a stable value, as confirmed by wide‐scan XPS (Figure 2c and Figure S8, Supporting Information). Given that the ureido groups provide the only HB sites in the entire polymer, the percentage of bonded N–H (i.e., stable HB) shows a similar trend as the atomic percentage of N in the elastomer (Figures S9 and S10, Supporting Information). Both the HB and hydrophobic interactions lead to the self‐assembly and microphase separation in PDUO, which is confirmed by modulated differential scanning calorimetry (MDSC), atomic force microscopy (AFM), and small‐angle X‐ray scattering (SAXS). The endothermic peak at ≈78 °C in the non‐reversing and total MDSC curves correspond to the dissociation of HB domains (Figure 2d).^{[ 18 ]} However, the melting endotherm disappears in the immediate secondary run, but reappears after aging at room temperature for 1 day (Figure S11, Supporting Information). This confirms the reformation of dissociated HB domains resulting from the relaxation of polymer chains, a process which requires a longer time.^{[ 18 ]} It also suggests the potential for self‐healing at elevated temperatures owing to the reversible HB, as reported in a previous study encompassing HB‐based elastomers.^{[ 12e ]} Furthermore, two distinct structures are observed in the AFM phase image (Figure 2e), indicating the well‐defined micro‐phase separation, resulting from the clustering of ureido groups due to HB, and the aggregation of PDMS chains because of hydrophobic interaction.^{[ 15 ]} The distinct peak in the 1D SAXS spectrum (Figure 2f) and the clear isotropic ring in the 2D SAXS pattern (inset) further confirm the formation of periodic, homogeneously distributed HB domains. The periodicity (interdomain distance) is calculated to be 7.9 nm based on Bragg's law.^{[ 15} , ^{19 ]} Moreover, since the HB domains are sufficiently small, the prepared PDUO film has a high average light transmittance of 92.7% in the wavelength range from 400 to 800 nm (Figure S12, Supporting Information).^{[ 20 ]} This is consistent with the inserted photo of the elastomer in Figure S12, Supporting Information, which shows a transparent, defect‐free, and compact film. Such high optical transparency demonstrates the macroscale homogeneity of the prepared elastomer.^{[ 20b ]} These results reveal the multiscale structure of PDUO, which includes atomic scale HB, nanoscale HB domains, and macroscopic homogeneity. Such a multiscale structure is highly beneficial for toughening and stiffening and at the same time attractive for applications requiring optical transparency in possible combination with autonomous self‐healing.

Figure 2.

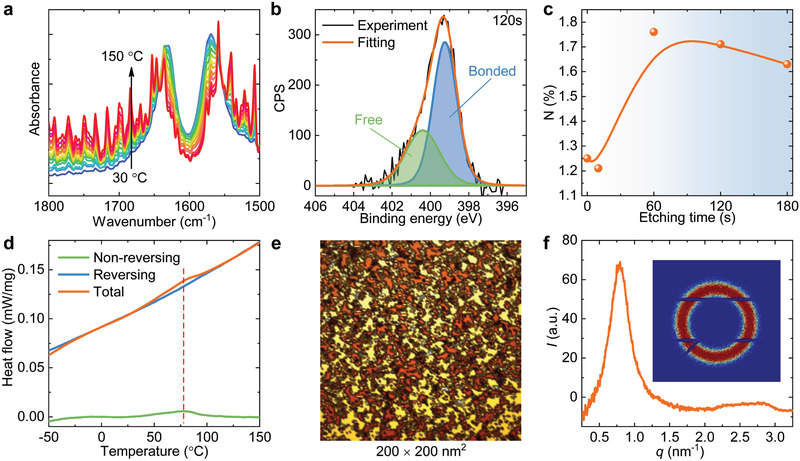
Characteristics of PDUO5000. a) FTIR spectra at an increasing temperature from 30 to 150 °C. The peak at 1630 cm^–1 exhibits a blueshift to 1636 cm^–1 and reduction of intensity as temperature increases from 30 to 150 °C, while several peaks arise at higher wavenumber (1647, 1653 cm^–1 and so on), revealing the transition of hydrogen‐bonded C=O to free C=O (Figure 2a). Furthermore, the decrease of signals at 1569 and 3336 cm^–1, and arising of peaks at 1559–1500 cm^–1 and 3400–3600 cm^–1 with increasing temperature indicate the conversion of hydrogen‐bonded N–H to free N–H (also shown in Figure S6, Supporting Information).^{[ 16a–c ]} b) Narrow‐scan XPS spectra of N 1s orbital and their fitting curves indicate the presence of both bonded N–H (blue) and free N–H (green) groups. c) The atomic percentage of N as a function of etching time by wide‐scan XPS provides (the etching time is proportional to etching depth on the sample surface). d) MDSC curves of the PDUO in the temperature range of −50 to 150 °C. The red dashed line denotes the melting peak. e) AFM phase image showing the distinct micro‐phase‐separation, where the yellow and brown colours represent the PDMS‐rich phase and HB domain, respectively. f) 1D SAXS spectrum and 2D SAXS pattern (inset) monitored from the sample.

Microstructures are often considered to play a key role in enhancing the mechanical properties of soft polymers.^{[ 2} , ^{21 ]} Herein, the strength of nanodomains is vital in amplifying the toughening and stiffing effects. For comparison, we prepare a control sample (PDUQ3000) containing quadruple HB sites (Figure 1b and Figure S13, Supporting Information). A peak can be found from the 1D SAXS spectrum of PDUQ3000 (although it is not as distinct as that of PDUO5000), confirming the formation of HB domains with a periodic distance of 4.9 nm (Figure S14, Supporting Information). Compared with the traditional covalently crosslinked silicone (Sylgard 184, Γ < 500 J m⁻²),^{[ 22 ]} PDUQ3000 indeed has a relatively higher fracture toughness of 6855 J m⁻² owing to the sacrificial HB domains (Figure 1c and Figure S15, Supporting Information). Nevertheless, it exhibits a lower Young's modulus of 1.27 MPa (Figure 1c and Figure S15, Supporting Information) due to the weaker nature of the quadruple HB. PDUQ3000 is therefore located beneath the current upper bound in the toughness versus stiffness diagram (Figure 1c). In distinct contrast, PDUO5000 can break through the trade‐off and demonstrates fracture toughness and Young's modulus ≈2.4 and ≈3.4 times as high as that of PDUQ3000, respectively, because the strength of octuple HB plays an important role in amplifying the toughening and stiffening effect of the microstructure.^{[ 2} , ^{23 ]} To further gain insight into the amplifying effect of the strong HB and the corresponding domains, we conduct density functional theory (DFT) calculations and molecular dynamic (MD) simulations. The Vienna Ab initio Simulation Package (VASP) is utilized for comparing the tensile and shearing mechanics of two polymer chain segments with ureido groups forming ideal quadruple and octuple HB, respectively (Figure 3a ,b; Figures S16 and S17, Supporting Information). To mimic the deformation, the bottom molecule is kept fixed, while the upper one is incrementally shifted upward (tensile; green arrow in Figure 3a) or rightward (shear; red arrow in Figure 3a). The changes in the total energy of the HBs upon deformation are monitored and used to determine the strength between molecules during the tensile and shear tests. It is clear that both the tensile and shearing forces of the octuple HB are much larger than those of the quadruple HB (Figure 3b). It should be noted that the first peaks of force in the shear tests result from the breakage of the HBs, while the second peaks of shear tests are attributed to the atomistic steric effect. Furthermore, the periodic HB domains formed by octuple and quadruple HB are investigated by MD simulations to demonstrate the crucial role of the strength of nanodomains (Figure 3c–e). We apply uniaxial tensile and shear strains (green and red arrow in Figure 3c, respectively) on the formed HB domains. Remarkably, our results show that the tensile and shear stresses of the octuple HB domain are more than twice as high as that of quadruple HB domains. It should be noted that the PDMS phase presents much lower tensile strength compared with HB domains (Figure S18, Supporting Information). The DFT calculations and MD simulations verify that the octuple HB and corresponding nanodomains indeed are considerably stronger than the quadruple HB, thus supporting the optimal enhancement of mechanical properties in dragline spider silk from which our designed synthetic elastomer is inspired by.

Figure 3.

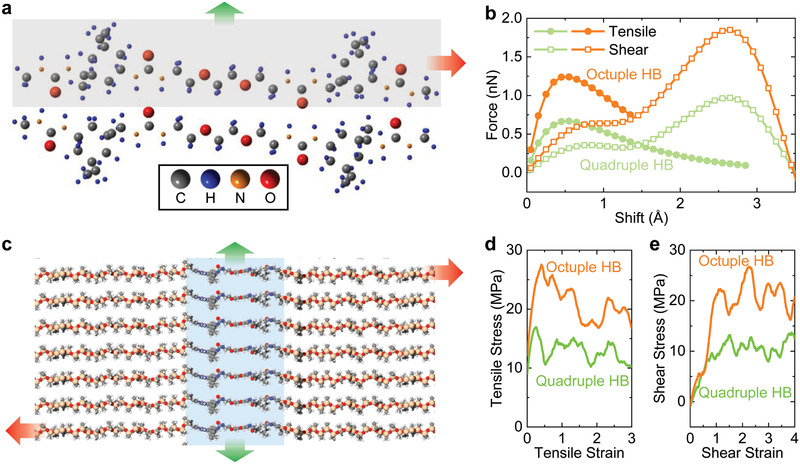
DFT calculation and MD simulations of HB mechanics. a) Tensile (green arrow) and shear (red arrow) deformations of octuple HBs by DFT calculations. The bottom molecule is fixed. b) The tensile and shearing force of octuple and quadruple HBs obtained in DFT calculation by the incremental shifting of 0.1 Å of the upper molecule. c) Tensile (green arrow) and shearing (red arrow) deformations of octuple HB domains by MD simulation. d,e) MD tensile and shearing stress–strain curves of octuple and quadruple HB domains. The DFT calculations and MD simulations demonstrate the higher strength of octuple HB and corresponding nanodomains, respectively, as compared with quadruple HB.

To gain deeper insight into the toughening and stiffening mechanisms, we conduct in situ SAXS measurements upon the uniaxial stretching of PDUO by a homemade drawing instrument (Figure S19a, Supporting Information). The evolution of 2D SAXS patterns (Figure 4a and Movie S1, Supporting Information) and the corresponding stress–Hencky strain (σ–ε_H) curve (Figure 4b) are recorded synchronously during stretching. The SAXS pattern shows a circular ring before stretching (ε_H = 0, Figure 4a), indicating isotropically orientated HB domains. In the initial stretch, the scattering ring turns into an ellipse with the major axis along the transverse direction (TD) (ε_H = 0.35). Upon further stretching, the signal along the TD decays gradually, resulting in two separated crescentic patterns (ε_H = 1), suggesting alignment of the nanodomains along the stretching direction (SD).^{[ 24 ]} From ε_H = 3.2 to ε_H = 4.05, the signal along TD is slightly enhanced. The evolution of signal along TD and SD are detailed by 1D integrated SAXS curves (Figure S19b–d, Supporting Information) and corresponding contour maps (Figure 4c,d). To quantify the change of domains, we extract interdomain distances (d) along the TD (d _TD) and SD (d _SD) (Figure 4e) from the 1D SAXS spectra (Figure S19c,d, Supporting Information) by Bragg's law. The curves of d can be divided into three zones (Figure 4e). In zone I (ε_H = 0–1.0), d _TD decreases from 7.9 (d ₀) to 6.3 nm, while d _SD increases from 7.9 to 12.1 nm. Specifically, in the very initial stages of strain (ε_H < 0.35), the change of d is close to that of affine deformations for incompressible materials, that is, $d_{\text{SD}}=e^{{\epsilon }_{\mathrm{H}}}\times d_0$, $d_{\text{TD}}={(e^{{\epsilon }_{\mathrm{H}}})}^{-0.5}\times d_0$ (Supporting Information),^{[ 15 ]} indicating the affine deformation of the PDMS network and straightening of the chains between conjunction points (Figure 4e).^{[ 24 ]} With the further increase of ε_H in zone I, both d _TD and d _SD gradually deviate from the affine deformation curve due to the deformation of HB domains along SD, where the HB domains become anisotropic.^{[ 25 ]} Moreover, the modulus (derivative of the σ–ε_H curve in Figure 4b) decreases with increasing strain in zone I, resulting from the dissociation of HBs during deformation.^{[ 19 ]} In zone II (ε_H = 1.0–3.2), both d _TD and d _SD barely change with increasing strain, while the modulus decreases and then keeps steady. This can be attributed to the further breakage of HB domains and the slippage of polymer chains.^{[ 19 ]} In zone III (ε_H > 3.2), the slight increase of both d _TD and modulus demonstrates that PDUO is subjected to strain hardening due to further stretch of polymer chains before breakage. In addition, the peaks in TD and SD become broader during stretching (full‐width‐at‐half‐maximum increases; Figure S19e, Supporting Information), indicating the generation of defects, which is the result of reconfiguration of HB domains.^{[ 26 ]} According to the SAXS results, we schematically illustrate the microstructure evolution of PDUO (Figure 4f). Before stretching, the HB domains (orange) and the PDMS‐rich phase (light blue) are distributed homogeneously, showing a bicontinuous structure (Figure 4f–i), consistent with the AFM image in Figure 2e. In zone I, the PDMS chain networks first follow affine deformation, and then the HB domains deform and realign along the SD (Figure 4f‐ii). In this zone, a portion of HBs will break to facilitate the redistribution of HB domains. In zone II, the dissociation of HBs occurs, followed by slippage of polymer chains (Figure 4f‐iii). In zone III, further stretching results in the rupture of the soft PDMS‐rich phase (Figure 4f‐iv). In short, the affine deformation in the initial stage leads to the high Young's modulus of PDUO due to the contribution of strong intact HB domains. In zone I and II, the transformation (including reorientation, rotation, deformation, breakage) of HB domains and friction of polymer chains can dissipate more energy and diminish the stress concentration. In zone III, the rupture of polymer chains further dissipates the energy. All of these microstructure evolutions work synergistically and lead to high fracture toughness and high modulus.

Figure 4.

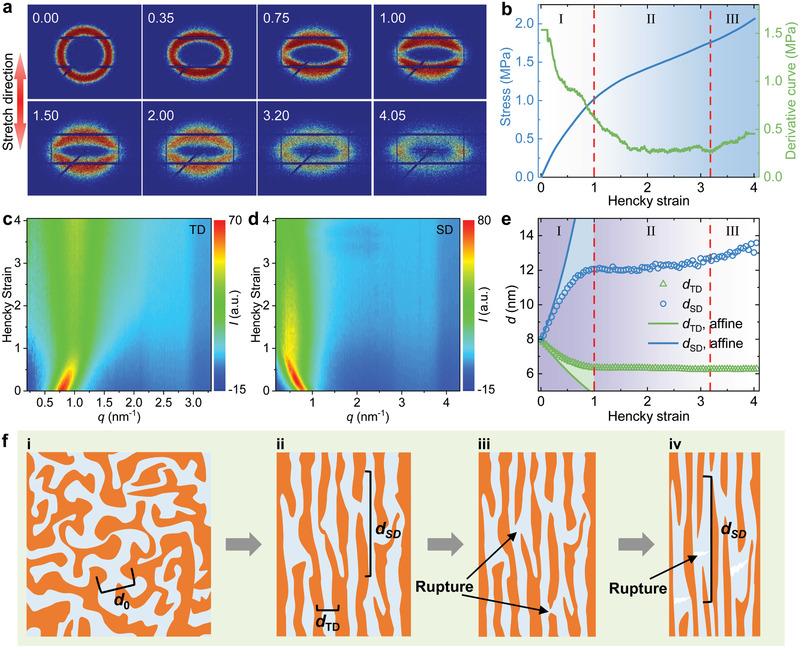
Revealing the microstructural evolution of a stretched PDUO5000 by in situ SAXS experiments. a) The evolution of the 2D SAXS pattern during sample stretching. The inset numbers correspond to the Hencky strains. b) The monitored stress–Hencky strain and its derivative curves during in situ SAXS experiments. c,d) Contour maps of 1D integrated SAXS curves (Figure S19c,d, Supporting Information) in the transverse direction (TD) and the stretch direction (SD), respectively. Upon stretching, the peak along TD moves to a higher scattering vector (q) and then stays at ≈1 nm^–1, while its intensity first decreases and then increases slightly. This is consistent with the evolution of the 2D pattern (Figure 4c; Figure S19c, Supporting Information). The peak along SD moves to low q value and then stays at ≈0.5 nm^–1, while its intensity initially increases followed by a decrease during stretching (Figure 4d; Figure S19d, Supporting Information). e) The change of interdomain distance along the TD (d _TD) and SD (d _SD) with the Hencky strain. The solid blue and green curves indicate the affine deformations for an incompressible material (Supporting Information). f) Schematic of the arrangement of PDUO5000 under different strains. Before stretching, the HB domains (orange) and PDMS‐rich phase (light blue) form a bicontinuous network (i). At the end of zone I, the HB domains align along the SD (ii). After zone I, the rupture of HB domains occurs (iii). When the strain reaches a threshold, the rupture of the PDMS‐rich phase occurs (iv).

Finally, in order to further investigate the tear resistance of PDUO at the microscale, we study the evolution of the region around the notch tip in a pre‐cracked specimen during loading and unloading by in situ scanning electron microscopy (SEM) (Figure 5 ; Movie S2 and Figure S20, Supporting Information). The notch does not propagate through the specimen but instead opens up and blunts at the beginning of the stretching (Figure 5a–c), similar to tough biological materials such as rabbit skin.^{[ 26 ]} Such blunting alleviates the stress concentration at the crack tip.^{[ 26} , ^{27 ]} As the strain further increases, fiber‐like flaws are generated around the crack tip at the edge of the specimen (Figure 5d,e), followed by the delamination (Figure 5f–h).^{[ 28 ]} The specimen does not fracture during the loading because of the limitation on the maximum displacement (Δd _max = 6.7 mm; gauge length ≈ 6 mm, as shown in Figure S20, Supporting Information) of the test device. During the unloading of the specimen (Figure 5i–l), the local damage can clearly be observed at the crack tip (Figure 5i,j). The delamination along the stretching direction, that is, crack deflection, can be attributed to the stiffness mismatch between HB domains and PDMS‐rich phase. Such mismatch in stiffness can stop the propagation of cracks across the specimen (Cook–Gordan crack‐stopping mechanism; Figure 5m).^{[ 29 ]} During the crack deflection, the crack not only turns the original propagating direction but also branches into two new ones (Figure 5k,l). Such crack branching has also been observed in other tough materials with a soft matrix and stiff fibers.^{[ 12g ]} For comparison, a pure Sylgard 184 specimen exhibits a distinctly different crack propagation due to the absence of microphase separation (Movie S3, Figures S21 and S22, Supporting Information). The pre‐crack grows straight without generation of fiber‐like flaws below a relatively low extension (Δd = 1.1 mm). In addition, no reversing crack is observed around the notch tip after the loading/unloading cycle (Δd _max = 1.0 mm). During stretching of the pre‐cracked PDUO, the straightening of polymer chains, the dissociation of HBs and the transformation of HB domains give rise to large strains, allowing large shape changes around the crack tip, thus permitting the blunting of crack tip to alleviate the stress concentration.^{[ 26 ]} Furthermore, both the deflection and branching of cracks can dissipate energy and further contribute to the redistribution of the stresses at the notch tip.^{[ 26} , ²⁷ , ^{30 ]} From the results above, the in situ SEM images demonstrate that the multiscale structure of PDUO can not only function at atomic‐ and nanoscale to increase the fracture energy but also modulate the failure process at the microscale to enhance the tear resistance.

Figure 5.

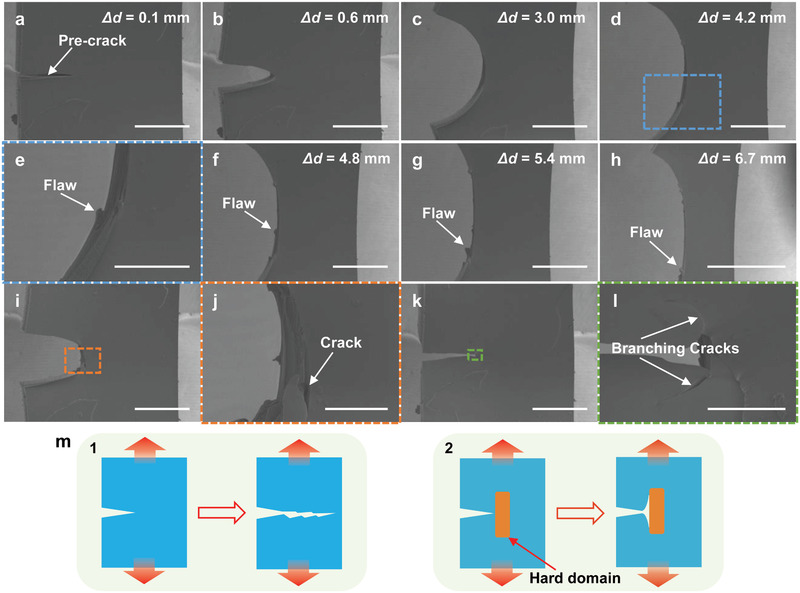
In situ SEM observation of a pre‐cracked specimen of PDUO during a loading and unloading test. Gauge length: ≈6 mm (as shown in Figure S20, Supporting Information). a–c) The pre‐crack opens and blunts in the initial state of loading (Δd = 0.1–3.0 mm, scale bar: 1.00 mm). d,e) A fiber‐like flaw is generated under loading at the edge of the specimen (scale bars: 1.00 mm and 400 µm, respectively). f–h) Additional flaws are generated and propagate along the stretch direction (scale bars: 1.00, 1.00, and 2.00 mm, respectively). i,j) Obvious cracks are observed during unloading (scale bars: 1.00 mm and 200 µm, respectively). k,l) Crack deflection and branching observed in the final unloading state. The cracks change direction rather than propagating in the original direction (scale bars: 1.00 mm and 100 µm, respectively). m) Schematic of the crack propagation pattern. The pre‐crack propagates across the transverse direction due to the homogeneity and brittle nature (1). Cook–Gordan crack‐stopping mechanism: the crack tip is stopped by hard domains followed by the deflection and branching (2). The PDUO behaves according to this mechanism.

To further optimize the mechanical properties of the PDUO, we reduce the molecular weight of the NH₂‐PDMS‐NH₂ segment to 3000 and 1000 Dalton (where the corresponding products are termed PDUO3000 and PDUO1000, respectively) to bring the HB clusters closer together. In the synthesis of PDUO1000, precipitation and failure of synthesis is observed when adding chain extender, suggesting that molecular weights around 1000 Dalton and below are too low for this purpose. This is attributed to the aggregation of polymer chains in the solvent due to highly concentrated HB sites separated by relatively short PDMS chains. PDUO3000, which has shorter PDMS macromonomers compared with PDUO5000, exhibits even higher Young's modulus of 14.7 MPa and similar fracture toughness of 17 016 J m⁻² (Figure 1c; Figure S1, Supporting Information). This observation is due to the effective higher number of HB clusters per unit volume, resulting in a striking improvement capable of exceeding the current trade‐off to an even greater extent. This further supports the profound toughening and stiffening effects of the octuple HB and indicates that as short chains as synthetically possible would yield the best combination of mechanical properties.

3. Conclusion

Inspired by spider silk, we built homogeneous and energy dissipative networks to toughen and stiffen unfilled elastomers by introducing locally dense HB sites into linear PDMS chains. We then revealed the toughening and stiffening mechanisms by a combination of multiscale experiments and atomistic simulations. The results demonstrated that the elastomer possessed a multiscale structure. At the atomic scale, the formed strong octuple HBs increases the friction of polymer chains and the dissipation energy, thus resulting in enhanced stiffness and toughness. At molecular scale, homogeneous polymer networks derived from macromonomers evenly distribute the stress to each polymer chain, thereby reducing the stress concentrations, consequently, enhancing the stretchability and delaying fracture. At the nanoscale, the formed strong HB domains and the resulted bicontinuous structure can increase the stiffness by restricting the network mobility and improve the toughness by dissipating mechanical energy during transformation between different configurations. The ultrastrong HB domains form a continuous phase, enabling the elastomers with enhanced stiffness, while their realignment, slippage, and breakage under loading can dissipate more energy and release stress concentration, therefore leading to ultrahigh fracture toughness. Moreover, during crack propagation, the alignment of HB domains along the stretch direction, as well as the stiffness mismatch between hard HB domains and the soft PDMS‐rich phase, can induce the deflection and branching of the crack, further dissipating energy and alleviating local stress. At the macroscale, the absence of macroscopic defects can delay fracture and grant the materials large extensibility. Consequently, the prepared elastomers demonstrate an unprecedented improvement in both stiffness and toughness, circumventing the current trade‐off between toughness and stiffness. This work paves the way for preparing a new generation of multifunctional unfilled elastomers with simultaneously high toughness and stiffness. Combined with optical transparency and the potential to self‐heal at elevated temperatures, the designed elastomers are expected to impact many areas of research that require exceptionally high mechanical durability, for example, serving as substrates or base materials in applications like wearable devices, flexible electronics, and soft robotics.

Conflict of Interest

Y.Z., Z.Z., and J.H. are involved in commercialization efforts for the materials that are being explored by NTNU Technology Transfer AS.

Supporting information

Supporting Information

Supplemental Movie 1

Supplemental Movie 2

Supplemental Movie 3

Zhuo Y., Xia Z., Qi Y., Sumigawa T., Wu J., Šesták P., Lu Y., Håkonsen V., Li T., Wang F., Chen W., Xiao S., Long R., Kitamura T., Li L., He J., Zhang Z., Simultaneously Toughening and Stiffening Elastomers with Octuple Hydrogen Bonding. Adv. Mater. 2021, 33, 2008523. 10.1002/adma.202008523

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.