The Role of Additives in Suppressing the Degradation of Liquid‐Exfoliated WS₂ Monolayers

Abstract

Group VI transition metal dichalcogenides (TMDs) are considered to be chemically widely inert, but recent reports point toward an oxidation of monolayered sheets in ambient conditions, due to defects. To date, the degradation of monolayered TMDs is only studied on individual, substrate‐supported nanosheets with varying defect type and concentration, strain, and in an inhomogeneous environment. Here, degradation kinetics of WS₂ nanosheet ensembles in the liquid phase are investigated through photoluminescence measurements, which selectively probe the monolayers. Monolayer‐enriched WS₂ dispersions are produced with varying lateral sizes in the two common surfactant stabilizers sodium cholate (SC) and sodium dodecyl sulfate (SDS). Well‐defined degradation kinetics are observed, which enable the determination of activation energies of the degradation and decouple photoinduced and thermal degradation. The thermal degradation is slower than the photoinduced degradation and requires higher activation energy. Using SC as surfactant, it is sufficiently suppressed. The photoinduced degradation can be widely prevented through chemical passivation achieved through the addition of cysteine which, on the one hand, coordinates to defects on the nanosheets and, on the other hand, stabilizes oxides on the surface, which shield the nanosheets from further degradation.

The degradation of liquid‐exfoliated WS₂ monolayers is studied in situ through photoluminescence as function of time and temperature in two surfactant systems (sodium cholate—SC; sodium dodecyl sulfate—SDS). The kinetics reveal that a photoinduced degradation (activation energy ≈25 kJ mol⁻¹) is dominant in SC, while an additional thermal degradation (activation energy ≈50 kJ mol⁻¹) is observed in SDS.

1. Introduction

Since the demonstration that group VI transition metal chalcogenides undergo a transition from an indirect‐bandgap semiconductor in the bulk to a direct‐bandgap semiconductor in the monolayer in 2010,^{[ 1 ]} tremendous research efforts have been devoted to the investigation of their optical properties in light of potential applications in (opto)electronics.^{[ 2 ]} While group VI TMD monolayers have been considered stable in ambient conditions, awareness is growing that oxidative degradation can indeed occur. Understanding the degradation behavior of 2D materials is crucial in order to judge their applicability in devices, as they should withstand the fabrication and operation conditions for extended periods of time. For example, it has already been demonstrated in 2013 that the on‐current in MoS₂ field effect transistors irreversibly decreases (accompanied with a shift in the threshold voltage) in the presence of O₂.^{[ 3 ]} This can be rationalized through adsorption of O₂ to sulfur vacancies and subsequent permanent doping due to the relatively high adsorption energies that were calculated to be 3.4 eV through density functional theory.^{[ 4 ]} Such high adsorption energies and the irreversible nature of the adsorption can be classified as chemisorption, or put in other words, oxidation of the material.

To date, several experimental and theoretical studies have investigated the oxidation and degradation of group VI TMD monolayers. Most studies consider CVD‐grown or micromechanically exfoliated WS₂ and MoS₂ on either SiO₂ or sapphire. An overview of observations and types of materials is listed in Table 1 .

Table 1.

Selected overview of experimental results for the degradation of sulfide TMD nanosheets

Observation	Material–synthesis–substrate	Ref.
At elevated temperatures degradation in ambient or oxygen atmosphere is observed.	MoS2–micromech.–Au(111); WS2/MoS2–CVD–SiO2/Al2O3; MoS2–bulk	[ 6 , 7 , 8 , 9 , 10 ]
Ageing under ambient conditions leads to degradation of the material.	MoS2–micromech.–Au(111); WS2/MoS2–CVD–Al2O3	[ 6 – 8b ]
Irradiation above a fluence threshold degrades the material.	WS2/WSe2/MoS2–CVD–SiO2/Al2O3	[ 11a – 13 ]
Moisture increases the degradation rate.	WS2/MoS2–CVD–SiO2/Al2O3	[ 7 , 11 , 12 ]
Heating leads to elevation at grain boundaries, which is likely caused by oxides.	WS2–CVD–graphene/SiO2	[ 8 , 9 ]
Degradation decreases the PL emission.	WS2/MoS2–CVD–Al2O3	[ 7 ]
Degradation increases the PL emission near to defect regions.	MoS2–micromech.–SiO2	[ 10 ]
Graphene is found to quench excitons preventing oxidation of WS2.	WS2–CVD–graphene	[ 14 ]

The theoretical studies found pristine basal planes to be very resilient to an attack by molecular oxygen, even though their oxidation, particularly by molecular oxygen, is thermodynamically favorable.^{[ 5 ]} These findings are rationalized by very high dissociation energies of molecular oxygen on the basal plane, which are thermally inaccessible.

Nonetheless, incorporation of oxygen into the crystal lattice was observed by STM upon ageing of MoS₂.^{[ 6 ]} Similar results are reported by Koratkar and co‐workers,^{[ 7 ]} who use optical microscopy and X‐ray photoelectron spectroscopy (XPS), to investigate the impact of ageing in moisture‐rich and dry environments. The presence of a desiccant in the storage container greatly improved material stability over the course of 1 year and therefore a catalytic effect on the oxidation was ascribed to water.^{[ 7 ]} As a result of ageing, the authors observed formation of holes and cracks on the sheets and a decreased A‐exciton photoluminescence (PL). These findings strongly suggest that sulfur vacancies can be the origin of oxidation resulting in incorporation of oxygen.

Similar to vacancies, edges and grain boundaries are generally believed to be centers of reactivity.^{[ 8 ]} The increased reactivity of grain boundaries causes their preferential oxidation, which can be exploited to visualize such features.^{[ 8} , ^{9 ]} Localized edge oxidation is also reported by Ni and co‐workers, who investigated micromechanically cleaved MoS₂.^{[ 10 ]} After annealing at 500 °C and subsequent exposure to ambient oxygen, they find formation of Mo^+VI oxides by XPS. In contrast to most other studies, an increase in PL emission upon oxidation is observed. They ascribe this increase to oxygen‐induced p‐doping, which presumably compensates intrinsic n‐doping of their starting material.

Furthermore, it was reported that degradation can be photoinduced. The susceptibility of CVD‐grown WSe₂ toward UV‐light has been reported.^{[ 11 ]} The observed effect was at first ascribed to UV‐light‐induced formation of oxygen radicals, which then react with the material, e.g., the material itself was not assumed to be activated. A study by Atkin et al.^{[ 12 ]} suggests that this is not necessarily the case, as degradation of WS₂ nanosheets was observed by irradiation with a 440 nm laser. At this wavelength, the photon energy is insufficient to form reactive oxygen species without a catalyst.^{[ 13 ]} During consecutive PL measurements at different laser fluences, it was found that the reaction does not proceed at fluences of ≈2 mJ µm⁻² and lower.^{[ 12 ]} These findings were further elaborated by Fuhrer and co‐workers,^{[ 13 ]} who used laser scanning confocal microscopy to study the light‐induced degradation of CVD‐grown WS₂ on sapphire. Here, the fluence threshold necessary for oxidation is assumed to be much lower than anticipated by Atkin et al.,^{[ 12 ]} hypothesizing no barrier at all. Further, a wavelength dependence showed that oxidation preferrentially occurs when electronic transitions in WS₂ are excited.

Since the mentioned publications deduce degradation behavior from substrate supported samples, an influence on the degradation behavior is expected. However, substrate effects on material degradation are rarely discussed and remain ambiguous as, e.g., graphene is reported to greatly increase, as well as eliminate material degradation.^{[ 9} , ^{14 ]}

The studies summarized above illustrate the complexity of the degradation, point to significant substrate effects and challenges of precisely monitoring degradation. In all cases, individual CVD‐ grown or micromechanically exfoliated nanosheets were analyzed microscopically and spectroscopically. However individual nanosheets can show differences in composition, edge species, contaminants, and defect densities^{[ 15 ]} in addition to substrate effects which all might affect the oxidation. In addition, only localized information on individual sheets is accessible and it is extremely challenging to gather significant statistics to access the average properties. Therefore, to complement the locally resolved picture, it is required to study large ensembles of nanosheets in a homogeneous environment.

In light of the degradation of TMD monolayers, it is important to devise passivation strategies to suppress this degradation. Since it was observed in different studies that sulfur vacancies (SVs) are readily filled with oxygen,^{[ 6} , ^{16 ]} it is reasonable to assume that further oxidation can occur starting from these defect sites. A number of studies have shown that thiols can bind to sulfur vacancies, in particular in ultrahigh vacuum conditions^{[ 17 ]} or in the case of chemically exfoliated TMDs in the 1T polymorph.^{[ 18 ]} While a recent report suggests that thiol functionalization can also be achieved in the case of liquid‐exfoliated 2H‐MoS₂,^{[ 19 ]} this is still under debate, as other studies have confirmed that this does not seem to be the case.^{[ 20 ]} Different possible reaction pathways have been theoretically investigated^{[ 21 ]} and revealed that the most likely reaction pathway is strongly dependent on the presence of different types of defects (e.g., S‐adatoms, S‐vacancies or both). As such, defect passivation through coordination of thiols to SVs may or may not be achievable, depending on the type of sample. This makes it important to compare samples produced from different techniques.

A complementary approach to study degradation and the potential of defect passivation would be to use samples with a distribution of sizes in the liquid phase. These can be prepared by liquid‐phase exfoliation (LPE), which is a widely used top down production technique.^{[ 22 ]} In LPE, exfoliation is achieved mechanically in the liquid environment through sonication or shearing. Aggregation of nanosheets is then prevented by suitable solvents with matching solubility parameters or surfactants.^{[ 23 ]} While size and thickness distributions are initially extremely broad,^{[ 24 ]} they can be narrowed by size selection techniques.^{[ 25 ]} For example, it has been demonstrated that high quality, monolayer‐rich TMD dispersions can be prepared through liquid cascade centrifugation,^{[ 26 ]} which exhibit optical properties similar to micromechanically exfoliated nanosheets, e.g., narrow linewidth photoluminescence and characteristic thickness dependent shifts of the excitonic features with layer number.^{[ 26} , ^{27 ]} Notably, LPE can be applied to a broad range of layered materials and previous work on nanosheets prone to oxidation such as black phosphorus,^{[ 28 ]} TiS₂,^{[ 29 ]} MoO₂,^{[ 30 ]} MXenes^{[ 31 ]} or NiPS₃ ^{[ 32 ]} has shown that degradation of the material can be tracked through optical extinction spectroscopy measured as function of time. This approach presents an interesting opportunity, since the liquid environment can be exchanged allowing to draw some conclusion on the oxidation pathway. For example, in the case of black phosphorus^{[ 28 ]} and TiS₂,^{[ 29 ]} it was demonstrated that degradation can be significantly slowed down in some organic solvents such as N‐methyl‐2‐pyrrolidone opposed to aqueous surfactant media. While this suppressed degradation is an advantage of using organic solvents over surfactants, monolayers can be more conveniently isolated in aqueous surfactant solution compared to solvents.^{[ 33 ]}

To date, the degradation of LPE group VI TMDs in ambient atmosphere has not yet been studied in detail. Possibly, this is due to the fact that they are still somewhat more stable than the materials mentioned above. In this study, we address this point. Using established protocols of size selection,^{[ 26 ]} we enrich WS₂ exfoliated in aqueous surfactant solution in monolayers and track the degradation as function of time and temperature through photoluminescence spectroscopy. Note that, in contrast to extinction spectroscopy which is typically used to study degradation of LPE nanosheets, the PL measurement allows us to selectively track monolayers due to the negligible contribution of few‐layers to the emission.^{[ 1 ]} Since it was recently observed that the reactivity of LPE WS₂ depends on the chemical nature of the stabilizer,^{[ 34 ]} we compare the degradation in the surfactant sodium cholate (SC) and sodium dodecyl sulfate (SDS). Well‐defined degradation kinetics are observed that allow us to determine activation energies of the oxidation. The experiments were designed in such a way that it is possible to distinguish between a photoinduced and a thermal degradation pathway—the latter one playing a minor role in SC. Finally, we demonstrate that the elaborated protocol and analysis can be used to devise passivation strategies to suppress degradation.

2. Results and Discussion

The dispersions of WS₂ nanosheets stabilized in water by the two different surfactants, SC and SDS, were produced by tip sonication followed by liquid cascade centrifugation^{[ 26 ]} to increase the monolayer content (see the Experimental Section). To confirm that the samples are of suitable optical quality, the dispersions were first subjected to room‐temperature extinction, Raman, and fluorescence spectroscopy (Figure S1, Supporting Information). It was possible to isolate three size‐selected fractions (denoted as small s‐WS₂, medium m‐WS₂, and large l‐WS₂) with sufficient A‐exciton PL primarily stemming from monolayers.^{[ 26 ]} This can be evaluated by conducting Raman measurements on liquid droplets with an excitation wavelength of 532 nm, where the photoluminescence is recorded simultaneously with the vibrational modes^{[ 26 ]} (see Figure S1C,D, Supporting Information). From our experience, samples with PL/Raman ratio > 5 can conveniently be measured in standard fluorescence spectrometers (see the Experimental Section) as exemplarily shown by the photoluminescence excitation contour plots in Figure S1E,F of the Supporting Information. From the optical extinction spectra, average lateral sizes and layer numbers were estimated (Table S1, Supporting Information) using established metrics.^{[ 26 ]} The average lateral sizes range from ≈35 nm in s‐WS₂ to ≈70 nm in l‐WS₂. The nanosheets are thus much smaller than micromechanically exfoliated or CVD‐grown monolayers so that we expect some edge effects to be discernible. The lateral dimensions were confirmed through atomic force microscopy (AFM) after dip‐coating of Si/SiO₂ coated with (3‐aminopropyl)triethoxysilane. This deposition method (see the Experimental Section), results in minimal aggregation and contamination from solvent/surfactant as outlined in detail in literature.^{[ 24} , ^{35 ]} The AFM images (Figures S2–S4, Supporting Information) reveal morphologies characteristic of nanosheets (e.g., sharp edges) in spite of the small lateral dimensions. The overall appearance, size, and thickness is comparable in the SC and SDS‐exfoliated samples with the exception that the thinnest observable sheets in SDS have a lower apparent AFM thickness (1.5–2 nm) on the basal plane with an elevated thickness (≈1 nm) at the edge opposed to the nanosheets in SC which have a more homogeneous apparent AFM height of 2.5–3 nm. This is discussed in more detail in the Supporting Information (Figures S4 and S5, Supporting Information). While these apparent AFM heights are much larger than the crystallographic thickness of one layer or indeed the height of CVD‐grown or micromechanically exfoliated monolayers, previous studies confirm that LPE TMD nanosheets exfoliated in SC with an apparent AFM height of 2.5–3 nm are indeed monolayers^{[ 36 ]} that appear thicker in the AFM, presumably due to adsorbed surfactant.

Due to the remaining polydispersity of the samples in spite of the size selection, it is important to verify that the observed PL feature shows the typical characteristics of the A‐exciton response of WS₂ monolayers. To this end, we subjected the size‐selected dispersions to photoluminescence measurements at different temperatures. Note that the temperature range is restricted to 5–80 °C to avoid freezing and evaporation of the solvent (water), respectively. In spite of this restricted temperature regime, we observe a redshift of the PL, an increase in linewidth and decrease in intensity with increasing temperature (Figures S6 and S7, Supporting Information) in agreement with measurements on micromechanically exfoliated monolayers.^{[ 37 ]} While the linewidth and position is restored when cooling the sample back down (Figure S7B,C, Supporting Information), the PL intensity does not fully recover (Figure S7A, Supporting Information). This effect is more pronounced for the fraction containing the smallest nanosheets and, as will be elaborated in detail below, is attributed to a degradation of the monolayers at elevated temperatures and under irradiation. This initial experiment suggests that the degradation of liquid‐suspended WS₂ can be tracked by measuring the photoluminescence as function of time and temperature.

To investigate this in more detail, the samples were heated to different temperatures in the PL spectrometer and their PL spectra were acquired after varying time intervals. During the measurements, the samples were continuously irradiated with light from a 450 W xenon arc lamp at a wavelength of 440 nm. Note that in contrast to excitation with a laser (e.g., during measurements in Raman spectrometers), the excitation power is intrinsically relatively low in such a setup (here 9 µW). Since the temperature has a pronounced impact on the excitonic emission as described above, the samples were cooled back to room temperature after certain time intervals of heating (15–30 min) to also acquire the corresponding room temperature spectra. The measurement protocol is schematically summarized in Figure 1A. Examples of PL spectra of s‐WS₂ in SC heated to 50 °C are shown in Figure 1B,C, with Figure 1B displaying spectra measured at room temperature and Figure 1C showing measurements at an elevated temperature. All spectra can be fitted well to a single Lorentzian corresponding to an excitonic emission as observed previously for LPE WS₂ stabilized in a surfactant solution.^{[ 26} , ^{27 ]} From these fits, the PL area, intensity, position, and full width at half maximum (FWHM) were extracted for each spectrum. Both the measurement at room temperature and at 50 °C show a drop in the PL intensity with time. In some data sets, a redshift of up to 10 meV is observed after heating/irradiation. The origin of this shift is discussed in Section S3.1 of the Supporting Information.

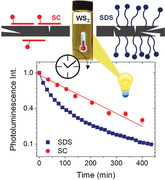
Figure 1.

Fluorescence of s‐WS₂‐SC as function of time and temperature. A) Schematic of the measurement profile involving iterative heating and cooling cycles (vertical lines). Measurements were taken both at elevated temperature and 20 °C as indicated by the black dots. B,C) Photoluminescence spectra of s‐WS₂‐SC with 440 nm excitation acquired at different time intervals measured at 20 °C (B) and elevated temperature, in this case 50 °C (C). The data is fit to a single Lorentzian as indicated by the solid lines to extract PL height, area, position, and full width at half maximum. D) Decay kinetics of the PL response of s‐WS₂‐SC heated to 50 °C. PL area and height of the data sets measured at 20 and 50 °C, respectively, is compared. The data was normalized to the value of the initial measurement prior to heating, as well as the first measurement at elevated temperatures, respectively. E) Normalized PL area (measured at 20 °C) of s‐WS₂‐SC heated to different temperatures as function of time. The data is described well by a single exponential fit (solid lines). F,G) Lifetimes (F) and portion of reacted material (G) as function of inverse temperature extracted from the fits in (E).

In Figure 1D, the PL intensity normalized to the respective value of the initial measurement prior to heating and irradiation is plotted as function of time for s‐WS₂‐SC (50 °C). Both PL area and intensity are plotted from the two data sets acquired at room temperature and elevated temperature, respectively. All the data follows the same functionality and can be described by a single exponential fit function. A similar behavior is observed for heating/irradiation at temperatures between 40 and 80 °C (Figure 1E). It is clear that the decay in PL is accelerating with increasing temperature. Fitting the data using a single exponential function allows us to extract the half‐life of the decay and the portion of reacted material in analogy to previous reports where degradation of LPE nanosheets was tracked through extinction spectroscopy.^{[ 28} , ²⁹ , ^{32 ]} The lifetimes and portion of reacted material are plotted as function of the inverse temperature in Figure 1F,G. While the reaction rate increases with increasing temperature (Figure 1F), there is only a minor effect on the portion of reacted material. Already at 40 °C, the PL almost disappears completely (after infinite time) suggesting severe degradation of the monolayers.

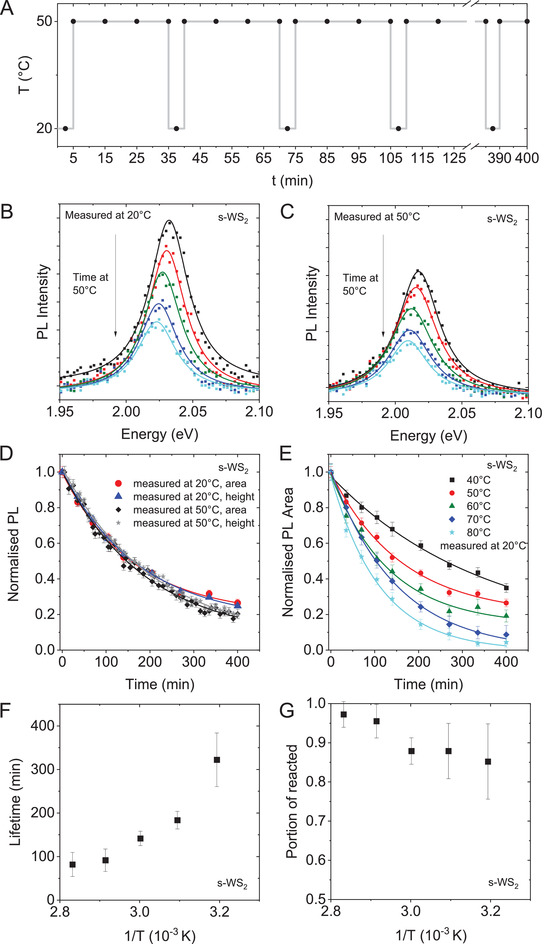
To investigate this in more detail, all three fractions of size‐selected WS₂ dispersions stabilized both in SC and SDS were subjected to the same type of measurements. In Figure 2A, the evolution of the normalized PL area as function of time is shown for s‐WS₂ and l‐WS₂ in SC heated and irradiated to 50 °C. The complete data sets are shown in Figures S8 and S9 of the Supporting Information. The data linearizes on the semilogarithmic plot, which allows to determine the lifetime with greater precision than in exponential fits which have more degrees of freedom for the fit. This linearization points to (pseudo) first order degradation kinetics. The lifetimes extracted from the linear fits of s‐WS₂ and l‐WS₂ measured at different temperatures are plotted as function of inverse temperature on a semilogarithmic scale in Figure 2B. Again, the data linearizes which means that the activation energies (E _A) of the degradation of monolayer WS₂ can be extracted from the slope according to the Arrhenius equation. While the decay is faster for s‐WS₂ compared to l‐WS₂, the activation energies are in a similar range (20–30 kJ mol⁻¹, see Table 2 ). This is similar to the activation energy of the oxidation of LPE NiPS₃ ^{[ 32 ]} and agrees with theoretical predictions of an edge‐centered oxidation mechanism of monolayered MoS₂.^{[ 38 ]}

Figure 2.

Comparison of degradation of WS₂ in sodium cholate and sodium dodecyl sulfate. A) Normalized PL area as function of time of small (black) and large (red) WS₂ heated to 50 °C in the presenence of light in aqueous SC on a semilogarithmic scale. The data linearizes suggesting first order decay kinetics with one dominant reaction pathway. B) Lifetime as function of inverse temperature for s‐ and l‐WS₂ in SC from the linearized fits in (A) on a semilogarithmic scale. Smaller nanosheets degrade more rapidly than larger ones. Arrhenius‐type behavior is found that allows to determine the activation energies as 20.0 (± 5.6) kJ mol⁻¹ (s‐WS₂) and 28.7 (± 2.3) kJ mol⁻¹ (l‐WS₂). C) Normalized PL area as function of time of small (black) and large (red) WS₂ heated to 50 °C in the presence of light in aqueous SDS on a semilogarithmic scale. The SDS data does not linearize and is fit to a biexponential decay pointing to two parallel reaction pathways. D) Plot of the short and long lifetime components as function of inverse temperature for s‐ and l‐WS₂ in SDS from the biexponential fits in (C) on a semilogarithmic scale. No linearization and no clear nanosheet size dependence are observed.

Table 2.

Activation energies of the size‐selected WS₂ samples exfoliated and stabilized in sodium cholate and sodium dodecyl sulfate, respectively

	E A photoinduced [kJ mol−1]	E A thermal [kJ mol−1]
SC
l‐WS2 (1–5k g)	28.7 ± 2.3
m‐WS2 (5–10k g)	27.8 ± 8.8
s‐WS2 (10–30k g)	20.0 ± 5.6
SDS
l‐WS2 (1–5k g)	24.3 ± 5.4	54.8 ± 9.1
m‐WS2 (5–10k g)	21.8 ± 3.0	38.9 ± 5.6
s‐WS2 (10–30k g)	29.6 ± 3.6	51.5 ± 6.0

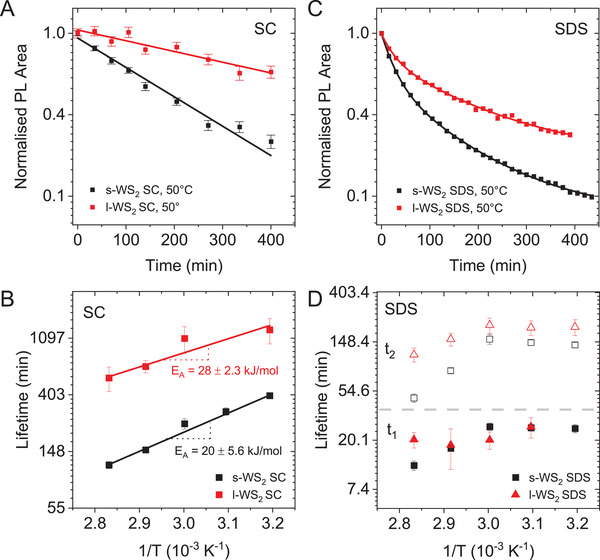
Interestingly, a different degradation behavior is observed in SDS‐stabilized WS₂ dispersions. As is shown in Figure 2C for s‐WS₂ and l‐WS₂‐SDS heated/irradiated to 50 °C, the decay kinetics of the PL area do not linearize on the semilogarithmic scale. To fit the data, several other kinetic models were tested, to determine which decay law describes the observed behavior best. The best R ² values, as well as the most likely continuation of the curves in both linear and semilogarithmic decays were obtained with the biexponential decay, indicating two parallel (pseudo) first order reactions following the decay law

$$\left[\mathrm{A}\right]=\left[{\mathrm{A}}_1\right]{\mathrm{e}}^{-\frac{t}{{\tau }_1}}+\left[{\mathrm{A}}_2\right]{\mathrm{e}}^{-\frac{t}{{\tau }_2}}+\left[{\mathrm{A}}_{\mathrm{constant}}\right]$$ (1)

where [A_constant] is the material unaffected by both reactions, [A_1/2] are the amount of material decaying via pathway 1 or 2, and τ_1/2 are the respective lifetimes. Note that the portions of concentration being affected by reaction 1 or 2 apply to different fractions of [A], likely associated with an attack on different reaction sites on the nanosized objects. Otherwise a parallel reaction would still follow a (pseudo) first order degradation and thus show linear behavior in semilogarithmic plots.

This fitting was applied to all other measured data of small, medium, and large WS₂ stabilized in SDS at temperatures ranging from 40 to 80 °C. In all cases, the data was well described by the biexponential decay model (Figure S10, Supporting Information). From these fits, the lifetimes of the two decay pathways were extracted and plotted as function of inverse temperature in Figure 2D. In the case of the WS₂‐SC data (Figure 2B), the data can be linearized according to the Arrhenius equation to extract activation energies as described above. However, this is clearly not the case for WS₂‐SDS. The lifetimes, which were extracted by using Equation (1), show parallel slow and fast reaction pathways, neither of which seem to follow a linear curve in the Arrhenius plot in Figure 2D. Additionally, the large material fraction shows considerable variation of τ₁ likely due to a larger uncertainty in the overall evaluation procedure associated with the lower initial PL intensity.

The presence of two decay pathways might suggest a thermal and photoinduced reaction. To test this, s‐WS₂ stabilized in SC and SDS, respectively was heated ex situ to 80 °C in the absence of light for 400 min. The PL spectra normalized to the PL intensity prior to heat treatment are displayed in Figure 3A,B for SC (Figure 3A) and SDS (Figure 3B) in comparison to the data from simultaneous heating and irradiation. In the case of SC, heating in the absence of light does not change the PL response (Figure 3A) in contrast to SDS, where a decrease in the PL intensity is also observed for heating in the absence of light, albeit less severe than for simultaneous heating and irradiation. This suggests that only a photoinduced degradation occurs in WS₂‐SC, whereas both photoinduced and thermal degradation take place in WS₂‐SDS.

Figure 3.

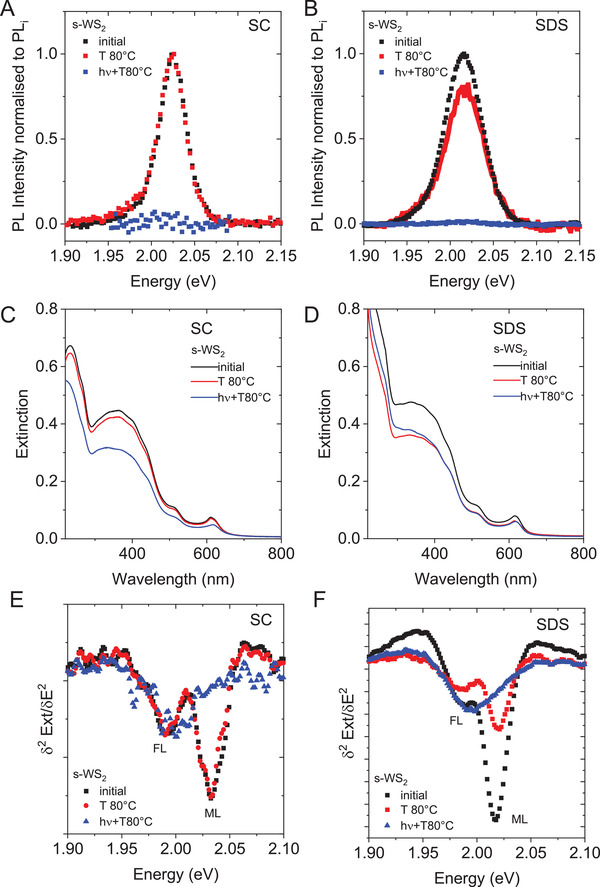
Photoinduced versus thermal degradation of s‐WS₂ in sodium cholate and sodium dodecyl sulfate. A,B) PL spectra of s‐WS₂ in SC (A) and SDS (B) after heating the dispersion in the absence of light to 80 °C for 400 min (ex situ heating, red) and in the presence of light (in the fluorescence spectrometer, 440 nm excitation, blue). The PL intensity was normalized to the initial value prior to temperature treatment. C,D) Extinction spectra of the dispersions in (A) and (B). While only minor changes are observed after heating the dispersion in SC, a drop in intensity is observed for the sample heated and irradiated (C). In SDS (D), a drop in intensity is observed in both cases. E,F) Second derivative on the A‐exciton region in the extinction spectra. Initially, both the monolayer (ML) and few‐layer (FL) component are visible. In SC (E), no change of the second derivative is observed after heat treatment suggesting that no aggregation occurs at elevated temperatures. After heating and irradiation, the monolayer component is reduced in intensity. In SDS (F), both monolayer and few‐layer component are reduced in intensity after heating, while heating and irradiation reduces the intensity of the monolayer more drastically.

For a complementary analysis, the samples were subjected to extinction spectroscopy. The corresponding spectra are displayed in Figure 3C,D for s‐WS₂‐SC (Figure 3C) and s‐WS₂‐SDS (Figure 3D). The complete data sets are shown in Figures S9 and S11 of the Supporting Information. In agreement with the PL spectra, the extinction of s‐WS₂‐SC is fairly unaffected by the isolated heat‐treatment (red), while a significant drop in intensity is observed for the heat‐treated and irradiated sample (blue). In contrast, the extinction spectra of s‐WS₂‐SDS show a decrease in intensity in both cases. Note that in contrast to PL, extinction spectra will show contributions from both monolayer and few‐layered nanosheets. Due to the exponential blueshift of the A‐exciton with decreasing nanosheet thickness in group VI TMDs,^{[ 26} , ²⁷ , ^{39 ]} in combination with the narrow linewidth of the A‐exciton response in LPE WS₂,^{[ 27 ]} the A‐exciton typically shows a splitting of monolayer WS₂ absorbance and the sum of all few‐layers in the extinction spectra, which can be best observed in the second derivative.^{[ 26 ]} This is plotted in Figures 3E,F for s‐WS₂‐SC and s‐WS₂‐SDS, respectively. Indeed, the monolayer component at ≈2.03 eV can be clearly resolved in both cases in the samples prior to the heat treatment at higher energy than the few‐layer peak at ≈1.99 eV. After the heat treatment in the absence of light, the A‐exciton resonance of s‐WS₂‐SC remains unaltered (Figure 3E). This agrees well with the (unaltered) emission observed in this sample. In addition, this data emphasizes that the decrease in PL caused by heating/irradiation is indeed a result of degradation, rather than aggregation at elevated temperature, as no aggregation is observed in the heat‐treated sample that was not exposed to light. The samples of s‐WS₂‐SC that were simultaneously heated and irradiated show a significant decrease of the A‐exciton response stemming from monolayers, while few‐layers are largely unaffected. This points to a selective degradation of monolayers. In the case of s‐WS₂‐SDS (Figure 3F), both the monolayer and few‐layer component decrease in intensity in the sample that was heated in the absence of light, while the heated/irradiated dispersion shows a more significant loss of the monolayer A‐exciton component. This suggests a degradation of both monolayers and few‐layers through the thermal degradation pathway with SDS as surfactant.

To confirm this, WS₂‐SC and WS₂‐SDS prior to and after heating (4 h, 80 °C), as well as heating and simultaneous irradiation (4 h, 80 °C, 440 nm) were subjected to AFM. Samples of m‐WS₂ were chosen as compromise between lateral size and monolayer content. When depositing the samples of the reaction mixture, mostly ill‐defined and small particles (at the resolution limit of our AFM) are observed (Figure S12, Supporting Information). While these can be the degradation products, we cannot exclude that the deposits are surfactant due to the low WS₂ concentration in the experiment (initially ≈0.01 gL⁻¹ WS₂ in 0.1 gL⁻¹ detergent). To examine the morphology of the nanosheets that remained intact after heating and heating/irradiation, the samples were centrifuged at 30k g, the supernatant decanted and discarded and the sediment redispersed in deionized (DI) water in 1/3 of the volume. Representative images are shown in Figure 4A,B and Figures S13 and S14 (Supporting Information). In both SC (Figure 4A; Figure S13, Supporting Information) and SDS (Figure 4B; Figure S14, Supporting Information), the characteristic nanosheet morphology is well retained after heating in the absence of light. After heating and simultaneous irradiation, edges are less well defined. Some aggregated objects are also observed which seem to be primarily connected at edges in the case of SC in contrast to SDS.

Figure 4.

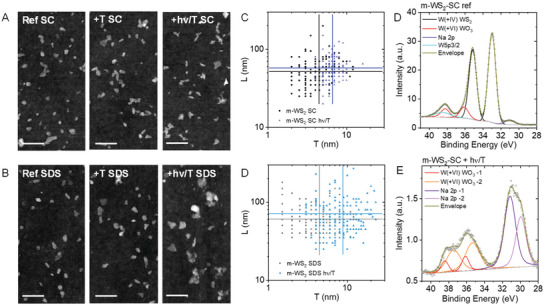
Additional characterization of the samples after heating and irradiation. A,B) AFM images of m‐WS₂ in SC (A) and SDS (B) of the reference, the samples after heating (+T, 4 h at 80 °C), and after heating and simultaneous irradiation (+hν/T, 4 h at 80 °C, 440 nm). Scale bars: 100 nm. Samples were deposited after removing the degradation products as supernatant after centrifugation to be able to investigate the morphology of the WS₂ that is still intact after the degradation experiment. C,D) Statistical analysis of the nanosheet dimensions prior to and after heating/irradiation in SC (C) and SDS (D). The vertical and horizontal lines indicate the arithmetic average. E,F) Fitted W4f XPS core‐level spectra of m‐WS₂‐SC drop‐cast on ITO (without washing) prior to (E) and after (F) heating/irradiation.

For a more quantitative assessment of the morphology, the lateral size and thickness of ≈150 individual nanosheets (no aggregates) was measured in each sample. The resultant distribution histograms are shown in Figures S15 and S16 of the Supporting Information. The effect of the heating and heating/irradiation can best be observed in a scatter plot of length as function of thickness, as shown in Figure 4C,D and Figure S17 (Supporting Information). In such a plot, each data point represents an individual nanosheet. After heating in the absence of light, the nanosheet size distribution did not change in the case of SC (Figure S17A, Supporting Information), while fewer of the smallest/thinnest sheets are observed in SDS (Figure S17C, Supporting Information). After heating and simultaneous irradiation, no nanosheets with an apparent AFM thickness of <4 nm are detected in SC (Figure 4C) suggesting selective destruction of monolayers. This is similar in SDS (Figure 4D), but with a lower thickness cut‐off of 3 nm. In SC, the length distribution remained comparable (Figure S15A,E, Supporting Information), while it broadened and extended to larger dimensions in SDS (Figure S15B,F, Supporting Information). In SDS, this effect is also observed in the thickness histograms (Figure S16B,F, Supporting Information). As discussed in more detail in the Supporting Information, this is consistent with degradation of both monolayers and small few‐layers in the case of SDS. Thus, the AFM confirms the conclusions drawn from the optical spectra.

In an attempt to characterize the degradation products, X‐ray photoemission spectroscopy (XPS) was performed. Initially, samples were filtered onto alumina membranes and washed with deionized water prior to the measurement to minimize contributions from surfactant. In this case, the spectra showed no difference between the reference and the heated/irradiated samples (Figure S18, Supporting Information) with very minor oxidation (6% in the reference and 3.5% in the heated/irradiated sample based on the fitting of the W4f core level spectra, Table S2, Supporting Information). This strongly suggests that degradation products are water soluble and removed by filtration, which would be expected for tungstates and sulfates.

Therefore, the reaction mixtures of the m‐WS₂ sample sets were deposited on ITO‐coated glass without employing any washing steps. Note that in this case, a pronounced contribution from the surfactant to the XPS spectra is expected, in particular in the case of the more dilute samples after heating and heating/irradiation. The data is displayed in Figure 4E,F and Figures S19 and S20 (Supporting Information). The W4f core level spectra of the m‐WS₂‐SC reference (Figure 4E), can be fit well with two sets of doublets in addition to two singlets. The singlet at ≈31 eV is attributed to the Na2p core level and stems from the surfactant (purple trace). The singlet at 38.5 eV is attributed to the W5p_3/2 orbital (cyan trace). Thus, only the two doublets correspond to the W4f core level. The doublet at lower binding energy (at a W4f_7/2 binding energy of ≈33 eV, black trace) is assigned to tungsten in the oxidation state +IV, i.e., WS₂. At higher binding energy (W4f_7/2 binding energy of ≈36 eV), W(+VI) species are observed which are assigned to WO₃ (red trace). These constitute 13% of the W4f core level. After heating in the absence of light, a larger contribution from Na is observed in the spectra (Figure S19B, Supporting Information) due to the lower concentration of WS₂ relative to the surfactant. In addition, the signals broaden, but no significant increase in the tungsten oxide content is observed which confirms that WS₂ is thermally stabilized with SC as surfactant. Similar to the temperature‐treated sample in the absence of light, the contribution of Na2p from the surfactant is significant in the sample after heating and simultaneous irradiation (Figure 4F, purple traces). Further, the doublet at intermediate binding energy (≈30–35 eV) that would correspond to W(+IV), i.e., WS₂ cannot be resolved. In the binding energy region of W(+VI), two sets of doublets are observed (red and orange traces). Thus, XPS suggests almost complete degradation of WS₂ to tungsten(VI) oxides. Note that this is certainly an overestimate, as XPS on filtered samples revealed the presence of intact WS₂, absorbance spectroscopy still showed the characteristic spectrum of WS₂ (Figure 3C,D) and nanosheets were still observed in AFM (after removal of the degradation products). In addition, the Raman modes of WS₂ in these samples are completely unaffected by the heat treatment and irradiation (Figures S22 and S23, Supporting Information). This is due to the fact that WS₂ is resonantly excited in Raman spectroscopy in contrast to oxides as described recently for TMDs elsewhere.^{[ 40 ]}

A similar picture is observed for the samples of m‐WS₂‐SDS (Figure S20, Supporting Information). However, in contrast to m‐WS₂‐SC, an increase in the oxide content from 8.3% to 23.5% is observed in the W4f core level spectra after heating in the absence of light. This confirms that a purely thermal degradation occurs with SDS as surfactant. Overall, the S core level spectra also confirm the conclusions drawn from the W4f core level spectra (Figures S19 and S20, Supporting Information). However, a detailed analysis is hampered through the presence of sulfates that are already present in the reference samples. Since sulfates are the charged head group in the surfactant SDS, this is to be expected in this case. With SC as surfactant, the presence of sulfates is more difficult to rationalize. However, we note that sulfates are common contaminants in water and sodium cholate (see for example Sigma‐Aldrich safety data sheet of sodium cholate, CAS number 206986‐87‐0 and product number C6445).

The data discussed above suggest that both a thermal and photoinduced degradation occurs in WS₂‐SDS in contrast to WS₂‐SC and that the photoinduced degradation predominantly affects monolayers in contrast to thermal degradation, which occurs for both monolayers and few‐layers. It is thus of great interest to deconvolute the lifetimes of both pathways in the WS₂‐SDS samples as accurately as possible with the goal to determine activation energies of both processes and gain a deeper understanding that allows to hypothesize a mechanism for such degradation pathways. Since one of the reaction paths is considerably faster, it can be approximated as having no more impact on the reaction after considerable reaction progression. The highest lifetime for the “fast” reaction was found to be τ₁ = 37.36 min for m‐WS₂‐SDS at 40 °C, with a corresponding “slow” lifetime of τ₂ = 234 min. For this set of values, after 3 h, only 0.3% of A₁ will be left while 27.8% of A₂ remain as PL signal. Separation of both reaction pathways can thus potentially be achieved by extracting information about the slow reaction pathway from the last data points in any given set. The last 6 values of the PL degradation kinetics of WS₂‐SDS were analyzed by linear fitting on a semilogarithmic plot to allow for an extrapolation to shorter times. The result of this data treatment is shown as blue curves in Figure 5A,B for s‐WS₂ (Figure 5A) and l‐WS₂ (Figure 5B) for the samples heated/irradiated to 80 °C. The obtained slow decay kinetics can then be subtracted from the full dataset (i.e., the measured data), leaving the degradation curve of the fast decay (magenta traces in Figure 5A,B). The complete data sets are shown in Figure S24 of the Supporting Information. In Figure 5A,B, data from the ex situ heating experiment in the absence of light is included (orange data points). With an appropriate scaling, the ex situ thermal decay agrees well with the slower decay of the heated/irradiated samples. This slower decay is thus attributed to purely thermal degradation and the faster decay to photoinduced degradation.

Figure 5.

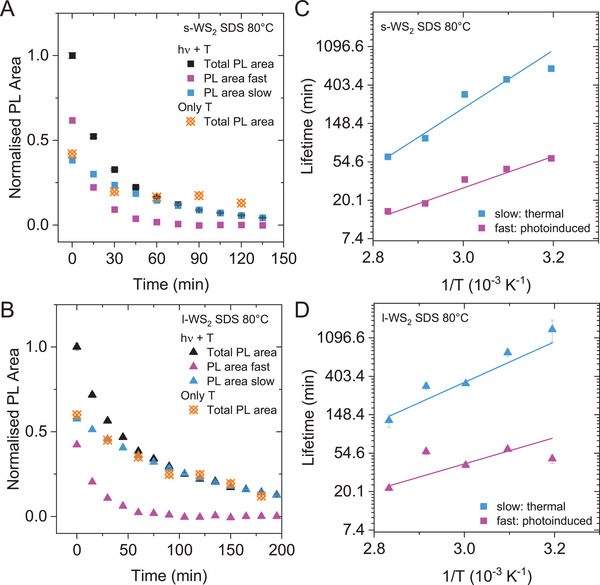
Deconvolution of the thermal and photoinduced decay of WS₂ in sodium dodecyl sulfate. A,B) Normalized PL area of s‐WS₂ (A) and l‐WS₂ (B) in SDS after heating and irradiation to 80 °C as function of time. The long‐lived component (blue) was extracted by fitting a first order exponential decay at longer times (>90 min) and subtracted from the measured data to obtain the decay kinetics of the faster reaction (magenta). Data from the ex situ heating in the absence of light is included for comparison (orange) showing a similar decay as the slow reaction which is therefore attributed to a thermal decay. C,D) Lifetimes of the thermal and photoinduced decay of s‐WS₂ (C) and l‐WS₂ (D) as function of inverse temperature on a semilogarithmic scale. The activation energies were determined from the linear fits.

The thus obtained deconvoluted photoinduced and thermal decays of WS₂‐SDS were fitted individually to extract lifetimes (and portion of reacted material, see Section S5.2, Supporting Information). The resultant lifetimes for the slow, thermal decay (blue) and fast, photoinduced decay (magenta) are plotted as a function of inverse temperature for s‐WS₂‐SDS and l‐WS₂‐SDS in Figure S5C (Supporting Information) and Figure 5D, respectively (for m‐WS₂ see Figure S25, Supporting Information). In spite of some scatter, the data linearizes, which allows to estimate activation energies of the thermal and photoinduced degradation according to the Arrhenius equation, which are summarized in Table 2. Overall, the activation energy of the photoinduced degradation is 20–30 kJ mol⁻¹, i.e., in the same range as the activation energy of WS₂‐SC, which agrees well with the observation that no thermal decay was observed for WS₂‐SC so that the degradation should be photoinduced in this case. The slower, thermal degradation, which is suppressed in SC, has a higher activation energy of ≈50 kJ mol⁻¹. The m‐WS₂‐SDS data shows a lower activation energy. However, we attribute this to experimental error due to the multistep analysis and greater scatter in the data for m‐WS₂‐SDS due to larger time increments between the PL measurements.

In spite of this scatter in the data, it is clear that E _A is higher for the thermal pathway (which was also found to be slower) indicating that at low temperatures, the photochemical pathway might have a more significant impact on ageing also in WS₂‐SDS where both processes occur. We note that the photochemical pathway is not spontaneous (i.e., it requires elevated temperatures), which indicates that the rate determining step is not overcome photochemically, but rather a thermal kinetic barrier is present. The reaction is probably photoinitiated and then the nanosheets are oxidized through a thermally accessed transition state. This means that both thermal and photochemical decay can be slowed by reducing the temperature, which is why storage at low temperature is beneficial to suppress both degradation pathways. Furthermore, within the scatter of the data, the activation energy is widely constant across nanosheet dispersions with different (average) lateral sizes. This implies that the overall reactions are the same on the molecular level irrespective of the sheet size. In such a scenario, the activation energy will be independent of sheet size regardless of whether degradation occurs on the edge or the basal plane. However, based on simple geometric assumptions, we would expect the portion of reacted material to show some size dependence. This is analyzed and discussed in detail in Section S5.2 of the Supporting Information. In brief, we indeed find that the portion of degraded WS₂ increases with decreasing sheet size for the photoinitiated reaction, which points toward a predominantly edge‐centered reaction. This behavior is not clearly observed for the thermal degradation. We therefore believe that the thermal degradation predominantly affects the basal plane. The suppression of the thermal degradation pathway in SC is in line with the reported hypothesis that the facial amphiphile preferentially adsorbs on the basal plane of WS₂ resulting in shielding of the basal plane toward oxidation.^{[ 34 ]}

In light of the relatively severe degradation of LPE WS₂ monolayers—in particular in the presence of light demonstrated above—it is important to devise passivation strategies to suppress this degradation. In the following, we demonstrate that the measurement and analysis protocol elaborated in this report has great potential to identify suitable reagents. For this proof of concept, we tested whether it would be possible to passivate SVs with thiols in our LPE WS₂. Due to the reported filling of SC with oxygen,^{[ 6} , ^{16 ]} we have decided to add the thiol during the sonication‐assisted exfoliation with the rational that it might be possible to passivate SV the moment they are exposed to the environment. As a model substance, we have chosen the amino acid l‐cysteine (cys) due to its water solubility and absence of the characteristic thiol odor. After exfoliation, the dispersions were size‐selected as before and the photoluminescence measured as function of time and temperature following the protocols described above.

Figure 6A,B shows the PL decay kinetics for s‐WS₂‐SC (Figure 6A) and s‐WS₂‐SDS (Figure 6B) at 60 °C heating and irradiation in the presence (blue) and absence (black) of cysteine. In both cases, degradation was significantly suppressed when cysteine was added, in particular for s‐WS₂‐SC, where the PL remained almost constant as function of time. Encouraged by this finding, we investigated the s‐WS₂‐SC‐cys in more detail. The decay kinetics of the PL area at different temperatures are depicted in Figure 6C. Only minor degradation is observed for temperatures <70 °C. In fact, the PL height hardly changed (Figure S28, Supporting Information). The discrepancy between the decay kinetics of PL area and height are due to a change in PL width, as illustrated in Figure 5D. Upon heating and irradiation at temperatures of 70 °C and below, a decrease in PL linewidth is observed reaching a room‐temperature FWHM of ≈23 meV. Note that this is close to the theoretical limit of the room temperature linewidth, which is governed by electron–phonon scattering^{[ 37a ]} in the absence of inhomogeneous broadening through defects and dielectric disorder.^{[ 41 ]} Since the PL linewidth can be regarded as quality indicator, a decrease in PL width suggests selective destruction of defective nanosheets or nanosheets with an inhomogeneous dielectric environment. Note that this was not observed in the absence of cysteine, where the decay kinetics of PL areas and height were identical within error (Figure 1D).

Figure 6.

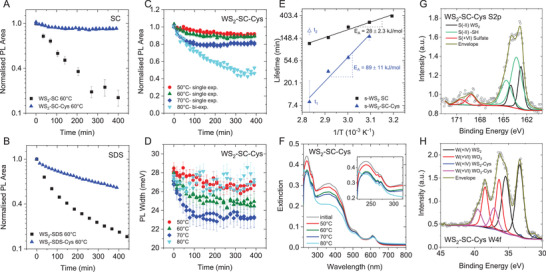
Effect of passivation through the addition of cysteine. A,B) Normalized PL area as function of time for s‐WS₂ after heating and irradiation to 60 °C in SC (A) and SDS (B) with (blue) and without (black) cysteine added during the exfoliation. Degradation is significantly slowed down and reduced through the presence of cysteine, in particular in SC. C) Normalized PL area of s‐WS₂‐SC‐cys as function of time for different temperatures. The decay kinetics at 50, 60, and 70 °C can be described through a single exponential, while a double exponential fit is required for the data acquired at 80 °C. D) PL full width at half maximum of s‐WS₂‐SC‐cys as function of time for different temperatures. E) Lifetimes extracted from the fits in (C) as function of inverse temperature on a semilogarithmic scale in comparison to s‐WS₂ in the absence of cysteine (black). The lifetime of the long‐lived component of the biexponential decay at 80 °C is similar to the lifetime of the reference sample, while the shorter component linearizes with the s‐WS₂‐SC‐cys data obtained at lower temperatures. Activation energies determined from the linear fits are indicated. F) Extinction spectra of the s‐WS₂‐SC‐cys samples before and after heat treatment and irradiation. In the UV region (inset), two additional peaks are observed that suggest the presence of oxides. G,H) Fitted X‐ray photoelectron spectroscopy core levels of WS₂‐SC‐cys. G) S2p core level. H) W4f core level.

When attempting to fit the decay kinetics of s‐WS₂‐SC‐cys (Figure 6C), we found that only the data for temperatures below 70 °C could be fit with a single exponential, while a biexponential function was required for the 80 °C data set. Similar to the WS₂‐SDS dispersions discussed above, this suggests the presence of two reaction pathways. The lifetimes from the fits of the PL area decays are plotted as function of inverse temperature on a semilogarithmic scale in comparison to the data set of s‐WS₂‐SC in the absence of cysteine in Figure 6E. For the 80 °C data set, both the short (τ₁) and long (τ₂) lifetimes are included. The long lifetime is in a similar range as the s‐WS₂‐SC reference data at the same temperature, while all other lifetimes fall significantly below the reference curve. The short lifetime τ₁ is a linear progression of the other three data points at lower temperatures on the semilogarithmic plot, which allows to determine the activation energy as ≈90 kJ mol⁻¹, i.e., significantly higher as the typical thermal and photoinduced degradation in the absence of cysteine. We therefore believe that a different reaction takes place on the molecular level even though the elaboration of detailed reaction mechanisms is beyond the scope of this manuscript.

The improved stability of the s‐WS₂‐SC‐cys dispersions is also confirmed by the UV–vis extinction spectra displayed in Figure 6F, which show a less significant decrease in extinction as compared to the reference in the absence of cysteine (compare Figure S9, top, Supporting Information) after heating and irradiation. These findings of successful passivation of the nanosheets through the addition of cysteine might suggest successful coordination of thiols to sulfur vacancies. However, other factors can play a role. For example, a closer inspection of the extinction spectra reveals well‐resolved small peaks in the UV region for both the initial s‐WS₂‐SC‐cys dispersion, as well as after heat treatment and irradiation (Figure 6F, inset). In particular, tungstates and WO₃ absorb light in this spectral region so that these features could be a manifestation of oxides. Note that these additional features were absent when diluting the reference sample with aqueous cysteine solution (Figure S29, Supporting Information).

To investigate this in more detail, WS₂‐SC‐cys prior to heating and irradiation was subjected to XPS after drop‐casting the dispersion onto indium tin oxide substrates without applying any washing steps. In contrast to the XPS on the drop‐cast samples after heating and irradiation described in Figure 4 and Figures S19 and S20 (Supporting Information), the high concentration sample after LCC was used for deposition to minimize the contribution from the surfactant to the spectra. The fitted S2p and W4f core level spectra are shown in Figure 6G,H, for additional data see Section S6.3 of the Supporting Information. The sulfur core level spectra (Figure 6F) can be fitted with three doublets. The lowest energy doublet with an S2p_3/2 binding energy of 162.7 eV (black) is close in energy to the sulfur species in the WS₂ reference (Table S5, Supporting Information) and is thus assigned to WS₂. Note that some variations in binding energies can occur in the cysteine sample, where it is not possible to reference the binding energy to adventitious carbon due to the presence of organic carbon from cysteine in the sample. The second doublet with an S2p_3/2 binding energy of 163.7 eV (green) is also attributed to S in the oxidation state −II and agrees well in energy with the thiol in the cysteine reference (Figure S30E and Table S5, Supporting Information). It is thus assigned to the thiol group of cysteine. In addition, a third doublet is observed at significantly higher S2p_3/2 binding energies of 169.1 eV (red). Based on the energy, it is assigned to S in the oxidation state +VI, e.g., in the form of sulfates. While such a feature might not be expected, we note that it is also present in the WS₂‐SC reference (Figure S19, Supporting Information), as well as in the cysteine‐SC reference solution (without WS₂) drop‐cast on ITO (Figure S30E, Supporting Information). This strongly suggests that it is a contamination, very likely in the sodium cholate or deionized water. We note that the intensity of the sulfate increases in intensity in the cysteine‐SC reference solution after sonication (Figure S30E, Supporting Information), which hints to partial oxidation of cysteine by sonication.

To fit the W4f core level spectra (Figure 6H), four doublets are required. Based on the binding energies (see Table S5, Supporting Information), two of the four species are assigned to tungsten in the oxidation state +IV and the other two to W(+VI). One of the doublets at a W4f_7/2 binding energy of 33.1 eV is very close to the binding energy of the W(+IV) in the WS₂ reference and is thus assigned to WS₂ (black). Accordingly, the lowest energy doublet with a W4f_7/2 binding energy of 31.3 eV (blue) must be a W(+IV) species with higher electron density than tungsten in the pristine WS₂. It can be anticipated that cysteine acts as a donor toward WS₂ so that this feature is attributed to an interaction of cysteine with WS₂. This indeed suggests some successful coordination of cysteine to WS₂. However, these two W(+IV) components only constitute ≈39% of the W species. The majority of the tungsten signal detected in XPS stems from W in the oxidation state +VI. Here, the lower energy doublet has a W4f_7/2 binding energy of 36.4 eV (red) and is similar to the traces of WO₃ observed in the WS₂ reference. Another less intense doublet is located at a W4f_7/2 binding energy of 37.3 eV (magenta), which can be again attributed to coordination of cysteine which seems to act as an electron acceptor relative to the WO₃. Overall, this high oxide content is surprising since the optical properties of this sample were dominated by WS₂. We attribute this to the surface sensitivity of XPS in combination with a low absorbance cross‐section of oxides at significantly higher energies than WS₂. Thus, a quantitative statement of the oxide content should be avoided. In addition, we note that the samples were fairly inhomogeneous due to the deposition by drop‐casting and different spectra were obtained in different sample regions. As shown in Figure S30B,D of the Supporting Information, the sulfate content in the S2p core level spectra can reach up to 33%. Interestingly, this coincides with an increased relative intensity of the WS₂‐cys component and a disappearance of the WO₃‐cys component in the W4f core level spectra.

While a quantitative assessment is not accessible, XPS clearly demonstrates i) successful coordination of cysteine to tungsten and ii) the presence of a significant amount of W(+VI)‐oxide prior to heating/irradiation, which is likely the origin of the features in the UV region of the extinction spectra that are not observed in sonication‐assisted LPE of WS₂ in the absence of cysteine or when cysteine is added on dilution of WS₂‐SC. The presence of these oxides is surprising and cannot easily be rationalized. On the one hand, it is possible that cysteine coordinates to WS₂ oxidation products produced on sonication and binds them to the WS₂ surface so that they are not released as water‐soluble tungstates. On the other hand, the presence of cysteine might result in an enhanced oxidation of WS₂ during exfoliation. Presumably, both the oxide and the cysteine coordinate to WS₂ and serve as passivation layer and prevent the progression of the oxidative degradation of WS₂ on heating and irradiation. Further experiments are required to elucidate the passivation mechanism in more detail.

3. Conclusion

The oxidative degradation of WS₂ monolayers was investigated in the presence of water and oxygen by studying the photoluminescence of liquid‐exfoliated nanosheet aqueous dispersions as function of time and temperature. In each measurement, an ensemble of thousands of nanosheets is probed giving access to the average information in contrast to spatially resolved techniques on individual nanosheets commonly applied. Furthermore, the liquid environment can be—on average—regarded as homogeneous compared to substrate‐supported nanosheets. The result from exfoliation and stabilization in two common surfactants was compared—one being a stereotypical linear amphiphile (SDS), one being classified as facial amphiphile (SC), which was previously suggested to adsorb preferentially on the basal plane.^{[ 34 ]} In both cases, three samples with different nanosheet size distributions were prepared to gain information on the role of edges in the degradation.

In general, well‐defined decays of the PL as function of time were observed. Using SC as surfactant, these followed (pseudo) first order decay kinetics with one predominant degradation pathway that was assigned to be a photoinduced degradation with an activation energy of ≈25 kJ mol⁻¹. In contrast, an additional thermal degradation was evidenced in SDS with an estimated activation energy of ≈50 kJ mol⁻¹. In both cases, no clear dependence of the nanosheet lateral size was observed for the activation energies. However, smaller nanosheets degraded more quickly compared to larger ones and more completely in the case of the thermal degradation which would be consistent with a degradation pathway preferentially occurring on the basal plane. AFM in combination with extinction spectroscopy showed that the degradation in SC is selective to monolayers, while (laterally small) few‐layers are also destroyed in SDS. XPS suggests that degradation products are tungstates and sulfates.

The overall methodology of sample fabrication, measurement and analysis does not require specialized equipment and is thus ideal to investigate potential chemical defect passivation schemes that can suppress degradation. This was demonstrated in a case study, where an additional passivation agent was added during exfoliation, size selection, and measurement. Here, we chose the amino acid cysteine as an example. While a remarkable stabilization toward degradation was observed, the mechanism could not be fully elucidated. XPS suggests that cysteine coordinates to defect sites of WS₂ and at the same time prevents oxides formed as degradation product to be dissolved, which results in an overall efficient passivation layer.

The work presented significantly adds to the understanding of the degradation of monolayered group VI TMDs using nanosheets suspended in a liquid environment. In particular, the complexity of the degradation process is highlighted and the insights will be of importance for further processing and applications of the nanosheets in devices. Furthermore, the elaborated protocol provides an ideal foundation to study efficient defect passivation strategies, for example through chemical functionalization in the future.

4. Experimental Section

Sample Preparation

WS₂ dispersions were prepared by probe sonicating the WS₂ powder (Sigma‐Aldrich 243639) with an initial concentration 20 gL⁻¹ in an aqueous SC or SDS solution, respectively. The powder was immersed in 80 mL of aqueous surfactant solution (C _surf = 6 gL⁻¹) in a stainless steel beaker. The mixture was subjected to a two‐step sonication, which serves the purpose to remove impurities present in the powder in the first step. 1) The mixture was sonicated for 1 h at 60% amplitude (the amplitude was attuned according to the energy input of the sonicator) in a 8 s on, 2 s off pulse sequence, using a Sonics Vibracell VCX 500 (500 W), equipped with a threaded probe and a replaceable tip. The dispersion was kept at 5 °C in a cryostat cooled water bath to avoid heating of the sample during sonication. After the sonication, the dispersion was centrifuged at 3800 × g for 1.5 h in a Hettich Mikro 220R centrifuge, equipped with a 1016 fixed‐angle rotor at 15 °C, to remove water‐soluble impurities in the dispersion. The supernatant was discarded and the sediment redispersed in 80 mL of 2 gL⁻¹ aqueous surfactant solution. 2) This dispersion was then again sonicated for 5 h at 60% amplitude in a 6 s on, 2 s off pulse sequence. For the experiments with cysteine, 6 × 10⁻³ m cysteine was added to the dispersion prior to sonication in addition to the detergents.

To select nanosheets by size and increase the monolayer content, liquid cascade centrifugation was used with sequentially increasing rotation speeds (2 h each step, 15 °C). Centrifugation conditions are expressed as relative centrifugal field (RCF) in units of 10³ x g (or k g) with g being the gravitational force. Two different rotors were used. For centrifugation at <10 000 g, the JA25.50 fixed angle rotor and a Beckman Coulter Avanti centrifuge was used with 50 mL centrifuge tubes (VWR, order number 525‐0402) filled with 20 mL of dispersion each. For centrifugation at >10 000 × g, the JA25.15 rotor was used with 14 mL vials (Beckman Coulter, order number 331374), filled with 10 mL dispersion each. As size selection steps, 1k g, 5k g, 10k g, and 30k g were chosen. The sediments were collected in 0.1 g L⁻¹ surfactant solution with reduced volume (in total ≈5 mL per size‐selected fraction) to increase the concentration. The sediment yielded after centrifugation at 1k g and the supernatant yielded at 30k g were discarded as the material is either too large or too small for efficient PL emission. Each sample was denoted x‐yk g, y being the RCF at which the sample sedimented and x the RCF used in the size selection step prior to sedimentation. For convenience, the sample 1–5k g is abbreviated as l‐WS₂, 5–10k g as m‐WS₂, and 10–30k g as s‐WS₂. The size‐selected high concentration samples were stored at 4 °C in amber vials.

Characterization

Optical extinction was measured on a Varian Cary 6000i in quartz cuvettes with a pathlength of 0.4 cm in 0.5 nm increments and integration times of 0.1 s nm⁻¹. The obtained sediments after LCC were diluted with an aqueous surfactant solution containing (0.1 gL⁻¹, and 6 × 10⁻³ m cysteine in case of the samples denoted as WS₂‐cys) such that their optical densities (OD) after background subtraction at 440 nm are OD = 0.40 ± 0.05 with respect to 10 mm path length (corresponding to a nanosheet concentration of ≈0.01 gL⁻¹), in order to assure similar light absorption at 440 nm excitation during PL experiments.

Photoluminescence was measured using a Horiba Scientific Fluorlog‐3 spectrometer equipped with a Xe arc lamp (450 W) and a Sincerity CCD camera as detector using double monochromators for excitation and emission with a 1200 l mm⁻¹ grating with 330 nm blaze in excitation. For the PLE contour plots, a 1200 l mm⁻¹ grating with 500 nm blaze was used in emission, while the single spectra for the degradation kinetics (440 nm excitation) were recorded using a 100 l mm⁻¹ grating with 780 nm blaze. The quartz cuvettes with 0.4 × 1 cm dimensions were placed inside the sample chamber so that the excitation light passed through the 0.4 cm side of the cuvette. A piezocooled temperature controller (TLC50/Horiba4) was used to adjust the external temperature. Emission was collected in a 90° angle, i.e., after having passed through the 1 cm side. Excitation bandwidths were typically 8 nm. In this setup, this results in a power of the exciting light of ≈9 µW spread over an area of ≈1.5 × 0.5 cm². Emission bandwidths were 5 nm, increments 1 nm and acquisition times 0.4 s nm⁻¹. To avoid artefacts from scattering of the nanomaterial dispersion, a 550 nm cut‐off filter was placed on the emission side. The excitation was corrected for the light intensity.

For XPS, the s‐WS₂ dispersions before and after in situ and ex situ heating and irradiation were filtered on alumina membranes, as well as drop‐cast on ITO to also capture the signal from soluble oxidation products. Note that these dispersions were very dilute (optical density of 0.4 at 440 nm). The cysteine‐treated dispersion was drop‐cast on ITO using the high concentration after the size selection. XPS measurements were carried out with an ESCALAB 250Xi (Thermo Scientific) in ultrahigh vacuum, an XR6 monochromated Al Kα source (hν = 1486.6 eV), and a pass energy of 20 eV. Except for the cysteine‐treated sample and the WS₂‐SC reference on ITO (where no charging was observed), XPS was measured with charge compensation employing a flood electron source.

For AFM measurements, the samples were deposited on Si/SiO₂ (300 nm oxide) coated with (3‐aminopropyl)triethoxysilane (APTS). To prepare the substrate, a solution (1:40) of DI water and (APTS was used to activate the substrate surface to facilitate deposition. Initially, the Si/SiO₂ substrate was immersed in the APTS solution for 15 min. This will form a monolayer covering the entire substrate. Subsequently, the substrate was removed, washed repeatedly with DI water, and finally dried with nitrogen. Once the substrate was prepared, the nanomaterial dispersion (concentration ≈0.01 gL⁻¹) was dropped onto the substrate and held for ≈20 s. Subsequently, the drop was discarded (e.g., blown off with pressurized nitrogen) and the sample repeatedly cleaned with DI water. For imaging, a Dimension ICON3 scanning probe microscope (Bruker AXS S.A.S.) was used in ScanAsyst mode (noncontact) in air under ambient conditions using aluminum‐coated silicon cantilevers (OLTESPA‐R3). Typical image sizes were 2 × 2 µm² scanned with 1024 lines at scan rates of ≈0.4 Hz and peak force setpoints of ≈0.03 V.

Raman spectroscopy was carried out on a Renishaw InVia‐Reflex confocal Raman microscope in air under ambient conditions using a 532 and 633 nm laser as excitation source, respectively. The Raman emission was collected by a 50× long working distance objective lens in streamline mode and dispersed by a 2400 l mm⁻¹ (532 nm) or 1200 l mm⁻¹ (633) grating with 1% (532 nm) and 10% (633) of the laser power (all <25 µW). The spectrometer was calibrated to a silicon reference sample prior to the measurement to correct for the instrument response. 5–10 spectra in different samples areas were recorded and averaged. In addition to the measurements on drop‐cast samples on ITO, spectra were acquired from the high concentration dispersions after LCC, but prior to degradation experiments (532 nm 1% power). Here, the WS₂ dispersions were dropped on aluminum foil. The laser was focused to the surface of the droplet, since focusing inside the droplet lowers the PL intensity due to innerfilter and reabsorption effects. After acquisition the spectra were averaged, baseline corrected and normalized to the 2LA(M) Raman mode.

In Situ Heating and Irradiation

To follow the degradation by heating and simultaneous irradiation (440 nm, ≈9 µW spread over an area of ≈1.5 × 0.5 cm²) in the fluorescence spectrometer, temperature ramps were programmed. Each temperature profile switches between the target temperature of 40–80 °C and 20 °C, being held at the target temperature for the same amount of time in between measurements. Prior to measurement, the samples were allowed to equilibrate for 5 min both when being heated up to the target temperature and when cooled down to 20 °C. Initially, the length of each heating interval was chosen to be ≈30 min, which provided insufficient resolution in some cases, in particular for the SDS data series. Therefore, some samples were measured with shorter time increments. The cuvettes were sealed to avoid evaporation of water at elevated temperatures.

Ex Situ Heating

Complementary to decay studies in the PL spectrometer, sample decay under exclusion of light was studied. Initial experiments were conducted in a large Schlenk tube ≈50 mL equipped with a stir bar and a septum filled with ≈15 mL diluted dispersion. The tube was then wrapped in aluminum foil in order to ensure exclusion of ambient light, and samples were extracted using a syringe after the denoted time elapsed. This approach exhibited a strong dependence on the tube size and on whether the septum was taken off during sample extraction. Such effects are probably caused by an interaction with ambient oxygen in the gas phase above the solution. In order to achieve reproducible decay results for the series of experiments with SDS stabilizer (where this was more relevant), the samples were split into multiple amber screw‐neck vials each containing ≈1 mL of dispersion. The vials were then heated for varying time periods and left to cool without opening them. The vials were heated using a block of solid aluminum with precise cut outs for each vial. The temperature was set by introducing another vial containing silicone oil with the thermometer attached to the vial.

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Karger L., Synnatschke K., Settele S., Hofstetter Y. J., Nowack T., Zaumseil J., Vaynzof Y., Backes C., The Role of Additives in Suppressing the Degradation of Liquid‐Exfoliated WS₂ Monolayers. Adv. Mater. 2021, 33, 2102883. 10.1002/adma.202102883

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.