Ultrastrong and Ductile Soft Magnetic High‐Entropy Alloys via Coherent Ordered Nanoprecipitates

Abstract

The lack of strength and damage tolerance can limit the applications of conventional soft magnetic materials (SMMs), particularly in mechanically loaded functional devices. Therefore, strengthening and toughening of SMMs is critically important. However, conventional strengthening concepts usually significantly deteriorate soft magnetic properties, due to Bloch wall interactions with the defects used for hardening. Here a novel concept to overcome this dilemma is proposed, by developing bulk SMMs with excellent mechanical and attractive soft magnetic properties through coherent and ordered nanoprecipitates (<15 nm) dispersed homogeneously within a face‐centered cubic matrix of a non‐equiatomic CoFeNiTaAl high‐entropy alloy (HEA). Compared to the alloy in precipitate‐free state, the alloy variant with a large volume fraction (>42%) of nanoprecipitates achieves significantly enhanced strength (≈1526 MPa) at good ductility (≈15%), while the coercivity is only marginally increased (<10.7 Oe). The ordered nanoprecipitates and the resulting dynamic microband refinement in the matrix significantly strengthen the HEAs, while full coherency between the nanoprecipitates and the matrix leads at the same time to the desired insignificant pinning of the magnetic domain walls. The findings provide guidance for developing new high‐performance materials with an excellent combination of mechanical and soft magnetic properties as needed for the electrification of transport and industry.

Ultrastrong and ductile bulk high‐entropy alloys with excellent soft magnetic properties are achieved by introducing a high volume fraction of coherent and ordered nanoprecipitates into the alloy matrix. The high lattice coherency between the homogeneously dispersed nanoprecipitates and the alloy matrix creates only negligible distortion fields on magnetic domain wall motion and contributes significantly to the strength of the material.

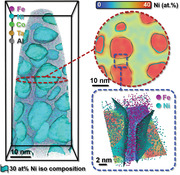
1. Introduction

Soft magnetic materials (SMMs), such as Fe‐3wt%Si based alloys^{[ 1 ]} and Permalloy,^{[ 2 ]} are standard materials that serve in electrical power generation and transformation and as sensors since the beginning of the twentieth century.^{[ 3 ]} SMMs have high saturation magnetization, permeability, and resistivity as well as low coercivity and core losses.^{[ 4 ]} With the growing demand for SMMs to operate under mechanically highly loaded conditions (e.g., high‐speed rotation, torque, vibration),^{[ 5} , ^{6 ]} advanced SMMs require not only excellent soft magnetic performance but also high strength and good ductility.^{[ 4 ]} This creates a fundamental microstructure design conflict, as conventional means to enhance mechanical strength reduce domain wall motion and vice versa. Although several amorphous soft magnetic alloys have a good combination of strength and soft magnetic properties,^{[ 7} , ^{8 ]} they have not been widely applied due to their brittleness and limited dimensions. This leads to the motivation of developing novel bulk soft magnetic alloys with excellent mechanical properties.

Since the original proposition in 2004, high‐entropy alloys (HEAs) emerged as a new design concept that has significantly broadened the compositional spectrum of materials.^{[ 9} , ^{10 ]} Besides many detailed investigations about their mechanical properties,^{[ 11} , ^{12 ]} few studies have also addressed their functional properties,^{[ 13 ]} including magnetic,^{[ 14} , ¹⁵ , ¹⁶ , ^{17 ]} thermal,^{[ 18} , ^{19 ]} and electrical ones^{[ 20 ]} as well as their resistance to corrosion and hydrogen embrittlement.^{[ 21 ]} For example, a non‐equiatomic CoFeMnNiAl alloy displays a high saturation magnetization (M_s ) of 147.9 Am² kg⁻¹,^{[ 22 ]} which is 15–35% above that of FeNi soft magnetic alloys (M_s  ≈95–135 Am² kg⁻¹).^{[ 23 ]} Hence, a highly promising and challenging field of HEA research is the combination of (often mutually exclusive) mechanical and functional properties, due to the huge accessible compositional space which allows realizing a large variety of nanostructure features.^{[ 24 ]} Recently, a fair balance between strength and soft magnetic properties was achieved in an ultrafine grain FeCoNiCu_0.2Si_0.2 HEA produced via melt‐spinning.^{[ 25 ]} The small grain size was used for enhancing strength, through the Hall–Petch effect. Although the improvement in strength and soft magnetic properties was accompanied by only modest ductility (≈7%), this work revealed the potential of HEAs to combine high strength with good magnetic properties. Yet, when aiming at higher strength levels and production of materials with bulk dimensions, a fundamental dilemma lies in the fact that most mechanical strengthening approaches increase magnetic hysteresis losses.^{[ 26} , ²⁷ , ²⁸ , ²⁹ , ^{30 ]} This is due to that the microstructure barriers that impede dislocation motion, such as interfaces and dislocations, also tend to pin magnetic domain walls.^{[ 31 ]} Thus, most microstructure features that increase mechanical strength deteriorate soft magnetic properties in terms of an increased coercivity (H _c).^{[ 31 ]}

Here, to realize an optimal balance among the strength, ductility and soft magnetic properties in SMMs, we introduce a high volume fraction of coherent and ordered nanoprecipitates into the HEA matrix. This idea was partially inspired by previous studies in which Cu nano‐precipitates with a size below the domain wall thickness do not deteriorate the alloy's coercivity.^{[ 32} , ³³ , ^{34 ]} This is due to the fact that precipitates of such small size (a few nm) do not interact with Bloch walls which have a thickness varying from ≈50 nm to a few micrometers in soft magnetic materials.^{[ 31 ]} Another possibility to achieve mechanical strength while maintaining a low hysteresis loss is introducing coherent precipitates into the alloy matrix. High lattice coherency between precipitates and matrix creates only negligible distortion fields, thus entailing modest pinning of domain walls, but coherent phases can impede dislocation motion through the work required for forming new interfaces by shear.^{[ 23 ]} Also, a good combination of mechanical and soft magnetic properties was observed when increasing the degree of superlattice ordering in a nanocrystalline alloy.^{[ 35 ]} Therefore, we hypothesize that a HEA with well‐tuned composition allows forming coherent and ordered nanoprecipitates embedded in a HEA matrix, to enhance strength without sacrificing coercivity. We probe this concept with a non‐equiatomic Fe_{35‐ x /3}Co_{30‐ x /3}Ni_{30‐ x /3}Ta₅Al _x (x = 3, 5, 7 at%) HEA system. Fe, Co and Ni are ferromagnetic elements that form a strong and ductile magnetic matrix, whereas Ta and Al are likely to create ordered nanoprecipitates that are coherent with the matrix.

2. Results and Discussion

We investigated the base Fe₃₅Co₃₀Ni₃₀Ta₅ (at%) HEA and the corresponding aluminum‐alloyed variants Fe_{35‐ x /3}Co_{30‐ x /3}Ni_{30‐ x /3}Ta₅Al _x (at%) (x = 3, 5, 7). The as‐cast HEAs plates (10‐mm thick) were hot‐rolled at 1473 K to 50% thickness reduction, followed by 10‐min homogenization at the same temperature and water quenching (see Experimental Section). The homogenized alloys containing 3 at%, 5 at%, and 7 at% Al are hereafter denoted as 3Al‐HEA, 5Al‐HEA, and 7Al‐HEA, respectively, whereas the homogenized Al‐free base alloy is referred to be B‐HEA (where “B” stands for “base”). For the 7Al‐HEA, apart from the face‐centered cubic (fcc) matrix phase, diffraction peaks corresponding to an L1₂ structure are identified in the X‐ray diffraction (XRD) patterns shown in Figure 1a. In contrast, the diffractogram of the B‐HEA shows a single fcc phase structure (Figure S1a, Supporting Information). Electron‐backscatter diffraction (EBSD) analysis shown in Figure 1a reveals equiaxed grains of the 7Al‐HEA matrix with an average size of 65.3 ± 10.3 µm (excluding annealing twin boundaries). According to the analogous EBSD analysis, the B‐HEA (Figure S1a, Supporting Information) shows an average grain size of 64.8 ± 9.8 µm, suggesting that the average grain size changes are <1 µm, compared to that of the 7Al‐HEA.

Figure 1.

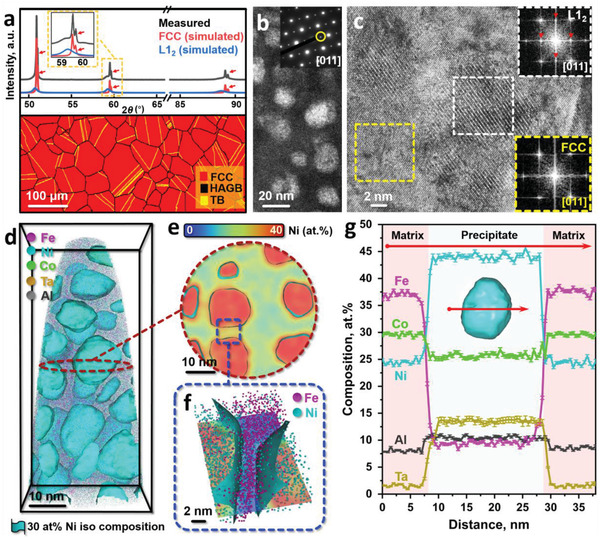
Microstructure of the 7Al‐HEA from micro‐ to near atomic‐scale. a) XRD pattern and EBSD phase map. The Cu Kα2 radiation causes additional diffraction peaks, marked by the red arrows. b) Centered dark‐field TEM image of the precipitates using the (011) superlattice spot (see inset, highlighted by a yellow circle). c) HRTEM image of the nanoprecipitation hardened HEA. The fast Fourier transformation (FFT) image (bottom right) acquired from the region highlighted by the yellow rectangle confirms the fcc structure with the zone axis of [011]. By contrast, the white rectangle region's FFT image (top right) reveals a pattern with pronounced superlattice spots. d) 3D reconstruction map of an APT tip highlighting the nanoprecipitates. e) 2D projection of the Ni concentration slice acquired from the central part of the APT tip shown in (d). f) Enlarged view of the groove region showing the distribution of Fe and Ni atoms. g) 1D compositional profiles showing the compositional changes across a selected precipitate along the red arrow shown in the inset. Error bars in (g) refer to the standard deviations of data points.

We further characterized the 7Al‐HEA down to near‐atomic scale by atom probe tomography (APT) and transmission electron microscopy (TEM). Figure 1b shows the g ₀₁₁ dark‐field (DF) TEM image of the homogeneously distributed nanoprecipitates with an average size of 13.5 ± 2.5 nm. Figure 1c displays a high‐resolution (HR) TEM image of the alloy. The corresponding fast Fourier transformation (FFT) pattern acquired from a nanoprecipitate (white dashed square) reveals an ordered structure. A full coherency relationship between the precipitate and the fcc matrix is confirmed by comparing their FFT patterns. Figure 1d visualizes the near‐spherical L1₂ precipitates in terms of a three‐dimensional (3D) reconstruction of a typical APT tip. The data show that the average volume of the L1₂ nanoprecipitates (2,294 ± 125 nm³) is below the critical size for the sphere‐to‐cuboid shape transition. This transition is based on Khachaturyan's theory,^{[ 36} , ^{37 ]} which suggests a more spherical shape of nano‐precipitates when their interfacial free energy prevails over the free energy associated with their elastic distortion field. Figure 1e provides a cross‐sectional two‐dimensional (2D) concentration plot in terms of a 30 at% Ni threshold value, acquired from the center region of the APT tip (Figure 1d). From Figure 1e, we selected two representative precipitate/matrix interfaces for further characterization (blue dashed square). The corresponding enlarged view of these precipitate/matrix interfaces is shown in Figure 1f. These results evidence Ni enrichment in the precipitates and Fe enrichment in the matrix, respectively. Figure 1g shows 1D compositional profiles acquired across a selected precipitate (see red arrow in the inset of Figure 1g). These profiles indicate that Ni, Ta and Al are preferentially partitioned into the L1₂ nanoprecipitates whose stoichiometry is given by Ni₄₂Co₂₄Ta₁₄Al₁₁Fe₉ (at%), whereas the fcc matrix holds a Fe and Co enriched composition of Fe₃₇Co₃₀Ni₂₄Al₈Ta₂ (at%). Also, the nanoprecipitates prevail homogeneously in the other Al‐containing HEAs (Figure S2a, Supporting Information). The chemical compositions of the fcc and the L1₂ phases were derived and averaged from several APT sub‐volumes, as detailed in Figure S2b, Supporting Information. The results show that by increasing the global Al content of the alloys, the fcc matrix monotonously gets enriched in Fe and Al, while Ni, Ta, and Al are preferentially partitioned to the L1₂ phase. The Movies S1–S3, Supporting Information further show the 3D distribution of L1₂ nanoprecipitates in 3Al‐HEA, 5Al‐HEA, and 7Al‐HEA, respectively.

In contrast to the Al‐doped alloys containing ordered nanoprecipitates, the B‐HEA has a single fcc crystal structure without superlattice diffraction spots, as shown in the TEM analysis (Figure S1b, Supporting Information). Further, APT measurements reveal the absence of nano‐segregation at near atomic‐scale for this alloy (Figure S1c–e, Supporting Information). The statistical binomial frequency distribution and the normalized homogenization parameters also confirm that all the elements are randomly distributed (Figure S1e, Supporting Information). The investigated APT specimen displays an overall composition of Fe_34.7Co_30.2Ni_30.3Ta_4.8 (at%), which is close to the bulk one determined by wet‐chemical analysis, that is, Fe_34.5Co_30.3Ni_30.2Ta_5.0 (at%).

Figure 2a shows the representative tensile stress–strain curves of the investigated HEAs. Compared with the single‐phase B‐HEA, which has a relatively low yield strength (σ_y) of 501 MPa and high tensile elongation (TE) of 53.4%, the 7Al‐HEA exhibits a significantly enhanced σ_y of 1202 MPa at a TE of 15.3%. In addition, the 7Al‐HEA has an ultimate tensile strength (σ_UTS) of 1526 MPa and displays a pronounced work‐hardening behavior during plastic straining, an important feature that renders the material damage‐tolerant. The σ_UTS–TE profiles shown in Figure 2b suggests that the HEAs investigated here have unprecedented strength‐ductility combinations, exceeding those reported for other soft magnetic alloys.

Figure 2.

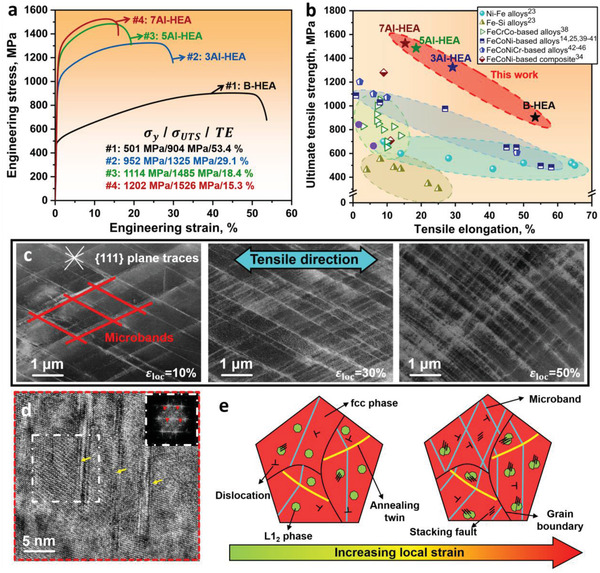
Mechanical behavior and deformation mechanisms of the 7Al‐HEA. a) Room temperature tensile stress–strain curves for the B‐HEA, 3Al‐HEA, 5Al‐HEA, and 7Al‐HEA. σ_y, σ_UTS, and TE represent the yield strength, the ultimate tensile strength and the tensile elongation, respectively. b) σ_UTS–TE profiles of various classes of soft magnetic materials,^{[ 14} , ²³ , ²⁵ , ³⁴ , ^{38 – 46 ]} including the newly developed soft magnetic HEAs investigated in this work. c) Electron channeling contrast imaging analysis revealing the evolution of the substructure in the 7Al‐HEA with increasing local strain during tensile deformation; the distance between the parallel microbands decreases with increasing local strain. d) HRTEM image of a region at ε_loc= 50% showing that the L1₂ nanoprecipitates have been sheared by nano‐spaced stacking faults (SFs); the inserted FFT pattern confirms the ordered structure of the nanoprecipitates in the fcc matrix. e) Schematic illustration of the micro‐processes in the precipitate‐containing HEAs during plastic straining.

To understand the relevant deformation mechanisms, we investigated the deformed microstructures at various local strain (ε_loc) levels by electron channeling contrast imaging (ECCI) and TEM. Figure 2c and Figures S3–S5, Supporting Information show the evolution of the deformation substructures developed in the HEAs during tensile straining. Dislocation generation and pile‐ups are indicated at the early deformation stage (ε_loc= 5%), which facilitate the formation of microbands consisting of a high density of dislocations, as shown in Figure S3, Supporting Information. Moreover, a more significant dynamic microband refinement behavior was observed in the HEA with higher aluminum content (Figure S4, Supporting Information). For instance, with increasing local strain in the 7Al‐HEA from 30% to 50%, the mean distance between the parallel microbands has been considerably reduced from 735 ± 251 nm to 163 ± 35 nm. The quantification of dynamic microband refinement in all the currently studied HEAs is shown for different local strains in Figure S5, Supporting Information. These results show that the dynamic microband refinement acts as the primary strain hardening mechanism in the investigated HEAs, as the reduced microband spacing requires inversely higher stresses for dislocations to pass on neighboring bands. The beneficial effect of microband refinement was also observed in other fcc alloys, for example, high manganese steels,^{[ 47} , ^{48 ]} and demonstrated to be responsible for high strain hardening rates during deformation. No deformation twinning was detected in the alloys, independent of their Al content. Furthermore, the HRTEM image in Figure 2d shows that the L1₂ nanoprecipitate can be sheared by a stacking fault (SF). The schematics in Figure 2e summarize the strengthening mechanisms activated during deformation.

We next reveal the magnetic response of the HEAs, measured by vibrating sample magnetometry (VSM). The saturation magnetization (M _s) and coercivity (H _c) of the HEAs were acquired from the magnetization curves displayed in Figure 3a,b. The values of M _s monotonously increase with increasing the (Fe+Co+Ni)‐to‐Al ratio, that is, it varies from 88 Am² kg⁻¹ (7Al‐HEA) to 105 Am² kg⁻¹ (3Al‐HEA), displaying a slight difference of only 17 Am² kg⁻¹. The coercivity has been evaluated via an M_x H protocol correction with extremely fine step size, as outlined in the Experimental Section. The obtained values of H _c slightly increase from 8.6 Oe (3Al‐HEA) to 10.7 Oe (7Al‐HEA). The relatively small H _c values suggest that the investigated HEAs fall into the class of soft magnetic materials.^{[ 4} , ^{49 ]}

Figure 3.

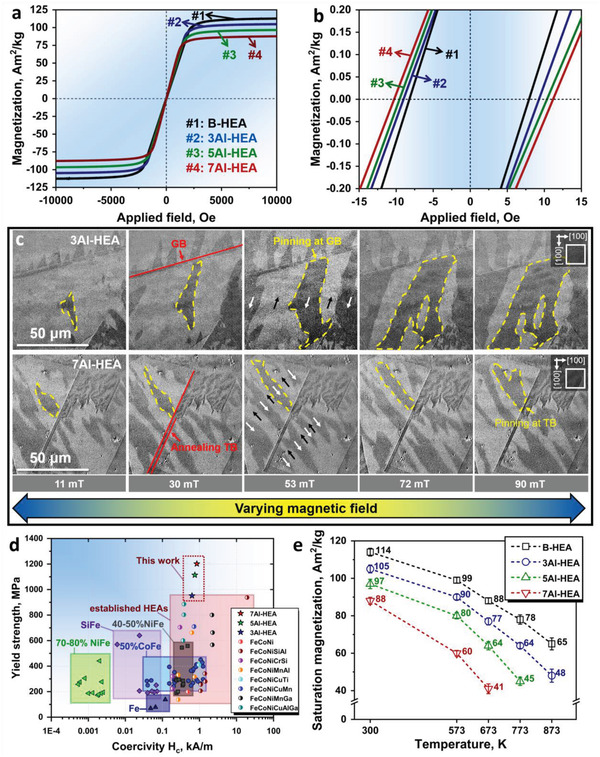
Soft magnetic behavior of the HEAs and associated Bloch wall pinning mechanisms. a) Hysteresis loops acquired up to ±10 000 Oe at room temperature. b) Hysteresis loops measured at a fine step size of 2 Oe per second, showing the coercivity of the alloys. c) Growth of the magnetic domain structure in the 3Al‐HEA and 7Al‐HEA, imaged by Kerr‐microscopy, under external magnetic fields. d) Yield tensile strength–coercivity profiles of the investigated soft magnetic HEAs compared to those of other soft magnetic materials, such as NiFe,^{[ 54} , ^{55 ]} CoFe,^{[ 38} , ^{56 ]} SiFe,^{[ 23 ]} Fe,^{[ 57 ]} and established HEAs.^{[ 14} , ²⁵ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁵⁸ , ⁵⁹ , ^{60 ]} e) Plot of the temperature dependence of the saturation magnetization of the investigated HEAs.

We also analyzed the magnetic domain structure of the grains using magneto‐optical Kerr‐microscopy. The deviation of the probed grain orientations from the ideal {100} orientation is kept below 5^°. The actual domain size evolution was tracked under a hysteresis loop varying the external applied magnetic field from −1000 to 1000 Oe, and the results are depicted in Figure 3c. We use the average magnetic domain width (W _SD) to describe their size since their shape is approximately oblate. We found that the W _SD decreases with the increase of the global Al content of the alloys. More specifically, the 3Al‐HEA has a W _SD of 23.5 ± 5.8 µm whereas the W _SD in the 7Al‐HEA is 12.3 ± 2.3 µm. These W _SD values are smaller than the average grain size, that is, ≈65 µm. A similar trend of magnetic domain refinement was observed in the electrical Fe‐Si steels with comparable W _SD.^{[ 23 ]} This behavior can be ascribed to the fact that Al/Si enrichment within the matrix (as a solid solution) changes the magnitude of the magnetic anisotropy constant (K ₁) of the matrix material and in turn also the domain wall energy.^{[ 50 ]} Such changes affect the overall balance between magnetostatic, volume and interfacial domain wall energies, resulting in a variation in the domain size.^{[ 51 ]} Moreover, the nanoscale chemical heterogeneity associated with nanoprecipitation can also impact the material's magnetic anisotropy, contributing to the observed refinement of the magnetic domains.^{[ 51 ]} These changes, along with different structural defects (e.g., 1D dislocations and 2D grain boundaries) that interact with moving domain walls and lead to different magnetization reversal processes, can increase coercivity.^{[ 51} , ^{52 ]}

By tracking the Bloch walls’ movement under different applied magnetic fields (yellow dashed area in Figure 3c), we see that the domain's growth is relatively smooth within the grains while it appears to be pinned at the grain and twin boundaries. This observation confirms that the coherent nanoscaled L1₂ precipitates do not exert notable magnetic pinning forces on the domain walls’ movement, in any case very small when compared to those at grain/twin boundaries.^{[ 51 ]} The Figure S6, Supporting Information shows a schematic representation of the Bloch wall pinning mechanisms for the HEAs with different precipitate sizes.

To establish a useful combination of mechanical and magnetic properties for the investigated HEAs, we constructed a “yield strength versus coercivity” diagram as a new kind of “Ashby‐plot” for this material class in Figure 3d. In this spirit, the properties of conventional SMMs are also included in the property chart for comparison. The HEAs of this work show excellent values of yield and ultimate tensile strength which outperform those of other SMMs, yet preserving good coercivity, with values below 11 Oe (0.87 kA m⁻¹). Figure 3e shows the saturation magnetization of the investigated alloys at high temperatures up to 873 K, suggesting that the magnetic properties of the HEAs also have good temperature resistance. For instance, the 3Al‐HEA can maintain 86%, 73%, and 61% of its room temperature M _s value at the temperatures of 573 K, 673 K, and 773 K, respectively. This observation can be attributed to the high thermal stability of the L1₂ phase along with the Fe‐Co rich matrix.^{[ 53 ]} This result indicates the substantial potential of the new alloys for applications where soft magnetic parts are exposed to elevated temperatures, for example, in high‐performance electric motors and transformers as well as in the vicinity of battery packs in electric vehicles.

Figure 4a shows the volume distribution of the L1₂ precipitates in the Al‐containing HEAs together with the corresponding volume fraction (inset of Figure 4a) obtained from the statistical analysis conducted on the APT data sets.^{[ 61 ]} The average volume of the nanoprecipitates increases from 168 ± 27 nm³ in the 3Al‐HEA to 2,294 ± 125 nm³ in the 7Al‐HEA. Figure 4b shows the changes in the lattice parameter and lattice misfit with increasing global Al content of the alloys according to XRD analysis. The volume fraction of the L1₂ precipitates and the corresponding lattice misfit increase with the global Al content (Figure 4a,b). Considering that the lattice strain at the coherent interface may also exert a pinning effect on the Bloch walls motion,^{[ 31 ]} we further measured the lattice strain distribution between the L1₂ nanoprecipitates and the fcc matrix by 4D‐STEM measurements, as outlined in the Experimental Section. Figure 4c shows the local strain map and the corresponding STEM phase map for the 3Al‐HEA and 7Al‐HEA. The localized strain caused during the sample preparation process was eliminated by subtracting the local average strain in each area (Figure S7, Supporting Information). Figure 4d illustrates the 1D local strain distribution along the arrows marked in Figure 4c. The estimated strain varies between −0.2% and 0.2% for the alloy with the smaller precipitate size (3Al‐HEA), whereas the alloy containing larger precipitates (7Al‐HEA) shows a higher average strain level varying within the range of −0.2% and 0.5%.

Figure 4.

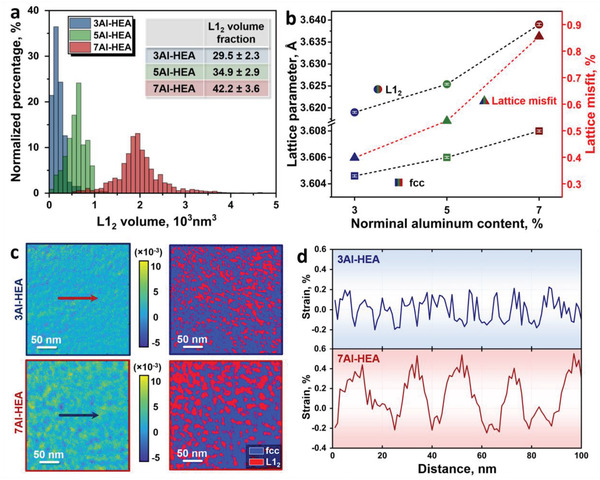
Statistic volume distribution of the L1₂ nanoprecipitates and quantitative lattice misfit and lattice strain in the HEAs. a) Normalized percentage with respect to the single precipitate volume, the inset shows the overall volume fractions of L1₂ precipitates. b) Lattice parameter and lattice misfit of the L1₂ and fcc phases. The lattice misfit (ε) is calculated using the equation ε = 2(a _L12 − a_fcc )/(a _L12 + a_fcc ), where a _L12 and a_fcc are the lattice parameters of the L1₂ and fcc phases, respectively.^{[ 36 ]} c) Local strain distribution map and corresponding phase distribution map of the 3Al‐HEA and 7Al‐HEA. d) 1D strain distributions along the arrows in (c).

We show that the proposed HEAs, containing ordered and coherent nanoprecipitates, exhibit ultrahigh yield strength values, varying from 952 MPa (3Al‐HEA) to 1202 MPa (7Al‐HEA), ultimate tensile strengths within the range of 1325 MPa (3Al‐HEA) and 1526 MPa (7Al‐HEA) and good elongation values between 15% (7Al‐HEA) and 29% (3Al‐HEA). They also present a good soft magnetic behavior with saturation magnetization (M _s) values ranging from 105 Am² kg⁻¹ (3Al‐HEA) to 88 Am² kg⁻¹ (7Al‐HEA) and low coercivity (H _c) whose values slightly vary from 8.6 Oe (3Al‐HEA) to 10.7 Oe (7Al‐HEA) at room temperature.

The current strategy by introducing the coherent and ordered nanoprecipitates in the Al‐containing HEAs enables a significant increase in yield strength by ≈245% (7Al‐HEA) compared to that of the base alloy which is devoid of nanoprecipitation. Simultaneously, the H _c only slightly increases by 2.1 Oe, at an overall value below 11 Oe at room temperature (7Al‐HEA). Note that the typical H _c values of conventional SMMs are lower than 13 Oe (1 kA m⁻¹).^{[ 4 ]} These observations reveal the potential of the investigated HEAs as promising soft magnetic material candidates for application scenarios with high mechanical loads. The considerable improvements in the mechanical properties derive from multiple strengthening mechanisms (detailed calculations are shown in Experimental Section): First, the high concentrations of the multiple elements (e.g., 32% Fe, 28% Ni, 28% Co, 7% Al, and 5% Ta for the 7Al‐HEA) in the fcc matrix provide massive solid solution strengthening^{[ 24 ]} and adjust the stacking fault (SF) energy into a regime where dislocation glide becomes planar. The increase of solid solution strengthening due to the Al addition compared to the base alloy is then evaluated to be: 87 MPa (3Al‐HEA) to 134 MPa (7Al‐HEA). Second, the high volume fraction of the ordered nanoprecipitation provides a remarkable precipitation strengthening effect. The HEA with a higher volume fraction of L1₂ nanoprecipitates and larger precipitate size may also require higher shear stress for the dislocations and SFs to cut through, thus effectively strengthening the alloys.^{[ 62} , ^{63 ]} The precipitation strengthening based on the particle shearing mechanism is evaluated to be in the range between 339 MPa (3Al‐HEA) and 528 MPa (7Al‐HEA). Third, dynamic microband refinement is responsible for the high strain hardening rates and the high uniform deformation. The theoretical calculation results on the contributions of various strengthening effects to the yield strengths of the current HEAs are summarized in Figure S8, Supporting Information, exhibiting good consistency with the experimental findings. Additionally, the lattice parameter of the L1₂ nanoprecipitates is larger than that of the fcc matrix. This leads to a positive lattice misfit that is beneficial for the high‐temperature mechanical behavior of the alloys compared with a negative lattice misfit, as reported for other superalloys and HEAs.^{[ 53} , ^{64 ]}

The mechanisms behind the soft magnetic behaviors are explained as follows. Firstly, the saturation magnetization (M _s) of the HEAs is slightly decreased by Al addition because the composition determines the fcc‐based HEAs’ M _s.^{[ 13 ]} More specifically, Ta and Al do not show any magnetic moment in the fcc and L1₂ phases as non‐ferromagnetic elements while Fe, Co, and Ni are ferromagnetic elements that exhibit high average magnetic moments.^{[ 13 ]} Therefore, the higher concentration of non‐ferromagnetic principal elements reduces the total magnetization per formula unit and leads to a slightly lower M _s (88 at% of ferromagnetic elements for 7Al‐HEA and 92 at% of ferromagnetic elements for 3Al‐HEA).^{[ 13 ]} Secondly, the coercivity (H _c) of SMMs is controlled by the displacement/movement of the magnetic domain walls. These processes are strongly affected by interfaces such as grain/twin boundaries and incoherent phase interfaces.^{[ 3 ]} The average grain size (≈65 µm) of the HEAs is comparable to that of conventional SMMs (50 µm to 1 mm). Therefore, it can be inferred that the grain boundaries in these HEAs are not acting as a deteriorating factor for the relatively low H _c (<11 Oe) required for soft magnetic applications.^{[ 14 ]} The slightly increased H _c observed for the Al‐doped HEAs (Figure 3b) is mainly associated with the increasing volume fraction of the L1₂ phase (Figure 4a) and the corresponding lattice misfit (Figure 4b). Nevertheless, according to the in‐situ observations of domain wall movement (Figure 3c), the pinning effect on the Bloch walls movement exerted by the precipitates is insignificant compared to that from high angle and twin boundaries.

3. Conclusions

We showed here that a non‐equiatomic FeCoNiTaAl HEA system can be turned into a material with a good property profile of strength, ductility and soft magnetic response, by introducing homogeneously distributed coherent and ordered nanoprecipitates. The formation of these nanoprecipitates is due to the strong interaction among Al‐Ta and Al‐Ni, respectively, which promotes the formation of intermetallic phases with some solid solution variation on the sublattices. The good combination of strength and ductility derives from massive solid solution, nanoprecipitation and dynamic microband strengthening, yielding mechanical features beyond those reported before for soft magnetic materials. The full coherency of the ordered nanoprecipitates and the matrix contributes significantly to the strength with only a slight increase in coercivity. The alloy design concept opens a pathway for developing novel soft magnetic materials with improved mechanical properties, such as needed for the electrification of industry and transportation.

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Supplemental Movie 1

Supplemental Movie 2

Supplemental Movie 3

Han L., Rao Z., Souza I. R. Filho, Maccari F., Wei Y., Wu G., Ahmadian A., Zhou X., Gutfleisch O., Ponge D., Raabe D., Li Z., Ultrastrong and Ductile Soft Magnetic High‐Entropy Alloys via Coherent Ordered Nanoprecipitates. Adv. Mater. 2021, 33, 2102139. 10.1002/adma.202102139

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.