Light Intensity Analysis of Photovoltaic Parameters for Perovskite Solar Cells

Abstract

The number of publications on perovskite solar cells (PSCs) continues to grow exponentially. Although the efficiency of PSCs has exceeded 25.5%, not every research laboratory can reproduce this result or even pass the border of 20%. Unfortunately, it is not always clear which dominating mechanism is responsible for the performance drop. Here, a simple method of light intensity analysis of the JV parameters is developed, allowing an understanding of what the mechanisms are that appear in the solar cell and limit device performance. The developed method is supported by the drift‐diffusion model and is aimed at helping in the explanation of parasitic losses from the interface or bulk recombination, series resistance, or shunt resistance in the perovskite solar cell. This method can help not only point toward the dominating of bulk or interface recombination in the devices but also determine which interface is more defective. A detailed and stepwise guidance for such a type of light intensity analysis of JV parameters is provided. The proposed method and the conclusions of this study are supported by a series of case studies, showing the effectiveness of the proposed method on real examples.

Light intensity analysis of photovoltaic parameters is introduced as a simple method, allowing understanding of the dominating mechanisms limiting the device performance in perovskite solar cells. The method is based on the drift‐diffusion model and is aimed at helping in the explanation of parasitic losses from the trap‐assisted recombination or ohmic losses in devices.

1. Introduction

There are more than ten years since the discovery of perovskite solar cells (PSCs). The number of studies on perovskite semiconductor materials and devices, and in particular PSCs, continue to grow exponentially. Although the efficiency of PSCs exceeded 25.5%, not every research group can reproduce this result or even pass the border of 20%. Detailed guidance on how to make perovskite solar cells with an efficiency of over 20% was proposed by Saliba et al.^{[ 1 ]} The work provides a comprehensive, reproducible description of the device fabrication protocols. However, progress in the field requires modifications in the device architectures and used materials. These deviations from the protocols will affect the performance of the devices, therefore an additional understanding of the changes in JV parameters such as fill‐factor (FF) and open‐circuit voltage (V _oc) is required. Interpretation of V _oc and its improvement is rather straight forward and therefore a lot of studies are dedicated to this.^{[ 2} , ^{3 ]} The V _oc reduction is typically associated with energy alignment and recombination in perovskite solar cells.^{[ 2 ]} While ideality factor points where bimolecular or trap‐assisted recombination are dominating in the devices. The interpretation of FF is more complicated first of all, it is very much linked to the short‐circuit photocurrent (J _sc) and V _oc of the devices, but also many parameters are influencing these JV characteristics, such as series^{[ 4 ]} and shunt resistance,^{[ 5 ]} and recombination processes in the PSC.^{[ 6} , ^{7 ]}

It is very well accepted that interfaces are the most critical for perovskite solar cells.^{[ 8} , ^{9 ]} Therefore, a lot of research is focused on interface engineering.^{[ 10} , ¹¹ , ^{12 ]} Several works have been reported where scientists try to correlate the FF with the processes occurring in the solar cell.^{[ 13} , ^{14 ]} Thus, the JV characteristics of the devices can provide some hints about performance‐limiting factors, however, due to the complexity of the processes in PSC devices, it often happens that more than one performance‐limiting mechanism is present in the devices. A lot of publications now show performance improvement, because the scientists understand and solve one of the issues within the devices. Despite the reported improvements, often, the performance of the reported devices is still far away from the state‐of‐the‐art. The complex analysis of understanding the performance‐limiting factor is still missing for perovskite solar cells. With most of the existing methods, we can conclude about possible mechanisms limiting the performance but often cannot distinguish the dominating one if more than one parameter affecting the JV characteristics. Simulations of the PSC device performance are currently used to explain the dominant mechanism of the performance in PSC devices. However, it is very effective for the research groups that are able to perform these simulations, while other research groups are still puzzling at understanding of performance‐limiting mechanisms occurring in their manufactured devices. Light intensity study of the JV parameters has become more popular in the last few years, claiming for example that it can make a correlation between trap densities and cell performances.^{[ 15 ]}

In this study, we introduce a simple method of FF and V _oc analysis as a function of light intensity to understand the performance‐limiting mechanism. So far there are no comprehensive studies that would help to fully understand the effect of these parameters (especially FF) on the operation of the solar cell. Although this method is based on the simulation results, the general conclusions can be easily transferable to only experimental methods and can be used for improving solar cells by scientists from the perovskite community. And therefore, the method can be applied in any, even not well‐equipped research group. This simple method will help both highly experienced and nonexpert laboratories to understand the main issues with their devices, and thereby motivating for improvement and fabrication of highly efficient solar cells.

2. Results and Discussion

2.1. Numerical Modeling

The interpretation of light intensity‐dependent characteristics of PSCs which we obtain experimentally was supported by the drift‐diffusion model developed for the investigated reference PSC system. The model quantitatively describes the generation, transport, and recombination mechanisms with the use of continuous equations for electron and hole charge carriers. Here, for the modeling, we neglect the effect of ions. The recombination processes include Shockley–Read–Hall, modified Langevin, and Auger models. The model has been discretized with the Scharfetter–Gummel method using Chebyshev polynomials for spatial grid discretization and solved by forwarding iteration in time to find steady‐state current for each applied voltage. To study the full perovskite solar cell stack, we have used the method of generalized potentials to not neglect energy differences between solar cell layers. The model includes electron and hole continuous equations to describe the generation, transportation, and recombination processes quantitatively:

$$\begin{array}{l}\frac{\partial n}{\partial t}=G-R_{\mathrm{m}}-R_{\mathrm{b}}-R_{\mathrm{t}}+\frac{1}{q}\nabla ·J_{\mathrm{n}}\\ \frac{\partial p}{\partial t}=G-R_{\mathrm{m}}-R_{\mathrm{b}}-R_{\mathrm{t}}-\frac{1}{q}\nabla ·J_{\mathrm{p}}\end{array}$$ (1)

where n and p are electron and hole charge carrier concentrations, respectively. G is a generation, R _m represents trap‐assisted recombination, R _b is radiative recombination, R_t represents Auger recombination mechanism. Also, q is an elementary charge and J _n and J _p are drift‐diffusion currents for electrons are holes, respectively. Both of the charge carrier concentrations are connected with the Poisson equation which is used to calculate the electric potential generated from free charge carriers:

$$\nabla ·F=\frac{q}{{\epsilon }_0{\epsilon }_{\mathrm{r}}}\left(p-n+N_{\mathrm{D}}-N_{\mathrm{A}}\right)$$ (2)

where ε₀ is the permittivity of vacuum, ε_r describes the permittivity of the material, and N _D and N _A represent the donor and acceptor concentrations, respectively. A more detailed description of the model is given in our previous work.^{[ 16 ]}

In this work we use p–i–n semitransparent perovskite solar cell with the following stack: glass/ITO/PTAA/perovskite/PCBM/SnO₂/ITO. The dual cation perovskite Cs_0.15FA_0.85Pb(I_0.98Br_0.02)₃ layer is used as a perovskite absorber. Table 1 summarizes all the parameters used for the simulation of PSCs if not stated otherwise. Here, we have considered only steady‐state conditions and do not study the dynamical effect of ions which results in hysteresis. We have already shown that ions in steady‐state conditions affect the operation of solar cells negligibly.^{[ 17 ]} The generation profile is calculated using the optical transfer‐matrix model.^{[ 18} , ^{19 ]} It has been calculated using the optical real and imaginary refractive index in function of wavelength for PTAA, perovskite, PCBM,^{[ 16 ]} and SnO₂ ^{[ 20 ]} layers. The electrical parameters are based on the literature or from the fitting procedure. For the hole‐transporting layer (HTL), PTAA material is used and the electrical parameters are adopted from the literature.^{[ 21} , ²² , ^{23 ]} Perovskite material is defined as an active layer with electrical parameters taken from the literature^{[ 24 ]} or from fitting to experimental data.^{[ 16 ]} For the electron‐transporting layer (ETL), we use PCBM material with electrical parameters adopted from the literature.^{[ 16} , ²⁵ , ²⁶ , ²⁷ , ^{28 ]} The SnO₂ material is used as a buffer layer and the electrical parameters are adopted from the literature.^{[ 29} , ^{30 ]}

Table 1.

Parameters used in the simulation of PSCs. The parameters for holes are written in the brackets and for electrons without the brackets.

	Name	Unit	PTAA	2C perovskite	PCBM	SnO2
L	Thickness	nm	14	535	40	45
εr	Permittivity		2.67	24.1	3.75	9.86
μn(p)	Mobility	cm2 V–1 s–1	(0.006)	6.845 (6.845)	0.002	0.002
C n(p)	Capturing rate	m3 s–1	–	1 (1) × 10–14	–	–
N t	Bulk trap density	m–3	–	9.896 × 1021	–	–
	ETL interface trap density	m–2	–	1.259 × 1014	–	–
	HTL interface trap density	m–2	–	7.943 × 1013	–	–
Γ n(p)	Auger constant	m6 s–1	–	1.55 (1.55) × 10–40	–	–
ζ	Langevin constant		–	5.2 × 10–5	–	–
E c(ν)	Energy level	eV	(−5.391)	−3.88 (−5.46)	−3.900	−3.904
N D(A)	Doping concentration	m–3	(0)	5.28 × 1020	0	1022
N c(ν)	Effective density of states	m–3	2.5 × 1025	1.2 × 1024	2.5 × 1025	2.5 × 1025
W a	Cathode work function	eV	(−5.288)
W c	Anode work function	eV	−4.00
R s	Series resistance	Ω	67.82
R sh	Shunt resistance	Ω	1.335 × 107

The first validations of the drift‐diffusion model were shown in our previous studies.^{[ 16} , ^{17 ]} The model was further elaborated by fitting the parameters of the solar cells measured under different light intensities. To increase the reliability of the proposed model, the simulation and validation of the results were performed for semitransparent devices with front and rear sides illumination measured under different light intensities. The usage of one set of parameters for two optical pathways and validation of the model with semitransparent devices significantly increases the accuracy of the simulation tool. The parameters used in the simulation were either adopted from the literature or obtained experimentally, all parameters are summarized in Table 1. The defined parameters point that the bulk and interface recombination are competing with each other. Thus, the model can determine whether the dominant trap recombination process occurs at the interfaces or in the bulk of the active material. It should be mentioned that for simplicity of the analysis at the initial stage we considered symmetrical recombination for electrons and holes, assuming that both interfaces Per/ETL and Per/HTL have the same level of defects. This model does not indicate which interface is more affected by the recombination processes, or in the other words, which interface is more defective. However, it allows us to make a clear distinction of whether bulk or interface recombination dominates. Getting this understanding, we further elaborated the model for asymmetric interfaces to point out the most defective interface. All conclusions obtained from the model are supported by the set of experiment results.

The experimental and simulated JV characteristics of the devices for the range of light intensities from 1 sun to 10^–4 suns are shown in Figure S1 (Supporting Information). The Figure represents the data obtained with front (glass/ITO) and back illumination. At the initial stage, the back‐side illumination was used for validation and improvement of the model reliability. The front and rear side illuminations will also be very important at the later stage of our research when we discuss asymmetric interface defect densities in the devices. Now, as can be observed from Figure S1 (Supporting Information) there is a very good correlation between the experiment and modeling. The shape of the experimental JV curves is well simulated not only between short‐circuit (SC) to open‐circuit (OC) range of applied voltage but also above OC which is mostly related to diffusion currents. The accurate matching between the experimental and simulated results was obtained because the buffer layer was included in the model, while in many simulations this layer is not included and the model is limited by the perovskite absorber and the surrounding ETL and HTL.^{[ 17} , ³¹ , ³² , ³³ , ^{34 ]} Figure 1 shows calculated and experimental photovoltaic parameters of the investigated reference devices for both front and rear side illuminations. The linear trend of V _oc in the semilog scale first of all will allow calculation of the ideality factor (n _id) and will help to find the dominant recombination processes, especially as it is negligibly affected by transport losses in the solar cell. The FF as a function of light intensity is very sensitive to the changes in defect states and ohmic losses. This will be further discussed in more detail. From the experimental results is observed that the FF measured from the front side is slightly higher than from the rear side. This difference arises from asymmetrical charge carrier density distribution in the perovskite layer. We have been able to reproduce that effect with modeling using donor doping in the absorber, which is well aligned with literature showing that the self‐doping affects the type of electronic conductivity making perovskite n‐type.^{[ 35 ]} The linearity of the J _sc on the log–log scale shows that the trap recombination (monomolecular) is the dominant one at SC conditions.^{[ 36 ]} However, deep analysis and interpretation of J _sc losses would require both optical and electrical characterizations, while here we only focus on electrical characterization. Therefore, our analysis will only be focused on FF and V _oc losses.

Figure 1.

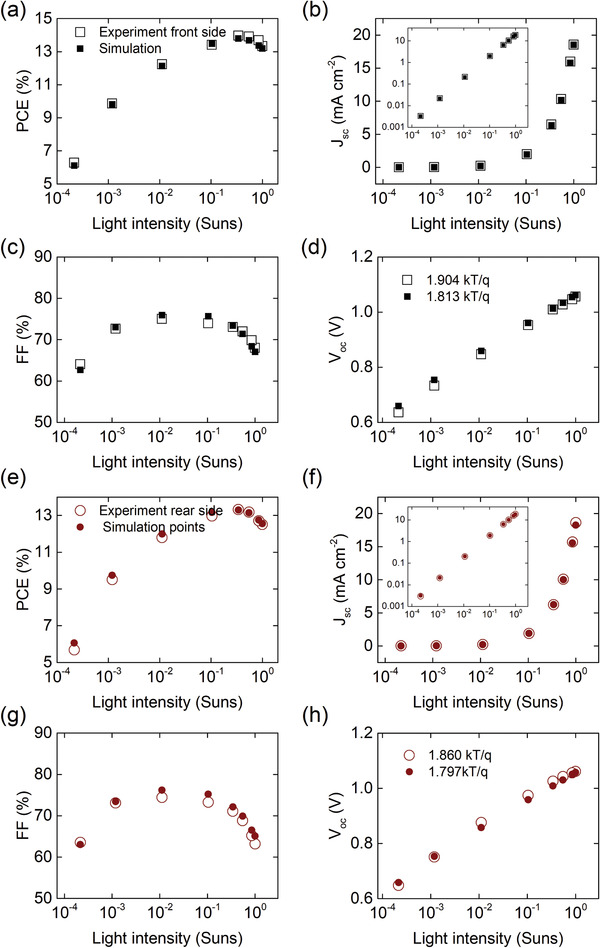
a–h) Photovoltaic experimental (open symbols) and simulation (close symbols) results for different light intensities for front illumination (a–d) and for rear illumination (e–h).

As the developed theoretical model can nicely describe the experimental results, with excellent fit, by changing different performance‐determining parameters, we can observe their influence on the device performance and see the trend of the FF and V _oc change. At the beginning of this study, we only show the results of the devices with front illumination. With the assumption of symmetric interfacial defects, the trend of the devices with rear illumination will be the same. Thus, Figure 2 shows the modification of the simulated outcome after complete removal either trap‐assisted recombination, resistive losses, or both. The PSC devices without trap recombination and resistive losses are only limited by the radiative recombination and its transport properties. Such devices will reach the Shockley–Queisser (SQ) limit that gives the upper limit of FF around 90% and V _oc equal to approximately 1.307 V for a 1.579 eV bandgap.^{[ 37 ]} The Auger recombination is so small that it starts to take domination only at a very high charge carrier concentration so only with concentrated light ranging in hundreds of suns. Devices without trap‐assisted recombination, with keeping resistive losses, demonstrate FF drop at 1 sun illumination compared to SQ devices. Decreasing the light intensity leading to increasing of FF, and reaching the FF's SQ limit at about 10^–2 suns. However, the FF drops again at very low light intensities values. These changes in the FF on both sides of the light intensity range are related to both series and shunt resistances, however, the distinguishing between these two will be discussed later. Now, keeping resistive losses at zero, but introducing trap‐assisted recombination leads to uniform shifting of the FF over the entire range of the light intensities downwards compare to the SQ limit. This uniform shift of FF over the entire range of light intensity is caused by trap recombination, however, the distinguishing between bulk and interface recombination will be analyzed later. The simulation of real reference devices illustrated the presence of both resistive losses and trap‐assisted recombination. The analysis of V_oc shows that the reduction or complete removing of trap states in reference devices will increase the V _oc value reaching the SQ limit of 1.307 V for perovskite absorber with 1.579 eV. The ideality factor also changes from 1.915 kT/q in real reference devices to almost 1 kT/q in the devices without trap recombination, as shown in Figure 2b. While the removing of resistive losses will not have any observed changes in V _oc and ideality factor compared to reference devices. These observations point out that V _oc and FF can change at a low light intensity and the character of the change depends on such factors as series and shunt resistances, as well as trap‐assisted recombination at the interfaces and in the bulk. However, often the distinguishing between each parameter and its influence on the JV parameters is not straightforward. There are quite a few works pointing to light intensity dependence of FF as a function of series resistance,^{[ 4} , ^{38 ]} and quite a lot of publications discuss the light intensity dependence of V _oc influencing by trap‐assisted recombination.^{[ 39 ]} However, deep analysis of the JV parameters in relation to each individual performance‐limiting factor has never been discussed before. However, the outcome of such investigation can be very useful and can provide very good guidance for the interpretation of the obtained results which will help to reveal the dominant mechanisms of PCE drop in the manufactured devices and help to produce perovskite solar cells with improved PCE.

Figure 2.

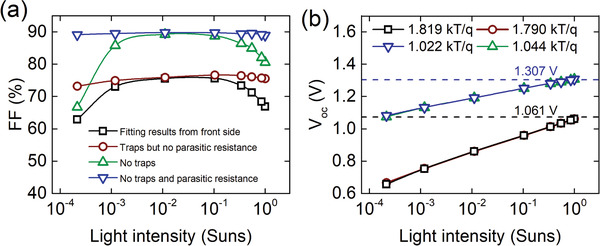
Simulation results for PSCs under different light intensities. The fitting (black square symbols), no traps (red open symbols), and no losses from trap recombination and parasitic resistance (green triangle symbols) results for FF (a) and V _oc (b).

Thus, in this study, using the developed model, we perform reverse engineering starting from the SQ perovskite solar cell, which has negligible losses of FF and with V _oc reaching SQ‐limited for the bandgap of 1.579 eV. Once the SQ limit is reached, charge‐carrier extraction will be limited only by radiative bimolecular recombination of electrons with holes.^{[ 40 ]} However, here we do not discuss bimolecular recombination, as it is determined by the intrinsic properties of the materials and it is lower by a few orders of magnitudes than trap‐assisted recombination.^{[ 41 ]} We gradually introduce resistive losses, and then, trap‐assisted recombination into the SQ devices and observe the JV parameters modifications in the range of different light intensities. In this way, we move from the SQ limit toward the simulated real devices but discuss all the details on the way.

2.2. Series Resistance

The first step of the analysis was focused only on resistive losses in the devices. Starting from SQ devices (no traps, no ohmic losses), we introduce additional resistances (either series resistance or shunt resistance) into the simulated SQ devices. Figure 3a demonstrates the effect of series resistance on FF, which appears to be pronounced only at high light intensities. The series resistance is often caused by the lateral conductivity of the transparent electrode.^{[ 4 ]}  However, it should be also mentioned that the series resistance value from the modeling is always higher than the one measured from the electrodes experimentally. It is related to the geometry of the electrodes and cells that influences the series resistance from the model. Series resistance is a very general parameter but its quantitative analysis helps a lot in determining the losses that are appearing under AM1.5 conditions. However, the determination of the series resistance value is only accurate with the use of more than one point of FF in light intensity function. From the figure, it is obvious, that the higher the series resistance in the devices, the lower is FF. Comparison of experimental and modeled results (no traps) allows us to determine the series resistance on the reference devices, which is 67.82 Ω. We correlate these losses with the high sheet resistance of sputtered back ITO electrodes and the geometry of the produced devices. A high sheet resistance of ITO in semitransparent devices is responsible for FF drop by about 5%–20% depends on the ITO manufacturing method. For the opaque devices with metal electrodes, the effect of electrode series resistance is much lower. But in this case, the series resistance of the devices is limited by the sheet resistance of the bottom ITO electrode, and of course by the geometry of the devices. For example, it was shown^{[ 4 ]} that increase the cell dimension from 0.09 to 1 cm² leads to FF drop from 76% to 69% for the devices with ITO sheet resistance of 10 Ω □⁻¹, and from 73% to 45% for the flexible devices with the sheet resistance of the ITO electrode of 60 Ω □⁻¹, measured at 1 sun illumination. The effect of series resistance on FF becomes less significant with a reduction of light intensity.^{[ 42 ]} And for certain cell geometry and certain light intensity it reaches saturation level, as shown in Figure 3a. As has been already mentioned, the effect of series resistance on V _oc is negligible and there is no V _oc change observed with increasing series resistance (see Figure 3b).

Figure 3.

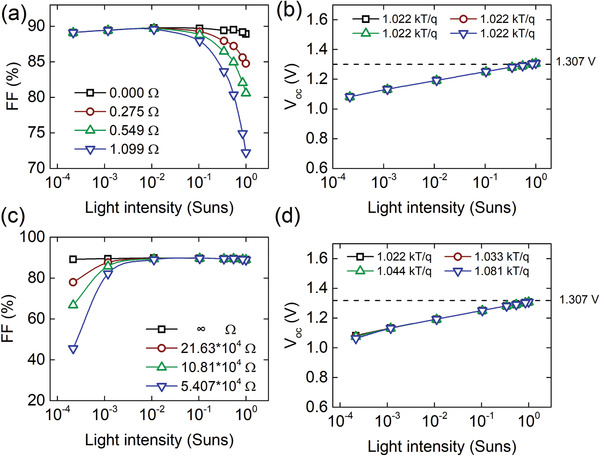
Simulated results for FF and V _oc of PSCs with front side illumination under different light intensities. a) −FF and b) −V _oc of the simulated devices having only series resistance as a performance‐limiting factor. c) −FF and d) −V _oc of the simulated devices having only shunt resistance as a performance‐limiting factor in the devices.

2.3. Shunt Resistance

Figure 3c demonstrates the other type of ohmic loss related to shunt resistance. The simulation shows only shunt resistance introduced into the SQ cells affecting FF in lower light intensities. The lower the value, the more detrimental the effect. Lower shunt resistance becomes visible even at higher light intensities, but high shunt resistance is only visible at very low light intensities. From the model, we determined that the value of shunt resistance in the reference devices acquired from the fitting was equal to 1.335 × 10⁷ Ω. Our reference samples have pretty low shunt resistance, and therefore the effect is highly observed. Moreover, from our experience and the literature,^{[ 43} , ^{44 ]} it is clear that further lowering of shunt resistance in the samples will also impact V _oc. In our case, because the range of the shunt resistances is not going to very low values, the effect can be observed only at very low light intensity values (see Figure 3d). Low values of shunt resistance are usually related to pinholes or nonuniformities in the perovskite layer. The small pinholes in the layer do not necessarily will lead to shunting the sample but might lead to contact between ETL and HTL layers directly which will drastically affect the operation of the solar cell, and it will be observed on both FF and V _oc change. More severe the shunts, it will be easy to observe at higher light intensities. However, for most of the samples, this is only observed under lower light intensity operation which is another point to make such an analysis. Even without the modeling tool the issue with shunt resistance can be pretty easily recognized performing dark JV measurements. ^{[ 45 ]} There are a lot of techniques for improving the quality of the layer and eliminating or reducing the shunt resistance.^{[ 46} , ^{47 ]}

2.4. Trap‐Assisted Recombination

At the next stage of the study, we introduce recombination losses into the modeled device. It is well accepted that trap‐assisted recombination is dominating the recombination mechanism in perovskite solar cells and limits their efficiency.^{[ 41} , ^{48 ]} The primary trap‐assisted recombination channels in the devices are grain boundaries and interfaces. To separate the effect of bulk and interface recombination, starting from SQ devices, we introduce only one type of efficiency‐loss mechanism, namely: bulk recombination (Figure 4a,b), or interface recombination (Figure 4c,d). For each scenario, four cases of bulk recombination effect were illustrated, namely: no bulk recombination (SQ device), and scenarios with the bulk defect states of 1 × 10²⁰, 1 × 10²¹, and 1 × 10²² m^–3, which are called low, intermediate, and high bulk defect densities, respectively. Same for the bulk recombination, four scenarios were illustrated: devices with zero recombination (SQ devices) for the reference, and three cases of defect concentration at the interfaces, equal to 5 × 10¹⁴, 2.5 × 10¹⁵, and 1 × 10¹⁶ m^–2, which are also called low, intermediate, and high interface defect densities, respectively. As was mentioned already, at the initial stage, we assume that both interfaces are symmetric, therefore the values of the defect concentration are equal at the HTL/perovskite and perovskite/ETL interface.

Figure 4.

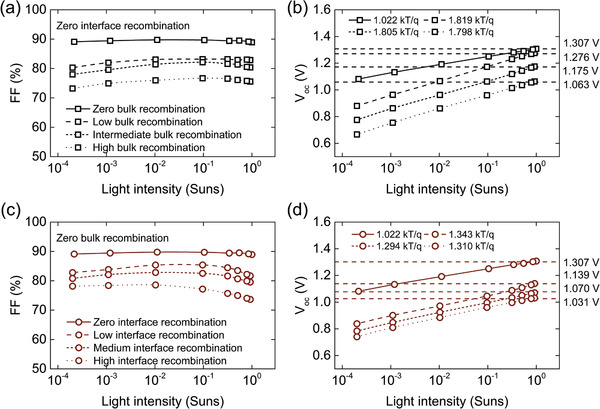
Simulated results for FF and V _oc of PSCs with front side illumination under different light intensities. a) –FF and b) −V _oc of the simulated devices having only bulk recombination as a performance‐limiting factor. c) −FF and d) −V _oc of the simulated devices having only interface recombination as a performance‐limiting factor in the devices.

The introduction of either bulk (Figure 4a) or interface recombination (Figure 4c) has a significant effect on FF leading to its reduction. The FF drops down with an increasing number of defect states. However, analyzing the light intensity dependency in both cases reveal some difference in the FF behavior in cases where either only bulk or interface recombination is present. In case when only bulk recombination present (Figure 4a), the drop in FF compare to SQ‐limited FF is almost the same over the entire range of light intensities. There is only a very slight slope is observed with increasing light intensities. This behavior can be explained by the fact that parallel resistance can also be non‐Ohmic,^{[ 49 ]} and can be observed in the devices with high trap densities. The recombination processes might appear to be slightly asymmetric due to illumination from one side only which generates more charge carriers at the incident side. However, it is much less visible for the bulk recombination process, where the whole perovskite film has uniform trap distribution.

In case when only interface recombination is present in the devices, with zero bulk recombination (Figure 4c), the light intensity behavior is slightly different. The drop of FF at 1 sun illumination is almost similar to the case of only bulk recombination, namely: FF of 75.5% vs 73.6% was observed for high bulk and high interface recombination at 1 sun, respectively. However, comparison between Figure 4a,c implies that bulk recombination results in a larger FF drop in the low light intensity region. The reason is that the zero bulk defect densities let the domination of the surface recombination which usually is considered to have higher defect concentration at the few nanometers interface. It has been already shown that such behavior might happen in the perovskite solar cell, where the total domination of the interface recombination is present.^{[ 50 ]} However, decreasing light intensity leads to some increase of FF, which at a certain level of decreased light intensity reaches the saturation level, similar to the case of series resistance (Figure 3a). Interestingly, with the lower level of defect densities at the interfaces (low interface recombination), sooner the saturation level can be reached during the reduction of light intensity. The devices with very high interface recombination can reach the maximum value of FF only at a light intensity of 10^–4 sun. But even then, the value of FF is still much lower than the possible SQ limit of the FF for this bandgap. To be more precise, if the SQ‐limited FF for the bandgap of reference devices is around 90%, the simulated devices with only interface recombination (and without any other performance‐limiting factors) will have FF at 1 sun of 64% (26% difference). Meanwhile, the FF reached 73% at very low light intensity, thereby reducing the gap between the SQ limit to 17%. In general, the interface recombination processes are dominating in the high light intensities as we have shown in our previous work.^{[ 16 ]} This is related to higher free charge carrier concentration at higher light intensities. Therefore, at higher charge carrier concentration more charge carriers can reach the surface of the material, and therefore potentially recombine nonradiative. This also explains the asymmetry of the FF comparing to the zero interface recombination case. The illumination is done at either front or rear side. In the case of bulk trap defect densities that are uniform across the device, the recombination might happen at any position depending, where the photon is being absorbed. However, the surface recombination is only happening at the interface between two materials. Therefore, all the photons that are absorbed in the bulk (lower energy photons) might recombine at the interface with a lower probability than in the case of bulk. It is independent of the symmetricity of the interface defect densities.

The light intensity dependency of V _oc is also very important in the analysis of trap‐assisted recombination. As was mentioned already the light intensity dependence of V _oc can allow calculation of the ideality factor using the following equation:

$$n_{\text{id}}=\frac{q}{k_{\mathrm{B}}\times T}\times \frac{\mathrm{d}{V}_{\text{oc}}}{\mathrm{d}\left(\ln \left(I\right)\right)}$$ (3)

where n _id is the ideality factor, k _B is the Boltzmann constant, T is the temperature of the system, q is the charge constant, and Iis the normalized light intensity.

The ideality factor can demonstrate which type of recombination is dominating in solar cells, whether the recombination type is SRH (n _id > 1) or bimolecular (n _id  =  1).^{[ 51 ]} This simplified explanation has been well accepted in the solar cell community. However, it has been also shown recently that the ideality factor can help to understand the domination of surface or bulk nonradiative recombination.^{[ 39 ]}

It is important to repeat that, at the initial stage of the modeling, the defect densities at both interfaces are counted as symmetrical, the effect of changing two interfaces simultaneously leads to a much smaller effect on V _oc than if we would change the interface defects asymmetrically, especially when change only one interface to higher values of interface recombination. This case will be discussed later. Continuing to keep symmetrical interfacial defects, we characterize the changes of the V _oc over the range of light intensity when both bulk and interface recombination is introduced into the PV system. The light intensity dependency of V _oc and the ideality factor are intensively described in the literature,^{[ 50} , ⁵² , ⁵³ , ^{54 ]} but here we split bulk and interface recombination and correlate our findings with the FF.

In the case of zero interface recombination, applying even low bulk recombination immediately increases the ideality factor from 1 (SQ case) to around 1.8, see Figure 4b. The change of ideality factor is mostly due to large loss of V _oc in lower light intensities, where bulk defect recombination has higher domination than in the high light intensities. The bulk trap recombination affects the V _oc in lower light intensity, where lower charge carrier concentration is present and thus all traps in the bulk can be effectively used. Further increase of bulk recombination does not increase ideality factor, however, lowers the V _oc. It can be explained with a very symmetric model of the device, where we assumed the same mobilities and recombination rates for electrons and holes. In our previous work to simulate the operation of different perovskite solar cells, it has been necessary to make calculations with asymmetric values and the density of states (DOS) to describe the trap distributions to get a good fit with experimental results and to achieve an ideality factor higher than 2 kT/q.^{[ 41 ]} The slight drop of ideality factor must be related to the small nonlinearity of the V _oc to light intensity relation. However, when calculating the ideality factor only in the low range of light intensity (10^–4 to 10^–2 suns) we would obtain values equal to 1.759, 1.764, and 1.840 kT/q. It is an increasing trend which is easily explained by the fact that bulk trap recombination is always more affecting V _oc in lower light intensities. Therefore, the discrepancy of decreasing ideality factor is coming from the numerical approach to assume uniform trap defects throughout the absorber which leads to some interface recombination. However, it could be considered to be a negligible effect only observed for the nonrealistic case with zero interface recombination.

For the zero bulk recombination, we observe a very similar trend to the previous case, when increasing symmetrically interface recombination, as shown in Figure 4d. The ideality factor increases to around 1.3 kT/q and shows slightly nonlinear V _oc behavior at high light intensity for the case of low interface recombination (see Figure S3 in the Supporting Information). The increase of surface recombination would expect to lower the ideality factor for higher interface recombination. This is observed if calculating the ideality factor for high light intensity (10⁰ to 10^–1 suns), where the ideality factor is equal to 1.619, 1.305, 1.231 kT/q, low, medium, and high interface recombination, respectively. However, symmetric interface recombination makes it resemble bulk recombination as described before. This is also clearly visible from the increasing trend of the ideality factors equal to 1.257, 1.324, and 1.357 kT/q at low light intensity (10^–2 to 10^–4 suns) for low, medium, and high interface recombination, respectively. Therefore, the increase of surface recombination with zero bulk defect is similar to a slight increase of the bulk defect densities from the V _oc point of view. For the same reason, we observe small nonlinearity in the V _oc behavior at a high light intensity which is more affected by the interface recombination mechanism. This makes it even more important to understand FF and V _oc relation at the same time.

2.5. Complex Analysis

A description of individual performance‐limiting factors makes a clear picture of how each factor can influence FF and V _oc in the devices. However, in real devices the bulk and interface defects are always present, therefore the cases described in Figure 4, are not realistic. It is always a competition between the domination of either interface or bulk trap‐assisted recombination. Thus, real devices never have only one limiting factor, but the combination of all of them which are high or low to a certain extend. In such a case interpretation of light intensity dependencies of FF and V _oc becomes more complex. Therefore, below we will discuss how to distinguish the dominating mechanism of the performance drop in real devices. Thus, in the following analysis we started not from the SQ devices, but from the devices having both series and shunt resistance. The values of series and shunt resistances were chosen to be equal to those defined in the reference device, namely: 67.82 Ω and 1.335 × 10⁷ Ω, respectively. And we introduce both bulk and interface recombination into the simulated JV parameters keeping bulk recombination at a low, medium, and high level, and the same for interface recombination demonstrating low, medium, and high level of the defect states (the same as in Figure 4). It will give in total nine variations (see Figure 5 ).

Figure 5.

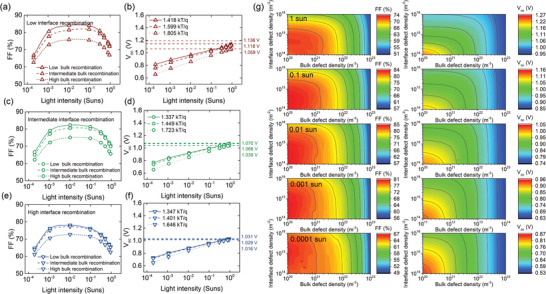
Simulated results for FF and V _oc of PSCs with front side illumination under different light intensities. a,c,e) –FF and b,d,f) −V _oc of the simulated devices with fixed series and shunt resistance (67.82 Ω, and 1.335 × 10⁷ Ω, respectively), and varied interface and bulk defect densities responsible for bulk and interface recombination. Here the bulk defect densities of 10²⁰ m^–3, 10²¹ m^–3, and 10²² m^–3 represent the cases of the low, medium, and high bulk recombination, respectively. The interface defect density of 5.0 × 10¹⁴ m^–3, 2.5 × 10¹⁵ m^–3, and 1.0 × 10¹⁶ m^–3 represent the cases of the low, medium, and high interface recombination respectively. g) 3D graphs of light‐intensity‐dependent FF and V _oc in the PSC with front illumination considering different levels of bulk and interface defect densities, responsible for bulk and interface recombination.

As has been already mentioned, both interfaces are assumed to be symmetrical, therefore the values of the defect concentration are equally the same at the HTL/perovskite and perovskite/ETL interface. Figure 5a shows the FF in light intensity function for low interface recombination. It is clearly visible that changing the bulk defect density from low level to high reduces FF uniformly by about 9%. This effect is also visible on V _oc relation, where the drop is mostly observed at the low light intensity, see Figure 5b. The ideality factor goes up from 1.418 to 1.805 kT/q which clearly shows the trend of the dominating bulk defect densities. These values are already at the level of competition between the domination of interface and bulk trap‐assisted recombination. Figure S4 (Supporting Information) shows the ideality factor change in 3D mode with changing both bulk and interface recombination. From the figure, it is clear that although interfacial defects have a strong effect on the ideality factor, the effect of bulk defects is higher. It should be also mentioned that the bulk defects are always present in the perovskite material, therefore the drop of FF is observed. However, if the ideality factor is in the range of 1–1.5 kT/q it points to dominating of interface recombination but most likely not the lack of defects. At the same time, the increase of bulk defect concentration reduces V _oc by 77 mV at 1 sun. In general, the bulk recombination affects low light intensity which leads to an increase of ideality factor, however, the interface recombination affects the high light intensity range. This could be explained again with the fact that bulk defects are uniformly distributed across the bulk of the perovskite layer and all photons independently on the absorption position would recombine with the same probability. Therefore, the lower light intensity that generates fewer free charge carriers in the bulk allows recombining with higher probability. Comparing that to higher light intensity, where more charge carriers are generated and fill more traps, decreases the probability of recombination.

Figure 5c,d shows the FF and V _oc in light intensity function for intermediate interface recombination. The trend in the FF drop with higher bulk recombination does not change comparing to lower interface recombination. However, we can see the shape of FF for the whole range to be slightly changed due to higher domination of interface recombination. We can see that it is mostly due to a slight drop of FF at high light intensity. Also, the drop of FF from low to high bulk recombination is 7%, suggesting that the domination of bulk is slightly reduced and the effect on the perovskite efficiency is decreased. This small observed change of FF shape in the whole range of light intensity is because the interface recombination is mostly dominating at a higher light intensity, where more electrons are generated and can reach the surface of the material and potentially recombine. If the free charge carrier concentration is lower, other processes might dominate its operation. For the same reason, V _oc at 1 sun also dropped down by 31 mV from low bulk recombination to a high one, while this difference at the lowest light intensity is 115 mV. It is also reflected in the ideality factor which now changes from 1.337 to 1.723 kT/q for low to high bulk recombination. Meaning, the interphase recombination once dominating the device reduces the effect of the bulk on the operation of the device. Most of the measured cells in our group lie in this condition and allow us to reach the maximum V _oc of around 1.1 V. The reason is that by changing only interface or bulk at one variation, the efficiency is still highly limited by the other mechanism. Even the best improvements are still leading to only a small increase of V _oc. Therefore, it is very important to know how much improvement of V _oc is possible when applying a new experimental method.

The previous observations are even more visible for the case of high interphase recombination, see Figure 5e,f. We can clearly see that the peak value of FF is not extremely affected by the interphase processes since the effect is mostly visible for high light intensity. Therefore, the increase of symmetric surface recombination leads to a further decrease of FF but mostly in that region. This makes the shape of the FF looks to shift from high light intensity to low one. In general, the shape of FF over different light intensities is very important for a good understanding of the dominant process in the operation of the device. Also, it can be noticed now that the drop of FF from low to high bulk recombination is now only 6%. However, this drop is less uniform especially at 1 sun, where the domination of surface recombination keeps FF at the lower range. The same observations are made for V _oc, which drops down mostly in the low light intensity. Only in the low light intensity region, the bulk recombination has a certain effect and reduces V _oc which leads to a small increase of ideality factor from 1.347 to 1.646 kT/q. Both numbers suggest strong competition between these two mechanisms in the operation of the perovskite solar cell.

Figure 5g shows FF and V _oc values in function of the bulk and interface recombination under different light intensities simulated from the front side. Very similarly the rear side simulations are shown in Figure S2 (Supporting Information). The range of values is higher than in Figure 5a–f to complete the already described trends. We can also clearly see that FF is mostly dominated by the bulk recombination in all light intensities. Interface recombination is only affecting FF at higher light intensities, and also only at high defect densities. In very low light intensities, the effect of surface recombination is barely visible. On the other hand, the V _oc is highly affected by both recombination processes. However, bulk recombination is more dominant in low light intensity and interface recombination is more noticeable at high light intensities.

From the above analysis, we could clearly see that the bulk recombination is always observed in PSCs and it is only a matter of how much it dominates the operation of the solar cell. The light intensity analysis is helpful only if we cover the measurement range wide enough to find the maximum peak point of FF. Also, there are needed more than three points to be able to calculate the ideality factor. The peak of FF tells us what is the total loss due to trap‐assisted recombination. The best‐prepared samples obtained in our group so far are showing FF around 81% at 1 sun, and surprisingly it always shows the maximum value of FF at around 0.01 suns light intensity where ohmic losses are the least observed. As it has been already discussed, the SQ FF limit is around 90%.

Because bulk and interface recombination are always competing, influencing the FF, depending on how high is the bulk recombination, the interface recombination might be more or less visible in the meaning of the ideality factor. For low bulk recombination, the interface can change the ideality factor drastically and try to dominate the solar cell. However, for higher bulk recombination, the ideality factor will keep closer to around 2 kT/q and even high interface recombination will not change it. Further, using the analysis, one should check the losses of V _oc by comparing to the SQ limit at 1 sun for a given bandgap. If losses are high with a low ideality factor that would be the suggestion of interface defects domination.

2.6. Asymmetric Interfaces

The symmetrical interface recombination has been used so far throughout the analysis for simplicity. However, in the real samples, it is quite unique to have such a scenario, where both interfaces are exactly in the same way affected by the trap defects recombination. It is challenging to define which interface has been dominating the sample and how much losses it generates. This knowledge can give an advantage in the experiment to define the potential side of improvements. Therefore, here, we focus on the asymmetric interface and its impact on the performance of the perovskite solar cell. To the best of our knowledge, we are the first to report a technique that allows for such a clear distinction between the domination of the interface based on the JV characteristics of the full device. However, it should be also acknowledged that now it is possible to achieve only using semitransparent devices. For simplicity, we refer to ETL and HTL interfaces which are related to perovskite/ETL and HTL/perovskite interfaces, respectively.

With this in mind, we perform the next step of research and apply asymmetric interfaces in the developed model. However, the main question is how to distinguish these two interfaces if illumination always occurs through only one side. This explains why most of the models existing so far apply symmetric interfaces. To overcome this issue, we use semitransparent devices in this study and illuminate our devices from both sides. Also, the model is developed and proven for illumination from both sides. This allows us to look into the device by illumination either from the ETL or the HTL side. The FF and V _oc of the devices with front and rear illumination, in relation to the interface defect densities at both interfaces, are shown in Figure 6 . From the figure, it is clearly visible that the losses of FF are higher at the recombination side where the light is incident. This means that, if the sample is illuminated from the front side, the FF losses are generated mostly at the HTL interface. The same is observed for the rear side and ETL interface. This is observed for all light intensities (Figures S5 and S6, Supporting Information) in the same way, but the highest losses are generated at high light illumination, e.g., 1 sun. This is for the same reason as discussed before, where interface recombination always dominates at high light intensity. For the V _oc losses, the explanation is the same, both interfaces generate higher V _oc losses respectively to the illumination side. However, the losses are still observed from the other interface. Figure S7 (Supporting Information) shows changes in the ideality factor over different recombinations for both interfaces. It is especially interesting to observe the difference of the ideality factors obtained with the front‐ (n _id,front) and rear‐ (n _id,rear) side illumination, also called Δn _id, as shown in Figure 6e. We can clearly see that these differences become very large when having high interface recombination at a specific interface. For the symmetrical surface recombination, we can see that Δn _id gets closer to zero. However, it is slightly higher than zero due to the presence of intrinsic donor doping, which makes the distribution of charge carriers in the device intrinsically asymmetric. Due to that fact, even very high HTL interface recombination might lead to only slightly negative Δn _id. However, the trend is clearly visible, where positive Δn _id means high ETL interface trap recombination as a dominant process. Oppositely, the negative Δn _id would suggest highly defected HTL interface recombination. Of course, it is valid for p–i–n devices, where the HTL is closer to the glass substrate. To differentiate from donor/acceptor asymmetrical doping, it is worth following the analysis with the FF at 1 sun from both sides. As was discussed before, highly intrinsically donor doped perovskite would give a higher FF at the front side, oppositely to acceptor doping, where the FF from the rear side would be the dominating one. This technique of experimental measurement allows definition of the dominant interface recombination when one is higher than another by two to five times. However, for a more quantitative analysis, only highly precise electrical modeling is needed. Also, this difference of the ideality factor is only related to interface recombination and other asymmetrical mechanisms in the device that make it independent of the bulk recombination process, which is considered symmetric.

Figure 6.

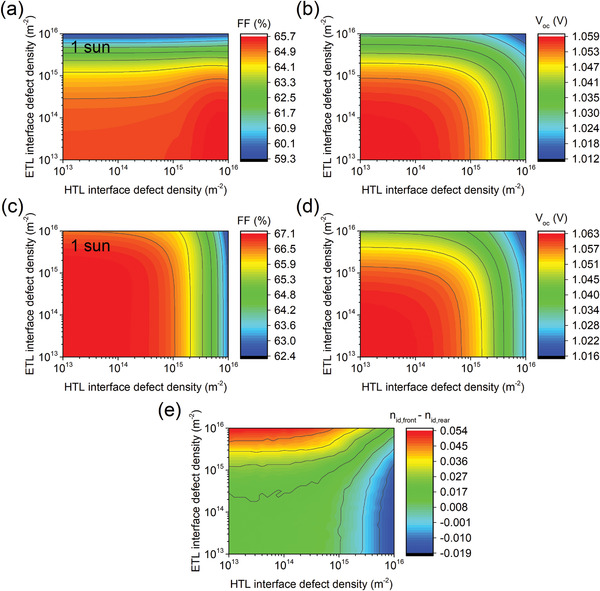
a,b) 3D graphs of FF (a) and V _oc (b) at 1 sun illumination of the semitransparent PSC with asymmetric interfaces, considering different levels of interface defect densities at HTL and ETL interfaces, for the device with front illumination (through the HTL side). c) FF and d) V _oc for the devices with rear illumination (through the ETL side). e) The ideality factor difference Δn _id (n _id,front − n _{id, rear}) in semitransparent devices with front and rear illumination.

2.7. Extraction Barrier

In the previous analysis, we mostly focused on the effect of the recombination processes on the performance of the PSCs. In the analyzed sample, we do not observe visible transportation losses due to potential energy misalignment of the transporting layers to perovskite material. Such an energy difference, even a small one, leads to high transportation losses. However, it should be mentioned that such losses are not a separate effect as series or shunt resistance but appear together with recombination processes. Meaning, the high extraction barrier between perovskite and transporting layer would lead to the accumulation of charge carriers at the interface. However, such an accumulation would not lead to observed losses due to a very low recombination loss which would not reduce the concentration of charge carriers. In this case, the time response of such a device would be affected but in the steady‐state condition, the operation of the aforementioned solar cell is still the same. Figure S8 (Supporting Information) shows simulated perovskite solar cells with different extraction barriers and without resistance and recombination losses. It is clearly seen that changing the energy level of ETL by 20, 90, and 120 meV does not show any difference in FF and V _oc.

In comparison with Figure S8 (Supporting Information), the simulation presented in Figure 7 is made taking into account interface and bulk recombinations. Figure 7 presents the simulated results of the light intensity study of the devices where the energy level of PCBM is also changed by 20, 90, and 120 meV. The choice of such asymmetric values is explained with the operation of the model, where the energy differences between layers are described with a Boltzmann distribution, where the exponential factor explains charge carrier concentration being lost when transported from absorber layer to the ETL. Also, we have decided to keep metal electrodes at the same energy levels and all other parameters exactly the same as in Table 1 except for the PCBM/SnO₂ conduction band. Therefore, the values are changed between the perovskite conduction band and anode work‐function. From the fitting parameters, we can clearly see that this extraction barrier is equal to 20 meV. However, deviation by 90 and 120 meV shows a linear decrease of FF, especially visible in the high light intensity. It is again, related to higher charge concentration thus more accumulation can appear and reduce the performance of the device, see Figure 7a. The V _oc in this range of values is slightly reduced, which also affect the ideality factor, as shown in Figure 7b. Changing the extraction barrier affects the device performance similarly to changing the series resistance. The reason is that changing the extraction barrier is the same as would be the increase of resistance of the device. However, one would notice that the effect is rather covering a wider range of FF in the function of light intensity. Therefore, these two mechanisms should be still possible to separate each other. Especially that if considering series resistance only to be influenced by the electrodes properties and the geometrical factor. Both are easier to define experimentally than the change of energy level of the transportation layers.

Figure 7.

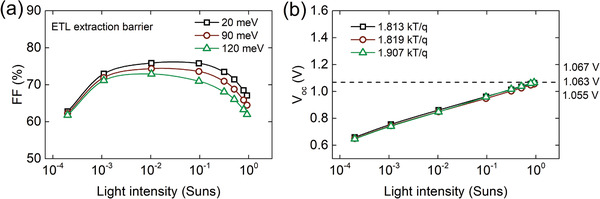
a,b) Simulated results for FF (a) and V _oc (b) of semitransparent PSCs with front side illumination under different light intensities. The ETL extraction barrier is changed by 20, 90, and 120 meV.

3. Case Study

3.1. Example 1: Series Resistance

To illustrate the effect of series resistance we compare semitransparent devices with rear ITO electrodes, having a sheet resistance of 60 Ω □⁻¹ with the identical devices where rear ITO is surrounded by evaporated Au busbar (fingers), thereby reducing the series resistance. The evaluated device stack is identical to the reference devices described above, namely: glass/ITO/PTAA/Cs_0.15FA_0.85Pb(I_0.98Br_0.02)₃/PCBM/SnO₂/ITO. The JV measurements of two devices at 1 sun reveal the difference in FF, 54.8% versus 60.9% for the devices without and with busbar, respectively. The difference is attributed to the reduction of the geometrical series resistance using evaporated busbars. The series resistance of the rear electrode can be further reduced using opaque devices with evaporated Cu electrodes. The FF races to 79.19% (see Table 2A). Additionally, we observe J _sc improvement due to the reflectivity of the rear metal electrode. To prove that the change of FF causing by the series resistance of the rear electrode, we refer to the light intensity study of the investigated devices, as shown in Figure 8A.

Table 2.

JV parameters of the perovskite solar cells measured with 1 sun illumination.

A. Example 1. Series resistance.
	Samples		V oc [V]	J sc [mA cm−2]	FF [%]	PCE [%]
1	Glass/ITO/PTAA/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/SnO2/ITO		0.998	18.25	54.80	10.00
2	Glass/ITO/PTAA/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/SnO2/ITO/Au fingers		0.992	18.21	60.80	10.99
3	Glass/ITO/PTAA/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/SnO2/Cu		1.043	19.66	79.19	16.24
B. Example 2. Shunt resistance.
(Glass/ITO/PTAA/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/SnO2/ITO/Au gold finger)

	Samples		V oc [V]	J sc [mA cm−2]	FF [%]	PCE [%]
1	–//–		1.027	20.26	58.86	12.25
2	–//–		1.021	20.04	61.28	12.54
C. Example 3. Trap recombination in the bulk.
(Glass/ITO/PTAA/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/SnO2/ITO/Au gold finger)

	Sample		V oc [V]	J sc [mA cm−2]	FF [%]	PCE [%]
1	Freshly made		1.017	19.92	60.24	12.21
2	After aging		0.972	14.52	51.66	7.29
D. Example 4. Interface recombination.
(Glass/ITO/HTL/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/BCP/Au)

	Samples / HTL		V oc [V]	J sc [mA cm−2]	FF [%]	PCE [%]
1	Cu:NiO x /PTAA		1.074	20.41	76.02	16.66
2	Cu:NiO x		0.999	19.51	75.55	14.73
E. Example 5. Interface recombination.
(Glass/ITO/PTAA/Cs0.15FA0.85Pb(I0.98Br0.02)3/PCBM/BCP/Au)

	Samples		V oc [V]	J sc [mA cm−2]	FF [%]	PCE [%]
1	With PCBM		1.054	20.80	77.05	16.91
2	Without PCBM		0.946	14.25	31.55	4.26

Figure 8.

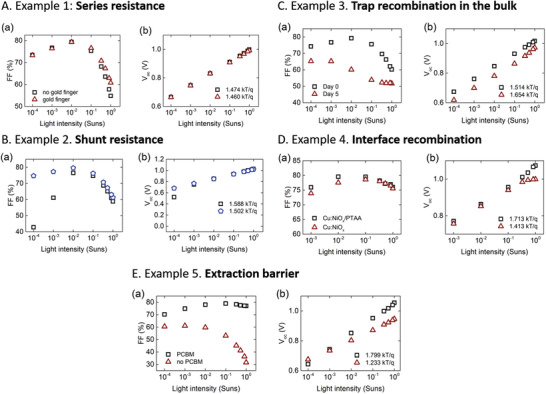
a,b) Light intensity study of the samples −FF (a) and −V _oc (b). A) Example 1: semitransparent devices with rear ITO electrode with and without Au busbars (fingers) and opaque devices. B) Example 2: two different devices with the same device architecture (sample to sample variation). C) Example 3: freshly made and after 5 d of the accelerated degradation under AM1.5G light. D) Example 4: devices with different HTL to show the interface recombination effect. E) Example 5: Light intensity study of two devices with and without a PCBM layer.

The figure demonstrates that the difference in the FF becomes negligible at the illumination of 10^–2 suns, there is no change in V _oc and ideality factor between these two devices. Because no difference in the FF at a low light intensity, it points that there is no difference in the bulk recombination in these two samples, and it clearly points that the only difference between these two devices is in the series resistance.

3.2. Example 2: Shunt Resistance

In the second example, we want to demonstrate the effect of shunt resistance in the devices. This factor very often remains hidden in the devices. Identical devices with different levels of shunt resistance can have demonstrated identical device performance. But due to the processing condition, the level of pinholes or layer uniformity can vary from device to device. Initial measurements of the performance do not reveal this difference. However, during the storage or especially aging of the devices, we might observe a different trend in the performance losses, which can be attributed to the difference in the shunt resistance in the devices. However, this difference in the shunt resistance can be easily identified in the devices from the same batch by performing a light intensity study.

As is clear from Table 2B that two identical devices produced in the same batch have very similar PCE and all JV parameters. However, performing a light intensity study reveals the difference in FF when light intensity goes to 10^–4 suns (Figure 8B). The V _oc of both devices is also identical at 1 sun illumination. However light intensity study reveals nonlinearity in the V _oc at a low light intensity, which also clearly points to the low shunt resistance in one of the devices. As was shown before, the shunt resistance, when very low might start to affect V _oc but only at the very low light intensity. Due to that, the ideality factor is also lowered and V _oc becomes nonlinear in the light intensity function. Thus, although the initial performance of the samples is identical these two samples are expected to have different behavior under aging because the difference in the shunt resistance can influence the device lifetime.

3.3. Example 3: Trap Recombination in the Bulk

To demonstrate the case with high defectivity of the perovskite layer and increased bulk recombination, we used freshly made and degraded devices identical to the reference devices used in this study. The encapsulated devices were aged at an elevated temperature of 40 °C over 5 d under constant light illumination. The JV parameters of freshly made and degraded samples are given in Table 2C. The light intensity study (see Figure 8C) reveals few things. First of all, the FF difference at low light intensity indicates that the degraded device has an issue with increased bulk recombination, which, of course, is easy to expect in the degraded sample, especially given that we are using full light spectrum, which includes UV light and degrades the perovskite layer much severely. The bulk degradation can be observed in the peak FF value, which drastically decreased from fresh to degraded sample, but also in the decrease of V _oc. The change of V _oc is followed by the increase of ideality factor which shows higher domination of the bulk recombination mechanism. However, it should be mentioned that such degradation might also create interface defects, especially on the illumination side.

3.4. Example 4: Interface Recombination

To highlight the effect of interface recombination, we demonstrate a case that was recently published by our group elsewhere.^{[ 16 ]} The architecture of the presented devices was the following: glass/ITO/HTL/Cs_0.15FA_0.85Pb(I_0.98Br_0.02)₃/PCBM/BCP/Au. As a hole transporting layer (HTL) either coper‐dopped nickel oxide (Cu:NiO_x) or an additional layer of PTAA on top of Cu:NiO _x (Cu:NiO _x /PTAA) was used. The JV parameters of both devices are shown in Table 2D. In the study, it was shown that significant recombination losses were observed in the devices with only Cu:NiO _x as an HTL, while the introduction of PTAA improves the interface and as a result, the performance, and especially V _oc was improved. This effect of high interface recombination in Cu:NiO _x ‐containing devices is easy to observe on the graph of light intensity dependency of V _oc and FF (Figure 8D). In addition to the improvement of V _oc at 1 sun illumination, we can observe the change of ideality factor from 1.413 to 1.713 kT/q when the interface recombination was reduced by the introduction of the PTAA layer. The difference of FF for both devices is very insignificant, indicating that the difference in the defect densities in the two devices has very little effect on the FF.

3.5. Example 5: Extraction Barrier

In the next case study, we would like to compare the devices with and without the PCBM layer. For that, two opaque samples were made in the same batch, however, one with spin‐coated PCBM and BCP layers and one only with BCP layer. PCBM is electron transporting material and BCP acts as a buffer layer in p‐i‐n configuration, respectively. The JV parameters of both devices are shown in Table 2E. Figure 8Ea clearly shows that the device without PCBM is losing PCE due to the drastic drop of FF in the whole range of light intensity. However, the most intense loss is at a higher light range. This suggests the extraction losses due to the mismatch of the energy level between perovskite and buffer layer, and also potentially with the metal electrode. This change is much more severe than what we have discussed in the manuscript. It can be easily understood when knowing that BCP is an isolator material that modifies the work‐function of the metal electrode, and it might work differently when put on the top of the perovskite material instead of the PCBM layer. We can also disclude the effect of series resistance since we have used the same geometry of electrodes and ITO substrates in one batch.

The losses of V _oc and change of ideality factor follow the trend of higher interface recombination, see Figure 8Eb. This is similar to what has been shown by Shao et al.,^{[ 56 ]} where it was shown that the role of PCBM is also related to the passivation of the interface defects. Thus, the loss of V _oc by around 100 mV and change of ideality factor from 1.799 to 1.233 kT/q can be accounted for the increase of interface recombination, which is in line with our previous description of the mechanism in the manuscript.

4. Summary and Guidelines for Interpretation of the Light Intensity Study

To summarize our study, we would like to propose guidelines for light intensity study which even without modeling can help to understand the major mechanisms dominating in the devices. Understanding the main issues in the poor‐performing devices can guide researchers toward the improvement and help in the manufacturing of highly efficient devices.

I. Light intensity measurements. The light intensity study is more efficient if: i) more measurement points are included in the study and ii) the measurements are performed up to a very low light intensity level. If it is not possible, at least the level of 10^–2 suns should be achieved.

II. Evaluation of FF in the range of low light intensities. Comparison of the FF can be done between two manufactured devices, or a comparison of the manufactured devices with an SQ‐limited FF for a certain bandgap. Plot FF as a function of light intensity and define the maximum value of FF. The value of light intensity where the FF will reach the maximum depends on the size of the devices, the distance between the active area and the contact points, and the sheet resistance of the electrodes. However, typically the maximum is reached at a medium light intensity of 10^–2 suns. Check whether the difference in FF at 1 sun remains when the maximum value of the FF is reached or not:

1. If FFs are different at 1 sun but demonstrate no difference at maximum FF values, then it is a classic case of high series resistance.

2. If FFs at maximum points are the same but demonstrate the difference at a very low light intensity, then it is a classic case of high shunt resistance. Basically, the issue of shunt resistance can also be easily recognized from the slope of the JV cure near J _sc on light (1 sun) or dark measured JV curves.

3. If the FFs at their maximum points of light intensity dependency are different, or the maximum FF does not reach the SQ limit, it points to the traps in the devices. Important to note that the effect of bulk recombination on FF is always higher. It is impossible to get a case with “zero” bulk recombination but having only interface recombination, bulk recombination is always present in the devices. Then even with low bulk recombination, it will be two competing factors influencing FF. With low interface recombination, the bulk recombination will dominate. However, if interface recombination will be very high, it starts to dominate in the FF drop. As both bulk and interface recombination contribute to FF drop, it is hard to define the dominating mechanism without V _oc analysis. The light intensity study of V _oc is discussed below.

4. Often there can be cases where both recombination and ohmic losses are present. In such a case, the difference in FFs at their maximum should be compared with the difference of FFs at 1 sun, and extremely low light intensity cases. If the difference in FFs at 1 sun is higher than the difference at maximum FF values, then both trap‐assisted recombination and series resistance issues are present in the device. Similarly, if the difference in FFs at extremely low light intensity is much higher than the difference in maximum FF values, then there is a combination of two issues: trap‐assisted recombination and shunt resistance.

5. As the effect of bulk and interface recombination will be finally concluded with V _oc light intensity analysis, the FF still can point to which interface is more defective. However, this technique so far is only applicable for the semitransparent device. For such analysis, the semitransparent devices should be measured with front and rear side illumination. If the FF of both measurements is the same, then we have a case of symmetric interface defect densities. However, if it is not the same, the lower FF from the given illumination side will point to the more defective interface. This conclusion can be further supported by the V _oc analysis (case 3d).

III. Evaluation of Voc in the range of low light intensities.Plot V _oc as a function of light intensity, and determine the ideality factor.

1. In the case of high trap‐assisted recombination (as defined in point 2c) and if the ideality factor is close to 2 kT/q, then the bulk defects are dominating.

2. In the case of high trap‐assisted recombination, and if the ideality factor is lower than 1.5 kT/q, then we are dealing with both high bulk recombination and even higher interface recombination. This will be observed in high V _oc losses which should be around 300 mV.

3. In the case of low trap‐assisted recombination (as defined in point 2c), and if the ideality factor is close to 1 kT/q, this is a case of very good devices with low bulk recombination and very good interfaces. This should be also observed in high V _oc of around 1.25 V for a PSC with a 1.56 eV bandgap.

4. The V _oc analysis is also very important in the interpretation of asymmetric interfacial defects in semitransparent devices. The same as FF can point on the more defective interface (point 2e), V _oc can support those conclusions. If the difference between the ideality factor from the front and rear illumination side is equal to zero, then we have a case of symmetric interface defect densities. However, if the difference of the ideality factors is positive, the ETL interface is more affected by the recombination (in the case of p–i–n devices). However, if the difference of the ideality factors from the front to the rear side is negative, then the HTL is more affected by the interface recombination. If apply it generally for any type of device: the higher ideality factor will point to the more defective interface.

5. Conclusion

The light intensity analysis of JV parameters in combination with the drift‐diffusion modeling was used to analyze PSCs to identify the recombination and ohmic losses in the cell. To increase the reliability of the model and perform its validation, the semitransparent sample has been measured and simulated from both sides. An important conclusion was made using both sides illumination, namely: the effect of self‐doping was recognized in the samples based on both sides’ analysis of the semitransparent devices and their losses of FF if illuminated from the rear side. Based on the developed model, we performed a stepwise analysis of different factors influencing device performance such as ohmic losses (series and shunt resistance) and trap‐assisted recombination (bulk and interface defects). The performed analysis guides how to assess the different mechanisms in the PSC without simulations, but only using light intensity analysis of the JV parameters. This technique gives the possibility to find operation mechanisms of the solar cell that would not be possible with only AM1.5 illumination.

The ohmic losses have been characterized by the series and shunt resistance and both have been attributed to the operation of PSCs. The series resistance is correlated with the ITO layer with poorer conductivity which results in FF loss at high light intensity. The shunt resistance is attributed to perovskite coverage and its pinholes that might affect the FF and even V _oc at low light intensities. The trap‐assisted recombination losses are differentiated between interface and bulk one. It has been shown that by using the method, it is possible to define which recombination is the dominant one in the PSCs. The details are given to understand these losses based on the results of FF and V _oc in light illumination intensity function. The recombination losses are described for three cases, where bulk defect density might be low, intermediate, or high. We have pointed out that these three cases are widely observed and should be covering the analysis for most of the samples. Moreover, we have developed a unique method to distinguish the most defective interface in the devices. It was possible due to the initial development of the model using semitransparent devices, and modeling both side illumination conditions. Applying the findings of the simulation into real semitransparent devices allows the use of a simple light intensity analysis to determine the most defective interface.

Generally, the proposed light intensity analysis of the JV parameters can help without complicated simulations to determine the main performance‐limiting mechanisms in a PSC. Using a series of simple measurements, which can be easily realized in any research lab, this method can help in understanding the main mechanisms occurring in the PSC and will create a solid base for efficiency improvement.

6. Experimental Section

Device Fabrication

The precursors for a perovskite Cs_0.15FA_0.85Pb(I_0.98Br_0.02)₃ solution was prepared using commercial lead iodide (PbI₂) (99.99%, TCI), formamidinium iodide (FAI) (GreatCell Solar), cesium iodide (CsI) (99.999%, Alfa Aesar), cesium bromide (CsBr) (99.999%, Alfa Aesar), dimethylformamide (DMF) solvent (99.8%, Sigma‐Aldrich) and 1‐methyl‐2‐pyrrolidinone (NMP) solvent (99.5%, ACROS Organics). The precursor solution was produced by mixing 1.4 m PbI₂, 1.19 m FAI, 0.126 m CsI and 0.084 m CsBr. The perovskite compositions were dissolved in DMF:NMP (9:1 volume ratio) solvent mixture and stirred overnight at room temperature.

The patterned glass/ITO substrates were ultrasonically cleaned, and also UV–ozone treated for 30 min. The solar cell was prepared inside the glovebox with an N₂ environment and the oxygen and moisture levels were at about 1 ppm. First, the HTL was spin‐coated using 4 mg mL⁻¹ of poly(triaryl amine) (PTAA) (Solaris) solution dissolved in toluene, at 5000 RPM for 35 s and with an acceleration equal to 5000 RPM s⁻¹ that gives approximately 18 nm layer thickness. Subsequently, the sample was annealed at 100 °C for 10 min. Further, the perovskite solution was dynamically spin‐coated with the gas quenching method.^{[ 16 ]} Using 150 µL of the precursor, the two‐step spin‐coating program was used to acquire desired thickness of approximately 535 nm. First, at 2000 RPM rotational speed for 10 s and with acceleration 200 RPM s^–1, second at 5000 RPM for 30 s with 2000 RPM s^–1. After 15 s of spin‐coating, the perovskite layer was quenched by using a nitrogen gun for 15 s at 6 bars pressure with 10 cm vertical distance from the substrate. After quenching, the perovskite samples were placed immediately on the hot plate with 100 °C for 10 min long. The ETL solution was prepared with [6,6]‐phenyl C61 butyric acid methyl ester (PCBM) (99%, Solenne) material dissolved in chlorobenzene solvent to acquire 20 mg mL^–1 solution, and further stirred overnight at 60 °C. Subsequently, the solution was spin‐coated with 1500 RPM speed for 50 s and 3000 RPM s^–1 acceleration that gives about 40 nm thickness of the layer. The buffer layer has been prepared using tin oxide (SnO₂) (Avantama N‐31) nanoparticles 2.5 wt% with a mixture of butanol filtered with a 0.2 µm polypropylene filter. The SnO₂ solution was spin‐coated with 3000 RPM speed for 50 s and 3000 RPM s^–1 acceleration and annealed at 80 °C for 5 min on a hot plate. The resulting thickness of the SnO₂ layer was approximately 60 nm. Afterward, the cleaning of the ITO contacts was accomplished in air with DMF:chlorobenzene solution at 1:6 volume ratio to remove all the layers at the ITO contact. Lastly, the ITO electrodes were sputtered with shadow masks placed on top of the ETLs to acquire a thickness of 180 nm. The samples have been finished with 100 nm gold busbars (outside of the active area) evaporated under 10^–6 mbars vacuum pressure to improve the conducting properties of the ITO electrodes.

Device Electrical Characterization

The current–voltage (J–V) characteristics (Keithley 2400) of perovskite solar cells were measured in N₂ conditions under a white light halogen lamp and illumination mask to define the active area of the illuminated cell equal to 0.09 cm². The light intensity was simulating AM1.5 conditions, and therefore it was calibrated to 100 mW cm⁻² with a silicon reference cell. Also, a set of ND filters was used to obtain 1, 0.83, 0.53, 0.33, 0.1, 0.01 and 0.001 sun illumination intensities. The maximum‐power‐point tracking was performed for 2 min before the JV measurements as a pre‐conditioning. The samples were kept in steady‐state condition when changing the filters by creating some time gap between the measurements and not switching the light off. The J–V curves were measured with a scanning rate equal to 0.165 V s⁻¹ with a 20 mV step and without preconditioning. The scanning direction was performed in forward (from −0.1 to 1.1 V) and reverse (from 1.1 to −0.1 V) bias directions to analyze the hysteresis effect.

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Glowienka D., Galagan Y., Light Intensity Analysis of Photovoltaic Parameters for Perovskite Solar Cells. Adv. Mater. 2022, 34, 2105920. 10.1002/adma.202105920

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.