Electrical Generation and Deletion of Magnetic Skyrmion‐Bubbles via Vertical Current Injection

Abstract

The magnetic skyrmion is a topologically protected spin texture that has attracted much attention as a promising information carrier because of its distinct features of suitability for high‐density storage, low power consumption, and stability. One of the skyrmion devices proposed so far is the skyrmion racetrack memory, which is the skyrmion version of the domain‐wall racetrack memory. For application in devices, skyrmion racetrack memory requires electrical generation, deletion, and displacement of isolated skyrmions. Despite the progress in experimental demonstrations of skyrmion generation, deletion, and displacement, these three operations have yet to be realized in one device. Here, a route for generating and deleting isolated skyrmion‐bubbles through vertical current injection with an explanation of its microscopic origin is presented. By combining the proposed skyrmion‐bubble generation/deletion method with the spin–orbit‐torque‐driven skyrmion shift, a proof‐of‐concept experimental demonstration of the skyrmion racetrack memory operation in a three‐terminal device structure is provided.

A new route to generate and delete magnetic skyrmion‐bubbles electrically is presented using a vertical current path. The vertical current path concept is easy to integrate with a widely used spin–orbit torque device. Using the vertical current path with a spin–orbit‐torque device, core operations for a skyrmion racetrack memory device in a three‐terminal device are demonstrated.

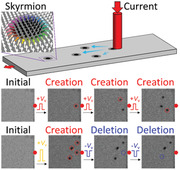
1. Introduction

Since its first discovery,^{[ 1} , ^{2 ]} the magnetic skyrmion has attracted much attention because of its topological characteristics and potential in spintronic applications.^{[ 3} , ^{4 ]} Various skyrmion devices have been proposed based on their distinct advantages of low power consumption, facile integration into logic devices,^{[ 5 ]} neuromorphic operations,^{[ 6 ]} or reservoir computing.^{[ 7 ]} One of these proposals is the skyrmion racetrack memory,^{[ 8} , ^{9 ]} in which information is encoded by magnetic skyrmions in a magnetic wire structure. Skyrmion racetrack memory has been considered as an appealing alternative to next‐generation memory technology because of its small skyrmion size, high‐speed operation, and stability.^{[ 8} , ⁹ , ^{10 ]} The minimum size of skyrmion can be smaller than that of the magnetic domain wall,^{[ 11 ]} where the minimum size determines the maximized device density. In addition, based on additional topological stability, the critical depinning current density in the skyrmion racetrack memory device is four orders of magnitude lower than that in the domain‐wall racetrack memory. Skyrmion racetrack memory requires the sequential operation of electrical generation, deletion, and shifting of individual skyrmions in a single racetrack device.^{[ 12 ]} Hence, the realization of skyrmion racetrack memory has been considered to be a challenging issue, and the feasibilities of the three main operations of generation/deletion/shift have typically been demonstrated individually. Specifically, since the experimental observations of magnetic skyrmions at room temperature,^{[ 13} , ^{14 ]} various approaches have been proposed for skyrmion generation using magnetic fields,^{[ 13} , ¹⁵ , ^{16 ]} current‐induced spin torque,^{[ 14} , ¹⁷ , ¹⁸ , ¹⁹ , ^{20 ]} voltage‐controlled magnetic anisotropy,^{[ 21 ]} and thermal energy.^{[ 22} , ^{23 ]} The deletion and shift of skyrmions have been successively achieved by current‐induced spin–orbit torque (SOT).^{[ 13} , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ^{20 ]} In the manipulation of skyrmions, the inevitable skyrmion Hall effect, which must be removed for skyrmion racetrack application, has also been experimentally observed,^{[ 24} , ^{25 ]} but can be suppressed using ferrimagnetic or synthetic antiferromagnetic systems.^{[ 26 ]} At this stage, the remaining experimental challenge toward achieving skyrmion racetrack memory is the implementation of all these three operations within a single device. Büttner et al.^{[ 17 ]} reported the two operations of generating and shifting skyrmion in one device using a tailored pinning site, whereas Woo et al.^{[ 18 ]} achieved the electrical generation and deletion of a single skyrmion in one device using device‐compatible geometry. In addition, Yu et al.^{[ 27 ]} realized a skyrmion shift device using writing and shifting skyrmions in one device. However, whether all three operations of generation/deletion/shift can be realized on a single device has not been experimentally proven. Here, we introduce a practical method for generating and deleting isolated skyrmions via vertical current injection. Our approach utilizes a 3D vertical conducting path on the track for skyrmion writing and deleting that allows the device density to be maximized and a skyrmion to be generated and annihilated at any position in the racetrack, whereas previous approaches can only be used at the end or edge of the racetrack. Additionally, we experimentally implemented core operations of skyrmion racetrack memory using the vertically injected current for the skyrmion generation and deletion operations in combination with the in‐plane current injection for the skyrmion shift. Although we do not provide the detection operation in this work, the read‐out operation of stored information can be achieved by integrating a magnetic tunnel junction (MTJ) unit directly onto the racetrack;^{[ 28 ]} the MTJ technology has been well‐established with the advance in spin transfer torque (STT)‐magnetic random access memory technology.

2. Skyrmion‐Bubble Generation via Vertical Current Injection

A multilayer of W (5 nm)/CoFeB (1.3 nm)/Ta (0.08 nm)/MgO (1 nm)/TaO _x (2 nm) on a Si/SiO₂ substrate with perpendicular magnetic anisotropy (PMA) was investigated (Figure  1a). In this stack, a thin Ta layer was inserted to tune the PMA degree, which originates from the CoFeB/MgO interface.^{[ 29 ]} The bottom W layer serves to induce the Dzyaloshinskii–Moriya interaction (DMI), which favors the formation of a Néel‐type skyrmion.^{[ 30 ]} The W/CoFeB/Ta/MgO/TaO _x film was patterned into a plate shape (the navy dashed line in Figure 1b). Then, GdO _x /Pt (2 nm each layer) was deposited on the magnetic wire (the green dashed line region in Figure 1b) using photolithography and the lift‐off process (for detailed information for the oxide material choice, see Section S1, Supporting Information). A sufficiently thin Pt top electrode allows the use of magneto‐optical Kerr effect (MOKE) microscopy to obtain the magnetic images of the CoFeB layer through the Pt layer. MOKE images in the black box region of Figure 1b with the z‐axis magnetic fields of 0 and 0.43 mT are presented in Figure 1c. The dark (light) gray represents the −z (+z) magnetization as described in the color bar. Under zero field, the film exhibits a half‐filled stripe domain with a rotational symmetry with a width of 1.2 µm. The stripe domain width is defined by the yellow arrows in Figure 1c. The stripe domain patterns in both regions with and without the top insulator are well‐connected with an identical stripe domain width. It indicates that the magnetic properties in the two regions are almost identical. Application of +z‐axis magnetic field (+μ₀ H_z ) breaks the symmetry along the z‐axis by lowering the energy of +z domains, so they expand, whereas the −z domains remain in the form of a stripe domain at +μ₀ H_z . Then, a vertical voltage input (V _v in Figure 1b) through the top Pt electrode usually induces an electric field between the top Pt and W/CoFeB layers if the oxide layer (MgO/TaO _x /GdO _x ) acts as an ideal insulating layer. However, in this work, an insulating layer with a conducting path was used to achieve vertical current injection into the magnetic layer (Figure 1d). The conducting path is expected to be a pinhole, which was possibly created during the device fabrication process. Therefore, the V _v input creates a current flow through the conducting path (red column in Figure 1d) and the current extends radially from the contact point in the magnetic film (yellow arrows in Figure 1d). The presence of the conducting path and its consequent current distribution in the magnetic film were confirmed by observing the evolution of the stripe domain during V _v application (see Section S2, Supporting Information). A V _v pulse of 2.5 V was applied for 300 ms under a μ₀ H_z of 0.43 mT, where the presence of μ₀ H_z stabilizes the skyrmions after generation (see Section S3, Supporting Information). Starting from the initial state (Figure 1e), MOKE images were taken every 100 ms along with V _v pulse injection. The initial state (Figure 1e) is a uniform magnetization along +z due to the presence of a sufficient +μ₀ H_z . When a V _v pulse was injected, reversal of magnetization was observed near the conducting path (red dot in Figure 1f). The MOKE images in Figure 1e–j are averaged over ten successive measurements where a single image measurement takes 10 ms, and therefore, blurred images can be observed because the magnetization state changes faster than the image capture speed. During the V _v application, the formation of several bubble domains was clearly observed near the conducting path, and the bubble domains remained stable even after the V _v pulse was turned off (Figure 1i,j). The bubble domains observed here would be considered a “skyrmion‐bubble” because they present magnetic properties of both chiral skyrmions and magnetic bubble domains.^{[ 31 ]} Interestingly, skyrmion‐bubbles are only generated toward the left side of the conducting path with regard to the asymmetric current distribution (see Section S4, Supporting Information). With this experimental observation of skyrmion‐bubble generation by vertical current injection, micromagnetic simulations were carried out to understand the microscopic origin of skyrmion‐bubble generation as described below.

Figure 1.

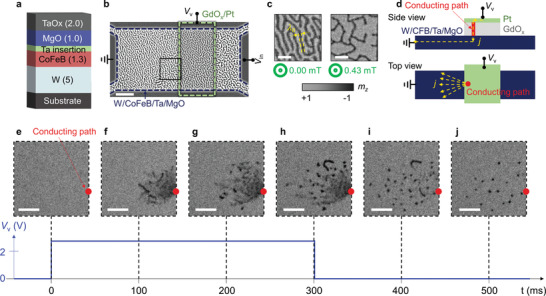
Isolated skyrmion‐bubble generation via vertical current injection. a) The magnetic film structure: substrate/W (5 nm)/Co₂₀Fe₆₀B₂₀ (1.3 nm)/Ta (0.08 nm)/MgO (1 nm)/TaO _x (2 nm). b) The three‐terminal device pattern. The magnetic film is patterned into a plate shape as marked in the navy dashed line and a GdO _x /Pt stack (2 nm each layer) is deposited on the green dashed region. Scale bar: 20 µm. c) The stripe domain under μ₀ H_z of magnitudes 0 and 0.43 mT. Light and gray represent the +z and −z magnetization as described in the color bar; m _z is the normalized z‐axis magnetization. The yellow arrows indicate the stripe domain width (λ₀). Scale bars: 5 µm. d) Schematics of the vertical current injection structure. e–j) Time‐dependent magneto‐optical Kerr effect images after application of a V _v pulse of 2.5 V for 300 ms. The red circle indicates the conducting path. Scale bars: 5 µm.

3. Micromagnetic Simulation of Skyrmion‐Bubble Generation

To illustrate the microscopic mechanism of skyrmion‐bubble generation via vertical current injection, we performed a spin dynamics simulation based on the Landau–Lifshitz–Gilbert equation using MuMax3 software^{[ 32 ]} at 0 K. An example for MuMax3 is provided in Section S5 in the Supporting Information. Material parameters were chosen to form a typical stripe domain at zero field and stabilize magnetic skyrmion‐bubbles under a μ₀ H_z (Figure  2a–c). The magnetization configurations under various magnitudes of μ₀ H_z agreed well with the experimentally measured images in Figure 1c,j. First, we consider the high current density through the conducting path and its consequent Joule heating effect on the magnetic film near the conducting path. Magnetic properties, including saturation magnetization (M _s), PMA energy (K _eff), and exchange stiffness (A), decrease with increasing temperature (Joule heating).^{[ 33 ]} Therefore, the heating region near the conducting path could have a lower energy for magnetization reversal compared with other regions of the magnetic film, leading to the magnetization reversal of the conducting path region by the dipole field generated from the other magnetizations. In the simulation, the magnetization reversal by the dipole field corresponds to a fixed reversal magnetization at the center (Figure 2d). The red dot in Figure 2d represents the conducting path. When the current through the conducting path reaches the magnetic film, the current extends radially, and the current density is inversely proportional to the distance from the conducting path. The SOT induced by the current in the magnetic film pushes out the magnetic domain wall formed at the boundary of the reversed magnetization toward the direction of current flow. Because all the magnetic properties and the defect distribution are symmetric in the film plane, the SOT forces exerted on the domain wall (F_j in Figure 2d) should extend the domain wall into a symmetric circular shape (the red dashed circle in Figure 2d). However, the presence of a field μ₀ H_z of 150 mT stabilizes small‐sized skyrmion‐bubbles rather than large domains (see Figure 2c). Therefore, the symmetric F_j by the radial current flow expands the domain wall in an irregular shape (see Figure 2e), and finally, a one‐stripe domain elongates from the fixed magnetization (see the red box in Figure 2f). The width of the elongated stripe domain is almost identical to that of the skyrmion‐bubble in Figure 2c. The generated stripe domain continues to elongate (Figure 2g), and the unstable stripe domain is eventually cut to form a magnetic skyrmion‐bubble as the magnetic skyrmion‐bubbles are more stable than stripe domains (see Figure 2h).^{[ 14} , ^{34 ]} It has repeatedly been confirmed that many skyrmion‐bubbles can remain after the skyrmion‐bubble generation process as described above (Figure 2i). To determine the cause of the formation of a skyrmion‐bubble, we simulated it with a small (≈50 nm) skyrmion‐bubble. Note that smaller skyrmion‐bubbles tend to be found in larger perpendicular magnetic fields,^{[ 2} , ³ , ¹³ , ¹⁴ , ¹⁹ , ²² , ²⁴ , ²⁵ , ^{27 ]} so that the required perpendicular magnetic field in simulations is larger than that in experimental situations. However, because the size of skyrmion‐bubbles is irrelevant to the two main generation mechanisms—the radial current distribution and the concentrated current density at the conducting path—it is expected that the large skyrmion‐bubbles would form similarly. The aforementioned simulations have been done with simplified assumptions to obtain the results within a short period of time. The effect of temperature is simplified to the formation of an initial reversed domain at the center. The temperature rises near the conducting path so that magnetization can change easily. Consequently, there will be a reversed magnetization zone near the conducting path. A stripe domain will emerge from these reversed magnetization areas and become skyrmion‐bubbles. An important mechanism here is that the spreading current breaks the stripe domain into skyrmion‐bubbles, as shown in the simulation. In addition to the aforementioned scenario, four additional supporting phenomena can be considered (see details in Section S6, Supporting Information).

Figure 2.

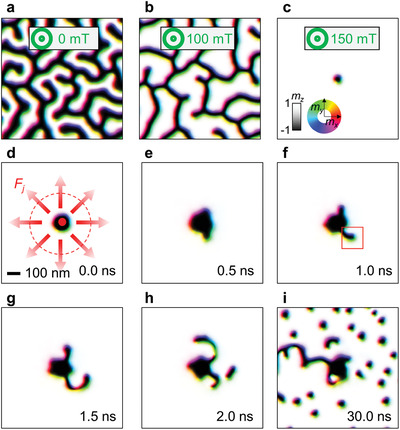
Micromagnetic simulation of skyrmion‐bubbles generated via vertical current injection. a–c) Magnetization configurations at a μ₀ H_z magnitude of 0 mT (a), 100 mT (b), and 150 mT (c). The direction of magnetization is described by the color. d) Initial state with reversed magnetization by the Joule heating effect at the center; the red arrows indicate a symmetric spin–orbit torque force on the domain wall of the reversed magnetization by the radial current flow. e–i) Time‐dependent evolution of magnetization configurations. i) A bunch of skyrmion‐bubbles generated by the vertical current injection and radial current flow.

4. Generation and Deletion of Magnetic Skyrmion‐Bubbles via Vertical Current Injection

Based on the experimental demonstration and simulation of generation of magnetic skyrmion‐bubbles via vertical current injection, we investigated the detailed operations of generation and deletion in a three‐terminal device with a vertical current path (Figure  3a). First, the simulation in Figure 2 is also valid when the polarity of all domain magnetizations and magnetic fields is reversed because the Joule heating effect by the vertical current is an even function with respect to the current. Therefore, when the +V _v pulse under +μ₀ H_z generates skyrmion‐bubbles with a m_z  = −1 core (skyrmion number = −1) (Figure 3b), the +V _v under −μ₀ H_z generates skyrmion‐bubbles with opposite polarity (skyrmion number = +1) (Figure 3c). The polarity of V _v is identical for the   ±1 skyrmion‐bubble generation. That is, the role of the vertical current is to generate Joule heating, as shown in the simulation, and the current must stretch out in the magnetic film for the generation. Interestingly, skyrmion‐bubbles are more generated on the bottom side of the vertical current path in Figure 3b, but are more accumulated on the top side in Figure 3c. This is the result of the skyrmion Hall effect because the skyrmion Hall angle is inverted when the skyrmion polarity is reversed.^{[ 24 ]} Second, we studied the dependence of the magnitude of the V _v pulse on the number of generated skyrmion‐bubbles. We set a +z uniform magnetization state under a μ₀ H_z value of +0.43 mT as the initial state (see Figure 3d). From the initial state, a 300 ms V _v pulse of varying magnitude was injected for the skyrmion‐bubble generation. The image of the generated skyrmion‐bubbles after the V _v pulse injections is shown in Figure 3e–i, where the number of generated skyrmion bubbles is roughly proportional to the magnitude of the V _v pulse, which can be explained by the simulation result. The above simulation has demonstrated that a skyrmion bubble was generated from the elongated stripe domain, which was generated from the reversed magnetization near the conducting path by SOT. In other words, a stronger SOT exerted on the domain wall leads to a larger number of elongated stripe domains, generating more skyrmion‐bubbles. Therefore, the higher the magnitude of a V _v pulse, the more skyrmion‐bubbles are generated. A single skyrmion‐bubble is generated by applying a V _v pulse of 1.0 V (Figure 3e). Therefore, skyrmion‐bubbles can accumulate using successive single skyrmion‐bubble generations using a V _v pulse injection. To verify the skyrmion‐bubble accumulation experimentally, from the initial state (Figure 3j), we generated a single skyrmion‐bubble using one V _v pulse of 1.0 V (the red dashed circle in Figure 3k). Then, another V _v pulse injection of 1.0 V generates another skyrmion‐bubble (the red dashed circle in Figure 3l). Further V _v pulse injections also generate single skyrmion‐bubbles and they are all accumulated (the red dashed circles in Figure 3m–o). Interestingly, a V _v pulse injection for the generation of a single skyrmion‐bubble also slightly displaces the existing skyrmion‐bubbles because the V _v pulse also generates a spreading current in the magnetic film plane and a consequent SOT.

Figure 3.

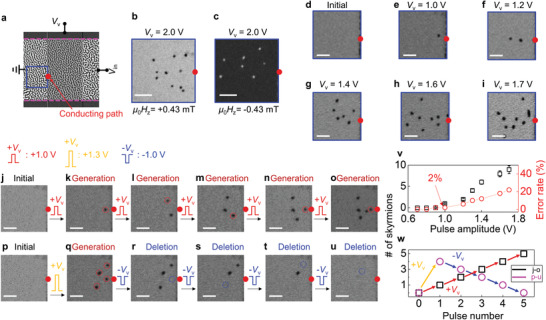
Skyrmion‐bubble generation and deletion. a) The three‐terminal device with the vertical voltage terminal (V _v) and the horizontal voltage terminal (V _in). b,c) Generation of several skyrmion‐bubbles with the −z magnetization core under a μ₀ H_z of +0.43 mT (b) and the +z magnetization core under −0.43 mT (c). d–i) Dependence of the V _v pulse magnitude on the number of generated skyrmion‐bubbles. d–i) From the initial state (d), the magneto‐optical Kerr effect images are presented after applying a V _v pulse of 1.0 (e), 1.2 (f), 1.4 (g), 1.6 (h), and 1.7 V (i). j–u) Skyrmion‐bubble generation and deletion. Red, yellow, and blue pulses indicate a pulse of +1.0, +1.3, and −1.0 V for 300 ms, respectively. j–o) Generation and accumulation of a single skyrmion‐bubble. From the initial state (j), a single skyrmion‐bubble is generated by successive +V _v pulses and is accumulated (k–o). p–u) A single skyrmion‐bubble deletion. From the initial state (p), after generation of four skyrmion‐bubbles (q), a single skyrmion‐bubble is deleted by successive −V _v pulses. v,w) Summary graphs for the skyrmion‐bubble generation and deletion. All scale bars: 5 µm.

If we applied a negative voltage of a V _v pulse, the current in the magnetic film plane would flow toward the conducting path point, absorbing the domain walls or skyrmion‐bubbles into the conducting path and effectively serving as an operation of skyrmion‐bubble deletion. To demonstrate the skyrmion‐bubble deletion operation experimentally by applying a negative voltage to a V _v pulse, we generated four skyrmion‐bubbles by applying a V _v pulse of 1.3 V (the red circles in Figure 3q). Next, one skyrmion‐bubble was deleted after applying a V _v pulse of −1.0 V (the blue dashed circle in Figure 3r). Then, further V _v pulses of −1.0 V delete one of the existing skyrmion‐bubbles and eventually return to the initial state (Figure 3u). Figure 3v,w presents summary curves for skyrmion‐bubble generation, accumulation, and deletion operations. It is clearly shown that an optimized positive (negative) voltage of a V _v pulse can generate (delete) single skyrmion‐bubbles one‐by‐one or, with a certain voltage pulse, a finite number of skyrmion‐bubbles can be generated or deleted at once. The error bar in the black squares graph in Figure 3v is the standard deviation obtained from 100 individual generation operations. The error rate (red circles graph in Figure 3v) is the probability to generate the wrong number of skyrmion‐bubbles, where the targeted number is set to the closest integer to the average value. The graph of the error rate shows an error rate of only 2% in the case of generating one skyrmion‐bubble (1.0 V pulse), where the two error events were nongeneration of skyrmion‐bubbles (histograms are provided in Section S7, Supporting Information).

5. Successive Generation/Shift/Deletion Operations of Magnetic Skyrmion‐Bubbles

The generated skyrmion‐bubbles cannot be distinguished with a nonchiral bubble domain on static MOKE images. A useful approach to verify the chirality of the generated skyrmion‐bubbles is the observation of the SOT‐induced movement of the skyrmion‐bubbles because a nonchiral bubble domain would not move by the action of SOT. We set a +z uniform magnetization state under a μ₀ H_z of +0.43 mT as the initial state (Figure  4a). From the initial state, two skyrmion‐bubbles were generated via vertical current injection by applying two successive V _v pulses of 1.0 V (the red and yellow circles in Figure 4b). Then, we applied a voltage pulse across the film plane (V _in) as defined in Figure 1b, which induces the SOT exerting on individual skyrmion‐bubbles. Skyrmion‐bubble shift operation toward the left is achieved by application of a V _in pulse of 1.0 V, as clearly shown in Figure 4c–e. Starting from the state in Figure 4f, the skyrmion‐bubble shift operation toward the right was also demonstrated by applying a negative V _in pulse injection (Figure 4g). The skyrmion‐bubble that returns near the conducting point can be deleted by applying a negative V _v pulse injection (the yellow dashed circle in Figure 4h). After that, another negative V _in pulse moved the remaining skyrmion‐bubble toward the right again (Figure 4i), followed by a deletion operation by a negative V _v pulse (Figure 4j). Here, the current‐driven skyrmion‐bubble motion direction is always along the current flow direction. Because STT moves the skyrmion‐bubbles along the electron flow direction, observation from Figure 4 demonstrates that our skyrmion‐bubble motion is dominated by SOT. Moreover, it also confirms that our skyrmion‐bubbles have Néel‐type chirality because the Bloch‐type skyrmion motion by SOT is perpendicular to the current direction.^{[ 18} , ^{35 ]} In shifting skyrmion‐bubbles, the skyrmion Hall effect is clearly observed in a counterclockwise direction with respect to the current direction. To confirm the skyrmion Hall effect quantitatively, we investigated 15 skyrmion‐bubble shifts of under application of a V _in pulse of 1.0 V. The averaged skyrmion‐bubble Hall angle is 10.6° with a standard deviation of 9.6°. The relatively large standard deviation is attributed to the creep dynamics of skyrmion‐bubbles because the next position that a skyrmion‐bubble jumps to by a pulse is also determined by the pinning distribution.^{[ 24 ]} When the skyrmion‐bubbles move to the left (Figure 4b–e), the red‐circle skyrmion‐bubble freely moves by SOT, while the yellow circle skyrmion‐bubble motion is relatively restrained. This phenomenon can be explained by skyrmion–skyrmion repulsion. This repulsion can affect the motion of skyrmions, in particular between Figure 4c,d, because it is inversely proportional to the distance between two skyrmions. At this stage, although the effect of the skyrmion–skyrmion repulsion on their motion is not clear, it should be verified in the future for more accurate operation.

Figure 4.

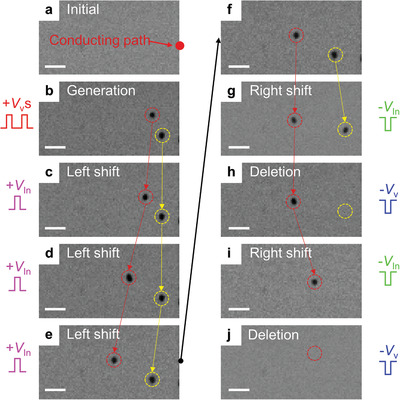
Skyrmion‐bubbles shift operation with generation and deletion. a) The initial state of the +z uniform magnetization. b) Generation of two isolated skyrmion‐bubbles by two positive V _v pulses marked as red and yellow circles. c–f) Skyrmion‐bubble shift operation to the left by applying positive V _in pulses. g) Skyrmion‐bubble shift operation to the right by applying a negative V _in pulse. h) Deletion of one skyrmion‐bubble by a negative V _v pulse. i) Skyrmion‐bubble shift to the right by a negative V _in pulse. j) Deletion of one skyrmion‐bubble by a negative V _v pulse described by a red circle. All scale bars: 5 µm.

6. Obtaining Skyrmion Racetrack Memory

Fert et al.^{[ 8} , ^{9 ]} proposed the concept of skyrmion racetrack memory, where the information is encoded by magnetic skyrmions. In other words, the skyrmion racetrack memory requires the generation and removal of a single skyrmion to write and delete information. The information stream shift should correspond to the skyrmion stream‐shift operation. Therefore, having experimentally established the skyrmion‐bubble generation, deletion, and shift operations, we present an experimental demonstration of the three core operations for skyrmion racetrack memory in a three‐terminal structure, including the vertical and in‐plane current injection paths. First, we encoded the decimal number 21 in its binary form (10101) using skyrmion racetrack memory. We start with a +z uniform magnetization state, which is arbitrarily divided into five regions by blue dashed lines (Figure  5a). Each region represents one bit, which corresponds to “0” if the region does not contain a skyrmion‐bubble, and “1” if the region contains one skyrmion‐bubble. Therefore, the initial state of Figure 5a corresponds to (00000). Then, the information is written as “1” at the rightmost bit by generating a single skyrmion‐bubble (a yellow circle in Figure 5b) by a positive V _v pulse, which results in (00001) (Figure 5b). Next, two information shifts toward the left by two positive V _in pulses were operated in sequence (Figure 5c,d). Now, the bit stream corresponds to (00100). To write “1” at the rightmost bit again, a skyrmion‐bubble is generated by a positive V _v pulse (the red circle in Figure 5e), resulting in the bit stream of (00101). Then, two shift operations were performed to the left using two positive V _in pulses (Figure 5f,g). During the two shift operations, the information is correctly shifted (from (00101) to (10100)) because two skyrmion‐bubbles are shifted together by a similar distance by an identical V _in pulse while maintaining the distance between them. Finally, the writing process is operated again (the white circle in Figure 5h). After all operations, the final bit stream indicates (10101) (Figure 5h), which is the binary number of the decimal number 21.

Figure 5.

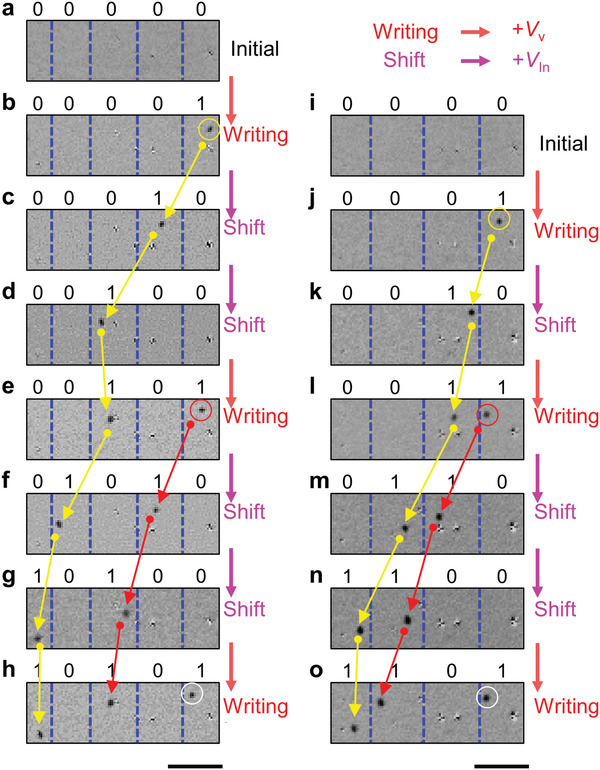
Operation of the skyrmion racetrack memory. a–h) Writing (10101). a) The initial state with (00000). b) Writing “1” at the rightmost bit by a single skyrmion‐bubble generation (00001). c,d) Two shifting operations by applying two positive V _in pulses (00100). e) Writing “1” by a single skyrmion bubble generation in (00101). f,g) Two shifting operations (10100). h) Writing “1” in (10101). i–o) Writing (1101). i) The initial state of (0000). j) Writing “1” in (0001). k) One shifting operation (0010). l) Writing “1” in (0011). m,n) Two shifting operations (1100). o) Writing “1” in (1101). The scale bars below the figures represent 10 µm.

Another example is (1101), which is the binary number of the decimal number 13. It also starts with the +z uniform magnetization state with four regions divided by blue dashed lines (Figure 5i). To write “1” at the rightmost bit, a single skyrmion‐bubble is generated by a positive V _v pulse (the yellow circle in Figure 5j), leading to (0001). Then, one shift operating to the left by a positive V _in pulse as in Figure 5k (0010), followed by a writing operation for “1” at the rightmost bit (the red circle in Figure 5l), resulting in (0011). After that, two shift operations by two V _in pulses are performed because two skyrmion‐bubbles are moved together toward the left while maintaining the distance between them (Figure 5m,n). Finally, the writing operation by generating a skyrmion‐bubble at the rightmost bit (Figure 5o) makes the final bit stream (1101), which is the binary number of the decimal number 13.

Here, the skyrmion racetrack width is much larger than the size of the skyrmion‐bubble. However, for future application, the track width should be comparable to the stabilized size of the skyrmion‐bubble. When the skyrmion racetrack width is slightly larger than the stabilized skyrmion‐bubble size, the repulsion force from the track edge can be considered.^{[ 9 ]} Although the edges can cause skyrmion destruction above a certain velocity,^{[ 36 ]} the boundary repulsion can also better stabilize the skyrmion racetrack memory operation because of the suppression of the skyrmion Hall effect.

7. Conclusion

We have introduced a method to generate and delete isolated skyrmion‐bubbles using vertical current injection, in which two processes are caused by thermal fluctuation because of the high‐density current through the vertical current path and the radial current flow. It is expected that the vertical current injection approach can adapt easily to a three‐terminal device geometry; thus, we have demonstrated experimental core operations of the skyrmion racetrack memory operation in a three‐terminal geometry, where the vertical terminal is used for the generation/deletion operations and the horizontal terminal is used for the shift operation by the current‐induced SOT. We have used a created filament path as a vertical conducting path; however, for the future application of the vertical conducting path concept, a more controlled method for the vertical conducting path is needed, which is discussed in Section S8 in the Supporting Information. Our experimental demonstration showed that several remaining problems, such as the skyrmion Hall effect, the requirement for a z‐axis magnetic field, and pinning or scaling issues, must be solved for further application. However, some of the issues can be eliminated by the previously reported approaches, including the use of ferrimagnetic or synthetic antiferromagnetic systems^{[ 26 ]} or biased magnetic field structures.^{[ 37} , ^{38 ]} For example, the existence of magnetic skyrmions in synthetic antiferromagnets was recently demonstrated by using interlayer coupling from an adjacent exchange‐biased layer.^{[ 36 ]} This means that the exchange bias from the adjacent layer can act as an external magnetic field. Another example^{[ 39 ]} is to achieve field‐free SOT switching using an in‐plane exchange‐biased magnetic layer separated by nonmagnetic Ru. Therefore, the external magnetic field can be replaced using the exchange‐biased layer. In this paper, we show a proof‐of‐concept experimental operation with relatively slow motion of skyrmion‐bubble. This is mainly due to the fact that the pattern size used was wide so that the current density could not be large. Thus, relatively many random motions occurred because of thermal release and trap at pinning sites. However, in the future, it will be possible to achieve a high density of skyrmion racetrack memory if thin wire structures with few defects and small‐size skyrmions are obtained. Our findings provide a milestone for the application of magnetic skyrmions in various types of devices, including skyrmion racetrack memory.

8. Experimental Section

Fabrication and Measurement

Samples of the magnetic channel W (5)/CoFeB (1.3)/Ta (0.08)/MgO (1)/TaO _x (2) were deposited on Si/SiO₂ substrates using a magnetron sputtering system at room temperature, followed by a post‐annealing process at 350 °C for 30 min under vacuum conditions below ≈1  ×  10⁻⁶ Torr with a 3 T perpendicular magnetic field. The deposited films were patterned into a wire shape by photolithography and Ar ion milling. Then, GdO _x (2)/Pt (2) layers were deposited using a magnetron sputtering system and patterned by a photolithography lift‐off process (the numbers in parentheses are the dimensions in nm).

Magnetic images were taken by a homemade MOKE microscope equipped with a perpendicular electromagnet and an electrical probing system. Real‐time images of skyrmion‐bubble generation were observed with a video rate using a charge‐coupled device camera placed at the focal plane of the microscope.

Micromagnetic Simulations

To show the mechanism by which the radial current forms skyrmion‐bubbles, we simulated the formation of small (≈50 nm) skyrmion‐bubbles. In Figure 2, the following conditions are used: saturation magnetization (M _S) = 10⁶ A m⁻¹, exchange stiffness constant (A) = 10⁻¹¹ J m⁻¹, PMA (K _u1) = $K_{\text{eff}}+\frac{{\mu }_0}{2}{M}_{\mathrm{S}}^2$ = 6.8 × 10⁵ J m⁻³, interfacial DMI (D _ind) = −2 × 10⁻³ J m⁻², damping constant (α) = 0.1, grid size (N_x , N_y , N_z ) = (400, 400, 1), cell size = (2 nm, 2 nm d), and magnetic layer thickness (d) = 1 nm. Grains with 5 nm lateral size were introduced. K _u1 had a 10% value variation per grain, and A _ex had a 90% value between grains. These parameters stabilized a skyrmion‐bubble of ≈50 nm size when the external perpendicular magnetic field was 0.15 T. It was assumed that the region of 50 nm radius at the center had the magnetization fixed in the −z direction. A total current of 3 mA was injected at the center of the structure and became the radial current in the heavy metal underlayer (5 nm thick). The local current density (j _rad) was determined by the total current conservation. The unit vector of pumped spin (σ  ) was $\widehat{z}\times \widehat{r}$, where $\widehat{r}$ is the radial direction. The spin Hall angle (θ_SH, the efficiency of converting the charge current to the spin current) was assumed to be 0.1.

MuMax3 was used to run simulations. MuMax3 solved the following Landau–Lifshitz–Gilbert equation, including the damping‐like SOT

$$\dot{m}=-\gamma \mathbf{m}\times {\mathbf{H}}_{\text{eff}}+\alpha \mathbf{m}\times \dot{m}-\gamma {\tau }_{\mathrm{d}}\mathbf{m}\times \left(\mathbf{m}\times \sigma \right)$$ (1)

where, m is a unit vector of the local magnetization, γ is the gyromagnetic ratio, H _eff is an effective magnetic field, and ${\tau }_{\mathrm{d}}=\left(\frac{\hslash {\theta }_{\text{SH}}{j}_{\text{rad}}}{2e{M}_{\text{sat}}d}\right)$ is the coefficient of the damping‐like SOT. (See Section S5, Supporting Information for an example file of MuMax3 for Figure 2d–i.)

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Supplemental Video 1

Supplemental Video 2

Yang S., Moon K.‐W., Ju T.‐S., Kim C., Kim H.‐J., Kim J., Tran B. X., Hong J.‐I., Hwang C., Electrical Generation and Deletion of Magnetic Skyrmion‐Bubbles via Vertical Current Injection. Adv. Mater. 2021, 33, 2104406. 10.1002/adma.202104406

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.