Abstract
One of the fundamental goals of particle physics is to gain a microscopic understanding of the strong interaction. Electromagnetic form factors quantify the structure of hadrons in terms of charge and magnetization distributions. While the nucleon structure has been investigated extensively, data on hyperons are still scarce. It has recently been demonstrated that electron-positron annihilations into hyperon-antihyperon pairs provide a powerful tool to investigate their inner structure. We present a method useful for hyperon-antihyperon pairs of different types which exploits the cross section enhancement due to the effect of vacuum polarization at the J/ψ resonance. Using the 10 billion J/ψ events collected with the BESIII detector, this allows a precise determination of the hyperon structure function. The result is essentially a precise snapshot of the transition process, encoded in the transition form factor ratio and phase. Their values are measured to be R = 0.860 ± 0.029(stat.) ± 0.015(syst.), and . Furthermore, charge-parity (CP) breaking is investigated in this reaction and found to be consistent with CP symmetry.
Subject terms: Experimental particle physics, Experimental nuclear physics
Investigating the inner structure of baryons is important to further our understanding of the strong interaction. Here, the BESIII Collaboration extracts the absolute value of the ratio of the electric to magnetic form factors and its relative phase for e + e − → J/ψ → ΛΣ decays, enhancing the signal thanks to the vacuum polarisation effect at the J/ψ peak.
Introduction
One distinctive feature of the strong nuclear interaction and a prerequisite for our existence is the confinement of nearly massless quarks into stable and massive hadrons such as protons or neutrons that constitute the matter we are made of. A coherent understanding of the dynamics of the strong interaction, however, remains one of the most intriguing puzzles of physics. The main challenge is the very nature of confinement: the quarks and gluons cannot be observed as bare particles, but are dressed by the strong interaction into quasi-particles, or constituent quarks, that form the bound systems we know as hadrons. The distribution and motion of quarks inside hadrons is quantified in terms of, e.g., electric and magnetic form factors (GE and GM), which offer an empirical tool to study the strong dynamics. The proton, as the most stable composite particle we know, with a lifetime much longer than the age of the Universe, offers an excellent testing ground for the strong interaction. The space-like form factors of the proton have been the subject of rigorous studies since 1956, when Hofstadter introduced the electron scattering techniques1. To this day, new and surprising features are being discovered2–7 and debated8–10.
A common strategy to achieve a deeper understanding of these features is to investigate the impact of introducing heavy and unstable quarks into the bound system. The lightest siblings of the proton are the Λ and the Σ0 hyperons, both consisting of an up-quark (u), a down-quark (d) and a heavy and unstable strange-quark (s), in contrast to the proton with a uud structure of only light quarks. Since hyperons are unstable, they cannot be studied in conventional electron scattering experiments (e−Y → e−Y, where Y represents the hyperon)9, which require stable beams or targets. Hyperon-antihyperon annihilation processes (such as ) are even more challenging and do not constitute a realistic alternative. Instead, time-like form factors of hyperons can be accessed in electron-positron annihilations with the subsequent production of a hyperon-antihyperon pair, such as . In this scenario, hyperon and antihyperon are quantum spin correlated with same or opposite helicity states for spin-1/2 hyperons, which signifies that the transition from the initial electron-positron pair to the final baryon-antibaryon pair involves amplitudes for both helicity conservation and helicity flip11. If there is a non-vanishing phase between the transition amplitudes for these different helicity states, we can observe the polarization of baryons through the angular distribution of the final-state particles. In light of this, the modulus and phase of the ratio GE/GM in time-like region can be accessed directly from the measurement of the polarization of one of the outgoing baryons along the direction orthogonal to the scattering plane. The time-like form factors can be seen as snapshots of the time evolution of a hyperon-antihyperon pair. In particular, the modulus and phase of the ratio GE/GM in the time-like region are very sensitive to the specifics of the hyperon interaction. Therefore, by dispersive calculations we can constrain the form factors also in the space-like region, gaining profound insight into the inner structure9,12–14. The dispersive relation has demonstrated an unprecedented capability to ascertain the intricate nature of the ratio based on its modulus and phase measured at the BESIII Collaboration at a single energy point9,15. However, the absence of data makes the predictions quite uncertain. In addition, the asymptotic behaviour of the form factor phase is of special interest at large energies, where the time-like and the space-like form factors should converge to the same real value. Hence, there should be a scale at which the phase approaches an integer multiple of π. Therefore, gathering additional data at different energy points would be essential to bolster the predictive capacity of the dispersive relation and to reveal additional remarkable attributes of baryons. Precise data at a relatively high energy would therefore be a pivotal step forward in the understanding of dynamics underlying the interaction of hyperons. Especially the transition, it is particularly interesting since it is the only ground-state transition for which we can gather data both in the high-energy time-like region (this work) and in the very low-energy region (via Dalitz decays, i.e. Σ0 → Λe+e−)9. The prospect of in the future comparing these two different energy regions is therefore unique.
In recent years, the BESIII collaboration has performed pioneering studies of hyperon form factors16. In particular, the self-analyzing hyperon decays can be used to measure the hyperon polarization, thereby completely determining the form factors of the Λ hyperon15. However, time-like form factors need to be studied in processes where a one-photon exchange is the dominating process, as shown in Fig. 1d. For a hyperon-antihyperon pair of the same type, e.g. , this means that the electron-positron annihilation must occur at an energy far from any vector meson resonances that can decay strongly into a hyperon-antihyperon pair. For a pair where the hyperon and the antihyperon from J/ψ are of different type, e.g. or , since the process is isospin-violating, the purely strong amplitude is suppressed by the small dimensionless factor , where the mu, md and mc represent the mass of u quark, d quark and c quark, respectively. Therefore, the suppressed strong process involving an intermediate ggg state from the J/ψ decay (Fig. 1a) with a branching fraction of 64.1% according to the Particle Data Group (PDG)17 is negligible compared to γgg (8.8%) (Fig. 1(b)) and γ* (13.5%) (Fig. 1c) mediated decays. Furthermore, the agreement between the expected coupling to the J/ψ decay and the value extracted from cross section data in the electromagnetic continuum18, indicates a clear absence of the γgg process in the Hence, must be a purely electromagnetic process mediated by , namely the hadronic vacuum polarization effect, as depicted in Fig. 1c, which has the same final production vertex as Fig. 1d. Accordingly, the electric and magnetic form factors of Fig. 1d can be extracted from Fig. 1c by correcting for the well-known vacuum polarization, which exhibits a notable enhancement attributed to the J/ψ resonance.
Fig. 1. The Feynman diagrams for e+e− → hadrons in the vicinity of the J/ψ.
a strong process with intermediate J/ψ mediated by gluons (ggg), (b) the mixed strong-electromagnetic process of J/ψ decay mediated by γgg, (c) electromagnetic process through the vacuum polarization of one virtual photon (γ*) to J/ψ, (d) continuum process without the J/ψ intermediate state but only one virtual photon.
In this work, using the available (10087 ± 44) × 106 J/ψ events produced in e+e− annihilations19 at BESIII, almost one order of magnitude larger than the data sample used in the previous measurement11, we investigate the form factors in the reaction with the polarized and spin correlated pairs, baryons and antibaryons simultaneously produced with correlated spins as defined in refs. 20,21. With the hadronic vacuum polarization at the J/ψ resonance resulting in a significantly enhanced signal, we probe the same vertex as the one-photon exchange process and attain the structure at the J/ψ resonance. The inclusion of charge-conjugate processes is implied hereafter unless explicitly mentioned otherwise.
Results and discussion
BESIII detector and candidates selection
The BESIII detector22 records symmetric e+e− collisions provided by the BEPCII storage ring23, which operates with a peak luminosity of 1033 cm−2s−1 in the centre-of-mass energy () range from 2.0 to 4.95 GeV. In this cylindrical system, tracks of charged particles in the detector are reconstructed from track-induced signals and the momenta are determined from the track curvature in the main drift chamber (MDC). The flight time of charged particles is recorded by a plastic scintillator time-of-flight system (TOF). Showers from photon clusters are reconstructed and energy deposits are measured in the electromagnetic calorimeter (EMC). The signal of is extracted from (10087 ± 44) × 106 J/ψ events19 at GeV, equivalent to an integrated luminosity of 3083 pb−1 19. The is reconstructed using decays and Σ0 from γΛ decays. The specific requirements of event reconstruction and selection criteria are described in the Methods below. The resulting signals of (Λ) and are clearly observed, as shown in Supplementary Figs. 1 and 2. The possible background events are investigated with an inclusive Monte Carlo (MC) sample generated with all known J/ψ decays. To estimate the number of background events coming directly from the continuum light hadron (QED) process, the same analysis is performed on the data sample at GeV, corresponding to an integrated luminosity of 166.3 pb−1 19. With an extended unbinned maximum likelihood fit to the γΛ () invariant mass distribution shown in Supplementary Fig. 3, the final signal yields are determined to be 26260 ± 181 and the QED background are 39 ± 7. The details of backgrounds analysis and fit are described in the Methods.
The vacuum polarisation effect in
Based on the studies of e+e− μ+μ− and ηπ+π− in ref. 24 the relative phase between the hadronic vacuum (Fig. 1c) and the continuum (Fig. 1d) processes is zero in case of a purely electromagnetic decay, and it has a line shape similar to the cross section of the purely electromagnetic process. Consequently, the ratio of the cross section at the J/ψ peak to that at any specific energy is the same for different purely electromagnetic processes as illustrated by both e+e− → μ+μ− and ηπ+π−. With the measured cross sections in ref. 24 the corresponding ratios of these two processes are calculated to be 24.20 ± 0.81 and 28.81 ± 8.52, respectively, both in good agreement with each other. Here, the uncertainties are statistical only since the systematic uncertainties cancel in the calculation of the ratio. We also performed a measurement of the cross sections of at the J/ψ peak and 3.08 GeV, determining the corresponding ratio to be 33.72 ± 6.06. This value is consistent with those from the above processes within the uncertainties, thus providing further evidence for as a purely electromagnetic decay, which implies a way to extract the electromagnetic form factor with the hadronic vacuum polarization at the J/ψ peak.
Since the imaginary part of form factors is non-zero at centre-of-mass energies above the two-pion threshold12,25, the relative phase ΔΦ between the electric and magnetic form factors, GE and GM, is expected to be non-zero. In the case of , a non-vanishing ΔΦ also demonstrates the polarization of Λ and in the direction perpendicular to the production plane. Since the electron mass is negligible in comparison to the J/ψ mass, the initial electron and positron helicities have to be the opposite. This implies that the angular distribution and polarization can be described uniquely by only two quantities, the relative phase and the angular distribution parameter 26, where and MY is the mass of the final hyperon. For , MY is replaced by 27. The feasibility of extracting the form factors in the production and cascade decays of is described by the six kinematic variables as described in Methods, expressed as the helicity angles shown in Fig. 2.
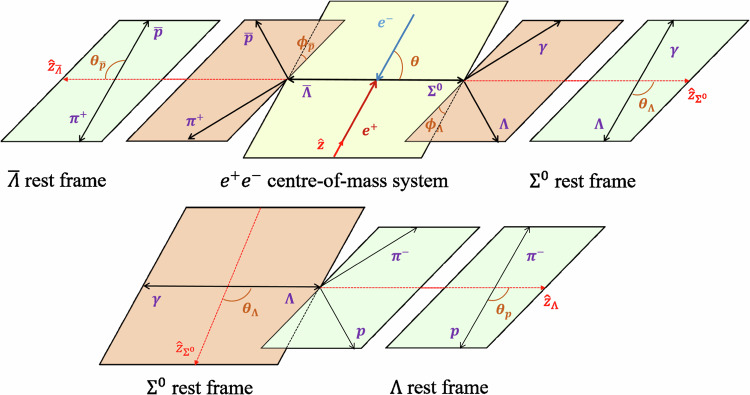
Fig. 2. Definition of the helicity angles for .
The angles θ, θΛ, θp, are the polar helicity angles of the Σ0, Λ, p and in the e+e− centre-of-mass system, Σ0 rest frame, Λ rest frame and rest frame, respectively. The angles between different decay or production planes, ϕΛ and , are the azimuthal helicity angles of the Λ and in the Σ0 rest frame and Λ rest frame, respectively. In the e+e− centre-of-mass system, the z is along the e+ momentum direction, and the zΣ is along the Σ0 outgoing direction. In the Σ0 rest frame, the polar axis is zΣ, yΣ is along z × zΣ and zΛ is along the Λ outgoing direction. In the Λ rest frame, the polar axis is zΛ, and yΛ is along zΣ × zΛ. In the rest frame, the polar axis is , and is along .
Here, we denote the angular distribution parameter, the relative phase and decay asymmetries for Σ0 → γΛ, Λ → pπ−, and as αJ/ψ, ΔΦ, αγ, αΛ, and , respectively. Subsequently, to extract the form factors, the helicity analysis is performed for based on the angular distribution as described in detail in the Methods. Although and are two independent reactions, their helicity amplitudes are simply related before and after charge-conjugate and parity transformation. In accordance with the Standard Model (SM), CP violation is absent in electromagnetic processes. As a result, the relative phases ΔΦ of these two decays are expected to satisfy , where and denote the relative phases of time-like electric and magnetic form factors for and , respectively. Therefore, a simultaneous measurement of and offers the possibility of exploring CP violation by evaluating , which is required to be zero from CP invariance within the SM. In this case, these processes are also of interest for searching for additional sources of CP violation beyond the SM.
In the Σ mass region, a combined helicity analysis is performed for and and the parameters αΛ and are fixed to be αΛ = 0.7519 and 28 from previous high-precision measurements of . Using the average magnitude for both has a negligible effect on fit results. Due to the electromagnetic part of the decay chain, Σ0 → γΛ, where the photon polarization is not measured29, the αγ is presumed to be 0. The free parameters, including αJ/ψ and the relative phase () for , are optimized with an unbinned maximum likelihood fit defined in Methods. These parameters are measured by incorporating the transverse polarization of in the joint angular distribution. The global fit is represented by the multidimensional angular distributions shown in Supplementary Figs. 4 and 5 with a specific fitting technique as well as systematic uncertainties described in Methods.
Extraction of the form factor ratio and test of the CP violation
From the global fit, a prominent polarization and strong correlation of the relative phase between the two processes are observed, characterized by Py elucidating the spin transverse polarization and Cxz representing the particular relationship between and . Their strong dependence on the direction angle θ, defined in the Methods, is seen in Fig. 3. To illustrate the fit quality, the fit results in each cos bin are also shown using points with error bars in Fig. 3. Apart from the difference caused by the fluctuations from the complex background channels, the points of each bin are consistent with the globally fitted curves. The fit yields αJ/ψ = 0.418 ± 0.028(stat.) ± 0.014(syst.), , and . The ratio is determined to be 0.860 ± 0.029(stat.) ± 0.015(syst.), giving the ratio and relative phase of the electric and magnetic form factors GE and GM for at GeV, with clear transverse spin polarizations of the Λ and observed. The sum of these two relative phases, , is in good agreement with the expected value of π. is calculated to be 0.003 ± 0.133(stat.) ± 0.014(syst.), which is consistent with zero and indicates no evident direct CP violation in the decays of and . This is the measurement that the time-like structure for is extracted at GeV with high precision by using the hadronic vacuum polarization enhancement at the J/ψ. In addition, unlike e+e− annihilation into hyperon anti-hyperon pairs, Λ and are not charge conjugates of each other, which enables us to explore direct CP violation by comparison of polarizations from both and . While currently statistically limited, it provides a way to search for possible new sources of CP violation. In the future, the BESIII experiment may provide even greater sensitivity to direct CP violation30, with further improvement expected from the next generation experiments, e.g., the next-generation tau-charm physics facility31 and PANDA32.
Fig. 3. Polarization in and spin correlations of the reaction.
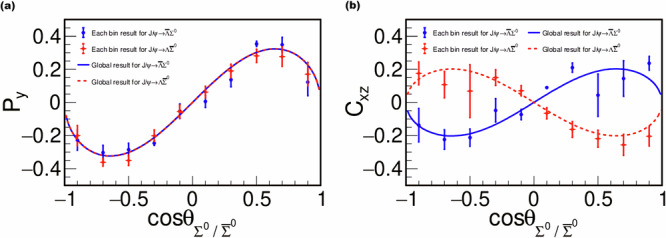
The points with error bars, blue solid dot for and red open double diamond for , are extracted in each () bin, and the blue solid curves denote the global expected dependence on ( for the red dotted curve).
Methods
Monte Carlo simulation
The optimization of the event selection criteria and the estimation of physics background as well as the determination of efficiency are performed using MC simulated samples. The GEANT4-based33 MC package includes the geometric description of the BESIII detector and the detector response. The inclusive MC sample includes both the production of the J/ψ resonance and the continuum processes incorporated in KKMC34. All particle decays are modelled with EVTGEN35,36 using branching fractions either taken from the Particle Data Group (PDG)17, when available, or otherwise estimated with LUNDCHARM37,38. For the signal , the MC samples are produced using the angular distribution formula shown in the Methods of Helicity amplitudes. For the determination of the cross section, the generator CONEXC39 was used. For the background channels , , the exclusive MC samples were generated in accordance with their decay amplitudes11,40.
Initial selection criteria
Candidates for are required to have four charged tracks with net zero charge and at least one photon.
Charged tracks are selected in the MDC within ±20 cm of the interaction point in the beam direction and within 10 cm in the plane perpendicular to the beam. The polar angles of these tracks are required to be within the MDC fiducial volume, , where θ is defined with respect to the z-axis, which is the symmetry axis of the MDC. No particle identification is used to maintain high efficiency.
To reconstruct the decays Λ → pπ− and , we loop over all the combinations of positive and negative charged track pairs and require that at least one (pπ−)() track hypothesis successfully passes the vertex finding algorithm41 of Λ and . If more than one accepted combination satisfies the vertex fit requirement, the one with the minimum value of is chosen, where is the invariant mass and MΛ is the nominal Λ mass17.
For good photon selection, showers in the EMC identified as photon candidates are required to satisfy fiducial and shower-quality requirements. For the barrel region, showers must have a minimum energy deposition of 25 MeV with the polar angle of each track satisfying , while those from the end cap region must have at least 50 MeV and the polar angle is required to be . To suppress background noise unrelated to the event, the difference between the EMC time and the event start time (TDC) has to fulfil 0 ≤ TDC ≤ 700 ns. To suppress showers generated by charged particles, the photon candidate angular separation from the nearest charged track is required to be at least 10∘.
The selected events are subjected to a four-constraint energy momentum conservation kinematic fit (4C fit) with the hypothesis of . The kinematic fit adjusts the reconstructed particle energy and momentum within the measured errors so as to satisfy energy and momentum conservation for the given event hypothesis. This improves resolution and reduces background. When there are multiple photon candidates in an event, the combination with the smallest is retained. The kinematic fit is very powerful to suppress background events with multiple photon candidates in the final states, e.g., and .
Final selection criteria
After the initial selection, the scatter plot of versus of the accepted candidates is shown in Supplementary Fig. 1, where the clear cluster corresponds to the decays of Λ → pπ− and . The Λ and signal candidates are selected by requiring MeV/c2 and MeV/c2. To further suppress backgrounds and improve the mass resolution, the 4C kinematic fit must satisfy . In addition, GeV/c2 and MγΛ > 1.135 GeV/c2 are required in the further analysis for and , respectively, which has a pronounced effect on suppressing the background events from . After applying the above requirements, the invariant mass spectrum of is shown in Supplementary Fig. 2, where the prominent peak of is clearly observed.
Background analysis
Possible background sources are investigated with an inclusive MC sample of 10 billion J/ψ decays. Using the same selection criteria, with the help of a generic event type analysis tool42, the surviving background events mainly originate from , and (including a resonant contribution from γηc), but none of these produce an evident peak in the Σ0 mass region. The exclusive MC samples of these background channels are generated with the corresponding helicity amplitudes and their contributions are shown in Supplementary Fig. 2. To estimate the number of background events coming directly from the e+e− annihilation, the same analysis is performed on data taken at 3.080 GeV, where the number of background events, 39 ± 7 is also extracted by fitting the γΛ (or ) mass spectrum as shown in Supplementary Fig. 3. The background events are then normalized to the J/ψ data after taking into account the luminosities and energy-dependent cross sections of continuum processes43, with the scaling factor calculated as
| 1 |
Here, , s, and ϵ are the integrated luminosity, the square of the centre-of-mass energy, and the detection efficiency at the two centre-of-mass energies, respectively. the number of background events for is normalized to be 669 ± 120. It should be pointed out that there is no interference between the QED background and the J/ψ resonance since this is a purely electromagnetic process according to ref. 18.
Signal extraction
The signal yields are obtained from an extended unbinned maximum likelihood fit to the γΛ () mass spectrum. The total probability density function (PDF) consists of a signal and various background contributions. The signal component is modelled as the MC simulated signal shape convolved with a Gaussian function to account for the difference in the mass resolution between data and MC simulation. The background components, , , and , as well as the reflection from signal conjugation decay mode, are described with the simulated shapes derived from the dedicated MC samples, while the magnitudes of different components are left free to account for the uncertainties of the branching fractions of these decays and other intermediate decays. The fit to the MγΛ/ spectrum, as displayed in Supplementary Fig. 2, gives events.
Helicity amplitude
The structure of the six dimensional angular distribution is determined by global parameters independent of the Σ0 scattering angle, , and is written in a modular form as
| 2 |
where the Cμν(θ; αJ/ψ, ΔΦ) is a 4 × 4 spin density matrix, describing the spin configuration of the spin correlated hyperon-antihyperon pair. The matrix elements are expressed as
| 3 |
where Py governs the polarization of the Σ0 and Cij characterizes its spin correlations. Both Py and Cij can be written in terms of or as
| 4 |
where f(θ), a common function dependent on the direction angle θ, is expressed as
| 5 |
The matrices in Eq. (2) represent the propagation of the spin density matrices in the sequential decays. The full expressions for Cμν and are given in refs. 44,38.
Global fit of parameters
A non-zero phase angle difference ΔΦ indicates transverse hyperon polarization, which allows us to measure these parameters at the same time. A simultaneous fit is performed to the two conjugate channels, and . The likelihood function constructed from the probability density function for an event characterized by ξi is
| 6 |
where is the detection efficiency, N is the number of the surviving data events after all selection criteria, the normalization factor , with defined in Eq. (2), and is the probability to produce event i based on the measured parameters ξi and the set of observables ω. Based on the likelihood function defined in Eq. (6), the objective function is written as
| 7 |
where and are the likelihood functions for and and the background events from simulation, respectively. In order to optimize the free parameters (αJ/ψ, and ) and minimize the objective function, the normalization factor in Eq. (6) is obtained by MC integral generated by phase space through all event selection criteria. We adjust the weights of the phase space sample events to match the momentum distribution of the final-state particles to the data. The weighted phase space events can then be employed to construct distributions of various physical quantities, thus displaying the fit results. To compare the fit with data, the moments directly related to helicity amplitude are defined as:
| 8 |
where Nk is the number of events in the bin and is the unit vector in the direction of the nucleon (anti-nucleon) in the rest frame of Σ0 () for , as illustrated in Fig. 2. The resulting Ti and helicity angle distributions for data and the fit results are shown in Supplementary Figs. 4 and 5, and the difference between T3 and T4 results from the transverse polarization of , which allows the relative phase between GE and GM to be determined from the global fit of polarization with the modulus of the ratio between GE and GM obtained from .
Systematic uncertainty
The uncertainties in the measurement of the form factors are mainly from the reconstruction, the 4C kinematic fit, and the background estimation. For the reconstruction, a correction to the MC efficiency is made. We also use the control sample of to obtain the efficiencies of the data and MC simulation in the Λ and reconstruction, and then correct the MC efficiencies by the observed data-MC efficiency differences. In order to reduce the impact of statistical fluctuations, the fit with the corrected MC sample is performed 400 times by varying the correction factor randomly within one standard deviation. The differences between the results with and without correction are taken as the systematic uncertainties. For the 4C kinematic fit, the MC sample in the polarization fit is altered by changing the helix parameters of charged tracks, and the same fit procedure is performed to the same data sample. The relative differences of the fit results are assigned as the uncertainties. The systematic uncertainty arising from the background estimate for each background source is assigned by varying the normalization factor by one standard deviation, the maximum change of the result is assigned as the associated systematic uncertainty. The total systematic uncertainty due to the background estimate is obtained by adding all effects of various background sources in quadrature. The uncertainties due to the are estimated by varying the quoted value from ref. 28 within one standard deviation. The systematic uncertainties for the polarization measurement, as discussed above, are listed in Supplementary Table 1.
Supplementary information
Acknowledgements
The BESIII collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support. This work is supported in part by National Key R&D Program of China under Contracts Nos. 2020YFA0406300, 2020YFA0406400; National Natural Science Foundation of China (NSFC) under Contracts Nos. 11635010, 11735014, 11835012, 11875115, 11935015, 11935016, 11935018, 11961141012, 12022510, 12025502, 12035009, 12035013, 12075250, 12165022, 12192260, 12192261, 12192262, 12192263, 12192264, 12192265, 12225509; the Chinese Academy of Sciences (CAS) Large-Scale Scientific Facility Program; Joint Large-Scale Scientific Facility Funds of the NSFC and CAS under Contract No. U1832207; the CAS Center for Excellence in Particle Physics (CCEPP); 100 Talents Program of CAS; The Institute of Nuclear and Particle Physics (INPAC) and Shanghai Key Laboratory for Particle Physics and Cosmology; Yunnan Fundamental Research Project under Contract No. 202301AT070162; ERC under Contract No. 758462; European Union’s Horizon 2020 research and innovation programme under Marie Sklodowska-Curie grant agreement under Contract No. 894790; German Research Foundation DFG under Contracts Nos. 443159800, 455635585, Collaborative Research Center CRC 1044, FOR5327, GRK 2149; Istituto Nazionale di Fisica Nucleare, Italy; Ministry of Development of Turkey under Contract No. DPT2006K-120470; National Science and Technology fund; National Science Research and Innovation Fund (NSRF) via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation under Contract No. B16F640076; Olle Engkvist Foundation under Contract No. 200-0605; STFC (United Kingdom); Suranaree University of Technology (SUT), Thailand Science Research and Innovation (TSRI), and National Science Research and Innovation Fund (NSRF) under Contract No. 160355; Polish National Science Centre under Contract 2019/35/O/ST2/02907; The Royal Society, UK under Contracts Nos. DH140054, DH160214; The Knut and Alice Wallenberg Foundation (Sweden); The Swedish Research Council; The Swedish Foundation for International Cooperation in Research and Higher Education (STINT); U. S. Department of Energy under Contract No. DE-FG02-05ER41374.
Author contributions
All the authors have contributed to this publication, being variously involved in the design and construction of the detectors, writing software, calibrating sub-systems, operating the detectors, acquiring data and analysing the processed data.
Peer review
Peer review information
Nature Communications thanks Ulrik Egede and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The raw data generated in this study have been deposited in the Institute of High Energy Physics mass storage silo database. The source data are available under restricted access for the complexity and large size, access can be obtained by contacting to besiii-publications@ihep.ac.cn.
Code availability
All algorithms used for data analysis and simulation are archived by the authors and are available on request to besiii-publications@ihep.ac.cn.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A list of authors and their affiliations appears at the end of the paper.
Contributor Information
The BESIII Collaboration, Email: besiii-publications@ihep.ac.cn
The BESIII Collaboration:
M. Ablikim, M. N. Achasov, P. Adlarson, M. Albrecht, R. Aliberti, A. Amoroso, M. R. An, Q. An, Y. Bai, O. Bakina, R. Baldini Ferroli, I. Balossino, Y. Ban, V. Batozskaya, D. Becker, K. Begzsuren, N. Berger, M. Bertani, D. Bettoni, F. Bianchi, E. Bianco, J. Bloms, A. Bortone, I. Boyko, R. A. Briere, A. Brueggemann, H. Cai, X. Cai, A. Calcaterra, G. F. Cao, N. Cao, S. A. Cetin, J. F. Chang, W. L. Chang, G. R. Che, G. Chelkov, C. Chen, Chao Chen, G. Chen, H. S. Chen, M. L. Chen, S. J. Chen, S. M. Chen, T. Chen, X. R. Chen, X. T. Chen, Y. B. Chen, Z. J. Chen, W. S. Cheng, S. K. Choi, X. Chu, G. Cibinetto, F. Cossio, J. J. Cui, H. L. Dai, J. P. Dai, A. Dbeyssi, R. E. de Boer, D. Dedovich, Z. Y. Deng, A. Denig, I. Denysenko, M. Destefanis, F. De Mori, Y. Ding, Y. Ding, J. Dong, L. Y. Dong, M. Y. Dong, X. Dong, S. X. Du, Z. H. Duan, P. Egorov, Y. L. Fan, J. Fang, S. S. Fang, W. X. Fang, Y. Fang, R. Farinelli, L. Fava, F. Feldbauer, G. Felici, C. Q. Feng, J. H. Feng, K. Fischer, M. Fritsch, C. Fritzsch, C. D. Fu, H. Gao, Y. N. Gao, Yang Gao, S. Garbolino, I. Garzia, P. T. Ge, Z. W. Ge, C. Geng, E. M. Gersabeck, A. Gilman, K. Goetzen, L. Gong, W. X. Gong, W. Gradl, M. Greco, L. M. Gu, M. H. Gu, Y. T. Gu, C. Y. Guan, A. Q. Guo, L. B. Guo, R. P. Guo, Y. P. Guo, A. Guskov, W. Y. Han, X. Q. Hao, F. A. Harris, K. K. He, K. L. He, F. H. Heinsius, C. H. Heinz, Y. K. Heng, C. Herold, G. Y. Hou, Y. R. Hou, Z. L. Hou, H. M. Hu, J. F. Hu, T. Hu, Y. Hu, G. S. Huang, K. X. Huang, L. Q. Huang, X. T. Huang, Y. P. Huang, Z. Huang, T. Hussain, N. Hüsken, W. Imoehl, M. Irshad, J. Jackson, S. Jaeger, S. Janchiv, E. Jang, J. H. Jeong, Q. Ji, Q. P. Ji, X. B. Ji, X. L. Ji, Y. Y. Ji, Z. K. Jia, P. C. Jiang, S. S. Jiang, X. S. Jiang, Y. Jiang, J. B. Jiao, Z. Jiao, S. Jin, Y. Jin, M. Q. Jing, T. Johansson, S. Kabana, N. Kalantar-Nayestanaki, X. L. Kang, X. S. Kang, R. Kappert, M. Kavatsyuk, B. C. Ke, I. K. Keshk, A. Khoukaz, R. Kiuchi, R. Kliemt, L. Koch, O. B. Kolcu, B. Kopf, M. Kuemmel, M. Kuessner, A. Kupsc, W. Kühn, J. J. Lane, J. S. Lange, P. Larin, A. Lavania, L. Lavezzi, T. T. Lei, Z. H. Lei, H. Leithoff, M. Lellmann, T. Lenz, C. Li, C. Li, C. H. Li, Cheng Li, D. M. Li, F. Li, G. Li, H. Li, H. Li, H. B. Li, H. J. Li, H. N. Li, J. Q. Li, J. S. Li, J. W. Li, Ke Li, L. J. Li, L. K. Li, Lei Li, M. H. Li, P. R. Li, S. X. Li, S. Y. Li, T. Li, W. D. Li, W. G. Li, X. H. Li, X. L. Li, Xiaoyu Li, Y. G. Li, Z. X. Li, Z. Y. Li, C. Liang, H. Liang, H. Liang, H. Liang, Y. F. Liang, Y. T. Liang, G. R. Liao, L. Z. Liao, J. Libby, A. Limphirat, C. X. Lin, D. X. Lin, T. Lin, B. J. Liu, C. Liu, C. X. Liu, D. Liu, F. H. Liu, Fang Liu, Feng Liu, G. M. Liu, H. Liu, H. B. Liu, H. M. Liu, Huanhuan Liu, Huihui Liu, J. B. Liu, J. L. Liu, J. Y. Liu, K. Liu, K. Y. Liu, Ke Liu, L. Liu, Lu Liu, M. H. Liu, P. L. Liu, Q. Liu, S. B. Liu, T. Liu, W. K. Liu, W. M. Liu, X. Liu, Y. Liu, Y. B. Liu, Z. A. Liu, Z. Q. Liu, X. C. Lou, F. X. Lu, H. J. Lu, J. G. Lu, X. L. Lu, Y. Lu, Y. P. Lu, Z. H. Lu, C. L. Luo, M. X. Luo, T. Luo, X. L. Luo, X. R. Lyu, Y. F. Lyu, F. C. Ma, H. L. Ma, L. L. Ma, M. M. Ma, Q. M. Ma, R. Q. Ma, R. T. Ma, X. Y. Ma, Y. Ma, F. E. Maas, M. Maggiora, S. Maldaner, S. Malde, Q. A. Malik, A. Mangoni, Y. J. Mao, Z. P. Mao, S. Marcello, Z. X. Meng, J. G. Messchendorp, G. Mezzadri, H. Miao, T. J. Min, R. E. Mitchell, X. H. Mo, N. Yu Muchnoi, Y. Nefedov, F. Nerling, I. B. Nikolaev, Z. Ning, S. Nisar, Y. Niu, S. L. Olsen, Q. Ouyang, S. Pacetti, X. Pan, Y. Pan, A. Pathak, Y. P. Pei, M. Pelizaeus, H. P. Peng, K. Peters, J. L. Ping, R. G. Ping, S. Plura, S. Pogodin, V. Prasad, F. Z. Qi, H. Qi, H. R. Qi, M. Qi, T. Y. Qi, S. Qian, W. B. Qian, Z. Qian, C. F. Qiao, J. J. Qin, L. Q. Qin, X. P. Qin, X. S. Qin, Z. H. Qin, J. F. Qiu, S. Q. Qu, K. H. Rashid, C. F. Redmer, K. J. Ren, A. Rivetti, V. Rodin, M. Rolo, G. Rong, Ch. Rosner, S. N. Ruan, A. Sarantsev, Y. Schelhaas, C. Schnier, K. Schoenning, M. Scodeggio, K. Y. Shan, W. Shan, X. Y. Shan, J. F. Shangguan, L. G. Shao, M. Shao, C. P. Shen, H. F. Shen, W. H. Shen, X. Y. Shen, B. A. Shi, H. C. Shi, J. Y. Shi, Q. Q. Shi, R. S. Shi, X. Shi, J. J. Song, W. M. Song, Y. X. Song, S. Sosio, S. Spataro, F. Stieler, P. P. Su, Y. J. Su, G. X. Sun, H. Sun, H. K. Sun, J. F. Sun, L. Sun, S. S. Sun, T. Sun, W. Y. Sun, Y. J. Sun, Y. Z. Sun, Z. T. Sun, Y. X. Tan, C. J. Tang, G. Y. Tang, J. Tang, L. Y. Tao, Q. T. Tao, M. Tat, J. X. Teng, V. Thoren, W. H. Tian, Y. Tian, I. Uman, B. Wang, B. Wang, B. L. Wang, C. W. Wang, D. Y. Wang, F. Wang, H. J. Wang, H. P. Wang, K. Wang, L. L. Wang, M. Wang, M. Z. Wang, Meng Wang, S. Wang, S. Wang, T. Wang, T. J. Wang, W. Wang, W. H. Wang, W. P. Wang, X. Wang, X. F. Wang, X. L. Wang, Y. Wang, Y. D. Wang, Y. F. Wang, Y. H. Wang, Y. Q. Wang, Yaqian Wang, Z. Wang, Z. Y. Wang, Ziyi Wang, D. H. Wei, F. Weidner, S. P. Wen, D. J. White, U. Wiedner, G. Wilkinson, M. Wolke, L. Wollenberg, J. F. Wu, L. H. Wu, L. J. Wu, X. Wu, X. H. Wu, Y. Wu, Y. J. Wu, Z. Wu, L. Xia, T. Xiang, D. Xiao, G. Y. Xiao, H. Xiao, S. Y. Xiao, Y. L. Xiao, Z. J. Xiao, C. Xie, X. H. Xie, Y. Xie, Y. G. Xie, Y. H. Xie, Z. P. Xie, T. Y. Xing, C. F. Xu, C. J. Xu, G. F. Xu, H. Y. Xu, Q. J. Xu, X. P. Xu, Y. C. Xu, Z. P. Xu, F. Yan, L. Yan, W. B. Yan, W. C. Yan, H. J. Yang, H. L. Yang, H. X. Yang, S. L. Yang, Tao Yang, Y. F. Yang, Y. X. Yang, Yifan Yang, M. Ye, M. H. Ye, J. H. Yin, Z. Y. You, B. X. Yu, C. X. Yu, G. Yu, T. Yu, X. D. Yu, C. Z. Yuan, L. Yuan, S. C. Yuan, X. Q. Yuan, Y. Yuan, Z. Y. Yuan, C. X. Yue, A. A. Zafar, F. R. Zeng, X. Zeng, Y. Zeng, X. Y. Zhai, Y. H. Zhan, A. Q. Zhang, B. L. Zhang, B. X. Zhang, D. H. Zhang, G. Y. Zhang, H. Zhang, H. H. Zhang, H. H. Zhang, H. Q. Zhang, H. Y. Zhang, J. L. Zhang, J. Q. Zhang, J. W. Zhang, J. X. Zhang, J. Y. Zhang, J. Z. Zhang, Jianyu Zhang, Jiawei Zhang, L. M. Zhang, L. Q. Zhang, Lei Zhang, P. Zhang, Q. Y. Zhang, Shuihan Zhang, Shulei Zhang, X. D. Zhang, X. M. Zhang, X. Y. Zhang, X. Y. Zhang, Y. Zhang, Y. T. Zhang, Y. H. Zhang, Yan Zhang, Yao Zhang, Z. H. Zhang, Z. L. Zhang, Z. Y. Zhang, Z. Y. Zhang, G. Zhao, J. Zhao, J. Y. Zhao, J. Z. Zhao, Lei Zhao, Ling Zhao, M. G. Zhao, S. J. Zhao, Y. B. Zhao, Y. X. Zhao, Z. G. Zhao, A. Zhemchugov, B. Zheng, J. P. Zheng, W. J. Zheng, Y. H. Zheng, B. Zhong, C. Zhong, X. Zhong, H. Zhou, L. P. Zhou, X. Zhou, X. K. Zhou, X. R. Zhou, X. Y. Zhou, Y. Z. Zhou, J. Zhu, K. Zhu, K. J. Zhu, L. X. Zhu, S. H. Zhu, S. Q. Zhu, T. J. Zhu, W. J. Zhu, Y. C. Zhu, Z. A. Zhu, J. H. Zou, and J. Zu
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51802-y.
References
- 1.Mcallister, R. W. & Hofstadter, R. Elastic scattering of 188-MeV electrons from the proton and the alpha particle. Phys. Rev.102, 851 (1956). [Google Scholar]
- 2.Punjabi, V. et al. The structure of the nucleon: elastic electromagnetic form factors. Eur. Phys. J. A51, 79 (1956). [Google Scholar]
- 3.Puckett, A. J. R. et al. Final analysis of proton form factor ratio data at Q2 = 4.0, 4.8, and 5.6 GeV2. Phys. Rev. C85, 045203 (2012). [Google Scholar]
- 4.Ablikim, M. et al. Measurement of proton electromagnetic form factors in the time-like region using initial state radiation at BESIII. Phys. Lett. B817, 136328 (2021). [Google Scholar]
- 5.Buttimore, N. H. & Jennings, E. Polarisation observables in lepton-antilepton-to-proton-antiproton reactions including lepton mass. Eur. Phys. J. A31, 9 (2007). [Google Scholar]
- 6.Gao, H. & Vanderhaeghen, M. The proton charge radius. Rev. Mod. Phys.94, 015002 (2022). [Google Scholar]
- 7.Lin, Y. H., Hammer, H. W. & Meißner, U. G. New insights into the nucleon’s electromagnetic structure. Phys. Rev. Lett.128, 052002 (2022). [DOI] [PubMed] [Google Scholar]
- 8.Lin, Y. H., Hammer, H. W. & Meißner, U. G. High-precision determination of the electric and magnetic radius of the proton. Phys. Lett. B816, 136254 (2021). [Google Scholar]
-
9.Mangoni, A., Pacetti, S. & Tomasi-Gustafsson, E. First exploration of the physical Riemann surfaces of the ratio
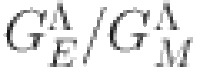 . Phys. Rev. D104, 116016 (2021). [Google Scholar]
. Phys. Rev. D104, 116016 (2021). [Google Scholar] - 10.Segovia, J., Cloet, I. C., Roberts, C. D. & Schmidt, S. M. Nucleon and Δ elastic and transition form factors. Few Body Syst.55, 1185 (2014). [Google Scholar]
- 11.Ablikim, M. et al. Polarization and entanglement in baryon-antibaryon pair production in electron-positron annihilation. Nature Phys.15, 631 (2019). [Google Scholar]
- 12.Pacetti, S., Ferroli, R. B. & Tomasi-Gustafsson, E. Proton electromagnetic form factors: basic notions, present achievements and future perspectives. Phys. Rep.550, 1 (2015). [Google Scholar]
- 13.Granados, C., Leupold, S. & Perotti, E. The electromagnetic Sigma-to-Lambda hyperon transition form factors at low energies. Eur. Phys. J. A53, 117 (2017). [Google Scholar]
- 14.Lin, Y. H., Hammer, H. W. & Meißner, U. G. The electromagnetic Sigma-to-Lambda transition form factors with coupled-channel effects in the space-like region. Eur. Phys. J. A59, 54 (2023). [Google Scholar]
- 15.Ablikim, M. et al. Complete measurement of the Λ electromagnetic form factors. Phys. Rev. Lett.123, 122003 (2019). [DOI] [PubMed] [Google Scholar]
- 16.Schönning, K., Batozskaya, V., Adlarson, P. & Zhou, X. R. Production and decay of polarized hyperon-antihyperon pairs. Chin. Phys. C47, 052002 (2023). [Google Scholar]
- 17.Zyla, P. A. et al. Review of particle physics. Prog. Theor. Exp. Phys.2022, 083C01 (2022). [Google Scholar]
-
18.Ferroli, R. B., Mangoni, A. & Pacetti, S. The cross section of
 as a litmus test of isospin violation in the decays of vector charmonia into
as a litmus test of isospin violation in the decays of vector charmonia into 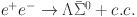 Eur. Phys. J. C80, 903 (2020). [Google Scholar]
Eur. Phys. J. C80, 903 (2020). [Google Scholar] - 19.Ablikim, M. et al. Number of J/ψ events at BESIII. Chin. Phys. C46, 074001 (2022). [Google Scholar]
-
20.Törnqvist, N. A. Suggestion for Einstein-Podolsky-Rosen experiments using reactions like
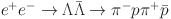 . Found. Phys.11, 171–177 (1981). [Google Scholar]
. Found. Phys.11, 171–177 (1981). [Google Scholar] - 21.Hiesmayr, B. Limits of quantum information in weak interaction processes of hyperons. Sci. Rep.5, 11591 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ablikim, M. et al. Design and construction of the BESIII detector. Nucl. Instrum. Meth. A614, 345 (2010). [Google Scholar]
- 23.Yu, C. H. et al. BEPCII Performance and Beam Dynamics Studies on Luminosity.Proc. IPAC2016, Busan, Korea.10.18429/JACoW-IPAC2016-TUYA01 (2016).
- 24.Ablikim, M. et al. Measurement of the phase between strong and electromagnetic amplitudes of J/ψ decays. Phys. Lett. B791, 375 (2019). [Google Scholar]
-
25.Dubnickova, A. Z., Dubnička, S. & Rekalo, M. P. Investigation of the baryon electromagnetic structure by polarization effects in
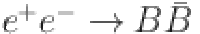 processes. Nuovo. Cimento. A109, 241 (1996). [Google Scholar]
processes. Nuovo. Cimento. A109, 241 (1996). [Google Scholar] -
26.Fäldt, G. & Kupsc, A. Hadronic structure functions in the
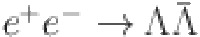 reaction. Phys. Lett. B772, 16 (2017). [Google Scholar]
reaction. Phys. Lett. B772, 16 (2017). [Google Scholar] - 27.Haidenbauer, J., Meißner, U. G. & Dai, L. Y. Hyperon electromagnetic form factors in the time-like region. Phys. Rev. D103, 014028 (2021). [Google Scholar]
-
28.Ablikim, M. et al. Precise measurements of decay parameters and CP asymmetry with entangled
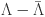 pairs. Phys. Rev. Lett.129, 131801 (2022).
[DOI] [PubMed] [Google Scholar]
pairs. Phys. Rev. Lett.129, 131801 (2022).
[DOI] [PubMed] [Google Scholar] - 29.Fäldt, G. Production and sequential decay of charmed hyperons. Phys. Rev. D97, 053002 (2018). [Google Scholar]
- 30.Ablikim, M. et al. Future physics programme of BESIII. Chin. Phys. C44, 040001 (2022). [Google Scholar]
- 31.Salone, N., Adlarson, P., Batozskaya, V., Leupold, S. & Tandean, J. Study of CP violation in hyperon decays at super-charm-tau factories with a polarized electron beam. Phys. Rev. D105, 116022 (2022). [Google Scholar]
- 32.Barucca, G. et al. The potential of Λ and Ξ− studies with PANDA at FAIR. Eur. Phys. J. A57, 154 (2021). [Google Scholar]
- 33.Agostinelli, S. et al. Geant4-a simulation toolkit. Nucl. Instrum. Meth. A506, 250 (2003). [Google Scholar]
- 34.Jadach, S., Ward, B. F. L. & Was, Z. Coherent exclusive exponentiation for precision Monte Carlo calculations. Phys. Rev. D63, 113009 (2001). [Google Scholar]
- 35.Lange, D. J. The EvtGen particle decay simulation package. Nucl. Instrum. Meth. A462, 152 (2001). [Google Scholar]
- 36.Ping, R. G. Event generators at BESIII. Chin. Phys. C32, 599 (2008).
- 37.Chen, J. C., Huang, G. S., Qi, X. R., Zhang, D. H. & Zhu, Y. S. Event generator for J/ψ and ψ(2S) decay. Phys. Rev. D62, 034003 (2000). [Google Scholar]
- 38.Yang, R. L., Ping, R. G. & Chen, H. Tuning and validation of the lundcharm model with J/ψ decays. Chin. Phys. Lett. 31, 061301 (2014).
- 39.Ping, R. G. An exclusive event generator for e+e− scan experiments. Chin. Phys. C38, 083001 (2014). [Google Scholar]
-
40.Zhong, B., Ping, R. G. & Xiao, Z. J. Study of
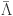 decay parameter in
decay parameter in 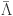 decay. Chin. Phys. C32, 692 (2008). [Google Scholar]
decay. Chin. Phys. C32, 692 (2008). [Google Scholar] - 41.Xu, M. et al. Decay vertex reconstruction and 3-dimensional lifetime determination at BESIII. Chin. Phys. C33, 428 (2009). [Google Scholar]
- 42.Zhou, X. Y., Du, S. X., Li, G. & Shen, C. P. TopoAna: A generic tool for the event type analysis of inclusive Monte-Carlo samples in high energy physics experiments. Comput. Phys. Commun.258, 107540 (2021). [Google Scholar]
- 43.Brodsky, S. J. & Farrar, G. R. Scaling laws at large transverse momentum. Phys. Rev. Lett.31, 1153 (1973). [Google Scholar]
- 44.Perotti, E., Fäldt, G., Kupsc, A., Leupold, S. & Song, J. J. Polarization observables in e+e− annihilation to a baryon-antibaryon pair. Phys. Rev. D99, 056008 (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The raw data generated in this study have been deposited in the Institute of High Energy Physics mass storage silo database. The source data are available under restricted access for the complexity and large size, access can be obtained by contacting to besiii-publications@ihep.ac.cn.
All algorithms used for data analysis and simulation are archived by the authors and are available on request to besiii-publications@ihep.ac.cn.