Regional tuning of photoreceptor adaptation in the primate retina

Abstract

Adaptation in cone photoreceptors allows our visual system to effectively operate over an enormous range of light intensities. However, little is known about the properties of cone adaptation in the specialized region of the primate central retina called the fovea, which is densely packed with cones and mediates high-acuity central vision. Here we show that macaque foveal cones exhibit weaker and slower luminance adaptation compared to cones in the peripheral retina. We find that this difference in adaptive properties between foveal and peripheral cones is due to differences in the magnitude of a hyperpolarization-activated current, I_h. This I_h current regulates the strength and time course of luminance adaptation in peripheral cones where it is more prominent than in foveal cones. A weaker and slower adaptation in foveal cones helps maintain a higher sensitivity for a longer duration which may be well-suited for maximizing the collection of high-acuity information at the fovea during gaze fixation between rapid eye movements.

Light adaptation in the primate fovea is poorly understood. Here, Saha et al. show that cone photoreceptors in the fovea exhibit weaker and slower light adaptation than cones in the peripheral retina due to differences in ion-channel properties.

Introduction

Adaptation is a fundamental property of all sensory systems which mediates efficient encoding of the sensory landscape by dynamically matching the neural gain to the prevailing stimuli in the environment¹. This is exemplified in the visual system which is faced with the challenge of operating over the trillion-fold range of light levels encountered from a moonless night to a bright sunny day². In addition, light levels at a given point in time can differ by ~1000-fold^2,3 across a single visual scene. Rapid saccadic eye movements which direct our high-acuity central vision to different locations within a visual scene add a temporal challenge to adaptation in the visual system necessitating adaptational mechanisms to operate on fast time scales to maintain visual sensitivity. Previous studies in peripheral primate retina show that during daytime vision it is the cone photoreceptors that mediate the majority of adaptation to mean light intensity⁴. In fact, adaptation of cone photoreceptor signal and noise across background light levels sets the absolute detection threshold for human cone-mediated vision^5,6. However, the basic properties of light adaptation are largely unknown for cones in the fovea, the specialized region of the primate retina with the highest cone density and responsible for our high- (spatial and chromatic) acuity vision^7–9. This is particularly important as recent work has shown that in addition to the well-known differences in cone density and morphology between foveal and peripheral primate retina^8–10 (Fig. 1A), there is a striking regional difference in cone function between the two locations^11,12. Foveal cones are two-fold slower in their response kinetics compared to peripheral cones and this regional difference in the time course of cone signals persists both in the retinal output, as well as at the level of perception^11,13. However, the possibility that the light adaptation of cones could be different in the primate fovea vs the peripheral retina has not been investigated. This creates a disconnect when linking physiology to perception because most of what we know about cone adaptation in primates comes from studies conducted in the peripheral retina, whereas most behavioral studies of light adaptation target foveal vision^12,14–18.

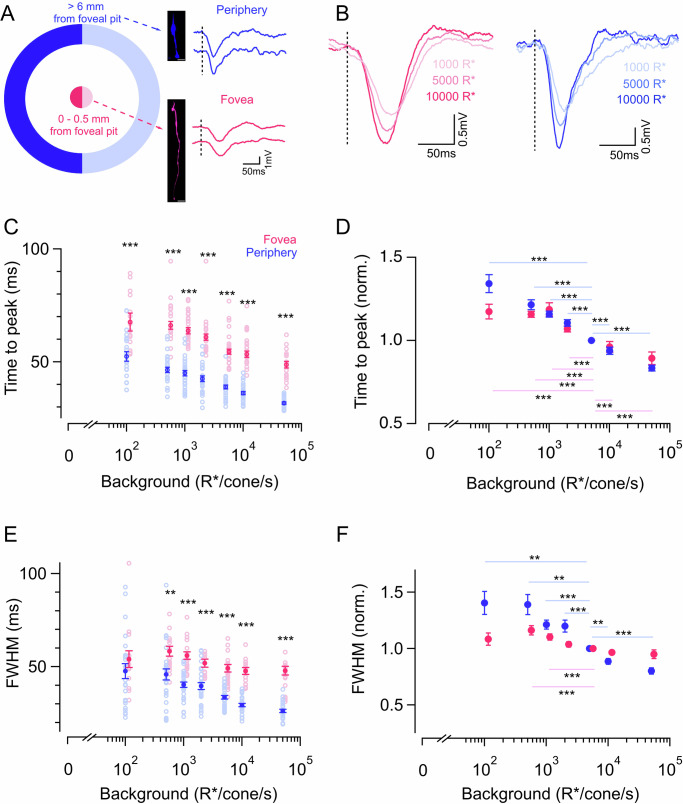
Fig. 1. Cone kinetics accelerate in the foveal and peripheral retina with increasing background luminance.

A Schematic showing the exact location of the foveal and peripheral retina and colors used throughout the figures. Measured from the center of the foveal pit, 0–0.5 mm was defined as foveal (magenta) and >6 mm was defined as peripheral (blue) retina. Insets show a cell-fill image of a foveal cone (scale bar - 35 µm) and peripheral cone (scale bar - 10 µm) and exemplar voltage responses of a foveal and peripheral cone to a 10 ms light flash (300% contrast) delivered on a background of 5000 R^*/s. The vertical dotted lines denote the timing of the light flash. B Exemplar voltage response from a foveal cone (left) and peripheral cone (right) to 10 ms light flashes (300% contrast) at three background light levels. Note the speeding up of voltage responses with higher background light levels. C Times to peak of cone flash responses in foveal and peripheral retina across background light levels. The number of foveal and peripheral cones are denoted as n_f and n_p, respectively for all figures. Time to peak of foveal and peripheral cone responses at 100 (n_f = 16; n_p = 24), 500 (n_f = 21; n_p = 28), 1000 (n_f = 25; n_p = 30), 2000 (n_f = 19; n_p = 28), 5000 (n_f = 30; n_p = 30), 10,000 (n_f = 25; n_p = 30), and 50,000 R^*/s (n_f = 19; n_p = 28) background light intensities, respectively. Empty circles represent individual data points and filled circles with error bars indicate the mean ± standard error of the mean (sem) for all figures. The time to peak of foveal cone responses is significantly slower compared to that of the peripheral cone responses. D Mean ± sem relative times to peak across backgrounds in foveal and peripheral cones. In each cell, the time to peak at each background was normalized by the time to peak at 5000 R^*/s in that cell (calculated from cells represented in B). Note the decrease in the relative times to peak for both foveal and peripheral cones with increasing background light levels. E Full-width at half maxima (FWHM) of foveal and peripheral cone flash responses shown in C across the same background light levels. The FWHM of foveal cone responses is significantly slower compared to that of the peripheral cone responses for most of the background light levels. F Mean ± sem relative FWHM across backgrounds in foveal and peripheral cones. In each cell, the FWHM at each background was normalized by the FWHM at 5000 R^*/s in that cell (calculated from cells in E). Source data are provided as a Source data file. For C, E, we performed multi-way ANOVA with multi-way comparison depending on the number of conditions compared. We used a one-sample t-test for (D, F). The significance threshold was placed at α = 0.05 (n.s., p > 0.05; *p < 0.05; **p < 0.01; ***p < 0.001).

Two characteristic features of luminance adaptation that are observed for cone-mediated vision at the perceptual level, as well as at the level of cone photoreceptor function is the reduction in sensitivity and acceleration of signal kinetics as mean luminance increases^{4,5,12,19–21}. The proportionate decrease in the gain of cone signals with increasing luminance can be described by the classical Weber Law and dictates signal adaptation in the downstream retinal circuitry across a broad range of background light levels^4,5,12,22,23. Such adaptation of gain permits cones to encode variations in luminance (i.e., contrast) independent of mean luminance². Acceleration of cone signals during light adaptation is due to preferential attenuation of low temporal frequency signals⁴. Similar temporal filtering of cone signals is also seen in the downstream retinal circuitry^24,25. Thus, light adaptation causes progressive compression of cone signals, both in magnitude and kinetics, with increasing background luminance^5,12,22. The time scale of such adaptive changes in cone signals will govern visual sensitivity under conditions when light inputs are rapidly changing, for instance, as we are sampling our visual environment during eye movements^2,26. But none of these features of light adaptation are known for cones in the fovea. Given the gap in knowledge of cone adaptation in the fovea, our goal in this study is to (i) determine differences in the properties (gain and kinetics) and timescale of luminance adaptation in the primate foveal vs peripheral cones and (ii) identify underlying mechanisms that create such regional differences in cone adaptation.

By performing whole cell patch clamp recordings from cones in isolated macaque retina and measuring light-evoked voltage responses, we show that adaptation of signal gain and kinetics to varying mean luminance is significantly weaker in foveal cones compared to peripheral cones. Adaptive changes occur on a much slower timescale in foveal cones compared to peripheral cones. Both of the above differences in properties and dynamics of light adaptation are potentially mediated by a hyperpolarization-activated current mediated by cyclic nucleotide-gated HCN channels, that seem to contribute larger currents in peripheral cones than in foveal cones²⁷. In addition to region-specific variations in cone adaptation between fovea and periphery, we also find differences in adaptation across cone spectral types where primate blue (short wavelength-sensitive, S) cones exhibit a weaker and slower luminance adaptation than red (long wavelength-sensitive, L) and green (medium wavelength-sensitive, M) cones, also most likely due to a lower magnitude of the HCN channel current in the S cones.

Results

Luminance-induced acceleration of foveal cone kinetics is lower than that of peripheral cones

To determine if cone adaptation is distinct in the primate fovea compared to the peripheral primate retina, we measured the responses of red and green cones to light stimuli across mean light intensities ranging from those seen in darkness (0 photopigment, R^*, activation/s) to daylight (~50,000 R^*/s). We then evaluated the impact of light adaptation on two salient cone response properties: (i) kinetics, and (ii) gain/sensitivity. Cone responses in the peripheral primate retina and in other mammalian species accelerate with increasing background light level^12,28. To test if this acceleration of cone kinetics is similar in the fovea, we recorded voltage responses to brief (10 ms duration) light flashes in the presence of varying background light levels (Fig. 1A, B). We quantified cone response kinetics at each background light level as the time to reach peak amplitude and full width at half maximum response (FWHM) (Fig. 1C–F). For both foveal and peripheral cones, the time to peak fell as the background light level increased, demonstrating that foveal cone light responses also accelerated with increasing background luminance (Fig. 1B–D). To account for cell-to-cell variability, each cone’s time to peak was normalized by the time to peak at the background light of 5000 opsin isomerization/s (R^*/s) (Fig. 1D). These normalized responses similarly show a robust reduction in the time to peak for both foveal and peripheral cones with increasing background light level. This acceleration of cone responses with increasing background luminance, especially in the fovea is consistent with previous perceptual work targeting foveal vision and reported a similar increase in temporal sensitivity to high-frequency flickering light^13,29. Fitting a line to the normalized time to peak vs logarithm of background luminance yielded a steeper slope for peripheral cones when compared to foveal ones, thus indicating that the rate at which the time to peak decreases with increased luminance is faster in the peripheral cones (Supplementary Fig. 1A, B). Similar to the time to peak measurements, the FWHM measurements also decreased with increased background luminance for peripheral cones at most background light levels (Fig. 1F). However, in foveal cones this change in FWHM was significantly smaller (Fig. 1F), and fitting a line to these data yielded a much steeper slope in peripheral cones compared to the foveal ones (Supplementary Fig. 1C). In addition, this difference in acceleration between foveal and peripheral cones was greater for FWHM than for the time-to-peak comparison. Overall, this suggests that there was a less pronounced acceleration of response kinetics with increasing background light level in the foveal than in the peripheral cones (Fig. 1D, F and Supplementary Fig. 1B, C).

Foveal cones exhibit weaker net gain adaptation than peripheral cones

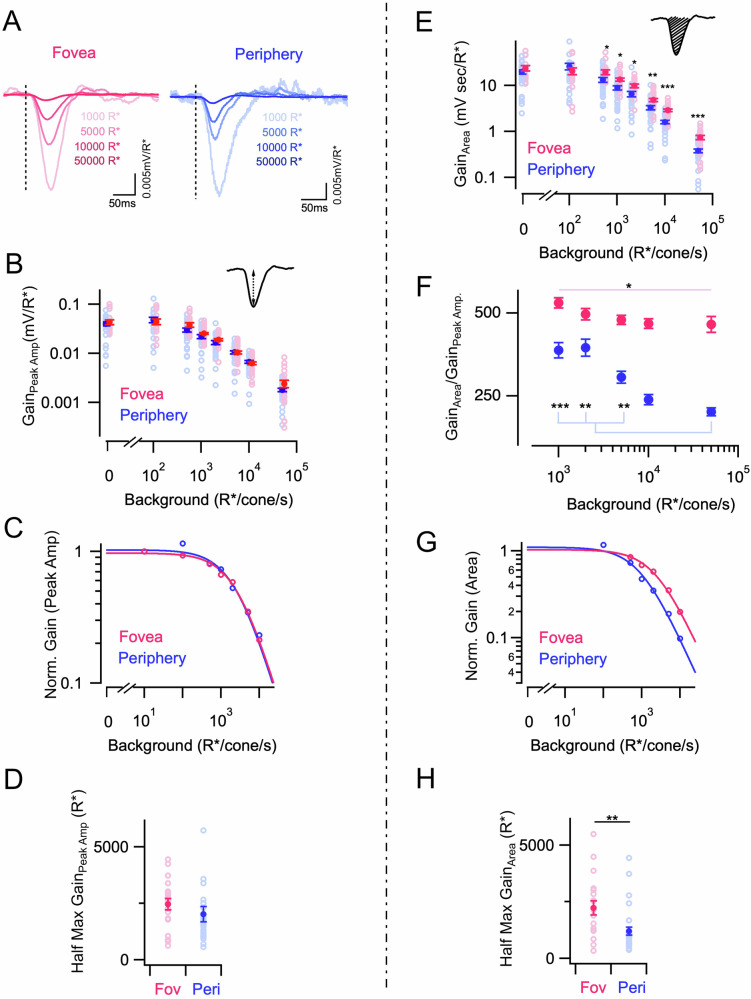
Adaptation in the cone photoreceptors of peripheral primate retina and other species is well characterized by Weber law, i.e., response gain is inversely proportionate to background light level^5,12,21,30. Given that foveal cones have overall slower kinetics than peripheral cones and exhibit a lower acceleration of response kinetics with increasing background light levels, we next wanted to compare cone response gain and characterize its dependence on background light level. The gain was quantified as response per activated opsin (R^*) and calculated by dividing peak response amplitudes by the strength of the light flashes (in R^*) (Fig. 2A). Response gain of cones estimated this way displayed a nonlinear decrease with brighter background light levels (Fig. 2B). Interestingly, foveal and peripheral cone response gain exhibited a similar dependence on background light level, both being well described by a Weber–Fechner function (Equation 1; Fig. 2C) and having similar half-desensitizing background light intensities (luminance at which gain reduces by 50%) (Fig. 2D). These results suggest that despite the difference in the cone response kinetics, the peak amplitude/gain of the response is similar between foveal and peripheral cones across all background light levels tested here (Fig. 2D). This means that the foveal cone response is essentially a time-dilated version of the peripheral cone response. Therefore the integrated response of a foveal cone i.e., area under the curve, should be greater than that of a peripheral cone because the response has the same peak amplitude but lasts longer in duration (Fig. 2E). This was indeed the case. However when using the integral of the voltage response as a measure of gain, we find that foveal cones not only have a higher response gain at most background light levels compared to their peripheral counterparts but also reduce their gain to a lesser extent than peripheral cones with increasing background light levels(Fig. 2E). In other words, the peripheral cones exhibit a stronger overall  response compression with increasing luminance than foveal cones. This is because they are more compressed in width (time) while maintaining an equal compression in height (amplitude) with increasing background luminance when compared to the responses of foveal cones. As a result, the integrated response of peripheral cones decreases more sharply than peak amplitude with increasing background luminance. This is reflected in the ratio of integrated response gain (area/R^*) to peak amplitude gain (amplitude/R^*) which exhibits a significant reduction in background luminance in peripheral cones as compared to foveal cones (Fig. 2F).

Fig. 2. Foveal cones exhibit weaker luminance adaptation than peripheral cones.

A Exemplar response of a foveal (left) and peripheral cone (right) to 10 ms light flashes at different background light levels. Responses have been converted into gain (mV/R^*). Both foveal and peripheral cone responses show a reduction in gain with increasing background luminance. B Adaptation of peak response amplitude in foveal and peripheral cones. Peak response gains were measured at 0 (darkness; n_f = 21; n_p = 28), 100 (n_f = 16; n_p = 24), 500 (n_f = 21; n_p = 28), 1000 (n_f = 26; n_p = 30), 2000 (n_f = 18; n_p = 28), 5000 (n_f = 30; n_p = 30), 10,000 (n_f = 26; n_p = 30) and 50,000 R^*/s (n_f = 20; n_p = 28) background light intensities, respectively. Peak response gain is not significantly different between foveal and peripheral cones across background luminance. Lighter open circles represent values from individual cells and points with error bars represent mean ± sem for all panels. C Normalized response gains (peak amplitude) across the luminance of an exemplar foveal and peripheral cone were fit to Eq. 1 described in the methods section. The solid line shows fit of Eq. 1 to an exemplar foveal and peripheral cone, demonstrating that cone adaptation is well described by this equation. D Half-maximal background luminance estimated from fits of peak amplitude gain across luminance to Weber–Fechner curve (Eq. 1) for foveal (n_f = 19) and peripheral (n_p = 30) cones. Half-maximum background luminance is not significantly different between foveal and peripheral cones. E Adaptation of integrated responses (area under the curve) in foveal and peripheral cones shown in (C). Integrated response gains were calculated at the same background light intensities as (C). Integrated response gain is significantly different between foveal and peripheral cones starting at 500 R^*/s background luminance. F Ratio of peak response amplitude and response integral (area under the curve) in foveal and peripheral cones across 1000 (n_f = 25; n_p = 30), 2000 (n_f = 18; n_p = 28), 5000 (n_f = 25; n_p = 30), 10,000 (n_f = 26; n_p = 30) and 50,000 R^*/s (n_f = 10; n_p = 28) background luminance. G Normalized response gains (area under the curve) across the luminance of an exemplar foveal and peripheral cone were fit to Eq. 1 described in the methods section. The solid line shows the fit of Eq. 1 to an exemplar foveal and peripheral cone, demonstrating that cone adaptation is well described by this equation. H Half-maximal background luminance estimated from fits of integrated gain across luminance to Weber–Fechner curve (Eq. 1) for foveal (n_f = 19) and peripheral (n_p = 30) cones. The half-maximal background is significantly different between the foveal and peripheral cones. Source data are provided as a Source Data file. For figure panels with multiple comparison groups, we performed multi-way ANOVA with multi-way comparison depending on the number of conditions compared. We used the unpaired t-test for panels with two comparison groups (D, H). For figure panels with multiple comparison groups, we performed multi-way ANOVA with multi-way comparison depending on the number of conditions compared (B, E, andF). The significance threshold was placed at α = 0.05 (n.s., p > 0.05; *p < 0.05; **p < 0.01; ***p < 0.001).

Fitting the curve of normalized integrated response gain vs background light intensity with a Weber–Fechner function yielded a significantly higher estimate of half-desensitizing background light intensity for foveal cones than peripheral cones (Fig. 2G, H). In fact, the estimate of half-desensitizing background luminance was lower by ~2-fold for peripheral cones when the integrated response is taken as a measure of Weber gain instead of peak amplitude (Fig. 2D, H and Supplementary Fig. 2A). This suggests that overall response compression with increasing background light level is stronger for peripheral cones than it is for foveal cones and is primarily driven by stronger temporal filtering and attenuation of low frequencies in the periphery. We further quantified the dynamic range of the Weber adaptation curve for integrated response gain and found a higher estimate for foveal than peripheral cones (Supplementary Fig. 2B). Together the above results show that a smaller adaptive change in response kinetics across mean luminance, gives rise to a net weaker light adaptation in foveal cones which can potentially allow them to maintain higher gain at brighter lighting conditions.

Foveal cones exhibit a slower timescale of light adaptation compared to peripheral cones

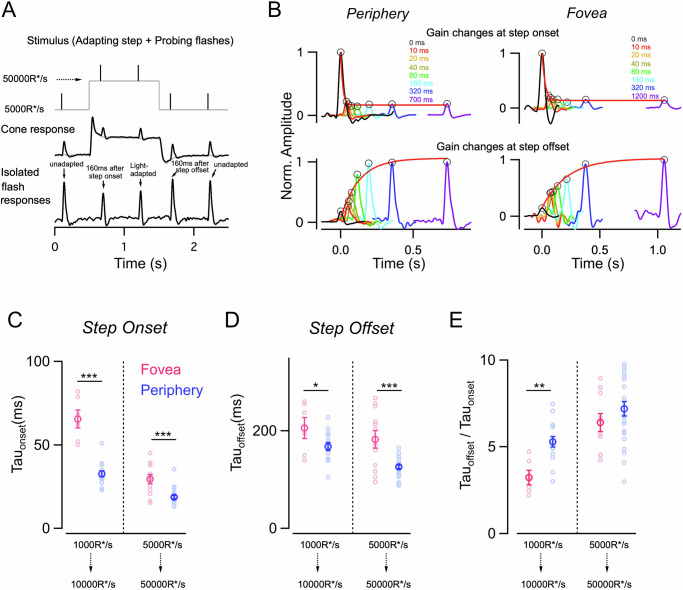
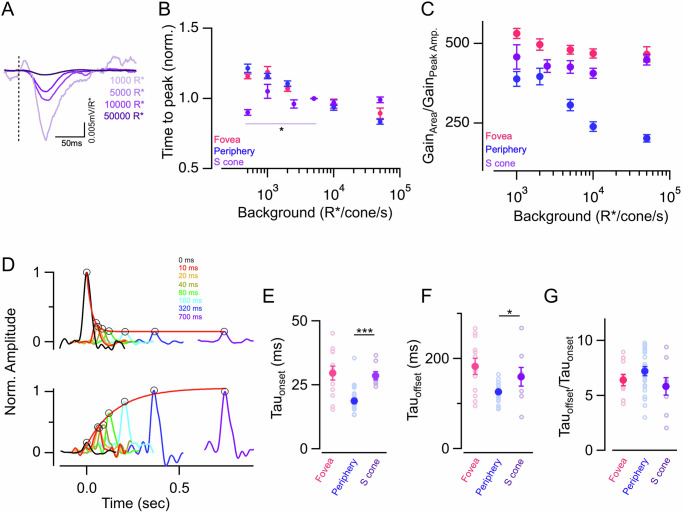
Is the difference in response kinetics and net gain (integrated response) between the foveal and peripheral retina reflected in the timescale of cone adaptation at the two retinal locations? This is a key feature of our everyday visual experience as we constantly shift our gaze to direct our high-resolution foveal vision for exploring different objects in a natural scene^31,32. Cones experiencing rapid changes in light intensity during such saccadic eye movements would need to adapt their gain on a fast timescale as recently demonstrated for cones in the peripheral primate retina²⁶. However, the timescale of adaptation remains unknown for cones in the fovea which is subject to fast and large changes in luminance as our eyes fixate from one location to the next while actively sampling a visual scene. To test if the timescale of light adaptation is different in foveal vs peripheral cones, we measured the magnitude and time course of light adaptation by probing response gain as a function of time following a sudden increase or decrease in background light level as previously described²⁶. Brief 10 ms light flashes were delivered at different time delays following either the onset or offset of a background light step while measuring the cone voltage response (Fig. 3A). Responses to light flashes were isolated by subtracting the response to a light step alone (Fig. 3A). Response gain was estimated as above by dividing the response amplitude by the strength of the light flash. Gains were then normalized to the unadapted gain which was measured by delivering a flash at a fixed timing well before the background step increment or well after the step decrement (Fig. 3A). Fully adapted gain was measured by delivering a flash at the end of the step, just before the offset (Fig. 3A). The gradual decrease in cone response gain following the light increment and  the corresponding increase following light decrement represents the time course of cone adaptation (Fig. 3B).

Fig. 3. Gain changes during light adaptation occur on a slower timescale in foveal compared to peripheral cones.

A Light stimulus used to assess the time course of rapid gain changes during light adaptation. Five brief light flashes (black trace) were superimposed on an adapting light step (gray trace); the first, third, and fifth flashes were fixed in time (black), and the second and fourth were presented at variable time delay from step onset and offset. In this exemplar trace, time delay = 160 ms. The middle panel shows the mean response of a peripheral cone to the adapting step in combination with the five flashes (black trace) for time delay = 160 ms, as well as to the light step alone (gray trace). The bottom panel shows flash responses isolated by subtracting the response to the light step alone. The first and fifth light flashes are the unadapted responses, whereas the smaller and faster response to the third flash (near the end of the step) is the adapted response. The light flashes following step onset and offset evoke cone responses that adapt from a lower to higher mean luminance, as well as responses that adapt from a higher to lower mean luminance. B The top panel shows rapid gain changes of the peripheral (left) and foveal (right) cone in (A) at light onset. Response gains for each of the flashes were obtained by dividing the response by the flash strength and normalizing to the response gain of the flash at lower background luminance (far left black trace; unadapted flash); the steady-state adapted gain is denoted by the far right purple trace and colored traces in between correspond to flashes with a variable delay from the step onset. The kinetics of the gain changes were tracked by identifying the peaks and fitting their time course with a single exponential function. The time constant of the best-fit exponential was tau_On = 13.5 ms (red smooth line) for the peripheral cone and 30.92 ms for the foveal cone. The bottom panel shows the time course of gain changes at light offset (gains normalized to response gain of the flash delivered well after light offset). Black trace corresponds to the initial steady-state adapted gain (far left) and the purple trace corresponds to the final steady-state gain after step offset (far right). Colored traces correspond to flashes with a variable delay from the step offset (same delays as in the top panel). The time constant of the best-fit exponential for this exemplar peripheral cone was tau_Off = 127.3 ms (red smooth line) for the peripheral cone and 250.63 ms for the foveal cone. C–E Time course of gain changes at step onset of foveal and peripheral cones for light steps of two distinct magnitudes 1000–10,000 R^*/s (n_f = 6; n_p = 15) and 5000–50,000 R^*/s (n_f = 12; n_p = 23). The foveal cones show a significantly slower time course of adaptation both at light onset and offset. E Gain changes several folds more rapidly during step onset than at step offset. The ratio of tau_onset over tau_offset was above 1 for both foveal and peripheral cones and significantly different between foveal and peripheral cones for only the 1000–10,000 R^*/s light step. Lighter open circles represent peak response gains from each cell. Points with error bars represent mean ± sem. Source data are provided as a Source Data file. We used the unpaired t-test for all the statistical analyses in this figure. The significance threshold was placed at α = 0.05 (n.s., p > 0.05; *p < 0.05; **p < 0.01; ***p < 0.001).

To precisely quantify the time course of cone adaptation, the gain changes following light onset and offset were fit with a single exponential function (Fig. 3B and Supplementary Fig. 3A). The time constants of adaptation at both light onset and offset were significantly larger for foveal cones compared to peripheral cones indicating that foveal cones have a slower time course of adaptation than their peripheral counterparts (Fig. 3C, D). Even though, there was a consistent speeding up of the adaptation time course for a larger step change (1000–10,000 R^* vs 5000–50,000 R^*) for both foveal and peripheral cones, adaptation kinetics remained substantially slower for foveal cones compared to peripheral cones (Fig. 3C, D). This shows that foveal cones need longer to adapt to fast gain changes compared to peripheral cones. The mean voltage response to the light step alone exhibited a much slower timescale than the rapid gain changes of the flash responses (Supplementary Fig. 3B, C). This slow adaptation of the steady-state response contributes to the encoding of the mean light intensity unlike the rapid adaptation probed by the flashes, which allows for fast contrast encoding²⁶. The decay kinetics of the steady-state step response were similar between foveal and peripheral cones (Supplementary Fig. 3C).

As previously shown for cone photocurrents in peripheral primate retina²⁶, the time course of gain changes at light offset is much slower than at light onset (Fig. 3B–D). This held true for both foveal and peripheral cone voltage responses and this asymmetry between light onset and offset was persistent irrespective of the size of the light step (Fig. 3C, D). To compare the asymmetry in the kinetics of adaptation at light onset vs offset between foveal and peripheral cones we estimated a asymmetric adaptation index by taking the ratio of the time constant of adaptation following light offset to that following light onset (Fig. 3E). We found that this asymmetric adaptation index was slightly smaller for foveal cones than peripheral cones at the lower light levels. At brighter background light levels, the asymmetric adaptation index is much higher for both foveal and peripheral cones but not significantly different from each other (Fig. 3E).

Foveal and peripheral cones exhibit similar response asymmetry to light increments and decrements

Both foveal and peripheral cones exhibit strong asymmetry in the time course of adaptation between light increments and decrements which raised the question of whether their response magnitudes are also similarly asymmetric. Light increment/decrement asymmetries in cone signals have previously been reported in amphibian, fish, and peripheral primate cones^21,26,33, as well as later in the retinal circuitry and visual pathway in the visual cortex^26,34–36. This motivated us to look at this asymmetry in foveal vs peripheral cones using positive and negative light steps of equal contrast. Responses of cones in the fovea and periphery to light increments and decrements were of equal amplitude up to ~25% contrast and started becoming strongly asymmetric at contrasts greater than 50% with responses to negative contrasts exceeding in magnitude compared to responses to positive contrasts (Fig. 4A–C). The contrast response curve of both foveal and peripheral cones looked nonlinear and identical at the lower background light levels but distinct at higher background light levels (Fig. 4C). Such asymmetric and rectified responses are most likely because cones can depolarize to a far more positive membrane potential for a negative contrast than they can hyperpolarize to for an equal and opposite positive contrast given their resting membrane potential sits at ~−45 mV²⁵. We estimated the response asymmetry to positive and negative contrasts by quantifying the ratio of the mean (steady-state) voltage response at the end of a given negative contrast step to that of its equivalent positive contrast step (Fig. 4D). This ratio was largely similar for both foveal and peripheral cones with both exhibiting higher asymmetry for higher contrasts and for higher background light level (Fig. 4D). Given the asymmetry in cone response amplitude to light increments and decrements, we next probed if the response kinetics also similarly differ for foveal and peripheral cones. This is important given previous observations that the OFF pathway has a higher temporal sensitivity than the ON pathway and human perception of dark stimuli is faster than that of light stimuli^{34,35,37–39}. To compare the kinetics of cone responses to light increments vs decrements, we measured responses to brief, 10 ms, light increments, and decrements at the brightest background luminance (50,000 R^*/cone/s) where the response asymmetry is the largest. Responses to brief light flashes allowed us to get a defined peak (Fig. 4E) which was missing in the responses to longer light decrement steps (Fig. 4A, B). Upon comparison, we found no difference in the response time to peak between light increment and decrement for both foveal and peripheral cones (Fig. 4F). Overall, these results show that foveal cones, like their peripheral counterparts, exhibit strong nonlinear sensitivity to light increments/decrements which most likely contribute to such asymmetry in downstream visual circuits and perception, especially for high contrast stimuli^34,40. However, the similar cone response kinetics to brief 10 ms flashes of light increment and decrement may suggest that differences in the kinetics of OFF signals relative to ON signals originate later on in the visual pathway downstream of cones.

Fig. 4. Asymmetric responses of foveal and peripheral cones to light increments and decrements.

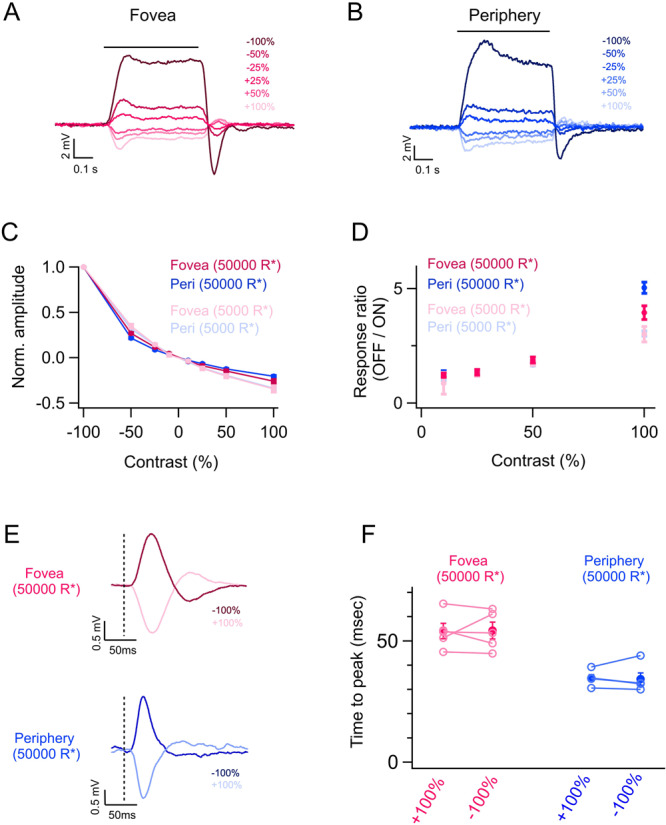
A, B Exemplar foveal and peripheral cone voltage responses to a series of light increments and decrements at a background light level of 50,000 R^*/s. C Normalized contrast response curves of foveal and peripheral cones at a lower (5000 R^*/s) and higher (50,000 R^*/s) background light level. The contrast responses are equally asymmetric between foveal (n_f = 4 for 5000 and 50,000 R^*/s background luminance) and peripheral cones (n_p = 16 and 15 for 5000 and 50,000 R^*/s background luminances, respectively). D The ratio of mean responses to equal and opposite contrast steps (OFF/ON ratio) as a function of contrast magnitude calculated for the cones in (C). E Exemplar foveal and peripheral cone voltage responses to a brief (10 ms) light increment and decrement flashes at a background light level of 50,000 R^*/cone/s. F Times to the peak of foveal (n_f = 5) and peripheral cone (n_p = 5) voltage responses to positive (+) and negative (−) 100% contrast flash at a background light level of 50,000 R^*/cone/s were similar. Lighter open circles represent peak response gains from each cell. Points with error bars represent mean ± sem. Source data are provided as a Source Data file. We used the paired t-test for the statistical analysis in (F). The significance threshold was placed at α = 0.05 (n.s., p > 0.05).

A role for HCN channels in causing regional differences in primate cone adaptation

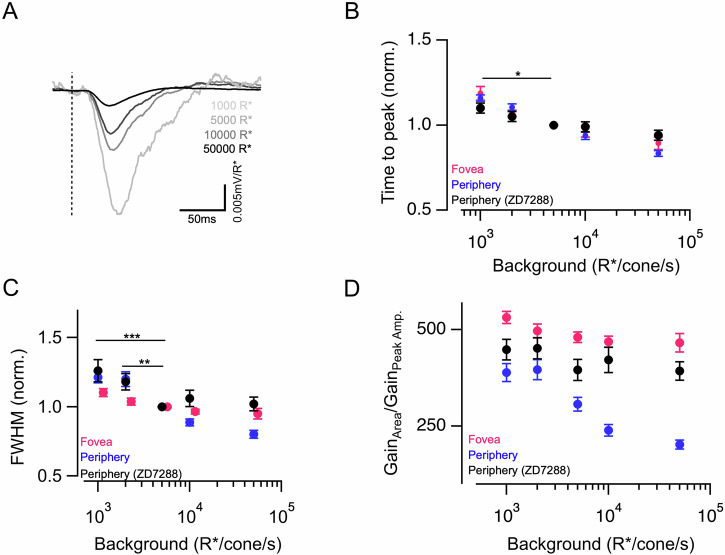
What could be a potential mechanism that causes the peripheral cones to accelerate their signals faster than the foveal cones as background light becomes brighter and hence results in differences in gain adaptation? Furthermore, could the same mechanism also be responsible for the faster timescales of adaptation seen in peripheral cones compared to foveal cones? Previous studies have attributed the role of HCN channels to the acceleration of photoreceptor voltage responses in a light-dependent manner^41,42. Moreover, it has recently been shown that the magnitude of HCN channel-mediated current is remarkably different between peripheral and foveal cones²⁷. These findings motivated us to determine if HCN channels are involved in shaping the adaptation of cone kinetics, as well as the dynamics of luminance adaptation. We first measured the magnitude of HCN channel-mediated currents in peripheral and foveal cones in response to hyperpolarizing voltage steps and observed a much larger current in peripheral than foveal cones consistent with previous findings²⁷ (Supplementary Fig. 4A, B). We then used an HCN channel-specific blocker, ZD7288, which abolished inward currents at hyperpolarized membrane potentials in peripheral cones (Supplementary Fig. 4A, B) and measured the impact on the voltage responses to brief 10 ms light flashes across a range of background luminance as mentioned above (Fig. 5A). HCN channel blocker significantly slowed down the acceleration of peripheral cone kinetics with increasing luminance and the dependence of peripheral cone kinetics (both time-to-peak and FWHM) vs mean luminance seemed more like that of the foveal cones with a shallower slope (Fig. 5B, C and Supplementary Fig. 4C–F). The effect of HCN channel block on cone kinetics was also much more pronounced at higher light levels where cones are relatively more hyperpolarized and cause a larger activation of these channels. Since HCN channel blocker also changes the amplitude of the cone signals, instead of comparing the absolute gain values across cones we compared the ratio of the response integral (area) gain (Supplementary Fig. 4H) to peak amplitude gain (Supplementary Fig. 4G) for each cone (Fig. 5D). Given that peripheral cone kinetics accelerate less with mean luminance in presence of the blocker, this ratio also showed little or no change across background light levels akin to that observed for foveal cones. This provides evidence in favor of a key role for HCN channels in shaping the luminance-driven acceleration of response kinetics for peripheral cones. We next tested the role of HCN channels in regulating the dynamics of luminance adaptation with the light stimuli used in Fig. 3. The time course of adaptation for peripheral cones was slowed down, especially at the onset with no effect at the offset of the light step in presence of the HCN channel blocker (Supplementary Fig. 5). This is presumably due to hyperpolarization-induced activation of the HCN channels at light onset as opposed to that at light offset which causes these channels to close due to membrane depolarization. The selective effect on the adaptation dynamics at the onset of the light step led to a lower asymmetric  adaptation index for peripheral cones in the presence of the blocker (Supplementary Fig. 5D). Overall, these results show that HCN channels contribute significantly towards making luminance adaptation stronger and faster in peripheral cones in comparison to that observed in foveal cones.

Fig. 5. Impact of HCN channel blocker on luminance adaptation in peripheral cones.

A Exemplar responses of a peripheral M/L cone to 10 ms light flashes at four different background light levels in the presence of HCN channel blocker ZD7288. Response amplitude has been converted into gain (mV/R^*). B Mean ± sem relative times to peak across backgrounds of peripheral cones in the presence of ZD7288 compared to that of foveal and peripheral cones without ZD7288 (replotted from Fig. 1). In each cell, the time to peak at each background was normalized by the time to peak at 5000 R^*/s in that cell. C Mean ± sem relative FWHM across backgrounds of peripheral cones in the presence of ZD7288 compared to that of foveal and peripheral cones without ZD7288 (replotted from Fig. 1). In each cell, the FWHM at each background was normalized by the FWHM at 5000 R^*/s in that cell. D The ratio of peak response amplitude and response integral of peripheral cones in the presence of ZD7288 (n = 1) compared to that of foveal and peripheral cones without ZD7288 (replotted from Fig. 2). Points with error bars represent mean ± sem response gains across a range of background luminance starting from 1000 R^*/s. Source data are provided as a Source Data file. We performed multi-way ANOVA with a multi-way comparison with three conditions. The significance threshold was placed at α = 0.05 (n.s., p > 0.05; *p < 0.05; **p < 0.01; ***p < 0.001).

Peripheral S cones exhibit weaker and slower luminance adaptation compared to L/M cones

Our results thus far show that a slower rate of change in response kinetics with increasing luminance, as observed in foveal L/M cones and in ZD7288-treated peripheral L/M cones, causes a net weaker gain adaptation. We wanted to further validate this idea by testing it in a scenario where there is minimal change in cone kinetics with changes in mean luminance. This is a well-established feature of light adaptation in primate short wavelength (S) sensitive cones and this constancy of kinetics of S cone signals across luminance is conserved even at the circuit and perceptual level^12,43,44. We used a previously published dataset of peripheral S cone voltage responses to light flashes across a range of background luminance for testing whether S cones exhibit a net weaker adaptation compared to peripheral L/M cones when using the response integral as a measure of gain¹² (Fig. 6A). We first confirmed that the S cone kinetics showed minimal change across luminance (Fig. 6B and Supplementary Fig. 6). Next, across luminance the response gain, using peak amplitude as a metric, wasn’t significantly different for S cones when compared to peripheral L/M cones for nearly all background light levels (Supplementary Fig. 6 vs Fig. 2). However, when we compared luminance-driven compression of responses between S and L/M cones by estimating the ratio of the integrated (area) gain and the peak amplitude gain, it stayed almost constant across background luminance unlike that in peripheral L/M cones but mimicking the pattern seen in the foveal L/M cones (Fig. 6C). This indicates that the net gain adaptation of S cones is weaker than that of L/M cones due to the minimal adaptation of their response kinetics with luminance.

Fig. 6. Weaker and slower luminance adaptation in peripheral S vs L/M cones.

A Exemplar responses of a peripheral S cone to 10 ms light flashes at four different background light levels. Responses have been converted into gain (mV/R^*). S cone responses show a reduction in gain with increasing background luminance. B Mean ± sem relative times to peak across backgrounds in foveal M/L, peripheral S, and peripheral M/L cones. In each cell, the time to peak at each background was normalized by the time to peak at 5000 R^*/s in that cell. Note that, the relative times to peak for peripheral S cones do not change with increasing background light level. Normalized times to peak were plotted from n = 14, 9, 8, 25, 10, 25 peripheral S cones at 500, 1000, 2500, 5000, 10,000, and 50,000 R^*/s background light intensities, respectively. Data for foveal and peripheral M/L cones replotted from Fig. 1. C Ratio of peak response amplitude and response integral in foveal M/L, peripheral S, and peripheral M/L cones. The ratio of amplitude vs integrated response gain was measured from n = 9, 8, 10, 10, 10 peripheral S cones at 1000, 2500, 5000, 10,000, and 50,000 R^*/s background light intensities, respectively. Data for foveal and peripheral M/L cones replotted from Fig. 2. D The top panel shows rapid gain changes of the peripheral S cone at the light onset. The kinetics of the gain changes were estimated similarly to that in Fig. 3. The time constant of the exponential fit was tau_onset = 34.5 ms (red smooth line). The bottom panel shows the time course of gain changes at light offset. The time constant of the exponential fit for this exemplar peripheral S cone was tau_offset = 384.7 ms (red smooth line). E–G The time course of gain changes at step onset of foveal, peripheral S, and peripheral M/L cones for light steps (5000–50,000 R^*/s). The time constant at light onset, offset, and their ratios were calculated from n = 8 S cones. Lighter open circles represent peak response gains from each cell. Foveal and peripheral M/L cone data have been replotted from Fig. 3. Points with error bars represent mean ± sem. Source data are provided as a Source Data file. We performed multi-way ANOVA with a multi-way comparison with three conditions. The significance threshold was placed at α = 0.05 (n.s., p > 0.05; *p < 0.05; **p < 0.01; ***p < 0.001).

We next performed similar experiments as above to estimate the timescale of adaptation for S cones and test if it is slower than that in the L/M cones (Fig. 6D). The time constants of adaptation at both the light onset and offset were significantly higher for peripheral S cones compared to that of the peripheral L/M cones and in fact similar to the foveal L/M cone time constants (Fig. 6E, F). However, the asymmetric adaptation index was not different across cone types (Fig. 6G). We next tested if S cones like foveal cones also have a smaller hyperpolarization-activated current which may be responsible for the lack of luminance-dependent response acceleration and a slower time course of adaptation. Indeed, estimation of the current to hyperpolarizing steps revealed a much smaller magnitude in peripheral S cones than L/M cones and identical to foveal L/M cones indicating that HCN channels play a key role in regulating temporal properties of cone adaptation in peripheral L/M cones (Supplementary Fig. 4B). Overall, our S cone results are consistent with the idea that lower hyperpolarization-activated current causes weaker temporal filtering of S cone responses at brighter light levels and potentially a slower timescale of luminance adaptation than that of L/M cones.

Discussion

Despite the importance of the fovea for our everyday vision, as well as the well-known perceptual differences between foveal and peripheral vision, little is known about how the early stages of visual processing differ among cone photoreceptors between these regions. Recent work has identified two-fold slower response kinetics in foveal cones compared to peripheral cones, which persists through the retinal output and into perception^11–13. However, challenges and sparsity of intracellular recordings from the fovea have prevented a detailed regional comparison of fundamental features of cone function such as light adaptation in the primate retina. By performing whole-cell patch clamp recordings from a sizeable population of cones in the primate fovea and peripheral retina we find that foveal cones not only exhibit slower response kinetics than peripheral cones across a broad range of background luminance but also show a relatively smaller change in kinetics with increasing luminance compared to peripheral cones (Fig. 1 and Supplementary Fig. 1). We then find that this slower acceleration of kinetics causes a weaker adaptation of foveal cone responses in comparison to peripheral cones (Fig. 2 and Supplementary Fig. 2). A smaller acceleration in response kinetics across light levels was accompanied by a slower time scale of adaptation in foveal cones compared to that in the peripheral cones (Fig. 3 and Supplementary Fig. 3). Our results further reveal that response asymmetry to light increments and decrements seems to be nearly identical between foveal and peripheral cones (Fig. 4). This will be an important consideration in understanding the origin of such asymmetries to light and dark stimuli in higher visual centers, as well as at the level of visual perception^33–35,40.

We also uncovered a key component of the mechanism underlying regional differences in cone adaptation which relies on the hyperpolarization-activated current mediated by HCN channels. Pharmacologically blocking this voltage-gated channel in peripheral cones reduces the adaptive changes in kinetics across luminance and slows the dynamics of adaptation converting the adaptive features of a peripheral cone to that of a foveal cone (Fig. 5 and Supplementary Figs. 4 and 5). Finally, we find that peripheral S cones, known to be more sluggish than L/M cones, share similar features of light adaptation as foveal L/M cones and rely on similar changes in temporal filtering and dynamics of luminance adaptation (Fig. 6 and Supplementary Fig. 6).

Response integral vs peak amplitude as a measure of signal gain

Although the peak amplitude measures of response gain did not explain the difference in adaptation between foveal and peripheral cones, taking the time-integrated response provided this insight. There is a rich history of human behavioral studies measuring the threshold of detection vs background light intensity which show that the gain of human cone-mediated vision decreases proportionately with luminance following the classical Weber law^2,23,45. Our results show that this dependence of gain on luminance is present in both cones in the fovea and in the periphery (Fig. 2). However, a key feature that is typically not captured in this behavioral threshold vs intensity measurements is the impact of luminance on the kinetics of the cone signals. Instead, this is well-captured in the increased perceptual sensitivity to high-frequency flickering light at brighter background illumination⁴³. We show that such luminance-dependent changes in temporal sensitivity of cone-mediated vision are present in both foveal and peripheral cones albeit to a different extent (Fig. 1). We find an identical reduction in peak amplitude of light responses with increasing background luminance in both foveal and peripheral cones but a faster acceleration of response kinetics only in peripheral cones. This causes a bigger reduction in the peripheral cone integrated response ‘integrated gain’ when compared to foveal cones across increasing background luminance. In other words, a slower acceleration of foveal cone response kinetics at brighter background light levels causes a weaker response compression (in time) compared to peripheral cones. Thus, for foveal cones adaptation is identical whether estimated using the peak amplitude or response integral as a measure of gain. This is also the case for the peripheral S cones where due to a lack of change in response kinetics across mean luminance, adaptation remains the same when considering peak amplitude or response integral as a metric of gain (Fig. 6). These results suggest that retinal location and spectral type specific attenuation of low temporal frequencies leads to different degrees extent of Weber adaptation in the different types of primate cones^4,12. Such differences in adaptive changes of temporal filtering coupled with an overall slower response kinetics seem to be coincident with a slower timescale of luminance adaptation in foveal L/M cones and peripheral S cones compared to peripheral L/M cones.

A role of HCN channels in primate cone adaptation

Acceleration of mammalian cone kinetics at brighter background light levels has been attributed to both phototransduction intrinsic and extrinsic mechanisms^46,47. Phototransduction intrinsic mechanisms include an increased rate of cGMP turnover, increased inactivation of the photopigment, and increased rate of CNG (cyclic nucleotide-gated) channel gating all of which are mediated by calcium feedback^46,48–53. Although such calcium feedback mechanisms have an important role in luminance-dependent changes in cone response gain^46,54, our findings provide evidence that luminance-driven changes in primate cone kinetics rely significantly on a phototransduction extrinsic mechanism, mediated by HCN channels, that causes a strong response acceleration of peripheral L/M cones at brighter light levels. Previous studies in mouse and goldfish retinas have shown that HCN-channel mediated current, I_h, in cones, is not only essential for the fast response kinetics but also crucial for light-dependent adaptive changes in temporal filtering such as those exhibited by peripheral primate cones^41,42. Our results further show that this hyperpolarization-activated current also shapes the time course of luminance adaptation in primate cones with a larger impact at higher than lower background light levels (Fig. 5 and Supplementary Figs. 4 and 5). Brighter background luminance and larger modulations around the mean light intensity lead to a stronger hyperpolarization of the cone membrane potential and hence activation of the I_h current. This causes the HCN channels to have a more pronounced effect at higher than lower light levels in peripheral primate cones consistent with our results. Our study also sheds light on how differences in the magnitude of the I_h current can cause regional and cone-type-specific differences in the adaptive tuning of response kinetics and in the time course of luminance adaptation in primate retinas. In fact, our results, as well as recent studies show that foveal cones have a much smaller amplitude of the I_h current compared to peripheral cones²⁷, which has implications for both cone adaptation, as well as for efficient signal propagation down the long axons of foveal cones²⁷. In addition, S cones in goldfish retina lack a prominent I_h current and consequently do not exhibit any adaptive changes in response kinetics⁴¹. Our results also show a smaller hyperpolarization-activated current mediated by HCN channels in S vs L/M cones which is perhaps one of the major contributors to the differences in luminance adaptation between primate S and L/M cones (Supplementary Figs. 4 and 6). We cannot rule out the role of calcium-dependent regulation of the phototransduction cascade in mediating some of the luminance-based differences in response kinetics and adaptation dynamics⁴⁶. This is especially the case for lower background light levels, where I_h current magnitude is smaller, and at light decrements, when HCN channels are closed. In fact, studies show that the phototransduction machinery in both foveal L/M cones and primate S cones differ from that in peripheral L/M cones because they share certain elements of the rod phototransduction machinery that are typically lacking in peripheral L/M cones^55,56. This is thought to be responsible for their overall slower response kinetics compared to peripheral L/M cones. However, whether such phototransduction-intrinsic differences between cones play a role in shaping adaptive changes in kinetics and in controlling the time course of adaptation will be grounds for future studies.

Potential impact of cone adaptation on downstream retinal circuitry

Do the regional differences in adaptation we observe at the level of cones shape adaptation later in the circuitry? This question is particularly important for the foveal midget pathway where each midget ganglion cell (MGC) derives its signal from a single cone and is responsible for the high spatial and chromatic sensitivity of our central vision^10,57. We predict that the impact of regional differences in cone adaptation will be more prominent in the midget pathway than other retinal circuits for the following reasons: (i) Our previous study shows that foveal MGCs exhibit an overall slower response kinetics than the peripheral MGCs and this difference in temporal filtering is largely inherited from the cones themselves¹¹. (ii) Due to a private one-to-one line of communication between a single cone and an MGC in the fovea, the pooling of signals from multiple cones necessary for post-receptor adaptation is missing and we predict light adaptation in the cones to dictate light adaptation at the level of foveal MGCs^4,57,58. (iii) If the luminance-dependent acceleration of foveal MGC responses is smaller than in peripheral MGCs like we observe in the cones, then it may be likely that the slower timescale of cone adaptation in the fovea is also inherited by the foveal MGCs. Furthermore, given that foveal MGCs lack synaptic inhibition¹¹, a common mechanism of gain control and temporal filtering, adaptation in the foveal midget pathway may be largely dictated by cone adaptation rather than downstream circuit mechanisms. Future studies will be essential to test these predictions and reveal differences in receptor vs post-receptor mechanisms of light adaptation between the fovea and the rest of the primate retina.

Linking cone physiology to perception

To understand how the performance of human daylight vision is governed by properties of cone function, we need to estimate both signal and noise inherent in the cone responses. Even though measurements of absolute behavioral thresholds vs background luminance for human cone-mediated vision are derived from studies that target foveal vision, most of what we know about properties of cone signal and noise in the primate retina comes from studies in the peripheral primate retina^5,12,14–18. Despite this regional discrepancy, previous cone recordings in the peripheral primate retina have suggested that the decrease in behavioral sensitivity with increasing luminance follows Weber's law^5,12. This is because adaptation may be entirely driven by signal adaptation against a relatively fixed level of noise from the CNG channels, which is independent of background luminance⁵. In light of our findings which reveal that cone signal adaptation is distinct between the peripheral retina and the fovea, a systematic analysis of noise in foveal cones and its luminance-dependent adaptation is required to determine the fundamental limits imposed by cone signal and noise on the sensitivity of high-definition foveal vision. Despite this gap, our estimate of background luminance that halves the cone response gain in the fovea (~2000 R^*/cone/s) is close to previous psychophysical measures of half desensitizing luminance (1–2 log td) which suggest that signal adaptation in foveal cones might dictate behavioral adaptation of foveal vision⁵⁹.

Finally, what is the perceptual and behavioral significance of a weaker and slower cone adaptation in the fovea compared to a stronger and rapid adaptation in the peripheral primate retina? Our high acuity foveal vision has evolved for resolving fine spatial and chromatic details which perhaps require the cones in the fovea to have a slower response kinetics so that they can integrate more photons over an extended time period akin to using a longer exposure time in a digital camera when acquiring high-resolution images. The integration time of foveal cones also seems to change less across luminance than peripheral cones which leads to a net “weaker” light adaptation. This allows foveal cones to maintain a higher sensitivity over a range of light levels than peripheral cones. In addition, a slower time scale of adaptation enables foveal cones to maintain a higher sensitivity for a longer duration. Such differences in adaptive filtering of signals between foveal and peripheral cones suggest a regional optimization in cone integration times for maximizing spatial over temporal sensitivity in the fovea and vice-versa in the periphery. In the periphery, a faster time scale of adaptation in cones might be better suited to meet the demands of the higher temporal sensitivity of peripheral vision such that it is able to detect rapidly changing inputs such as those encountered during motion^19,60. Another functional reason for a stronger and quicker luminance adaptation could be because of a potentially smaller dynamic range of signaling in peripheral cones than in foveal cones. Thus, to avoid saturation, adaptation occurs sooner and at lower light levels in peripheral cones.

Weaker and slower adaptation in foveal cones could be particularly well-suited to maximize sensitivity for efficient encoding during the fixations between saccadic eye movements, when the gaze is stationary. In fact, the typical duration of fixation (300–500 ms)^31,61 seems better matched to the slower response kinetics, slower acceleration of response kinetics with luminance, and slower time course of gain adaptation in foveal cones than that of peripheral cones. Overall, our results uncover an elegant strategy employed by the primate retina: to fine-tune light adaptation in the foveal cone photoreceptors such that higher sensitivity is achieved at the expense of speed, thus meeting the demands for maximal encoding of high-definition information between saccadic eye movements.

Methods

Tissue preparation and electrophysiology

Electrophysiological recordings were performed on primate retinas from the Tissue Distribution Program of the Wisconsin National Primate Research Center (WNPRC) and Washington National Primate Research Center (WaNPRC). Recordings were made from isolated retinas from Macaca fascicularis, Macaca nemestrina, and Macaca mulatta of both sexes, aged 2 through 20 years. All primate tissue use was done in accordance with the University of Wisconsin and the University of Washington Institutional Animal Care and Use Committee. Tissue was obtained and prepared as described previously^11,12. In brief, dark-adapted (>1 h) retina stored in warm (~32 °C), oxygenated Ames medium was placed photoreceptor side up on a poly-lysine-coated coverslip (BD Biosciences) that served as the floor of our recording chamber. Throughout recordings, the retina was continuously perfused with warm, oxygenated Ames solution. After identifying the foveal pit in the retina, recordings were made from the inner segments of cones that were within 0.5 mm of the pit (fovea) and >6 mm from the pit (peripheral retina). Whole-cell patch-clamp recordings were performed from individual cones in the current-clamp configuration (holding current = 0 pA) to measure light-evoked voltage responses^11,12. Data were low pass-filtered at 3 kHz, digitized at 10 kHz, and acquired using a Multiclamp 700B amplifier. All recordings were controlled using the MATLAB-based Symphony Data Acquisition Software, a piece of open-source electrophysiology software (https://github.com/symphony-das). To study the role of HCN channels in shaping light adaptation, a specific blocker of HCN channels, ZD7288 (Sigma-Aldrich), was diluted in oxygenated Ames solution at a concentration of 0.1 mM and applied to the bath solution. This was followed by light-evoked whole-cell recordings from peripheral cones. To isolate the HCN‐mediated currents voltage-clamp recordings were performed in cones which presented voltage steps from −80 to −10 mV, in increasing steps of 10 mV from a holding membrane potential of −60 mV. Membrane potentials reported in this study have not been corrected for the liquid junction potential. S cones in the peripheral macaque retina were identified and targeted for whole-cell recordings, to measure adaptation dynamics (Fig. 6D, G), based on previously described morphological features⁶².

Light stimulation

Stimuli were presented using computer-driven LEDs with peak wavelengths of 410 nm, 505 nm, and 650 nm to allow effective stimulation of all 3 cone types. Data presented in this study is from green (M) or red (L) cones except in Fig. 6, Supplementary Figs. 4B and 6 which present results from blue (S) cones. Light stimuli covered a ~500 μm disk centered on the cell being recorded from. All stimulus protocols were generated using custom-written MATLAB-based extensions of Symphony Data Acquisition Software and delivered at 10 kHz. To determine cone isomerization rates, we used measured LED power output, measured LED spectra, primate photoreceptor spectra from Baylor et al.⁶³, and an effective collecting area of 0.37 μm^2 18. For comparison with perceptual studies, one photopic troland (td) is assumed to be 10–30 R^*/cone/s^18,64.

Cell selection criteria

Cells for data collection were included based on the magnitude of their responses to a flash of bright light. Cones with flash responses >8 mV were selected. These assumptions were based on previously described criteria¹¹. These criteria help us limit our analysis to cells whose responses are representative of primate cone responses in vivo. We also limited our recording time to 4 mins post breaking into the cell to prevent washout of intracellular components, which affects response quality^5,11,12.

Analysis

All analysis was performed using custom-written MATLAB and Igor Pro analysis routines. Data in Fig. 6A–C and Supplementary Fig. 6 were obtained and re-analyzed from a previous study, ref. ¹².

Flash response analysis

Time to peak, peak amplitude, full width at half maxima, and area under the curve were calculated from a cell’s average response to repeated brief flashes of light. In some cases, especially for lower background light levels, we used a fitting-based approach to account for any noise in the responses around the peak to estimate the peak amplitude and time to peak as described previously¹².

Weber adaptation curves

Average responses to a light flash for each cell across different background light levels were first converted to gain i.e., response amplitude per isomerization (mV/R^*), by dividing the peak amplitude by the light intensity. Similarly, we also computed the integrated response gain by estimating the area under the curve of the voltage response and then dividing it by the flash intensity. In both cases, the response gains across different background light levels were normalized to the response gain in darkness. This normalized gain curve across the background light level was then fit with the Weber–Fechner function^5,12 described by the equation below:

$$\frac{{\gamma }_B}{{\gamma }_D}=\frac{1}{\left(1+\frac{I_B}{I_0}\right)}$$ 1

where γ_Β is the gain at a given background (in mV or mVs/R^*), γ_D is the gain in darkness (in mV or mVs/R^*), I_B is the intensity of the background illumination (in R^*/s), and I₀ is the background light where gain decreased by 50%. We obtained the best-fit values through automatic fitting routines in Matlab (nlinfit and lsqfit).

Adaptation timescale analysis

The time scale of adaptation analysis followed a structure similar to what was described previously^5,26. Brief flashes were delivered with variable delay with respect to the onset/offset of a light step. Raw data was smoothed with a Savitzky–Golay filter with a 50 ms window to help with isolating responses. Responses to the flashes were isolated by subtracting the response to the step alone. Flashes were delivered before the step and well after the step to obtain unadapted responses. A flash delivered before the step offset was used as a fully adapted response.

Isolated responses were fit with a slanted-gaussian to approximate the response amplitude:

$$R\left(x\right)=a{e}^{-\frac{{\left(x-b\right)}^2}{2c^2}}+mx+d$$ 2

Response amplitudes were divided by the flash intensity to calculate the gain for that response. All gain values were normalized by the unadapted response (pre-step for onset, post-step for offset). To approximate the timescale of adaptation for the step onset, a plot of normalized gain vs time-from-onset was constructed. The peak time of each response (the variable “b” in the slanted Gaussian) was subtracted by the time of step onset to obtain the abscissa values for the plot. The unadapted response was placed at t = 0. The offset plot was made in the same way except the response times were subtracted by the time of step offset, and the adapted response was placed at t = 0. Both plots were fit with a monophasic exponential function and the timescale parameter was extracted from the fit.

Statistical analysis

We used the unpaired t-test for all the statistical analyses except in Fig. 1 D, F where a one-sample t-test was used. Error bars indicate SEM. The significance threshold was placed at α = 0.05 (n.s., p > 0.05; *p < 0.05; **p < 0.01; and ***p < 0.001). For figure panels with multiple comparison groups, we performed multi-way ANOVA with multi-way comparison depending on the number of conditions compared.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

The experiments were conceived and designed by R.S. and J.B. All electrophysiology experiments were conducted by R.S., J.B., and A.S. Data were analyzed by A.S., T.B., and R.S. R.S. wrote the manuscript with feedback from all the authors.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

Source data are provided with this paper. All other data are available from the lead contact, Raunak Sinha (raunak.sinha@wisc.edu), upon request. Source data are provided as a Source Data file. Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53061-3.