Time delayed fractional diabetes mellitus model and consistent numerical algorithm

Abstract

The diabetes mellitus model (DMM) is explored in this study. Many health issues are caused by this disease. For this reason, the integer order DMM is converted into the time delayed fractional order model by fitting the fractional order Caputo differential operator and delay factor in the model. It is proved that the generalized model has the advantage of a unique solution for every time t. Moreover, every solution of the system is positive and bounded. Two equilibrium states of the fractional model are worked out i.e. disease free equilibrium state and the endemic equilibrium state. The risk factor indicator, R₀ is computed for the system. The stability analysis is carried out for the underlying system at both the equilibrium states. The key role of R₀ is investigated for the disease dynamics and stability of the system. The hybridized finite difference numerical method is formulated for obtaining the numerical solutions of the delayed fractional DMM. The physical features of the numerical method are examined. Simulated graphs are presented to assess the biological behavior of the numerical method. Lastly, the outcomes of the study are furnished in the conclusion section.

Introduction

Diabetes is a metabolic disease caused by ineffective regulation of the body’s supply of glucose. This happens when the body does not use the insulin that is produced by the pancreas, or when the amount of insulin released by the beta cells in the pancreas is inadequate. As a result the biological system does not work properly, which causes abnormal blood glucose levels^1–3. The pancreas and the liver regulate insulin and glucose synthesis, respectively, to keep glucose levels regular. This process is known as the glycose-insulin regulation system, and it is essential for preserving general health. The pancreas secretes insulin, which is necessary for glucose to be used as fuel by cells. When this system does not control insulin, the blood sugar levels rise, which can lead to diabetes because of either inadequate insulin or insulin resistance. Diabetes can cause several long-term health issues. Diabetes that is not under control might produce life threatening complications. Most diabetic cases are not recognized at the early stages globally, and complications frequently occur when diabetes is not immediately diagnosed or controlled. Diabetes-related problems fall into two categories, acute complications need immediate medical intervention, and chronic complications develop gradually. Diabetes is associated with a higher risk of infections, cognitive and mental disorders, blindness, renal failure, and cardiovascular disease. It results in abnormal blood circulation in the extremities, loss of sensory and motor function, as well as impeded wound healing. Cardiovascular disease and chronic renal disease are the two main killers of diabetics patients^4,5. Obesity, smoking, aging, and a low-fiber diet are common risk factors for diabetes⁶. Diabetes has been linked to both Group B streptococci and TB, two illnesses that frequently coexist with diabetes^7,8. Diabetes and TB can interact to slow down healing and increase the chance of mortality, resistance, and recurrence⁸. Furthermore, diabetes and the HIV co-occur, which increase the risk of premature deaths⁹. Death rates associated with diabetes are rising, despite declines in other non-communicable illnesses such as cancer, stroke, and cardiovascular disease¹⁰. In 2010, the World Health Organization (WHO) reported that diabetes, excluding fatalities from cardiovascular disease and chronic renal disease, was responsible for 2.8% of all deaths globally. Worldwide, diabetes was linked to 13% of stroke deaths and 21% of deaths from coronary heart diseases¹¹. Moreover, the International Diabetes Federation (IDF) revealed that diabetes is a contributing factor in 5 million adult deaths yearly, or 8.4% of all fatalities globally^12–15. In different fields of study, fractional and delayed fractional systems are useful for simulating intricate dynamic behaviors. Their contributions to the study and prediction of real-world occurrences in several scientific and technical domains are noteworthy as they provide valuable insights into systems that exhibit memory effects, temporal delays, and non-local interactions. Due to continuous investigation into the mathematical underpinnings its real-world applications across several fields, became larger are increasing rapidly^18–23.

Classical delay differential equations (DDE) based mathematical models are useful, especially when the description of the systems under investigation relies not only on the system’s current condition but also on its historical status. Different kinds of DDEs exist, each with a unique kind of delay, including time-dependent, neutral, stochastic, constant, and state-dependent delays. In many applied disciplines, including biology, electrical networks, life science, environmental sciences, mechanics, physiology, and population dynamics, DDEs play crucial role^24–26.

Although delays are ubiquitous in real-world systems and the study of DDEs has attracted attention, FDDEs are a relatively new field of research. A generalization of the DDE to any non-integer order is the FDDE. For modeling real-world challenges, FDDEs have garnered significant attention due to their ability to produce large effects with minimal delays. Many, delay fractional mathematical models are used to incorporate the real world phenomenon in many fields of sciences and engineering’s. Moreover, many numerical methods are applied to solve the mathematical models^27–33.

Recent research has thoroughly examined the intricacies of epidemic models with generic incidence functions, providing new understandings of delayed optimum control and stochastic bifurcation³⁴. Similarly, dynamic nature of hepatitis B model, which is a severe health concern in the global community is studied in³⁵. The study of complex behaviors in multifaceted systems such as numerical analysis of mathematical models of fractional-order drinking in³⁶. In³⁷ a fractional mathematical model specific to allergies caused by antacids under the fractional mathematical models to explain the complexity of food allergies.

The unpredictability of real-life scenarios, a nonlinear stochastic cholera epidemic model under the influence of noise is studied in³⁸. New studies in³⁹ reveals that comprehending the dissemination of worms in WSNs has become contingent on stochastic models. Using harmonic mean type incidence rates to model the COVID-19 pandemic may help to capture the fractional character of its dynamics and stability⁴⁰. Computer virus spread are modeled using deterministic and fractional approaches⁴¹. Vaccination and asymptomatic carriers are incorporated into fractional-order epidemic models⁴².

To study computer virus transmission, fractional and deterministic methodologies are adopted in⁴³. Thus, the harmonic mean type incidence rates are useful for constructing any epidemic models, the model studied in⁴⁴ for rabies, for the theoretical and numerical analysis. The important information on the dynamics of the COVID-19 epidemic using actual data and fractional modeling, in particular with the help of the ABC operator in⁴⁵. An investigation of nonlinear dengue epidemic model is made on the basis of deterministic and fractional techniques⁴⁶. To highly non-linear epidemic model, including the ones mentioned for Cutaneous Leishmania⁴⁷. The dynamics of cholera spread has been properly studied and eradicated using generalized fractional derivatives⁴⁸. The model of HIV/AIDS on control theories and bifurcation analysis are studied in⁴⁹. The process of bifurcation analysis and fractional optimum control model have improved the dynamics of transmission of the Human Syncytial Respiratory Virus⁵⁰.

The research work on modeling and analysis of the direct transmission of cholera and HIV and their optimum control is studied in⁵¹. The bifurcation analysis have been employed to study the dynamic transmission of co-infections including cholera and HIV, significant results in⁵². The study of viral infections dynamics in light of innovations in fractional order model for the Hepatitis C virus in⁵³. The SIR models with fractional order derivatives⁵⁴ have explained the impact of treatment cure rates on the spread of the disease. The dynamics of hepatitis B viral infections is studied for generalized fractional model in⁵⁵. Viral model covering lytic and non-lytic adaptive immunity have constituted a strongly extensive overview of immune reactions⁵⁶.

In this article, we examine many facets of viral propagation inside a time delayed fractional order DM model. An integer order model is not sufficient to capture the intricate dynamics of viral propagation, particularly when the current state of the system has to be represented by considering prior stages. Alternatively, by accounting for memory effects and the history of state variables, fractional order derivatives provide a deeper insight to the disease phenomenon. This advancement enables a more thorough and accurate analysis of disease propagation.

The rest of this work is as follows, in “Preliminaries” provides a quick summary of key definitions of non-integer order calculus. “Model conversion to fractional delay” introduces the dynamics of the diabetes mellitus model for non-integer order instances, as well as local stability analysis with the existence and uniqueness of solution. “Numerical results” introduces a novel numerical approximation technique for addressing the suggested fractional derivatives model. In this section, we present numerical experiments that demonstrate the dynamics under consideration for several orders of fractional derivatives.

Preliminaries

We presented basic definitions from fractional calculus^9,16,17,23.

Definition 2.1

The gamma function is defined as,

.

Definition 2.2

Let (0, t) with where (0,t) is a finite interval. Then Caputo fractional derivative is,

, is called Caputo fractional derivative.

Where is the arbitrary or non-integer order of the derivative.

Remark 2.3

The Mittage-Leffler function is described as,

.

Remark 2.4

The Mittage-Leffler function in two variables is defined as,

.

Definition 2.5

The biologically feasible region for the system is defined as,

, which is positively invariant.

ABC operator⁵⁷

The fractional derivative operator proposed by Atangana-Baleanu, characterized by a non-local and non-singular kernel for a function of is expressed as,

.

Caputo-Fabrizio operator⁵⁷

The fractional derivative operator proposed by Caputo and Fabrizio, characterized by exponential and non-singular kerel for a function of , is defined as,

.

Classical model of DM

For studying and evaluating diabetes model is the most effective way to better understand the processes underlying the disease and forecast its course. Because of this, we will examine the following diabetes mellitus model in this research¹,

Subject to initial conditions of the form

Model conversion to fractional delay

The state variables in the model are P(t), Q(t), X(t), and Y(t) which describe the sensitive, exposed (pre-diabetic), infected without treatment, infected with treatment individuals respectively, and the parameters are enlisted below. Numerous critical parameters are important in the context of population dynamics and disease transmission. The number of people born within a certain period is represented by the symbol , which indicates the birth rate. On the other hand, represents the total number of fatalities in the population during a certain period, which represents the mortality rate. The case fatality rate, or percentage of a certain disease’s affected population that eventually passed away, is indicated by the δ. The , describes the disease-related mortality rate while taking treatment effects into account. The product of δ and indicates the rate of disease transmission, in the absence of therapy, from pre-diabetic to diabetic. Finally, shows the risk factor causing disease. Each of these parameters plays a crucial role in the overall dynamics and outcomes of the system under consideration and is the time delay factor. Placing Caputo fractional derivative instead of integer order derivative in¹, the time delayed fractional DMM is represented by system (1). Where is the fractional order parameter.

1

,

where initial conditions are,

.

Theorem 3.1

For any initial positive values, the system (1) is positive invariant in .

Proof

Consider the 1st equation of the system (1),

,

,

Taking Laplace Transformation

,

,

. Now applying the Laplace inverse

,

,

,

.

Similarly, the positivity results holds for other equations of the system (1).

Theorem 3.2

For every time t, the solution of the system (1) will exist and the solution will be unique.

Proof

Define the region as,

Let ,

then, ,

,

,

.

Therefore (P) satisfies the Lipchitz condition. Moreover, for contraction mapping

.

Let, .

Similarly, we have,

Let, .

Therefore,

,

for, , are contraction mappings.

Therefore, , satisfy Lipshitz conditions. Therefore, according to Banach’s fixed point theorem, the unique solution of the time delayed fractional differential system exists.

Theorem3.3

For positive initial conditions, the system (1) is bounded for all t [0, t_m).

Proof

Consider,

,

,

,,

.

Taking Laplace transformation

,

,

.

Now applying Laplace inverse transformation, we get

,

,

,

let .

Then we have,

.

As ,

,

,

.

Which completes the result.

Equilibrium points

The infection free points of the DMM is listed below,

, and endemic equilibrium points is . Where

,

,

,

.

Risk factor indicator ()

The of the DMM is calculated with the help of next-generation matrix theory and is given as below.

Let us consider the translation and transmission matrix from the system (1) as,

, and

,

.

Where is the spectral radius of ,

.

Sensitivity analysis of R0

Sensitivity analysis helps to understand how the parameters effects the R_0. For this, we proceed as follows

,

,

,

,

,

.

The parameters increase the risk factor , while decrease the risk factor of time delayed DMM.

Theorem 3.7

The disease-free equilibrium is locally asymptotically stable if and unstable if.

Proof

Using the system (1), finding partial derivatives and applying disease-free equilibrium point in it. We have

.

The eigenvalues of the above matrix are described as follows,

Numerical eigenvalues of the system (1) are,

-0.1387.

-0.2052.

-1.1387.

-1.1365.

This shows that all the eigenvalues are negative, so the system is locally stable.

Lemma 3.8

Let be a continuous function, and let. Then for anytime, and, then following inequality hold.

.

Theorem 3.9

The system is globally asymptotically stable at disease-free equilibrium point, if .

Proof

Consider a Voltera-type candidate Lyapunov function,

,

,

By using Lemma 3.8, .

,

,

.

Using DFE point,

.

Hence, using LaSalle’s invariance theorem, the system (1) is globally asymptotically stable.

Theorem 3.10

The system is globally asymptotically stable at the endemic equilibrium point if, if .

Proof

Let a Voltera-type candidate Lyapunov function be,

where are the endemic points.

.

Since, .

,

.

Here we set , so we have

.

Hence, by LaSalle’s invariance theorem, the system (Eq. 1) is globally asymptotically stable.

Numerical results

In this section, we develop the numerical scheme and will check its positivity and boundedness.

Hybridized numerical scheme

Here we will formulate the Grunwald Letnikov finite difference scheme for the system (1), the Grunwald-Letnikov approximation [23] is described as,

.

Now we will consider the 1st equation of system (1) and proceed as given below,

.

Some straight forward calculations exhibits that,

.

Similarly, the other equations will be as follows,

,

,

.

Lemma 4.2

Suppose that all the state variables and control parameters are non-negative with Then .

Proof

Consider the form,

.

For ,

.

Since all the parameters are positive.

Therefore

By following the principle of mathematical induction we reach at the conclusion, that

.

Similarly,

Hence the proposed numerical scheme preserve the positivity property for .

Lemma 4.3

Suppose that are finite and positive, i.e. Then, .

Proof

Consider,

,

,

For ,

,

.

For ,

,

.

Similarly for .

.

Finally, we have .

Numerical experiment

In this section, we have performed the numerical example. For this, the parametric values and intial data is listed in Table 1.

Table 1.

The biological assumptions for the underlying model are as, the homogeneity of the population, and constant birth rate and natural death rate.

Parameter symbol	Parameter values Per person per day	Source
	0.9	1
	0.13869	1
	0.0009	1
	0.06654	1
	1	1
	0.5	Assumed
	2	Assumed
	0.88187	1
	0.9, 0.85,0.8,0.75	1
P(0)	20,000	Assumed
Q(0)	8000	Assumed
X(0)	4000	Assumed
Y(0)	3000	Assumed

Simulated graphs

The simulated graphs for the above test example are given below.

Graphical discussion

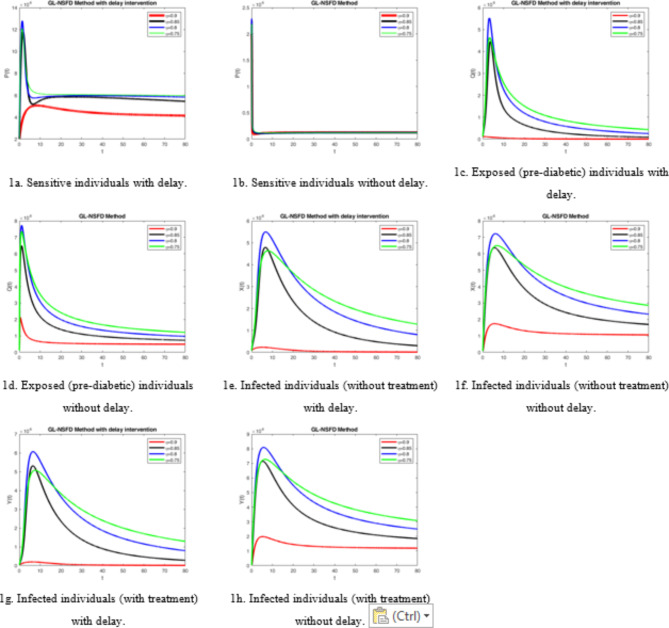
In this section, we have presented the simulated graphs for the better perception and progressive behavior of the state variables involved with underlying model (when ). The graphs are plotted with and without delay factors. First, we explain the graphical behavior of the sensitive populace in Fig. 1a and b. The graphs in the Fig. 1a reflects that the number of sensitive individuals are greater as compared with the sensitive populace, when the delay factors are not adopted biologically and physically. The different trajectories of the graph illustrate the role of , the fractional order parameter. The different values of the show that the greater value of , the graph converges fastly towards the endemic equilibrium point. The value of risk factor indicators R₀ is greater than one. When the value of is smaller than the rate of convergence is slower. Similarly the graph in Fig. 1e and f reveals the progressive behavior of the exposed (pre-diabetic) individuals with delay and without delay factors.

Fig. 1.

Simulated graphs at endemic equilibrium point.

The graphs in Fig. 1c and d illustrate the dynamical behavior of the exposed (pre-diabetic) i.e. the number of pre- diabetic individuals decrease when the delay factors are adopted, while other parametric values are kept fixed for both the cases. Infected when the individuals, do not follow the diet plan, spends the sedately life style and do not take the proper treatment, then the risk factor of the diabetic mellitus increases. On the other hand, the populace size of the infected individuals increases who do not take the treatment. So, when the delay-strategies are adopted without treatment, the number of infected individuals decreases considerably. On the contrary, the number of individuals are greater when the delay factors are followed physically and biologically but the treatment is not taken. In the last two figures Fig. 1g and h, we have considered the infected with treatment for both with delay factor and without delay factor. When delay factors are considered along with the treatment factor, the number of infected individuals may be reduced up to the specific level. While, the size of infected populace with treatment in the absence of delay strategy is large, which shows that the delay factor plays a significant role in controlling the diabetic mellitus.

Similarly, the graphs at the disease free equilibrium point can be explained in the biological background (when ). For instance, when the precautionary measures i.e. diet plan, physical activities, socio economic conditions are considered, the diabetic mellitus patients become zero s shown in Fig. 2b. Similarly, all other classes in Fig. 2c and d become zero except the sensitive class represented by Fig. 2a whose value is .

Fig. 2.

Visualization of the disease-free equilibrium point.

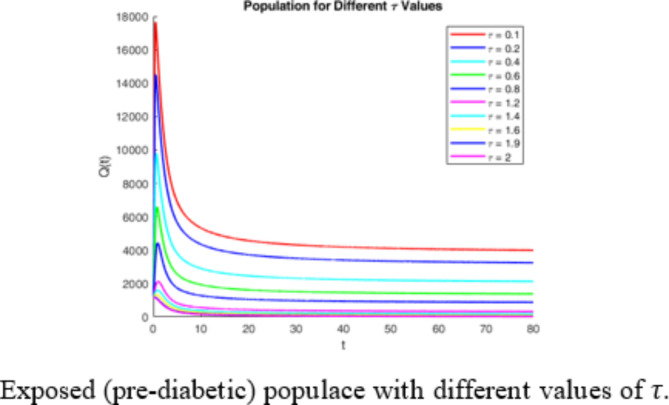
Figure 3 reveals the role of delay factor in controlling the diabetic mellitus. The different graphs are plotted against the different values of as mentioned in the Fig. 3. The graph exhibits that when the value of increases i.e. the various diabetic controlling factors are followed the exposed (pre-diabetic) case decrease. Therefore, by adopting the maximum possible control factors, the exposed class may be reduced, remarkably.

Fig. 3.

Effect of delay parameter on exposed (pre-diabetic).

Conclusions

In this work, a classical integer order model is successfully converted into the time delayed fractional diabetes mellitus model for analyzing the disease dynamics. The fractional Caputo differential operator and some appropriate delay factors are included in the model. It is investigated that the governing model has a unique solution, which is also positive and bounded. Moreover, the initial values of the state variables do not affect the steady state of the model. So, the model is mathematically stable, well-posed and biologically in line with the disease dynamics. Therefore, this model is suitable for investigating the DM disease phenomenon. Also, the time delayed fractional system has two steady states i.e. disease free and endemic equilibrium. It is examined that the system is locally and globally stable at these steady states. The risk factor indicator is computed analytically for the model and described biologically that if the diet, physical activities, socio economic conditions and similar factors are ignored, the risk of DM increases and vice versa. Mathematically such situations, the numeric value of exceeds one and the sensitive individuals become pre-diabetic and ultimately to diabetic. So, the role of is very crucial in describing the disease dynamics and DM control strategies. In addition, the exact solution of the model cannot be found. To overcome this issue, a hybridized numerical scheme, coined as GL-NSFD scheme is designed to find the numerical solution of the model. The formed scheme provides with the positive and bounded approximate solutions to the said model. The simulated graphs illustrate the positivity, boundedness and converges towards the exact steady states. A graphical comparison is made to detect the impact of delay factor. To this end, two types of graphs i.e. with delay and without delay are sketched. These graphs reveals the difference between the disease dynamics. Furthermore, the role of delay factor are graphically investigated and it is observed that the higher value of plays a significant role in fixing and controlling the disease dynamics. For further perspective, this model may be applied to study the dynamics of contagious diseases.

Author contributions

M.R. Conceptualization, Methodology, M.A.U.R: Software. Writing- Original draft preparation. M.R.: Simulations, Visualization, Z.I.: Investigation, analysis. N.A: Numerical computations, H.A.: results and discussion, S.N.: Revision, Reviewing, I.K.: Methodology, Writing- Original draft, software. All the authors reviewed the manuscript.

Data availability

Data used in this work is available from the corresponding author base on a reasonable request.

Declarations

Competing interests

The authors declare no competing interests.