Abstract
The reliable operation of railway embankments traversing degrading permafrost regions is challenged by climate warming. This study examines performances of four main types of railway embankments on the Qinghai-Tibet Plateau in thermally stabilizing permafrost foundation over warm permafrost using numerical modelling and 10-year monitoring data. Then, a reinforcement measure that combines a thermal conductivity variable system (TCVS) was designed to improve the cooling capacity of the crushed-rock sloped embankment (CRSE) by countering the heat absorption of slopes during summers. A coupled thermal-fluid-solid model was built to simulate and assess the cooling performance and reinforcing capacity of the new design. Results show that the crushed-rock embankments can produce convection cooling on the permafrost subgrade but the performances vary with different structures. The CRSE has insufficient cooling capacity to withstand the underlying permafrost degradation in warm permafrost regions. The optimized CRSE that combines the TCVS can effectively cool the underlying warm permafrost and decrease the shady-sunny slope effect under a warming climate, and can be used as an effective reinforcement measure. This study confirms the application of air-cooled embankments in protecting permafrost subgrade and provides guidance for structural design of embankment traversing degrading permafrost.
Keywords: Cooling performance, Cooling reinforcement, Crushed rock, Permafrost, Thermal conductivity variable system
1. Introduction
The world’ s greatest low-latitude permafrost region is found in the Qinghai-Tibet Plateau (QTP). Under the conditions of global warming and increasing human engineering activities, the heat balance in permafrost is broken, leading to an increase in permafrost temperature or melting, which in turn triggers diseases such as roadbed subsidence, pavement cracking and depressions, resulting in the destruction of roads and seriously affecting traffic safety [1]. The Qinghai-Tibet Railway (QTR) traverses about 275 km of warm sections with an average ground temperature exceeding −1 °C and 221 km of permafrost areas characterized by a high ice content [2]. The QTR stands as the inaugural transportation infrastructure planned in the permafrost area of the QTP, taking into account the impacts of climate warming [3].This railway employs a range of engineering measures including ventilation ducts, crushed rocks, sun-shadings and thermosyphons, to actively cool the roadbed and lower the temperature of warm permafrost by regulating the heat transfer mechanisms. This ensures the safety and stable operation of the QTR [4,5].
The crushed-rock embankment, an air-cooled technique, is the most commonly used subgrade for mitigating the impact of permafrost degradation, and its ability to protect permafrost has been verified by a large number of field tests [[6], [7], [8]]. The crushed-rock layer, serving as a porous medium with high permeability, varies in thermal conductivity due to natural convection in its pores. It accelerates winter heat extraction and facilitates summer heat transfer primarily through conduction [9]. The cooling mechanism of a crushed-rock embankment involves enhancing winter cooling efficiency and diminishing summer warming efficiency [10]. The crushed-rock layer strongly impacts permafrost distribution, potentially inducing permafrost development in areas with positive annual average temperatures [[11], [12], [13]]. The most common subgrade forms of QTR are traditional embankment (TE), crushed-rock basement embankment (CRBE), crushed-rock sloped embankment (CRSE) and U-shaped crushed-rock embankment (UCRE) [14], which are significantly different in terms of heat transfer processes [14,15].
At present, researchers mainly focus on the analysis results of field monitoring data and the reinforcement measures of cooling-roadbed embankments with different configurations since the operation of QTR [7]. Crushed-rock test conducted on the Alaska Highway in the United States has showcased outstanding cooling performance [9]. In the experimental section of the Beiluhe section of QTR, the crushed-rock embankment demonstrates efficient cooling, preserving the thermal stability of the permafrost underneath the subgrade [16]. 8 monitoring profiles of crushed-rock embankments were studied in QTR, and it is concluded that the cooling performance varies considerably between different roadbeds [14]. Ten years of monitoring data from three different types of embankment in QTR shows that crushed-rock structures exhibit a cooling impact, but are generally ineffective in warm permafrost areas [17]. Using the soil temperature monitoring data spanning the period from 2005 to 2015, the thermal dynamics of permafrost under roadbeds have been studied, and the results reveal that there are many variables affecting the cooling of crushed-rock embankments, such as the shady-sunny slope effect, the geological conditions of their location, and rainfall [18]. Amidst the challenges of global warming and the growing frequency of climate extremes, it remains uncertain if the crushed-rock embankments will possess adequate cooling capabilities in the future [19].
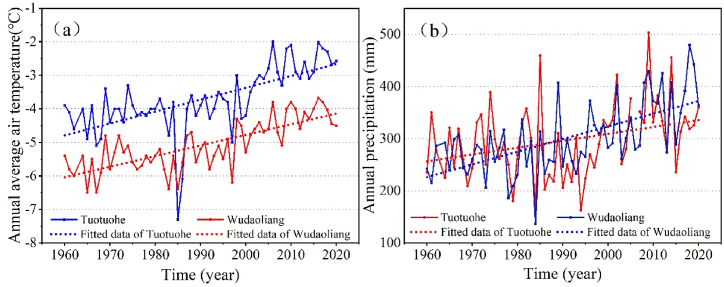
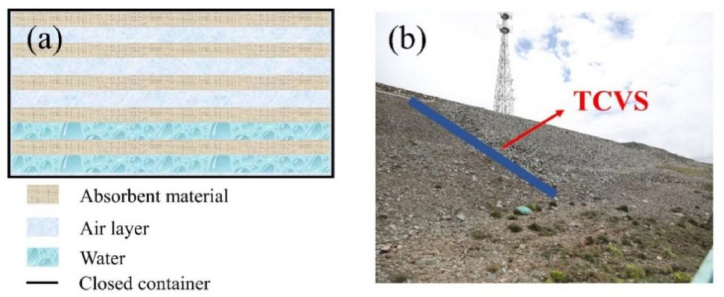
Since the initiation of the QTR in 2006, the subgrade in the permafrost zone has been stabilized as a whole, but there are still large settlement deformations in some sections [18]. Moreover, if no drainage measures are taken for the subgrade, the average annual settlement rate of both shoulders of CRSE is about 22 mm·a−1 [20]. Meanwhile, under the influence of the complex plateau environment, there is the problem of weathering of blocks stone and aeolian-sand (Fig. 1a and b), resulting in the blockage of porous media and weakening of convection cooling within the crushed-rock layer [21], and based on statistics, there are about 200 km of aeolian-sand road sections on the QTR [22]. Previous studies have indicated that in the permafrost region of the Qinghai-Tibet Railway, the large wind, cold temperatures, and strong radiation in the plateau area can cause sand and weathered rock debris to clog the rock layer, as well as burial, which results in a reduction in the porosity of the porous medium, consequently diminishing the cooling effect of the crushed-rock layer. This process can lead to the warming of the underlying permafrost, further posing a potential threat to the integrity and stability of the Qinghai-Tibet Railway [23]. In addition, the permafrost on the Tibetan Plateau confronts trials from climate warming [24]. As depicted in Fig. 2a and b, the annual average air temperature and annual precipitation in the Wudaoliang and Tuotuohe regions along the QTR have increased nearly 2 °C and 100 mm respectively over the past 60 years from 1960 to 2020. Research on the sensitivity of permafrost to climate warming indicates that by 2100, the average annual ground temperature of permafrost on the QTP is projected to rise by be 2.6 ± 0.3 °C, accompanied by an increase in the active layer thickness of by 3.0 ± 1.0m [24]. Therefore, under the impacts of climate warming, persistent attention must be directed towards ensuring the long-term safety and steadiness of the cooled subgrade in the permafrost zone along the QTR to guarantee its continued operation [[25], [26], [27], [28]].
Fig. 1.
Pore filling of crushed-rock embankments on the QTR. (a) Weathering of blocks stone at the Beiluhe section; (b) aeolian-sand damage at Honglianghe section.
Fig. 2.
Variations of air temperature and precipitation in Tuotuohe and Wudaoliang. (a) Annual average air temperature; (b) annual precipitation.
In this study, a coupled thermal-fluid-solid model for permafrost embankment was established, and then validated by field ground temperature data. Thermal performances of four main railway embankments including TE, CRBE, CRSE, and UCRE along the QTR, were numerically investigated based on the model. Cooling efficiency of the crushed-rock embankments was evaluated considering climate warming. Then, a reinforcement measure that combines the CRSE and a thermal conductivity variable device (TCVS) was presented to enhance the cooling efficiency of the embankment and weaken the shady-sunny slope effect. Numerical simulations are conducted to determine the cooling capacity and thermal characteristics of this new design. It is expected that this study provides essential guidance for protecting the subgrade in warm permafrost areas.
2. Numerical modeling
2.1. Study site
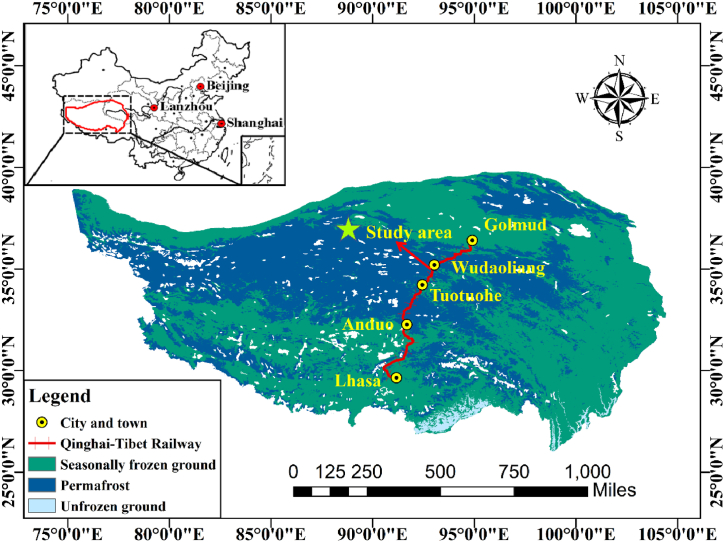
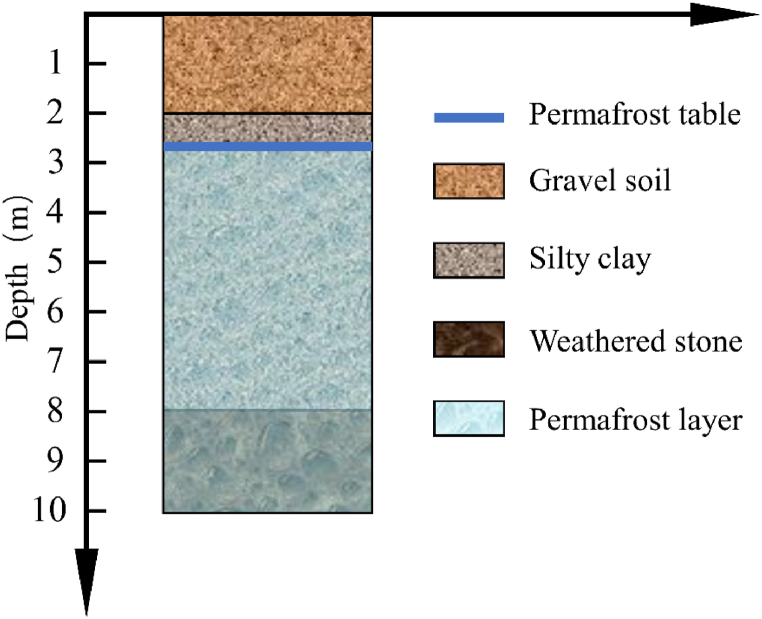
The embankments examined in this study are mainly concentrated in the Wudaoliang area beside the Qinghai-Tibet Railway, which is situated at an elevation of about 4600 m above sea level (Fig. 3). The climate is cold, and the permafrost warm is thaw-sensitive, with a ground temperature average of more than −1.0 °C every year. Based on the drilling investigation, In the Wudaoliang region, the range of the permafrost table is 2.5–3.0 m. We have installed a 10-m deep borehole located 30 m from the toe of the Qinghai-Tibet Railway embankment within the Wudao Liang study area. The results show that the stratum in this area is primarily composed of gravel soil, silty clay, and weathered mudstone (Fig. 4).
Fig. 3.
Location of study site in the permafrost area of the QTP. Data of permafrost distribution were from the China Cold and Arid Scientific Data Center (http://westdc.westgis.ac.cn/).
Fig. 4.
Geological conditions in the study site of Wudaoliang.
2.2. Computational domain
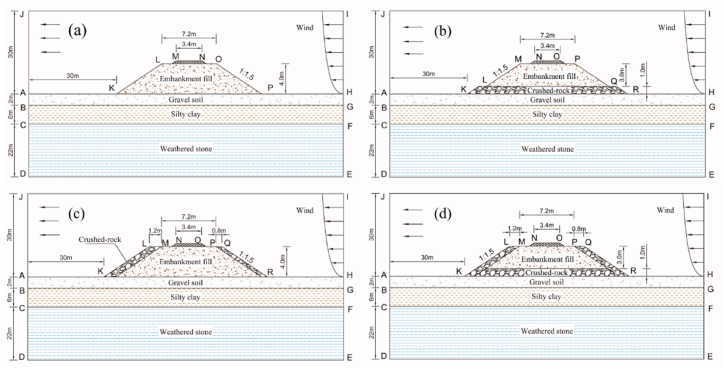
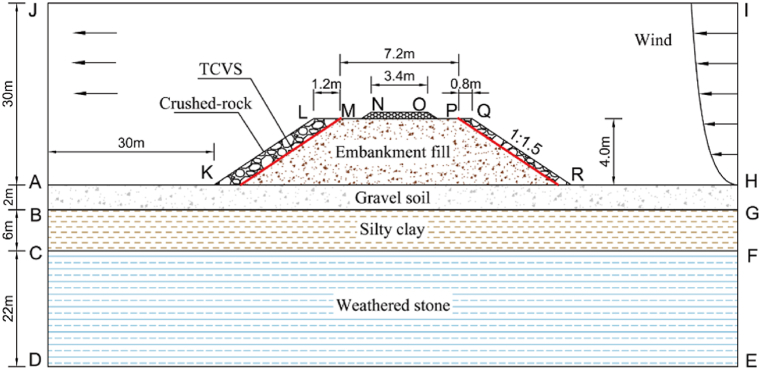
Considering the influence of external wind, a numerical model has been established for the subgrade of the QTR under open field conditions. Owing to the arid and gusty winter conditions prevalent in the QTP, the drifted snow is not taken into account [5]. This model is depicted in Fig. 5. Up to this point, the three primary categories of crushed-rock embankments have found extensive application in railways within permafrost zones. However, in certain sections, TE structural roadbeds have been employed. This choice is attributed to the more challenging implementation of cooling measures in these specific areas [18]. The calculation domain extends 30m above and below the natural ground and 30m horizontally from the base of the subgrade. The sunny slope side features a crushed-rock layer measuring 1.2m in thickness, while the shady slope side has a layer of 0.8m. The basement layer beneath the subgrade is 1.5m thick. The TE and the crushed-rock embankments are at 4.0m (Fig. 5a, b, 5c, 5d). The roadbed follows a slope ratio of 1:1.5. The geological composition of the lower part of the roadbed includes a 2.0-m layer of gravel soil, followed by a 2.0–8.0-m layer of silty clay, and below 8.0m, there is weathered mudstone.
Fig. 5.
Geometrical model of the computed embankments. (a) TE; (b) CRBE; (c) CRSE; (d) UCRE.
2.3. Governing equations
Given the diverse heat transfer properties exhibited by various media, three zones make up the calculation model of the embankment when it is under open conditions: air region, crushed-rock region and soil layer region, in which crushed-rock region is regarded as a porous media region [29]. To simplify the calculation, the gas is assumed to be incompressible, and the Boussinesq hypothesis is used, that is, only the density of air in the gravitational term is variable. The assumption is made that the porous medium is isotropic and in a state of local thermal equilibrium with the fluid within it. Based on the above basic assumptions, the governing equations of each region are stated as follows [[30], [31], [32], [33], [34]].
2.3.1. Air region
This region is a fluid region, and the following governing equation is used.
Continuity equation:
| (1) |
the variables and denote air speed along x and y axes, respectively (Eq. (1)).
Momentum equation:
| (2) |
| (3) |
where ρ is air density, p is air pressure and μ is dynamic viscosity (Eq. (2) and (Eq. (3)).
Energy equation:
| (4) |
where cp and λa are air specific heat capacity and air specific heat capacity, respectively (Eq. (4)).
2.3.2. Crushed-rock region
Given its elevated permeability, the designated area is treated as a porous medium in this computational analysis [35]. The thermal convection within the crushed rock entails an unsteady interplay of heat and mass transfer. In order to complete this computation, we consider only the movement of lacunal air. The governing equations are as follows: [36].
Continuity equation:
| (5) |
In Eq. (5), the components of air seepage velocity in the x and y directions are denoted by and , respectively [37].
Momentum equation:
| (6) |
| (7) |
where kr is permeability of rock layer, Br is the inertial drag coefficient (Eq. (6) and (Eq. (7)).
Energy equation:
| (8) |
In Eq. (8), and represent the equivalent volume heat capacity and equivalent thermal conductivity, respectively.
The Boussinesq hypothesis has been adopted to establish the correlation between air density and its temperature T [34]:
| (9) |
where is the thermal expansion coefficient of air (Eq. (9)).
2.3.3. Soil layer region
Since the heat conduction term during the freezing and thawing of soil is much larger than the convective term (about 2-3 orders of magnitude), the convective heat transfer within the soil can be disregarded in this scenario [38]. Therefore, the predominant mode of heat transfer within foundations and embankment fills is thermal conduction involving a phase change, and it can be expressed as Eq. (10) [32,34],:
| (10) |
Under the assumption that the phase transition occurs within a specified temperature range , the expressions for and can be derived using the sensible heat capacity method [30].
| (11) |
| (12) |
The subscripts f and u are used to denote the frozen and unfrozen areas, respectively. The parameter L corresponds to the latent heat associated with the phase change (Eq. (11) and Eq. (12)).
2.4. Thermal parameters
In the embankment model (Fig. 5), air, railway ballast, embankment fill, gravel soil, silty clay, and weathered stone are shown in order from top to bottom, with the location of the crushed-rock layer (CRL) varying according to the form of the subgrade.
The CRL possesses an average diameter measuring 0.25 m (with a diameter range spanning from 0.1 m to 0.3 m), an inertial resistance factor denoted as B = 333.60 m-1, and an intrinsic permeability specified as k = 1.50 × 10−6 m2 [33,34,39]. At an altitude of 4500 m, the air has the following characteristics: its density is 0.641 kg m−3, its specific heat is 1.004 × 103 J kg−1 °C−1, its thermal conductivity is 0.02 W·m−·1 °C−1, and its dynamic viscosity is 1.75 × 10−5 kg m−1 s−1 [40]. The thermal parameters of the relevant materials are given in Table 1 [30,36,41].
Table 1.
Thermal parameters of materials incorporated in the model.
| Physical parameters | (W·m−1·°C−1) | (J·m−3·°C−1) | (W·m−1·°C−1) | (J·m−3·°C−1) | L (J·m−3) |
|---|---|---|---|---|---|
| Embankment fill | 2.053 | 1.625 × 106 | 1.794 | 1.982 × 106 | 2.04 × 107 |
| Silty clay | 1.351 | 1.879 × 106 | 1.125 | 2.357 × 106 | 6.03 × 107 |
| Gravel soil | 2.610 | 1.863 × 106 | 1.910 | 2.401 × 106 | 2.32 × 107 |
| Weathered stone | 1.824 | 2.122 × 106 | 1.474 | 2.413 × 106 | 3.81 × 107 |
| Railway ballast | 0.346 | 1.006 × 106 | 0.346 | 1.006 × 106 | 0 |
| Crushed-rock layer | 0.442 | 1.016 × 106 | 0.442 | 1.016 × 106 | 0 |
| Air | 0.020 | 0.664 × 103 | 0.020 | 0.664 × 103 | 0 |
2.5. Boundary conditions
To streamline the computations, annual harmonic temperatures are directly applied to the air, natural ground surfaces, and embankment surfaces, and can be formulated by the following equations [34,42]:
| (13) |
where represents the average yearly surface temperature, denotes the annual amplitude of air temperatures, signifies the time, and represents the increasing rate of air temperature, set at 0.052 °C/year. This assumption is grounded on the projection that for the next 50 years, there will be a 2.6 °C increase in the mean annual air temperature [43]. This assumption is also based on the predictions from the IPCC Sixth Assessment Report (2021), which indicates that under a low emission scenario with robust mitigation measures, global temperatures could rise by 2.0 °C–2.6 °C.
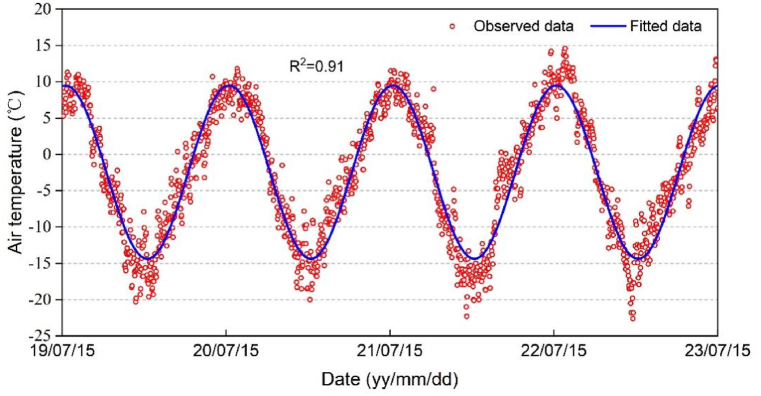
As shown in Fig. 6, from 2019 to 2023, we deployed meteorological stations in the study area of the Wudaoliang section of the Qinghai-Tibet Railway, conducted field observations and recorded temperature data. According to the analysis of the observed data, the results obtained after fitting with the sine function show that the R2 of the fitting function is 0.91, while the standard errors for and are 0.07 and 0.09, respectively for air temperatures. At the meantime, the coefficients and in Eq. (13), representing the temperature and natural ground boundaries, were determined through fitting the respective function.
Fig. 6.
Observed air temperatures at the Wudaoliang section of QTR.
Table 2 summarizes the sine function parameters for temperature pertaining to additional boundaries, specifically embankment surface, derived from the adherent layer theory [44] and relevant researches [34,42]. In the computational model, the heat flux at the lower boundary is assumed to maintain a constant value of 0.06 W m−2 and adiabatic conditions are applied in the lateral boundaries [36,40,45].
Table 2.
Thermal boundary parameters incorporated in Eq. (13).
| Boundaries | (°C) | (°C) |
|---|---|---|
| Air | −4.5 | 11.5 |
| Natural ground surfaces | −0.52 | 12.0 |
| Sunny slope shoulder | 2.18 | 9.29 |
| Shady slope shoulder | −1.24 | 12.58 |
| Railway ballast | 2.0 | 15.0 |
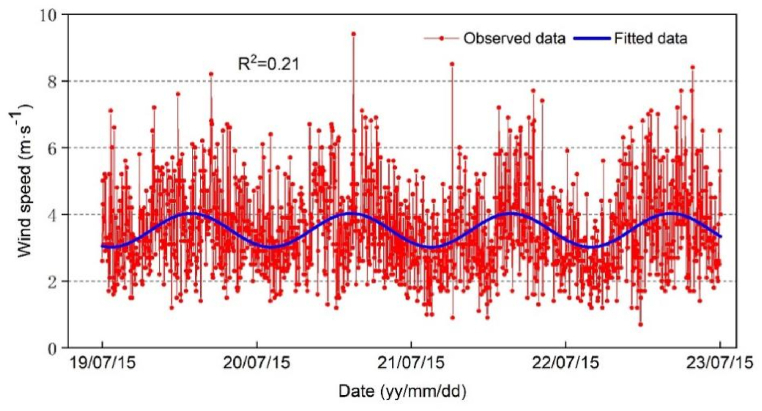
Thermal convection processes in rock layer is influenced by winds. In the Qinghai-Tibet Plateau, wind speeds are higher during the cold season and lower during the warm season. Consequently, more cold air enters the porous medium layer in the cold season, while less heat penetrates during the warm season, resulting in overall heat dissipation from the embankment. This allows more cold air to reach the permafrost beneath the embankment, thereby effectively protecting the permafrost foundation of the Qinghai-Tibet Railway. The observed wind speed at a height of 10 m in the Wudaoliang section of the QTR between 2019 and 2023, are shown in Fig. 7. These data were collected by the meteorological stations we deployed in the Wudaoliang research area. The results show that wind speeds were generally higher in winter and lower in summer, meanwhile, all boundary parameter values are derived from field monitoring. In accordance with the monitoring data and the power law governing wind profile [46], the prevailing external wind speed can be indicated as follows:
| (14) |
| (15) |
Fig. 7.
Observed wind speeds at the height of 10 m in the Wudaoliang of QTR.
In Eq. (14) and Eq. (15), and represent the wind speeds at 10 m and arbitrary height from the ground, respectively.
2.6. Initial conditions
The permafrost region of the Tibetan Plateau experiences extremely cold temperatures in winter, making construction impractical. Since the filling of the embankment was carried out during the hottest season and the embankment fill brought and transferred the most heat energy, it was postulated that the construction of the embankment would be finalized on July 15. The initial value for each soil layer of the foundation is established at −0.56 °C, derived from the average annual ground temperature observed at the test site prior to construction. Subsequent to this, a sequence of calculations is carried out to obtain the initial temperature distribution within the foundations as of July 15, employing a prolonged transient solution until a thermally stable condition is attained and the upper boundary (Eq. (13)) is determined, excluding considerations of global warming. If the calculated temperature field obtained on 15 July matches the observed temperature field closely, it will be employed as the foundational initial temperature field. The original temperature distribution within the embankment is established as a constant value based on that day's observations.
2.7. Model validation
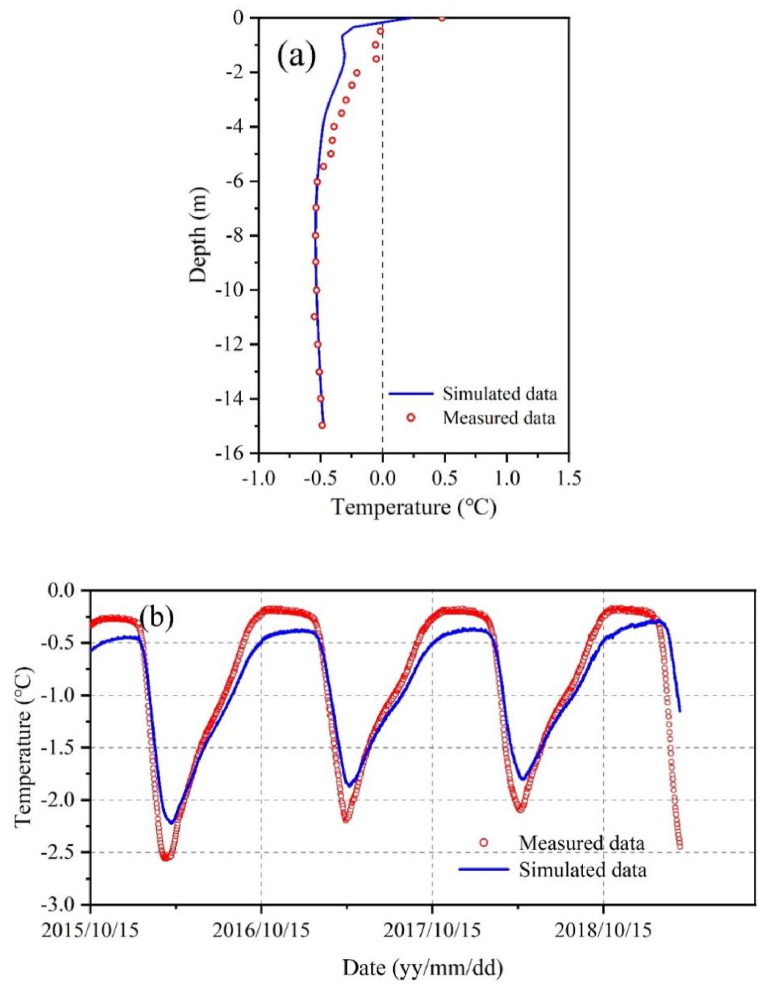
To confirm the modeling results, measured and simulated data are used to compare the centreline borehole profiles of the CRSE on 15 October of the 3rd year, as shown in Fig. 8a. After almost 3 years of service, the modeled ground temperatures exhibit a broad concurrence with the measured values, and there is a good agreement between the observed and calculated values for the annual average ground temperature and the permafrost upper boundary. However, there are also some differences in the part of the ground depth above 5m, which may be due to the streamlining of the boundary and geological environment. The long-term ground monitoring data of Wudaoliang (K1082 + 575) in the QTR permafrost area from 2015 to 2019 were also used to validate simulation results, as depicted in Fig. 8b, which indicates that the simulated temperature trend is similar to and can be well matched with the measured temperature curve changes, with a difference of about 0.3 °C at the extreme point, which may be due to the complexity of the plateau climate. The above comparison results show that the utilized model in this investigation can better reflect the cooling capacity of embankments and simulate the thermal evolution of different types of roadbeds on permafrost.
Fig. 8.
Comparison of measured and simulated ground temperatures. (a) Profiles of the CRSE centerline borehole from October 15 in 3rd service year; (b) temperatures at a depth of 2m beneath the embankment centre from October 2015 to March 2019.
3. Simulation results and analysis
The ground temperature of embankments in permafrost zones plays a crucial role in determining the stability of road embankments. Within permafrost areas of the QTP, the embankment typically reaches its maximum thawing depth in October annually, a parameter also designated as the permafrost table (PT) [34,47]. Hence, we simulate and compare the thermal state of four types of embankments (TE, CRBE, CRSE and UCRE) of the QTR within a 30-year post-construction timeframe, mainly analyzing the ground temperature distribution within the embankment on 15 October and variations in PT.
3.1. Ground temperature distributions
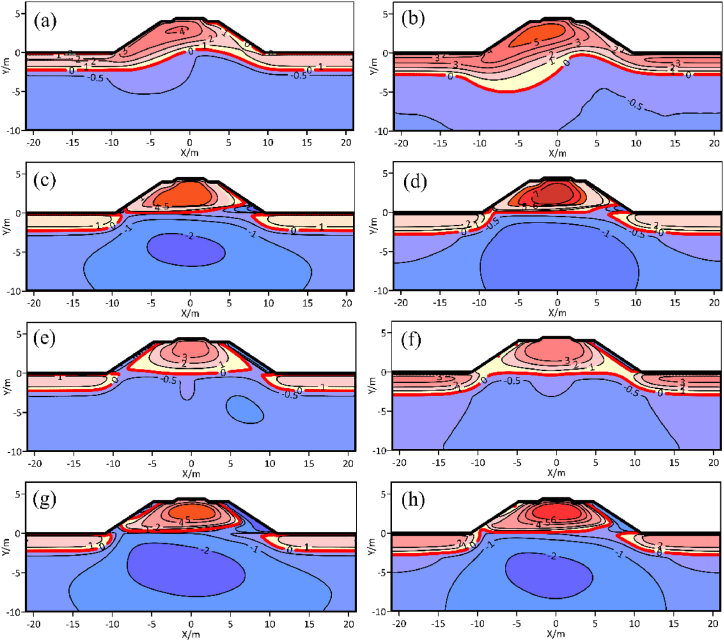
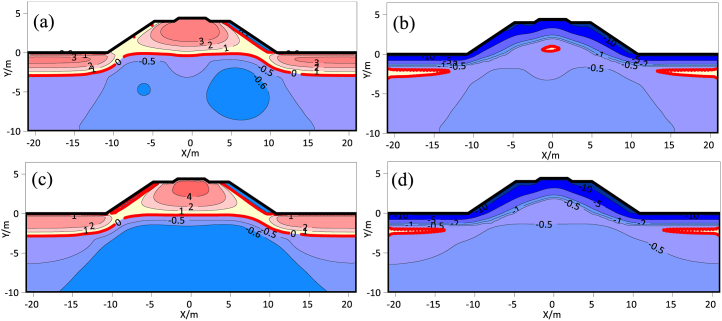
The temperature distribution differences of the four kinds of embankments on October 15, following construction, are depicted in Fig. 9. From Fig. 9a, it is evident that after the TE construction, the PT beneath the embankment was lifted to some extent due to the increased thermal resistance of the soil, but after the PT was lifted, an obvious warm permafrost layer larger than −0.5 °C appeared near the original PT, and the range of the warm permafrost layer was enlarged year by year along with the operation of the roadbed. Influence by the effect of the shady-sunny slope, the temperature field of the embankment has an apparent asymmetric distribution state, and the PT beneath the left shoulder is also significantly lower than beneath the right shoulder. Due to the absence of cooling effect, the ground temperature of TE shows a tendency to increase year after year. And the PT below the left shoulder also shows a decreasing trend, by the 30th year, the PT below the left shoulder has consistently remained approximately 1.5 m lower than that below the natural surface. A large range of warm permafrost above −0.5 °C appeared beneath the left shoulder. Therefore, the distribution of permafrost ground temperature field and the PT are detrimental to the stability of permafrost embankment, which presents a serious risk to QTR's continued safe functioning.
Fig. 9.
Geotemperature fields on October 15 in the 5th and 30th service year. (a) TE in the 5th year; (b) TE in the 30th year; (c) CRBE in the 5th year; (d) CRBE in the 30th year; (e) CRSE in the 5th year; (f) CRSE in the 30th year; (g) UCRE in the 5th year; (h) UCRE in the 30th year.
The distribution of the ground temperature field for the CRBE and UCRE roadbeds since the 5th and 30th years of operation at the period of maximum melting depth are given in Fig. 9c–d, Fig. 9g and h, respectively. It is evident that both types of crushed-rock structures show a good cooling effect, the temperature and PT distribution within the embankment demonstrate satisfactory symmetry, notwithstanding the impact of the shady-sunny slope effect. In the fifth year of roadbed operation, the part beneath the roadbed showed a −2.0 °C cold zone in addition to the −1.0 °C cold zone, and the range of the UCRE cold core was larger than that of the CRBE, which covering most part beneath the embankment and the surrounding areas. When the roadbed was in its 30th year of operation, the cold core still covered most part beneath the roadbed, although the range of the cold core was reduced owing to the influence of global warming. Therefore, CRBE and UCRE demonstrate enhanced capability in preserving the durability of the thermal stability of permafrost roadbeds.
From Fig. 9e and f, the distribution of the geotemperature of CRSE for the period of maximum thaw depth in the 5th and 30th year of roadbed operation are shown. After the 5th year of roadbed's utilization, the roadbed exhibits a cooling procedure from the side slopes, and the PT beneath the roadbed is lifted to the original natural ground attachment as a whole. However, the cooling effect in the central part of the roadbed is weaker than that on both side slopes, showing a warm range of −0.5-0 °C. Meanwhile, as a result of the shady-sunny slope effect, a −1.0 °C cold zone appeared beneath the shady slope of the roadbed, which is smaller than that of UCRE and CRBE in the lateral area, and shallower than that of CRBE and UCRE in the depth. When the roadbed is operated up to the 30th year, the cold core under the roadbed disappears, but the temperature is still lower than that of the natural site, suggesting that the crush-rocked structure provides some cooling effect for permafrost protection, but the cooling effect is relatively insufficient, meanwhile, with relation to global warming, the cold from the slope of the roadbed cannot cool the central part of the roadbed, resulting in the central part of the roadbed starting to produce a warm region of −0.5°C–0°C. In summary, for the warm permafrost region, CRSE has insufficient cooling effect for the deep layer and the center of the roadbed in permafrost, and some reinforcement measures should be taken.
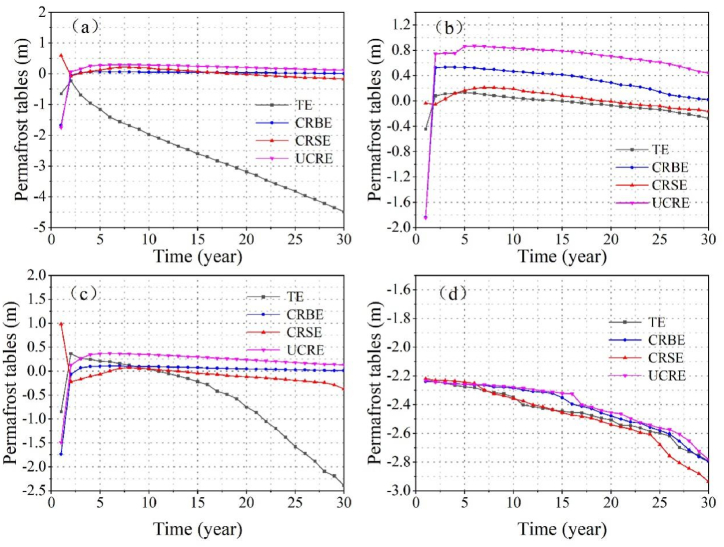
3.2. Permafrost table variations beneath the embankments
Fig. 10 shows the change process of the PT beneath the four types of roadbed structures in the 30 years since the construction of the roadbed. Using the initial surface of the earth as a reference, the depth of the pavement in the figure is computed. Positive values indicate that the PT has been raised to the interior of the roadbed above initial surface of the earth, and negative values indicate that the PT is below the initial surface of the earth. The PT beneath the sunny slope of TE was first lifted by more than 0.50 m (Fig. 10a), but began to decrease dramatically year by year after the roadbed was operated for 3 years, and it decreased by nearly 3.0 m when it was operated for 30 years, whereas the PT beneath the shady slope decreased over the years but remained relatively stable (Fig. 10b). The effect of shady and sunny slopes leads to a significant asymmetry in the PT distribution of TE, which is aggravated gradually, and is very likely to lead to non-uniform settlement of the roadbeds, affecting the prolonged stability of the roadbeds.
Fig. 10.
Permafrost table variations underneath the embankments. (a) left shoulder; (b) right shoulder; (c) embankment center; and (d) natural site.
Regarding the crushed-rock embankment, there were no discernible variations in the PT depth beneath the sunny and shaded slopes, PT beneath the shady slope was lifted slightly faster than that beneath the sunny slope. The depth of PT under the two shoulders has shown better symmetry, and since then the uplift speed has been slower, the PT has basically entered a stable state, but the PT exhibits a declining trend due to the impact of global warming. As can be seen in Fig. 10, on account of the weak cooling impact of crushed-rock slope, regardless of the position of the PT, the CRSE is lower than the CRBE and UCRE, especially in the center of the pavement, the difference is nearly 0.5m (Fig. 10c and d), which also indicates that the cooling performance of CRSE is poor, and reinforcing measures should be used.
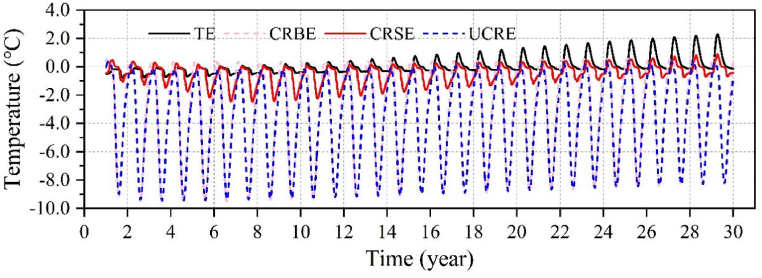
The distinct cooling impacts of the four embankments are also assessed utilizing Fig. 11, which illustrates variations of the centerline temperature at a depth of 0 m beneath the embankments during the 30 years. In the case of the TE, extensive thawing intervals during the warm season and brief freezing periods during the cold season cause the soil at the original ground surface below the embankment centerline to experience a constant warming trend without the implementation of any cooling technique. In comparison, the UCRE and CRBE embankments are significantly cooler than the TE throughout the 30-year freeze-thaw cycle period, with temperatures never exceeding 0.5 °C. The average temperatures of both embankments are substantially lower than those of CRSE. UCRE, in particular, consistently remains below 0 °C after the 10th year, demonstrating its superior cooling performance. On the contrary, because of the limited cooling efficacy of CRSE, its center temperature always remains at −0.5 °C–0 °C after the 20th year, which belongs to the warm permafrost, and the temperature increases each year. Thereby, it may said that CRSE's cooling impact is insufficient to meet the demands of climate warming.
Fig. 11.
Variations in ground temperature over 30 service years at the original ground surface below the centerline of the four embankments.
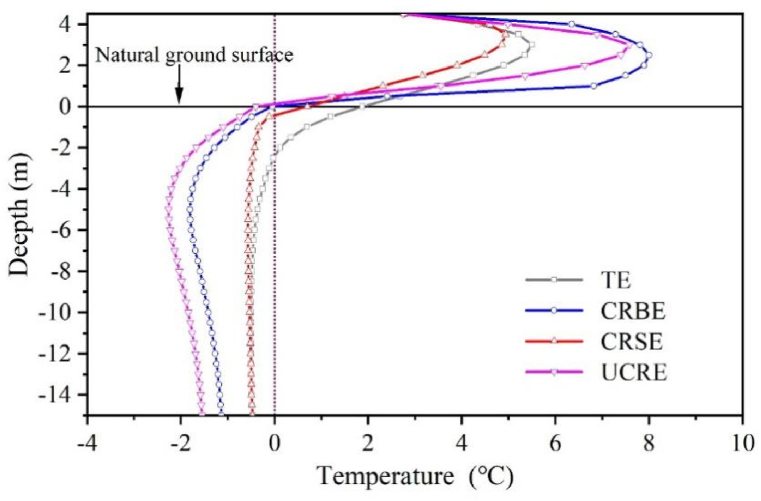
The ground temperature profiles below the centerlines on October 15, 30th service year, are shown in Fig. 12. It can be found that the highest ground temperatures below the TE, particularly above depths of −4.0 m, are much higher than the other three types of structures, while the PT under the TE has melted to approximately 2.5m below the embankment. The cooling effect of the UCRE and CRBE is significantly better, and the permafrost under these two structures is effectively cooled, and temperatures at depths of 1.5 m–15.0 m beneath the embankment are maintained below −1.5 °C and −1.0 °C after 30 years of operation, respectively. However, the cooling capacity of CRSE exhibits a comparatively restricted cooling capacity, leading to warm permafrost with temperatures exceeding −0.5 °C beneath the embankment's centerline and the cooling efficiency on deep permafrost is not significant, which proves that CRSE does not meet the stability requirements of roadbeds in permafrost regions.
Fig. 12.
Temperature variation with depth along the centerline of four embankments on October 15 in the 30th service year.
4. Optimization and reinforcement of CRSE
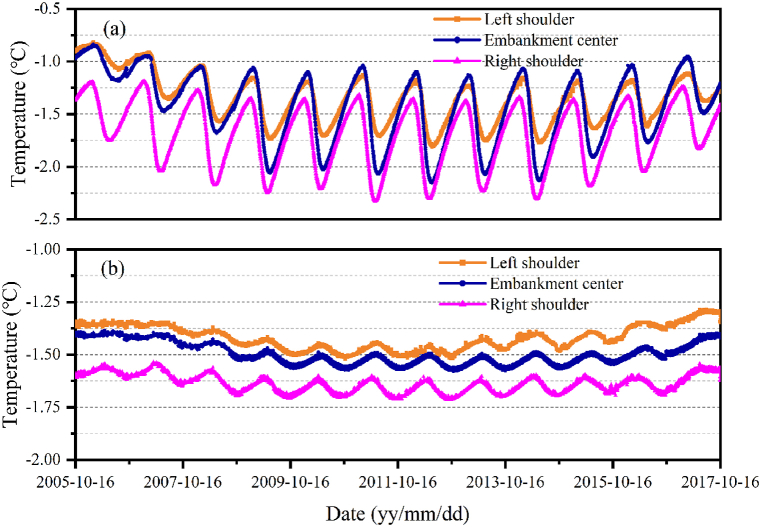
For a further assessment of the CRSE's cooling capacity, long-term geotemperature monitoring data at depths of 5m and 10m beneath the CRSE at QTR permafrost K1082 + 575 (QTR design milepost) within the Wudaoliang study area are used, as shown in Fig. 13. As can be seen in Fig. 13a, it is evident that after the embankment started to be used, the soil temperature beneath the right shoulder (shady side), the middle of the road and the left shoulder (sunny side) all showed a decreasing and then increasing trend, and the maximum temperature discrepancy between the left and right shoulders was more than 1 °C. After 2017, temperatures at a depth of 5m were above −1.5 °C at all locations, and particularly above −1 °C at the left shoulder and the center, showing a decreasing trend.
Fig. 13.
Monitored geotemperatures below section K1082 + 575 of the QTR. (a) temperatures at 5m deep; and (b) temperatures at 10m deep.
Fig. 13b depicts temperature variations at a depth of 10m beneath the CRSE. The data reveals that temperatures at this depth are generally lower than those at 5m. At 10 m, temperatures in the left shoulder, right shoulder, and center of the embankment also show a pattern of initially decreasing and then increasing, though the variation range is significantly smaller compared to the 5-m depth. This suggests that permafrost at 10m is relatively stable. Nonetheless, temperatures at this depth increased by 0.1 °C over the 10-year period, with a rise of 0.2 °C observed at the left shoulder. Additionally, since 2017, the temperature difference between the left and right shoulders has reached 0.3 °C. The above results also indicate again that the cooling capacity of the CRSE is insufficient and the shady-sunny slope effect in the temperature field of CRSE is quite pronounced.
In response to rising ground temperatures beneath the crushed-rock slope embankment, railway authorities have implemented several mitigation measures. These include increasing the thickness of the rock fill, adjusting the size of the rocks, and incorporating thermal rods. Despite these efforts, the effectiveness of these measures has been relatively slow. Considering the future global warming and the inadequate thermal stability in the warm permafrost zone, it is not possible to ensure the CRSE's prolonged thermal stability and reinforcement measures should be taken.
4.1. Improved methodology
When water freezes, its thermal conductivity changes from 0.56 W/(m.°C) to 2.2 W/(m.°C) with an increase of 4.0 %. By exploiting the characteristics of the change in thermal conductivity of the phase change of water, a type of thermal conductivity variable system (TCVS), that can act as a thermal semiconductor was presented [48], as shown in Fig. 14a. The TCVS comprises a closed container, and an air layer, an absorbent material layer and a water layer in the container. The absorbent material in TCVS is selected from a highly absorbent polymer system combining absorbent sponge, polyacrylic acid and polyacrylamide, and the shell is a building material with strength, such as concrete, and the purpose is to prevent the internal moisture from emanating and to protect the internal structure. Despite the harsh and variable natural environment of the Qinghai-Tibet Plateau, the shell of the TCVS, made from concrete and other construction materials, exhibits excellent stability and durability. It is resistant to freeze-thaw cycles and less susceptible to degradation from weathering. Additionally, the timely maintenance of the Qinghai-Tibet Railway further ensures that TCVS can be used effectively for a long time in such extreme natural conditions. The TCVS needs no power to take advantage of the temperature changes in nature throughout the year, and is characterised by a lower thermal conductivity at positive temperatures in summer and a larger thermal conductivity at negative temperatures in winter.
Fig. 14.
The application of TCVS for optimizing CRSE. (a) Sketch of TCVS; (b) field CRSE with the TCVS.
A new embankment cooling structure, which combines CRL and TCVS, is proposed. In this design, a 20 cm thick TCVS is applied to the CRSE between the CRL and the embankment fill, as shown in Fig. 14b. To assess its cooling efficacy, the thermal qualities of the optimized CRSE were investigated using numerical modelling to assess its future thermal condition and compare it with the CRSE (Fig. 15). To better estimate the improvement of the cooling capacity of TCVS, the thermal boundaries of the slopes on both sides of the embankment, the shoulders and the natural ground surface, the size of the embankment and the initial temperature conditions are consistent with thermal boundary conditions in section 2.5, and the thermal parameters of TCVS are shown in Table 3.
Fig. 15.
Geometric physical model of the optimized CRSE.
Table 3.
Thermal parameters of TCVS.
| Time | Thermal conductivity(W·m−1·K−1) |
|---|---|
| Temperature >0 °C | 0.21 |
| Temperature <0 °C | 1.22 |
4.2. Simulation results and comparison
Fig. 16 gives the temperature distribution for CRSE and the optimized CRSE on October 15 and January 15 in the 30th service year. From the comparison of Fig. 16a and b, it can be seen that during the 30th year of roadbed service, under the impact of global warming, for CRSE, during the warm season, the cold from the slope of the roadbed is unable to cool down the central part of the embankment, which leads to the central part beneath the embankment to produce a high temperature region of −0.5°C–0°C. In the cold season, there is a temporal and spatial hysteresis of the cooling effect, leading to the existence of a high temperature regions of −0.5°C–0°C and even above 0 °C beneath the central part, all these indicate that CRSE with CRL reinforcing measure alone cannot avoid the degradation of permafrost beneath the embankment in warm permafrost zones due to global warming. The optimized CRSE effectively avoids this and the added TCVS proves effective in mitigating the heat from the pavement. Comparing Fig. 16a and c, it is clear that, compared to CRSE, the optimized CRSE not only eliminates the high temperature zone below the center of the embankment, but also significantly raises the −0.5 °C isotherm. At the same time, the optimized CRSE effectively extends the range of the −0.6 °C cold core from a discontinuous regional distribution to a continuous distribution, which mitigates the permafrost degradation under the roadbed to some extent. In addition, the temperature distributions of the optimized CRSE have good symmetry and effectively avoids the shady-sunny slope effect.
Fig. 16.
Ground temperature fields on October 15 and January 15 in the 30th service year for the CRSE and the optimized CRSE. (a) CRSE on October 15; (b) CRSE on January 15; (c) the optimized CRSE on October 15; (d) the optimized CRSE on January 15.
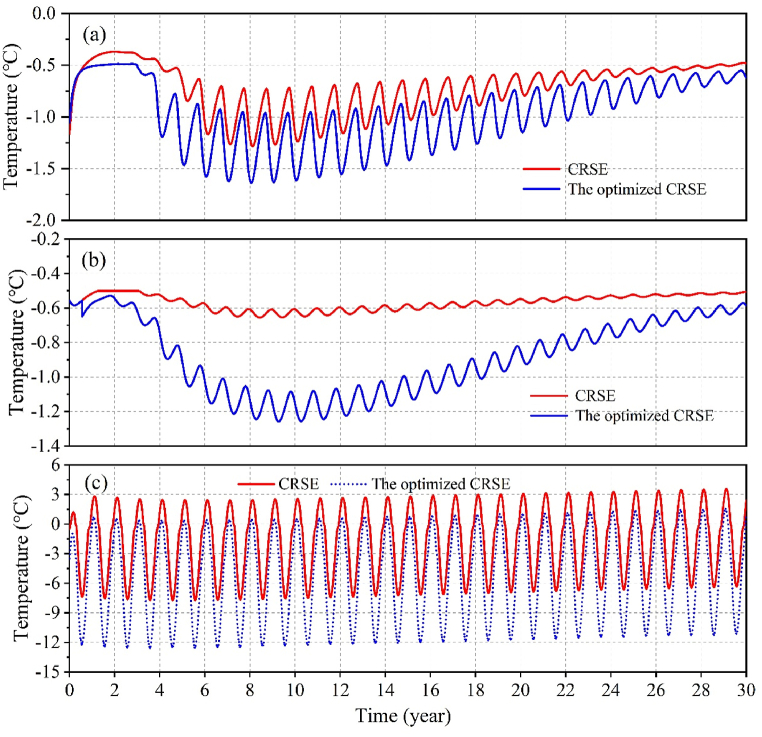
Fig. 17 reveals the permafrost temperature variations at each location for both types of embankments. Capitalizing on the heat resistance provided by the TCVS during warm seasons, the embankment fill can receive the cold energy obtained by the CRL, significantly reducing the geotemperature below the optimized CRSE. At a depth of 4.0 m, the largest variation in temperature between the two structures can be up to 0.3 °C (Fig. 17a), and at a depth of 8.0 m, the maximum temperature difference between the two structures is 0.6 °C (Fig. 17b). In addition, both structures under the two depths experienced a cooling process by the 10th service year, and then warmed up due to the impact of global warming, and by the 30th year, the temperature at the depth of 4 m under the CRSE structure will be close to −0.5 °C, and warm permafrost will be formed, while the temperature at the depth of 4 m under the optimized CRSE is about −0.7 °C. Leveraging the thermal resistance of insulating material, its effectiveness in reducing heat exchange in the roadbed and strong insulation of the road surface from heat in summer, in a sunny slope environment, the optimized CRSE's temperature at the slope location is still lower than that of the CRSE, with a peak of nearly 3 °C during warm seasons and 5 °C during cold seasons, respectively (Fig. 17c). These results proved that the effective cooling performance of the optimized CRSE, so it can be seen that the stability of CRSE in QTR can be improved through utilization of the optimized CRSE structure with the combination of CRL and TCVS.
Fig. 17.
Variations of ground temperatures underneath the two embankments during 30 service years. (a) temperatures at 4.0 m deep; (b) temperatures at 8.0 m deep; and (c) 0.5m beneath the center of the sunny slope.
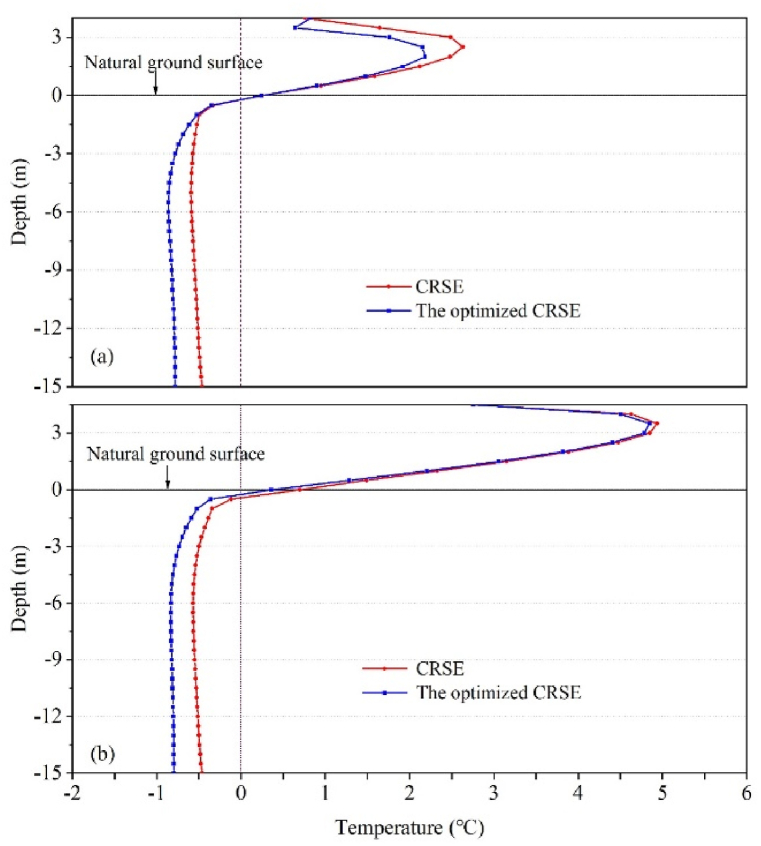
To compare the cooling performance of the CRSE and the optimized CRSE, we present the ground temperature profiles below two positions on October 15 in the 30th year (Fig. 18). It is apparent that the overall geotemperature under the optimized CRSE is lower than that of CRSE, and both temperatures show a clear downward trend, and the cooling effectiveness of the CRSE embankment, employing only CRL, is very restricted, leading to a permafrost temperature beneath the embankment that exceeds −0.5 °C. The temperature difference between CRSE and the optimized CRSE at the sunny side and roadbed center are all close to 0.32 °C at a depth of 15.0 m. Meanwhile, the temperature of the optimized CRSE is lower than that of CRSE by more than 0.5 °C under the left shoulders at height of 0.0 m–4.0 m (Fig. 18a), which also proved that TCVS could effectively inhibit the thermal disturbance of the embankment fill by external heat. After 30 years of operation, the temperatures at two locations under the optimized CRSE 15m are below −0.5 °C and close to −1 °C (Fig. 18a and b), which all indicate that the optimized CRSE structure is more effective in cooling. Therefore, the comparison affirms that the novel design is improving the cooling capacity of the original CRSE, which can contribute to the enduring stability of the CRSE in the QTR, as well as improving the CRSE's ability to cope with global climate warming and humidification.
Fig. 18.
Temperature variation with depth along the centerline of embankments on October 15 in the 30th service year. (a) Left shoulder; and (b) roadbed center.
4.3. Mechanism of the optimized CRSE
Under conditions of positive and negative temperature changes throughout the year, the thermal conductivity of TCVS can differ significantly between positive and negative temperatures in both states. This allows for control of heat flow between the environment and the protected object, ultimately achieving stabilization and protection of permafrost. TCVS consists of alternating layers of absorbent material and air in a sealed container with an internal body of water with a high thermal capacity stored at the bottom. During the warm season, the low thermal conductivity of the air layers prevents external heat from reaching the underlying permafrost, thereby reducing the overall thermal conductivity of the device. In the cold season, the top layer of water-absorbing material cools down, adsorbs water vapor from the air, and forms an ice layer that develops in successive layers, eventually converting all the water in the bottom reservoir into frost within the air layers. The higher thermal conductivity of the ice increases the thermal conductivity of the device, facilitating the transfer of external cold into the underlying permafrost and the dissipation of heat.
Due to the permafrost area, the duration of the cold season surpasses that of the warm season. Therefore, the device can store cold energy in the winter to protect the lower permafrost. The airtight container serves the purpose of preventing water loss from the interior and effectively protects the internal laminated structure from external loads.
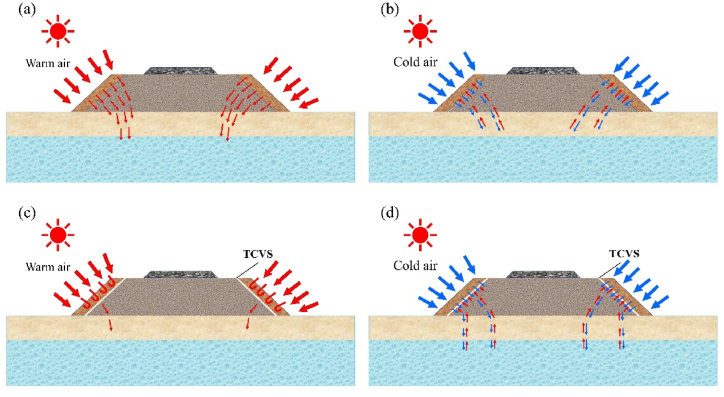
Fig. 19 demonstrates the mechanism of the optimized CRSE for cooling the roadbed. The new structure reduces heat absorption during the warm season and increases the overall heat dissipation, thereby enhancing the cooling effect (Fig. 19a and c). The two side slopes of the CRSE are the main conduits for heat to enter the roadbed, due to the fact that they exhibit a significantly greater surface area compared to the top surface. Applying the TCVS between the CRL and embankment fill can efficiently inhibit the effects of heat conduction and convection, preventing warm heat from entering the embankment and affecting its thermal stability. The TCVS and CRL accelerates the absorption of cold air throughout the winter, which enhances the cooling efficiency of the embankment slopes (Fig. 19b and d). This process facilitates the transfer of cooling from the slope to the core, ensuring efficient cooling in the embankment. Overall, TCVS slows down the rate of cryogenic and thermal transitions in the soil and reduces the risk of settlement and damage to the foundations, which, when combined with the crushed stone layer, helps to maintain the stability and durability of the infrastructure.
Fig. 19.
Brief mechanism for the optimized CRSE. (a) CRSE in warm seasons; (b) CRSE in cold seasons. (c) the optimized CRSE in warm seasons; (d) the optimized CRSE in cold seasons.
The TCVS can be manufactured in units ranging from 1 to 2 m2 to meet engineering requirements and installed using construction techniques similar to those employed for thermal insulation material. It should be positioned axially and horizontally between the crushed-rock layer and the embankment along CRSE of the railway. This arrangement facilitates comprehensive heat flow control for permafrost engineering and stabilizes the permafrost temperature field. Although optimizing the existing CRSE with the new structure will incur higher economic costs, under the backdrop of global climate change, failing to maintain and reinforce the Qinghai-Tibet Railway embankments would severely threaten the safety and quality of the railway due to permafrost degradation caused by rising temperatures. Therefore, relevant maintenance departments invest substantial financial resources annually for these activities. In the future, we will build on the results of this research to further optimize the structure using low-cost new materials, aiming to achieve cost reduction and improved effectiveness.
5. Conclusions
In this study, a coupled thermal-fluid-solid model was developed and validated to examine the cooling performance of four types of permafrost embankments regularly used on the Qinghai-Tibet Plateau. A reinforcement measure that combining the TCVS was presented to improve the cooling capacity of the existing CRSE. Its cooling efficiency and thermal properties are ascertained using numerical simulations. The main conclusions were drawn.
-
(1)
Numerical simulations and field monitoring elucidate that the adoption of crushed-rock embankments manifests as a potent strategy for protecting permafrost subgrade. The efficacy of this convective cooling varies among distinct embankment structures. Significantly, UCRE emerges as a particularly efficacious intervention, substantially cooling the ground temperature and concurrently ensuring the stabilization of the embankments on the QTP.
-
(2)
The cooling capacity of CRSE is insufficient to withstand the degradation of the underlying permafrost in warm permafrost areas. Specifically, CRSE does not have a significant cooling effect on deep permafrost and causes the widespread warming of the underlying permafrost.
-
(3)
The optimized CRSE with a combination of TCVS not only mitigates the thermal impact on the warm permafrost beneath the roadbed, but also reduces the shady-sunny slope effect. The optimized CRSE is particularly instrumental in curbing heat accumulation at the embankment center, thereby averting the occurrence of large warm permafrost zones beneath this region. Additionally, the optimized CRSE shows robust protective capabilities against deep permafrost. Therefore, the optimized CRSE stands out as a viable and effective reinforcement measure and can be used as a mitigation measure for degrading permafrost in railway embankment maintenance engineering on QTP.
Data availability
The authors do not have permission to share data.
CRediT authorship contribution statement
Bingyan Li: Writing – review & editing, Methodology, Formal analysis. Minghao Liu: Writing – review & editing, Supervision, Funding acquisition. Jing Luo: Resources. Xin Ju: Resources. Fei Yin: Resources.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (Grant No. U2268216, 42271152), the Key Science and Technology Program of Gansu Province, China (Nos. 23ZDFA017, 22ZD6FA004), the Program of the Key Laboratory of Cryospheric Science and Frozen Soil Engineering of Chinese Academy of Sciences, China (Grant No. CSFSE-ZZ-2405), and the West Light Foundation of Chinese Academy of Sciences, China (Granted to Dr. Minghao Liu).
References
- 1.Qin Y., Wang T., Yuan W. Wind-driven device for cooling permafrost. Nat. Commun. 2023;14:7558. doi: 10.1038/s41467-023-43375-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cheng G.D. A roadbed cooling approach for the construction of Qinghai-Tibet Railway. Cold Reg. Sci. Technol. 2005;42:169–176. [Google Scholar]
- 3.Dore G., Niu F., Brooks H. Adaptation methods for transportation infrastructure built on degrading permafrost. Permafr. Periglac. Process. 2016;27:352–364. [Google Scholar]
- 4.Ma W., Cheng G., Wu Q. Preliminary study on Technology of cooling foundation in permafrost regions. J. Glaciol. Geocryol. 2002;24:579–587. [Google Scholar]
- 5.Cheng G.D., Sun Z.Z., Niu F.J. Application of the roadbed cooling approach in Qinghai-Tibet railway engineering. Cold Reg. Sci. Technol. 2008;53:241–258. [Google Scholar]
- 6.Wu Q.B., Lu Z.J., Zhang T., Wei M., Liu Y.Z. Analysis of cooling effect of crushed rock-based embankment of the Qinghai-Xizang Railway. Cold Reg. Sci. Technol. 2008;53:271–282. [Google Scholar]
- 7.Niu F.J., Liu M.H., Cheng G.D., Lin Z.J., Luo J., Yin G.A. Long-term thermal regimes of the Qinghai-Tibet Railway embankments in plateau permafrost regions. Sci. China Earth Sci. 2015;58:1669–1676. [Google Scholar]
- 8.Mu Y.H., Ma W., Liu Y.Z., Sun Z.H. Monitoring investigation on thermal stability of air-convection crushed-rock embankment. Cold Reg. Sci. Technol. 2010;62:160–172. [Google Scholar]
- 9.Goering D., Saboundjian S. Cold Regions and Construction Conference. ASCE/CSCE/IWCSEAA; 2004. Design of passive permafrost cooling system for an interior Alaska roadway. [Google Scholar]
- 10.Esch D.C. Roads and Airfields in Cold Regions. ASCE; 1996. Road and airfield design for permafrost conditions; pp. 121–150. [Google Scholar]
- 11.Herz T., King L., Gubler H. 8th International Conference on Permafrost, Zurich, Switzerland. 2003. Microclimate within coarse debris of talus slopes in the alpine periglacial belt and its effect on permafrost; pp. 383–387. [Google Scholar]
- 12.Harris S.A., Pedersen D.E. Thermal regimes beneath coarse blocky materials. Permafr. Periglac. Process. 1998;9:107–120. [Google Scholar]
- 13.Gorbunov A., Seversky E. Extended Abstracts, International Symposium on Mountain and Arid Land Permafrost. Urlah Erdem Publishing Ulaanbaatar; 2001. Influence of coarsely fragmental deposits on permafrost formation; pp. 24–25. [Google Scholar]
- 14.Ma W., Feng G.L., Wu Q.B., Wu J.J. Analyses of temperature fields under the embankment with crushed-rock structures along the Qinghai-Tibet Railway. Cold Reg. Sci. Technol. 2008;53:259–270. [Google Scholar]
- 15.Cheng G., Sun Z., Niu F. Application of roadbed cooling methods in the qinghai-tibet railway construction. J. Glaciol. Geocryol. 2006;28:797–808. [Google Scholar]
- 16.Sun Z.Z., Ma W., Li D.Q. In situ test on cooling effectiveness of air convection embankment with crushed rock slope protection in permafrost regions. J. Cold Reg. Eng. 2005;19:38–51. [Google Scholar]
- 17.Tai B.W., Wu Q.B., Zhang Z.Q., Xu X.M. Cooling performance and deformation behavior of crushed-rock embankments on the Qinghai-Tibet Railway in permafrost regions. Eng. Geol. 2020;265 [Google Scholar]
- 18.Wu Q.B., Zhao H.T., Zhang Z.Q., Chen J., Liu Y.Z. Long-term role of cooling the underlying permafrost of the crushed rock structure embankment along the Qinghai-Xizang railway. Permafr. Periglac. Process. 2020;31:172–183. [Google Scholar]
- 19.Luo J., Niu F.J., Liu M.H., Lin Z.J., Yin G.A. Field experimental study on long-term cooling and deformation characteristics of crushed-rock revetment embankment at the Qinghai-Tibet Railway. Appl. Therm. Eng. 2018;139:256–263. [Google Scholar]
- 20.Mu Y.H., Ma W., Li G.Y., Mao Y.C., Liu Y.Z. Long-term thermal and settlement characteristics of air convection embankments with and without adjacent surface water ponding in permafrost regions. Eng. Geol. 2020;266 [Google Scholar]
- 21.Han F., Zhang X., Yu W., Wei L., Zhou J. Analysis on the cooling performance properties of block-stone embankment in permafrost regions under the scenario of aeolian-sand. J. Glaciol. Geocryol. 2018;40:528–538. [Google Scholar]
- 22.Chen L., Yu W., Han F., Liu W., Yi X. Impacts of aeolian sand on cooling effect of crushed-rock embankment of Qinghai-Tibet Railway. J. Glaciol. Geocryol. 2015;37:147–155. [Google Scholar]
- 23.Liu M.-h., Li G.-y., Niu F.-j., Lin Z.-j., Shang Y.-h. Porosity of crushed rock layer and its impact on thermal regime of Qinghai− Tibet Railway embankment. J. Cent. S. Univ. 2017;24:977–987. [Google Scholar]
- 24.Zhang G.F., Nan Z.T., Hu N., Yin Z.Y., Zhao L., Cheng G.D., Mu C.C. Qinghai-Tibet Plateau permafrost at risk in the late 21st century. Earth's Future. 2022;10 [Google Scholar]
- 25.Chen R., von Deimling T.S., Boike J., Wu Q.B., Langer M. Simulating the thermal regime of a railway embankment structure on the Tibetan Plateau under climate change. Cold Reg. Sci. Technol. 2023:212. [Google Scholar]
- 26.Liu H., Huang S.B., Xie C., Tian B.S., Chen M., Chang Z.Q. Monitoring roadbed stability in permafrost area of qinghai-tibet railway by MT-InSAR Technology. Land. 2023;12:474. [Google Scholar]
- 27.Wu Q., Zhang Z., Liu G. Relationships between climate warming and engineering stability of permafrost on Qinghai-Tibet Plateau. J. Eng. Geol. 2021;29:342–352. [Google Scholar]
- 28.Xu Y.Z., Shen M.D., Zhou Z.W., Ma W., Li G.Y., Chen D. Investigating characteristics of the long-term settlement of railway embankments in warm permafrost areas. Front. Environ. Sci. 2023;11 [Google Scholar]
- 29.Lai Y.M., Zhang L.X., Zhang S.J., Mi L. Cooling effect of ripped-stone embankments on Qing-Tibet railway under climatic warming. Chin. Sci. Bull. 2003;48:598–604. [Google Scholar]
- 30.Zhang M.Y., Lai Y.M., Dong Y.H. Numerical study on temperature characteristics of expressway embankment with crushed-rock revetment and ventilated ducts in warm permafrost regions. Cold Reg. Sci. Technol. 2009;59:19–24. [Google Scholar]
- 31.Xiangyan K., Jianbing W. A bifurcation study of non-Darcy free convection in porous media. ACTA MECHANICA SINICA-CHINESE EDITION- 2002;34:177–185. [Google Scholar]
- 32.Tao W.Q. second ed. Xi'an Jiaotong University Press; Xi'an: 2004. Numerical Heat Transfer. [Google Scholar]
- 33.Nield D.A., Bejan A. Springer; 2006. Convection in Porous Media. [Google Scholar]
- 34.Lai Y.M., Zhang M.Y., Li S.Y. Science Press; Beijing: 2009. Theory and Application of Cold Regions Engineering. [Google Scholar]
- 35.Li X., Li X.K. A soil freezing-thawing model based on thermodynamics. Cold Reg. Sci. Technol. 2023;211 [Google Scholar]
- 36.Liu M.H., Zheng H., Niu F.J., Fang J.H., Lin Z.J., Luo J., Yin G.A. Cooling performance enhancement of a new expressway embankment in the Tibetan Plateau permafrost zone. Cold Reg. Sci. Technol. 2021:190. [Google Scholar]
- 37.Li X.K., Li X., Liu S., Qi J.L. Thermal-seepage coupled numerical simulation methodology for the artificial ground freezing process. Comput. Geotech. 2023;156 [Google Scholar]
- 38.Wd A. Lanzhou Univ. Press; Lanzhou: 1990. Interaction Among Temperature, Moisture and Stress Fields in Frozen Soil. [Google Scholar]
- 39.Zhang M.Y., Lai Y.M., Li D.Q., Chen W., Tong G.Q. Experimental study on ventilation characteristics of a concrete-sphere layer and a crushed-rock layer. Int. J. Heat Mass Tran. 2013;59:407–413. [Google Scholar]
- 40.Lai Y.M., Zhang M.Y., Liu Z.Q., Yu W.B. Numerical analysis for cooling effect of open boundary ripped-rock embankment on Qinghai-Tibetan railway. Sci. China Earth Sci. 2006;49:764–772. [Google Scholar]
- 41.Xu X.Z., Wang J.C., Zhang L.X. Science Press; Beijing: 2001. Physics of Frozen Soils. [Google Scholar]
- 42.Cheng G., Jiang H., Wang K., Wu Q. Thawing index and freezing index on the embankment surface in permafrost regions. J. Glaciol. Geocryol. 2003;25:603–607. [Google Scholar]
- 43.Qin D., Ding Y., Wang S., Wang S., Dong G., Lin E., Liu C., She Z., Sun H., Wang S., Wu G. A study of environment change and its impacts in Western China. Earth Sci. Front. 2002;9:321–328. [Google Scholar]
- 44.Zhu L.N. Study of the adherent layer on different types of ground in permafrost regions on the qinghai-xizang plateau. J. Glaciol. Geocryol. 1988;01:8–14. [Google Scholar]
- 45.Zhang M.Y., Pei W.S., Li S.Y., Lu J.G., Jin L. Experimental and numerical analyses of the thermo-mechanical stability of an embankment with shady and sunny slopes in a permafrost region. Appl. Therm. Eng. 2017;127:1478–1487. [Google Scholar]
- 46.Zhao M., Miao M.Q., Wang Y.C. Meteorological Press; Beijing: 1991. Boundary Layer Meteorology. [Google Scholar]
- 47.Zhang M., Zhang X., Li S., Wu D., Pei W., Lai Y. Evaluating the cooling performance of crushed-rock interlayer embankments with unperforated and perforated ventilation ducts in permafrost regions. Energy. 2015;93:874–881. [Google Scholar]
- 48.Yu Q.H. 2004-03-03. Thermal Conductivity Variable Device and Application, in, Vol. 03108089.8, China. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors do not have permission to share data.