Similarity-based multimodal regression

Summary

To better understand complex human phenotypes, large-scale studies have increasingly collected multiple data modalities across domains such as imaging, mobile health, and physical activity. The properties of each data type often differ substantially and require either separate analyses or extensive processing to obtain comparable features for a combined analysis. Multimodal data fusion enables certain analyses on matrix-valued and vector-valued data, but it generally cannot integrate modalities of different dimensions and data structures. For a single data modality, multivariate distance matrix regression provides a distance-based framework for regression accommodating a wide range of data types. However, no distance-based method exists to handle multiple complementary types of data. We propose a novel distance-based regression model, which we refer to as Similarity-based Multimodal Regression (SiMMR), that enables simultaneous regression of multiple modalities through their distance profiles. We demonstrate through simulation, imaging studies, and longitudinal mobile health analyses that our proposed method can detect associations between clinical variables and multimodal data of differing properties and dimensionalities, even with modest sample sizes. We perform experiments to evaluate several different test statistics and provide recommendations for applying our method across a broad range of scenarios.

1 Introduction

Complex health outcomes are understood as a byproduct of intricate biological pathways that are rarely captured in a single measurement. Advances in technology have enabled researchers to collect a large number of measurements on a single individual, spanning domains such as genomics, imaging, and physical activity. These individual data types are often called modalities, and the aggregation of several modalities on the same subject is called multimodal data. The availability of large multimodal data has increased considerably in the past decade, with studies such as the UK Biobank releasing multimodal data on roughly half a million individuals (Sudlow et al. 2015).

We focus on two large-scale multimodal studies, one collecting multimodal neuroimaging data and the other collecting a multitude of mobile health data. The Philadelphia Neurodevelopmental Cohort (PNC; Satterthwaite et al., 2014) consists of over 1,600 subjects with multimodal imaging including structural magnetic resonance imaging (MRI), functional MRI (fMRI), and diffusion tensor imaging (DTI). With the goal of understanding neurodevelopmental trajectories, studies have leveraged the PNC data to understand the effect of brain development on matrix-valued brain connectivity (Baum et al. 2020) and high-dimensional measures of cortical structures (Vandekar et al. 2015), among many other measures. For mobile health data, the National Institute of Mental Health (NIMH) Family Study of Affective Spectrum Disorders collects real-time data on over 200 participants on their physical activity and emotional state through actigraphy and ecological momentary assessment (EMA) administered through mobile devices (Merikangas et al. 2014, 2019). Through the NIMH Family Study, researchers have identified differences among participants with mood disorders such as bipolar disorder in their patterns of sleep, mood, and physical activity (Merikangas et al. 2019). In both studies, there is a need for flexible methods to handle multimodal data, allowing further analyses while minimizing loss of information from the original data.

The emergence of these multimodal studies has driven methods for integration of multiple data modalities, often called multimodal data fusion. These methods vary considerably in their models and applications but generally involve extensions of traditional multivariate analysis techniques such as independent component analysis, canonical correlation analysis, and singular value decomposition (Lahat et al. 2015). While these techniques work very well for certain types of data for which model constraints are satisfied, they are difficult to generalize to others. In neuroimaging for example, methods for integrating multiple modalities of functional imaging data may not directly apply to simultaneous analysis of structural and functional imaging. For more generally applicable models, several deep learning frameworks have been extended and enable prediction using multimodal data (Gao et al. 2020). However, these machine learning approaches are tailored for prediction tasks and are not suited for inference.

For analysis of data having arbitrary dimension and structure, distance-based and kernel-based methods provide inference through similarity metrics computed between subjects. Distance correlation and the HilbertSchmidt independence criterion are used for independence testing and are equivalent under certain choices of the distance and kernel (Sejdinovic et al. 2013; Shen and Vogelstein 2020). Maximum mean discrepancy is used for two-sample kernel testing (Gretton et al. 2007) and permutational analysis of variance for multiple group distance-based tests (Anderson 2001), with asymptotic properties recently investigated (Shinohara et al. 2020). For regression, multivariate distance matrix regression (MDMR; McArdle and Anderson, 2001) and kernel machine regression (KMM; Suykens et al., 2002; Liu et al., 2007) are both widely used and have been shown to be equivalent under certain conditions on the corresponding distance and kernel matrices (Pan 2011). For multiple kernels computed on the same data, the microbiome regression-based kernel association test, an extension of KMM, allows for testing based on the minimum of P-values across kernels (Zhao et al. 2015). Another extension of KMM can incorporate multiple data modalities and their interactions in regression on outcomes with distributions in the exponential family (Li and Cui 2012). To the best of our knowledge, none of these methods are designed to perform regression on multiple data modalities through their distances or kernels.

We propose a distance-based model for simultaneous regression of multimodal data of arbitrary types, which we call similarity-based multimodal regression (SiMMR). We develop two test statistics that are appropriate for different settings and compare them through simulation and applications to the PNC and NIMH Family Study data. We demonstrate that our test statistics outperform existing distance-based methods and provide high power for detection of associations across all data types considered. Our method introduces a novel framework for multimodal data fusion, which we demonstrate to be a flexible and powerful model for regression of multimodal data.

2 Methods

2.1 Multivariate distance matrix regression

We briefly review a standard distance-based method for regression of a single data modality called multivariate distance matrix regression (MDMR; McArdle and Anderson, 2001; Anderson, 2001; Schork and Zapala, 2012). Let $(\Omega ,d)$ be a semimetric space and Y be a random object taking values in Ω. Suppose, we observe independent draws y_i for each subject $i=1,2,\dots ,n$ and let $D={(d_{ij})}_{n\times n}$ denote the sample dissimilarity matrices where $d_{ij}=d(y_i,y_j)$. Define the doubly centered dissimilarity matrix $G=(I-11^T)A(I-11^T)$ where $A={(-\frac{1}{2}{d}_{ij}^2)}_{n\times n}$. Let X be an n × p design matrix with corresponding projection matrix $H=X{(X^{T}X)}^{-1}{X}^T$.

MDMR tests for an association of Y and X via the pseudo-F statistic

$$F=\frac{\text{tr}(\mathit{HGH})}{\text{tr}[(I-H)G(I-H)]},$$

where statistical significance is typically evaluated through permutation. With a univariate outcome and Euclidean distance, it is equivalent to the standard regression F-statistic if appropriate degrees of freedom are accommodated (McArdle and Anderson 2001). For testing subsets of covariates, the numerator can be replaced by $\text{tr}[(H-H_r)G(H-H_r)]$, where H_r is the projection matrix from the reduced model (Li et al. 2009; Reiss et al. 2010).

Recent papers investigate the asymptotic null distribution of the MDMR test statistic, deriving distributions based on ${\chi }^2$ random variables weighted by the eigenvalues of G. McArtor et al. (2017) reformulate the statistic in terms of multidimensional scaling (MDS) scores and derive the asymptotic distribution as a quotient of weighted sums of central ${\chi }^2$ random variables by making assumptions about the distribution of MDS scores. By assuming matrix normal error and limiting their scope to Euclidean and Mahalanobis distances, Li et al. (2019) find the distribution to be a weighted quotient of noncentral ${\chi }^2$ random variables. For distance-based analysis of variance, Shinohara et al. (2020) represent the pseudo-F statistic as a U-statistic to identify the limiting distribution as a weighted sum of central ${\chi }^2$ random variables. Shi et al. (2021) adapt results from kernel-based testing to derive the asymptotic null distribution as a weighted sum of noncentral ${\chi }^2$ random variables, making no assumptions about the error structure or limitations on the distance function.

2.2 Similarity-based multimodal regression model

Let $({\Omega }_1,d_1),({\Omega }_2,d_2),\dots ,({\Omega }_m,d_m)$ be semimetric spaces. We consider random objects $Y_1,Y_2,\dots ,Y_m$ taking values in ${\Omega }_1,{\Omega }_2,\dots ,{\Omega }_m$, respectively and a vector-valued random variable for covariates X. Suppose we observe independent draws $\{y_{1i},y_{2i},\dots ,y_{mi}\}$ as the multimodal outcome and x_i as the corresponding vector of covariates of dimension length p for each subject $i=1,2,\dots ,n$. Let $D_k={(d_{\mathit{kij}})}_{n\times n}$ denote sample dissimilarity matrices defined based on appropriately chosen distance metrics for each individual data modality where $d_{\mathit{kij}}=d_k(y_{ki},y_{kj})$ for $k=1,2,\dots ,m$.

Our goal is to assess the joint association between $Y_1,Y_2,\dots ,Y_m$ and X through their respective dissimilarity matrices $D_1,D_2,\dots ,D_m$. Define weighted doubly centered dissimilarity matrices $G_1,G_2,\dots ,G_m$, where $G_k=w_k(I-\frac{1}{n}11^T)A_k(I-\frac{1}{n}11^T)$ and $A_k={(-\frac{1}{2}{d}_{\mathit{kij}}^2)}_{n\times n}$. In our analyses, the weights $w_k>0$ are chosen as the largest eigenvalue of G_k following recommendations from previous literature on integration of multiple distance matrices (Abdi et al. 2005). Weights based on other properties of G_k may alternatively be selected, or weights can be chosen to place particular emphasis on certain modalities.

Our model tests for an association between these weighted doubly centered dissimilarity matrices and the covariates of interest. These G_k admit the decompositions $G_k=Z_k{Z}_k^T$, where $Z_k={\left[\begin{array}{cccc}{z}_{k1}& z_{k2}& \cdots & z_{kn}\end{array}\right]}^T$ are the n × n matrices of classical multidimensional scaling (cMDS) scores (McArdle and Anderson 2001). Note that for non-Euclidean distances, G_k is not guaranteed to be positive semidefinite and cMDS scores may include imaginary values. One solution is to discard imaginary cMDS axes; however, McArdle and Anderson (2001) show that this might lead to conservative tests. The recommended solution is to add a constant to off-diagonal elements of each distance matrix prior to computation of cMDS, which has a solution derived in Cailliez (1983) and recently applied in the formulation of partial distance correlation (Székely and Rizzo 2014).

Let $Z=\left[\begin{array}{cccc}{Z}_1& Z_2& \cdots & Z_m\end{array}\right]$ denote the n × mn matrix of concatenated cMDS scores; this concatenation was first proposed in Faraway (2014). We propose similarity-based multimodal regression (SiMMR) as the multivariate regression model

$$Z=XB+E,$$ (2.1)

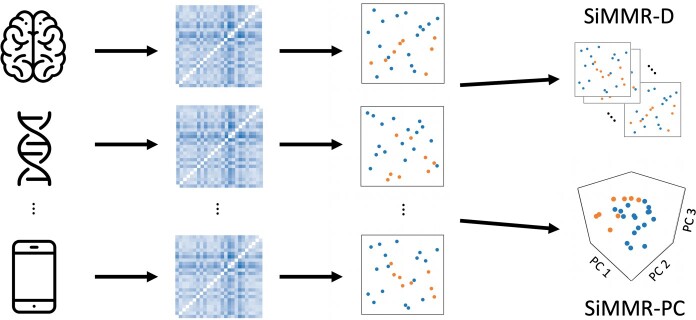
where $X={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]}^T$ is the n × p design matrix, B is a p × mn matrix of regression coefficients and E is an n × mn error matrix. In Fig. 1, we illustrate the SiMMR model and two proposed test statistics which we describe in 2.3.

Fig. 1.

Illustration of similarity-based multimodal regression. In SiMMR, distance matrices are computed separately on each modality, followed by representation in Euclidean space via classical multidimensional scaling (cMDS). SiMMR then concatenates these cMDS coordinates and performs inference using either Dempster’s trace (SiMMR-D) or Pillai’s trace after dimension reduction using principal components (SiMMR-PC).

2.3 SiMMR-D and SiMMR-PC test statistics

We propose two statistics to test the null hypothesis that a subset of covariates has no association with the joint cMDS scores Z. Let $B={\left(\begin{array}{cc}{B}_1& B_2\end{array}\right)}^T$ where B  ₂ are the regression coefficients for the covariates of interest. Our goal is to test the null hypothesis $H_0:B_2=0$ against $H_a:B_2\ne 0$. Certain test statistics for multivariate regression require Z to be full-rank and compare the sum of squares and cross products (SSCP) matrices of the hypothesis $\tilde{R}=Z^T(H-H_r)Z$ and the SSCP error matrix $\tilde{E}=Z^T(I-H)Z$, where $H=X{(X^{T}X)}^{-1}{X}^T$ and H_r is the hat matrix from the reduced model. In our case, Z is rank deficient since mn > n for m > 1. To perform regression in this high-dimensional setting, we propose two alternative approaches. First, we adapt the Dempster trace (Dempster 1958) to our setting, which we denote by T_D, the SiMMR Dempster trace (SiMMR-D). Directly applying the original formulation of Dempster trace, SiMMR-D is the ratio between the traces of the SSCP matrices,

$$T_D=\frac{\text{tr}(Z^T(H-H_r)Z)}{\text{tr}[Z^T(I-H)Z]}.$$ (2.2)

Using the idempotency of H and the cyclical property of the trace, we can rewrite this as

$$T_D=\frac{\text{tr}[(H-H_r)(\sum _{k=1}^m{G}_k)(H-H_r)]}{\text{tr}[(I-H)(\sum _{k=1}^m{G}_k)(I-H)]}.$$ (2.3)

This equality shows that SiMMR-D is equivalent to performing MDMR using the sum of the dissimilarity matrices, which connects SiMMR-D directly to this classic distance-based regression framework. Theoretical results derived for MDMR thus apply directly to our method, which include the asymptotic null distribution of the MDMR pseudo-F statistic previously discussed in Section 2.1.

The SiMMR-D test statistic is a natural extension of MDMR, but it discards cross-product terms in the SSCP matrices that capture the correlations among modalities. As an alternative solution, we propose another test statistic that leverages the correlations of the cMDS scores. We first address the rank deficiency of the SSCP matrices by performing dimension reduction on the cMDS scores using principal component analysis (PCA). We then construct Pillai’s trace from the first K PC scores represented in the n × K matrix W. This test statistic, which we denote by $T_{\text{PC}}$ and we call SiMMR principal components (SiMMR-PC(K)), is defined through the corresponding K × K SSCP matrices ${\tilde{R}}_{\text{PC}}=W^T(H-H_r)W$ and ${\tilde{E}}_{\text{PC}}=W^T(I-H)W$ as

$$T_{\text{PC}}(K)=\text{tr}[{\tilde{R}}_{\text{PC}}{({\tilde{E}}_{\text{PC}}+{\tilde{R}}_{\text{PC}})}^{-1}].$$ (2.4)

For the design matrix of dimensions n × p, $T_{\text{PC}}(K)$ is defined for $K<n-p-1$. We investigate the choice of K through simulation and applications in Sections 4.1 and 4.2.

SiMMR-PC performs inference based on the cMDS scores of each modality, which are not unique since any orthogonal rotation of the optimal scores is also optimal (see e.g. page 396 in Mardia et al. (1979)). Orthogonal rotation of each cMDS solution can be represented as a rotation of the concatenated cMDS scores. However, owing to rotational invariance of the Pillai’s trace test statistic (Langsrud 2004), any set of cMDS solutions yields the same $T_{\text{PC}}$ test statistic.

Testing for both SiMMR-D and SiMMR-PC statistics proceeds via permutation. The permutational null distribution is generated by permuting the rows of the design matrix and computing the chosen SiMMR test statistic. The P-value for the permutation test is then the proportion of permuted test statistics less than the test statistic computed using the original design matrix. Throughout our analyses, we perform 999 permutations for computation of each SiMMR p-value.

The computational complexity of SiMMR depends on the choice of test statistic. We first assume that the vector of covariates is reasonably small so that computation of the hat matrices does not impact the complexity. For SiMMR-D, the most expensive computations are the matrix multiplications involving the $n\times nm Z$ matrices to obtain the SSCP matrices. These multiplications have a time complexity of up to $O(n^3{m}^2)$. For SiMMR-PC(K), we first apply PCA to the Z matrices, which have time complexity of $O(n^3{m}^3)$ using standard implementations. We then select the top K PCs, leading to SSCP matrix construction having a lower time complexity of $O(n^{2}K+n{K}^2)$. Thus, the relative complexity of SiMMR-D versus SiMMR-PC depends on a number of factors, but SiMMR-D should be faster when both n and m are large. For all SiMMR test statistics, the dimension of each modality q impacts the complexity of distance matrix computations but does not impact SiMMR. Empirical results for the runtime of each test statistic are presented in Section 3.2.

2.4 Alternative methods

Few other methods exist for regression of multimodal outcomes taking values in arbitrary semimetric spaces. However, we can compare our SiMMR methodology to other methods that test similar hypotheses.

For Euclidean distances computed on a single modality, MDMR is equivalent to multivariate multiple regression (MMR) using a pseudo-F statistic (McArdle and Anderson 2001). We thus compare our SiMMR test statistics to MMR on the concatenation of multimodal outcomes. When the dimensionality of the multimodal outcomes are sufficiently small ($k<n-p-1$, where k is the dimension of the outcome and p is the dimension of the covariates), we can compare our SiMMR-PC test statistic to multivariate regression using Pillai’s trace. In our analyses, Pillai’s trace is only applicable in simulations.

We can also compare SiMMR to performing individual MDMR tests while controlling for multiple comparisons (MC-MDMR). This method tests against the null hypothesis that none of the modalities are associated with the covariates of interest. We apply MDMR to each modality separately and adjust using the Bonferroni correction.

Kernel machine regression (KMR) provides an alternative framework that enables regression on complex data through kernels. For MDMR with a univariate continuous covariate, KMR is equivalent to MDMR when the kernel is equal to the doubly centered dissimilarity matrix from MDMR (Pan 2011). Unlike MDMR however, KMR requires a positive semidefinite kernel matrix. Let y be an $n\times 1$ vector of continuous outcomes, X be a n × p matrix of covariates with rows ${\mathit{x}}_i$, and ${\mathit{z}}_1,{\mathit{z}}_2,\dots ,{\mathit{z}}_m$ be n-dimensional vectors of multimodal data where n is the number of subjects. For subject i, we consider a KMR model for multimodal complex data as

$$y_i={\mathit{x}}_i^T\beta +h_1(z_{1i})+h_2(z_{2i})+\cdots +h_m(z_{mi})+e_i,$$

where $\mathit{\beta }$ is a $p\times 1$ vector of regression coefficients, $h_j,j=1,2,\dots ,m$ are unknown functions, and e_i are independent errors with variance ${\sigma }^2$. A variance components test has been proposed for testing $H_0:h_1(·)=h_2(·)=\cdots =h_m(·)$ using the score test statistic

$$S({\sigma }^2)=\frac{1}{2{\sigma }^2}{\mathit{y}}^T{P}_0\left(\sum _{j=1}^m{K}_j\right)P_0\mathit{y},$$

where $P_0=I-X{(X^{T}X)}^{-1}{X}^T$ is the projection matrix under the null hypothesis. By making several assumptions of normality and using an estimator for ${\sigma }^2$, the approximate distribution of $S({\widehat{\sigma }}^2)$ is obtained using the Satterthwaite method (Li and Cui 2012).

We compare SiMMR to KMR by treating our covariate of interest as the outcome and using the doubly centered dissimilarity matrices as kernels. That is, we choose K_j = G_j for $j=1,2,\dots ,m$, where G_j are defined in Section 2.3. For non-Euclidean distances, the G_j are not necessarily positive semidefinite and KMR may not apply. Furthermore, KMR cannot be applied in settings with other types of outcomes, including categorical and ordinal responses.

3 Simulation study

We evaluate the efficacy of our proposed SiMMR methodology through a simulation study with varying sample size, number of features, number of modalities, and correlation structure. We compare our method to MDMR, KMR, and multivariate multiple regression (MMR) where applicable.

3.1 Data generation

We simulate a multimodal dataset with correlations within and between modalities through the following setup. Let N be the simulation sample size, M be the number of modalities, and Q be the number of features per modality. Let $Y=(Y_1,Y_2,\dots ,Y_M)$ denote the full MQ-dimensional vector of multimodal data and $x\sim \text{Binomial}(0.5)$ denote a simulated binary covariate. We additionally consider settings with a continuous covariate, $x\sim N(0,1)$.

We draw the N multimodal observations from a multivariate normal distribution with correlation structure Σ of dimension MQ × MQ, where the covariate shifts the observations in directions of the eigenvectors of Σ. For a covariate effect of rank L, $Y=x\sum _{l=1}^L{c}_l{\mathit{\varphi }}_l+ϵ$, where $ϵ\sim N(0,\Sigma )$, Σ is the chosen correlation structure, and ${\mathit{\varphi }}_l,\hspace{0.17em}l=1,2,\dots ,MQ$ are the eigenvectors of Σ. In additional simulations, we will also consider the case where the covariate is only associated with one modality. To achieve this, we use the same simulation design but modify the elements of ${\mathit{\varphi }}_l$ to be 0 for features that are not part of the first modality, Y  ₁.

We propose three simulation settings by modifying the correlation structure. In our first scenario, Σ is an exchangeable correlation matrix with parameter $\rho =0.25$ to simulate multimodal data that have low correlations within modality and between modalities. Our second scenario uses an exchangeable correlation structure with $\rho =0.75$ so that the simulated multimodal data has high correlations. The third scenario has Σ instead as a first-order autoregressive structure, or AR(1), with parameter $\tau =0.9$. The AR(1) structure yields correlations that are generally higher within modality than between modalities.

In each scenario, we vary the rank and magnitude of the covariate effect. We choose L as 1, $\lfloor MQ/4\rfloor ,\hspace{0.17em}\lfloor MQ/2\rfloor$, and MQ to provide simulation settings with varying complexity of covariate effects. The contribution of each eigenvector of Σ to the covariate effect varies across settings to ensure that the strength of the effect remains similar. In particular, L = 1 has $c_1=3,\hspace{0.17em}L=\lfloor MQ/4\rfloor$ has $c_1=c_2=\cdots =c_{\lfloor MQ/4\rfloor }=0.7,\hspace{0.17em}L=\lfloor MQ/4\rfloor$ has $c_1=c_2=\cdots =c_{\lfloor MQ/2\rfloor }=0.7$, and L = MQ has $c_1=c_2=\cdots =c_{MQ}=0.15$.

For each simulation setting, we generate 1,000 multimodal datasets. In each dataset, we compare SiMMR to three competing methods: multivariate multiple regression (MMR), KMR, and multivariate distance matrix regression applied to each modality correcting for multiple comparisons using Bonferroni correction (MC-MDMR). For simulation settings where $MQ<N-2$, we perform MMR by computing Pillai’s trace based on the simulated data Y. SiMMR-PC is computed with the number of PCs K ranging from 2 to 25. For SiMMR-PC with $K\ge N-2$, all PCs are included.

3.2 Simulation results

Type I error is well-controlled across simulation settings and SiMMR test statistics. In Table 1, we display the type I error and power of MMR, KMR, MC-MDMR, SiMMR-D, and SiMMR-PC(3) across simulation settings. Supplementary Table 1 shows results for AR(1) correlation settings while also including SiMMR-PC(10) and SiMMR-PC(15). We find that the type I error rates for SiMMR test statistics are well-controlled across simulation settings, but MC-MDMR is overly conservative at high numbers of modalities M, especially in the exchangable correlation settings. Across correlation structures at sample size 100 and 10 modalities, MMR has a slightly conservative type I error. In simulations with a continuous covariate, MC-MDMR and MMR have type I error closer to 0.05 (Supplementary Tables 2 and 3).

Table 1.

Simulation results across varying sample size, number of features, covariate effect, and correlation structure.

				Exchangeable, low correlation					Exchangeable, high correlation					AR(1) correlation
PC	N	M	Q	MMR	MCM	KMR	SiMMR-D	SiMMR-PC(3)	MMR	MCM	KMR	SiMMR-D	SiMMR-PC(3)	MMR	MCM	KMR	SiMMR-D	SiMMR-PC(3)
			5	0.054	0.045	0.043	0.047	0.049	0.054	0.032	0.051	0.048	0.049	0.054	0.042	0.048	0.048	0.051
		2	100		0.017	0.039	0.032	0.034		0.017	0.032	0.032	0.035		0.036	0.037	0.037	0.042
			5		0.034	0.062	0.053	0.042		0.014	0.058	0.051	0.05		0.032	0.05	0.048	0.033
	25	10	100		0.007	0.051	0.044	0.052		0.005	0.047	0.041	0.054		0.05	0.042	0.041	0.04
			5	0.051	0.054	0.053	0.055	0.048	0.051	0.038	0.057	0.058	0.046	0.051	0.052	0.057	0.055	0.05
		2	100		0.033	0.052	0.043	0.054		0.028	0.048	0.045	0.052		0.044	0.047	0.046	0.038
			5	0.04	0.039	0.05	0.045	0.052	0.04	0.013	0.053	0.052	0.046	0.04	0.029	0.05	0.05	0.06
None	100	10	100		0.011	0.05	0.044	0.046		0.006	0.042	0.045	0.047		0.051	0.055	0.055	0.045
			5	0.54	0.948	0.968	0.964	0.89	0.215	0.664	0.732	0.732	0.512	0.233	0.671	0.714	0.714	0.521
		2	100		0.104	0.151	0.138	0.097		0.041	0.064	0.065	0.053		0.157	0.182	0.182	0.18
			5		0.328	0.498	0.475	0.32		0.086	0.195	0.194	0.131		0.21	0.347	0.349	0.237
	25	10	100		0.019	0.074	0.061	0.06		0.005	0.052	0.053	0.051		0.084	0.083	0.084	0.092
			5	1	1	1	1	1	0.953	1	1	1	0.997	0.976	1	1	1	0.999
		2	100		0.459	0.554	0.524	0.326		0.171	0.23	0.223	0.154		0.689	0.764	0.755	0.743
			5	0.253	0.946	0.982	0.98	0.928	0.092	0.448	0.652	0.646	0.476	0.185	0.81	0.929	0.928	0.871
1	100	10	100		0.052	0.161	0.145	0.095		0.018	0.084	0.084	0.057		0.248	0.418	0.411	0.311
			5	0.103	0.125	0.127	0.132	0.138	0.196	0.066	0.083	0.086	0.25	0.078	0.081	0.065	0.068	0.125
		2	100		0.083	0.129	0.113	0.889		0.025	0.048	0.044	1		0.151	0.23	0.23	0.154
			5		0.169	0.168	0.155	0.363		0.048	0.078	0.074	0.951		0.09	0.114	0.115	0.106
	25	10	100		0.048	0.183	0.145	1		0.009	0.065	0.065	1		0.227	0.787	0.796	0.517
			5	0.488	0.407	0.465	0.458	0.416	0.931	0.177	0.2	0.201	0.809	0.241	0.291	0.231	0.231	0.418
		2	100		0.987	1	0.997	1		0.127	0.196	0.188	1		0.951	1	1	0.304
			5	0.984	0.892	0.916	0.898	0.939	1	0.43	0.181	0.183	1	0.9	0.409	0.576	0.568	0.222
25%	100	10	100		0.795	1	0.999	1		0.044	0.188	0.191	1		1	1	1	0.92
			5	0.272	0.303	0.264	0.279	0.339	0.749	0.124	0.118	0.123	0.838	0.616	0.125	0.117	0.117	0.574
		2	100		0.318	0.503	0.436	0.999		0.042	0.071	0.069	1		0.393	0.635	0.632	0.317
			5		0.37	0.44	0.414	0.818		0.084	0.116	0.11	1		0.136	0.238	0.233	0.187
	25	10	100		0.194	0.577	0.492	1		0.013	0.091	0.084	1		0.554	1	1	0.954
			5	0.989	0.947	0.957	0.957	0.917	1	0.655	0.652	0.64	1	1	0.583	0.651	0.651	0.987
		2	100		1	1	1	1		0.475	0.863	0.836	1		1	1	1	0.542
			5	1	1	1	1	1	1	0.788	0.81	0.772	1	1	0.959	1	1	0.322
50%	100	10	100		1	1	1	1		0.174	0.882	0.857	1		1	1	1	1

Rejection rates are shown across varying number of subjects (N), number of modalities (M), number of features per modality (Q), and number of principal components included in the binary covariate effect (PC). The highest power among tests within each simulation setting is bolded. MMR, multivariate multiple regression using Pillai’s trace; MCM, multiple MDMR statistics after Bonferroni correction; KMR, kernel machine regression.

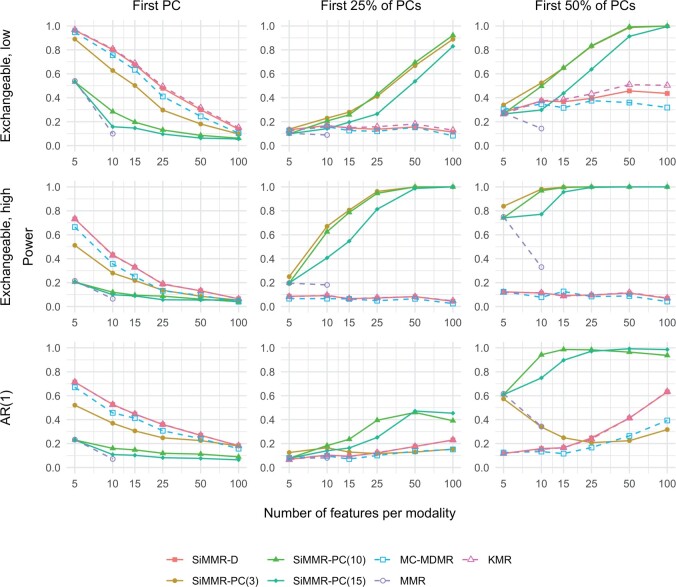
SiMMR outperforms MC-MDMR across simulation settings. For covariate effects in the first PC direction, SiMMR-D shows equal or greater power than MC-MDMR and MMR across all simulations. For more complex covariate effects, we observe that SiMMR-PC(3) yields greater power than MC-MDMR across the exchangeable correlation settings with especially large differences in the high correlation setting. Supplementary Table 1 shows that either SiMMR-PC(10) or SiMMR-PC(15) outperform MC-MDMR across all AR(1) correlation settings. Figure 2 and Supplementary Fig. 1 compare test statistics for settings with two modalities and show that these results hold across number of features Q per modality. Supplementary Figure 6 demonstrates that SiMMR particularly outperforms MC-MDMR in settings where only one modality is associated with the covariate.

Fig. 2.

Power results in simulations with exchangeable and AR(1) correlation structures for a sample size of 25. Each trace represents a different test statistic. Different simulation settings are distinguished by correlation structure across rows and by rank of the binary covariate effect across columns. Exchangeable refers to an exchangeable correlation structure with low or high correlation and AR(1) refers to a first-order autoregressive structure. MDMR, multivariate distance matrix regression; MC-MDMR, multiple MDMR statistics after Bonferroni correction; MMR, multivariate multiple regression using Pillai’s trace.

SiMMR yields comparable power with MMR and KMR. SiMMR-D and KMR produce similar power results across all settings, with KMR slightly outperforming in certain settings. In settings with $MQ<N-2$, we can apply MMR and compare the power results to SiMMR. At a sample size of 25, we find that SiMMR-PC yields similar or greater power than MMR across all settings. SiMMR-PC(10) and SiMMR-PC(15) show particularly higher power in exchangeable, high correlation, and AR(1) correlation settings (Supplementary Table 1). Across settings with a sample size of 100, Supplementary Table 1 and Supplementary Fig. 1 show that SiMMR-PC(3) has comparable or lesser power than MMR but SiMMR-PC(10) and SiMMR-PC(15) yield equal or greater power than MMR. In our setting where only one modality is associated with the covariate, we find that all of our multimodal analyses decrease in performance as the number of unassociated modalities increases (Supplementary Fig. 6).

Relative performance of SiMMR-D and SiMMR-PC depends on correlation structure and covariate effect. In settings with a covariate effect in the first PC direction, Table 1 shows that SiMMR-D yields equal or higher power than SiMMR-PC and Supplementary Figs. 2 and 3 show that this relationship holds across SiMMR-PC test statistics for 2 through 25 PCs. For exchangeable correlation structures and covariate effects in 25% or 50% of the PC directions, SiMMR-PC outperforms across sufficiently low number of PCs in the low correlation setting and across all choices in the high correlation setting. For settings with an AR(1) correlation structure, the performance of SiMMR-PC relative to SiMMR-D depends on the complexity of the covariate effect and number of features per modality. SiMMR-PC with large numbers of PCs performs better in settings with more complex covariate effects and larger number of features. Supplementary Table 1 numerically compares SiMMR-PC test statistics for AR(1) correlation settings and shows that SiMMR-PC(3) performs the best for covariate effects with 25% of PCs and 5 features per modality, but SiMMR-PC(10) and SiMMR-PC(15) outperform in other settings. Supplementary Tables 2 and 3 and Supplementary Fig. 5 show that these results hold in settings with a continuous covariate. In Supplementary Fig. 6, we observe that SiMMR-PC considerably outperforms SiMMR-D when only one modality is associated with the covariate. Supplementary Figure 7 shows running times in the high correlation setting, demonstrating that SiMMR-D runs faster than SiMMR-PC(1) in most settings considered. One notable exception is the $N=100,M=50$ setting where SiMMR-D runs in 12.03 min and SiMMR-PC(1) runs in 9.2 min on a Intel Core i9-13900H (24M Cache, up to 5.40 GHz).

4 Data applications

We apply SiMMR to two studies with novel and distinct types of multimodal data. Our first application involves neuroimaging data from the Philadelphia Neurodevelopmental Cohort (PNC; Satterthwaite et al., 2014), where we are interested in testing for age-related changes in brain connectivity and cortical structure. Our second application uses mobile health data from the National Institute of Mental Health (NIMH) Family Study of Affective Spectrum Disorders (Merikangas et al. 2014), where we test for differences in mood and physical activity measures among subjects with mood disorders. Our SiMMR applications involve vector-valued cortical thickness and sulcal depth measurements from the PNC, matrix-valued structural and functional connectivity from the PNC, and time series observations of mobile health data from the NIMH Family Study of Affective Spectrum Disorders.

4.1 Philadelphia Neurodevelopmental Cohort

We apply the SiMMR methodology to two multimodal neuroimaging datasets collected as part of the PNC (Satterthwaite et al. 2014). All participants, or their parent or guardian, provided informed consent, and minors provided assent. The study was approved by the institutional review boards of both the University of Pennsylvania and the Children’s Hospital of Philadelphia. The PNC includes 9,498 subjects between the ages of 8 and 23. Multimodal imaging was acquired on a subset of 1,601 subjects using a Siemens TIM Trio 3-T scanner with a 32-channel head coil and the same imaging sequences and parameters for every subject. Included participants in the PNC were medically healthy, were not taking psychoactive medication, and passed strict quality-assurance procedures for their imaging.

4.1.1 Image acquisition and preprocessing

In this study, we first examine a subset of 912 PNC subjects with high-quality cortical thickness (CT) and sulcal depth (SD) measurements computed from T1-weighted images (demographic details in Table 2 under “PNC Cortical Structure”). The acquisition and preprocessing for these data was originally described in Vandekar et al. (2015) and in subsequent studies (Vandekar et al. 2016; Weinstein et al. 2021). Cortical reconstruction of the T1-weighted structural images was completed using FreeSurfer (version 5.3). These cortical measurements were resampled to the fsaverage5 atlas, which has 10,242 vertices in each brain hemisphere. Cortical thickness was computed as the minimum distance between pial and white matter surfaces (Dale et al. 1999) and sulcal depth as the height of gyri (Fischl et al. 1999).

Table 2.

Demographics of the imaging and mobile health datasets.

	PNC Connectivity	PNC Cortical Structure	NIMH Family Study
Number of subjects	727	912	77
Age, mean (SD)	15.88 (3.23)	14.80 (3.50)	49.31 (17.73)
Male, n (%)	307 (42.2)	415 (45.5)	31 (40.3)
Diagnosis, n(%)
Healthy Control			34 (44.2)
MDD			26 (33.8)
Bipolar Type I			6 (7.8)
Bipolar Type II			11 (14.3)

Age, sex, and diagnosis status (applicable only to the NIMH Family Study) are shown for all subjects included in this study. The two PNC datasets are different subsets of the full PNC dataset with some overlap. PNC, Philadelphia Neurodevelopmental Cohort; FC, functional connectivity; SC, structural connectivity; CT, cortical thickness; SD, sulcal depth; NIMH, National Institute of Mental Health; MDD, major depressive disorder.

Our second application involves a set of subjects from the PNC with structural connectivity, resting-state functional connectivity, and n-back functional connectivity measurements. Acquisition and preprocessing for this sample has previously been discussed in Baum et al. (2020). In summary, 727 participants are included after strict quality assurance procedures (demographic details in Table 2 under “PNC Connectivity”). Structural connectivity is calculated from diffusion-weighted imaging using probabilistic tractography. Entries of each subject’s structural connectivity (SC) matrices are computed as the number of probabilistic streamlines connecting each pair of 400 brain regions, normalized by the total edge weight across all network connections. Functional connectivity matrices are computed separately for functional magnetic resonance imaging (fMRI) acquired while the participant is at rest (rsFC) and during the n-back task (n-back FC). Functional connectivity between each pair of the 400 brain regions is computed as the Pearson correlation coefficient between the mean regional blood-oxygen-level-dependent (BOLD) time series.

4.1.2 Application of SiMMR

Previous studies of the PNC have demonstrated neurodevelopmental changes in cortical thickness (Vandekar et al. 2015) and the coupling between cortical thickness and sulcal depth (Vandekar et al. 2016). We apply SiMMR to the cortical structure data for regression on age while controlling for sex. We construct dissimilarity matrices based on the Euclidean distance. We compare SiMMR to KMR by treating age as the outcome while treating sex as a nuisance covariate.

Using SC and FC matrices from the PNC, Baum et al. (2020) demonstrated neurodevelopmental changes in a coupling metric computed between SC and n-back FC while separately examining coupling between SC and rsFC. In our application, we incorporate all three modalities and apply SiMMR to determine if there is an association between SC, n-back FC, and rsFC jointly with age while controlling for sex and relevant quality metrics. The quality metrics are identical to those in Baum et al. (2020), which includes mean relative framewise displacements calculated on the resting-state and n-back fMRI scans and mean relative displacement from interspersed volumes with a b value of 0 s/mm² calculated from the diffusion-weighted images. We choose to compute dissimilarities between functional connectivity matrices using the log-Euclidean distance (Arsigny et al. 2006), which addresses several issues with using Frobenius distances for positive semidefinite matrices. For structural connectivity, we use the Frobenius distance since the matrices are not guaranteed to be positive semidefinite. We compare SiMMR to KMR by using the doubly centered dissimilarity matrices as kernels while treating age as the outcome and sex and quality metrics as nuisance covariates.

To assess rejection rate in these applications, we use a resampling-based approach to evaluate rejection of the null hypothesis in smaller sample sizes. That is, we draw 1,000 samples without replacement and compute P-values for all test statistics for each sample. The rejection rate is then calculated as the proportion of p-values with value less than our nominal type I error rate of 0.05.

4.1.3 Results

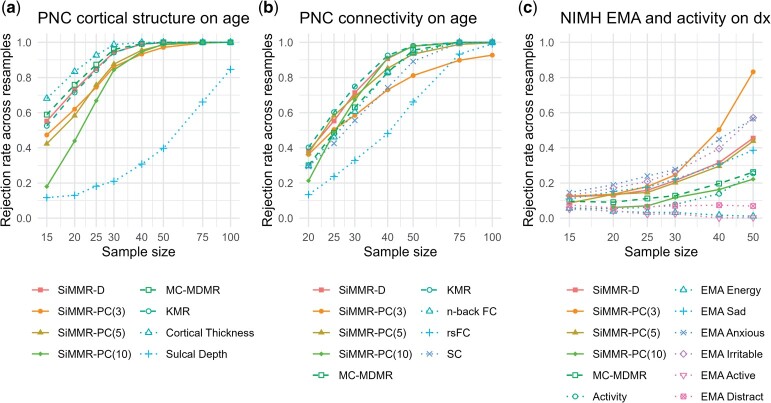
For changes of cortical structure during brain development, joint analysis of cortical thickness and sulcal depth does not outperform unimodal analysis of cortical thickness. MDMR on cortical thickness has a 83.3% rejection rate to detect an age association at a sample size of 20, whereas MC-MDMR, KMR, and SiMMR-D only have a 75.9%, 71.5%, and 72.9% rejection rate, respectively. At the same sample size, MDMR on sulcal depth only has a 13.0% rejection rate. These results are consistent with a previous study finding age-related changes in cortical thickness using the PNC study (Vandekar et al. 2015). We find that age-related changes in sulcal depth require a larger sample size to detect, which leads inclusion of sulcal depth to reduce rejection rate in our multimodal analyses. Our results do not contradict previous reports of age-related patterns in the coupling between cortical thickness and sulcal depth (Vandekar et al. 2016); however, this relationship does not drive higher rejection rate for detection of age when jointly analyzing the two modalities.

In PNC structural and functional connectivity data, Fig. 3a shows that SiMMR-D and KMR have a high rejection rate for detecting age-related changes in connectivity, achieving rejection rates of 90.7% and 92.5%, respectively at a sample size of 40. Comparing this multimodal analysis to unimodal analyses, only MDMR on structural connectivity achieves similar results with a 83.1% rejection rate at the same sample size and combining all three unimodal analyses via MC-MDMR yields a rejection rate of 82.9%. These results suggest that multimodal structural and functional analysis via SiMMR and KMR is better able to detect changes in brain connectivity than any unimodal analysis or the combination of unimodal analyses. Supplementary Figure 4 shows that using the Frobenius distance for functional connectivity matrices leads to lesser rejection rate for both multimodal and unimodal analyses of rsFC and n-back FC.

Fig. 3.

Rejection rates across resamples in applications of SiMMR to imaging and mobile health data. Each trace represents a different test statistic. Power curves for individual modalities are obtained through multivariate distance matrix regression (MDMR). PNC, Philadelphia Neurodevelopmental Cohort; FC, functional connectivity; rsFC, resting-state functional connectivity; SC, structural connectivity; EMA, ecological momentary assessment; MC-MDMR, multiple MDMR statistics after Bonferroni correction; MMR, multivariate multiple regression using Pillai’s trace.

4.2 NIMH Family Study

We also apply SiMMR to mobile health data collected as part of the National Institute of Mental Health (NIMH) Family Study of Affective Spectrum Disorders, an observational cohort study of subjects recruited from the greater Washington, DC, metropolitan area (Merikangas et al. 2014). All participants provided informed consent, and the study was approved by the Combined Neuroscience Institutional Review Board at the National Institutes of Health. Each participant was evaluated for mental disorders via a comprehensive semistructured diagnostic interview, with mental disorders defined by Diagnostic and Statistical Manual for Mental Disorders, IVth Edition (DSM-IV) criteria. Further details on the recruitment and exclusion criteria can be found in Merikangas et al. (2014).

4.2.1 Mobile health data preprocessing

For our study, we examine the subset of 384 participants with actigraphy and ecological momentary assessment (EMA) data. Physical activity data were collected via accelerometers (Actiwatch Spectrum, Philips Respironics, Murrysville, PA, USA), which produced activity counts for every minute of the day measured via movement-related voltage signals recorded by the accelerometer. Participants completed EMA four times a day approximately four hours apart through a smartphone during the same 2-week assessment period when accelerometry data are being collected. For our analyses, we include self-reported mood variables in EMA, which consist of 7-point Likert scales to measure the degree to which participants felt active, anxious, energetic, sad, distracted, and irritable. Further details on the actigraphy, EMA data collection, and activity data processing were presented in Johns et al. (2019), Lamers et al. (2018), Merikangas et al. (2019), and Shou et al. (2017).

For our analysis, we include 77 subjects with at least 1 week of data. We summarize the activity and EMA time series by averaging time points within each weekday across 2 weeks. The time points consist of 1,440 min per day for activity data and 4 times per day for EMA data. For time points with missing data for either week, we use the single available measurement. We exclude subjects from our analyses who are missing both measurements for any time point of EMA data. Our mobile health dataset consists of 77 participants with 10,080 activity time points and 28 EMA time points for each of the six EMA variables. Demographic details are available in Table 2.

4.2.2 Application of SiMMR

A previous study used mobile health data from the NIMH Family Study to understand the joint relationship between physical activity and mood, and to identify diagnosis-related differences in the association between activity, energy, mood, and sleep (Merikangas et al. 2019). This study summarized the activity data into four bins per day to align with the EMA measurements, which only included measures of sadness and energy. We use SiMMR to identify diagnosis effects while leveraging the full activity time series as well as all six EMA variables. For each modality, we calculate dissimilarity matrices using the Euclidean distance between time series. Our analysis is performed by using SiMMR to simultaneously regress activity and the EMA variables on diagnosis status while controlling for age and sex. KMR cannot be applied in this setting since our covariate of interest is categorical. To assess rejection rate across resamples in this application, we use the approach previously described in Section 4.1.2.

4.2.3 Results

Figure 3c demonstrates that SiMMR-PC can detect diagnosis-related changes jointly among physical activity and EMA measurements of mood with a high rejection rate at larger sample sizes. Multimodal analysis using SiMMR-PC(3) has a rejection rate of 83.2% at sample size 50, which far outperforms unimodal MDMR analyses where the highest rejection rate is 57.1% from MDMR on EMA-measured feelings of irritability. EMA-measured feelings of anxiety and sadness and measures of physical activity as assessed by accelerometers also show associations with diagnosis, having rejection rates of 56.6%, 38.6%, and 25.5%, respectively at sample size 50. Other unimodal analyses show notably lower rejection rates across sample sizes considered. Combining these unimodal analyses via MC-MDMR yields a low rejection rate as a result with MC-MDMR having a rejection rate of 26.2% for the same number of subjects. These observations suggest that joint analysis of physical activity and mood measurements using SiMMR can identify diagnosis-related changes more effectively than use of existing methodologies for unimodal or combined unimodal analyses.

4.3 Selection of SiMMR-PC

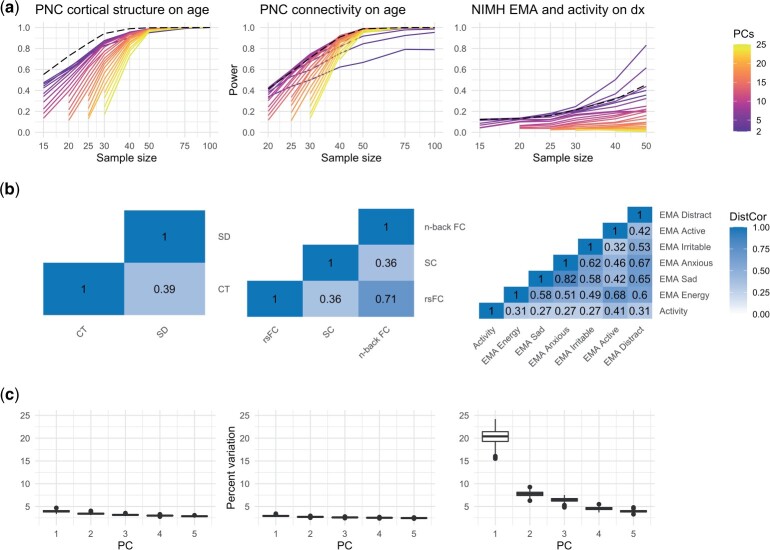
In our applications, selection of the number of PCs included in SiMMR-PC is important to detect associations of interest. Figure 4a shows that in our application to PNC cortical thickness and sulcal depth, SiMMR-D outperforms SiMMR-PC across all numbers of PCs considered. Figure 4b shows in our PNC connectivity study that SiMMR-D and SiMMR-PC show comparable performance at varying numbers of PCs. However, Fig. 4c shows that SiMMR-PC(3) and SiMMR-PC(4) have higher power for detection of diagnosis than SiMMR-D at higher sample sizes in the NIMH Family Study application. To investigate possible explanations for these results, we compute the distance correlation (Székely et al. 2007) between each modality using data from all subjects. Figure 4a shows that the distance correlation between PNC cortical thickness and sulcal depth is relatively low (0.39) and the distance correlations among certain EMA measurements in the NIMH Family Study are considerably higher ($>0.60$ for certain pairs of modalities). Figure 4c further shows that the percent of variation explained by the first few PCs across resamplings of 50 subjects is considerably higher in the NIMH Family Study application. These findings demonstrate that distance correlation and scree plots from PCA can inform when to use SiMMR-PC and how to select the number of PCs included. Based on our observations, we suggest use of SiMMR-PC in applications with high distance correlation among modalities and choosing PCs that explain a large portion of the variation among MDS scores.

Fig. 4.

SiMMR-PC results across number of PCs and related exploratory analyses in real data applications. (a) shows the rejection rate across resamples for SiMMR-PC test statistics across number of PCs compared to SiMMR-D (dashed line). (b) displays the distance correlation (DistCor) among modalities in each application using the full sample. (c) shows the percent of variation explained by PCs across the 1,000 resamplings of size 50 in each application. PNC, Philadelphia Neurodevelopmental Cohort; EMA, ecological momentary assessment.

5 Discussion

The emergence of technology and organized efforts for collection of multiple types of health data provides a great opportunity to jointly examine associations between multimodal assessments and health outcomes. To integrate and perform inference in multimodal settings, we develop a flexible distance-based testing framework called SiMMR, which can incorporate data from arbitrary semimetric spaces. We demonstrate in simulation and real data that our test statistics can identify associations with relatively small sample sizes and across a wide range of data structures. We propose two alternative test statistics that provide higher power in certain settings, generally outperforming existing distance-based methods.

We find that relative performance of SiMMR versus unimodal analysis depend on the included modalities and their correlation. In our simulations and applications, the benefit of performing SiMMR is limited when modalities show lesser correlation. Furthermore, in simulations where most modalities are not associated with simulated covariates, we found that our multimodal tests decreased in performance as more data modalities were added. We also observe through our application to PNC cortical structure that modalities with weak associations can reduce power of a multimodal analysis, even when the correlation between modalities is known to be important (Vandekar et al. 2016). Our results emphasize that knowledge about the data structure should inform whether application of SiMMR is appropriate and the choice of modalities to include.

Comparing SiMMR test statistics and KMR, SiMMR-PC generally outperforms SiMMR-D when the correlation among modalities is high and the effect of interest is sufficiently complex. SiMMR-D and KMR show comparable performance across our simulations and applications; however, KMR could not be applied when considering categorical outcomes and cannot be applied when using non-Euclidean dissimilarity metrics. For selection among SiMMR-PC statistics, we found that the first three or four PCs provided optimal power across most of our settings, with additional PCs needed in simulations with complex correlation structures. We used standard scree plots to choose among PCs that explain the most variation; however, other investigations have suggested that PCs explaining less variation may be more closely associated with outcome measures (Liu et al. 2020). While our choices of SiMMR-PC statistics performed well across our analyses, further investigation may suggest alternative data-driven approaches for choosing the optimal number of PCs.

We choose to use Euclidean and log-Euclidean distances throughout our analyses; however, other distances could be employed. Several studies have compared choices of distance in various data types including positive semidefinite matrices (Dryden et al. 2009), time series (Wang et al. 2013), and brain connectivity maps (Shehzad et al. 2014). Future investigations could further examine how the choices of distance measures influences SiMMR results, particularly when different types of distances (e.g. Euclidean and non-Euclidean) are chosen.

The SiMMR-PC test statistic performs multivariate regression through the principal components of the outcome variable, which is related to previous work in multivariate regression. In particular, SiMMR-PC resembles PC-based test statistics in the multiple phenotype setting with multiple outcome variables and a single covariate (Liu and Lin 2019); but these statistics do not apply to our settings with multiple covariates. Our investigation is closely related to previous work performing likelihood ratio tests on PCs, which also tested other approaches such as regularization and shrinkage applied to covariance estimates (Ullah and Jones 2015). Future studies of SiMMR could incorporate other PC-based statistics and alternative high-dimensional test statistics.

6 Software

SiMMR is implemented as an R package. SiMMR and the simulation code used in this article are available at https://github.com/andy1764/SiMMR. Analysis codes for our data applications are available on request from the corresponding author (chenandr@musc.edu).

Funding

This work was supported by the National Institute of Neurological Disorders and Stroke (grant numbers R01 NS085211 and R01 NS060910), the National Multiple Sclerosis Society (RG-1707-28586), the National Institute of Mental Health (R01 MH123550, R01 MH112274, and R01 MH119219), the National Science Foundation Graduate Research Fellowship Program, and a seed grant from the University of Pennsylvania Center for Biomedical Image Computing and Analytics (CBICA). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.

Conflict of interest statement. None declared.

Data availability

Data used in this article to support our findings are from the Philadelphia Neurodevelopmental Cohort (PNC) Study and the NIMH Family Study of Affective Spectrum Disorders. The PNC data are openly available at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2. The NIMH Family Study data are not shared.