Summary Paragraph
Hippocampal representations that underlie spatial memory undergo continuous refinement following formation1. To track the spatial tuning of neurons dynamically during offline states we used a novel Bayesian learning approach based on the spike-triggered average decoded position in ensemble recordings from freely-moving rats. Measuring these tunings, we found spatial representations within hippocampal sharp-wave ripples that were stable for hours during sleep and were strongly aligned with place fields initially observed during maze exploration. These representations were explained by a combination of factors that included pre-configured structure before maze exposure and representations that emerged during theta oscillations and awake sharp-wave ripples on the maze, revealing the contribution of these events in forming ensembles. Strikingly, the ripple representations during sleep predicted the future place fields of neurons during re-exposure to the maze, even when those fields deviated from previous place preferences. In contrast, we observed tunings with poor alignment to maze place fields during sleep and rest before maze exposure and in the later stages of sleep. In sum, the novel decoding approach allowed us to infer and characterize the stability and retuning of place fields during offline periods, revealing the rapid emergence of representations following novel exploration and the role of sleep in the representational dynamics of the hippocampus.
Introduction
Memories are continuously refined after they form. Different stages of sleep play important roles in the transformations that memories undergo, but many aspects of these offline processes remain unknown. Memories that involve the hippocampus are particularly affected by sleep, which alters molecular signaling, excitability and synaptic connectivity of hippocampal neurons 2,3. Memories are considered to be represented by the activity of ensembles of neurons that form upon experience 4. In the rat hippocampus, these ensembles are tuned to locations within a maze environment 5. Indeed, an animal’s position can be decoded from the spike trains recorded from a population of neurons (Fig. 1a)6. Spatial representations, however, do not remain stationary following initial formation. In many cases the place fields (PFs) of hippocampal neurons develop and shift during traversals of an environment 7,8, remap upon exposure to different arenas 9, and reset or remap even with repeated exposure to the same place 1,10. This presents a challenge to traditional decoding approaches that rely on the assumption that hippocampal neuron always represent the same maze positions as they do on a specific behavioral session 11, including mazes that the animal has yet to experience 12.
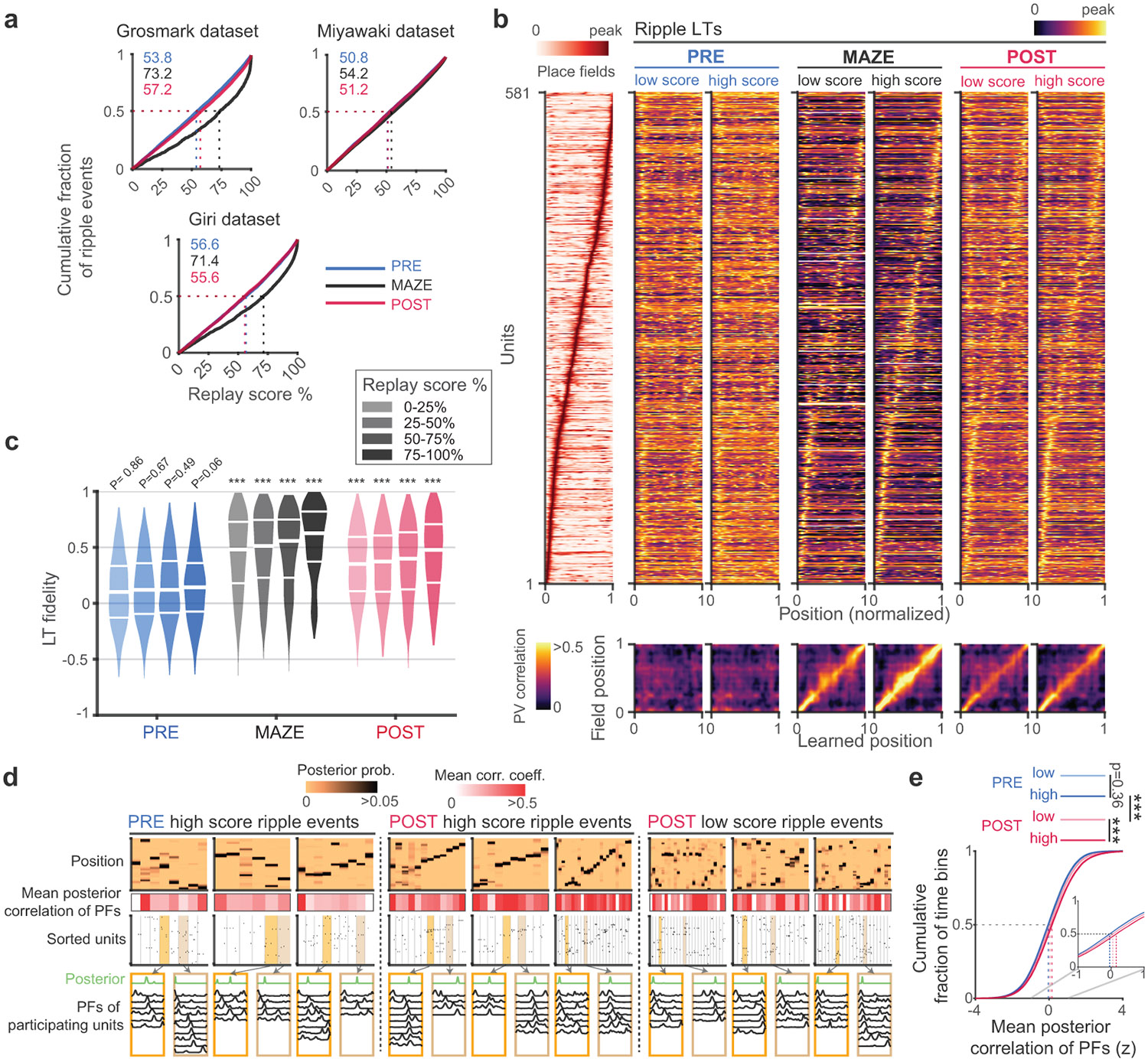
Fig.1. Bayesian learning of hippocampal spatial tunings during offline states.
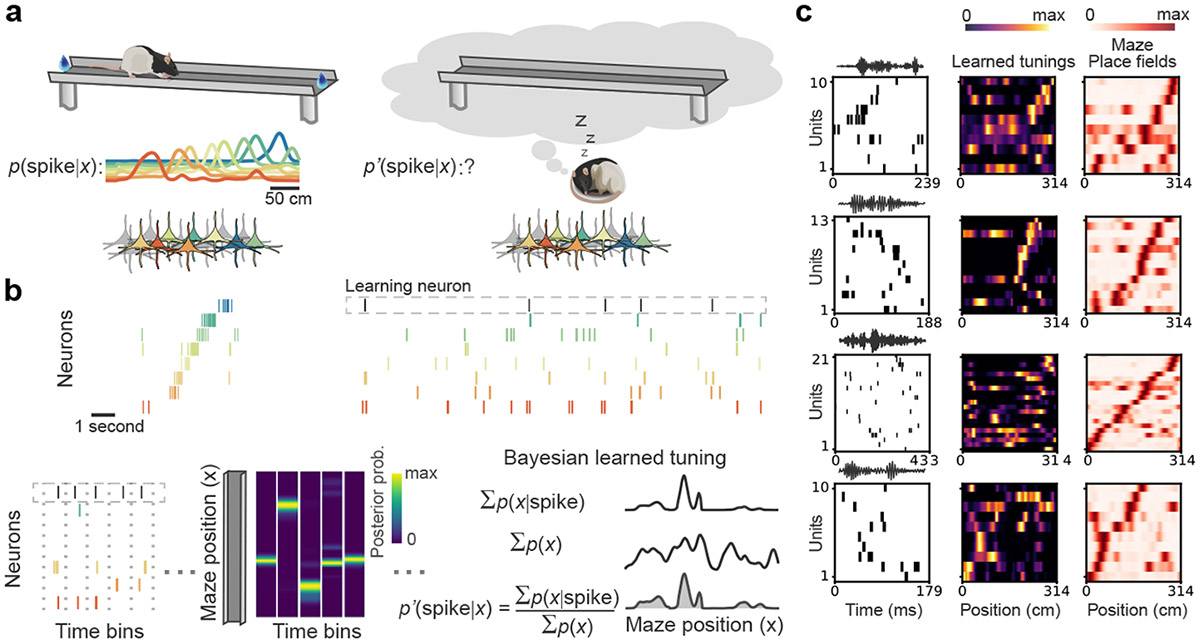
(a) Hippocampal place cells show tuning to specific locations (place fields) on a linear track maze. When animals sleep or rest outside of the maze, the spiking of these neurons is no longer driven by maze location but may represent an internally generated simulation of or another location. (b) We employed Bayesian learning to assess each neuron’s tuning for internally generated cognitive space, , using the place fields of all other neurons recorded on the maze, under the assumption of conditional independence among Poisson spiking neurons conditioned on space (see Methods). Top left, sample spike raster during an example maze traversal. Top right, spiking patterns of the same cells during a brief window in sleep. For each iteration, one cell is selected as the learning neuron. Bottom, left to right, population activity extracted for time bins in which the learning neuron spikes. Next, posterior probability distributions are constructed using the spikes and track tunings of the other neurons during these time-bins. The Bayesian learned tuning is equal to the summation of the posterior distributions over these time-bins (), normalized by the overall likelihood of each track location () obtained across the entire offline period. (c) Example tunings derived from single ripple events recorded during rest and sleep in the home cage following maze exposure. For each offline ripple event, shown are the spike raster (left) with ripple band power above, tunings learned for each unit from the raster (middle), and the place fields on the maze (right). While in principle, tunings can be derived from individual events, in practice they are best evaluated by combining across multiple ripple events (Extended Data Fig. 1).
We conjectured that modifications of spatial representations would take place during sleep when connections between some neurons are strengthened while those between other neurons are weakened 2,13. Consistent with this conjecture, cells that become active in a new environment continue to reactivate for hours during sharp-wave ripples in sleep 14, suggesting that offline processes during sleep involve the spatial representations of hippocampal neurons. Moreover, the collective hippocampal map of space shows changes following sleep 15 and some cells express immediate early genes during this period which can mark them for sleep-dependent processing 16. However, while spatial representations are readily measured from the spiking activities of neurons when animals explore a maze environment, access to these non-stationary representations is lost when animals cease exploring, making it challenging to evaluate how spatial representations are shaped over time.
To evaluate and track the spatial preferences of a neuron across online and offline periods, we developed a novel method based on Bayesian learning 17 (Fig. 1b-c). Under the assumption of conditional independence of Poisson spike counts from hippocampal neurons conditioned on location, we derived the Bayesian learned tuning (LT) of a neuron from the spike-triggered average of the posterior probability distribution of position determined from the simultaneous spiking patterns of all other neurons in the recorded ensemble, including for time periods when animals were remote from the maze locations for which position was specified. In this formalism, the internally generated preference of a neuron for a location is revealed through its consistent coactivity with other neurons in the ensemble associated with that position. These Bayesian learned tunings allowed us to track, for the first time, the place preferences of neurons as they evolved in exceptionally long-duration (up to 14 h) hippocampal unit recordings, enabling us to identify those periods and events in which the firing activities of neurons were consistent or inconsistent with place fields on the maze and to characterize the plastic offline changes in tuning relative to the broader ensemble.
Spatial tunings during ripples in post sleep align with place fields on the maze.
We first examined how tuning curves are impacted by an animal’s experience on a maze by characterizing the representations of neurons from spike trains recorded from the rat hippocampus in experiments where rest and sleep in a home cage both preceded (PRE) and followed (POST) exposure to a novel track (MAZE), where rats ran for water reward. To examine spatial tunings in each brain state separately, we first separated unit and local field potential data recorded from hippocampal region CA1 into different states using general criterion (see Methods) for rapid eye movement sleep (REM, sleep featuring prominent hippocampal theta), ripple periods during rest and sleep (150-250 Hz band power accompanied by high multi-unit firing rates), slow-wave sleep (SWS) periods exclusive of ripples, and active wake (with prominent theta). We calculated place fields and the learned tunings for each epoch for all pyramidal units with peak spatial firing rates > 1 Hz on the maze (Fig. 2a-c). We limited the initial analysis to the first 4h of POST, during which we expect greater similarity with maze firing patterns 14. Learned tunings showed a wide distribution of fidelity to place fields from PRE to POST depending on brain state. Population vector (PV) correlations between spatial bins in place fields and learned tunings (Fig. 2b) and LT-PF Pearson correlation coefficients (Fig. 2c) demonstrated that the highest fidelities to place fields were observed in spatial representations during theta and ripples on the maze, as expected 18-20. However, among offline periods only spatial tunings evidenced during POST, particularly those during ripples, showed significant correlations with unit place fields in MAZE, and notably not those during PRE. LTs that displayed fidelity to MAZE PFs could be composed from individual ripple events (Fig. 1c) but improved upon averaging over multiple events (Extended Data Fig. 1). These differences were not due to differences in the proportion of time in rest versus sleep or in the number of active firing bins (Extended Data Fig. 1c). The fidelity of LTs further varied during SWS; tunings derived from ripples during periods of high delta (0.5-4 Hz) and high spindle (8-16 Hz) power displayed higher PF fidelities compared to periods with low power (Extended Data Fig. 2a-c). Interestingly, we observed weak but significantly aligned representations consistent with the maze during POST REM sleep, when vivid dream episodes are frequently experienced 21. These representations were best aligned at the trough and descending phase of REM theta (Extended Data Fig. 2f) which may reflect that only specific time windows during REM sleep correspond to previous experience 22. Overall, these findings provide a measurement of the temporal variations in hippocampal ensemble firing patterns and indicate that place fields maintain internal tunings consistent with their place fields on the maze primarily during ripples in POST SWS.
Fig. 2. Bayesian learned tunings during MAZE and offline states.
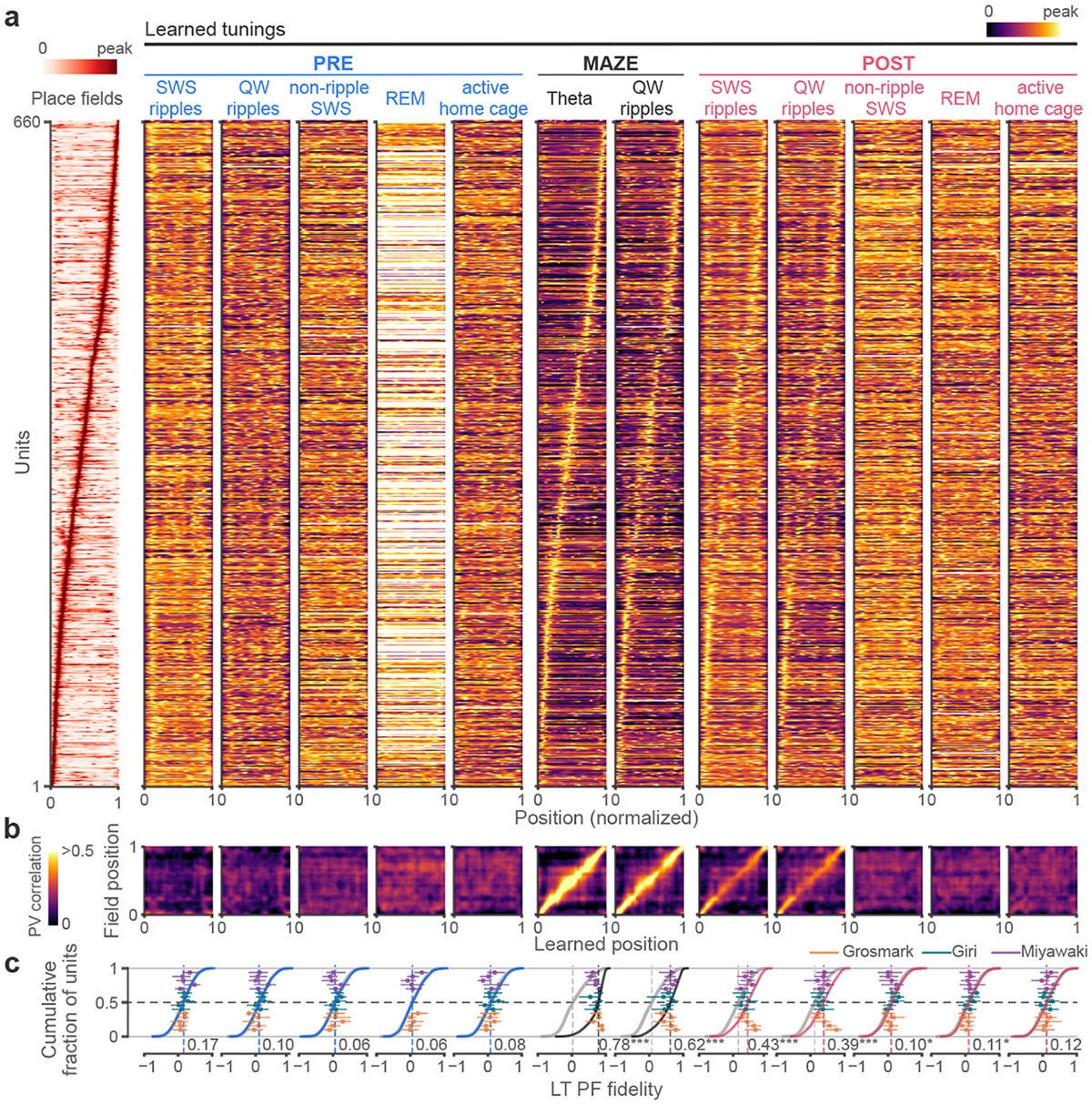
(a) Place fields (PFs) of hippocampal units pooled across sessions (n = 660 units from 15 sessions and 11 rats) alongside Bayesian learned tunings (LTs) calculated separately for each behavioral epoch (PRE, MAZE, POST) and brain state (ripples in slow-wave sleep (SWS) and quiet waking (QW), non-ripple SWS, REM, and active home cage). Blanks reflect instances without neuronal firing for the specified state and epoch (e.g. no REM activity in PRE). Only tunings learned on the MAZE and POST bear a visual resemblance to place fields, particularly those during ripples. (b) The LT-PF correlations of the population vectors across space calculated between place fields and each set of learned tunings in (a). (c) Cumulative distributions of PF fidelity for each set of LTs in (a), defined as Pearson correlation coefficients between the LTs and PFs (LT-PF fidelity), compared to null distributions obtained from unit identity shuffles (gray, but occluded in many instances). Individual session medians (dots) and corresponding interquartile range (IQR; horizontal lines) are overlaid. Only tunings learned on the MAZE and POST displayed significant median fidelities compared (one-sided) to null distributions obtained from 104 unit identity shuffles (PRE; SWS ripples: p = 0.24; QW ripples: p = 0.93; non-ripple SWS: p = 0.17; REM: p = 0.53; active home cage: p = 0.21; MAZE; theta: p < 10−4; ripples: p < 10−4; POST; SWS ripples: p < 10−4; QW ripples: p < 10−4 ; non-ripple SWS: p = 0.04; REM: p = 0.02; active home cage: p = 0.12; see also Extended Data Fig. 2). * p < 0.05, *** p < 0.001.
Spatial representations are more stable in post-maze sleep.
We next tracked the learned tunings of neurons over time and examined the consistency of their place preferences within different epochs. We calculated LTs from all ripple events within 15 min windows sliding in 5 min steps during each session, from PRE through MAZE and the first 4 h of POST. Sample unit tunings from a recording session are shown in Fig. 3a (additional examples provided in Extended Data Fig. 3). These examples show stable LTs for multiple successive time windows during POST, and in some instances also during PRE. To quantify the overall stability of LTs for each unit, we used Pearson correlation coefficients to assess the consistency of the learned tunings across time windows within and between behavioral epochs (Fig. 3b). High off-diagonal values in the correlation matrices within an epoch indicated that the LT remained stable during that epoch. For the example units in Fig. 3a we compared the median LT stability values from each epoch against shuffle distributions generated by randomizing the unit identities of the LTs at each time window (Fig. 3c). This z-scored LT stability was > 0 in both PRE and POST in this session (Fig. 3d) and for data pooled across all sessions (Fig. 3e), but it was significantly higher in POST compared to PRE, revealing that POST sleep representations were more stable than those in PRE. When we measured the LT stability across time windows from PRE to POST epochs, to examine their consistency from before and after the novel maze exposure when place fields first form, the PRE w/ POST LT stability was not significantly > 0 in the example session (median = 0.65, p = 0.16), rose to significance in the pooled data (p < 10−4, Wilcoxon signed rank test (WSRT, n = 660)), but remained significantly lower than the stabilities observed within PRE and POST (PRE vs PRE w/ POST: p < 10−4; POST vs PRE w/ POST: p < 10−4, WSRT (n = 660)), thus signaling that only a small minority of units maintained the same consistent spatial tuning from before to after maze exposure.
Fig. 3. Stability of learned tunings during ripples in PRE and POST.
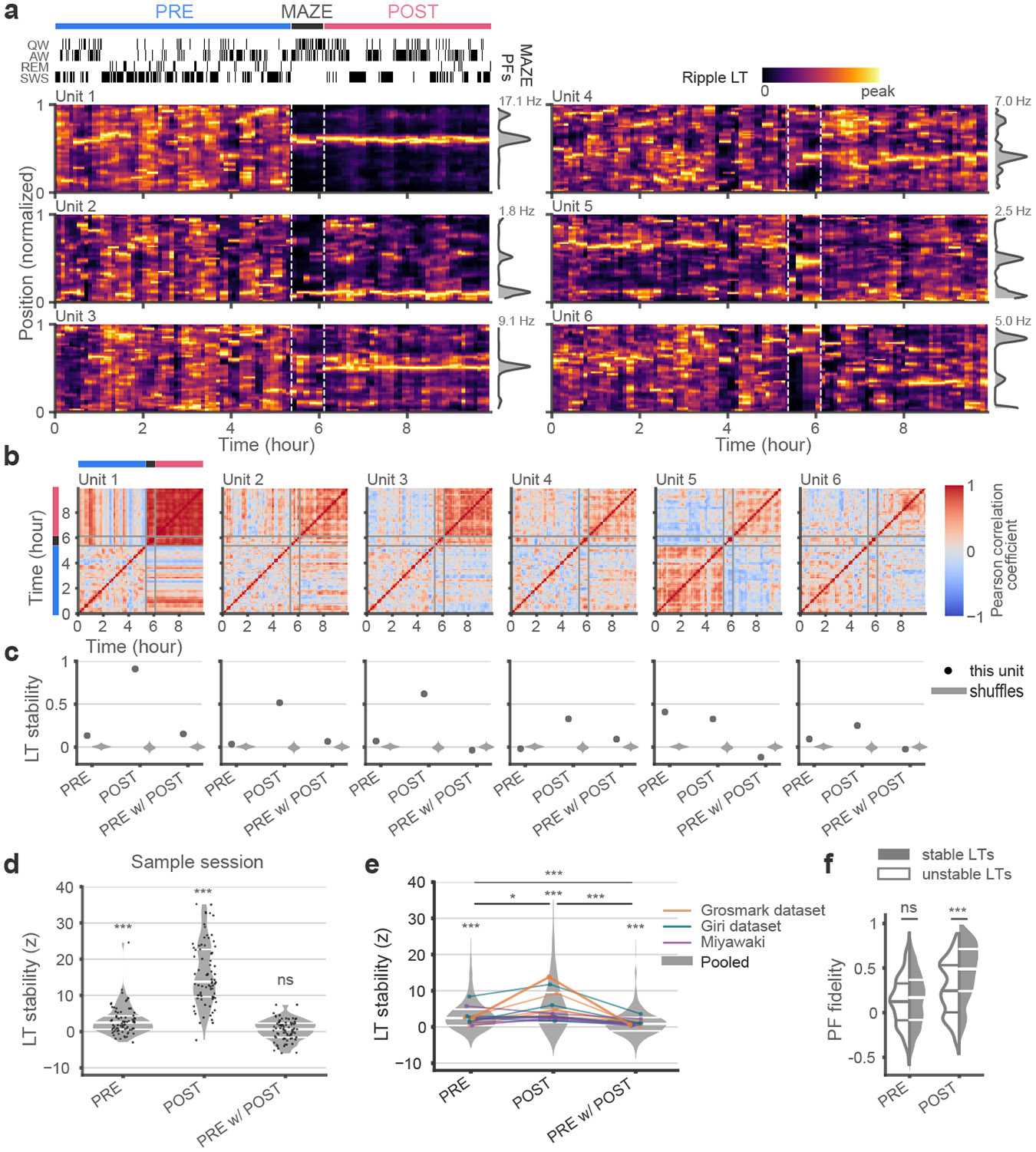
(a) Heat maps of LTs exclusively during ripples for sample units in sliding 15 min windows (hypnogram on top left indicates quiet waking (QW), active waking (AW), rapid eye movement (REM) sleep, and slow-wave sleep (SWS) states) from PRE through POST (maze PFs in gray, vertical on right) show stable LTs during POST. Units 5 and 6 show stable tunings during PRE ripples that do not align with their maze PFs. (b) The matrix of LT correlation coefficients across time for units in (a). (c) Stability of the LTs (black) for units in (a), defined as the median of the correlation coefficient between LTs from non-overlapping 15-min windows. Violin plots (gray) show chance distributions obtained from non-identical units randomly scrambled across windows (1000x). While LTs of units 5 and 6 were stable within PRE and POST, they were not consistent across these epochs. (d and e) Unit LT stabilities z-scored against unit ID shuffles were significantly > 0 for the sample session (d) (PRE: median = 2.51, p = 3.9 x 10−9; POST: median = 13.78, p = 2.8 x 10−14; PRE-POST: median = 0.65, p = 0.16, two-sided Wilcoxon signed rank test (WSRT; n = 77)) with individual units shown as dots, and (e) all sessions pooled together (PRE: median = 2.47, p = 4.4 x 10−67; POST: median=3.10, p = 4.6 x 10−79; across PRE w/ POST median = 0.95, p = 1.1 x 10−13, two-sided WSRT (n = 660)). LT stability was higher in POST than in PRE (p = 0.02) or between PRE w/ POST (p < = 1.9 x 10−70, two-sided WSRT (n = 660)). Median values from individual sessions overlaid and color coded by dataset. (f) Distributions of PF fidelity (r(LT, PF)) for units with stable (z > 2) versus unstable (z < 2) LTs showed no difference in PRE (p = 0.29) but were higher for stable units in POST (p = 2.1 x 10−11, two-sided Mann Whitney U Test (n = 660)). *p<0.05, ***p < 0.001.
A subset of units showed remarkably stable learned tunings during PRE which compelled us to consider whether the LTs of those units might show higher fidelity with maze PFs. To test this conjecture, we divided units into “stable” and “unstable” by whether their z-scored LT stability was > or < 2 (PRE: 371 stable vs. 289 unstable; POST: 454 stable vs. 206 unstable), respectively, in both PRE and POST (Fig. 3f). In POST, units with both stable and unstable LTs showed significant PF fidelity (p < 10−4, comparison against 104 unit identity shuffles). However, the PF fidelity of units with stable LTs was significantly higher compared to units with unstable LTs in POST. Importantly, in PRE there was no significant difference between PF fidelities of stable and unstable units, and neither of these subsets showed significantly greater PF fidelity compared to a surrogate distribution obtained by shuffling unit identities (PRE stable LTs: p = 0.06; PRE unstable LTs: p = 0.35; vs. POST stable LTs: p < 1e-4; POST unstable LTs: p = 2x10−4)). Next, we tested whether the subset of ripple events in PRE that featured high replay scores (Supplementary Information and Extended Data Fig. 4) might show better PF fidelity. However, we found little alignment of between maze PFs and LTs constructed from these events. These findings demonstrate that although some units in PRE display stable learned spatial tunings, these tunings do not typically anticipate the future place fields of these neurons but rather show a broad distribution of alignments with the maze place preferences. In contrast, LTs constructed from low replay score events from POST showed strong fidelity to maze PFs, despite the absence of sequential trajectories in low score events (Supplementary Information and Extended Data Fig. 4). Thus, events that would typically be classified as non-replays in POST maintain representations that are faithful to the maze place-fields.
While the stability and fidelity of spatial tunings were significantly greater in POST, these features did not last indefinitely. In our data that involved multiple hours of POST, we observed decreases in both the fidelity and stability of Bayesian learned tunings over the course of sleep (Fig. 4). The similarity of sleep representations to maze place-fields decreased progressively over POST, eventually reaching levels similar to PRE. The stability of spatial tunings also decreased over this period, indicating that at the ensemble level these representations become less coherent in later periods of sleep. The dissolution of representational alignment with the maze over the course of sleep may reflect an additional important aspect of sleep, distinct from that of reactivation and replay 23,24.
Fig. 4. Spatial representations are randomized over the course of sleep.
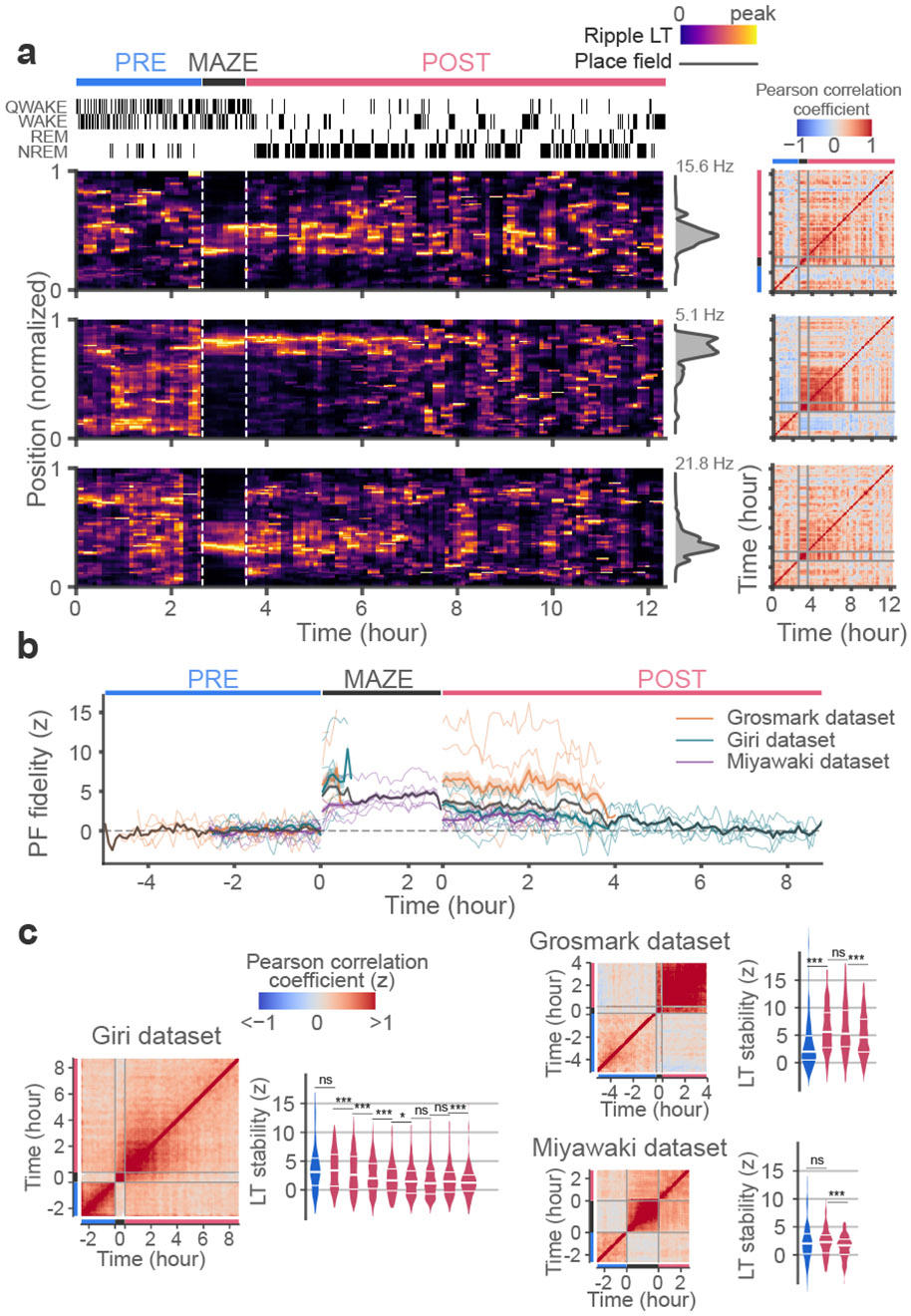
(a) Heat maps of ripple LTs for sample units in sliding 15 min windows throughout a sample long duration session show gradual decreases in LT stability over time. A matrix of correlation coefficients between LTs from different time windows is provided on the right for each unit. (b) PF fidelity (correlation coefficient between LTs and PFs) shows a gradual decrease over time in POST. The color traces show median values across units within each individual session. The black trace and gray shade depict the median and interquartile range of the pooled data. PRE and MAZE epochs of differing durations were aligned to the onset of MAZE while POST epochs were aligned to the end of MAZE. (c) Left panels show LT stability correlation matrices averaged over all recorded units, shown separately for each dataset. Here, the matrix for each unit was z-scored against unit-ID shuffles prior to averaging. Right panels show the distribution of z-scored LT stability in overlapping 2-hour blocks during POST, separately for each dataset. Comparisons across blocks were performed using two-sided Mann Whitney U Tests with no correction for multiple comparisons (Giri dataset; p = 0.81, p < 10−4, p < 10−4, p < 10−4, p = 0.04, p = 0.08, p = 0.77, p = 0.005; Grosmark dataset; p < 10−4, p = 0.75, p < 10−4; Miyawaki dataset; p = 0.47, p = 2x10−4). *p < 0.05, **p < 0.01, ***p < 0.001.
Stability and retuning of representations during sharp-wave ripples in sleep
Recent studies report that place fields drift and frequently remap upon repeat exposures to the same environment 1,10,15,25-27 though it is unclear when and how these representational changes emerge. Given that the tunings learned during POST ripples display a diversity of place-field fidelities, some aligned but others misaligned with maze PFs, we asked whether these representations relate to the future spatial tunings of the cells. In three recording sessions from two animals, we re-exposed rats back to the maze environment after ~9 h of POST rest and sleep (Fig. 5a). We labelled these epochs “reMAZE” and compared the place fields across maze exposures with the ripple LTs from the intervening POST period (Fig. 5b-d). POST ripple LT’s showed significant correlations with place fields from both maze exposures, indicating a continuity of representations across these periods. However, PFs were not identical between MAZE and reMAZE (Fig. 5b), illustrating that neuronal representations drift and remap in the rat hippocampus 1 (see also Extended Data Fig. 5). Consistent with our hypothesis that representational remapping emerging during POST could account for the deviations in PFs observed between repeated exposures to the maze, in instances where we saw reMAZE PFs congruent with MAZE PFs (top panel, Fig. 5e), the POST LTs for those cells showed strong fidelity with the maze period. However, in instances where reMAZE PFs deviated from the MAZE PFs (bottom panel, Fig. 5e, and time-evolved examples in Fig. 5h and Extended Data Fig. 6), the POST LTs for those units predicted the PFs observed during maze reexposure. Likewise, we observed a significant correlation between PF fidelities in POST and the reMAZE-MAZE similarity (Fig. 5f). These correlations were significant for cells with both weak and strong PF stability on the MAZE (Extended Data Fig. 5e, f) and were stronger for tunings learned from SWS than from quiet waking (Extended Data Fig. 5g, h). To better examine whether ripple representations during POST can presage representational changes across maze exposures, we performed a multiple regression analysis to test the extent to which reMAZE PFs are explained by MAZE PFs and LTs from PRE or POST (first 4 h). We also included the average LTs (over PRE and POST) to control for the general deviations of LTs that were not specific to any unit, as well as “latePOST” LTs constructed from the last 4 h of POST prior to reMAZE (Fig. 5g). This regression demonstrated a significant contribution (beta coefficient) for MAZE PFs, as expected, indicating that there is significant continuity in place-fields across maze exposures. However, it also revealed that POST LTs, but not PRE LTs, impact the PF locations in maze reexposure. Remarkably, we found no significant contribution from the late POST LTs, indicating that our observations do not simply arise from temporal proximity between POST sleep and the maze reexposure, nor from general dissolution and instability of LTs in time (see also Extended Data Fig.5i), but rather reflect rapid changes in representations that are manifested in the initial hours of sleep. Inspection of individual LTs (Fig. 5h) showed multiple instances in which LTs from early POST periods showed spatial preferences that shifted away from MAZE place-fields but were better aligned with their future reMAZE tunings. Overall, these results demonstrate the critical role of POST sleep in stabilizing and reconfiguring the spatial representations of hippocampal neurons across exposures to an environment.
Fig. 5. POST ripple tunings predict future place fields on maze re-exposure.

(a) Timeline for sessions (n=3) in which the animal was re-exposed to the same maze track (reMAZE) after > 9 h from initial exposure (MAZE). We used the first 4 h of POST to calculate LTs. (b) Cumulative distribution of PF similarity between MAZE and reMAZE, compared (one-sided) to null distributions obtained from unit identity shuffles (gray) (p < 10−4). (c) Cumulative distribution of POST PF fidelity (correlation coefficient between POST LTs and MAZE PFs) (p < 10−4). (d) Cumulative distribution of correlation coefficient between POST LTs and reMAZE PFs (p < 10−4). In panels b-d, p-values were obtained by comparing the median (one-sided) against those from surrogate distributions from 104 unit-identity shuffles. (e) Example units with high MAZE/reMAZE similarity and high POST PF fidelity (top row), or low MAZE/reMAZE similarity and low POST PF fidelity (bottom row). The rightmost column shows the degree of similarity between the reMAZE PFs and POST LTs for each unit. (f) MAZE/reMAZE similarity correlated with POST PF fidelity. The best linear fit and 95% confidence intervals are overlaid with black line and shaded gray, respectively. (g) Multiple regression analysis for modeling reMAZE PFs using PRE LTs, MAZE PFs, POST LTs, and latePOST LTs (beyond 1st 4 h) as regressors (R2 = 0.19, p < 10−4, c0 =0, c1 =0.13, β1 =−0.02, p = 0.77, β2 =0.31, p < 10−4, β3 =0.14, p < 10−4; β4 = −0.01, p = 0.58 ; p-values were obtained by comparing the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of reMAZE PFs). The overlaid circular markers depict regression coefficients obtained by leaving out one session at a time. (h) Heatmaps of ripple LTs for sample units in sliding 15 min windows from different sessions (session hypnograms on top, as in Fig. 3; MAZE and reMAZE place fields and LTs during PRE, POST, and latePOST on the right). Note the rapid emergence of learned tunings during POST that showed alignment with their future place fields upon reMAZE. ***p <0.001
Sleep representations are driven by awake ripples and theta oscillations.
Our findings thus far indicate that the neuronal firing patterns during POST ripples reflect both stable and retuned place-field representations following the maze. We next investigated the factors that conspire to establish these patterns. Two recent studies 28,29 indicate that, more so than place field activity, the spike patterns of neurons during waking theta oscillations provide the necessary conditions for establishing the firing patterns observed during POST sleep. Other studies, however, suggest that waking ripples are a primary mechanistic candidate for generating stable representations 30,31. Adding further complication, several studies have indicated that PRE and POST ripples share overlapping activity structure 14,32,33, suggesting limits on the flexibility of sleep representations. To better understand the respective contributions of these different factors on the representations in POST sleep, we performed a multiple regression to test the extent to which POST LTs are explained by: PRE LTs, MAZE PFs, LTs of MAZE theta periods, and LTs of MAZE ripples (Fig. 6a). Remarkably, we found that the beta coefficients for all of these regressors were significant. The beta coefficient for MAZE theta LTs was significant, indicating that waking theta oscillations, particularly at the trough of theta (Extended Data Fig. 7e, f), are important for the formation of ensemble representations 28,29. Consistent with this, the stability of PFs on the MAZE was significantly predictive of the stability and fidelity of LTs during POST (Extended Data Fig. 7 and Extended Data Fig. 8). However overall, MAZE ripple LTs had the largest beta coefficient, indicating that firing patterns during waking ripples on the maze have the most lasting impact on POST ripple activity 30,31. Surprisingly, the second largest beta coefficients were observed for PRE ripple LTs, indicating that next to MAZE patterns, patterns configured in PRE also provide an important determinant of POST sleep activity 32-34. Consistent with this, we observed a significant correlation between the PF fidelity in PRE and the PF fidelity in POST (Fig. 6b).
Fig. 6. Ensemble patterns during awake theta and ripples and a diversity of pre-existing representations impact the tunings in POST sleep.
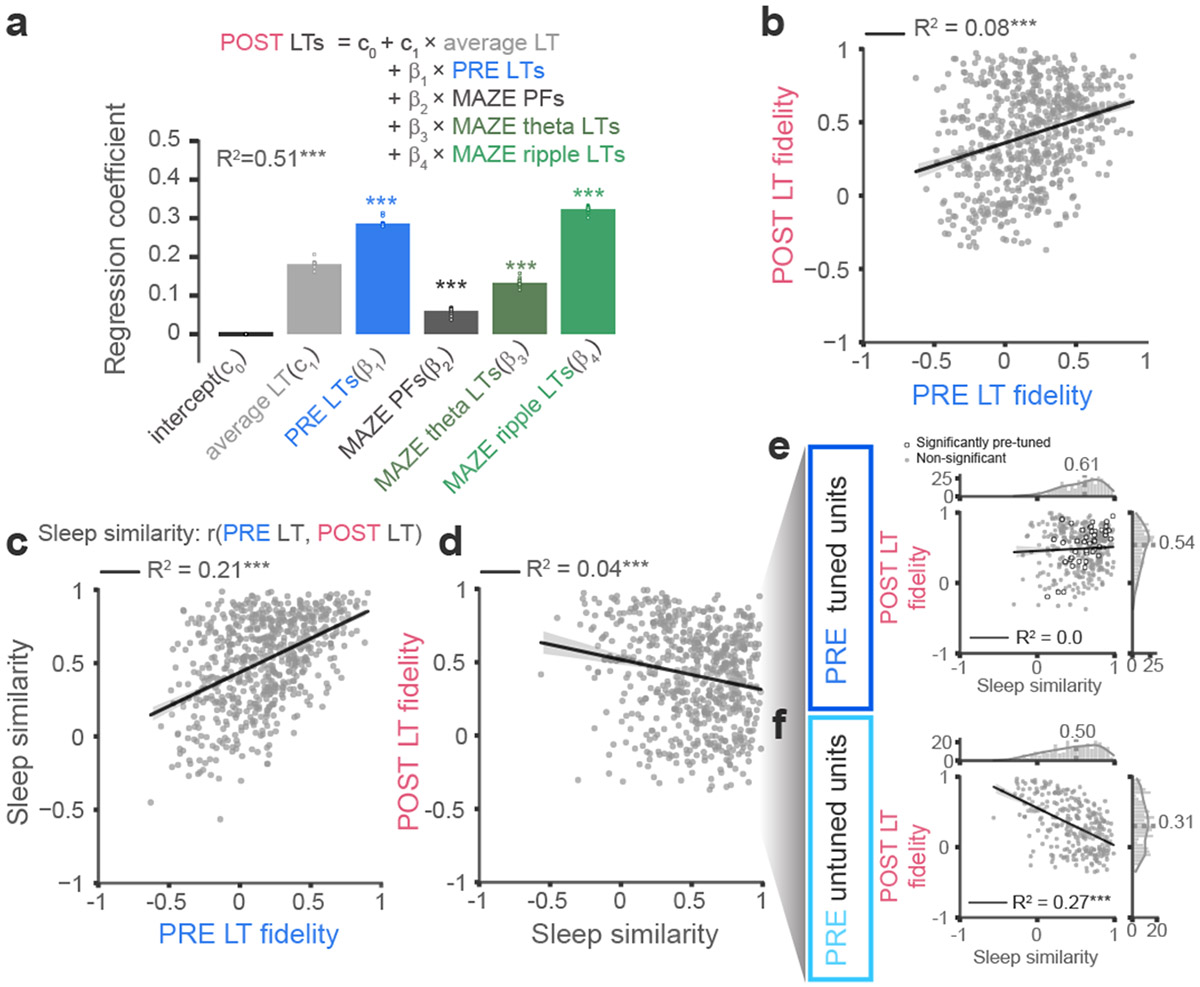
(a) Multiple regression analysis for estimating the dependence of POST LTs on PRE LTs, MAZE PFs, MAZE theta LTs, and MAZE ripple LTs shows that POST LTs were most significantly impacted by PRE LTs and MAZE ripple LTs (R2 = 0.51, p < 10−4, c0 = 0, c1 =0.18, β1 = 0.29, p < 10−4, β2 =0.06, p < 10−4, β3 = 0.13, p < 10−4, β4 = 0.32, p < 10−4, p-values were obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of POST LTs). The overlaid circles mark regression coefficients obtained by leaving out one session at a time. (b) PF fidelity (correlation with MAZE PF) was significantly correlated between PRE and POST LTs. In b-f, the best linear fits and 95% confidence intervals are overlaid with black line and shaded gray, respectively. (c) Sleep similarity (correlation between PRE and POST LTs) was correlated with PRE PF fidelity, indicating that high fidelity PRE LTs are preserved in POST. (d) An overall negative correlation between sleep similarity and POST PF fidelity. When we split units into PRE-tuned (PRE PF fidelity > median of shuffle distribution) and PRE-untuned units (PRE PF fidelity < median of shuffle distribution), (e) sleep similarity and POST fidelity were both high for PRE-tuned cells, with a positive correlation (R2 = 0.50, p = 0.0004) for significantly PRE-tuned cells (white circles, 46 out of all 660 units). (f) For PRE-untuned cells, a negative correlation between POST PF fidelity and sleep similarity indicates a continuum of flexible retuning to maze PF. *** p < 0.001.
These observations suggest that despite the absence of maze tuning in PRE sleep, some cells maintain similar representations between PRE and POST. Sleep similarity, which measures the consistency of LTs across PRE and POST by assessing the correlation between PRE LTs and POST LTs, was significantly correlated with PF fidelity in PRE (Fig. 6c); thus, PRE LTs that aligned with maze PFs, presumably by chance, maintained those LTs in POST (see also individual examples in Extended Data Fig. 3, e.g. in Rat N). On the other hand, sleep similarity showed a weak negative correlation with the PF fidelity in POST, consistent with the notion that these measures respectively reflect neuronal rigidity and flexibility. To better understand the difference between PRE and POST LTs, we separated units into relatively “PRE-tuned” cells (PRE PF fidelity > median of shuffles), and “PRE-untuned” cells (PRE PF fidelity < median of shuffles). PRE-tuned cells showed generally high POST PF fidelity along with high sleep similarity (Fig. 6e), with a positive correlation in these variables in the further subset of cells that were significantly PRE-tuned cells relative to unit-ID shuffles. In contrast, PRE-untuned cells showed a significant negative correlation between sleep similarity and POST fidelity (Fig. 6f); those with high sleep similarity were poorly tuned in POST, while those that reconfigured from PRE to POST, showed better fidelity to maze PFs. These analyses therefore reveal the contribution of PRE sleep to maze representations and POST activities; cells whose representations are already aligned with maze place fields in PRE maintain those same representations in POST, but other neurons display a broad range of flexible reconfiguration that is inversely proportional to their rigidity 34 across PRE and POST.
Discussion
The observations of dynamic representations in offline states made possible by Bayesian learning have important implications for our understanding of how learning and sleep impact the place-field representations of hippocampal neurons. First, we found that neural patterns occurring in PRE reconfigure during exposure to a novel environment. While ripple events during pre-exposure occasionally scored highly for replays, spatial representations were not coherent among active neurons during these periods, as cells with very divergent place fields often fire within the same time bins (e.g. Extended Data Fig. 4d, e). These observations suggest that continuous patterns in the decoded posteriors of spike trains could emerge spuriously. Consistent with this notion, it has been noted that the measures and shuffles used to quantify replays inevitably introduce unsupported assumptions about the nature of spontaneous activity 11,33,35,36. We propose that only for those periods and events in which there is strong correspondence between the Bayesian learned tunings and neurons’ place-fields, can it be considered valid to apply Bayesian decoding to offline spike trains 11.
Among the brain states we examined, sharp-wave ripples in early sleep offered the representations that best aligned with the place fields on the maze. These early sleep representations emerged from a confluence of factors, including carryover of firing patterns from pre-maze sleep (in both PRE-tuned and PRE-untuned units)33. Most notably, however, our analysis revealed a key role in awake activity patterns during theta oscillations, particularly at the trough of theta, which corresponds to the encoding phase 37,38 (whereas the peak of theta corresponds to greater dispersion and prospective exploration 39,40) and more prominently, those during sharp-wave ripples, in generating the ensemble coordination that underlies spatial representations during sleep. This may indicate a greater similarity in co-firing across awake and sleep ripples, compared to theta 18, though we note that theta and ripple LTs both provide strong PF fidelity (Fig. 2). These observations are consistent with the hypothesis that an initial cognitive map of space is first laid down during theta oscillations 19,28,29,41, then stabilized and continuously updated by awake replays based on the animal’s (rewarded and/or aversive) experiences on the maze 30,31,42-44. Once ensembles are established, they reactivate during the early part of sleep 14,45. However, sleep representations were not always exact mirror images of the maze place-fields, and our Bayesian learning approach allowed us to measure those deviations for individual neurons. Remarkably, we found that these early-sleep ripple representations proved predictive of place fields on re-exposure to the maze. Based on these observations, we propose that representational drift in fact arises rapidly from retuning that takes place during early sleep sharp-wave ripples rather than noisy deviations that develop spontaneously over time. This could reflect the possibility that single-trial plasticity rules that give rise to new place fields 46-48 are also at work when animals go to sleep. Furthermore, we conjecture that hippocampal reactivations during sleep does not play a passive role in simply recapitulating the patterns already seen during learning but represents a key optimization process generating and integrating new spatial tunings within the recently formed spatial maps.
Overall, representations remained stable and consistent with the maze for hours of sleep in POST, despite the absence of strong sequential replay trajectories during ripples in POST sleep. Reconciling observations based on studies that measure neuronal reactivation using pairwise or ensemble measures with those that focus on trajectory replays has until now represented a challenge to the field 49. Our study consolidates these views by demonstrating that faithful representations, which are consistent with pairwise and ensembles measures of reactivation, persist for hour-long durations. However, the trajectories produced by these cell ensembles do not necessarily provide continuous high-momentum sweeps through the maze environment 50,51, as we found high fidelity spatial tunings even among low replay score ripple events in post-maze sleep. Instead, trajectories simulated by the hippocampus during sleep ripples may explore pathways that were not directly experienced during waking but can serve to better consolidate a cognitive map of space 42,52. Additionally, we found increasing instability and drift in the spatial representations of neurons over the course of sleep, indicating that late sleep, like PRE, features more randomized activity patterns 23,53. It is also worth noting that we found weak alignment between maze place fields and learned spatial tunings during REM sleep, but that this alignment was best at the trough of theta 54,55. It may be that under a different behavioral paradigm such as with frequently repeated maze exposures56 or salient fear memories 57, , we might have uncovered tunings more generally consistent with dream-like replays of maze place-fields 58. On the other hand, it is also worth noting that most dreams do simply not reprise awake experiences 22. The randomization of representations, as we see during the bulk of REM and late stages of slow-wave sleep, may reflect an important function of sleep, driving activity patterns from highly-correlated ensembles to those with greater independence 23,24,59, which may be important for resetting the brain in preparation for new experiences 13.
In sum, the Bayesian learning approach provides a powerful means of tracking the stability and plasticity of representational tuning curves of neurons over time, which provides significant insights into how ensembles patterns form and reconfigure during offline state. Provided a sufficient number of units are randomly sampled (Extended Data Fig. 1), a similar approach can be readily extended to investigate the dynamics of internally-generated representations in other neural systems during both sleep and awake states, including within rehearsal, rumination, or episodic simulation 52,60.
Methods
Behavioral task and data acquisition.
We trained four water-deprived rats to alternate between two water wells in a previously habituated home box. Due to the large number of recorded units obtained from each animals, such sample sizes of are typical for demonstrating consistency among subjects. The selections of animals and recorded hippocampal units were essentially random, but experimenters were not blind to experimental condition. Water rewards during the alternation were delivered via water pumps interfaced with custom-built Arduino hardware. After the animals learned the alternation task, they were surgically implanted under deep isoflurane anesthesia with 128 channel silicon probes (8 shanks, Diagnostic Biochips, Glen Burnie, MD) either unilaterally (one rat) or bilaterally (three rats) over the dorsal hippocampal CA1 subregions (AP: −3.36 mm, ML:± 2.2 mm). Following recovery from surgery, the probes were gradually lowered over a week to the CA1 pyramidal layer, which was identified by sharp wave-ripple polarity reversals and frequent neuronal firing. After ensuring recording stability, the animals were exposed to novel linear tracks during one (three rats) or two (one rat) behavioral sessions (in total five sessions from the four rats). During each session, the implanted animal was first placed in the home box (PRE, ~ 3 hours) with ad libitum sleep (during the dark cycle). Then, the animal was transferred to a novel linear track with two water wells that were mounted on platforms at either end of the track (MAZE, ~ 1 hour). After running on the linear track for multiple laps for water rewards, the animal was returned to the home box (aligned with the start of the light cycle) for another ~10 hours of ad libitum sleep (POST). In four of these sessions, following POST the rats were re-exposed to the same linear track for another ~ 1h of running for reward (reMAZE).
Wideband extracellular signals were recorded at 30 kHz using an OpenEphys board 61 or an Intan RHD recording controller during each session. The wideband activity was high-pass filtered with a cut-off frequency of 500 Hz and thresholded at five standard deviations above the mean to extract putative spikes. The extracted spikes were first sorted automatically using SpykingCircus 62, followed by a manual passthrough using Phy 63 (https://github.com/cortex-lab/phy/). Only units with less than 1% of total number of spikes in their refractory period (based on the units’ autocorrelograms) were included in further analysis. Putative neurons were classified into pyramidal and interneurons based on peak waveform shape, firing rate, and interspike intervals 64,65. For analysis of local field potentials (LFP, 0.5-600 Hz), signals were filtered and downsampled to 1250 Hz.
The animal’s position was tracked using an Optitrack infrared camera system (NaturalPoint Inc, Corvalis, OR) with infrared-reflective markers mounted on a plastic rigid body that was secured to the recording headstage. 3D position data was extracted online using the Motive software (Version 2.1.1), sampled at either 60 Hz or 120 Hz, and later interpolated for aligning with the ephys data. Although, we attempted to track the animal’s position during each entire session, including in the home cage, the cage limited visual access from our fixed cameras. Additionally, in one session the position data for reMAZE was lost during the recording. All animal procedures followed protocols approved by the Institutional Animal Care and Use Committees (IACUC) at the University of Michigan and conformed to guidelines established by the United States National Institutes of Health.
These data comprised the Giri dataset used in our study. We also took advantage of previously published data described in detail in a previous report 14. These data consisted of recordings of unit and local field potential from the rat hippocampus CA1 region performed using Cheetah software (Version 5.6.0) on a Neuralynx (Bozeman, MT) DigitalLynx SX data-acquisition system, with PRE rest and sleep, exposure to a novel MAZE, and POST rest and sleep: the Miyawaki dataset (3 rats, 5 sessions; PRE, MAZE, POST, each ~ 3 hours)14,23 and the Grosmark dataset (4 rats, 5 sessions; PRE, and POST, each ~ 4 hours and MAZE, ~ 45 minutes)34,66. Vectorized rat images used in the manuscript were generously provided by Etienne Ackermann https://github.com/kemerelab/ratpack/.
Units.
In all of these data, we quantified the stability of units across sleep epochs; PRE and POST in Miyawaki and Grosmark sessions and PRE, POST, and latePOST in Giri datasets (Extended Data Fig. 8). Consistency in isolation distance and firing rate over the sleep epochs were used as stability measures 23. Units with isolation distance > 15 and firing rate that remained above 33% of the overall session mean during all epochs were considered stable. For all of the analyses in the paper, we required stability during PRE and POST but for reMAZE prediction analyses (Fig. 5 and Extended Data Fig. 5), we required stability across PRE, POST, and latePOST. See Supplementary Tables 1-3 for further details of each session. These data are available upon request from the corresponding author.
Place field calculations.
To calculate place fields, we first linearized the position by projecting each two-dimensional track position onto a line that best fit the average trajectories taken by the animal over all traversals within each session. The entire span of the linearized position was divided into 2 cm position bins and the spatial tuning curve of each unit was calculated as occupancy-normalized spike counts across the linearized position bins. We only considered pyramidal units with MAZE place-field peak firing rate > 1 Hz for further analyses, except in Fig. 5h and Extended Data Fig. 3 where all stable pyramidal units were included.
Place field stability.
In each session, the MAZE epoch was divided into 6 blocks with matching number of laps and then the place fields were separately calculated for each block. Each unit’s PF stability was defined as the median correlation coefficient of place fields across every pair of blocks.
Spatial Information.
The spatial information 67 was calculated, as the information content (in bits) that each unit’s firing provides regarding the animal’s location:
in which is the unit’s firing rate in position bin i, is the unit’s overall mean firing rate, and is the probability of occupancy of bin .
Local field potential analysis and brain state detection.
We estimated a broadband slow wave metric using the irregular-resampling auto-spectral analysis (IRASA) approach 68, following code generously shared by Dan Levenstein and the Buzsaki lab (https://github.com/buzsakilab/buzcode). This procedure allows calculation of the slope of the power spectrum which was used to detect slow-wave activity. The slow-wave metric for each session followed a bimodal distribution with a dip that provided a threshold to distinguish slow-wave sleep (SWS) from other periods. A time-frequency map of the local field potential (LFP) was also calculated in sliding 1s windows, step size of 0.25 s, using the Chronux toolbox (Version 2.12)69. To identify high theta periods, such as during active waking or REM sleep 23,70, the theta/non-theta ratio was estimated at each time point as the ratio of power in theta (4-9 Hz in home cage and 6-11 Hz on the linear track, as we typically observe a small shift in theta between these periods 70) to a summation of power in delta frequency band (1-4 Hz) and the frequency gap between the first and second harmonics of theta (10-12 Hz during home cage awake and REM epochs and 11–15 Hz during MAZE). To calculate the ripple power, multichannel LFP signals were filtered in the range of 150-250 Hz. The envelope of the ripple LFP was calculated using the Hilbert transform, z-scored and averaged across the channels. Only channels with the highest ripple power from each electrode shank were used in the averaging.
Detection of ripple events.
For each recording session, multi-unit firing rates (MUA) were calculated by binning the spikes across all recorded single units and multi-units in 1 ms time bins. Smoothed MUA was obtained by convolving the MUA with a Gaussian kernel with and z-scoring against the distribution of firings rates over the entire session. Ripple events were first marked by increased MUA firing, periods when the smoothed MUA crossed 2z and the boundaries were extended to the nearest zero-crossing time points. The ripple events that satisfied the following criteria were considered for further analysis: a) duration between 40 and 600 milliseconds, b) occurrence during SWS with a theta-delta ratio < 1 and ripple power > 1.s.d. or during quiet waking (QW) with ripple power > 3 s.d. of the mean, and c) concurrent speed of the animal below 10 cm/sec (when available). All ripple events were subsequently divided into 20 millisecond time bins. The onsets and offsets of the events were adjusted to first time bins with at least two pyramidal units firing. We split ripples with silent periods > 40 ms into two or more events. Histograms of ripple durations are reported in Extended Data Fig. 2d.
Bayesian learned tunings.
Consider the following. We recorded from a set of independent neurons during a maze session and parametrized their spatial tuning curves for positions on the maze. However, subsequent to the session, we lose the tuning curve for one of the neurons, neuron . Or maybe this neuron was inaccessible during the maze session, because of faulty electronics, but we regain access to it in sleep afterward the maze. Is there any way that we can learn the tuning curve of neuron , using information gleaned from firing activity of the other neurons over some period of time T?
While this may initially seem impossible, if the neurons are all indeed conditionally dependent on position , and if some internal estimate, thought, or imagination of continues to drive the spiking activity of these neurons, then with enough observation it should be possible to extract the tuning curve through Bayesian learning. Intuitively, if neuron , has a preference for some position , then whenever the animal is thinking of , even if it is no longer on the maze, the neuron should fire alongside all of the other neurons that have a similar preference for . But if neuron fires randomly with different neurons, then it cannot be said to have any particular spatial tuning for .
In this paper, we are concerned with estimating tuning curves based on internal representations of position, rather than an external marker. Our motivating hypothesis is that if during the periods of estimation, while some neurons may change their tuning functions, the ensemble largely maintains its internal consistency, and thus it is informative to measure the tuning curves of individual neurons during these periods. Bayesian decoding has been long used to analyze the position information encoded by the ensemble during offline periods. However, it relies on the assumption that the position preference of neurons does not change over time and experience, which is known to be false for hippocampal neurons.
We model hippocampal neurons as conditionally independent Poisson random variables with firing rates that vary over discretized spatial bins. When an animal explores the maze the firing rate parameters (i.e., tuning curves) of observed neurons, , are typically calculated using the occupancy normalized spike-triggered average position:
| (1) |
where the indicator function during periods in which the animal is in position bin and otherwise. In this work, we also account for directional tuning curves, as discussed below. We define the learned tuning curve for neuron as as the rate parameter of the distribution , for which we may have some prior beliefs .
The likelihood of the observed data during the learned tuning period can be described as
| (2) |
where we’ve taken the tuning curves of the other neurons as known parameters. Using Bayes’ rule, we can directly formulate the likelihood of from this equation, and then calculate a maximum likelihood estimate. Note that because the position is considered unobserved during our period of interest, it does not enter into this equation. However, we can introduce it:
| (3) |
| (4) |
where in the last line, we’ve taken advantage of the independence of the position and the activity of the other neurons on the parameters. In Bayesian estimation, the prior, , allows for the integration of other information into the estimate. For example, we could assume a bias towards a previous measurement that is refined over time or choose a prior such that the shape of reflects general previous observations of the tuning curves of neurons during behavior, or more generally one that enforces smoothness over position 71. In this work, we assume a general uninformative prior. In such a case, it can be shown (see section Bayesian learned tuning with uninformative prior) that the maximizing values for the tuning curve are:
| (5) |
Examining this equation, we see that it is quite similar to the normal occupancy-normalized tuning curve estimate, except that we now have the posterior distribution of rather than binarized counts of occupancy. Moreover, note that this is not actually a closed form solution, as the parameters appear on both sides of the equality. To avoid an iterative solution, we approximate , which is sensible in the case of large numbers of neurons, as the position dependency on any single neuron is small. Thus, we arrive at our estimator for the learned tuning of neuron .
| (6) |
Finally, note that the denominator here represents the estimated average occupancy during the period in which we are calculating LTs. For the illustrations and analyses where LTs are evolved over very short time windows (e.g. for 15 min sliding windows in Fig. 4 and elsewhere, defined as ), we used the estimated average occupancy over the entirety of such periods in the recording (e.g. ripples over all of POST in Fig. 4) in the denominator. Thus, for these short windows:
| (7) |
For the tuning curves of the observed neurons, since the majority of the sessions (16 out of 17) consisted of two running directions on the track, we first calculated the posterior joint probability of position and travel direction and then marginalized the joint probability distribution over travel direction 72:
| (8) |
in which signifies the travel direction. With the assumption of independent Poisson-distributed firings of individual units conditioned on maze position and direction 6,72, we have:
| (9) |
In equation (9), characterizes the mean firing rate of unit at position bin and direction and is the bin duration used for decoding, which was chosen = 20 ms in our analyses. By marginalizing the left hand side of equation (9) over direction , we obtain
| (10) |
which we have used above to calculate in each time bin.
We note that while this approach relies on the place fields of neurons measured on the maze to calculate the posterior probability of , a given neuron’s LT does not depend on its own place field but is learned based on the coherence of its firing with the other neurons in the ensemble. A neuron that fires mostly randomly with other neurons in a sample epoch will produce a spatial LT that will be diffuse across locations, whereas a neuron that fires only with neurons the encode a specific segment of the maze will produce an LT that represents that same segment. Critically, if the learned tuning curve of a neuron learned from activity during an epoch, E, does not match its maze place preference, then it cannot reasonably be said to “encode” that same location during epoch E. The LT therefore allows us to examine for which time periods and which neurons we can use Bayesian decoding following more standard methods 11,72.
This approach can be readily generalized to other neural systems where tuning curves have been recorded, provided a sufficiently large number of units are recorded to sample the stimulus space. In the case of 1D MAZE locations and place fields, we find that > 40 simultaneously recorded units are needed to reliably obtain high fidelity PFs (Extended Data Fig. 1). For larger or multiple environments, a greater number of units may be needed, as insufficient neuronal sampling or inherent preferences in the dataset (e.g. for reward locations) may result in some biases across the stimulus space. Significance testing should therefore be performed against unit-ID shuffles across available units. Prior to evaluating offline LTs, validation can be performed against online data to confirm adequate sampling resolution.
Additional restrictions to avoid potential confounds from unit waveform clustering:
To avoid potential confounds from spike misclassification of units detected on the same shank 73, we placed additional inclusion requirements for LT calculations. We determined the L-ratios 74 between unit and each other unit recorded on the same shank, yielding the cumulative probability of the other units’ spikes belonging to unit . Since the range of L-ratio depends on the number of included channels, to provide a consistent threshold for all datasets, the L-ratio for each pair was calculated using the four channels that featured the highest spike amplitude difference between each pair of units. Only units with L-ratio > 10−3 (see Extended Data Fig. 3) were used to calculate LTs for each cell.
Fidelity of the learned tunings across epochs.
To quantify the degree to which tuning curves in LTs or PFs relate across epochs, we used a simple Pearson correlation coefficient across position bins. We obtained consistent results with the Kullback-Leibler divergence (not shown). The median for each epoch were compared against a surrogate distribution of such median values obtained by shuffling (104 times) the unit identities of the PFs within each session. Thus, we tested against the null hypothesis that learned tunings in each session may have trivial non-zero correlations with PFs. For each epoch we obtained p-values based on the number of such surrogate median values that were ≥ those in the original data. With the exception of Fig. 2 only units that participated in > 100 ripple events in PRE or POST were included in the analysis.
Learned tuning stability and dynamics.
We further evaluated the dynamics of LTs across time in non-overlapping 15 min windows (except for illustration purposes only, in time evolved LTs in Fig. 3a, Fig. 4a, Fig. 5h, and Extended Data Fig. 3, where we used overlapping 15 min windows with a 5 min step size). A unit’s LT stability was defined as the median Pearson correlation coefficient between that unit’s LTs in all different pairs of time windows within a given epoch. Thus, units that had stable and consistent LTs across an epoch yield higher correlations in these comparisons than those with unstable LTs. These unit LT stability values were z-scored against a null distribution of median correlation coefficients based on randomizing the LTs’ unit identities within each 15 min time window (1000 shuffles). Normalized stability correlation matrices in Fig. 4c were calculated by z-scoring each correlation coefficient against a surrogate distribution based on shuffling the LTs’ unit identities. To investigate the changes in POST LT stability over time in Fig. 4c, we calculated LT stability within overlapping 2-hour blocks with a step size of one hour.
Ripple event replay scores.
The posterior probability matrix () for each ripple event was calculated based on previously published methods. Replays were scored using the absolute weighted correlation between decoded position () and time bin () 36:
| (11) |
| (12) |
where and are time bin and position bin indices, respectively, and
| (13) |
Each replay score was further quantified as a percentile relative to surrogate distributions obtained by shuffling the data according to the commonly used within-event time swap, in which time bins are randomized within each ripple event 72. We preferred this method over the circular spatial bin shuffle (or column cycle shuffle 72) as it preserves the distribution of peak locations across time bins within each event (see also related discussion in ref 33). Each ripple event was assigned to one of four quartiles based on the percentile score of the corresponding replay relative to shuffles.
Place fields’ overlap with decoded posterior.
A Pearson correlation coefficient was calculated between the PF of each unit firing (participating) in a time-bin and the posterior probability distribution for that bin based on the firings of all units. The mean posterior correlation of PFs was calculated over all participating units. Since this mean posterior correlation might be inflated when there is a low number of participating units, for each time bin with firing unit count we generated surrogate distribution of mean posterior correlation by randomly selecting units. Then, the mean posterior correlation in the original data was z-scored against the corresponding surrogate distribution for randomly participating units.
Theta learned tuning variations with oscillation characteristics.
We investigated how learned tunings during periods dominated by theta oscillations, such as MAZE active running periods and REM periods, were influenced by oscillation characteristics, such as power, phase, frequency. Theta power was determined by computing the power spectrum of the LFP recorded from the channel exhibiting maximum ripple power (typically in the pyramidal layer) in two-second windows with one-second overlap, using the Chronux toolbox (Version 2.12) and averaging the power within the theta frequency range (5 – 10 Hz). Theta frequency within each window was identified as the frequency exhibiting peak power within the theta frequency range. Theta phase was obtained by band-pass filtering the LFP within theta frequency range and computing the phase of the analytic signal derived from the Hilbert transform of the theta LPF. Theta periods were divided into 20 ms time bins, and theta power, frequency, and phase were calculated within each bin using linear interpolation. Time bins were then categorized into low versus high theta power or frequency along the medians of the distribution of theta power or frequency across all time bins within each session. To categorize theta time bins based on theta phase, we first aligned the instantaneous phase signal such that the theta trough corresponded with maximum population firing across all units compensating for potential misalignment with the LFP signal. Subsequently, theta time bins were divided into trough (−π/4 – π/4), ascending (π/4 – 3π/4), peak (3π/4 – 5π/4) and descending (5π/4-7π/4) phases. The learned tunings were calculated separately for each distinct subset, as depicted in Extended Data Fig. 2f and Extended Data Fig. 7e. REM periods were restricted to intervals lasting at least six seconds to minimize false positives. For analyses of MAZE active running periods, theta periods were restricted to intervals where the animal’s velocity exceeded 10 cm/S and we matched the number of firing bins for each unit across all data splits to control for such differences. LT variations with respect to animal’s velocity during MAZE active running periods were determined by calculating LTs for distinct subsets of time bins, divided along the median velocity distribution across all MAZE theta time bins within each session.
Multiple regression analyses.
To examine the extent to which a spatial tuning curve (LT or PF) within a given epoch was impacted by the tuning curves in other epochs, we performed multiple regression analyses. E.g. we modeled POST LTs using:
| (14) |
and reMAZE PFs using
| (15) |
The dependent variables and regressors were calculated over all position bins from all units. The average LT in the analyses were calculated by averaging all unit LTs over PRE and POST. and are the regression coefficients.
In order to test the statistical significance of the regression values and each regression coefficient, we compared these against distributions of surrogates (n = 104 shuffles) calculated by randomizing the unit identities of the dependent variable’s tuning curves. For each coefficient and values, we obtained a p-value based on the number of surrogates that were ≥ those in the original data.
Bayesian learned tuning with uninformative prior.
We’ll define as the vector of spike observations for all neurons except the -th, and is the observation at time . is the posterior probability distribution of positions as already defined (calculated using the firing rate estimates from place fields using a uniform prior over position).
Define our observations at time , . Assume that the neuron that we care for exhibits Poisson spiking over the spatial bins , with parameter ; in other words, . Thus, our estimation problem is specifically to find the best estimates of the parameters, .
In general, the Bayesian data likelihood is found using Bayes rule:
Thus, for all of our observations, we can write:
where in the last line, we’ve taken advantage of the conditional independence of the spiking of the neurons in each time bin conditioned on the position in that bin, and the activity of the other neurons on the parameters.
In order to find the best parameters, we will maximize the logarithm of this quantity by taking the derivative with respect to each and setting equal to zero.
We will assume that our neurons are Poisson distributed, that is:
Note that the derivative with respect to the parameter can be expressed as
Thus, we have:
To bias the results as little as possible, we will use a flat prior for (note that this is an “improper” prior as it does not integrate to 1, but the posterior is still proper 75). Another alternative might be to shape the parameter distribution using a conjugate prior with parameters determined using information from the behavioral period or from the statistics of the other neurons. With an uninformative prior,
Rearranging,
This can be interpreted as a normalized spike triggered average posterior probability distribution over space, triggered on the spikes of the neuron whose learned tuning we’re calculating.
Extended Data
Extended Data Fig. 1. The factors that impact learned tunings.
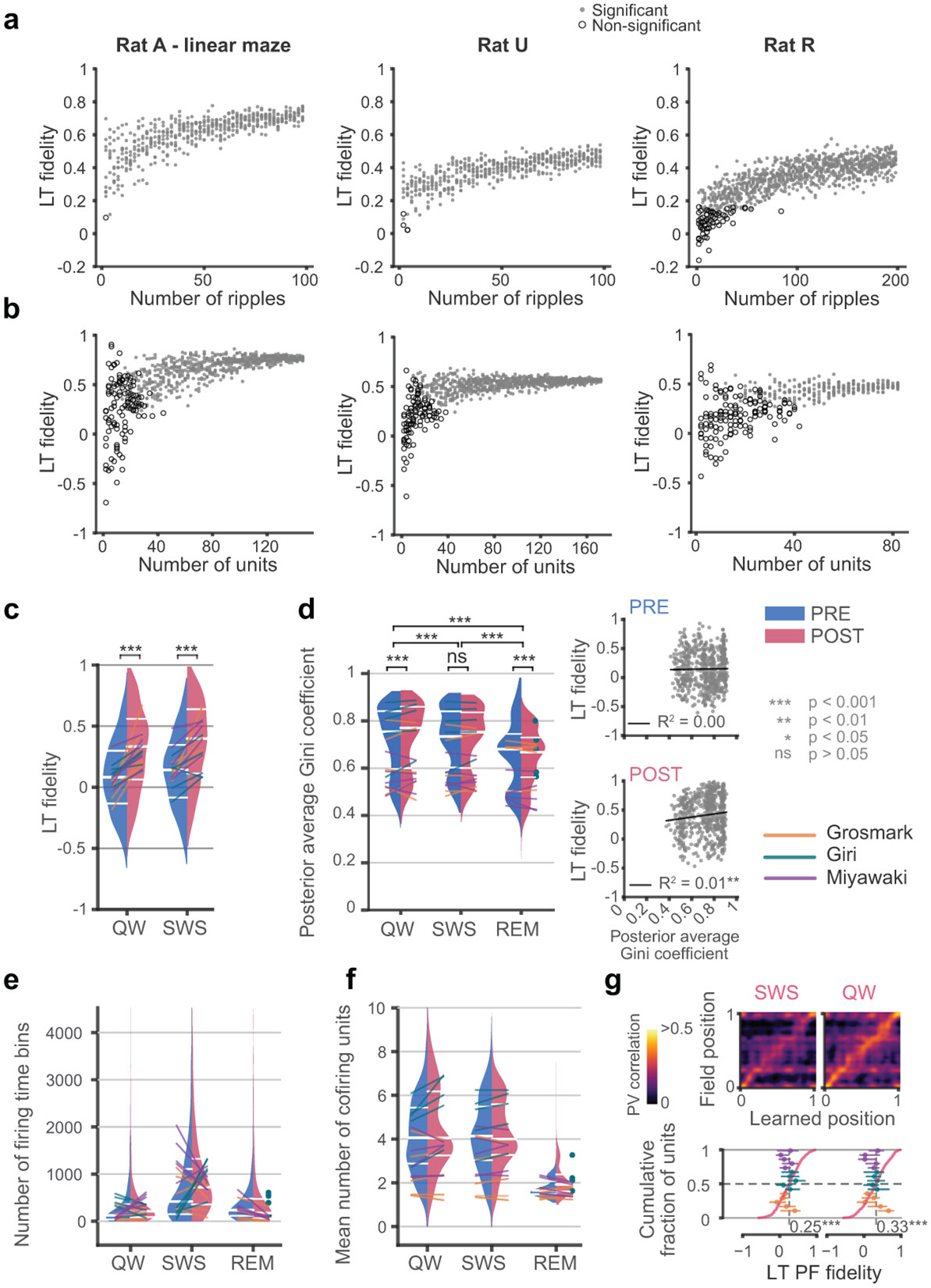
In three sample maze sessions we calculated LTs by (a) randomly varying the number and subset of awake ripple events, or (b), varying the number of units included, and tested the effects on the quality of learned tunings (LTs), as reflected by place field (PF) fidelity. Samples that yielded with significant median LT fidelities (r(LT, PF), p < 0.01 relative to unit ID shuffle) are represented in gray dots, while non-significant samples are indicated by empty circular markers. The median LT fidelity increases as more ripples and units are incorporated. Based on these results, we estimate that approximately 40 simultaneously recorded units are needed to obtain quality LTs, while the minimum number of ripples could vary across sessions, with as few as five ripples needed to generate LTs with significant PF fidelities in some cases. (c) The distribution of PF fidelities corresponding to quiet wake (QW), or slow-wave sleep (SWS), when the number of firing time bins utilized for calculation of each unit’s LT were matched between PRE and POST via subsampling the firing time bins, indicated significant difference between PRE and POST within each event category (QW: p = 2.0 x 10−35; SWS: p = 2.7 x 10−43, two-sided Wilcoxon signed-rank tests with no correction for multiple comparisons). (d) Left, the distribution of the mean sharpness of the posterior probability distribution over position (quantified by the Gini coefficient, see Methods) used in LT calculations for units in each event category. There was a significant effect of event category (p = 1.5 x 10−151, Friedman’s test) with both QW and SWS had higher median Gini coefficients (i.e. sharper posteriors) than REM (QW versus REM: p < = 4.3 x 10−98; SWS versus REM: p = 3.8 x 10−97, two-sided WSRT with no correction for multiple comparisons). The overlaid lines (dots for sessions with no REM in PRE) connect median values corresponding to individual sessions. PRE and POST also exhibited slightly different Gini coefficients during QW (p = 5.0 x 10−11) or REM (p = 8.6 x 10−11) but not during SWS (p = 0.95), though the effect sizes of the difference were small (QW: 0.20; SWS: 0.04; REM: −0.29). Right, the correlation between the PF fidelity and posterior Gini coefficient for PRE (top) and POST (bottom) by pooling across all event categories was weak in both PRE and POST, and significant during POST (p = 0.004) but not PRE (p = 0.72), indicating that the sharpness of posteriors was not a major driver of differences between PRE and POST LTs. (e) The distributions of the number of bins with spikes used to calculate LTs in quiet wake ripples (QW), slow wave sleep ripples (SWS), and rapid-eye movement (REM) sleep during PRE or POST epochs in Fig. 2a. The overlaid lines (dots for sessions with no REM in PRE) connect median values corresponding to individual sessions. (f) The distributions of the average number of units that cofired with the learning unit when calculating LTs during each epoch. (g) Population vector correlation matrices (top) and cumulative distributions of PF fidelity (bottom) for SWS and QW LTs during POST, recalculated following subsampling of each unit’s SWS and QW firing bins to match the number of firing bins during the corresponding REM periods.
Extended Data Fig. 2. The impact of sleep oscillations on LT quality.
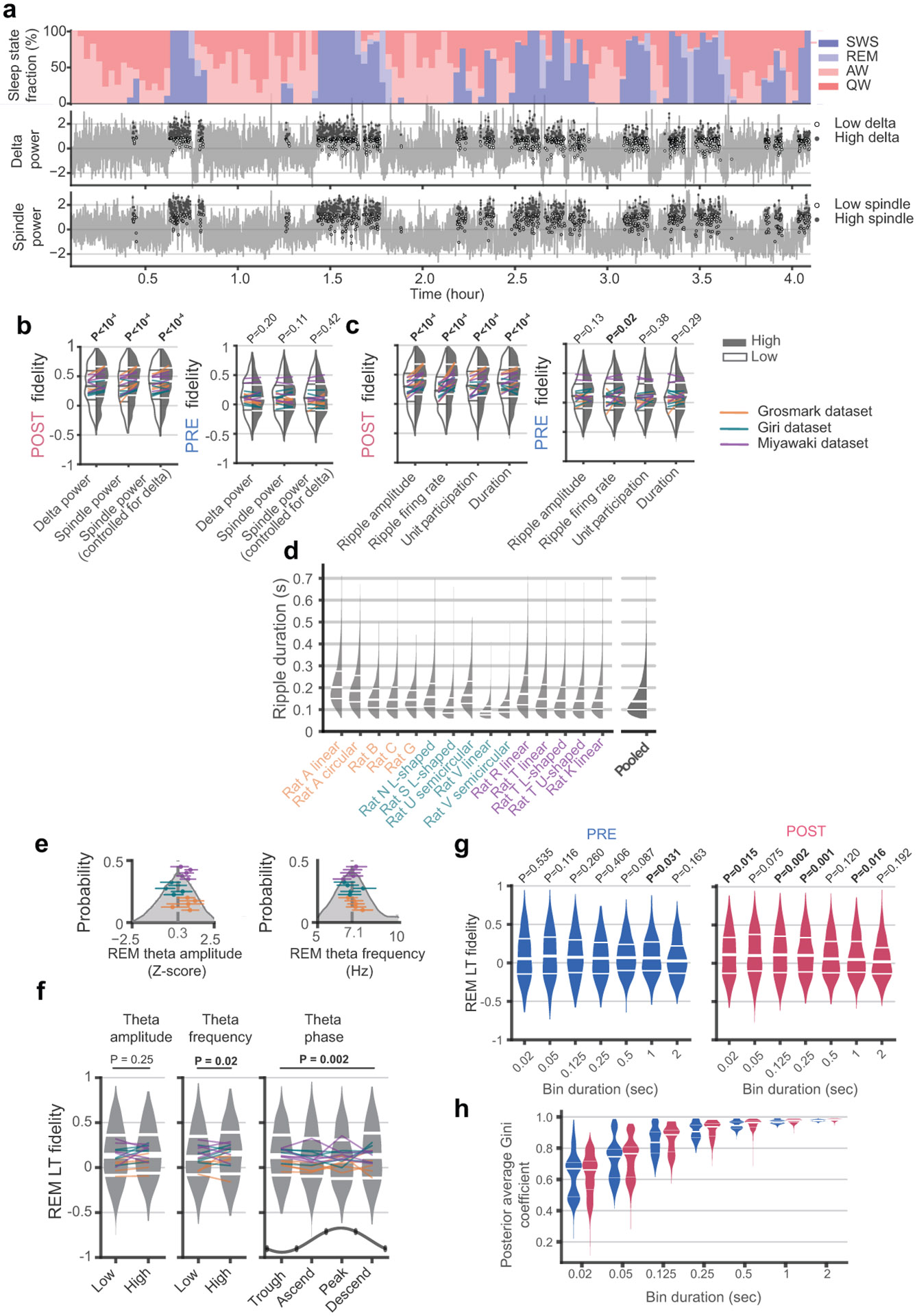
(a) Top row, the fraction of each sleep state in 2-minute sliding windows during POST from a sample session. Middle row, the power of delta oscillations (1-4Hz) in 2-second sliding windows (gray) across POST. Filled and empty dots indicating SWS ripple events with high (≥ median) or low (< median) delta power for that session. Bottom row, similar to the middle panel, but for spindle power (9-18Hz) calculated in 500 ms sliding windows (gray). (b) In POST, but not PRE, SWS ripples separated into those occurring during high vs. low delta power (left) and high vs. low spindle power (middle) resulted in higher fidelity when the oscillations were present at higher power. When we split each 2-s delta window into two 500 ms periods with higher and two windows with lower spindle power, to isolate the impact of spindles at each level of delta, we observed higher fidelity LTs for ripples that occurred during high spindle power. (c) LTs calculated based on events with high (≥ median) ripple (120-250Hz) amplitude, multi-unit firing rate, unit participation rate, or ripple event duration, all exhibited significantly higher PF fidelity compared to those with low (< median) values in POST. In all comparisons in (b) and (c), LTs were calculated based on matched number of bins and p-values (inset) were derived from Wilcoxon signed-rank tests. (d) Distributions of the duration of ripple events obtained from each session in each dataset. (e) The distribution of theta amplitude (z-scored over REM, left) and theta frequency (right) during the REM periods in POST (n = 813613 20 ms time bins pooled across all sessions), with individual session medians (dots) and interquartile ranges (horizontal lines) superimposed. (f) PF fidelity of LTs in POST REM calculated based on distinct subsets of 20 ms time bins separated according to high and low theta amplitude (left panel) or frequency (middle panel) separated by the median values in each session. There was a significant effect of frequency (p = 0.02, two-sided WSRT, n = 660). Similarly, REM LTs calculated based on separating windows according to theta phase (right panel) into trough (−π/4 – π/4), ascending (π/4 – 3π/4), peak (3π/4 – 5π/4) and descending (5π/4-7π/4) phase. Median PF fidelities significantly differed across theta phase (p = 0.0015, Friedman’s test, n = 660) (g) We tested the effect of different sized time bins on REM LT-PF fidelities in PRE (left) and POST (right). While the effect was subtle and not significantly different across different sized bins (Friedman’s test), LTs using 125 ms and 250 ms bin durations exhibited significantly aligned LT-PF fidelities (median fidelities compared (one-sided) to null distributions obtained from 104 unit identity shuffles without multiple comparison corrections). (h) The posteriors used to calculate LTs exhibits greater sparsity for larger bin sizes in both PRE and POST REM. This is because larger bins result in more active neurons within each bin, producing increasingly sharper posteriors (see equation (9), Methods).
Extended Data Fig. 3. Additional examples of the evolution of LTs from PRE to POST.
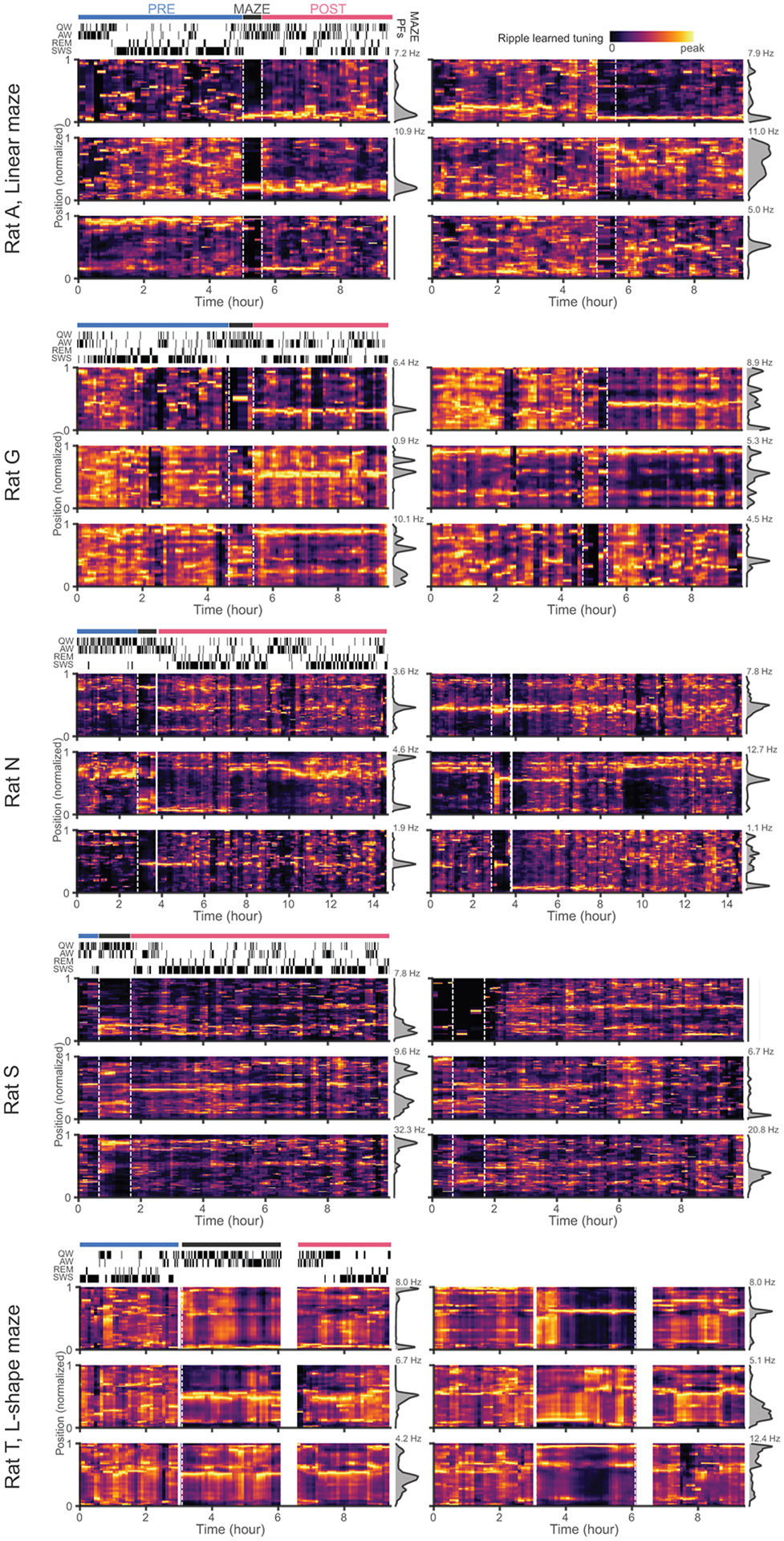
Similar to Fig. 3a, heat maps of ripple LTs in sliding 15 min windows from PRE through MAZE to POST (maze place fields in gray on right) for 6 sample units from each of 5 different sessions (hypnogram on top left indicating the brain state, quiet waking (QW), active waking (AW), rapid eye movement (REM) sleep, and slow-wave sleep (SWS) at each timepoint)).
Extended Data Fig. 4. Place field fidelities do not strictly correlate with replay score.
(a) Distribution of replay scores in the different datasets calculating as percentile against time shuffled bins. Median scores for different epochs are shown with dashed lines (chance median score = 50; see Methods). (b) Ripple events were divided into quartiles according to replay score. Top panels show the place fields and sets of LTs calculated based on low and high quartile replay score events within PRE, MAZE, and POST. Bottom panels show population vector (PV) correlations between position bins in the PFs versus different sets of LTs. (c) Distribution of PF fidelity for each ripple subset. Median PF fidelities were significantly greater compared (one-sided) against surrogate distributions (from 104 unit identity shuffles, without multiple comparison corrections) in all subsets during MAZE and POST but not during PRE (PRE; p = 0.86, p = 0.67, p = 0.49, p = 0.06 for first to forth quartiles, respectively. MAZE and POST: p < 10−4 for all quartiles). (d) Place fields of participating units in replays show differing amounts of overlap with the decoded posteriors. Example events with high replay scores in PRE and POST, and low replay scores in POST showing posterior probability matrices and corresponding spike rasters of units sorted by place field order. The middle row depicts the mean correlation of the participating units’ place fields with the decoding posterior in each time bin. The bottom panels show the place fields and decoded positions of participating units for example time bins. Note that even bins with poor place-field coherence display sharp posteriors, because of the multiplication rule in Bayes formula, whereby spatial tunings of participating units are multiplied by each other. (e) Mean posterior correlation of PFs and decoded positions show increased place-field overlap in both low and high score replays in POST compared to PRE. Low and high replay score events in PRE did not differ significantly (PRE low versus high: p = 0.36; POST low versus high: p = 1.8x10−66; POST high versus PRE high: p = 1.1x10−282; POST low versus PRE high: p = 1.1x10−59; two-sided Mann Whitney U Test). ***p < 0.001.
Extended Data Fig. 5. Additional details and variations on MAZE/reMAZE analyses.
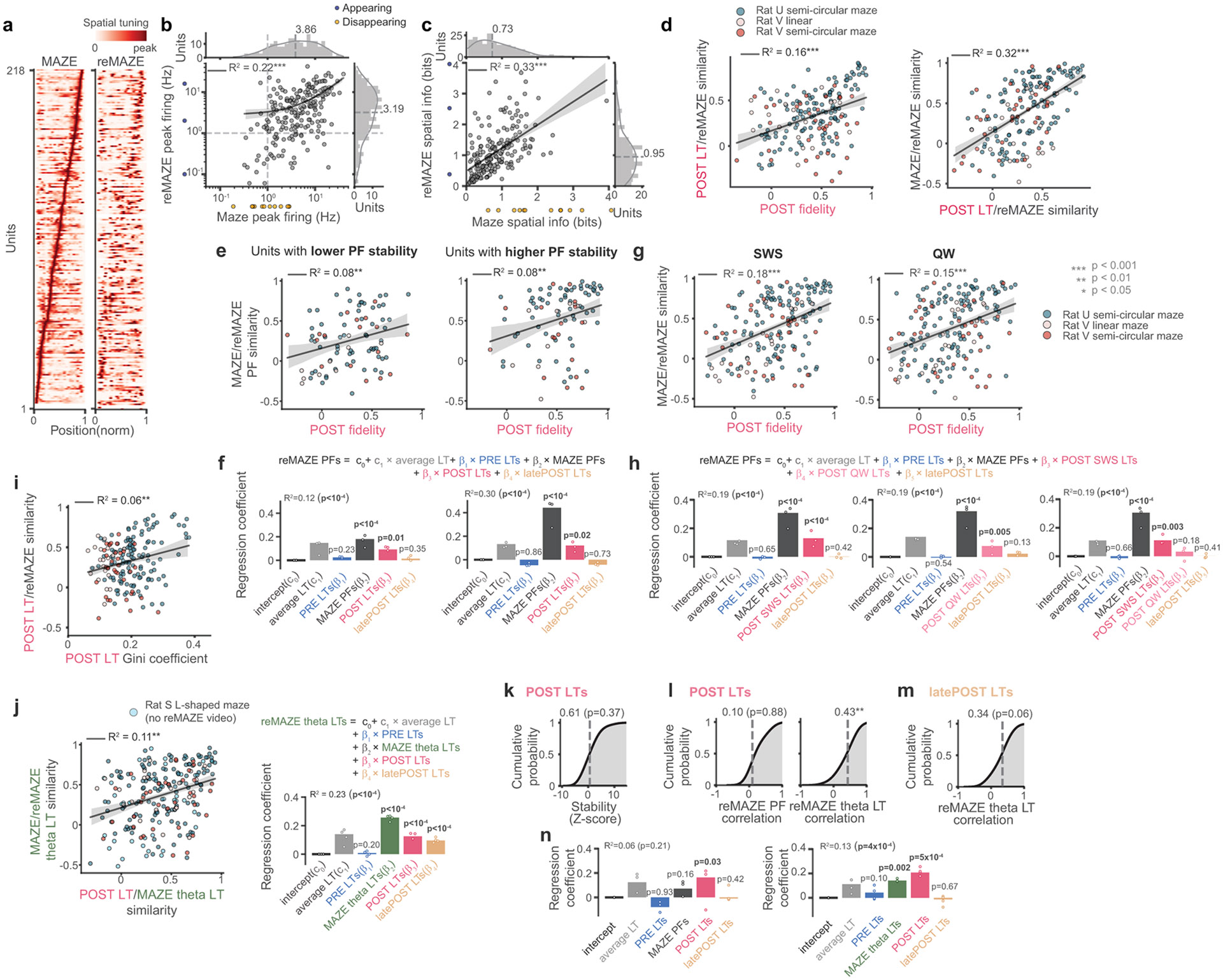
(a) Place fields from MAZE and reMAZE for all units used for analyses in Fig. 5. (b) Place field peak firing rates during MAZE and reMAZE and their marginal histograms. Despite an apparent modest decrease in peak firing rates during reMAZE and disappearance or appearance of a small subset of units (orange dots), peak firing rates in reMAZE and MAZE remained significantly correlated. In this and subsequent panels, best linear fit and 95% confidence intervals are overlaid with black line and shaded gray, respectively. (c) The same as (b) but for spatial information between MAZE and reMAZE spatial tunings across units. (d) . POST LT fidelity to MAZE PFs (left) is correlated with the similarity to the reMAZE PF. Likewise, POST LT similarity to reMAZE PFs (right) is correlated with the similarity between MAZE and reMAZE PFs. (e) MAZE/reMAZE similarity correlation with POST PF fidelity (as in Fig. 5f) separately for units with lower (left) or higher (right) PF stabilities relative to each session’s median. Higher POST fidelity was predictive of greater MAZE/reMAZE similarity in both sets. (f) Multiple regression separately for each panel directly above in (e) The regressors were more predictive (higher R2) for units with more stable MAZE PFs, but POST LTs beta coefficients were similar between units with lower or higher PF stabilities (both p values = 0.02). p-values were obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of reMAZE PFs. (g) PF fidelities of POST LTs calculated exclusively based on slow-wave sleep (SWS; left) or quiet wake (QW; right) ripple events both predicted similarity between MAZE and reMAZE place fields. However, a stronger correlation was observed for SWS LTs. (h) The same multiple regression analysis for modeling reMAZE PFs as in Fig. 5g but with the inclusion of POST SWS LTs (left panel), POST QW LTs (middle panel), or both (right panel), as regressors. While both SWS and QW POST LTs were predictive of reMAZE (p < 10−4 and p < 0.01, p-values obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of reMAZE PFs), the POST SWS LTs offered the stronger prediction. (i) The Gini coefficients of POST LT’s (measuring sparsity, i.e. sharpness of tuning) were significantly correlated with their similarity to reMAZE place fields. This demonstrates that sparser (as opposed to more diffuse) POST LTs display higher similarity with the upcoming place fields during maze re-exposure. (j) Similar to Fig. 5f & 5g, but using tunings learned during theta (active periods) on MAZE and reMAZE. This analysis also allowed us to add data from an additional session (from Rat S) for which video tracking was lost during the reMAZE epoch). Left panel, the similarity of POST LTs with MAZE theta LTs predicted the similarity between MAZE and reMAZE theta LTs. Right panel, POST LTs remained predictive of reMAZE theta LTs in this control comparison. (k) The stability of POST LTs (z-scored against unit-id shuffles, as in Fig. 3d) for units with MAZE PF peak firing rate < 1 Hz (threshold used in this paper) were not significantly > 0. (l) In the same set of units, the POST LTs did not display a significant correlation with reMAZE PFs (left) but still showed a significant correlation with reMAZE theta LTs (right). (m) The correlation with reMAZE theta LT was absent for latePOST LTs. (n) Multiple regression analyses for modeling the reMAZE PFs (left) or reMAZE theta LTs (right) for these low-firing units both resulted in significant regression coefficients for POST LTs. *p < 0.05, **p < 0.01, ***p < 0.001.
Extended Data Fig. 6. Additional examples of the evolution of LTs from PRE to reMAZE.

Similar to Fig. 5h, heat maps of ripple LTs in sliding 15 min windows from PRE through MAZE, POST, and latePOST for sample units from 4 different sessions (hypnogram on top left indicate the brain state, quiet waking (QW), active waking (AW), rapid eye movement (REM) sleep, and slow-wave sleep (SWS) at each timepoint)). MAZE and reMAZE place fields and LTs during PRE, POST, and latePOST are plotted on the right of each panel, except for Rat S for which we plot reMAZE theta LTs (rather than reMAZE PFs) because video tracking was lost during reMAZE for this session.
Extended Data Fig. 7. The correlation between the learned tuning of units and their intrinsic and MAZE tuning properties.
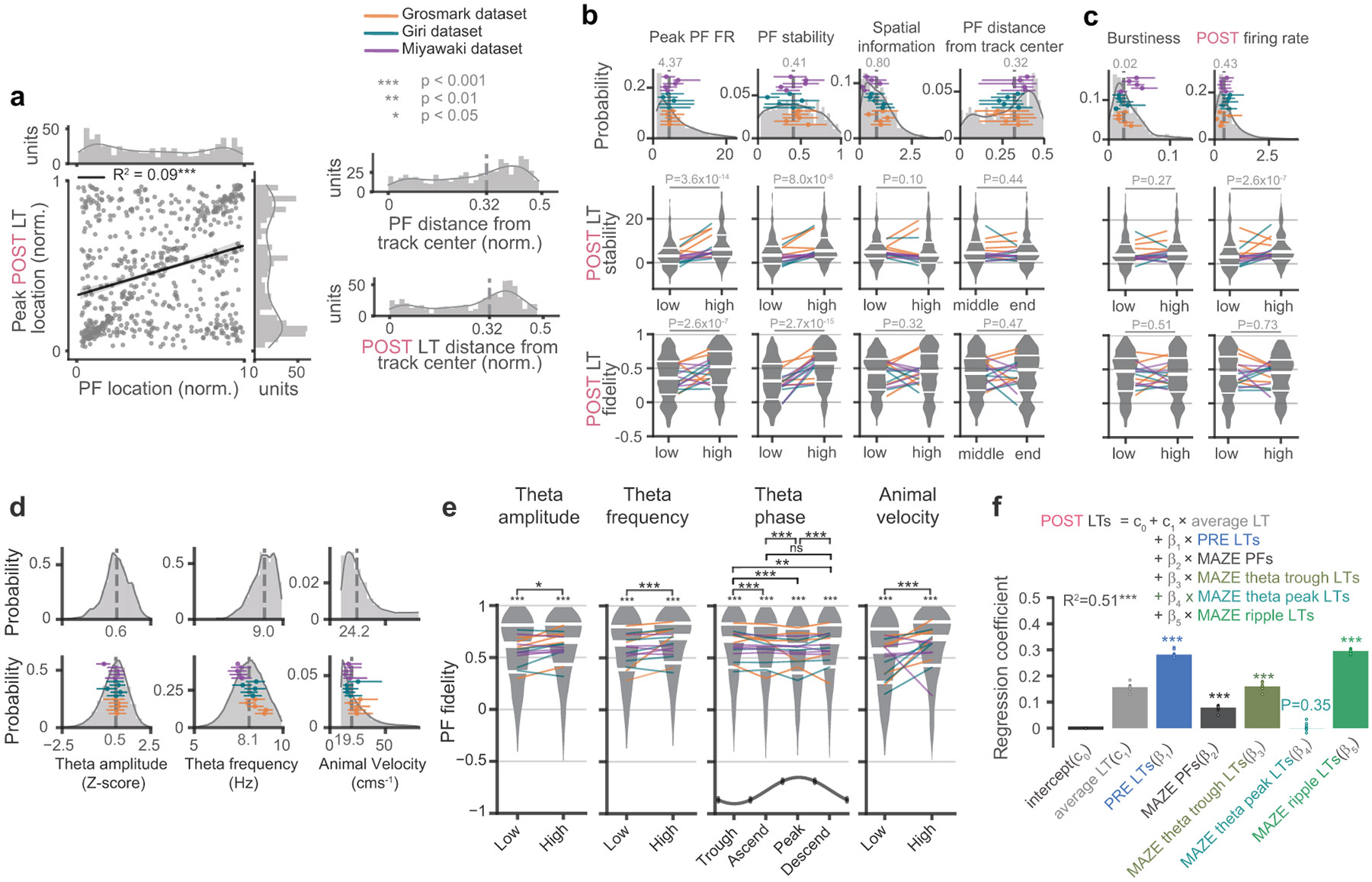
(a) Left, the distribution of locations of peak tuning across POST ripple LTs and maze place field (PFs). Right, the marginal distributions of peak locations relative to the center of the track show similar distributions between POST LTs (top) and PFs (bottom). (b) Relationship between PF features and stability and fidelity of the POST LTs. First row, distribution of each MAZE spatial tuning metric by pooling units across all sessions (n = 660 units). The median and interquartile ranges corresponding to individual sessions are depicted using overlaid lines. To analyze the connection between the POST stability and fidelity with each MAZE spatial tuning metric, the set of units within each session was divided into low or high categories according to the median. Among the spatial tuning metrics, peak place field firing rate (peak PF FR), and PF stability were predictive of the POST LT fidelity and stability. We saw no effect from metrics such as spatial information or PF distance from the track center. Cross-group comparisons used two-sided Mann Whitney U Tests. (c) Similar analysis on unit firing characteristics indicates that firing burstiness is not a factor driving LT stability or fidelity. Additionally, higher firing rates during the POST ripples affected the stability of POST LTs but not their fidelity. Median and interquartile ranges corresponding to individual sessions are superimposed with colored dots and lines. Cross-group comparisons used two-sided Mann Whitney U Tests. (d) The distribution of theta amplitude (z-scored), frequency, and velocity of the animal observed during MAZE theta periods for a sample session (top row) and for overall distributions (bottom row) by pooling over all sessions (n = 2250347 20 ms time bins). Median and interquartile ranges corresponding to individual sessions are superimposed with colored dots and lines. (e) From left to right, PF fidelity of MAZE theta LTs calculated based on distinct subsets of 20 ms time bins into Low/High relative to session medians showed significant effects for theta amplitude (1st column) (p = 0.01) or frequency (2nd column) (p = 7.9x10−16). The impact of theta phase (3rd column) on MAZE theta LTs was investigated by calculating the LTs based on distinct set of 20 ms time bins according to theta phase: Trough (−π/4 to π/4), Ascend (π/4 to 3π/4), Peak (3π/4 to 5π/4), Descend (5π/4 to 7π/4). LTs associated with the trough and descending phase of theta displayed higher PF fidelity than other theta phases (cross-group comparison using Friedman’s test; p = 2.2x10−13 with post hoc comparisons within each pair; Trough vs. Ascend: p = 2.1x10−5; Trough vs. Peak: p = 2.2x10−12; Trough vs. descend: p = 0.002; Ascend vs. Peak: p = 3.6x10−5; Ascend vs. descend: p = 0.12; Peak vs. descend: p = 9.2x10−8). Theta periods split according to the animal’s velocity (4th column) during the theta periods (p = 6.7x10−18). These panels indicate significant differences compared to chance levels (vs. unit-ID shuffle surrogates) within each group, as well as comparisons across groups (two-sided Wilcoxon Signed-Rank Tests). (f) Multiple regression analysis revealed that learned tunings calculated based on firing during MAZE theta trough, but not theta peak, strongly predict POST learned tunings, along with MAZE ripple LTs (theta peak LTs: p = 0.35; theta trough, PRE, ripple LTs, and MAZE PFs: p < 10−4). p-values were obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of POST LTs. Results obtained by leaving out individual sessions are superimposed with dots. *p < 0.05, ** p <0.01, *** p < 0.001.
Extended Data Fig. 8. Unit stability and isolation.
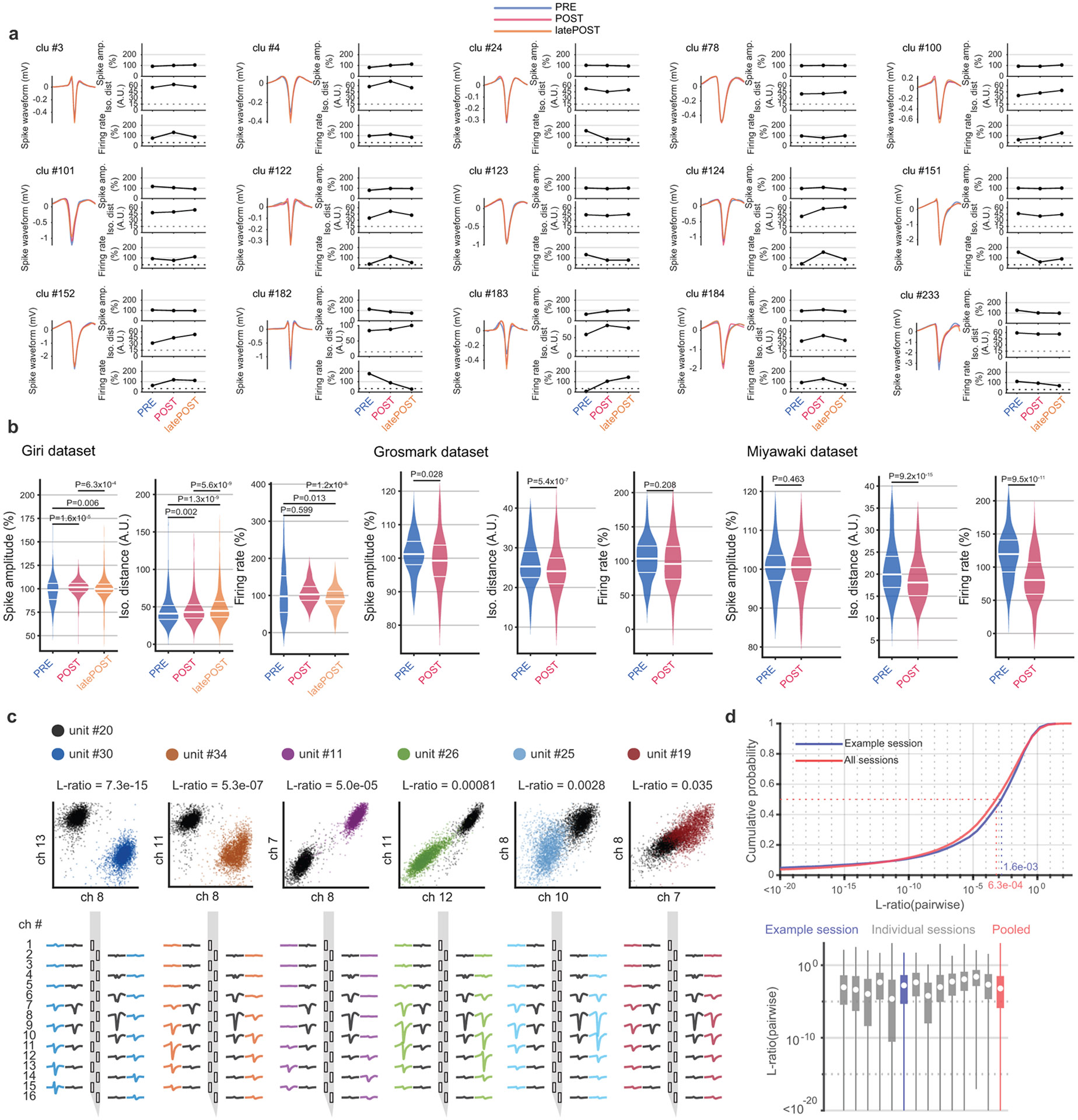
(a) Sample units (from Rat U) depicting mean spike waveform and unit stability assessed by spike amplitude, isolation distance, and firing rate over three sleep epochs (PRE, POST, and latePOST). Inclusion thresholds for isolation distance and firing rates are shown with dashed lines. (b) The distribution of unit stability measures by pooling across all units in sessions shown for each dataset. See Methods for further details on unit inclusion criteria. Within-group comparisons used two-sided Wilcoxon Signed Rank Tests. (c) The L-ratio was used to quantify the degree of overlap in the spike feature space between each pair of units. Each scatterplot (top row) shows the spikes of the reference unit #20 (black) and other units (colored) recorded on the same shank in an example recording session from the Giri dataset. The axes in each scatterplot correspond to the spike amplitude on two channels with maximal distinction between the pairs, showing a range of overlap with unit #20. For example, unit #30 on the leftmost inset showed almost no overlap, while unit 19 on the rightmost inset significantly overlapped. The L-ratio (e.g. between unit #20 and the other units) was obtained by calculating the probability of spikes from the second unit belonging to the reference unit. An L-ratio threshold of 10−3 was applied to include only isolated units for determining the LTs of each reference cell. Corresponding mean spike waveforms (bottom row) provided for each pair of units across recording electrodes. (d) The cumulative distributions of L-ratios for this example session and across all sessions (top) (n = 40207 unit pairs). The L-ratios for each individual session (bottom), showing mean (dots), the full range (whiskers) and interquartile range (boxes).
Supplementary Material
Acknowledgements
We thank Asohan Amarasingham, Ted Abel, George Mashour, Matthijs van der Meer, Nat Kinsky, Pho Hale, and Rachel Wahlberg for valuable comments on the manuscript. This work was funded by NINDS R01NS115233 and NIMH R01MH117964.
Footnotes
Competing Interests
The authors declare no competing interests.
Data Availability
The Grosmark dataset is publicly available at https://crcns.org/data-sets/hc/hc-11. The Miyawaki and Giri datasets are available upon request from the corresponding author.
Code Availability
Custom-written MATLAB and python code supporting this study is available at https://github.com/diba-lab/Maboudi_et_al_2022
References
- 1.Mankin EA, et al. Neuronal code for extended time in the hippocampus. PNAS 109, 19462–19467 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Klinzing JG, Niethard N & Born J Mechanisms of systems memory consolidation during sleep. Nat Neurosci 22, 1598–1610 (2019). [DOI] [PubMed] [Google Scholar]
- 3.Havekes R & Abel T The tired hippocampus: the molecular impact of sleep deprivation on hippocampal function. Curr Opin Neurobiol 44, 13–19 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hebb DO The organization of behavior, (Wiley, New York, NY, 1949). [DOI] [PubMed] [Google Scholar]
- 5.O'Keefe J & Dostrovsky J The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34, 171–175 (1971). [DOI] [PubMed] [Google Scholar]
- 6.Zhang K, Ginzburg I, McNaughton BL & Sejnowski TJ Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. J Neurophysiol 79, 1017–1044 (1998). [DOI] [PubMed] [Google Scholar]
- 7.Frank LM, Stanley GB & Brown EN Hippocampal plasticity across multiple days of exposure to novel environments. J Neurosci 24, 7681–7689 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dong C, Madar AD & Sheffield MEJ Distinct place cell dynamics in CA1 and CA3 encode experience in new environments. Nat Commun 12, 2977 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alme CB, et al. Place cells in the hippocampus: eleven maps for eleven rooms. Proc Natl Acad Sci U S A 111, 18428–18435 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ziv Y., et al. Long-term dynamics of CA1 hippocampal place codes. Nat Neurosci 16, 264–266 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.van der Meer MAA, Kemere C & Diba K Progress and issues in second-order analysis of hippocampal replay. Philos Trans R Soc Lond B Biol Sci 375, 20190238 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dragoi G & Tonegawa S Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 469, 397–401 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cirelli C & Tononi G The why and how of sleep-dependent synaptic down-selection. Semin Cell Dev Biol 125, 91–100 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Giri B, Miyawaki H, Mizuseki K, Cheng S & Diba K Hippocampal Reactivation Extends for Several Hours Following Novel Experience. J Neurosci 39, 866–875 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grosmark AD, Sparks FT, Davis MJ & Losonczy A Reactivation predicts the consolidation of unbiased long-term cognitive maps. Nat Neurosci 24, 1574–1585 (2021). [DOI] [PubMed] [Google Scholar]
- 16.Pettit NL, Yap EL, Greenberg ME & Harvey CD Fos ensembles encode and shape stable spatial maps in the hippocampus. Nature 609, 327–334 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wiskott L. Lecture Notes on Bayesian Theory and Graphical Models. (2013). [Google Scholar]
- 18.Diba K & Buzsaki G Forward and reverse hippocampal place-cell sequences during ripples. Nat Neurosci 10, 1241–1242 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dragoi G & Buzsaki G Temporal encoding of place sequences by hippocampal cell assemblies. Neuron 50, 145–157 (2006). [DOI] [PubMed] [Google Scholar]
- 20.Tirole M, Huelin Gorriz M, Takigawa M, Kukovska L & Bendor D Experience-driven rate modulation is reinstated during hippocampal replay. eLife 11(2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Siclari F, et al. The neural correlates of dreaming. Nat Neurosci 20, 872–878 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vertes RP Memory consolidation in sleep; dream or reality. Neuron 44, 135–148 (2004). [DOI] [PubMed] [Google Scholar]
- 23.Miyawaki H & Diba K Regulation of Hippocampal Firing by Network Oscillations during Sleep. Curr Biol 26, 893–902 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Norimoto H., et al. Hippocampal ripples down-regulate synapses. Science 359, 1524–1527 (2018). [DOI] [PubMed] [Google Scholar]
- 25.Kinsky NR, Sullivan DW, Mau W, Hasselmo ME & Eichenbaum HB Hippocampal Place Fields Maintain a Coherent and Flexible Map across Long Timescales. Curr Biol 28, 3578–3588 e3576 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Geva N, Deitch D, Rubin A & Ziv Y Time and experience differentially affect distinct aspects of hippocampal representational drift. Neuron 111, 2357–2366 e2355 (2023). [DOI] [PubMed] [Google Scholar]
- 27.Khatib D, et al. Active experience, not time, determines within-day representational drift in dorsal CA1. Neuron 111, 2348–2356 e2345 (2023). [DOI] [PubMed] [Google Scholar]
- 28.Drieu C, Todorova R & Zugaro M Nested sequences of hippocampal assemblies during behavior support subsequent sleep replay. Science 362, 675–679 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Liu C, Todorova R, Tang W, Oliva A & Fernandez-Ruiz A Associative and predictive hippocampal codes support memory-guided behaviors. Science 382, eadi8237 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roux L, Hu B, Eichler R, Stark E & Buzsaki G Sharp wave ripples during learning stabilize the hippocampal spatial map. Nat Neurosci 20, 845–853 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yagi S, Igata H, Ikegaya Y & Sasaki T Awake hippocampal synchronous events are incorporated into offline neuronal reactivation. Cell Rep 42, 112871 (2023). [DOI] [PubMed] [Google Scholar]
- 32.Liu K, Sibille J & Dragoi G Preconfigured patterns are the primary driver of offline multi-neuronal sequence replay. Hippocampus 29, 275–283 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Farooq U, Sibille J, Liu K & Dragoi G Strengthened Temporal Coordination within Pre-existing Sequential Cell Assemblies Supports Trajectory Replay. Neuron 103, 719–733 e717 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Grosmark AD & Buzsaki G Diversity in neural firing dynamics supports both rigid and learned hippocampal sequences. Science 351, 1440–1443 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Foster DJ Replay Comes of Age. Annu Rev Neurosci 40, 581–602 (2017). [DOI] [PubMed] [Google Scholar]
- 36.Silva D, Feng T & Foster DJ Trajectory events across hippocampal place cells require previous experience. Nat Neurosci 18, 1772–1779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hasselmo ME What is the function of hippocampal theta rhythm?--Linking behavioral data to phasic properties of field potential and unit recording data. Hippocampus 15, 936–949 (2005). [DOI] [PubMed] [Google Scholar]
- 38.Siegle JH & Wilson MA Enhancement of encoding and retrieval functions through theta phase-specific manipulation of hippocampus. eLife 3, e03061 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ujfalussy BB & Orban G Sampling motion trajectories during hippocampal theta sequences. eLife 11(2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Olypher AV, Lansky P & Fenton AA Properties of the extra-positional signal in hippocampal place cell discharge derived from the overdispersion in location-specific firing. Neuroscience 111, 553–566 (2002). [DOI] [PubMed] [Google Scholar]
- 41.Monaco JD, Rao G, Roth ED & Knierim JJ Attentive scanning behavior drives one-trial potentiation of hippocampal place fields. Nat Neurosci 17, 725–731 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gupta AS, van der Meer MA, Touretzky DS & Redish AD Hippocampal replay is not a simple function of experience. Neuron 65, 695–705 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mattar MG & Daw ND Prioritized memory access explains planning and hippocampal replay. Nat Neurosci 21, 1609–1617 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cheng S & Frank LM New experiences enhance coordinated neural activity in the hippocampus. Neuron 57, 303–313 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wilson MA & McNaughton BL Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679 (1994). [DOI] [PubMed] [Google Scholar]
- 46.Bittner KC, Milstein AD, Grienberger C, Romani S & Magee JC Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357, 1033–1036 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Geiller T., et al. Local circuit amplification of spatial selectivity in the hippocampus. Nature 601, 105–109 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vaidya SP, Chitwood RA & Magee JC The formation of an expanding memory representation in the hippocampus. bioRxiv, 2023.2002.2001.526663 (2023). [Google Scholar]
- 49.Tingley D & Peyrache A On the methods for reactivation and replay analysis. Philos Trans R Soc Lond B Biol Sci 375, 20190231 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Krause EL & Drugowitsch J A large majority of awake hippocampal sharp-wave ripples feature spatial trajectories with momentum. Neuron 110, 722–733 e728 (2022). [DOI] [PubMed] [Google Scholar]
- 51.Stella F, Baracskay P, O'Neill J & Csicsvari J Hippocampal Reactivation of Random Trajectories Resembling Brownian Diffusion. Neuron 102, 450–461 e457 (2019). [DOI] [PubMed] [Google Scholar]
- 52.Diba K. Hippocampal sharp-wave ripples in cognitive map maintenance versus episodic simulation. Neuron 109, 3071–3074 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Genzel L, Kroes MC, Dresler M & Battaglia FP Light sleep versus slow wave sleep in memory consolidation: a question of global versus local processes? Trends Neurosci 37, 10–19 (2014). [DOI] [PubMed] [Google Scholar]
- 54.Poe GR, Nitz DA, McNaughton BL & Barnes CA Experience-dependent phase-reversal of hippocampal neuron firing during REM sleep. Brain Res 855, 176–180 (2000). [DOI] [PubMed] [Google Scholar]
- 55.Zielinski MC, Shin JD & Jadhav SP Hippocampal theta sequences in REM sleep during spatial learning. bioRxiv, 2021.2004.2015.439854 (2021). [Google Scholar]
- 56.Louie K & Wilson MA Temporally structured replay of awake hippocampal ensemble activity during rapid eye movement sleep. Neuron 29, 145–156 (2001). [DOI] [PubMed] [Google Scholar]
- 57.Boyce R, Glasgow SD, Williams S & Adamantidis A Causal evidence for the role of REM sleep theta rhythm in contextual memory consolidation. Science 352, 812–816 (2016). [DOI] [PubMed] [Google Scholar]
- 58.Hobson JA REM sleep and dreaming: towards a theory of protoconsciousness. Nat Rev Neurosci 10, 803–813 (2009). [DOI] [PubMed] [Google Scholar]
- 59.Colgin LL, Kubota D, Jia Y, Rex CS & Lynch G Long-term potentiation is impaired in rat hippocampal slices that produce spontaneous sharp waves. J Physiol 558, 953–961 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Schacter DL, Addis DR & Buckner RL Episodic simulation of future events: concepts, data, and applications. Ann N Y Acad Sci 1124, 39–60 (2008). [DOI] [PubMed] [Google Scholar]
- 61.Siegle JH, et al. Open Ephys: an open-source, plugin-based platform for multichannel electrophysiology. J Neural Eng 14, 045003 (2017). [DOI] [PubMed] [Google Scholar]
- 62.Yger P., et al. A spike sorting toolbox for up to thousands of electrodes validated with ground truth recordings in vitro and in vivo. eLife 7(2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rossant C, et al. Spike sorting for large, dense electrode arrays. Nat Neurosci 19, 634–641 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bartho P., et al. Characterization of neocortical principal cells and interneurons by network interactions and extracellular features. J Neurophysiol 92, 600–608 (2004). [DOI] [PubMed] [Google Scholar]
- 65.Petersen PC, Siegle JH, Steinmetz NA, Mahallati S & Buzsaki G CellExplorer: A framework for visualizing and characterizing single neurons. Neuron 109, 3594–3608 e3592 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Grosmark AD, Long JD & Buzsáki G Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning. (CRCNS.org, 2016). [Google Scholar]
- 67.Skaggs W, Mcnaughton B & Gothard K An information-theoretic approach to deciphering the hippocampal code. Advances in neural information processing systems 5(1992). [Google Scholar]
- 68.Wen H & Liu Z Separating Fractal and Oscillatory Components in the Power Spectrum of Neurophysiological Signal. Brain Topogr 29, 13–26 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bokil H, Andrews P, Kulkarni JE, Mehta S & Mitra PP Chronux: a platform for analyzing neural signals. J Neurosci Methods 192, 146–151 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Buzsaki G. Theta oscillations in the hippocampus. Neuron 33, 325–340 (2002). [DOI] [PubMed] [Google Scholar]
- 71.Park M, Weller JP, Horwitz GD & Pillow JW Bayesian active learning of neural firing rate maps with transformed gaussian process priors. Neural Comput 26, 1519–1541 (2014). [DOI] [PubMed] [Google Scholar]
- 72.Davidson TJ, Kloosterman F & Wilson MA Hippocampal replay of extended experience. Neuron 63, 497–507 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Quirk MC & Wilson MA Interaction between spike waveform classification and temporal sequence detection. J Neurosci Methods 94, 41–52 (1999). [DOI] [PubMed] [Google Scholar]
- 74.Schmitzer-Torbert N, Jackson J, Henze D, Harris K & Redish AD Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience 131, 1–11 (2005). [DOI] [PubMed] [Google Scholar]
- 75.Murphy KP Machine learning : a probabilistic perspective, (MIT Press, Cambridge, MA, 2012). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The Grosmark dataset is publicly available at https://crcns.org/data-sets/hc/hc-11. The Miyawaki and Giri datasets are available upon request from the corresponding author.
Custom-written MATLAB and python code supporting this study is available at https://github.com/diba-lab/Maboudi_et_al_2022


