Abstract
Knowledge of reliable geometries and associated intermolecular interaction energy (ΔE) values at key fragments of the potential energy surface (PES) in the gas phase is indispensable for the modeling of various properties of the pyrene dimer (PYD) and other important aggregate systems of a comparatively large size (ca. 50 atoms). The performance of the domain-based local pair natural orbital (DLPNO) variant of the coupled-cluster theory with singles, doubles and perturbative triples in the complete basis set limit [CCSD(T)/CBS] method for highly accurate predictions of the ΔE at a variety of regions of the PES was established for a representative set of pi-stacked dimers, which also includes the PYD. For geometries with the distance between stacked monomers close to a value of such a distance in the ΔE minimum structure, an excellent agreement between the canonical CCSD(T)/CBS results and their DLPNO counterparts was found. This finding enabled us to accurately characterize the lowest-lying configurations of the PYD, and the physical origin of their stabilization was thoroughly analyzed. The proposed DLPNO-CCSD(T)/CBS procedure should be applied with the aim of safely locating a global minimum of the PES and firmly establishing the pertaining ΔE of even larger dimers in studies of packing motifs of organic electronic devices and other novel materials.
Keywords: intermolecular interactions, potential energy surfaces, pyrene dimer, CCSD(T), DLPNO
1. Introduction
From among the many research directions in the area of intermolecular noncovalent interactions, of particular importance are studies into the structure, stability and electronic properties of dimers of organic aromatic molecules. Their importance is mainly due to the numerous applications of related systems in, for instance, supramolecular junctions [1,2], scaffolds used in the design of organic semi-conductors [3,4] and stimuli-responsive luminescent materials [5,6]. Most recently, a number of joint experimental/theoretical investigations of these dimers appeared, where spectral measurements were accompanied by high-level quantum chemical predictions of the intermolecular interaction energy in the gas phase (abbreviated as ΔE in the following) and other properties and where significant structural conclusions were reached (for examples, see references [7,8,9,10] and works cited therein). In this type of study, ΔE values were usually obtained from the dispersion-corrected density-functional theory [11] (DC DFT) computations. Notable exceptions are calculations of the ΔE performed for pyridine dimers in reference [12] using the explicitly correlated variant [13] of the coupled-cluster theory with singles, doubles and perturbative triples [CCSD(T)] (see the review [14] for background) and for 2-naphthalenethiol dimers in reference [15] using the domain-based local pair natural orbital (DLPNO) approximation [16,17,18] to the CCSD(T). It is noted that currently the “golden standard” ΔE predictions require an application of the canonical CCSD(T) computations and extrapolations of pertinent energies to their complete basis set (CBS) limit (see the most recent discussions in references [19,20]), but because of the exceedingly high computational cost of the CCSD(T)/CBS procedure, it cannot be routinely applied yet to larger dimers (with more than about 30 atoms if sufficiently large basis sets were to be used and if the system was of a low symmetry; see reference [21]) to directly support their experimental investigations. It is also noted that the local natural orbital (LNO) CCSD(T) scheme was used to estimate the CBS extrapolated ΔE values of systems with more than 100 atoms, but only in their equilibrium geometries [22]. Thus, it should be of interest to obtain the canonical CCSD(T)/CBS ΔE results for a mid-sized dimer featuring aromatic stacking, and also in non-equilibrium geometries, to be able to compare these data to their counterparts predicted by some of the reduced-scaling variants of the CCSD(T). This comparison is the first of two main goals of the present paper. In particular, a performance of the focal-point “silver standard” DLPNO-CCSD(T)/CBS approach [23], which involves the iterative treatment of triple excitations within the CCSD(T) [24] together with an application of large basis sets (see Section 4), was inspected in highly complicated bonding scenarios of the cluster containing 52 atoms, namely, the pyrene dimer (PYD). Prior such comparison was carried out in this work, however, the level of the accuracy of the present canonical CCSD(T)/CBS ΔE computations themselves was established. This was carried out for ten pi-stacked dimers, each in eight geometries along the dissociation curve, which were taken from the S66x8 set [25] (see Section 2.1). The procedure expressed by Equation (1) in Section 4 was found to be highly accurate and was applied also to a region of the potential energy surface (PES) of the benzene dimer (BD). Namely, 125 structures around the global minimum (GM) of the BD [26] were considered (see Section 2.2). The DLPNO-based method was concomitantly applied to these sets of the S66x8 and BD structures. Based on the quite successful DLPNO-CCSD(T)/CBS results for the challenging smaller systems, the aforementioned comparison with the canonical CCSD(T)/CBS ΔE data in an important fragment of the PES was performed for one of the configurations of the PYD, which is a complex frequently studied by calculations and experiments (see references [27,28,29,30,31,32] for the most recent examples, as well as the important solid-state investigation [33] and works cited therein). Specifically, the two sets of CCSD(T)/CBS results were obtained along the dissociation curve of the PYD (see Section 2.3). Importantly, an outstanding level of agreement between the canonical and DLPNO-CCSD(T)/CBS ΔE data was found in the region around a minimum of the investigated stacking coordinate. This finding enabled us to attain the second main goal of the present paper, namely, to accurately characterize the ΔE minima of the most stable configurations of the PYD (see Section 2.4 for details) and to reveal its GM. The physical origin of the stabilization of these low-lying regions of the PES of the PYD was discussed in Section 3. The DLPNO-CCSD(T)/CBS procedure validated here may be applied in robust searches for the GM of even larger adducts [34].
2. Results
2.1. Systems from the S66x8 Set
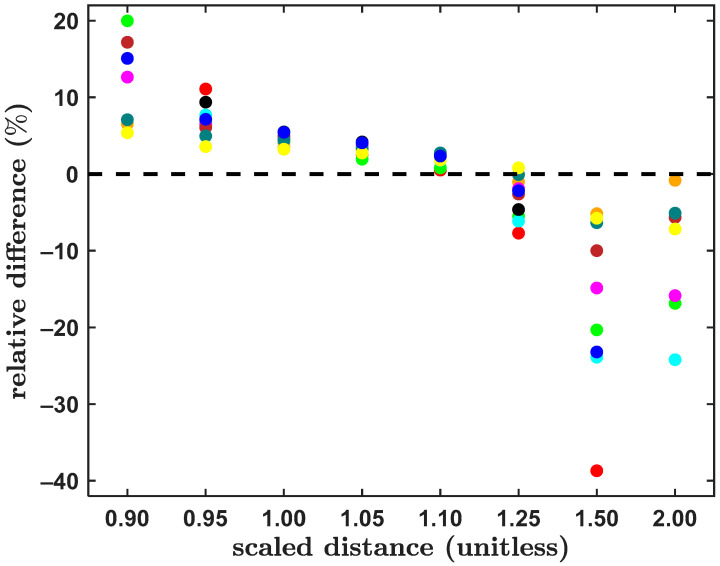
The “golden standard” ΔE values from the widely recognized S66x8 benchmark set of small dimers [25] were repeatedly reinvestigated (see references [19,20] and works cited therein). Here, a subset of the S66x8 database was considered. Specifically, all ten pi-stacked systems from the S66x8 set (see Table 1) were used to carefully check the level of the accuracy of the present procedure for obtaining the reference CCSD(T)/CBS ΔE data. This procedure is detailed in Section 4. In brief, it applies the pertinent augmented correlation-consistent polarized valence X-tuple basis sets [35,36] (aXZ) to assess contributions to the ΔE of Hartree–Fock (HF) energy, the second-order Møller–Plesset correlation energy (MP2) and higher-order correlation energy. In the shorthand notation used in Section 2 and Section 3, these terms are denoted as , and , respectively. Of course, a total contribution of the correlation energy, , to the ΔE is , and . Importantly, a large aTZ basis set was used to estimate the term in the focal-point approach (see Equation (1) in Section 4), and the counterpoise correction (CP) [37] was applied throughout. All underlying absolute energies for the ΔE estimation using Equation (1) are provided in the Supporting Information in Excel spreadsheets whose names begin with “canonical_”. The CCSD(T)/CBS ΔE values obtained in this way for the MP2/cc-pVTZ minima [25] of the aforementioned complexes are listed in Table 1 together with their counterparts from references [19,20] and, wherever available, [22]. Further, a computationally even more demanding procedure was applied to these ten dimers, and its results are also shown in Table 1. Namely, total canonical CCSD(T) energies were obtained while adopting the series of {aDZ; aTZ; aQZ} basis sets, and pertinent values were extrapolated to the CBS limit using the mixed Gaussian/exponential form [38] (see Equation (2) in Section 4) to estimate the ΔE. An inspection of Table 1 reveals that the two sets of present results agree very well (within less than 0.2 kJ/mol) with each other, and they also agree with estimates from the literature [19,20,22]. This comparison shows that a very large aQZ basis set is not needed in order to obtain highly accurate CCSD(T)/CBS ΔE values. It also shows that the procedure expressed by Equation (1) provides results of benchmark quality. Hence, this procedure was applied also to non-equilibrium geometries of the investigated dimers from the S66x8 set to obtain the reference ΔE data. Concomitantly the focal-point method described by Equation (3) of Section 4 was used to approximate the DLPNO-CCSD(T)/CBS ΔE values (all pertinent absolute energies can be found in Excel spreadsheets in the Supporting Information). For a total of 80 investigated differences between the DLPNO-CCSD(T)/CBS ΔE and their canonical CCSD(T)/CBS counterparts, the mean of absolute values and the mean squared deviation amount to 0.598 and 0.724 kJ/mol, respectively. The highest absolute value of these differences equals ca. 2.8 kJ/mol and is found for the uracil dimer with the relative intermonomer separation, , of 0.95, where is the MP2/cc-pVTZ equilibrium distance between monomers [39]. It is stressed that the benchmark value of the ΔE, which amounts to –39.162 kJ/mol, agrees well with its “sterling silver” level counterpart of –38.769 kJ/mol from reference [19]. Furthermore, an application of the model expressed by Equation (2) to this highly challenging system [40] yields a very similar result, namely, –39.147 kJ/mol. Relative to these data, the DLPNO-CCSD(T)/CBS value of ca. –36.8 kJ/mol is overestimated by about 7%. Nonetheless, the differences of the DLPNO and canonical CCSD(T) results exhibit a practically uniform (and very interesting) pattern. This is apparent from an inspection of Figure 1, where the relative differences of the two data sets are plotted (it has to be mentioned that seven points with underlying smaller than 1.0 kJ/mol were excluded from analysis so that a division of very small numbers was avoided). In brief, the DLPNO-CCSD(T)/CBS results are systematically underestimated regarding their absolute values for short intermonomer separations, namely, in structures with = 0.90 and 0.95, and overestimated for large intermonomer separations, that is, for dimers with = 1.50 and 2.00, while there is a quite high level of agreement between the two sets of CCSD(T)/CBS values in the intermediate region, both in absolute and relative terms. The relative differences become the smallest for structures with = 1.10 (see Figure 1), with a mean value of 2.0%. Regarding the absolute differences obtained for these geometries, their mean absolute value and the mean squared deviation is as low as 0.334 and 0.263 kJ/mol, respectively. This is important because the minima of the CCSD(T)/CBS dissociation curves would be often located in between of 1.05 and 1.10 (see Table 1 in reference [19]). As a consequence, the DLPNO approximation to the CCSD(T) can be expected to work very well at “true” minimal geometries. It is worth noting that that mean absolute value of the differences for structures with = 0.90 and 0.95 is even higher than 1.0 kJ/mol, amounting to 1.215 and 1.029 kJ/mol, respectively. For these structures, the relative differences can be as high as 20%, which is found for the pyridine dimer with = 0.90. It is also worth noting that the highest relative differences occur for structures with = 1.50 (see Figure 1). The biggest value of these differences is found for the pertinent geometry of the benzene dimer and amounts to 38%. In this case the DLPNO-CCSD(T)/CBS computations overestimated the ΔE by 0.772 kJ/mol with respect to a rather small reference value of –1.995 kJ/mol. Further results for the BD are presented in the subsequent paragraph.
Table 1.
Comparison of the predicted interaction energy values for minima of ten pi-stacked complexes from the Set66 [25].
| System (Designation in S66 Set) |
CCSD(T)/CBS |ΔE| Estimate/kJ/mol | ||||
|---|---|---|---|---|---|
| From Equation (1) | From Equation (2) | From Ref. [22] (a) | From Ref. [20] (b) | From Ref. [19] (c) | |
| benzene–benzene (S24) |
10.926 | 10.762 | 11.171 ± 0.293 | 11.238 | 10.548 |
| pyridine–pyridine (S25) |
15.462 | 15.340 | 15.481 ± 0.335 | 15.731 | 15.104 |
| uracil–uracil (S26) |
40.578 | 40.593 | 40.203 ± 0.418 | 40.652 | 40.246 |
| benzene–pyridine (S27) |
13.561 | 13.428 | 13.724 ± 0.293 | 13.824 | 13.205 |
| benzene–uracil (S28) |
23.239 | 23.101 | 22.928 ± 0.460 | 23.200 | 22.866 |
| pyridine–uracil (S29) |
27.905 | 27.774 | 27.656 ± 0.377 | 27.870 | 27.514 |
| benzene–ethene (S30) |
5.570 | 5.482 | — | 5.619 | 5.310 |
| uracil–ethene (S31) |
13.860 | 13.800 | — | 13.823 | 13.627 |
| uracil–ethyne (S32) |
15.362 | 15.333 | — | 15.376 | 15.008 |
| pyridine–ethene (S33) |
7.455 | 7.378 | — | 7.464 | 7.201 |
(a) Obtained using the LNO scheme; (b) the “14k-GOLD” level result; (c) the “sterling silver” level result.
Figure 1.
Plot of relative differences between the approximate and canonical interaction energies, which are described in the text, for structures of ten pi-stacked dimers from the S66x8 set [25] in geometries defined by the scaled distance between monomers. Data points are color-coded with the benzene dimer in red, pyridine dimer in green, uracil dimer in orange, benzene–pyridine in cyan, benzene–uracil in magenta, pyridine–uracil in brown, benzene–ethene in black, uracil–ethene in teal, uracil–ethyne in yellow and pyridine–ethene in blue color.
2.2. The Benzene Dimer Structures
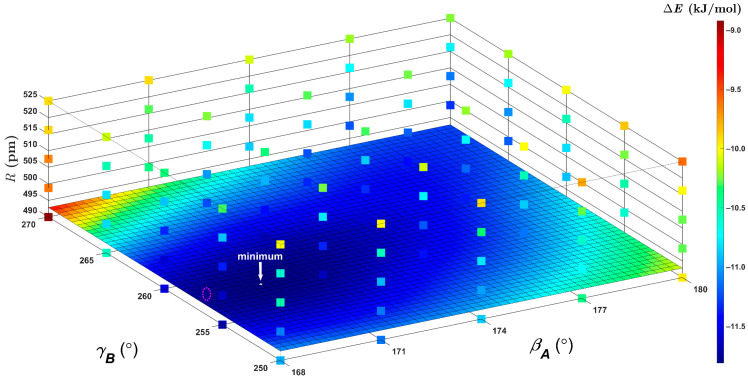
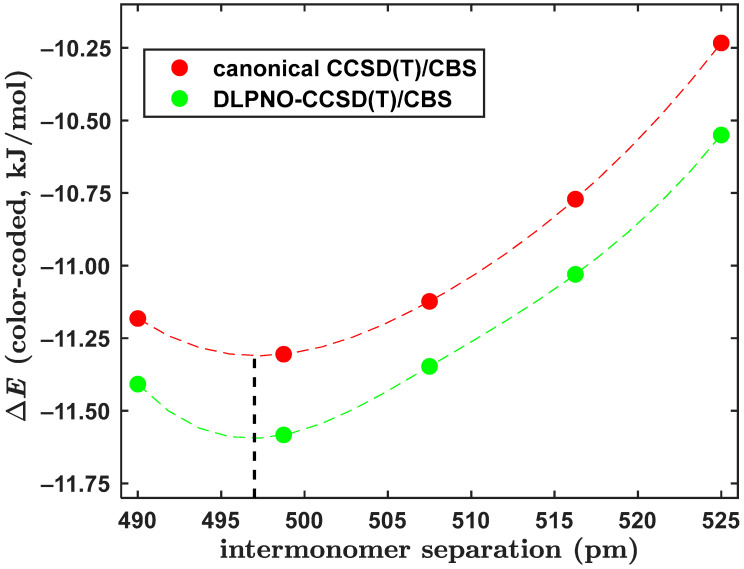
The canonical CCSD(T)/CBS ΔE values were predicted using Equation (1) also for an important region of the PES of the BD. The investigated region covered T-shaped structures on the three-dimensional (3D) grid of one radial () and two angular (, ) coordinates, which were adopted from reference [41]. Values of these coordinates were chosen in sufficiently wide intervals to contain both the tilted (of Cs symmetry) and fully symmetric (that is, of C2v symmetry) geometries of T-shaped BD structures and to also encompass a position of the GM. Pertinent absolute energies obtained on this 3D grid of 5 × 5 × 5 points are collected in Excel spreadsheets in the Supporting Information together with the Cartesian coordinates of all 125 structures. Figure 2 graphically presents the data. The canonical CCSD(T)/CBS ΔE results span values from a relatively large interval of about 2.80 kJ/mol in a fairly complicated landscape, and their minimum located by 3D interpolation is essentially the same as the one found on a smaller, but tighter, grid in reference [23]. Hence, they served as a stringent test of the DLPNO-CCSD(T)/CBS results obtained by an application of Equation (3). Differences between the two ΔE data sets have values between –0.597 and 0.664 kJ/mol, with an average and a median value equal to –0.248 and –0.275 kJ/mol, respectively. The mean squared deviation of these differences is very small, namely, 0.155 kJ/mol. As already mentioned, positions of the GM were obtained by the 3D interpolation of the data (see Figure 2 for a visualization). Despite the fact that the PES around a position of the GM is very flat [26,41,42,43], an agreement within 3 pm in the radial and 2° in the angular coordinates of the DLPNO and canonical CCSD(T)/CBS minima was found. The corresponding ΔE values in these minima differ by about a quarter of kJ/mol only. It is worth noting that for and fixed at 180° and 270°, respectively, the dependence captures a minimum of the fully symmetric geometry of the T-shaped arrangement. The canonical and DLPNO-CCSD(T)/CBS calculations exhibit such a minimum at around the same value of , namely, = 497 pm (see Figure 3). Importantly, this value agrees with the result of = 497.4 pm that was obtained in reference [26] from a robust fit of 19 points predicted by the same canonical CCSD(T)/CBS computational procedure as the one used here. Moreover, the DLPNO-CCSD(T)/CBS ΔE data are only slightly and quite uniformly (see Figure 3) overestimated in their absolute value relative to their canonical counterparts. In particular, an average difference between the two sets of ΔE values is as low as –0.261 kJ/mol. These results thus confirm an outstanding performance of the present DLPNO-CCSD(T)/CBS approach in regions close to the minima of the PES. In the next part, results for the pyrene dimer are presented.
Figure 2.
The three-dimensional plot of the intermolecular interaction energies of the benzene dimer that are discussed in the text. The canonical computations place the global minimum with ΔE = –11.81 kJ/mol at around = 493.9 pm, = 170.0° and = 257.4°, as indicated by the white arrow, and the cut through interpolated data is shown for a value of in this minimum. The reduced-scaling computations, which were performed on a different grid, predict the global minimum with ΔE = –12.15 kJ/mol at around = 491.3 pm, = 168.5° and = 257.4° (shown schematically as the dotted ellipse in magenta).
Figure 3.
Plot of the distance dependence of the intermolecular interaction energy of the fully symmetric T-shaped dimer of benzene. The respective data points are connected by a spline. An approximate position of the minimum is indicated by the dashed black line drawn at = 497 pm.
2.3. Dissociation of the Pyrene Dimer
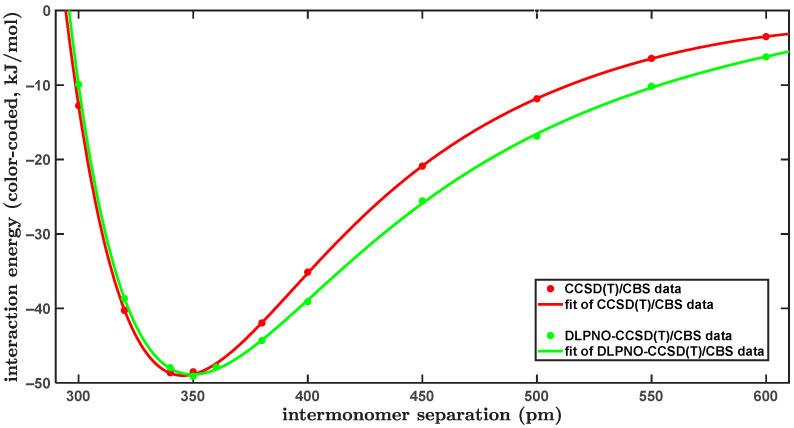
The computational models expressed by Equations (1) and (3) were applied to one of the slipped-parallel configurations of the PYD. Here, this topology of the PYD is called “L” in order to use the notation from reference [44] (briefly, the designation “L” refers to a displacement of one of the monomers along the long axis of the reference monomer; see Section 2.4 for further details). The interplane distance, , was varied in a very wide interval from 300 to 600 pm, and the canonical and DLPNO-approximated CCSD(T)/CBS ΔE values were obtained at eleven geometries of this configuration. The geometry of rigid monomers was taken from the Supplementary Information to reference [44]. It is noted that the canonical CCSD(T) calculations were computationally very demanding, as they applied 1932 basis functions of the aTZ basis set to estimate terms in a fully reliable way [45]. The same form of a modified Dunham expansion (see Section 4) was employed to accurately fit both sets of the CCSD(T)/CBS data, which are listed in Supporting Information Table S1. Figure 4 graphically presents the results. The curve fitted to canonical CCSD(T)/CBS values has a minimum of –49.0 kJ/mol at equal to 346 pm. The corresponding DLPNO-CCSD(T)/CBS minimum lies very close, namely, at = 350 pm, and has almost the same ΔE value of –48.9 kJ/mol, as might be expected on the basis of results for smaller systems described in preceding paragraphs. Also following these expectations, there is a significant under-binding by the DLPNO-CCSD(T)/CBS computations in the region of short intermolecular distances and a quite strong over-binding for larger values (see Figure 4). In particular, the canonical CCSD(T)/CBS curve has an inflexion point at 393 pm with the corresponding ΔE of –37.5 kJ/mol. At this intermolecular separation, which can be considered as intermediate, the DLPNO-CCSD(T)/CBS ΔE amounts to –40.8 kJ/mol and is thus by about 9% higher in absolute value than its canonical counterpart. Furthermore, the DLPNO-CCSD(T)/CBS curve has an inflexion point at = 403 pm with the associated ΔE of –38.1 kJ/mol, while the canonical CCSD(T)/CBS ΔE result for this distance is lower by ca. 11% in absolute value, as it amounts to –34.2 kJ/mol. These apparent deficiencies of the DLPNO-CCSD(T)/CBS data are analyzed in Section 3.1 in terms of the respective and contributions.
Figure 4.
Plot of the distance dependence of the intermolecular interaction energy of the “L” configuration of the pyrene dimer.
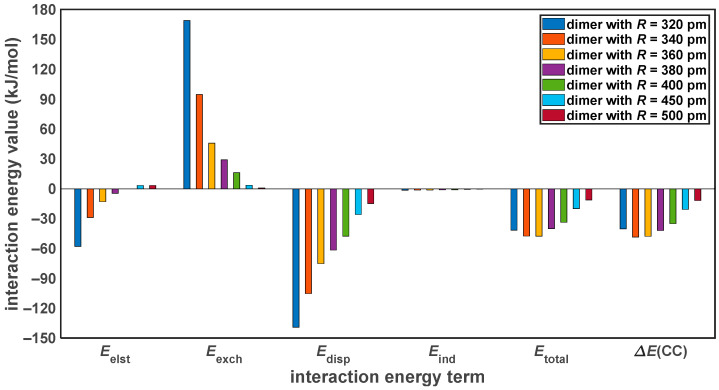
It is worthwhile to apply the symmetry-adapted perturbation theory (SAPT) of intermolecular interactions [46] and inspect the physical contributions to noncovalent binding in the investigated PYD structures. The SAPT treatment was combined with the DFT-based description of monomers [47] and with extrapolations of all of the SAPT terms to the CBS limit as in our previous work [48] (see Section 4 for technical details and a full set of references). The resulting approach is referred to as SAPT-DFT/CBS and provides reliable values of the electrostatic, , Pauli exchange, , London dispersion, , and induction, , contributions to a total intermolecular interaction energy, , with . These contributions are shown in Figure 5 together with the canonical CCSD(T)/CBS interaction energy data, which are denoted as to clearly distinguish them from the SAPT result. Within the PYD geometries with the distance varied in an interval from 320 to 500 pm, the two sets of total interaction energy values agree well. In particular, a value of the mean squared deviation of the seven investigated differences equals 1.056 kJ/mol. Significantly, the distance dependence of respective contributions to follows the trends typical for systems with aromatic stacking [49,50] and are in accord with results from reference [44]. This SAPT-DFT/CBS approach is thus utilized in the discussion of a stabilization of various PYD configurations in Section 3.2.
Figure 5.
Components of the intermolecular interaction energy at various distances in the “L” configuration of the pyrene dimer.
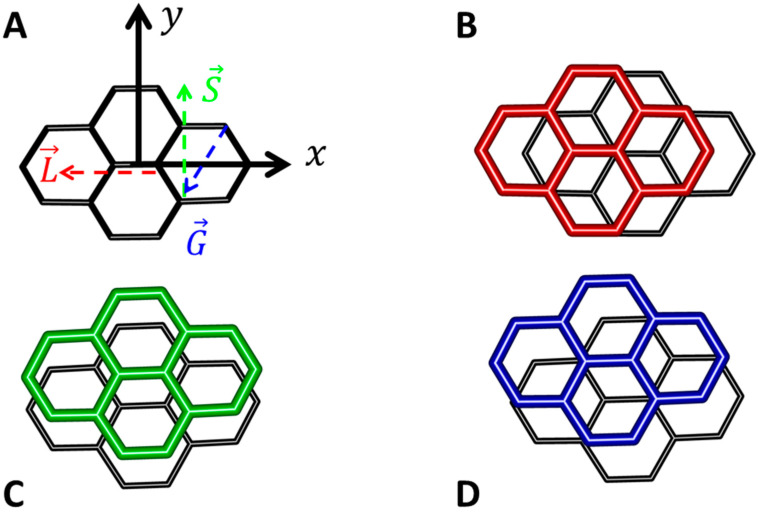
2.4. Minima of the Pyrene Ddimer
An outstanding performance of the DLPNO-CCSD(T)/CBS ΔE calculations in regions of the PES minima was found for various benchmark sets, as described in previous sections. Consequently, these calculations were used to locate the GM of the PYD by a direct search approach in the rigid-monomer approximation. Due to a relatively high computational cost of some of the underlying computations (in particular, of the iterative CCSD(T) performed with 3704 basis functions of the aQZ basis set), this search was restricted to the lowest-lying fragments of the PES that had been scanned by DFT-based methods in older references [44,51]. The monomer geometry was optimized at the MP2/aTZ level assuming the D2h symmetry. A resulting structure agreed with the experimental geometry of the ground electronic state, that is, S0 1Ag [52]. Specifically, measured values of rotational constants {A, B, C} are {1.001, 0.5593, 0.3610} GHz when rounded, while their MP2/aTZ counterparts accordingly amount to {1.015, 0.5589, 0.3603} GHz. Coordinates of this MP2/aTZ structure are provided in Table S2 together with the atom numbering as employed in setting the angular configurations through translation vectors , and (see Figure 6). These vectors are listed in Table S3 and used as in the important study [44] to define the “L”, “S” and “G” topology, respectively, of the PYD. In the coordinate system shown in Figure 6A, the L and S configuration was obtained by offsetting one of the monomers along its long (designated as x) and short (y) axes, respectively, and keeping the other monomer in its reference geometry. These two parallel-displaced configurations are accordingly pictured in Figure 6B,C. The G (graphite-like) configuration forms a honeycomb pattern, which is shown in Figure 6D. Also investigated here is the “X” (crossed) topology. In this configuration, axes x and y of one of the monomers are interchanged with respect to the reference orientation, and the resulting dimer resembles a cross. Other structures of the PYD would lie too high on its PES and were not considered as candidates for the GM, while it should be noted that some of the higher-energy structures feature C–H∙∙∙π interactions (see Table III in reference [51]). Thus, the direct search for a minimum of the interplanar distance, , was carried out for the aforementioned four configurations within their symmetry group, which is specified in Table 2. First the DLPNO-CCSD(T)/CBS ΔE values were obtained for distances spanning an interval from 330 to 380 pm with ten pm step and the resulting curve was inspected. Then, several additional data points were suitably added in five pm steps for an accurate fit to the functional form given by Equation (4). The final results are presented in Table 2. They indicated the L configuration with the DLPNO-CCSD(T)/CBS optimal of 343 pm and associated ΔE = –52.1 kJ/mol to be the GM, while it should be noted that there were only small differences in the DLPNO-CCSD(T)/CBS minima of respective configurations, as values of these differences remained within about four kJ/mol and eleven pm for the ΔE and data, respectively (see Table 2). However, the ΔE difference between the lowest-lying minima, namely, of the L and G configurations, was relatively big, amounting to almost two kJ/mol. Moreover, geometries of these two configurations and of an isolated pyrene molecule were fully optimized using the DC DFT method PBE0-D3/TZVPP (see Section 4 for specifications), and the deformation energy of the respective PYD structures was estimated from relevant DLPNO-CCSD(T)/CBS energies. The resulting deformation energy was found to be fairly small, and similar in value, for the L and G configurations (it amounted to 0.396 and 0.462 kJ/mol, respectively). Furthermore, the zero-point energy (ZPE) of these two configurations was estimated through the PBE0-D3/TZVPP harmonic vibrational analysis. A (ZPE(L)–ZPE(G)) difference was found to be 0.316 kJ/mol, which would not change the ordering of the stabilization of the investigated PYD structures. The DLPNO-CCSD(T)/CBS and PBE0-D3/TZVPP-based results thus revealed the L configuration as the GM of the PYD. Interestingly, this configuration was correctly taken as the ground electronic state in the investigation of pyrene excimers, while only the DC DFT calculations of its structure were performed in that work [53] and while two previous DFT-based computations [44,51] both predicted the G configuration to have the highest binding (see also reference [54]). In Section 3.2, a preference for the formation of respective PYD structures is analyzed. By combining the canonical CCSD(T)/CBS ΔE of the L configuration (–51.1 kJ/mol), the aforementioned deformation energy of ca. 0.4 kJ/mol and the (ZPE(L)—2 × ZPE(monomer)) difference of 1.6 kJ/mol obtained from the PBE0-D3/TZVP calculations, the dissociation energy of the PYD is predicted to be about –49 kJ/mol.
Figure 6.
Pictorial representation of the pyrene dimers (all structures are shown to the same scale). (A) The reference frame (its z axis points towards the viewer and is not shown). (B) The slipped-parallel structure of “L” configuration. (C) The slipped-parallel structure of “S” configuration. (D) The graphene-like structure of “G” configuration.
Table 2.
Computational results for the four low-lying configurations of the pyrene dimer.
| Parameter | Configuration (Symmetry) | |||
|---|---|---|---|---|
| L (C2h) | G (Cs) | S (C2h) | X (D2h) | |
| /pm | 344 | 347 | 350 | 355 |
| ΔE/kJ/mol | –52.1 | –50.3 | –49.1 | –48.4 |
3. Discussion
3.1. Discrepancies between the Canonical and DLPNO CCSD(T)/CBS Results
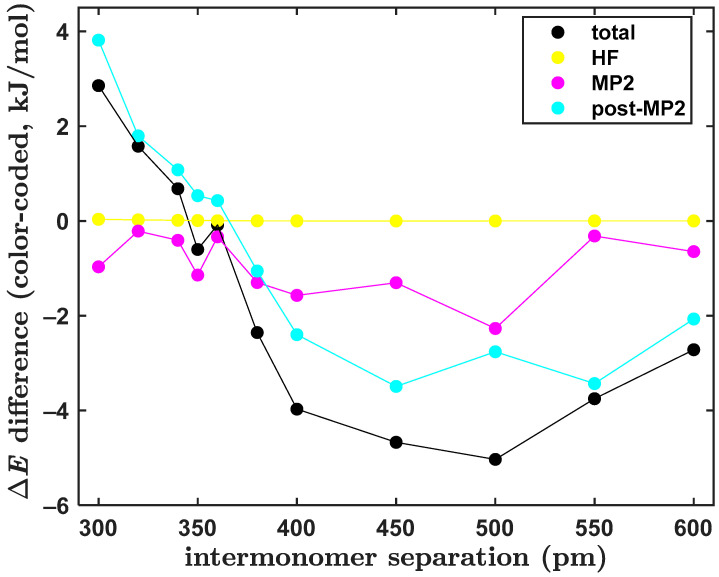
Due to their size and complexity, the investigated configurations of the PYD present a challenge to the CCSD(T)/CBS computations. Specifically, a total ΔE value of these structures is obtained as a relatively small sum of some large, repulsive , even larger, but attractive and a non-negligible, repulsive components. Hence, it is of interest to inspect the values of these contributions to the data along the dissociation curve of the PYD since, in Section 2.3, significant differences between the canonical and DLPNO CCSD(T)/CBS ΔE results were obtained at small and large interplanar distances . The underlying data are listed in Table S4. Values of respective components of the ΔE vastly vary throughout the investigated range of distances. In particular, the canonical CCSD(T)/CBS , and contributions change by ca. 174, –258 and 74 kJ/mol, respectively, between = 300 and 600 pm (see Table S4). Figure 7 presents differences of the DLPNO-approximated and canonical CCSD(T)/CBS values of the total and of its components. A positive value of the differences implies that a weaker binding was predicted by the DLPNO-CCSD(T)/CBS calculation than by its canonical counterpart. Differences of the total interaction energy have values between ca. 2.9 kJ/mol (found at = 300 pm, which is the shortest distance considered here) and –5.0 kJ/mol (occurs at = 500 pm). Importantly, these differences are lower than the “spectroscopic accuracy” value of one kJ/mol in an interval from 340 to 360 pm, that is, at around the minima of the investigated dependences (see Section 2.3, in particular Figure 4). An inspection of Figure 7 reveals that small values of the ΔE differences in this region originate from a compensation of errors in the and contributions. Namely, differences of the data are negative for all investigated values of , while differences in the data are positive from = 300 up to 360 pm. At the same time, it should be noted that there are essentially no differences between the two sets of the values throughout the whole range of interplanar distances (see Figure 7). The differences shown in Figure 7 also immediately explain a relatively poor performance of the DLPNO-CCSD(T)/CBS approach in the region of larger values of . In this part of the data curves, differences in the and data are of the same sign and both contribute to resulting discrepancies. Specifically, at the data point with = 500 pm, the and differences amount to ca. –2.3 and –2.7 kJ/mol, respectively, which leads to the highest absolute value (of 5.0 kJ/mol) of differences between the canonical and DLPNO-CCSD(T)/CBS interaction energies along the investigated curve of the PYD. In this case, also the relative difference is quite high, as it constitutes about 42% of the canonical CCSD(T)/CBS ΔE value of ca. –11.8 kJ/mol at = 500 pm. As a consequence, an application of the DLPNO-CCSD(T)/CBS method, which is computationally quite costly, should be limited to regions lying close to the PES minima in order to obtain the ΔE data of benchmark quality. This would likely hold for other “difficult” complexes of a similar and bigger size due to an expected error accumulation of the DLPNO approximation [55].
Figure 7.
Plot of the distance dependence of the interaction energy differences of the pyrene dimer that are discussed in the text.
3.2. Stacking Preferences of the Pyrene Dimers
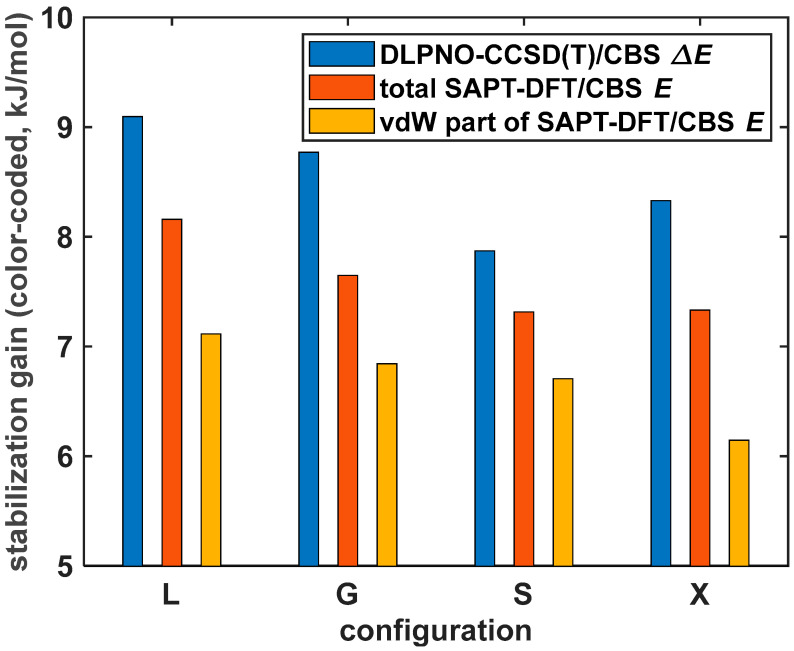
Values of the SAPT-DFT/CBS energy terms are fairly similar for the four PYD configurations described in Section 2.4. This was, of course, expected on the basis of results reported in reference [44]. An illustration of respective contributions to data for the set of {L; G; S; X} structures with the same interplanar distances = 345 and 355 pm is anyway provided in Tables S5 and S6, respectively. The chosen values of span over a region of the PES minima of the considered configurations (see Table 2). The DLPNO-CCSD(T)/CBS ΔE data of these structures are listed in Tables S5 and S6 as well. Importantly, the two sets of total interaction energies have the same ordering, despite a slight overestimation of the binding by the SAPT-DFT/CBS calculations relative to their ab initio counterparts (see Tables S5 and S6). This further confirms, in addition to results from Section 2.3, the reliability of the present SAPT-DFT/CBS computational approach. Hence, it was applied also to the cofacial π∙∙∙π stacked (called “sandwich”) arrangement of the PYD in order to explore a source of the offset stacking of respective {L; G; S; X} structures [56]. The interplanar distance of 370 pm was chosen for this investigation because it is a value found in the SAPT-DFT/CBS minimum of the sandwich geometries, which were prepared from the same MP2/aTZ monomer as the one used in Section 2.4. The corresponding DLPNO-CCSD(T)/CBS minimum was located at = 371 pm, with ΔE = –38.2 kJ/mol (see Table 2 for reference). Thus, for the sandwich and {L; G; S; X} structures, all , , and contributions to were inspected in terms of their absolute values and of differences between the sandwich and respective slipped arrangements. Various combinations of the SAPT terms were checked, too, in an attempt to interpret the stacking preferences of the PYD. The “van der Waals” contributions, [57], , turned out to be useful in this respect, contrary to, for instance, sums of the first-order terms of the SAPT expansion () that were most recently invoked in an analysis of the GM of the benzene dimer [26]. Figure 8 shows various stabilization energies, which were obtained as a difference between the given interaction energy in the sandwich and slipped structures (underlying data are provided in Table S7). Quite similar values of this stabilization were predicted for all four slipped structures. In particular, an average stabilization obtained from the DLPNO-CCSD(T)/CBS ΔE and SAPT-DFT/CBS results amounted to 8.5 and 7.6 kJ/mol, respectively. The data captured quite well absolute values of the studied differences (their average is 6.6 kJ/mol). This indicates that π∙∙∙π aromatic interactions are governed by a competition between the and contributions, at least in this part of the PES [58]. However, the ordering of stabilization was swapped by the results for S and X configurations relative to the DLPNO-CCSD(T)/CBS ΔE data, while almost the same values were obtained from SAPT-DFT/CBS (see Figure 8 and Table S7).
Figure 8.
Differences between the interaction energy of {L; G; S; X} configuration and of the fully stacked “sandwich” configuration of the pyrene dimer, which were obtained for the pertinent geometries with the same interplanar separation of = 370 ppm to describe the stabilization gain of a formation of the investigated structures.
4. Materials and Methods
The canonical CCSD(T)/CBS interaction energy obtained with the CP procedure to reduce the basis set superposition error [37], , was predominantly estimated using Equation (1):
| (1) |
where subscripts denote the respective energy terms, namely, the total Hartree–Fock energy (“HF”), the MP2 correlation energy (“MP2”) and the higher-order correlation energy (“post-MP2”; taken as a difference of the CCSD(T) and MP2 contributions to the total energy [45]), and superscripts specify the augmented correlation-consistent polarized-valenced basis set [35,36], denoted as aXZ, that was used to compute the respective term. In some cases, the value was also established through the model expressed by Equation (2):
| (2) |
where superscript denotes an application of the aXZ basis set, (aDZ; aTZ; aQZ), for obtaining the total CCSD(T) energy, while the corresponding integer value of is 2, 3 and 4, respectively. Thus, three equations in three unknowns (namely, , and ) were formed in this model and solved analytically for a value of . Calculations of all the aforementioned CCSD(T) energies were performed in the Molpro version 2022.2 [59]. The HF/a5Z and MP2/a5Z energies for Equation (1) were computed using the Turbomole version 7.1 [60]. The MP2/a5Z correlation energies were obtained in the resolution-of-the-identity integral approximation [61,62] while applying the relevant auxiliary basis sets [62].
The DLPNO-CCSD(T)/CBS interaction energy (denoted simply as ΔE below) was estimated using the previously developed procedure [63]. This procedure is described by Equation (3) (the notation as in Equation (1) is used, and the right arrow symbol indicates an application of the two-point extrapolation formula from reference [64]):
| (3) |
Of course, the underlying CCSD(T) and MP2 correlation energies were obtained in the DLPNO approximation [16,17,18,65], and the CP was applied. The ORCA version 5.0.3 [66] was used. The HF calculations applied “VeryTightSCF” accuracy settings. The default method of the orbital localization was adopted, and the “T1” option for the iterative treatment of triple excitations within the CCSD(T) method [24] was used. The electron-correlation space was truncated through the “TightPNO” set of parameters.
The density-fitting variant of the SAPT-DFT method [67] was used as implemented in Molpro 2022.2. Previously developed computational protocol [68] was applied in order to estimate the respective SAPT-DFT/CBS terms. In brief, the , , and contributions to the total interaction energy, , are related to the underlying interaction energy terms as follows: and are the electrostatic polarization and Pauli exchange energy contributions, respectively, arising in the first order of the perturbation theory of intermolecular interactions [69]; is the London dispersion energy contribution obtained as a sum of the second-order terms and [70]; and is the induction energy contribution approximated by a sum of the second-order terms and [71] and of the correction term , which is computed at the HF level [72].
The least-squares fit of pertinent data employed the following functional form:
| (4) |
where and is the interplanar distance. The trust-region-reflective algorithm from the “lsqcurvefit” function of MATLAB® Optimization Toolbox™ was applied to obtain final sets of results.
The PBE0-D3/def2-TZVPP approach (the PBE0 hybrid-functional [73] applied together with the D3 empirical dispersion correction [74] and the triple zeta valence basis set from reference [75]) was used to optimize the geometries for an assessment of the deformation energy. It was also used to obtain the harmonic vibrational frequencies for an estimation of the ZPE differences. In the underlying calculations, the Gaussian 16 revision C.01 [76] was applied with default algorithms and settings.
5. Conclusions
To conclude, this study has achieved two major goals. The first major goal was to obtain fully reliable canonical CCSD(T)/CBS ΔE values along the π∙∙∙π stacking coordinate in a large adduct, namely, the PYD containing 52 atoms, for the purpose of their comparison to the “silver standard” DLPNO-CCSD(T)/CBS ΔE results. The comparison revealed an excellent agreement of the two sets of ΔE data around the minima. In fact, these minima were found to be almost identical. However, this agreement was shown to be a result of the compensation of errors of the DLPNO-based and contributions to the intermolecular binding relative to their canonical counterparts. Consequently, the canonical CCSD(T)/CBS calculations would be needed for obtaining the benchmark ΔE values at non-equilibrium geometries of similarly complex systems. The second major goal was to exploit the aforementioned agreement and use the DLPNO-CCSD(T)/CBS strategy for an accurate characterization of the most stable PYD structures. Namely, four low-lying regions of the PES were investigated, which corresponded to {L; G; S; X} configurations around their minima. From among them, the “L” configuration with the DLPNO-CCSD(T)/CBS optimal stacking distance of 343 pm and associated ΔE = –52.1 kJ/mol was found to be the GM. These values are recommended for use in investigations involving the ground electronic state of the PYD [77]. Using the computed data for the GM and an isolated pyrene, the dissociation energy of the PYD in the gas phase was estimated to be about –49 kJ/mol, which awaits experimental verification.
Acknowledgments
The support of the Ministry of Education, Youth and Sports (through the project New Technologies for Translational Research in Pharmaceutical Sciences/NETPHARM CZ.02.01.01/00/22_008/0004607 co-funded by the European Union) is gratefully acknowledged. The computational resources were provided by the e-INFRA CZ project (ID:90254) and by the ELIXIR-CZ project (ID:90255), which are part of the international ELIXIR infrastructure.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/ijms251910762/s1.
Author Contributions
Conceptualization, J.C. and J.B.; investigation, J.C.; writing, J.C.; validation, J.B.; funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the article and in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding Statement
The Czech Science Foundation through the joint GAČR–NCN project 24-15057L.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Li X., Ge W., Guo S., Bai J., Hong W. Characterization and Application of Supramolecular Junctions. Angew. Chem. 2023;62:202216819. doi: 10.1002/anie.202216819. [DOI] [PubMed] [Google Scholar]
- 2.Zhou P., Fu Y., Wang M., Qiu R., Wang Y., Stoddart J.F., Wang Y., Chen H. Robust Single-Supermolecule Switches Operating in Response to Two Different Noncovalent Interaction. J. Am. Chem. Soc. 2023;145:18800–18811. doi: 10.1021/jacs.3c03282. [DOI] [PubMed] [Google Scholar]
- 3.Poriel C., Rault-Berthelot J. Dihydroindenofluorenes as building units in organic semiconductors for organic electronics. Chem. Soc. Rev. 2023;52:6754–6805. doi: 10.1039/D1CS00993A. [DOI] [PubMed] [Google Scholar]
- 4.Roy R., Brouillac C., Jacques E., Quiton C., Poriel C. π-Conjugated Nanohoops: A New Generation of Curved Materials for Organic Electronics. Angew. Chem. 2024;63:e202402608. doi: 10.1002/anie.202402608. [DOI] [PubMed] [Google Scholar]
- 5.Zhao W., Ding Z., Yang Z., Lu T., Yang B., Jiang S. Remarkable Off–On Tunable Solid-State Luminescence by the Regulation of Pyrene Dimer. Chem. Eur. J. 2024;30:e202303202. doi: 10.1002/chem.202303202. [DOI] [PubMed] [Google Scholar]
- 6.Liao Q., Huang A., Wang J., Chang K., Li H., Yao P., Zhong C., Xie P., Wang J., Li Z., et al. Controllable π–π coupling of intramolecular dimer models in aggregated states. Chem. Sci. 2024;15:4364–4373. doi: 10.1039/D3SC05533G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Du W., Zheng Y., Wang X., Lei J., Wang H., Tian X., Zou S., Bloino J., Gou Q., Caminati W., et al. Scissor-like Face to Face π−π Stacking: A Surprising Preference Induced by the Isocyano Group in the Self-Assembled Dimer of Phenyl Isocyanide. J. Phys. Chem. Lett. 2022;13:9934–9940. doi: 10.1021/acs.jpclett.2c02807. [DOI] [PubMed] [Google Scholar]
- 8.Germer S., Bauer M., Hübner O., Marten R., Dreuw A., Himmel H.-J. Isolated Dimers Versus Solid-State Dimers of N-Heteropolycycles: Matrix-Isolation Spectroscopy in Concert with Quantum Chemistry. Chem. Eur. J. 2023;29:e202302296. doi: 10.1002/chem.202302296. [DOI] [PubMed] [Google Scholar]
- 9.Miao X., Preitschopf T., Sturm F., Fischer F., Fischer I., Lemmens A.K., Limbacher M., Mitric R. Stacking Is Favored over Hydrogen Bonding in Azaphenanthrene Dimers. J. Phys. Chem. Lett. 2022;13:8939–8944. doi: 10.1021/acs.jpclett.2c02280. [DOI] [PubMed] [Google Scholar]
- 10.Torres-Hernández F., Pinillos P., Li W., Saragi R.T., Camiruaga A., Juanes M., Usabiaga I., Lessari A., Fernández J.A. Competition between O−H and S−H Intermolecular Interactions in Conformationally Complex Systems: The 2-Phenylethanethiol and 2-Phenylethanol Dimers. J. Phys. Chem. Lett. 2024;15:5674–5680. doi: 10.1021/acs.jpclett.4c00903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Goerigk L., Hansen A., Bauer C., Ehrlich S., Najibi A., Grimme S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017;19:32184–32215. doi: 10.1039/C7CP04913G. [DOI] [PubMed] [Google Scholar]
- 12.Hübner O., Thusek J., Himmel H.-J. Pyridine Dimers and Their Low-Temperature Isomerization: A High-Resolution Matrix-Isolation Spectroscopy Study. Angew. Chem. 2023;62:e202218042. doi: 10.1002/anie.202218042. [DOI] [PubMed] [Google Scholar]
- 13.Ma Q., Werner H.-J. Explicitly correlated local coupled-cluster methods using pair natural orbitals. WIREs Comput. Mol. Sci. 2018;8:e1371. doi: 10.1002/wcms.1371. [DOI] [PubMed] [Google Scholar]
- 14.Calvin J.A., Peng C., Rishi V., Kumar A., Valeev E.F. Many-Body Quantum Chemistry on Massively Parallel Computers. Chem. Rev. 2021;121:1203–1231. doi: 10.1021/acs.chemrev.0c00006. [DOI] [PubMed] [Google Scholar]
- 15.Saragi R.T., Calabrese C., Juanes M., Pinacho R., Rubio J.E., Pérez C., Lessari A. π-Stacking Isomerism in Polycyclic Aromatic Hydrocarbons: The 2-Naphthalenethiol Dimer. J. Phys. Chem. Lett. 2023;14:207–231. doi: 10.1021/acs.jpclett.2c03299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Riplinger C., Neese F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013;138:034106. doi: 10.1063/1.4773581. [DOI] [PubMed] [Google Scholar]
- 17.Riplinger C., Pinski P., Becker U., Valeev E.F., Neese F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016;144:024109. doi: 10.1063/1.4939030. [DOI] [PubMed] [Google Scholar]
- 18.Riplinger C., Sandhoefer B., Hansen A., Neese F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013;139:134101. doi: 10.1063/1.4821834. [DOI] [PubMed] [Google Scholar]
- 19.Santra G., Semidalas E., Mehta N., Karton A., Martin J.M.L. S66x8 noncovalent interactions revisited: New benchmark and performance of composite localized coupled-cluster methods. Phys. Chem. Chem. Phys. 2022;24:25555–25570. doi: 10.1039/D2CP03938A. [DOI] [PubMed] [Google Scholar]
- 20.Nagy P.R., Gyevi-Nagy L., Lőrincz B.D., Kállay M. Pursuing the basis set limit of CCSD(T) non-covalent interaction energies for medium-sized complexes: Case study on the S66 compilation. Mol. Phys. 2022;121:e2109526. doi: 10.1080/00268976.2022.2109526. [DOI] [Google Scholar]
- 21.Donchev A.G., Taube A.G., Decolvenaere E., Hargus C., McGibbon R.T., Law K.-H., Gregersen B.A., Li J.-L., Palmo K., Siva K., et al. Quantum chemical benchmark databases of gold-standard dimer interaction energies. Sci. Data. 2021;8:55. doi: 10.1038/s41597-021-00833-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Al-Hamdani Y.S., Nagy P.R., Zen A., Barton D., Kállay M., Bradenburg J.G., Tkatchenko A. Interactions between large molecules pose a puzzle for reference quantum mechanical methods. Nat. Commun. 2021;12:3927. doi: 10.1038/s41467-021-24119-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Czernek J., Brus J. Reliable Dimerization Energies for Modeling of Supramolecular Junctions. Int. J. Mol. Sci. 2024;25:602. doi: 10.3390/ijms25010602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Guo Y., Riplinger C., Becker U., Liakos D.G., Minenkov Y., Cavallo L., Neese F. Communication: An improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)] J. Chem. Phys. 2018;148:011101. doi: 10.1063/1.5011798. [DOI] [PubMed] [Google Scholar]
- 25.Řezáč J., Riley K.E., Hobza P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theory Comput. 2011;7:2427–2438. doi: 10.1021/ct2002946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Czernek J., Brus J. Revisiting the Most Stable Structures of the Benzene Dimer. Int. J. Mol. Sci. 2024;25:8272. doi: 10.3390/ijms25158272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang X., Fu Z., Jiang X., Yang Z., Wang S., Wang K., Wu Z., Zhang S.-T., Liu H., Yang B. Robust formation of discrete non-covalent pyrene dimers in an amorphous film by strong π-π interaction. Chem. Commun. 2022;58:8250–8253. doi: 10.1039/D2CC02125K. [DOI] [PubMed] [Google Scholar]
- 28.Shao C., Zhai Y., Cardenas-Salvarez A., Zhang W., Grajales-Gonzales E., Bai X., Li Y., Monge-Palacios M., Sarathy S.M. High-resolution mass spectrometry of pyrene dimers formed in a jet-stirred reactor. Combust. Flame. 2023;255:112886. doi: 10.1016/j.combustflame.2023.112886. [DOI] [Google Scholar]
- 29.Feng X., Wang X., Redshaw C., Tang B.Z. Aggregation behaviour of pyrene-based luminescent materials, from molecular design and optical properties to application. Chem. Soc. Rev. 2023;52:6715–6753. doi: 10.1039/D3CS00251A. [DOI] [PubMed] [Google Scholar]
- 30.Leboucher H., Simon A., Rapacioli M. Structures and stabilities of PAH clusters solvated by water aggregates: The case of the pyrene dimer. J. Chem. Phys. 2023;158:114308. doi: 10.1063/5.0139482. [DOI] [PubMed] [Google Scholar]
- 31.Xia Z.-A., Yao M., Wang S., Yang D., Wang Z., Wu R., Zhang S.-T., Liu H., Yang B. Tailoring pyrene excimer luminescence via controlled sulfur oxidation. J. Mater. Chem. C. 2024;12:9305–9311. doi: 10.1039/D4TC01348D. [DOI] [Google Scholar]
- 32.Shao C., Wang Q., Zhang W., Bennett A., Li Y., Guo J., Im H.G., Roberts W.L., Violi A., Sarathy M. Elucidating the polycyclic aromatic hydrocarbons involved in soot inception. Commun. Chem. 2023;6:223. doi: 10.1038/s42004-023-01017-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gong Y.-B., Zhang P., Gu Y., Wang J.-Q., Han M.-M., Chen C., Zhan X.-J., Xie Z.-L., Zou B., Peng Q., et al. The Influence of Molecular Packing on the Emissive Behavior of Pyrene Derivatives: Mechanoluminiscence and Mechanochromism. Adv. Opt. Mater. 2018;6:1800198. doi: 10.1002/adom.201800198. [DOI] [Google Scholar]
- 34.Gray M., Herbert J.M. Assessing the domain-based local pair natural orbital (DLPNO) approximation for non-covalent interactions in sizable supramolecular complexes. J. Chem. Phys. 2024;161:054114. doi: 10.1063/5.0206533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dunning T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989;90:1007–1023. doi: 10.1063/1.456153. [DOI] [Google Scholar]
- 36.Kendall R.A., Dunning T.H., Jr. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992;96:6796–6806. doi: 10.1063/1.462569. [DOI] [Google Scholar]
- 37.Boys S.F., Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970;19:553–566. doi: 10.1080/00268977000101561. [DOI] [Google Scholar]
- 38.Peterson K.A., Woon D.E., Dunnig T.J., Jr. Benchmark calculations with correlated wave functions. J. Chem. Phys. 1994;100:7410–7415. doi: 10.1063/1.466884. [DOI] [Google Scholar]
- 39.The Benchmark Energy & Geometry Database (BEGDB) [(accessed on 28 August 2024)]. Available online: http://www.begdb.org/
- 40.Kesharwani M.K., Karton M., Sylvetsky N., Martin J.M.L. The S66 Non-Covalent Interactions Benchmark Reconsidered Using Explicitly Correlated Methods Near the Basis Set Limit. Austr. J. Chem. 2018;71:238–248. doi: 10.1071/CH17588. [DOI] [Google Scholar]
- 41.Podeszwa R., Bukowski R., Szalewicz K. Potential Energy Surface for the Benzene Dimer and Perturbational Analysis of π−π Interactions. J. Phys. Chem. A. 2006;110:10345–10354. doi: 10.1021/jp064095o. [DOI] [PubMed] [Google Scholar]
- 42.Schnell M., Erlekam U., Bunker P.R., von Helden G., Grabow J.-U., Meijer G., van der Avoird A. Structure of the Benzene Dimer—Governed by Dynamics. Angew. Chem. Int. Ed. 2013;52:5180–5183. doi: 10.1002/anie.201300653. [DOI] [PubMed] [Google Scholar]
- 43.Herman K.M., Aprà E., Xantheas S.S. A critical comparison of CH···π versus π···π interactions in the benzene dimer: Obtaining benchmarks at the CCSD(T) level and assessing the accuracy of lower scaling methods. Phys. Chem. Chem. Phys. 2023;25:4824–4838. doi: 10.1039/D2CP04335A. [DOI] [PubMed] [Google Scholar]
- 44.Podeszwa R., Szalewicz K. Physical origins of interactions in dimers of polycyclic aromatic hydrocarbons. Phys. Chem. Chem. Phys. 2008;10:2735–2746. doi: 10.1039/b719725j. [DOI] [PubMed] [Google Scholar]
- 45.Marshall M.S., Burns L.A., Sherrill C.D. Basis set convergence of the coupled-cluster correction: Best practices for benchmarking non-covalent interactions and the attendant revision of the S22, NBC10, HBC6, and HSG databases. J. Chem. Phys. 2011;135:194102. doi: 10.1063/1.3659142. [DOI] [PubMed] [Google Scholar]
- 46.Patkowski K. Recent developments in symmetry-adapted perturbation theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020;10:e1452. doi: 10.1002/wcms.1452. [DOI] [Google Scholar]
- 47.Shahbaz M., Szalewicz K. Evaluation of methods for obtaining dispersion energies used in density functional calculations of intermolecular interactions. Theor. Chem. Acc. 2019;138:25. doi: 10.1007/s00214-019-2414-5. [DOI] [Google Scholar]
- 48.Czernek J., Brus J., Czerneková V., Kobera L. Quantifying the Intrinsic Strength of C–H⋯O Intermolecular Interactions. Molecules. 2023;28:4478. doi: 10.3390/molecules28114478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Henrichsmeyer J., Thelen M., Bröckel M., Fadel M., Behnle S., Sekkal-Rahal M., Fink R.F. Rationalizing Aggregate Structures with Orbital Contributions to the Exchange-Repulsion Energy. ChemPhysChem. 2023;24:e202300097. doi: 10.1002/cphc.202300097. [DOI] [PubMed] [Google Scholar]
- 50.Gray M., Herbert J.M. Origins of Offset-Stacking in Porous Frameworks. J. Phys. Chem. C. 2023;127:2675–2686. doi: 10.1021/acs.jpcc.2c08413. [DOI] [Google Scholar]
- 51.Rapacioli M., Spiegelman F., Talbi D., Mineva T., Goursot A., Heine T., Seifert G. Correction for dispersion and Coulombic interactions in molecular clusters with density functional derived methods: Application to polycyclic aromatic hydrocarbon clusters. J. Chem. Phys. 2009;130:244304. doi: 10.1063/1.3152882. [DOI] [PubMed] [Google Scholar]
- 52.Baba M., Saitoh M., Kowaka Y., Taguma K., Yoshida K., Semba Y., Kasahara S., Yamanaka T., Ohshima Y., Hsu Y.-C., et al. Vibrational and rotational structure and excited-state dynamics of pyrene. J. Chem. Phys. 2009;131:224318. doi: 10.1063/1.3270136. [DOI] [PubMed] [Google Scholar]
- 53.Hoche J., Schmitt H.-C., Humeniuk A., Fischer I., Mitrić R., Röhr M.I.S. The mechanism of excimer formation: An experimental and theoretical study on the pyrene dimer. Phys. Chem. Chem. Phys. 2017;19:25002–25015. doi: 10.1039/C7CP03990E. [DOI] [PubMed] [Google Scholar]
- 54.Sabbah H., Biennier L., Klippenstein S.J., Sims I.R., Rowe B.R. Exploring the Role of PAHs in the Formation of Soot: Pyrene Dimerization. J. Phys. Chem. Lett. 2010;1:2962–2967. doi: 10.1021/jz101033t. [DOI] [Google Scholar]
- 55.Sandler I., Chen J., Taylor M., Sharma S., Ho J. Accuracy of DLPNO-CCSD(T): Effect of Basis Set and System Size. J. Phys. Chem. A. 2021;125:1553–1563. doi: 10.1021/acs.jpca.0c11270. [DOI] [PubMed] [Google Scholar]
- 56.Carter-Fenk K., Herbert J.M. Reinterpreting π-stacking. Phys. Chem. Chem. Phys. 2020;22:24870–24886. doi: 10.1039/D0CP05039C. [DOI] [PubMed] [Google Scholar]
- 57.Carter-Fenk K., Herbert J.M. Electrostatics does not dictate the slip-stacked arrangement of aromatic π–π interactions. Chem. Sci. 2020;11:6758–6765. doi: 10.1039/D0SC02667K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cabaleiro-Lago E.M., Rodríguez-Otero J., Vázquez S.A. Electrostatic penetration effects stand at the heart of aromatic π interactions. Phys. Chem. Chem. Phys. 2022;24:8979–8991. doi: 10.1039/D2CP00714B. [DOI] [PubMed] [Google Scholar]
- 59.Werner H.J., Knowles P.J., Manby F.R., Black J.A., Doll K., Hesselmann A., Kats D., Kohn A., Korona T., Kreplin D.A., et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020;152:144107. doi: 10.1063/5.0005081. [DOI] [PubMed] [Google Scholar]
- 60.Balasubramani S.G., Chen G.P., Coriani S., Diedenhofen M., Frank M.S., Franzke Y.J., Furche F., Grotjahn R., Harding M.E., Hättig C., et al. TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations. J. Chem. Phys. 2020;152:184107. doi: 10.1063/5.0004635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Weigend F., Häser M. RI-MP2: First derivatives and global consistency. Theor. Chem. Acc. 1997;97:331–340. doi: 10.1007/s002140050269. [DOI] [Google Scholar]
- 62.Weigend F., Häser M., Patzelt H., Ahlrichs R. RI-MP2: Optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998;294:143–152. doi: 10.1016/S0009-2614(98)00862-8. [DOI] [Google Scholar]
- 63.Czernek J., Brus J., Czerneková V. A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes. Int. J. Mol. Sci. 2022;23:15773. doi: 10.3390/ijms232415773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Halkier A., Helgaker T., Jørgensen P., Klopper W., Koch H., Olsen J., Wilson A.K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998;286:243–252. doi: 10.1016/S0009-2614(98)00111-0. [DOI] [Google Scholar]
- 65.Pinski P., Riplinger C., Valeev E.F., Neese F. Sparse maps–A systematic infrastructure for reduced-scaling electronic structure methods. I. An efficient and simple linear scaling local MP2 method that uses an intermediate basis of pair natural orbitals. J. Chem. Phys. 2015;143:034108. doi: 10.1063/1.4926879. [DOI] [PubMed] [Google Scholar]
- 66.Neese F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022;12:e1606. doi: 10.1002/wcms.1606. [DOI] [Google Scholar]
- 67.Heßelmann A., Jansen G. Density-functional theory-symmetry-adapted intermolecular perturbation theory with density fitting: A new efficient method to study intermolecular interaction energies. J. Chem. Phys. 2005;122:014103. doi: 10.1063/1.1824898. [DOI] [PubMed] [Google Scholar]
- 68.Czernek J., Brus J., Czerneková V. A computational inspection of the dissociation energy of mid-sized organic dimers. J. Chem. Phys. 2022;156:204303. doi: 10.1063/5.0093557. [DOI] [PubMed] [Google Scholar]
- 69.Heßelmann A., Jansen G. First-order intermolecular interaction energies from Kohn–Sham orbitals. Chem. Phys. Lett. 2002;357:464–470. doi: 10.1016/S0009-2614(02)00538-9. [DOI] [Google Scholar]
- 70.Heßelmann A., Jansen G. Intermolecular dispersion energies from time-dependent density functional theory. Chem. Phys. Lett. 2003;367:778–784. doi: 10.1016/S0009-2614(02)01796-7. [DOI] [Google Scholar]
- 71.Heßelmann A., Jansen G. Intermolecular induction and exchange-induction energies from coupled-perturbed Kohn–Sham density functional theory. Chem. Phys. Lett. 2002;362:319–325. doi: 10.1016/S0009-2614(02)01097-7. [DOI] [Google Scholar]
- 72.Moszynski R., Heijmen T.G.A., Jeziorski B. Symmetry-adapted perturbation theory for the calculation of Hartree–Fock interaction energies. Mol. Phys. 1996;88:741–758. doi: 10.1080/00268979650026262. [DOI] [Google Scholar]
- 73.Adamo C., Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999;110:6158–6170. doi: 10.1063/1.478522. [DOI] [Google Scholar]
- 74.Grimme S., Antony J., Ehrlich S., Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 75.Weigend F., Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 76.Frish M.J., Trucks J.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Petersson G.A., Nakatsuji H., et al. Gaussian 16. Gaussian, Inc.; Wallingford, CT, USA: 2019. Revision C.01. [Google Scholar]
- 77.Dai Y., Rambaldi F., Negri F. Eclipsed and Twisted Excimers of Pyrene and 2-Azapyrene: How Nitrogen Substitution Impacts Excimer Emission. Molecules. 2024;29:507. doi: 10.3390/molecules29020507. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented in this study are available in the article and in the Supplementary Materials.