Abstract
Among C60’s diverse functionalities, its potential application in CO2 sequestration has gained increasing interest. However, the processes involved are sensitive to the molecule’s electronic structure, aspects of which remain debated and require greater precision. To address this, we performed structural optimization of fullerene C60 using the QM MP2/6–31G* method. The nonplanarity of the optimized icosahedron is characterized by two types of dihedral angles: 138° and 143°. The 120 dihedrals of 138° occur between two hexagons intersecting at C–C bonds of 1.42 Å, while the 60 dihedrals of 143° are observed between hexagons and pentagons at C–C bonds of 1.47 Å. NBO analysis reveals less pyramidal sp1.78 hybridization for carbons at the 1.42 Å bonds and more pyramidal sp2.13 hybridization for the 1.47 Å bonds. Electrostatic potential charges range from −0.04 a.u. to 0.04 a.u. on the carbon atoms. Second-order perturbation analysis indicates that delocalization interactions in the C–C bonds of 1.42 Å (143.70 kcal/mol) and 1.47 Å (34.98 kcal/mol) are 22% and 38% higher, respectively, than those in benzene. MP2/Def2SVP calculations yield a correlation energy of 13.49 kcal/mol per electron for C60, slightly higher than the 11.68 kcal/mol for benzene. However, the results from HOMO-LUMO calculations should be interpreted with caution. This study may assist in the rational design of fullerene C60 derivatives for CO2 reduction systems.
Keywords: fullerene C60, MP2 method, delocalization, bond–antibond interaction, correlation, HOMO-LUMO gap
1. Introduction
Fullerene C60, also known as Buckminsterfullerene, was first discovered by Kroto et al. in 1985, who earned the Nobel Prize in Chemistry in 1996 [1]. This carbon allotrope was made accessible for practical applications through the synthetic technique developed by Kratschmer et al. [2]. Due to its unique structural, chemical, and mechanical properties, fullerene has been functionalized for numerous applications, including cosmetics, food additives, materials science, fuel cells, electrochemistry, and drug delivery [3,4,5,6]. The structural and electronic properties of fullerene C60 have been extensively investigated using experimental [2,7,8,9,10,11,12,13,14,15,16,17,18,19], classical mechanical [16,20,21,22,23,24,25,26,27,28,29,30,31], and quantum mechanical methods [7,16,19,29,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. With its delocalized conjugated π system on a nonplanar spheroidal geometry, there has been ongoing debate about its aromaticity [62]. The high positive heat of formation suggests that fullerene C60 is anti-aromatic rather than aromatic [12]. Electron correlation plays a crucial role in calculating the low-lying excited T1u states of C60’s delocalized conjugated π bonds [43], and the HOMO-LUMO energy gap has been closely linked to the molecule’s reactivity [42]. Most quantum mechanical studies on fullerene C60 have utilized hybrid density functional theory (DFT). Electron correlation effects in the fullerene cage have revealed different local minimum geometries for C20, with varying DFT functionals showing differences in predicting the relative ordering of C20 isomer energies [63]. Moreover, hybrid DFT performance has been found to degrade with increased pentagon–pentagon strain energy and the percentage of Hartree–Fock (HF) exchange in the DFT method [39,64]. The QM MP2 natural bond orbitals (NBO) analysis offers valuable insights into the structural properties of fullerene in terms of molecular orbitals [65,66,67,68]. Fullerene-based CO2 sequestration has shown potential for converting environmental CO2 into carbohydrates [17,58,59]. Characterizing fullerene C60 using MP2-based NBO analysis can deepen our understanding of the structural and electronic properties of its nonplanar carbon cage, facilitating the development of fullerene C60 derivatives, including nanobuds, for applications such as CO2 reduction [32].
2. Materials and Methods
The structures of fullerene C60 and benzene were initially constructed and verified using visual molecular dynamics (VMD) [69] as the starting point for structural optimization. The optimized geometry is shown in Figure 1a, and the representative atoms C1, C2, and C6 are indicated in Figure 1b (the cartesian coordinates of the optimized structure for fullerene C60 are available in the Supplementary Materials). Computational simulations were performed using coupled cluster single and double with perturbative triples (CCSD(T)), second-order Møller–Plesset perturbation theory (MP2), primarily MP2/6–31G*, and density functional theory (DFT) methods through the Gaussian 16 software package by Frisch et al. [70]. The DFT optimization was conducted using Becke’s three-parameter hybrid functional for exchange and the Lee–Yang–Parr correlation functional (B3LYP) [71,72], as well as the Becke–Perdew (BP86) [73,74,75] functional. For single-point calculations, the 3–21G*, 6–31G*, and two Karlsruhe basis sets were employed: the valence double-ζ basis set with polarization functions (def2-SVP) and the valence triple-ζ basis set with polarization functions on main-group elements (def2-TZVP) [76].
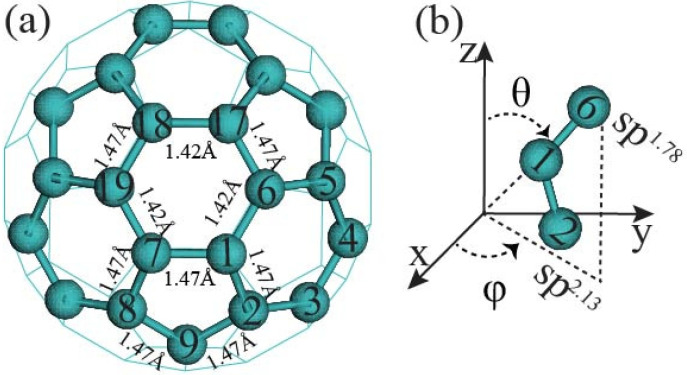
Figure 1.
Structure of fullerene C60. (a) The hexagon and pentagon in CPK representation of fullerene C60; (b) The C1–C6 natural hybrid orbital (NHO) directionality described by a vector in a coordinating system. All figures are prepared using the visual molecular dynamics package [69].
3. Results
3.1. Bond Length, Bond Angle, and Dihedral Angles of Fullerene
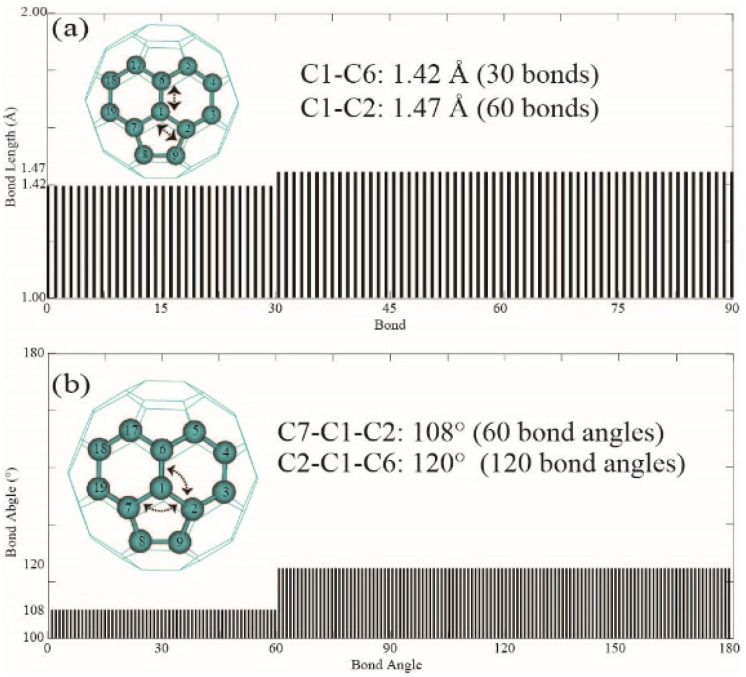
The structural optimization of fullerene C60 was performed using the MP2/6–31G* method. The bond lengths, bond angles, dihedral angles, and Merz–Kollman (MK) electrostatic partial charges (ESP) of the optimized geometry are summarized and depicted in Figure 2a, Figure 2b, Figure 3a and Figure 3b, respectively. A comparison of atomic partial charges for the carbon atoms in fullerene C60 is provided in Table 1. As shown in Figure 1a, the optimized structure features two types of C=C bonds: 30 double bonds with a length of 1.42 Å, and 60 bonds with a length of 1.47 Å. The C1=C6 double bonds shared between two hexagons have a bond length of 1.42 Å, while the C1=C2 bonds of 1.47 Å connect a hexagon and a pentagon. These bond lengths align well with the experimental value of 1.45 Å reported by David et al. [26]. Both bond lengths are slightly longer than the 1.39 Å typical for benzene but shorter than the 1.54 Å of typical C-C σ single bonds. This suggests that the bonds in fullerene C60 are somewhat similar to the conjugated π bonds in benzene but with fewer degrees of conjugation. The curvature of the fullerene surface influences the C-C bonding, as the σ bonds span a non-planar surface crossing both five-membered and six-membered rings. The curvature affects the s and p orbital character, resulting in intermediate hybridization and corresponding bond lengths [9]. In Figure 2b, it is evident that there are 60 bond angles of 108° in the icosahedral symmetry, corresponding to the 12 pentagons, with each pentagon having five bond angles of 108°. Additionally, there are 120 bond angles of 120° corresponding to the 20 hexagonal rings that make up the C60 framework.
Figure 2.
Profiles of bond lengths and bond angles of C60. (a) Bond lengths of C60; (b) Bond angles of C60.
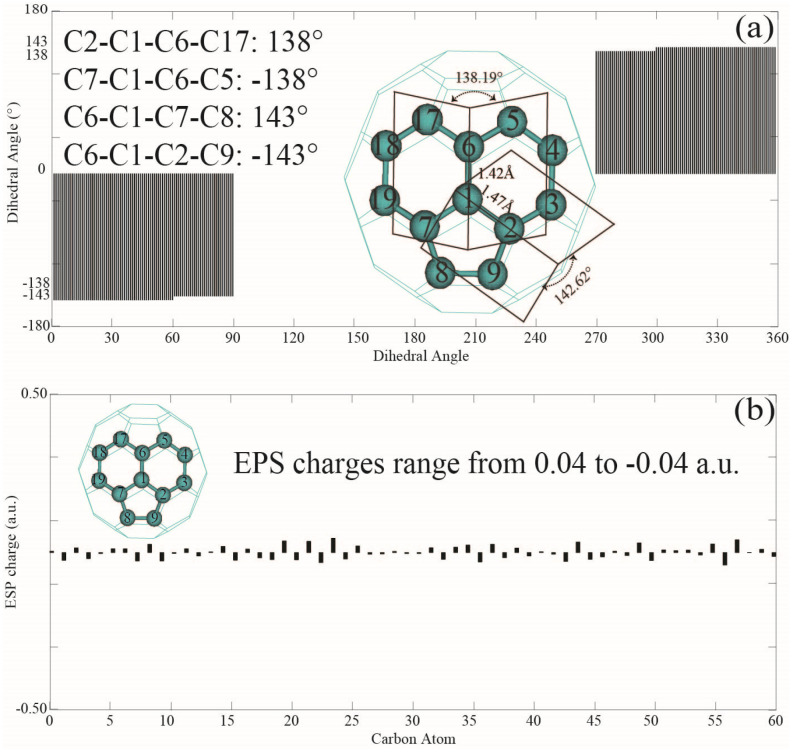
Figure 3.
Dihedral angle and ESP partial charge of C60. (a) Dihedral angles of C60; (b) ESP charges of fullerene C60.
Table 1.
Ranges of partial charges of Fullerene C60.
| Model | C1 | C6 | C2 | Minimum | Maximum | Median |
|---|---|---|---|---|---|---|
| ESP | −0.031000 | 0.009000 | −0.035000 | −0.040000 | 0.040000 | 0.0 |
| NBO | −0.000020 | 0.000010 | 0.000010 | −0.000030 | 0.000030 | 0.0 |
| Mulliken | 0.000011 | −0.000022 | −0.000022 | −0.000049 | 0.000046 | 0.0 |
| Hirshfeld | −0.000020 | 0.000013 | 0.000010 | −0.000022 | 0.000023 | 0.0 |
| CM5 | −0.000020 | 0.000013 | 0.000010 | −0.000022 | 0.000023 | 0.0 |
Dihedral angles reflect the relative orientations or curvature of the five-membered and six-membered rings in fullerene C60. Figure 3a shows that fullerene C60 exhibits two types of dihedral angles: those shared between two hexagons and those between a hexagon and a pentagon. The dihedral angle between two hexagons is 138°, while the hexagon-pentagon intersection exhibits an angle of 143°. These results are consistent with previous findings by Schein et al. [77]. The negative sign of a dihedral angle indicates the same numerical value but in the opposite direction, defined by different sets of atoms from the two rings. For instance, the dihedral angles C7–C1–C6–C17 at 138° and C2–C1–C6–C5 at −138° refer to identical hexagons in Figure 3a. Additionally, the 30 dihedral angles of 138° correlate with the 30 C=C bonds of 1.42 Å in fullerene C60. Similarly, the presence of 60 dihedral angles of 143° is consistent with the 60 C=C bonds of 1.47 Å. The most widely used electrostatic potential (ESP) scheme defines atomic partial charges by fitting a classical Coulomb model to the quantum mechanical electrostatic field [78]. As shown in Table 1, the ESP charges for C1, C6, and C3 are −0.031, 0.009, and −0.035 a.u., respectively. In contrast, the NBO scheme assigns charges of −0.00002, 0.00001, and 0.00001 a.u. to C1, C6, and C2, respectively, while the Mulliken charge assignments give lower values of 0.000011, −0.000022, and −0.000049 a.u. for the same atoms. Lastly, Hirshfeld and CM5 partial charge assignments yield values of −0.00002, 0.000023, and −0.000022 a.u. for C1, C6, and C2, respectively. As seen in Table 1 and Figure 3b, the ESP charges of carbon atoms in fullerene C60 range from −0.04 a.u. to 0.04 a.u. Although all five partial charge definitions have a median value of 0.00 a.u., the ESP partial charges are magnitudes higher (by a factor of 1000) than those calculated using NBO, Hirshfeld, Mulliken, and CM5 charge schemes for fullerene C60. These significant discrepancies in partial charge assignments will be further investigated in future work.
3.2. Natural Bond Analysis
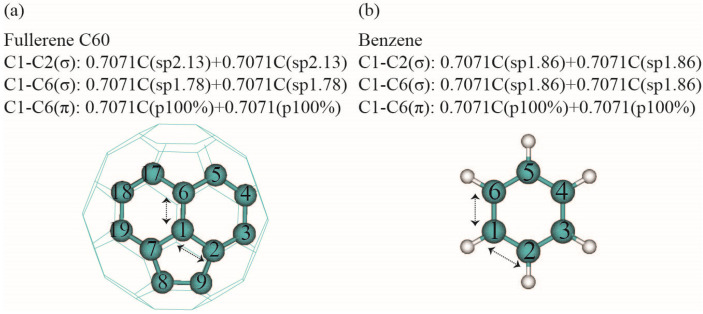
Natural bond analyses were conducted for the optimized structures of fullerene C60 and benzene, focusing on the C1–C6 and C1–C2 bonds using the MP2/6–31G* and CCSD(T)/aug-cc-pVTZ methods [68]. The directionality of natural hybrid orbitals (NHOs) is depicted in Figure 1b and compared between fullerene C60 and benzene in Table 2. Natural bond coefficients and hybridization are described in Figure 4. The extent of delocalization interactions for the C1–C2, C1–C6 (σ), and C1–C6 (π) bonds is presented in Table 3, while the delocalization energies of the major natural bonds are summarized in Table 4 and illustrated in Figure 4b. The use of localized NBOs offers conceptual simplicity and flexibility over canonical molecular orbitals (CMOs) [68]. NHOs represent a group of natural localized orbitals (NLOs) that transition from atomic basis orbitals to molecular orbitals and are expressed as linear combinations of natural atomic orbitals (NAOs). The NHO orientation is described using azimuthal (Φ) and polar (θ) angles, defining the directionality of the p-component (Figure 1b). As shown in Table 2, planar benzene exhibits a polar angle (θ) deviation of 4.1° for both the C1–C2 and C1–C6 σ bonds (see Figure 1). In contrast, the NHOs in fullerene C60 deviate from the center line between the nuclei by 13.1° and 15.1°, respectively. This indicates that the C1–C2 and C1–C6 σ bonds in fullerene C60 bend 9° and 11° more from the center line compared to the corresponding bonds in benzene. Furthermore, the NHOs for the C1–C6 π bond in fullerene C60 exhibit a polar angle (θ) of 75.8° from the center line, compared to the typical 90° in benzene. This 14.2° deviation reflects the impact of structural non-planarity on the C1–C6 π bond in fullerene C60. Tracking the bond bending due to pyramidalization provides valuable insight into the reactivity and stability of crosslinked nanobuds.
Table 2.
Angular properties of natural hybrid orbitals.
| Bond | Line of Center between Two Nuclei | Hybrid 1 | Hybrid 2 | |||||
|---|---|---|---|---|---|---|---|---|
| Hybrid 1–2 | θ (Theta) | φ (Phi) | θ | φ | Dev | θ | φ | Dev |
| Fullerene C60 | ||||||||
| C1–C2 (σ) | 129.4 | 264.9 | 140.6 | 255.2 | 13.1 | 62.4 | 91.8 | 13.1 |
| C1–C6 (σ) | 47.9 | 167.4 | 58.7 | 154.1 | 15.1 | 140.8 | 5.5 | 15.1 |
| C1–C6 (π) | 47.9 | 167.4 | 50.3 | 276.1 | 75.8 | 71.9 | 297.4 | 75.8 |
| Benzene | ||||||||
| C1–C2 (σ) | 90.0 | 22.7 | 90.0 | 17.9 | 4.1 | 90.0 | 207.6 | 4.1 |
| C1–C6 (σ) | 90.0 | 142.7 | 90.0 | 147.6 | 4.1 | 90.0 | 317.9 | 4.1 |
| C1–C6 (π) | 90.0 | 142.7 | 0.0 | 0.0 | 90.0 | 0.0 | 0.0 | 90.0 |
Figure 4.
(a) Natural bond orbital coefficients and hybrids of fullerene C60; (b) natural bond orbital coefficients and hybrids of benzene.
Table 3.
Statistics of delocalization interactions larger than 0.5 kcal/mol.
| Molecule | Bond | Energy (Hartree) | Geminal | Vicinal | Energy (kcal/mol) |
|---|---|---|---|---|---|
| Fullerene C60 | C1–C2 (σ) | −0.88405 | 4 | 12 | 34.98 |
| Total | C1–C2 | 4 | 12 | 34.98 (100% + 38%) | |
| C1–C6 (σ) | −0.93273 | 4 | 8 | 26.33 | |
| C1–C6 (π) | −0.34383 | 4 | 8 | 110.14 | |
| Total | C1–C6 | 8 | 16 | 143.70 (100% + 22%) | |
| Benzene | C1–C2 (σ) | −0.90988 | 4 | 6 | 21.74 |
| Total | C1–C2 | 4 | 6 | 21.76 (100%) | |
| C1–C6 (σ) | −0.91019 | 4 | 6 | 21.76 | |
| C1–C6 (π) | −0.29735 | 0 | 4 | 87.66 | |
| Total | C1–C6 | 4 | 10 | 111.70 (100%) |
Table 4.
Delocalization energies for C1–C2 and C1–C6 bond of both fullerene and benzene using second order perturbation theory with MP2/631G* and/CCSD(T)/aug-cc-pvtz.
| Fullerene C60 | Benzene(MP2/6–31G*/CCSD(T)/aug-cc-pvtz) | ||||||
|---|---|---|---|---|---|---|---|
| Donor | Type | Acceptor | E (kcal/mol) | Donor | Type | Acceptor | E (kcal/mol) |
| C1–C2 (σ) |
Rydberg | C3 | 0.8 | C1–C2 (σ) |
Rydberg | C3 | 1.36/0.92 |
| Rydberg | C3 | 1.64 | Rydberg | C3 | 2.02/1.93 | ||
| Rydberg | C6 | 0.8 | Rydberg | C6 | 1.36/0.92 | ||
| Rydberg | C6 | 1.64 | Rydberg | C6 | 2.02/1.93 | ||
| Rydberg | C7 | 1.31 | Antibond | C1–C6 | 3.24/2.25 | ||
| Rydberg | C9 | 1.31 | Antibond | C1–H7 | 1.49/0.91 | ||
| Antibond | C1–C6 | 3.91 | Antibond | C2–C3 | 3.24/2.25 | ||
| Antibond | C1–C7 | 2.05 | Antibond | C2–H8 | 1.49/0.91 | ||
| Antibond | C2–C3 | 3.91 | Antibond | C3–H9 | 2.77/3.15 | ||
| Antibond | C2–C9 | 2.05 | Antibond | C6-H12 | 2.77/3.15 | ||
| Antibond | C3–C11 | 3.48 | Total | C1–C2 | 10 | 21.76/18.32 | |
| Antibond | C6–C17 | 3.48 | C1–C6 (σ) |
Rydberg | C2 | 1.36/0.92 | |
| Antibond | C7–C19 | 3.8 | Rydberg | C2 | 2.02/1.93 | ||
| Antibond | C7–C19 | 0.5 | Rydberg | C5 | 1.36/0.92 | ||
| Antibond | C9–C10 | 3.8 | Rydberg | C5 | 2.02/1.93 | ||
| Antibond | C9–C10 | 0.5 | Antibond | C1–C2 | 3.24/2.25 | ||
| Total | C1–C2 | 16 | 34.98 | Antibond | C1–H7 | 1.50/0.91 | |
| C1–C6 (σ) |
Rydberg | C2 | 1.61 | Antibond | C2–H8 | 2.77/3.15 | |
| Rydberg | C5 | 1.61 | Antibond | C5–C6 | 3.24/2.25 | ||
| Rydberg | C7 | 1.61 | Antibond | C5–H11 | 2.77/3.15 | ||
| Rydberg | C7 | 1.61 | Antibond | C6–H12 | 1.50/0.91 | ||
| Antibond | C1–C2 | 3.68 | Total | 10 | 21.78/18.32 | ||
| Antibond | C1–C7 | 3.68 | C1–C6 (π) |
Rydberg | C2 | 2.57/1.88 | |
| Antibond | C2–C9 | 1.75 | Rydberg | C5 | 2.57/1.88 | ||
| Antibond | C5–C6 | 3.68 | Antibond | C2–C3 | 42.39/41.94 | ||
| Antibond | C5–C15 | 1.75 | Antibond | C4–C5 | 42.39/41.94 | ||
| Antibond | C6–C17 | 3.68 | Total | 4 | 89.92/87.64 | ||
| Antibond | C7–C8 | 1.75 | |||||
| Antibond | C6–C17 | 1.75 | |||||
| Total | 12 | 28.16 | |||||
| C1–C6 (π) |
Rydberg | C1 | 0.53 | ||||
| Rydberg | C2 | 1.75 | |||||
| Rydberg | C5 | 1.75 | |||||
| Rydberg | C6 | 0.53 | |||||
| Rydberg | C7 | 1.75 | |||||
| Rydberg | C17 | 1.75 | |||||
| Antibond | C1–C2 | 1.2 | |||||
| Antibond | C1–C7 | 1.2 | |||||
| Antibond | C2–C3 | 25.66 | |||||
| Antibond | C4–C5 | 25.66 | |||||
| Antibond | C5–C6 | 1.2 | |||||
| Antibond | C6–C17 | 1.2 | |||||
| Antibond | C7–C19 | 25.66 | |||||
| Antibond | C17–C18 | 25.66 | |||||
| Total | 14 | 115.54 | |||||
| Total | C1–C6 | 26 | 143.70 (122%) | Total | C1–C6 | 14 | 111.70 (100%) |
| Total | C1–C2 | 16 | 34.98 (138%) | Total | C1–C2 | 10 | 21.76 (100%) |
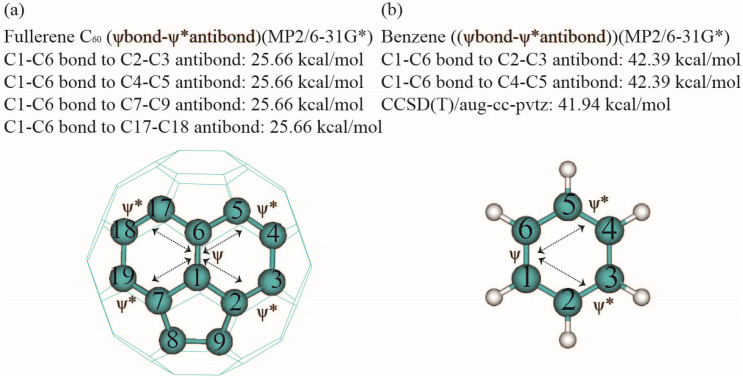
As shown in Figure 4, our calculations reveal that the hybrids at C1 and C6 in the C1–C6 NBO of fullerene C60 exhibit sp1.78 hybridization, slightly smaller than the sp1.84 hybridization found in benzene. Meanwhile, the hybrids at C1 and C2 in the C1–C2 NBO display sp2.13 hybridization, indicating more pyramidalization compared to the sp1.84 hybridization in the C1–C6 bond of benzene. This suggests that the C1–C6 bond in fullerene is similar to the “1.5 bond” found in benzene, whereas the C1–C2 bond resembles a single bond [9]. Bond–antibond interactions were evaluated using second-order perturbative calculations on the NBO basis. The C1–C6 orbital experiences delocalization interactions with various unoccupied orbitals, including non-Lewis core electron pairs, valence lone pairs, Rydberg orbitals, and antibonding orbitals. As indicated in Table 3, both the C1–C6 σ and π orbitals have 4 geminal and 8 vicinal interactions, compared to 2 geminal and 4 vicinal interactions for C1–C6 in benzene. Among these interactions, the most significant involves the less pyramidalized sp1.78 bond–antibond interactions in the C1–C6 π bond of fullerene C60. Our results, shown in Figure 5 and Table 4, indicate that the strongest delocalization provides an interaction energy of 25.66 kcal/mol between the C1–C6 π bond and four other π antibonds (C2–C3, C4–C5, C7–C18, and C7–C19) in fullerene C60. Including additional delocalizations, the total delocalization energy for the C1–C6 π bonds amounts to 115.54 kcal/mol, while the 12 delocalizations involving the C1–C6 σ bond contribute 28.16 kcal/mol. Altogether, the C1–C6 σ and π bond delocalizations generate a total interaction energy of 143.70 kcal/mol. In contrast, the C1–C2 σ bond, which lacks a π bond, only generates 34.98 kcal/mol from its 16 delocalizations. Compared to the typical delocalization in benzene (Table 3), the delocalization energies of 34.98 kcal/mol for the C1–C2 bond and 143.70 kcal/mol for the C1–C6 bond in fullerene C60 are approximately 38% higher than the corresponding 21.76 kcal/mol for the C1–C2 bond and 111.70 kcal/mol for the sum of the C1–C6 σ and π bonds in benzene. This increase is primarily due to the presence of six additional vicinal delocalizations for the C1–C2 bond, four additional geminal and six additional vicinal delocalizations for the C1–C6 bond in fullerene C60, as shown in Table 3. Notably, the C1–C6 π bond in fullerene C60 undergoes strong delocalization interactions with alternating antibonds, while in benzene, only two antibond acceptors interact with the C1–C6 Lewis-type donor bonds. Despite this, the delocalization energy of 25.66 kcal/mol for the C1–C6 bond in fullerene C60 is weaker than the 42.39 kcal/mol observed for the delocalization in benzene. For consistency, we have listed the results of the CCSD(T)/aug-cc-pVTZ calculations alongside those from MP2/6–31G* for benzene in Table 4 and Figure 5. The MP2/6–31G* results show a delocalization energy of 42.39 kcal/mol, closely matching the 41.94 kcal/mol obtained from CCSD(T)/aug-cc-pVTZ calculations for the strongest delocalization. Our calculations suggest that the C1–C2 and C1–C6 bonds in fullerene C60 contribute 38% and 22% more enthalpy, respectively, than those bonds in benzene, which may account for the thermochemical stability of fullerene C60 [14,49,50]. These findings imply that both non-planarity and formation entropy should be carefully considered when interpreting the thermostability of fullerene [52,79].
Figure 5.
(a) Natural bond orbital delocalization of fullerene C60; (b) natural bond orbital delocalization of benzene. The star indicates antibond, the arrow indicates bond–antibond interaction.
3.3. Correlation Energy and HOMO-LUMO Gap of α Electrons of Fullerene C60
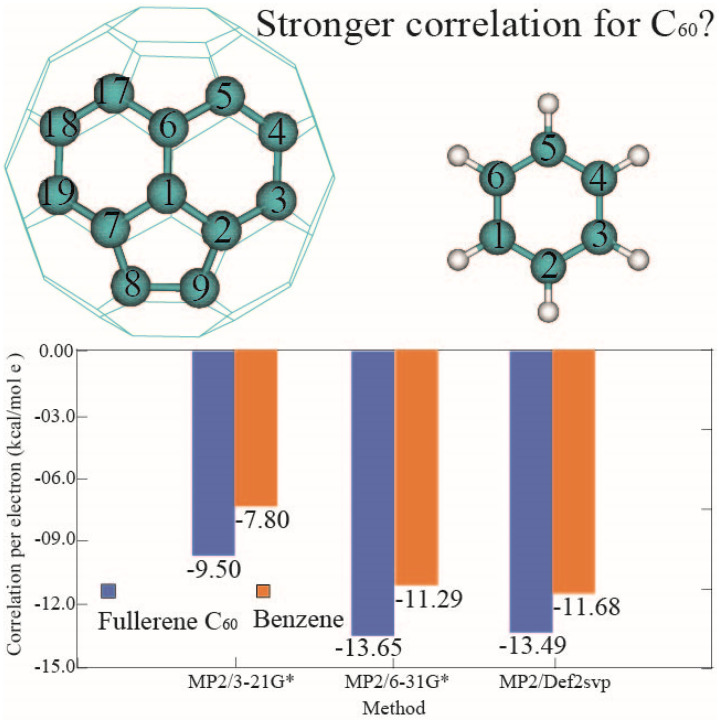
Single-point MP2 and Hartree–Fock (HF) energies were calculated using various basis sets based on the optimized geometries. The energy discrepancies between MP2 and Recovering electron correlation energy is a fundamental and challenging task in quantum chemistry. Correlation energy typically refers to the difference between the true total energy and the Hartree–Fock limit. It consists of two main components: static and dynamic correlation [80]. Static correlation arises from the fact that HF treats the many-body wavefunction as a single Slater determinant, whereas the exact total energy requires a combination of many determinants in the non-relativistic Schrödinger equation [81]. Dynamic correlation, or Pauli correlation, results from the mean-field approximation in HF, where instantaneous Coulomb repulsion is approximated by treating other electrons as an average charge distribution. HF already accounts for static exchange correlation between parallel spin electrons based on the anti-symmetry principle. MP2, through its perturbative potential, recovers electron correlation by considering electron-electron interactions [82]. The MP2-HF energy difference has been widely applied in evaluating correlation energy and the electron density matrix [83]. The MP2-HF discrepancy provides a major component of the electron correlation energy in C60, which has a delocalized π bond system [84]. As shown in Table 5 and Figure 6, the MP2-HF energy differentials for fullerene C60 are −9.50, 13.65, and −13.49 kcal/mol per electron for calculations at MP2/3–21G*, MP2/6–31G, and MP2/Def2SVP, respectively. The MP2/Def2SVP basis set yields the same correlation energy per electron as MP2/6–31G*, while MP2/6–31G* shows a notable improvement of 4.15 kcal/mol per electron compared to MP2/3–21G*. A similar pattern is observed in the MP2-HF energy discrepancies for benzene across different basis sets. Notably, our calculations consistently show that fullerene C60 provides 2.30, 2.36, and 1.81 kcal/mol more correlation energy per electron than benzene at MP2/3–21G*, MP2/6–31G*, and MP2/Def2SVP, respectively. It is also worth mentioning that the CCSD(T)/aug-cc-pVTZ method produces significantly larger correlation energy (15.54 kcal/mol per electron) than all other results computed at the MP2 level, which motivates future CCSD(T) calculations on fullerene C60 derivatives. The importance of correlation energy is well-established in small delocalized π systems [85]. Aromaticity, a fundamental concept in organic chemistry [86], refers to the stabilization of conjugated cycloalkenes due to delocalized π-electrons following the 4n + 2 rule and exhibiting no diamagnetic properties in a magnetic field. The precise definition of aromaticity is still debated, but it has been evaluated from structural [87], energetic [88], reactivity [89], and magnetic perspective [90]. Fullerene C60 has been considered antiaromatic rather than aromatic due to its high positive heat of formation (610 kcal/mol) [12]. However, its aromaticity has also been evidenced both experimentally [18] and theoretically [16]. Magnetic shielding effects of frontier orbitals have been demonstrated in endohedral complexes of small molecules (e.g., helium or formaldehyde) encapsulated within fullerene C60 [19,60,61]. Therefore, other electronic factors influencing electron correlation in fullerene, such as strain destabilization energy, will be explored in future work [45].
Table 5.
The major correlation energy of fullerene C60 and benzene in addition to exchange component.
| Method | MP2 (Hartree) | HF (Hartree) | MP2—HF (kcal/mol) |
(MP2—HF)/ (kcal/mol e) |
|---|---|---|---|---|
| Fullerene C60 | ||||
| MP2/3–21G* | −2264.4378913 | −2258.9901941 | −3418.48 | −9.50 |
| MP2/6–31G* | −2279.6317630 | −2271.8025400 | −4912.92 | −13.65 |
| MP2/def2svp | −2277.8316660 | −2270.0928633 | −4865.21 | −13.49 |
| Benzene (The CCSD(T)/aug-cc-pvtz recovered correlation is counted by CCSD(T)-HF) | ||||
| MP2/3–21G* | −229.9376703 | −229.4155101 | −327.657 | −7.80 |
| MP2/6–31G* | −231.4577321 | −230.7018849 | −474.302 | −11.29 |
| MP2/def2svp | −231.3162080 | −230.5345726 | −490.477 | −11.68 |
| CCSD(T)/aug-cc-pvtz | −231.8204089 | −230.7804015 | −652.615 | −15.54 |
Figure 6.
Comparison of correlation energy per electron between fullerene C60 and benzene.
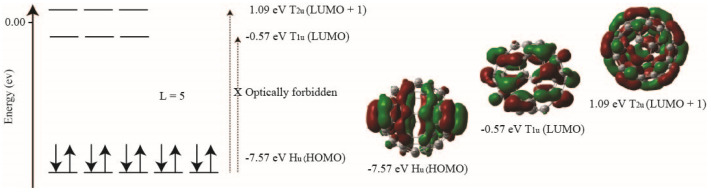
The calculation of the LUMO energy for C60 has enabled the evaluation of designed fullerene derivatives for their potential use in organic photovoltaic applications [15,91] and reactivity studies [42]. According to quantum mechanics, the electron density of a perfect spherical molecule is confined to its surface. Spherical harmonic wavefunctions can be obtained by solving Schrödinger’s equation for such molecular systems. The energy levels corresponding to these harmonic states are determined based on the radius of the molecular system and angular momentum quantum numbers, following the Aufbau principle, Pauli exclusion principle, and Hund’s rule. Although fullerene C60 has an icosahedral symmetry rather than a perfect spherical geometry, its electronic energy scheme can be derived by expanding the energy level diagram for spherical symmetry harmonics with respect to angular momentum (l) [92]. The lower symmetry of the icosahedral group in C60 splits the degeneracies of the highest occupied molecular orbitals (HOMO) from spherical harmonic states [9,93], though a maximum molecular orbital degeneracy of five is still possible due to the icosahedral symmetry of fullerene C60. As shown in Figure 7, the HOMO of C60 has H1u symmetry with a fivefold degeneracy, while the LUMO has a threefold degeneracy in T1u symmetry. The LUMO+1 orbital, which is located just above the LUMO, also exhibits triply degenerate T2u symmetry [94]. The transition from the HOMO to LUMO is optically forbidden due to the Ag symmetry of the ground state with icosahedral symmetry [13,44], so the HOMO-LUMO separation values in Table 6 are provided for reference. We focus on comparing the experimentally measured reduction potential with the HOMO to LUMO+1 transition. As shown in Table 6, the HOMO-LUMO+1 gap calculated using MP2/3–21G* is −8.94 eV, which is larger than the −8.66 eV gap obtained using MP2/6–31G*, suggesting that larger basis sets may yield more accurate HOMO-LUMO+1 gaps compared to the experimental value of 4.90 eV. The deviations from the experimental value are −4.04 eV and −3.76 eV for MP2/3–21G* and MP2/6–31G*, respectively [7]. In contrast, the HOMO-LUMO separations from the B3LYP/Def2SVP and BP86/Def2SVP calculations are 2.28 eV and 2.03 eV, respectively, which are lower than the experimental reduction potential. It is worth noting that MP2 calculations may yield more accurate results with larger basis sets. However, there remains significant room for improvement in the B3LYP/Def2SVP and BP86/Def2SVP calculations, as Def2SVP is already a basis set of reasonable size. Therefore, the results of the HOMO-LUMO+1 transition from B3LYP/Def2SVP and B3LYP/6-31G should be interpreted with caution in future work.
Figure 7.
Energy level diagram of the L = 5 for fullerene C60 based on the results computed using MP2 method.
Table 6.
Comparison of the HOMO-LUMO gaps of α electrons for fullerene C60 using different methods (HOMO H1u, LUMO T1u, and LUMO + 1 T2u α MOs).
| Method (α Electron) |
HOMO H1u (eV) |
LUMO T1u (eV) | LUMO + 1 T2u (eV) | H1u to T1u (eV) |
H1u to T2u (eV) |
|---|---|---|---|---|---|
| MP2/3-21G* | −8.19 | −0.92 | 0.75 | −7.27 | −8.94 |
| MP2/6–31G* | −7.57 | −0.57 | 1.09 | −7.00 | −8.66 |
| Experimental [7] | −4.90 | ||||
| B3LYP/Def2svp | −7.63 | −5.95 | −5.01 | −1.68 | −2.62 |
| BP86/Def2svp | −5.94 | −4.13 | −3.07 | −1.81 | −2.87 |
4. Discussion
Our calculations show relatively large deviations in the HOMO-LUMO gap compared to the available experimental value of −4.9 eV. Therefore, further studies on the HOMO-LUMO gap calculations for fullerene C60 will be pursued. Jaworski et al. reported that the state-of-the-art DLPNO-CCSD(T) method provides more accurate predictions for IR, Raman, UV-vis, ionization potential, NMR chemical shifts (1H and 13C), spin–spin coupling, and thermodynamic stability of fullerene, accounting for the effects of the structural Faraday cage [57]. To improve the accuracy of our results, we plan to apply higher-level methods, such as CCSD(T)/aug-cc-pVTZ, in future studies. These methods will be used to refine our HOMO-LUMO gap calculations and to explore delocalization, including bond–antibond interactions and Rydberg effects, in non-planar fullerene, in contrast to planar benzene, to better understand aromaticity.
5. Conclusions
The MP2 structural simulation of fullerene C60 confirms that its non-planarity is characterized by two types of dihedral angles—138° and 143°—in the optimized icosahedral structure. The 120 dihedral angles of 138° occur between two intersecting hexagon planes, while 60 dihedral angles of 143° are observed between a hexagon and a neighboring pentagon. The polyhedral structure has bond lengths of 1.42 Å for C–C bonds shared between two hexagons and 1.47 Å for C–C bonds connecting a hexagon and a pentagon. Our NBO analysis suggests that carbon atoms in the C–C bonds of 1.42 Å (shared by hexagons) exhibit sp1.78 hybridization, while those in the C–C bonds of 1.47 Å (connecting hexagons and pentagons) undergo sp2.13 hybridization. The ESP charge range for carbon atoms, from −0.04 a.u. to 0.04 a.u., represents a significantly larger magnitude than that of other charge types in fullerene C60. Second-order perturbation evaluations indicate that delocalization interaction energies involving C1–C6 and C1–C2 bonds in fullerene C60 are 22% and 38% higher, respectively, than the corresponding delocalization energies in planar benzene. These calculations highlight the significance of delocalization interactions in contributing to the formation of enthalpy and the thermostability of fullerene C60. Moreover, the major correlation energy per electron at MP2/Def2SVP for fullerene C60 yields a value of 13.49 kcal/mol, which is comparable to the 11.68 kcal/mol observed for benzene. This work establishes a solid benchmark foundation for future mechanistic studies of fullerene C60 derivatives for CO2 reduction systems.
Acknowledgments
Y.L., Y.G. and D.L. acknowledge the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0024495. T.A. and B.I.Y. acknowledge the Taif University Research Support Project TURSPHC2024/1, Saudi Arabia. Y.L. would like to express profound gratitude to Bruce R. Johnson for his generous support.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano14191576/s1, Table S1: Cartesian coordinates of the optimized structure for fullerene C60.
Author Contributions
Conceptualization, Y.L., Y.G., and B.I.Y.; methodology, Y.L.; software, Y.L.; validation, Y.L.; formal analysis, Y.L.; investigation, Y.L., and B.I.Y.; resources, Y.L.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L., Y.G., T.A. and B.I.Y.; visualization, Y.L.; supervision, Y.L. and Y.G.; project administration, Y.L. and Y.G.; funding acquisition, Y.G., Y.L., D.-J.L., T.A., and B.I.Y. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding Statement
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0024495. T.A. and B.I.Y. acknowledge the Taif University Research Support Project TURSPHC2024/1, Saudi Arabia.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Kroto H.W., Heath J.R., O’Brien S.C., Curl R.F., Smalley R.E. C60: Buckminsterfullerene. Nature. 1985;318:162–163. doi: 10.1038/318162a0. [DOI] [Google Scholar]
- 2.Krätschmer W., Lamb L.D., Fostiropoulos K.H.D.R., Huffman D.R. Solid C60: A new form of carbon. Nature. 1990;347:354–358. doi: 10.1038/347354a0. [DOI] [Google Scholar]
- 3.Paukov M., Kramberger C., Begichev I., Kharlamova M., Burdanova M. Functionalized Fullerenes and Their Applications in Electrochemistry, Solar Cells, and Nanoelectronics. Materials. 2023;16:1276. doi: 10.3390/ma16031276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lalwani G., Sitharaman B. Multifunctional fullerene-and metallofullerene-based nanobiomaterials. Nano Life. 2013;3:1342003. doi: 10.1142/S1793984413420038. [DOI] [Google Scholar]
- 5.Mousavi S.Z., Nafisi S., Maibach H.I. Fullerene nanoparticle in dermatological and cosmetic applications. Nanomedicine. 2017;13:1071–1087. doi: 10.1016/j.nano.2016.10.002. [DOI] [PubMed] [Google Scholar]
- 6.Fjodorova N., Novič M., Venko K., Rasulev B., Türker Saçan M., Tugcu G., Sağ Erdem S., Toropova A.P., Toropov A.A. Cheminformatics and Machine Learning Approaches to Assess Aquatic Toxicity Profiles of Fullerene Derivatives. Int. J. Mol. Sci. 2023;24:14160. doi: 10.3390/ijms241814160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sohlberg K., Foster M.E. What’s the gap? A possible strategy for advancing theory, and an appeal for experimental structure data to drive that advance. RSC Adv. 2020;10:36887–36896. doi: 10.1039/D0RA07496A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Blase X., Attaccalite C., Olevano V. First-principles GW calculations for fullerenes, porphyrins, phtalocyanine, and other molecules of interest for organic photovoltaic applications. Phys. Rev. B. 2011;83:115103. doi: 10.1103/PhysRevB.83.115103. [DOI] [Google Scholar]
- 9.Haddon R.C. Electronic structure, conductivity and superconductivity of alkali metal doped (C60) Acc. Chem. Res. 1992;25:127–133. doi: 10.1021/ar00015a005. [DOI] [Google Scholar]
- 10.Yannoni C.S., Bernier P.P., Bethune D.S., Meijer G., Salem J.R. NMR determination of the bond lengths in C60. J. Am. Chem. Soc. 1991;113:3190–3192. doi: 10.1021/ja00008a068. [DOI] [Google Scholar]
- 11.Meirzadeh E., Evans A.M., Rezaee M., Milich M., Dionne C.J., Darlington T.P., Bao S.T., Bartholomew A.K., Handa T., Rizzo D.J., et al. A few-layer covalent network of fullerenes. Nature. 2023;613:71–76. doi: 10.1038/s41586-022-05401-w. [DOI] [PubMed] [Google Scholar]
- 12.Chen Z., Chen Z., Wu J.I., Corminboeuf C., Bohmann J., Lu X., Hirsch A., von Rague Schleyer P. Is C60 buckminsterfullerene aromatic? Phys. Chem. Chem. Phys. 2012;14:14886–14891. doi: 10.1039/c2cp42146a. [DOI] [PubMed] [Google Scholar]
- 13.Yamaguchi S., Tahara T. Observation of an optically forbidden state of C60 by nondegenerate two-photon absorption spectroscopy. Chem. Phys. Lett. 2004;390:136–139. doi: 10.1016/j.cplett.2004.03.146. [DOI] [Google Scholar]
- 14.Hoke S.H., II, Molstad J., Dilettato D., Jay M.J., Carlson D., Kahr B., Cooks R.G. Reaction of fullerenes and benzyne. J. Org. Chem. 1992;57:5069–5071. doi: 10.1021/jo00045a012. [DOI] [Google Scholar]
- 15.Su Y.-W., Lan S.-C., Wei K.-H. Organic photovoltaics. Mater. Today. 2012;15:554–562. doi: 10.1016/S1369-7021(13)70013-0. [DOI] [Google Scholar]
- 16.Jarvis S.P., Sang H., Junqueira F., Gordon O., Hodgkinson J.E., Saywell A., Rahe P., Mamone S., Taylor S., Sweetman A., et al. Chemical shielding of H2O and HF encapsulated inside a C60 cage. Commun. Chem. 2021;4:135. doi: 10.1038/s42004-021-00569-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Andreoli E., Barron A.R. Activation Effect of Fullerene C60 on the Carbon Dioxide Absorption Performance of Amine-Rich Polypropylenimine Dendrimers. ChemSusChem. 2015;8:2635–2644. doi: 10.1002/cssc.201500605. [DOI] [PubMed] [Google Scholar]
- 18.Sternfeld T., Thilgen C., Hoffman R.E., del Rosario Colorado Heras M., Diederich F., Wudl F., Scott L.T., Mack J., Rabinovitz M. An Insight into the Aromaticity of Fullerene Anions: Experimental Evidence for Diamagnetic Ring Currents in the Five-Membered Rings of C606− and C706−. J. Am. Chem. Soc. 2002;124:5734–5738. doi: 10.1021/ja012649p. [DOI] [PubMed] [Google Scholar]
- 19.Vyas V.K., Bacanu G.R., Soundararajan M., Marsden E.S., Jafari T., Shugai A., Light M.E., Nagel U., Rõõm T., Levitt M.H., et al. Squeezing formaldehyde into C60 fullerene. Nat. Commun. 2024;15:2515. doi: 10.1038/s41467-024-46886-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Froimowitz M. Molecular geometries and heats of formation of C60 and C70 as computed by MM2-87. J. Comput. Chem. 1991;12:1129–1133. doi: 10.1002/jcc.540120911. [DOI] [Google Scholar]
- 21.Friedrich M., Piovano P., Stefanelli U. The Geometry of C60: A Rigorous Approach via Molecular Mechanics. SIAM J. Appl. Math. 2016;76:2009–2029. doi: 10.1137/16M106978X. [DOI] [Google Scholar]
- 22.Liu T., Dennis T.J.S. Conformational Analysis of [60]PCBM from DFT Simulations of Electronic Energies, Bond Strain and the 13C NMR Spectrum: Input Geometry Determination and Ester Bond Rotation Dynamics. C. 2021;7:66. doi: 10.3390/c7030066. [DOI] [Google Scholar]
- 23.Kitjanon J., Khuntawee W., Phongphanphanee S., Sutthibutpong T., Chattham N., Karttunen M., Wong-Ekkabut J. Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations. Polymers. 2021;13:4044. doi: 10.3390/polym13224044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang C.I., Hua C.C., Chen S.A. Dynamic solvation shell and solubility of C60 in organic solvents. J. Phys. Chem. B. 2014;118:9964–9973. doi: 10.1021/jp506572p. [DOI] [PubMed] [Google Scholar]
- 25.Hedberg K., Hedberg L., Bethune D.S., Brown C.A., Dorn H.C., Johnson R.D., De Vries M. Bond Lengths in Free Molecules of Buckminsterfullerene, C60 from Gas-Phase Electron Diffraction. Science. 1991;254:410–412. doi: 10.1126/science.254.5030.410. [DOI] [PubMed] [Google Scholar]
- 26.David W.I.F., Ibberson R.M., Matthewman J.C., Prassides K., Dennis T.J.S., Hare J.P., Kroto H.W., Taylor R., Walton D.R. Crystal structure and bonding of ordered C60. Nature. 1991;353:147–149. doi: 10.1038/353147a0. [DOI] [Google Scholar]
- 27.Yang Y., Arias F., Echegoyen L., Chibante L.F., Flanagan S., Robertson A., Wilson L.J. Reversible Fullerene Electrochemistry: Correlation with the HOMO-LUMO Energy Difference for C60, C70, C76, C78, and C84. J. Am. Chem. Soc. 1995;117:7801–7804. doi: 10.1021/ja00134a027. [DOI] [Google Scholar]
- 28.Tans S.J., Devoret M.H., Groeneveld R.J., Dekker C. Electron–electron correlations in carbon nanotubes. Nature. 1998;394:761–764. doi: 10.1038/29494. [DOI] [Google Scholar]
- 29.Ugwumadu C., Nepal K., Thapa R.A.J.E.N.D.R.A., Lee Y.G., Al Majali Y., Trembly J., Drabold D.A. Simulation of multi-shell fullerenes using Machine-Learning Gaussian Approximation Potential. Carbon Trends. 2023;10:100239. doi: 10.1016/j.cartre.2022.100239. [DOI] [Google Scholar]
- 30.Zhao Y., Yakobson B.I., Smalley R.E. Dynamic Topology of Fullerene Coalescence. Phys. Rev. Lett. 2002;88:185501. doi: 10.1103/PhysRevLett.88.185501. [DOI] [PubMed] [Google Scholar]
- 31.Zhao Y., Smalley R.E., Yakobson B.I. Coalescence of fullerene cages: Topology, energetics, and molecular dynamics simulation. Phys. Rev. B. 2002;66:195409. doi: 10.1103/PhysRevB.66.195409. [DOI] [Google Scholar]
- 32.Scuseria G.E. Ab Initio Calculations of Fullerenes. Science. 1996;271:942–945. doi: 10.1126/science.271.5251.942. [DOI] [Google Scholar]
- 33.Wang H., Liu F.L. (C=C=C=C)@C(60): A Bonding C(60)-Endohedral Molecular Allotrope of Carbon. ACS Omega. 2020;5:26933–26937. doi: 10.1021/acsomega.0c04233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sattarova A.F., Biglova Y.N., Mustafin A.G. Quantum-chemical approaches in the study of fullerene and its derivatives by the example of the most typical cycloaddition reactions: A review. Int. J. Quantum Chem. 2022;122:e26863. doi: 10.1002/qua.26863. [DOI] [Google Scholar]
- 35.Kłos J., Tiesinga E., Kotochigova S. Quantum scattering of icosahedron fullerene C60 with noble-gas atoms. Sci. Rep. 2024;14:9267. doi: 10.1038/s41598-024-59481-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Argaman U., Makov G. Structure and properties of graphullerene: A semiconducting two-dimensional C60 crystal. NPJ Comput. Mater. 2023;9:211. doi: 10.1038/s41524-023-01167-5. [DOI] [Google Scholar]
- 37.Orozco-Ic M., Charistos N.D., Muñoz-Castro A., Islas R., Sundholm D., Merino G. Core-electron contributions to the molecular magnetic response. Phys. Chem. Chem. Phys. 2022;24:12158–12166. doi: 10.1039/D1CP05713H. [DOI] [PubMed] [Google Scholar]
- 38.Trzaskowski B., Adamowicz L., Beck W., Muralidharan K., Deymier P.A. Impact of Local Curvature and Structural Defects on Graphene–C60 Fullerene Fusion Reaction Barriers. J. Phys. Chem. C. 2013;117:19664–19671. doi: 10.1021/jp405301e. [DOI] [Google Scholar]
- 39.Karton A. Fullerenes Pose a Strain on Hybrid Density Functional Theory. J. Phys. Chem. A. 2022;126:4709–4720. doi: 10.1021/acs.jpca.2c02246. [DOI] [PubMed] [Google Scholar]
- 40.An W., Shao N., Bulusu S., Zeng X.C. Ab initio calculation of carbon clusters. II. Relative stabilities of fullerene and nonfullerene C24. J. Chem. Phys. 2008;128:084301. doi: 10.1063/1.2831917. [DOI] [PubMed] [Google Scholar]
- 41.Vance S.J., Desai V., Smith B.O., Kennedy M.W., Cooper A. Aqueous solubilization of C60 fullerene by natural protein surfactants, latherin and ranaspumin-2. Biophys. Chem. 2016;214-215:27–32. doi: 10.1016/j.bpc.2016.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Aihara J.-i. Correlation found between the HOMO–LUMO energy separation and the chemical reactivity at the most reactive site for isolated-pentagon isomers of fullerenes. Phys. Chem. Chem. Phys. 2000;2:3121–3125. doi: 10.1039/b002601h. [DOI] [Google Scholar]
- 43.Fukuda R., Ehara M. Electronic excitations of C60 fullerene calculated using the ab initio cluster expansion method. J. Chem. Phys. 2012;137:134304. doi: 10.1063/1.4757066. [DOI] [PubMed] [Google Scholar]
- 44.Martins J.L., Troullier N., Weaver J.H. Analysis of occupied and empty electronic states of C60. Chem. Phys. Lett. 1991;180:457–460. doi: 10.1016/0009-2614(91)85149-Q. [DOI] [Google Scholar]
- 45.Suresh C.H., Lincy T.L., Mohan N., Rakhi R. Aromatization Energy and Strain Energy of Buckminsterfullerene from Homodesmotic Reactions. J. Phys. Chem. A. 2015;119:6683–6688. doi: 10.1021/acs.jpca.5b01157. [DOI] [PubMed] [Google Scholar]
- 46.Panahian Jand S., Nourbakhsh Z., Site L.D. Nuclear quantum effects in fullerene-fullerene aggregation in water. Front. Chem. 2022;10:1072665. doi: 10.3389/fchem.2022.1072665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Moztarzadeh O., Jamshidi M., Taherpour A.A., Babuska V. Molecular modelling of fullerene C60 functionalized by nitric oxide for use in biological environment. Sci. Rep. 2024;14:2565. doi: 10.1038/s41598-024-53050-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Aouane M., Armstrong J., Walkey M., Hoffman G., Bacanu G.R., Whitby R.J., Levitt M.H., Rols S. A combined inelastic neutron scattering and simulation study of the 3He@C60 endofullerene. Phys. Chem. Chem. Phys. 2023;25:20295–20301. doi: 10.1039/D3CP02253F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Karton A., Chan B., Raghavachari K., Radom L. Evaluation of the Heats of Formation of Corannulene and C60 by Means of High-Level Theoretical Procedures. J. Phys. Chem. A. 2013;117:1834–1842. doi: 10.1021/jp312585r. [DOI] [PubMed] [Google Scholar]
- 50.Chan B. Fullerene Thermochemical Stability: Accurate Heats of Formation for Small Fullerenes, the Importance of Structural Deformation on Reactivity, and the Special Stability of C60. J. Phys. Chem. A. 2020;124:6688–6698. doi: 10.1021/acs.jpca.0c04732. [DOI] [PubMed] [Google Scholar]
- 51.Choi C.H., Kertesz M., Mihaly L. Vibrational Assignment of All 46 Fundamentals of C60 and C606−: Scaled Quantum Mechanical Results Performed in Redundant Internal Coordinates and Compared to Experiments. J. Phys. Chem. A. 2000;104:102–112. doi: 10.1021/jp991420h. [DOI] [Google Scholar]
- 52.Sabirov D.S., Osawa E. Information Entropy of Fullerenes. J. Chem. Inf. Model. 2015;55:1576–1584. doi: 10.1021/acs.jcim.5b00334. [DOI] [PubMed] [Google Scholar]
- 53.Zhao Y., Lin Y., Yakobson B.I. Fullerene shape transformations via Stone-Wales bond rotations. Phys. Rev. B. 2003;68:233403. doi: 10.1103/PhysRevB.68.233403. [DOI] [Google Scholar]
- 54.Häser M., Almlöf J., Scuseria G.E. The equilibrium geometry of C60 as predicted by second-order (MP2) perturbation theory. Chem. Phys. Lett. 1991;181:497–500. doi: 10.1016/0009-2614(91)80301-D. [DOI] [Google Scholar]
- 55.Bühl M., Patchkovskii S., Thiel W. Interaction energies and NMR chemical shifts of noble gases in C60. Chem. Phys. Lett. 1997;275:14–18. doi: 10.1016/S0009-2614(97)00733-1. [DOI] [Google Scholar]
- 56.Shameema O., Ramachandran C.N., Sathyamurthy N. Blue Shift in X−H Stretching Frequency of Molecules Due to Confinement. J. Phys. Chem. A. 2006;110:2–4. doi: 10.1021/jp056027s. [DOI] [PubMed] [Google Scholar]
- 57.Jaworski A., Hedin N. Local energy decomposition analysis and molecular properties of encapsulated methane in fullerene (CH4@C60) Phys. Chem. Chem. Phys. 2021;23:21554–21567. doi: 10.1039/D1CP02333K. [DOI] [PubMed] [Google Scholar]
- 58.Meloni G., Giustini A., Park H. CO2 Activation within a Superalkali-Doped Fullerene. Front. Chem. 2021;9:712960. doi: 10.3389/fchem.2021.712960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ridassepri A.F., Umejima Y., Nakamura J. B-Doped Fullerene as a Potential Metal-Free Catalyst Material for CO Reduction Reaction. J. Phys. Chem. C. 2024;128:9513–9519. doi: 10.1021/acs.jpcc.4c01468. [DOI] [Google Scholar]
- 60.Vícha J., Vaara J., Straka M. The essential role of symmetry in understanding 3He chemical shifts in endohedral helium fullerenes. Phys. Chem. Chem. Phys. 2023;25:10620–10627. doi: 10.1039/D3CP00256J. [DOI] [PubMed] [Google Scholar]
- 61.Cioslowski J. Endohedral Magnetic Shielding in the C60 Cluster. J. Am. Chem. Soc. 1994;116:3619–3620. doi: 10.1021/ja00087a066. [DOI] [Google Scholar]
- 62.Bühl M., Hirsch A. Spherical Aromaticity of Fullerenes. Chem. Rev. 2001;101:1153–1184. doi: 10.1021/cr990332q. [DOI] [PubMed] [Google Scholar]
- 63.Cleland D.M., Fletcher E.K., Kuperman A., Per M.C. Electron correlation effects in isomers of C20. J. Phys. Mater. 2020;3:025006. doi: 10.1088/2515-7639/ab7e41. [DOI] [Google Scholar]
- 64.Karton A., Waite S.L., Page A.J. Performance of DFT for C60 Isomerization Energies: A Noticeable Exception to Jacob’s Ladder. J. Phys. Chem. A. 2019;123:257–266. doi: 10.1021/acs.jpca.8b10240. [DOI] [PubMed] [Google Scholar]
- 65.Liu Y., Ma R., Fan H., Johnson B.R., Briggs J.M. Pharmacophore Oriented MP2 Characterization of Charge Distribution for Anti-SARS-CoV-2 Inhibitor Nirmatrelvir. J. Mol. Struct. 2023;1290:135871. doi: 10.1016/j.molstruc.2023.135871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Liu Y., Gallo A.A., Liu Y., Hall M.B., Johnson B.R. QM evaluation of the intramolecular aromatic π-π interactions of Ir(I) complex transition states. J. Mol. Struct. 2023;1291:135907. doi: 10.1016/j.molstruc.2023.135907. [DOI] [Google Scholar]
- 67.Liu Y., Sulaiman H.F., Johnson B.R., Ma R., Gao Y., Fernando H., Amarasekara A., Ashley-Oyewole A., Fan H., Ingram H.N., et al. QM/MM study of N501 involved intermolecular interaction between SARS-CoV-2 receptor binding domain and antibody of human origin. Comput. Biol. Chem. 2023;102:107810. doi: 10.1016/j.compbiolchem.2023.107810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Weinhold F., Landis C.R., Glendening E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016;35:399–440. doi: 10.1080/0144235X.2016.1192262. [DOI] [Google Scholar]
- 69.Humphrey W., Dalke A., Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 70.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Petersson G.A., Nakatsuji H., et al. Gaussian 16 Rev. C.01. Gaussian, Inc.; Wallingford, CT, USA: 2016. [Google Scholar]
- 71.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- 72.Becke A.D., Density-functional thermochemistry III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
- 73.Perdew J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B. 1986;33:8822–8824. doi: 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- 74.Becke A.D. Density functional calculations of molecular bond energies. J. Chem. Phys. 1986;84:4524–4529. doi: 10.1063/1.450025. [DOI] [Google Scholar]
- 75.Becke A.D., Johnson E.R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005;123:154101. doi: 10.1063/1.2065267. [DOI] [PubMed] [Google Scholar]
- 76.Weigend F., Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 77.Schein S., Sands-Kidner M. A geometric principle may guide self-assembly of fullerene cages from clathrin triskelia and from carbon atoms. Biophys. J. 2008;94:958–976. doi: 10.1529/biophysj.107.110817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Singh U.C., Kollman P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984;5:129–145. doi: 10.1002/jcc.540050204. [DOI] [Google Scholar]
- 79.Johari G.P. Entropy of buckminsterfullerene at 0 K. J. Chem. Phys. 1994;100:2220–2222. doi: 10.1063/1.466519. [DOI] [Google Scholar]
- 80.Šulka M., Šulková K., Jurečka P., Dubecký M. Dynamic and Nondynamic Electron Correlation Energy Decomposition Based on the Node of the Hartree-Fock Slater Determinant. J. Chem. Theory Comput. 2023;19:8147–8155. doi: 10.1021/acs.jctc.3c00828. [DOI] [PubMed] [Google Scholar]
- 81.Löwdin P.-O. Quantum Theory of Many-Particle Systems. III. Extension of the Hartree-Fock Scheme to Include Degenerate Systems and Correlation Effects. Phys. Rev. 1955;97:1509–1520. doi: 10.1103/PhysRev.97.1509. [DOI] [Google Scholar]
- 82.Møller C., Plesset M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934;46:618–622. doi: 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
- 83.Kristensen K., Høyvik I.M., Jansik B., Jørgensen P., Kjærgaard T., Reine S., Jakowski J. MP2 energy and density for large molecular systems with internal error control using the Divide-Expand-Consolidate scheme. Phys. Chem. Chem. Phys. 2012;14:15706–15714. doi: 10.1039/c2cp41958k. [DOI] [PubMed] [Google Scholar]
- 84.Nordholm S. Analysis of Bonding by Quantum Chemistry─Resolving Delocalization Stabilization in a Mechanistic Basis and New Hückel Model. J. Phys. Chem. A. 2023;127:3449–3471. doi: 10.1021/acs.jpca.2c08497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Damour Y., Véril M., Kossoski F., Caffarel M., Jacquemin D., Scemama A., Loos P.F. Accurate full configuration interaction correlation energy estimates for five- and six-membered rings. J. Chem. Phys. 2021;155:134104. doi: 10.1063/5.0065314. [DOI] [PubMed] [Google Scholar]
- 86.Grunenberg J. Ill-defined chemical concepts: The problem of quantification. Int. J. Quantum Chem. 2017;117:e25359. doi: 10.1002/qua.25359. [DOI] [Google Scholar]
- 87.Krygowski T.M., Cyrański M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001;101:1385–1420. doi: 10.1021/cr990326u. [DOI] [PubMed] [Google Scholar]
- 88.Cyrański M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005;105:3773–3811. doi: 10.1021/cr0300845. [DOI] [PubMed] [Google Scholar]
- 89.Feixas F., Matito E., Poater J., Solà M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015;44:6434–6451. doi: 10.1039/C5CS00066A. [DOI] [PubMed] [Google Scholar]
- 90.Zanasi R., Lazzeretti P., Malagoli M., Piccinini F. Molecular magnetic properties within continuous transformations of origin of the current density. J. Chem. Phys. 1995;102:7150–7157. doi: 10.1063/1.469109. [DOI] [Google Scholar]
- 91.Matsumoto F., Iwai T., Moriwaki K., Takao Y., Ito T., Mizuno T., Ohno T. Design of Fullerene Derivatives for Stabilizing LUMO Energy using Donor Groups Placed in Spatial Proximity to the C60 Cage. J. Org. Chem. 2012;77:9038–9043. doi: 10.1021/jo3015159. [DOI] [PubMed] [Google Scholar]
- 92.Saito S., Oshiyama A. Cohesive mechanism and energy bands of solid C60. Phys. Rev. Lett. 1991;66:2637–2640. doi: 10.1103/PhysRevLett.66.2637. [DOI] [PubMed] [Google Scholar]
- 93.Weaver J.H., Martins J.L., Komeda T., Chen Y., Ohno T.R., Kroll G.H., Troullier N., Haufler R.E., Smalley R.E. Electronic structure of solid C60: Experiment and theory. Phys. Rev. Lett. 1991;66:1741–1744. doi: 10.1103/PhysRevLett.66.1741. [DOI] [PubMed] [Google Scholar]
- 94.Golden M.S., Knupfer M., Fink J., Armbruster J.F., Cummins T.R., Romberg H.A., Roth M., Sing M., Schmidt M., Sohmen E. The electronic structure of fullerenes and fullerene compounds from high-energy spectroscopy. J. Phys. Condens. Matter. 1995;7:8219. doi: 10.1088/0953-8984/7/43/004. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data are available from the corresponding author upon reasonable request.