Characterizing Spatial Information Loss for Wastewater Surveillance Using crAssphage: Effect of Decay, Temperature, and Population Mobility

Abstract

Populations contribute information about their health status to wastewater. Characterizing how that information degrades in transit to wastewater sampling locations (e.g., wastewater treatment plants and pumping stations) is critical to interpret wastewater responses. In this work, we statistically estimate the loss of information about fecal contributions to wastewater from spatially distributed populations at the census block group resolution. This was accomplished with a hydrologically and hydraulically influenced spatial statistical approach applied to crAssphage (Carjivirus communis) load measured from the influent of four wastewater treatment plants in Hamilton County, Ohio. We find that we would expect to observe a 90% loss of information about fecal contributions from a given census block group over a travel time of 10.3 h. This work demonstrates that a challenge to interpreting wastewater responses (e.g., during wastewater surveillance) is distinguishing between a distal but large cluster of contributions and a near but small contribution. This work demonstrates new modeling approaches to improve measurement interpretation depending on sewer network and wastewater characteristics (e.g., geospatial layout, temperature variability, population distribution, and mobility). This modeling can be integrated into standard wastewater surveillance methods and help to optimize sewer sampling locations to ensure that different populations (e.g., vulnerable and susceptible) are appropriately represented.

Graphical Abstract

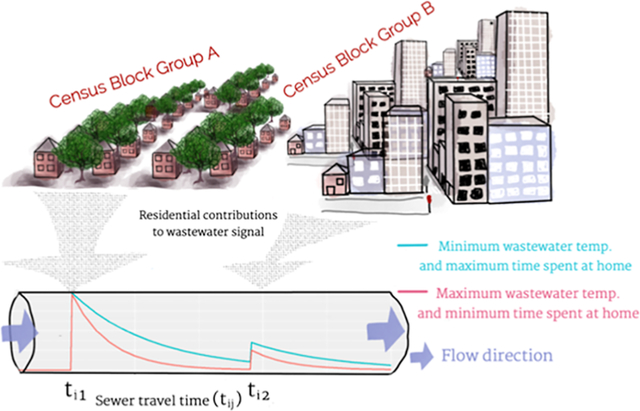
1. INTRODUCTION

Wastewater surveillance (WWS) has been used to complement the clinical surveillance of SARS-CoV-2, norovirus, and other public health concerns (e.g., drug and pharmaceutical use, antimicrobial resistance, and exposures to external stressors).^1–3 However, microbial responses are known to decay in wastewater, so the varying proximity of populations to wastewater treatment plants (WWTPs) can confound spatial associations between the total sewershed population and measured wastewater influent data, when contributions are assumed to be homogeneous, introducing bias to WWS.^4–8 This bias can reduce the ability to predict the initial loadings of microbial responses at their source (i.e., the locations of spatially distributed populations contributing to wastewater). A reduced ability to predict spatially and temporally distributed loadings from WWS data (herein called “information loss”) obscures inferences made with WWS data about represented populations. Based on studies relating microbial responses to sources, we hypothesize that natural processes (e.g., decay, adsorption, desorption, detachment from biofilms⁹), measurement error, and information diffusion losses (i.e., loss of accuracy in modeled associations between spatially and temporally distributed data) can contribute to this information loss in sewer networks. See Figure 1 for concrete examples pertaining to molecular microbial responses.¹⁰

Figure 1.

Types of information losses that may reduce the ability to detect a microbial response signal from distributed sources.

A critical step forward in WWS of microbial targets (e.g., SARS-CoV-2, influenza, norovirus, or antimicrobial resistance) is characterizing this information loss to improve the accuracy of measurement interpretation.¹¹ For chemical responses (e.g., illicit drug use), mechanistic modeling approaches have been applied.⁵ While simulations demonstrate how microbial information may be lost over wastewater travel times from spatially distributed populations,⁷ no current study with observational data challenges the implicit assumption that microbial responses measured from wastewater influents equally represent the whole sewershed community.³ Mechanistic models would be ideal to apply to microbial data, but loadings and transport processes are not well-characterized. Research supports the fact that the fate and transport of microbial responses vary vastly between water types.¹² Recent research shows that sewer pipe type (e.g., gravity or pressurized) and biofilm presence significantly affect microbial decay.^9,13,14 These works demonstrate that there is much to be discovered about in-sewer fate and transport prior to the application of completely mechanistic fate and transport models.

Spatial predictor models (SPMs) from the microbial Find, Inform, and Test (FIT) framework,¹⁵ employing a land-use regression approach, offer an intermediary solution. These hydrologically influenced, spatially explicit models do not require detailed knowledge of the underlying process dynamics. The SPMs leverage the signal decay hyperparameter, ${\alpha }_{\mathrm{p}}$, which represents the distance at which we would expect to see a p % loss of information from source locations.^10,16–18

In this study, SPMs are tailored for sewer networks, redefining populations as sources and adapting models to available information such as sewer travel times estimated with hydraulic–hydrologic models. We investigate the loss of information about fecal contributions to wastewater collection systems. Since fecal input to these systems is an important denominator in the population-level interpretation of microbial responses during WWS, we apply these SPMs to relate spatially distributed populations to observed crAssphage measurements (i.e., Carjivirus communis, a human-associated fecal marker that is shed by most, if not all people in Western populations¹⁹ and which is frequently measured in WWS contexts) at WWTPs to help fix some factors in the information loss profile about fecal shedding.^20–25

In addition to normalizing WWS responses by fecal markers, WWS researchers are generally in consensus about using flow-adjusted disease markers (sometimes called flow normalization) in wastewater to better correlate microbial targets in wastewater with respective case data.^23,26,27 We expect that we can improve on correlations between flow-adjusted crAssphage (i.e., crAssphage load) responses and population data by using a spatially explicit representation of population impacts and temperature effects, which are known to affect the decay of genetic markers in water and wastewater,^5,25,27,28 including crAssphage^4,29–31 Given that people shed feces in various locations and that population mobility influences the levels of biomarkers measured from wastewater data,^32,33 we also explore the impact of population mobility on crAssphage loads.

This work expands SPMs for suitability in sewer networks, applying them to crAssphage measured at WWTPs to 1) estimate the spatial information loss to evaluate disproportionately represented populations; 2) quantify the modifying effect that wastewater temperature has on fecal contributions; and 3) explore population mobility effects on WWS responses. Lastly, we challenge our initial assumptions about the types of information loss that we capture with the signal decay hyperparameter, ${\alpha }_{\mathrm{p}}$ (representing a travel time instead of distance) using a sensitivity analysis to see the impact of adding errors to spatially distributed population estimates, crAssphage measurements, and precisely estimated travel times from a well-developed Stormwater Management Model (i.e., a dynamic hydraulic–hydrologic model). Results of this work have important implications to the normalization of SARS-CoV-2 measurements by crAssphage during WWS.

2. MATERIALS AND METHODS

2.1. Sampling and Quantification of crAssphage in WWTP Influents.

Weekly or biweekly 24 h flow-weighted composite samples were collected from four WWTPs in Hamilton County, Ohio, from August 2020 to October 2021. The four WWTPs serve the Mill Creek, Taylor Creek, Muddy Creek, and Little Miami catchment areas of the greater Cincinnati area with populations of 488,000, 34,000, 76,000, and 143,000, respectively, estimated by the Metropolitan Sewer District of Greater Cincinnati (MSD). From here on, we refer to these names for each of the WWTPs. Mill Creek, Muddy Creek, and Little Miami are combined sewer systems, whereas Taylor Creek is a separate sewer system. One-liter composite samples were taken to the U.S. EPA AWBERC facility in Cincinnati, OH, for processing as part of a broader SARS-CoV-2 monitoring study.²¹ Samples were prepared by transferring two 225 mL of composite influent samples to sterile 250 mL conical tubes and amending them with 25 mL of 10× PBS. For analysis of crAssphage, each subsample was mixed, and 0.2 mL was removed and extracted using the DNeasy PowerWater Kit (Qiagen, Germantown, MD) as per the manufacturer’s instructions, eluting nucleic acids in 125 μL of RNase-free water. Quantification of crAssphage gene fragments was determined by droplet digital PCR (ddPCR) using the previously described crAv056 assay.³⁴ For details on sample collection, nucleic acid extraction, and ddPCR quantification of crAssphage gene fragments, refer to the methods in Nagarkar et al. 2022.²⁶

For modeling purposes, we calculated the daily load of crAssphage (log₁₀ copies-crAv056-per-day), $z_i$, from the estimated wastewater concentration (crAv056-copies-perliter) $y_i$ and the daily flow $q_i$ (liter-wastewater-per-day) for the ith space/time sample

$$z_i={\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(y_i{q}_i\right)$$ (1)

Flows were continuously recorded and totalized to report the daily flow.

2.2. Hydrologically and Hydraulically Influenced Land-Use Regression Framework for Wastewater Surveillance Signals.

In this study, a previously developed microbial land-use regression framework¹⁵ is adapted for wastewater surveillance signals. The model predicts a WWS response $z_i$ by incorporating sewer characteristics $x_i^{\left(w\right)}$ that affect microbiological responses in sewer networks. We expand the model to integrate the mechanistic hydraulic and hydrologic characteristics of the sewer network by estimating wastewater travel times with the EPA’s Stormwater Management Model with mass pollutant routing. We designate spatially distributed populations at residential locations as sources and denote the contribution at space/time sample $i$ from upstream residential populations as $s_i\left(\mathit{\alpha }\right)$ where the spatial extent of populations contributing to the ith sample is defined by upstream populations, sewer travel time, signal decay hyperparameter, and modifiers $\mathit{\alpha }$. For assessing the impacts of distributed populations and associated factors, we focus on hyperparameter ${\alpha }_{90}$, the travel time for which 90% of original source information is lost from a wastewater treatment plant influent sample. We define a linear model with one source term and variables representing sewershed characteristics, $x_i^{\left(w\right)}$, (i.e., daily wastewater pH, daily ambient temperature (°C), daily wastewater temperature (°C), average industrial flow (MGD), binary sewer type [separate or combined], compound variable describing 48 h precipitation [inches] for sewersheds with a combined sewer type, and population mobility factors represented as % time spent at the location compared to a baseline)

$$z_i={\beta }_0+{\beta }_1{s}_i(\mathit{\alpha })+\{\sum _{w=1}^W{\beta }_w{x}_i^{(w)}\}$$ (2)

Here, ${\beta }_0$ is an intercept. Each of the predictors is standardized such that associated regression coefficients ${\beta }_1$ and ${\beta }_{\mathrm{w}}$ represent the increase in the response for a 1 standard deviation increase in the source and sewershed characteristic terms, respectively. We also included supplementary methods and analysis to explore population mobility as a modifying factor (S8).

We construct a source predictor $s_i(\mathit{\alpha })$ to relate spatially distributed populations to WWS responses from samples at other locations using SPMs of increasing sophistication: (1) the original Euclidean distance sum of exponentially decaying contributions (SEDC) model with distance replaced by sewer pipe travel times;¹⁵ (2) the travel time SEDC model, but with the hyperparameter, ${\alpha }_{90}$, modified by wastewater temperature (SEDC-T), and (3) the travel time SEDC model, but with ${\alpha }_{90}$ modified by both wastewater temperature and population mobility (SEDC-TM). The value of $s_i\left({\alpha }_{90}\right)$ in the sewer network is calculated using the SEDC from the $j$th population location connected to each sample $i$

$${\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90}\right)=\sum _{j=1}^N{P}_{0j}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-2.3t_{ij}}{{\alpha }_{90}}\right)$$ (3.1)

$$s_i(\mathit{\alpha })=s_i\left({\alpha }_{90}\right)={\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90}\right)/\mathrm{s}\mathrm{t}\mathrm{d}\left({\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90}\right)\right)$$ (3.2)

where $P_{0j}$ is the population at each jth location of populations of the N connected to sample $i$ via the sewer network locations (i.e., upstream census block group populations) and $t_{ij}$ is the travel time in hours from $j$ to $i$ through the sewer. ${\alpha }_{90}$ is the signal decay hyperparameter that describes the travel time at which you would expect to see a 90% loss of the information that could be obtained by sampling directly at each jth location. For example, if ${\alpha }_{90}$ is very small, then the microbial response at wastewater sampling sites is highly dictated by the population information at very close locations relative to farther ones (i.e., for which travel times $\gg {\alpha }_{90}$). As ${\alpha }_{90}$ approaches infinity, the sum of sewershed population contributions will directly explain the microbial responses in wastewater.

Due to the evidence of temperature-modified decay of microbial markers,^4,12,35,36 and for crAssphage in particular,^29,31 we expand the second SPM approach (SEDC-T). We let ${\alpha }_{90}$ exponentially decrease with wastewater temperature by setting ${\alpha }_{90}={\alpha }_{90,\mathrm{T}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\gamma }_1{T}_i\right)$ where $T_i$ is the z-scored wastewater temperature (with a mean of 0 and standard deviation of 1), ${\gamma }_1<0$ is a fitted hyperparameter that captures the exponential decrease of ${\alpha }_{90}$ with z-scored temperature, and ${\alpha }_{90,\mathrm{T}}$ is the value of ${\alpha }_{90}$ at the average wastewater temperature (i.e., when Ti = 0) of 18.3 °C for this study (see Supporting Information 3 for more descriptive statistics). The SPM is

$${\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90,T},{\gamma }_1,T_i\right)=\sum _{j=1}^N{P}_{0j}\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{-2.3t_{ij}}{{\alpha }_{90,T}\mathrm{e}\mathrm{x}\mathrm{p}\left({\gamma }_1{T}_i\right)}\right]$$ (4.1)

$$\begin{gathered} s_i(\mathit{\alpha })=s_i\left({\alpha }_{90,T},{\gamma }_1,T_i\right) \\ ={\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90,T},{\gamma }_1,T_i\right)/\mathrm{s}\mathrm{t}\mathrm{d}\left({\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90,T},{\gamma }_1,T_i\right)\right) \end{gathered}$$ (4.2)

For a 1 standard deviation increase in the wastewater temperature (i.e., when Ti increases by 1), ${\alpha }_{90}$ decreases by a factor of $\mathrm{e}\mathrm{x}\mathrm{p}(\gamma 1)$ Since temperature changes with time, the SPM no longer represents a uniquely spatial variable but a spatial–temporal variable. However, the physical influence that wastewater temperature has on the signal decay hyperparameter may be entangled with temporal factors that affect residential population contributions to the sewer network, such as seasonal behavior changes.

In the next SPM (eq 5.1), the SEDC with temperature and mobility (SEDC-TM), we acknowledge that mobility may modify how spatially distributed population information is lost over travel times due to population mobility factors. In this model, ${\alpha }_{90}$ exponentially decreases with Ti and exponentially increases with the percent of time spent at home from baseline (i.e., a population mobility factor) by using ${\alpha }_{90}={\alpha }_{90,\mathrm{T}\mathrm{M}}\mathrm{e}\mathrm{x}\mathrm{p}(\gamma 1\mathrm{T}\mathrm{i}+\gamma 2\mathrm{M}\mathrm{o}\mathrm{b}\mathrm{i}$), where Mobi is the z-scored mobility factor (mean of 0 and standard deviation of 1), $\gamma 2>0$ is a fitted parameter that captures the exponential increase of ${\alpha }_{90}$ with the z-scored population mobility factor, and ${\alpha }_{90,\mathrm{T}\mathrm{M}}$ is the value of ${\alpha }_{90}$ at an average wastewater temperature (i.e., when $T_i=0$) and population mobility conditions (i.e., when ${\mathrm{M}\mathrm{o}\mathrm{b}}_i=0$). The SEDC-TM SPM is

$$\begin{array}{l}{\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90,\mathrm{T}\mathrm{M}},{\gamma }_1,T_i,{\gamma }_2,{\mathrm{M}\mathrm{o}\mathrm{b}}_i\right)\\ ={\sum }_{j=1}^N{P}_{0j}\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{-2.3t_{ij}}{{\alpha }_{90,\mathrm{T}\mathrm{M}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\gamma }_1{T}_i+{\gamma }_{2}Mo{b}_i\right)}\right]\end{array}$$ (5.1)

$$\begin{gathered} s_i(\mathit{\alpha })=s_i\left({\alpha }_{90,\mathrm{T}\mathrm{M}},{\gamma }_1,T_i,{\gamma }_2,{\mathrm{M}\mathrm{o}\mathrm{b}}_i\right) \\ ={\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90},{\gamma }_1,T_i,{\gamma }_2,{\mathrm{M}\mathrm{o}\mathrm{b}}_i\right)/\mathrm{s}\mathrm{t}\mathrm{d} \\ \left({\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{90,\mathrm{T}\mathrm{M}},{\gamma }_1,T_i,{\gamma }_2,{\mathrm{M}\mathrm{o}\mathrm{b}}_i\right)\right) \end{gathered}$$ (5.2)

2.3. Databases of Spatially Distributed Information.

This model requires spatially distributed locations, $j$, of residences and associated populations, $P_{0j}$, and septic systems (to differentiate from sewered locations), Sep_j. Additionally, wastewater travel times from the jth population locations to the ith sampling site, $t_{ij}$, are needed as are data representing meteorological and mobility factors of interest.

The 2019 U.S. Census is the most up-to-date database of spatially distributed populations at residential locations. Population data were represented at census block group resolution to match how health data are represented to protect privacy. The census population information was aggregated to the census block group level using the tidycensus package in R4.1.0.³⁷ Septic system locations were obtained from the Hamilton County Health Department and geocoded with the ggmap package³⁸ in R. Sewershed boundaries were provided by MSD. Since census block group and sewershed boundaries do not align, the population in each jth intersection of a census block group³⁹ with a given sewershed $\left(P_{0,j}\right)$ was calculated as follows

$$P_{0j}=\left(P^{(\mathrm{C}\mathrm{B}\mathrm{G})}\right)\left(\frac{A_j^{\text{(sewered})}}{A_j^{\text{(total)}}}\right)-p^{\mathrm{h}\mathrm{h}}{\mathrm{S}\mathrm{e}\mathrm{p}}_j$$ (6)

Where $P^{(\mathrm{C}\mathrm{B}\mathrm{G})}$ is the census block group population according to the 2019 Census, $A_j^{\text{(total)}}$ is the total area of the census block group in square feet, ${A_j}^{\text{(sewered)}}$ represents the area of that census block group that is sewered in square feet, Sep_j represents the number of septic systems in area ${A_j}^{\text{(sewered)}}$, and $p^{\text{hh}}=2.41$ is the median persons per household for Ohio based on 2016–2020 Census data.⁴⁰ To our knowledge, only two studies of crAssphage shedding dynamics exist^41,42 and do not outline population-level shedding rates, so our model is independent of any assumptions about fecal shedding. In other words, we assume each Census Block Group has a sufficiently large population size (approximately 150–4500 people, see Table S3 in the Supporting Information) for the law of large numbers to apply, and we assume that each census block group will shed the same load of crAssphage per-capita on average. We note that this assumption may fail for small census block groups and if the distributions of shedding are particularly heavy tailed (e.g., Cauchy).

The travel time, $t_{ij}$, from each spatially distributed population location $j$ to the location of each ith sample associated with a unique WWTP was obtained from MSD’s collection system models. The models are built using U.S. EPA’s Stormwater Management Model (SWMM), and adaptations were made specifically for this study by adding in pollutant mass routing. See S1.9 for details on travel time estimation using tracer experiments and the underlying collection system models. We also calculated Euclidean distances $D_{ij}$ for model comparison (see S1.8).

Spatially distributed data by sewershed were also obtained for our analyses. Recorded daily flow (million gallons per day; MGD), average industrial flow (MGD), daily wastewater temperature (°C), daily wastewater pH (measured with continuous in-line meters with critical values typically reported as mean on the day of the sample), and sewer type (i.e., whether the system was combined or separate) were obtained from MSD. Daily ambient temperature (°C) and precipitation (millimeters) data were obtained using the rnoaa package.⁴³

Lastly, population mobility was represented by freely available COVID-19 Google community mobility data.⁴⁴ These data represent daily mobility at the county level expressed as the percent time spent at different location types (e.g., home, transit, retail or recreation, grocery stores or pharmacies, or work) from a baseline value obtained from the 5 weeks Jan 3 to Feb 6, 2020; i.e., prior to the disruptive impacts of the COVID-19 pandemic.⁴⁴

For details on data sources and processing in ArcMap10.5 and R, see Supporting Information Section S1 and for a table that summarizes sewershed characteristics, Census Block Group information, and mobility variables across the sewersheds, see S3.

2.4. Implementation of the Hydrologically Informed Land-Use Regression.

Hyperparameters (i.e., ${\alpha }_{90},{\alpha }_{90,\mathrm{T}},{\alpha }_{90,\mathrm{T}\mathrm{M}},{\gamma }_1$, and ${\gamma }_2$) were obtained by maximizing the model fit to ${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ crAssphage load as represented by Pearson’s $R^2$ from a univariate regression between the modeled source terms $s_i(\alpha )$ and the response with each SPM of increasing sophistication (i.e., SEDC, SEDC-T, and SEDC-TM). We used the optim function in R and set an objective function to $1-R^2$, where the range of hyperparameter values ${\alpha }_{90},$ ${\alpha }_{90,\mathrm{T}}$, or ${\alpha }_{90,\mathrm{T}\mathrm{M}}$ were constrained to a lower bound of 0 and upper bound of 90 h. ${\gamma }_1$ had lower bounds of –2 and upper bounds of 0, and ${\gamma }_2$ had lower bounds of 0 and upper bounds of 2. An in-depth tutorial on optimizing SEDC hyperparameters can be found at https://mserre.sph.unc.edu/BMElab_web/SEDCtutorial/index.html.

In addition to the ${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ crAssphage load $z_i={\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(y_i{q}_i\right)$ as a response, we explored the crAssphage concentration ${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(y_i\right)$ as a response as an additional way to learn about this novel modeling approach.

The three SPMs used for calculating population contributions were compared with a 10-fold cross-validation evaluated with mean square error (MSE) to select a population contribution SPM with the fewest parameters and within the best-performing model’s MSE.⁴⁵ Finally, we implemented the hydrologically influenced land-use regression model (eq 2) using a standard least absolute shrinkage and selection operation (LASSO) regression with glmnet package⁴⁶ in R to assess sewershed factors (i.e., $x_i^{(w)}$) that influence crAssphage load. A 10-fold cross-validation was applied to the LASSO to determine the shrinkage parameter ${\lambda }_{\text{min}}$ that minimized the MSE and ${\lambda }_{1\text{se}}$, which corresponded to the largest value of $\lambda$ such that the error was within 1 standard deviation of the cross-validated errors of ${\lambda }_{\text{min}}$. We determined which variables would be included in the model based on ${\lambda }_{\text{1se}}$ with a standard LASSO and ran a bootstrap resampling of the data (10,000 simulations) to obtain regression coefficients with 95% interval estimates and measures of model fit ($R^2$ and adjusted $R^2$). We visually evaluated the normality of the resulting model residuals.

2.5. Mapping the Spatial Information Loss Rate.

To represent the rate of information loss about population fecal shedding captured from each census block group given the sampling sites at the WWTPs, we express the information loss rate $(r_{ij}^{(\mathrm{S}\mathrm{P}\mathrm{M})})$ for each location $j$ for the ith space/time sample with the resulting hyperparameters from different SPMs

$$r_{ij}^{\text{SEDC}}=1-\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-2.3t_{ij}}{{\alpha }_{90}}\right)$$ (7.1)

$$r_{ij}^{\text{SEDC-T}}=1-\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-2.3t_{ij}}{{\alpha }_{90,T}\mathrm{e}\mathrm{x}\mathrm{p}\left({\gamma }_1{T}_i\right)}\right)$$ (7.2)

$$r_{ij}^{\text{SEDC-TM}}=1-\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-2.3t_{ij}}{{\alpha }_{90,\mathrm{T}\mathrm{M}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\gamma }_1{T}_i+{\gamma }_2{\mathrm{M}\mathrm{o}\mathrm{b}}_i\right)}\right)$$ (7.3)

We used minimum and maximum values of $T_i$ and ${\mathrm{M}\mathrm{o}\mathrm{b}}_i$ to explore “best case” and “worse case” scenarios, i.e., those conditions that result in the least and most information losses, respectively. Maps were generated using R with the sf⁴⁷ and ggplot⁴⁸ packages.

2.6. Sensitivity Analysis for Different Types of Information Loss.

Our initial assumptions about the signal decay hyperparameter, ${\alpha }_{\mathrm{p}}$, is that it captures three types of information loss (Figure 1). For losses from natural processes, we added error to the travel times $t_{ij}$ estimated from a well-developed EPA SWMM model of the sewer networks (see Supporting Information 1.9). For losses from measurement error, we added error to the measured crAssphage load $z_i$. For information diffusion losses, we added error to the estimates of spatially distributed populations at residential locations $P_{0j}$. We tested how the extra errors on model components associated with these processes affect 1) the optimized hyperparameter ${\alpha }_{90}$; 2) resulting regression coefficient ${\beta }_1$; and 3) model fit $R^2{\alpha }_{90}$. We obtained $t_{ijk}^{\prime },$ $z_{ik}^{\prime }$, and $P_{0jk}^{\prime }$ for $k=1$ iterations, which are a function of the original values, $t_{ij},$ $z_{ij}$, and $P_{0j}$ from our databases as well as their standard deviations and normal random error.

$${t_{ijk}}^{\prime }=t_{ij}+0.1{\hat{\sigma }}_{t_{ij}}{\epsilon }_{jk}$$ (8.1)

$${z_{ik}}^{\prime }=z_i+0.1{\hat{\sigma }}_{z_i}{\epsilon }_{ik}$$ (8.2)

$${P_{0jk}}^{\prime }=P_{0j}+0.1{\hat{\sigma }}_{P_{0j}}{\epsilon }_{jk}$$ (8.3)

where ${\epsilon }_{jk}$ and ${\epsilon }_{ik}$ are matrices with each column representing $j$ or $i$ rows randomly generated from a normal distribution with a mean of 0 and standard deviation of 1 and ${\hat{\sigma }}_{tij},$ ${\hat{\sigma }}_{zi}$, and ${\hat{\sigma }}_{P0j}$ are the standard deviations of $P_{0j},t_{ij}$, and $z_i$, respectively.

We then ran the hyperparameter optimization using each $k$ th set of values from ${t_{ijk}}^{\prime }$, while fixing the original $P_{0j}$ and $z_i$. We repeated this approach with each $k$ th set of values from ${z_{ik}}^{\prime }$ fixing $P_{0j}$ and $t_{ij}$ and again for ${P_{0jk}}^{\prime }$, fixing $t_{ij}$ and $z_i$. From this, we obtained ${\alpha }_{90k}{\mathrm{*}}^{(\text{(input)}},{\hat{\beta }}_{1\mathrm{k}}^{(\text{input)}}$, and $R_k^{2(\text{input)}}$ for $\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}=\left\{P_{0j},t_{ij}\right.,\left.z_i\right\}$. We estimated the mean and variance of ${\alpha }_{90k}{\mathrm{*}}^{(\text{(input)}},{{\hat{\beta }}_{1\mathrm{k}}}^{\text{(input)}}$, and $R_k^{2(\text{input)}}$ for each iteration $k$ where ${{\hat{\beta }}_{1\mathrm{k}}}^{\text{(input)}}$ was the univariate standardized regression coefficient for contributions from spatially distributed populations at residential locations. We noted the percent change in the hyperparameter values from the original analysis and the variance around those estimates across the $k$ simulations to determine to which inputs the hyperparameter is most sensitive.

To reflect realistic conditions where septic system locations and sewer travel times may be unknown and contributing to information diffusion losses, we ran an additional sensitivity analysis by not accounting for septic systems in the census block group population count $P_{0j}$ such that

$$P_{0j}^{\prime }=(P^{(\mathrm{C}\mathrm{B}\mathrm{G})})\left(\frac{A_j^{(\text{sewered})}}{A_j^{(\text{total})}}\right)$$ (9)

Additionally, we wanted to understand how this modeling approach performs when SWMM travel times are not available for a municipality, so we replaced travel time with Euclidean distance (i.e., natural processes poorly captured).

$${\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{D90}\right)=\sum _{j=1}^N{P}_{0j}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-2.3D_{ij}}{{\alpha }_{D90}}\right)$$ (10.1)

$$s_i(\mathit{\alpha })=s_i\left({\alpha }_{D90}\right)={\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{D90}\right)/\mathrm{s}\mathrm{t}\mathrm{d}\left({\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{c}}_i\left({\alpha }_{D90}\right)\right)$$ (10.2)

Here, $D_{ij}$ is the Euclidean distance in meters from the centroid of each census block group to the wastewater treatment plant and ${\alpha }_{D90}$ is the distance at which we would expect to see a 90% loss of information from the spatially distributed census block group centroid locations.

3. RESULTS AND DISCUSSION

3.1. Signals from Distributed Input Locations Decay over Travel times.

We discuss here the results of using the crAssphage load. Please see S6 for summary of results and discussion about using concentration versus load. We find that the optimized signal decay hyperparameter values, ${{\alpha }_{90}}^{\mathrm{*}}$, ${{\alpha }_{90,\mathrm{T}}}^{\mathrm{*}}$, or ${{\alpha }_{90,\mathrm{T}\mathrm{M}}}^{\mathrm{*}}$, are less than 1 day (<24 h) for all models using crAssphage load (log10-copies-per-day) as a response (Table 1). The signal decay hyperparameter is estimated to be 10.3 h when using the simple SEDC, representing 43.6, 40.7, 29.2, and 28.4% of the sewered populations at residential locations in Muddy Creek, Little Miami, Taylor Creek, and Mill Creek, respectively (i.e., the SEDC value divided by the total sewershed population; see S10).

Table 1.

Model Comparison between the SEDC with crAssphage Concentration as the Response, SEDC with crAssphage Load as the Response, SEDC Modified by Temperature (SEDC-T) with crAssphage Load as the Response, and SEDC Modified by Temperature and Mobility (SEDC-TM) with crAssphage Load as the Response^a

spatial predictor model k = no. of variables	response	β(residential) (95% CI)	Adj. R2	MSE10-fold (1-MSE CI)	informed hyperparameter values
					${{\alpha }_{90}}^{\mathrm{*},}{{\alpha }_{90,\mathrm{T}}}^{\mathrm{*}}$,or ${{\alpha }_{90,\mathrm{T}\mathrm{M}}}^{\mathrm{*}}$	${{\gamma }_1}^{\mathrm{*}}$	${{\gamma }_2}^{\mathrm{*}}$
SEDC k = 1	crAssphage concentration ${\text{log}}_{10}(y_i)$	−0.242 (−0.282, −0.202)	0.309	0.133 (0.0106, 0.160)	<1	NA	NA
SEDC k = 1	crAssphage load $z_i={\text{log}}_{10}(y_i{q}_i)$	0.370 (0.332, 0.409)	0.529	0.120 (0.115, 0.125)	10.3	NA	NA
SEDC-T k = 2	crAssphage load $z_i={\text{log}}_{10}(y_i{q}_i)$	0.383 (0.346, 0.420)	0.565	0.120 (0.115, 0.125)	9.68	−0.143	NA
SEDC-TM k = 3	crAssphage load $z_i={\text{log}}_{10}(y_i{q}_i)$	0.388 (0.352, 0.424)	0.581	0.121 (0.116, 0.126)	9.61	−0.107	0.106

^aShown are the standardized regression coefficients for the residential signal contributions, β^{(residential)} with 95% confidence intervals (CI), the adjusted Pearson’s correlation efficient using all the data, Adj. R², the 10-fold cross-validation mean square error, MSE_10-fold, and the informed hyperparameter values from the full data set: the optimized signal decay hyperparameter value, ${{\alpha }_{90}}^{\mathrm{*}},{{\alpha }_{90,\mathrm{T}}}^{\mathrm{*}}$, or ${{\alpha }_{90,\mathrm{T}\mathrm{M}}}^{\mathrm{*}}$ the optimized temperature modification hyperparameter value, ${{\gamma }_1}^{\mathrm{*}}$, and the mobility modification hyperparameter value, ${{\gamma }_2}^{\mathrm{*}}$, as described in Section 2.5.

Previous work has characterized heterogeneous population contributions using chemical markers in wastewater,^5,7 but we estimate and depict this for microbial markers for the first time. From our work, we see that WWTP influent samples do not represent a homogeneously pooled sample but rather a sample biased toward nearer populations. Furthermore, we tested the relative importance of estimated contributions from residential locations compared with other sewershed characteristics with a LASSO regression. The contributions remain important and their effect on crAssphage load is greater in magnitude compared to other sewershed characteristics selected with the LASSO (i.e., industrial flow, combined sewer, population mobility variables, precipitation for combined sewer networks, and pH) (see S7).

Using our modeling approach, locations with high spatial information loss rates can be identified, and information could be recuperated by sampling wastewater at localized points on the sewer network in addition to WWTP influents. Furthermore, by comparing the map of spatially distributed populations from Census data (Figure 2a) and the information loss obtained with the SEDC SPM (Figure 2b), it is possible to identify locations where large populations are poorly represented. Sampling points within the sewer networks could then be selected to better characterize the distributed populations of interest.

Figure 2.

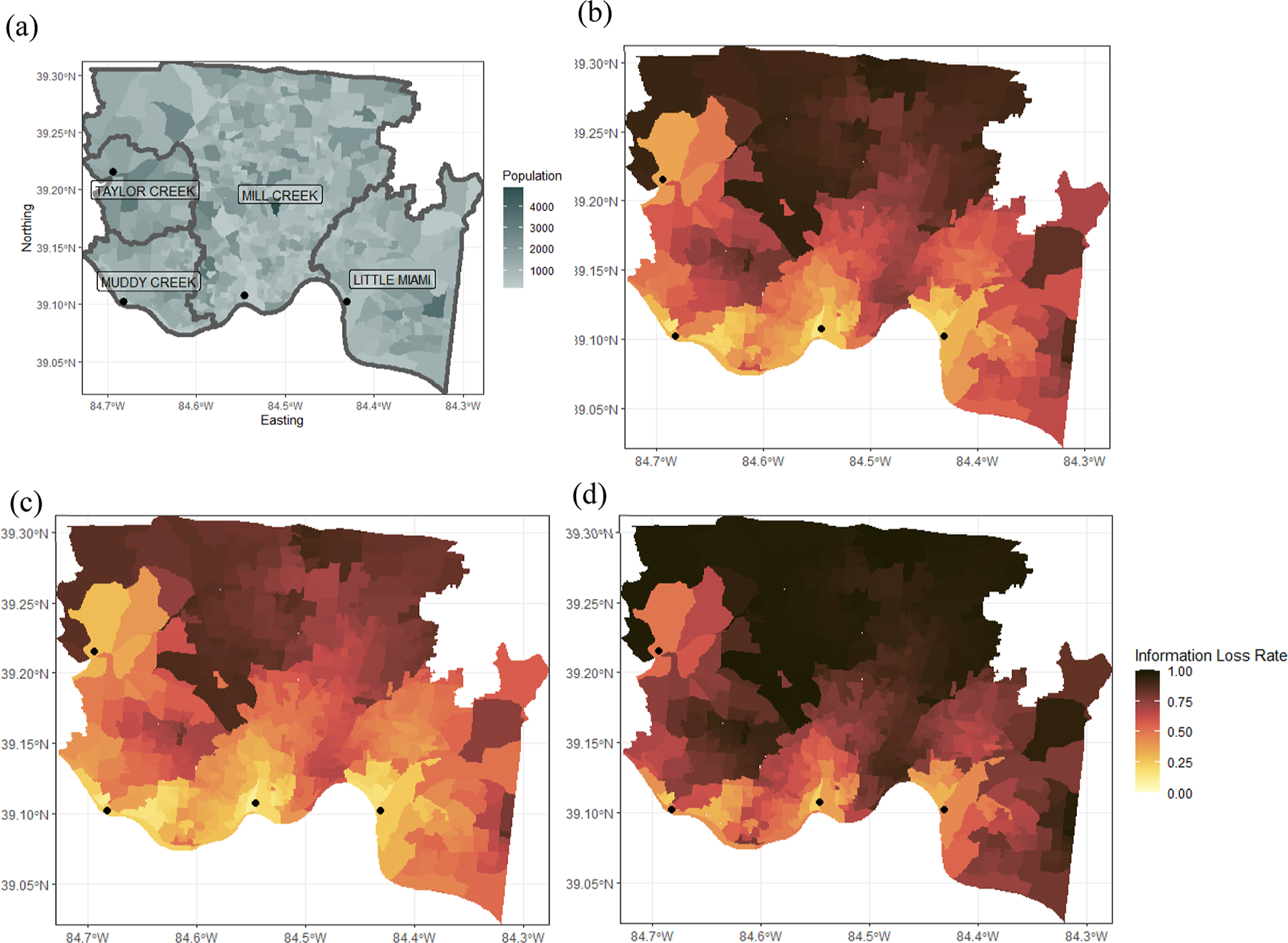
(a) Census block group population and sewershed delineations followed by (b–d) spatial information loss rate from distributed residential sources (represented by census block groups) to the crAssphage load signal measured at the wastewater treatment plant. Hyperparameters were obtained with the (b) base SEDC SPM where ${\alpha }_{90}=10.3$; the (c) “best case” SEDC SPM with temperature and mobility modification (SEDC-TM) showing the spatial information loss rate given the lowest wastewater temperature (12.3 C) and the greatest percent of time spent at home above a baseline (15%); and the (d) “worst case” SEDC-TM SPM showing the spatial information loss rate given the highest wastewater temperature (25.4 C) and the least percent of time spent at home above a baseline (−2%). The WWTP locations are depicted as small black circles.

The advantage of using an SEDC SPM is that it captures attenuation of spatially distributed information from multiple known and unknown processes during transport, not only physical decay, and does not rely on a laboratory $k$. For example, if we modeled information loss as only a function of pre-established temporal decay estimates for crAssphage (T₉₀ between 2.4 and 13.6 days in wastewater-spiked freshwater mesocosms),^29,31,49 we would expect the total sewershed population to be well-represented because all travel times to the studied WWTPs are within 2.4 days (maximum of 14.0 h). We now reject that hypothesis with our finding of a signal decay hyperparameter ${\alpha }_{90}\mathrm{*}=10.3\mathrm{h}$, which expresses a 90% loss over that shorter travel time. Consequently, our signal decay hyperparameter value suggests that decay is likely not the only process contributing to information loss or that crAssphage decays considerably faster (approximately 5–30×) in wastewater itself than when diluted into freshwater. Other transport dynamics (e.g., adsorption, sedimentation, biofilm interactions, inflow, and infiltration^9,12) may also hasten signal reduction and information diffusion losses. These types of information diffusion losses are likely increased for disease marker data, where contributions from cases are further affected by fecal shedding patterns for the disease and case reporting limitations (e.g., at home testing of a disease and asymptomatic cases). Statistical techniques like smoothing wastewater response data or including lag terms and asymptomatic corrections for case data may therefore improve correlations to epidemiologic data.⁵⁰

3.2. The Ability to Capture Signals from Distributed Locations Is Influenced by Wastewater Temperature.

From optimization of hyperparameters from the SEDC-T model, we find that the baseline signal decay hyperparameter, ${\alpha }_{90,T}\mathrm{*}$, is 9.68 h (Table 1). We find a 1 standard deviation increase in wastewater temperature (${\sigma }_{{\mathrm{T}}_i}={3.75}^{\circ }\mathrm{C}$) diminishes the signal decay hyperparameter to 86.7% of its baseline value [i.e., $9.68\mathrm{h}e{\gamma }_1^{\mathrm{*}}=9.68\mathrm{h}{e}^{-0.143}=(9.68\mathrm{h})(0.867)=8.39\mathrm{h}$]. This indicates that signals from farther away residential locations are better captured under colder wastewater conditions. In other words, warmer wastewater is associated with greater spatial information loss, consistent with its impact on physical decay processes.^4,29–31

Previous work has found that temperature modifies the decay of crAssphage based on sewage-spiked mesocosms sampled during average winter (14.5 °C) and summer temperatures (25 °C) in Spain,^35,51 and from sewage in freshwater microcosms representing winter and summer kept at 15 and 25 °C.³¹ Our work extends the knowledge of this relationship to real-world wastewater matrices. The decay modification by wastewater temperature has also been observed for SARS-CoV-2^4,27 and murine hepatitis virus RNA in untreated wastewater.⁴ Previously, a meta-analysis found that correlations between SARS-CoV-2 in wastewater and case numbers were affected by variations in temperature.²⁵ The extent to which this modifying effect on decay is similar between crAssphage and SARS-CoV-2 or other WWS markers of interest would have implications for using crAssphage as a normalization factor; if they are similar, then the adjustment would not need to account for differential temperature impacts. Overall, seasonal or long-term trends (e.g., climate change) should be considered when evaluating WWS data. For example, during the winter, there may be more gastrointestinal illnesses that are known to increase crAssphage shedding.⁴² Precipitation also varies seasonally, impacting flow.

3.3. The Ability to Capture a Signal from Specific Locations Is Influenced by Population Mobility.

From the optimization of the hyperparameters from the SEDC-TM model, we find that the baseline signal decay hyperparameter, ${\alpha }_{90,\mathrm{T}\mathrm{M}}^{\mathrm{*}}$, is 9.61 h (Table 1). Our primary finding from this model is that for a 1 standard deviation increase in the percent of time that people stay at home, we find an 11% increase in the signal decay hyperparameter [i.e., $e{{\gamma }_2}^{\mathrm{*}}=9.61\times \left.{10}^{-0.106}=(9.61)(1.11)=10.7\mathrm{h}\right]$. This increase in ${{\alpha }_{90,\mathrm{T}\mathrm{M}}}^{\mathrm{*}}$ indicates that when people stay home more, population information at spatially distributed residential locations is better captured by wastewater influent data.

Figure 2c depicts the information loss rate given the minimum wastewater temperature and the maximum percent time spent at home (“best-case”), whereas Figure 2d depicts this rate given the maximum wastewater temperature and the minimum percent time spent at home (“worst-case”). The extent of change across these maps highlights the importance of accounting for temporal factors, such as changes in wastewater temperature and population mobility. In general, these maps show that to best associate geocoded residential population data with wastewater data for health reporting and disease surveillance, models are needed that incorporate fate and transport, wastewater temperature, and population mobility data. To our knowledge, only one previous study examines population mobility data in a microbial WWS context, where population mobility was accounted for with cell phone data and a validated biomarker (i.e., 5-HIAA) to provide accurate representation of population.³² Higher levels of 5-HIAA were found on weekdays, when there were more people in the sewershed based on mobile phone data compared to weekends. 5-HIAA-normalized SARS-CoV-2 wastewater data were also reported to better correlate with COVID-19 cases. Our work supports this conclusion in showing that wastewater responses are impacted by population mobility and newly shows that like 5-HIAA, crAssphage loads measured in wastewater can represent population and capture variations in population mobility.

3.4. The Signal Decay Hyperparameter from SEDC SPMs can Be Estimated Using Alternative Databases, but with Loss of Information.

Some study areas may not have databases corresponding to septic system locations or calibrated SWMM models that can estimate travel times accurately. We therefore conducted a sensitivity analysis to evaluate the impact of errors in key inputs for the SEDC SPM (i.e., spatially distributed residential population information, $P_{0j}$, estimated travel times, $t_{ij}$, or the ${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ transformed wastewater response, $y_i$) on model outputs (i.e., optimized ${{\alpha }_{90}}^{\mathrm{*}}$, standardized regression coefficient estimation ${\hat{\beta }}_1$, and model fit $R^2$).

Table 2 shows that introducing a normal random error within 10% of the standard deviation to spatially distributed populations had negligible effects on model outputs (i.e., ${{\alpha }_{90}}^{\mathrm{*}},{\beta }_1$, and $R^2$). These estimates were all within 1 standard deviation of the mean output values from this sensitivity analysis, indicating that the modeling approach is not very sensitive to this type of noise (i.e., 10% of ${P_{0j}}^{\prime }s$ standard deviation). However, in supplemental analyses where populations on septic systems were not removed from the census block group population estimates (see eq 9 and S5 for details), we observed a slight increase in spatial information loss (i.e., ${{\alpha }_{90}}^{\mathrm{*}}=10.0\mathrm{h}$ instead of 10.3), suggesting that by removing populations associated with septic systems, we create a more accurate representation of spatially distributed populations at residential locations that contribute to the sewer network. However, this slight decrease is within 1 standard deviation of the mean of ${{\alpha }_{90}}^{\mathrm{*}}$ across k iterations of noise ($\mathrm{E}\left[{{\alpha }_{90k}}^{\mathrm{*}}\right]$). We recommend that, if databases of septic systems are available, populations on septic systems should be removed (eqs 3.1 and 3.2), acknowledging the small impact.

Table 2.

Sensitivity Analysis Results Showing the Mean and Variance around Optimized Signal Decay Hyperparameter ${{\mathit{\alpha }}_{90\mathit{k}}}^{\mathrm{*}}$, Estimated Standardized Regression Coefficient ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_{1\mathbf{k}}$, and Model Fit Pearson’s ${{\mathit{R}}_{\mathit{k}}}^2$ for k = 1–100 Random Draws of Noise ${\mathit{ϵ}}_{\mathit{j}\mathit{k}}$ Applied to Spatially Distributed Residential Population Information ${\mathit{P}}_{0\mathit{j}}$ and Estimated Travel Times ${\mathit{t}}_{\mathit{i}\mathit{j}}$, or ${\mathit{\epsilon }}_{\mathit{i}\mathit{k}}$ Applied to the Observed crAssphage Load Response ${\mathit{z}}_{\mathit{i}}$

	noise added to travel time values ${\hat{\sigma }}_{t_{ij}}=3.02$	noise added to population values ${\hat{\sigma }}_{P_{0j}}=540$	noise added to crAssphage load ${\hat{\sigma }}_{Z_{0j}}=0.510$
${\mathit{\alpha }}_{90}\mathrm{*}$ mean across k iterations	8.96 h	10.3 h	10.3 h
${\alpha }_{90}\mathrm{*}$ variance across k iterations	8.86	0.0289	0.0581
${\hat{\beta }}_1$ mean across k iterations	0.363	0.370	0.371
${\hat{\beta }}_1$ variance across k iterations	6.14 × 10−4	2.05 × 10−7	6.16 × 10−6
R2 mean across k iterations	0.510	0.528	0.525
R2 variance across k iterations	3.98 × 10−3	1.67 × 10−6	2.75 × 10−5

Contrastingly, normal random error within 10% of the standard deviation added to travel times decreased the hyperparameter value, ${{\alpha }_{90}}^{\mathrm{*}}$, by 13% (from 10.3 to 8.96 h; Table 2). Additionally, this estimate was associated with a large variance (8.86 h). This indicates the model sensitivity to travel times. An additional analysis using Euclidean distance (see eqs 10.1, 10.2 and S5) as a proxy for travel times yielded an ${{\alpha }_{90}}^{\mathrm{*}}$ of 100 m. Based on typical conditions for these sewersheds, we estimate 100 m to correspond with a travel time of less than 1 h (see S11), much lower than the ${{\alpha }_{90}}^{\mathrm{*}}$ obtained in our main analysis (10.3 h) and outside of the 1 standard deviation boundary. From this, we conclude that Euclidian distance is a poor proxy for sewer travel time, highlighting the need for dynamic hydraulic–hydrologic sewer models (e.g., SWMM) and tracer experiments to accurately estimate travel times. While previous work has found that travel times had little effect on SARS-CoV-2 concentrations entering a WWTP,²⁷ these travel times were approximated with pipe distance and flow velocity and did not benefit from tracer experiments conducted with a calibrated hydraulic model. Our work indicates that it is possible to obtain a wide range of ${{\alpha }_{90}}^{\mathrm{*}}$ when there is error on the travel times, demonstrating an observable effect of travel time estimates on WWS responses.

Lastly, we considered variations in laboratory methods that may introduce error into quantified wastewater responses⁵² and the effect on modeled outputs. We found that normal random error within 10% of the standard deviation on crAssphage load response gave approximately the same SPM outputs from our original analysis (within 1 standard deviation; Table 2). This suggests that a minor measurement uncertainty within a single laboratory using the same method may be acceptable. Our analysis did not explore larger differences across laboratories using different methods,⁵³ highlighting a potential area for future investigation.

3.5. Implications, Limitations, and Future Research.

Here, we used the microbial FIT framework to depict, for the first time, the loss of spatially distributed information about fecal contributions to the sewer system over travel times using crAssphage genetic markers. Previous WWS research has used crAssphage and other markers (e.g., PMMoV) to normalize SARS-CoV-2 concentrations to account for variability in wastewater responses.^{21–24,54,55} However, our work reveals that information degradation and sewershed characteristics influence crAssphage load, impacting the proportional pathogen prevalence modeled using fecal marker normalization methods.^2,56

We note some advantages of our semimechanistic, semi-statistical approach over fully mechanistic models. A fully mechanistic model would require loadings at sources (i.e., individual household level), which may be difficult to obtain due to low or biased case reporting, and case reporting rates are one major reason that wastewater surveillance is so attractive as a tool to understand changes in disease prevalence. Additionally, modeling fecal shedding at the individual household level results in geoprivacy issues because fecal shedding at the individual level may be considered health data.⁵⁷ While work may be done to better characterize fecal shedding of different markers at the individual level, our modeling approach allows for that shedding information to be aggregated to larger population groups, so that identities of individuals or vulnerable populations are protected.

There is room to refine sampling and microbial response measurements to reduce measurement error, address the locational accuracy of spatially distributed populations, and improve characterization of other confounding sources in the system (e.g., flows from precipitation and industry) to reduce information diffusion losses during WWS. Above all, this study emphasizes that calibrated hydraulic sewer models to characterize travel times and dilution of flows are particularly beneficial when assessing these sewershed transport processes. Furthermore, understanding the impacts of the temperature and population mobility on microbial loads in wastewater may benefit WWS.

Results across the different SPMs (Table 1) demonstrate the modification of signal decay by the temperature and population mobility. While the predictive value shows only incremental benefits, the effects on signal decay have major implications to WWS. For example, if a large population cluster (e.g., a university campus) has an illness (e.g., norovirus) and is located at the end of the spatial extent that the WWS data can capture (i.e., in our study about 10.3 h of travel time away), the WWS data would poorly reflect that cluster, especially during periods of warmer wastewater temperature or when people are less often at home [see Figure 2c,d]. We would expect that as cases go from being very mixed in their spatial distribution in the population to very clustered, the more important modification from temperature, population mobility, or other potential factors become.

A previous systematic review of correlations between WWS SARS-CoV-2 data and COVID-19 cases demonstrated that variability in ambient air temperature and sewershed catchment size negatively impacts correlations between WWS data and reported cases.²⁵ Our work provides a generalizable modeling approach to address these processes without requiring knowledge of mechanistic phenomena. While our study was limited to four adjacent sewersheds and the applicability of these information loss patterns to other locations is unknown, the model itself can be generalized to other locations and WWS data. This approach can be applied to any measurable microbial response that is emerging or not well-characterized (i.e., unknown parameters for in-sewer fate and transport). We also provide evidence for the influence of population mobility on correlations and positive implications to standardizing WWS responses by fecal indicators (e.g., crAssphage) if transport dynamics are expected to be similar between a WWS response and the fecal indicator used for standardization. Our findings and modeling framework can be used to design representative WWS programs, choose sampling sites that accurately capture population contributions, and help public health agencies better interpret WWS data on SARS-CoV-2 and other targets of emerging interest.

ABBREVIATIONS

ddPCR

droplet digital polymerase chain reaction

FIT

the microbial Find, Inform, and Test framework

LASSO

least absolute shrinkage and selection operator

MGD

million gallons per day

MM

mobility as modifiers

MX

mobility as sewershed characteristics

SEDC

sum of exponentially decaying contributions

SPM

spatial predictor model

SWMM

Storm Water Management Model

WWS

wastewater surveillance

WWTP

wastewater treatment plant