Abstract
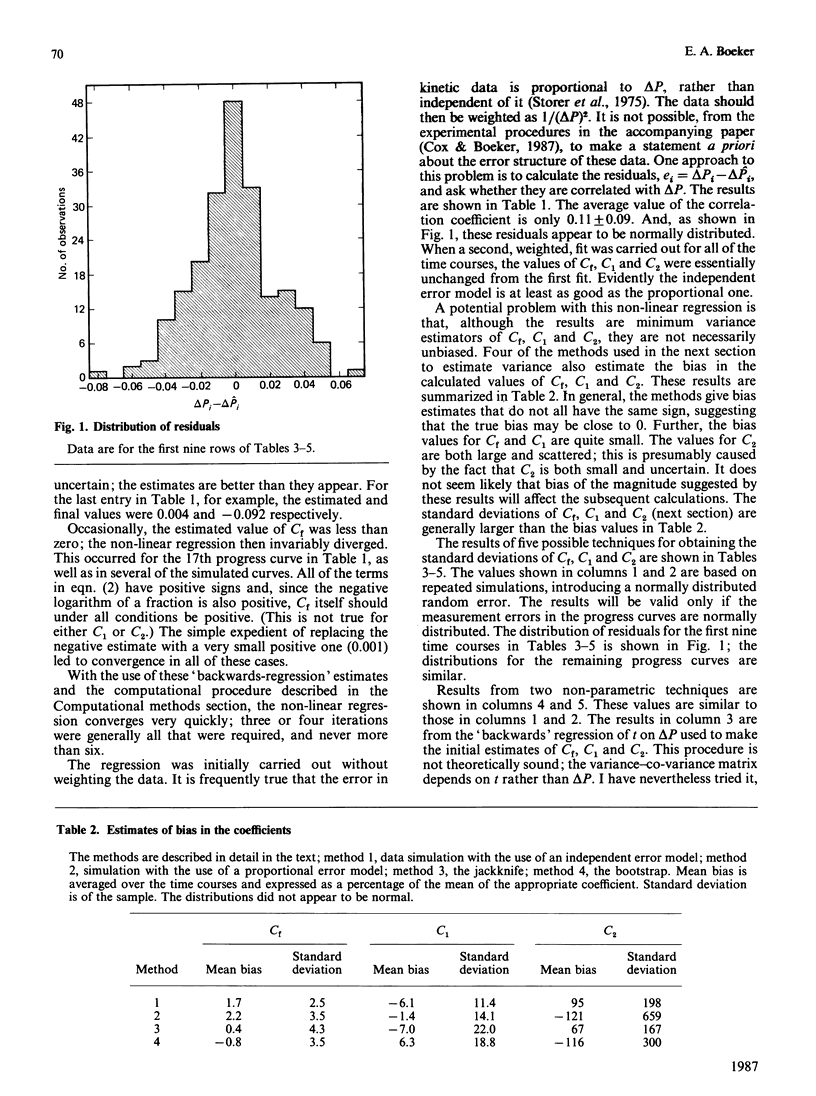
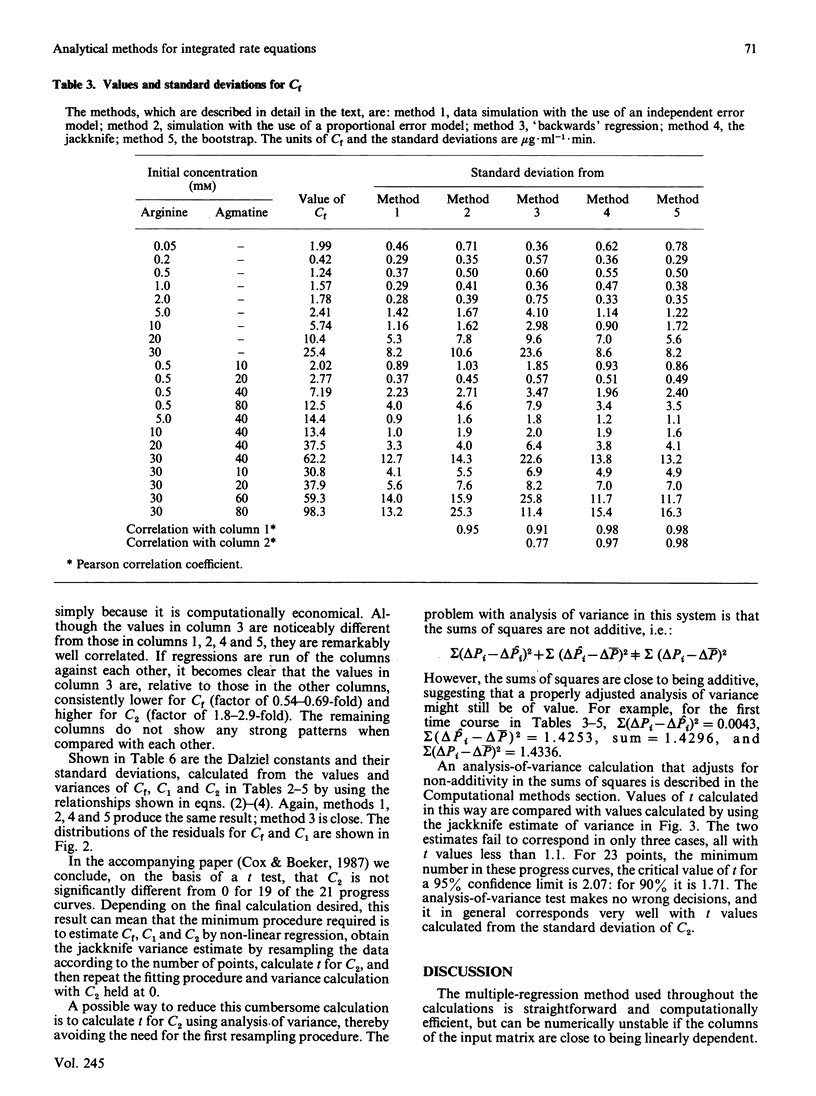
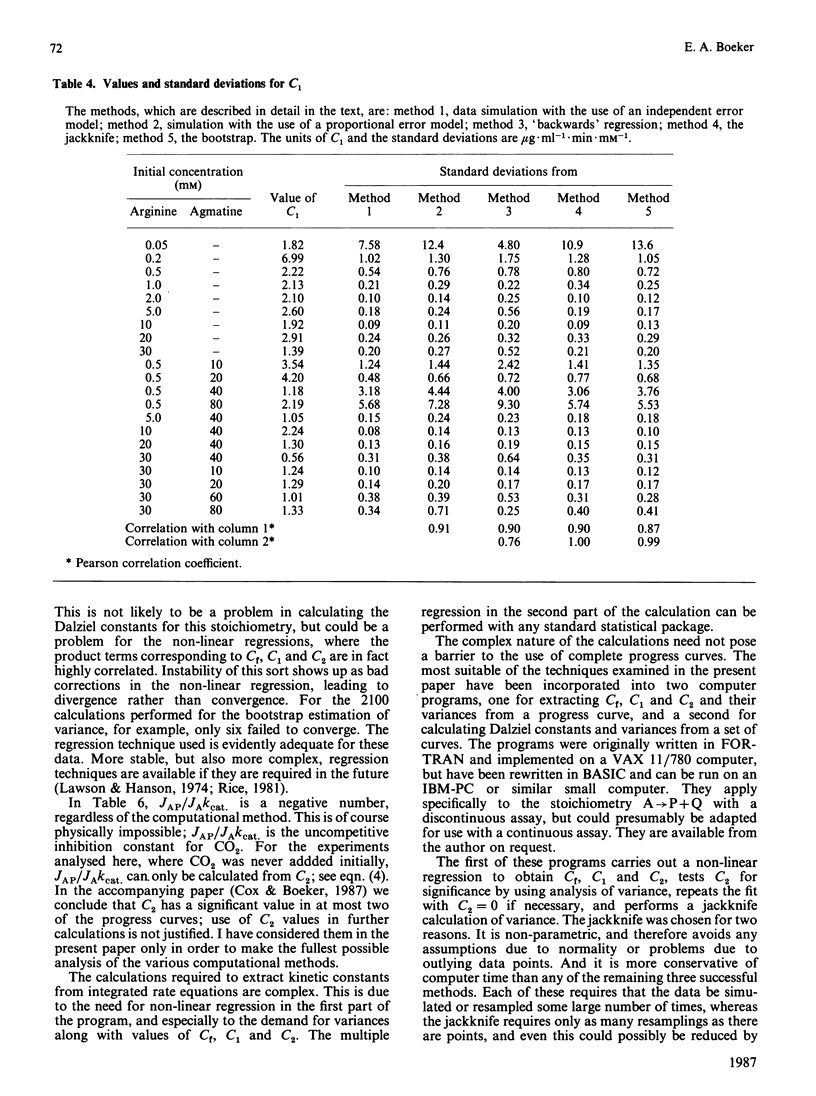
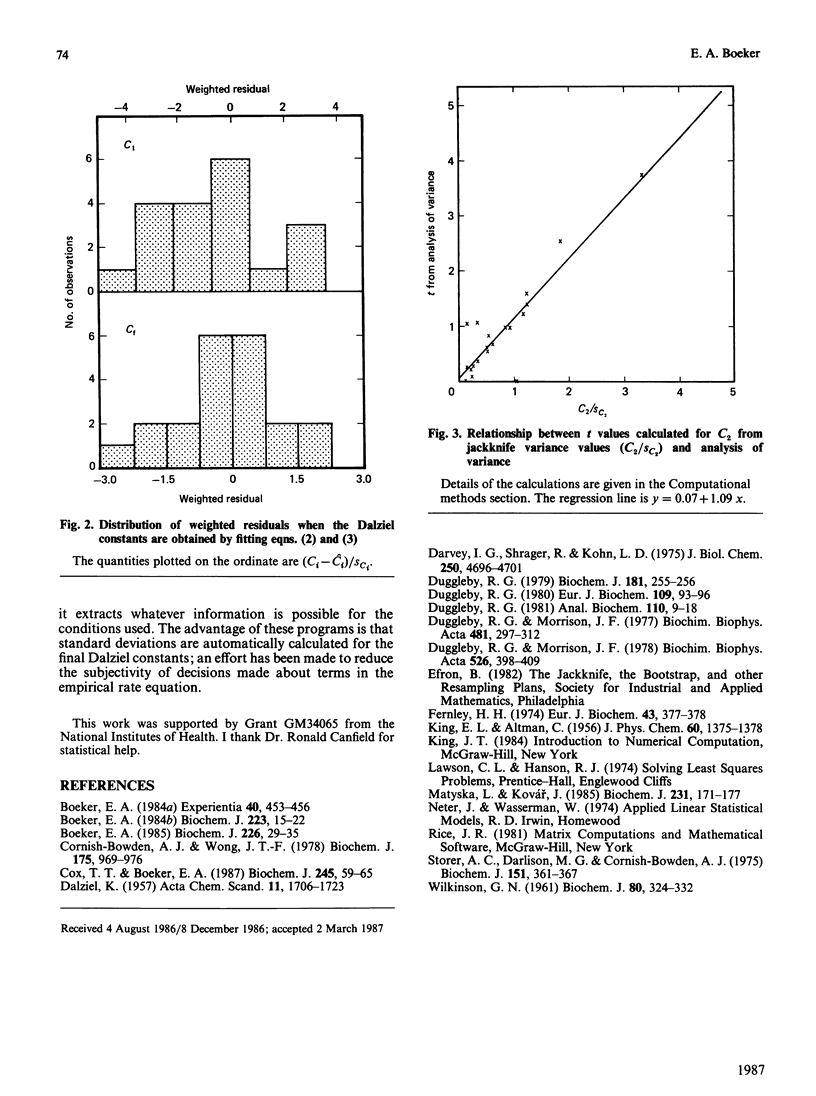
The integrated rate equation for reactions with stoichiometry A----P + Q is: e0t = -Cf . ln(1-delta P/A0) + C1 delta P + 1/2C2(delta P)2 where the coefficients C are linear or quadratic functions of the kinetic constants and the initial substrate and product concentrations. I have used the 21 progress curves described in the accompanying paper [Cox & Boeker (1987) Biochem. J. 245, 59-65] to develop computer-based analytical and statistical techniques for extracting kinetic constants by fitting this equation. The coefficients C were calculated by an unweighted non-linear regression: first approximations were obtained from a multiple regression of t on delta P and were refined by the Gauss-Newton method. The procedure converged in six iterations or less. The bias in the coefficients C was estimated by four methods and did not appear to be significant. The residuals in the progress curves appear to be normally distributed and do not correlate with the amount of product produced. Variances for Cf, C1 and C2 were estimated by four resampling procedures, which gave essentially identical results, and by matrix inversion, which came close to the others. The reliability of C2 can also be estimated by using an analysis-of-variance method that does not require resampling. The final kinetic constants were calculated by standard multiple regression, weighting each coefficient according to its variance. The weighted residuals from this procedure were normally distributed.
Full text
PDF



Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Boeker E. A. Integrated rate equations for enzyme-catalysed first-order and second-order reactions. Biochem J. 1984 Oct 1;223(1):15–22. doi: 10.1042/bj2230015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boeker E. A. Integrated rate equations for irreversible enzyme-catalysed first-order and second-order reactions. Biochem J. 1985 Feb 15;226(1):29–35. doi: 10.1042/bj2260029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornish-Bowden A., Wong J. T. Evaluation of rate constants for enzyme-catalysed reactions by the jackknife technique. Application to liver alcohol dehydrogenase. Biochem J. 1978 Dec 1;175(3):969–976. doi: 10.1042/bj1750969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox T. T., Boeker E. A. Analysis of enzyme kinetics by using integrated rate equations. Arginine decarboxylase. Biochem J. 1987 Jul 1;245(1):59–65. doi: 10.1042/bj2450059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darvey I. G., Shrager R., Kohn L. D. Integrated steady state rate equations and the determination of individual rate constants. J Biol Chem. 1975 Jun 25;250(12):4696–4701. [PubMed] [Google Scholar]
- Duggleby R. G. A comment on the 'jack-knife' technique for analysing enzyme-kinetic data. Biochem J. 1979 Jul 1;181(1):255–256. doi: 10.1042/bj1810255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duggleby R. G. A nonlinear regression program for small computers. Anal Biochem. 1981 Jan 1;110(1):9–18. doi: 10.1016/0003-2697(81)90104-4. [DOI] [PubMed] [Google Scholar]
- Duggleby R. G. Estimation of the reliability of parameters obtained by non-linear regression. Eur J Biochem. 1980 Aug;109(1):93–96. doi: 10.1111/j.1432-1033.1980.tb04771.x. [DOI] [PubMed] [Google Scholar]
- Duggleby R. G., Morrison J. F. Progress curve analysis in enzyme kinetics: model discrimination and parameter estimation. Biochim Biophys Acta. 1978 Oct 12;526(2):398–409. doi: 10.1016/0005-2744(78)90131-6. [DOI] [PubMed] [Google Scholar]
- Duggleby R. G., Morrison J. F. The analysis of progress curves for enzyme-catalysed reactions by non-linear regression. Biochim Biophys Acta. 1977 Apr 12;481(2):297–312. doi: 10.1016/0005-2744(77)90264-9. [DOI] [PubMed] [Google Scholar]
- Fernley H. N. Statistical estimations in enzyme kinetics. The integrated Michaelis equation. Eur J Biochem. 1974 Apr 1;43(2):377–378. doi: 10.1111/j.1432-1033.1974.tb03423.x. [DOI] [PubMed] [Google Scholar]
- Matyska L., Kovár J. Comparison of several non-linear-regression methods for fitting the Michaelis-Menten equation. Biochem J. 1985 Oct 1;231(1):171–177. doi: 10.1042/bj2310171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storer A. C., Darlison M. G., Cornish-Bowden A. The nature of experimental error in enzyme kinetic measurments. Biochem J. 1975 Nov;151(2):361–367. doi: 10.1042/bj1510361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WILKINSON G. N. Statistical estimations in enzyme kinetics. Biochem J. 1961 Aug;80:324–332. doi: 10.1042/bj0800324. [DOI] [PMC free article] [PubMed] [Google Scholar]


