Abstract
We present the use of stimulated Brillouin scattering spectroscopy to achieve rapid measurements of cell biomechanics in a flow cytometer setup. Specifically, our stimulated Brillouin scattering flow cytometry can acquire at a rate of 200 Hz, with a spectral acquisition time of 5 ms, which marks a 10x improvement compared to previous demonstrations of spontaneous Brillouin scattering flow cytometry. We experimentally validate our stimulated Brillouin scattering flow cytometer by measuring cell populations of normal breast epithelial cells and metastatic breast epithelial cancer cells.
1. Introduction
Cells are complex machines that sense and respond to their environmental cues, thus making their biomechanical behavior an important process to study. The mechanical interactions they experience can alter cellular functions, i.e. migration tendencies [1,2], cell proliferation [3], and gene expression [4], as well as affecting morphogenesis [5] and metastasis [6]. In recent years, biomechanics has been shown to be a critical player with respect to the progression of cancer [7–9]. Consequently, there have been numerous methods developed to extract biomechanical markers, specifically elastic modulus, on the cellular level: atomic force microscopy (AFM) [10], micropipette aspiration [11], microrheology [12], and deformable microbeads [13] to name a few. While these methods have uncovered a plethora of information and have gained great interest in the field, all these instruments either require contact, are significantly invasive, or only gather global mechanical information from the samples.
This evidence unveils an interesting relationship: that there is a clear tradeoff between how much mechanical information can be ascertained using a given modality and its respective measurement throughput [14]. To give a specific example, cell deformability-based methods, such as using optical stretcher [15] and adding acoustic pressure [16] which only access whole cell mechanical signatures, have begun to be integrated with flow cytometry [17–19] thus achieving measurements of >1000 cells per experiment, but critically lack the resolution to illustrate subcellular structures like the cell nucleus. Ideally, a system would exist with subcellular resolutions to analyze vast biomechanical information while also having high measurement throughput. To address this gap in the field, spontaneous Brillouin scattering was proposed in combination with a flow cytometry scheme [20,21], but lacked the spectral acquisition speeds to truly be considered ‘high throughput’ as it could only measure ∼200 cells per hour. Another time-domain Brillouin microscopy-based cytometry applied impulsive stimulated Brillouin scattering to microfluidic channel [22], with single-shot pump pulses, CW probe, and time-domain detection, but only application in liquid samples was shown because of low spatial resolution, high pump power and long exposure time (∼50 ms). As such, there is a need to speed up spectral acquisitions to make Brillouin microscopy more suitable for high throughput measurements of large-scale mechanical phenotyping and to fill the gap in the field of biomechanical analysis, breaking free of the tradeoff between measurement throughput and mechanical information content from which current instruments suffer.
Brillouin microscopy is unique among other mechanical characterizations in its all optical (non-contact and label-free) ability to use the Brillouin-extracted storage modulus ( ) as a contrast mechanism for probing cell mechanics [23–25]. While, as previously mentioned, spontaneous Brillouin scattering has been demonstrated in a flow cytometry scheme, the reliance of this method on the inefficient scattering method ultimately limited throughput on the basis of the sampling rate of the spectrometer (∼50 ms) in order to reach ∼10 MHz precision for highly-sensitive measurements. While lower measurement times have been achieved (∼20 ms) in conjunction with confocal microscopy [26,27], spontaneous Brillouin scattering has essentially reached its fundamental limit in biological samples. As such, there is need to speed up spectral acquisitions to make Brillouin microscopy more suitable for higher throughput measurements of large-scale mechanical phenotyping with speeds more in line with the prior art [19,28].
The use of stimulated Brillouin scattering (SBS) in microscopy applications began with continuous wave (CW) lasers for both pump and probe counterpropagating beams, which has been demonstrated in liquids (∼2-5 ms) [29–31] and C. elegans (∼20 ms) [32] with modest acquisition times and similar signal-to-noise ratios compared to spontaneous Brillouin methods. For SBS, the frequency difference between the external light beams is known a priori and is tuned to efficiently drive the coupling between acoustical and optical waves. As the frequency difference between the pump ( ) and probe ( ) is tuned near the phonon frequency, the scattered light acquires a Lorentzian distribution of frequency shift centered at with a linewidth of where the linewidth of the gain spectrum is related to the lifetime of the acoustic wave ( ). Experimentally, we can ascertain the SBS signal from the gain observed in the transmitted probe beam.
Since Brillouin light scattering is inherently a non-contact, non-perturbative approach, it is particularly suitable for measurements where cells cannot be easily accessed such as within microfluidic channels. Furthermore, with the nonlinear interaction utilized in SBS, the process has a much stronger Brillouin signal available; therefore, resulting in faster possible spectral acquisition. This speed-up can be leveraged specifically in the flow cytometry application where acquisition time is directly correlated with overall throughput of the system. Moreover, the spectral resolution of SBS microscopy is higher than that of spontaneous Brillouin microscopy since the system is not based on spectrally dispersive elements (∼500 MHz resolution) but rather on laser interactions (∼100kHz resolution). In this manner, we aim to take advantage of the ability to, at high throughput, probe the mechanical signatures of two cell populations: a genetically stable, nontumorigenic epithelial breast cell line (MCF10A), and metastatic breast epithelial cancer cells (MDA-MB-231), an invasive breast cancer cell line. It has been shown, using AFM, that metastatic cells are generally softer than normal, healthy cells [33]. This has been confirmed with other techniques that provide mechanotyping but are limited in that they either require direct contact with the cells [34] or perturb the cell [35] in order to gain the mechanical information and must grow the cells on flat substrates, that are typically much stiffer than physiological tissue stiffness. In this work, we will demonstrate the ability of a state-of-the-art CW SBS spectrometer to directly measure the cell signatures of these two cell lines in a flow cytometry system with high throughput. We found a higher Brillouin shift of the nontumorigenic MCF10A cell line as compared to the metastatic MDA-MB-231.
2. Theory
Unlike its spontaneous counterpart, stimulated Brillouin scattering leverages a nonlinear resonant effect between optical light waves and acoustic phonons. A stimulated Brillouin scattering event is the result of fluctuations coming from the presence of an external light field and manifests as a nonlinear interaction between the pump and Stokes fields via a moving acoustic wave. The nonlinear exponential growth achieved in the Stokes wave is what enables SBS to have much higher efficiency than spontaneous Brillouin. Two counterpropagating fields, pump and probe, beat together and generate a moving acoustic wave through electrostriction. The material undergoes changes in optical properties, namely refractive index, that cause scattering of the pump light. It can be understood as creating a moving Bragg grating in the medium at the acoustic velocity ( ). The frequency of the scattered light is subsequently downshifted due to the Doppler shift of the traveling acoustic phonon. By design, the resultant frequency matches that of the probe beam and will combine to generate more acoustic phonons which in turn generate more scattering and so on. For our purposes, operating in an SBS amplifier configuration, the frequency difference between the external light fields is known a priori and is tuned to efficiently drive the coupling between acoustic and optical waves [36].
| (1) |
As the frequency difference between the pump ( ) and probe ( ) is tuned near the phonon frequency, the scattered light acquires a Lorentzian distribution of frequency shift centered at with a linewidth of . Where these quantities can be described as the following:
| (2) |
| (3) |
where n is the refractive index, is the speed of sound, c is the speed of light, is the photon frequency, is the scattering angle, and is the damping parameter. The linewidth of the gain spectrum is inversely proportional to the lifetime of the acoustic wave ( ). Since the measured Brillouin frequency shift is related to the speed of sound in the material, Brillouin spectroscopy probes the local longitudinal modulus of the material [37]. From Eq. (2), the Brillouin shift is proportional to the longitudinal modulus by: , where is the density and is the real part of the complex longitudinal modulus which is expressed as . In solid materials, the longitudinal modulus is the uniaxial stress-strain ratio at frequency , thus . The Brillouin linewidth is related to the imaginary part of the complex longitudinal modulus . As such, Brillouin measurements extract the mechanical information of the material and an empirical relationship between the real part of the complex longitudinal modulus ( ) and the more widely measured Young’s modulus ( ) has been shown in biological samples previously [23,38,39]. Experimentally, we can ascertain the SBS signal from the gain observed in the transmitted probe beam.
| (4a) |
| (4b) |
| (4c) |
The gain in the transmitted probe beam, as shown in Eq. (4a), is related to the intensity of the pump ( ), the interaction length (L), and the Lorentzian shaped gain factor. The peak value of the Brillouin gain factor occurs at and is also known as the line-center gain factor ( ) which depends on a number of material properties such as the electrostrictive constant ( ) and the mass density ( ).
3. Methods
3.1. Experimental configuration and acquisition
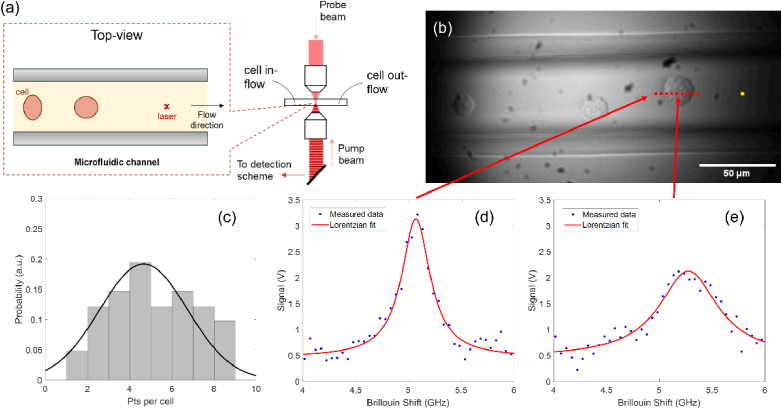
As an example, to illustrate how Brillouin microscopy can be used to investigate the mechanical properties of suspended cells in flow, we built a high-speed Brillouin flow cytometer, see Fig. 1(a), based on our state-of-the-art CW SBS microscope [31]. In this case, a 1 MHz amplitude modulated CW pump laser ( ) illuminates the sample from below while a counterpropagating CW probe ( ) is focused from above. Using the known frequency difference between the pump and probe, we can extract the peak position through Lorentzian least-square fitting of the measured spectra. The acquisition time of each measured spectra is 5 ms. Figure 1(b) is a widefield image of our flow cytometry measurements in a 50μm × 50μm straight polymethyl methacrylate (PMMA) microfluidic channel (microfluidic ChipShop, GmbH). A syringe pump is connected to the channel and controls the flow rate of the cells suspended in a 10% OptiPrep medium. We experimentally determined that this concentration of density gradient medium resulted in the best conditions for flow with albeit moderate clumping of cells in flow. As the cells flow through the channel, we take continuous Brillouin spectra measurements. Both the pump and probe are focused through a 20x objective lens with an NA of 0.45 (Olympus, LUCPlanFLN). We co-located our widefield camera to focus inside the microfluidic channel for a better alignment with the SBS spectrometer. When a cell passes through the interaction region of the pump and probe beams, we collect the Brillouin signal of the cell. Figure 1(c) shows the distribution of the number of points collected per cell where the cell diameter is roughly 20μm. On average, we obtain ∼4-5 points per cell which is dependent on a number of factors namely: laser power, cells size, the position of the cell in the channel, and the relative speed of the cell. An important tradeoff between operating parameters arises because low flow rates and high laser power can provide more points per cell and higher precision but induce the risk of optical trapping. As a result, we experimentally determined what flow rate and input laser power would avoid optical trapping and provide enough points per cell at high precision. It should be noted that using a sheath flow configuration would result in less spread in the distribution of points per cell as a larger number of cells would flow through the center of the channel and consequently the focus of the counterpropagating laser beams. However, a previous demonstration of spontaneous Brillouin flow cytometry validated that obtaining ∼4-5 points per cell was sufficient to recapitulate the cell population in flow compared with 2D Brillouin images [21]. In Figs. 1(d) and 1(e), an experimental example of the acquired water and cell spectra are shown respectively. The frequency shift is determined via Lorentzian least-square fitting of the data.
Fig. 1.
(a) Simplified schematic of the experimental setup used in this work. The inset sketch shows a magnified top-view of the microfluidic channel. (b) Widefield image of cells flowing through the microfluidic channel. Yellow dot represents the laser interaction region with red dots representing example sampling points. (c) Distribution of the number of sampled points per cell over a typical experiment. Experimentally attained Brillouin spectra of (d) medium and (e) the cell at experimental conditions.
3.2. Experimental setup
Our CW SBS spectrometer (see Supplement 1 (1,003.7KB, pdf) ) uses two CW single-frequency, tunable lasers at 780 nm with low-noise (∼100kHz linewidth) that feed the probe (Toptica DL pro) and pump (Toptica TA pro) arms. Along the pump path, the frequency is locked to an 85Rb absorption in rubidium atom D2 line using a vapor-based locking module paired with two Bragg gratings (Optigrate BP-780) that reject (∼15 dB) extraneous noise. Then the pump is intensity modulated using an acousto-optic modulator (AOM, AOMO 3080-125, Crystal Technologies) at 1 MHz. The AOM is driven by a function generator that also provides the lock-in amplifier (LIA, Zurich Instruments UHF) with a reference signal used for demodulation of the detected signal. Meanwhile, on the probe path, the beam is constantly being scanned around the acoustic wave resonance by sweeping the piezo voltage of the laser and is ultimately the transmitted beam that is detected by the amplified photodetector (Thorlabs PDA36A2). Once detected, the signal is split with a bias tee (MiniCircuits ZFBT-4R2GW+) into DC and AC signals. The DC is used to monitor the baseline probe signal level whereas the AC is sent to the LIA, who is referenced by the pump modulation frequency, to extract the amplified Brillouin signal from the high probe background level. Background modulated pump stray light is reduced by using the combination of a spatial filter and a hot 85Rb vapor cell (Precision Glassblowing) before the photodetector. The beam frequency between the pump and probe beams is monitored by a signal analyzer (Keysight N9000B) which provides the frequency axis component of the extracted SBS spectra. A fast data acquisition card (DAQ) is used to synchronize the frequency sweeping signal of probe and detected signals from LIA and send data to a Labview program. Brillouin spectra are then fitted with a Lorentzian function using a home-built MATLAB script.
4. Flow cytometer characterization
4.1. Stimulated Brillouin scattering system performance
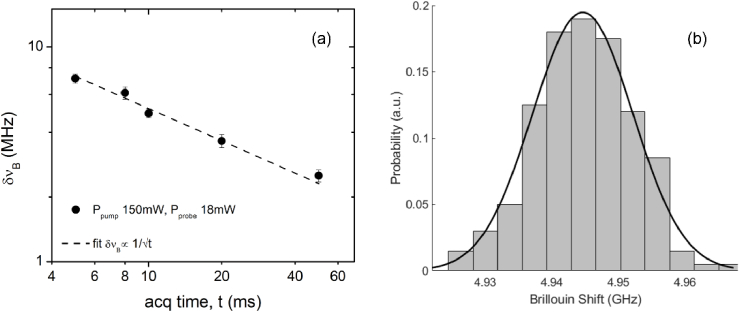
Figures 2(a) and 2(b) show the shot noise limited operation of our system down to 5 ms acquisition time taken at experimental conditions of 150 mW of pump average power and 18 mW of probe average power. Regarding potential cell damage, it has been shown that keeping the total (pump and probe) average power below ∼200 mW and the peak power below ∼2W avoids both thermal and ablation damage in biological samples [26,32]. Our experimental condition of 168 mW total average power is below that and would avoid cell damage. To acquire the Brillouin spectra, the probe frequency, tuned by sweeping the piezo voltage of the laser, is scanned (at 400 GHz/s) over a 2 GHz range (from ∼4 GHz to ∼6 GHz) for experiments of water and cells. For proper Nyquist sampling, the read rate of the DAQ was set to be greater than twice the bandwidth of the lock-in amplifier. For the data shown below, 100 samples of water spectra were acquired in a 50μm × 50μm straight microfluidic channel, and each spectrum was fit with a Lorentzian to estimate the Brillouin shift and linewidth. The frequency precision ( ) is then defined as the standard deviation of the Brillouin shift estimates over the 100 spectra acquired. As expected, our frequency precision measurements follow a Gaussian distribution as seen in Fig. 2(b). We achieve ∼7.5 MHz precision at our experimental conditions which is known to give high-quality Brillouin measurements for cells. At our shortest exposure condition, 5 ms, we are capable of ∼7.5 MHz precision meaning we could theoretically run shorter exposure while still maintaining the 10 MHz precision limit; however, our system is technically limited by the scanning mechanisms of the probe laser, i.e. the piezo inside the probe laser module. To reach the ultimate scanning speed, an external scanning module would have to be used; either an acousto-optic modulator (AOM) or an electro-optic modulator (EOM).
Fig. 2.
Experimental data of water to demonstrate system performance. (a) Shift precision ( ) for 100 spectra of water in the 50μm × 50μm straight microfluidic channel with typical measurement conditions while varying acquisition time. Pump and probe average powers were held constant at 150 mW and 18 mW respectively. Dashed line represents linear fit of the data. Error bars are the standard deviation over the 100 acquisitions. (b) Distribution of the 100 Brillouin shifts fit with a Gaussian.
4.2. Throughput capability
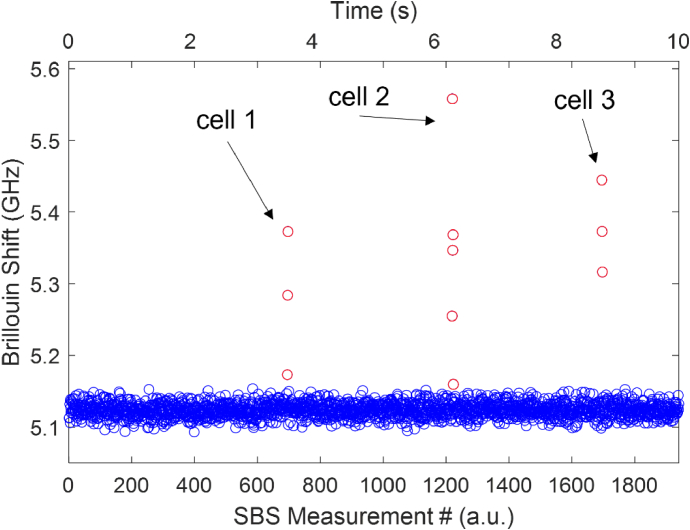
To estimate our SBS flow cytometer speed capabilities we consider a representative measurement segment (∼10s in length) as shown in Fig. 3. This measurement segment is one of many taken over the course of a measurement trial and contains the Lorentzian-fit Brillouin shifts recorded in a small time window as cells flow through the Brillouin interaction region in the microfluidic channel. As our home-built LabView program is continuously acquiring the Brillouin signal, the measurement segments collect signatures from both the medium and cells which are later analyzed by our post-processing procedure. Figure 3 demonstrates that, at our experimental conditions of 5 ms spectral time with the measurement segment window of ∼10s, we are capable of collecting the information of the 3 unique cells. Between 0-2 s in the window there are no cells passing through the interaction region therefore we can extrapolate from experimental data that our SBS flow cytometer throughput is 3 cells per 8s or 0.375 cells per second.
Fig. 3.
Demonstration of individual measurement segment. Segment of continuously acquired Brillouin shift data as 3 cells flow across the Brillouin interaction region. Total time of measurement segment is ∼10s. Circles represent individual 5 ms spectral measurements where blue circles are measurements of medium and red circles are measurements of the cells. Arrows indicate different cells.
It should be noted that theoretically our throughput could be much higher given our measurement rate of 200 Hz. Our flow cytometer is mainly limited by nonoptimal flow conditions. For example, the clumping of cells reduces the cell flow rate over the course of the measurement trial and employing sheath flow and hydrodynamic focusing [40–43] or droplet microfluidics [44–47] could greatly increase the number of cells passing through the Brillouin interaction region. Assuming adequate control of the relative spacing between consecutive cells, ∼5pts per cell and 5 pts between the next subsequent cell, an SBS flow cytometer with our measurement time could reach an overall throughput of ∼20 cells per second.
5. Cell measurements
5.1. Sample preparation
MCF10A cells were gifted by Michele Vitolo and cultured with DMEM/F-12 (Gibco #11330033), 5% Horse Serum (Gibco #16050122), EGF (Peprotech #AF-100-15), Hydrocortisone (Sigma #H-0888), Cholera Toxin (Sigma #C-8052), Insulin (Sigma #I-1882), and Pen/Strep (Gibco #15070063). The MCF10A cells were verified to be mycoplasm free, checked routinely every 3-6 months. The cells were cultured in a 1:1 mixture of Dulbecco's modified Eagle's medium and F12 medium (DMEM-F12) supplemented with 5% horse serum, hydrocortisone (0.5 μg/ml), insulin (10 μg/ml), epidermal growth factor (20 ng/ml), cholera toxin (100 ng/ml), and penicillin-streptomycin (100 μg/ml each). MDA-MB-231 were acquired from ATCC (ATCC #HTB-26) and cultured with DMEM (ATCC #30-2002), 10% FBS (ATCC #30-2020), and Pen/Strep (Gibco #15070063). Both cell types were prepared for flow experiments by resuspension in DPBS (Gibco #14190144) or 10% OptiPrep (Sigma #C974P05).
5.2. Post-processing of flow data
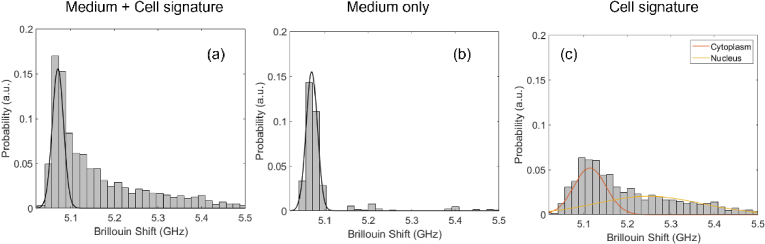
As described previously, we used a 50μm × 50μm microfluidic channel with a syringe pump to flow cells and collect their Brillouin signal. Once the prepared cells in suspension are loaded into the syringe, we collect measurements of the cells in flow over the course of a ∼45 min measurement trial. With our home-built LabView acquisition program, we acquire many smaller segments (∼10s) of data which are comprised of individual spectral measurements (∼2000 × 5 ms). During these segments, cells flow across the Brillouin interaction region and are sampled at multiple points by our spectrometer. In post-processing, our home-built MATLAB script uses a single peak Lorentzian least-square fit of each individual spectral measurement and collects the respective Brillouin information. This collection of spectral information can then be represented as a histogram, see Fig. 4(a), which, due to our continuous acquisition, contains data from both the medium used in flow and the cells. We remove the medium signature by fitting a Gaussian to measurements of only the medium and subtracting it from the overall distribution, see Fig. 4(b). Once removed, we are left with the cell signature which is composed of both the cytoplasm and nucleus as is shown in Fig. 4(c). We can distinguish the two by fitting the cell signature with a linear combination of two Gaussians where the lower Brillouin shift peak position corresponds to the cytoplasm, which is known to be less stiff than the nucleus, and the higher Brillouin shift peak position is the nucleus. Similar post-processing methodology has been demonstrated before and has combined spontaneous Brillouin with fluorescent imaging to confirm that cell nuclei tend to have higher Brillouin shifts when compared to the cytoplasm [21].
Fig. 4.
Histograms represent flow experiment data post-processing. (a) Experimental data with Brillouin shift signatures from both the medium and the cells. (b) Experimental data of Brillouin shift of only the medium. Black line represents Gaussian fit to be subtracted from overall measurement. (c) Extracted cell signature with medium removed. Orange and yellow lines are each Gaussian fits of the cytoplasm and nucleus respectively.
Importantly, we have previously demonstrated that since the height of the channel is larger than the cell size, not all cells will be sampled through their center in the height direction. As a result, when averaging over the whole cell population, the flow data represent equivalent information to what would be obtained from histograms of cross-sectional Brillouin images [21].
5.3. Brillouin shift analysis
During each experiment, our CW SBS flow cytometer sampled hundreds of cells each sampled at multiple points. With our post-processing, described in the previous section, we construct representative cell signature distributions which allow us to understand the mechanical properties of the cell lines at high throughput and compare them. We analyze the Brillouin shift of the nucleus and cytoplasm of each of the two cell lines.
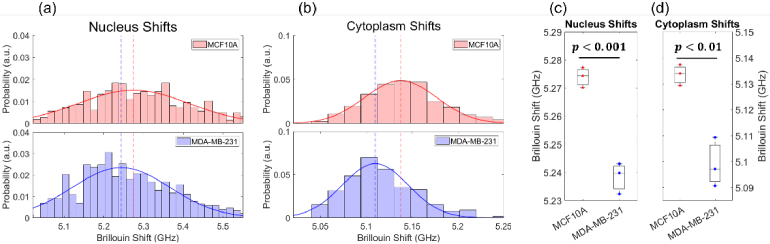
In order to confirm our prediction that MCF10A will have a higher Brillouin shift than MDA-MB-231, we can analyze the Brillouin shifts of the cell lines using our population distributions of three separate experiments for each cell line. As previously mentioned, the cell signatures can be broken down into nucleus and cytoplasm contributions. A representative experiment of MCF10A, shown in Fig. 5(a) and 5(b) in red, captures the overall mechanics of the population having higher Brillouin shift and thus higher stiffness compared to MDA-MB-231, shown in Fig. 5(a) and 5(b) in blue. The nucleus shift central peak location of MCF10A for this experiment is at GHz while MDA-MB-231 is at GHz. The cytoplasm shift central peak location of MCF10A is GHz and MDA-MB-231 is GHz. We performed a two-sample t-test to confirm the statistical significance between the two cell line nucleus shifts, Fig. 5(c), as well as the cytoplasm shifts, Fig. 5(d). In both cases of nucleus and cytoplasm, we observe significantly higher Brillouin shifts in MCF10A than MDA-MB-231 in flow.
Fig. 5.
Brillouin cell signature results. Representative experiments of MCF10A (top, 280 cells) and MDA-MB-231 (bottom, 311 cells) separated into (a) nucleus signatures and (b) cytoplasm signatures. The red lines depict the Gaussian fits of the MCF10A distributions, and the blue lines show the Gaussian fits of the MDA-MB-231 distributions. The dashed lines in each plot show the central peak location of each fit. (c) and (d) show the Brillouin shift population central peak location for the nucleus and cytoplasm respectively. Three separate experiment runs for both cell lines were conducted. Statistical significance between the two cell lines was analyzed using a two-sample t-test.
These findings are consistent with gold-standard mechanical analyses of metastatic potential [16,48–52] and provide validation of our flow cytometer. The resultant lower Brillouin shift, and subsequently softer, signature seen in the metastatic MDA-MB-231 when compared to MCF10A can be largely attributed to cytoskeleton alterations and thus is linked to a characteristic reduction in adhesion [53] and higher invasiveness [54] of cancer cells. One of the main benefits of using Brillouin for these measurements is the fidelity it provides with respect to being all-optical and thus not perturbing the cell such as other current technologies, thus alleviating any artifacts due that cells are prone to through mechanical stimulation. Furthermore, with flow cytometry being an ideal application for SBS where two counterpropagating beams are required, the ability to measure cell mechanics in flow is highly relevant to metastasis through the bloodstream compared to other methods of its kind.
6. Conclusion
In this work, we presented the combination of state-of-the-art CW SBS with flow cytometry to achieve higher throughput mechanical measurements of cells. We analyzed the Brillouin shift signatures of both the nucleus and cytoplasm of MCF10A and MDA-MB-231. Our CW SBS flow cytometry setup is capable of measuring continuously at a rate of 200 Hz, given by the 5 ms spectral acquisition speeds which marks a 10x improvement in measurement time compared to a previous implementation of spontaneous Brillouin flow cytometry [21]. This resulted in an overall throughput of 0.375 cells per second. Our throughput is limited by nonoptimal flow conditions and clumping of cells, which in turn slows down the flow rates and frequency of cells passing through the interaction region. Further improvements to a setup such as this one could utilize advanced microfluidic techniques and circulating cell models, such as Jurkat cells, to fully exploit the speedup potential that CW SBS systems offer. With a more suitable microfluidic system and circulating cell model, the theoretical throughput of a system leveraging microfluidic techniques such as these could exceed ∼20 cells per second. This is much lower than traditional flow cytometers (>10 K cells/second) and deformability cytometers [18] but provides unique mechanical contrast for the cell nucleus. Further improvements on the SBS cytometer will also include the characterization of the linewidth to provide additional mechanical contrast linked to viscosity enabled by the much higher spectral resolution of SBS spectroscopy. For the application, nearly 90% of human solid tumors are epithelial carcinomas that disseminate through the free-floating environments of the bloodstream or lymphatics during metastasis (PMID: 9124038). Given the importance of tumor cell mechanics for traversing the steps in the metastatic cascade (PMID: 33238151), this state of the art CW SBS flow cytometry system provides new approaches to measure tumor cell mechanics in the free-floating environments relevant to metastasis.
Supplemental information
Funding
National Cancer Institute10.13039/100000054 (P30-CA134274, R01-CA124704, R21CA258008).
Disclosures
None.
Data availability
Data and methods are available upon request to the authors.
Supplemental document
See Supplement 1 (1,003.7KB, pdf) for supporting content.
References
- 1.Pelham R. J., Wang Y., “Cell locomotion and focal adhesions are regulated by substrate flexibility,” Proc. Natl. Acad. Sci. U.S.A. 94(25), 13661–13665 (1997). 10.1073/pnas.94.25.13661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lo C.-M., Wang H.-B., Dembo M., et al. , “Cell movement is guided by the rigidity of the substrate,” Biophys. J. 79(1), 144–152 (2000). 10.1016/S0006-3495(00)76279-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Huang S., Ingber D. E., “The structural and mechanical complexity of cell-growth control,” Nat Cell Biol 1(5), E131–E138 (1999). 10.1038/13043 [DOI] [PubMed] [Google Scholar]
- 4.Chiquet M., “Regulation of extracellular matrix gene expression by mechanical stress,” Matrix Biol. 18(5), 417–426 (1999). 10.1016/S0945-053X(99)00039-6 [DOI] [PubMed] [Google Scholar]
- 5.Huang S., Ingber D. E., “Cell tension, matrix mechanics, and cancer development,” Cancer Cell 8(3), 175–176 (2005). 10.1016/j.ccr.2005.08.009 [DOI] [PubMed] [Google Scholar]
- 6.Levental K. R., Yu H., Kass L., et al. , “Matrix crosslinking forces tumor progression by enhancing integrin signaling,” Cell 139(5), 891–906 (2009). 10.1016/j.cell.2009.10.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paul C. D., Mistriotis P., Konstantopoulos K., “Cancer cell motility: lessons from migration in confined spaces,” Nat Rev Cancer 17(2), 131–140 (2017). 10.1038/nrc.2016.123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chaudhuri P. K., Low B. C., Lim C. T., “Mechanobiology of Tumor Growth,” Chem. Rev. 118(14), 6499–6515 (2018). 10.1021/acs.chemrev.8b00042 [DOI] [PubMed] [Google Scholar]
- 9.Schroeder A., Heller D. A., Winslow M. M., et al. , “Treating metastatic cancer with nanotechnology,” Nat Rev Cancer 12(1), 39–50 (2012). 10.1038/nrc3180 [DOI] [PubMed] [Google Scholar]
- 10.Franze K., “Atomic force microscopy and its contribution to understanding the development of the nervous system,” Curr. Opin. Genet. Dev. 21(5), 530–537 (2011). 10.1016/j.gde.2011.07.001 [DOI] [PubMed] [Google Scholar]
- 11.Hochmuth R. M., “Micropipette aspiration of living cells,” J. Biomech. 33(1), 15–22 (2000). 10.1016/S0021-9290(99)00175-X [DOI] [PubMed] [Google Scholar]
- 12.Fabry B., Maksym G. N., Butler J. P., et al. , “Scaling the Microrheology of Living Cells,” Phys. Rev. Lett. 87(14), 148102 (2001). 10.1103/PhysRevLett.87.148102 [DOI] [PubMed] [Google Scholar]
- 13.Serwane F., Mongera A., Rowghanian P., et al. , “In vivo quantification of spatially varying mechanical properties in developing tissues,” Nat. Methods 14(2), 181–186 (2017). 10.1038/nmeth.4101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Guck J., Chilvers E. R., “Mechanics Meets Medicine,” Sci. Transl. Med. 5(212), 1 (2013). 10.1126/scitranslmed.3007731 [DOI] [PubMed] [Google Scholar]
- 15.Guck J., Ananthakrishnan R., Mahmood H., et al. , “The Optical Stretcher: A Novel Laser Tool to Micromanipulate Cells,” Biophys. J. 81(2), 767–784 (2001). 10.1016/S0006-3495(01)75740-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hartono D., Liu Y., Tan P. Lin, et al. , “On-chip measurements of cell compressibility via acoustic radiation,” Lab Chip 11(23), 4072–4080 (2011). 10.1039/c1lc20687g [DOI] [PubMed] [Google Scholar]
- 17.Hur S. C., Henderson-MacLennan N. K., McCabe E. R. B., et al. , “Deformability-based cell classification and enrichment using inertial microfluidics,” Lab Chip 11(5), 912 (2011). 10.1039/c0lc00595a [DOI] [PubMed] [Google Scholar]
- 18.Otto O., Rosendahl P., Mietke A., et al. , “Real-time deformability cytometry: on-the-fly cell mechanical phenotyping,” Nat. Methods 12(3), 199–202 (2015). 10.1038/nmeth.3281 [DOI] [PubMed] [Google Scholar]
- 19.Yankaskas C. L., Thompson K. N., Paul C. D., et al. , “A microfluidic assay for the quantification of the metastatic propensity of breast cancer specimens,” Nat Biomed Eng 3(6), 452–465 (2019). 10.1038/s41551-019-0400-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang J., Alisafaei F., Nikolić M., et al. , “Nuclear Mechanics within Intact Cells Is Regulated by Cytoskeletal Network and Internal Nanostructures,” Small 16(18), 1907688 (2020). 10.1002/smll.201907688 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang J., Nou X. A., Kim H., et al. , “Brillouin flow cytometry for label-free mechanical phenotyping of the nucleus,” Lab Chip 17(4), 663–670 (2017). 10.1039/C6LC01443G [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Meng Z., Petrov G. I., Yakovlev V. V., “Flow cytometry using Brillouin imaging and sensing via time-resolved optical (BISTRO) measurements,” Analyst 140(21), 7160–7164 (2015). 10.1039/C5AN01700A [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Scarcelli G., Polacheck W. J., Nia H. T., et al. , “Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy,” Nat. Methods 12(12), 1132–1134 (2015). 10.1038/nmeth.3616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Scarcelli G., Besner S., Pineda R., et al. , “In Vivo Biomechanical Mapping of Normal and Keratoconus Corneas,” JAMA Ophthalmol 133(4), 480 (2015). 10.1001/jamaophthalmol.2014.5641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nikolić M., Scarcelli G., Tanner K., “Multimodal microscale mechanical mapping of cancer cells in complex microenvironments,” Biophys. J. 121(19), 3586–3599 (2022). 10.1016/j.bpj.2022.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nikolić M., Scarcelli G., “Long-term Brillouin imaging of live cells with reduced absorption-mediated damage at 660 nm wavelength,” Biomed. Opt. Express 10(4), 1567 (2019). 10.1364/BOE.10.001567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang J., Scarcelli G., “Mapping mechanical properties of biological materials via an add-on Brillouin module to confocal microscopes,” Nat Protoc 16(2), 1251–1275 (2021). 10.1038/s41596-020-00457-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gossett D. R., Tse H. T. K., Lee S. A., et al. , “Hydrodynamic stretching of single cells for large population mechanical phenotyping,” Proc. Natl. Acad. Sci. U.S.A. 109(20), 7630–7635 (2012). 10.1073/pnas.1200107109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Remer I., Bilenca A., “Background-free Brillouin spectroscopy in scattering media at 780 nm via stimulated Brillouin scattering,” Opt. Lett. 41(5), 926 (2016). 10.1364/OL.41.000926 [DOI] [PubMed] [Google Scholar]
- 30.Ballmann C. W., Thompson J. V., Traverso A. J., et al. , “Stimulated Brillouin Scattering Microscopic Imaging,” Sci. Rep. 5(1), 18139 (2015). 10.1038/srep18139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zanini G., Scarcelli G., “Localization-assisted stimulated Brillouin scattering spectroscopy,” APL Photonics 7(5), 056101 (2022). 10.1063/5.0087697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Remer I., Shaashoua R., Shemesh N., et al. , “High-sensitivity and high-specificity biomechanical imaging by stimulated Brillouin scattering microscopy,” Nat. Methods 17(9), 913–916 (2020). 10.1038/s41592-020-0882-0 [DOI] [PubMed] [Google Scholar]
- 33.The Physical Sciences - Oncology Centers Network. Agus D. B., Alexander J. F., Arap W., et al. , “A physical sciences network characterization of non-tumorigenic and metastatic cells,” Sci. Rep. 3(1), 1449 (2013). 10.1038/srep01449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Remmerbach T. W., Wottawah F., Dietrich J., et al. , “Oral Cancer Diagnosis by Mechanical Phenotyping,” Cancer Res. 69(5), 1728–1732 (2009). 10.1158/0008-5472.CAN-08-4073 [DOI] [PubMed] [Google Scholar]
- 35.Tse H. T. K., Gossett D. R., Moon Y. S., et al. , “Quantitative Diagnosis of Malignant Pleural Effusions by Single-Cell Mechanophenotyping,” Sci. Transl. Med. 5(212), 1 (2013). 10.1126/scitranslmed.3006559 [DOI] [PubMed] [Google Scholar]
- 36.Boyd R. W., Nonlinear Optics , 3rd ed. (Academic Press, 1992). [Google Scholar]
- 37.Randall J., Vaughan J. M., “The measurement and interpretation of Brillouin scattering in the lens of the eye,” Proc. R. Soc. Lond. B. 214(1197), 449–470 (1982). 10.1098/rspb.1982.0021 [DOI] [PubMed] [Google Scholar]
- 38.Scarcelli G., Kim P., Yun S. H., “In Vivo Measurement of Age-Related Stiffening in the Crystalline Lens by Brillouin Optical Microscopy,” Biophys. J. 101(6), 1539–1545 (2011). 10.1016/j.bpj.2011.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Webb J. N., Su J. P., Scarcelli G., “Mechanical outcome of accelerated corneal crosslinking evaluated by Brillouin microscopy,” Journal of Cataract and Refractive Surgery 43(11), 1458–1463 (2017). 10.1016/j.jcrs.2017.07.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mao X., Waldeisen J. R., Huang T. J., ““Microfluidic drifting”—implementing three-dimensional hydrodynamic focusing with a single-layer planar microfluidic device,” Lab Chip 7(10), 1260 (2007). 10.1039/b711155j [DOI] [PubMed] [Google Scholar]
- 41.Paiè P., Bragheri F., Vazquez R. M., et al. , “Straightforward 3D hydrodynamic focusing in femtosecond laser fabricated microfluidic channels,” Lab Chip 14(11), 1826–1833 (2014). 10.1039/C4LC00133H [DOI] [PubMed] [Google Scholar]
- 42.Chiu Y.-J., Cho S. H., Mei Z., et al. , “Universally applicable three-dimensional hydrodynamic microfluidic flow focusing,” Lab Chip 13(9), 1803 (2013). 10.1039/c3lc41202d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Huang D., Wang H., Wang X., et al. , “Investigation of Optimal Coupling Velocities of the Sample and Sheath Flows for Hydrodynamic Focusing,” JMSE 8(8), 601 (2020). 10.3390/jmse8080601 [DOI] [Google Scholar]
- 44.Moragues T., Arguijo D., Beneyton T., et al. , “Droplet-based microfluidics,” Nat Rev Methods Primers 3(1), 32 (2023). 10.1038/s43586-023-00212-3 [DOI] [Google Scholar]
- 45.Anna S. L., Bontoux N., Stone H. A., “Formation of dispersions using “flow focusing” in microchannels,” Appl. Phys. Lett. 82(3), 364–366 (2003). 10.1063/1.1537519 [DOI] [Google Scholar]
- 46.Mazutis L., Gilbert J., Ung W. L., et al. , “Single-cell analysis and sorting using droplet-based microfluidics,” Nat Protoc 8(5), 870–891 (2013). 10.1038/nprot.2013.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Thibault D., Jensen P. A., Wood S., et al. , “Droplet Tn-Seq combines microfluidics with Tn-Seq for identifying complex single-cell phenotypes,” Nat Commun 10(1), 5729 (2019). 10.1038/s41467-019-13719-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Swaminathan V., Mythreye K., O’Brien E. T., et al. , “Mechanical Stiffness Grades Metastatic Potential in Patient Tumor Cells and in Cancer Cell Lines,” Cancer Res. 71(15), 5075–5080 (2011). 10.1158/0008-5472.CAN-11-0247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Guck J., Schinkinger S., Lincoln B., et al. , “Optical Deformability as an Inherent Cell Marker for Testing Malignant Transformation and Metastatic Competence,” Biophys. J. 88(5), 3689–3698 (2005). 10.1529/biophysj.104.045476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cross S. E., Jin Y.-S., Tondre J., et al. , “AFM-based analysis of human metastatic cancer cells,” Nanotechnology 19(38), 384003 (2008). 10.1088/0957-4484/19/38/384003 [DOI] [PubMed] [Google Scholar]
- 51.Nikkhah M., Strobl J. S., Schmelz E. M., et al. , “Evaluation of the influence of growth medium composition on cell elasticity,” J. Biomech. 44(4), 762–766 (2011). 10.1016/j.jbiomech.2010.11.002 [DOI] [PubMed] [Google Scholar]
- 52.Corbin E. A., Kong F., Lim C. T., et al. , “Biophysical properties of human breast cancer cells measured using silicon MEMS resonators and atomic force microscopy,” Lab Chip 15(3), 839–847 (2015). 10.1039/C4LC01179A [DOI] [PubMed] [Google Scholar]
- 53.Cavallaro U., Christofori G., “Cell adhesion and signalling by cadherins and Ig-CAMs in cancer,” Nat. Rev. Cancer 4(2), 118–132 (2004). 10.1038/nrc1276 [DOI] [PubMed] [Google Scholar]
- 54.Byun S., Son S., Amodei D., et al. , “Characterizing deformability and surface friction of cancer cells,” Proc. Natl. Acad. Sci. U.S.A. 110(19), 7580–7585 (2013). 10.1073/pnas.1218806110 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and methods are available upon request to the authors.