Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Oct 1;63(41):19074–19086. doi: 10.1021/acs.inorgchem.4c02299

Two P, Ten P, White P, Red P: Mechanistic Exploration of the Oligomerization of Red Phosphorus from Diphosphorus with the Ab Initio Nanoreactor

Nathan D Yoshino 1,*, Lee-Ping Wang 1,*
PMCID: PMC11483771  PMID: 39352782

Abstract

graphic file with name ic4c02299_0015.jpg

Phosphorus is critical to humans on many fronts, yet we do not have a mechanistic understanding of some of its most basic transformations and reactions—namely the oligomerization of white phosphorus to red. With heat or under ultraviolet (UV) exposure, it has been experimentally demonstrated that white phosphorus dissociates into diphosphorus units which readily form red phosphorus. However, the mechanism of this process is unknown. The ab initio nanoreactor approach was used to explore the potential energy surface of phosphorus clusters. Density functional theory and metadynamics simulations were used to characterize potential reaction pathways. A mechanism for oligomerization is proposed to take place via diphosphorus additions at π-bonds and weak σ-bonds through three membered ring intermediates. Downhill paths through P6 and P8 clusters eventually result in P10 clusters that can oligomerize into red phosphorus chains. The initial, rate limiting step for this process has an energy barrier of 24.2 kcal/mol.

Short abstract

Phosphorus cluster reactivity is a relatively underexplored area despite phosphorus being critical in our technological advances. The oligomerization of red phosphorus is explored using density functional theory and ab initio molecular dynamics with the Nanoreactor and metadynamics. A mechanism for oligomerization is proposed and new insights to the reactivity of diphosphorus and the stability of phosphorus clusters are uncovered.

Introduction

Phosphorus (P) is an essential element in the genetic code and cellular metabolism,1 as well as many industrially produced materials and organic compounds such as pharmaceuticals, foodstuffs,2 semiconductors (e.g., gallium phosphide)3 and fertilizer.4 With this many applications, an optimal process for producing elemental phosphorus is necessary. Elemental phosphorus is classified into three allotropes:

  • 1.

    White phosphorus—tetrahedral P4 with a low melting point (44.15 °C)5

  • 2.

    Black phosphorus—stacked 2D honeycomb lattice similar to graphite6

  • 3.

    Red phosphorus—many forms with varying levels of structure7

Current industrial phosphorus generation uses a thermal process to convert phosphates into white P and subsequently phosphorus trichloride2 as a feedstock for other compounds, but this requires large amounts of energy and uses hazardous chlorine gas.

Alternative methods of more direct phosphorus generation are of great interest in order to omit chlorine from the process.8−14 Experimental research efforts led by Cummins et al. have included ultraviolet (UV) photolysis of P4 to incorporate diphosphorus (P2) units directly into synthetic schemes.15 This work is inspired by the observation that P4 oligomerization to red P can be initiated by photolysis of P4 into P2 units under UV light16 (Figure 1) or at high temperatures (>275 °C).2,7,17,18 Red P is known to exist in at least five forms from amorphous7 (form I) to the well-defined tubular structure of fibrous red phosphorus19 (form IV) and Hittorf’s violet phosphorus (form V).20,21 Changes between forms are induced at high temperatures (>450 °C) and are irreversible.7

Figure 1.

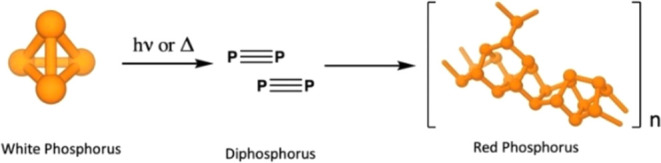
Figure 1

Open in a new tab

White phosphorus dissociates to P2, which oligomerizes to red phosphorus. Some red phosphorus forms contain repeated P10 and P11 subunits. P11 subunits in different chains cross-link to form an extended network.

Red phosphorus itself has compelling, unexplored potential. Historically, its main uses are in flame retardants and matchboxes.22 However, there is a great body of work suggests Red P will play a key role in sustainable energy.23,24 Initial efforts by Wang et al.25 with Red P microparticles demonstrated high levels of hydrogen gas evolution for an elemental photocatalyst. Compared to its metal-based counterparts, Red P has several advantages such as stability, nontoxicity, and cost. Many other studies have confirmed the photocatalytic hydrogen evolution potential of Red P in other forms or when combined with other photocatalysts.26−39 In addition, Red P’s photocatalytic use could extend to pollutant degradation40−43 and bacterial inactivation to clean water.43−45 Recent work has also shown Red Phosphorus to be useful for energy storage as a candidate for use in anodes of ion batteries. Carbon/Red P materials have been extensively studied and demonstrated areal capacities of up to 10 mA h cm2–,46 boosted ion storage and good stability.46−55

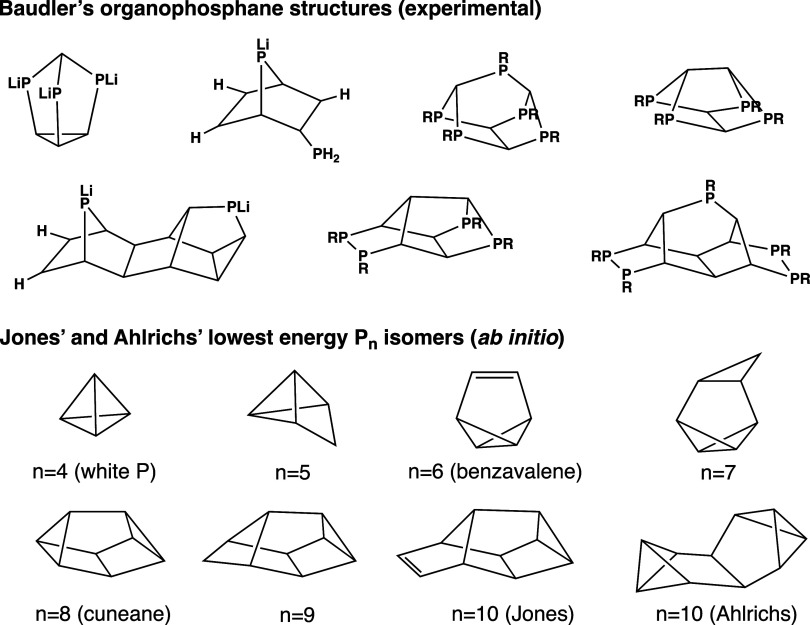
The reaction pathways of red P formation from P2 may involve traversing a landscape of oligophosphorus and polyphosphorus molecules. Clues are provided in the rich chemistry of organophosphane compounds, in which a great number of Pn-containing structural motifs were described by Baudler,56 Weigand,57,58 Hey-Hawkins,59 and others. Some of these compounds have versatile metal coordination capabilities,60−65 and may be used as precursors to metal phosphides,59,66 which are challenging to synthesize but have potential to replace precious metal catalysts in reactions such as hydrogen evolution. Therefore, studies of Pn cluster growth of intermediate cluster sizes could further guide the discovery of novel polyphosphorus compounds and derived functional materials.

The first to speculate on the structure of Red P and phosphorus clusters was Pauling, who initially proposed a structural model of red P based on X-ray analysis6 consisting of linked units of tetrahedral white P with one bond broken.67 The structure of Hittorf’s phosphorus was later characterized by Thurn and Krebs,20 followed by the discovery of similar structural motifs in amorphous red P by Fasol et al.21 Subsequently, Baudler characterized a vast array of monocyclic and polycyclic phosphanes (Figure 2). The vertices of all skeletal structures from here on will indicate a phosphorus atom unless otherwise specified., showing that the parallel, tubular structure of red P could be synthesized from nucleophilic additions of compounds containing P2 and P4 subunits.68−73 These studies generally observed that organophosphorus clusters will maximize the number of five-membered rings formed while avoiding four and seven-membered rings; three-membered rings are also more thermally stable than six-membered rings.56

Figure 2.

Figure 2

Open in a new tab

Previously studied phosphorus clusters by Baudler, Jones, and Ahlrichs.

While experimental isolation of small elemental P clusters has not yet been achieved, mass spectroscopy (MS) has provided some insights. Early work by Kerwin74,75 using electron ionization MS suggested that Pn clusters, n = 2–4 (particularly P4) dominate red P vapors at temperatures from 100–300 °C, along with trace amounts of P8.76,77 This was followed by discovery of larger clusters including up to P24 in red P vapor78 and up to P89 in laser desorption ionization experiments.79−82

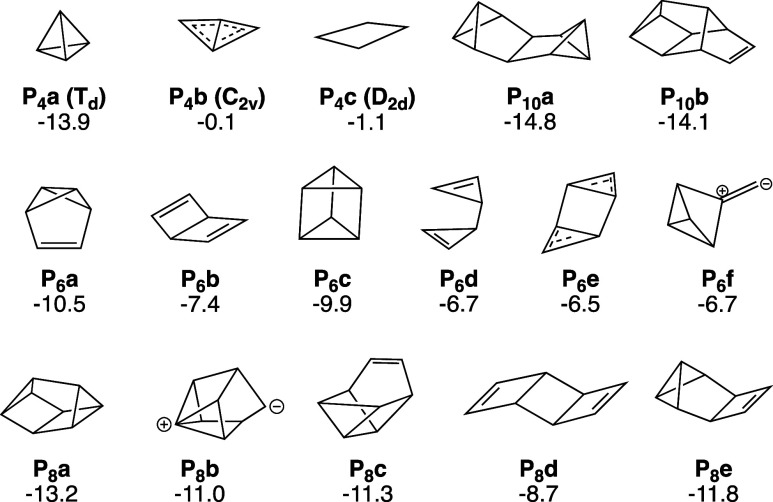
In the past few decades, small P clusters have been extensively characterized with theoretical methods. Early studies83−85 found repulsive interactions between parallel P–P bonds in four-membered rings, consistent with experimental observations disfavoring these structures.56 Ahlrichs et al. studied the most stable even-numbered isomers of Pn clusters up to n = 28 with the Hartree–Fock (HF) and MP2 methods86 and hypothesized that these structures were intermediates in red P formation. Concurrently, Jones et al.87−89 carried out density functional theory (DFT) studies for neutral and ionic P clusters up to n = 11. Both studies largely agreed on the most stable structures of P clusters with one exception being P10 (Figure 2)—Jones’ structure was later favored by more accurate CCSD(T) calculations by Häser.53 These initial studies, together with neutron diffraction experiments90 suggest that amorphous red P contains cuneane-like P8 clusters reminiscent of the tubular structure of Hittorf’s (form V) and fibrous (form IV) red P. Häser’s theoretical studies73,91,92 revealed the following trends: Pn clusters with n ≥ 10 are more stable relative to P4 and those with n = 6–8 are less stable. Islands of stability do not exist beyond n = 4, but stability gradually increases with cluster size due to increasing the number of strain-free five-membered rings.73 Gimarc and Warren’s exploration93−95 of strain energies in P clusters affirms this, estimating cuneane P8 as having the smallest ring strain for P8 isomers. DFT studies on ionic P clusters revealed similar cuneane-like structural motifs and noted that odd-numbered clusters were more stable than even-numbered ones.80,96−99 New families of stable ionic cluster structures were found using DFT simulated annealing, suggesting that broad exploration of the potential energy surface is useful for finding new isomers.100

With the abundance of experimental and theoretical investigations of organophosphanes and P clusters, their structural patterns and the factors that contribute to their stabilities are well understood. However, the chemical transformations between these species have not been thoroughly explored. While Häser and Ahlrichs have proposed mechanisms for the oligomerization of red P,86 their analyses were based solely on energetic minima of phosphorus clusters on the PES and did not examine the kinetic feasibility of the proposed pathways. It is the purpose of this work to propose a kinetically reasonable mechanism for the oligomerization of red P by characterizing the reaction network that connect small phosphorus clusters of varying size.

Many mechanistic investigations start with informed hypotheses from known reactions or by chemical intuition, but the reactivity of elemental P has a much smaller body of experimental knowledge and the derived chemical intuition is also greatly reduced. Moreover, Jones87,88 and Xue100 previously demonstrated with their simulated annealing studies that computational methods that reduce bias and the need for guesswork are highly useful for improved understanding of these systems. The recent decade has seen the development of many methods for automatic generation and characterization of reaction pathways, including those based on the automated application of elementary reaction rules,101−106 and molecular dynamics (MD) simulations on reactive potential energy surfaces.107−111 Ab initio quantum chemistry and DFT are the most reliable methods for discovering previously unknown reactivity as they have the least amount of empirical fitting but are computationally very expensive. To mitigate this, ab initio molecular dynamics (AIMD)-based reaction discovery methods employ various methods to increase the frequency of reaction events relative to ambient conditions. Within this class of approaches, the ab initio nanoreactor112 is an attractive option for simulating red P oligomerization, as it accelerates reactivity by inducing molecular collisions without relying on user-specified collective variables and can generate new hypotheses outside of any mechanistic space determined by rules. For these reasons the nanoreactor was chosen as the primary reaction discovery approach for this study.

Herein, we will first discuss how the ab initio nanoreactor was used to generate novel mechanistic hypotheses for the oligomerization of red P. Our initial simulations found P2 oligomerization reactions that result in many of the stable isomers discussed above (Figure 3 and Table S1). We observed that diphosphorus units tend to add to existing phosphorus clusters via pseudopericyclic reactions to form three-member rings at π-bonds and weak σ-bonds, and we propose that this is a key step in the formation of red P. The reaction network results in forming Jones’ P10 units which then oligomerize through the π-bonds at the bridging P atoms. Our work shows for the first time a detailed, mechanistic exploration of the P cluster reaction space and demonstrates that ab initio molecular dynamics can facilitate reaction discovery in chemical spaces that are largely unintuitive.

Figure 3.

Figure 3

Open in a new tab

Small phosphorus clusters (P2–P10) observed in initial nanoreactor simulations with their per-atom energy (kcal/mol) relative to diphosphorus.

Results and Discussion

From over 90 nanoreactor simulations, a large set of reaction pathways were characterized. Reactions that are perhaps most significant to a mechanism or were observed multiple times in simulations are summarized in Scheme 1. The numbers given are the electronic activation energy followed by the reaction energy in kcal/mol. Reactions without bold arrows were directly observed in the nanoreactor or during the path refinement process. Reactions with bolded arrows were inspired by nanoreactor results and modeled separately. Reactions stated as “<1.0” were calculated to be barrierless association reactions with our methods. It is notable that there are multiple pathways that lead toward cuneane P8 and Cs P10 (Jones’s P10), which are fundamental building blocks for red P chains. Many of these pathways do not have particularly high barriers considering the temperatures that oligomerization occurs.

Scheme 1. Reactions Discovered in and Inspired by the Nanoreactor Simulations.

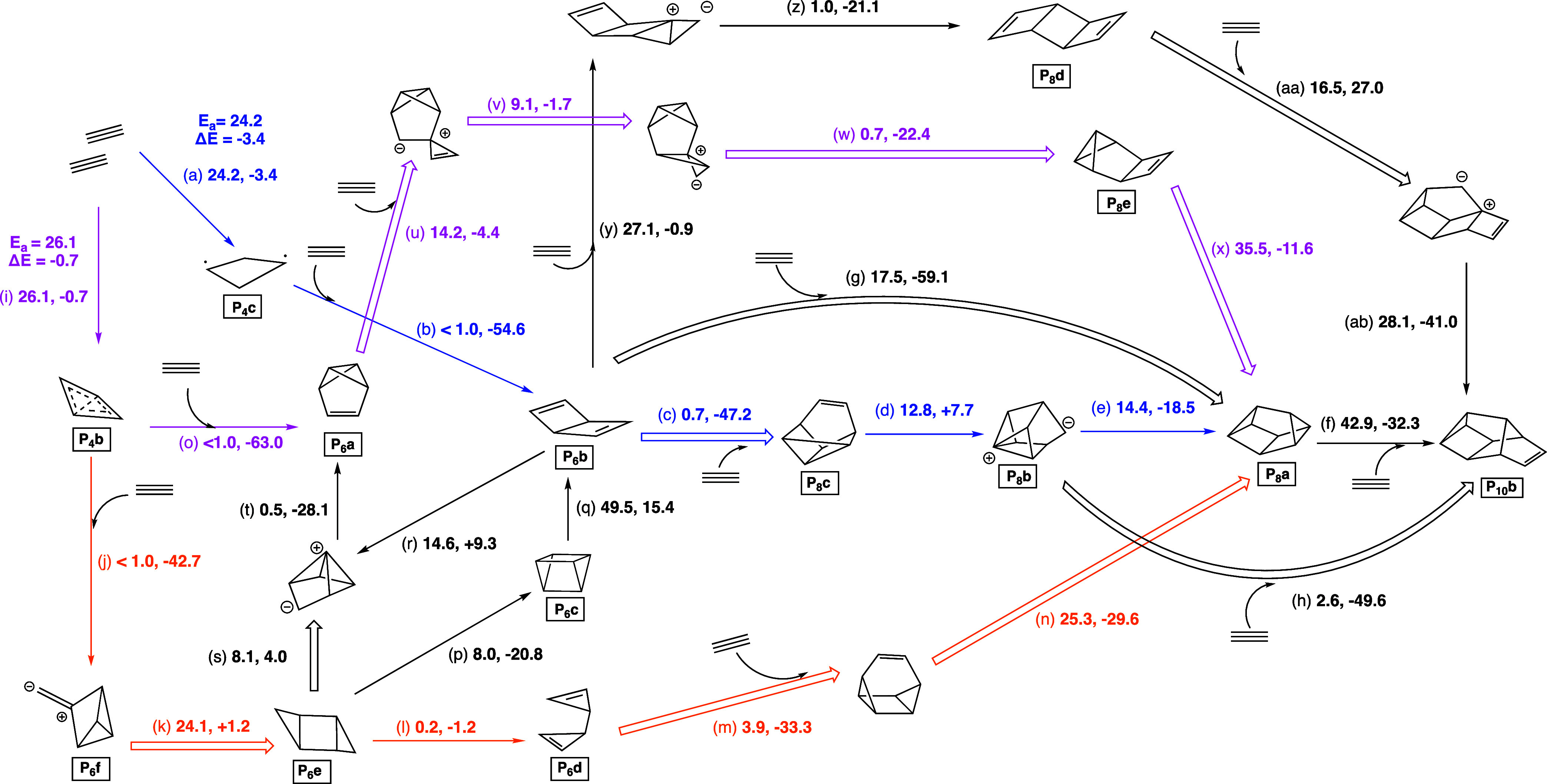
Scheme 1

Open in a new tab

As amorphous forms of red P contain many structural motifs from forms V (Hittorf’s) and IV,90 we suggest that diphosphorus could follow the pathways in Scheme 1 as it oligomerizes into cuneane structures (Figure 4). Particularly the pathway (blue) starting from P4c through to P6b seems plausible. Even if P6b isomerizes into P6a–the most stable P6 isomer–through reactions r and t, there is still a downhill path (pink) to cuneane P8 via a P2 addition at the π-bond. P6b will also readily react with any diphosphorus nearby (reaction c) minimizing the isomerization to P6a. If P4b is formed, it can react with another diphosphorus in two ways, forming P6a through reaction o or P6f through reaction j (gold) depending on the orientation of diphosphorus. Reaction o is likely preferred as it leads to the most stable P6a isomer. The gold pathway through P6f also contains P6d which was by far the most common P6 isomer observed in nanoreactor simulations. All three pathways seem plausible to form P8a, and phosphorus clusters may isomerize between these paths as they traverse the potential energy surface downward toward the cuneane subunit of Red P.

Figure 4.

Figure 4

Open in a new tab

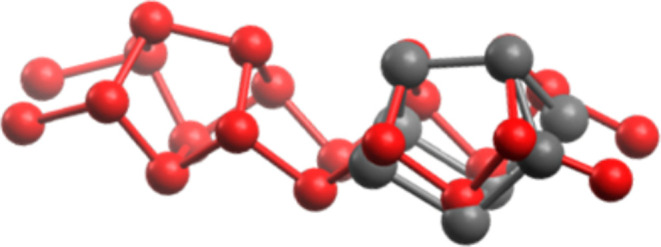
Optimized geometry of the main product (P8a) from Scheme 1 (gray) corresponds to one subunit of Red P (red).

With these pathways characterized, we are also able to verify our choice of methods with previous work. In particular, in comparison to ref (113), which calculated the relative energies of several P4 energy minima and the energy barriers between them using third order Rayleigh–Schrödinger perturbation theory (CASSCF-RSPT3 (4,9)) and an aug-cc-pVTZ basis set, our ωB97X-D3/def-TZVP calculations agree to within 0.2 eV for the activation energy for 2P2 → P4c (Figure S1) and the reaction energy of 2P2 → P4a (Table S2), and moderate agreement is found for the relative energies of other P4 clusters (to within 0.5 eV). We think the smallest clusters are the most problematic for DFT due to the open-shell character of P4b and P4c and the breaking of multiple bonds in their reaction pathways;114 these phenomena were not observed for the larger clusters in this study.

Pseudopericyclic P2 Addition at π-Bonds

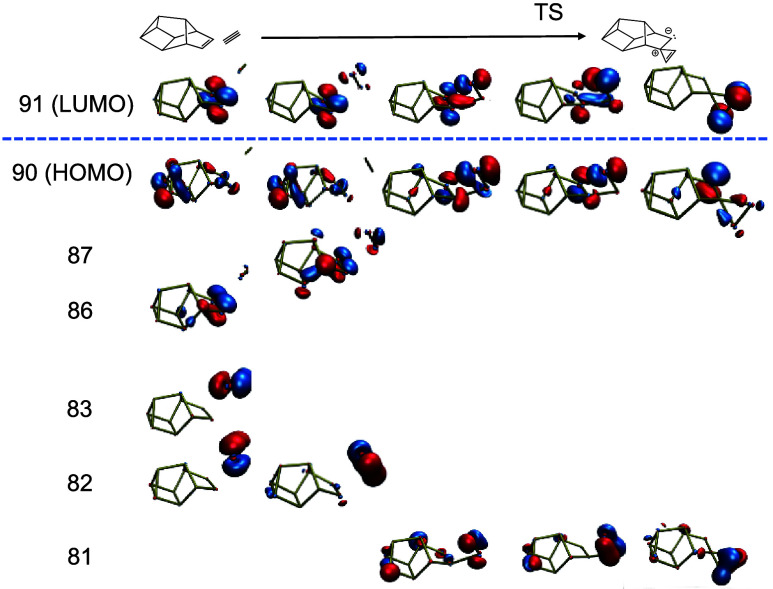
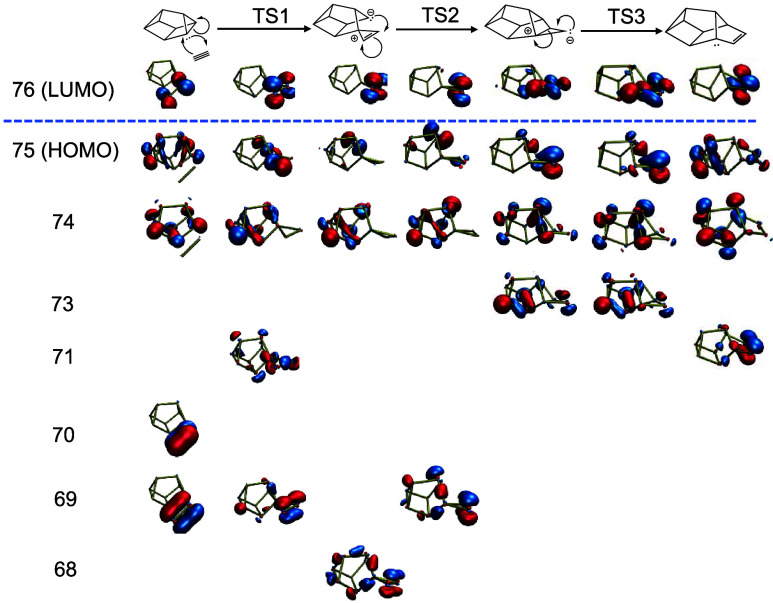
Addition of diphosphorus units through pseudopericyclic reactions emerged as a common motif in the nanoreactor simulations (Scheme 2). Scheme 2a shows a sterically strained three-membered ring intermediate but is the most energetically effective way to add a P2 to the π-bond in P10b whereas Scheme 2b corresponds to a [2 + 2] cycloaddition. Following Woodward–Hoffmann rules, the cycloaddition forces the newly formed ring into a supra/antara conformation that must undergo a phosphorus inversion to reach the same product. Relevant molecular orbitals (MO’s) for the pseudopericyclic addition of diphosphorus is shown in Figure 5. Three MO’s with distinct π-bond character are visible in the reactant (MO 82, 83 and 86). One π-bond (82 → 81) stays consistent throughout the reaction coordinate. The π-bond character of the other P2 π-bond and the P10 π-bond start to disappear during the association (87). During the association, the highest occupied molecular orbital (HOMO) develops a p-orbital character, which is consistent with the interpretation of the π-bond moving to become a lone pair on the back phosphorus. The lowest unoccupied molecular orbital (LUMO) of the transition state shows a clear overlap between the π* orbitals of disappearing π-bonds. This overlap appears along the new formed σ-bond. The HOMO of the final product shows a clear p-orbital on the back phosphorus and some σ-bond character along the newly formed bonds.

Scheme 2. Reactions that Result from P2 Addition to Jones’ P10.

Scheme 2

Open in a new tab

(a) Pseudopericyclic addition of P2 at a π-bond. (b) [2 + 2] supra/antara cycloaddition of P2 at a π-bond. (c) Comparison of [2 + 2] and pseudopericyclic addition of subsequent P2. (d) Third structure in (a) cannot form bicyclic product.

Figure 5.

Figure 5

Open in a new tab

Relevant molecular orbitals for the pseudopericyclic addition of diphosphorus to Jone’s P10, following Scheme 2a.

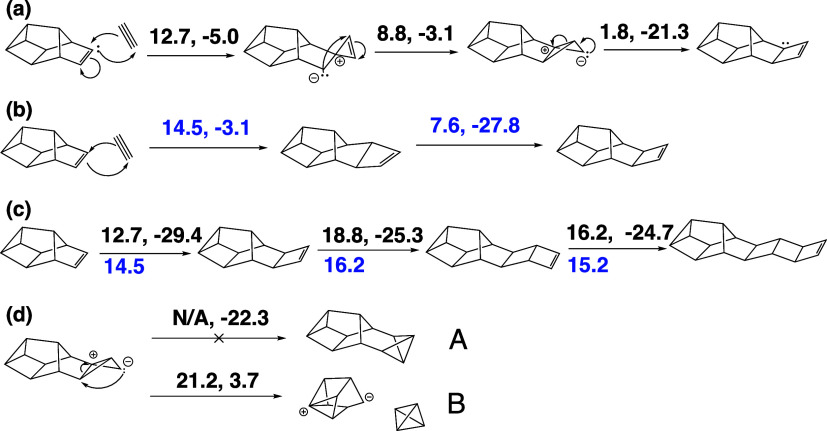
The barriers for these mechanisms starting from even-numbered chains P10–P16 are summarized in Scheme 2c. Although there is no consistent trend for which pathway is preferred, both mechanisms have activation energies below 20 kcal/mol and so would be plausible even at low temperatures. Continued addition of P2 units could result in increasingly long “ladder-like” structures. Other reaction paths following P2 addition were considered; in particular the bicyclic intermediate (the third structure in Scheme 2a) bears resemblance to P6a and Ahlrichs’ P10, both of which were the most stable isomers for their size. An alternate product (Scheme 2d, product A) would contain only σ-bonds and is more stable by 1.1 kcal/mol compared to the “ladder” motif. However, an attempt to locate the TS for Scheme 2d, product A instead led to product B consisting of white P and P8b with a much higher activation energy than the final reaction in Scheme 2a. The reverse of this reaction, with a barrier of 17.5 kcal/mol (ΔErxn= −3.7 kcal/mol), could also reasonably be part of the oligomerization process if white P were present.

From the structures in Scheme 2c, pathways to red P chains were modeled by adding a bridging P2 on top of the ladder. Scheme 3a shows an addition of diphosphorus on top of two σ-bonds, while Scheme 3b shows the formation of a cuneane-like structure can that could occur after an addition of diphosphorus at a terminating π-bonds. These steps have similar barriers to the reactions in Scheme 2 However, these mechanisms involve multiple endothermic steps and rate limiting barriers of >34 kcal/mol in the elementary step where the bridging P2 completes the cage unit, cleaving a ladder σ-bond in the process. While some experimental conditions involving red P production are known to happen at high temperatures, this barrier is larger than most steps studied so far. These findings initially suggested that diphosphorus addition at σ-bonds would be mechanistically avoided.

Scheme 3. Cleavage of σ-Bonds with P–P π-Bonds.

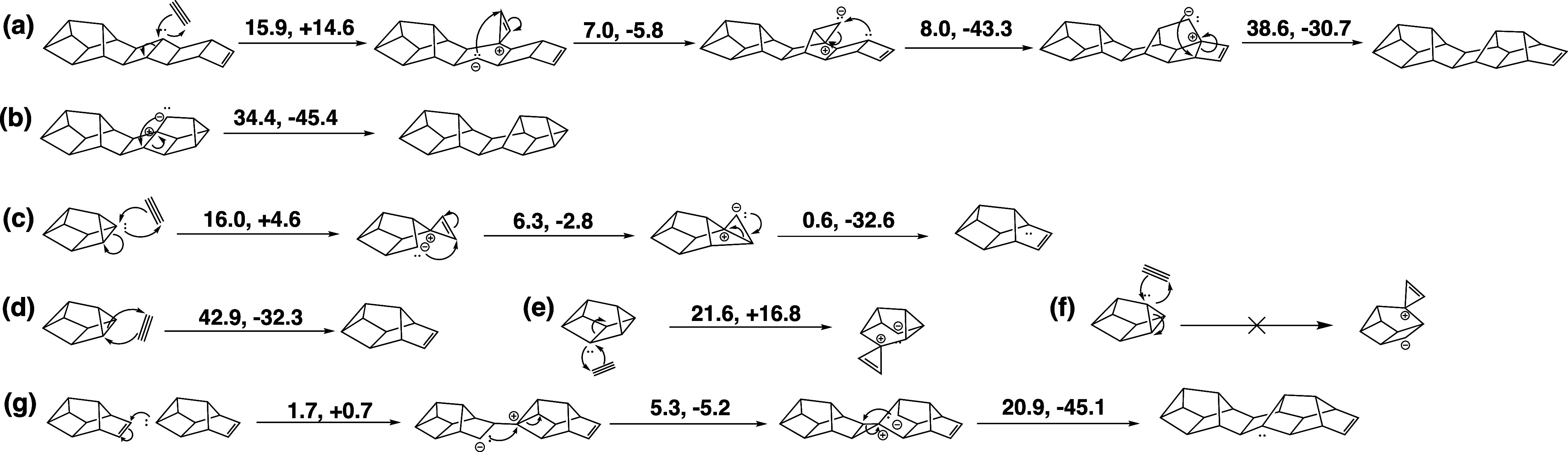
Scheme 3

Open in a new tab

(a, b) Energetically costly addition of diphosphorus at ladder σ-bonds. (c) Pseudopericyclic addition of diphosphorus at three-membered ring σ-bonds of cuneane P8. (d–f) Other possible P2 additions to σ-bonds of cuneane P8. (g) Oligomerization of Jones’ P10 through σ-bond cleavage.

Low-Energy Pathway for P–P σ-Bond Activation

Cuneane P8 is clearly a very stable minimum on the potential energy surface of P clusters, and it showed little reactivity in the nanoreactor simulations. As in Scheme 1, the activation energy of adding P2 to cuneane P8 was found to be 42.9 kcal/mol in the nanoreactor. Inspired by the pseudopericyclic reactions at π-bonds, a new mechanistic path to larger P clusters was found. Addition of P2 at the three-membered rings on cuneane P8 have surprisingly low reaction barriers (16.0 kcal/mol) despite the occurrence of σ-bond cleavage (Scheme 3c). The resulting cluster is P10b, or Jones’ P10, which is significant as Jones’ P10 can be considered as one unit of red P. Diphosphorus additions at other atoms on cuneane P8 were also considered (Scheme 3d–f). These have higher barriers (Scheme 3d,e), are significantly more endothermic (Scheme 3e), or were unable to be characterized with our methods (Scheme 3f). Addition at the three-membered rings of cuneane P8 (Scheme 3c) may be more favorable due to the formation of a five-membered ring in the intermediate simultaneous with the breaking of a four-member ring. Overall, this indicates that Jones’ P10 would be the favored product between cuneane P8 and P2 (Figure 6).

Figure 6.

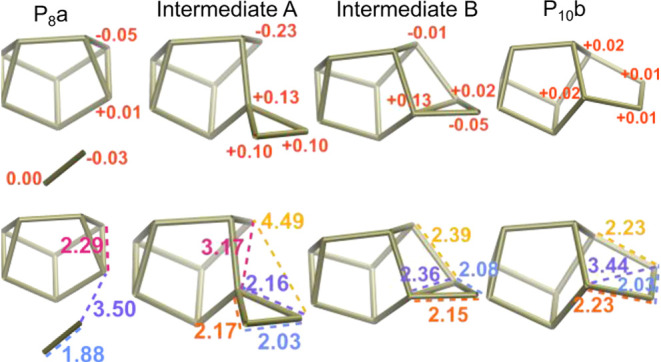
Figure 6

Open in a new tab

RESP charges (top) and bond distances (Å, bottom) for the reaction in Scheme 3c. All atoms without charges listed are smaller in magnitude than 0.05 a. u.

Similar to P2 addition of P10, the LUMO (Figure 7) for the sequence in Scheme 3c shows π* character. In TS1, the π character of MO 70 starts to disappear as it approaches p-orbital lone-pair like character of P10 (MO 71). As with the P2 addition to a π-bond in Figure 5, the HOMO and second HOMO display lone-pair character on the back phosphorus. This lone pair character diminishes in the last two reaction steps as that electron density forms new bonds. The second π-bond (MO 69) is conserved through the first reaction step, and becomes more localized on the rightmost phosphorus with lone-pair character through TS2 (MO 73). However, the π character is re-established through TS3 into the final product (MO 71).

Figure 7.

Figure 7

Open in a new tab

Relevant molecular orbitals for the addition of diphosphorus to cuneane P8.

This mechanism of using a π-bond to cleave cuneane P8 can be extrapolated to devise a mechanism for oligomerization of P10 units (Scheme 3g). Here, the π-bond on one of the P10 units acts similarly to a P2 and is attacked by the lone pair on the vertex of 3, 4, and 5-membered rings. Again, there is disappearance of the π character on the P10 unit (Figure 8, MO 126) as orbital density is developed like a lone pair (HOMO and second HOMO) first onto the P10 unit through TS1, and then onto the bottom-left phosphorus of P8 through TS2. The lone pair character of the HOMO diminishes through TS3 as one σ-bond between the two units is broken and another is formed (MO’s 113–115, 127).

Figure 8.

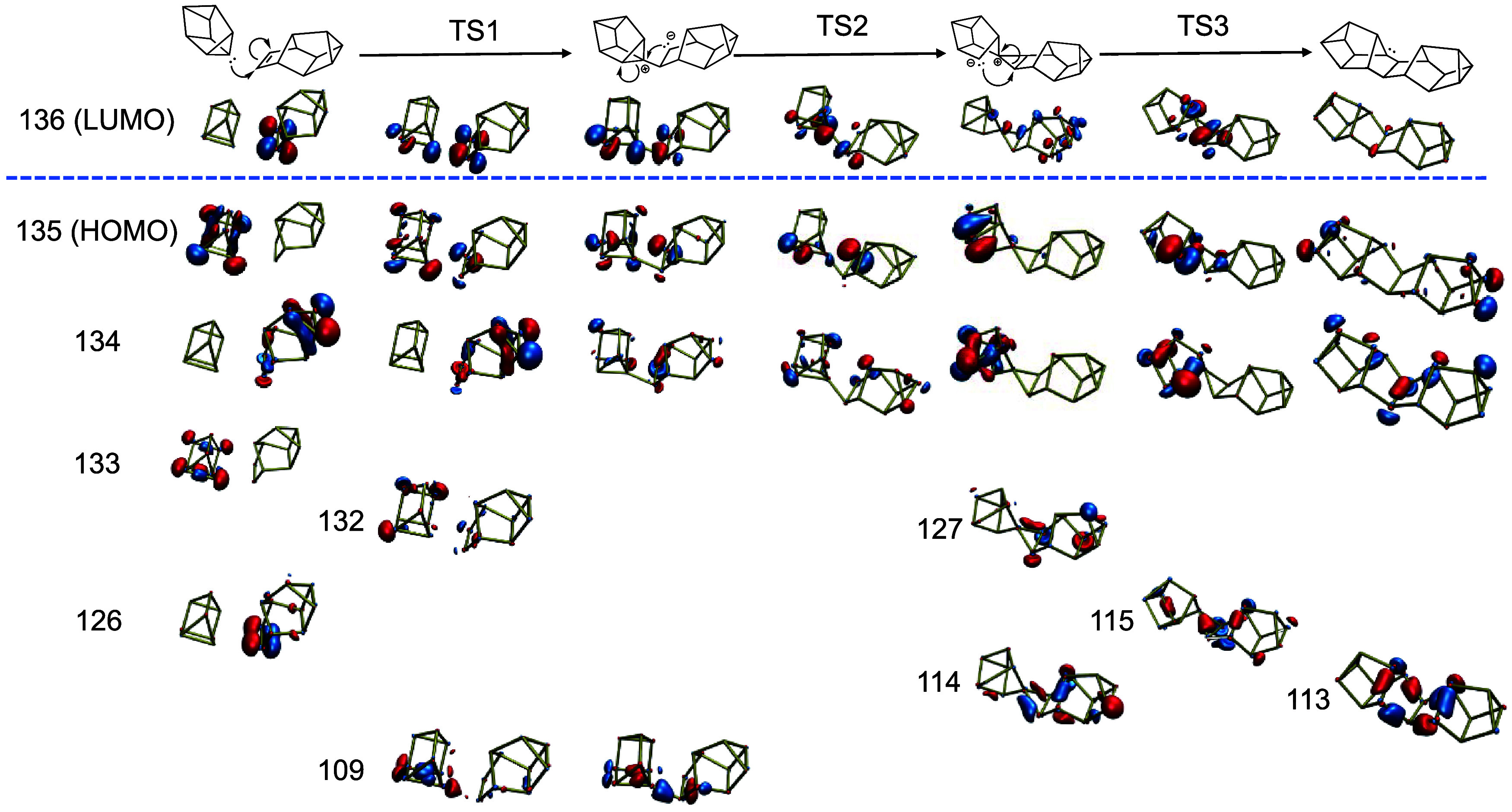
Figure 8

Open in a new tab

Relevant molecular orbitals for the dimerization of two cuneane P8 units of red P.

These mechanisms generally proceed through three-membered cyclic, zwitterionic intermediate before rearranging to the tubular structure of red P. However, Kollman RESP charge calculations show more nuance in these intermediates (Figure 6). It seems that 3-member rings delocalize electron density. The quaternary phosphorus in Intermediate A is expected to show a distinct positive charge. However, the whole 3-member ring shows a significant positive charge (>0.10 a.u.). The lengths of the bonds in this ring also indicate delocalization as the newly formed single bonds (orange and purple) are not as long as typical P–P single bonds (>2.2 Å). In Intermediate B, the expected single bonds of the secondary phosphorus (blue and orange) are 2.08 and 2.15 Å, closer to the length of a typical P=P double bond (2.03 Å). The lack of a distinct negative charge on the secondary phosphorus also hints at the delocalized nature. Bond lengths and RESP charges for the dimerization reaction can be found in Figures S4 and S5, and similar patterns can be observed. The seeming tendency for electron delocalization in three-member rings is likely a contributing factor in the high occurrence and unusual stability they show in phosphorus clusters.

Nonetheless, the formal charges used to represent the work herein are still a useful heuristic for communicating mechanism and electron movement as shown in the MO’s. With the reactions in Schemes 1 and 3c leading to the formation of P10b and this oligomerization step of P10b, a pathway to red P chains is clear starting from P2. This pathway is summarized in Scheme 4. On path from the P6b (C2v) Dewar benzene structure (blue), another path from the Pba benzavalene isomer (pink path), and another path from P6f (gold path). The pink versus orange pathway depends on the orientation of the diphosphorus unit as it approaches P4b. The pink path has the largest single reaction step barrier of 35.5 kcal/mol–plausible at some experimental temperatures (>275 °C), and seemingly necessary as no paths with smaller barriers were found that lead out from this P6 global minimum. The orange path is an alternative path from P4b that has no barriers larger than 25 kcal/mol. The blue pathway has similar barriers, but requires adding a P2 unit to a less stable isomer of P6.

Scheme 4. Electronic Potential Energy Surface of the Calculated Pathways from Diphosphorus to a Unit of Red Phosphorus.

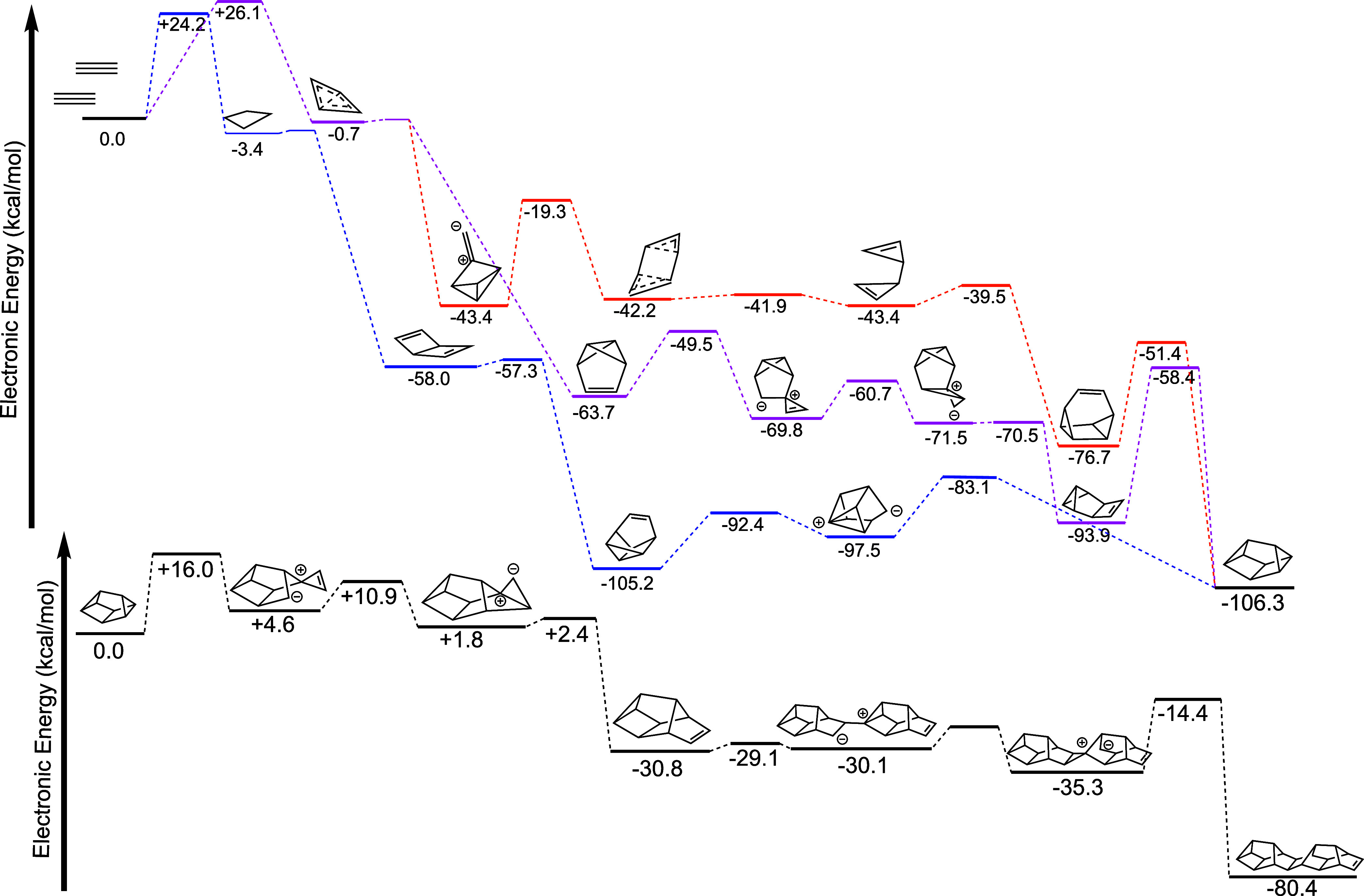
Scheme 4

Open in a new tab

Disphosphorus from addition steps are implied but not explicitly shown.

Harmonic Free Energy Corrections May Not Be Sufficiently Accurate

To fully assess the plausibility of these pathways, evaluating the activation free energies is required. We computed the free energy barriers and reaction free energies using the harmonic approximation at 500 K. While the relative size of most reactions steps and barriers remained largely the same, bimolecular steps involving P2 additions had consistently higher activation free energies by about 10–20 kcal/mol compared to the electronic activation energies (SI, Figure S2). This resulted in some key steps of the mechanism with barriers upward of 40+ kcal/mol and positive reaction free energies of almost 30 kcal/mol, which would not support the proposed mechanism.

However, the methods used to calculate free energies may not be appropriate for this system, as ideal gas approximations begin to break down with heavier and larger species. Additionally, further investigations of the normal modes along the free energy surface revealed that the transition state structures for many of the diphosphorus addition steps contain a large number of low frequency vibrations corresponding to large amplitude motion. These motions are not properly described by a harmonic potential as typically done. To more rigorously characterize the free energy surface of diphosphorus additions, ab initio metadynamics were used as the method of choice.

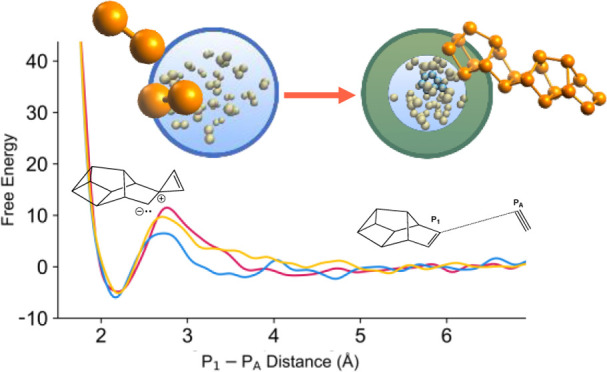
Due to the high computational cost and the challenges involved in defining an appropriate collective variable (CV) for many of the reactions, we chose to study a single reaction, that of P2 addition to Jones’ P10. In this reaction, the CV was chosen as the distance between a chosen P atom on the diphosphorus (PA) and the atom labeled P1 on the π-bond of P10 (Jones’ isomer). The free energy simulation results using three different initial conditions are shown in Figure 9 and Table 1. The results suggest that the free energy barrier is in the range of 6–12 kcal/mol, much lower than the harmonic approximation result (26.6 kcal/mol). The reaction free energies have good agreement, ranging from −5.96 to −4.83 kcal/mol, significantly lower than the harmonic approximation of +9.92 kcal/mol. To summarize, these free energy simulations strongly suggest that the harmonic approximations are overestimating the barrier height and reaction free energies for P2 addition reactions.

Figure 9.

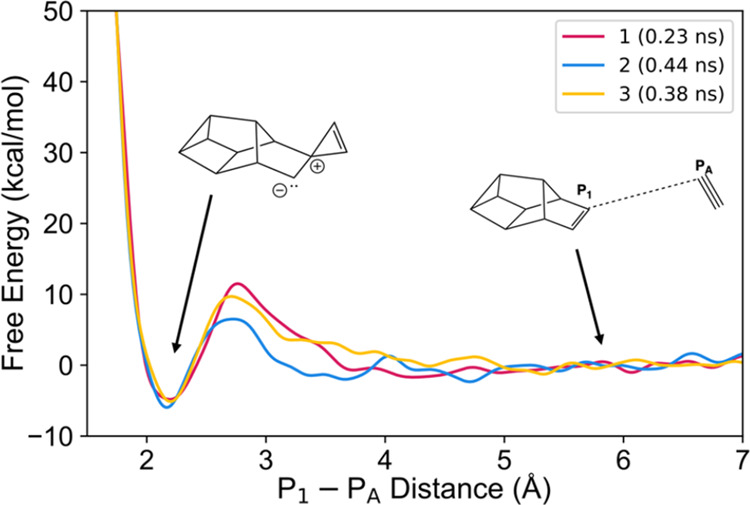
Figure 9

Open in a new tab

Free energy surface from metadynamics simulations for the P2 addition to Jones’ P10.

Table 1. Free Energies and Barriers Generated from Metadynamics Simulations of P10b and P2.

  free energy barrier (kcal/mol) reaction free energy (kcal/mol)
1 (0.23 ns) 11.5 –4.83
2 (0.44 ns) 6.51 –5.96
3 (0.38 ns) 9.71 –5.13
Open in a new tab

Conclusions

From the data gathered, a plausible mechanism for how diphosphorus oligomerizes to red P clusters can be proposed. Our mechanism suggests that diphosphorus units tend to add to clusters at π-bonds and weak σ-bonds through three membered ring intermediates. Downhill paths through P6 and P8 clusters eventually result in P10 clusters that may oligomerize into various red P forms, with forms IV and V consisting of repetitions of said P10 clusters. This mechanism has the largest barrier of 24.2 kcal/mol at the start with two diphosphorus units coming together to form a P4 species. Our methods of choice are supported by free energy simulations and multireference methods. While this study has largely focused on closed-shell species, more work can be done to explore open-shell mechanisms or mechanisms that involve ionic species.

Looking forward, another key mechanistic step that was not explored was the formation of P11 red P subunits by cross-linking P10 subunits with P2. We anticipate that similar diphosphorus addition steps as the ones found here could play a part in the reaction pathway. Additionally, investigating paths with open-shell methods or ionic species could open a new realm of possibilities toward the formation of red P. Electron paramagnetic resonance analysis of the formation of red P could provide insights if radical formation is a crucial step in this process. Additionally, nuclear magnetic resonance could be of some use in determining the ring size of intermediate species during oligomerization. Finally, our findings have also demonstrated the ability of the ab initio nanoreactor to inspire unique chemical hypotheses from the ground up. This suggests that further applications of the nanoreactor may be successful in generating reaction networks in systems that do not follow conventional rules, such as reactions dominated by noncarbon elements, ions, and/or radicals.

Computational Methods

The bulk of the calculations in this paper are in two categories—(1) the ab initio nanoreactor simulations for reaction discovery, and (2) conventional hypothesis testing involving the modeling and optimization of energy minima, transition states (TSs), and minimum energy paths (MEPs). The nanoreactor simulations were started from geometries consisting of P2 molecules and P2/P4 mixtures for consistency with experimental demonstration of red P oligomerization from diphosphorus.16−18 The reactions that are observed in the nanoreactor trajectories were converted into optimized MEPs in an automated procedure called energy refinement.112 Furthermore, the study of the nanoreactor pathways helped to inspire chemically similar mechanistic hypotheses that were not directly observed in the trajectories; these we modeled and investigated “manually”. We also incorporated potentially important reaction intermediates into the starting species of further nanoreactor simulations. In this way, the development of the reaction network involved several rounds of feedback between reaction discovery and hypothesis testing.

The ab initio nanoreactor simulations generally consisted of a number of randomly positioned and oriented P2 units and other small P clusters with a total of 40–80 atoms. Due to the exploratory nature of these simulations, various combinations of simulation parameters were employed as described in the Supporting Information (Table S3). A representative simulation used the B3LYP hybrid density functional with the 6-31G* basis set and DFT-D3 dispersion correction, with the simulation time step set to 1 fs and a Langevin thermostat set to 1000 K and a damping time of 0.150 ps. Each simulation was propagated for an average of 20 ps. The simulations were carried out with the TeraChem115−119 quantum chemistry software and initial conditions were generated using the PackMol120 software.

The accelerated reactivity is generated through the combination of high temperature—which is close to the experimental conditions of red P formation—and a time-dependent external potential that is the nanoreactor’s distinguishing feature (eq 1).

graphic file with name ic4c02299_m001.jpg
graphic file with name ic4c02299_m002.jpg 1

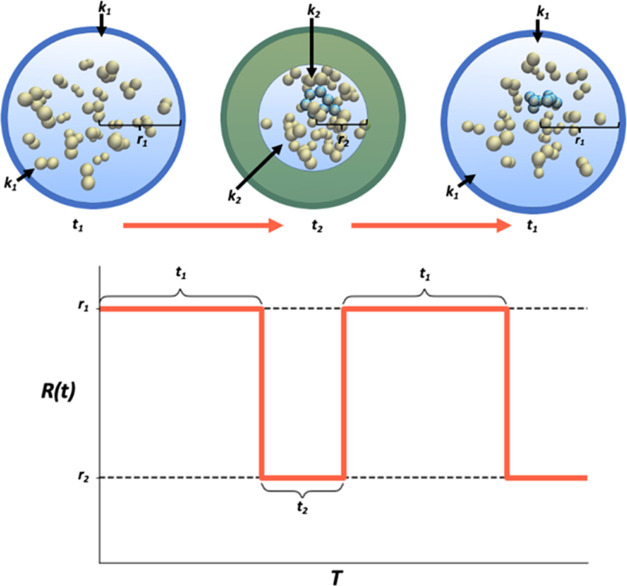
Here, m is the atomic mass, R1 and R2 are radius parameters (R2 < R1), and k1 and k2 are force constants. Equation 1 describes a flat-bottomed harmonic boundary potential with time-dependent parameters in which molecules are free to move within a sphere of R1 for some time period t1. After period t1, the radius of the spherical region with zero potential shrinks to R2; atoms outside of this radius are uniformly accelerated inward due to the mass-weighted force. The oscillating action induces high-velocity collisions that increase the number of observed reactions (Figure 10). Different combinations of the boundary potential parameters were tried to optimize the frequency of observing reactions that gave chemically reasonable activation barriers after energy refinement; recommended values are given in Rows 4 and 5 of Table S3.

Figure 10.

Figure 10

Open in a new tab

Nanoreactor oscillates between two boundary potentials. During t2-intervals with the more restricted boundary potential, molecules outside the r2-sphere are accelerated inward, inducing collisions and reactions. This process repeats as the molecules relax into the r1-sphere during the t1-intervals.

Reactions observed in the nanoreactor trajectories were automatically identified and extracted from the trajectory, then input into an energy refinement procedure112 in which the reactant, product, and transition state structures were optimized. This was followed by vibrational analysis of the TS structure and intrinsic reaction coordinate (IRC) calculations to verify the correctness of the MEP.121 These calculations were performed at a higher level of theory compared to the nanoreactor simulations, namely the ωB97X-D3 range-separated functional122 and the def-TZVP basis set.123 This density functional has been benchmarked against gold standards (CCSDT(T)) and showed a mean absolute errors of 2.1 and 3.0 kcal/mol for reaction barriers and reaction energies, respectively.124 It is also a computationally efficient choice, which is necessary due to the number of reactions explored and also the size of some of these systems (300+ electrons). Therefore, it is a reasonable choice for exploring our system. Approximate Gibbs free energies using the ideal gas/rigid rotor/harmonic oscillator approximation (abbreviated as “harmonic approximation”) were calculated with vibrational analysis of the transition state, product, and reactant structures. The optimizations were done in translation-rotation internal coordinates with the geomeTRIC software interfaced with TeraChem.125

We also performed metadynamics simulations of selected reactions to assess the margin of error of the harmonic approximation for Gibbs free energies, particularly for bimolecular association reactions. Well-tempered metadynamics simulations were carried out using TeraChem with the PlumEd126−128 plug-in, the ωB97X-D3 functional,122 and the def-TZVP Gaussian basis set.123 Simulations used a time step of 1 fs and were propagated for 500 ps. The Langevin thermostat was set to 500 K with a damping time of 150 fs. A bias factor of 5 was used with initial Gaussian height of 0.001 au, approximately 2% of the energy barrier, with a new biasing potential added every 100 fs. The collective variable was chosen to be the distance between the two phosphorus atoms forming a bond in the reaction of interest; a repulsive potential was placed at 15.0 Bohr.

Acknowledgments

We thank Kit Cummins for inspiring this project and initial guidance in addition to his former students Tiansi Xin and Mike Geeson for their feedback on this work and manuscript.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.4c02299.

  • Free energy comparisons; nanoreactor parameters; multi-reference schemes; xyz coordinates (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ic4c02299_si_001.pdf (2.1MB, pdf)

References

  1. Kolodiazhnyi O. I. Phosphorus Compounds of Natural Origin: Prebiotic, Stereochemistry, Application. Symmetry 2021, 13 (5), 889 10.3390/sym13050889. [DOI] [Google Scholar]
  2. Schrodter K.; Bettermann G.; Staffel T.; Wahl F.; Klein T.; Hofmann T.. Industrial Phosphorus. In Ullman’s Encyclopedia of Industrial Chemistry; Wiley, 2012; pp 503–519. [Google Scholar]
  3. Aparna A. R.; Brahmajirao V.; Karthikeyan T. V. Review on Synthesis and Characterization of Gallium Phosphide. Procedia Mater. Sci. 2014, 6, 1650–1657. 10.1016/j.mspro.2014.07.150. [DOI] [Google Scholar]
  4. Sahrawat K. L.; Abekoe M. K.; Diatta S.. Application of Inorganic Phosphorus Fertilizer. In Sustaining Soil Fertility in West Africa, SSSA Special Publications; Wiley, 2015; p 225. [Google Scholar]
  5. Rumble J. R.CRC Handbook of Chemistry and Physics, 102nd ed.; CRC Press/Taylor & Francis: Boca Raton, FL, 2021. [Google Scholar]
  6. Hultgren R.; Gingrich N. S.; Warren B. E. The Atomic Distribution in Red and Black Phosphorus and the Crystal Structure of Black Phosphorus. J. Chem. Phys. 1935, 3 (6), 351–355. 10.1063/1.1749671. [DOI] [Google Scholar]
  7. Smith A. J.; Roth W. L.; DeWitt T. W. Polymorphism of Red Phosphorus. J. Am. Chem. Soc. 1947, 69 (11), 2881–2885. 10.1021/ja01203a072. [DOI] [PubMed] [Google Scholar]
  8. Transue W. J.; Velian A.; Nava M.; Martin-Drumel M. A.; Womack C. C.; Jiang J.; Hou G. L.; Wang X. Bin.; McCarthy M. C.; Field R. W.; Cummins C. C. A Molecular Precursor to Phosphaethyne and Its Application in Synthesis of the Aromatic 1,2,3,4-Phosphatriazolate Anion. J. Am. Chem. Soc. 2016, 138 (21), 6731–6734. 10.1021/jacs.6b03910. [DOI] [PubMed] [Google Scholar]
  9. Geeson M. B.; Cummins C. C. Phosphoric Acid as a Precursor to Chemicals Traditionally Synthesized from White Phosphorus. Science 2018, 359 (6382), 1383–1385. 10.1126/science.aar6620. [DOI] [PubMed] [Google Scholar]
  10. Pham Minh D.; Ramaroson J.; Nzihou A.; Sharrock P. One-Step Synthesis of Sodium Trimetaphosphate (Na3P3O9) from Sodium Chloride and Orthophosphoric Acid. Ind. Eng. Chem. Res. 2012, 51 (10), 3851–3854. 10.1021/ie201085b. [DOI] [Google Scholar]
  11. Geeson M. B.; Cummins C. C. Let’s Make White Phosphorus Obsolete. ACS Cent. Sci. 2020, 6 (6), 848–860. 10.1021/acscentsci.0c00332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Popp F. D.; McEwen W. E. Polyphosphoric Acids As A Reagent In Organic Chemistry. Chem. Rev. 1958, 58 (2), 321–401. 10.1021/cr50020a004. [DOI] [Google Scholar]
  13. Scheschkewitz D. A Convenient P-Source. Nat. Chem. 2020, 12 (9), 785–787. 10.1038/s41557-020-0534-0. [DOI] [PubMed] [Google Scholar]
  14. Frenette B. L.; Trach J.; Ferguson M. J.; Rivard E. Frustrated Lewis Pair Adduct of Atomic P(−1) as a Source of Phosphinidenes (PR), Diphosphorus (P2), and Indium Phosphide. Angew. Chem., Int. Ed. 2023, 62 (10), e202218587 10.1002/anie.202218587. [DOI] [PubMed] [Google Scholar]
  15. Tofan D.; Cummins C. C. Photochemical Incorporation of Diphosphorus Units into Organic Molecules. Angew. Chem., Int. Ed. 2010, 49 (41), 7516–7518. 10.1002/anie.201004385. [DOI] [PubMed] [Google Scholar]
  16. Rathenau G. Optische Und Photochemische Versuche Mit Phosphor. Physica 1937, 4 (6), 503–514. 10.1016/S0031-8914(37)80084-1. [DOI] [Google Scholar]
  17. Melville H. W. The Photochemistry of Phosphine. Proc. R. Soc. London, Ser. A 1932, 138 (836), 374–395. 10.1098/rspa.1932.0190. [DOI] [Google Scholar]
  18. Melville H. W.; Gray S. C. Polymerization of Phosphorus. Trans. Faraday Soc. 1936, 32, 271–285. 10.1098/rspa.1932.0190. [DOI] [Google Scholar]
  19. Ruck M.; Hoppe D.; Wahl B.; Simon P.; Wang Y.; Seifert G. Fibrous Red Phosphorus. Angew. Chem., Int. Ed. 2005, 44 (46), 7616–7619. 10.1002/anie.200503017. [DOI] [PubMed] [Google Scholar]
  20. Thurn H.; Krebs H. Über Struktur Und Eigenschaften Der Halbmetalle. XXII. Die Kristallstruktur Des Hittorfschen Phosphors. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1969, 25 (1), 125–135. 10.1107/S0567740869001853. [DOI] [Google Scholar]
  21. Fasol G.; Cardona M.; Hönle W.; von Schnering H. G. Lattice Dynamics of Hittorf’s Phosphorus and Identification of Structural Groups and Defects in Amorphous Red Phosphorus. Solid State Commun. 1984, 52 (3), 307–310. 10.1016/0038-1098(84)90832-9. [DOI] [Google Scholar]
  22. Scheer M.; Balázs G.; Seitz A. P4 Activation by Main Group Elements and Compounds. Chem. Rev. 2010, 110 (7), 4236–4256. 10.1021/cr100010e. [DOI] [PubMed] [Google Scholar]
  23. Fung C. M.; Er C. C.; Tan L. L.; Mohamed A. R.; Chai S. P. Red Phosphorus: An Up-and-Coming Photocatalyst on the Horizon for Sustainable Energy Development and Environmental Remediation. Chem. Rev. 2022, 122 (3), 3879–3965. 10.1021/acs.chemrev.1c00068. [DOI] [PubMed] [Google Scholar]
  24. Tian H.; Wang J.; Lai G.; Dou Y.; Gao J.; Duan Z.; Feng X.; Wu Q.; He X.; Yao L.; Zeng L.; Liu Y.; Yang X.; Zhao J.; Zhuang S.; Shi J.; Qu G.; Yu X. F.; Chu P. K.; Jiang G. Renaissance of Elemental Phosphorus Materials: Properties, Synthesis, and Applications in Sustainable Energy and Environment. Chem. Soc. Rev. 2023, 52 (16), 5388–5484. 10.1039/D2CS01018F. [DOI] [PubMed] [Google Scholar]
  25. Wang F.; Ng W. K. H.; Yu J. C.; Zhu H.; Li C.; Zhang L.; Liu Z.; Li Q. Red Phosphorus: An Elemental Photocatalyst for Hydrogen Formation from Water. Appl. Catal., B 2012, 111–112, 409–414. 10.1016/j.apcatb.2011.10.028. [DOI] [Google Scholar]
  26. Wang F.; Li C.; Li Y.; Yu J. C. Hierarchical P/YPO4Microsphere for Photocatalytic Hydrogen Production from Water under Visible Light Irradiation. Appl. Catal., B 2012, 119–120, 267–272. 10.1016/j.apcatb.2012.03.011. [DOI] [Google Scholar]
  27. Dang H.; Dong X.; Dong Y.; Fan H.; Qiu Y. Enhancing the Photocatalytic H2 Evolution Activity of Red Phosphorous by Using Noble-Metal-Free Ni(OH)2 under Photoexcitation up to 700 Nm. RSC Adv. 2014, 4 (84), 44823–44826. 10.1039/C4RA06867J. [DOI] [Google Scholar]
  28. Cheng Z.; Fang W.; Zhao T.; Fang S.; Bi J.; Liang S.; Li L.; Yu Y.; Wu L. Efficient Visible-Light-Driven Photocatalytic Hydrogen Evolution on Phosphorus-Doped Covalent Triazine-Based Frameworks. ACS Appl. Mater. Interfaces 2018, 10 (48), 41415–41421. 10.1021/acsami.8b16013. [DOI] [PubMed] [Google Scholar]
  29. Chen J.; Huang S.; Long Y.; Wu J.; Li H.; Li Z.; Zeng Y.-J.; Ruan S. Fabrication of ZnO/Red Phosphorus Heterostructure for Effective Photocatalytic H2 Evolution from Water Splitting. Nanomaterials 2018, 8 (10), 835 10.3390/nano8100835. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Liu E.; Qi L.; Chen J.; Fan J.; Hu X. In Situ Fabrication of a 2D Ni2 P/Red Phosphorus Heterojunction for Efficient Photocatalytic H2 Evolution. Mater. Res. Bull. 2019, 115, 27–36. 10.1016/j.materresbull.2019.03.011. [DOI] [Google Scholar]
  31. Liu Y.; Hu Z.; Yu J. C. Liquid Bismuth Initiated Growth of Phosphorus Microbelts with Efficient Charge Polarization for Photocatalysis. Appl. Catal., B 2019, 247, 100–106. 10.1016/j.apcatb.2019.01.092. [DOI] [Google Scholar]
  32. Zhang M.; Liu J.; Liu L.; Sun K.; Liang X.; Wan J.; Fu F. A New High-Yield Fabrication Approach for Porous Red Phosphorus Nanosheets Using N-Methyl-2-Pyrrolidone with Multiple Photocatalytic Reduction Applications. Ceram. Int. 2020, 46 (14), 23165–23172. 10.1016/j.ceramint.2020.06.096. [DOI] [Google Scholar]
  33. Wang M.; Qin Z.; Diao Z.; Li R.; Zhong J.; Ma D.; Chen Y. Red Phosphorus/Carbon Nitride van Der Waals Heterostructure for Photocatalytic Pure Water Splitting under Wide-Spectrum Light Irradiation. ACS Sustainable Chem. Eng. 2020, 8 (35), 13459–13466. 10.1021/acssuschemeng.0c04372. [DOI] [Google Scholar]
  34. Zhu Y.; Lv C.; Yin Z.; Ren J.; Yang X.; Dong C.-L.; Liu H.; Cai R.; Huang Y.-C.; Theis W.; Shen S.; Yang D. A [001]-Oriented Hittorf’s Phosphorus Nanorods/Polymeric Carbon Nitride Heterostructure for Boosting Wide-Spectrum-Responsive Photocatalytic Hydrogen Evolution from Pure Water. Angew. Chem., Int. Ed. 2020, 59 (2), 868–873. 10.1002/anie.201911503. [DOI] [PubMed] [Google Scholar]
  35. Jia J.; Bai X.; Zhang Q.; Hu X.; Liu E.; Fan J. Porous Honeycomb-like NiSe2/Red Phosphorus Heteroarchitectures for Photocatalytic Hydrogen Production. Nanoscale 2020, 12 (9), 5636–5651. 10.1039/C9NR09757K. [DOI] [PubMed] [Google Scholar]
  36. Xu M.; Jiang L.; Wang J.; Feng S.; Tremblay P. L.; Zhang T. Efficient Photocatalytic Hydrogen Evolution with High-Crystallinity and Noble Metal-Free Red Phosphorus-CdS Nanorods. Int. J. Hydrogen Energy 2020, 45 (35), 17354–17366. 10.1016/j.ijhydene.2020.04.200. [DOI] [Google Scholar]
  37. Guo C.; Du H.; Ma Y.; Qi K.; Zhu E.; Su Z.; Huojiaaihemaiti M.; Wang X. Visible-Light Photocatalytic Activity Enhancement of Red Phosphorus Dispersed on the Exfoliated Kaolin for Pollutant Degradation and Hydrogen Evolution. J. Colloid Interface Sci. 2021, 585, 167–177. 10.1016/j.jcis.2020.11.055. [DOI] [PubMed] [Google Scholar]
  38. Hu L.; Xu J.; Zhao S.; Li X.; Li L.; Ran L. Red/Black Phosphorus Z-Scheme Heterogeneous Junction Modulated by Co-MOF for Enhanced Photocatalytic Hydrogen Evolution. Catal. Lett. 2021, 151 (9), 2658–2672. 10.1007/s10562-020-03507-2. [DOI] [Google Scholar]
  39. Chen N.; Cao J.; Guo M.; Liu C.; Lin H.; Chen S. Novel NiO/RP Composite with Remarkably Enhanced Photocatalytic Activity for H2 Evolution from Water. Int. J. Hydrogen Energy 2021, 46 (37), 19363–19372. 10.1016/j.ijhydene.2021.03.091. [DOI] [Google Scholar]
  40. Ansari S. A.; Cho M. H. Highly Visible Light Responsive, Narrow Band Gap TiO2 Nanoparticles Modified by Elemental Red Phosphorus for Photocatalysis and Photoelectrochemical Applications. Sci. Rep. 2016, 6, 25405 10.1038/srep25405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhou H.; Xu S.; Zhang D.; Chen S.; Deng J. One Step in Situ Synthesis of Core-Shell Structured Cr2O3:P@fibrous-Phosphorus Hybrid Composites with Highly Efficient Full-Spectrum-Response Photocatalytic Activities. Nanoscale 2017, 9 (9), 3196–3205. 10.1039/C6NR09584D. [DOI] [PubMed] [Google Scholar]
  42. Wang J.; Pi M.; Zhang D.; Chen S. The Visible-Light Photocatalytic Activity for Enhancing RhB Degradation and Hydrogen Evolution from SrTiO3 Nanoparticles Decorated Red Phosphorus Nanorods as Photocatalysts. J. Phys. D: Appl. Phys. 2020, 53 (8), 085501 10.1088/1361-6463/ab58df. [DOI] [Google Scholar]
  43. Athira T. K.; Roshith M.; Babu T. G. S.; Kumar D. V. R. Fibrous Red Phosphorus as a Non-Metallic Photocatalyst for the Effective Reduction of Cr(VI) under Direct Sunlight. Mater. Lett. 2021, 283, 128750 10.1016/j.matlet.2020.128750. [DOI] [Google Scholar]
  44. Wang W.; Li G.; An T.; Chan D. K. L.; Yu J. C.; Wong P. K. Photocatalytic Hydrogen Evolution and Bacterial Inactivation Utilizing Sonochemical-Synthesized g-C3N4/Red Phosphorus Hybrid Nanosheets as a Wide-Spectral-Responsive Photocatalyst: The Role of Type I Band Alignment. Appl. Catal., B 2018, 238, 126–135. 10.1016/j.apcatb.2018.07.004. [DOI] [Google Scholar]
  45. Roshith M.; Kumar M. S.; Kumar A. K. N.; Ramasubramanian S.; Stanley J.; Babu T. G. S.; Kumar D. V. R. Urchin-like Fibrous Red Phosphorus as an Efficient Photocatalyst for Solar-Light-Driven Disinfection of E. Coli. J. Photochem. Photobiol., A 2019, 384, 112034 10.1016/j.jphotochem.2019.112034. [DOI] [Google Scholar]
  46. Kaur H.; Konkena B.; Gabbett C.; Smith R.; McCrystall M.; Tian R.; Roy A.; Carey T.; Vega-Mayoral V.; Nicolosi V.; Coleman J. N. Amorphous 2D-Nanoplatelets of Red Phosphorus Obtained by Liquid-Phase Exfoliation Yield High Areal Capacity Na-Ion Battery Anodes. Adv. Energy Mater. 2023, 13 (6), 2203013 10.1002/aenm.202203013. [DOI] [Google Scholar]
  47. Kim Y.; Park Y.; Choi A.; Choi N. S.; Kim J.; Lee J.; Ryu J. H.; Oh S. M.; Lee K. T. An Amorphous Red Phosphorus/Carbon Composite as a Promising Anode Material for Sodium Ion Batteries. Adv. Mater. 2013, 25 (22), 3045–3049. 10.1002/adma.201204877. [DOI] [PubMed] [Google Scholar]
  48. Liu W.; Ju S.; Yu X. Phosphorus-Amine-Based Synthesis of Nanoscale Red Phosphorus for Application to Sodium-Ion Batteries. ACS Nano 2020, 14 (1), 974–984. 10.1021/acsnano.9b08282. [DOI] [PubMed] [Google Scholar]
  49. Kong W.; Xu S.; Yin J.; Yang H.; Feng W.; Cui L.; Wen Z. A Novel Red Phosphorus/Reduced Graphene Oxide-C3N4 Composite with Enhanced Sodium Storage Capability. J. Electroanal. Chem. 2021, 902, 115819 10.1016/j.jelechem.2021.115819. [DOI] [Google Scholar]
  50. Zhu Z.; Pei Z.; Liu B.; Sun D.; Fang Y.; Lei X.; Liu X.; Niu S.; Pan H.; Zhou J.; Qian Y.; Wang G. Hierarchical Ion/Electron Networks Enable Efficient Red Phosphorus Anode with High Mass Loading for Sodium Ion Batteries. Adv. Funct. Mater. 2022, 32 (16), 2110444 10.1002/adfm.202110444. [DOI] [Google Scholar]
  51. He S.-A.; Liu Q.; Cui Z.; Xu K.; Zou R.; Luo W.; Zhu M. Red Phosphorus Anchored on Nitrogen-Doped Carbon Bubble-Carbon Nanotube Network for Highly Stable and Fast-Charging Lithium-Ion Batteries. Small 2022, 18 (7), 2105866 10.1002/smll.202105866. [DOI] [PubMed] [Google Scholar]
  52. Sun Y.; Wu Q.; Zhang K.; Liu Y.; Liang X.; Xiang H. A High Areal Capacity Sodium-Ion Battery Anode Enabled by a Free-Standing Red Phosphorus@N-Doped Graphene/CNTs Aerogel. Chem. Commun. 2022, 58 (51), 7120–7123. 10.1039/D2CC02265F. [DOI] [PubMed] [Google Scholar]
  53. Song J.; Peng X.; Liu D.; Li H.; Wu M.; Fang K.; Zhu X.; Xiang X.; Tang H. On-Site Conversion Reaction Enables Ion-Conducting Surface on Red Phosphorus/Carbon Anode for Durable and Fast Sodium-Ion Batteries. J. Energy Chem. 2023, 80, 381–391. 10.1016/j.jechem.2023.01.027. [DOI] [Google Scholar]
  54. Luan Q.; Xue X.; Feng H.; Tao L.; Zhou D.; Chen T.; Tan M.; Dong W. In-Plane Carrier Regulation and Hydrogen Adsorption/Desorption Optimization of P4 Molecule Anchored Vs-ZnIn2S4–x for Improve Photocatalytic Activity. Appl. Catal., B 2023, 337, 122932 10.1016/j.apcatb.2023.122932. [DOI] [Google Scholar]
  55. Huang H.; Xie D.; Zheng Z.; Zeng Y.; Xie S.; Liu P.; Zhang M.; Wang S.; Cheng F. Recycled Graphite from Spent Lithium-Ion Batteries as a Conductive Framework Directly Applied in Red Phosphorus-Based Anodes. ACS Appl. Mater. Interfaces 2023, 15 (45), 52686–52695. 10.1021/acsami.3c13615. [DOI] [PubMed] [Google Scholar]
  56. Baudler M.; Glinka K. Monocyclic and Polycyclic Phosphanes. Chem. Rev. 1993, 93, 1623–1667. 10.1021/cr00020a010. [DOI] [Google Scholar]
  57. Hennersdorf F.; Weigand J. J. A Tetracyclic Octaphosphane by Successive Addition, Inversion, and Condensation Reactions. Angew. Chem., Int. Ed. 2017, 56 (27), 7858–7862. 10.1002/anie.201703953. [DOI] [PubMed] [Google Scholar]
  58. Hennersdorf F.; Frötschel J.; Weigand J. J. Selective Derivatization of a Hexaphosphane from Functionalization of White Phosphorus. J. Am. Chem. Soc. 2017, 139 (41), 14592–14604. 10.1021/jacs.7b07704. [DOI] [PubMed] [Google Scholar]
  59. Eilrich V. J.; Grell T.; Lönnecke P.; Hey-Hawkins E. Coordination Chemistry of Hepta-Tert-Butylnonaphosphane. Dalton Trans. 2022, 51 (29), 10887–10897. 10.1039/D2DT01691E. [DOI] [PubMed] [Google Scholar]
  60. Ziegler C. G. P.; Maier T. M.; Pelties S.; Taube C.; Hennersdorf F.; Ehlers A. W.; Weigand J. J.; Wolf R. Construction of Alkyl-Substituted Pentaphosphido Ligands in the Coordination Sphere of Cobalt. Chem. Sci. 2019, 10 (5), 1302–1308. 10.1039/C8SC04745F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Gendy C.; Valjus J.; Roesler R.; Tuononen H. M. Haptotropism in a Nickel Complex with a Neutral, π-Bridging Cyclo-P4 Ligand Analogous to Cyclobutadiene. Angew. Chem., Int. Ed. 2022, 61 (18), e202115692 10.1002/anie.202115692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Wang S.; Sears J. D.; Moore C. E.; Rheingold A. L.; Neidig M. L.; Figueroa J. S. Side-on Coordination of Diphosphorus to a Mononuclear Iron Center. Science 2022, 375 (6587), 1393–1397. 10.1126/science.abn7100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Edgar M.; Elsegood M. R. J.; Liu P.; Miles C. R.; Smith M. B.; Wu S. Dinuclear Palladium(II) and Platinum(II) Complexes of a Readily Accessible Bicyclic Diphosphane. Eur. J. Inorg. Chem. 2022, 2022 (12), e202200017 10.1002/ejic.202200017. [DOI] [Google Scholar]
  64. Yang C.; Jiang X.; Chen Q.; Leng X.; Xiao J.; Ye S.; Deng L. Signet-Ring-Shaped Octaphosphorus-Cobalt Complexes: Synthesis, Structure, and Functionalization Reactions with Carbene Analogs. J. Am. Chem. Soc. 2022, 144 (45), 20785–20796. 10.1021/jacs.2c08647. [DOI] [PubMed] [Google Scholar]
  65. Senthil S.; Gau M. R.; Mindiola D. J. A Contiguous Tricyclic [P6]2-Framework Spanning Across Two Vanadium(III) Centers. Organometallics 2023, 42 (11), 1048–1051. 10.1021/acs.organomet.2c00638. [DOI] [Google Scholar]
  66. Eilrich V. J.; Hey-Hawkins E. Cyclooligophosphanes and Their Coordination Chemistry. Coord. Chem. Rev. 2021, 437, 213749 10.1016/j.ccr.2020.213749. [DOI] [Google Scholar]
  67. Pauling L.; Simonetta M. Bond Orbitals and Bond Energy in Elementary Phosphorus. J. Chem. Phys. 1952, 20 (1), 29–34. 10.1063/1.1700191. [DOI] [Google Scholar]
  68. Baudler M.; Ternberger H.; Faber W.; Hahn J. Li3P7, Ein Polyphosphid Mit Fluktuierenden Bindungen: Synthese Aus P2H4 Und Überführung in P7H3. Z. Naturforsch. 1979, 34, 1690–1697. 10.1515/znb-1979-1214. [DOI] [Google Scholar]
  69. Baudler M.; Faber W. Einfache Darstellung von Trilithium-heptaphosphid Aus Farblosem Phosphor Und Lithiumdihydrogenphosphid. Chem. Ber. 1980, 113 (10), 3394–3395. 10.1002/cber.19801131032. [DOI] [Google Scholar]
  70. Baudler M.; Heumüller R.; Langerbeins K. Dilithium-Hydrogenheptaphosphid, LiHP7 - Ein Teilmetalliertes Derivat von P7H3: Darstellung Und Strukturelle Charakterisierung. Z. Anorg. Allg. Chem. 1984, 514, 7–17. 10.1002/zaac.19845140702. [DOI] [Google Scholar]
  71. Baudler M.; Heumüller R.; Germeshausen J.; Hahn J. Dilithium-Dihydrogentetradecaphosphid, Li2H2P14: Darstellung Und Strukturelle Charakterisierung. Z. Anorg. Allg. Chem. 1985, 526, 7–14. 10.1002/zaac.19845140702. [DOI] [Google Scholar]
  72. Baudler M.; Heumüller R. Lithium-Tetrahydrogenheptaphosphid Und Lithium-Octahydrogenheptaphosphid. Z. Anorg. Allg. Chem. 1988, 559, 49–56. 10.1002/zaac.19845140702. [DOI] [Google Scholar]
  73. Böcker S.; Häser M. Covalent Structures of Phosphorus: A Comprehensive Theoretical Study. Z. Anorg. Allg. Chem. 1995, 621 (2), 258–286. 10.1002/zaac.19956210215. [DOI] [Google Scholar]
  74. Kerwin L. Some Mass Spectrometric Data on Phosphorus. Can. J. Phys. 1954, 32 (12), 757–758. 10.1139/p54-082. [DOI] [Google Scholar]
  75. Carette J.-D.; Kerwin L. Une Étude Du Phosphore Rouge Par Spectrométrie de Masse. Can. J. Phys. 1961, 39, 1300–1319. 10.1139/p61-155. [DOI] [Google Scholar]
  76. Kane J. S.; Reynolds J. H. Mass Spectrometer Study of the Vapors from Red Phosphorus and Arsenic. J. Chem. Phys. 1956, 25 (2), 342–349. 10.1063/1.1742883. [DOI] [Google Scholar]
  77. Smets J.; Coppens P.; Drowart J. Photoionization with Mass Spectkometric Analysis of the Tetraphosphorus Molecule. Chem. Phys. 1977, 20, 243–251. 10.1016/0301-0104(77)85028-3. [DOI] [Google Scholar]
  78. Martin T. P. Compound Clusters. Z. Phys. D At., Mol. Clust. 1986, 3 (2), 211–217. 10.1007/BF01384809. [DOI] [Google Scholar]
  79. Huang R.; Li H.; Lin Z.; Yang S. Experimental and Theoretical Studies of Small Homoatomic Phosphorus Clusters. J. Phys. Chem. A 1995, 99 (5), 1418–1423. 10.1021/j100005a009. [DOI] [Google Scholar]
  80. Chen M. D.; Li J. T.; Huang R. B.; Zheng L. S.; Au C. T. Structure Prediction of Large Cationic Phosphorus Clusters. Chem. Phys. Lett. 1999, 305 (5–6), 439–445. 10.1016/S0009-2614(99)00403-0. [DOI] [Google Scholar]
  81. Sládková K.; Houška J.; Havel J. Laser Desorption Ionization of Red Phosphorus Clusters and Their Use for Mass Calibration in Time-of-Flight Mass Spectrometry. Rapid Commun. Mass Spectrom. 2009, 23 (19), 3114–3118. 10.1002/rcm.4230. [DOI] [PubMed] [Google Scholar]
  82. Kolářová L.; Prokeš L.; Kučera L.; Hampl A.; Peňa-Méndez E.; Vaňhara P.; Havel J. Clusters of Monoisotopic Elements for Calibration in (TOF) Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2017, 28 (3), 419–427. 10.1007/s13361-016-1567-x. [DOI] [PubMed] [Google Scholar]
  83. Trinquier G.; Malrieu J.; Daudley J.-P. Ab Initio Study of the Regular Polyhedral Molecules N4, P4, As4, N8, P8 and As8. Chem. Phys. Lett. 1981, 80 (3), 552–557. 10.1016/0009-2614(81)85076-2. [DOI] [Google Scholar]
  84. Ahlrichs R.; Brode S.; Ehrhardt C. Theoretical Study of the Stability of Molecular P2, P4 (Td), and P8 (Oh). J. Am. Chem. Soc. 1985, 107 (25), 7260–7264. 10.1021/ja00311a005. [DOI] [Google Scholar]
  85. Schiffer H.; Ahlrichs R.; Häser M. Theoretical Investigation of next Neighbour Interactions and Ring Strain in Linear and Monocyclic Phosphanes. Theor. Chim. Acta 1989, 75 (1), 1–10. 10.1007/BF01151229. [DOI] [Google Scholar]
  86. Haeser M.; Schneider U.; Ahlrichs R. Clusters of Phosphorus: A Theoretical Investigation. J. Am. Chem. Soc. 1992, 114 (24), 9551–9559. 10.1021/ja00050a039. [DOI] [Google Scholar]
  87. Jones R. O.; Hohl D. Structure of Phosphorus Clusters Using Simulated Annealing - P2 to P8. J. Chem. Phys. 1990, 92 (11), 6710–6721. 10.1063/1.458306. [DOI] [Google Scholar]
  88. Jones R. O.; Seifert G. Structure of Phosphorus Clusters Using Simulated Annealing. II. P9, P10, P11, Anions P42-, P102-, P113-, and Cations PN+ to N = 11. J. Chem. Phys. 1992, 96 (10), 7564–7572. 10.1063/1.462408. [DOI] [Google Scholar]
  89. Ballone P.; Jones R. O. Density Functional Study of Phosphorus and Arsenic Clusters Using Local and Non Local Energy Functionals. J. Chem. Phys. 1994, 100, 4941–4946. 10.1063/1.467213. [DOI] [Google Scholar]
  90. Elliott S. R.; D J. C.; M E. The Structure of Amorphous Phophorus. J. Phys. Colloq. 1985, 46 (C8), 349–353. 10.1051/jphyscol:1985852. [DOI] [Google Scholar]
  91. Haeser M. Structural Rules of Phosphorus. J. Am. Chem. Soc. 1994, 116 (15), 6925–6926. 10.1021/ja00094a053. [DOI] [Google Scholar]
  92. Häser M.; Treutler O. Calculated Properties of P2, P4, and of Closed-Shell Clusters up to P18. J. Chem. Phys. 1995, 102, 3703–3711. 10.1063/1.468552. [DOI] [Google Scholar]
  93. Warren D. S.; Gimarc B. M. Valence Isomers of Benzene and Their Relationship to Isomers of Isoelectronic P6. J. Am. Chem. Soc. 1992, 114 (13), 5378–5385. 10.1021/ja00039a058. [DOI] [Google Scholar]
  94. Gimarc B. M.; Warren D. S. Relative Energies and Strain Energies of Proposed Structures for Octaphosphorus. Inorg. Chem. 1993, 32 (9), 1850–1856. 10.1021/ic00061a050. [DOI] [Google Scholar]
  95. Warren D. S.; Gimarc B. M. Maximum Hardness in P6 Isomers. Int. J. Quantum Chem. 1994, 49 (3), 207–213. 10.1002/qua.560490312. [DOI] [Google Scholar]
  96. Chen M. D.; Huang R. B.; Zheng L. S.; Au C. T. The Prediction of Isomers for the Phosphorus Clusters P7+. Main Group Met. Chem. 1999, 22 (8), 479–483. 10.1515/MGMC.1999.22.8.479. [DOI] [Google Scholar]
  97. Chen M. D.; Luo H. B.; Liu M. H.; Zhang Q. E.; Au C. T. A Theoretical Study of the Isomers of Phosphorus Clusters P11, P11+ and P11–. Main Group Met. Chem. 2000, 23 (7), 361–367. 10.1515/MGMC.2000.23.7.361. [DOI] [Google Scholar]
  98. Chen M. D.; Chen Q. B.; Liu J.; Zheng L. S.; Zhang Q. E.; Au C. T. Parity Alternation of Ground-State Pn– and PN+ (n = 3–15) Phosphorus Clusters. J. Phys. Chem. A 2007, 111 (2), 216–222. 10.1021/jp0669355. [DOI] [PubMed] [Google Scholar]
  99. Guo L.; Wu H.; Jin Z. First Principles Study of the Evolution of the Properties of Neutral and Charged Phosphorus Clusters. J. Mol. Struct.: THEOCHEM 2004, 677, 59–66. 10.1016/j.theochem.2004.02.014. [DOI] [Google Scholar]
  100. Xue T.; Luo J.; Shen S.; Li F.; Zhao J. Lowest-Energy Structures of Cationic P2m+1+ (m = 1–12) Clusters from First-Principles Simulated Annealing. Chem. Phys. Lett. 2010, 485 (1–3), 26–30. 10.1016/j.cplett.2009.12.019. [DOI] [Google Scholar]
  101. Zimmerman P. M. Navigating Molecular Space for Reaction Mechanisms: An Efficient, Automated Procedure. Mol. Simul. 2015, 41 (1–3), 43–54. 10.1080/08927022.2014.894999. [DOI] [Google Scholar]
  102. Dewyer A. L.; Zimmerman P. M. Finding Reaction Mechanisms, Intuitive or Otherwise. Org. Biomol. Chem. 2017, 15 (3), 501–504. 10.1039/C6OB02183B. [DOI] [PubMed] [Google Scholar]
  103. Jafari M.; Zimmerman P. M. Uncovering Reaction Sequences on Surfaces through Graphical Methods. Phys. Chem. Chem. Phys. 2018, 20 (11), 7721–7729. 10.1039/C8CP00044A. [DOI] [PubMed] [Google Scholar]
  104. Matheu D. M.; Dean A. M.; Grenda J. M.; Green W. H. Mechanism Generation with Integrated Pressure Dependence: A New Model for Methane Pyrolysis. J. Phys. Chem. A 2003, 107 (41), 8552–8565. 10.1021/jp0345957. [DOI] [Google Scholar]
  105. Gao C. W.; Allen J. W.; Green W. H.; West R. H. Reaction Mechanism Generator: Automatic Construction of Chemical Kinetic Mechanisms. Comput. Phys. Commun. 2016, 203, 212–225. 10.1016/j.cpc.2016.02.013. [DOI] [Google Scholar]
  106. Bergeler M.; Simm G. N.; Proppe J.; Reiher M. Heuristics-Guided Exploration of Reaction Mechanisms. J. Chem. Theory Comput. 2015, 11 (12), 5712–5722. 10.1021/acs.jctc.5b00866. [DOI] [PubMed] [Google Scholar]
  107. Martínez-Núñez E. An Automated Method to Find Transition States Using Chemical Dynamics Simulations. J. Comput. Chem. 2015, 36 (4), 222–234. 10.1002/jcc.23790. [DOI] [PubMed] [Google Scholar]
  108. Martínez-Núñez E. An Automated Transition State Search Using Classical Trajectories Initialized at Multiple Minima. Phys. Chem. Chem. Phys. 2015, 17 (22), 14912–14921. 10.1039/C5CP02175H. [DOI] [PubMed] [Google Scholar]
  109. Varela J. A.; Vázquez S. A.; Martínez-Núñez E. An Automated Method to Find Reaction Mechanisms and Solve the Kinetics in Organometallic Catalysis. Chem. Sci. 2017, 8 (5), 3843–3851. 10.1039/C7SC00549K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  110. Pietrucci F.; Andreoni W. Graph Theory Meets Ab Initio Molecular Dynamics: Atomic Structures and Transformations at the Nanoscale. Phys. Rev. Lett. 2011, 107 (8), 085504 10.1103/PhysRevLett.107.085504. [DOI] [PubMed] [Google Scholar]
  111. Wang L. P.; Titov A.; McGibbon R.; Liu F.; Pande V. S.; Martínez T. J. Discovering Chemistry with an Ab Initio Nanoreactor. Nat. Chem. 2014, 6 (12), 1044–1048. 10.1038/nchem.2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  112. Wang L. P.; McGibbon R. T.; Pande V. S.; Martinez T. J. Automated Discovery and Refinement of Reactive Molecular Dynamics Pathways. J. Chem. Theory Comput. 2016, 12 (2), 638–649. 10.1021/acs.jctc.5b00830. [DOI] [PubMed] [Google Scholar]
  113. Wang L. P.; Tofan D.; Chen J.; Van Voorhis T.; Cummins C. C. A Pathway to Diphosphorus from the Dissociation of Photoexcited Tetraphosphorus. RSC Adv. 2013, 3 (45), 23166–23171. 10.1039/c3ra43940b. [DOI] [Google Scholar]
  114. Vitillo J. G.; Cramer C. J.; Gagliardi L. Multireference Methods Are Realistic and Useful Tools for Modeling Catalysis. Isr. J. Chem. 2022, 62 (1–2), e202100136 10.1002/ijch.202100136. [DOI] [Google Scholar]
  115. Ufimtsev I. S.; Martínez T. J. Quantum Chemistry on Graphical Processing Units. 1. Strategies for Two-Electron Integral Evaluation. J. Chem. Theory Comput. 2008, 4 (2), 222–231. 10.1021/ct700268q. [DOI] [PubMed] [Google Scholar]
  116. Ufimtsev I. S.; Martinez T. J. Quantum Chemistry on Graphical Processing Units. 2. Direct Self-Consistent-Field Implementation. J. Chem. Theory Comput. 2009, 5 (4), 1004–1015. 10.1021/ct800526s. [DOI] [PubMed] [Google Scholar]
  117. Ufimtsev I. S.; Martinez T. J. Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics. J. Chem. Theory Comput. 2009, 5 (10), 2619–2628. 10.1021/ct9003004. [DOI] [PubMed] [Google Scholar]
  118. Snyder J. W.; Curchod B. F. E.; Martínez T. J. GPU-Accelerated State-Averaged Complete Active Space Self-Consistent Field Interfaced with Ab Initio Multiple Spawning Unravels the Photodynamics of Provitamin D3. J. Phys. Chem. Lett. 2016, 7 (13), 2444–2449. 10.1021/acs.jpclett.6b00970. [DOI] [PubMed] [Google Scholar]
  119. Liu F.; Sanchez D. M.; Kulik H. J.; Martínez T. J. Exploiting Graphical Processing Units to Enable Quantum Chemistry Calculation of Large Solvated Molecules with Conductor-like Polarizable Continuum Models. Int. J. Quantum Chem. 2019, 119 (1), e25760 10.1002/qua.25760. [DOI] [Google Scholar]
  120. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30 (13), 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  121. Fukui K. The Path of Chemical Reactions - the IRC Approach. Acc. Chem. Res. 1981, 14 (12), 363–368. 10.1021/ar00072a001. [DOI] [Google Scholar]
  122. Lin Y. S.; Li G.-D.; Mao S. P.; Chai J.-D. Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections. J. Chem. Theory Comput. 2013, 9 (1), 263–272. 10.1021/ct300715s. [DOI] [PubMed] [Google Scholar]
  123. Eichkorn K.; Weigend F.; Treutler O.; Ahlrichs R. Auxiliary Basis Sets for Main Row Atoms and Transition Metals and Their Use to Approximate Coulomb Potentials. Theor. Chem. Acc. 1997, 97 (1–4), 119–124. 10.1007/s002140050244. [DOI] [Google Scholar]
  124. Goerigk L.; Hansen A.; Bauer C.; Ehrlich S.; Najibi A.; Grimme S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19 (48), 32184–32215. 10.1039/C7CP04913G. [DOI] [PubMed] [Google Scholar]
  125. Wang L. P.; Song C. Geometry Optimization Made Simple with Translation and Rotation Coordinates. J. Chem. Phys. 2016, 144 (21), 214108 10.1063/1.4952956. [DOI] [PubMed] [Google Scholar]
  126. Bonomi M.; Branduardi D.; Bussi G.; Camilloni C.; Provasi D.; Raiteri P.; Donadio D.; Marinelli F.; Pietrucci F.; Broglia R. A.; Parrinello M. PLUMED: A Portable Plugin for Free-Energy Calculations with Molecular Dynamics. Comput. Phys. Commun. 2009, 180 (10), 1961–1972. 10.1016/j.cpc.2009.05.011. [DOI] [Google Scholar]
  127. Tribello G. A.; Bonomi M.; Branduardi D.; Camilloni C.; Bussi G. PLUMED 2: New Feathers for an Old Bird. Comput. Phys. Commun. 2014, 185 (2), 604–613. 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
  128. Promoting Transparency and Reproducibility in Enhanced Molecular Simulations. Nat. Methods 2019, 16 (8), 670–673. 10.1038/s41592-019-0506-8. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic4c02299_si_001.pdf (2.1MB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES