Spatial Modeling With Spatially Varying Coefficient Processes

Abstract

In many applications, the objective is to build regression models to explain a response variable over a region of interest under the assumption that the responses are spatially correlated. In nearly all of this work, the regression coefficients are assumed to be constant over the region. However, in some applications, coefficients are expected to vary at the local or subregional level. Here we focus on the local case. Although parametric modeling of the spatial surface for the coefficient is possible, here we argue that it is more natural and flexible to view the surface as a realization from a spatial process. We show how such modeling can be formalized in the context of Gaussian responses providing attractive interpretation in terms of both random effects and explaining residuals. We also offer extensions to generalized linear models and to spatio-temporal setting. We illustrate both static and dynamic modeling with a dataset that attempts to explain (log) selling price of single-family houses.

1. INTRODUCTION

The broad availability of fast, inexpensive computing along with the development of very capable, user-friendly geographic information systems (GIS) software has led to the increased collection of spatial and spatio-temporal data in such diverse fields as real estate/finance, epidemiology, environmetrics/ecology, and communications. In turn, this has fueled increased spatial modeling and data analysis activity within the statistical community.

In many applications, the objective is to build regression models to explain a response variable observed over a region of interest, say $D$, under the assumption that the responses are spatially associated. That is, whereas some spatial modeling may be accomplished through the mean, it is still anticipated that the responses are dependent and that this dependence becomes stronger as pairs of responses become closer in space. With continuous response that is point referenced, if a normality assumption (perhaps on a transformed scale) seems plausible, this dependence is typically modeled directly using a Gaussian process. The literature here is enormous. The book by Cressie (1993) is perhaps a place to start. In the case of, say, binary or count response, a hierarchical model is often adopted using an exponential family model at the first stage and then introducing normally distributed spatial random effects into the mean structure on a transformed scale related by a link function (see, e.g., Diggle, Tawn, and Moyeed 1998).

In nearly all of this work, the regression coefficients are assumed to be constant across the region. In certain applications, this would not be appropriate. The coefficients may be expected to vary at the local or subregion level. For instance, Assunçao, Gamerman, and Assunçao (1999) introduced a Bayesian space varying parameter model to examine microregion factor productivity and the degree of factor substitution in the Brazilian agriculture. Agarwal, Gelfand, Sirmans, and Thibadeau (2003), in the context of locally stationary spatial modeling, introduced local regression models for factors affecting house price at the school district (and sub-school district) level. A flexible modeling approach for space-varying regression models was developed with a simulation study by Gamerman, Moreira, and Rue (2001). These authors all made the rather restrictive assumption that for a given coefficient, it is constant on specified areal units. The levels of the surface on these units is modeled using independent or conditionally autoregressive specifications. Concerns arise about the arbitrariness of the scale of resolution, the lack of smoothness of the surface, and the inability to interpolate the value of the surface to individual locations. When working with point-referenced data, it will be more attractive to allow the coefficients to vary by location, to envision a spatial surface for a particular coefficient. For instance, in our application we also model the (log) selling price of single family houses. Customary explanatory variables include the age of the house, the square feet of living area, the square feet of other area, and the number of bathrooms. If the region of interest is a city or greater metropolitan area, then it is evident that the capitalization rate (e.g., for age), will vary across the region. Older houses will have higher value in some parts of the region than in other parts. By allowing the coefficient of age to vary with location, we can remedy the foregoing concerns. With practical interest in mind, say real estate appraisal, we can predict the coefficient for arbitrary properties, not just for those that sold during the period of investigation. Similar issues arise in modeling environmental exposure to a particular pollutant, where covariates might include temperature and precipitation.

One possible approach would be to model the spatial surface for the coefficient parametrically. In the simplest case this would require the rather arbitrary specification of a polynomial surface function; a range of surfaces too limited or inflexible might result. More flexibility could be introduced using a spline surface over two-dimensional space (see, e.g., Luo and Wahba 1998). However, this requires selection of a spline function and determination of the number of and locations of the knots in the space. Also, with multiple coefficients, a multivariate specification of a spline surface is required. The approach that we adopt here is arguably more natural and at least as flexible. We model the spatially varying coefficient surface as a realization from a spatial process. For multiple coefficients, we use a multivariate spatial process model. In fact, we use a stationary specification in which desired degree of smoothness of process realization can be modeled through the choice of covariance function (e.g., the Matèrn class). Kent (1989) and Stein (1999a) have provided discussions of univariate process; Banerjee and Gelfand (2003), of multivariate process. A nonstationary model results for the data.

We adopt a Bayesian approach for our modeling framework. This is attractive in the proposed setting, because we are specifically interested in inference for the random spatial effects. In particular, we obtain an entire posterior for the spatial coefficient process at both observed and unobserved locations, as well as posteriors for all model parameters. Interpolation for a process that is neither observed nor arising as a residual seems inaccessible in any other framework. For Gaussian responses, although some inference is possible through likelihood methods, it is more limited, and in particular, interval estimation relies on possibly inappropriate asymptotics. For non-Gaussian data, approximations will almost surely be required, possibly in the form that we provide in Section 7, but still inference will be limited.

To clarify interpretation and implementation, we first develop our general approach in the case of a single covariate, and thus we have two spatially varying coefficient processes, one for “intercept” and one for “slope.” We then turn to the case of multiple covariates. Because even in the basic multiple regression setting, coefficient estimates typically reveal some strong correlations, the collection of spatially varying coefficient processes is expected to be dependent. Hence we use a multivariate process model. Indeed, we present a further generalization to build a spatial analog of a multivariate regression model (see, e.g., Goldstein 1995). We also consider flexible spatio-temporal possibilities. The previously mentioned real estate setting provides site level covariates whose coefficients are of considerable practical interest and a dataset of single-family home sales from Baton Rouge, LA enables illustration. Except for regions exhibiting special topography, we anticipate that a spatially varying coefficient model will prove more useful than, for instance, a trend surface model. That is, incorporating a polynomial in latitude and longitude into the mean structure would not be expected to serve as a surrogate for allowing the variability across the region of a coefficient for say age or living area of a house.

The article is organized as follows. Section 2 details the Gaussian modeling approach for a single covariate. Section 3 addresses the multiple-covariate case. Section 4 proposes a sequence of varying coefficient specifications in the spatio-temporal setting. Section 5 comments briefly on model comparison. Section 6 presents an example using the aforementioned single-family home sales data. Section 7 concludes with some discussion of the generalized linear model setting.

2. THE MODELING APPROACH FOR A SINGLE COVARIATE

Recall the usual Gaussian stationary spatial process model as in, for example, Cressie (1993),

$$Y\left(\mathbf{s}\right)=\mu \left(\mathbf{s}\right)+W\left(\mathbf{s}\right)+ϵ\left(\mathbf{s}\right),$$ (1)

where $\mu (\mathbf{s})=\mathbf{x}(\mathbf{s}{)}^T\mathbf{\beta }$ and $ϵ(\mathbf{s})$ is a white noise process, that is, $\mathrm{E}(ϵ(\mathbf{s}))=0,$ $\mathrm{v}\mathrm{a}\mathrm{r}(ϵ(\mathbf{s}))={\tau }^2,$ $\mathrm{c}\mathrm{o}\mathrm{v}\left(ϵ(\mathbf{s}),ϵ\left({\mathbf{s}}^{\prime }\right)\right)=0$, and $W(\mathbf{s})$ is a second-order stationary mean 0 process independent of the white noise process; that is, $\mathrm{E}(W(\mathbf{s}))=0,\mathrm{v}\mathrm{a}\mathrm{r}(W(\mathbf{s}))={\sigma }^2,$ $\mathrm{c}\mathrm{o}\mathrm{v}\left(W(\mathbf{s}),W\left({\mathbf{s}}^{\prime }\right)\right)={\sigma }^2\rho \left(\mathbf{s},{\mathbf{s}}^{\prime };\varphi \right)$, where $\rho$ is a valid two-dimensional correlation function.

The $W(\mathbf{s})$ are viewed as spatial random effects, and (1) implicitly defines a hierarchical model. Letting $\mu (\mathbf{s})={\beta }_0+{\beta }_{1}x(\mathbf{s})$, write $W(\mathbf{s})={\beta }_0(\mathbf{s})$ and define ${\tilde{\beta }}_0(\mathbf{s})={\beta }_0+{\beta }_0(\mathbf{s})$. Then ${\beta }_0(\mathbf{s})$ can be interpreted as a random spatial adjustment at location $\mathbf{s}$ to the overall intercept ${\beta }_0$. Equivalently, ${\tilde{\beta }}_0(\mathbf{s})$ can be viewed as a random intercept process. For an observed set of locations ${\mathbf{s}}_1,{\mathbf{s}}_2,\dots ,{\mathbf{s}}_n$ given ${\beta }_0,{\beta }_1,\left\{{\beta }_0\left({\mathbf{s}}_i\right)\right\}$ and ${\tau }^2$, the $Y\left({\mathbf{s}}_i\right)={\beta }_0+{\beta }_{1}x\left({\mathbf{s}}_{\mathbf{i}}\right)+{\beta }_0\left({\mathbf{s}}_{\mathbf{i}}\right)+ϵ\left({\mathbf{s}}_{\mathbf{i}}\right),$ $i=1,\dots ,n$, are conditionally independent. The first-stage likelihood is

$$\begin{array}{r}L\left({\beta }_0,{\beta }_1,\left\{{\beta }_0\left({\mathbf{s}}_i\right)\right\},{\tau }^2;\mathbf{y}\right)={\left({\tau }^2\right)}^{-\frac{n}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{1}{2{\tau }^2}\sum \left(Y\left({\mathbf{s}}_i\right)\right.\right.\\ \left.\left.-{\left({\beta }_0+{\beta }_{1}x\left({\mathbf{s}}_i\right)+{\beta }_0\left({\mathbf{s}}_i\right)\right)}^2\right)\right\}.\end{array}$$ (2)

In obvious notation, the distribution of ${\mathbf{\beta }}_0=\left({\beta }_0\left({\mathbf{s}}_1\right),\dots \right.,{\left.{\beta }_0\left({\mathbf{s}}_n\right)\right)}^T$ is

$$f\left({\mathbf{\beta }}_0\mid {\sigma }_0^2,{\varphi }_0\right)=N\left(0,{\sigma }_0^2{H}_0\left({\varphi }_0\right)\right),$$ (3)

where ${\left(H_0\left({\varphi }_0\right)\right)}_{ij}={\rho }_0\left({\mathbf{s}}_i-{\mathbf{s}}_j;{\varphi }_0\right)$. For all of the discussion and examples that follow, we adopt the Matèrn correlation function, $\rho (\mathbf{h},\varphi )\propto (\gamma (\Vert \mathbf{h}\Vert ){)}^v{K}_v(\gamma (\Vert \mathbf{h}\Vert ))$. Here $K_v$ is a modified Bessel function, $\varphi =(\gamma ,v)$, where $\gamma$ is a decay parameter and $v$ is a smoothness parameter (see Stein 1999a for a more in-depth discussion). With a prior on ${\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2$, and ${\varphi }_0$, specification of the Bayesian hierarchical model is completed. Under (2) and (3), we can integrate over ${\mathbf{\beta }}_0$, obtaining the marginal likelihood

$$\begin{array}{l}L\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\varphi }_0;\mathbf{y}\right)\\ ={\left|{\sigma }_0^2{H}_0\left({\varphi }_0\right)+{\tau }^{2}I\right|}^{-\frac{1}{2}}\\ \times \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{1}{2}{\left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right)}^T{\left({\sigma }_0^2{H}_0\left({\varphi }_0\right)+{\tau }^{2}I\right)}^{-1}\right.\\ \left.\times \left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right)\right\},\end{array}$$ (4)

where $\mathbf{x}={\left(x\left({\mathbf{s}}_1\right),\dots ,x\left({\mathbf{s}}_n\right)\right)}^T$.

We note analogies with usual Gaussian random-effects models where $Y_{ij}={\beta }_0+{\beta }_1{x}_{ij}+{\alpha }_i+e_{ij}$, with ${\alpha }_i\mathrm{i}\mathrm{i}\mathrm{d}N\left(0,{{\sigma }_{\alpha }}^2\right)$ and ${ϵ}_{ij}\text{iid}N\left(0,{{\sigma }_{ϵ}}^2\right)$. In this case, replications are needed to identify (separate) the variance components. Because of the dependence between the ${\beta }_0\left(s_i\right)$, replications are not needed in the spatial case, as (4) reveals. Also, if $U(\mathbf{s})$ denotes the total error in the regression model, then $U(\mathbf{s})$ is partitioned into “intercept process” error and “pure” error.

If the Bayesian model is fitted using the marginal likelihood in (4) with simulation-based model fitting, then samples essentially from the posterior $f\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,\varphi \mid y\right)$ are obtained. But then samples from ${\mathbf{\beta }}_0\mid \mathbf{y}$ can be obtained one-for-one because

$$\begin{gathered} f\left({\mathbf{\beta }}_0\mid \mathbf{y}\right)=\int f\left({\mathbf{\beta }}_0\mid {\beta }_0,{\beta }_1,{\tau }^2,\right.\left.{\sigma }_0^2,{\varphi }_0,\mathbf{y}\right) \\ \times f\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\varphi }_0\mid \mathbf{y}\right) \end{gathered}$$ (5)

where

$$\begin{array}{l}f\left({\beta }_0\mid {\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\varphi }_0,\mathbf{y}\right)\\ =N\left({\left(\frac{1}{{\tau }^2}I+\frac{1}{{\sigma }_0^2}{H}_0^{-1}\left({\varphi }_0\right)\right)}^{-1}\frac{1}{{\tau }^2}\left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right),\right.\\ \left.{\left(\frac{1}{{\tau }^2}I+\frac{1}{{\sigma }_0^2}{H}_0^{-1}\left({\varphi }_0\right)\right)}^{-1}\right).\end{array}$$

We can also obtain samples from the posterior of the ${\beta }_0(\mathbf{s})$ process at a new location, say ${\mathbf{s}}_{new}$, to provide interpolation for the ${\beta }_0(\mathbf{s})$ surface. Specifically,

$$f\left({\beta }_0\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right)=\int f\left({\beta }_0\left({\mathbf{s}}_{\mathit{new}}\right)\mid {\mathbf{\beta }}_0,{\sigma }_0^2,{\varphi }_0\right)f\left({\mathbf{\beta }}_0,{\sigma }_0^2,{\varphi }_0\mid \mathbf{y}\right).$$ (6)

The first density under the integral is a univariate normal that can be written down directly from the specification of ${\beta }_0(\mathbf{s})$. For the prediction of $y\left({\mathbf{s}}_{\mathit{new}}\right)$ given $\mathbf{y}$, we require

$$\begin{array}{l}f\left(y\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right)=\int f\left(y\left({\mathbf{s}}_{\mathit{new}}\right)\mid {\beta }_0,{\beta }_1,{\beta }_0\left({\mathbf{s}}_{new}\right),{\tau }^2\right)\\ \times f\left({\beta }_0\left({\mathbf{s}}_{new}\right)\mid {\mathbf{\beta }}_0,{\sigma }_0^2,{\varphi }_0\right)\\ \times f\left({\mathbf{\beta }}_0,{\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\varphi }_0\mid \mathbf{y}\right).\end{array}$$ (7)

The first term under the integral sign is a normal density. Again, it is straightforward to obtain samples from this predictive distribution.

The foregoing development immediately suggests how to formulate a spatially varying coefficient model. Suppose that we write

$$Y\left(\mathbf{s}\right)={\beta }_0+{\beta }_{1}x\left(\mathbf{s}\right)+{\beta }_1\left(\mathbf{s}\right)x\left(\mathbf{s}\right)+ϵ\left(\mathbf{s}\right).$$ (8)

In (8), ${\beta }_1(\mathbf{s})$ is a second-order stationary mean 0 Gaussian process with variance ${\sigma }_1^2$ and correlation function ${\rho }_1\left(\cdot ;{\varphi }_1\right)$. Also, let ${\tilde{\beta }}_1(\mathbf{s})={\beta }_1+{\beta }_1(\mathbf{s})$. Now ${\beta }_1(\mathbf{s})$ can be interpreted as a random spatial adjustment at location $\mathbf{s}$ to the overall slope ${\beta }_1$. Equivalently, ${\tilde{\beta }}_1(\mathbf{s})$ can be viewed as a random slope process. In effect, we are using an infinite-dimensional function to explain the relationship between $x(\mathbf{s})$ and $Y(\mathbf{s})$.

Expression (8) yields an obvious modification of (2) and (3). In particular, the resulting marginalized likelihood becomes

$$\begin{array}{l}L\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_1^2,{\varphi }_1;\mathbf{y}\right)\\ ={\left|{\sigma }_1^2{D}_x{H}_1\left({\varphi }_1\right)D_x+{\tau }^{2}I\right|}^{-\frac{1}{2}}\\ \times \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{1}{2}{\left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right)}^T{\left({\sigma }_1^2{D}_x{H}_1\left({\varphi }_1\right)D_x+{\tau }^{2}I\right)}^{-1}\right.\\ \left.\times \left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right)\right\},\end{array}$$ (9)

where $D_x$ is diagonal with ${\left(D_x\right)}_{ii}=x\left({\mathbf{s}}_i\right)$. Moreover, with ${\mathbf{\beta }}_1={\left({\beta }_1\left({\mathbf{s}}_1\right),\dots ,{\beta }_1\left({\mathbf{s}}_n\right)\right)}^T$, we can sample $f\left({\mathbf{\beta }}_1\mid \mathbf{y}\right)$ and $f\left({\beta }_1\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right)$ using obvious analogs of (5) and (6).

Note that (8) provides a heterogeneous, nonstationary process for the data regardless of the choice of covariance function for the ${\beta }_1(\mathbf{s})$ process. Here, $\mathrm{v}\mathrm{a}\mathrm{r}\left(Y(\mathbf{s})\mid {\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_1^2,{\varphi }_1\right)=x^2(\mathbf{s}){\sigma }_1^2+{\tau }^2$ and $\mathrm{c}\mathrm{o}\mathrm{v}\left(Y(\mathbf{s}),Y\left({\mathbf{s}}^{\prime }\right)\mid {\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_1^2,{\varphi }_1\right)={\sigma }_1^{2}x(\mathbf{s})x\left({\mathbf{s}}^{\prime }\right){\rho }_1\left(\mathbf{s}-{\mathbf{s}}^{\prime };{\varphi }_1\right)$. As a result, we observe that in practice, (8) is sensible only if we have $x(\mathbf{s})>0$. In fact, centering and scaling, usually advocated for better-behaved model fitting, is inappropriate here. With centered $x(\mathbf{s})$’s, we would find the likely untenable behavior that $\mathrm{v}\mathrm{a}\mathrm{r}(Y(\mathbf{s}))$ decreases and then increases in $x(\mathbf{s})$. Worse, for an essentially central $x(\mathbf{s})$, we would find $Y(\mathbf{s})$ essentially independent of $Y\left({\mathbf{s}}^{\prime }\right)$ for any ${\mathbf{s}}^{\prime }$. Also, scaling the $x(\mathbf{s})$’s accomplishes nothing. ${\beta }_1(\mathbf{s})$ would be inversely rescaled, because the model identifies only ${\beta }_1(\mathbf{s})x(\mathbf{s})$.

This leads to concerns regarding possible approximate collinearity of $\mathbf{x}$, the vector of $x\left({\mathbf{s}}_i\right)$’s, with the vector $1$. Expression (9) shows that a badly behaved likelihood will arise if $\mathbf{x}\approx c1$. Fortunately, we can reparameterize (8) to $Y(\mathbf{s})={\beta }_0^{\prime }+{\beta }_1^{\prime }\tilde{x}(\mathbf{s})+{\beta }_1(\mathbf{s})x(\mathbf{s})+ϵ(\mathbf{s})$, where $\tilde{x}(\mathbf{s})$ is centered and scaled with obvious definitions for ${\beta }_0^{\prime }$ and ${\beta }_1^{\prime }$. Now ${\tilde{\beta }}_1(\mathbf{s})={\beta }_1^{\prime }/s_x+{\beta }_1(\mathbf{s})$, where $s_x$ is the sample standard deviation of the $x(\mathbf{s})$’s.

As after (4), we can draw an analogy with usual longitudinal linear growth curve modeling where $Y_{ij}={\beta }_0+{\beta }_1{x}_{ij}+{\beta }_{1i}{x}_{ij}+{ϵ}_{ij}$, that is, a random slope for each individual. Also, $U(\mathbf{s})$, the total error in the regression model (8), is now partitioned into “slope process” error and “pure” error.

The general specification encompassing (1) and (7) would be

$$Y\left(\mathbf{s}\right)={\beta }_0+{\beta }_{1}x\left(\mathbf{s}\right)+{\beta }_0\left(\mathbf{s}\right)+{\beta }_1\left(\mathbf{s}\right)x\left(\mathbf{s}\right)+ϵ\left(\mathbf{s}\right).$$ (10)

Expression (10) parallels the usual linear growth curve modeling by introducing both an intercept process and a slope process. The model in (10) requires a bivariate process specification to determine the joint distribution of ${\mathbf{\beta }}_0$ and ${\mathbf{\beta }}_1$. We return to this in Section 3, but, under independence of the processes, (10) can be easily marginalized over ${\mathbf{\beta }}_0$ and ${\mathbf{\beta }}_1$, yielding

$$\begin{array}{l}L\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\sigma }_1^2,{\varphi }_0,{\varphi }_1;\mathbf{y}\right)\\ ={\left|{\sigma }_0^2{H}_0\left({\varphi }_0\right)+{\sigma }_1^2{D}_x{H}_1\left({\varphi }_1\right)D_x+{\tau }^{2}I\right|}^{-\frac{1}{2}}\\ \times \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{1}{2}{\left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right)}^T\right.\\ \times {\left({\sigma }_0^2{H}_0\left({\varphi }_0\right)+{\sigma }_1^2{D}_x{H}_1\left({\varphi }_1\right)D_x+{\tau }^{2}I\right)}^{-1}\\ \left.\times \left(\mathbf{y}-{\beta }_{0}1-{\beta }_1\mathbf{x}\right)\right\}.\end{array}$$ (11)

Again, simulation from $f\left({\mathbf{\beta }}_0\mid \mathbf{y}\right),$ $f\left({\beta }_1\mid \mathbf{y}\right),$ $f\left({\beta }_0\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right),f\left({\beta }_1\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right)$, and $f\left(y\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right)$ is straightforward. The possibility of predicting the spatial surface at arbitrary locations makes a compelling case for a Bayesian inference approach. Classical kriging methods cannot address this problem, because no ${\beta }_0\left({\mathbf{s}}_i\right)$ or ${\beta }_1\left({\mathbf{s}}_i\right)$ are observed. Also, in (10), the total error has been partitioned into three independent pieces with obvious interpretation. The relative sizes of the error components at any ${\mathbf{s}}_i$ can be studied through $E\left({\beta }_0\left({\mathbf{s}}_i\right)\mid \mathbf{y}\right),E\left({\beta }_1\left({\mathbf{s}}_i\right)x\left({\mathbf{s}}_i\right)\mid \mathbf{y}\right)$, and $E\left(ϵ\left({\mathbf{s}}_i\right)\mid \mathbf{y}\right)$. To compare the relative variability contributions, we could calculate $E\left({\tau }^2\mid \mathbf{y}\right),E\left({\sigma }_0^2\mid \mathbf{y}\right)$, and ${\bar{x}}^{2}E\left({\sigma }_1^2\mid \mathbf{y}\right)$, where $\bar{x}=\sum x\left({\mathbf{s}}_i\right)/n$. In the case where ${\rho }_0$ and ${\rho }_1$ are isotropic, posteriors for the ranges can be obtained to compare spatial range of the intercept process with that of the slope process. The posterior mean surfaces $E\left({\beta }_0(\mathbf{s})\mid \mathbf{y}\right)$ and $E\left({\beta }_1(\mathbf{s})\mid \mathbf{y}\right)$ can be obtained over an arbitrary grid of locations and displayed graphically using standard software.

Bayesian models using the marginal likelihoods in either (4), (9), or (11) are easily fitted using a slice Gibbs sampler as discussed by Agarwal and Gelfand (2001) (see Neal 2002, as well). In particular, under, say (11), we add an auxiliary variable $U~unif\left(0,L\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\sigma }_1^2,{\varphi }_0,{\varphi }_1;\mathbf{y}\right)\right)$. Then the posterior $\left({\beta }_0,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\sigma }_1^2,{\varphi }_0,{\varphi }_1,U\mid \mathbf{y}\right)\propto I\left(U<L\right)\pi \left({\beta }_0\right.,{\beta }_1,{\tau }^2,{\sigma }_0^2,{\sigma }_1^2,{\varphi }_0,{\varphi }_1$), where $\pi$ is the prior on the marginalized parameters. The slice Gibbs sampler updates $U$ with a uniform draw and updates the other parameters with a prior draw subject to the indicator restriction. This algorithm is “off-the-shelf,” requiring no tuning. It converges faster than Metropolis alternatives and avoids the autocorrelation problem that often arises with these alternatives.

3. A MULTIVARIATE SPATIALLY VARYING COEFFICIENT MODEL

Here we turn to the case of a $p\times 1$ multivariate covariate vector $\mathbf{X}(\mathbf{s})$ at location $\mathbf{s}$, where, for convenience, $\mathbf{X}(\mathbf{s})$ includes a 1 as its first entry to accommodate an intercept. We generalize (10) to

$$Y\left(\mathbf{s}\right)={\mathbf{X}}^T\left(\mathbf{s}\right)\tilde{\mathbf{\beta }}\left(\mathbf{s}\right)+ϵ\left(\mathbf{s}\right),$$ (12)

where $\tilde{\beta }(\mathbf{s})$ is assumed to follow a $p$-variate spatial process model. With observed locations ${\mathbf{s}}_1,{\mathbf{s}}_2,\dots ,{\mathbf{s}}_n$, let $X^T$ be $n\times np$ block diagonal having as block for the ith row ${\mathbf{X}}^T\left({\mathbf{s}}_i\right)$. Then we can write $\mathbf{Y}=X^T\tilde{\mathbf{\beta }}+ϵ$, where $\tilde{\mathbf{\beta }}$ is $np\times 1$, the concatenated vector of the $\tilde{\beta }(\mathbf{s})$ and $ϵ~N\left(0,{\tau }^{2}I\right)$.

In practice, to assume that the component processes of $\tilde{\mathbf{\beta }}(\mathbf{s})$ are independent is likely inappropriate. That is, in the simpler case of simple linear regression, negative association between slope and intercept is usually seen. (This is intuitive if one envisions overlaying random lines that are likely relative to a fixed scattergram of data points.) The dramatic improvement in model performance when dependence is incorporated is shown in the example of Section 6. To formulate a multivariate Gaussian process for $\tilde{\mathbf{\beta }}(\mathbf{s})$, we require the mean and the cross-covariance function. For the former, following Section 2, we take this to be ${\mathbf{\mu }}_{\beta }={\left({\beta }_1,\dots ,{\beta }_p\right)}^T$. For the latter, we require a valid $p$-variate choice. In the sequel we work with a computationally convenient separable choice following Mardia and Goodall (1993) (see also Banerjee and Gelfand 2002 in this regard).

More precisely, let $\mathit{C}\left(\mathbf{s},{\mathbf{s}}^{\prime }\right)$ be the $p\times p$ matrix with $(l,m)$ entry $\mathrm{c}\mathrm{o}\mathrm{v}({\tilde{\mathbf{\beta }}}_l(\mathbf{s}),{\tilde{\mathbf{\beta }}}_m\left({\mathbf{s}}^{\prime }\right))$ and let

$$C{\left(\mathbf{s},{\mathbf{s}}^{\prime }\right)}_{lm}=\rho \left(\mathbf{s}-{\mathbf{s}}^{\prime };\varphi \right){\tau }_{lm},$$ (13)

where $\rho$ is a valid scalar correlation function in two dimensions and $T_{p\times p}$ is such that $(T{)}_{lm}={\tau }_{lm}$ is positive-definite symmetric. In other words, $T$ is the covariance matrix associated with an observation vector at any spatial location, and $\rho$ captures the attenuation in association across space. If we collect the set of $\rho \left(\mathbf{s}-{\mathbf{s}}^{\prime };\varphi \right)$ into an $n\times n$ matrix $H(\varphi )$ as in the previous section, then, with $\otimes$ denoting the Kronecker product, the distribution of $\mathbf{\beta }$ is

$$\tilde{\mathbf{\beta }}~N\left(1_{n\times 1}\otimes {\mathit{\mu }}_{\beta },H\left(\varphi \right)\otimes T\right).$$ (14)

As in the previous section, if $\tilde{\mathbf{\beta }}=\mathrm{\beta }+1_{n\times 1}\otimes {\mathbf{\mu }}_{\beta }$, then we can write (12) as

$$Y\left(\mathbf{s}\right)={\mathbf{X}}^T\left(\mathbf{s}\right){\mathbf{\mu }}_{\beta }+{\mathbf{X}}^T\left(\mathbf{s}\right)\mathit{\beta }\left(\mathbf{s}\right)+ϵ\left(\mathbf{s}\right).$$ (15)

In (15), the total error in the regression model is partitioned into $p+1$ pieces each with an obvious interpretation. Following Section 2, using (12) and (14), we can integrate over $\mathbf{\beta }$ to obtain

$$\begin{array}{l}L\left({\mathbf{\mu }}_{\beta },{\tau }^2,T,\varphi ;\mathbf{y}\right)\\ ={\left|X(H(\varphi )\otimes T)X^T+{\tau }^{2}I\right|}^{-\frac{1}{2}}\\ \times \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{1}{2}{\left(\mathbf{y}-X\left(1\otimes {\mathbf{\mu }}_{\beta }\right)\right)}^T{\left(X(H(\varphi )\otimes T)X^T+{\tau }^{2}I\right)}^{-1}\right.\\ \left.\times \left(\mathbf{y}-X\left(1\otimes {\mathbf{\mu }}_{\beta }\right)\right)\right\}.\end{array}$$ (16)

The possibly daunting form (16) still involves only $n\times n$ matrices.

The Bayesian model is completed with a prior $f\left({\mathbf{\mu }}_{\beta }\right.,{\tau }^2,T,\varphi$ ) which we assume to take the product form $f\left({\mathbf{\mu }}_{\beta }\right)f\left({\tau }^2\right)f(T)f(\varphi )$. Later, these components are normal, inverse gamma, inverse Wishart and gamma, and gamma, where $\varphi =(\gamma ,\nu )$ under the Matèrn correlation function. The model using (16) and such a prior is readily fitted through a sliced Gibbs sampler similar to that described at the end of the previous section.

With regard to prediction analogous to (5), $f(\tilde{\mathbf{\beta }}\mid \mathbf{y})$ can be sampled one-for-one with the posterior samples from $f\left({\mathbf{\mu }}_{\beta },{\tau }^2,T,\varphi \mid \mathbf{y}\right)$ using $f\left(\tilde{\mathbf{\beta }}\mid {\mathit{\mu }}_{\beta },{\tau }^2,T,\varphi ,y\right)$, which is $N(B\mathbf{b},B)$, where $B={\left(X^{T}X/{\tau }^2+H^{-1}(\varphi )\otimes T^{-1}\right)}^{-1}$ and $\mathbf{b}=X^T\mathbf{y}/{\tau }^2+\left(H^{-1}(\varphi )\otimes T^{-1}\right)\left(1\otimes {\mathbf{\mu }}_{\beta }\right).$ $B$ is $np\times np$, but for sampling $\tilde{\mathbf{\beta }}$, only a Cholesky decomposition of $B$ is needed and only for the retained posterior samples. Prediction at a new location, say ${\mathbf{s}}_{\mathit{new}}$, requires, analogous to (6), $f\left(\tilde{\mathbf{\beta }}\left({\mathbf{s}}_{\mathit{new}}\right)\mid \right.\left.\tilde{\mathbf{\beta }},{\mathbf{\mu }}_{\beta },{\tau }^2,T,\varphi \right)$. Defining ${\mathbf{h}}_{\mathit{new}}(\varphi )$ to be the $n\times 1$ vector with ith row entry $\rho \left({\mathbf{s}}_i-{\mathbf{s}}_{\mathit{new}};\varphi \right)$, this distribution is normal with mean ${\mathbf{\mu }}_{\beta }+\left({\mathbf{h}}_{new}^T(\varphi )\otimes T\right)\left(H^{-1}(\varphi )\otimes T^{-1}\right)\left(\tilde{\mathbf{\beta }}-1_{nx1}\otimes {\mathbf{\mu }}_{\beta }\right)={\mathbf{\mu }}_{\beta }+\left({\mathbf{h}}_{\mathit{new}}^T(\varphi )H^{-1}(\varphi )\otimes I\right)\left(\tilde{\mathbf{\beta }}-1_{nx1}\otimes {\mathbf{\mu }}_{\beta }\right)$ and covariance matrix $T-\left({\mathbf{h}}_{\mathit{new}}^T(\varphi )\otimes T\right)\left(H^{-1}(\varphi )\otimes T^{-1}\right)\left({\mathbf{h}}_{\mathit{new}}(\varphi )\otimes T\right)=\left(I-{\mathbf{h}}_{\mathit{new}}^T(\varphi )H^{-1}(\varphi ){\mathbf{h}}_{\mathit{new}}(\varphi )\right)T$. Finally, the predictive distribution for $Y\left({\mathbf{s}}_{\mathit{new}}\right),f\left(Y\left({\mathbf{s}}_{\mathit{new}}\right)\mid \mathbf{y}\right)$ is sampled analogously to (7).

We conclude this section by noting an extension of (12) when we have repeated measurements at location $\mathbf{s}$. That is, suppose that we have

$$Y\left(\mathbf{s},l\right)={\mathbf{X}}^T\left(\mathbf{s},l\right)\mathbf{\beta }\left(\mathbf{s}\right)+ϵ\left(\mathbf{s},l\right),$$ (17)

where $l=1,\dots ,L_{\mathbf{s}}$ with $L_{\mathbf{s}}$ the number of measurements at $\mathbf{s}$ and the $ϵ(\mathbf{s},l)$ still white noise. As an illustration, in the real estate context that we mentioned earlier, $\mathbf{s}$ might denote the location for an apartment block and $l$ indexes apartments in this block that have sold, with the lth apartment having characteristics $\mathbf{X}(\mathbf{s},l)$. Suppose further that $\mathbf{Z}(\mathbf{s})$ denotes an $r\times 1$ vector of site level characteristics. For an apartment block, these characteristics might include amenities provided or distance to the central business district. Then (17) can be extended to a multilevel model in the sense of Goldstein (1995) or Raudenbush and Bryk (2002). In particular, we can write

$$\mathbf{\beta }\left(\mathbf{s}\right)=\left(\begin{array}{c}{\mathbf{Z}}^T\left(\mathbf{s}\right){\mathbf{\gamma }}_1\\ ⋮\\ {\mathbf{Z}}^T\left(\mathbf{s}\right){\mathbf{\gamma }}_p\end{array}\right)+\mathbf{W}\left(\mathbf{s}\right).$$ (18)

In (18), ${\mathbf{\gamma }}_j$ is an $r\times 1$ vector associated with ${\tilde{\beta }}_j(\mathbf{s})$ and $\mathbf{W}(\mathbf{s})$ is a mean $0$ multivariate Gaussian spatial process as, for example, earlier. In (18), if the $\mathbf{W}(\mathbf{s})$ were independent, then we would have a usual multilevel model specification. In the case where $\mathbf{Z}(\mathbf{s})$ is a scalar capturing just an intercept, we return to the initial model of this section.

4. SPATIALLY VARYING COEFFICIENTS MODELS WITH SPATIO-TEMPORAL DATA

A natural extension of the modeling of the previous sections is to the case in which data are correlated at spatial locations across time. Such data frequently arise in ecological, environmental, and meteorological settings. If we assume that time is discretized to a finite set of equally spaced points on a scale, then we can conceptualizea time series of spatial processes that are observed only at the spatial locations ${\mathbf{s}}_1,\dots ,{\mathbf{s}}_n$.

Adopting a general notation that parallels (10), let

$$Y\left(\mathbf{s},t\right)={\mathbf{X}}^T\left(\mathbf{s},t\right)\tilde{\mathbf{\beta }}\left(\mathbf{s},t\right)+ϵ\left(\mathbf{s},t\right),t=1,2,\dots ,M.$$ (19)

That is, we introduce spatio-temporally varying intercepts and spatio-temporally varying slopes. Alternatively, if we write $\tilde{\mathbf{\beta }}(\mathbf{s},t)=\mathbf{\beta }(\mathbf{s},t)+{\mathbf{\mu }}_{\beta }$, then we are partitioning the total error into $p+1$ spatio-temporal intercept pieces including $ϵ(\mathbf{s},t)$, each with an obvious interpretation. So we continue to assume that the $ϵ(\mathbf{s},t)$ are iid $N\left(0,{\tau }^2\right)$, but we need to specify a model for $\tilde{\mathbf{\beta }}(\mathbf{s},t)$. Regardless, (19) defines a nonstationary process with $E(Y(\mathbf{s},t))={\mathbf{X}}^T(\mathbf{s},t)\tilde{\mathbf{\beta }}(s,t),$ $\mathrm{v}\mathrm{a}\mathrm{r}(Y(\mathbf{s},t))={\mathbf{X}}^T(\mathbf{s},t){\mathrm{\Sigma }}_{\tilde{\mathbf{\beta }}(\mathbf{s},t)}\mathbf{X}(\mathbf{s},t)+{\tau }^2,$ and $\mathrm{c}\mathrm{o}\mathrm{v}\left(Y(\mathbf{s},t),Y\left({\mathbf{s}}^{\prime },t^{\prime }\right)\right)={\mathbf{X}}^T(\mathbf{s},t){\mathrm{\Sigma }}_{\tilde{\mathbf{\beta }}(\mathbf{s},t),\tilde{\mathbf{\beta }}\left({\mathbf{s}}^{\prime },t^{\prime }\right)}\mathbf{X}\left({\mathbf{s}}^{\prime },t^{\prime }\right)$.

We propose four models for $\mathbf{\beta }(\mathbf{s},t)$. Paralleling the customary longitudinaldata modeling assumption when the time series are usually short, we could set

$$\text{model}1:\mathrm{\beta }(\mathbf{s},t)=\mathrm{\beta }(\mathbf{s}),$$

where $\mathrm{\beta }(\mathbf{s})$ is modeled as in the previous sections. Model 1 can be viewed as a local linear growth curve model.

Next, we have

$$\text{model}2:\mathrm{\beta }(\mathbf{s},t)=\mathrm{\beta }(\mathbf{s})+\alpha (t),$$

where $\mathrm{\beta }(\mathbf{s})$ is again as in model 1. In modeling $\alpha (t)$, we examine two possibilities. The first possibility treats the ${\alpha }_k(t)$ as time dummy variables, taking this set of $pM$ variables to be a priori independent and identically distributed. The second possibility models the $\mathit{\alpha }(t)$ as a random walk or autoregressive process. The components could be assumed to be independent across $k$, but for greater generality, we take them to be dependent, using an analog of (13), replacing $\mathbf{s}$ with $t$ and $\rho$, now a valid correlation function in one dimension. Such additivity in space and time has been discussed in the case of usual modeling of the error structure by, for example, Gelfand, Ecker, Knight, and Sirmans (2003).

In model 3 we consider an analog of the nested-effects areal unit specification of Waller, Carlin, Xia, and Gelfand (1997). (see also Gelfand et al. 2002). In particular, we have

$$\text{model}3:\mathbf{\beta }(\mathbf{s},t)={\mathbf{\beta }}^{(t)}(\mathbf{s})$$

Here we have spatially varying coefficient processes nested within time. The processes are assumed to be independent across $t$ (essentially time dummy processes) and permit temporal evolution of the coefficient process. Following Section 3, the process ${\mathbf{\beta }}^{(t)}(\mathbf{s})$ would be mean 0, second-order stationary Gaussian with cross-covariance specification at time $t,C^{(t)}\left(\mathbf{s},{\mathbf{s}}^{\prime }\right)$, where ${(C^{(t)}\left(\mathbf{s},{\mathbf{s}}^{\prime }\right))}_{lm}=\rho (\mathbf{s}-{\mathbf{s}}^{\prime };{\varphi }^{(t)}){\tau }_{lm}^{(t)}$. We have specified model 3 with a common ${\mathbf{\mu }}_{\beta }$ across time, which enables some comparability with the other models that we have proposed. However, we can increase flexibility by replacing ${\mathbf{\mu }}_{\beta }$ with ${\mathbf{\mu }}_{\beta }^{(t)}$.

Finally, model 4 proposes a separable covariance specification in space and time, extending work of Gelfand, Zhu, and Carlin (2001):

$$\text{model}4:\mathbf{\beta }(\mathbf{s},t)\text{such}\text{that}{\text{Σ}}_{\left[\beta \left(\mathbf{s},t\right),\beta \left({\mathbf{s}}^{\prime },t^{\prime }\right)\right]}={\rho }^{\left(1\right)}\left(\mathbf{s}-{\mathbf{s}}^{\prime };\varphi \right)\times {\rho }^{\left(2\right)}\left(t-t^{\prime };\gamma \right)T,$$

where ${\rho }^{(1)}$ is a valid two-dimensional correlation function, ${\rho }^{(2)}$ is a valid one-dimensional choice, and $T$ is positive-definite symmetric. Here ${\rho }^{(1)}$ obtains spatial association as in the earlier sections, which is attenuated across time by ${\rho }^{(2)}$. The resulting covariance matrix for the full vector $\mathbf{\beta }$, blocked by site and time within site, has the convenient form $H_2(\gamma )\otimes H_1(\varphi )\otimes T$.

In each of the aforementioned models, we can marginalize over $\mathbf{\beta }(\mathbf{s},t)$ as we did in the earlier sections. Depending on the model, it may be more computationally convenient to block the data by site or by time. We omit the details, noting only that with $n$ sites and $T$ time points, the resulting likelihood will involve the determinant and inverse of an $nT\times nT$ matrix.

Note that all of the foregoing modeling can be applied to the case of cross-sectional data in which the set of observed locations varies with $t$. This is the case with, for instance, our real estate data. We observe a selling price only at the time of a transaction. With $n_t$ locations in year $t$, the likelihood for all but model 3 will involve a $\sum n_t\times \sum n_t$ matrix.

5. MODEL COMPARISON

In either the purely spatial case or the spatio-temporal case, we may seek to compare models. For instance, in the spatial case from Sections 2 and 3, we can consider models in which only a subset of the coefficients vary spatially, where the coefficient processes are independent, or where the multivariate dependence version is assumed. In the spatio-temporal case, we can consider models 1–4 (with possible submodels in the cases of models 2 and 3).

We use the posterior predictive loss approach of Gelfand and Ghosh (1998). Illustrating in the spatio-temporal context, for each ($\mathbf{s},t$) in (19), let $Y_{\mathit{new}}(\mathbf{s},t)$ be a new observation obtained at that location and time for the given $\mathbf{X}(\mathbf{s},t)$. If under a particular model, $\mu (\mathbf{s},t)$ and ${\sigma }^2(\mathbf{s},t)$ denote the mean and variance of the predictive distribution of $Y_{\mathit{new}}(\mathbf{s},t)$ given $Y_{\mathit{obs}}$ (the set of all observed $Y$’s), then the criterion becomes

$$D_k=\sum _{(\mathbf{s},t)}{(Y_{obs}(\mathbf{s},t)-\mu (\mathbf{s},t))}^2+k\sum _{(\mathbf{s},t)}{\sigma }^2(\mathbf{s},t).$$ (20)

In (20), the first term is a goodness-of-fit component $(G)$, and the second term is a penalty for model complexity component $(P)$. The constant $k$ weights these components and is often set to 1. The model yielding the smallest value of (20) is chosen.

6. AN EXAMPLE

We draw our data from a database of real estate transactions in Baton Rouge, LA, during the 8-year period 1985–1992. In particular, we focus on modeling the log selling price of single family homes. In the literature it is customary to work with log selling price in order to achieve better approximate normality. A range of house characteristics are available. We use four of the most common choices: age of house, square feet of living area, square feet of other area (e.g., garages, carports, storage) and number of bathrooms. For the static spatial case, a sample of 237 transactions was drawn from 1992. Figure 1 shows the parish of Baton Rouge and the locations contained in an encompassing rectangle within the parish.

Figure 1.

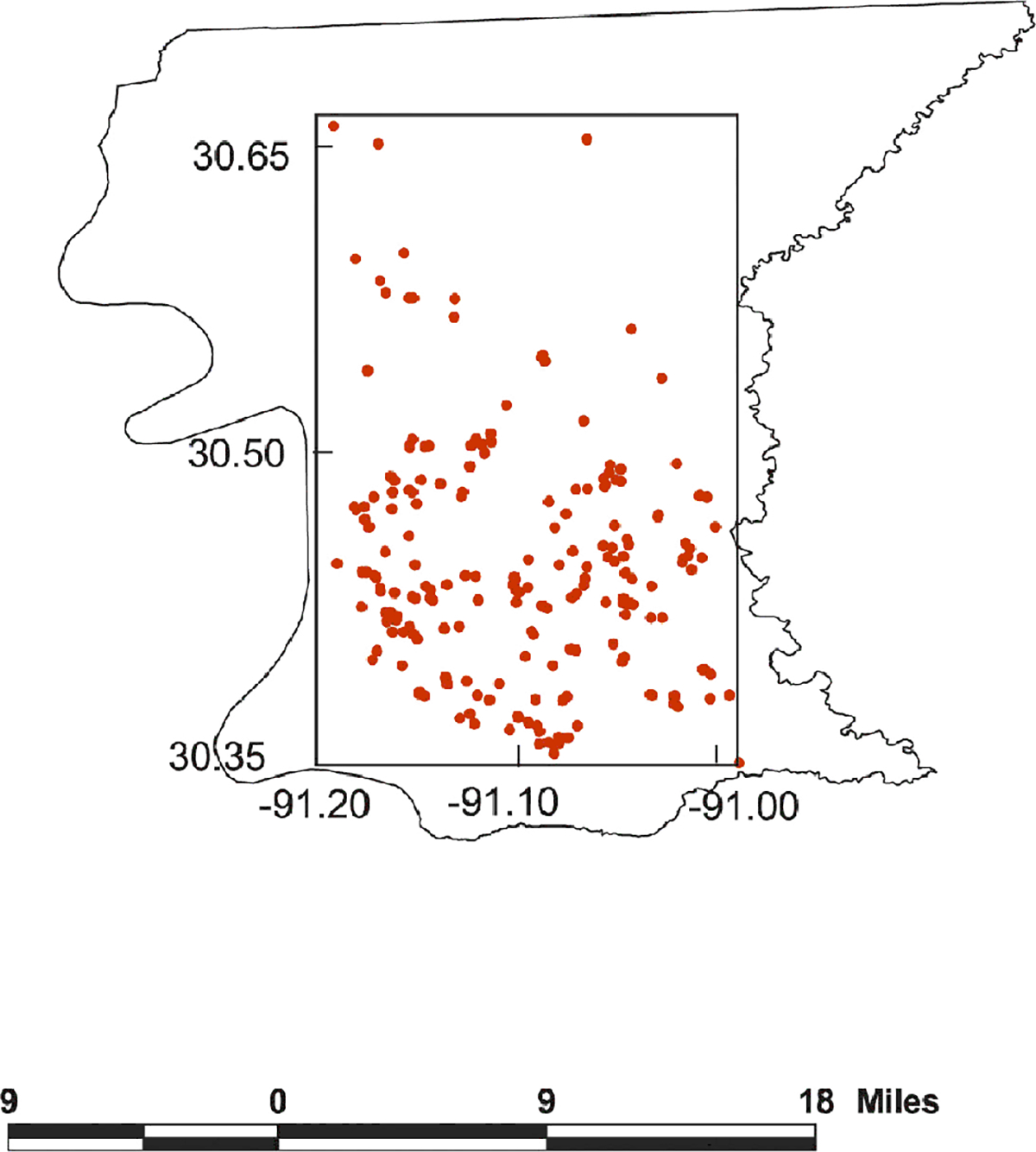
Locations Sampled Within the Parish of Baton Rouge for the Static Spatial Models.

We fitted the following collection of models. In all cases the correlation function is from the Matèrn class, that is, $\rho \left(\mathbf{s}-{\mathbf{s}}^{\prime };\varphi \right)\propto {\left(\gamma ‖\mathbf{s}-{\mathbf{s}}^{\prime }‖\right)}^{\nu }{K}_v\left(\gamma ‖\mathbf{s}-{\mathbf{s}}^{\prime }‖\right)$. We used priors that are fairly noninformative and comparable across models as sensible. We began with a spatial-varying intercept and one spatially varying slope coefficient. (The remaining coefficients do not vary). The intercept and coefficient processes follow a two-dimensional version of (13). There are four such models. The model comparison results are given in Table 1. The model with a spatially varying living area coefficient is best here. We then introduce two spatially varying slope coefficient processes along with a spatially varying intercept using a three-dimensional version of (13). There are six models here. Table 2 shows that the model with spatially varying age and living area is best. Finally, we allow five spatially varying processes; an intercept and four coefficients. We tried a model with five independent processes along with a five-dimensional version of (13). From Table 3 the five-dimensional model using (13) is far superior, and the independence model is clearly worst, supporting our earlier intuition.

Table 1.

Values of Posterior Predictive Model Choice Criterion for Two-Dimensional Models (intercept process is always included)

Model	G	P	D
Living area	69.87	46.24	116.11
Age	74.52	44.58	119.10
Other area	70.24	49.87	120.11
Bathrooms	78.02	52.93	130.95

Table 2.

Values of Posterior Predictive Model Choice Criterion for Three-Dimensional Models (intercept process is always included)

Model	G	P	D
Age, living area	61.38	47.83	109.21
Age, other area	63.80	48.45	112.25
Age, bathrooms	67.25	48.66	114.91
Living area, other area	72.35	50.75	123.10
Living area, bathrooms	78.47	49.28	127.75
Other area, bathrooms	74.58	47.44	122.02

Table 3.

Values of Posterior Predictive Model Choice Criterion (over all models)

Model	G	P	D
Five-dimensional model	42.21	36.01	78.22
Three-dimensional model (best)	61.38	47.83	109.21
Two-dimensional model (best)	69.87	46.24	116.11
Independent process model	94.36	59.34	153.70

The prior specification used for the five-dimensional dependent process model are as follows. We take vague $N\left(0,{10}^{5}I\right)$ for ${\mathit{\mu }}_{\beta }$; a five-dimensional inverted wishart, $IW(5,diag(.001))$, for $T$, and inverted gamma, $IG(2,1)$, for ${\tau }^2$ (mean 1, infinite variance). For the Màtern correlation function parameters $\varphi$ and $v$, we assume gamma priors $G(2,.1)$ (with mean 20 and variance 200). For all of the models, three parallel chains were run to assess convergence. Satisfactory mixing was obtained within 3,000 iterations for all the models; another 2,000 samples were generated and retained for posterior inference. The resulting posterior inference summary is provided in Table 4. We note a significant negative overall age coefficient with significant positive overall coefficients for the other three covariates. These are as expected. The contribution to spatial variability from the components of $\mathbf{\beta }$ is captured through the diagonal elements of the $T$ matrix scaled by the corresponding covariates after the discussion at the end of Section 2. We see that the spatial intercept process contributes most to the error variability with, perhaps surprisingly, the “bathrooms” process second. Clearly, spatial variability overwhelms the pure error variability $\left({\tau }^2\right)$, showing the importance of the spatial model. The dependence between the processes is evident in the posterior correlation between the components. In fact, under (13), it is straightforward to calculate that $\mathrm{c}\mathrm{o}\mathrm{v}\left({\tilde{\beta }}_l(\mathbf{s}),{\tilde{\beta }}_m(\mathbf{s}+\mathbf{h})\right)/\sqrt{\mathrm{c}\mathrm{o}\mathrm{v}\left({\tilde{\beta }}_l(\mathbf{s}),{\tilde{\beta }}_l(\mathbf{s}+\mathbf{h})\right)\mathrm{c}\mathrm{o}\mathrm{v}\left({\tilde{\beta }}_m(\mathbf{s}),{\tilde{\beta }}_m(\mathbf{s}+\mathbf{h})\right)}=T_{lm}/\sqrt{T_{ll}{T}_{mm}}$, regardless of $\mathbf{h}$. We find the anticipated negative association between the intercept process and the slope processes (apart from that with the “other area” process). Under the Matérn correlation function, by inverting $\rho (\cdot ;\varphi )=.05$ for a given value of the decay parameter $\gamma$ and the smoothing parameter $v$, we obtain the range, that is, the distance beyond which spatial association becomes negligible. Posterior samples of $(\gamma ,\nu )$ produce posterior samples for the range. The resulting posterior median is roughly 4 km over a somewhat sprawling parish, which measures roughly 22 km × 33 km. The smoothness parameter suggests processes with mean squared differentiable realizations $(v>1)$. Figure 2 shows the posterior mean spatial surfaces for each of the processes. The contour plots are evidently quite different. Table 5 considers a sample of 20 holdout sites on which the model can be validated; in fact, the validation is done with all of the models from Table 3. The entries in bold indicate validation failures. We find that for the first model, 19 of 20 predictive intervals contain the true value while for the independence model, 18 of 20 do so. More importantly, notice how much shorter these intervals are using the five-dimensional model.

Table 4.

Inference Summary for the Five-Dimensional Multivariate Spatially Varying Coefficients Model

Parameter	2.5 %	50 %	97.5 %
${\beta }_0$ (intercept)	9.908	9.917	9.928
${\beta }_1$ (age)	−.008	−.005	−.002
${\beta }_2$ (living area)	.283	.341	.401
${\beta }_3$ (other area)	.133	.313	.497
${\beta }_4$ (bathrooms)	.183	.292	.401
$T_{11}$	.167	.322	.514
${\bar{x}}_1^2{T}_{22}$	.029	.046	.063
${\bar{x}}_2^2{T}_{33}$	.013	.028	.047
${\bar{x}}_3^2{T}_{44}$	.034	.045	.066
${\bar{x}}_4^2{T}_{55}$	.151	.183	.232
$T_{12}/\sqrt{T_{11}{T}_{22}}$	−.219	−.203	−.184
$T_{13}/\sqrt{T_{11}{T}_{33}}$	−.205	−.186	−.167
$T_{14}/\sqrt{T_{11}{T}_{44}}$	.213	.234	.257
$T_{15}/\sqrt{T_{11}{T}_{55}}$	−.647	−.583	−.534
$T_{23}/\sqrt{T_{22}{T}_{33}}$	−.008	.011	.030
$T_{24}/\sqrt{T_{22}{T}_{44}}$	.061	.077	.098
$T_{25}/\sqrt{T_{22}{T}_{55}}$	−.013	.018	.054
$T_{34}/\sqrt{T_{33}{T}_{44}}$	−.885	−.839	−.789
$T_{35}/\sqrt{T_{33}{T}_{55}}$	−.614	−.560	−.507
$T_{45}/\sqrt{T_{44}{T}_{55}}$	.173	.232	.301
$\varphi$ (decay parameter)	.51	1.14	2.32
$v$ (smoothness parameter)	.91	1.47	2.87
range (in km)	2.05	4.17	9.32
${\tau }^2$	.033	.049	.077

Figure 2.

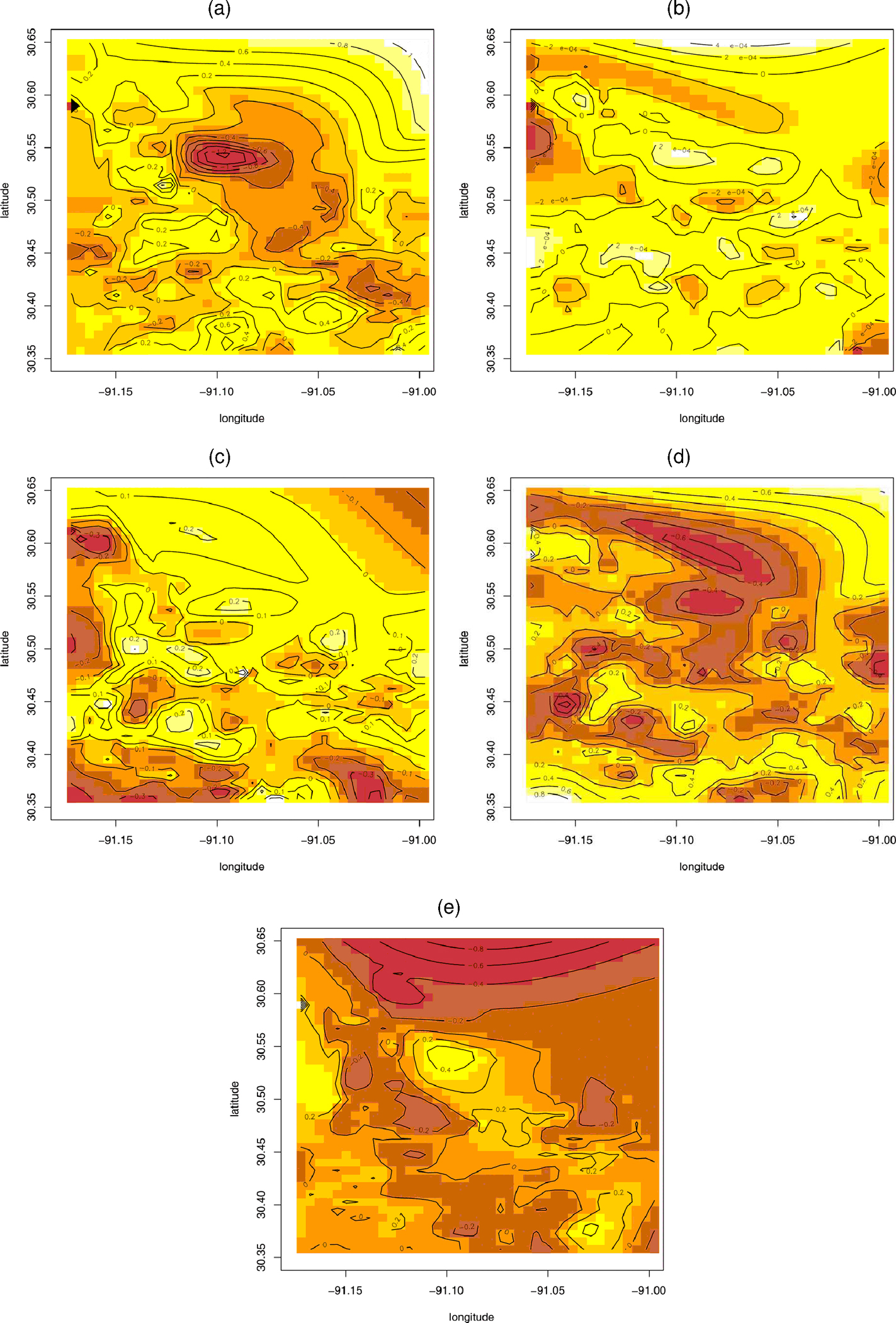
Mean Posterior Spatial Surfaces for the 5-D SVC Model: (a) Intercept Process, (b) Age Process, (c) Living Area Process, (d) Other Area Process, (e) Bathrooms Process.

Table 5.

Cross-Validatory Posterior Predictive Intervals for 20 Locations in Baton Rouge

True value	Five-dimensional	Three-dimensional (best)	Two-dimensional (best)	Independent
11.18	(10.85, 11.53)	(10.74, 11.68)	(10.56, 11.52)	(10.44, 11.79)
10.86	(10.54, 11.22)	(10.47, 11.31)	(10.52, 11.35)	(10.71, 12.08)
11.16	(11.05, 11.68)	(11.03, 11.96)	(10.97, 11.98)	(10.68, 12.06)
11.46	(11.39, 11.78)	(11.28, 12.11)	(11.35, 12.26)	(11.51, 12.34)
12.29	(12.01, 12.72)	(12.09, 12.94)	(12.06, 13.01)	(11.87, 13.24)
10.18	(9.81, 10.59)	(9.80, 10.60)	(9.73, 10.88)	(9.68, 10.75)
11.26	(11.03, 11.51)	(11.17, 11.76)	(11.08, 11.72)	(11.21, 12.13)
10.97	(10.82, 11.42)	(11.00, 11.97)	(10.77, 11.35)	(10.71, 11.52)
11.55	(11.27, 11.91)	(11.21, 11.86)	(11.28, 12.01)	(11.27, 12.08)
12.22	(12.11, 12.76)	(12.20, 12.84)	(12.15, 13.05)	(12.29, 13.25)
12.05	(11.81, 12.55)	(11.85, 12.53)	(11.85, 12.51)	(11.78, 12.49)
11.68	(11.50, 11.89)	(11.47, 11.92)	(11.49, 11.90)	(11.53, 12.18)
11.95	(11.60, 12.22)	(11.72, 12.24)	(11.64, 12.18)	(11.52, 12.21)
12.22	(11.77, 12.35)	(11.62, 12.27)	(11.89, 12.84)	(11.74, 12.82)
11.34	(11.02, 11.76)	(11.23, 11.86)	(11.22, 11.90)	(11.26, 11.85)
11.05	(11.10, 11.75)	(10.96, 11.78)	(11.01, 11.81)	(11.12, 12.09)
10.53	(10.04, 10.86)	(10.05, 10.89)	(10.07, 10.86)	(10.05, 10.88)
11.42	(11.26, 11.64)	(11.18, 11.82)	(11.16, 11.88)	(11.18, 12.05)
10.68	(10.58, 11.29)	(10.76, 11.53)	(10.73, 11.78)	(10.57, 11.58)
12.16	(11.66, 12.19)	(11.85, 12.62)	(11.94, 12.89)	(11.78, 12.82)

Turning to the dynamic models proposed in Section 5, we returned to the Baton Rouge database, drawing a sample of 120 transactions at distinct spatial locations for the years 1989–1992. We compare models 1–4. In particular, we have two versions of model 2; 2a has the $\mathit{\alpha }(t)$ as four iid time dummies, and 2b uses the multivariate temporal process model for $\mathit{\alpha }(t)$. We also have two versions of model 3; 3a has a common ${\mathbf{\mu }}_{\beta }$ across $t$, whereas 3 b uses ${\mathbf{\mu }}_{\beta }^{(t)}$. In all cases, we used the five-dimensional spatially varying coefficient model for $\mathbf{\beta }$’s. Table 6 gives the results. Model 3, in which space is nested within time, turns out to be the best, with model 4 following closely behind. Finally Table 7 summarizes the posterior inference summary for model 3b. The overall coefficients $({\mathbf{\mu }}_{\beta }^{(t)})$ do not change much over time; however, there is some indication that spatial range does change over time.

Table 6.

Model Choice Criteria for Various Spatio-Temporal Process Models (see Sec. 6)

Model	G	P	D
Independent process
Model 1	88.58	56.15	144.73
Model 2a	77.79	50.65	128.44
Model 2b	74.68	50.38	125.06
Model 3a	59.46	48.55	108.01
Model 3b	57.09	48.41	105.50
Model 4	53.55	52.98	106.53
Dependent process
Model 1	54.54	29.11	83.65
Model 2a	47.92	26.95	74.87
Model 2b	43.38	29.10	72.48
Model 3a	43.74	20.63	64.37
Model 3b	42.35	21.04	63.39
Model 4	37.84	26.47	64.31

Table 7.

Inference Summary for the 5-Dimension Multivariate Spatio-Temporal Model 3 (space nested within time)

Parameter	1989	1990	1991	1992
β0 (intercept)	9.697 (9.438, 9.956)	9.164 (8.782, 9.613)	9.56 (9.237, 9.860)	9.716 (9.445, 9.980)
β1 (age)	−.005 (−.007, −.001)	−.004 (−.007, −.002)	−.004 (−.007, −.002)	−.005 (−.008, −.002)
β2 (living area)	.383 (.314, .490)	.357 (.252, .460)	.402 (.232, .574)	.348 (.278, .416)
β3 (other area)	.246 (.068, .410)	.248 (.075, .422)	.305 (.137, .486)	.326 (.146, .515)
β4 (bathrooms)	.301 (.195, .407)	.296 (.193, .395)	.311 (.197, .420)	.304 (.201, .416)
ϕ (decay parameter)	1.63 (.68, 3.52)	1.77 (.85, 3.15)	1.05 (.42, 2.33)	1.17 (.57, 2.38)
ν (smoothness parameter)	1.48 (.92, 3.05)	1.51 (.93, 3.05)	1.54 (.86, 3.16)	1.47 (.88, 2.92)
range (in km)	2.95 (1.40, 7.04)	2.80 (1.55, 5.65)	4.55 (2.07, 11.31)	4.11 (2.03, 8.4)
τ 2		.038 (.024, .082)

7. THE GENERALIZED LINEAR MODEL SETTING

We briefly consider a generalized linear model version of (12), replacing the Gaussian first stage with

$$f\left(y\left({\mathbf{s}}_i\right)\mid \theta \left({\mathbf{s}}_i\right)\right)=h\left(y\left({\mathbf{s}}_i\right)\right)\exp \left(\theta \left({\mathbf{s}}_i\right)y\left({\mathbf{s}}_i\right)-b\left(\theta \left({\mathbf{s}}_i\right)\right)\right),$$ (21)

where, using a canonical link, $\theta \left({\mathbf{s}}_i\right)={\mathbf{X}}^T\left({\mathbf{s}}_i\right)\tilde{\mathbf{\beta }}\left({\mathbf{s}}_i\right)$. The specification generates the models of Diggle et al. (1998). In (19), we could include a dispersion parameter with little additional complication.

The resulting first-stage likelihood becomes

$$L\left(\tilde{\mathbf{\beta }}:\mathbf{y}\right)=\exp \left\{\sum y\left({\mathbf{s}}_i\right){\mathbf{X}}^T\left({\mathbf{s}}_i\right)\tilde{\mathbf{\beta }}\left({\mathbf{s}}_i\right)-b\left({\mathbf{X}}^T\left({\mathbf{s}}_i\right)\tilde{\mathbf{\beta }}\left({\mathbf{s}}_i\right)\right)\right\}.$$ (22)

Taking the prior on $\tilde{\mathbf{\beta }}$ in (14), the Bayesian model is completely specified with a prior on $\varphi ,$ $T$, and ${\mathbf{\mu }}_{\beta }$.

This model can be fitted using a conceptually straightforward Markov chain Monte Carlo algorithm in the form of a Gibbs sampler, which would update the components of ${\mathbf{\mu }}_{\beta }$ and $\tilde{\mathbf{\beta }}$ using adaptive rejection sampling (Gilks and Wild 1992). With an inverse Wishart prior on $T$, the resulting full conditional of $T$ is again inverse Wishart. Updating $\varphi$ is usually very awkward, because it enters in the Kronecker form in (14). Metropolis updates are hard to design but offer perhaps the best possibility. Also problematic is the repeated componentwise updating of $\tilde{\mathbf{\beta }}$. This hierarchically centered parameterization (Gelfand, Sahu, and Carlin 1995, 1996) is preferable to working with ${\mathbf{\mu }}_{\beta }$ and $\mathit{\beta }$, but the algorithm still runs very slowly with autocorrelation problems.

An alternative to componentwise updating is to introduce blocked Metropolis updating through a Langevin diffusion (see, e.g., Roberts, Gelman, and Gilks 1997; Christensen, Möller, and Waagepetersen 2000). Updating the entire $np\times 1$ vector $\tilde{\mathbf{\beta }}$ seems unrealistic. Blocking $\tilde{\mathbf{\beta }}$ by component process is essentially computationally intractable, and blocking $\tilde{\mathbf{\beta }}$ by site creates strong autocorrelation problems. Clearly, more work is needed to provide efficient model-fitting strategies for these models.