Rapid patient-specific organ dose estimation in computed tomography scans via integration of radiomics features and neural networks

Abstract

Background

Computed tomography (CT) offers detailed cross-sectional images of internal anatomy for disease detection but carries a risk of solid cancer or blood malignancies due to exposure to X-ray radiation. This study aimed to develop a new method to quickly predict patient-specific organ doses from CT examinations by training neural networks (NNs) based on radiomics features.

Methods

CT Digital Imaging and Communications in Medicine (DICOM) image data were exported to DeepViewer, a clinical autosegmentation software, to segment the regions of interest (ROIs) for patient organs. Radiomics feature extraction was performed based on the selected CT data and ROIs. Reference organ doses were computed using Monte Carlo (MC) simulations. Patient-specific organ doses were predicted by training a NN model based on radiomics features and reference doses. For the dose prediction performance, the relative root mean squared error (RRMSE), mean absolute percentage error (MAPE), and coefficient of determination (R²) were evaluated on the test sets. The robustness of the NN model was evaluated via the random rearrangement of patient samples in the training and test sets.

Results

The maximal difference between the reference and predicted doses was less than 1 mGy for all investigated organs. The range of MAPE was 1.68% to 5.2% for head organs, 11.42% to 15.2% for chest organs, and 5.0% to 8.0% for abdominal organs; the maximal R² values were 0.93, 0.86, and 0.89 for the head, chest, and abdominal organs, respectively.

Conclusions

The radiomics feature-based NN model can achieve accurate prediction of patient-specific organ doses at a high speed of less than 1 second using a single central processing unit, which supports its use as a user-friendly online clinical application.

Introduction

Computed tomography (CT) is the prevalent diagnostic modality for various diseases owing to its capacity to generate cross-sectional images of the internal structures of organs and tissues (1-3). CT imaging is a diagnostic modality that enables the identification of various pathological conditions, such as infectious, traumatic, inflammatory, and hemorrhagic disorders (4-6). However, exposure of patients to ionizing radiation from CT scans may result in DNA damage, which could potentially lead to the development of solid cancers (7-11). A retrospective cohort study from Australia reported there to be a significant association between CT radiation exposure and overall cancer incidence, with a relative risk of 1.24 (95% confidence interval: 1.20–1.29) among pediatric patients exposed to radiation (12). Therefore, the estimation of patient-specific organ doses from CT scans is necessary for the evaluation and management of the potential carcinogenic risk associated with radiation exposure.

The main methods used to calculate patient-specific organ doses include size-specific dose estimation (SSDE), Monte Carlo (MC) simulation, and neural networks (NNs) (13-18). SSDE adopts a phantom-based the volume CT dose index (CTDI_vol) and patient size-related equivalent water diameter (D_w) to calculate patient-specific organ doses. NN models apply fully connected networks (FCNs) or convolutional neural networks (CNNs) to account for anatomical characteristics beyond patient size and can achieve a relatively better performance than can SSDE in predicting patient-specific organ doses. However, NN-based prediction models may require a large number of patient samples to be allocated to the training and test sets to ensure that the prediction accuracy remains robust if the patient sample allocation strategy changes. MC can conduct precise dose calculations directly based on patients’ three-dimensional CT Hounsfield unit (HU) measurements for exacting accurate organ doses. Thus, MC is presently the benchmark data for other dose prediction methods (19-21). However, owing to the large number of transport simulations for photons and electrons, MC requires intensive computational resources, including central processing units (CPUs), graphics processing units (GPUs), and even computing time. This reduces MC’s user-friendliness in the context of quickly completing clinical online prediction tasks. Thus, it is necessary to devise new methods to predict patient-specific organ doses from CT scans with high accuracy, fast speed, and stable prediction performance.

In this study, organ doses computed with MC were used as reference doses. The robust FCN model was trained based on radiomics features and MC-calculated organ doses to predict patient-specific organ doses within a short time, with relatively better robustness and use of minimal computational resources. Radiomics features are highly condensed numerical features that include a considerable greater amount of intensity, anatomical, and tissue properties beyond the D_w or patient size used by the SSDE. The FCN model trained based on radiomics features sufficiently reflects the correlation between patients’ complex characteristics and organ doses, thus precisely predicting patient-specific organ doses. The performance of the FCN model was evaluated by calculating the relative root mean squared error (RRMSE), mean absolute percentage error (MAPE), and coefficient of determination (R²) of the test sets. The robustness of the FCN model was verified via the random allocation of patient samples to the training and test sets at a ratio of 8:2.

Methods

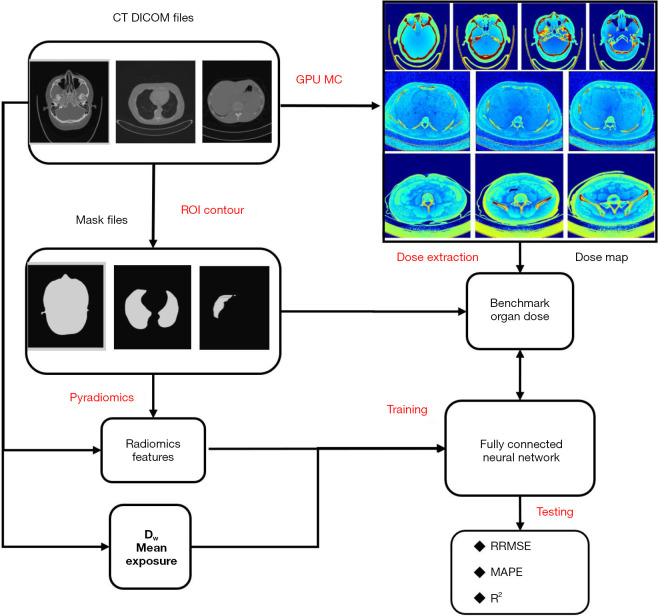
The materials and methods included source patient data, data processing, and dose prediction methods. As indicated in the flowchart in Figure 1, in the workflow, it is necessary to process CT data, generate mask data, extract radiomics features, and compute reference organ doses before training and evaluation of the FCN organ dose prediction model. In this section, the first part introduces the patient data collection and data processing. The second part shows the technical workflow for radiomics feature extraction and selection. The third part outlines the calculation of the reference organ doses for head, chest, and abdominal CT data using a GPU-based MC. The fourth part explains how we constructed, trained, and evaluated the FCN model.

Figure 1.

General workflow for training and evaluating the FCN model to predict patient-specific organ doses for the head, chest, and abdomen in patients. CT, computed tomography; DICOM, Digital Imaging and Communications in Medicine; GPU, graphics processing unit; MC, Monte Carlo; ROI, region of interest; D_w, water diameter; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination.

Data collection

We selected 237 head, 247 abdominal, and 723 thoracic CT cases from the Shanghai Zhongye Hospital. The inclusion criteria were as follows: age between 18 and 75 years, no history of surgery or trauma, and no contraindications to a CT scan. The exclusion criteria were incomplete or corrupted CT images, the presence of metal implants or foreign bodies in the abdomen, and severe motion artifacts. The CT images of the selected patients were exported to DeepViewer autosegmentation system (22), which is a deep learning-based software that can automatically segment regions of interest (ROIs) from CT images. The ROIs segmented by DeepViewer were the body, liver, stomach, bowel, left kidney, right kidney, pancreas, and spinal cord. The CT images and corresponding ROIs of each patient were converted from Digital Imaging and Communications in Medicine (DICOM) format to the Neuroimaging Informatics Technology Initiative (NIfTI; nii) format using “dcmstruct2niiz’ (23), a Python package that converts DICOM RT-Struct files to NIfTI masks. Conversion was necessary to generate CT and mask data for radiomics feature extraction. The scan voltage of the CT machine was set to 120 keV for the head and chest patients and 100 keV for the abdomen.

The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by Institutional Review Board of Shanghai Zhongye Hospital (No. LS0001). Individual consent for this retrospective analysis was waived.

Radiomics feature extraction

The purpose of this study was to use radiomics features extracted from CT images and ROIs to train an FCN model that can predict patient-specific organ doses from CT scans. The Pyradiomics module (24) was used to extract radiomics features from each patient’s CT scans and ROIs. The Pyradiomics module is a Python library that calculates various radiomics features from medical images and masks. The main procedures of the feature extraction and selection process included image preprocessing, feature calculation, and feature selection.

In the first step, we performed image preprocessing to standardize the radiomics feature calculation and enhance the robustness of the FCN model. We resampled the spatial resolution of the CT and masks for each patient to 1, 1, and 5 mm, respectively, using the Pyradiomics parameter “resamplePixelSpacing”. The “resamplePixelSpacing” parameter in Pyradiomics resamples the entire image volume, including all voxels, by interpolating the intensity values based on the specified spacing. This interpolation process inherently takes into account all voxels, including those at the boundaries of different structures (e.g., organs) within the image. We also performed data augmentation (25-27) to increase the size and diversity of the training data.

In the second step, we calculated 107 radiomics features for each organ of the patient without using filters that preprocess medical images to emphasize specific patterns, textures, or structures. The radiomics features were divided into seven types: gray-level co-occurrence matrix, first-order statistics, neighboring gray-tone difference matrix, gray-level dependence matrix, gray-level run-length matrix, shape-based, and gray-level size zone matrix. These features can capture the texture, shape, and intensity characteristics of the ROIs and reflect their correlation, homogeneity, contrast, and intensity distribution. The features were stored in a CSV file and used as input data to train the FCN model.

In the third step, we selected the relevant features to avoid overfitting (28,29) and enhance the robustness of the FCN model. Overfitting is a problem that occurs when the model learns excessively from the training data and fails to generalize to new data. We used the f-regression function from the scikit-learn library (30,31) to select features that had a high correlation with the output variables (age and gender). The f-regression function can compute the F value and P value for each feature and output variable pair and rank the features accordingly. The top 100 features for each output variable were selected and used to train the FCN model according to F values. Feature extraction and selection were performed using double AMD EPYC 7,551 CPUs from Advanced Micro Devices, Inc. in the United States, in the Anaconda 3 (32) environment. Anaconda 3 is a platform that provides various Python packages and tools for data science and machine learning.

Reference organ dose calculation

Organ doses are the amount of radiation absorbed by the organs during the CT scan and are important for assessing the radiation risk and optimizing the scan parameters. To train the FCN model, we obtained the reference organ doses for each patient, which were calculated using a GPU-based MC particle transport code, GGEMS (33).

GGEMS is software that can simulate the interaction of photons and electrons with matter, and it can handle complex geometries, heterogeneous materials, and multiple radiation sources. GGEMS can run on GPUs, which are specialized hardware devices that can perform parallel computations much faster than CPUs. By using GPUs, GGEMS can process MCs much faster than can CPU-based MC codes almost without sacrificing organ dose calculation accuracy. GGEMS has been applied to compute dose distributions in brachytherapy (34).

To carry out organ dose simulation, SPEKTR3.0 software was used to generate the energy spectrum of X-ray, and the equivalent spectrum was validated by measuring the half-value layer (HVL) method. The equivalent spectrum was then randomly sampled with an interval of 1 keV for further simulations of the X-ray spectrum (35). Tube Current Modulation (TCM) information was extracted from the DICOM image headers to generate the number of source particles of each slice. The tube current was proportional to the number of photons in the simulation. In order to obtain the real CT dose. We obtained the conversion coefficient by the ratio of the CTDI value measured under a 100-mAs tube current and a CTDI value calculated in the MC. Finally, the coefficient was applied to the MC module dose. No secondary particles were simulated during the simulation since the mean free path of secondary particles were considered smaller than the size of voxels of CT images.

For each patient, we used GGEMS to calculate the organ doses of the brain, eyes, lens, optical nerves, pituitary, lungs, heart, esophagus, trachea, liver, stomach, bowel, left kidney, right kidney, pancreas, and spinal cord from the CT image and masks. We also considered autotube current modulation, which is a technique that can adjust the tube current according to the patient’s anatomy and reduce the radiation dose. We performed GPU-based MC simulations using two Nvidia RTX-4090 graphics cards from Shenzhen Colorful Technology and Development CO., LTD., which are high-performance GPUs that can support large-scale simulations. We obtained the slice-wise dose distribution for each patient, with an error of less than 2% in each voxel. A voxel is the smallest unit of volume in a three-dimensional (3D) image and contains the intensity value of the image. The GPU-calculated organ doses were used as the reference organ doses when training the FCN model to predict organ doses from radiomics features.

Organ dose prediction model

The FCN is an effective machine-learning algorithm that can provide an efficient solution to regression problems by learning the complex nonlinear relationship between the input and output variables. A regression problem is a type of supervised learning problem that involves predicting a continuous value based on the input features. The FCN model consists of multiple layers of artificial neurons that can process and transform the input data. The FCN model can maximally reduce the loss by modulating the weighting matrix according to the reference y-values. The loss function is a measure of how well the model fits the data, and the weighting matrix is a set of parameters that determines how the neurons are connected and activated. A well-trained FCN model can achieve better performance in terms of speed, accuracy, and interpretability as compared to traditional regression methods. The trained FCN regression model could reflect the relationship between the input radiomics features and the reference organ doses and accurately predict personalized organ doses.

The FCN structure used in this study contained six dense layers: an input layer, an output layer, and four hidden layers. A dense layer is a type of layer that connects every neuron in the previous layer to every neuron in the current layer. The input layer receives the radiomics features as input data, and the output layer produces the organ doses as the output data. We split each of the head, chest, and abdomen datasets into training and test sets at a ratio of 0.8:0.2 using the “train_test_split” function from the scikit-learn module. The hidden layers perform nonlinear transformations and learn high-dimensional features from the input data. For each dense layer, we applied regularization techniques by using batch normalization and “dropout” to improve the generalization and robustness. Batch normalization is a technique that can normalize the input data for each layer and reduce the internal covariate shift. The internal covariate shift occurs when the distribution of the input data changes owing to updates of the parameters in the previous layers. Meanwhile, the dropout technique can randomly drop out some neurons during the training process and prevent overfitting. Overfitting is a problem that occurs when the model learns excessively from the training data and fails to generalize to new data. We set the dropout parameter to 0.2, meaning that 20% of the neurons were removed for each layer.

The performance of the trained FCN model was assessed using the regression metrics of the RRMSE, MAPE), and R² on the test sets for the ROIs, including the head, chest, and abdomen. The test set was a subset of the data that was not used for training the model and was used to evaluate how well the model could predict new data. Regression metrics are numerical measures that can quantify the accuracy and goodness of fit of the model. RRMSE is the ratio of the root mean square error to the mean value of the output variable and indicates the relative error of the model. MAPE is the average absolute value of the difference between the predicted and reference values divided by the reference value for all predictions, and it indicates the overall error of the model. R² is the proportion of variance in the output variable that is explained by the input variable, and it indicates the strength of the relationship between the input and output variables. The mathematical equations for RRMSE, MAPE, and R² are as follows:

$$\text{RRMSE}=\frac{\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}}{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{y}}_i}}\times 100\text{\%}$$ [1]

$$MAPE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|}\times 100\text{\%}$$ [2]

$$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle {\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$ [3]

where, n is the number of patients, $y_i$ is the reference organ dose, ${\widehat{y}}_i$ is the predicted organ dose, and $\overline{y}$ is the mean value of reference dose. The robustness of the model was verified by the random assignment of patient samples to the training and test sets, with the ratio of the two sets being maintained at 0.8:0.2, and through the comparison of the regression metrics of different patient sample assignment strategies. The robustness of a model is its ability to maintain its performance under different conditions and scenarios. Residual network 50 (ResNet50) models were employed on the CT images datasets to assess the accuracy and generality of CNNs in predicting patient-specific organ doses from CT scans.

Results

In this section, the first part reports the mean predicted and reference organ doses as the standard deviation (SD). The second part lists the computed regression metrics of the FCN prediction model. The third part contains the regression metrics for different patient sample allocation strategies on the training and test sets for evaluation of the robustness of the FCN prediction model.

Predicted organ doses on the test sets

Tables 1-3 list the FCN-predicted organ doses for the head, chest, and abdomen. Table 1 shows the comparison of the reference and predicted doses, indicating good agreement. For the investigated head organs, the mean reference doses ranged from 20.43 mGy (pituitary) to 39.79 mGy (right lens), while the mean predicted doses closely matched these values. The SD were generally low, ranging from 2.1 to 7.9 mGy for the reference doses and 2.19 to 7.01 mGy for the predicted doses. The agreement between reference and predicted doses, coupled with low SDs, supported the accuracy of the FCN model.

Table 1. Mean predicted and reference doses for the head CT scans on the test sets.

Organ	Mean reference dose (mGy)	SD of the reference dose (mGy)	Mean predicted dose (mGy)	SD of the predicted dose (mGy)
Brain	26.94	2.61	26.89	2.89
Eye_L	33.28	6.97	33.22	7.01
Eye_R	32.25	4.85	32.34	4.19
Len_L	38.87	5.95	38.93	6.41
Len_R	39.79	7.82	39.25	7.90
Nerve_L	23.42	2.70	23.25	2.10
Nerve_R	24.29	4.23	23.71	3.51
Pituitary	20.43	4.31	20.49	4.26

CT, computed tomography; SD, standard deviation; Eye_L, left eye; Eye_R, right eye; Len_L, left lens; Len_R, right lens; Nerve_L, left nerve; Nerve_R, right nerve.

Table 2. Mean predicted and reference doses for chest CT scans on the test sets.

Organ	Mean reference dose (mGy)	SD of the reference dose (mGy)	Mean predicted dose (mGy)	SD of the predicted dose (mGy)
Lung_L	16.31	7.39	16.49	6.08
Lung_R	16.44	6.74	16.54	6.05
Heart	13.86	5.53	13.38	4.34
Spinal cord	11.51	3.71	11.19	2.70
Esophagus	13.41	4.81	13.011	3.85
Trachea	9.43	4.17	9.04	3.52

CT, computed tomography; SD, standard deviation; Lung_L, left lung; Lung_R, right lung.

Table 3. Mean predicted and reference doses for abdominal CT scans on the test sets.

Organ	Mean reference dose (mGy)	SD of the reference dose (mGy)	Mean predicted dose (mGy)	SD of the predicted dose (mGy)
Bowel	25.28	5.01	25.14	4.66
Kidney_L	26.16	4.62	25.89	3.91
Kidney_R	26.21	5.12	25.84	4.34
Liver	30.25	6.26	29.57	5.11
Pancreas	24.19	4.19	24.34	3.15
Spinal cord	17.06	3.04	17.08	2.51

CT, computed tomography; SD, standard deviation; Kidney_L, left kidney; Kidney_R, right kidney.

As seen in Table 2, the mean reference doses varied across organs, from 9.43 mGy (trachea) to 16.44 mGy (right lung), while the mean predicted doses closely tracked these values. The SDs ranged from 3.71 to 7.39 mGy for reference doses and 2.70 to 6.08 mGy for predicted doses. Despite interorgan differences, the agreement between the reference and predicted doses remained consistently robust.

As seen from Table 3, the mean reference doses ranged from 17.06 mGy (spinal cord) to 30.25 mGy (liver), with the mean predicted doses being closely aligned with these values. The SDs ranged from 3.04 to 6.26 mGy for the reference doses and 3.15 to 5.11 mGy for the predicted doses across these organs. The close concordance between the reference and predicted doses, along with the relatively low SDs, indicates the accuracy of the FCN for a diverse set of abdominal organs.

Computed regression metrics on the test sets

As observed in Table 4, the RRMSE for various head organs ranged from 3.89% for the brain to 11.24% for the right eye. The MAPE results indicate the FCN model was effective, with values ranging from 1.68% for the brain to 5.19% for the pituitary gland. The R² values showed strong correlations between the predicted and reference organ doses, with the brain yielding an R² score of 0.93.

Table 4. Regression metrics for the head CT scans on the test sets.

Organ	RRMSE (%)	MAPE (%)	R2
Brain	3.89	1.68	0.93
Eye_L	5.04	4.66	0.90
Eye_R	11.24	4.92	0.84
Len_L	8.15	4.61	0.88
Len_R	5.44	5.13	0.89
Nerve_L	8.21	4.22	0.80
Nerve_R	5.66	4.68	0.86
Pituitary	5.24	5.19	0.89

CT, computed tomography; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination; Eye_L, left eye; Eye_R, right eye; Len_L, left lens; Len_R, right lens; Nerve_L, left nerve; Nerve_R, right nerve.

As seen in Table 5, the RRMSE values, ranging from 8.15% for the left lung to 10.58% for the heart, attest to the ability of the FCN model to minimize the prediction errors across various chest organs. Meanwhile, the MAPE, ranging from 11.42% for the spinal cord to 15.18% for the trachea, provides insights into the prediction bias, with relatively low values indicating favorable predictions. Notwithstanding some variations, the R² values were between 0.74 and 0.86.

Table 5. Regression metrics for the chest CT scans on the test sets.

Organ	RRMSE (%)	MAPE (%)	R2
Lung_L	8.15	14.38	0.86
Lung_R	8.23	13.52	0.85
Heart	10.58	14.19	0.75
Spinal cord	8.83	11.42	0.74
Esophagus	9.86	12.97	0.77
Trachea	9.71	15.18	0.78

CT, computed tomography; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination; Lung_L, left lung; Lung_R, right lung.

As evidence from Table 6, the RRMSE values ranged from 7.71% for the bowel to 11.90% for the right kidney. Meanwhile, the MAPE ranged from 5% for the bowel to 8.34% for the right kidney, indicating a low incidence of errors and high accuracy in the prediction of patient-specific abdominal organ doses. Finally, the R² values, which ranged from 0.74 to 0.89, confirm the strength of the correlation between the predicted and reference doses.

Table 6. Regression metrics for abdominal CT scans on the test sets.

Organ	RRMSE (%)	MAPE (%)	R2
Bowel	7.71	5.0	0.89
Kidney_L	10.4	6.38	0.78
Kidney_R	11.9	8.34	0.75
Liver	9.93	7.97	0.78
Pancreas	11.73	7.06	0.74
Spinal cord	11.53	7.47	0.75

CT, computed tomography; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination; Kidney_L, left kidney; Kidney_R, right kidney.

Robustness of the FCN model

The patient samples in the training and test sets were randomly reallocated 20 times with the ratio being maintained at 0.8:0.2. The RRMSE, MAPE, and R² values were computed for each training-test split. For the head, chest, and abdomen, the organ doses of different training-test splits are plotted as box charts for each organ in Figures 2-4.

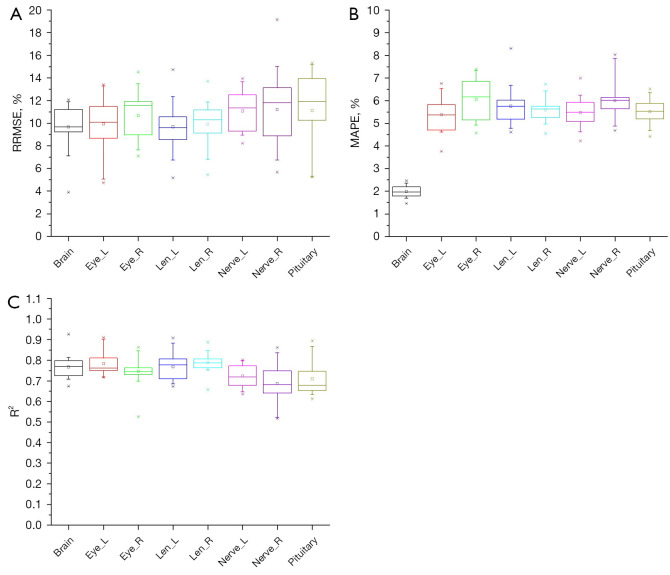
Figure 2.

Box charts of (A) RRMSE, (B) MAPE, and (C) R² for the head doses of 20 random patient allocation strategies. Eye_L, left eye; Eye_R, right eye; Len_L, left lens; Len_R, right lens; Nerve_L, left nerve; Nerve_R, right nerve; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination.

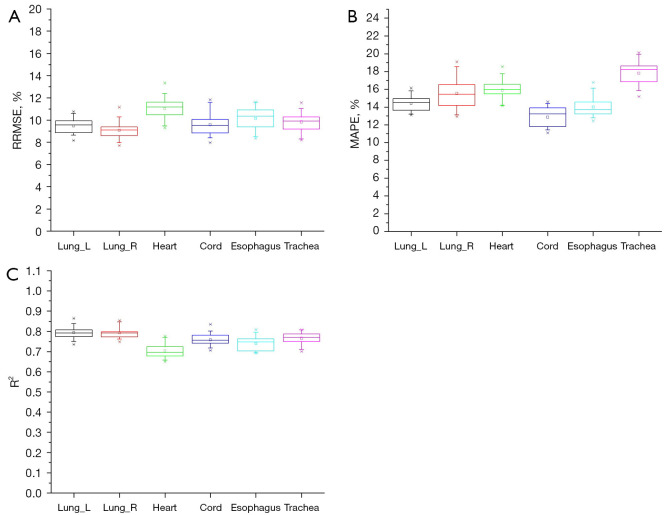
Figure 3.

Box charts of (A) RRMSE, (B) MAPE, and (C) R² for the chest doses of 20 random patient allocation strategies. Lung_L, left lung; Lung_R, right lung; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination.

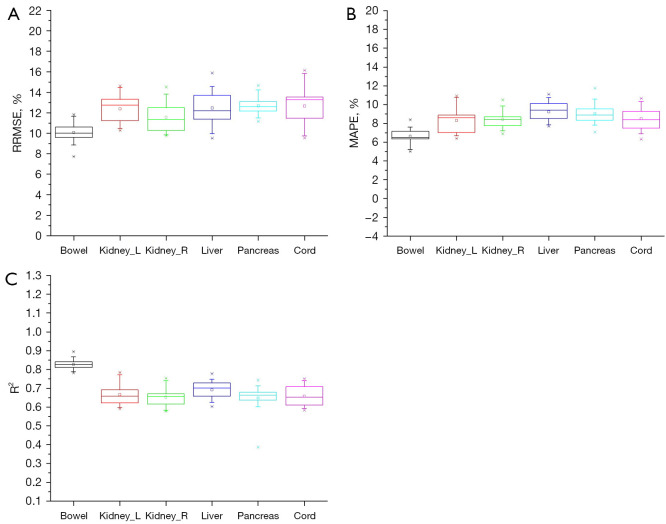
Figure 4.

Box charts of (A) RRMSE, (B) MAPE, and (C) R² for the abdominal doses of 20 random patient allocation strategies. Kidney_L, left kidney; Kidney_R, right kidney; RRMSE, relative root mean squared error; MAPE, mean absolute percentage error; R², R-square is the coefficient of determination.

As seen in Figure 2A, the brain had the highest precision with the lowest median RRMSE (9.62) and interquartile range (IQR) (1.89), indicating more accurate predictions. The pituitary showed a lower accuracy, with the highest median RRMSE (11.23) and IQR (3.16). Eyes, lenses, and nerves exhibited median RRMSE values from 10.2% to 11.3%. The brain exhibited high accuracy with a low MAPE of approximately 1.8% and a narrow IQR, reflecting consistent predictions (Figure 2B). Meanwhile, the eyes and lenses exhibited higher MAPE values, ranging from 4.5% to 7.4%, and their IQR values had modest data variability. Similarly, the nerves and the pituitary had high MAPE values (approximately 4.6–8.3%). These findings emphasize the overall effectiveness of the FCN model in predicting patient-specific head organ doses.

As can be surmised from Figure 2C, the FCN model demonstrated good accuracy, as indicated by R² values exceeding 0.7 for all organs. The brain, left eye, and right eye exhibited particularly strong fits, with R² values ranging from approximately 0.70 to 0.92, indicating good predictive performance. The left lens, right lens, left nerve, right nerve, and pituitary also maintained high R² values, indicating robust model fit. The IQR values for these head organs suggested stable and consistent predictions, further emphasizing the ability of the FCN model to provide precise estimates of patient-specific head organ doses.

Meanwhile, the heart yielded the lowest precision (Figure 3A), with the highest median RRMSE (10.5%) and IQR (1.34). The esophagus showed similar accuracy, with a median RRMSE of 10.5% and an IQR of 1.7. The predictive performance for the lungs, spinal cord, and trachea was better than for the heart and esophagus, with median RRMSE values ranging from 8.6% to 10.1%.

Figure 3B shows that both the left and right lungs exhibited low MAPE values of approximately 13.5%, indicating highly accurate prediction. The IQR values for the chest organs, while showing some variability, reflected a consistent model performance. Similarly, the heart maintained a low MAPE of approximately 15.7%, suggesting accurate predictions. The spinal cord, esophagus, and trachea yielded MAPE values ranging from 11.1% to 14.6%, indicating effective prediction accuracy.

As can be observed from Figure 3C, the model demonstrated robust accuracy, with R² values exceeding 0.65 for all organs. The left lung, right lung, and heart showed strong fits, with R² values ranging from approximately 0.76 to 0.86, highlighting the model’s excellent predictive performance for the chest organs. The spinal cord, esophagus, and trachea maintained high R² values, verifying the reliability of the FCN model. The IQR values for these organs suggest consistent and stable predictions.

As seen in Figure 4A, the liver exhibited the highest accuracy, with a low median RRMSE (11.83) and IQR (2.39), indicating precise prediction. The bowel displayed a lower accuracy, with the highest median RRMSE (10.47) and IQR (2.51). The kidneys, pancreas, and spinal cord yielded median RRMSE values ranging from 8.5% to 8.9%.

Figure 4B shows that the bowel, left kidney, and right kidney had effective prediction accuracy, with MAPE values ranging from 6.3% to 7.2%. These values suggest that the FCN model provides precise estimates for these abdominal organs. The liver, pancreas, and spinal cord also exhibited MAPE values of approximately 8.7%, indicating reliable prediction.

As seen in Figure 4C, the FCN model showed solid predictive accuracy, with R² values exceeding 0.6 for the examined abdominal organs. Particularly noteworthy are the bowel, left kidney, right kidney, and liver, which exhibited strong fits, with R² values ranging from approximately 0.7 to 0.83. This indicated the effectiveness of the FCN model in accurately predicting abdominal organ doses.

Discussion

This study aimed to explore a novel and robust for accurately predicting a personalized organ doses when the resources for prediction are minimized to a single CPU core. A CPU core is the basic unit of processing power in a computer that can execute one task at a time. Minimizing the resources for prediction means that the prediction method can be run on a low-end computer with limited computational power and memory. Unlike previous studies, we investigated personalized organ doses by training the FCN prediction model based on radiomics features and GPU-calculated organ doses. Radiomics features are quantitative features that can describe the texture, shape, and intensity characteristics of ROIs in medical images. The GPU-calculated organ doses were the reference organ doses obtained using a GPU-based MC particle transport code. A GPU is a specialized hardware device that can perform parallel computations much faster than can a CPU. The MC particle transport code is a software that can simulate the interaction of radiation with matter.

The performance of the radiomics feature-based FCN model was assessed using the regression metrics RRMSE, MAPE, and R² on the test set for the ROIs in the liver, stomach, bowel, left kidney, right kidney, pancreas, and spinal cord. Regression metrics are numerical measures that can quantify the accuracy and goodness of fit of a model. The results of this study suggest that radiomics features can reflect the head, chest, and abdominal organ features (e.g., geometric shape, size, tissue, and anatomy). We further found that the FCN model could accurately and robustly predict patient-specific organ doses based on radiomics features.

In previous studies (13,14) that adopted size-specific dose estimates (SSDEs), NNs, CNNs, etc., only patient size, tube voltage, or some other simple features were considered, and the robustness of these models was not validated via random assignment of patient samples to the training and test sets. These methods have certain limitations; for example, they ignore the patient’s anatomy, tissue, and geometry and are sensitive to data distribution and quality. In previous MC studies, a massive amount of computing resources of multiple CPUs or GPUs was required for using MC to calculate personalized organ doses. MC is the gold standard method for accurately simulating the interaction of radiation with matter, but it is also very time-consuming and complex to implement.

In this study, we proposed a novel method to predict patient-specific organ doses using an FCN prediction model based on radiomics features and GPU-calculated organ doses. Radiomics features are quantitative features that can describe the texture, shape, and intensity characteristics of ROIs in medical images. The GPU-calculated organ doses were the reference organ doses obtained using a GPU-based MC particle transport code. The FCN model is a machine learning algorithm that can learn the complex nonlinear relationship between the input and output variables. The trained FCN model only requires a simple Python script to predict organ doses in one second, with minimal computing resources, even a single CPU. Thus, this study represents a significant advance in the development of a fast, accurate, and easy-to-use organ dose prediction method.

To assess the accuracy and generality of CNNs in predicting patient-specific organ doses from CT scans, we employed ResNet50 models on the datasets for head, chest, and abdomen CT images. The ResNet50 models achieved the following MAPE values: 5.56%, 6.03%, 5.49%, and 5.88% for the left eye, right eye, left lens, and right lens, respectively; 14.31% and 13.16% for the left lung and right lung, respectively; and 12.27% and 13.01% for the left kidney and right kidney, respectively. The corresponding R² values were 0.68, 0.71, 0.72, and 0.74 for the left eye, right eye, left lens, and right lens, respectively; 0.75 and 0.81 for the left lung and right lung, respectively; and 0.38 and 0.26 for the left kidney and right kidney, respectively. The ResNet50 models likely demonstrated worse generality (R²) for kidneys because the limited abdomen data set was not adequate for achieving sufficient predictive generality with ResNet50. The maximum predictive discrepancy between the radiomics-based models and the ResNet models was within 3% for MAPE and 0.5 for R². The radiomics-based models slightly outperformed the ResNet50 models, likely due to the generalized features from radiomics and simpler FCN structure being better suited to the smaller dataset compared to the complex ResNet50 models, which require training on a larger number of parameters.

This study had several limitations that should be addressed. First, we only trained the FCN prediction model using the radiomics features of patients diagnosed at our institution. The accuracy and robustness of the model can vary across institutions owing to different patient populations, scan protocols, and image quality. Therefore, collaboration with multiple institutions is necessary to verify the effectiveness of the proposed method. Second, the GPU-calculated reference organ doses were only validated using the CTDI_vol of the CT device at our institution. The CTDI_vol is a standardized measure of the radiation dose output of a CT scanner; however, it does not reflect the reference organ doses of the patients. It is also possible that different types of CT devices have different radiation characteristics and dose distributions. Therefore, it is necessary to train the FCN model for multiple CT device types and compare the GPU-calculated organ doses with the reference organ doses measured by dosimeters. Third, we did not include other tissues or organs, such as the skin and spleen, in this study. The skin and spleen are also exposed to radiation during the CT scan, and they may have different radiomics features and organ doses compared to other ROIs. Therefore, it is necessary to develop a predictive model for these tissues and organs in the future.

Conclusions

This study found a correlation between radiomics features and personalized organ doses using a well-trained FCN prediction model. The range of MAPE was from 1.68% to 5.2% for head organs, 11.42% to 15.2% for chest organs, and 5.0% to 8.0% for abdominal organs; the maximal R² values were 0.93, 0.86, and 0.89 for the head, chest, and abdominal organs, respectively. Good accuracy and robustness were achieved by the FCN in 1 second with a single CPU core for organ dose prediction. This suggests a new direction for predicting organ dose from CT examinations through building FCN models that combine radiomics features and GPU-calculated organ dose.

Supplementary

The article’s supplementary files as

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by Institutional Review Board of Shanghai Zhongye Hospital (No. LS0001). The requirement for individual consent was waived due to the retrospective nature of the study.