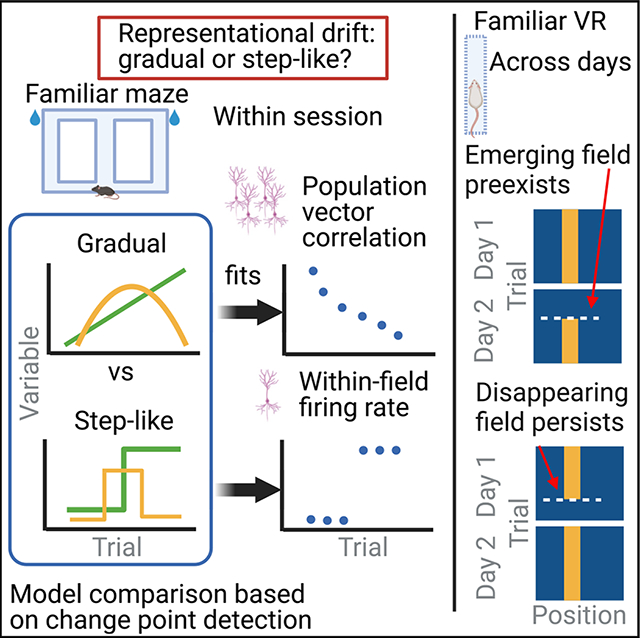
SUMMARY
Representation of the environment by hippocampal populations is known to drift even within a familiar environment, which could reflect gradual changes in single-cell activity or result from averaging across discrete switches of single neurons. Disambiguating these possibilities is crucial, as they each imply distinct mechanisms. Leveraging change point detection and model comparison, we find that CA1 population vectors decorrelate gradually within a session. In contrast, individual neurons exhibit predominantly step-like emergence and disappearance of place fields or sustained changes in within-field firing. The changes are not restricted to particular parts of the maze or trials and do not require apparent behavioral changes. The same place fields emerge, disappear, and reappear across days, suggesting that the hippocampus reuses pre-existing assemblies, rather than forming new fields de novo. Our results suggest an internally driven perpetual step-like reorganization of the neuronal assemblies.
In brief
Zheng et al. systematically analyze drift in hippocampal place fields and show that, while the population-level representation gradually drifts, the peak firing rates of individual place fields are better described by abrupt changes. The step-like changes are not driven by measured behavioral variables and are biased by the pre-existing assemblies.
Graphical Abstract
INTRODUCTION
Balance between stability and flexibility is crucial for hippocampal function. Although hippocampal place cells have long been assumed to be stable within the same environment,1,2 recent studies have found that population-wide representations become progressively dissimilar as time lapses, without external perturbations.3–5 These gradual changes, termed “representational drift,” have timescales ranging from minutes to weeks. They have also been reported in the piriform cortex6 and several neocortical areas,7 although Jensen et al.8 reported the lack of drift in single neurons in the motor system.
While representational drift is often defined as the “gradual” decorrelation in the population over time, it remains an unresolved question regarding whether the mechanism is “gradual” or “discrete” at the level of single neurons. This distinction is crucial for a mechanistic understanding of the phenomenon. Hebbian spike-timing-dependent plasticity (STDP)9,10 is expected to change synaptic strength over many repetitions and, thus, gradually. On the other hand, behavioral timescale synaptic plasticity11–15 (BTSP) provides a mechanism for abrupt changes in neural firing rate. Intracellular and imaging experiments in vivo have demonstrated that spontaneously emerging ON fields often coincide with dendritic “plateau potentials” in CA1 pyramidal neurons, attributed to the temporal coordination of their entorhinal and CA3 inputs.12,16 Thus, representational drift in the hippocampus could conceivably consist of either gradual or discrete changes in single-neuron activity patterns.
Studies of BTSP focus on the emergence of place fields (also translocation, i.e., emergence in one and abolishment in another field, see Milstein et al.14) but not disappearance (note: spontaneous emergence and disappearance of place fields within session is visible in a previous paper17). Furthermore, it is unclear whether neurons exhibit other forms of spontaneous abrupt changes, such as up- or down-modulation of firing rate (or “rate remapping”18,19). The apparent lack of evidence could be due to difficulties in detecting abrupt changes. The emergence of place fields is relatively well defined and can be detected by looking at when the within-field activity goes above thresholds.15,20 Similarly, rate remapping is often induced by changing some experimental condition (e.g., the wall color of the maze) and studied in a trial-averaged fashion.18,19 On the other hand, spontaneous rate remapping is difficult to study without an unsupervised method for detecting abrupt and sustained changes on a single-trial level.
We developed a statistical framework that allowed us to detect, determine, and link the type of changes occurring on the single-cell and population levels. By analyzing large datasets of simultaneous recordings of the hippocampal CA1 pyramidal neurons, we show that population vectors of the CA1 pyramidal cells are decorrelated as a function of elapsed trials gradually, akin to the gradual drift view. In contrast, changes at the individual place cell level are better characterized by step-like emergence and disappearance of place fields or steep changes in within-field firing, which we call “switching.” We found that, although spatial position, trial number, and novelty may modulate the probability of place field turnover, switching can happen on every trial and in all parts of the test environment without apparent behavioral changes. Switching is not a single-cell property: neurons with multiple place fields can sustain stability in one field and change in another field, and neurons with switching fields in one environment may remain stable in another. Instead, switching appears to be driven by circuit dynamics, as place fields co-switch together on the same trial more than expected by chance. Finally, the spontaneous emergence of place fields on one day does not mean a de novo formation of a place field but rather a “reuse” of pre-existing assemblies, as emerging/disappearing fields on one day could pre-exist/reappear on the previous/next day. These findings bridge together single-cell and population features—the step-like and gradual views—and illustrate that pre-existing cell assembly blocks continuously reorganize themselves without external perturbations.
RESULTS
We examined the stability of single units and populations of hippocampal CA1 pyramidal cells while mice performed a spontaneous alternation task in a figure-8 maze in either a familiar or a novel environment21 (schematics in Figure 4K; see STAR Methods). For multiple-day comparisons, CA1 neurons detected by two-photon imaging were used as mice traversed a 1D virtual hallway.22
Figure 4. Spatial-temporal and behavioral modulation of switching.
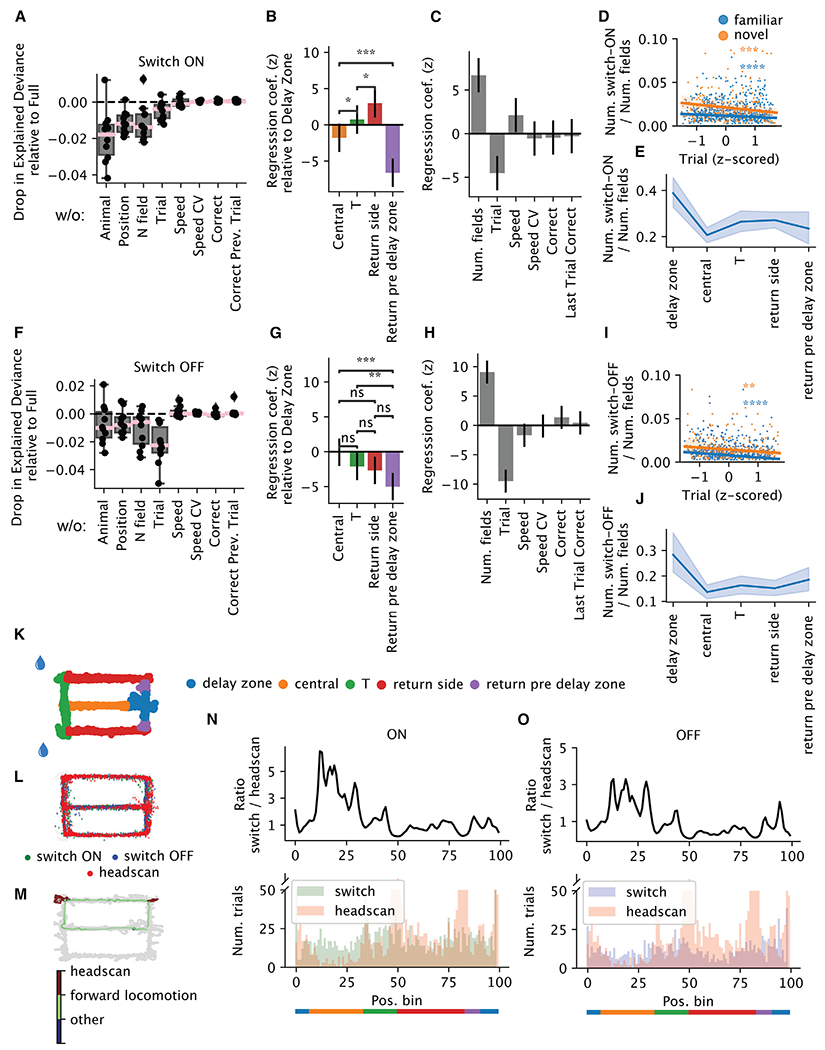
(A–C) Poisson generalized linear model (GLM) predicting the number of switch-ON occurrences per arm and trial within one session (n = 5,131 arms × trials from 46 sessions from 11 animals). (A) Drop in explained deviance relative to the full model when one predictor is removed in the GLM. Each dot is one random split in the 5-fold cross-validation. (B) Spatial regression coefficients, in standardized units: each variable represents the gain in the probability of switching when the animal is in one arm relative to the delay zone. Error bars reflect 95% confidence intervals (CIs), based on asymptotic standard errors from the Fisher information matrix. (C) The rest of the regression coefficients.
(D) The number of switch-ON occurrences normalized by the number of fields as a function of trial (Z scored within each session for comparison across sessions with different numbers of trials). Blue, familiar; orange, novel (familiar: n = 1,029 trials, Pearson r = −0.15, p = 1.3 × 10−6; novel: n = 281 trials; Pearson correlation r = −0.23, p = 1.3 × 10−4).
(E) The number of switch-ON occurrences normalized by the number of fields as a function of the arms. Each data point is one session. Shaded region reflects the 95% CI.
(F–J) Similar to (A)–(E), but for switching OFF occurrences. (I) Familiar: Pearson r = −0.2, p = 3.3 × 10−11; novel: Pearson r = −0.18, p = 2.7 × 10−3).
(K) Schematic of the maze, with each arm colored differently.
(L) Detected head-scanning events projected onto the maze.
(M) Distribution of the head scans and switches on the maze for one example session.
(N and O) Top: the ratio as a function of position between the number of trials when switch-ON (N)/-OFF (O) occurs and the number of trials when head scans occur. Bottom: the number of trials when switches (green or purple)/head scans (pink) occur as a function of position.
Within-session representational drift is driven by discrete switching of place fields
As animals traversed the figure-8 maze, the dorsal CA1 population activity exhibited largely similar sequential firing over the entire session (Figure 1A; place cells with place fields1). Yet, a subset of neurons changed their firing rates substantially from the beginning to the end of the session (Figure 1B). To relate our initial observations to previous reports, we first analyzed the correlation between population vectors (PVs) as a function of trial lag (Figure 1C). The correlation decreased as a function of the lag between trials, suggesting drift within both the familiar and the novel environment (Figure 1D). Linear regression revealed that drift was significantly faster in novel environments (larger negative slope) within the first 1–10 trial lags, but we failed to detect a significant difference between novel and familiar environments over a range of 11–20 or 21–30 trial lags (Figure 1E). Thus, our analysis supports the idea that novelty destabilizes the network15,23,24 but also highlights a surprising degree of spontaneous drift that persists in familiar environments.
Figure 1. Stability and change of single units and population activity.
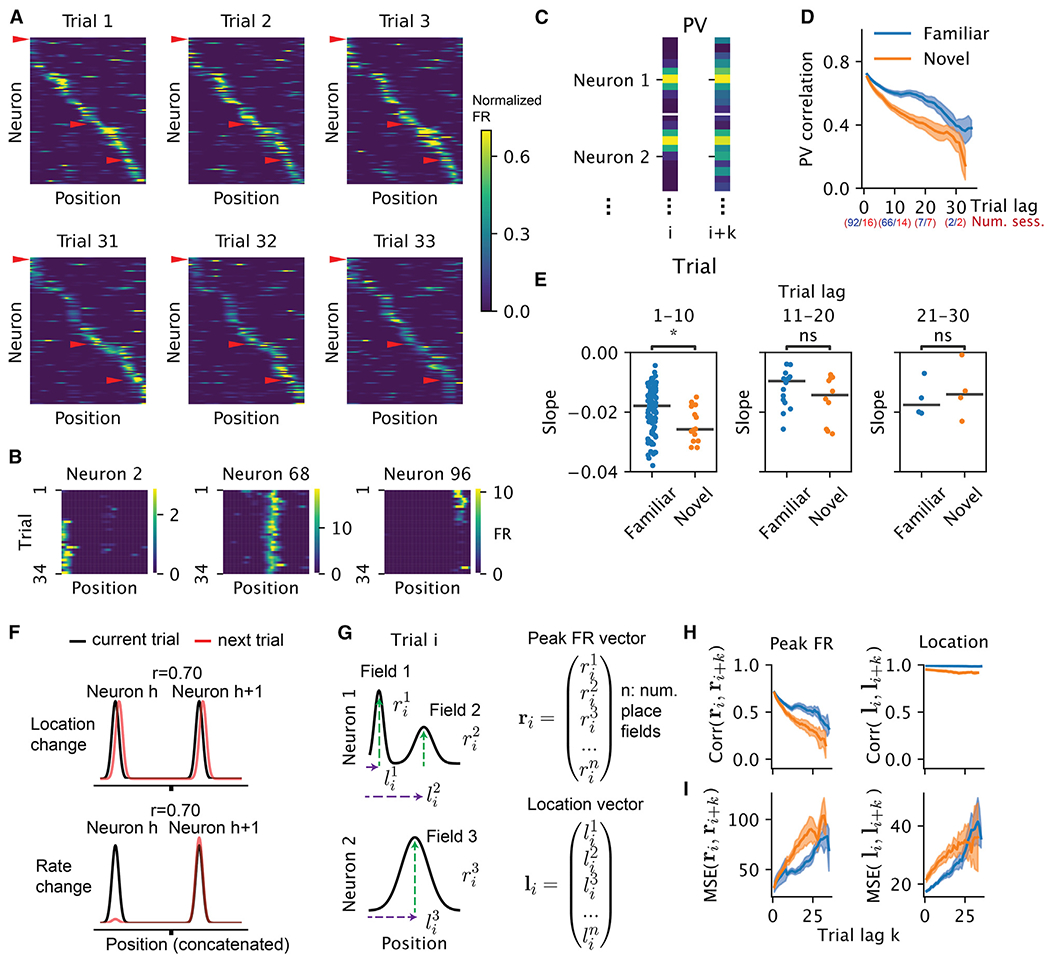
(A) Population rate maps of hippocampal place cells during early and late trials. Place cells were sorted by the peak of the place fields on trial 1. (When there were multiple fields, we used the fields with the largest within-field peak firing rates. Only place cells with spatial information larger than 1 bit/spike are displayed here for ease of visualization; n = 114 of 264 place cells for one direction of turn in the figure-8 maze.) Color represents normalized firing rate.
(B) Rate maps of three example neurons, marked by red arrowheads in (A), showing place field emergence (left), stable firing (middle), and place field disappearance (right).
(C) Schematic for constructing the population vectors (PVs) in (D). The rate maps for all neurons were concatenated on a given trial to form a PV. The Pearson correlation between PVs from a pair of trials was computed. All trial pairs with lag k were averaged to produce the mean PV correlation per trial lag.
(D) Population rate map correlations as a function of trial lag (only place cells are included). Blue and orange correspond to familiar and novel sessions, respectively. Shaded area corresponds to 95% confidence interval, where each data point is the correlation between two trials within one session. The numbers of included sessions for blocks of trials are indicated in parentheses.
(E) Comparing the slope of PV correlation decay between familiar and novel environments in three ranges of trial lags. Trial lag 1–10, n = 106, Wilcoxon rank-sum test, p = 0.02, Cohen’s d = 0.58; trial lag 11–20, n = 26, p = 0.3, Cohen’s d = 0.54; trial lag 21–30, n = 8, p = 0.68, Cohen’s d = −0.35. Asterisks indicate the significance level for all figures (*0.01 < p ≤ 0.05; **0.001 < p ≤ 0.01, ***0.0001 < p ≤ 0.001; ****p ≤ 0.0001). We note that the lack of significance could be due to fewer sessions present at the later ranges.
(F) Schematics of different hypothetical mechanisms inducing a population-level decorrelation. Each Gaussian bump represents the tuning curve of one place cell. The Pearson correlation r is taken between the black (current trial) and red (next trial) curves.
(G) Schematics for how the within-field peak firing-rate vector and place field location vector were constructed in (H) and (I).
(H) Correlation of within-field peak population firing rate (left) and peak location (right) of place cells as a function of trial lag.
(I) Similar to (H), but instead of correlation, the normalized squared Euclidean distance (equivalent to mean squared error, MSE) is shown as a function of trial lags.
In principle, representational drift could be driven by a change in place field location or its firing rate, among other possibilities (Figure 1F). We found the vector of the peak firing rate of all place fields decorrelated as a function of trial lag, whereas the vector of the field locations remained stable (Figures 1G and 1H). We emphasize, though, that the lack of decorrelation does not mean the field locations do not change as a function of trial. In fact, the average squared Euclidean distance as a function of trial lag increased significantly (Figure 1I). We focus on the decorrelation due to changes in firing rate for the rest of this paper.
The decorrelation of the population vectors could arise from either a gradual change (as implied by the term “drift”3,4) or a relatively sudden (“quantal”) jump11 at the single-cell level. Qualitative inspection suggested discrete and sustained changes in the within-field firing rates (quantal change; Figures 2A and 2B). We refer to such step-like increases/decreases in firing rates as “switching ON/OFF.” To investigate switching quantitatively, we leveraged a change-point detection model to fit a piece-wise constant function to the peak within-field firing rates across trials. The trials at which these step functions change values are determined to be change points25 (see STAR Methods). To select the numbers of change points objectively, we compared the observed fit to models fit on shuffled data where trial order was randomly permuted (Figure 2C). To rule out changes that were too small, we required change points to result in at least a 40% change in firing rate (relative to the maximum). This restriction ruled out only 7% of the putative switching fields (n = 212/3,184). The combination of the shuffle and the criteria on the magnitude ruled out 99.9% of the false positives in simulations from a null model using a homogeneous Poisson process (Figures S13F and S13G), demonstrating the robustness of our framework. Figures 2A and 2B show examples of switching ON and switching OFF fields. Importantly, the switching includes not only a sudden appearance or disappearance of place fields but also drastic changes in firing rates of existing fields (see examples in Figures S3 and S10C). Overall, 19% (2,310/12,311) of the place fields showed significant switching (14% ON, 9% OFF) in the familiar environment (Figure 2D) and 31% (662/2,127; 25% ON, 18% OFF) in the novel environment (Figure 2D), echoing the finding of a higher rate of BTSP in novel environments.15 Furthermore, a subgroup of animals exposed to both familiar and novel environments had less training than the animals exposed to only the familiar environment. These animals had higher fractions of switching fields (“Familiar” in Figure 2E) than the “Familiar only” animals (see caveats in the discussion). Thus, novelty seemed to induce instability in the network in a graded way.
Figure 2. Place cells exhibit discrete switching of firing rate.
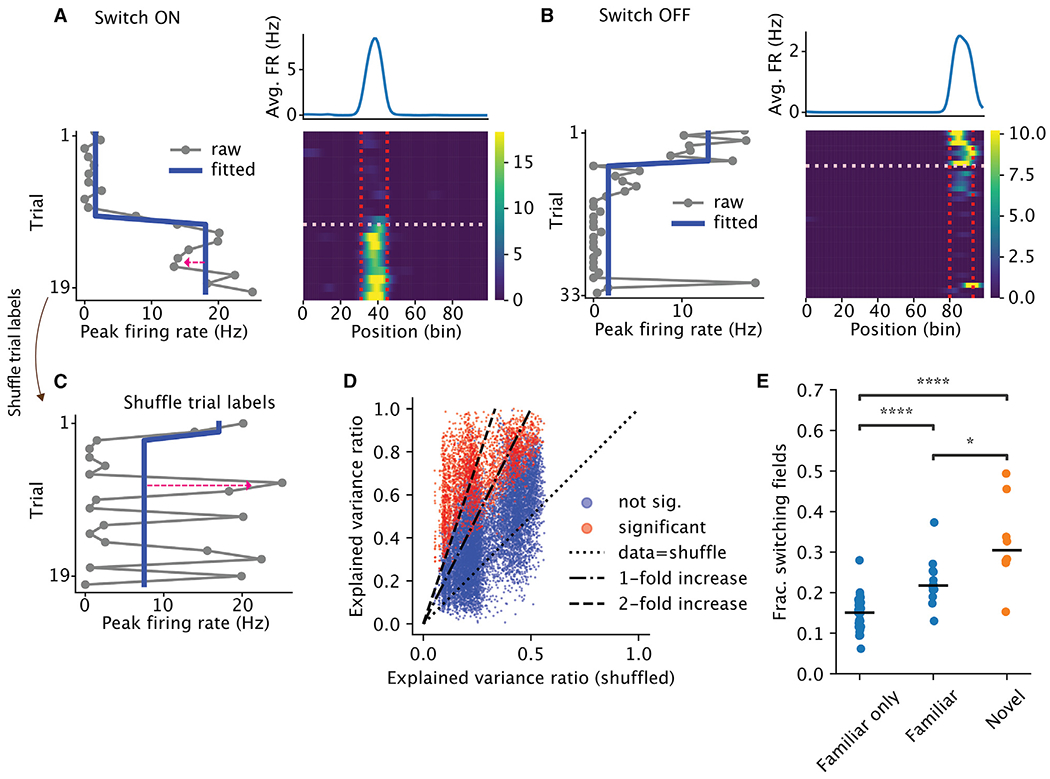
(A and B) Examples of place cells with place fields that switched ON (A) or OFF (B). Bottom right is the rate map, i.e., firing rate (color) as a function of position (x axis) and trial (y axis). Vertical lines mark the boundary of the place fields. The horizontal line marks the switch trial. Bottom left is the peak within-field firing rate across trials. The red arrow in (A) highlights the reconstruction error. The blue line is the fitted step function. Top right is the trial-averaged rate map.
(C) Peak within-field firing rate from (A), with the trial label shuffled.
(D) Explained variance ratio from the best change-point model, data vs. shuffle. Each dot is a place field, colored by whether the field had significant switching.
(E) Each dot is the fraction of switching fields from one session, grouped by whether the session came from an animal that experienced only the familiar environment (“Familiar only,” n = 34, median = 0.15), the session was a familiar-environment session but came from an animal that also experienced the novel environment on that day (“Familiar,” n = 12, median = 0.22), or the session was a novel environment (“Novel,” n = 8, median = 0.3). Horizontal bars are the medians. Two-sided Wilcoxon rank-sum test: Familiar only vs. Familiar, p = 4 × 10−5; Familiar vs. Novel, p = 0.01; Familiar only vs. Novel, p = 1.7 × 10−5.
A potential artifactual source of these observations is electrode drift in the tissue, resulting in the spurious appearance/disappearance or changing firing rates of the recorded neurons. Several observations and control analyses mitigate against such an explanation. First, the majority of place fields were stable across the entire session, and the switching neurons were embedded among them (Figure 1A). Second, comparison of the spike amplitudes during pre-experience and post-experience sleep demonstrated that the firing waveforms across the two sleep sessions did not vary differentially between switching and stable neurons (Figure S1A). Third, neurons with multiple place fields simultaneously showed stable and switching place fields (see examples in Figure 5E; Figure S1C). Finally, neurons recorded on the same site with a switching neuron had unchanged waveforms before and after the switch (Figures S1D–S1H), a strong support for the recording stability despite switching fields. Furthermore, switching was not related to the expression of channelrhodopsin (ChR) in a small subset of the neurons in the dataset (Figure S2).
To demonstrate the accuracy of the change-point model in capturing the firing-rate dynamics across trials, we compared it to an alternative model, which poorly captures abrupt, step-like changes in firing rate, but which can accurately describe the gradual emergence or disappearance of place fields. Specifically, we ran a polynomial regression on each place field’s firing rate with the trial number as the independent variable. Importantly, we matched the number of free parameters between the change point and the polynomial regression models. For instance, a one-change-point model has two parameters specifying the means of the two segments and was compared with a linear regression model (which also has two parameters: slope and intercept). An N-change-point model has N + 1 parameters and was compared with a regression model with Nth order polynomial (Figures 3A–3C; more examples in Figure S3). The change-point models explained more variance for more than 96% of the place fields across all model complexities (Figures 3D–3F, left column). In contrast, polynomial regression explained more variance than the change-point model for the population vector decorrelation (Figures 3D–3F, right column). Altogether, these analyses revealed that individual place fields tend to exhibit discrete and step-like changes in contrast to gradual and continuous changes in the population-level representation.
Figure 3. Discrete and continuous models of the trial-to-trial changes of within-field firing rates and population vectors.
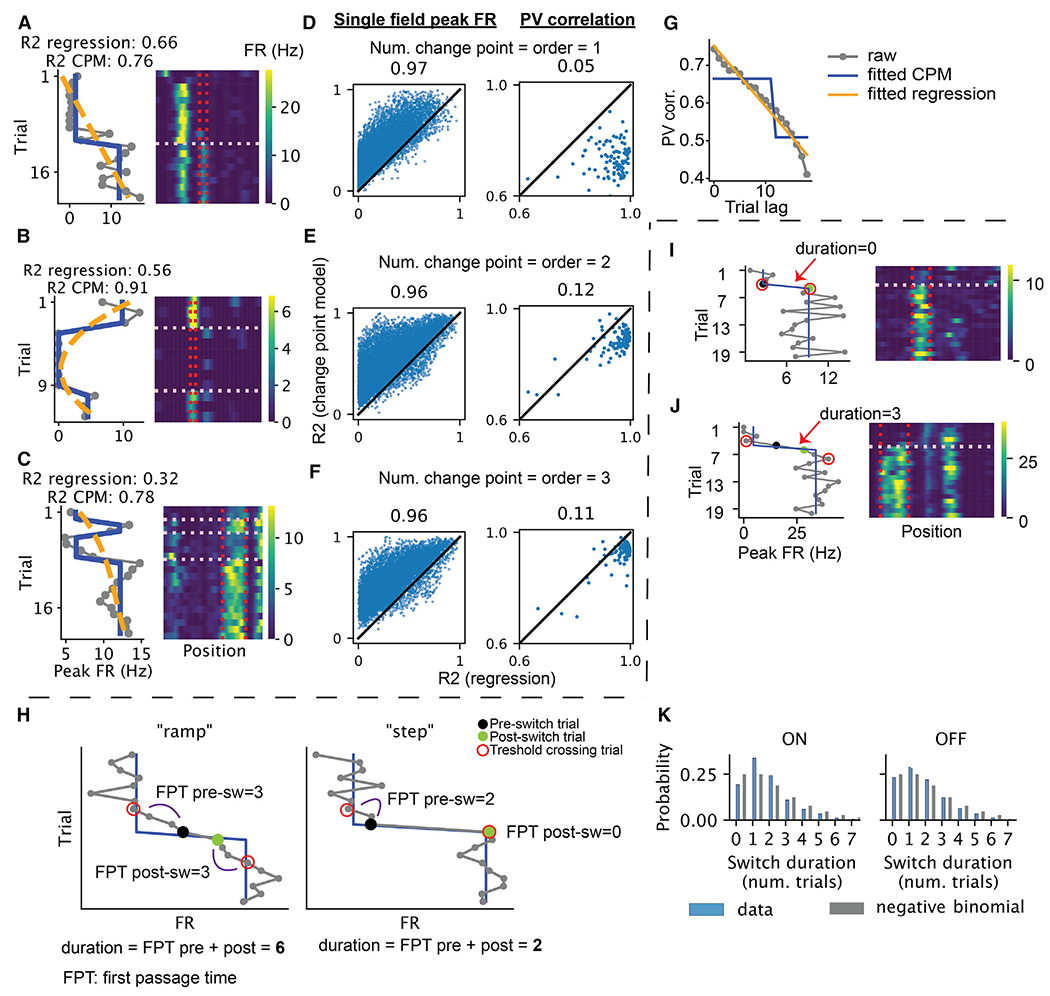
(A–C) Example neurons illustrate the comparison between change-point model and a continuous polynomial regression model. Left: gray, within-field peak firing rate as a function of trial; blue, fitted change-point model (i.e., a step function); orange, fitted polynomial regression. Right: rate maps of the selected neuron. The vertical lines mark the boundary of the place field, while the horizontal lines mark the detected change points. Neurons A, B, and C have one, two, and three change points/polynomial order, respectively.
(D–F) Explained variance ratio of the change-point model vs. that of the polynomial regression for each place field (left) and the population vector from each session (right, different turns of the T maze and different directions of the linear maze were treated separately). For individual place fields, the models are fitted to the within-field firing rate across trials. For population vectors, the models are fitted to predict population vector correlation (averaged across trial pairs) using trial lag.
(G) Example of the comparison between a discrete change-point model and a continuous polynomial regression model (CPM) for the population vector correlation as a function of trial lag.
(H) Schematics demonstrating the differences in first passage time (FPT) of threshold crossing in data better characterized as a “ramp” (left) vs. a “step” (right). Threshold crossing is defined as above the predicted firing rate by the step model post-switch-ON and below the predicted pre-switch-ON firing rate and vice versa for OFF. Post-switch trial is the change point given by the change point detection, and pre-switch trial is one trial before.
(I and J) Examples demonstrating switching with different switch durations, measured by the number of trials between the first pre-switch and the post-switch threshold crossing trial (red circle) minus one.
(K) Distributions of the switch durations for switch-ON and -OFF (blue), compared with a negative binomial (p = 0.5) with two successes (gray).
One might object that averaging across trial pairs might smooth out potential “jumps” in the population vector. We therefore applied the model comparison to the population vectors themselves (instead of the correlations previously) (see STAR Methods). We found that the two models were largely comparable at explaining the data, with more sessions (60%–70%) better explained by the gradual model and the distribution of R2 significantly biased toward continuous models (Figure S4G). These analyses confirmed that overall, the change in population was relatively gradual, but did not rule out the possibility of occasional jumps that were difficult to distinguish from gradual (e.g., Figures S4A–S4C).
A change-point model stipulates an instantaneous “step-like” change in firing rate. Are these changes really abrupt, or do they emerge over a small number of trials? We reasoned that if the firing rate were slowly ramping up (resp. down), it would take multiple trials to move above (resp. below) the model’s predicted firing rate after a change point (Figure 3H, left). Alternatively, if the firing rate were an abrupt step, the first passage time above or below the predicted firing rate would be quicker (Figure 3H, right). Indeed, assuming that trial-to-trial firing-rate fluctuations following an instantaneous step up/down are symmetric around the mean, the distribution of first passage times follows a negative binomial distribution (see STAR Methods). Empirically, we found that 75%–77% of first passage times happened in fewer than two trials, and the distribution of passage times resembled the expected negative binomial distribution (Figures 3I–3K). Therefore, calling the changes “discrete” or “step-like” is warranted.
We have so far shown that a continuous drift model better characterizes the population change within a session, whereas a discrete step model better describes the changes of the individual place cells. We next sought to establish a relationship between the two. In other words, how much does switching contribute to the drift of the population vector? Even though it is intuitive that switchers should contribute to the drift of the population vector, it is still conceivable that non-switchers could exhibit other forms of variability and play a larger role in the observed continuous drift of the population. To answer this question, we grouped the place cell population into the “switchers” (cells with at least one switching field) and “non-switchers” (cells with no switching fields). The population vector of the switching population decorrelated faster than that of the non-switching population in both familiar and novel environments (Figure S5).
Factors that affect the rate of switching
Are “switches” in place field activity affected by sensory, cognitive, or behavioral factors? To investigate, we used a Poisson generalized linear model to predict the number of place field switches per trial within five distinct segments of the maze (delay zone, central arm, left/right choice arm, return side arm, and pre-delay zone; Figure 4K). The number of switches was predicted from four categorical variables—animal identifier, maze segment (“position”), current trial correct/incorrect, and previous trial correct/incorrect—and three numeric variables: trial number, average speed, and number of active place fields. The model explained 20% of the deviance for switching ON and 14% for switching OFF. We examined the importance of each predictor by leaving it out and computing the decrease in cross-validated explained deviance compared to the full model. We found that the variables that explained most of the variance were the animal labels (i.e., individual differences), the maze corridors, and the number of place fields, for both switching ON and switching OFF fields (Figures 4A–4C, 4F, and 4G). Trial numbers (Z scored within a session) contributed less to switching ON but more to switching OFF. The contribution from position and trial suggested that the occurrence of switching was not homogeneous across space and time. Although the distribution of switching across arms was variable across sessions and animals (Figure S6), consistently more ON/OFF switching occurred in the delay zone (Figures 4B–4G, 4E, and 4J). However, we did not find any reliable behavioral signature (average speed, variability of speed, or fraction of time spent locomoting; see STAR Methods) or neural signature (average pyramidal cell or interneuron activities or excitation/inhibition [E/I] ratio) that separated the delay zone from other parts of the maze (Figure S7). As expected, switching probability decreased as a function of the trial number, reflecting the graded influence of novelty discussed above15 (Figures 4D and 4I). By contrast, average locomotion speed did not change as a function of trial (Figure S8C). Correct or incorrect arm choice on the current or previous trial did not predict the occurrence of switching (Figures 4C and 4H). Leaving out locomotion speed or coefficient of variation (CV) of speed did not reduce the model’s ability to predict held-out data (Figures 4A and 4F). Nor did we find a clear linear relationship between speed and the normalized (i.e., divided by the number of fields) switching count (Figures S8A and S8B). We note that even though space and time made significant contributions, the effect sizes were small, suggesting these behavioral correlates were not determining factors of switching.
Although we failed to find generic behavioral correlates of place field switching, it is possible that some specific behaviors could induce novel place fields or make them disappear. Indeed, it has been reported that exploratory head scanning in rats was predictive of the emergence of novel place fields.26 In our experiments, most head scans were detected in the reward area (position 50, between green and red sections), while head scans in the central arm were rare (Figures 4N and 4O). We found no reliable relationship between field switching and incidence of head scanning (Figures 4O and 4P). Thus, even without behavior triggers, discrete drift continues to occur.
Field switching was not restricted to spatial tuning. The firing rates within place fields can vary substantially in the central arm of the maze, depending on the animal’s future choice in the coming turn, known as “splitter fields.”27,28 We found that the splitter feature of hippocampal neurons could also switch ON and OFF at any trial of the session, similar to place fields (Figure S9). Thus, field switching is not confined to space but appears to be a generic property of hippocampal neurons.
Switching exhibits signatures of BTSP
We next tested whether switching exhibits signatures of BTSP. Some signatures have been shown in intracellular recordings11,12 and calcium imaging15,20,29 during rapid place field formations. We observed a significant correlation between the place field width and the running speed on the trial when the field switched ON (Figure S13A), after controlling for the spatial inhomogeneity of place field width (Figure S13B). The shift of the place field peak on the trial after the switch-ON trial could be backward or forward (relative to the animal’s motion), but the distribution skewed toward backward (Figure S13C), although it is not significant in the novel environment. Dong et al.20 found that CA1 place fields tended to shift forward in the first few trials and then revert to backward. It could be that in novel contexts switch-ON happened more in early trials (Figure 4D), resulting in larger fractions of forward shifting fields.
Intracellular recordings showed burst firing associated with the plateau potential as a signature for BTSP.11,12 We did not find higher within-field peak firing rate (which strongly correlates with burst probability) on the switch trial (Figure S13D) relative to the trial after the switch trial. This could be a limitation of extracellular recording or could have occurred because both BTSP- and non-BTSP-mediated sudden potentiations were present in the data. Interestingly, there was a significant ramp before the switch-ONs not present in the null simulation consisting of homogeneous Poisson firing across trials (Figures S13D and S13E), suggesting a preparatory potentiation before the large jump in firing rate.
Switching: Neuron or circuit property?
Is switching an intrinsic property of the neuron or is it controlled by the circuit in which the neuron is embedded? If switching were an intrinsic property, we would expect each neuron to exhibit the property consistently (i.e., switch or not switch) in different environments. We observed individual neurons with a switching field in a familiar context and a stable field in a novel context and vice versa, suggesting switching might not be intrinsic to the neuron (e.g., Figures 5A and 5B). To quantify this observation, we developed a continuous metric to measure the extent to which the trial-to-trial variability of the neuron is dominated by discrete switching (see STAR Methods). We found no correlation of the switchiness across the two contexts (i.e., familiar and novel; Figure 5C, left). In contrast, two other measures of variability were correlated across environments (Figure 5C, right two columns): (1) the CV of the mean within-field firing rate across trials, which measures how noisy the within-field firing is, and (2) the lap-to-lap correlation of the firing-rate maps, which measures how jittery the spatial tuning is (examples in Figure S10). To be sure that the results are not affected by the conservation of firing rates across contexts,30 the correlations were performed on the residual of the metrics, after the mean firing rate during non-rapid eye movement (NREM) sleep was regressed out (Figures 5C and 5D). Overall, these findings suggest that some forms of firing variability, but not switchiness, are intrinsic to individual neurons.
Figure 5. Switching is not a single-neuron property.
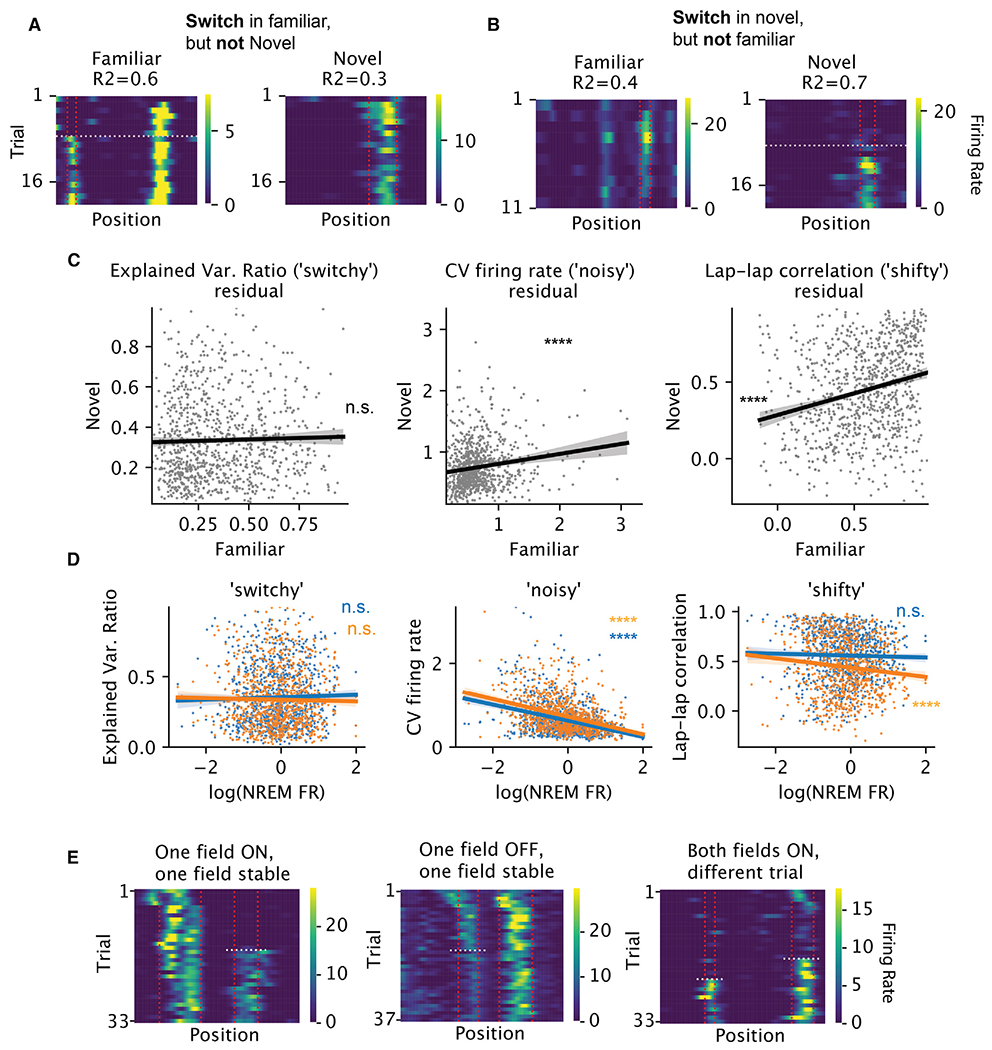
(A) Example neuron with no switch-ON field in the familiar and with switch-ON field in the novel maze. R2: explained variance ratio of the one-change-point model. Vertical lines mark the field boundary and the horizontal line marks the switch trial.
(B) Example neuron with switch-ON field in the familiar but no switch-ON field in the novel maze.
(C) For each neuron (per dot, n = 955), the relationship between familiar and novel maze for each metric of variability (per column) is shown, after regressing out the effect of firing rate during NREM sleep. The firing rates were first log-transformed. The residuals are significantly correlated across environments for CV of within-field peak firing rate (left, standardized linear regression coefficients t = 4.8, R2 = 0.02, p < 10−5) and lap-lap rate map correlation (middle, t = 7.9, R2 = 0.06; p < 10−14), but not for the explained variance ratio from the change-point model (right, t = 0.9, R2 = 0.0008, p = 0.37). The error bands show 95% CI for the regressions.
(D) For each neuron (per dot), the relationship between each metric of variability (per column) and its log-firing rate during NREM sleep. Blue and orange: familiar and novel environments, respectively. (Standardized linear regression coefficients and p values: noisy: familiar, t = −11.1, p = 3.6 × 10−27; novel, t = −12.6, p = 1.5 × 10−33; shifty: familiar, t = −0.8, p = 0.4; novel, t = −3.6, p = 0.000326; switchy: familiar, t = 0.9, p = 0.4; novel, t = −0.6, p = 0.5).
(E) Examples of subfields of a neuron showing different switching behavior.
Switching appeared to stabilize within-field firing rates for the new place fields. Specifically, switch-ON fields had lower CV of firing rates within the five trials after the switch, relative to trial-to-trial variability in non-switching fields over five trials taken either from the beginning or from the middle of the session (Figures S12A and S12D). Further, we observed neurons with two or more place fields whose individual fields switched ON/OFF independent of one another. In some cases, one field was stable while the other field switched (Figure 5E, left and middle; quantifications in Figures S11A–S11D). In other cases, switching in one field occurred on different trials compared with switching in another field (Figure 5E, right). Of 781 place field pairs that belonged to the same place cell and both switched, only 41 (5%) switched on the same trial. Together, these results suggest that switchiness is not an intrinsic property of individual neurons.
If switching is not a cell-intrinsic property, it may be driven by a circuit-level mechanism. For example, BTSP-induced plateau potentials may co-occur in multiple neurons in the same trial, suggesting the possibility that groups of neurons “co-switch” ON. We found that in each trial, a small subset of the place fields (up to 5%) switched ON/OFF and sometimes tiled the track (see example in Figures 6A–6C). We examined whether these fields switched together in the same trial (which we call “co-switching”) or by chance. We created a null distribution for the number of pairs of place fields that co-switched ON/OFF on at least one trial by circularly shifting the switch trials for each field independently by a random amount (Figure 6D). We then tested whether the number of pairs of fields that co-switched exceeded the shuffled pairs and found that 17% (20%) of the familiar sessions and 57% (29%) of the novel sessions showed at least one trial with significant co-switching ON (OFF) (Figure 6E). The pairwise test was chosen because it had a higher power of detecting potential interactions among the neurons. The small fraction of place fields that switched together suggests that switching is largely asynchronous (Figure 6F), thus creating a perpetually changing population. Yet the shuffle test highlights the non-independence of switching. Together, these findings suggest that the switching feature of a field is not an intrinsic property of the neuron. The non-independence of switching could reflect the flexible partnership between the neuron and the different assemblies or the non-stationarity in the rate of switching in the population.
Pre-existing dynamics bias switching
Can a spontaneously emerging place field emerge anywhere on the track? BTSP induction experiments suggested that a place field could form anywhere on the track, if enough current is injected into the cell to form a plateau potential.11 Other place field induction experiments stimulating a larger number of neurons simultaneously failed to induce place fields in a highly localized manner,31,32 highlighting how the network can limit the degrees of freedom on the formation and remapping of place fields.33 We therefore hypothesized that pre-existing dynamics, reflected through the subthreshold activities before the formation, could bias the formation of place fields. Further, the disappearance of place fields should not eliminate the spatial bias in the subthreshold activities post-disappearance.
To examine the spontaneous emergence and disappearance of place fields, we focused on the subset of switching fields whose average within-field peak firing rate pre-switch-ON/post-switch-OFF was below the threshold of place field detection (60% of the switching ON, 20% of the switching OFF). Indeed, we found that, even before the emergence of the new place field, the firing rates within the future place fields were already elevated relative to the mean rate recorded outside of the future place field for the majority of the neurons (Figures S14A, S14C, and S14E). Similarly, the firing rates remained elevated within the previous place field after the field had switched OFF (Figures S14B, S14D, and S14F). Thus, within-session switching seems to reflect “unmasking”/“masking” of pre-existing/persisting place fields.34,35
A natural next question regards the timescale at which place fields pre-exist/persist. Spatial representation drifts across days,36 and place fields can form spontaneously via BTSP.11,12,15 It is therefore plausible that place fields that emerged during the experiment were “brand new” and did not exist on the previous day, reflecting drift across days. However, we found the opposite. We examined a two-photon calcium imaging dataset,22 where mice ran on a virtual linear track for multiple days. Every 5–10 trials, the mice were teleported between a familiar environment and an environment that was novel on the first day of the experiment (Figures 7A and 7B). In many cases, we observed that place fields that switched within session made repeated appearances across multiple days, suggesting a pre-existing bias on where place fields can be expressed for a given place cell. For example, a place field that switched ON on day 2 could be found stably on day 1 (Figure 7C). In another example, a field switched OFF on day 1 and reemerged on day 2. Overall, we found that even on the day before the emergence of the new place field, the firing rates within the future place fields were already significantly elevated relative to the mean rate recorded outside of the future place field (Figures 7E and 7G). Similarly, the firing rates remained elevated on the next day within the previous place field after the field had switched OFF (Figures 7F and 7H). Thus, even when the place fields are silent for an extended period (i.e., before switching ON or after switching OFF), they are still subject to the biasing effect imposed by the network.
Figure 7. Switching is biased by pre-existing fields.
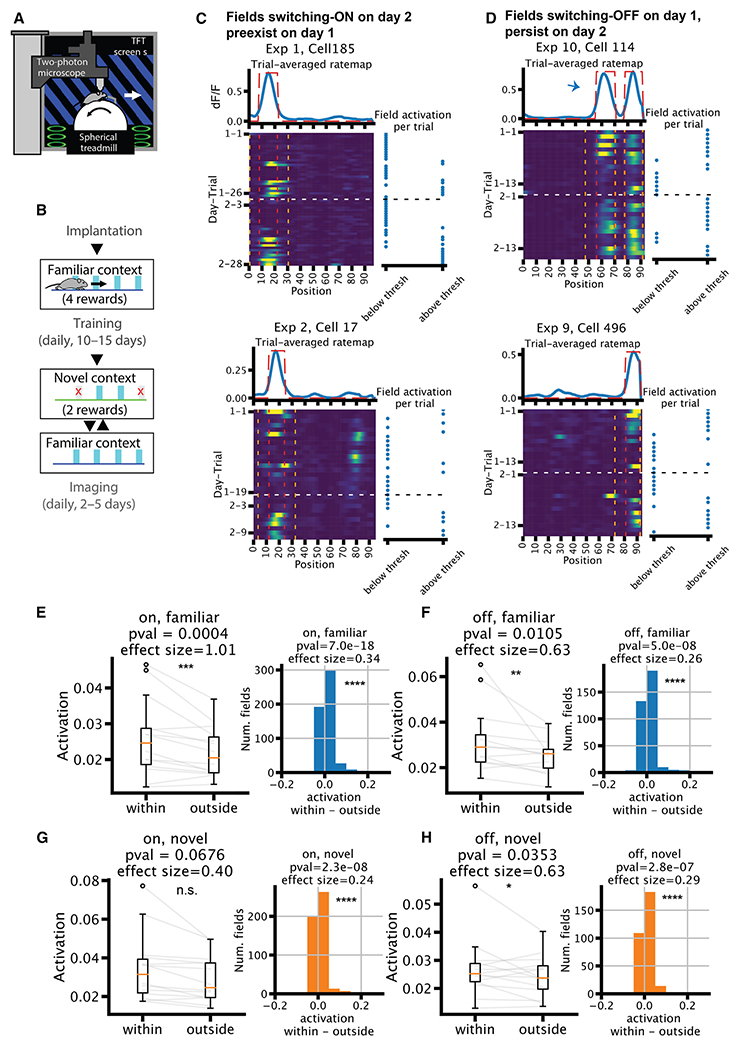
(A) Experimental setup of the imaging experiment.
(B) Behavior timeline.
(C and D) Example neurons that had a place field that switched ON on day 2 (C) or was OFF on day 1 (D). Top: trial-averaged rate map in blue, with field mask in dotted red line. Bottom left: rate map; red vertical lines mark the boundary of the fields, while orange vertical lines mark the “outside” region for the quantifications in (E)–(H). White horizontal line marks the change in the day. Bottom right: binary variable of whether the within-field activation is above the place field detection threshold at each trial. Arrow in (D) (top) marks the place field of interest among the two fields. Note: (D) (bottom) is an example for both scenarios in (C) and (D).
(E–H) Quantifications of within- vs. outside-of-field activation (n = 14). For fields that switch ON (E and G) on the second day, the quantification is done on the first day using the field detected on the second day. The opposite is true for fields that switch OFF (F and H), i.e., detected on the first day and quantified on the second day. Left: median dF/F across trials, averaged across all fields within one session, separated into within vs. outside of the place fields. Right: histogram of within minus outside-of-field dF/F of all fields pooled across sessions. Wilcoxon rank-sum tests and Cohen’s d are used for significance test and effect size.
A potential caveat is that a shift in the imaging plane could lead to a coordinated change (some increase and some decrease) in the fluorescent calcium indicator GCaMP fluorescence, resulting in an appearance of switching. Such shift would cause a large absolute change in the baseline GCaMP on trials where many neurons switched. We therefore correlated the average absolute change in baseline fluorescence (see methods in Hainmueller and Bartos22) across cells in a given image field with the number of switching fields per trial but did not observe a significant correlation (Figure S15). This result indicates that there was no relationship between the trial-to-trial image stability and place field switching, making image drift an unlikely confounder.
DISCUSSION
We found that hippocampal place fields can abruptly and spontaneously appear, disappear, or change firing rates over the course of a recording session, resulting in consistent trial-to-trial turnover and gradual population-level drift in the spatial representation. These switches in individual place fields occurred in any part of the maze without apparent behavioral correlates. Switching was not exclusive to place fields, as choice-predicting (splitter) fields also showed regular turnover. The rate of drift was accelerated by novelty. Switching was not an intrinsic property carried by single neurons: different place fields belonging to the same neuron could have independent switching properties. But pairs of place fields from different neurons switched on the same trial more often than by chance, reflecting population-level coordination. Finally, when place fields formed spontaneously, the locations were constrained by the pre-existing spatial bias in the subthreshold activities before the formation. The bias also persisted after the disappearance. These biases extended beyond single sessions into multiple days.
Robustness of the change-point model
Representational drift is often studied in a trial-averaged manner and described as “gradual” in both population activity and single neurons3,4,6,36–40 (but see Marks and Goard7 and Eliav et al.17). However, these reports relied on qualitative reports of aggregated statistics and did not explicitly model the drift dynamics of single neurons. We leveraged change point detection, shuffle tests, and comparison to polynomial regression to rigorously arbitrate the issue of gradual vs. sudden change. Decorrelations of population vector averaged across trial pairs were gradual, while changes in the peak within-field firing rate were sudden, highlighting the necessity of careful model comparison with single-cell and single-trial resolution. Our modeling framework also allowed us to detect changes in within-field firing rates beyond simple emergence of place fields, which was the focus of studies of BTSP.11,12,15 By expanding our analysis to a broader variety of firing-rate changes, we gained a more complete picture of the sudden and persistent changes of place field features. They also gave us the power to determine the contribution of the switchers to the population level drift and to examine the coordination of switching in the population. More generally, leveraging rigorous model comparison to determine whether neural activities are gradual or discrete has been fruitful in deepening our understanding of the neural mechanism of perceptual decision making in macaque lateral intraparietal cortex (LIP).41
Interpretations of representational drift
The term “representational drift” refers to the changing relationship between external variables (image, odor, space, etc.) and neuronal activity. One interpretation hypothesized the homeostatic readjustment of synapses and firing rates42,43 as a driver for drift. An implication is that the longer the elapsed time between retesting, the larger the drift. In support of this hypothesis, longer testing intervals lead to larger decorrelation.4,36 However, recent experiments showed a greater role of the amount of awake experience in the degree of drift than time per se.38,39 The within-session drift we observed is consistent with these observations.
Another potential driver for drift could be changing attentional and behavioral states. The implicit assumption of drift is that spiking patterns correspond to or “represent” some external physical features.1,44 Thus, the spiking patterns can change when the animal attends to different external features.45–47 Consequently, drift could be induced by changes in an animal’s behavior or attentional states.48–51 In particular, Monaco et al.26 reported that exploratory head movement can reliably induce novel place fields in rats. We found, though, that such “stereotypical” behavior was not necessary to induce firing-rate changes in mice. In addition, switching could occur everywhere and all the time, suggesting that it is not induced by particular events.
Here, we offer an alternative explanation for the drift and suggest the neuronal circuits are perpetually reorganized through their internal dynamics.52,53 Fluctuations in the nervous system may trigger spontaneous plateau potentials that induce BTSP and change the tuning,11 corresponding to the switch-ONs. Alternatively, Kispersky et al.54 showed in a biophysical model that small changes in α-amino-3-hydroxy-5-methyl-4-isoxazole-propionic acid (AMPA) conductance could lead to an abrupt increase in firing rate due to the dynamic properties of the ionic currents. Switch-OFFs (which were not explicitly described via BTSP) might be triggered by the switch-ONs in other pyramidal cells via interneurons to maintain E/I balance.55,56 In support of this interpretation, optogenetic stimulation of hippocampal pyramidal cells led to the appearance and disappearance of place fields (“remapping”) both inside and outside the stimulated part of the maze, by affecting monosynaptic drive of interneurons.31,33,57 Similarly, long-term potentiation of the CA3-CA1 connections both induced and abolished place fields transiently but reverted to their default fields with extended time.55
Our postulation that perpetual changes in neuronal dynamics are internally organized does not diminish the role of behavioral effects and external inputs. Indeed, we showed that place fields in the delay zone had a higher rate of switching ON/OFF, and place fields tended to switch more frequently in earlier trials, which could be due to different behavioral, attentional, and motivational states at particular places and times. Head scanning, active exploration, and attention to novel and salient cues may effectively trigger instantaneous or slow modification of firing patterns and/or affect the temporal rate of population vector decorrelations. Thus, STDP-induced slow and BTSP-induced quantal plasticity mechanisms likely co-exist and combine the advantages offered by each mechanism.
Consistent with previous reports that novelty induces instability in the network,15,17,23 we showed higher probability of switching in novel contexts. Even in the familiar context, animals exposed to both familiar and novel (“Familiar”) had more switching than animals exposed to only the familiar context (“Familiar only”). We caution, though, that the higher fraction of switching in the “Familiar” sessions compared to the “Familiar only” sessions could be due to multiple reasons, (1) exposure to novel contexts, (2) less training, and (3) additional experience, as opposed to not novelty per se. Furthermore, increased experience with the novel environment,23,58 especially when structured attention is required,51 stabilizes the representation and reduces drift,59 an avenue that we did not explore in our current work.
Properties of the pre-existing bias
The presence of subthreshold place fields in “silent” neurons has been shown by unmasking their spiking fields by sustained or transient depolarization.34,60 These subthreshold fields are hypothesized to reflect pre-existing bias imposed by hippocampal cell assemblies. Consistent with this hypothesis, we observed persistent place fields that spontaneously formed and disappeared across multiple days. Given that switching comprises pre-existing/persistent place fields, it is possible that fluctuations of excitation and inhibition could unmask the place field even without the need for BTSP or other forms of drastic plasticity34,54,60 by moving population activity from one attractor to the next. The attractor dynamics does not require recurrent excitation,61 and the attractor property of CA1 has been demonstrated in Zutshi et al.,62 where momentary silencing of the medial entorhinal cortex led to an instantaneous but reversible reconfiguration of the place field sequences without the need for plasticity.62
Given the biasing effect on place field locations that we observed across 2 days, how could large changes in population-level representation happen across many weeks4? We emphasize that the pre-existing bias does not fully determine the expression of place fields. On a timescale of 2 days, place fields exhibit mostly ON and OFF switching in a fixed range of locations. On a slower timescale, however, we hypothesize that the tendency of ON and OFF switching could change. For instance, a neuron might switch ON less frequently and eventually develop a new place field in a different location. The bias itself reflects the population activity and connectivity and therefore could also slowly change as the population drifts, making it easier for cells to develop place fields in new locations. Our findings and explanation are consistent with work from Geva et al.,38 which finds that place field location shifts over days are not random but become progressively larger over longer time intervals. We find that this bias is present even for unstable fields that emerge and disappear on the timescale of trials.
Limitations of the study
The present study focuses on the change in the peak firing rate of the place fields, while changes in location of the place fields have also been shown to play a role in representational drift38 across days. Furthermore, higher-resolution behavior tracking might reveal subtler behavior correlates of switching in future experiments.
RESOURCE AVAILABILITY
Lead contact
Requests for further information and resources and reagents should be directed to and will be fulfilled by the lead contact, György Buzsáki (gyorgy.buzsaki@nyulangone.org).
Materials availability
This study did not generate new unique reagents.
Data and code availability
The electrophysiological dataset analyzed for the present study has been made publicly available in the Buzsáki lab repository (https://buzsakilab.nyumc.org/datasets). The calcium imaging dataset that supports the findings of this study is available from Marlene Bartos (bartos@physiologie.uni-freiburg.de) upon request.
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
| AAV1.Syn.GCaMP6f.WPRE.SV4 | University of Pennsylvania Vector Core | Addgene plasmid #100837 |
| Deposited data | ||
| High density CA1 recordings on a figure-8 maze | (Huszár et al., 2022)21 | https://doi.org/10.48324/dandi.000552/0.230630.2304 |
| Experimental models: Organisms/strains | ||
| Mouse: C57BL/6J | Charles River Laboratory or in house | RRID:MGI:3028467 |
| Mouse: B6;129P2-Pvalbtm1(cre)Arbr/J | The Jackson Laboratory | RRID:IMSR_JAX:017320 |
| Mouse: B6.Cg-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J | The Jackson Laboratory | RRID:IMSR_JAX:007909 |
| Software and algorithms | ||
| Python | N/A | https://www.python.org/ |
| Ruptures | (Truong et al., 2020)63 | https://centre-borelli.github.io/ruptures-docs/ |
| Statesmodels | (Seabold and Perktold, 2010)64 | https://github.com/statsmodels/statsmodels/ |
| Custom analysis scripts | This paper | https://doi.org/10.5281/zenodo.13247193 |
| Matlab 2019 | MathWorks | https://www.mathworks.com/matlabcentral/answers/601606-download-matlab-2019a |
| Custom Matlab algorithms for image analysis | (Hainmueller and Bartos, 2018)22; | https://github.com/ThomasHainmueller/HainmuellerCazala_et_al_2023 |
STAR★METHODS
EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS
We refer to Huszár et al.21 and Hainmueller & Bartos22 for details on the mice used for the electrophysiological dataset and the two-photon calcium imaging dataset, respectively. For the electrophysiological dataset, time-pregnant C57BL/6J female mice were either bred in-house or obtained from Charles River Laboratory. The animals were manipulated with in utero electroporation (see Methods in Huszár et al.21). For the calcium imaging dataset, B6;129P2-Pvalbtm1(cre)Arbr/J mice (PV-Cre; The Jackson laboratory) crossed with B6.Cg-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J mice (Ai9-reporter; The Jackson laboratory) were used for all experiments at an age of 7–15 weeks. Mice were housed on a 12-h light–dark cycle in groups of 2–5 mice. After the start of the post-window-implantation training and food restriction, mice were housed individually.
METHOD DETAILS
Datasets
For details on animal surgery, training, recording, data preprocessing, and spike sorting / cell body segmentation, we refer to Huszár et al.21 and Hainmueller & Bartos22 for the electrophysiological dataset and the two-photon calcium imaging dataset, respectively. In brief, for the electrophysiological dataset, we used the chronic silicon probe recordings from hippocampal CA1 region in n=11 mice. The animals were trained on a spatial alternation task on a figure-eight maze. Animals were water restricted before the start of experiments and familiarized to a customized 79 × 79 cm2 figure-eight maze raised 61 cm above the ground. Over several days after the start of water deprivation, animals were shaped to visit alternate arms between trials to receive a water reward. A 5-s delay in the start area (delay area) was introduced between trials. The position of head-mounted red LEDs (light-emitting diodes) was tracked with an overhead camera at a frame rate of 30 Hz. Animals were required to run at least ten trials along each arm (at least twenty trials total) within each session. In all sessions that included maze behavior, animals spent ~120 min in the homecage before running on the maze and another ~120 min in the homecage afterward for sleep recordings. All behavioral sessions were performed in the mornings (start of the dark cycle). A subset of n=3 mice were exposed to novel environments in addition to the familiar figure-eight maze. After the shaping phase described above, animals underwent recording sessions consisting of a ~120-min homecage period, running on the figure-eight maze, ~60-min homecage period, running in a never-before experienced environment, followed by a final ~120-min homecage period. The novel environments included two distinct linear mazes and a different figure-eight maze. Mazes were placed in distinct recording rooms, or in different corners of the same recording room, with distinct enclosures to ensure unique visual cues. We required that the familiar sessions had no fewer than 20 trials in total and 7 trials per turn, and no fewer than 50 putative pyramidal cells. Overall, we included 46 familiar sessions and 8 novel sessions. For the co-switching analysis, we further excluded a novel session because it had too few trials.
Identification of light responsive pyramidal neurons was performed as described in Huszár et al., 2022. Briefly, ChR2 was introduced into hippocampal pyramidal neurons via in-utero electroporation to achieve a sparse expression profile. ChR2 expressing pyramidal neurons were identified via trains of 2ms pulses of blue light delivered at 5Hz. Stimulation was performed at the end of each recording session following a prolonged rest period in the homecage. Light was never delivered during behavior on the figure-8 maze. Light-responsive, putatively ChR2-expressing neurons were identified by their reliable and short-latency spiking following light pulse offset (see Methods in Huszár et al.21). Pyramidal neurons were subselected based on their waveform shape.
For the calcium imaging dataset, mice were injected with AAV1.Syn.GCaMP6f.WPRE.SV4 to express the calcium indicator GCaMP6f pan-neuronally in the dorsal CA1. The mice were then implanted with a 3 mm diameter transcortical window over the external capsule after aspiration of the overlying cortex and imaged with a resonant-scanning two-photon microscope (for details see Hainmueller and Bartos22). For imaging experiments, the mice were head-fixed and ran in a virtual environment resembling a linear track. The track consisted of textured walls, floors and other 3D rendered objects at the tracks sides as visual cues. Potential reward locations were marked with visual and acoustic cues, and 4 μl of soy milk was gradually dispensed through a spout in front of the mouse as long as the mouse waited in a rewarded location. The forward gain was adjusted so that 4 m of distance travelled along the circumference of the ball equaled one full traversal along the linear track. When the mouse had reached the end of the track, screens were blanked for 5–10 s and the mouse was ‘teleported’ back to the start of the linear track. The virtual environment was displayed on four TFT monitors (19″ screen diagonal, Dell) arranged in a hexagonal arc around the mouse and placed ~25 cm away from the head, thereby covering ~260° of the horizontal and ~60° of the vertical visual field of the mouse. Mice were first trained in the familiar virtual environment for 4-5 days. After the window implantation surgery, mice were re-habituated in the familiar virtual environment until consistent reward licking. From the first day of the imaging session, mice were introduced to a novel context. which had different visual cues, floor and wall textures but had the same dimensions as the familiar context including the four marked reward locations. On the novel track, two of these reward sites were disabled (that is, the auditory cue was still given, but no reward was dispensed). Mice alternatingly ran on the two tracks for a total of 15–30 runs on each track and day. The mice made 1–5 runs on one track and then an equal number of runs on the other. The length of these trial blocks was randomly varied. Imaging was performed in the same set of contexts for two to five consecutive days. We only considered the CA1 recording for two days, 14 experiments in 11 animals, with 9828 pyramidal cells (150-1765 per session).
Significant calcium transients were identified, which mainly reflect burst firing of principal cells. In brief, calcium traces were corrected for slow changes in fluorescence by subtracting the eighth percentile value of the fluorescence-value distribution in a window of ~8 s around each time point from the raw fluorescence trace. We obtained an initial estimate on baseline fluorescence and standard deviation (s.d.) by calculating the mean of all points of the fluorescence signal that did not exceed 3 s.d. of the total signal and would therefore be likely to be part of a significant transient. We divided the raw fluorescence trace by this value to obtain a ΔF/F trace. We used this trace to determine the parameters for transient detection that yielded a false positive rate (defined as the ratio of negative to positive oriented transients) <5% and extracted all significant transients from the raw ΔF/F trace. Definitive values for baseline fluorescence and baseline s.d. were then calculated from all points of this trace that did not contain significant transients. For further analysis, all values of this ΔF/F trace that did not contain significant calcium transients were masked and set to zero.
Behavior segmentation
From the 2D position tracking, we computed the velocity in x and y directions within each time bin and smoothed it with a gaussian filter (std = 10 bins), and then computed the speed using . We categorized the animal’s behavior on the maze into forward locomotion, immobility, and headscan. We first defined immobility as times when the speed was <1cm/s. We then detected headscan using a simplified version of the method used in Monaco et al26. Headscan events were detected by first finding times when the distance between the animal’s head position (reflected by the LED tracking) and the track was above a threshold of 3 cm. We then extended the time both forward and backward till when the head position was “on-track”, distance < 1 cm. Both thresholds were manually adjusted to minimize type I and type II error. Among these putative events, those that were shorter than 0.4s in time, and those whose start and end locations had a distance greater than 20 bins were excluded. The rest of the events were merged if the end of one and the start of the next were within 0.4s in time. We computed the distance to the maze from one point by first sampling positions that were on the maze, and then calculated the smallest Euclidean distance from that point to the position samples. We sampled positions on the maze by: 1) selecting the time points where the speed was > 10cm/s; 2) using these points to construct a map from the linearized coordinates back to the 2D coordinates using linear interpolation; 3) evenly sampling 200 linearized coordinates; and 4) mapping them back to the 2D coordinates. Excluding the times of immobility and headscan, as well as occasional backtracking, the rest was considered forward locomotion.
Ratemap calculation
Only time points when animals were moving forward were included. Spikes were binned by bins of 2.2cm. The spike counts and occupancies within each bin were smoothed by a gaussian filter with standard deviation of 2.5. We obtained ratemaps per trial by dividing the smoothed spike counts by smoothed occupancies. We then averaged over trials to obtain a trial-averaged ratemap. For the imaging dataset, we first mask the dF/F traces and performed the same operations on the masked traces in place of spikes.
Place field detection
For the electrophysiological dataset, we circularly shuffled animal’s positions in time and constructed trial-averaged ratemaps 1000 times to obtain a null distribution of the average ratemaps per neuron. Place fields were defined as contiguous chunks of positions where: 1) the empirical average ratemaps were above the 95th percentile of the null distribution; 2) the size was between 4 and 30 bins; and 3) the peak firing rate within the field was above 1Hz. For the imaging dataset, we circularly shuffled the animal’s position labels in the ratemaps per trial and then averaged to obtain a null distribution of the average ratemaps per neuron. Place fields were defined as contiguous chunks of positions where: 1) the empirical average ratemaps were above a threshold. The threshold for each neuron was computed as: 0.25 times the difference between the peak of the average ratemap and the baseline. The baseline was defined as the 25th percentile of the activity rate among all the positions and trials. The baseline was either defined using the current session or all days, giving rise to a threshold and a “pooled” threshold. The final threshold was the maximum between the threshold and 0.6 * pooled threshold. Including a pooled threshold ensured that small fluctuations on one day would not be classified as place field activity if the neuron had high activity on the other day. 2) The in-field gain, measured by the average within-field activity/average outside activity had to be >3.3) The peak within-field activity rate had to be higher than the 80th percentile of the null distribution. After detecting the place fields, we computed the peak within-field firing rate per trial and the peak locations per trial. For the analysis of preexisting fields, we obtained the outside region for each place field by extending the field in both directions, each for 10% of the track length, until it hit the boundary of the maze or another field.
For the figure 8-maze data, we separated place fields into fields that were common for both turns (on the central arm) and fields that were specific for one type of turn (on non-central arms or splitter cells on the central arm). The field was determined to be common to both turns if the peaks detected from both turns were less than 5 bins apart and lied on the central arm, and that the peak firing rates per trial were not significantly different between two turns (using independent t-test). If they were, then the field was deemed a splitter field. Analysis on the place field parameters (firing rate, location) were performed using all trials for the turn-common fields, and only trials for one turn for the turn-specific fields.
Detection of discrete switching
We used a change point detection algorithm called optimal partitioning25. Given the number of change points (K), it searches for K changes points that partitions the time series x1:T into K + 1 segments, where T is the length of the signal. Each segment is associated with a cost. In our case the cost was the sum of squared error of fitting a constant function within a segment: , where is the average of x within u and v. The objective is to find change points that minimize the total cost: where the left hand side denotes the minimal cost from 1 till T given K change points (K + 1 segments). At its core, the search utilizes a recursive relation that relates the optimal value of the cost function within a segment given m change points to the optimal cost within a subsection from the start of the segment to the last change point (given m − 1 change points): . Starting from C1(u, v) for all pairs of u, v, it recursively computes for K + 1 ≥ m ≥ 2. Finally, it backtracks to find the set of change points: starting from given The time complexity is O(KT2), compared to O(TK) in the naïve way. For a more detailed description we refer to Truong et al.63 for a review. We used the Python package ruptures63 to perform change point detection on the time series of within-field peak firing rate over trials. We set the parameter of the minimal segment length to be two.
To determine the significance of the change points and further determine the number of change points that suited the data the best, we noticed that if a step-function like structure existed in the data, shuffling the data would break the structure and incur a higher cost from the change point model than in the original data. This observation allowed us to determine whether there was any significant discrete jump in the data. We could further determine the optimal number of change points by selecting the number that led to the highest increase in cost in shuffle compared to data. This way, overfitting with many change points was avoided, because increasing the number of change points would also decrease the cost in the shuffle, counterbalancing the decrease in the cost of the data. In practice, for each place field, we shuffled the within-field peak firing rate over trials 1000 times and fit each shuffle with change point models from one change point up to min(5, ⌋ num. trials / 4 ⌊) and obtained the costs. The empirical costs were compared against the shuffle to compute the P-values. We then performed a Bonferroni corrected test (with a P-value threshold of 5%) to determine whether a field had any significant change points. Next, the optimal number of change points to each field that had significant change points was determined to be the one whose empirical cost had the lowest percentile in shuffle. Finally, we filtered change points whose step sizes were < 40% of the max firing rate across trials to include only relatively large changes. Although the shuffle test already tended to favor large and sustained changes, the final filter filtered out only a small fraction of events.
Metrics of variability
We used two traditional metrics of variability: CV of the firing rate (“noisy”) and the lap-to-lap ratemap correlations (“shifty”), plus one new metric based on the change point detection (“switchy”), to measure the variability of the space-related activities of the place cells. The “noisiness” measured the total amount of fluctuations of the within-field peak firing rate and was computed as the standard deviation divided by the mean of the within-field peak firing rate across trials. We then averaged them across fields to get one measure for one neuron. The shiftiness was the Pearson correlation between the ratemaps from a pair of trials, averaged over all pairs of trials, and primarily measured the shift in the location or distribution of the ratemap. Neither of these metrics captured the degree of step-function like switching, which we called switchiness and defined to be the fraction of variance of the within-field peak firing rate explained by the change point model with one change point. (Fixing one change point is to make place fields that have different optimal numbers of change points comparable). We then average the switchiness per field to assign a score to each neuron.
Continuous model of trial-dependent change
We compared the discrete switching model with a continuous model for explaining both the change in single place field’s activity over trials and also the decay in the population vector correlations as a function of trial lags. The continuous model was a polynomial regression y(t) ~ b0 + b1t + b2t2 + …bktk, where y(t) was either the peak within-field firing rate of one place field in trial t or the population vector correlation averaged over all trials pairs t trials apart, bis were the coefficients and k was the order of the model. The fitting was done using the Python library statsmodels64.
Model comparison applied to the population vectors
To further determine whether the population vectors evolve gradually or abruptly while ruling out the effect of trial averaging, we apply the change point or regression models to the population vectors themselves (instead of the correlations previously). To simultaneously speed up the computation and reduce the noise, we first reduced the dimensionality of the matrix of population vectors (n_trial-by-(n_neuron x n_position)) to n_trial-by-n_feature, where n_feature is chosen to preserve just above 95% of the variance, usually n_trial-2. Now the fitted piece-wise constant function from the change point model are vector-valued functions, with change points shared across the feature dimensions. The cost for one section is now the sum of the cost over all dimensions. The polynomial regression models are fitted to each feature dimension independently. This choice is justified since gradual changes of each dimension would add up to a gradual change of the population, whereas if sudden changes occur at different times across each dimension, we would not necessarily regard the population as having jumps. The explained variance ratio can be obtained as usual.
Switch duration quantification and comparison
If the trial-to-trial firing rate fluctuations before and after an instantaneous step up/down are symmetric around the mean, the distribution of first passage times (FPTs) follows a negative binomial distribution. The negative binomial distribution models the number of tails in a sequence of coin tosses before k heads occur. In our case, the coin was fair (p = 0.5). We defined thresholds as the firing rates (FRs) predicted by the change point model. For switch-ONs, the first threshold crossing post-switch was defined as the first trial when the actual FR went above the predicted FR after the switch. The first threshold crossing pre-switch was the first trial (counting backwards from the switch) when the actual FR was below the predicted FR before the switch. Vice versa for switch-OFFs. The FPTs were defined as the number of trials between the post/pre-switch trial and the first threshold crossing. The post-switch trial was the change point given by the change point detection, while the pre-switch trial was the trial before the post-switch trial. For each switching, we summed the FPTs pre- and post-switch to get the switch duration. Since each of the FPT was expected to follow a negative binomial distribution with k = 1, the switch duration was compared with a negative binomial distribution with k = 2, i.e. the sum of two independent negative binomial variables with k = 1.
Contribution of switching neurons to drift
We grouped the place cell population into the “switchers” (cells with at least one switching field) and “non-switchers” (cells with no switching fields). To ensure the sizes of the groups were comparable, we sampled non-switchers to match the size of the switchers for each session ten times and averaged the analysis results for Figures 4A and 4B. For each subpopulation, we computed the population vector correlation and took the median across all trial pairs given a trial lag for each session. We next measured the magnitude of decorrelation per session by fitting a linear regression on the population vector correlation, using trial lag as the regressor.
Generalized linear model of switching
We used a generalized linear model (GLM) to predict the number of switching ON/OFF per trial and arm (familiar maze only). The relevant variables were aggregated per trial and arm for each session and concatenated across sessions and animals. The full model was log(y) ~ C(Animal) + C(Position) + N_field + Trial + Speed + CV_speed + C(Correct) + C(Prev_correct), where y was the number of switching C(·) indicates categorical variables. “Position” refers to the arm of the maze. “N_field” refers to the number of fields whose peak lied in that arm. “Trial” and “Speed” were z-scored within session to aid comparison across sessions and animals. “Speed” refers to the average speed within the arm at the trial. “CV_speed” refers to the coefficient of variation of the speed within the arm at the trial. “Correct” refers to whether the animal made the correct turn on the current trial, and “Prev_correct” whether the previous trial was correct. We used a Poisson likelihood function. The variable selection was performed by repeating a 5-fold stratified cross-validation 10 times (grouped by animal to make sure the relative sample size for different animals were maintained). The fitting and cross-validations were done via the Python library sklearn.
Quantification of pre-existing constraint
To quantify the extent to which the place field preexisted (before switch-ONs) or persisted (after switch-OFFs), we computed the difference between the mean within-field firing rate (or dF/F for imaging) and the mean outside-of-field firing rate (or dF/F). The “outside” was defined by extending the field boundary in both directions by 10% of the track length, until it hit the end of track or the onset of another place field. This way we ensured that the quantification was not obfuscated by the existence of multiple fields. We then took the median across trials for each neuron and plotted the distribution in Figures 7E–7H (left panels). To make sure the result is robust across sessions, we also averaged the within and outside dF/F across all fields within a session (Figures 7E–7H, right panels).
QUANTIFICATION AND STATISTICAL ANALYSIS
All statistical details, including the specific statistical tests, are specified in the corresponding figure legends. In general, for one sample and paired two samples we performed two-sided Wilcoxon signed rank tests. For unpaired two samples we performed two-sided Wilcoxon rank sums test. We used the Pearson correlation coefficient to measure linear correlation. Effect sizes were reported using Cohen’s d. All statistical analyses were conducted using Python.
Supplementary Material
Figure 6. Network coordination of switching.
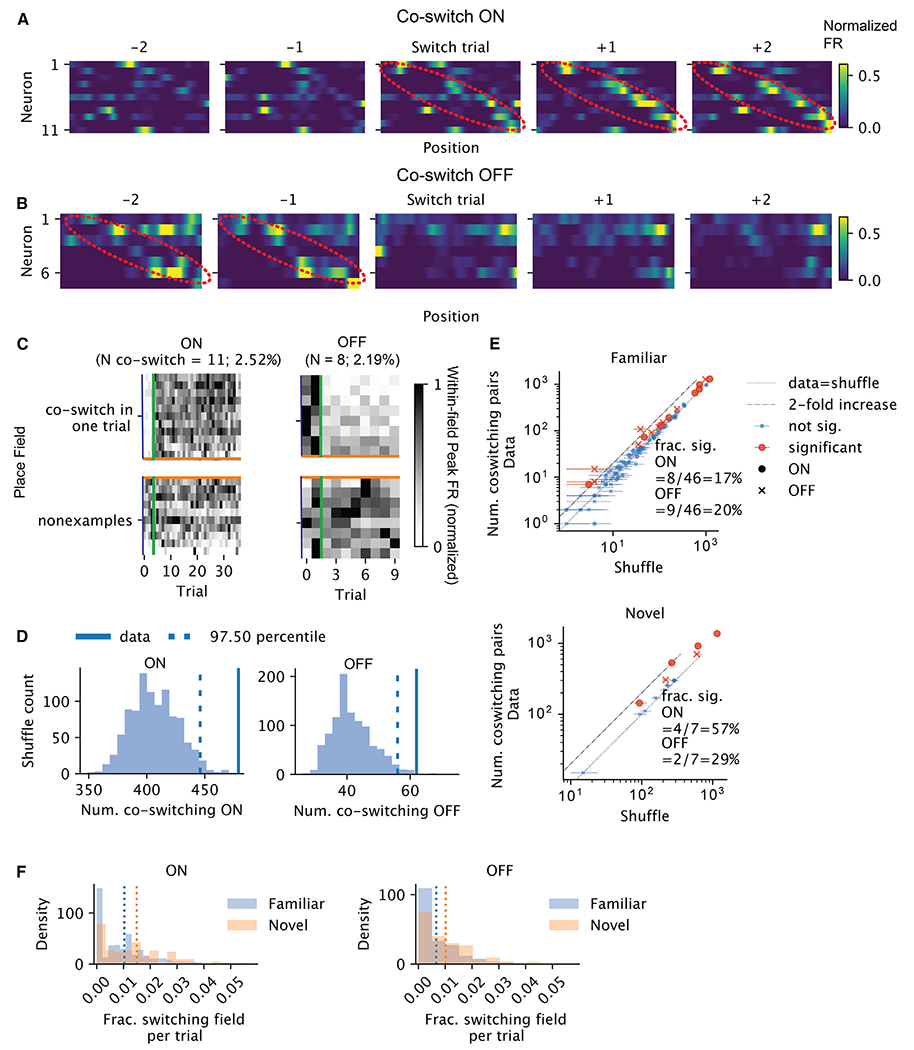
(A) Activities of example neurons whose fields co-switched ON in the vicinity of the co-switching trial. Each heatmap is the rate map for different neurons (row) for one trial. The rows are sorted by the locations of the place fields that switched together. The color reflects the normalized firing rate. The x axis is position. The emerging sequence is highlighted in red ellipsoids.
(B) Similar to (A), but for fields that switched OFF together. The fading sequence is highlighted in red ellipsoids.
(C) Within-field peak firing rates per field across trials (normalized across all trials), for the same set of neurons as in (A). Each row is a field. Above the orange lines are the fields that co-switched ON at the trial marked by the green vertical lines, whereas below are the randomly selected fields that did not switch ON that trial. Left contains the fields of the neurons shown in (A) and right contains the fields of the neurons shown in (B).
(D) Shuffle test result for the number of pairs of fields that co-switched ON on some trials, for the sessions in (A) (left) and (B) (right).
(E) For each session, the number of co-switching pairs vs. shuffle median. The error bars mark the 95% CI from shuffle tests. Red dots are sessions with significant co-switching of neurons. Circles and crosses correspond to co-switching ON and cross OFF fields, respectively. Top, familiar, and bottom, for novel context.
(F) Histograms of the fraction of switching fields for ON (left) and OFF (right) in each trial (excluding the first and last two trials). Blue is familiar and orange is novel context. Vertical lines mark the means.
Highlights.
Hippocampal neurons exhibit representational drift within a session
Step-like switches in individual firing rates underlie gradual population drift
Pre-existing assemblies bias spontaneous (dis)appearance of fields across days
ACKNOWLEDGMENTS
We thank Isabel Low for comments on the manuscript. We thank Caleb Kemere and members of the Williams and Buzsáki laboratories for feedback and support. This work was supported by NIH MH122391, 1RF1MH133778, and U19 NS107616.
Footnotes
DECLARATION OF INTERESTS
G.B. is a member of the advisory board of Neuron.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2024.114702.
REFERENCES
- 1.O’Keefe J, and Nadel L (1978). The Hippocampus as a Cognitive Map (Clarendon Press; ). [Google Scholar]
- 2.Thompson LT, and Best PJ (1990). Long-term stability of the place-field activity of single units recorded from the dorsal hippocampus of freely behaving rats. Brain Res. 509, 299–308. 10.1016/0006-8993(90)90555-. [DOI] [PubMed] [Google Scholar]
- 3.Manns JR, Howard MW, and Eichenbaum H (2007). Gradual Changes in Hippocampal Activity Support Remembering the Order of Events. Neuron 56, 530–540. 10.1016/j.neuron.2007.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, and Schnitzer MJ (2013). Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci 16, 264–266. 10.1038/nn.3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sheintuch L, Geva N, Baumer H, Rechavi Y, Rubin A, and Ziv Y (2020). Multiple Maps of the Same Spatial Context Can Stably Coexist in the Mouse Hippocampus. Curr. Biol 30, 1467–1476.e6. 10.1016/j.cub.2020.02.018. [DOI] [PubMed] [Google Scholar]
- 6.Schoonover CE, Ohashi SN, Axel R, and Fink AJP (2021). Representational drift in primary olfactory cortex. Nature 594, 541–546. 10.1038/s41586-021-03628-7. [DOI] [PubMed] [Google Scholar]
- 7.Marks TD, and Goard MJ (2021). Stimulus-dependent representational drift in primary visual cortex. Nat. Commun 12, 5169. 10.1038/s41467-021-25436-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jensen KT, Kadmon Harpaz N, Dhawale AK, Wolff SBE, and Ölveczky BP (2022). Long-term stability of single neuron activity in the motor system. Nat. Neurosci 25, 1664–1674. 10.1038/s41593-022-01194-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Markram H, Lübke J, Frotscher M, and Sakmann B (1997). Regulation of Synaptic Efficacy by Coincidence of Postsynaptic APs and EPSPs. Science 275, 213–215. 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- 10.Magee JC, and Johnston D (1997). A Synaptically Controlled, Associative Signal for Hebbian Plasticity in Hippocampal Neurons. Science 275, 209–213. 10.1126/science.275.5297.209. [DOI] [PubMed] [Google Scholar]
- 11.Bittner KC, Grienberger C, Vaidya SP, Milstein AD, Macklin JJ, Suh J, Tonegawa S, and Magee JC (2015). Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat. Neurosci 18, 1133–1142. 10.1038/nn.4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bittner KC, Milstein AD, Grienberger C, Romani S, and Magee JC (2017). Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357, 1033–1036. 10.1126/science.aan3846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fan LZ, Kim DK, Jennings JH, Tian H, Wang PY, Ramakrishnan C, Randles S, Sun Y, Thadhani E, Kim YS, et al. (2023). All-optical physiology resolves a synaptic basis for behavioral timescale plasticity. Cell 186, 543–559.e19. 10.1016/j.cell.2022.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Milstein AD, Li Y, Bittner KC, Grienberger C, Soltesz I, Magee JC, and Romani S (2021). Bidirectional synaptic plasticity rapidly modifies hippocampal representations. Elife 10, e73046. 10.7554/eLife.73046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Priestley JB, Bowler JC, Rolotti SV, Fusi S, and Losonczy A (2022). Signatures of rapid plasticity in hippocampal CA1 representations during novel experiences. Neuron 110, 1978–1992.e6. 10.1016/j.neuron.2022.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grienberger C, and Magee JC (2022). Entorhinal cortex directs learning-related changes in CA1 representations. Nature 611, 554–562. 10.1038/s41586-022-05378-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Eliav T, Maimon SR, Aljadeff J, Tsodyks M, Ginosar G, Las L, and Ulanovsky N (2021). Multiscale representation of very large environments in the hippocampus of flying bats. Science 372, eabg4020. 10.1126/science.abg4020. [DOI] [PubMed] [Google Scholar]
- 18.Allen K, Rawlins JNP, Bannerman DM, and Csicsvari J (2012). Hippocampal Place Cells Can Encode Multiple Trial-Dependent Features through Rate Remapping. J. Neurosci 32, 14752–14766. 10.1523/JNEUROSCI.6175-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, and Moser M-B (2005). Independent Codes for Spatial and Episodic Memory in Hippocampal Neuronal Ensembles. Science 309, 619–623. 10.1126/science.1114037. [DOI] [PubMed] [Google Scholar]
- 20.Dong C, Madar AD, and Sheffield MEJ (2021). Distinct place cell dynamics in CA1 and CA3 encode experience in new environments. Nat. Commun 12, 2977. 10.1038/s41467-021-23260-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huszár R, Zhang Y, Blockus H, and Buzsaki G (2022). Preconfigured dynamics in the hippocampus are guided by embryonic birthdate and rate of neurogenesis. Nat. Neurosci 25, 1201–1212. 10.1038/s41593-022-01138-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hainmueller T, and Bartos M (2018). Parallel emergence of stable and dynamic memory engrams in the hippocampus. Nature 558, 292–296. 10.1038/s41586-018-0191-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Frank LM, Stanley GB, and Brown EN (2004). Hippocampal Plasticity across Multiple Days of Exposure to Novel Environments. J. Neurosci 24, 7681–7689. 10.1523/jneurosci.1958-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sheffield MEJ, Adoff MD, and Dombeck DA (2017). Increased prevalence of calcium transients across the dendritic arbor during place field formation. Neuron 96, 490–504.e5. 10.1016/j.neuron.2017.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jackson B, Scargle JD, Barnes D, Arabhi S, Alt A, Gioumousis P, Gwin E, San P, Tan L, and Tsai TT (2005). An algorithm for optimal partitioning of data on an interval. IEEE Signal Process. Lett 12, 105–108. 10.1109/LSP.2001.838216. [DOI] [Google Scholar]
- 26.Monaco JD, Rao G, Roth ED, and Knierim JJ (2014). Attentive Scanning Behavior Drives One-Trial Potentiation of Hippocampal Place Fields. Nat. Neurosci 17, 725–731. 10.1038/nn.3687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Frank LM, Brown EN, and Wilson M (2000). Trajectory Encoding in the Hippocampus and Entorhinal Cortex. Neuron 27, 169–178. 10.1016/S0896-6273(00)00018-0. [DOI] [PubMed] [Google Scholar]
- 28.Wood ER, Dudchenko PA, Robitsek RJ, and Eichenbaum H (2000). Hippocampal Neurons Encode Information about Different Types of Memory Episodes Occurring in the Same Location. Neuron 27, 623–633. 10.1016/S0896-6273(00)00071-4. [DOI] [PubMed] [Google Scholar]
- 29.Madar AD, Dong C, and Sheffield MEJ (2023). BTSP, not STDP, Drives Shifts in Hippocampal Representations During Familiarization. Preprint at bioRxiv. 10.1101/2023.10.17.562791. [DOI] [Google Scholar]
- 30.Mizuseki K, and Buzsáki G (2013). Preconfigured, Skewed Distribution of Firing Rates in the Hippocampus and Entorhinal Cortex. Cell Rep. 4, 1010–1021. 10.1016/j.celrep.2013.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McKenzie S, Huszár R, English DF, Kim K, Christensen F, Yoon E, and Buzsáki G (2021). Preexisting hippocampal network dynamics constrain optogenetically induced place fields. Neuron 109, 1040–1054.e7. 10.1016/j.neuron.2021.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Robinson NTM, Descamps LAL, Russell LE, Buchholz MO, Bicknell BA, Antonov GK, Lau JYN, Nutbrown R, Schmidt-Hieber C, and Häusser M (2020). Targeted Activation of Hippocampal Place Cells Drives Memory-Guided Spatial Behavior. Cell 183, 1586–1599.e10. 10.1016/j.cell.2020.09.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rolotti SV, Ahmed MS, Szoboszlay M, Geiller T, Negrean A, Blockus H, Gonzalez KC, Sparks FT, Solis Canales AS, Tuttman AL, et al. (2022). Local feedback inhibition tightly controls rapid formation of hippocampal place fields. Neuron 110, 783–794.e6. 10.1016/j.neuron.2021.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Valero M, Zutshi I, Yoon E, and Buzsáki G (2022). Probing subthreshold dynamics of hippocampal neurons by pulsed optogenetics. Science 375, 570–574. 10.1126/science.abm1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Samsonovich A, and McNaughton BL (1997). Path Integration and Cognitive Mapping in a Continuous Attractor Neural Network Model. J. Neurosci 17, 5900–5920. 10.1523/JNEUROSCI.17-15-05900.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rubin A, Geva N, Sheintuch L, and Ziv Y (2015). Hippocampal ensemble dynamics timestamp events in long-term memory. Elife 4, e12247. 10.7554/eLife.12247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Deitch D, Rubin A, and Ziv Y (2021). Representational drift in the mouse visual cortex. Curr. Biol 31, 4327–4339.e6. 10.1016/j.cub.2021.07.062. [DOI] [PubMed] [Google Scholar]
- 38.Geva N, Deitch D, Rubin A, and Ziv Y (2023). Time and experience differentially affect distinct aspects of hippocampal representational drift. Neuron 111, 2357–2366.e5. 10.1016/j.neuron.2023.05.005. [DOI] [PubMed] [Google Scholar]
- 39.Khatib D, Ratzon A, Sellevoll M, Barak O, Morris G, and Derdikman D, (2023). Active experience, not time, determines within-day representational drift in dorsal CA1. Neuron 111, 2348–2356.e5. 10.1016/j.neuron.2023.05.014. [DOI] [PubMed] [Google Scholar]
- 40.Mankin EA, Sparks FT, Slayyeh B, Sutherland RJ, Leutgeb S, and Leutgeb JK (2012). Neuronal code for extended time in the hippocampus. Proc. Natl. Acad. Sci. USA 109, 19462–19467. https://doi.org/10.1073/pnas.1214107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Latimer KW, Yates JL, Meister MLR, Huk AC, and Pillow JW (2015). Single-trial spike trains in parietal cortex reveal discrete steps during decision-making. Science 349, 184–187. 10.1126/science.aaa4056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tononi G, and Cirelli C (2006). Sleep function and synaptic homeostasis. Sleep Med. Rev 10, 49–62. 10.1016/j.smrv.2005.05.002. [DOI] [PubMed] [Google Scholar]
- 43.Watson BO, Levenstein D, Greene JP, Gelinas JN, and Buzsáki G (2016). Network Homeostasis and State Dynamics of Neocortical Sleep. Neuron 90, 839–852. 10.1016/j.neuron.2016.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.deCharms RC, and Zador A (2000). Neural Representation and the Cortical Code. Annu. Rev. Neurosci 23, 613–647. 10.1146/annurev.neuro.23.1.613. [DOI] [PubMed] [Google Scholar]
- 45.Fenton AA, Lytton WW, Barry JM, Lenck-Santini PP, Zinyuk LE, Kubík S, Bures J, Poucet B, Muller RU, and Olypher AV (2010). Attention-Like Modulation of Hippocampus Place Cell Discharge. J. Neurosci 30, 4613–4625. 10.1523/jneurosci.5576-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fenton AA, and Muller RU (1998). Place cell discharge is extremely variable during individual passes of the rat through the firing field. Proc. Natl. Acad. Sci. USA 95, 3182–3187. 10.1073/pnas.95.6.3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jackson J, and Redish AD (2007). Network dynamics of hippocampal cell-assemblies resemble multiple spatial maps within single tasks. Hippocampus 17, 1209–1229. 10.1002/hipo.20359. [DOI] [PubMed] [Google Scholar]
- 48.Kentros CG, Agnihotri NT, Streater S, Hawkins RD, and Kandel ER (2004). Increased Attention to Spatial Context Increases Both Place Field Stability and Spatial Memory. Neuron 42, 283–295. 10.1016/s0896-6273(04)00192-8. [DOI] [PubMed] [Google Scholar]
- 49.Pettit NL, Yuan XC, and Harvey CD (2022). Hippocampal place codes are gated by behavioral engagement. Nat. Neurosci 25, 561–566. 10.1038/s41593-022-01050-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sadeh S, and Clopath C (2022). Contribution of behavioural variability to representational drift. Elife 11, e77907. 10.7554/eLife.77907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zemla R, Moore JJ, Hopkins MD, and Basu J (2022). Task-selective place cells show behaviorally driven dynamics during learning and stability during memory recall. Cell Rep. 41,111700. 10.1016/j.cel-rep.2022.111700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. 10.1038/nature10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Pastalkova E, Itskov V, Amarasingham A, and Buzsáki G (2008). Internally Generated Cell Assembly Sequences in the Rat Hippocampus. Science 321, 1322–1327. 10.1126/science.1159775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kispersky T, White JA, and Rotstein HG (2010). The Mechanism of Abrupt Transition between Theta and Hyper-Excitable Spiking Activity in Medial Entorhinal Cortex Layer II Stellate Cells. PLoS One 5, e13697. 10.1371/journal.pone.0013697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dragoi G, Harris KD, and Buzsáki G (2003). Place Representation within Hippocampal Networks Is Modified by Long-Term Potentiation. Neuron 39, 843–853. 10.1016/S0896-6273(03)00465-3. [DOI] [PubMed] [Google Scholar]
- 56.Royer S, and Paré D (2003). Conservation of total synaptic weight through balanced synaptic depression and potentiation. Nature 422, 518–522. 10.1038/nature01530. [DOI] [PubMed] [Google Scholar]
- 57.Geiller T, Sadeh S, Rolotti SV, Blockus H, Vancura B, Negrean A, Murray AJ, Rózsa B, Polleux F, Clopath C, and Losonczy A (2022). Local circuit amplification of spatial selectivity in the hippocampus. Nature 601, 105–109. 10.1038/s41586-021-04169-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Vaidya SP, Chitwood RA, and Magee JC (2023). The formation of an expanding memory representation in the hippocampus. Preprint at bioRxiv. 10.1101/2023.02.01.526663. [DOI] [Google Scholar]
- 59.Nitzan N, Bennett C, Movshon JA, Olsen SR, and Buzsáki G (2024). Mixing novel and familiar cues modifies representations of familiar visual images and affects behavior. Cell Rep. 43, 114521. 10.1016/j.celrep.2024.114521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lee D, Lin B-J, and Lee AK (2012). Hippocampal Place Fields Emerge upon Single-Cell Manipulation of Excitability During Behavior. Science 337, 849–853. 10.1126/science.1221489. [DOI] [PubMed] [Google Scholar]
- 61.Couey JJ, Witoelar A, Zhang S-J, Zheng K, Ye J, Dunn B, Czajkowski R, Moser M-B, Moser EI, Roudi Y, and Witter MP (2013). Recurrent inhibitory circuitry as a mechanism for grid formation. Nat. Neurosci 16, 318–324. 10.1038/nn.3310. [DOI] [PubMed] [Google Scholar]
- 62.Zutshi I, Valero M, Fernández-Ruiz A, and Buzsáki G (2022). Extrinsic control and intrinsic computation in the hippocampal CA1 circuit. Neuron 110, 658–673.e5. 10.1016/j.neuron.2021.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Truong C, Oudre L, and Vayatis N (2020). Selective review of offline change point detection methods. Signal Process. 167, 107299. 10.1016/j.sigpro.2019.107299. [DOI] [Google Scholar]
- 64.Seabold S, and Perktold J (2010). Statsmodels: Econometric and Statistical Modeling with Python. SciPy 7, 92–96. 10.25080/Majora-92bf1922-011. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The electrophysiological dataset analyzed for the present study has been made publicly available in the Buzsáki lab repository (https://buzsakilab.nyumc.org/datasets). The calcium imaging dataset that supports the findings of this study is available from Marlene Bartos (bartos@physiologie.uni-freiburg.de) upon request.
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
| AAV1.Syn.GCaMP6f.WPRE.SV4 | University of Pennsylvania Vector Core | Addgene plasmid #100837 |
| Deposited data | ||
| High density CA1 recordings on a figure-8 maze | (Huszár et al., 2022)21 | https://doi.org/10.48324/dandi.000552/0.230630.2304 |
| Experimental models: Organisms/strains | ||
| Mouse: C57BL/6J | Charles River Laboratory or in house | RRID:MGI:3028467 |
| Mouse: B6;129P2-Pvalbtm1(cre)Arbr/J | The Jackson Laboratory | RRID:IMSR_JAX:017320 |
| Mouse: B6.Cg-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J | The Jackson Laboratory | RRID:IMSR_JAX:007909 |
| Software and algorithms | ||
| Python | N/A | https://www.python.org/ |
| Ruptures | (Truong et al., 2020)63 | https://centre-borelli.github.io/ruptures-docs/ |
| Statesmodels | (Seabold and Perktold, 2010)64 | https://github.com/statsmodels/statsmodels/ |
| Custom analysis scripts | This paper | https://doi.org/10.5281/zenodo.13247193 |
| Matlab 2019 | MathWorks | https://www.mathworks.com/matlabcentral/answers/601606-download-matlab-2019a |
| Custom Matlab algorithms for image analysis | (Hainmueller and Bartos, 2018)22; | https://github.com/ThomasHainmueller/HainmuellerCazala_et_al_2023 |


