Multimodal gradients of basal forebrain connectivity across the neocortex

Abstract

Cortical cholinergic projections originate from subregions of the basal forebrain (BF). To examine its organization in humans, we computed multimodal gradients of BF connectivity by combining 7 T diffusion and resting state functional MRI. Moving from anteromedial to posterolateral BF, we observe reduced tethering between structural and functional connectivity gradients, with the lowest tethering in the nucleus basalis of Meynert. In the neocortex, this gradient is expressed by progressively reduced tethering from unimodal sensory to transmodal cortex, with the lowest tethering in the midcingulo-insular network, and is also spatially correlated with the molecular concentration of VAChT, measured by [¹⁸F]fluoroethoxy-benzovesamicol (FEOBV) PET. In mice, viral tracing of BF cholinergic projections and [¹⁸F]FEOBV PET confirm a gradient of axonal arborization. Altogether, our findings reveal that BF cholinergic neurons vary in their branch complexity, with certain subpopulations exhibiting greater modularity and others greater diffusivity in the functional integration with their cortical targets.

The basal forebrain innervates the cortex with cholinergic projections via long-range branching projections. Using MRI and PET, the authors show that these projections exhibit gradients of increasing branch complexity traversing unimodal to transmodal cortex.

Introduction

The basal forebrain (BF) (Fig. 1) is a collection of subcortical cholinergic cell groups that provide the major sources of acetylcholine to the cortex and hippocampus¹. Structurally, the ascending cholinergic projections are highly branched, with individual cells often targeting multiple different cortical areas^2–4. The total arborization of a single human cholinergic BF neuron is estimated to have a length in excess of 100 meters⁴.

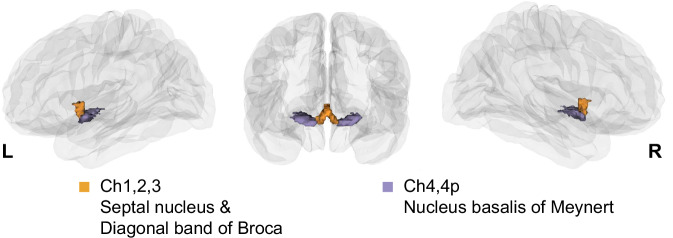
Fig. 1. A 3D view of histologically defined basal forebrain (BF) subdivisions defined by Zaborsky et al.⁴⁰ projected on a glass brain.

The anteromedial nuclei are displayed in yellow, and the posterolateral nuclei in purple.

The organization of ascending BF cholinergic projections may reflect complex spatial topographies of connectivity with the cortex^5,6. Axonal tracing studies in rats suggest that BF cholinergic neurons are grouped into ensembles that target functionally interrelated cortical areas⁷. In humans, patterns of functional connectivity in distinct BF subregions have been found to overlap with distinct cortico-cortical networks^8–10. Consistent with a spatial topography of projections, subregional structural changes in BF gray matter and white matter integrity are associated with distinct patterns of cortical degeneration and cognitive dysfunction^11–15. In neurodegenerative diseases such as Alzheimer’s (AD), early dysfunction or loss of specific BF cholinergic fibers may alter local neuronal functions in cholinoreceptive cortical areas¹⁶. Although these separate lines of evidence suggest that the cortex expresses topographies of BF structural and functional connectivity, the interrelationship of these topographies to one another is unknown.

At the cortico-cortical level, the degree to which interregional structural connectivity predicts functional integration, also known as structural-functional coupling or tethering, appears to decrease from unimodal to transmodal areas and to coincide with functional and cytoarchitectonic cortical hierarchies^17–20. How does the structural organization of ascending cholinergic BF projections relate to their functional integration in the cortex? One possibility is that BF structural and functional connectivity are closely tethered. This would be expected if white matter tracts emanating from local populations of BF cholinergic neurons target local patches of cortex⁵. In this scenario, BF functional connectivity would reflect these structurally segregated cortical modules. Alternatively, BF structural and functional connectivity might exhibit negligible overlap. This pattern would be expected if the BF white matter tracts are highly diffuse, with each local population of cholinergic neurons projecting to multiple distinct and overlapping cortical areas⁵. In this scenario, BF functional connectivity would reflect mixtures of these diffuse afferent inputs. Finally, a third possibility is that the profile of tethering between BF structural and functional connectivity varies depending on the properties of different cortical areas^18,21 and the biophysical constraints these properties may impose on the cholinergic projections^22,23. This pattern would be expected if populations of BF cholinergic neurons vary in their branch complexity, with certain subpopulations exhibiting greater modularity and others greater diffusivity in the functional integration of their cortical targets.

Here we addressed the relationship between structural and functional connectivity in the ascending BF projections. We used multimodal imaging combining high-resolution 7 Tesla (7 T) diffusion (dMRI) and resting state functional MRI (rsfMRI) in a cohort of 173 individuals from the Human Connectome Project (HCP)²⁴. From these datasets (Table 1), we derived gradients of the continuous transitions in BF functional and structural connectivity with the cortex using diffusion map embedding²⁵. Diffusion map embedding is a statistical technique that has recently gained traction to extract different topographies or gradients of the continuous transitions in structural and functional connectivity within the brain (i.e., entire cortex or individual regions^26,27). In both the dMRI and rsfMRI datasets, a single gradient dominated the explained variance in BF connectivity, characterized by an anteromedial to posterolateral axis spanning the BF nuclei. To quantify how these patterns of BF structural and functional connectivity were tethered, we computed the residual value between (a) the gradients of structural and functional connectivity within the BF and (b) the expression of these gradients on the cortical surface. Consistent with a gradient of branch complexity across the BF, we found closer tethering (lower residual values) between BF structural and functional connectivity in anteromedial areas of the BF, with stronger divergence (higher residual values) in posterolateral areas overlapping the nucleus basalis of Meynert (NbM). The cortical expression of BF structure-function tethering itself exhibited a gradient, with the closest tethering observed in primary sensory cortices and the greatest divergence in midcingulo-insular hubs of the ventral attention network^28–36. Using in vivo molecular imaging of the human^37,38 and mouse cortical cholinergic projections, in combination with anterograde viral labeling of individual BF cholinergic axons in mice² (Table 1), we provide confirmatory cell-type specific evidence that the observed gradient of tethering between BF structural and functional connectivity is likely shaped by the complexity of axonal arborization in BF cholinergic neurons. In mice and humans, BF cholinergic neurons with greater arborization appear to target evolutionarily conserved midcingulo-insular cortical areas, which exhibit among the highest concentrations of cortical cholinergic innervation.

Table 1.

Summary of datasets used in Chakraborty et al. with hyperlinked references to the original paper

Species	Reference	Imaging modality	Imaging target	Use in Chakraborty et al.	Strain	Age (y or m)	Sex (M:F)
Human	HCP	7 T MRI	White matter fiber bundles	Gradient calculation, residual analysis (Figs. 2–8 and Supplementary Fig. S1–S6)	N/A	22-35 y	69:104
			Resting-state BOLD signal
Human	Kanel	PET	[18F]FEOBV	Principal correlation analysis of structure-function tethering and cholinergic innervation (Figs. 4, 8)	N/A	24.5 (4.9) y	10:3
Human	Aghourian	PET	[18F]FEOBV	Replication correlation analysis of structure-function tethering and cholinergic innervation (Supplementary Fig. S5)	N/A	66.8 (6.8) y	5:13
Human	Bedard	PET	[18F]FEOBV	Replication analysis of structure-function tethering and cholinergic innervation (Supplementary Fig. S5)	N/A	68.3 (3.1) y	4:1
Human	Tuominen	PET	[18F]FEOBV	Replication analysis of structure-function tethering and cholinergic innervation (Supplementary Fig. S5)	N/A	37 (10.2) y	3:1
Mouse	Li (SI Appendix Fig, 7)	fMOST	AAV-CAG-flex-GFP	Unimodal versus transmodal cholinergic neuron branch counts with retrospective mouse data (Fig. 7 and Supplementary Fig. S7)	ChAT-ires-Cre	3 m	N/A
Mouse	N/A	microPET	[18F]FEOBV	Cross-validation of human cortical cholinergic innervation with prospective mouse data (Fig. 7 and Supplementary Fig. S7)	VAChTflox/flox	6 m	3:3
				Cross-validation of human cortical cholinergic innervation with prospective mouse data (Fig. 7 and Supplementary Fig. S7)	C57BL/6 J		2:3

fMOST fluorescence micro-optical sectioning tomography, y   years, m   months, M   male, F   female. Ages are given as mean $\pm$SD, where applicable.

Results

Primary BF structural and functional gradients

We built dMRI and rsfMRI connectomes of the BF using high-resolution 7 T MRI HCP data (n = 173; Table 1)³⁹ and a well-validated stereotactic BF atlas, which provides annotations for its separate nuclei (Fig. 1)⁴⁰. For each individual, the structural and functional connectomes were separately defined by an M-by-N matrix, where M represents the voxels in the entire BF and N represents the cortical parcels of the HCP multimodal parcellation (HCP-MMP)⁴¹. For rsfMRI data, the matrices encode the interregional temporal correlations in blood oxygenation level-dependent (BOLD) signals. For dMRI data, the matrices encode the streamline counts between different regions of the brain and BF. We confirmed that the probabilistic tractography of the BF streamlines recapitulates prior ex vivo anatomical tracing⁴² and in vivo diffusion mapping^14,43 work on the human BF projection system, which distinguish midline cingulum and lateral capsular/perisylvian white matter projection routes (Supplemental Fig. 1).

For the dMRI and rsfMRI datasets, we computed gradients of connectivity using the BrainSpace toolbox⁴⁴. Starting from the input matrices (Supplemental Fig. 2A) encoding the dMRI and rsfMRI data (averaged across individuals), we used a kernel function to build an affinity matrix encoding interregional similarity of features within the BF (Supplemental Fig. 2B). These matrices were decomposed via nonlinear dimension reduction into a set of eigenvectors describing axes of BF connectivity with cortical targets. The axes were then projected back to the BF space (Supplemental Fig. 2C).

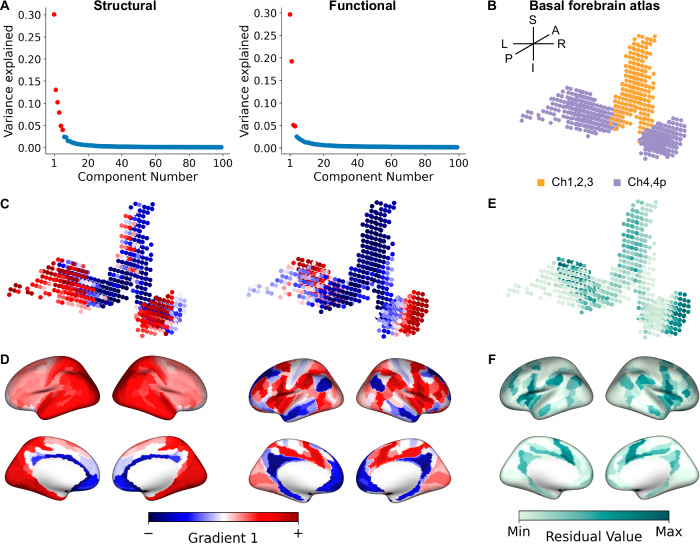
The first gradient for both BF structural and functional connectivity data explained the most (30%) variance, with a drop to 15% explained variance for the second gradient (Fig. 2A). We, therefore, focused on the first principal gradient, which exhibited a smooth continuous transition from anteromedial to posterolateral BF for both the structural and functional connectomes (Fig. 2B, C). The connectivity profiles are consistent with findings from the histological mapping of the individual BF nuclei^12,40 and in prior cluster-based parcellations of the BF from rsfMRI^8–10. Note that the hemispheric asymmetry in these gradients is due to the original stereotaxic mapping of the BF atlas (Fig. 2B; “Methods”).

Fig. 2. Basal forebrain (BF) gradients of structural and functional connectivity.

A Scree plots showing the variance explained by each gradient of structural (left) and functional connectivity (right). Gradients falling above the knee-point⁴⁶ are denoted as red. Source data are provided as a Source Data file (see Data Availability). B The BF atlas projected into 599 voxels color-coded according to a priori histologically defined anteromedial or posterolateral nuclei. C The first principal gradient of the BF based on structural (sG1; left) and functional (fG1; right) connectivity both revealed an anteromedial to posterolateral axis. The lower bound of gradient values is represented by blue (−), while the upper bound is represented by red (+). D Gradient-weighted cortical maps corresponding to sG1 (left) and fG1 (right). E Residual values encoding tethering between structural and functional connectivity at each BF voxel. Darker green values indicate lower tethering (higher values, max squared residual value = 7.32 × 10⁻²), while lighter green indicates higher tethering (lower values, min squared residual value = 5.16 × 10⁻⁷) between structural and functional connectivity. F Gradient-weighted cortical maps corresponding to structure-function tethering. Darker green values indicate lower tethering (higher values, max squared residual value = 1.004 × 10⁻³), while lighter green indicates higher tethering (lower values, min squared residual value = 2.36 × 10⁻¹¹) between structural and functional connectivity.

We next computed gradient-weighted cortical maps⁴⁵ to determine how BF gradients were expressed by the cortex. The gradient-weighted cortical maps were created by multiplying each row of the initial connectivity matrix (M_{BF voxels} x N_{cortical parcels}) with the corresponding structural principal gradient (sG1) or functional principal gradient (fG1) value to create a gradient-weighted connectivity matrix. Finally, all rows of this gradient-weighted matrix were averaged to produce a single cortical representation of the particular gradient (see Supplemental Fig. 2E and “Methods”). For the gradient-weighted cortical map corresponding to sG1 (sG1ctx; Fig. 2D left), we observed a smooth macroscale transition from the anteromedial to the posterolateral cortical surface. By contrast, the gradient-weighted cortical map corresponding to fG1 (fG1ctx; Fig. 2D right) exhibited a more patch-like pattern with moderate differentiation of gradient weights between midline and lateral cortical areas.

A gradient of structure-function tethering in BF connectivity

We examined the magnitude of shared variance, or tethering, between BF structural and functional gradients to determine their spatial similarity to one another. To do so, we computed voxel-wise regressions for the sG1 and fG1 structure-function gradient pair and extracted their corresponding residuals (see “Methods”). The residual map encoding BF structure-function tethering was projected back to BF space (Supplemental Fig. 2D), which revealed an anteromedial to posterolateral topography, with the lowest structure-function tethering localized in posterolateral subregions (Fig. 2E). We next computed the gradient-weighted cortical map encoding our residualized map of BF structure-function tethering. The resulting cortical map (Fig. 2F) exhibited decreased tethering moving from unimodal to transmodal cortex, with the lowest tethering in the anterior cingulate, insular, and frontal opercular cortices.

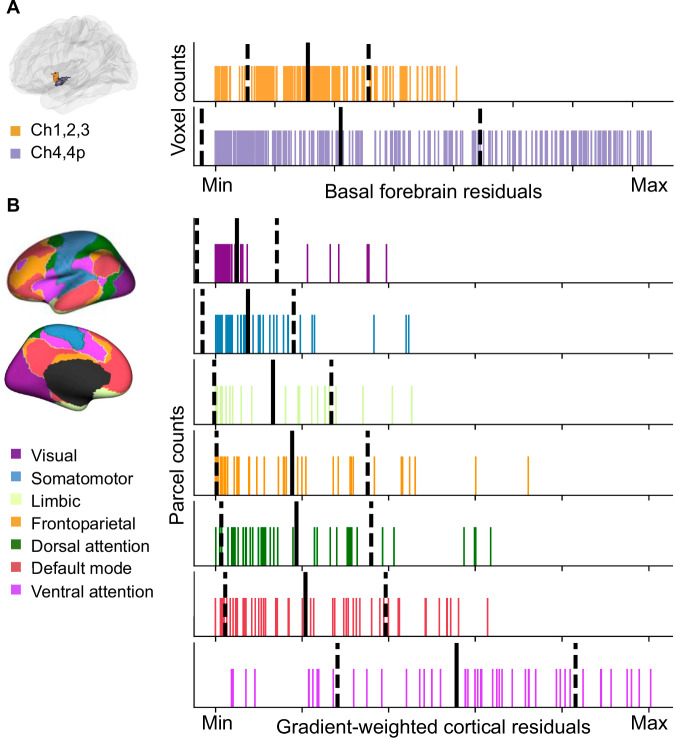
How does the smooth transition of tethering between BF structural and functional connectivity (Fig. 2E) align with the histologically defined boundaries of the BF anteromedial (Ch1,2,3) and posterolateral (Ch4,4p) nuclei (Fig. 2B)⁴⁰? To address this question, we examined if the distributions of residual values within Ch1,2,3 and Ch4,4p differed from one another. We performed permutation tests with fitted surrogate maps (see “Methods”) to compute the difference in both the means and dispersion between Ch1,2,3 and Ch4,4p. Dispersion was quantified by the coefficient of variation (CoV) defined as the ratio of the standard deviation to the mean of the data. The mean residual values were not different between Ch1,2,3 and Ch4,4p (p_perm = 0.40). However, the residual values in Ch4,4p exhibited significantly greater variability in comparison to Ch1,2,3 (p_perm = 0.01). This latter finding suggests that structure-function tethering within Ch4,4p was more inhomogeneous than Ch1,2,3 (Fig. 3A).

Fig. 3. Distributions of basal forebrain (BF) and cortical residuals.

A Rug plots showing the distribution of residuals within the a priori histologically defined anteromedial (Ch1,2,3) and posterolateral (Ch4,4p) BF nuclei⁴⁰. The solid black line indicates the mean, and the dashed lines indicate +/− one standard deviation. The minimum and maximum values correspond to the same scale as in Fig. 2E, with the minimum indicating lower squared residual values (higher tethering) and the maximum indicating higher squared residual values (lower tethering). B Rug plots showing the distribution of residuals within each of the 7 intrinsic resting-state networks identified by Yeo et al.³⁵. The color-coding for different networks is based on the original parcellation. The solid black line indicates the mean, and the dashed lines indicate +/− one standard deviation. The minimum and maximum values correspond to the same scale as in Fig. 2F. Source data are provided as a Source Data file.

We then asked how well the cortical residual-weighted map of BF structure-function tethering (Fig. 2F) aligns with the spatial topographies of intrinsic cortico-cortical resting state networks. To do so, we compared the mean and CoV of the distributions of residual values captured by each of the 7 Yeo macroscale resting state networks³⁵ covering the entire human cerebral cortex. A pattern in which the distributions of these residual values are well delineated from one another across the different cortico-cortical networks (distinct means, lower CoVs) would indicate that each network falls along a continuum of BF structure-function tethering defined by the observed anteromedial-to-posterolateral gradient. By contrast, a pattern in which the distributions of residuals are more spread out across the different cortico-cortical networks (overlapping means, higher CoVs) would indicate that each network exhibits a mixture of lower and higher BF structure-function tethering. We found that the mean of the residuals significantly differed among networks (F₆₃₆₀ = 47.55, p = 0.001, Fig. 3B), with the ventral attention network characterized by a significantly higher mean of the residuals  than the visual (p_perm = 0.001) and somatomotor networks (p_perm = 0.001). The mean of the residuals for the dorsal attention, limbic, frontoparietal and default mode networks exhibited an intermediate tendency for structure-function tethering. We also observed that the CoVs captured by each cortico-cortical network also differed. Again, the ventral attention network exhibited significantly greater heterogeneity in residual values than the visual (p_perm = 0.001) and somatomotor networks (p_perm = 0.001; Fig. 3B). Taken together, these findings support a continuum of BF structure-function tethering. Cortico-cortical networks with hubs primarily in the unimodal cortex (visual, somatomotor) tend to exhibit higher tethering, while networks with hubs primarily in the transmodal cortex tend to exhibit lower tethering.

To assess the stability of the dominant structural and functional connectivity gradients (sG1 and fG1) and the gradient of their tethering, we performed cross-validation analyses across the 173 individuals in the sample (see “Methods”). We found that each individual’s observed gradients were consistently highly correlated with the model (split-half or leave-one-out), consistent with stable gradient organization across individuals (Supplemental Fig. 3).

Having confirmed the stability of sG1, fG1, and their tethering across individuals, we next examined if gradients with lower explained variance, i.e., sG2 and fG2, may reveal additional profiles of BF structure-function tethering. To explore this possibility, we computed the knee-point in the curve of explained variance for the complete set of observed structural and functional gradients (see “Methods”), where the change in explained variance became negligible⁴⁶. The knee-point corresponded to sG6 for structural gradients and fG4 for functional gradients (Fig. 2A, red color gradient components). For each of the 24 structure-function gradient pairs in this 6 x 4 matrix (Supplemental Fig. 4A), we computed the structure-function tethering metric as before. When we examined the average of the 24 residual maps (Supplemental Fig. 4B), we observed a high degree of correspondence to the sG1-fG1 residual map (r = 0.918; Supplemental Fig. 4C), even when excluding sG1-fG1 pairing from the average (r = 0.878; Supplemental Fig. 4D). These findings imply that the gradient of tethering between BF structural and functional connectivity is captured by a single dominant profile (Fig. 2E).

BF structure-function tethering reflects an arborization gradient of cholinergic neurons

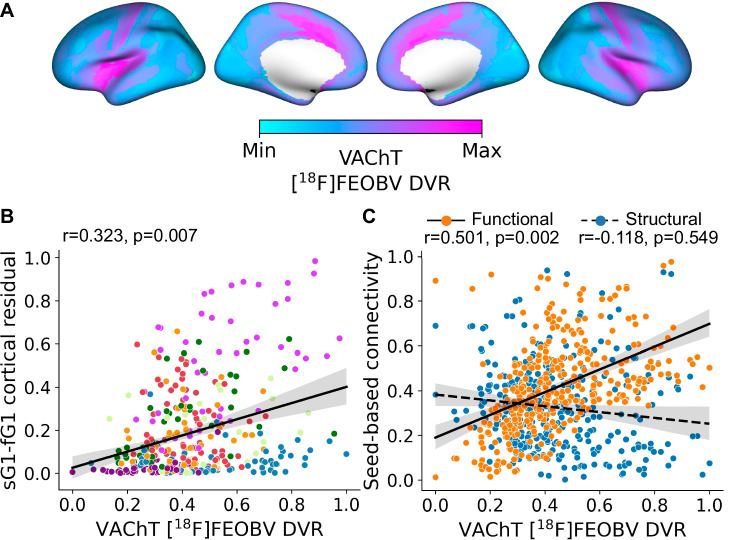
We next explored what properties of BF connectivity might shape the observed gradient profile of structure-function tethering in the cortex. Currently, [¹⁸F]FEOBV positron emission tomography (PET) provides the most direct in vivo assay of cortical cholinergic innervation in humans. The [¹⁸F]FEOBV radiotracer binds to the vesicular acetylcholine transporter (VAChT), a glycoprotein expressed solely by cholinergic neurons, with the highest density of expression on the presynaptic terminals⁴⁷. We used distribution volume ratios (DVR) of [¹⁸F]FEOBV binding from a group of healthy cognitively normal young adults (n = 13; mean age = 24.54, 3 females, Table 1)³⁷, and produced an average map representing BF cortical cholinergic innervation (Fig. 4A; see “Methods”). We then examined the correlation between the cortical expression of BF structure-function detethering (cortical residual map from Fig. 2F) and cholinergic innervation estimated from the average [¹⁸F]FEOBV map using spatial spin tests⁴⁸. Surprisingly, we found that cortical areas exhibiting lower BF structure-function tethering, i.e., more branching, exhibited a higher density of BF cholinergic input, i.e., higher VAChT concentration (r = 0.323, p_spin = 0.007; Fig. 4B). We replicated these associations with three other publicly available atlases of [¹⁸F]FEOBV PET^38,49,50 (Table 1) and found similar strong positive relationships (Supplemental Fig. 5).

Fig. 4. Multimodal gradients of basal forebrain (BF) connectivity in relation to in vivo molecular imaging of VAChT with [¹⁸F]FEOBV PET.

A Average VAChT concentrations for 13 cognitively normal younger adults reveal the density of presynaptic cholinergic terminals across the cortical surface. The values of each cortical parcel were rescaled¹¹⁵ between 0 (Min, light blue) and 1(Max, pink), Max indicating a higher concentration of cholinergic nerve terminals. B The spatial relationship of cortical VAChT concentrations (panel A) with the cortical map encoding BF structure-function tethering (Fig. 2F). Each point in the scatter plot represents cortical parcels based on HCP-MMP 1.0 parcellation⁴¹ color-coded according to the Yeo networks³⁵ (Fig. 3B). Spin tests⁴⁸, as implemented in the neuromaps toolbox³⁸, were used to calculate Pearson’s correlation and p-value based on n = 10k permutations. The solid line is the regression line. The shaded area represents the size of the 95% confidence interval for the regression estimate. The confidence interval is estimated using a non-parametric bootstrap procedure. C The spatial relationship of cortical VAChT concentrations (panel A) with seed-based connectivity for the BF structural (blue) and functional (orange) datasets. Spin tests⁴⁸, as implemented in the neuromaps toolbox³⁸, were used to calculate Pearson’s correlation and p-value based on n = 10k permutation. The solid line is the regression line. The shaded area represents the size of the 95% confidence interval for the regression estimate. The confidence interval is estimated using a non-parametric bootstrap procedure. Source data are provided as a Source Data file.

Why might BF structural and functional connectivity diverge in cortical regions more densely innervated by BF cholinergic input? One possibility is that cortical areas expressing lower tethering between BF structural and functional connectivity tend to receive inputs from more highly branched cholinergic neurons. Under this arborization gradient account, these cortical areas would exhibit strong BF functional connectivity and high VAChT concentration from multiple converging collateral arbors, but relatively weak structural connectivity due to greater diffusivity in the ascending tracts. To test this hypothesis, we computed seed-based connectivity of the BF with each HCP-MMP cortical parcel for both the dMRI (streamline counts) and rsfMRI (Pearson correlation r-values) datasets and then projected these to the cortical surface. We then examined the spatial relationship of cortical VAChT concentration with the seed-based estimates of BF streamline counts and resting-state correlations. Consistent with an arborization gradient, we observed a significant positive relationship of cortical VAChT concentrations with BF resting state correlations (r = 0.501, p_spin = 0.002), but not streamline counts (r = − 0.118, p_spin = 0.549; Fig. 4C). Moreover, the relationship of cortical VAChT with BF resting state correlations was significantly different than that observed for BF streamline counts (average difference between correlation coefficients = 0.608, 95% CI [0.727, 0.493], p_boot < 0.001, as revealed by bootstrap analysis), with greater divergence between BF resting state correlations and streamline counts in cortical parcels with higher VAChT concentrations.

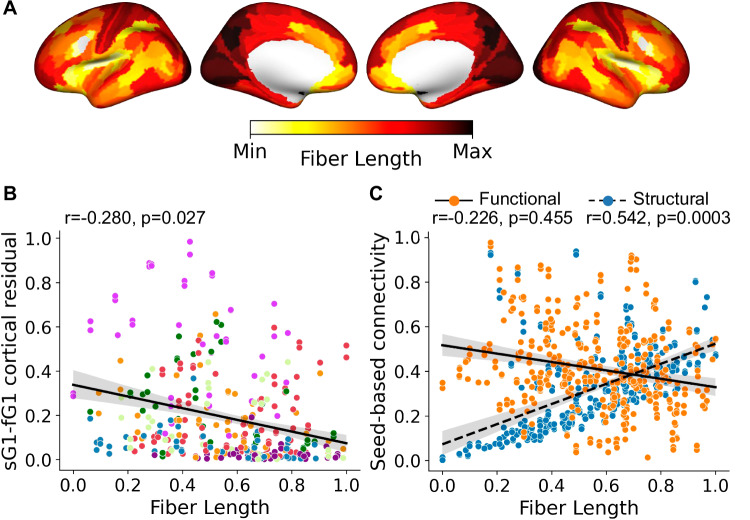
We noted that the observed arborization gradient tends to differentiate cortical areas according to their distance from the BF nuclei, implying that arborization may reflect a biophysical constraint on cholinergic projections. The brain organizes its connections to optimize communication while minimizing the biological resources required for these connections, or wiring cost^51–53. Neurons with long-range projections that extend from one brain region to another, therefore, often have fewer axonal branches than neurons with shorter-range projections. The BF cholinergic neurons may, therefore, balance longer distances traveled by their ascending axonal projections with fewer axonal arborizations. To test this hypothesis, we used diffusion tractography data to compute the average white matter fiber length from the BF ROI to each cortical parcel (“Methods”). The fiber length estimates were then projected to the cortical surface (see “Methods,” Fig. 5A) and compared to BF structure-function tethering using spin tests^38,48. Consistent with a distance/arborization tradeoff, we detected a significant negative relationship where cortical areas receiving longer fibers tend to exhibit a connectivity pattern of weak arborization, i.e., higher structure-function tethering (r = − 0.280, p_spin = 0.027, Fig. 5B) and lower VAChT concentration (r = − 0.483, p_spin = 0.004, Supplemental Fig. 6). In a distance/arborization tradeoff model, cortical areas at greater distances from the BF would require innervation from a larger number of individual BF neurons due to lower branching per neuron. This may necessitate greater numbers of BF streamlines to innervate distal cortical areas. Consistent with this prediction, we found that cortical areas innervated by longer fibers tend to receive higher BF streamline counts (Fig. 5C; r = 0.542, p_spin = 0.0003). Fiber length was not related to the strength of BF resting state correlations (r = -0.226, p_spin = 0.455). Moreover, the relationship of fiber lengths with BF streamline counts was significantly different than that observed with BF resting state correlations (difference between correlation coefficients = − 0.771, (95% CI [− 0.664, − 0.881], p_boot < 0.001). In sum, greater divergence between BF structural and functional connectivity, i.e., higher arborization, was observed in cortical parcels with higher VAChT concentration, stronger resting state correlations with BF, fewer direct streamlines, and shorter distances from BF.

Fig. 5. Multimodal gradients of basal forebrain (BF) connectivity in relation to diffusion tractography estimates of white matter fiber lengths.

A Average white matter fiber lengths for 173 cognitively normal younger adults reveal cortical areas receiving the longest BF projections located in the primary visual and somatomotor cortices. The values of each cortical parcel were rescaled¹¹⁵ between 0 (Min, yellow) and 1(Max, dark red), Max indicating the longest white matter fibers from the BF. B The spatial relationship of BF white matter fiber lengths (panel A) with the cortical map encoding BF structure-function tethering (Fig. 2F). Each point in the scatter plot represents cortical parcels based on HCP-MMP 1.0 parcellation⁴¹ color-coded according to the Yeo networks³⁵ (Fig. 3B). Spin tests⁴⁸, as implemented in the neuromaps toolbox³⁸, were used to calculate Pearson’s correlation and p-value based on n = 10k permutations. The solid line is the regression line. The shaded area represents the size of the 95% confidence interval for the regression estimate. The confidence interval is estimated using a non-parametric bootstrap procedure. C The spatial relationship of BF white matter fiber lengths (panel A) with seed-based connectivity for the BF structural (blue) and functional (orange) datasets. Spin tests⁴⁸, as implemented in the neuromaps toolbox³⁸, were used to calculate Pearson’s correlation and p-value based on n = 10k permutations. The solid line is the regression line. The shaded area represents the size of the 95% confidence interval for the regression estimate. The confidence interval is estimated using a non-parametric bootstrap procedure. Source data are provided as a Source Data file.

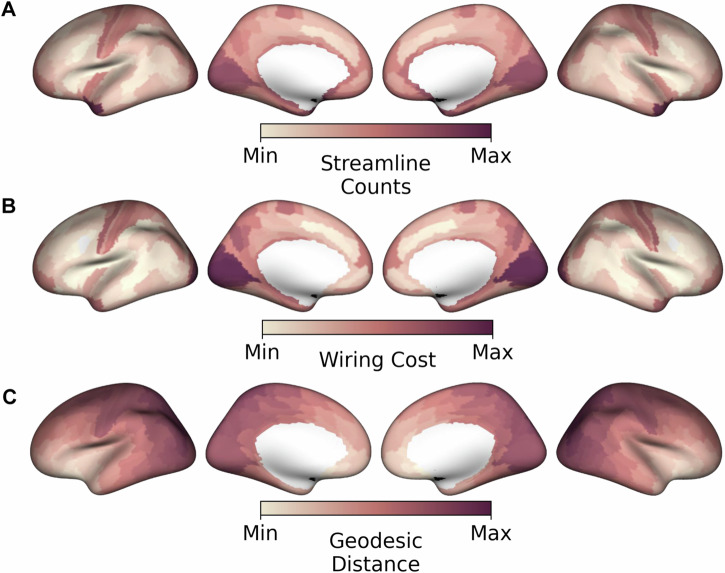
If more individual BF neurons are needed to provide innervation over longer distances due to lower branching, this pattern would be consistent with higher wiring costs in these regions. We, therefore, next computed an estimate of BF wiring cost^22,23 by multiplying the average fiber length with the total number of streamlines received from the BF (Fig. 6A and Supplemental dataset 1) for each HCP-MMP cortical parcel. In this fiber distance-weighted structural connectivity map (Fig. 6B), the further away and the higher the streamline counts, the larger the wiring cost. Expectedly, the highest wiring costs were observed in cortical areas that receive input from cholinergic neurons predicted to have the lowest branching, i.e., primary visual and somatomotor cortex. These cortical areas also tend to have the farthest geodesic distance from the BF (Fig. 6C).

Fig. 6. Cortical wiring costs and geodesic distances for basal forebrain (BF) projections.

A Streamline count representing the number of BF streamlines reaching each of the HCP-MMP cortical parcels⁴¹. The values of each cortical parcel were rescaled¹¹⁵ between 0 (Min) and 1(Max), Max indicating the highest streamline counts. B Wiring costs represent the BF white matter streamline counts for each cortical parcel weighted by their average fiber lengths, (Fig. 5A). The values of each cortical parcel were rescaled¹¹⁵ between 0 (Min) and 1(Max). Wiring costs are highest (Max) in primary visual and somatomotor cortices. C Geodesic distances from the BF to each parcel on the cortical surface. The values were rescaled¹¹⁵ between 0 (Min) and 1(Max), with Max encoding the longest geodesic distance from BF.

Cellular evidence for a gradient of arborization in BF cholinergic neurons

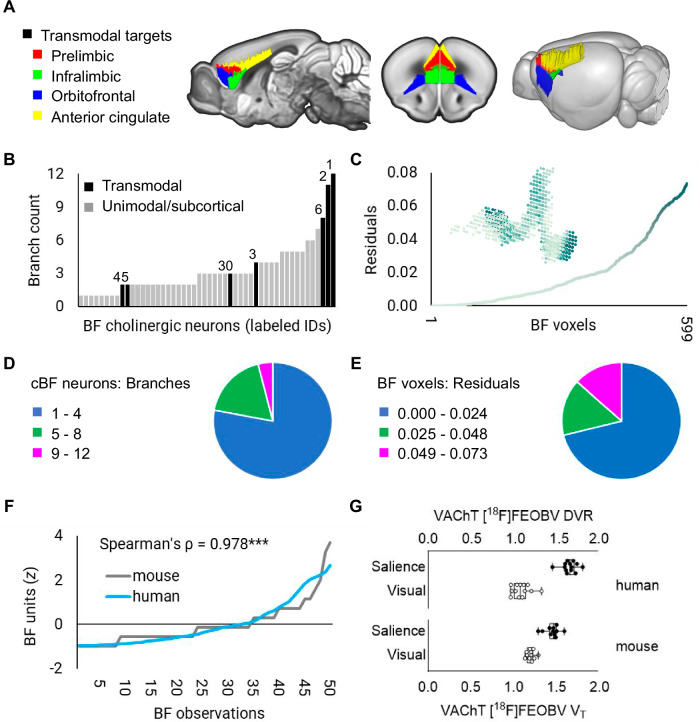
Thus far, the distance/arborization tradeoff observed in humans implies that the branching complexity of individual cholinergic neurons is shaped by a combination of the physical proximity and/or function of its cortical targets. However, a limitation of in vivo dMRI and rsfMRI techniques is that neither can resolve single-cell axonal branching of cholinergic neurons. To test the arborization gradient hypothesis more directly, we leveraged a whole brain atlas of mouse BF cholinergic projections² derived from cell-type specific anterograde viral labeling of individual BF cholinergic soma and axonal projections within the diagonal band of Broca (Table 1 and Supplemental Fig. 7A). For each neuron, the targets of its axonal branches were labeled using the Allen Mouse Brain Atlas⁵⁴, and classified according to whether any one of their branches targeted transmodal (iso)cortical areas. We identified 7/50 neurons fitting this criterion (Fig. 7A). The Allen Mouse Brain Atlas⁵⁵ annotations for the target areas include infralimbic and cingulate cortical areas within the mouse homologue of the salience network^56,57. The remaining 43 neurons target unimodal sensory, motor, or subcortical areas.

Fig. 7. A cortical gradient of basal forebrain (BF) arborization in mouse and human.

A In a whole brain atlas of mouse BF cholinergic neurons² (n = 50), 7/50 labeled neurons targeted transmodal (iso)cortical areas, color-coded on sagittal, coronal, and 3D renders of the Allen Mouse Brain Atlas⁵⁴. B The number of distinct brain-wide targets for each of the 50 BF cholinergic neurons (branch counts) were ranked low to high. Black bars denote neurons targeting transmodal areas (panel A), and numerical label IDs correspond to individual neurons in Supplemental Fig. 7 of Li et al.². C The residual values encoding BF structure-function tethering in humans across 599 voxels of the BF region-of-interest (inset) were ranked low to high. D and E For mouse and human, distributions of cholinergic basal forebrain (cBF) neuronal branching and BF voxel residuals were split into tertiles to examine the concentrations of values (higher versus lower) relative to the total number of observations. F The rank-ordered residuals across 599 BF voxels (downsampled to 50, blue) are superimposed over the branch counts of 50 mouse neurons (light gray) shown in panel (B). G Box-and-whiskers plots with individual values superimposed from in vivo [¹⁸F]FEOBV PET data for ventral attention and visual networks (human, n = 13) and salience network regions (panel A) and a visual cortical control ROI (mice, n = 11). Box hinges mark the 25th and 75th percentiles, whiskers extend to minimum and maximum values, and the middle line indicates the median. Source data are provided as a Source Data file. *** = p < 0.001.

We next counted the number of distinct brain-wide targets for each of the 50 BF cholinergic neurons. There was substantial variation in branch counts, ranging from neurons with only a single target to neurons with up to 12 different targets across the brain (Fig. 7B). Note that the upper bound of this branch count likely reflects an underestimate^2–4, given that cholinergic neurons originating in the NbM were not labeled in this study and the technique for quantifying the terminal fields was conducted at mesoscopic resolution. A permutation test comparing the number of branches between the transmodal targeting and unimodal/subcortical targeting cholinergic neurons revealed significantly higher branch counts in the transmodal targeting subset (10 k permutations, t = 3.2, p_perm = 0.004, see “Methods”). To compare the distributions of BF neuronal branching in mice with our metric of BF neuronal branching in humans (structure-function tethering), we sorted the BF residuals (Fig. 7C inset) from low to high across the 599 voxels comprising the full BF ROI. Consistent with mice, the distribution was right-skewed with a small concentration of higher residual values and a long left tail of smaller values (Fig. 7C). For mice and humans, we split the respective distributions of neuronal branching and voxel residuals into tertiles to examine the concentrations of values (higher versus lower) relative to the total number of observations (see “Methods”). For mice, the highest tertile contained only a small percentage (4%) of neurons with > 8 branches (Fig. 7D). Similarly, for humans, the highest tertile contained a relatively small percentage (13%) of BF voxels (Fig. 7E). In both species, BF cholinergic neurons with very high branching thus represent a relatively smaller proportion of the total neuronal population. The shapes of the continuous distributions for single cell branch counts (Fig. 7B) and for voxel residuals (Fig. 7C) were also highly similar to one another (Spearman’s rank correlation = 0.978, p < 0.0001; Fig. 7F, see “Methods”), despite the fact that they originate from separate species and measurement techniques.

To bridge the gap between measures of central cholinergic innervation in humans and mice, we acquired in vivo [¹⁸F]FEOBV microPET data in control mice (n = 11, Table 1) and quantified VAChT concentrations in the salience network regions (Fig. 7A) identified by the prior anterograde viral tracing study² and a control region of interest comprising Allen Mouse Brain Atlas annotations for the visual cortex (see “Methods”, Supplemental Fig. 7B). In humans, we extracted [¹⁸F]FEOBV PET measures of VAChT from the homologous ventral attention and visual networks, as defined from the a priori Yeo³⁵ networks (Fig. 3B). In both mice and humans, we found that VAChT concentrations were significantly higher in salience network hubs compared to the visual cortex (Fig. 7G; mouse: t₁₀ = 11.54, p < 0.0001; human: t₁₂ = 17.19, p < 0.0001). These findings provide further translational evidence that BF cholinergic neurons exhibit an arborization gradient which is shaped by the function and physical distance of their cortical targets.

To emphasize the features capturing the BF cholinergic arborization gradient in humans, we generated a cortical surface integrating measures of (1) BF structure-function tethering, (2) cortical VAChT concentration, and (3) fiber lengths of BF white matter projections (Fig. 8A). The highest convergence of these three features selectively colocalizes midcingulo-insular hubs of the ventral attention network (white boundaries). Altogether, our findings accord with a gradient of BF cortical cholinergic innervation, which captures both modular (more neurons, fewer branches) and diffuse (fewer neurons, more branches) properties of functional integration⁵, depending on the subregional point of origin within the BF and the cortical targets (Fig. 8B).

Fig. 8. Multimodal map of the human basal forebrain (BF) cholinergic innervation.

A A cortical surface emphasizing the arborization gradient of BF cholinergic neurons was constructed by summing the intensity normalized maps encoding (1) BF structure-function tethering, (2) cortical VAChT concentration, and (3) fiber lengths of BF white matter projections. The tethering and fiber length maps were sign flipped such that maximum values on the scale reflect higher VAChT, lower tethering, and shorter fiber lengths. The highest convergence of these three features selectively colocalizes midcingulo-insular hubs of the ventral attention network (white boundaries derived from Yeo et al.³⁵). B Depending on the subregional point of origin within the BF (anteromedial or posterolateral) and cortical target, BF cholinergic neurons may exhibit either a modular (more neurons, fewer branches) or diffuse (fewer neurons, more branches) profile of arborization.

Discussion

We examined how the structural organization of cholinergic BF projections relates to their functional integration in the human and mouse cortex. Our findings, derived from multimodal in vivo brain imaging and cell type-specific tracing of BF cholinergic axons, imply that the branching complexity of cholinergic projections may reflect the properties of the cortical areas they target. Moving up the cortical hierarchy, neuronal populations with both increasingly diverse repertoires of cortical-cortical connectivity and shorter projection distances from the BF receive input from increasingly branched BF cholinergic neurons.

We considered the spatial relationship of the BF arborization gradient (defined from the residuals between BF structural and functional connectivity) to an established set of the brain’s core resting state networks³⁵. Our findings indicate a pattern of cortical cholinergic innervation where shifts in axonal branching align spatially with the boundaries of cortico-cortical network hubs. Cholinergic neurons with the highest arborizations target hubs of the midcingulo-insular network. Moving down this arborization gradient, frontoparietal and temporal network hubs exhibit an innervation profile of intermediate branching. Finally, cholinergic neurons with the fewest arbors per cell appear to preferentially target unimodal sensory cortices. In this hierarchically organized projection pattern, cholinergic neurons with fewer branches would need to be more numerous than those with many branches in order to provide coverage of an equivalent cortical surface area. Consistent with this prediction, cortical areas that receive higher numbers of BF streamlines tend to be farther away from the BF in terms of fiber lengths (Fig. 5C). Moreover, when we split estimates of axonal branch counts into tertiles in both mouse (cells) and human (voxels), the lowest tertile comprised > 60% of observations (Fig. 7D, E), while the uppermost tertile comprised < 15%. Hence, the BF appears to be populated by a significantly larger proportion of neurons with relatively fewer branches.

What is the functional significance of a cholinergic arborization gradient in this hierarchical cortical architecture? Neuroimaging work examining the functional and structural connectivity of the brain’s cortico-cortical networks has consistently identified the midcingulo-insular in high-level selection and enhancement of both exogenous (sensory) and endogenous sources of input^28–36. These two streams of information are thought to reflect a fundamental division of labor in the brain’s network organization. Support for this division comes from work demonstrating that exogenous and endogenous networks tend to be functionally anticorrelated with one another^58–62, reflecting their competitive interactions for representational dominance of the outside sensory world versus internal mental content. The midcingulo-insular areas are unique in that they exhibit positive temporal correlations with networks in both the exogenous and endogenous processing streams, implying a superordinate role in selecting between the two^36,63–65. We also recently provided meta-analytic evidence that task-related midcingulo-insular activations, as measured by fMRI, exhibit among the strongest patterns of pharmaco-modulation by cholinergic agonists and task-related co-activations with the BF⁶⁶. The profile of BF cholinergic arborization and the strength of its modulatory regulation on the midcingulo-insular cortex provide further evidence of its privileged supervisory status.

Cortical cholinergic signaling is thought to play a central role in promoting the selection and processing of relevant stimuli while suppressing competing irrelevant information^5,67–69. Parallel lines of research in mouse and non-human primates have started to uncover the cortical circuit and computations which enable this core property of brain function⁷⁰. The BF cholinergic inputs form an integral component of a canonical disinhibitory microcircuit expressed throughout the cortex, composed of pyramidal neurons and multiple classes of interneurons^71–79, possibly organized at the columnar scale^80,81. Targeted release of acetylcholine in this microcircuit may bias mutually suppressive responses of neuronal populations competing for attentional resources^70,82–84, allowing one population to dominate over others. Moving up the cortical hierarchy, individual cholinergic neurons may require larger arborizations to bias competitive responses across increasingly large and spatially distributed populations of cortical neurons. We speculate that coalitions of BF cholinergic neurons may coordinate the release of acetylcholine^85,86 along this arborization gradient. These transient coordinated patterns of signaling may act to flexibly segregate⁸⁷ assemblies of neurons^88–91 across the cortical hierarchy to form coherent attentional episodes⁹².

A diversity of branch complexity in BF cholinergic neurons may also account for differences in their vulnerability to aging and disease. Cell type-specific labeling and transcriptomic analyses examining morphological and functional properties that increase a neuron’s vulnerability to age-related neurodegenerative diseases such as AD have consistently demonstrated large axonal projections as a key risk factor^4,93–95. The observed decreased structure-function tethering in the posterolateral BF, and in particular, the NbM is consistent with neurons exhibiting large arborizations. This morphofunctional property of NbM cholinergic neurons may increase their vulnerability to dysfunction in the aging brain. In parallel, our observation that the ventral attention network may receive input from the most highly branched NbM cholinergic neurons implies that these cortical areas might exhibit higher vulnerability to dysfunctional cholinergic signaling in the aging brain⁹⁶. It is also notable that the BF cholinergic neurons with fewer arborizations, which our findings suggest primarily target the primary and somatosensory cortices, constitute projection zones that are relatively spared by pathology in the early stages of AD⁹⁷.

Our findings are subject to several important methodological considerations. First, the basal forebrain is a small subcortical structure with poorly defined anatomical boundaries. We therefore used a probabilistic atlas to localize its constituent nuclei. However, when using probabilistic BF atlases in combination with data collected at spatial resolutions typical of 3 T structural (1.5 mm³) and functional MRI (3 mm³), aliasing of adjacent structures has been shown to systematically overestimate the BF gray matter⁹⁸. To mitigate this issue, we leveraged data that used optimized MRI protocols to acquire high spatial resolution dMRI (1.05 mm³) and rsfMRI (1.6 mm³) at 7 T^99,100. Second, our measures of structural connectivity were estimated using streamlined tractography on diffusion-weighted imaging, which can be susceptible to false positives and negatives in certain brain areas⁹⁸. It is, therefore, possible that the regional variation in BF structure-function correspondence is partly explained by regional variation in tractography performance. Another concern is the susceptibility-related spatial distortions near the BF region for fast readout scans, such as those used for the rsfMRI acquisitions by the HCP. Although corrected for using a separately acquired field map, these spatial distortions might lead to suboptimal probing of BF voxels due to possible contamination from white matter (WM) tissue and cerebrospinal fluids (CSF). To limit the impact of the latter on the functional time series analysis, additional denoising using the average WM and CSF timeseries was performed. Finally, the atlas provided by Li et al.². consists of cholinergic neurons sampled exclusively from the anteromedial nuclei of the basal forebrain. Complete morphologies of individual basal forebrain cholinergic neurons are needed over larger samples of neurons, with greater coverage of the mouse basal forebrain nuclei, and with quantification of both axonal and dendritic arborizations^3,4,6.

In sum, we demonstrate that multimodal gradients of BF connectivity reveal spatially inhomogeneous patterns of structure-function tethering in the cortex, with the lowest tethering in mid-cingulate and anterior insular cortical areas involved in salience detection and allocation of attentional resources throughout the brain. These cortical areas tend to be located proximal to the BF and receive disproportionately higher concentrations of cholinergic innervation. Our findings conform to a model in which this multimodal BF gradient is shaped in part by axonal branch complexity.

Methods

We used high-resolution minimally pre-processed HCP 7 T MRI data (n = 173)³⁹ and the existing stereotactic atlas of the BF⁴⁰ to build structural and functional connectomes. Any further pre- and postprocessing was done on the high-performance computing cluster of the Digital Research Alliance of Canada. Workflows were built using Snakemake¹⁰¹ with the full workflow available on GitHub (see Data and Code Availability statements for specifics). Individual connectomes were averaged and reduced to a 2-dimensional M-by-N matrix describing the pairwise connectivity strength between M BF ROI voxels and N cortical regions⁴¹. The BrainSpace toolbox⁴⁴ was used to capture the gradients which, as well as any further analysis, was done using Jupyter Notebooks¹⁰².

Human MRI datasets

High-resolution 7 T dMRI and rsfMRI data were downloaded from the HCP data repository²⁴. We used the minimally pre-processed 7 T data (described in Glasser et al.³⁹) consisting of 173 healthy subjects (69 male, 104 female) aged 22 to 35 years. The dMRI images were collected with a 1.05 mm³ isotropic voxel size, TR = 7000 ms, TE = 71.2 ms, b-values = 1000, 2000 s/mm², FOV = 210 x 210 mm². Resting-state fMRI images were collected with a 1.6 mm³ isotropic voxel size, TR = 1000 ms, TE = 22.2 ms, FOV = 208 mm², spanning 4 runs of 16-min duration each, per subject. For anatomical imaging, two T₁-weighted (T₁w) scans were obtained using a three-dimensional (3D) magnetization-prepared rapid gradient-echo (MPRAGE)¹⁰³ sequence with identical geometries and a 0.7 mm³ isotropic voxel size. Full details of the acquisition parameters can be found in the HCP S1200 release reference manual¹⁰⁴.

Basal forebrain mask

The BF ROI was created using the existing stereotactic atlas of the BF⁴⁰. This stereotactic BF atlas is based on histological sections obtained from 10 postmortem brains. The magnocellular cell groups were delineated in each slice, 3D reconstructed, and warped into the MNI single-subject reference space¹⁰⁵. The atlas consists of 4 subregions of the BF defined in the nomenclature: Ch1-2, Ch3, Ch4, and Ch4p¹⁰⁶. For each subregion, a stereotactic probabilistic map has a range of 0 to 10, indicating the number of brains containing the specific magnocellular cell groups in the given voxel. Note that this atlas is not left-right symmetrical; hence, our BF ROI is asymmetrical. Our BF ROI is created by thresholding these subregion masks to 50% first and then combining all to get a mask covering full BF. This BF ROI mask was then warped into the MNI152 non-linear 6^th generation atlas (MNI152Nlin6Asym).

Structural connectivity reconstruction

Diffusion tractography was performed to get a connectivity matrix for diffusion data. As part of the minimal preprocessing pipeline data release, all subjects underwent FreeSurfer processing (v5.3.0-HCP)¹⁰⁷. The BF ROI mask was then first resampled and transformed to the individual subjects’ minimally preprocessed volume space (0.7 mm³). Volumetric cortical labels were built by mapping the HCP-MMP 1.0 surface parcellation⁴¹ using Connectome Workbench’s ribbon-constrained label-to-volume-mapping function and FreeSurfer-derived surfaces. The BF ROI voxels were used as seeds, and the 180 cortical regions in each hemisphere were combined and used as targets to perform probabilistic tractography using FSL’s probtrackx¹⁰⁸ with 5000 streamlines per BF ROI voxel. The resulting probability maps (Supplemental Fig. 1B) in the BF quantified the number of streamlines that reached each target. The maps were resampled to MNI space¹⁰⁹ and 1.6 mm³ resolution to match the functional connectivity data and reduced to a 2-dimensional M-by-N matrix, where M represents the voxels in the BF ROI (599 voxels), and N is the cortical targets (180 each hemisphere) with their corresponding number of streamlines. In addition, the wiring cost connecting the BF ROI with the cortex was calculated by multiplying the number of streamlines with their average length for each cortical target²². The M-by-N connectivity feature matrix, as well as the cortical wiring cost map for all 173 subjects, were averaged to calculate the gradients and wiring cost, respectively.

Functional connectivity reconstruction

First, the BF ROI mask in the minimally preprocessed volume space was resampled to the 1.6 mm³ isotropic voxel size of the rsfMRI data and added to the subject’s subcortical parcellation. A functional connectivity matrix was then created for each subject by calculating the temporal correlation between BF voxels and cortical ROIs. All four runs (i.e., two sets of 16 min. runs with posterior-to-anterior and anterior-to-posterior phase-encoding) of the minimally preprocessed and ICA-FIX denoised rsfMRI data¹¹⁰ were used. Since the BF ROI is not included in the dense timeseries provided by HCP, these were regenerated using the updated subcortical parcellation to include the BF ROI voxels for further processing. Subsequent processing included ROI-constrained subcortical smoothing to match the cortical sampling density using the scripts provided by HCP¹⁰⁷, as well as additional signal filtering (i) based on the average WM and CSF timeseries using ciftify¹¹¹ and (ii) by applying a Wishart filter as proposed previously^112,113 to selectively smooth unstructured noise more than the structured blood oxygenation level-dependent signal. Average cortical ROI timeseries (concatenated across runs) were then extracted using the HCP-MMP 1.0 surface parcellation⁴¹. The 2-dimensional M-by-N functional connectivity matrices were constructed by calculating the Pearson’s correlation coefficient for each BF ROI voxel (M) to each of the cortical parcels (N, 180 each hemisphere) and averaged over all subjects to calculate group-wise gradients.

Gradient calculation

Connectivity gradients were calculated using the BrainSpace toolbox⁴⁴. Group averaged connectivity matrices were used as input to the GradientMaps function, using the normalized angle kernel and diffusion map embedding approach. This nonlinear dimension reduction method transforms the connectivity matrix into a low-dimensional representation to construct connectivity gradients and their corresponding lambda values (i.e., explained variance)²⁵. BF voxels that are characterized by similar connectivity patterns will have a gradient value closer together, whereas voxels with little or no similarity are farther apart. These gradients were then mapped back onto the BF voxel space to visualize continuous transitions in functional and structural connectivity patterns (Supplemental Fig. 2A–C).

In addition, gradient-weighted cortical maps were created by multiplying each row of the BF-cortical connectivity matrix with the corresponding gradient value of that BF voxel⁴⁵ (Supplemental Fig. 2E). The distribution of cortical gradient-weighted values was then decomposed into seven functional networks³⁵ using the HCP-MMP 1.0 parcellation-based 7 Yeo networks as defined in refs. ^35,114. These include the visual, somatomotor, dorsal attention, ventral attention, limbic, frontoparietal, and default mode networks.

Residual values (structure-function tethering) for each of the BF voxels and HCP-MMP parcels were calculated based on the regression between the structural and functional gradients for the BF and gradient-weighted cortical maps, respectively.

Human [¹⁸F]FEOBV PET dataset

Human [¹⁸F]FEOBV PET data acquisition and preprocessing are described in-depth by Kanel et al.³⁷. Briefly, all participants (n = 13; 10 males, 3 females; mean age = 24.5 years, SD = 4.9 years) provided written informed consent prior to scanning. Dynamic [¹⁸F]FEOBV PET imaging was performed in 3D list mode on an ECAT Exact HR + PET tomograph (Siemens Molecular Imaging) at the University of Michigan. Each subject’s [¹⁸F]FEOBV PET image was intensity normalized to a supratentorial white matter reference region to create parametric DVR [¹⁸F]FEOBV PET images. A group-level [¹⁸F]FEOBV template was computed from the average of all DVR [¹⁸F]FEOBV PET images, which was then smoothed with a 6 mm full-width at half-maximum (FWHM) Gaussian kernel, before transformation to 10k_fsavg surface-space and parcellation with the HCP-MMP 1.0⁴¹. The values of each cortical parcel encoding the relative concentration of cholinergic nerve terminals were rescaled¹¹⁵ and visualized on an inflated surface (Fig. 4A). Additional [¹⁸F]FEOBV maps^49,50 were obtained from the neuromaps toolbox³⁸ to examine the reproducibility of our results.

Mouse viral tracing dataset

Viral tracing of mouse cholinergic BF neurons is described in-depth by Li et al.². Briefly, a Cre-dependent adeno-associated virus (AAV) expressing FLEX-GFP under the CAG promoter (Serotype 9;UNC Gene Therapy Center Vector Core, Chapel Hill, NC) was injected into the Diagonal Band of Broca of Chat-ires-Cre mice to label cholinergic neurons. Whole-brain tissue was imaged using fMOST and the 3D data was aligned to the Allen Mouse Brain Atlas⁵⁴. Finally, the reconstruction of 50 cholinergic Diagonal Bands of Broca neurons was performed, and the axon-targeted areas were determined using the atlas-based region labels. The branch counts, and Allen Mouse Brain Atlas annotations for areas targeted by each branch are provided by Li et al.² in their Supplemental Appendix Fig. 7.

To investigate the relationship between cholinergic branch complexity and the cortical area each branch targets, the Allen Mouse Brain atlas annotations for the 50 labeled cholinergic Diagonal Band of Broca neurons were sorted according to whether they targeted unimodal sensory cortical and subcortical regions (group 1) or transmodal cortical areas (group 2). To assess the statistical significance of the mean difference in branch counts between the two groups, a permutation test with 10k iterations was conducted by randomly shuffling the combined data and recalculating the mean difference between the two groups for each permutation. The p-value was then computed as the proportion of permuted mean differences that were equal to or exceeded the observed mean difference in absolute value.

For the distributions of branch counts derived from (i) the 50 labeled cholinergic Diagonal Band of Broca neurons in mice and (ii) the residuals encoding tethering between BF structural and functional connectivity in humans, each dataset was divided into three equal parts (tertiles) based on a fixed-interval approach that uses the maximum value of the dataset as a reference point. This strategy groups the range of data in each distribution into lower, middle, and upper tertiles, where the size of each bin depends on the distribution of the data.

To assess the similarity between the distributions of branch counts derived from the 50 labeled cholinergic Diagonal Band of Broca neurons in mice and the residuals encoding tethering between BF structural and functional connectivity in humans, each dataset was first z-scored. To ensure both datasets had the same length, the human dataset was interpolated and downsampled from 599 to 50 points using linear interpolation. This procedure involved generating an interpolation vector that evenly spanned the original index range of the dataset, and then estimating the values at these new points, effectively reducing the dataset’s size while preserving its overall shape and trends. Spearman’s rank correlation analyses were then performed to evaluate the monotonic relationship between the two datasets. A permutation test with 10k iterations was conducted to assess the statistical significance of the observed correlation by randomly shuffling the data and recalculating the correlation coefficient for each permutation.

Mouse [¹⁸F]FEOBV PET acquisition

All small-animal imaging procedures were conducted in accordance with the Canadian Council of Animal Care’s current policies and were approved by the University of Western Ontario’s Animal Care Committee (Animal Use Protocols: 2020-162 and 2020-163) and the Lawson Health Research Institute’s Health and Safety board. Mice were housed as pairs in standard plexiglass cages in a temperature- and humidity-controlled environment at 22–25 °C and 40%–60%, respectively. Housing cages were situated in rooms on a 12-h light/12-h dark cycle, and food (regular chow) and water were made available to the animals ad libitum. Imaging experiments were performed during the light cycle (7:00 AM-7:00 PM), and the scanning order was balanced according to biological sex. All efforts were made to maximize animal welfare before, during, and after imaging experiments.

High-resolution 9.4 T MRI and [¹⁸F]FEOBV PET data were acquired at the Center of Functional and Metabolic Mapping (Agilent Animal MRI Scanner, Bruker) and the Lawson Health Research Institute’s Preclinical Imaging Facility (Inveon DPET, Siemens Healthineers), respectively. Data were acquired in 11 (5 male, 6 female) control mice, either C57BL/6 J or VAChT^flox/flox at 6 months of age. VAChT^flox/flox mice were generated on a C57BL/6 J background as previously described¹¹⁶.

In vivo, dynamic [¹⁸F]FEOBV PET data were acquired as 150-min list-mode emission scans, performed with a timing window of 3.432 ns and a 350–640 keV discrimination energy range. Mice were anesthetized (1.5–2.0% isoflurane in 1.0 L/min O_2(g)) and then injected intravenously with a ~ 20 Megabecquerel (MBq) dose of [¹⁸F]FEOBV. Data were binned into consecutive frames of increasing duration (n_frames = 43), consisting of 15 frames of 40 s, followed by 28 frames of 300 s. An OSEM3D algorithm with two iterations and 18 subsets was used to reconstruct [¹⁸F]FEOBV PET images with the following parameters: matrix dimensions: 128 mm × 128 mm × 159 mm; voxel resolution: 0.776 mm × 0.776 mm × 0.796 mm.

Given that (a) VAChT is expressed throughout cerebral², subcortical, and cerebellar gray matter regions of the mouse brain¹¹⁷, and (b) the spatial resolution of microPET cannot resolve [¹⁸F]FEOBV uptake within small white matter structures, no anatomical reference region was used for intensity normalization of mouse [¹⁸F]FEOBV PET data. Rather, parametric volume of distribution (V_T) images were estimated for each mouse by fitting the whole-brain [¹⁸F]FEOBV time-activity curves with the multi-time point graphical analysis methodology described by Logan et al. ¹¹⁸, where an image-derived input function (IDIF) served as the reference. The IDIF was obtained from a volume of interest placed in the lumen of the left ventricle of the mouse heart¹¹⁹, and the start of the linear portion (t*) was determined from the curve fitting, where t* = ~ 11.33 min.

Pre-processing of mouse [¹⁸F]FEOBV V_T images was performed using SPM12 in MATLAB R2020b. Preparation of [¹⁸F]FEOBV V_T images included resizing, centering, and re-orienting the images to follow the right-hand coordinate system (RAS). Each V_T image was then coregistered to its corresponding native space MRI image using normalized mutual information. Finally, all [¹⁸F]FEOBV V_T images were cropped to the native space MRI bounding box dimensions and nonlinearly warped to the study-specific anatomical mouse brain template (see below). To parcellate mouse [¹⁸F]FEOBV V_T images, we performed non-linear registration of the study-specific mouse brain template to the Allen Mouse Brain Atlas⁵⁴.

For anatomical MRI, mice were anesthetized (1.5–2.0% isoflurane in 1.5 L/min O_{2 (g)}) and then positioned in the center of a 30 mm RF volume coil (Bruker). Four iterations of magnetization transfer (MT)-weighted spoiled gradient-recalled echo (GRE) images were acquired using a fast low-angle shot 3D pulse sequence with the following parameters: FOV = 16 mm x 16 mm x 10 mm; matrix dimensions: 128 x 128 x 8; voxel resolution = 0.125 mm³, slice thickness = 10 μm; TR = 30 ms; TE = 2.77 ms; FA = 9^o; off-resonance saturation = 4.5 kHz (Gaussian pulse = 10 ms duration); effective FA = 900^{o, 120}.

Pre-processing of mouse anatomical brain images was performed using SPM12 in MATLAB R2020b. For each mouse, the anatomical brain images (n = 4) were first averaged, then resized, centered, and re-oriented to follow the RAS. Using normalized-cross correlation, the images were then coregistered to the mouse brain template from Hikishima et al.¹²¹, bias-corrected using MICO¹²², and then segmented using tissue prior probability maps for gray matter, WM, and CSF tissue compartments. For each mouse, the tissue segments from this step were combined to mask out the surrounding skull and tissue. Finally, the gray and white matter segmentations were used to create nonlinear transformations for diffeomorphic registration to a population-specific average template using geodesic shooting¹²³.

Geodesic distance

The geodesic distance along the cortical surface was calculated using the geodesic library (https://github.com/the-virtual-brain/tvb-gdist) based on the algorithm that approximates the exact distance along the shortest path between two nodes (or vertices) on a triangulated surface mesh¹²⁴. An average BF seed node was created for the left and right hemispheres separately by (i) projecting the BF mask onto the 59k_fs_LR white matter surface of the individual subjects using Connectome Workbench’s volume-to-surface-mapping function, (ii) averaging across all subjects to get a probability map, (iii) resampling to the 10k_fsavg surface-space as suggested by the HCP study (https://wiki.humanconnectome.org) and (iv) then by thresholding at 0.5 to obtain a final binary BF seed on the cortical surface. A distance value was then assigned to each cortical vertex based on the minimum geodesic distance along the 10k_fsavg pial surface to the BF seed node to avoid the medial wall. To match with the resolution of the cortical connectivity results, the geodesic distance map was parcellated using the HCP-MMP 1.0 atlas as implemented in the neuromaps toolbox³⁸, and rescaled to values between 0 and 1¹¹⁵.

Statistical analyses

Permutation tests with surrogate maps¹²⁵ were used to compute statistical significance for the BF gradients and the distribution of residuals. BF gradient values for structural and functional connectivities were first rescaled between 0 and 1, and Euclidean distance was used to calculate the distance matrix among all voxels within the original BF ROI. Variograms were then permuted (n = 1000) using the SurrogateMaps function implemented in the BrainSpace toolbox⁴⁴. Parameters were adjusted in the case of a suboptimal fit compared to the empirical data (pv = 60, random_state = 1234). The final variograms were used to build and compare the null probability for the mean and CoV between BF subregions.

To assess the stability of structural and functional connectivity gradients and the gradient of their tethering, we performed split-half and leave-one-out cross-validation analyses across the 173 individuals in the sample (Supplemental Fig. 3). For each split, or subject left out, the model was trained on the remaining individuals, and the predicted gradient was compared to the observed gradient for the left-out individual.

Spin tests⁴⁸, as implemented in the neuromaps toolbox³⁸, were used to compare cortical maps based on n = 10k permuted maps. All cortical maps were parcellated using the HCP-MMP 1.0 atlas⁴¹, and values were rescaled between 0 and 1¹¹⁵. In addition to the spin tests, a bootstrapping analysis was performed to quantify the difference between structural and functional connectivity and their correlation with [¹⁸F]FEOBV PET maps and fiber length. Here, bootstrapping was applied 10k times (by randomly selecting sets of regions during each iteration) to build a null probability of correlation coefficients for statistical inference based on the observed difference between the two connectomes.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

Author contributions: S.C., A.R.K., and T.W.S designed research. S.C., R.A.M.H., K.M.O., and A.R.K. performed research. A.R.K., R.A.M.H., and K.M.O. contributed new reagents/analytic tools. P.K. and K.M.O. conducted preprocessing of PET images. P.K. also reviewed and critiqued the paper. M.A.M.P. and V.P. provided the mouse lines. S.C. and R.A.M.H. analyzed data. S.C. and T.W.S. wrote the paper.

Peer review

Peer review information

Nature Communications thanks Elizabeth Coulson and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

For the origin and use of the multiple datasets described in this paper, see Table 1. The Human Connectome (HCP) project dataset is available at http://www.humanconnectomeproject.org. The main human [¹⁸F] FEOBV PET data was derived from Kanel et al.³⁷. The processed imaging data is available at https://github.com/sudesnac/HumanBF-Connectivity/tree/main/results/connectivity_distance, the human [¹⁸F] FEOBV PET data used in the supplemental analysis are available at neuromaps³⁸ https://netneurolab.github.io/neuromaps/index.html. The mouse [¹⁸F] FEOBV PET data was collected by K.M.O., and the processed images can be accessed at 10.5281/zenodo.13750996 by contacting tschmitz@uwo.ca. The viral tracing data were derived from Li et al.². and are available in their supplemental materials (SI Appendix Fig. 7). All source data for figures are provided in the Source Data file. Source data are provided in this paper.

Code availability

The workflow for reconstructing the structural connectivity matrix from the HCP data and a subcortical region of interest is available at https://github.com/sudesnac/diffparc-smk¹²⁶; and the functional connectivity workflow at https://github.com/khanlab/subcorticalparc-smk¹²⁷. All other code used to conduct the reported analyses and create the figures are available at https://github.com/sudesnac/HumanBF-Connectivity¹²⁸.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53148-x.