Fast singlet excited-state deactivation pathway of flavin with a trimethoxyphenyl derivative

Abstract

Incorporation of the trimethoxyphenyl group at position 7 of flavin can drastically change the photophysical properties of flavin. We show unique fast singlet ¹(π,π*) excited state deactivation pathway through nonadiabatic transition to the ¹(n,π*) excited- state, and subsequent deactivation to the ground electronic state (S₀), closing the photocycle. This mechanism explains the exceptionally weak fluorescence and the short excited–state lifetime for the flavin trimethoxyphenyl derivative and the lack of excited triplet T₁ state formation. Full recovery of flavin in its ground state takes place within a 15 ps time window after photoexcitation in a polar solvent such as acetonitrile. According to quantum chemical calculations, the C₍₂₎-O distance elongates by 0.16 Å in the ¹(n,π*) state, with respect to the ground state. Intermediate–state structures are predicted by theoretical ab initio calculations and their dynamics are investigated using broadband vis-NIR time-resolved transient absorption and fluorescence up-conversion techniques.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-75239-x.

Introduction

Flavins are important biologically active molecules with a structure characterized by isoalloxazine core (see Fig. 1)^1,2. Flavin cofactors, such as flavin mononucleotide (FMN) and flavin adenine dinucleotide (FAD), which are derived from riboflavin (Fig. 1), are mainly involved in dark enzymatic redox reactions. Nevertheless, the role of flavins in light-dependent processes³ such as bioluminescence, plant phototropism, nucleic acid repair, and the regulation of biological clocks, has been documented and is currently the subject of intensive research. Artificial flavin derivatives are also important compounds used in organocatalysis and in organic photoredox catalysis^2,4–8.

Fig. 1.

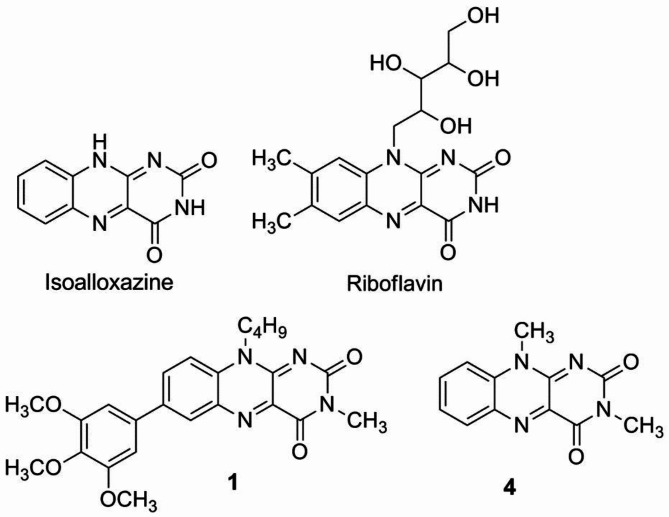
Structure of isoalloxazine as the parent structure of flavins, riboflavin as an example of naturally occurring flavins, and flavins 1 and 4 which are subject to investigation in this work.

Photophysics of flavin (Fl) derivatives is rich and well-studied^9–14. Their photoexcitation leads to the population of the ¹(π,π*) singlet excited state (S₁), which typically relaxes through S₁(π,π*) →S₀ radiative decay and S₁→T₁ intersystem crossing. In aerobic solutions, the nascent T₁ species sensitizes singlet oxygen (¹O₂) with a yield close to the Fl triplet formation quantum yield Φ_T1. For example, 3,10-dimethylisoalloxazine 4 (Fig. 1) in acetonitrile is characterized by a high yield of singlet oxygen sensitization, Φ_Δ = 0.56¹⁵. Moreover, its singlet excited-state lifetime τ_S1 is long (7.0 ns)¹⁶. To suppress triplet state formation and fluorescence, a very fast competing deactivation channel of the S₁ state is required.

Flavins are studied not only experimentally but also theoretically. A variety of quantum chemical methods have been applied to the study of flavins in their different oxidized and reduced forms. For a detailed discussion, readers are referred to an excellent review that describes several methods: starting from DFT gas-phase approaches and the simple polarizable continuum model, through the QM-cluster model, the fragment molecular orbital (FMO) method featuring molecular orbitals of fragments, the hybrid quantum mechanics molecular mechanics QM/MM method, the extrapolative scheme known as ONIOM (short for ‘Our own N-layered Integrated molecular Orbital and Molecular mechanics’), and up to the scheme of QM/MM calculations where the MM atoms are replaced with their partial (point) charges¹⁷. Particularly noteworthy are the papers in which the electronic structure of flavin has been discussed in a context of position and character of substituents^14,18–20 and effect of environment^21,22. In recent contribution a variety of electronic structure methods were studied to describe the energetics of the low-lying excited states ¹(π,π*) and ¹(n,π*) of flavin, including the potential-energy scans tracing the coordinates form the Franck-Condon point to ¹(π,π*) minimum and then towards ¹(n,π*) minimum²³.

Tuning the spectral and electronic properties of Fl is required for applications in Fl-mediated organocatalytic and photocatalytic reactions^{2,4,7,8,24–26}. So far, it is believed that fully oxidized flavins exhibit good fluorescence quantum yield, usually accompanied by high triplet quantum yield and the associated efficiency of singlet oxygen formation. Extreme cases are e.g. reduced flavins which are essentially nonfluorescent, having a quantum yield more than three orders of magnitude lower than oxidized flavins²⁷. As an example of typical flavin photophysics, compound 4 (Fig. 1) can be given, which has high fluorescence quantum yield (Φ_f = 0.35) and long ¹(π,π*) state lifetime (7 ns) in acetonitrile^15,16. Recent synthetic efforts have demonstrated effective methods for synthesis of Fl derivatives by installing aryl substituents at the position 7 via direct C − C bonding¹⁵. To our surprise, along newly synthesized flavin derivative 1 with trimethoxyphenyl group at the position 7 (Fig. 1), exhibits a very weak fluorescence which is unique among flavin derivatives. Thus, this work is devoted to elucidating the mechanism of enhancement in radiationless relaxation of the singlet excited state in the flavin substituted by 3,4,5-trimethoxyphenyl group in the position 7. Complementary experimental and theoretical studies show that incorporation of trimethoxyphenyl group into isoalloxazine activates a fast ¹(π,π*)→¹(n,π*)→S₀ nonradiative channel. This finding is expected to hold for flavins in general and can be used to tune their photophysics, when fast light-to-heat conversion is desired, without formation of the reactive species such as singlet oxygen, ¹O₂.

Experimental

Materials

The investigated flavin derivative, 7-(3,4,5-trimethoxyphenyl)isoalloxazine 1 (see Fig. 1), was prepared by Suzuki coupling starting from the corresponding 7-bromoisoalloxazine derivative¹⁵. The reference compound 3,10-dimethylisoalloxazine 4 was prepared according to literature²⁸.

Stationary fluorescence

Fluorescence emission spectra were recorded on a Horiba Jobin- Yvon-Spex Fluorolog 3–22 spectrofluorometer²⁹. Right-angle geometry was used in all of the steady-state emission measurements. The experiments were performed on 3.5 mL of sample solutions contained in a quartz cell (1 cm × 1 cm) using the linear fit method. Fluorescence spectra were collected with 3 nm excitation and 3 nm emission slits, using 0.1 s integration time. Lumichrome in acetonitrile with 0.028 fluorescence quantum yield (Φ_f) was used as a reference standard¹¹.

Femtosecond fluorescence up-conversion

Femtosecond fluorescence up-conversion measurements (Figure S1) were performed in a 2 mm thick quartz cell. Sample solution was stirred by a Teflon-coated bar. The sample of 1 was prepared in acetonitrile with absorbance A(2 mm) = 0.2 at the excitation wavelength 400 nm. The details of the experimental set-up is given in Supporting Information file. The molecular rotational diffusion effects were eliminated by using a magic-angle configuration. Fitting of the fluorescence kinetic was performed with a single-exponential function convoluted with Gaussian IRF using lmfit library in Python³⁰ optimization algorithm applied was Levenberg-Marquardt. Obtained FWHM of the IRF was 400 fs.

Femtosecond UV–Vis–NIR transient absorption

Femtosecond UV–vis-NIR transient absorption spectra were obtained using a commercially available system (Ultrafast Systems, Helios)^31,32. The solution of 1 were studied in a 2 mm thick quartz cell with a steering magnetic bar. Experiments were performed at the excitation wavelength of 500 nm, with 1 µJ energy per pulse (photon peak fluence ≈ 2 × 10¹⁵ photons per cm²). The pump diameter (FWHM) at the sample was ≈ 250 μm. Probing white light continuum pulse was generated in a sapphire plate (visible range) or in YAG crystal (NIR range). The recorded transient absorption spectra were corrected for the chirp using Surface Xplorer software. The kinetics were analyzed using fitting procedure (Surface Xplorer), satisfactory fits were typically obtained with two-exponential function. Convolution with the instrument response function (ca. 200 fs FWHM) was included into the fitting procedure.

Computational details

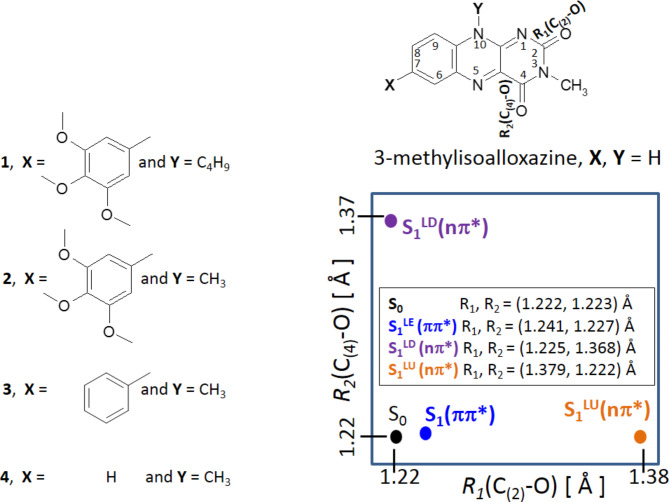
The photophysics of flavin derivatives 1–4 (see Fig. 6) were studied separately by means of ab initio methods both in the ground (S₀) and excited (S₁) electronic states. Each of molecules 2–4 have a single distinguished minimum in the ground electronic state (S₀). The molecule 1 has two close-in energy minima with the hydrogen-bonded minimum (H-bonded, Table 2) slightly lower, and this latter minimum has the reference energy of the whole system. The geometries in their closed-shell ground electronic state, S₀, were determined with the MP2 method³³ without symmetry constraint and the MP2 energy of this form (in the S₀-state) is the reference value for all other ground-state and excited-state structures. The excited-state (S₁) equilibrium geometries were determined with the second-order algebraic diagrammatic construction ADC(2) method^34–37. Each molecule has three equilibrium excited-state geometries: S₁^LE(π,π*), S₁^LD(n,π*) and S₁^LU(n,π*) and each of them was optimized without any symmetry constraints. In terms of the geometry, the most apparent difference between them lies in the length of the optimized C₍₂₎-O and C₍₄₎-O bond lengths (see Table 3) which make them coordinates for the S₁-state deactivation mechanism. All four geometries: one ground state and three excited states differ also with the interatomic distances of the carbon-carbon skeleton inside the flavin rings – especially one ring possessing carbonyl groups (see Table S1).

Fig. 6.

Enumeration of atoms (right above) in the Fl derivatives (numbered 1–4). In the rectangle (right below) shown is position of the ground, S₀, and three excited–state equilibrium forms: S₁^LE(π,π*), S₁^LD(n,π*), and S₁^LU(n,π*) for 1, in the [R₁, R₂] configuration space. Molecule 1 is 10-butyl-3-methyl-7-(3,4,5-trimethoxyphenyl)isoalloxazine, molecule 2 is 3,10-dimethyl-7-(3,4,5-trimethoxyphenyl)isoalloxazine, molecule 3 is 3,10-dimethyl-7-phenylisoalloxazine, molecule 4 is 3,10-dimethylisoalloxazine.

Table 2.

Absorption spectra of the studied molecules calculated with the CC2/aug-cc-pVDZ method at the geometry optimized at the MP2/cc-pVDZ theory level.

S0 form		ΔEVE[eV]	λabs[nm]	f	µe[D]
Molecule 1, H-bonded isomer
	S0	0.00a			µg = 6.5
	S0→S1(π,π*)	2.76	450	0.2071	10.1
	S0→S2(n,π*)	3.38	367	0.0010	1.6
	S0→S3(n,π*)	3.45	360	0.0013	3.1
	S0→S4(π,π*)	3.77	329	0.0146	21.9
	S0→S5(π,π*)	4.00	310	0.0432	1.7
	S0→S6(π,π*)	4.06	306	0.0269	21.6
Molecule 1, non-H-bonded isomer
	S0	0.026a			µg = 7.0
	S0→S1(π,π*)	2.89	429	0.2308	9.3
	S0→S2(n,π*)	3.37	368	0.0007	3.4
	S0→S3(n,π*)	3.53	352	0.0012	3.7
	S0→S4(π,π*)	3.94	315	0.0104	19.3
	S0→S5(π,π*)	4.05	306	0.0380	1.6
	S0→S6(n,π*)	4.16	298	0.0004	3.9
Molecule 2
	S0	0.0a			µg = 7.2
	S0→S1(π,π*)	2.77	448	0.2305	10.5
	S0→S2(n,π*)	3.30	376	0.0003	3.2
	S0→S3(n,π*)	3.46	359	0.0006	3.8
	S0→S4(π,π*)	3.75	331	0.0151	22.1
	S0→S5(π,π*)	3.94	315	0.0583	1.8
	S0→S6(π,π*)	4.06	306	0.0371	20.2
Molecule 3
	S0	0.0a			µg = 8.3
	S0→S1(π,π*)	2.83	439	0.2298	9.6
	S0→S2(n,π*)	3.30	376	0.0003	2.3
	S0→S3(n,π*)	3.46	359	0.0006	4.7
	S0→S4(π,π*)	3.93	316	0.0390	2.7
	S0→S5(π,π*)	4.05	306	0.0855	13.3
	S0→S6(n,π*)	4.08	304	0.0001	3.9
Molecule 4
	S0	0.0			µg = 7.9
	S0→S1(π,π*)	3.01	412	0.2138	7.9
	S0→S2(n,π*)	3.39	366	0.0004	1.5
	S0→S3(n,π*)	3.51	354	0.0005	4.4
	S0→S4(π,π*)	4.02	309	0.0955	2.9
	S0→S5(n,π*)	4.19	296	0.0000	4.7
	S0→S6(π,π*)	4.22	294	0.0723	11.4

Table 3.

Adiabatic energies, E^a (S₁) (in eV), fluorescence energy, E_fl. (in eV), oscillator strength, f, dipole moment, µ_e, and carbonyl bond distances of the S₁^LE(π,π^∗), S₁^LD(n,π*) and S₁^LU(n,π*) excited–state forms for three flavin derivatives optimized at the ADC(2)/cc-pVDZ theory level.

State	S1LE(π,π*)	S1LD(n,π*)	S1LU(n,π*)	S0
Molecule 1, roatmer H-bonded
Ea (S1)	2.374 eV	2.389 eV	2.043 eV	0.00
Efl.	1.71 eV (1.90 eV)	1.24 eV	0.47 eV	–
ffl.	0.1112	0.0000007	0.000004	–
µe	6.0 D	4.3 D	10.3 D	6.5 D
R1(C(2)-O)	1.241 Å	1.225 Å	1.379 Å	1.222 Å
R2(C(4)-O)	1.227 Å	1.368 Å	1.222 Å	1.223 Å
R3(C(4’)H—N(1))	2.488 Å	2.502 Å	2.558 Å	2.487 Å
Molecule 1, rotamer non-H-bonded
Ea (S1)	2.465	2.441	2.074	0.026 eV
Efl.	1.93 eV (2.09 eV)	1.27 eV	0.46 eV	–
ffl.	0.1581	0.000003	0.000004	–
µe	7.4 D	4.0 D	10.5 D	6.7 D
R1(C(2)-O)	1.234 Å	1.226 Å	1.379 Å	1.221 Å
R2(C(4)-O)	1.229 Å	1.367 Å	1.222 Å	1.223 Å
R3(C(4’)H—N(1))	5.264 Å	5.243 Å	5.266 Å	5.159 Å
Molecule 2
Ea (S1)	2.443 eV	2.376 eV	2.028 eV	0.0 eV
Efl.	1.98 eV	1.22 eV	0.43 eV	–
ffl.	0.1801	0.0000006	0.000003	–
µe	7.9 D	4.3 D	10.2 D	6.8 D
R1(C(2)-O)	1.234 Å	1.220 Å	1.380 Å	1.221
R2(C(4)-O)	1.229 Å	1.368 Å	1.222 Å	1.223
Molecule 3
Ea (S1)	2.474 eV	2.378 eV	2.038 eV	0.0 eV
Efl.	1.93 eV	1.22 eV	0.433 eV	–
ffl.	0.1679	0.0000006	0.00003	–
µe	7.8 D	3.4 D	9.6 D	6.6 D
R1(C(2)-O)	1.235 Å	1.224 Å	1.379 Å	1.220 Å
R2(C(4)-O)	1.228 Å	1.368 Å	1.222 Å	1.223 Å
Molecule 4
Ea (S1)	2.531 eV	2.384 eV	2.051 eV	0.00
Efl.	1.87 eV	1.22 eV	0.44 eV	–
ffl.	0.1342	0.0000006	0.000003	–
µe	8.9 D	3.2 D	10.0 D	7.6 D
R1(C(2)-O)	1.237 Å	1.224 Å	1.380 Å	1.220 Å
R2(C(4)-O)	1.228 Å	1.368 Å	1.222 Å	1.223 Å

Single point calculation of E_fl at the CC2/aug-cc-pVDZ level are given in parenthesis

To find fast singlet excited-state deactivation paths of 1, the three excited states were determined: one ππ* excited state, S₁(π,π*), and two (n,π*) excited states characterized by a substantial elongation of one of the two carbonyl bonds present in the molecules (marked LD and LU). To study this process, the relaxed potential-energy profiles were constructed, separately in the S₀ and the excited states: S₁^LE(π,π*), S₁^LD(n,π*) and S₁^LU(n,π*), along the R₁(C₍₂₎-O) distance driving coordinate. For each fixed value of a given R₁(C₍₂₎-O) coordinate the remaining 3N-7 internal nuclear coordinates were optimized. In this way each of the excited-state minimum of the given molecule is depicted in the excited-state potential-energy profile with its characteristic R₁(C₍₂₎-O) distance (see Fig. S3).

For each molecule, the correlation-consistent valence double-zeta basis set with polarization functions on all atoms (cc-pVDZ)³⁸ was used in these calculations as well as in the calculations of the potential-energy profiles.

To simulate the UV absorption spectra, the simplified version of the coupled clusters method was used, CC2^39,40 in conjunction with the aug-cc-pVDZ³⁸ basis set. All the calculations were performed using the TURBOMOLE program package⁴¹.

Experimental results

UV–Vis absorption spectra and weak fluorescence

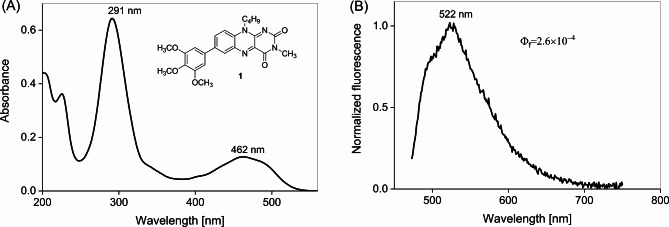
Compound 1 in acetonitrile shows an absorption band with a long wavelength maximum at 462 nm (2.69 eV) corresponding to π→π* transition (Fig. 2A). The determined extinction coefficient is ε(462 nm) = 8560 M⁻¹ cm⁻¹. This absorption band is consistent with the CC2/aug-cc-pVDZ calculated value for ΔE^VE(S₀→S₁(ππ*) of 2.76 eV for weakly H-bonded isomer and of 2.89 eV for just by 0.026 eV less stable non-hydrogen bonded isomer of 1 (see Table 2). The fluorescence spectrum recorded upon excitation at 463 nm shows an S₁→S₀ fluorescence band with maximum at 528 nm (2.35 eV) (Fig. 2B). The calculated fluorescence energy value from the relaxed emitting S₁(ππ*) state minima, E_fl., equals 1.93 eV (ADC(2)/cc-pVDZ) – for non-H-bonded rotamer, and 1.70 eV – for H-bonded excited state (see Table 3). Single point calculations at the CC2/aug-cc-pVDZ level for those two emitting forms give E_fl. values more close to experimental 2.35 eV value: 2.09 (non-H-bonded) and 1.90 eV (H-bonded), respectively. The experimentally determined fluorescence quantum yield is very low of Φ_f = 2.6 × 10⁻⁴ in acetonitrile, probably implying a very short τ_S1(π,π*) lifetime.

Fig. 2.

(A) Stationary UV-Vis absorption spectrum and (B) fluorescence spectrum of 1 in acetonitrile (λ_exc = 463 nm).

Emission kinetics recorded with fluorescence up-conversion spectroscopy

Excitation of compound 1 in acetonitrile at 400 nm results in kinetics showing a surprisingly fast S₁(π,π*)→S₀ fluorescence decay. A single-exponential fit of kinetics shown in Fig. 3, indicates a very short τ_S1(π,π*) lifetime of 0.41 ps, about 3 orders of magnitude shorter than typical τ_S1 lifetimes reported for Fls, including reference 4 (Table S2)⁹. This surprising property is caused by the presence of the trimethoxyphenyl group in compound 1. To get further insights into mechanism of S₁(π,π*) deactivation, transient absorption studies were performed.

Fig. 3.

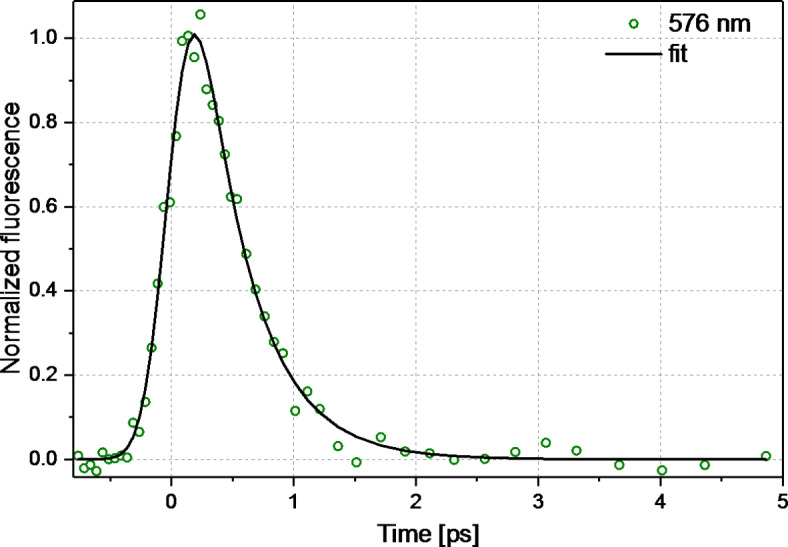
Kinetics of fluorescence of 1 (c = 3.0 × 10⁻⁴ M) in acetonitrile probed at 576 nm after excitation at 400 nm (0.25 µJ). The single exponential fit convolved with Gaussian with IRF = 400 fs, resulted in τ = 0.41 ps.

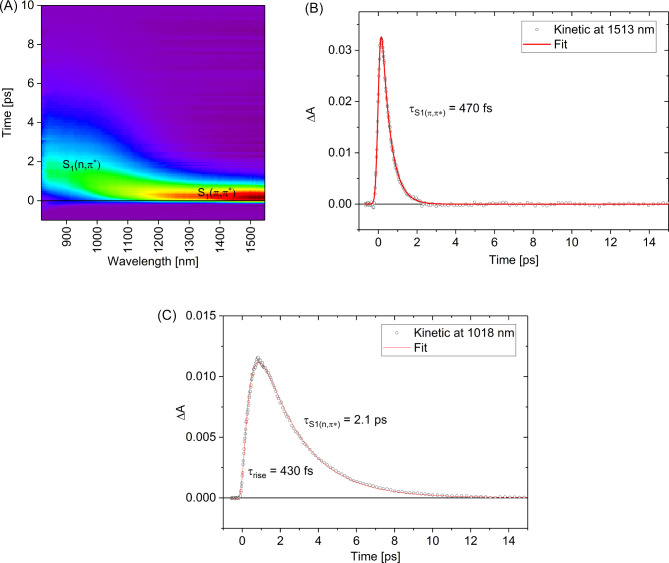
Transient species in NIR spectral range

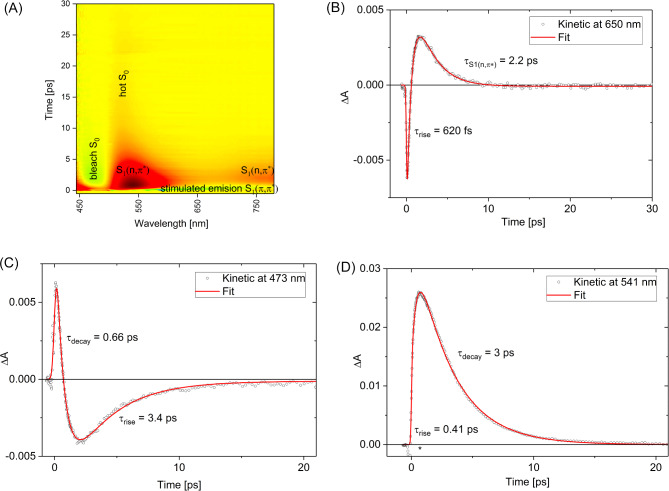
For transient absorption measurements of 1 in NIR spectral range, 500 nm (2.5 eV) excitation wavelength λ_ex has been selected in order to populate S₁(π,π*) state without significant excess of vibrational energy. This λ_ex lies little further in red than λ^max absorption band peak (Fig. 2). The transient absorption experiment reveals an instantaneous formation of the band centered about 1500 nm which can be assigned to the S₁(π,π*) state absorption (S₁→S_n transition, Fig. 4A). This band decays with a time-constant of ca. 470 fs which is the lifetime of the S₁(π,π*) state (Fig. 4B), in a good agreement with fluorescence up-conversion spectroscopy data (0.41 ps). Subsequently, we observed the appearance of the band at about 1000 nm (Fig. 4C), which can tentatively be assigned to the ¹(n,π*) state population as its rise (ca. 430 fs) matches the decay time-constant of the precursor − ¹(π,π*) state. The ¹(n,π*) population undergoes decay over time-scale of a few picoseconds, described by the time-constant τ_S1(n,π*) of 2.1 ps. In contrast to the NIR range, recorded transient absorption spectra in the visible spectral range show a higher complexity due to the contribution of the S₀ ground state bleaching and S₁(π,π*)→S₀ stimulated emission.

Fig. 4.

Transient absorption data in NIR spectral range for 1 (c = 3.9 × 10⁻⁴ M) in acetonitrile upon excitation at 500 nm (1 µJ). Contour plot (A) and selected representative kinetics at 1513 nm (B) and 1018 nm (C).

Transient species in the visible range

The transient absorption kinetics at 650 nm (Fig. 5B) reveal a rapidly-decaying negative signal corresponding to S₁(π,π*)→S₀ stimulated emission associated with a time constant of 0.62 ps. Disappearance of that signal is followed by a rise of the positive transient absorption signal, reaching maximum at a delay time of 1.5 ps. It can be assigned to¹(n,π*) population. The presence of a short-lived (0.66 ps, Fig. 5C) positive signal at 473 nm can also be attributed to the S₁(π,π*) population. The contour plot of the transient absorption data (Fig. 5A) gathers these signals together, illustrating the interplay between them.

Fig. 5.

Transient absorption data recorded in visible range for 1 (c = 3.9 × 10⁻⁴ M) in acetonitrile upon excitation at 500 nm (1 µJ). Contour plot (A) and selected representative kinetics at 650 nm (B), 473 nm (C) and 541 nm (D). (*) solvent contribution.

The kinetics probed at 541 nm is dominated by the absorption of S₁(n,π*) population (Fig. 5D). The decay occurs with a relatively long 3 ps time constant (not approximately 2.2 ps, as probed at 650 and 1015 nm, Table 1). This may be a manifestation of the additional contribution from the hot S₀ ground state population nascent upon ¹(n,π*) state decay. The nascent hot S₀ state may undergo absorption band narrowing upon shedding its excess heat to the solvent³¹. Indeed, inspection of the kinetics probed at 473 nm (Fig. 5C) shows that repopulation of the ground state S₀ occurs with a relatively long time constant of 3.4 ps, suggesting that S₀ vibrational cooling of compound 1 is likely the rate limiting step. Note that the complete recovery of the S₀ population observed within a 15 ps time window (Fig. 5A), indicates the return of molecules of compound 1 to their initial form, as existed before sample photoexcitation, and no longlived intermediates (such as triplet species) remain. This photobehavior of compound 1 is dramatically different from typical Fl photophysics, which are known for active triplet generation in the intersystem crossing T₁←S₁^9,11. For instance, the reference compound 4 after photoexcitation at 470 nm shows a gentle decay of the population of the S₁ state in a temporal window of 2.6 ns and the appearance of the absorption band of the T₁ state (Fig. S2A), similar characteristics have been reported for deazaflavin (3-butyl-10-methyl-5-deazaisoalloxazine)⁴².

Table 1.

Results of the fit of selected kinetic traces with single or double exponential function (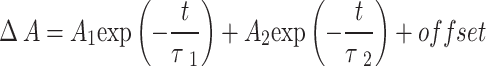) convoluted with instrument response function (ca. 200 fs, FWHM).

Probe wavelength [nm]	A1	τ1[ps]	A2	τ2[ps]	Offset
1513	0.0536	0.47	–	–	0.000022
1018	− 0.023	0.46	0.022	2.1	0.000023
650	− 0.020	0.62	0.010	2.2	− 0.000083
541	− 0.026	0.41	0.038	3.0	0.0000056
473	0.021	0.66	− 0.0087	3.4	− 0.00012

Accuracy of time constants is ca. ± 10%.

Comparison of the simulated UV–Vis absorption spectra and S₀-state geometry of molecule 1 with other Fl derivatives

The experimentally studied molecule 1 consists of the two moieties: an almost planar 3-methylisoalloxazine ring covalently bound to a trimethoxyphenyl group attached at the position 7. The presence of the additional butyl group – attached to the nitrogen atom N₍₁₀₎ – is the reason for existence of two low-energy rotamers (Table 2). The most stable one is a weakly hydrogen bonded rotamer in which the butyl group interacts with the N₍₁₎ atom with the intramolecular hydrogen bond distance C_(4’)H—N₍₁₎ is of 2.49 Å. The second-in-energy rotamer – in which the butyl group is tilted away from the flavin moiety– molecule is by 0.026 eV less stable (MP2/cc-pVDZ). The small energy difference between them make it possible that both rotamers coexist in thermal equilibrium, in experimental conditions - especially in polar solvent which should stabilize more polar non-H-bonded isomer (7D vs. 6.5D). To understand better a fast deactivation of the S₁ excited-state of molecule 1, three other molecules, 2, 3 and 4 were selected for calculations (Fig. 6). While the molecule 4 consists of just unsubstituted isoalloxazine skeleton, the remaining two, 2 ad 3, have an additional substituent – attached at the position 7 of flavin – with increasing electron donating character: phenyl (molecule 3) and trimethoxyphenyl (molecule 2). Note that in derivatives 2–4, the butyl substituent is replaced by the methyl group to study sole electronic effect of the step-by step substitution of the molecule 4. Moreover, 4 is an excellent reference (Fig. S2B), since its slow S₁-state deactivation (τ_s1 = 7 ns in acetonitrile) has been reported¹⁶.

The calculations were aimed to determine the geometry of the Fl derivatives in the electronic ground state S₀ and the excited states S₁(π,π*) and S₁(n,π*). Interestingly, the distances R₁(C₍₂₎-O) and R₂(C₍₄₎-O) were found to be substantially different in these states (Fig. 6).

Calculations show that for molecule 1 the twist angle (C-C-C-C dihedral) of the trimethoxyphenyl vs. isoalloxazine ring is approximately 39° in the minimum ground-state S₀, while both carbonyl bonds R₁(C₍₂₎-O) and R₂(C₍₄₎-O) are short, having length of 1.222 and 1.223 Å, respectively (see Table 3). Those geometrical parameters of 1 are very comparable to the derivatives: 2 and 3 (see Fig. 6) while the R₁ and R₂ distances also to 4. The calculated vertical excitation energies, ΔE^VE, to the lowest singlet excited states for molecules 1–4 are gathered in Table 2. According to these calculations, the S₀ → S₁ transition energy for H-bonded isomer of 1, ΔE^VE(S₀→S₁) of 2.76 eV (λ_abs = 450 nm, CC2/aug-cc-pVDZ), has a substantial oscillator strength, f of 0.2, which is the highest f value among all the S₀ → S_n transitions (up to n = 6). The S₀ → S₁(π,π*) transition is also the strongest for the remaining molecules studied: 2–4. What varies is the value of ΔE^VE(S₀ → S₁(π,π*)) which decreases in the series from 3.01 eV, for unsubstituted 4, through 2.83 eV, for phenyl-substituted 3, and 2.77 eV, for 7-trimethoxyphenylisoalloxazine 2 down to 2.76 eV for 1. In comparison to unsubstituted molecule 4, the presence of phenyl, in 3, and three methoxyphenyl groups, in 1 and 2, decreases the ΔE^VE value for the S₀ → S₁(π,π*) transition leaving the S₀ → S_n(n,π*) transitions almost unchanged. Both groups are strong π-electron donors^43,44 and they tend to stabilize the ¹π,π* excited states. Thus they lower either the vertical excitation energies, ΔE^VE(S₀→π,π*), or adiabatic energies, E^a, of the optimized (¹π,π*) excited state (see Tables 2 and 3). Similar substituent effect has been reported⁴⁵. As it is shown in Table S3, the presence of the π-electron donating methoxy group results in a shift of the electron density from the π occupied orbital localized on the trimethoxyphenyl to the π∗ unoccupied orbital localized solely on the flavin.

Table 3 shows that the state S₁(π,π*) has substantially high dipole moment µ_e, thus one can expect that the use of polar solvent can further stabilize this state.

The mechanism of the singlet excited-state deactivation

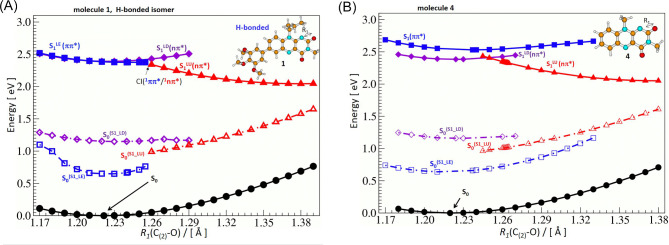
The S₀ ground state energy landscape of the molecule 1 consists of two close-in-energy minima related to H-bonded and non-H-bonded isomers (see Table 2), while the derivatives 2–4 have a single global minimum. All the minima have short C=O double bonds – with an increasing potential-energy when elongating one of the carbonyl bonds (see black filled circles in Fig. 7). The excited-state energy landscape is much more diverse and chemical structure dependent.

Fig. 7.

Excited-state (S₁) potential-energy profile of 1 (A) and 4 (B) (calculated with the ADC(2)/cc-pVDZ method) plotted as a function of the R₁(C₍₂₎-O) distance to describe the S₁-state deactivation process through a cascade of the S₁ states leading toward the region with a low S₀-S₁ state energy gap. Solid lines and full symbols denote the ground (S₀), and excited S₁-state minimum energy profiles. Dashed lines and open symbols (S₀^S1) denote energy profiles of the ground S₀ state calculated at the optimized geometry of the given S₁ state. Black circles indicate the S₀ state, blue squares - S₁(π,π*), violet diamonds- S₁^LD(n,π*), and red triangles - S₁^LU(n,π*).

The electronic structure of molecule 1 is determined mainly by its ground S₀ state and three singlet excited–state forms: one ¹ππ* and two ¹nπ* states. These excited–state equilibrium geometries, optimized without any symmetry constraint, differ mainly in terms of carbonyl bond elongation and by the C-C and C-N bond distances in their close vicinity, as in thymine⁴⁶. The twisting angle of the trimethoxyphenyl moiety vs. flavin is close to 40^o for those excited-state forms.

Each of the ¹nπ* state minima is characterized by the elongation of one of the C-O carbonyl bonds present in flavin moiety (as shown in Fig. 6). Each C-O elongation is related to the excitation of an electron from the orbital “n” lone pair of the given oxygen atom – localized on this C-O bond – to the antibonding orbital π* delocalized throughout the molecule. The described excitation can be traced in Table S3, where it is shown that both n and π* orbitals are localized on flavin which means that both the S₁(n,π*) states are the local states also of unsubstituted flavin. What is different for the S₁^LE(π,π*) excited state minimum is that the electron is photoexcited from the occupied π orbital localized also on trimethoxyphenyl substituent to the π∗ orbital localized exclusively on the flavin. This way, the π-electron donating character of the methoxy groups is seen as it pushes the electron density from phenyl towards flavin, in the S₁^LE(π,π*) state, favoring its stabilization vs. the S₁(n,π*) states.

We distinguish two: S₁^LD(n,π*) and S₁^LU(n,π*) singlet ¹nπ* excited states, each associated with the elongation of a different C-O bond. At the S₁^LD(n,π*) minimum, the C₍₄₎-O bond is much longer than the C₍₂₎-O bond (R₂ > R₁) while the proximal C₍₄₎-C and C₍₄₎-N₍₃₎ bonds are shorter than in the S₀-state geometry. In the case of the S₁^LU(n,π*) minimum, the C₂-O bond is much longer (R₂ < R₁) and the C₍₂₎-N₍₁₎ and C₍₂₎-N₍₃₎ bonds get substantially shrinked. To trace the excited–state decay mechanism, we will examine molecule 1 through computational studies and compare it with the profiles obtained for unsubstituted derivative 4 (molecules 2 and 3 are provided in Figure S3).

Upon photon absorption, the first locally excited state S₁^LE(π,π*) is populated as the S₀→S₁ transition is characterized by a high oscillator strength (Table 2). Initially, the system relaxes to the equilibrium form of this S₁^LE(π,π*) state, as its geometry closely resembles the geometry of the S₀-state, especially in terms of two short C-O bonds (see the blue curve Fig. 7A, for molecule 1, and Fig. 7B, for molecule 4). The S₁^LE(π,π*) state is predicted to be a fluorescent state, with the fluorescence energy, E_fl., for molecule 1 being 1.90 eV (λ_fl.^calc = 653 nm) for H-bonded isomer obtained by single-point CC2/aug-cc-pVDZ. However, the profile of the S₁(π,π*) state is very shallow (see blue filled squares along the solid line in Fig. 7A) with a tiny excited-state barrier of 0.001 eV (at R₁ = 1.255 Å). Behind the barrier, only two additional points were optimized in this state with slightly lower energy (up to R₁ = 1.258 Å) and further attempts in optimization of the first singlet state at little larger distances produced the molecule in the S₁^LU(n,π*) state. This is an indication that the molecule finds the CI region between the two excited states. We tried, however, to find more evidence of such a situation, and additional calculations were performed. (i) Optimization of the second excited state was performed at the few distances R₁ > 1.258 Å and those calculations ended up in finding two almost degenerate states: S₁^LE(π,π*) and S₁^LU(n,π*) suggesting existence of the crossing point. (ii) Second, the single-point calculations of the few lowest excited states were performed on top of the profiles of the S₁^LE(π,π*) and S₁(n,π*) exited states (LU and LD, Fig. S4). The S₁^LE(π,π*) state calculated with the geometry of the S₁^LU(n,π*) state for molecule 1 is quite close in energy to the lower S₁^LU(n,π*) state indicating the proximity of the region CI(¹ππ*/¹nπ*), at a distance of ~ 1.26 Å (See Fig. S4B).

Thus, we can conclude, that the S₁^LE(π,π*) will structurally evolve to populate equilibrium of the S₁(π,π*) state. In its proximity is located a convenient crossing point S₁(π,π*)/S₁^LU(n,π*) (Fig. 7A). The path S₁(π,π*)→S₁^LU(n,π*) is supported by close energy curve calculated S₁^LU(n,π*) for geometry of S₁(π,π*). This is not the case for the alternative path S₁(π,π*)→S₁^LD(n,π*), since the S₁^LD(n,π*) state calculated on top of the profile S₁^LE(π,π*) lands over 1 eV higher in energy (Fig. S4) that allows us to exclude it from the S₁(π,π*) depopulation mechanism.

We propose that S₁(π,π*)/S₁^LU(n,π*) conical intersection is responsible for short S₁(π,π*) state lifetime observed in the experiment (0.5 ps). Formed species in the S₁^LU(n,π*) state shows up evolution of the geometry of the molecule 1 due to the elongation of the C₍₂₎-O bond up to 1.38 Å (red curve, Fig. 7A). As the molecule relaxes in the S₁^LU(n,π*) state toward its minimum, internal conversion S₁^LU(n,π*)→S₀ becomes more probable since the respective energy difference ΔE(S₁^LU(n,π*), S₀) gets smaller down to ~ 0.4 eV for the given equilibrium geometry of the S₁^LU(n,π*) state (Fig. 7A). Such a behavior of the ¹nπ* excited state related to the C₍₂₎-O bond elongation as an important driving coordinate toward the conical intersection region has been reported for thymine⁴⁶. Consequently, one can expect a short excited–state lifetime τ_S1(n,π*) determined for molecule 1. The nascent molecule in the S₀-state undergoes relaxation by shortening the C₍₂₎-O bond, thereby recovering the initial structure and completing the photocycle.

Observing the changes in a series of the excited-state profiles for molecules 4, 3, 2 and 1 (Figure S3) one can notice that the S₁^LD(n,π*) and S₁^LE(π,π*) excited states become more proximal to each other in terms of energy what makes the S₁^LE(π,π*) state depopulation faster in 1. For instance, in the molecule 4 pattern of the excited-states energy profiles are less convenient for the deactivation, since equilibrium of the S₁(π,π*) state is more stable. The crossing point S₁(π,π*)/S₁^LU(n,π*) is substantially less convenient to reach for 4 in comparison to 1. The energy barrier is about 0.06 eV, at the C₍₂₎-O distance of ~ 1.29 Å for 4 (extended by 0.05 Å from its minimum) and the S₁(π,π*) state profile is monotonously increasing its energy towards longer C₍₂₎-O distances (Fig. S5). In 4 the access to the CI(¹ππ*/¹nπ*) point is more difficult, which rationalizes the experimental data showing a long S₁(π,π*) excited-state lifetime (7 ns)¹⁶.

We should emphasize that calculations are performed in the gas phase, while time-resolved experiments were performed in polar solvent as acetonitrile (compound 1 is not soluble in nonpolar solvent as n-hexane). One can expect that the selection of polar solvent influences the course of the potential-energy profiles of polar intermediates (see dipole moments in Table 3). Thus a direct comparison between the gas-phase calculation and experimental data recorded in the polar solvent is not straightforward. On the other hand, the calculations develop the mechanistic picture for ¹(π,π*)→¹(n,π*) path explaining a very fast ¹(π,π*) deactivation in 1.

The butyl group in molecule 1, as a weak electron-donor, has a weak influence on energy potential profiles (Figure S3) upon comparison of molecule 1 (with butyl group) and molecule 2 (with methyl group) at position N₍₁₀₎. Thus, the presence of trimethoxyphenyl substituent is a key factor influencing the unique photophysics of molecule 1. This conclusion corresponds to experimental values as other similar 10-butylisoalloxazines are characterized by usual “flavin” fluorescence parameters¹⁹

Conclusions

According to theoretical predictions for molecule 1, the presence of a trimethoxyphenyl group in flavin opens the ¹(π,π*)→¹(n,π*) deactivation channel. The electron donating group present in the studied molecules levels off the fluorescent ¹(π,π*) state relative to the dark ¹(n,π*) state, making S₁-state depopulation easier. The change in geometry occurring in the ¹(n,π*) state is related to the stretching of one of the C=O carbonyl bonds present in the isoalloxazine moiety. Consequently, there is a substantial decrease in the S₁(n,π*)-S₀ state energy gap, making the internal conversion channel effective and responsible for ¹(n,π*) excited-state depopulation to the S₀ ground state. This deactivation mechanism is unique and complements rare fast deactivation processes among flavin derivatives, e.g. “butterfly” bending motion described for partially or fully reduced isoalloxazine derivatives⁴⁷.

The effective internal conversion ¹(π,π*)→¹(n,π*) explains the experimental data obtained for molecule 1: a substantial shortening in the measured excited-state lifetimes (on the order of picoseconds for molecule 1) compared to unsubstituted flavins as 3,10-dimethylisoalloxazine 4 (on the order of nanoseconds) as well as other 7-aryl-10-butylisoalloxazines¹⁵. The laser-pulse induced photoprocess in molecule 1 occurs within a 15 ps time window in acetonitrile. The mechanism ¹(π,π*)→¹(n,π*)→S₀ is experimentally confirmed as the photoexcited ¹(π,π*) state population decays mainly through the ¹(n,π*) excited state intermediate, followed by recovery to the S₀ ground state. The absence of triplet excited state in the mechanism is also confirmed by the transient absorption spectroscopy. The emerging photoprocess is described by:

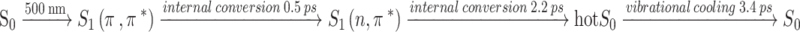with a minor contribution of fluorescence (yield Φ_f = 2.6 × 10⁻⁴). It should be mentioned that a significant weakening of fluorescence was also observed by the introduction of the 3,4,5-trimethoxyphenyl group into position 7 for 1,3-dimethylalloxazine and 5-phenyl-3,10-dimethyl-5-deazaisoalloxazine.¹⁵ Unique properties of these derivatives can be used in applications that require minimal side-reactions caused by the singlet oxygen (¹O₂) or for organocatalysis to avoid participation of an excited form of flavin at all.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

S. N.: data aquisition, apparatus construction, writing the manuscript & editing, N. V.: data aquisition, M. S. conceptualization, writing the manuscript & editing, T. T. : synthesis, E. S. : synthesis, R. C.: conceptualization, synthesis, writing the manuscript & editing, M. R.: calculations, conceptualization, visualization, writing the manuscript & editing, G. B.: data aquisition, formal analysis, conceptualization, visualization, writing the manuscript & editing All authors reviewed the manuscript.

Data availability

The datasets generated during the current study are available from the corresponding author on request.

Declarations

Competing interests

The authors declare no competing interests.