Abstract
Here, first-principles calculations have been employed to make a comparative study on structural, mechanical, electronic, and optical properties of new Ca3MF3 (M = As and Sb) photovoltaic compounds under pressure. The findings disclose that these two systems possess a direct band gap, showcasing a large tunable range under pressure, effectively encompassing the visible light spectrum. Adjusting various levels of hydrostatic pressure has effectively tuned both the band alignment and the effective masses of electrons and holes. Both compounds were initially identified as brittle materials at 0 GPa pressure; however, as the pressure increases, they transform, becoming highly anisotropic and ductile. Due to the material's mechanical robustness and enhanced ductility, as evidenced by its stress-induced mechanical properties, the Ca3MF3 (M = As and Sb) material shows potential for use in solar energy applications. Furthermore, as the influence of external pressure increases, the absorption edge seems to move slightly towards lower energy region. Optical properties show that the materials studied might be used from several optoelectronic devices in the visible and ultraviolet range area. Our findings show that pressure considerably influences the physicochemical properties of Ca3MF3 (M = As and Sb) compounds, which is a promising feature that can be useful for optoelectronic and photonic applications, for instance, light-emitting diodes, photodetectors, and solar cells.
Keywords: First-principles study, A3BX3 photovoltaic compound, Pressure effect, Optoelectronic properties, Mechanical properties
Graphical abstract
Highlights
-
•
Changes in the physical properties of Ca3AsF3 and Ca3SbF3 were observed in the range of hydrostatic pressures (0–50 GPa).
-
•
As pressure rises, there is a consistent decrease observed in the lattice parameter, volume, and bond lengths.
-
•
Effective mass values below 1.5m0 for Ca3MF3 (M = As and Sb) compounds suggest high mobility for the charge carriers.
-
•
The shifting of the dielectric function peak to lower photon energies is observed with the growth of pressure.
-
•
The crystal elastic constants satisfy the Born-stability criteria, confirming mechanical stability.
1. Introduction
Solar energy is among the most accessible and cost-effective long-term renewable alternatives currently available. Solar photovoltaics PV is a modern power technology for capturing solar energy and transforming it into electrical energy. The identification of novel optically anisotropic compounds is pivotal for the advancement of optoelectronic devices, a field that has recently garnered significant interest [[1], [2], [3]]. Two-dimensional (2D) materials such CdS monolayer [4], Ga-doped AlN monolayer [5], bilayer CdS [6], BN bilayer [7], GeSe, and black phosphine are regarded as promising substances for energy-related purposes including photovoltaic, optoelectronic and thermoelectric devices owing to their substantial less toxicity, optical anisotropy, moderate direct band gap, novel electronic properties and comparatively elevated mobility of charge carriers [[8], [9], [10], [11], [12]]. However, there is a shortage of materials exhibiting a direct band gap. Monolayer transition metal dichalcogenides, such as MoS2 and WSe2, are recognized for possessing direct band gap; nonetheless, their carrier mobility is relatively constrained. Halide perovskite materials based on lead, for instance, MAPbX3 (MA = CH3NH3+), have become increasingly prominent in the photovoltaic (PV) realm due to its remarkable PCE, appropriate band gaps, high mobility of photoinduced carriers [[13], [14], [15], [16]], and effective absorption of visible light [17] and extensive research has been conducted on it [18,19]. Lately, there has been considerable attention directed towards enhancing the efficiency of solar cells (SC) by utilizing the inorganic A3BX3 cubic photovoltaic compound family. Within this compound family, Mg3NF3 (pm m) exhibits a strong probability of transitions between states near the edge of the p-s band, that correlates strongly with its outstanding photovoltaic (PV) performance, whereas Ba3PI3, Ba3AsI3, and Ba3SbI3 emerge as stable PV materials, boasting an impressive efficiency of 25.9 %.
Hybrid perovskites have yielded solar cells exhibiting significant stability and remarkable power conversion efficiency in a short timeframe. However, the photo-physics of hybrid perovskite materials remains complicated [20], leaving many doubts unresolved regarding their structure-property relationships. Understanding how alterations in lattice structure affect the electronic configuration of perovskites is essential for identifying prospective perovskite and for controlling their electronic structure through geometrical and compositional manipulation. It might further help in understanding the evolution of electronic changes resulting from electron-phonon coupling on an ultrafast timescale and the impact of pressure variations on the electronic structure due to pressure-induced alterations in the energy surface of the ground and excited states [21]. To investigate the available stable crystal structures of perovskite, and their dependence on the elemental composition and selected geometrical parameters, we performed DFT simulations to study the impact of such changes in the crystal structure of perovskite on the electronic characteristics.
Regulating pressure throughout material production routes is a recognized strategy for introducing an alteration in the physical interactions and bonds within the crystal lattice of a structure [22]. Recent years have seen an increasing interest in examining the impact of pressure on metal halide perovskites [[23], [24], [25]]. Many experiments have used diverse strain application methods on halide perovskites, such as hydrostatic pressurization [[26], [27], [28]], electrostriction [29], annealing [30,31], applied pressure through van der Waals force [32], pressure through thermal expansion mismatch [33], heat-induced change of substrate conversion phase, among others [34]. Significant efforts have been devoted to unraveling the structure-property connections of perovskites [[35], [36], [37]], to our knowledge, there exists a lack of systematic research endeavors examining the influence of pressure variations on the electrical structure and characteristics of metal halide perovskites [38]. Faghihnasiri et al. [39] indicated that in CH3NH3PbX3 (X = Cl, Br, I) perovskites, the band gap broadens with the imposition of tensile strain, however, they display diverse responses under compressive strain. First-principles simulations based on DFT were employed to investigate the physical properties of the non-toxic perovskite compounds Sr3BCl3 (B = As, Sb) [40] at pressures reaching 25 GPa and the findings indicate that these materials have potential for versatile applications in optoelectronic technologies. Joifullah et al. [41]conducted computational analysis on Sr3PX3 (X = Cl, Br) and observed a red-shift in the spectral lines, indicating a shift toward lower energy, which suggests promising characteristics for optoelectronic applications.
As the majority of a material's physical attributes hinge on its phase stability, there is considerable interest in scrutinizing these stabilities prior to exploring other characteristics [42,43]. Prior to paying excessive experimental costs, utilizing efficient and economical software to conceptually investigate such materials is a sensible strategy [44]. Thus, this investigation centers on a comparative examination employing the Quantum Espresso simulation software to analyze the pressure-induced physical characteristics of our suggested Ca3MF3 (M = As and Sb) structural configurations. Changes in the physical properties of Ca3AsF3 and Ca3SbF3 were observed under various range of hydrostatic pressures (0–50 GPa). Through the modifying of its optoelectronic properties via hydrostatic pressure, one can design this photovoltaic compound to be a more viable candidate for use in optoelectronic and photovoltaic purposes.
2. Computational methodology
The structural and optoelectronic characteristics of Ca3AsF3 and Ca3SbF3 were computed utilizing Density Functional Theory (DFT) as executed in the Quantum Espresso software [45]. The calculations employed ultrasoft pseudopotentials [46] and the GGA-PBE functional [47] for the exchange-correlation energy. The input parameter contained the essential starting configurations, which encompassed the Brillouin zone grid, crystal structures, lattice constants, and kinetic cut-off energy. To improve the appropriateness and effectiveness of both structures, the kinetic energy cut-off and charge density cut-off were fixed at 60 Ry and 600 Ry, respectively. In the lattice optimization vc-relax computation, the k-point dimensions were set to 8 × 8 × 8. The optimization technique used to reduce the structure to its least energetic form which is the Broyden-Fletcher-Goldfarb-Shanno method [48]. The self-consistent field (SCF) computations were designated with a maximum force tolerance of less than 0.01 eV/Å and a convergence threshold of 10−6 a. u. In the relaxation computation for the ionic minimization, the tolerance of the force convergence was set to 10−3 a. u. The inaccuracy of band gap estimation in materials with d or f electrons is well recognized in GGA-PBE approximation. The Tran-Blaha modified Becke-Johnson (TB-mBJ) approximation [49] is employed in the Wien2k [50] code to analyze electronic properties. Utilizing a linearized augmented plane-wave basis set with lmax = 10 and RMTKmax = 7, we achieved convergence for both charge and energy. The first order time-dependent perturbation theory was employed to assess dynamic stability and investigate the optical characteristics of materials [51]. Subsequently, the examination of the photon energy spectrum resulted in the determination of absorption peaks in the complex dielectric function. The fundamental equation for calculating optical absorption coefficient is the complex dielectric function, represented as = + . The other optical features including absorption α(ω), reflectivity R(ω), refractive index n(ω), and extinction coefficient k(ω) are calculated by evaluating dielectric function using the formulas:
| (1) |
| (2) |
| (3) |
| (4) |
The elastic constants for the current investigation were calculated via the Thermo-PW package. The optimized structure of both materials was represented by VESTA software [52].
3. Results and discussions
3.1. Structural properties
Ca3MF3 (M = As, Sb) is a novel fluoride photovoltaic compound with a cubic structure while belonging to the space group pm m (#221) [53]. Fig. 1a shows the 2d view of Ca3MF3 (M = As, Sb) and the 3d representation of its structure is in Fig. 1b. The unit cells of these materials comprise a total of seven atoms. In this unit cell, the Ca atoms are located in the 3d Wyckoff site and at fractional coordinates of (0.5, 0, 0). The M (M = As, Sb) atoms are located at the 1a Wyckoff site with fractional coordinates (0, 0, 0), whereas the F atoms are found at the 3c Wyckoff site with fractional coordinates (0, 0.5, 0.5). When Ca2+ ions bond with two As3−/Sb3− ions and four F1− ions, CaM2F4 octahedra are created through the sharing of their corners and outer edges. As3+ creates AsCa6 octahedra by sharing corners with six distinct Ca2+ ions through covalent bonding. In Table 1, the optimized key geometric factors, such as optimized lattice constant (a0), unit cell volume (V0), bulk modulus (B), pressure derivative of bulk modulus (), and the ground state energy (E0) are listed. Ca3AsF3 has a smaller unit cell compared to Ca3SbF3. The Murnaghan equation of state [54] was used to calculate the energy variation (in terms of volume contrast):
| (5) |
In Fig. 2a and b, the energy vs. volume graph provides both materials' structural stability (see Fig. 2) (see Table 2). For Ca3AsF3, the ground state energy E0 of −392.65 Ry is located at the volume V0 = 153.13 Å3, which corresponds to a0 = 5.35 Å. Similarly, for Ca3SbF3, E0 of −391.94 Ry is presented at V0 = 173.74 Å3, which corresponds to a0 = 5.58 Å. The computed values of lattice constant for these compounds are comparable with the available literature [53]. Table 2 illustrates alterations in lattice parameters and volume due to pressure changes. It's observable that both the lattice constants and volumes decrease as pressure rises, as displayed in Fig. 3(a–b). Table 3 represents the bond lengths under various hydrostatic pressures. Since the volume of unit cells decreases due to increase in pressure levels, the bond lengths being directly correlated to the volume, also decrease as the pressure increases. As a result, this induces compressional strain within the lattice networks of Ca3AsF3 and Ca3SbF3, consequently reducing the band gap which alters the electronic characteristics (see Fig. 3).
Fig. 1.
Constructed (a) 2D and (b) 3D crystal structure of Ca3MF3 (M = As and Sb) compounds.
Table 1.
Structural parameters of the unit cell and band gap for cubic Ca3MF3 (M = As and Sb) compounds.
| Optimized Structural Parameters | Ca3AsF3 |
Ca3SbF3 |
||
|---|---|---|---|---|
| Present Work | Other Cal. | Present Work | Other Cal. | |
| Lattice constant (a0) in Å | 5.35 | 5.29 [53] | 5.58 | 5.35 [53] |
| Optimum volume V0 in Å3 | 153.13 | 173.74 | ||
| Bulk modulus (B) in GPa | 43.93 | 35.16 | ||
| Pressure derivative of bulk modulus B′ | 3.98 | 3.87 | ||
| Ground state energy E0 in Ry | −392.65 | −391.94 | ||
| Band Gap Eg (Γ- Γ) in eV | 2.27 (PBE) | 3.36 (HSE) [53] | 2.19 (PBE) | 3.00 (HSE) [53] |
Fig. 2.
Volume optimization of (a) Ca3AsF3 and (b) Ca3SbF3.
Table 2.
Calculated values of lattice constant (a) and unit cell volume (V) of Ca3AsF3 and Ca3SbF3 compounds under pressure.
| Phase | Compound | Calculated data | Pressure (GPa) |
|||||
|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | |||
| Cubic (pm m) | Ca3AsF3 | a (Å) | 5.35 | 5.10 | 4.93 | 4.81 | 4.71 | 4.63 |
| V (Å3) | 153.13 | 132.65 | 119.82 | 111.28 | 104.49 | 99.25 | ||
| Ca3SbF3 | a (Å) | 5.58 | 5.31 | 5.12 | 4.98 | 4.87 | 4.77 | |
| V (Å3) | 173.74 | 149.72 | 134.22 | 123.51 | 115.50 | 108.53 | ||
Fig. 3.
Pressure-induced reduction of lattice constant and unit cell volume of Ca3MF3 (M = As and Sb).
Table 3.
Determined bond length in Ca3AsF3 and Ca3SbF3 cubic compounds under various hydrostatic pressures.
| Pressure (GPa) | Bond length (Å) |
|||||
|---|---|---|---|---|---|---|
| Ca3AsF3 |
Ca3SbF3 |
|||||
| Ca-F | As-F | Ca-As | Ca-F | Sb-F | Ca-Sb | |
| 0 | 2.68 | 3.78 | 2.67 | 2.79 | 3.94 | 2.78 |
| 10 | 2.55 | 3.61 | 2.55 | 2.65 | 3.75 | 2.65 |
| 20 | 2.47 | 3.49 | 2.46 | 2.56 | 3.62 | 2.55 |
| 30 | 2.40 | 3.40 | 2.40 | 2.49 | 3.52 | 2.48 |
| 40 | 2.35 | 3.33 | 2.35 | 2.43 | 3.44 | 2.43 |
| 50 | 2.31 | 3.27 | 2.31 | 2.39 | 3.38 | 2.38 |
3.2. Electronic properties
Designing materials for specific applications in electronics, optics, and energy devices necessitates an understanding of their electronic features, such as band structure and density of states. The generalized gradient approximation (GGA-PBE) is generally inadequate in correctly predicting band profiles and band gaps for systems because of the self-interaction effect and limited capacity to capture highly localized states [55]. Hence, the TB-mBJ approximation has been utilized to accurately analyze electronic features of Ca3AsF3 and Ca3SbF3. TB-mBJ functional is a semi-local functional that includes certain non-local information such as gradient of electron density and kinetic energy density, in contrast to GGA-PBE functional, which happens to be a local functional [49]. Nevertheless, each one of the solutions has its limitations. However, current study considered the lack of accuracy of the bandgap obtained by the GGA approach and rectified by employing the TB-mBJ functional. The electronic band structure of two different materials Ca3AsF3 and Ca3SbF3 are calculated at various pressure condition, unstressed (0 GPa) and stressed (10–50 GPa) for better perceive of individual electronic properties of both compounds. Electrons behavior along the symmetric axes of the Brillouin zone (X-R-M--R) has a great impact on the energy dispersion of material. In accordance with semiconductor theory, comprehending the band structures near the Fermi level (EF) is crucial for understanding the physical characteristics of materials. Hence, the band structures of Ca3MF3 in proximity to the EF are presented in Fig. 4, Fig. 6a via TB-mBJ functional and Fig. 5, Fig. 7a via GGA-PBE functional in an unpressurized environment for Ca3AsF3 and Ca3SbF3, respectively. The figures clearly demonstrates that both materials exhibit a direct band gap as conduction band minimum (CBM) and valence band maximum (VBM) both are in point. For a system that is considered for optoelectronic device application, it is essential to possess direct bandgap [56]. Moreover, a direct band gap facilitates direct optical transitions with minimal alteration in the wave vector, thereby potentially boosting the efficiency of light absorption. The bandgap energy (Eg) for Ca3AsF3 (Ca3SbF3) is determined to be 3.54 (3.20) eV via TB-mBJ functional and 2.27 (2.19) eV via GGA-PBE functional under unstressed conditions.
Fig. 4.
Obtained band structure profile of Ca3AsF3 via TB-mBJ functional at various pressures: (a) 0 GPa, (b) 10 GPa, (c) 20 GPa, (d) 30 GPa, (e) 40 GPa, and (f) 50 GPa.
Fig. 6.
Obtained band structure profile of Ca3SbF3 via TB-mBJ at different pressures: (a) 0 GPa, (b) 10 GPa, (c) 20 GPa, (d) 30 GPa, (e) 40 GPa, and (f) 50 GPa.
Fig. 5.
Obtained band structure profile of Ca3AsF3 via GGA-PBE functional at various pressures: (a) 0 GPa, (b) 10 GPa, (c) 20 GPa, (d) 30 GPa, (e) 40 GPa, and (f) 50 GPa.
Fig. 7.
Obtained band structure profile of Ca3SbF3 via GGA-PBE functional at different pressures: (a) 0 GPa, (b) 10 GPa, (c) 20 GPa, (d) 30 GPa, (e) 40 GPa, and (f) 50 GPa.
The computed bandgaps of Ca3MF3 (M = As, Sb) compounds at various hydrostatic pressures are shown in Fig. 4, Fig. 5, Fig. 6, Fig. 7. It is observable that the bandgap energy of both compounds diminishes gradually as pressure goes up from 0 to 50 GPa, suggesting effective adjustability of the bandgap via pressure. Based on the Shockley–Queisser theory, an optimal optical absorption edge falls within the bandgap energy range of 1.3–1.5 eV, which is advantageous for enhancing the photoelectric performance of compounds and boosting the conversion efficiency of solar cells. The computed outcomes indicate that applying the appropriate compressive force can achieve the optimal bandgap energy (1.3–1.5 eV) for both materials, suggesting that pressure is an effective method to enhance the power conversion efficiency of Ca3AsF3 and Ca3SbF3 compounds. Due to increasing pressure from 0 to 50 GPa, the Eg value reduces from 3.54 to 1.47 eV via TB-mBJ and 2.27 to 0.37 eV via GGA-PBE functional for Ca3AsF3. The same behavior is seen for Ca3SbF3 in Fig. 6, Fig. 7, here at 50 GPa bandgap energy Eg is reduced to 0.95 eV via TB-mBJ and 0.11 eV via GGA-PBE functional. Fig. 8 illustrates that for both materials, the band gap diminishes linearly with increasing pressure. Moreover, the direct bandgap behavior uniformity remains unchanged under all applied pressure in both materials, indicating the possibility of both materials to be used in enhancing the efficiency of the solar cell. When the band gap decreases, the movement of electrons from the VB to the CB becomes very efficient which enhances light absorption and conductivity, this in turn makes materials more suitable for use in optoelectronics. Furthermore, as the Fermi level of the studied compounds is located closer to their valence bands, it is highly likely that the materials are p-type semiconductors.
Fig. 8.
The pressure-induced band gap narrowing of Ca3AsF3 and Ca3SbF3.
In this work, the band gap characteristics of Ca3AsF3 and Ca3SbF3 compounds were evaluated in terms of orbital contributions in the context of the Partial Density of States analysis. This section refers to the evaluation of orbital contributions as part of the analysis of the band gap features of studied compounds. The observations made on the results obtained from analysis of PDOS structures as shown in Fig. 9, Fig. 10, both for unpressurized and pressurized states of Ca3MF3 (M = As, Sb), indicated that different pressures led to significant changes in the distribution of electronic states at the band edges. These alterations involved changes in energy levels, modifications in orbital properties, and variations in the density of states, highlighting how pressure-induced structural changes affect the behavior of semiconductors. Fig. 9(a–f) and 10 (a-f) demonstrate that, for Ca3AsF3 (Ca3AsF3), the major contributions in the valence band (VB) originate from As-4p (Sb-5p) with a small contribution from Ca-3p and F-2p. In contrast, Ca-3p is the primary contributor in the conduction band (CB), with small contributions from Ca-4s and F-2p. The figures clearly shows that the shift of Ca-3p states in the direction of Fermi level with rising pressure is primarily accountable for altering the electronic band gap for both investigated materials. Increasing hydrostatic pressure increases the hybridization between As-4p (Sb-5p) and Ca-3p orbitals, leading to closer proximity of the CBs to the EF and a reduction in the band gap. In addition, the pressure-induced reduction in the Ca-As (Sb), Ca-F, and As-F (Sb-F) bond length (Table 3) may facilitate the hybridization of As-4p (Sb-5p) and Ca-3p orbitals within CB. Consequently, the electronic band gap of Ca3AsF3 (Ca3AsF3) reduces from 3.54 (3.20) to 1.47 (0.95) eV via TB-mBJ and 2.27 (2.19) to 0.37 (0.11) eV via GGA-PBE functional. Therefore, within the constituent Ca, As (Sb), and F atoms, the band gap mostly originates from the hybridization of electronic states between the Ca and As (Sb) atoms.
Fig. 9.
Calculated PDOS profile of novel Ca3AsF3 perovskite under pressure.
Fig. 10.
Calculated PDOS profile of novel Ca3SbF3 cubic perovskite under pressure.
Fig. 11(a–b) illustrates Total Density of States (TDOS) plots for Ca3MF3 (M = As, Sb), indicating that with increasing pressure, the conduction states move towards decreased energy levels more significantly than the valence states moving towards increased energy levels. This pressure-induced shift of energy states, which results in the band gap being tuned and decreasing, is also reflected in the band structure diagrams at the Γ point.
Fig. 11.
TDOS of (a) Ca3AsF3 and (b) Ca3SbF3 at different applied pressures.
The electron density reveals the charge distribution within the unit cell of materials, allowing for the determination of the type of chemical bonds present in those materials. Fig. 12(a–d) illustrates the charge density distribution of Ca3MF3 (M = As, Sb) at pressures of 0 and 50 GPa, depicted along the crystallographic plane (100). The electron density values are shown on the scale to the right, with red denoting high electron density and blue low electron density. At 0 GPa pressure, the spherical contour shapes surrounding the Ca and F atoms indicate ionic bonding between them, with no overlapping of the atoms (Fig. 12a & b). Conversely, the elliptical contour shapes around the Ca and As/Sb atoms exhibit slight overlapping, indicating a covalent bonding nature between them along the (100) direction. At a pressure of 50 GPa, the spherical contour shapes around the Ca and F atoms remain unchanged, indicating the continuation of ionic bonding (Fig. 12c & d). Overall, the shapes surrounding the Ca and As/Sb atoms get more elliptical as overlapping increases, signifying a stronger covalent bonding nature between them under pressure along the (100) plane.
Fig. 12.
Charge density distribution of Ca3MF3 (M = As and Sb) along (100) crystallographic plane at 0 and 50 GPa pressure.
3.3. Carrier transport properties
The effective mass of both holes (mh) and electrons (me) serves as a significant determinant of photovoltaic efficiency, greatly affecting carrier mobility, resistivity, and the optical sensitivity of free carriers. The effective masses of Ca3AsF3 and Ca3SbF3 were determined (Table 4) by fitting the VBM and CBM on the basis of the following formula [57]:
| (6) |
Table 4.
Effective mass of electron and hole, and ration of effective mass (D) of Ca3AsF3 and Ca3SbF3 under various pressure levels. The unit of mass is the electron rest mass m0.
| Pressure (GPa) | Ca3AsF3 |
Ca3SbF3 |
||||
|---|---|---|---|---|---|---|
| me | mh | D | me | mh | D | |
| 0 | 0.52 | 0.49 | 1.08 | 0.76 | 0.48 | 1.57 |
| 10 | 0.49 | 0.35 | 1.41 | 0.60 | 0.34 | 1.76 |
| 20 | 0.44 | 0.26 | 1.68 | 0.49 | 0.25 | 1.97 |
| 30 | 0.38 | 0.21 | 1.86 | 0.41 | 0.19 | 2.20 |
| 40 | 0.33 | 0.16 | 2.07 | 0.33 | 0.15 | 2.25 |
| 50 | 0.28 | 0.13 | 2.14 | 0.28 | 0.12 | 2.28 |
The wave vector along different axes, the reduced Planck constant, and the energy dispersion relation function are represented by the symbols k, ℏ, and ε(k), respectively. Typically, a greater dispersion at the bottom (top) of the CB (VB) corresponds to a smaller effective mass for electrons (holes), facilitating electron (hole) diffusion [58]. As pressure increases, mh and me in Ca3MF3 (M = As and Sb) compounds steadily decline (Fig. 13). As the effective mass reduces, electrons and holes in the absorption layer can diffuse more readily to the transport layer. Therefore, it can be inferred that applying hydrostatic pressure can enable carrier migration and increase the PCEs of Ca3MF3 cells. Since the effective mass is less than 1.5m0 for both materials, this suggest that Ca3AsF3 and Ca3SbF3 can be considered feasible materials for high-mobility solar applications.
Fig. 13.
Calculated effective masses of holes (mh) and electrons (me) of Ca3MF3 (M = As and Sb) under all applied pressure (0–50 GPa).
One of the foremost factors determining the photocatalytic property of a semiconductor is the rate at which photo-generated charge carriers are separated and diffused. If the effective mass of photo-generated carriers is reduced, they are more likely to reach surface response sites within their lifespan, thereby enhancing photocatalytic activity [59,60]. While the absolute value of the effective mass of a photoinduced carrier holds significance, the relative ratio of effective masses, which dictates the recombination rate of carriers, could potentially have a crucial function in separating the carriers. The relative ratio of effective mass (D) is determined through following formula [61,62].
| (7) |
For the D value that significantly deviates from 1, the mobility difference between electrons and holes becomes more considerable, thus, the rate of recombination of photo-generated pairs will also be reduced. As shown by the obtained results in Table 4, D values significantly differ from 1 at rising pressure for both materials. Hence, in the pressurized conditions Ca3MF3 (M = As and Sb), becomes more effective in the pair separation and has lower electron-hole recombination because of smaller effective mass compared to the unpressurized system.
3.4. Mechanical properties
The elasticity properties of solids are vital that create a considerable relationship between mechanical features. They provide significant insight into the inner forces of solids, thus giving essential details about their stability and power. These features include various factors, such as bulk and shear modulus, Young's modulus, the combination of flexibility and brittleness, as well as directionality. Concerning the material's mechanical properties, elastic constants of Ca3MF3 (M = As and Sb) are effectively used to determine its reaction to various pressures and tensions. The elastic constant Cij such as C11, C12, and C44 is determined over a pressure range (Table 5), which spans from 0 to 50 GPa in the context of events that apply an appropriate strain tensor that deforms the cubic unit cell. In order to ensure mechanical stability, this constant should safely comply with the equational inequalities that are often described as Born stability criteria [63]:
| C11 > 0, C44 > 0, C11-C12 > 0, C11 + 2C12 > 0 | (8) |
Table 5.
Calculated value of elastic constants (Cij), Cauchy pressure (Cp), Crystal stiffness (Cs), and Kleinman parameter (ζ) in Ca3MF3 (M = As and Sb) compounds under different hydrostatic pressures.
| Pressure (GPa) | Compound | C11 | C12 | C44 | Cp | Cs | ζ |
|---|---|---|---|---|---|---|---|
| 0 | Ca3AsF3 | 97.85 | 15.15 | 24.94 | −9.79 | 41.35 | 0.30 |
| Ca3SbF3 | 79.45 | 11.05 | 18.03 | −6.98 | 34.20 | 0.29 | |
| 10 | Ca3AsF3 | 191.92 | 25.94 | 24.37 | 1.57 | 82.99 | 0.29 |
| Ca3SbF3 | 173.03 | 21.96 | 16.62 | 5.34 | 75.53 | 0.28 | |
| 20 | Ca3AsF3 | 270.91 | 35.59 | 22.12 | 13.47 | 117.66 | 0.28 |
| Ca3SbF3 | 249.05 | 30.90 | 14.08 | 16.82 | 109.07 | 0.27 | |
| 30 | Ca3AsF3 | 350.20 | 47.75 | 18.96 | 28.79 | 151.22 | 0.28 |
| Ca3SbF3 | 322.54 | 40.25 | 10.74 | 29.51 | 141.14 | 0.27 | |
| 40 | Ca3AsF3 | 422.00 | 54.18 | 15.14 | 39.04 | 183.91 | 0.28 |
| Ca3SbF3 | 390.61 | 48.38 | 6.91 | 41.47 | 171.11 | 0.27 | |
| 50 | Ca3AsF3 | 488.78 | 63.22 | 10.78 | 52.44 | 212.78 | 0.27 |
| Ca3SbF3 | 452.89 | 54.05 | 2.51 | 51.54 | 199.42 | 0.26 |
Research states that both compounds resist fluctuating orders of pressure in addition to satisfying the Born stability criteria. Moreover, while the hydrostatic pressure increases, the assessed elastic constants also increase. However, the mathematical amount of C11 is significantly higher than C12 and C44, indicating that the analyzed compound also enabled resistance to force along the x-direction [64].
Studying the Cauchy pressure (Cp) value of a material offers a means to ascertain whether the material displays brittle or ductile behavior. Cauchy pressure (Cp) is expressed as:
| Cp = C12-C44 | (9) |
A material's ductility or brittleness is governed by the sign of its Cauchy pressure, which can be either positive or negative [65]. Table 5 shows the changes in Cauchy pressure (Cp) value under implementation of pressure up to 50 GPa. At ambient pressure, both materials show that they are brittle; therefore, the Cp value is negative. When pressure rises to higher levels, both materials demonstrate a change from brittleness to ductility [66] with Cp moving from negative to positive value, reflecting an increasing tendency to ductility.
The crystal stiffness (Cs) material's ability to oppose shear stress is calculated using the formula:
| (10) |
Table 5 shows the increasing nature of crystal stiffness (Cs) of Ca3MF3 (M = As and Sb) upon applied pressure. It indicates that both materials become more resistant to deformation as pressure increases.
The Kleinman parameter (ζ) quantifies the resistance of a crystal to bond stretching and bending. The top (ζ = 1) is associated with the objective of minimizing bond stretching, while the bottom (ζ = 0) corresponds to minimizing bond bending [67]. Kleinman parameter (ζ) is expressed as:
| (11) |
The values of the Kleinman parameter (ζ) are closer to the bottom (ζ = 0) for Ca3MF3 (M = As and Sb) in all the variations of pressure listed in Table 5, which indicates that bond stretching is more dominant than bond bending.
The bulk modulus (B), shear modulus (G), and Young's modulus (Y) of Ca3MF3 (M = As and Sb) has been estimated using the Voigt–Reuss–Hill (VRH) approach, and the estimated values are presented in Table 6 using the following formulas:
| (12) |
| (13) |
| (14) |
Table 6.
The calculated bulk modulus B (GPa), shear modulus G (GPa), young modulus E (GPa), Pugh's ratio B/GH, machinability index (μM), hardness factor H, and Poisson ratio ν, and Zener anisotropy factor A of Ca3MF3 (M = As and Sb).
| Pressure (GPa) | Compound | B | Y | G | B/GH | μM | Hv | ν | A |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Ca3AsF3 | 42.71 | 74.13 | 30.52 | 1.40 | 1.71 | 6.96 | 0.21 | 0.60 |
| Ca3SbF3 | 33.85 | 57.00 | 23.47 | 1.45 | 1.87 | 5.23 | 0.22 | 0.52 | |
| 10 | Ca3AsF3 | 81.27 | 104.70 | 40.80 | 2.00 | 3.33 | 4.83 | 0.28 | 0.29 |
| Ca3SbF3 | 72.32 | 83.54 | 32.21 | 2.25 | 4.35 | 2.91 | 0.30 | 0.22 | |
| 20 | Ca3AsF3 | 114.00 | 121.81 | 46.59 | 2.45 | 5.15 | 3.62 | 0.31 | 0.18 |
| Ca3SbF3 | 103.68 | 97.25 | 36.84 | 2.81 | 7.36 | 1.91 | 0.32 | 0.12 | |
| 30 | Ca3AsF3 | 148.59 | 133.92 | 50.53 | 2.94 | 7.83 | 2.61 | 0.32 | 0.12 |
| Ca3SbF3 | 134.31 | 106.16 | 40.00 | 3.36 | 12.50 | 1.19 | 0.33 | 0.07 | |
| 40 | Ca3AsF3 | 176.84 | 141.67 | 53.34 | 3.32 | 11.68 | 2.03 | 0.33 | 0.08 |
| Ca3SbF3 | 162.47 | 111.24 | 41.91 | 3.88 | 23.50 | 0.64 | 0.33 | 0.04 | |
| 50 | Ca3AsF3 | 205.15 | 145.03 | 54.57 | 3.76 | 19.02 | 1.40 | 0.33 | 0.05 |
| Ca3SbF3 | 187.00 | 112.77 | 42.70 | 4.38 | 74.50 | 0.19 | 0.32 | 0.01 |
Shear modulus (G) quantifies the capacity of a material to yield plastic deformation by a force from the external. A material bulk modulus denoted as B is a measure of its resistance to the external force that compels it to compress. Young's modulus (Y), often known as the modulus of elasticity, measures a material's capacity to withstand tensional or compressional force along the direction of its length. An increase in the values of G, B, and Y for both materials was found when pressure was applied. The development of these mechanical properties is caused by the rise in intermolecular or interatomic forces that ensue when an external pressure is forced. The increase boosts the capacity of a substance to withstand deviations in volume, shear deformation, or axial deformation.
Machinability index (μM) measure the easiness at which a solid object can be manufactured using cutting tools, and it is computed by the following equation:
| (15) |
From Table 6, the machinability index values for Ca3MF3 (M = As and Sb) increase with pressure. It implies that the machinability of these materials is improved when pressed. This suggests that these two materials can be machined more easily, with less tool wear and improved surface finish, and the productivity is enhanced thus new possibilities for machining opened.
The hardness factor influences the use of a material and can be used to deduce its elastic and plastic mode of deformation. The equation for finding a material's hardness is:
| (16) |
Table 6 displays the correlation between pressure and Vickers hardness. The material hardness of the two compounds is shown to decrease with increased pressure. The declining hardness factor indicates an enhancement in the machinability index.
The ductile and brittle nature of a substance can be found alongside Cauchy pressure (Cp) indication by examining two additional parameters: Pugh's ratio and Poisson's ratio. Pugh's ratio (B/GH) calculation involves dividing the bulk modulus by the shear modulus, whereas Poisson's ratio (v) computed through the following equation:
| (17) |
The critical values for recognizing any material's brittle or ductile quality are 1.75 for B/G and 0.26 for ν [68]. A substance turns out to be ductile if both B/GH and ν exceed their respective critical values; alternatively, it will be classified as brittle. Examining the calculated B/GH and ν values reveals that both compounds display brittle nature under ambient pressure condition (Table 6). However, as the pressure rises, the behavior shifts from brittle to ductile, which is also proved by the Cp value. Additionally, under high-pressure conditions, these two compounds exhibit improved ductility, which is verified by Fig. 14(a–b). Therefore, based on the findings the use of hydrostatic pressure is a suitable tactic whenever more ductility is required in the manufacture of optoelectronic devices. Thus, the implementation of hydrostatic pressure proves to be a viable strategy whenever there is a need for increased ductility in the production of optoelectronic devices. The confirmation of ductile nature of a compound for the optoelectronic field is necessary. Ductile materials are anticipated to demonstrate enhanced properties when utilized in thin films [69].
Fig. 14.
Variation of (a) Poisson's ratio and (b) Pugh's ratio of Ca3MF3 (M = As and Sb) compounds at different pressures.
The direction-dependent characteristics of a material provide certain indications of homogeneity. This is gauged by the anisotropy index A. In cubic materials, the Zener anisotropy factor (A) is determined on the basis of the following equation [70]:
| (18) |
If A deviates from unity, the material is anisotropic, whereas indicate its isotropic features. Table 6 shows that the value of anisotropic index does not tend to be 1 under any applied pressure conditions. In summary, we have discovered that the compound Ca3MF3 (M = As and Sb) shows elastic anisotropy, and the anisotropy remarkably increases with increasing pressure, as shown in Table 6.
To show the elasticity of a material with directional variation, the ELATE tool [71] was utilized to simulate the fluctuations of Young's modulus, shear modulus, and Poisson's ratio, as depicted in Fig. 15(a–d). The 3D spherical plots depict isotropic behavior, but any departure from a spherical form reveals material anisotropy. The figure clearly shows that departure from spherical plots is more pronounced under a pressure of 50 GPa compared to that observed under ambient pressure, indicating that the application of pressure could increase the degree of anisotropy of Ca3MF3 (M = As and Sb).
Fig. 15.
The anisotropic 3D illustration of (a) Young's modulus, (b) shear modulus, and (c) Poisson's ratio of Ca3MF3 (M = As and Sb) at 0 and 50 GPa pressure.
3.5. Sound velocity and debye temperature
Elastic waves pass through a medium and cause deformation or re-establishment of the deformation. Waves exist in solids, liquids, and gases, characterized by their capacity to restore the substance to its former condition after deformation. Elastic waves are primarily categorized into two types: longitudinal waves and transverse waves. Both compounds > indicate that transverse waves propagate at a reduced velocity relative to longitudinal waves within solids. The velocities of longitudinal and transverse elastic waves have been calculated using relevant bulk and shear values, as well as the density of these materials in the subsequent equation:
| (19) |
| (20) |
To calculate the average sound velocity within a solid, the Navier equation is utilized:
| (21) |
Large values of the mean velocities indicate strong interatomic bonding of any solid. The calculated mean sound velocities listed in Table 7 also indicate that the value of Ca3AsF3 is greater than that of Ca3SbF3, indicating that Ca3AsF3 exhibits stronger interatomic bonding than Ca3SbF3.
Table 7.
Pressure dependence of shear sound velocity (m/s), longitudinal sound velocity (m/s), average wave velocity (m/s), Debye temperatures (K) and melting temperature Tm (K) for Ca3MF3 (M = As and Sb).
| Pressure (GPa) | Ca3AsF3 |
Ca3SbF3 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tm±300 | Tm±300 | |||||||||
| 0 | 3343.52 | 5527.85 | 3695.87 | 393.37 | 1131.30 | 2861.00 | 4768.47 | 3165.01 | 323.20 | 1022.52 |
| 10 | 3597.21 | 6557.80 | 4010.34 | 447.97 | 1687.22 | 3113.00 | 5889.52 | 3479.93 | 373.63 | 1575.60 |
| 20 | 3652.37 | 7105.51 | 4090.26 | 472.32 | 2154.17 | 3151.81 | 6419.57 | 3539.34 | 394.14 | 2024.97 |
| 30 | 3662.80 | 7572.37 | 4116.69 | 487.71 | 2622.79 | 3151.49 | 6825.46 | 3550.18 | 406.49 | 2459.23 |
| 40 | 3647.51 | 7865.95 | 4108.23 | 496.97 | 3047.00 | 3118.53 | 7117.59 | 3521.19 | 412.37 | 2861.55 |
| 50 | 3592.63 | 8110.53 | 4054.61 | 499.13 | 3441.73 | 3059.46 | 7312.43 | 3460.47 | 413.02 | 3229.67 |
A key factor in thermodynamics is the Debye temperature , which is connected with the most energetic mode of vibration of the crystal [72]. The Debye temperature connects several basic properties e.g., specific heat, stability of the lattice, and melting point. The Debye temperature is:
| (22) |
where , , , , , , are constants. Table 7 illustrates the calculated Debye temperature values, which are higher for Ca3AsF3 compared to Ca3SbF3, and these values rise with pressure for both substances due to the coupling of atomic oscillations, resulting in the generation of a spectrum of frequencies. The rise of the Debye temperature causes an impact on the specific heat capacity of the studied compounds, and its value rises with the temperature rise. An increase in the specific heat takes place to be a measure of the thermodynamic stability of the studied materials [73]. The melting point is another important thermophysical property that becomes vital to evaluate the possibilities to use a material at high temperatures. For the cubic system, the melting temperature is [74]:
| (23) |
The computed melting point of Ca3MF3 (M = As and Sb) is presented in Table 7. Under ambient pressure conditions, the melting temperature of Ca3AsF3 (Ca3SbF3) is 1131.3 300 (1022.5 300) K, but this rises to 3441.7 300 (3229.6 300) K at a pressure of 50 GPa. Hence, the increased pressure results in the increase of the melting point for both investigated materials. Hence, it can be concluded that the phase of material stays stable even in high temperatures if exposed to pressure.
3.6. Optical properties
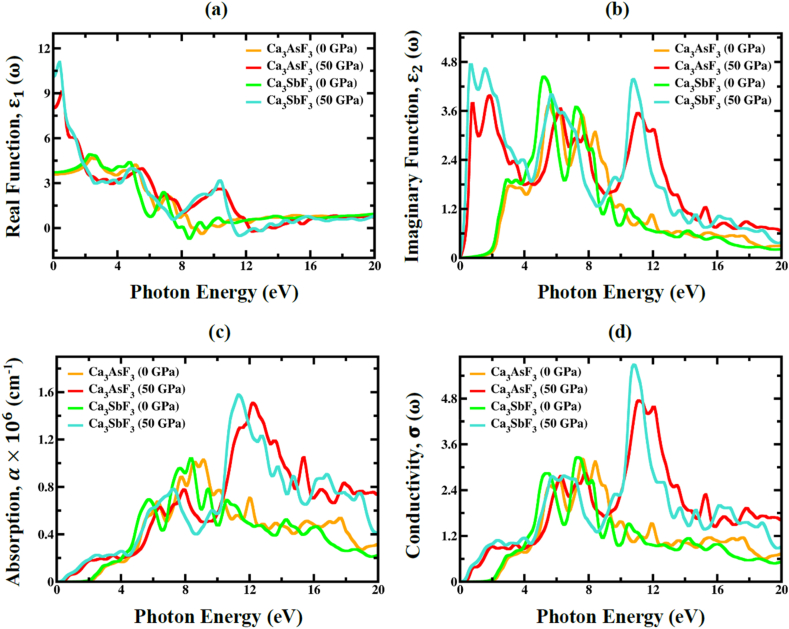
The complex dielectric function is an important characteristic that provides an understanding about the spectral characteristics of the photovoltaic material. Thus, the interest is directly related to the possibility of these materials being used in solar and optoelectronic systems. Optical performance of a given material can be improved using a thermodynamic technique known as hydrostatic pressure which modifies the electronic framework. In this paper, the various optical functions such as optical absorption, reflectivity, refractive index, extinction coefficient, and dielectric functions of this cubic Ca3MF3 (M = As and Sb) compounds have been analyzed, especially in the case of hydrostatic pressures of 0 GPa and 50 GPa. The optical behavior of the photovoltaic material can be determined based on the complex dielectric function, , equation [75]:
| (24) |
In this equation denotes the real component and signifies the imaginary component. Here the real portion of the dielectric function, , is associated with the electrical band structure and defines the absorptive behavior and the intensity of polarization a substance can involve in, whereas, the dissipation of the dielectric, is settled by the . A high dielectric constant decreases the possibility of charge-carrier recombination and boosts the efficiency of charge screening [76]. The real and imaginary portion of the for non-toxic Ca3MF3 (M = As and Sb), under various pressure scenarios, are displayed in Fig. 16(a–b). A comparative analysis of the obtained results indicates that applying pressure increases when comparing a pressurized and a non-pressurized system (Fig. 16a). This increase in is correlated with a lower energy gap (Eg) in the pressured system. As displayed in Fig. 16a, the determined static dielectric value, for Ca3AsF3 (Ca3SbF3) is 3.58 (3.72) at 0 GPa. Notably, when exposed to hydrostatic pressure, the initial value of for both materials notably rise, mainly because of a reduced rate of charge recombination, rendering these candidates more favorable for optoelectronic purposes. Moreover, the figure shows that the Ca3MF3 (M = As and Sb) compound under pressure exhibits the highest in the visible zone. Since , has a reversed relation with band gap, a larger value of energy gap corresponds to a smaller value of . Therefore, considering the Penn model [77], the obtained relationship expressed by the following equation can be presented:
| (25) |
Fig. 16.
The pressure-induced (a) real part ε1(ω), (b) imaginary part ε2(ω) of dielectric function, (c) absorption α(ω), (d) conductivity σ(ω) of Ca3MF3 (M = As and Sb) at pressure = 0, and 50 GPa.
The applied pressure leads to the rise of in the visible region, therefore, the peaks redshift to lower photon energies, observable in Fig. 16b. As a result, it is possible to infer that Ca3MF3 (M = As and Sb) absorbs effectively even under high pressure. The change in the peak position can be caused by the alterations of both the lattice constant and the bandgap. Moreover, the greater values of and at lower levels of photon energy, along with the smaller values at higher energy levels, emphasize the promising suitability of Ca3AsF3 and Ca3SbF3 for applications in microelectronics and integrated circuits.
The optical absorption coefficient, (α) serves as a vital determinant in comprehending a compound's ability to absorb photon energy, providing insightful perspectives on the efficiency of solar energy conversion. At pressures of up to 50 GPa, Fig. 16c shows how the absorption coefficient (α) of Ca3MF3 (M = As and Sb) varies in response to various photon energies. Upon examining Fig. 16c, it is obvious that absorption does not start at 0 eV; rather, it happens at the band gap value. As pressure rises, the absorption edge has clearly moved towards the lower photon energy area, a phenomenon known as redshift. It is also evident that the absorption coefficient for both materials at the visible spectra increases with rising hydrostatic pressure. Thus, the absorption coefficient for the two compounds is imperative when designing a solar cell. It is evidently possible to enhance the efficiency of the devices and their competitiveness against other types of solar cells by increasing the absorption coefficient of these two materials. Optical conductivity, σ(ω), represents the conductivity of photons within a material. Fig. 16d analyze the optical conductivity of Ca3AsF3 and Ca3SbF3 in terms of energy at pressures of 0 and 50 GPa. The conductivity spectra exhibit identical traits with absorption spectra, as demonstrated in Fig. 16c, due to the free carriers that material emits upon absorbing energy. The optical conductivity increases with applied pressure due to the heightened absorption coefficient, which rises with increasing pressure.
The refractive index n(ω) and extinction coefficient k(ω) of Ca3MF3 (M = As and Sb) are depicted in Fig. 17(a–b) across the photon energy spectrum from 0 to 20 eV. The refractive index n(ω) is the primary determinant that explains the degree of transparency exhibited by the material. Efficiency of the material increases with the reduction of refractive index values towards zero i.e. materials would become highly transparent. Conversely, near-zero refractive index values exhibit high absorbance i.e. large positive refractive index. At zero frequency of applied field, the behavior of n(ω) mirrors that of real part of ε1(ω) and is connected to it by the equation = ε1 (0). Moreover, the refractive index at zero frequency n(0) and ε1(0) precisely satisfy the criteria ε1 (0), as seen in Fig. 16, Fig. 17a. The increased value of n(0) of Ca3MF3 (M = As and Sb) under pressure can enhance the appropriateness of these materials for use in QLEDs, OLEDs, solar cells, and waveguides. The extinction coefficient k(ω) exhibits a comparable pattern to that of ε2(ω), as displayed in Fig. 17b.
Fig. 17.
The pressure-induced (a) Refractive index, (b) Extinction coefficient and (c) Reflectivity spectrum, and (d) loss function of Ca3MF3 (M = As and Sb) at pressure = 0, and 50 GPa.
Reflectivity refers to the ability of a material to bounce energy off its surface. Fig. 17c illustrates the spectrum curves of R(ω) plotted against photon energy while varying pressure for Ca3MF3 (M = As and Sb). The finding indicates that the greatest changes in reflectance occurred throughout the photon energy range of 0–16 eV. Increasing hydrostatic pressure leads to a rise in reflectivity of both material frameworks within the visible range. However, the comparatively reduced R (whether under pressure or not) in the low-energy range suggests the potential suitability of both compounds for use in solar cells. The energy that is lost by the electrons in a dielectric medium is known as the electron loss function. The electron loss function, , can be deduced through the following formula:
| (26) |
From the graph in Fig. 17d, the peak of the electron loss function for the Ca3MF3 (M = As and Sb) substances indicates that energy loss is experienced when the energy of the emitted photon exceeds the bandgap value. is closely linked to the concept of plasma oscillation and its frequency, which is often called plasma frequency (ωp). It was observed that at ambient pressure, in case of Ca3AsF3, the peak loss function is 10.6 eV, and for Ca3SbF3 is 9.23 eV. The findings provide approximate values for the plasma frequency of the Ca3MF3 materials. At higher frequencies than plasma frequencies both materials become transparent, and the electrons in those materials cannot gain the energy of the incoming light. With compressing, the peak in the loss function moves to larger energy values. The reduction in the number of active electrons, responsible for the intra-band and inter-band transitions, is observed as the peak moves to larger energies [78]. This is due to the compression of the material under pressure, which reduces the number of available states for the electrons.
4. Conclusions
For the first time, a simulation based on DFT was employed to investigate the impacts of hydrostatic pressure ranging from 0 to 50 GPa on the structural, electronic, mechanical, and optical properties of Ca3MF3 (M = As and Sb) materials systematically utilizing GGA-PBE and TB-mBJ functional. As pressure increases, there is a consistent decrease observed in the lattice parameter, volume, and bond lengths. Moreover, the effective masses of electrons and holes in Ca3MF3 (M = As and Sb) compounds reduce continuously in response to applied hydrostatic pressure. Effective mass values below 1.5m0 for Ca3MF3 (M = As and Sb) compounds suggest high mobility for the charge carriers. At high pressures, the band gap is notably lowered, which enhances the optical characteristics and makes these compounds promising for solar cells development. Additionally, the shifting of the dielectric function peak to lower photon energies is observed with the growth of pressure. The detailed investigation of optical properties revealed that in optoelectronic applications, Ca3MF3 (M = As and Sb) will have optimal performance as they have increased absorption and conductivity under high-pressure conditions. The computed value of elastic constants successfully meets the Born stability up to 50 GPa pressure, affirming the mechanical stability of both compounds throughout the entire range of applied pressure. Moreover, these materials show improved anisotropy and ductility under pressure. The results of this study are expected to stimulate further research aimed at utilizing the novel perovskites Ca3AsF3 and Ca3SbF3 in optoelectronic device applications.
Data availability statement
The data will be made available on request.
CRediT authorship contribution statement
Md. Adil Hossain: Writing – original draft, Software, Investigation, Formal analysis, Data curation, Conceptualization, Methodology, Validation, Writing – review & editing. Ali A. Sabi: Writing – original draft, Software, Methodology, Data curation, Writing – review & editing. Heider A. Abdulhussein: Writing – original draft, Software, Methodology, Formal analysis, Data curation, Writing – review & editing. Ahmad A. Mousa: Writing – original draft, Software, Methodology, Investigation, Formal analysis, Data curation. Mohammed S. Abu-Jafar: Writing – review & editing, Supervision, Project administration, Methodology, Investigation, Formal analysis. Redi Kristian Pingak: Writing – original draft, Software, Methodology, Investigation, Formal analysis, Data curation. Abbas H. Abo Nasria: Writing – original draft, Software, Methodology, Formal analysis, Data curation. Waqed H. Hassan: Writing – original draft, Software, Methodology, Investigation, Formal analysis, Data curation. Noorhan F. AlShaikh Mohammad: Writing – original draft, Software, Methodology, Investigation, Formal analysis, Data curation. Asif Hosen: Writing – review & editing, Supervision, Software, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization, Validation, Visualization, Writing – original draft.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors highly acknowledge the resources and technical support from University of Engineering & Technology (KUET), Bangladesh, the University of Kufa and the Ministry of Higher Education and Scientific Research, Iraq, and the Middle East University, Jordan.
Contributor Information
Mohammed S. Abu-Jafar, Email: mabujafar@najah.edu.
Asif Hosen, Email: asif@mse.kuet.ac.bd.
References
- 1.Hong T., Chamlagain B., Lin W., Chuang H.-J., Pan M., Zhou Z., Xu Y.-Q. Polarized photocurrent response in black phosphorus field-effect transistors. Nanoscale. 2014;6:8978–8983. doi: 10.1039/C4NR02164A. [DOI] [PubMed] [Google Scholar]
- 2.Zhao S., Wu J., Jin K., Ding H., Li T., Wu C., Pan N., Wang X. Highly polarized and fast photoresponse of black phosphorus-InSe vertical p–n heterojunctions. Adv. Funct. Mater. 2018;28 doi: 10.1002/adfm.201802011. [DOI] [Google Scholar]
- 3.Yuan H., Liu X., Afshinmanesh F., Li W., Xu G., Sun J., Lian B., Curto A.G., Ye G., Hikita Y., Shen Z., Zhang S.-C., Chen X., Brongersma M., Hwang H.Y., Cui Y. Polarization-sensitive broadband photodetector using a black phosphorus vertical p–n junction. Nat. Nanotechnol. 2015;10:707–713. doi: 10.1038/nnano.2015.112. [DOI] [PubMed] [Google Scholar]
- 4.Alaarage W.K., Abo Nasria A.H., Abdulhussein H.A. Computational analysis of CdS monolayer nanosheets for gas-sensing applications. Eur. Phys. J. B. 2023;96 doi: 10.1140/epjb/s10051-023-00601-3. [DOI] [Google Scholar]
- 5.Hussein T.A., Alaarage W.K., Abdulhussein H.A., Seriani N., Abo Nasria A.H. Ga-doped AlN monolayer nano-sheets as promising materials for environmental sensing applications. Comput Theor Chem. 2023;1223 doi: 10.1016/j.comptc.2023.114086. [DOI] [Google Scholar]
- 6.Alaarage W.K., Abo Nasria A.H., Hussein T.A., Abbood H.I. Investigation of the electronic and optical properties of bilayer CdS as a gas sensor: first-principles calculations. RSC Adv. 2024;14:5994–6005. doi: 10.1039/d3ra08741g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alaa Hussein T., Shiltagh N.M., Kream Alaarage W., Abbas R.R., Jawad R.A., Abo Nasria A.H. Electronic and optical properties of the BN bilayer as gas sensor for CO2, SO2, and NO2 molecules: a DFT study. Results Chem. 2023;5 doi: 10.1016/j.rechem.2023.100978. [DOI] [Google Scholar]
- 8.Kream Alaarage W., Abo Nasria A.H., Omran Alkhayatt A.H. A DFT investigation of an InP bilayer: a potential gas sensor with promising adsorption and optical response. Comput Theor Chem. 2023;1227 doi: 10.1016/j.comptc.2023.114223. [DOI] [Google Scholar]
- 9.Thomas S.P., Singh A., Grosjean A., Alhameedi K., Bjørn T., Plits R., Edwards A.J., Iversen B.B. The ambiguous origin of thermochromism in molecular crystals of dichalcogenides: chalcogen bonds versus Dynamic Se─Se/Te─Te bonds. Angew. Chem. Int. Ed. 2023;62 doi: 10.1002/anie.202311044. [DOI] [PubMed] [Google Scholar]
- 10.Ur Rehman S., Butt F.K., Tariq Z., Ul Haq B., Lin G., Li C. Cubic Germanium monochalcogenides (π-GeS and π-GeSe): emerging materials for optoelectronic and energy harvesting devices. Sol. Energy. 2019;185:211–221. doi: 10.1016/j.solener.2019.03.090. [DOI] [Google Scholar]
- 11.Ryder C.R., Wood J.D., Wells S.A., Yang Y., Jariwala D., Marks T.J., Schatz G.C., Hersam M.C. Covalent functionalization and passivation of exfoliated black phosphorus via aryl diazonium chemistry. Nat. Chem. 2016;8:597–602. doi: 10.1038/nchem.2505. [DOI] [PubMed] [Google Scholar]
- 12.Fei R., Yang L. Strain-Engineering the anisotropic electrical conductance of few-layer black phosphorus. Nano Lett. 2014;14:2884–2889. doi: 10.1021/nl500935z. [DOI] [PubMed] [Google Scholar]
- 13.Dong Q., Fang Y., Shao Y., Mulligan P., Qiu J., Cao L., Huang J. Electron-hole diffusion lengths > 175 μm in solution-grown CH3NH3PbI3 single crystals. Science. 2015;347:967–970. doi: 10.1126/science.aaa5760. 1979. [DOI] [PubMed] [Google Scholar]
- 14.Zhumekenov A.A., Saidaminov M.I., Haque M.A., Alarousu E., Sarmah S.P., Murali B., Dursun I., Miao X.-H., Abdelhady A.L., Wu T., Mohammed O.F., Bakr O.M. Formamidinium lead halide perovskite crystals with unprecedented long carrier dynamics and diffusion length. ACS Energy Lett. 2016;1:32–37. doi: 10.1021/acsenergylett.6b00002. [DOI] [Google Scholar]
- 15.Stranks S.D., Eperon G.E., Grancini G., Menelaou C., Alcocer M.J.P., Leijtens T., Herz L.M., Petrozza A., Snaith H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science. 2013;342:341–344. doi: 10.1126/science.1243982. 1979. [DOI] [PubMed] [Google Scholar]
- 16.Wehrenfennig C., Eperon G.E., Johnston M.B., Snaith H.J., Herz L.M. High charge carrier mobilities and lifetimes in organolead trihalide perovskites. Adv. Mater. 2014;26:1584–1589. doi: 10.1002/adma.201305172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kojima A., Teshima K., Shirai Y., Miyasaka T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009;131:6050–6051. doi: 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- 18.Endres J., Egger D.A., Kulbak M., Kerner R.A., Zhao L., Silver S.H., Hodes G., Rand B.P., Cahen D., Kronik L., Kahn A. Valence and conduction band densities of states of metal halide perovskites: a combined experimental–theoretical study. J. Phys. Chem. Lett. 2016;7:2722–2729. doi: 10.1021/acs.jpclett.6b00946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Haruyama J., Sodeyama K., Han L., Tateyama Y. First-principles study of ion diffusion in perovskite solar cell sensitizers. J. Am. Chem. Soc. 2015;137:10048–10051. doi: 10.1021/jacs.5b03615. [DOI] [PubMed] [Google Scholar]
- 20.Appavoo K., Nie W., Blancon J.-C., Even J., Mohite A.D., Sfeir M.Y. Ultrafast optical snapshots of hybrid perovskites reveal the origin of multiband electronic transitions. Phys. Rev. B. 2017;96 [Google Scholar]
- 21.Jaffe A., Lin Y., Karunadasa H.I. Halide perovskites under pressure: accessing new properties through lattice compression. ACS Energy Lett. 2017;2:1549–1555. [Google Scholar]
- 22.McMillan P.F. New materials from high-pressure experiments. Nat. Mater. 2002;1:19–25. doi: 10.1038/nmat716. [DOI] [PubMed] [Google Scholar]
- 23.Wang Y., Lu X., Yang W., Wen T., Yang L., Ren X., Wang L., Lin Z., Zhao Y. Pressure-induced phase transformation, reversible amorphization, and anomalous visible light response in organolead bromide perovskite. J. Am. Chem. Soc. 2015;137:11144–11149. doi: 10.1021/jacs.5b06346. [DOI] [PubMed] [Google Scholar]
- 24.Wang L., Wang K., Zou B. Pressure-induced structural and optical properties of organometal halide perovskite-based formamidinium lead bromide. J. Phys. Chem. Lett. 2016;7:2556–2562. doi: 10.1021/acs.jpclett.6b00999. [DOI] [PubMed] [Google Scholar]
- 25.Yuan G., Qin S., Wu X., Ding H., Lu A. Pressure-induced phase transformation of CsPbI3 by X-ray diffraction and Raman spectroscopy. Phase Transitions. 2018;91:38–47. [Google Scholar]
- 26.Hosen A., Hossain M.A., Abu-Jafar M.S., Pingak R.K., Mousa A.A. Unraveling lead-free Fr-based perovskites FrQCl3 (Q= Ca, Sr) and their pressure induced physical properties: DFT analysis for advancing optoelectronic performance. J. Phys. Chem. Solid. 2024;193 [Google Scholar]
- 27.Hosen A., Islam M.R., Park J. Pressure-induced band gap shifting from ultra-violet to visible spectrum of non-toxic RbCaBr3 cubic perovskite for enhancing optoelectronic applications. J. Inorg. Organomet. Polym. Mater. 2024:1–10. [Google Scholar]
- 28.Hosen A., Islam M.R., Badhan S.H. Exploring the influence of pressure-induced semiconductor-to-metal transition on the physical properties of cubic perovskites FrXCl3 (X= Ge and Sn) Heliyon. 2024;10 doi: 10.1016/j.heliyon.2024.e27581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang Y., Gao L., Yang Y., Xiang Y., Chen Z., Dong Y., Zhou H., Cai Z., Wang G.-C., Shi J. Nontrivial strength of van der Waals epitaxial interaction in soft perovskites. Phys. Rev. Mater. 2018;2 doi: 10.1103/PhysRevMaterials.2.076002. [DOI] [Google Scholar]
- 30.Zhu C., Niu X., Fu Y., Li N., Hu C., Chen Y., He X., Na G., Liu P., Zai H., Ge Y., Lu Y., Ke X., Bai Y., Yang S., Chen P., Li Y., Sui M., Zhang L., Zhou H., Chen Q. Strain engineering in perovskite solar cells and its impacts on carrier dynamics. Nat. Commun. 2019;10:815. doi: 10.1038/s41467-019-08507-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhao J., Deng Y., Wei H., Zheng X., Yu Z., Shao Y., Shield J.E., Huang J. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Sci. Adv. 2017;3 doi: 10.1126/sciadv.aao5616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen B., Li T., Dong Q., Mosconi E., Song J., Chen Z., Deng Y., Liu Y., Ducharme S., Gruverman A., De Angelis F., Huang J. Large electrostrictive response in lead halide perovskites. Nat. Mater. 2018;17:1020–1026. doi: 10.1038/s41563-018-0170-x. [DOI] [PubMed] [Google Scholar]
- 33.Wang Y., Lü X., Yang W., Wen T., Yang L., Ren X., Wang L., Lin Z., Zhao Y. Pressure-induced phase transformation, reversible amorphization, and anomalous visible light response in organolead bromide perovskite. J. Am. Chem. Soc. 2015;137:11144–11149. doi: 10.1021/jacs.5b06346. [DOI] [PubMed] [Google Scholar]
- 34.Liu G., Gong J., Kong L., Schaller R.D., Hu Q., Liu Z., Yan S., Yang W., Stoumpos C.C., Kanatzidis M.G., Mao H., Xu T. Isothermal pressure-derived metastable states in 2D hybrid perovskites showing enduring bandgap narrowing. Proc. Natl. Acad. Sci. USA. 2018;115:8076–8081. doi: 10.1073/pnas.1809167115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Castelli I.E., García-Lastra J.M., Thygesen K.S., Jacobsen K.W. Bandgap calculations and trends of organometal halide perovskites. Apl. Mater. 2014;2 [Google Scholar]
- 36.Lang L., Yang J.-H., Liu H.-R., Xiang H.J., Gong X.G. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites. Phys. Lett. 2014;378:290–293. [Google Scholar]
- 37.Mosconi E., Amat A., Nazeeruddin M.K., Gratzel M., De Angelis F. First-principles modeling of mixed halide organometal perovskites for photovoltaic applications. J. Phys. Chem. C. 2013;117:13902–13913. [Google Scholar]
- 38.Lü X., Yang W., Jia Q., Xu H. Pressure-induced dramatic changes in organic–inorganic halide perovskites. Chem. Sci. 2017;8:6764–6776. doi: 10.1039/c7sc01845b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Faghihnasiri M., Izadifard M., Ghazi M.E. Study of strain effects on electronic and optical properties of CH3NH3PbX3 (X= Cl, Br, I) perovskites. Physica B Condens Matter. 2020;582 doi: 10.1016/j.physb.2020.412024. [DOI] [Google Scholar]
- 40.Hosen A. Investigating the effects of hydrostatic pressure on the physical properties of cubic Sr3BCl3 (B= As, Sb) for improved optoelectronic applications: a DFT study. Heliyon. 2024;10 doi: 10.1016/j.heliyon.2024.e35855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Joifullah S., Hossain M.A., Al Yeamin M., Haque M.M., Pingak R.K., Mohammad N.F.A., Abu-Jafar M.S., Mousa A.A., Hosen A. First-principles investigation of pressure-modulated structural, electronic, mechanical, and optical characteristics of Sr3PX3 (X= Cl, Br) for enhanced optoelectronic application. Opt. Quant. Electron. 2024;56:1–28. [Google Scholar]
- 42.Fakharuddin A., Shabbir U., Qiu W., Iqbal T., Sultan M., Heremans P., Schmidt-Mende L. Inorganic and layered perovskites for optoelectronic devices. Adv. Mater. 2019;31 doi: 10.1002/adma.201807095. [DOI] [PubMed] [Google Scholar]
- 43.Wang C., Gao Y. Stability of perovskites at the surface analytic level. J. Phys. Chem. Lett. 2018;9:4657–4666. doi: 10.1021/acs.jpclett.8b00381. [DOI] [PubMed] [Google Scholar]
- 44.Zhou X., Jankowska J., Dong H., V Prezhdo O. Recent theoretical progress in the development of perovskite photovoltaic materials. J. Energy Chem. 2018;27:637–649. doi: 10.1016/j.jechem.2017.10.010. [DOI] [Google Scholar]
- 45.Giannozzi P., Baseggio O., Bonfà P., Brunato D., Car R., Carnimeo I., Cavazzoni C., de Gironcoli S., Delugas P., Ferrari Ruffino F., Ferretti A., Marzari N., Timrov I., Urru A., Baroni S. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020;152 doi: 10.1063/5.0005082. [DOI] [PubMed] [Google Scholar]
- 46.Perdew J.P., Ruzsinszky A., Csonka G.I., Vydrov O.A., Scuseria G.E., Constantin L.A., Zhou X., Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008;100 doi: 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
- 47.Garrity K.F., Bennett J.W., Rabe K.M., Vanderbilt D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014;81:446–452. [Google Scholar]
- 48.Fischer T.H., Almlof J. General methods for geometry and wave function optimization. J Phys Chem. 1992;96:9768–9774. doi: 10.1021/j100203a036. [DOI] [Google Scholar]
- 49.Tran F., Blaha P. Accurate band gaps of semiconductors and Insulators<? format?> with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009;102 doi: 10.1103/PhysRevLett.102.226401. [DOI] [PubMed] [Google Scholar]
- 50.Blaha P., Schwarz K., Madsen G.K.H., Kvasnicka D., Luitz J. vol. 60. 2001. (wien2k, an Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties). [Google Scholar]
- 51.Karsch F., Patkós A., Petreczky P. Screened perturbation theory. Phys. Lett. B. 1997;401:69–73. doi: 10.1016/S0370-2693(97)00392-4. [DOI] [Google Scholar]
- 52.Momma K., Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011;44:1272–1276. [Google Scholar]
- 53.Feng H.J., Zhang Q. Predicting efficiencies >25% A3MX3photovoltaic materials and Cu ion implantation modification. Appl. Phys. Lett. 2021;118 doi: 10.1063/5.0039936. [DOI] [Google Scholar]
- 54.Murnaghan F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA. 1944;30:244–247. doi: 10.1073/pnas.30.9.244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yakovkin I.N., Dowben P.A. The problem of the band gap in LDA calculations. Surf. Rev. Lett. 2007;14:481–487. [Google Scholar]
- 56.Noor N.A., Iqbal M.W., Zelai T., Mahmood A., Shaikh H.M., Ramay S.M., Al-Masry W. Analysis of direct band gap A2ScInI6 (A=Rb, Cs) double perovskite halides using DFT approach for renewable energy devices. J. Mater. Res. Technol. 2021;13:2491–2500. doi: 10.1016/j.jmrt.2021.05.080. [DOI] [Google Scholar]
- 57.Zhong S., Wu M., Lei X. First-principle calculations of effective mass of silicon crystal with vacancy defects. Materials Science- Poland. 2016;34:916–923. doi: 10.1515/msp-2016-0128. [DOI] [Google Scholar]
- 58.Yin W.-J., Yang J.-H., Kang J., Yan Y., Wei S.-H. Halide perovskite materials for solar cells: a theoretical review. J. Mater. Chem. A. 2015;3:8926–8942. doi: 10.1039/C4TA05033A. [DOI] [Google Scholar]
- 59.Liao P., Carter E.A. New concepts and modeling strategies to design and evaluate photo-electro-catalysts based on transition metal oxides. Chem. Soc. Rev. 2013;42:2401–2422. doi: 10.1039/C2CS35267B. [DOI] [PubMed] [Google Scholar]
- 60.Geng G., Chen P., Guan B., Jiang L., Xu Z., Di D., Tu Z., Hao W., Yi Y., Chen C., Liu M., Hu W. Shape-controlled metal-free catalysts: facet-sensitive catalytic activity induced by the arrangement pattern of noncovalent supramolecular chains. ACS Nano. 2017;11:4866–4876. doi: 10.1021/acsnano.7b01427. [DOI] [PubMed] [Google Scholar]
- 61.Fan H., Jiang T., Li H., Wang D., Wang L., Zhai J., He D., Wang P., Xie T. Effect of BiVO4 crystalline phases on the photoinduced carriers behavior and photocatalytic activity. J. Phys. Chem. C. 2012;116:2425–2430. doi: 10.1021/jp206798d. [DOI] [Google Scholar]
- 62.Zhang H., Liu L., Zhou Z. First-principles studies on facet-dependent photocatalytic properties of bismuth oxyhalides (BiOXs) RSC Adv. 2012;2:9224–9229. [Google Scholar]
- 63.Khan S., Ahmad R., Mehmood N., Hina F., Rehman A.U., Zaman S.U., Kim H.J. First-principles investigation of the physical properties of indium based fluoroperovskites InAF3 (A = Ca, Cd and Hg) Mater. Sci. Semicond. Process. 2021;121 doi: 10.1016/j.mssp.2020.105385. [DOI] [Google Scholar]
- 64.Khan U.A., Khan N.U., Abdullah, Alghtani A.H., Tirth V., Ahmed S.J., Sajjad M., Algahtani A., Shaheed T., Zaman A. First-principles investigation on the structural, electronic, mechanical and optical properties of silver based perovskite AgXCl3 (X= Ca, Sr) J. Mater. Res. Technol. 2022;20:3296–3305. doi: 10.1016/j.jmrt.2022.08.101. [DOI] [Google Scholar]
- 65.Eberhart M.E., Jones T.E. Cauchy pressure and the generalized bonding model for nonmagnetic bcc transition metals. Phys. Rev. B. 2012;86 doi: 10.1103/PhysRevB.86.134106. [DOI] [Google Scholar]
- 66.Khan M., Rahaman Md.Z., Ali Md.L. Pressure-induced band gap engineering of nontoxic lead-free halide perovskite CsMgI3 for optoelectronic applications. ACS Omega. 2023;8:24942–24951. doi: 10.1021/acsomega.3c01388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kleinman L. Deformation potentials in silicon. I. Uniaxial strain. Phys. Rev. 1962;128:2614–2621. doi: 10.1103/PhysRev.128.2614. [DOI] [Google Scholar]
- 68.Hossain Md.S., Haque Babu Md.M., Saha T., Hossain Md.S., Podder J., Rana Md.S., Barik A., Rani P. Pressure induced semiconductor to metal phase transition in cubic CsSnBr3 perovskite. AIP Adv. 2021;11 doi: 10.1063/5.0048979. [DOI] [Google Scholar]
- 69.Roknuzzaman M., Ken Ostrikov K., Wang H., Du A., Tesfamichael T. Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations. Sci. Rep. 2017;7 doi: 10.1038/s41598-017-13172-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zener C.M., Siegel S. Elasticity and anelasticity of metals. J. Phys. Colloid Chem. 1949;53:1468. doi: 10.1021/j150474a017. [DOI] [Google Scholar]
- 71.Gaillac R., Pullumbi P., Coudert F.-X. ELATE: an open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter. 2016;28 doi: 10.1088/0953-8984/28/27/275201. [DOI] [PubMed] [Google Scholar]
- 72.Qi L., Jin Y., Zhao Y., Yang X., Zhao H., Han P. The structural, elastic, electronic properties and Debye temperature of Ni3Mo under pressure from first-principles. J. Alloys Compd. 2015;621:383–388. doi: 10.1016/j.jallcom.2014.10.015. [DOI] [Google Scholar]
- 73.Noor N.A., Mahmood Q., Rashid M., Ul Haq B., Laref A. The pressure-induced mechanical and optoelectronic behavior of cubic perovskite PbSnO3 via ab-initio investigations. Ceram. Int. 2018;44:13750–13756. doi: 10.1016/j.ceramint.2018.04.217. [DOI] [Google Scholar]
- 74.Goyal M., Sinha M.M. Ab-initio study of mechanical and thermoelectric properties of topological semimetal: LaAuPb. Phys. Scripta. 2022;97 doi: 10.1088/1402-4896/ac46f6. [DOI] [Google Scholar]
- 75.Fried M., Lohner T., Aarnink W.A.M., Hanekamp L.J., van Silfhout A. Determination of complex dielectric functions of ion implanted and implanted‐annealed amorphous silicon by spectroscopic ellipsometry. J. Appl. Phys. 1992;71:5260–5262. doi: 10.1063/1.350587. [DOI] [Google Scholar]
- 76.Dzade N.Y. First-principles insights into the electronic structure, optical and band alignment properties of earth-abundant Cu2SrSnS4 solar absorber. Sci. Rep. 2021;11:4755. doi: 10.1038/s41598-021-84037-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Penn D.R. Wave-number-dependent dielectric function of semiconductors. Phys. Rev. 1962;128:2093–2097. doi: 10.1103/PhysRev.128.2093. [DOI] [Google Scholar]
- 78.Huang S., Li R.-Z., Qi S.-T., Chen B., Shen J. A theoretical study of the elastic and thermal properties of ScRu compound under pressure. Phys. Scripta. 2014;89 doi: 10.1088/0031-8949/89/6/065702. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data will be made available on request.