Spin–orbit-coupled Bose–Einstein condensates

Abstract

Spin–orbit (SO) coupling—the interaction between a quantum particle’s spin and its momentum—is ubiquitous in physical systems. In condensed matter systems, SO coupling is crucial for the spin-Hall effect^1,2 and topological insulators^3–5; it contributes to the electronic properties of materials such as GaAs, and is important for spintronic devices⁶. Quantum many-body systems of ultracold atoms can be precisely controlled experimentally, and would therefore seem to provide an ideal platform on which to study SO coupling. Although an atom’s intrinsic SO coupling affects its electronic structure, it does not lead to coupling between the spin and the centre-of-mass motion of the atom. Here, we engineer SO coupling (with equal Rashba⁷ and Dresselhaus⁸ strengths) in a neutral atomic Bose–Einstein condensate by dressing two atomic spin states with a pair of lasers⁹. Such coupling has not been realized previously for ultracold atomic gases, or indeed any bosonic system. Furthermore, in the presence of the laser coupling, the interactions between the two dressed atomic spin states are modified, driving a quantum phase transition from a spatially spin-mixed state (lasers off) to a phase-separated state (above a critical laser intensity). We develop a many-body theory that provides quantitative agreement with the observed location of the transition. The engineered SO coupling—equally applicable for bosons and fermions—sets the stage for the realization of topological insulators in fermionic neutral atom systems.

Quantum particles have an internal ‘spin’ angular momentum; this can be intrinsic for fundamental particles like electrons, or a combination of intrinsic (from nucleons and electrons) and orbital for composite particles like atoms. SO coupling links a particle’s spin to its motion, and generally occurs for particles moving in static electric fields, such as the nuclear field of an atom or the crystal field in a material. The coupling results from the Zeeman interaction $-\mathbf{\text{μ}}\cdot \mathbf{\text{B}}$ between a particle’s magnetic moment $\mathbf{\text{μ}}$, parallel to the spin $\mathbf{\text{σ}}$, and a magnetic field $\mathbf{\text{B}}$ present in the frame moving with the particle. For example, Maxwell’s equations dictate that a static electric field $\mathbf{\text{E}}=E_0\widehat{z}$ in the laboratory frame (at rest) gives a magnetic field ${\mathbf{\text{B}}}_{\text{SO}}=E_0\left(ħ/m{c}^2\right)\left(-k_y,k_x,0\right)$ in the frame of an object moving with momentum $ħ\mathbf{\text{k}}=ħ\left(k_x,k_y,k_z\right)$ where $c$ is the speed of light in vacuum and $m$ is the particle’s mass. The resulting momentum-dependent Zeeman interaction $-\mathbf{\text{μ}}\cdot {\mathbf{\text{B}}}_{\text{SO}}(\mathbf{\text{k}})\propto {\sigma }_x{k}_y-{\sigma }_y{k}_x$ is known as the Rashba⁷ SO coupling. In combination with the Dresselhaus⁸coupling $\propto -{\sigma }_x{k}_y-{\sigma }_y{k}_x$, these describe two-dimensional SO coupling in solids to first order.

In materials, the SO coupling strengths are generally intrinsic properties, which are largely determined by the specific material and the details of its growth, and are thus only slightly adjustable in the laboratory. We demonstrate SO coupling in an ⁸⁷Rb Bose–Einstein condensate (BEC) where a pair of Raman lasers create a momentum-sensitive coupling between two internal atomic states. This SO coupling is equivalent to that of an electronic system with equal contributions of Rashba and Dresselhaus⁹ couplings, and with a uniform magnetic field $\mathbf{\text{B}}$ in the $\widehat{y}-\widehat{z}$ plane, which is described by the single-particle Hamiltonian:

$$\widehat{H}=\frac{{ħ}^2{\widehat{\mathbf{\text{k}}}}^2}{2m}\check{1}-\left[\mathbf{\text{B}}+{\mathbf{\text{B}}}_{\text{SO}}(\widehat{\mathbf{\text{k}}})\right]\cdot \mathbf{\text{μ}}=\frac{{ħ}^2{\widehat{\mathbf{\text{k}}}}^2}{2m}\check{1}+\frac{\Omega }{2}{\check{\sigma }}_z+\frac{\delta }{2}{\check{\sigma }}_y+2\alpha {\widehat{k}}_x{\check{\sigma }}_y$$ (1)

$\alpha$ parametrizes the SO-coupling strength; $\Omega =-g{\mu }_{\text{B}}{B}_z$ and $\delta =-g{\mu }_{\text{B}}{B}_y$ result from the Zeeman fields along $\widehat{z}$ and $\widehat{y}$, respectively; and ${\check{\sigma }}_{x,y,z}$ are the $2\times 2$ Pauli matrices. Without SO coupling, electrons have group velocity, $v_x=ħk_x/m$ independent of their spin. With SO coupling, their velocity becomes spin-dependent, $v_x=ħ\left(k_x\pm 2\alpha m/{ħ}^2\right)/m$ for spin $|\uparrow \rangle$ and $|\downarrow \rangle$ electrons (quantized along $\widehat{y}$). In two recent experiments, this form of SO coupling was engineered in GaAs heterostructures where confinement into two-dimensional planes linearized the native cubic SO coupling of GaAs to produce a Dresselhaus term, and asymmetries in the confining potential gave rise to Rashba coupling. In one experiment a persistent spin helix was found⁶, and in another the SO coupling was only revealed by adding a Zeeman field¹⁰.

SO coupling for neutral atoms enables a range of exciting experiments, and importantly, it is essential in the realization of neutral atom topological insulators. Topological insulators are novel fermionic band insulators including integer quantum Hall states and now spin quantum Hall states that insulate in the bulk, but conduct in topologically protected quantized edge channels. The first-known topological insulators—integer quantum Hall states¹¹—require large magnetic fields that explicitly break time-reversal symmetry. In a seminal paper³, Kane and Mele showed that in some cases SO coupling leads to zero-magnetic-field topological insulators that preserve time-reversal symmetry. In the absence of the bulk conductance that plagues current materials, cold atoms can potentially realize such an insulator in its most pristine form, perhaps revealing its quantized edge (in two dimensions) or surface (in three dimensions) states. To go beyond the form of SO coupling we created, almost any SO coupling, including that needed for topological insulators, is possible with additional lasers^12–14.

To create SO coupling, we select two internal ‘spin’ states from within the ⁸⁷Rb $5{\text{S}}_{1/2}$, $F=1$ ground electronic manifold, and label them pseudo-spin-up and pseudo-spin-down in analogy with an electron’s two spin states: $|\uparrow \rangle =|F=1$, $m_F=0\rangle$ and $|\downarrow \rangle =\mid F=1$, $m_F=-1\rangle$. A pair of $\lambda =804.1\text{nm}$ Raman lasers, intersecting at $\theta ={90}^{\circ }$ and detuned by $\delta$ from Raman resonance (Fig. 1a), couple these states with strength $\Omega$; here $ħk_{\text{L}}=\sqrt{2}\pi ħ/\lambda$ and $E_{\text{L}}={ħ}^2{k}_{\text{L}}^2/2m$ are the natural units of momentum and energy. In this configuration, the atomic Hamiltonian is given by equation (1), with $k_x$ replaced by a quasimomentum $q$ and an overall $E_{\text{L}}$ energy offset. $\Omega$ and $\delta$ give rise to effective Zeeman fields along $\widehat{z}$ and $\widehat{y}$, respectively. The SO-coupling term $2E_{\text{L}}q{\check{\sigma }}_y/k_{\text{L}}$ results from the laser geometry, and $\alpha =E_{\text{L}}/k_{\text{L}}$ is set by $\lambda$ and $\theta$, independent of $\Omega$ (see Methods). In contrast with the electronic case, the atomic Hamiltonian couples bare atomic states $|\uparrow ,{\kappa }_x=q+k_{\text{L}}\rangle$ and $|\downarrow ,{\kappa }_x=q-k_{\text{L}}\rangle$ with different velocities, $ħ{\kappa }_x/m=ħ\left(q\pm k_{\text{L}}\right)/m$.

Figure 1 |. Scheme for creating SO coupling.

a, Level diagram. Two $\lambda \approx 804.1\text{nm}$ lasers (thick lines) coupled states $|F=1,m_F=0\rangle =|\uparrow \rangle$ and $|F=1,m_F=-1\rangle =|\downarrow \rangle$, differing in energy by a $ħ{\omega }_{\text{Z}}$ Zeeman shift. The lasers, with frequency difference $\text{Δ}{\omega }_{\text{L}}/2\pi =\left({\omega }_{\text{Z}}+\delta /ħ\right)/2\pi$, were detuned $\delta$ from the Raman resonance. $|m_F=0\rangle$ and $|m_F=+1\rangle$ had a $ħ\left({\omega }_{\text{Z}}-{\omega }_q\right)$ energy difference; because $ħ{\omega }_q=3.8E_{\text{L}}$ is large, $|m_F=+1\rangle$ can be neglected. b, Computed dispersion. Eigenenergies at $\delta =0$ for $\Omega =0$ (grey) to $5E_{\text{L}}$. When $\Omega <4E_{\text{L}}$ the two minima correspond to the dressed spin states $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$. c, Measured minima. Quasimomentum $q_{\uparrow ,\downarrow }$ of $|{\uparrow }^{\prime },{\downarrow }^{\prime }\rangle$ versus $\Omega$ at $\delta =0$, corresponding to the minima of $E_{-}(q)$. Each point is averaged over about ten experiments; the uncertainties are their standard deviation. d, Spin-momentum decomposition. Data for sudden laser turn-off: $\delta \approx 0,\Omega =2E_{\text{L}}$ (top image pair), and $\Omega =6E_{\text{L}}$ (bottom image pair). For $\Omega =2E_{\text{L}},|{\uparrow }^{\prime }\rangle$ consists of $|\uparrow ,{\kappa }_x\approx 0\rangle$ and $|\downarrow ,{\kappa }_x\approx -2k_L\rangle$, and $|{\downarrow }^{\prime }\rangle$ consists of $|\uparrow ,{\kappa }_x\approx 2k_L\rangle$ and $|\downarrow ,{\kappa }_x\approx 0\rangle$.

The spectrum, a new energy-quasimomentum dispersion of the SO-coupled Hamiltonian, is displayed in Fig. 1b at $\delta =0$ and for a range of couplings $\Omega$. The dispersion is divided into upper and lower branches $E_{\pm }(q)$, and we focus on $E_{-}(q)$. For $\Omega <4E_{\text{L}}$ and small $\delta$ (see Fig. 2a), $E_{-}(q)$ consists of a double well in quasi-momentum¹⁵, where the group velocity $\partial E_{-}(q)/\partial ħq$ is zero. States near the two minima are dressed spin states, labelled as $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$. As $\Omega$ increases, the two dressed spin states merge into a single minimum and the simple picture of two dressed spins is inapplicable. Instead, that strong coupling limit effectively describes spinless bosons with a tunable dispersion relation¹⁶ with which we engineered synthetic electric¹⁷ and magnetic fields¹⁸ for neutral atoms.

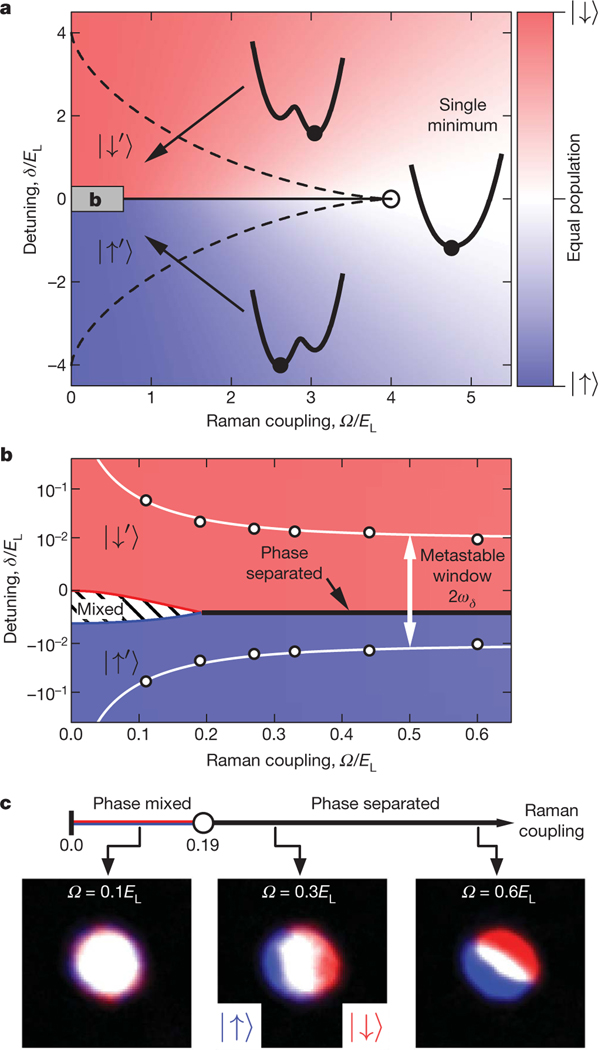
Figure 2 |. Phases of a SO-coupled BEC.

a, b, Mean field phase diagrams for infinite homogeneous SO-coupled ⁸⁷Rb BECs (1.5-kHz chemical potential). The background colours indicate atom fraction in $|\uparrow \rangle$ and $|\downarrow \rangle$. Between the dashed lines there are two dressed spin states, $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$. a, Single-particle phase diagram in the $\Omega -\delta$ plane. b, Phase diagram (enlargement of the grey rectangle in a), as modified by interactions. The dots represent a metastable region where the fraction of atoms $f_{{\uparrow }^{\prime },{\downarrow }^{\prime }}$ remains largely unchanged for $t_{\text{h}}=3\text{s}$. c, Miscible-to-immiscible transition. Phase line for mixtures of dressed spins and images after TOF (with populations $N_{\uparrow }\approx N_{\downarrow }$, mapped from $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$ showing the transition from phase-mixed to phase-separated within the ‘metastable window’ of detuning.

In the absence of Raman coupling, atoms with spins $|\uparrow \rangle$ and $|\downarrow \rangle$ spatially mixed perfectly in a BEC. By increasing $\Omega$ we observed an abrupt quantum phase transition to a new state where the two dressed spins spatially separated, resulting from a modified effective interaction between the dressed spins.

We studied SO coupling in oblate ⁸⁷Rb BECs with about $1.8\times {10}^5$ atoms in a $\lambda =1,064\text{-nm}$ crossed dipole trap with frequencies $(f_x,f_y,f_z)\approx (50,50,140)\text{Hz}$. The bias magnetic field $B_0\widehat{y}$ generated a ${\omega }_{\text{Z}}/2\pi \approx 4.81\text{MHz}$ Zeeman shift between $|\uparrow \rangle$ and $|\downarrow \rangle$. The Raman beams propagated along $\widehat{y}\pm \widehat{x}$ and had a constant frequency difference $\text{Δ}{\omega }_{\text{L}}/2\pi \approx 4.81\text{MHz}$. The small detuning from the Raman resonance $\delta =ħ\left(\text{Δ}{\omega }_{\text{L}}-{\omega }_{\text{Z}}\right)$ was set by $B_0$, and the state $|m_F=+1\rangle$ was decoupled owing to the quadratic Zeeman effect (see Methods).

We prepared BECs with an equal population of $|\uparrow \rangle$ and $|\downarrow \rangle$ at $\Omega$, $\delta =0$, then we adiabatically increased $\Omega$ to a final value up to $7E_{\text{L}}$ in 70 ms, and finally we allowed the system to equilibrate for a holding time $t_{\text{h}}=70\text{ms}$. We abruptly $\left(t_{\text{off}}<1\text{μs}\right)$ turned off the Raman lasers and the dipole trap—thus projecting the dressed states onto their constituent bare spin and momentum states—and absorption-imaged them after a 30.1-ms time of flight (TOF). For $\Omega >4E_{\text{L}}$ (Fig. 1d), the BEC was located at the single minimum $q_0$ of $E_{-}(q)$ with a single momentum component in each spin state corresponding to the pair $\left\{|\uparrow ,q_0+k_{\text{L}}\rangle ,|\downarrow ,q_0-k_{\text{L}}\rangle \right\}$. However, for $\Omega <4E_{\text{L}}$ we observed two momentum components in each spin state, corresponding to the two minima of $E_{-}(q)$ at $q_{\uparrow }$ and $q_{\downarrow }$. The agreement between the data (symbols), and the expected minima locations (curves), demonstrates the existence of the SO coupling associated with the Raman dressing. We kept $\delta \approx 0$ when turning on $\Omega$ by maintaining equal populations in bare spins $|\uparrow \rangle$, $|\downarrow \rangle$ (see Fig. 1d).

We experimentally studied the low-temperature phases of these interacting SO-coupled bosons as a function of $\Omega$ and $\delta$. The zero-temperature mean-field phase diagram (Fig. 2a, b) includes phases composed of a single dressed spin state, a spatial mixture of both dressed spin states, and coexisting but spatially phase-separated dressed spins.

This phase diagram can largely be understood as the result of non-interacting bosons condensing into the lowest-energy single particle state, and can be divided into three regimes (Fig. 2a). In the region of positive detuning marked $|{\downarrow }^{\prime }\rangle$, there are double minima at $q=q_{\uparrow },q_{\downarrow }$ in $E_{-}(q)$ with $E_{-}\left(q_{\downarrow }\right)<E_{-}\left(q_{\uparrow }\right)$ and the bosons condense at $q_{\downarrow }$. In the region marked $|{\uparrow }^{\prime }\rangle$ the reverse holds. The energy difference between the two minima is $\text{Δ}(\Omega ,\delta )=E_{-}\left(q_{\uparrow }\right)-E_{-}\left(q_{\downarrow }\right)\approx \delta$ for small $\delta$ (see Methods). In the third ‘single minimum’ regime, the atoms condense at the single minimum $q_0$. These dressed spins act as free particles with group velocity $ħK_x/m$ (with an effective mass $m^{\ast }\approx m$, for small $\Omega$), where $K_x=q-q_{\uparrow ,\downarrow ,0}$ for the different minima.

We investigated the phase diagram using BECs with initially equal spin populations prepared as described previously, but with $\delta \ne 0$ and $t_{\text{h}}$ up to 3 s. We probed the atoms after abruptly removing the dipole trap, and then ramping $\Omega \to 0$ in 1.5 ms. This approximately mapped $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$ back to their undressed counterparts $|\uparrow \rangle$ and $|\downarrow \rangle$ (see Methods). We absorption-imaged the atoms after a 30-ms TOF, during the last 20 ms of which a Stern-Gerlach magnetic field gradient along $\widehat{y}$ separated the spin components.

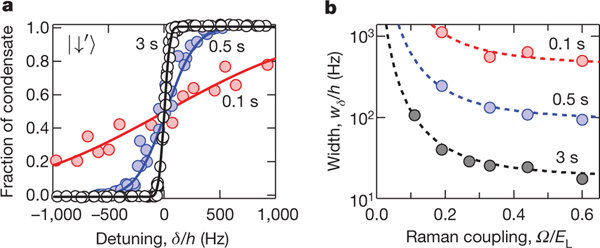
Figure 3a shows the condensate fraction $f_{{\downarrow }^{\prime }}=N_{{\downarrow }^{\prime }}/\left(N_{{\downarrow }^{\prime }}+N_{{\uparrow }^{\prime }}\right)$ in $|{\downarrow }^{\prime }\rangle$ at $\Omega =0.6E_{\text{L}}$ as a function of $\delta$, at $t_{\text{h}}=0.1\text{s}$, 1 s and 3 s, where $N_{{\uparrow }^{\prime }}$ and $N_{{\downarrow }^{\prime }}$ denote the number of condensed atoms in $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$, respectively. The BEC is all $|{\uparrow }^{\prime }\rangle$ for $\delta \lesssim 0$ and all $|{\downarrow }^{\prime }\rangle$ for $\delta \gtrsim 0$, but both dressed spin populations substantially coexisted for detunings within $\pm w_{\delta }$ (obtained by fitting $f_{{\downarrow }^{\prime }}$ to the error function where $\delta =\pm w_{\delta }$ corresponds to $f_{{\downarrow }^{\prime }}=0.50\pm 0.16$). Figure 3b shows $w_{\delta }$ versus $\Omega$ for hold times $t_{\text{h}}$. $w_{\delta }$ decreases with $t_{\text{h}}$; even by our longest $t_{\text{h}}$ of 3 s it has not reached equilibrium.

Figure 3 |. Population relaxation.

a, Condensate fraction $f_{{\downarrow }^{\prime }}$ in $|{\downarrow }^{\prime }\rangle$ at $\Omega =0.6E_{\text{I}}$ versus detuning $\delta$ at $t_{\text{h}}=0.1$, 0.5 and 3 s showing $w_{\delta }$ decrease with increasing $t_{\text{h}}$. The solid curves are fits to the error function from which we obtained the width $w_{\delta }$. b, Metastable detuning width. Width $w_{\delta }$ versus $\Omega$ at $t_{\text{h}}=0.1$, 0.5 and 3 s; the data fits well to $a\left[b+{\left(\Omega /E_{\text{L}}\right)}^{-2}\right]$ (dashed curves).

Conventional $F=1$ spinor BECs have been studied in ²³Na and ⁸⁷Rb without Raman coupling^19–21. For our $|\uparrow \rangle$ and $|\downarrow \rangle$ states, the interaction energy depends on the local density in each spin state, and is described by:

$${\widehat{H}}_{\text{I}}=\frac{1}{2}\int d^{3}r\left[\left(c_0+\frac{c_2}{2}\right){\left({\widehat{\rho }}_{\uparrow }+{\widehat{\rho }}_{\downarrow }\right)}^2+\frac{c_2}{2}\left({\widehat{\rho }}_{\downarrow }^2-{\widehat{\rho }}_{\uparrow }^2\right)+\left(c_2+c_{\uparrow \downarrow }^{\prime }\right){\widehat{\rho }}_{\uparrow }{\widehat{\rho }}_{\downarrow }\right]$$

where ${\widehat{\rho }}_{\uparrow }$ and ${\widehat{\rho }}_{\downarrow }$; are density operators for $|\uparrow \rangle$ and $|\downarrow \rangle$, and normal ordering is implied. In the ⁸⁷Rb $F=1$ manifold, the spin-independent interaction is $c_0=7.79\times {10}^{-12}{\text{Hz}\text{cm}}^3$, the spin-dependent interaction²² is $c_2=-3.61\times {10}^{-14}{\text{Hz}\text{cm}}^3$, and $c_{\uparrow \downarrow }^{\prime }=0$. Because $\left|c_0\right|\gg \left|c_2\right|$, the interaction is almost spin-independent, but $c_2<0$, so the two-component mixture of $|\uparrow \rangle$ and $|\downarrow \rangle$ has a spatially mixed ground state (is miscible). When ${\widehat{H}}_{\text{I}}$ is re-expressed in terms of the dressed spin states, $c_{\uparrow \downarrow }^{\prime }\approx c_0{\text{Ω}}^2/\left(8E_L^2\right)$ is non-zero and corresponds to an effective interaction between $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$. This modifies the ground state of our SO-coupled BEC (mixtures of $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$) from phase-mixed to phase-separated above a critical Raman coupling strength ${\Omega }_{\text{c}}$. This transition lies outside the common single-mode approximation²⁰.

The effective interaction between $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$ is an exchange energy resulting from the non-orthogonal spin part of $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$ (see Methods): a spatial mixture produces total density modulations¹⁵ with wavevector $2k_{\text{L}}$, in analogy with the spin-textures of the electronic case⁶. These increase the state-independent interaction energy in ${\widehat{H}}_{\text{I}}$ wherever the two dressed spins spatially overlap, contributing to the $c_{\uparrow \downarrow }^{\prime }$; term. (Such a term does not appear for radio-frequency-dressed states, which are always spin-orthogonal.) Because $c_{\uparrow \downarrow }^{\prime }$; and $c_2$ have opposite sign here, the dressed BEC can go from miscible to immiscible at the miscibility threshold¹⁹ for a two-component BEC $c_0+c_2+c_{\uparrow \downarrow }^{\prime }/2=\sqrt{c_0\left(c_0+c_2\right)}$, when $\Omega ={\Omega }_{\text{c}}$ (this result is in agreement with an independent theory presented in ref. 23).

Figure 2b depicts the mean field phase diagram including interactions, computed by minimizing the interaction energy $H_{\text{I}}$ plus the single particle detuning $\text{Δ}(\Omega ,\delta )\approx \delta$. This phase diagram adds two new phases, mixed (hashed) and phase-separated (bold line), to those present in the non-interacting case. The $c_2\left({\widehat{\rho }}_{\downarrow }^2-{\widehat{\rho }}_{\uparrow }^2\right)/2$ term in ${\widehat{H}}_{\text{I}}$ implies that the energy difference between a $|\uparrow \rangle$ BEC and a $|\downarrow \rangle$ BEC is proportional to $N^2{c}_2$. The detuning required to compensate for this difference slightly displaces the symmetry point of the phase diagram downwards. As evidenced by the width of the metastable window $2w_{\delta }$ in Fig. 2b, for $|\delta |<w_{\delta }$ the spin-population does not have time to relax to equilibrium. The miscibility condition does not depend on atom number, so the phase line in Fig. 2c shows the system’s phases for $|\delta |<w_{\delta }$: phase-mixed for $\Omega <{\Omega }_{\text{c}}$ and phase-separated for $\Omega >{\Omega }_{\text{c}}$ where ${\text{Ω}}_{\text{c}}\approx \sqrt{-8c_2/c_0}{E}_{\text{L}}\approx 0.19E_{\text{L}}$.

We measured the miscibility of the dressed spin components from their spatial profiles after TOF, for $\Omega =0$ to $2E_{\text{L}}$ and $\delta \approx 0$ such that $N_{\text{T}{\uparrow }^{\prime }}\approx N_{\text{T}{\downarrow }^{\prime }}$, where $N_{\text{T}{\uparrow }^{\prime },{\downarrow }^{\prime }}$ is the total atom number including both the condensed and thermal components in $|{\uparrow }^{\prime }\rangle$, $|{\downarrow }^{\prime }\rangle$. For each TOF image, we numerically re-centred the Stern-Gerlach-separated spin distributions (Fig. 2c, and see Methods), giving condensate densities $n_{{\uparrow }^{\prime }}(x,y)$ and $n_{{\downarrow }^{\prime }}(x,y)$. Given that the self-similar expansion of BECs released from harmonic traps essentially magnifies the in situ spatial spin distribution, these reflect the in situ densities²⁴.

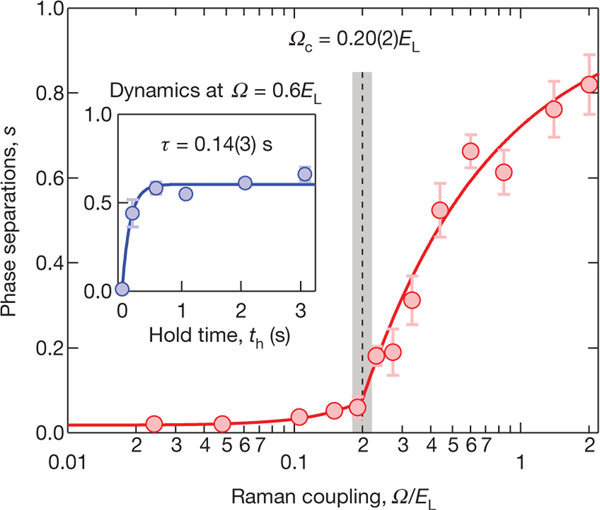
A dimensionless metric $s=1-\langle n_{{\uparrow }^{\prime }}{n}_{{\downarrow }^{\prime }}\rangle /{\left(\langle n_{{\uparrow }^{\prime }}^2\rangle \langle n_{{\downarrow }^{\prime }}^2\rangle \right)}^{\frac{1}{2}}$ quantifies the degree of phase separation (where $\langle \dots \rangle$ is the spatial average over a single image). $s=0$ for any perfect mixture $n_{{\uparrow }^{\prime }}(x,y)\propto n_{{\downarrow }^{\prime }}(x,y)$, and $s=1$ for complete phase separation. Figure 4 displays $s$ versus Raman coupling $\Omega$ with a hold time $t_{\text{h}}=3\text{s}$, showing that $s\approx 0$ for small $\Omega$ (as expected given our miscible bare spins) and $s$ abruptly increases above a critical ${\Omega }_{\text{c}}$. The inset to Fig. 4 plots $s$ as a function of time, showing that $s$ reaches steady state in 0.14(3) s, which is much less than $t_{\text{h}}$. To obtain ${\Omega }_{\text{c}}$, we fitted the data in Fig. 4 to a slowly increasing function below ${\Omega }_{\text{c}}$ and the power-law $1-{\left(\Omega /{\Omega }_{\text{c}}\right)}^{-a}$ above ${\Omega }_{\text{c}}$. The resulting ${\Omega }_{\text{c}}=0.20(2)E_{\text{L}}$ is in agreement with the mean field prediction ${\Omega }_{\text{c}}=0.19E_{\text{L}}$. This demonstrates a quantum phase transition for a two-component SO-coupled BEC, from miscible when $\Omega <{\Omega }_{\text{c}}$ to immiscible when $\Omega >{\Omega }_{\text{c}}$.

Figure 4 |. Miscible to immiscible phase transition.

Phase separation $s$ versus $\Omega$ with $t_{\text{h}}=3\text{s}$; the solid curve is a fit to the function described in the text. The power-law component of the fit has an exponent $a=0.75\pm 0.07$; this is not a critical exponent, but instead results from the decreasing size of the domain wall between the regions of $|{\uparrow }^{\prime }\rangle$ and $|{\downarrow }^{\prime }\rangle$ as $\Omega$ increases. Each point represents an average over 15 to 50 realizations and the uncertainties are the standard deviation. Inset, phase separation $s$ versus $t_{\text{h}}$ with $\Omega =0.6E_{\text{L}}$ fitted to an exponential showing the rapid 0.14(3)-s timescale for phase separation.

Even below ${\Omega }_{\text{c}}$, $s$ slowly increased with increasing $\Omega$. To understand this effect, we numerically solved the two-dimensional spinor Gross-Pitaevskii equation in the presence of a trapping potential. This demonstrated that the differential interaction term $c_2\left({\widehat{\rho }}_{\downarrow }^2-{\widehat{\rho }}_{\uparrow }^2\right)/2$ in ${\widehat{H}}_I$ favours slightly different density profiles for each spin component, while the $\left(c_2+c_{\uparrow \downarrow }^{\prime }\right){\widehat{\rho }}_{\uparrow }{\widehat{\rho }}_{\downarrow }$ term favours matched profiles. Thus, as $c_2+c_{\uparrow \downarrow }^{\prime }$ approached zero from below this balancing effect decreased, causing $s$ to increase.

An infinite system should fully phase separate $(s=1)$ for all $\Omega >{\Omega }_{\text{c}}$. In our finite system, the boundary between the phase-separated spins, set by the spin-healing length $({\xi }_{\text{s}}=\sqrt{{ħ}^2/2m\left|c_2+c_{\uparrow \downarrow }^{\prime }\right|n}$, where $n$ is the local density), can be comparable to the system size. We interpret the increase of $s$ above ${\Omega }_{\text{c}}$ as resulting from the decrease of ${\xi }_{\text{s}}$ with increasing $\Omega$.

We realized SO coupling in an ⁸⁷Rb BEC, and observed a quantum phase transition from spatially mixed to spatially separated. By operating at lower magnetic field (with a smaller quadratic Zeeman shift), our method extends to the full $F=1$ or $F=2$ manifold of ⁸⁷Rb or ²³Na, enabling a new kind of tuning for spinor BECs, without the losses associated with Feshbach tuning²⁵. Such modifications may allow access to the expected non-abelian vortices in some $F=2$ condensates²⁶. Because our SO coupling is in the small $\Omega$ limit, this technique is practical for fermionic ⁴⁰K, with its smaller fine-structure splitting and thus larger spontaneous emission rate²⁷. When the Fermi energy lies in the gap between the lower and upper bands (for example, Fig. 1b) there will be a single Fermi surface; this situation can induce $p$-wave coupling between fermions²⁸ and more recent work anticipates the appearance of Majorana fermions²⁹.

METHODS SUMMARY

System preparation.

Our experiments began with nearly pure ⁸⁷Rb BECs of approximately $1.8\times {10}^5$ atoms in the $|F=1,m_F=-1\rangle$ state³⁰ confined in a crossed optical dipole trap. The trap consisted of a pair of l,064-nm laser beams propagating along $\widehat{x}-\widehat{y}(1/e^2$ radii of $w_{\widehat{x}+\widehat{y}}\approx 120\text{μm}$ and $w_{\widehat{z}}\approx 50\text{μm}$) and $-\widehat{x}-\widehat{y}$ ($1/e^2$ radii of $w_{\widehat{x}-\widehat{y}}\approx w_{\widehat{z}}\approx 65\mu \text{m}$).

We prepared equal mixtures of $|F=1,m_F=-1\rangle$ and $|1,0\rangle$ using an initially off-resonant radio-frequency magnetic field $B_{\text{rf}}(t)\widehat{x}$. We adiabatically ramped $\delta \approx 0$ to in l5ms, decreased the radio-frequency coupling strength ${\Omega }_{\text{rf}}$ to about 150 Hz, which is much less than $ħ{\omega }_q$, in 6 ms, and suddenly turned off ${\Omega }_{\text{rf}}$, projecting the BEC into an equal superposition of $|m_F=-1\rangle$ and $|m_F=0\rangle$. We subsequently ramped $\delta$ to its desired value in 6 ms and then linearly increased the intensity of the Raman lasers from zero to the final coupling $\Omega$ in 70 ms.

Magnetic fields.

Three pairs of Helmholtz coils, orthogonally aligned along $\widehat{x}+\widehat{y}$, $\widehat{x}-\widehat{y}$ and $\widehat{z}$, provided bias fields ($B_{x+y}$, $B_{x-y}$, and $B_z$). By monitoring the $\mid F=1,m_F=-1\rangle$ and $|1,0\rangle$ populations in a nominally resonant radio-frequency dressed state, prepared as above, we observed a short-time (less than about 10 min) root-mean-square field stability $g{\mu }_{\text{B}}{B}_{\text{RMS}}/h\lesssim 80\text{Hz}$. The field drifted slowly on longer timescales (but changed abruptly when unwary colleagues entered through our laboratory’s ferromagnetic doors). We compensated for the drift by tracking the radio-frequency and Raman resonance conditions.

The small energy scales involved in the experiment meant that it was crucial to minimize magnetic field gradients. We detected stray gradients by monitoring the spatial distribution of $|m_F=-1\rangle -|m_F=0\rangle$ spin mixtures after TOF. Small magnetic field gradients caused this otherwise miscible mixture to phase-separate along the direction of the gradient. We cancelled the gradients in the $\widehat{x}-\widehat{y}$ plane with two pairs of anti-Helmholtz coils, aligned along $\widehat{x}+\widehat{y}$ and $\widehat{x}-\widehat{y}$, to $g{\mu }_{\text{B}}{B}^{\prime }/h\lesssim 0.7\text{Hz}{\text{μm}}^{-1}$.

METHODS

System preparation.

Our experiments began with nearly pure ⁸⁷Rb BECs of approximately $1.8\times {10}^5$ atoms in the $|F=1,m_F=-1\rangle$ state³⁰ confined in a crossed optical dipole trap. The trap consisted of a pair of 1,064-nm laser beams propagating along $\widehat{x}-\widehat{y}$ ($1/e^2$ radii of $w_{\widehat{x}+\widehat{y}}\approx 120\text{μm}$ and $w_{\widehat{z}}\approx 50\text{μm}$) and $-\widehat{x}-\widehat{y}$ ($1/e^2$ radii of $w_{\widehat{x}-\widehat{y}}\approx w_{\widehat{z}}\approx 65\text{μm}$).

We prepared equal mixtures of $|F=1,m_F=-1\rangle$ and $|1,0\rangle$ using an initially off-resonant radio-frequency magnetic field $B_{\text{rf}}(t)\widehat{x}$. We adiabatically ramped $\delta$ to $\delta \approx 0$ in 15 ms, decreased the radio-frequency coupling strength ${\Omega }_{\text{rf}}$ to about 150 Hz, which is much less than $ħ{\omega }_q$, in 6 ms, and suddenly turned off ${\Omega }_{\text{rf}}$ projecting the BEC into an equal superposition of $|m_F=-1\rangle$ and $|m_F=0\rangle$. We subsequently ramped $\delta$ to its desired value in 6 ms and then linearly increased the intensity of the Raman lasers from zero to the final coupling $\Omega$ in 70 ms.

Magnetic fields.

Three pairs of Helmholtz coils, orthogonally aligned along $\widehat{x}+\widehat{y}$, $\widehat{x}-\widehat{y}$ and $\widehat{z}$, provided bias fields ($B_{x+y}$, $B_{x-y}$, and $B_z$). By monitoring the $\mid F=1,m_F=-1\rangle$ and $|1,0\rangle$ populations in a nominally resonant radio-frequency dressed state, prepared as above, we observed a short-time (less than about 10 min) root-mean-square field stability $g{\mu }_{\text{B}}{B}_{\text{RMS}}/h\lesssim 80\text{Hz}$. The field drifted slowly on longer timescales (but changed abruptly when unwary colleagues entered through our laboratory’s ferromagnetic doors). We compensated for the drift by tracking the radio-frequency and Raman resonance conditions.

The small energy scales involved in the experiment meant that it was crucial to minimize magnetic field gradients. We detected stray gradients by monitoring the spatial distribution of $|m_F=-1\rangle -|m_F=0\rangle$ spin mixtures after TOF. Small magnetic field gradients caused this otherwise miscible mixture to phase-separate along the direction of the gradient. We cancelled the gradients in the $\widehat{x}-\widehat{y}$ plane with two pairs of anti-Helmholtz coils, aligned along $\widehat{x}+\widehat{y}$ and $\widehat{x}-\widehat{y}$, to $g{\mu }_{\text{B}}{B}^{\prime }/h\lesssim 0.7{\text{Hz}}^{\prime }\mu {\text{m}}^{-1}$.

SO-coupled Hamiltonian.

Our system³⁰ consisted of a $F=1$ BEC with a bias magnetic field along $\widehat{y}$ at the intersection of two Raman laser beams propagating along $\widehat{x}+\widehat{y}$ and $-\widehat{x}+\widehat{y}$ with angular frequencies ${\omega }_{\text{L}}$ and ${\omega }_{\text{L}}+\text{Δ}{\omega }_{\text{L}}$, respectively. The rank-1 tensor light shift of these beams produced an effective Zeeman magnetic field along the $z$ direction with Hamiltonian ${\widehat{H}}_{\text{R}}={\Omega }_{\text{R}}{\check{\sigma }}_{3,z}\cos \left(2k_{\text{L}}\widehat{x}+\text{Δ}{\omega }_{\text{L}}t\right)$, where ${\check{\sigma }}_{3,x,y,z}$ are the $3\times 3$ Pauli matrices and we define ${\check{\text{I}}}_3$ as the $3\times 3$ identity matrix. If we take $\widehat{y}$ as the natural quantization axis (by expressing the Pauli matrices in a rotated basis ${\check{\sigma }}_{3,y}\to {\check{\sigma }}_{3,z}$, ${\check{\sigma }}_{3,x}\to {\check{\sigma }}_{3,y}$ and ${\check{\sigma }}_{3,z}\to {\check{\sigma }}_{3,x}$) and make the rotating wave approximation, the Hamiltonian for spin states $\{|m_F=+1\rangle ,|0\rangle ,|-1\rangle \}$ in the frame rotating at $\text{Δ}{\omega }_{\text{L}}$ is:

$$\begin{gathered} {\widehat{H}}_3=\frac{{ħ}^2{\widehat{\mathbf{\text{k}}}}^2}{2m}{\check{1}}_3+\left(\begin{array}{ccc}3\delta /2+ħ{\omega }_q& 0& 0\\ 0& \delta /2& 0\\ 0& 0& -\delta /2\end{array}\right)+ \\ \frac{{\Omega }_{\text{R}}}{2}{\check{\sigma }}_{3,x}\cos \left(2k_{\text{L}}\widehat{x}\right)-\frac{{\Omega }_{\text{R}}}{2}{\check{\sigma }}_{3,y}\sin \left(2k_{\text{L}}\widehat{x}\right) \end{gathered}$$ (2)

As we justify below, $|m_F=+1\rangle$ can be neglected for large enough $ħ{\omega }_q$, which gives the effective two-level Hamiltonian:

$${\widehat{H}}_2=\frac{{ħ}^2{\widehat{\mathbf{\text{k}}}}^2}{2m}\check{1}+\frac{\delta }{2}{\check{\sigma }}_z+\frac{\Omega }{2}{\check{\sigma }}_x\cos \left(2k_{\text{L}}\widehat{x}\right)-\frac{\Omega }{2}{\check{\sigma }}_y\sin \left(2k_{\text{L}}\widehat{x}\right)$$

for the pseudo-spins $|\uparrow \rangle =|m_F=0\rangle$ and $|\downarrow \rangle =|-1\rangle$ where $\Omega ={\Omega }_{\text{R}}/\sqrt{2}$. After a local pseudo-spin rotation by $\theta (\widehat{x})=2k_{\text{L}}\widehat{x}$ about the pseudo-spin $\widehat{z}$ axis followed by a global pseudo-spin rotation ${\check{\sigma }}_z\to {\check{\sigma }}_y$, ${\check{\sigma }}_y\to {\check{\sigma }}_x$ and, ${\check{\sigma }}_x\to {\check{\sigma }}_z$ the $2\times 2$ Hamiltonian takes the SO-coupled form:

$${\widehat{H}}_2=\frac{{ħ}^2{\widehat{\mathbf{\text{k}}}}^2}{2m}\check{1}+\frac{\Omega }{2}{\check{\sigma }}_z+\frac{\delta }{2}{\check{\sigma }}_y+2\frac{{ħ}^2{k}_{\text{L}}{\widehat{k}}_x}{2m}{\check{\sigma }}_y+E_{\text{L}}\check{1}$$

The SO term linear in ${\widehat{k}}_x$ results from the non-commutation of the spatially dependent rotation about the pseudo-spin $z$ axis and the kinetic energy.

Effective two-level system.

For atoms in $|m_F=-1\rangle$ and $|m_F=0\rangle$ with velocities $ħ{\kappa }_x/m\approx 0$ and Raman-coupled near resonance, $\delta \approx 0$, the $|m_F=+1\rangle$ state is detuned from resonance owing to the $ħ{\omega }_q=3.8E_{\text{L}}$ quadratic Zeeman shift. For $\delta /4E_{\text{L}}\ll 1$ and $\Omega <4E_{\text{L}}$, we have $\text{Δ}(\Omega ,\delta )\approx \delta {\left[1-{\left(\Omega /4E_{\text{L}}\right)}^2\right]}^{1/2}$.

Effect of the neglected state.

In our experiment, we focused on the two-level system formed by the $|m_F=-1\rangle$ and $|m_F=0\rangle$ states. We verified the validity of this assumption by adiabatically eliminating the $|m_F=+1\rangle$ state from the full three-level problem. To second-order in $\Omega$, this procedure modifies the detuning $\delta$ and SO-coupling strength $\alpha$ in equation (1) by:

$${\delta }^{(2)}={\left(\frac{\Omega }{2}\right)}^2\frac{1}{4E_{\text{L}}+ħ{\omega }_q}\approx \frac{1}{32}\frac{{\Omega }^2}{E_{\text{L}}}$$

$${\alpha }^{(2)}={\left(\frac{\Omega }{2}\right)}^2\frac{\alpha }{{\left(4E_{\text{L}}+ħ{\omega }_q\right)}^2}\approx \frac{\alpha }{256}{\left(\frac{\Omega }{E_{\text{L}}}\right)}^2$$

In these expressions, we have retained only the largest term in a $1/{\omega }_q$ expansion. In our experiment, where $ħ{\omega }_q=3.8E_{\text{L}}$, $\delta$ is substantially changed at our largest coupling $\Omega =7E_{\text{L}}$. To maintain the desired detuning $\delta$ in the simple two-level model (that is, $\Delta \approx \delta +{\delta }^{(2)}=0$ in Fig. 1c), we changed $g{\mu }_{\text{B}}{B}_0$ by as much as $3E_{\text{L}}$ to compensate for ${\delta }^{(2)}$. We did not correct for the change to $\alpha$, which was always small.

Although both terms are small at the $\Omega =0.2E_{\text{L}}$ transition from miscible to immiscible, slow drifts in $B_0$ prompted us to locate $\Delta =0$ empirically from the equal-population condition, $N_{\text{T}{\uparrow }^{\prime }}=N_{\text{T}{\downarrow }^{\prime }}$. As a result, $\delta$ in equation (1) implicitly includes the perturbative correction ${\delta }^{(2)}$.

Origin of the effective interaction term.

The additional $c_{\uparrow \downarrow }^{\prime }$ term in the interaction Hamiltonian for dressed spins directly results from transforming into the basis of dressed spins, which are:

$$|{\uparrow }^{\prime },K_x\rangle \approx |\uparrow ,{\kappa }_x=K_x+q_{\uparrow }+k_{\text{L}}\rangle -\epsilon |\downarrow ,{\kappa }_x=K_x+q_{\uparrow }-k_{\text{L}}\rangle$$

and

$$|{\downarrow }^{\prime },K_x\rangle \approx |\downarrow ,{\kappa }_x=K_x+q_{\downarrow }-k_{\text{L}}\rangle -\epsilon |\uparrow ,{\kappa }_x=K_x+q_{\downarrow }+k_{\text{L}}\rangle$$ (3)

where $ħK_x/m$ is the group velocity, $K_x=q-q_{\uparrow }$ for $|{\uparrow }^{\prime }\rangle$ and $K_x=q-q_{\downarrow }$ for $|{\downarrow }^{\prime }\rangle$, and $\epsilon =\text{Ω}/8E_L\ll 1$. Thus, in second quantized notation, the dressed field operators transform according to:

$${\widehat{\psi }}_{\uparrow }(r)={\widehat{\psi }}_{{\uparrow }^{\prime }}(r)+\epsilon e^{2i{k}_{\text{L}}x}{\widehat{\psi }}_{{\downarrow }^{\prime }}(r)$$

and

$${\widehat{\psi }}_{\downarrow }(r)={\widehat{\psi }}_{{\downarrow }^{\prime }}(r)+\epsilon e^{-2i{k}_{L}x}{\widehat{\psi }}_{{\uparrow }^{\prime }}(r)$$

where $q_{\uparrow }\approx -\sqrt{1-4{\epsilon }^2}{k}_{\text{L}}\approx -k_{\text{L}}$ and $q_{\downarrow }\approx \sqrt{1-4{\epsilon }^2}{k}_{\text{L}}\approx k_{\text{L}}$. Inserting the transformed operators into:

$${\widehat{H}}_{\text{I}}=\frac{1}{2}\int d^{3}r\left[\left(c_0+\frac{c_2}{2}\right){\left({\widehat{\rho }}_{\downarrow }+{\widehat{\rho }}_{\uparrow }\right)}^2+\frac{c_2}{2}\left({\widehat{\rho }}_{\downarrow }^2-{\widehat{\rho }}_{\uparrow }^2\right)+c_2{\widehat{\rho }}_{\downarrow }{\widehat{\rho }}_{\uparrow }\right]$$

gives the interaction Hamiltonian (with normal ordering implied) for dressed spins which can be understood order-by-order (both $c_2/c_0$ and $\epsilon$ are treated as small parameters). In this analysis, the terms proportional to $c_2$ are unchanged to the order of $c_2/c_0$, and we only need to evaluate the transformation of the spin-independent term (proportional to $c_0$). At $O(\epsilon )$ and $O\left({\epsilon }^3\right)$ all the terms in the expansion include the high-spatial-frequency prefactors $e^{\pm 2i{k}_{\text{L}}x}$ or $e^{\pm 4i{k}_{\text{L}}x}$. For density distributions that vary slowly on the $\lambda /2$ length scale these average to zero. The $O\left({\epsilon }^2\right)$ term, however, has terms without these modulations, and is:

$${\widehat{H}}_{\text{I}}^{\left({\epsilon }^2\right)}=\frac{1}{2}\int {\text{d}}^{3}r\left(8c_0{\epsilon }^2{\widehat{\psi }}_{{\downarrow }^{\prime }}^{†}{\widehat{\psi }}_{{\uparrow }^{\prime }}^{†}{\widehat{\psi }}_{{\downarrow }^{\prime }}{\widehat{\psi }}_{{\uparrow }^{\prime }}\right)$$

giving rise to ${c^{\prime }}_{\uparrow \downarrow }=c_0{\Omega }^2/\left(8E_{\text{L}}^2\right)$.

Mean field phase diagram.

We compute the mean-field phase diagram for a ground-state BEC composed of a mixture of dressed spins in an infinite homogeneous system. This applies to our atoms in a harmonic trap in the limit of $R\gg {\xi }_s$, where $R$ is the system size, ${\xi }_{\text{s}}=\sqrt{{ħ}^2/2m\left|c_2+c_{\uparrow \downarrow }^{\prime }\right|n}$ is the spin healing length and $n$ is the density. We first minimize the interaction energy ${\widehat{H}}_{\text{I}}$ at fixed $N_{{\uparrow }^{\prime },\downarrow }$, with an effective interaction $c_{\uparrow \downarrow }^{\prime }$ as a function of $\Omega$. The two dressed spins are either phase-mixed, both fully occupying the system’s volume $V$, or phase-separated with a fixed total volume constraint $V=V_{{\uparrow }^{\prime }}+V_{{\downarrow }^{\prime }}$. For the phase-separated case, minimizing the free energy gives the volumes $V_{{\uparrow }^{\prime }}$ and $V_{{\downarrow }^{\prime }}$, determined by $N_{{\uparrow }^{\prime },{\downarrow }^{\prime }}$ and $V$. The interaction energy of a phase-mixed state is smaller than that of a phase-separated state for the miscibility condition $c_0+c_2+c_{\uparrow \downarrow }^{\prime }/2<\sqrt{c_0\left(c_0+c_2\right)}$, corresponding to $\Omega <{\Omega }_{\text{c}}$. This condition is independent of $N_{{\uparrow }^{\prime },{\downarrow }^{\prime }}$: for any $N_{{\uparrow }^{\prime },{\downarrow }^{\prime }}$ the system is miscible at $\Omega <{\Omega }_{\text{c}}$. Then, at a given $\Omega$, we minimize the sum of the interaction energy and the single-particle energy from the Raman detuning, $\left(N_{{\uparrow }^{\prime }}-N_{{\downarrow }^{\prime }}\right)\delta /2$, allowing $N_{{\uparrow }^{\prime },{\downarrow }^{\prime }}$ to vary. For the miscible case $\left(\Omega <{\Omega }_{\text{c}}\right)$, the BEC is a mixture with fraction $N_{{\downarrow }^{\prime }}/\left(N_{{\uparrow }^{\prime }}+N_{{\downarrow }^{\prime }}\right)\in (0,1)$ only in the range of detuning $\delta \in \left({\delta }_0-W_{\delta },{\delta }_0+W_{\delta }\right)$, where ${\delta }_0=c_{2}n/2$, $W_{\delta }=\left|{\delta }_0\right|{\left(1-\Omega /{\Omega }_{\text{c}}\right)}^{1/2}$ and $n=\left(N_{{\uparrow }^{\prime }}+N_{{\downarrow }^{\prime }}\right)/V$. For the immiscible case $\left(\Omega >{\Omega }_c\right),W_{\delta }=\left(c_2/8c_0\right)c_{2}n$ is negligibly small compared to $c_{2}n$.

Figure 2b shows the mean field phase diagram as a function of $(\Omega ,\delta )$, where $\delta /E_{\text{L}}$ is displayed with a quasi-logarithmic scaling, using the sign function $(\delta /E_{\text{L}})\left[{\log }_{10}\left(\left|\delta /E_{\text{L}}\right|+\left|{\delta }_{\min }/E_{\text{L}}\right|\right)-{\log }_{10}\left|{\delta }_{\min }/E_{\text{L}}\right|\right]$, in order to display $\delta$ within the range of interest. This scaling function smoothly evolves from logarithmic, that is, approximately $\text{sgn}\left(\delta /E_{\text{L}}\right){\log }_{10}\left|\delta /E_{\text{L}}\right|$ for $|\delta |\gg {\delta }_{\min }$, to linear, that is, approximately $\delta$ for $|\delta |\ll {\delta }_{\min }$, where ${\delta }_{\min }/E_{\text{L}}=0.001E_{\text{L}}=1.5\text{Hz}$.

In our measurement of the dressed spin fraction $f_{{\downarrow }^{\prime }}$ (see Fig. 3a), $\delta =0$ is determined from the $N_{\text{T}{\uparrow }^{\prime }}=N_{\text{T}{\downarrow }^{\prime }}$ condition. We identify this condition as $\delta ={\delta }_0$ and apply it for all hold times $t_{\text{h}}$. Because $\left|{\delta }_0\right|\approx 3\text{Hz}$ is below our approximately 80-Hz root-mean-square field noise, we are unable to distinguish ${\delta }_0$ from 0.

Recombining TOF images of dressed spins.

To probe the dressed spin states (equation (3)), each of which is a spin and momentum superposition, we adiabatically mapped them into bare spins, $|\uparrow ,{\kappa }_x=q_{\uparrow }+k_{\text{L}}\rangle$ and $|\downarrow ,{\kappa }_x=q_{\downarrow }-k_{\text{L}}\rangle$, respectively. Then, in each image outside an $\sim 90-\text{μm}$ radius disk containing the condensate for each spin distribution, we fitted $n_{\text{T}{\uparrow }^{\prime },\text{T}{\downarrow }^{\prime }}(x,y)$ to a gaussian modelling the thermal background and subtracted that fit from $n_{\text{T}{\uparrow }^{\prime },\text{T}{\downarrow }^{\prime }}(x,y)$ to obtain the condensate two-dimensional density $n_{{\uparrow }^{\prime },{\downarrow }^{\prime }}(x,y)$. Thus, for each dressed spin we readily obtained the temperature, total number $N_{\text{T}{\uparrow }^{\prime },\text{T}{\downarrow }^{\prime }}$, and condensate densities $n_{{\uparrow }^{\prime },{\downarrow }^{\prime }}(x,y)$.

To analyse the miscibility from the TOF images where a Stern-Gerlach gradient separated individual spin states, we re-centred the distributions to obtain $n_{{\uparrow }^{\prime }}(x,y)$ and $n_{{\downarrow }^{\prime }}(x,y)$. This took into account the displacement due to the Stern-Gerlach gradient and the non-zero velocities $ħ{\kappa }_x/m$ of each spin state (after the adiabatic mapping). The two origins were determined in the following way: we loaded the dressed states at a desired coupling $\Omega$ but with detuning $\delta$ chosen to put all atoms in either $|{\downarrow }^{\prime }\rangle$ or $|{\uparrow }^{\prime }\rangle$. Because $q_{\uparrow ,\downarrow }=\mp \left(1-{\Omega }^2/32E_{\text{L}}^2\right)k_{\text{L}}$ (see Fig. 1c), these velocities $ħ{\kappa }_x/m=ħ\left(q_{\uparrow }+k_{\text{L}}\right)/m,ħ\left(q_{\downarrow }-k_{\text{L}}\right)/m$ depend slightly on $\Omega$, and our technique to determine the origin of the distributions accounts for this effect.

Calibration of Raman coupling.

Both Raman lasers were derived from the same Ti:sapphire laser at $\lambda \approx 804.1\text{nm}$, and were offset from each other by a pair of acousto-optic modulators driven by two phase-locked frequency synthesizers near 80 MHz. We calibrated the Raman coupling strength $\Omega$ by fitting the three-level Rabi oscillations between the $m_F=-1,0$ and $+1$ states driven by the Raman coupling to the expected behaviour.