Foliage shedding in deciduous forests lifts up long-distance seed dispersal by wind

Abstract

Seed terminal velocity and release height are recognized as key biotic determinants of long-distance dispersal (LDD) of seeds by wind. Yet, potential determinants at the ecosystem level, such as seasonal dynamics in foliage density characterizing many deciduous forests, have received much less attention. We integrated detailed field observations and experiments with a mechanistic wind dispersal model to assess how seasonal variation in foliage density, estimated by leaf-area index (LAI), affects LDD in deciduous forests. We found that the model, previously shown to accurately predict seed dispersal by wind, also reliably describes the effects of LAI variation on wind statistics for a wide range of canopy types. Sparser canopies are characterized by more organized vertical eddy motion that promotes LDD by uplifting seeds to higher elevations where winds are stronger. Yet, sparser canopies are also characterized by reduced mean windspeed aloft. We showed that former effect more than compensates for the latter, i.e., conditions of low LAI are favorable for LDD. This may account for the tendency of many temperate tree species to restrict seed release to either early spring or late fall, when LAI is relatively low. Sensitivity analysis reveals that the typical seasonal variation in LAI can be more important to LDD of seeds by wind than the natural variation in seed terminal velocity. Because our model accurately describes the effects of LAI variation for distinctly different sites, species, and life forms, we suggest that its results reflect a general association between LDD and foliage density dynamics.

Deciduous trees, which shed leaves seasonally, dominate forest communities in many temperate regions and are also common in tropical and subtropical climates (1). The seasonal phenomenon of leaf shedding has been studied intensively (2–4) but seldom in relation to seed dispersal, another striking seasonal phenomenon of organ abscission in plants (5). The study of seed dispersal, on the other hand, has encompassed multiple aspects related mostly to seed and tree attributes (6–10), but the influence of forest canopy foliage dynamics has rarely been investigated. The two phenomena, however, are not independent, especially for species adapted for wind dispersal. Seasonal changes in forest foliage density, through their effects on wind flow patterns, affect seed dispersal by wind, particularly long-distance dispersal (LDD), and thus bear significant implications for plant population spread, species survival in fragmented landscapes, and gene flow patterns (10, 11).

Foliage density is often characterized by the leaf-area index (LAI), the one-sided leaf area per unit ground area (m²·m^-2). The annual course of LAI variation in deciduous temperate forests typically exhibits a square-wave-like pattern, increasing from near zero values in the late winter to some site-specific (12) peak values in the midst of the growing season during summer, and rapidly dropping with leaf abscission during fall (13). To assess how these seasonal changes in LAI affect LDD, it is necessary to explore their effects on wind flow patterns. Of particular interest are their effects on the size and characteristic duration (i.e., typical length and time scales) of turbulent eddies because only coherent updrafts are capable of uplifting seeds above the canopy. Such uplifting events constitute the key determinant of LDD not only in forested landscapes (14), but also in grasslands (15, 16).

Several laboratory, field, and numerical studies explored the statistical properties of turbulence within and above roughness elements such as vegetation canopies, and over a broad range of canopy densities (17–20). These studies conclude that winds above sparser canopies are usually weaker than winds above denser canopies, for the same mean shear stress at the canopy top (20). This implies that seeds escaping sparse canopies are transported by weaker winds thus are likely to travel shorter distances than seeds that escape a dense canopy. On the other hand, eddies near the top of sparse canopies appear to have larger mixing lengths when compared with their dense canopy counterparts (20). Hence, seeds that escape sparser canopies are likely to continue their upward trajectories to higher levels above the surface, where they encounter increasingly higher mean winds. The overall effect on LDD of these two conflicting mechanisms is difficult to quantify, thereby limiting our ability to formulate clear hypotheses about the relationship between canopy foliage variation and seed dispersal by wind.

We explore how seasonal variation in LAI affects seed dispersal by wind and LDD in particular. Focusing on trees in an eastern North American deciduous forest as a case study, we address this goal by combining field observations with a detailed mechanistic wind dispersal model that resolves the turbulent dynamics within the canopy. We used this model to formulate hypotheses about the relationship between the variation in LAI and turbulent wind statistics. We then tested these hypotheses both numerically and empirically, and evaluated the role of seasonal foliage dynamics, as compared with other dispersal determinants, on LDD.

Methods

The Model. We developed a coupled Eulerian–Lagrangian closure (CELC) modeling approach, which combines Eulerian closure principles for estimating turbulent wind statistics (21) with Lagrangian principles for describing trajectories of airborne particles (22), to model wind dispersal of seeds. This model was successfully tested against dispersal data collected in forests (14) and grasslands (16). It uses inputs similar to classic advection–diffusion models (23, 24), namely the seed terminal velocity (V_t) and the height of seed release (H_r). It also resolves the effects of organized canopy turbulence by explicitly incorporating turbulent excursions whose time scales are of a magnitude of tens of seconds. The Eulerian component of CELC computes the needed velocity statistics by using second-order moment-closure principles (18). The Lagrangian component follows, generating random velocity fluctuations at high temporal resolutions (fractions of seconds) while preserving the vertical variation of flow statistics computed by the Eulerian component. These fluctuations generate a synthetic turbulent flow field in three dimensions, incorporating stochasticity in all velocity components (and hence seed trajectories). The model does not intend to precisely (or instantaneously) mimic real velocity time series (which is impossible given the chaotic nature of turbulence). However, the synthetic turbulence it generates retains all of the key statistical attributes of real canopy turbulence relevant to dispersal including time scale of organized eddies, vertical attenuation of the first and second moments of the Eulerian velocity statistics, and the vertical decorrelation of the covariances between the three velocity components with decreasing height within the canopy. The general scheme, the mathematical formulations, and the parameterization of the CELC model are given in Supporting Methods, which is published as supporting information on the PNAS web site (see also refs. 14 and 16).

Research Site and Tree Species. The study site is located at the Blackwood Division of the Duke Forest near Durham, NC (35°58′41.430″N, 79°05′39.087″W, 163 m above sea level). We focused on a 1-ha (100 × 100 m) plot around a 45-m-high walkup tower, within an 80- to 100-year-old oak–hickory forest composed of mixed hardwood species with loblolly pine (Pinus taeda) as a minor component. The oldest individuals exceeded 180 years, and the maximum tree height was 33 m. The species include Quercus alba, Quercus michauxii, Carya tomentosa, Liriodendron tulipifera, and Liquidambar styraciflua as canopy dominant, and mostly Ostrya virginiana, Carpinus caroliniana, and Cornus florida in the understory. Tree density in 1997 was measured at 311 ha^-1. Thirty-four measurements of ground-level LAI were collected by using an LAI-2000 canopy analyzer within the 1-ha plot between early 2000 and late 2003 (D. Ellsworth, B. Poulter, C. Oishi, S. Palmroth, and R. Oren, personal communication). The mean ± SD LAI was 3.04 ± 1.45 m²·m^-2, ranging between 0.89 m²·m^-2 (January) and 4.82 m²·m^-2 (August–September). A detailed description of how all CELC's input parameters were determined is given in Supporting Methods.

Wind Measurements. A previous (1997–2001) study carried out in a pine stand adjacent to our study site demonstrated that the statistical distribution of mean wind velocity does not vary significantly either within or between seasons (25), implying that the site has relatively stationary mean wind conditions. This allows assessment of the role of seasonal variation in LAI in determining LDD, with minimal “interferences” from strong seasonal variation in wind conditions. We examined this assumption by comparing Weibull functions fitted to the measured friction velocity (u_*) time series recorded during five seasons in the present study [R² values ranging from 0.94 to 0.96, P_(slope=0) < 10^-5 in all cases]. The observed and fitted histograms for the five periods (Table 1 and Fig. 4, which are published as supporting information on the PNAS web site) clearly show that the seasonal variation in u_* is minor compared with the 5-fold (1 to 5) seasonal variation in LAI. Thus, as a first-order approximation, u_*, the key forcing term in CELC, can be considered as stationary with respect to the seasonal variation in foliage density.

Seed Sampling and Measurements. We placed 102 seed traps, each with a 0.20-m² sampling area, at 12 levels along the 45-m-high tower. Each of the lower nine levels contained eight traps, and each of the three upper levels, all above the top of the surrounding canopy (h = 33 m), contained 10 traps. We also randomly placed 48 traps on the ground within the 1-ha plot. Evidence for predation of trapped seeds was scarce, occurring almost exclusively on the ground traps. We added contact papers to further minimize predation and to avoid trapped seeds from bouncing off the tower traps. During the first dispersal season (fall 2000), we tested the efficiency of this procedure by placing marked seeds of three different species in traps at the upper three levels, revealing that the vast majority of the marked seeds were kept until the next census.

Seed traps were checked 92 times during the 27 months of this study (November 2000 to February 2003). A total of 54,596 seeds of eight wind-dispersed species were collected, 28,289 from the tower traps and 26,307 from the ground traps. In ref. 14, we analyzed the data collected during fall 2000, and here we concentrate on the data collected during fall 2001, spring 2002, and fall 2002.

The most abundant species in the traps were Liriodendron tulipifera and Liquidambar styraciflua, accounting for 66% and 28% of the total sample, respectively. The remaining 6% was distributed among the following six species, in order of descending abundance: Ulmus alata, C. caroliniana, Fraxinus americana, Acer rubrum, P. taeda, and O. virginiana. The last species was especially rare and therefore was excluded from the analysis.

Results

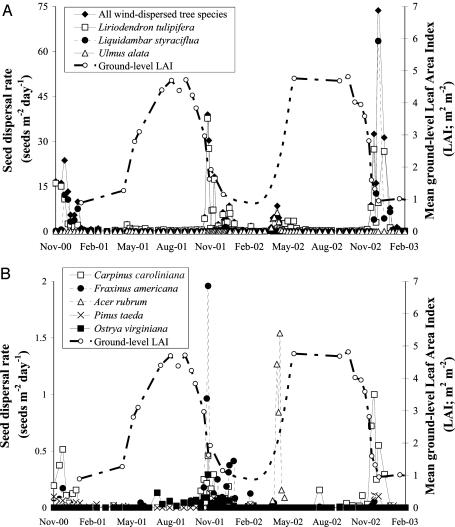
The observed seasonal dispersal dynamics was characterized by marked variation within and among seasons and years (Fig. 1). The most common species in the samples, Liriodendron tulipifera, was the only species dispersing all year long, with some seeds collected from traps in every single census. This species showed a dispersal peak during fall, either in October (2001), November (2000), or December (2002), and a secondary small peak in May. The second most common species, Liquidambar styraciflua, showed a biannual pattern with peaks in late November–early December in both 2000 and 2002, and very low dispersal in 2001. This species reached a dispersal rate (estimated from ground trap data) of 63 seeds per m per day in early December 2002, the maximum dispersal rate recorded for any species in this study. Other species dispersing mostly during fall were C. caroliniana, F. americana, and P. taeda. Two species, U. alata and A. rubrum, dispersed seeds during spring, particularly in 2002, peaking in early and mid-April, respectively.

Fig. 1.

Seasonal dynamics of seed dispersal and LAI observed near the meteorological tower at Duke Forest over 27 successive months. Note the difference in dispersal rates between species that were common (A) and rare (B) in the seed traps. The seasonal variation in LAI is shown in both panels for reference. LAI measurements were missing for the period between 2 December 2001 and 18 May 2002; the line drawn between these two points follows a second-order polynomial fitted for LAI data collected during the corresponding period in the previous and the subsequent (not shown) years.

We first tested the predictive skills of CELC's Eulerian component against published data representing a broad range of canopy structural differences. These comparisons (Table 2 and Fig. 5, which are published as supporting information on the PNAS web site) demonstrate the model's ability to reproduce the key features of wind flow patterns [R² values ranging from 0.60 to 0.92 for four major flow statistics, P_(slope=0) < 10^-5 in all cases]. We also found good agreement between the measured and modeled flow statistics for our study site [R² values ranging from 0.71 to 0.93, P_(slope=0) < 0.01 in all cases]. These results show that CELC's Eulerian component is able to relate variation in LAI to the corresponding variation in the major flow statistics. Thus, we examined whether the patterns predicted by CELC's Eulerian component are consistent with previous findings indicating that variation in LAI can possibility have conflicting effects on LDD by wind. We calculated how a typical 5-fold seasonal variation in LAI affects the following flow statistics: the 30-min time-averaged horizontal velocity (ū), the variance of the vertical velocity (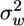), the turbulent shear stress (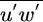), which measures the degree of interaction between the horizontal and vertical velocity turbulent excursions, and the mean turbulent kinetic energy dissipation rate (ε) at all levels within and above the canopy.

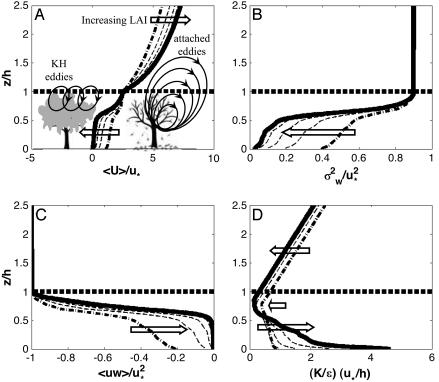
We found that a 5-fold seasonal variation in LAI, which has been measured in our study site and in many other deciduous forests (12), significantly changes the flow statistics both within and above the canopy (Fig. 2). In general, the principal flow statistics inside the canopy are more attenuated and less intercorrelated with increase in LAI. Increase in LAI tends to increase ū above the canopy and decrease 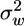and the inverse of ε for most of the vertical range where seeds are released. Consequently, the relaxation time scale (T_L), inversely related to ε but linearly related to 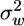, increases as LAI decreases, indicating that eddies above sparser canopies retain their kinetic energy over longer periods of time. Independently, we analyzed the high-frequency sonic anemometer data collected in our site, revealing, again, a more organized vertical eddy motion in periods of lower LAI: The long-term average vertical integral time scale I_w was 25% larger for the two winter months (low LAI) as compared with the two summer months (high LAI). Thus, these results are in close agreement with previous evidence for the existence of countering effects of more organized eddies as opposed to weaker windspeed above the canopy during periods of lower LAI.

Fig. 2.

Effects of LAI variation on major flow statistics needed by CELC. Increasing LAI (e.g., early spring to midsummer in temperate deciduous forests), indicated by the arrow, decreases mean horizontal wind velocity within the forest and has an opposite effect above the canopy (A). It also reduces the variance of the turbulent vertical velocity (B) and the turbulent covariance between horizontal and vertical winds (C), and decreases the so-called “relaxation time scale,” a measure of temporal organization of eddies in the vertical direction (D). The normalizing variables are the friction velocity above the canopy (u_*) and canopy height (h). In A we also provide a schematic representation of the primary mechanism that enhances LDD in sparse (low LAI) versus dense (high LAI) canopies, in which the dominant eddy motion is through attached and KH eddies, respectively.

Following the model evaluation steps, we explored its hypotheses about the effects of foliage density variation on wind (and therefore LDD) by running CELC simulations for a wide range of LAIs (= 1, 2,..., 5 m²·m^-2), seed release heights (H_r = 0.5 h, 0.55 h,..., 0.95 h, where h is the top canopy height), and terminal velocities (V_t = 0.45, 0.85,..., 1.65 m s^-1). Given the strong association between uplifting events and LDD (14–16), we focused on two response variables: the probability of uplifting (P_uplifted), estimated as the fraction of uplifting events from all dispersal events, and the mean distance traveled by uplifted seeds (D_uplifted). For the former variable, we also provide an empirical test for this relationship, using the fraction of seeds trapped above the canopy top as a rough estimate of the uplifting probability.

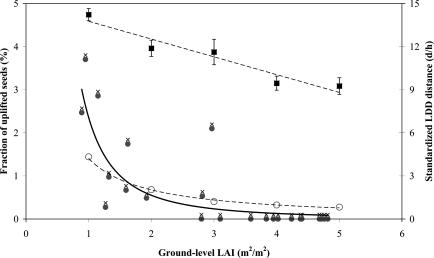
CELC's predictions suggest that lower LAI strongly promotes LDD (Fig. 3). The mean distance traveled by uplifted seeds (D_uplifted) increases linearly with decreasing LAI, whereas the increase in uplifting probability (P_uplifted) follows an inverse power law distribution. A power law relationship is also evident in our estimates of P_uplifted from the empirical dispersal data, which naturally show more scatter, but overall closely resemble the predicted relationship (Fig. 3).

Fig. 3.

The mean predicted distance traveled by uplifting seeds (filled squares), and the mean predicted (open circles) and observed (filled circles) uplifting probability, as a function of LAI. For generality, the dispersal distance (d) is standardized by the forest top canopy height (h), equal to 33 m in our site. The predicted values calculated by varying seed terminal velocity (V_t) from 0.5 to 2 m·s^-1, release height (H_r) from 0.5 to 0.95 h, and u_* are taken from the overall Weibull function (Table 1 and Fig. 4; u_* > 0.5 m·s^-1). The observed values are calculated as the fraction of seeds collected from traps above the top canopy height, from the total number of seeds collected from tower traps, for each census period (typically 1–2 weeks) for which LAI data were available. The predicted dispersal distances of uplifted seeds is a strong linear function of LAI (d/h = 15.00 - 1.24 LAI; R² = 0.92, P_(slope=0) < 0.001; upper dashed line). The predicted uplifted probability is very accurately described by an inverse power law function of LAI (d/h = 1.40 LAI^-1.05; R² = 0.99, P_(slope=0) < 0.001; lower dashed line). The observed estimates of uplifting probability include many zero values; hence, the distribution is not amenable for power law or exponential regression. A small increment of 0.1, indicated by crosses, gives a fair fit for the inverse power (d/h = 2.36 LAI^-2.10; R² = 0.76, P_(slope=0) < 0.001; solid line). We note that the parameter values for this inverse power function are extremely sensitive to the size of the increment, whereas the coefficient of determination is rather stable. This suggests that the inverse power law describes the observed pattern fairly well but precludes any interpretation from these specific parameter values.

In the last step of our model exploration, we run a formal sensitivity analysis to compare the relative impact of the observed variation in four major dispersal parameters (u_*, H_r, V_t, and LAI) on LDD. This formal sensitivity analysis (described in detail in Supporting Methods) reveals that under sparse canopy conditions (i) more seeds are uplifted (5 times more in LAI = 1 than in LAI = 5 for the same fecundity) and (ii) uplifted seeds travel longer distances, compared with dense canopy conditions (Fig. 6, which is published as supporting information on the PNAS web site). More specifically, it provides an order-of-magnitude formula for estimating the effects of u_*, H_r, V_t, and LAI on D_uplift approximately as

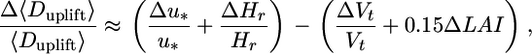leading to

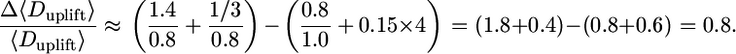Discussion

How Does Foliage Density Variation Affect Winds and Seed Dispersal by Wind? Our results strongly corroborate previous indications that the variation in canopy foliage affects wind flow in a manner that is likely to bear conflicting effects on LDD by wind. On the one hand, we confirm that the mean windspeed above the canopy increases as LAI increases, suggesting that uplifted seeds are likely to travel longer distances during periods of high LAI. On the other hand, we also provide evidence that vertical flow tends to be more organized as LAI decreases, suggesting that more seeds are likely to be uplifted and are expected to reach higher elevations (where windspeed is higher) and hence to travel longer distances during periods of low LAI. The clear linear negative correlation between the distance traveled by uplifted seeds and LAI (Fig. 3) suggests that the effects of more organized eddies in lower LAI are more important for LDD than the countering effects of weaker windspeed above the canopy.

To understand the principal mechanism underlying the non-trivial tendency for a higher degree of organization in lower LAI levels, we distinguish between two types of eddy motion within and above sparse versus dense canopies (Fig. 2 A). In sparse canopies, the flow is dominated by the so-called attached eddies, whose size increase linearly above the zero-plane displacement; they are primarily responsible for the existence of the logarithmic velocity profile in the atmospheric surface layer (26). The term “attached” is used because eddies are primarily impacted by the presence of a solid surface (boundary) and appear to originate from this (displaced) boundary. Dense canopies on the other hand, experience another type of eddy motion near the canopy top that resembles Kelvin–Helmholtz (KH) instabilities, often associated with mixing layers (rather than boundary layers). Mixing layers are formed when two coflowing fluids are injected at different velocities. The interface between these two fluids is known as a “free shear” layer, which is highly unstable and produces the KH instabilities (20). The mixing layer analogy to dense canopy flows becomes evident by noting that the mean velocity inside the canopy is considerably weaker than the mean velocity above the canopy (Fig. 2 A). This difference in flow velocity between the inside and above the canopy is responsible for the production of KH eddies. Unlike “attached” eddies, the KH eddies do not increase in size with increasing elevation; rather, their size is roughly constant and equals to 1/3–1/2 h.

Overall, we demonstrate that a decrease in LAI increases both dispersal distance and uplifting probability, chiefly the latter. Seeds dispersing late in the fall or early in spring (low LAI) are likely to encounter stronger winds within the canopy, with stronger and more frequent horizontal and vertical gusts, and more coherent eddies, compared with seeds dispersing in the midst of the growing season (high LAI). Each of these trends acts to enhance seed uplifting independently of the other trends. The combined outcome exhibits a synergetic effect, as reflected by the inverse power law relationship found, both numerically and empirically, between uplifting probability and LAI (Fig. 3) and in agreement with spore model calculations from pasture (27). In summary, lower foliage density should promote LDD by increasing the vertical (and therefore the horizontal) distance traveled by uplifted seeds, and mostly by increasing seed uplifting probability.

Relative Importance of Foliage Density Variation in Determining LDD. Our sensitivity analysis, which focuses on uplifted seeds because of their critical importance for LDD, suggests, in agreement with the previous studies (16, 28), that natural variation in wind velocity is still the most important singular agent controlling the distance traveled by uplifted seeds. Variation in windspeed is approximately two to three times more important than the variation in seed release height, terminal velocity, or foliage density taken separately and is equal to the combined effects of them all. The relative importance of the observed variation in LAI for LDD is equivalent to that of terminal velocity and seed release height. Note that for seed release height and especially for terminal velocity, the species-specific parameter range is considerably narrower than the range taken here for all species together (29). Thus, if we replace the global species values we selected for the sensitivity analysis equation with species-specific values, the effects of wind and LAI, being to a large extent species-independent, are likely to become even more significant. This corroborates the argument made by previous researchers (28–30), who questioned, at least for tree species, the traditional emphasis on seed terminal velocity as the key determinant of dispersal distance (31, 32). Overall, the results of this analysis highlight the important role of canopy foliage dynamics in LDD of seeds by wind, which is at least comparable to the effect of terminal velocity.

Ecological and Evolutionary Interpretations. Trees in temperate and tropical deciduous forests exhibit considerable variation in the timing of flowering, fruiting and dispersal (2–4). Studies of seed dispersal phenology, which may not necessarily coincide with fruiting phenology, emphasized links between seed dispersal and optimal conditions for survival and germination (3, 4). Most wind-dispersed species in seasonal tropical forests disperse during the end of the dry season, to coincide with the strong trade winds and the leaflessness of the forest canopies (3, 4). This has been vividly described by Daniel Janzen (33): “In the Central American lowland deciduous forests, heavy winds are common during the dry season. In the absence of foliage they occasionally reach the forest floor under the mature canopy. This is an excellent time for wide dispersal of airborne seeds.” The negative correlation between LDD and foliage density exemplified here may hold not only for seasonal phenological changes but also for natural disturbances. Hurricanes, ice storms, or wind damage act as a natural thinning processes, thereby reducing LAI and enhancing LDD.

Tree species in North American temperate deciduous forest are frequently classified into two major phenological groups (2, 34, 35). One group includes species that flower, fruit, disperse, and germinate within a short time early in the growing season. The second group includes trees that flower and fruit during the growing season, disperse their seeds at the end of the growing season, and germinate early in the following growing season. We found that both groups exhibit a common pattern in relation to the timing of seed dispersal: Their peak dispersal strongly coincides with the short period of a significant drop (in fall) or rise (in spring) of foliage density (Fig. 1), suggesting that both groups disperse seeds in low foliage conditions that give rise to LDD.

Seed production logically plays a critical role in the realization of the potential for LDD. Wind-dispersed trees generally produce large numbers of seeds annually (35). Dispersing seeds in relatively low foliage densities (LAI ≈ 1) at either the beginning or the end of the growing season, as has been observed in all of the seven tree species we investigated, has a 5-fold advantage as compared with dispersing seeds in high foliage densities (LAI ≈ 5) in the midst of the growing season (Fig. 3). That is, trees dispersing in full foliage conditions need to invest about five times more in seed production, for their seeds to escape the canopy and potentially experience an LDD equivalent to those seeds dispersing in leafless conditions.

Evaluating evolutionary interpretations of these findings is complicated by the fact that plant fitness is affected by numerous biotic and abiotic factors, each of which may select for a particular, possibly conflicting, phenological response. Moreover, it is difficult to separate causes and consequences: Do trees select to concentrate seed release in low foliage conditions to promote LDD, or are their seeds more likely to disperse in these periods because of the stronger winds? Whereas the former interpretation explicitly implies evolutionary strategy, the latter does not separate adaptive from random response. To tackle such complications, the study of the phenological strategy of plants in seasonal environments needs to incorporate different levels of complexity (3). Addressing this challenge for wind-dispersed species would necessitate a clear understanding of the role of internal and external factors, such as terminal velocity (at the seed level), physiology of seed abscission (at the branch level), the allocation of fruits along tree height (at the tree level), species composition (at the community level), and foliage density dynamics (at the ecosystem scale), all affecting the abscission of seeds and their movement through the air.