Development and comparison of model‐integrated evidence approaches for bioequivalence studies with pharmacokinetic end points

Abstract

By applying nonlinear mixed‐effect (NLME) models, model‐integrated evidence (MIE) approaches are able to analyze bioequivalence (BE) data with pharmacokinetic end points that have sparse sampling, which is problematic for non‐compartmental analysis (NCA). However, MIE approaches may suffer from inflation of type I error due to underestimation of parameter uncertainty and to the assumption of asymptotic normality. In this study, we developed a MIE BE analysis method that is based on a pre‐defined model and consists of several steps including model fitting, uncertainty assessment, simulation, and BE determination. The presented MIE approach has several improvements compared with the previously reported model‐integrated methods: (1) treatment, sequence, and period effects are only added to absorption parameters (such as relative bioavailability and rate of absorption) instead of all PK parameters; (2) a simulation step is performed to generate confidence intervals of the pharmacokinetic metrics for BE assessment; and (3) in an effort to maintain type I error, two more advanced parameter uncertainty evaluation approaches are explored, a nonparametric (case resampling) bootstrap, and sampling importance resampling (SIR). To evaluate the developed method and compare the uncertainty assessment methods, simulation experiments were performed for BE studies using a two‐way crossover design with different amounts of information (sparse to rich designs) and levels of variability. Based on the simulation results, the method using SIR for parameter uncertainty quantification controls type I error at the nominal level of 0.05 (i.e., the significance level set for BE evaluation) even for studies with small sample size and/or sparse sampling. As expected, our MIE approach for BE assessment exhibited higher power than the NCA‐based method, especially as the data becomes sparser and/or more variable.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Non‐compartmental analysis (NCA) is a standard method used in bioequivalence (BE) analysis. However, NCA typically requires rich pharmacokinetic (PK) sampling, which may not be feasible or practical in some situations. Model‐integrated evidence (MIE) approaches, based on nonlinear mixed‐effect modeling, may be useful for BE studies with sparse PK data, but may suffer from inflated type I errors.

• WHAT QUESTION DID THIS STUDY ADDRESS?

Can MIE approaches for BE analysis be improved to control type I errors, achieve high power, and have the ability to handle complicated PK models?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

Sampling importance resampling (SIR), a posterior distribution uncertainty assessment method that relaxes distributional assumption, is used in our novel MIE approach for BE assessment and shows maintained type I error in addition to high power. A simulation step in the method is able to handle models without analytical solutions for PK metrics, as well as use geometric mean ratio for BE inference.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Our novel MIE approach may provide an alternative to traditional BE approaches, especially in studies which require sparse PK sampling.

INTRODUCTION

In vivo bioequivalence (BE) studies typically compare the pharmacokinetics (PK) of two drug products or formulations. Such studies are required for most abbreviated new drug applications (ANDAs) when a biowaiver is not applicable, as well as new drug applications (NDAs) in the case of formulation changes during development or post‐approval. To evaluate the equivalence regarding the extent and rate of absorption of active ingredient or active moiety, PK metrics including area under the plasma concentration–time curve (AUC) and peak concentration (C _max) are compared between a reference product and a test product. ¹ In a conventional nonreplicated design (i.e., two‐treatment, two‐period, two‐sequence crossover study, also referred to as a two‐way crossover study), the 90% confidence interval (CI) of the test‐to‐reference geometric mean ratio (GMR) of a relevant PK metric should be within the regulatory criterion range of 0.8–1.25 to claim BE based on the two one‐sided tests (TOST) recommended by regulatory agencies. ² , ³ Common relevant PK metrics are AUC from 0 to the last sampling time (AUC_last), AUC from 0 to infinity (AUC_inf), and C _max. ¹

Non‐compartmental analysis (NCA) is widely used to analyze PK data for the calculation of individual PK metrics during BE analysis. However, NCA requires dense sampling times to achieve high accuracy, which may be problematic in special populations, such as oncology patients, or when sampling is collected from a biological matrix other than blood. On the other hand, nonlinear mixed‐effect (NLME) modeling applies a hierarchical model involving fixed effects for typical PK parameters and random effects accounting for individual variation from the typical values. In this approach, information is shared across subjects, and it is thus able to handle sparser data. In the literature, a series of methods that apply NLME for BE analysis have been proposed and evaluated. ⁴ , ⁵ , ⁶ , ⁷ Generally, the methods involve fitting an NLME model to the measured blood plasma drug concentrations in the BE study data, then using the model, parameter estimates, and uncertainty of those estimates to derive the ratios of model‐based PK metrics (AUC and C _max) and their uncertainty, which are used to assess BE based on the TOST.

However, the proposed methods have either failed to assess type I error ⁷ or have suffered from inflated type I error, likely due to either shrinkage for empirical Bayes estimates‐based BE analysis ⁵ , ⁶ or the application of an asymptotic approximation ⁴ that led to parameter uncertainty underestimation in the case of small sample sizes and/or sparse data. Recently, Loingeville et al. ⁸ explored three alternative methods to evaluate uncertainty of model parameters, based on which the standard error of related PK metrics is derived for BE tests. All three uncertainty methods proposed by Loingeville et al. ⁸ suggested a well‐controlled type I error. However, although the desired type I error was achieved, their developed methods depend on analytical solutions of AUC and C _max, which may not be available for complicated PK models, and furthermore, their proposed methods apply assumptions of normality to the uncertainty of parameters to construct the 90% CI of the metrics, which may cause type I problems in more complicated models.

In this work, we present a novel model‐integrated evidence (MIE) approach for BE assessment with improvements compared with the previous methods. Firstly, effects for treatment, sequence and period are only specifically added to absorption parameters, including bioavailability (to assess relative changes), because BE studies aim to test for the difference in drug absorption between two formulations and generally assume that the drug molecule behavior is the same after being absorbed into the system. Secondly, a simulation step to compute PK summary metrics is added in the analysis procedure as opposed to a dependence on distributional assumptions about the population and parameter uncertainty to calculate the 90% CI. In addition, the simulation step allows the method to handle complex PK models defined by ordinary differential equations (ODE) in addition to simple models with available analytical solutions. Lastly, two additional advanced parameter uncertainty methods are implemented to better control type I error. The first method is the nonparametric (case resampling) bootstrap method. Although the nonparametric bootstrap approach was first explored by Hu et al. ⁷ on PK BE data, there has not been any study reported to systematically evaluate its performance. The second method we investigate is sampling importance resampling (SIR), originally developed by Rubin, ⁹ and extended to NLME models by Dosne et al. ¹⁰ , ¹¹ These methods for uncertainty are compared with a variance–covariance matrix estimate of parameter uncertainty based on the sandwich estimator, ¹² a robust variance estimator that is widely used in population pharmacokinetic/pharmacodynamic (PK/PD) modeling but requires distributional assumptions when computing CIs of the required PK metrics for BE evaluation. An advantage of both bootstrap and SIR is that they generate a nonparametric, potentially asymmetric, uncertainty distributions ¹¹ unlike the covariance method. Moreover, SIR is often significantly faster than bootstrap. ¹¹

In this study, we also evaluated the presented MIE approach with three parameter uncertainty assessment methods, and compared this approach to the NCA‐based BE analysis in terms of type I error and power through simulation experiments with different levels of data sparsity and population variation. An ideal method is expected to achieve high power while maintaining type I error at a pre‐set significance level.

METHODS

Standard BE method

In the standard BE method, for a two‐way crossover study, a linear mixed‐effect model is fit on log‐transformed individual PK metrics measured using NCA. ²

$$\begin{array}{c}\log \left({\psi }_{\mathrm{mik}}\right)={\alpha }_m+{\beta }_{m,\mathrm{TRT}}{\mathrm{TRT}}_{\mathrm{ik}}+{\beta }_{m,\mathrm{SEQ}}{\mathrm{SEQ}}_{\mathrm{i}}\hfill \\ +{\beta }_{m,\mathrm{PER}}{\mathrm{PER}}_k+{\eta }_{\mathrm{mi}}+{\epsilon }_{\mathrm{mik}}\hfill \end{array}$$ (1)

where ${\psi }_{\mathrm{mik}}$ is the measured value of the mth PK metric (i.e., AUC_last, AUC_inf, or C _max) of the ith subject at the kth period. The covariates related to the BE study design include treatment (${\mathrm{TRT}}_{\mathrm{ik}}$), sequence (${\mathrm{SEQ}}_i$), and period (${\mathrm{PER}}_k$) with 0 for reference and 1 for the alternative. The corresponding coefficients are indicated by ${\beta }_{m,\mathrm{TRT}}$, ${\beta }_{m,\mathrm{SEQ}}$ and ${\beta }_{m,\mathrm{PER}}$. The intercept term of the regression level is indicated with ${\alpha }_m$. ${\eta }_{\mathit{mi}}$ is the random effect corresponding to between‐subject variation (BSV) and ${\epsilon }_{\mathrm{mik}}$ is the residual error accounting residual unexplained variation for single observations per occasion (AUC_last, AUC_inf, or C _max), including between‐occasion variation (BOV). Since the comparison of PK between the two treatments is of interest, the BE conclusion is based on the 90% CI of ${\beta }_{m,\mathrm{TRT}}$ that is built on its point estimate and standard error as well as a t‐distribution. The resultant CIs for all PK metrics should be completely within log(0.8) and log(1.25) to claim BE.

Model‐integrated evidence method

Herein, we present an MIE approach for BE evaluation, which is different from the standard BE method in several aspects (Table 1). The method consists of several steps including (1) model fitting, (2) parameter uncertainty assessment, (3) using the model and uncertainty to enumerate the differences in summary PK metrics between treatment and reference through population simulations, and (4) drawing a BE determination (Figure 1).

TABLE 1.

Comparison between the standard NCA‐based method and the model‐integrated evidence (MIE) approaches presented in this paper for BE evaluation.

Step	Standard BE method	Developed MIE approach
Model fitting	Linear mixed‐effect model on log‐transformed individual PK metrics measured using NCA	Nonlinear mixed‐effect model on observed concentrations
Random‐effect levels	BSV (per PK metric)	BSV (per parameter), BOV (per parameter)
Parameter uncertainty distribution assessment	Standard error (SE) for fixed effects calculated from the least square method, assuming t‐distribution	Parameter uncertainty is calculated by one of: Covariance matrix, assuming a normal distribution Sampling importance resampling (SIR) Case‐resampling bootstrap
Construction of a 90% confidence interval	From the estimate of the coefficient of treatment effect (${\beta }_{m,\mathit{TRT}}$) and the parameter uncertainty distribution	Population simulation of summary PK metrics from population PK model, parameters, and uncertainty distributions

FIGURE 1.

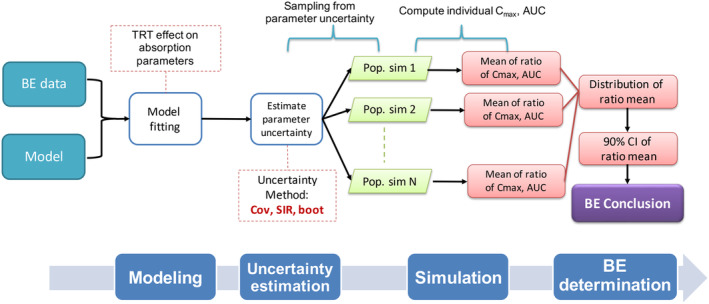
Overview of our developed model‐integrated evidence approaches for bioequivalence (BE) analysis. The method consists of four steps: (1) model fitting using a pre‐defined model for the reference product with additional treatment effect (TRT), sequence effect (SEQ), and period effect (PER) on absorption parameters including bioavailability (F, F is assumed to be 1 for the reference product); (2) uncertainty assessment using covariance matrix (Cov), sampling importance resampling (SIR), or nonparametric bootstrap (boot); (3) simulation for population (i.e., with a large subject number), which can be changed to simulation for a typical subject; and (4) conclusion based on the 90% confidence interval (CI) of the geometric mean ratio obtained from the simulation step.

Step 1: Model fitting

The pre‐defined NLME model for reference drug

In this work, we assume that there is a pre‐defined NLME model to describe the PK of the reference drug, which can be formulated as:

$$y_{\mathit{ijk}}=f\left({\mathit{\theta }}_{\mathit{ik}},t_{\mathit{ijk}}\right)+h\left(f\left({\mathit{\theta }}_{\mathit{ik}},t_{\mathit{ijk}}\right),{\epsilon }_{\mathit{ijk}}\right)$$ (2)

$${\theta }_{\mathit{lik}}=g\left({\mathrm{TV}}_l,{\eta }_{\mathit{li}},{\kappa }_{\mathit{lik}}\right)$$ (3)

The observed drug concentrations are indicated by $y_{\mathit{ijk}}$ for the ith subject at the jth sampling of the kth period. The PK model consists of a structural model defined by a vector of PK parameters, (${\mathit{\theta }}_{\mathit{ik}}$). The individual parameters of ${\mathit{\theta }}_{\mathit{ik}}$ are denoted as ${\theta }_{\mathit{lik}}$ which is specifically for the lth parameter. ${\theta }_{\mathit{lik}}$ is defined in Equation 3 by typical values of the parameter (${\mathrm{TV}}_l$), and potentially, random effects for BSV (${\eta }_{\mathit{li}}$) and BOV (${\kappa }_{\mathit{lik}}$) through the function $g$. The residual error is indicated by the function of $h\left(f\left({\mathit{\theta }}_{\mathit{ik}},t_{\mathit{ijk}}\right),{\epsilon }_{\mathit{ijk}}\right)$, and is assumed to be zero when ${\epsilon }_{\mathit{ijk}}$ is zero. ${\eta }_{\mathrm{l}i}$, ${\kappa }_{\mathrm{li}k}$, and ${\epsilon }_{\mathit{ijk}}$ are assumed to follow multivariate normal distributions with the mean of zero and variance matrices ($\mathrm{\Omega }$, $\mathrm{{\rm K}}$, and $\mathrm{\sum }$, respectively), the off‐diagonal elements of which represent variance (denoted by ${\omega }_l^2$, ${\gamma }_l^2$, and ${\sigma }^2$, respectively).

The model used in the model fitting step

The general purpose of a BE study is to compare the rate and extent of absorption of the active ingredient or moiety from two drug products or formulations. Therefore, extra parameters are added to the absorption parameters of the pre‐defined NLME model to generate a model to fit the BE data. Specifically, parameters defining treatment effect (${\beta }_{l,\mathrm{TRT}}$) are added to each absorption parameter in the model, such as the rate of absorption and bioavailability between test and reference compound (bioavailability is added to the reference model and fixed to 1 if not present in the pre‐defined model, thus ${\beta }_{F,\mathrm{TRT}}$ represents the relative change in bioavailability across treatments). In the case of crossover BE studies, additional parameters for sequence effect (${\beta }_{l,\mathrm{SEQ}}$) and period effect (${\beta }_{l,\mathrm{PER}}$) are added to each absorption parameter, in the following form:

$${\theta }_{\mathit{lik}}=g\left({\mathrm{TV}}_l,{\eta }_{\mathit{li}},{\kappa }_{\mathit{lik}}\right)·{\left({\beta }_{l,\mathrm{TRT}}\right)}^{{\mathrm{TRT}}_{\mathit{ik}}}·{\left({\beta }_{l,\mathrm{SEQ}}\right)}^{{\mathrm{SEQ}}_i}·{\left({\beta }_{l,\mathrm{PER}}\right)}^{{\mathrm{PER}}_k}$$ (4)

It should be noted that in certain design situations, a model with both BSV and BOV on all the parameters may not be identifiable. Therefore, the model used in the MIE approach for BE assessment may not include BSV and BOV on each parameter.

Estimation of model parameters is performed using NONMEM 7.4 (Icon Development Solutions, Hanover, MD) ¹³ facilitated by Perl‐speaks‐NONMEM (PsN) ¹⁴ with the first‐order conditional estimation method with interaction (FOCEI). Supplementary Material S1 provides examples of NONMEM model codes. To ensure the quality of the resultant model, the NONMEM fitting process is required to be free of warnings, such as rounding errors or estimates near boundaries. In addition, the method provides an option for testing the identifiability of models by detecting saddle points using the saddle‐reset ¹⁵ setting in NONMEM. Briefly, the estimation result is acceptable if changes are small in objective functions value (absolute change <1) and in parameter estimates (<10%) comparing before and after saddle‐reset.

Step 2: Uncertainty assessment

In order to build 90% CIs of PK metrics, parameter uncertainty (including the distribution of that uncertainty) needs to be assessed. There are three methods in our MIE approach to select for uncertainty assessment, all of which are implemented in NONMEM.

Covariance matrix

A covariance matrix for all model parameters is obtained using the sandwich estimator ¹² (the default “$COV” method in NONMEM). Based on the resultant covariance matrix as well as parameter estimates, a series of parameter vectors are sampled assuming a multivariate normal distribution for further model simulations.

Bootstrap

Nonparametric (case resampling) bootstrap is carried out. In this procedure, sampling with replacement for individual data is performed stratifying on sequence. Thereafter, each bootstrap dataset is analyzed through model fitting and the resultant parameter estimates from all the datasets describe the uncertainty of the model parameters.

Sampling importance resampling (SIR)

The SIR method consists of the steps of sampling, importance weighting, and resampling. ¹⁰ , ¹¹ It is possible to iterate the SIR steps multiple times. For the first iteration, the proposal distribution is a normal distribution or a t‐distribution with the parameter estimates as a mean vector and the covariance matrix estimated from the sandwich estimator. For the following iterations, the proposal distribution is the resultant distribution from the last iteration. The final result of SIR is parameter vectors resampled from the last iteration. To avoid uncertainty underestimation, options are provided to sample parameters in a wider range than the proposal distribution by setting the acceptance ratio less than 1 and/or sampling from a t‐distribution.

Step 3: Simulation

The purpose of the simulation step is to create a density distribution for the geometric mean of PK metrics (i.e., AUC and C _max) derived from the model, parameter estimates, and parameter uncertainty. Unlike clinical trial simulation (CTS), the simulation in this step aims to obtain C _max and AUC and their uncertainties informed by the fitted model. For example, the C _max based on the model is obtained either from available analytical solutions or from the maximal concentration of a simulated continuous PK curve but not the maximum observation in a CTS, which would also account for residual errors. For each simulation, one set of the model parameter vector obtained from the uncertainty distribution (Step 2) is used. The number of simulations should be large (e.g., 1000 simulations) to ensure the accuracy of the resultant distributions, from which the BE conclusions are drawn. In the methods presented here, there are two types of simulations available to choose from:

• (1)Simulation of a typical subject. In this type of simulation, only parameters of fixed effects are used to simulate a rich PK study for a single typical subject. As a result, the mean ratio is the metric ratio on the typical subject. In this type of simulation, it is assumed that the typical subject represents the geometric mean of the population.
• (2)Population simulation, where a PK study in a population is simulated including a large number of individuals (e.g., 1000 subjects). The individual PK parameters are randomly sampled from the random effect model.

Certain design aspects of the BE study during the simulation step are consistent with that of original BE study such as dosing and sampling duration. To specifically evaluate the estimate of treatment effect, other covariates are not included in the simulations, that is, no sequence or period effects in the case of crossover studies.

From each simulation, there are two ways to obtain metrics:

• (1)For models where analytical solutions are available for AUC and C _max, metric values are directly calculated based on PK parameters, either through typical value calculations (when simulating the typical subject), or individual predictions (when simulating populations).
• (2)For complicated models where analytical solutions for AUC and C _max are not available (e.g., a model with Michaelis–Menten elimination for nonlinear PK), PK profiles for a typical subject or individuals in a population are simulated using NONMEM based on ODE without considering residual errors, and the PK metrics are then calculated based on these simulated curves. We evaluated this calculation method for PK metric and it showed relative accuracies of above 99.9% with the default time step for the models investigated in this article, where both analytical and ODE solutions could be generated. Accuracy can be improved by adjusting the integration time step using MTIME in NONMEM. An example NONMEM simulation code (without MTIME) is provided in Supplementary Material S1.

After simulating PK profiles and computing PK metrics, the geometric mean of the ratio (either typical ratio or GMR for population simulation) is calculated for each simulation. Across all simulations, density distributions of mean ratios are obtained.

Step 4: BE determination

Based on the resultant density distributions of mean ratios, a conclusion is reached whether the two products are considered BE. Briefly, for each related PK metric, the nonparametric 5th and 95th percentiles are calculated from the distributions and form the 90% CI of the mean ratio. If the entire CI is within the regulatory limits of 80–125%, BE is concluded. Typically, for BE to be claimed, all metrics must show BE, otherwise, the tested product fails the BE test.

Simulation experiment

Simulation experiments were carried out using R to evaluate the performance of the presented MIE approach compared with the standard NCA‐based BE method. The simulation settings were similar to the previous studies, ⁴ , ⁵ , ⁶ which were based on PK data of the anti‐asthmatic drug theophylline.

Study design

A standard two‐treatment, two‐period, two‐sequence crossover design was applied for the simulation experiment with an oral dose of 4 mg. To evaluate BE analysis methods for different levels of data sparsity, datasets were simulated under four study designs, with different combinations of number of subjects (N) and number of samples (n):

• (1) N = 40, n = 10, sampling times at 0.25, 0.5, 1, 2, 3.5, 5, 7, 9, 12, 24;
• (2) N = 24, n = 10, sampling times at 0.25, 0.5, 1, 2, 3.5, 5, 7, 9, 12, 24;
• (3) N = 24, n = 5, sampling times at 0.25, 1.5, 3.35, 12, 24;
• (4) N = 40, n = 3, sampling times at 0.25, 3.35, 24;

Pharmacokinetic model

The model that was used to generate all the datasets for the simulation experiment was a one‐compartment PK model with first‐order absorption and first‐order elimination. The typical values of pharmacokinetic parameters for reference product were 40.36 mL/h for clearance (CL), 480 mL for volume of distribution (V), 1.48 h⁻¹ for rate of absorption (ka), and 1 for bioavailability (F). In order to guarantee the identifiability of model parameters in a non‐replicate crossover study, the following log‐normally distributed random effects were used: (1) low variance: ${\omega }_{\mathit{CL}}^2$ = ${\omega }_{\mathit{ka}}^2$ = 0.04; ${\omega }_V^2$ = 0.01, ${\gamma }_F^2$ = 0.01; (2) high variance: ${\omega }_{\mathit{CL}}^2$ = ${\omega }_{\mathit{ka}}^2$ = ${\omega }_V^2$ = 0.25, ${\gamma }_F^2$ = 0.0225. A proportional error model was used for residual variability with a variance σ ² = 0.01. No effect was included for sequence or period covariates (i.e., ${\beta }_{l,\mathit{SEQ}}$ = ${\beta }_{l,\mathit{PER}}$ = 1 for all individuals), while the treatment effect was only included in relative bioavailability (${\beta }_{F,\mathit{TRT}}$) but not on the rate of absorption. In that case, ${\beta }_{F,\mathit{TRT}}$ directly corresponds to the test‐to‐reference ratio of metrics. Therefore, ${\beta }_{F,\mathit{TRT}}$ was set to 0.8 or 1.25 to test for type I error, and ${\beta }_{F,\mathit{TRT}}$ was set to 0.9 to test for power. On the other hand, a treatment effect on the rate of absorption does not have such a simple relationship with metric ratios (Supplementary Material S2), and thus it was not included in the true model for the convenience of type I error and power evaluation.

Analysis

The simulated BE datasets were analyzed using the following methods for BE assessment:

MIE approach

The PK model used during the MIE approach for BE assessment was similar to the simulation model described above except that all covariate effects were estimated, that is, treatment, sequence, and period effects for absorption parameters (bioavailability and rate of absorption). All the three uncertainty methods (covariate matrix, SIR, and bootstrap) were evaluated. For SIR, the proposal distribution was set as a t‐distribution and IACCEPT was set as 0.4 to ensure that an initial sampling distribution was wide enough to encompass the potential parameter uncertainty distribution. SIR was performed for six iterations with 2000 samples generated for each iteration. From each of the three uncertainty methods, 1000 sets of population parameter vectors were generated from the parameter uncertainty distribution for the simulation step, and mean ratios of metrics were computed for the typical subject.

NCA‐based BE method

The NCA analysis of the simulated datasets was performed using the ncappc ¹⁶ package in R. AUC was calculated based on the linear‐up, log‐down trapezoidal rule. A linear mixed‐effect model was fit to the logarithm of metrics using the nlme R package ¹⁷ to estimate treatment, sequence, and period effects. The 90% CIs of the coefficient for treatment effect were obtained from the regression and used for hypothesis testing for BE based on TOST.

Evaluation

BE datasets were generated for each of the four investigated study designs in this simulation experiment and for three different values of the simulated treatment effect, with both high and low variation in the data (24 total scenarios, each with 500 simulations). For each scenario, the percentage of cases concluding BE was calculated for each analysis method and PK metric, respectively. The resultant percentage is the PK metric‐specific type I error (when the simulated treatment effect is 0.8 or 1.25) or study power (when the treatment effect is set to 0.9). For the design with only three sampling points, the result for AUC_inf with the NCA method was not included due to the difficulty of estimating extrapolated AUC. Lastly, the overall type I error or power was obtained by calculating the percentage of cases concluding BE for all the relevant PK metrics.

RESULTS

Figure 2a shows that the type I errors for the three PK metrics with the simulated treatment effect set to 0.8 were within the target range (computed as a 95% prediction interval based on the binomial distribution, that is, 3.2–7.0%), indicating that the observed type I error was not significantly different from 5% in an exact binomial test given a significance level of 5% and 500 simulations. However, the overall type I errors for the final BE determination (Figure 2b), based on all three PK metrics meeting the BE acceptance criteria, were deflated for the standard NCA method in 6 out of the 8 scenarios (1.8–2.6%). In other words, the overall type I errors were significantly lower than the target 5%, indicating the conventional NCA method was overly conservative in terms of the final BE determination. The MIE approach, on the other hand, maintained the overall type I errors around 5% for most scenarios.

FIGURE 2.

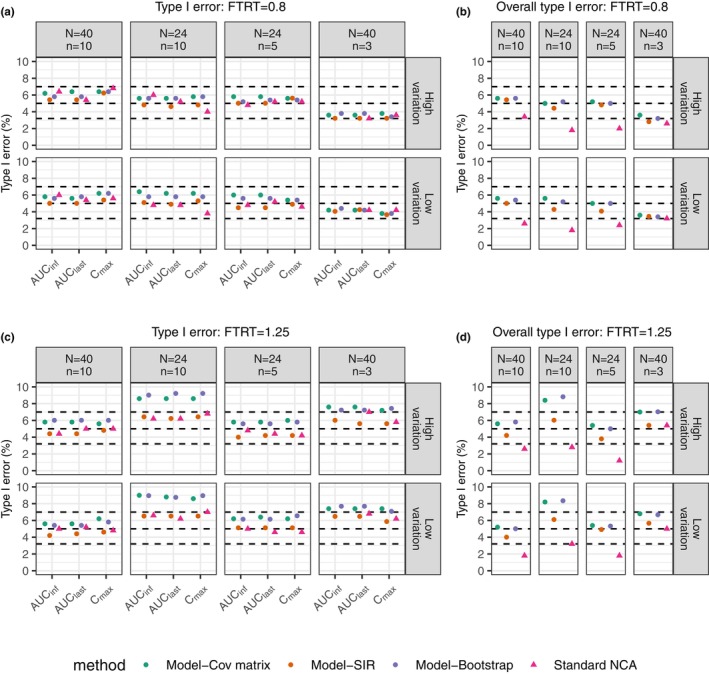
Comparison in type I error between the standard NCA‐based BE method and model‐integrated evidence approaches using different uncertainty assessment methods including covariance matrix (Cov matrix), SIR, and nonparametric bootstrap for true treatment effect set at 0.8 (a and b) and 1.25 (c and d). Left plots (a and c) show type I error of BE tests from individual PK metric. Right plots (b and d) show overall type I error of final results that concludes BE only when all related metrics pass BE. It is noted that the overall type I error is based on C _max, AUC_last, AUC_inf except for the scenario (N = 40, n = 3), where only C _max and AUC_last are involved since AUC_inf could not be correctly estimated using the standard NCA method. For the sake of comparison among methods, AUC_inf is not considered for any of the methods in this scenario. The horizontal dashed lines indicate nominal level (5%), as well as its 95% prediction interval (3.2%, 7%) for 500 simulations. N represents subject number and n represents the number of samples per person in each simulated dataset.

For the simulation experiment with the treatment effect equal to 1.25 (Figure 2c,d), the standard NCA method exhibited deflated overall type I errors (1.2–2.8%) in 5 out of the 8 scenarios, while the type I errors for each metric were around 5%. The MIE approach using the SIR uncertainty method had maintained type I errors in all simulation experiments (4.0–6.5% for all individual PK metrics and 3.8–6.1% for overall BE). On the other hand, the MIE approach with the covariance matrix and bootstrap methods for uncertainty assessment had inflated type I error in 4 out of 8 scenarios for the individual PK metrics (7.2–9.2%) and in 2 of 8 scenarios for the overall type I errors (8.2–8.8%). More investigation was performed by repeating the simulation experiment for one scenario (N = 24, n = 10 with high variation), the results of which are listed in Supplementary Material S3. The additional simulation experiment showed a type I error of around 7% for the MIE approach with the covariance matrix (Figures S3‐1 and S3‐2). The magnitude of difference among repeated simulation experiments is closely related to the simulation size. A simulation experiment with 500 simulations had a lower power to detect a deviation from the target of 5% compared with larger simulation numbers (Figure S3‐3). The MIE approach with SIR maintained the type I errors in all simulation scenarios, which is strong evidence for that SIR adequately estimated the parameter uncertainty distributions.

The power of the standard NCA method was lower than that of the MIE approaches for all scenarios (Figure 3). Larger differences between the standard NCA method and the MIE approaches are seen with high data variation and with lower numbers of subjects. It should be noted that the sampling times for the 3‐and 5‐sample scenarios were optimized for population parameter estimation based on optimal design theory in the previous study, ⁶ and this could be the reason that the number of individuals was more influential on the power than the number of observations. The overall powers (Figure 3b) of the MIE approaches were all above 80%, similar to its power for individual metrics. However, for the high variation case, the overall power for the standard NCA method was reduced to ~60% for the two scenarios with 24 subjects.

FIGURE 3.

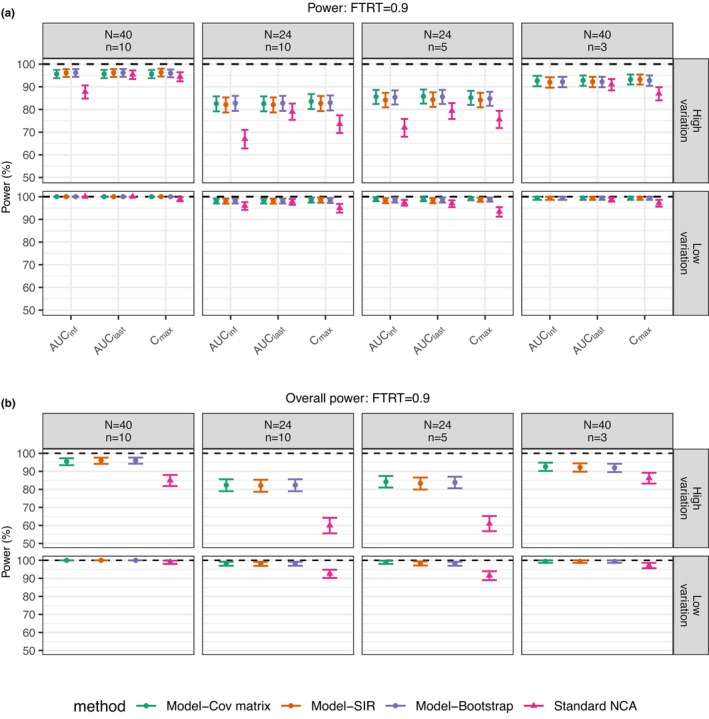
Comparison in power between standard NCA‐based BE method and model‐integrated evidence approaches using different uncertainty assessment methods including covariance matrix (Cov matrix), SIR, and nonparametric bootstrap with true treatment effect set at 0.9 for individual metrics (a) and final BE conclusion (b). It is noted that the overall power is based on C _max, AUC_last, AUC_inf except for the scenario (N = 40, n = 3), where only C _max and AUC_last are involved since AUC_inf could not be correctly estimated using the standard NCA method. For the sake of comparison among methods, AUC_inf is not considered for any of the methods in this scenario. The horizontal dashed lines indicate power at 100%. The error bar is 95% confidence interval for power based on the binomial distribution for 500 simulations. N represents the subject number and n represents the number of samples per person in each simulated dataset.

Figure 4a shows that the medians of the estimated means of the log(ratio) in each scenario from the 500 simulations were around the true value, log(1.25), indicating unbiased estimation for all the analysis methods. However, Figure 4b shows different uncertainty, indicated by the standard error (SE) for PK metrics, for different methods. Among the MIE approaches for BE assessment, the covariance matrix and bootstrap uncertainty methods exhibited lower uncertainty than the SIR uncertainty method, and may explain the inflated type I errors in certain scenarios due to underestimation of the uncertainty in the CIs of the PK metric GMRs. It is seen that the estimated uncertainty of the standard NCA approach was right‐skewed for AUCinf, with some cases having relatively large uncertainty, suggesting that an extrapolation problem of AUCinf estimation existed even for rich sampling in the case of high variation. This result may explain the low power of the standard NCA method in these situations (the corresponding plot is not shown here but is similar to Figure 4b).

FIGURE 4.

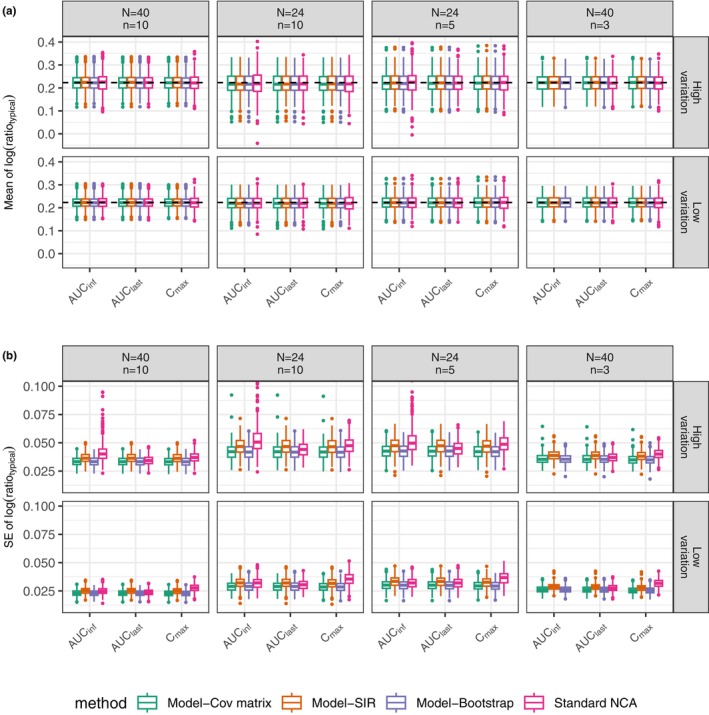
Boxplots for the mean of the natural logarithm of metric ratio for a typical subject (a) and its standard error (SE) (b) from the simulation experiment with the true treatment effect at 1.25. The comparison is between standard NCA‐based BE method and the model‐integrated evidence approaches using different uncertainty assessment methods including covariance matrix (Cov matrix), SIR, and nonparametric bootstrap. The natural logarithm of 1.25 (0.223) is indicated by the dashed horizontal line (a). N represents the subject number and n represents the number of samples per person in each simulated dataset.

To further compare the two simulation approaches (i.e., simulation for a typical subject and population simulation) of the MIE approach, additional simulations were performed with detailed methods and resulted in Supplementary Material S2. The results showed that the typical values of AUC_last and C _max were different from their geometric means (Figures S2‐1A, S2‐2A, S2‐3A). As for ratios, GMR and typical ratio were consistent if the two products differed in only bioavailability (Figure S2‐1B). While they exhibited discrepancy for AUC_last and C _max if the treatment effect was on the rate of absorption (Figures S2‐2B, S2‐3B, S2‐4).

The evaluation of the MIE approach was mainly performed for scenarios of different bioavailability between two products, implemented in the simulations via a treatment effect by changing the relative bioavailability. That treatment effect is equal to the true GMR for all PK metrics. In the scenario of different absorption rates, a treatment effect on KA will not be proportional to the GMR of C _max (Figure S2‐4). For example, to achieve a C _max GMR of 0.8 for type I error evaluation, the simulated treatment effect on KA would need to be set to 0.3, a large difference that is not common in real examples. Nevertheless, we investigated this scenario in the case with high variation, and simulations showed controlled type I error and high power (results not shown).

DISCUSSION

In the present work, we developed a MIE approach for evaluating BE that is capable of analyzing sparse PK data. Our study showed that our novel MIE approaches for BE assessment had higher power than the standard NCA method (Figure 3) while controlling type I errors (Figure 2) in a series of diverse scenarios. Larger differences in power between the MIE approach and the NCA‐based method were seen with high data variation and with lower numbers of individuals. These results should not be surprising as the MIE approach applies NLME modeling that shares information among all subjects (i.e., borrowing strength over subjects) and therefore achieves higher power, ¹⁸ especially with sparse sampling. On the other hand, NCA analyzes individual PK profiles separately and may present challenges with accurately estimating PK metrics in the case of sparse sampling. For example, the accuracy of C _max estimates tends to decline with sparse sampling. Furthermore, in the simulation experiment with only three samples, AUC_inf could not be calculated using the NCA approach because of the difficulty in AUC extrapolation to infinity. In addition, the NCA approach needs a long sampling duration. Otherwise, the AUC_inf measurement is sensitive to high variation PK, suggested by the high variation of AUC_inf shown in Figure 4b, which led to lower power compared with AUC_last and C _max when using the NCA approach (Figure 3a). It should be noted that it is recommended to collect 12–18 samples per subject per dose for BE studies. While the sampling times used in the presented experiment study were set the same as in previous publications to compare between different MIE approaches in different levels of sparsity. ⁴

In the case of BE tests, a BE conclusion is claimed only if the null hypotheses (bioinequivalence) are rejected for tests on all metrics, ² that is, accepting all alternative hypotheses (bioequivalence). Such multiple comparisons are one of the reasons that the overall type I error of the NCA‐based method was deflated for some scenarios. Similarly, the overall powers of the NCA‐based method were lower than the power for individual metrics (Figure 3b). However, this effect was not as pronounced with the MIE approaches. One explanation may be that the MIE approaches integrate the information over all samples for all tests by adding treatment effects on related absorption parameters so that the conclusion for each metric is based on all data instead of heavily depending on the information of certain sampling points. Although treatment effect is expected only for absorption parameters, it is possible that there exists period or sequence effects on other PK parameters. However, adding these effects on all parameters may lead to an unidentifiable model. As a result, we propose only adding these effects to absorption parameters for parsimony. Note that period and sequence effects on relative bioavailability will also affect other parameters, such as apparent clearance and apparent volume of distribution.

In an effort to control type I error of the presented MIE approaches for BE determination, we investigated a series of methods for uncertainty assessment. A good method of assessing parameter uncertainty is expected to control type I errors at a pre‐defined significance level. The covariance matrix method estimates uncertainty based on an asymptotic approximation to the inverse of the fisher information matrix (FIM) in combination with an assumption of a multivariate normal distribution. However, the asymptotic condition is not achieved when analyzing small sample size and/or sparse BE data, which may lead to underestimation of uncertainty and thus inflation of type I error. Loingeville et al. ⁸ have recently suggested that scaling the FIM‐based on the number of subjects and the number of parameters in a model may correct the inflated type I error due to this asymptotic assumption.

A second uncertainty assessment approach used in this work is a nonparametric (case resampling) bootstrap. The nonparametric bootstrap uses observed data as a guess of the population and assesses uncertainty by sampling from the “population” multiple times. Nevertheless, bootstrap methods may underestimate the coverage of the CI for a small sample that is not large enough to represent the population. ¹⁹ Furthermore, the bootstrap approach is more computationally intensive compared with other methods. ¹¹

The third approach to uncertainty estimation investigated was using the SIR procedure, which obtains a posterior distribution of parameter uncertainty based on the performance of sampled parameters in describing the data. It has been demonstrated in this work that SIR maintains type I error around the nominal level (Figure 2). Similarly, Loingeville et al. ⁸ also showed that another method for generating a posterior distribution, Hamiltonian Monte‐Carlo (HMC), controlled type I error in evaluating BE. Considering their performance in controlling type I errors and the relatively low computational burden compared with bootstrap, uncertainty methods based on a posterior distribution such as SIR and HMC are a promising strategy for controlling type I error in the MIE approaches.

The MIE approaches for BE determination investigated here include a simulation step, where each simulation is based on a sample drawn from the parameter uncertainty distribution, allowing for simulations based on non‐normal uncertainty distributions. This is in contrast to the approach suggested by Loingeville et al. ⁸ where different methods of uncertainty calculation are only used to more accurately assess the variance of an assumed normal distribution for parameter uncertainty when performing a Wald test. Although this normality assumption may be supported by the central limit theorem, it may not hold for small sample sizes.

In addition to handling models without explicit analytical solutions, the simulation step in the presented method allows for direct calculation of the GMR through population simulations instead of ratios calculated based on the typical subject. Supplementary Material S2 shows that the geometric means (for metrics and test‐to‐reference ratio of metrics) may be different from typical values depending on the difference between the products (i.e., the difference in the aspects of absorption, rate, or extent). To be in accordance with regulatory criteria, ² GMR is the better option for BE evaluation considering that the impact of formulation differences on the rate of absorption is unknown. The simulations also showed that the values of geometric means and GMR also depended on BSV and BOV, as well as their variation magnitudes (Figures S2‐1, S2‐2, and S2‐3). Thus, the PK model used in the MIE approach should contain random effects present in the data, especially BOV if possible. BOV can be added not only to bioavailability (as in the simulation experiments), but also to other PK parameters. It is also noted that in the presented simulation experiment the treatment effect was set on relative bioavailability, in which case the typical ratio and GMR are consistent (Figure S2‐1). As a result, we used a typical ratio for BE conclusion that was expected to give similar results to GMR for the purpose of shortening the running time of the simulation experiments.

In the current study, the MIE approaches with SIR for uncertainty estimation‐controlled type I error and had a high power for BE evaluation for sparse BE data. By using NLME, the MIE approaches for BE assessment may be a promising tool for other situations for generic drug evaluation, such as highly variable drugs and drug products with long half‐life. Möllenhoff et al. ²⁰ explored a different statistical approach, the bioequivalence optimal test, as an alternative to the TOST to improve the power for BE analysis in highly variable drugs. In future work, incorporating this approach into our method may give further improvements.

Previous and presented MIE approaches for BE assessment were evaluated under the situation that the analysis model was the data‐generating model. That may be approximately the case when there is a well‐developed population PK model available for reference products. However, there may not exist a well‐developed population PK model for certain products, in which case a model‐building procedure may be necessary. However, complex model exploration may impair the type I error of confirmative analyses. ⁷ One recommendation is to make a pre‐specified analysis plan or to prespecify model(s). ⁷ In this aspect, more efforts are needed to evaluate the impact of model misspecification on method performance.

In the current work, the simulation experiment was performed for oral drug examples. However, the developed MIE approaches can be used for drugs with other types of extravascular administration. It should be noted that some other extravascular administrations may lead to extremely sparse data (e.g., ophthalmic drugs) or require complicated absorption models (e.g., long‐acting injectables). In both scenarios, PK models may not be identifiable in a BE study design despite being available in the literature. One promising strategy for the above concerns is through model averaging, which performs analyses based on a series of pre‐defined models. ²¹ , ²² In addition, averaging over several models avoids the model‐building process and may help with the problem of model misspecification without assuming only one model. Current investigations are extending the proposed MIE approach by utilizing the model averaging approach. To ensure easy access to these proposed methods, an open‐access R package is also being developed that features an interactive web app using shiny. ²³

In summary, our MIE approach for BE assessment using SIR shows controlled type I error and higher power compared with NCA‐based method. Our study demonstrates that the presented method serves as a promising tool to analyze BE with sparse data.

AUTHOR CONTRIBUTIONS

X.C., H.B.N., M.D., L.Z., L.F., M.O.K., and A.C.H. wrote the manuscript; X.C., H.B.N., M.D., L.Z., L.F., M.O.K., and A.C.H. designed the research; X.C., H.B.N., and A.C.H. performed the research; X.C. and H.B.N. analyzed the data.

FUNDING INFORMATION

This work was supported by the Food and Drug Administration (FDA) under contract HHSF223201710015C.

CONFLICT OF INTEREST STATEMENT

M.D., L.Z., and L.F. are employed by the U.S. Food and Drug Administration. H.B.N. is a former employee of Uppsala University and is currently employed with Pharmetheus AB. A.C.H. and M.O.K. have received consultancy fees from, and own stock in Pharmetheus AB, all unrelated to this manuscript. The opinions expressed in this article are those of the authors and should not be interpreted as the position of the U.S. Food and Drug Administration. All other authors declared no competing interests in this work. As an Associate Editor for CPT: Pharmacometrics & Systems Pharmacology, Andrew Hooker was not involved in the review or decision process for this article.

Supporting information

Supplementary Material S1.

Supplementary Material S2.

Supplementary Material S3.

Chen X, Nyberg HB, Donnelly M, et al. Development and comparison of model‐integrated evidence approaches for bioequivalence studies with pharmacokinetic end points. CPT Pharmacometrics Syst Pharmacol. 2024;13:1734‐1747. doi: 10.1002/psp4.13216