Abstract
Lewis acidic boranes, especially tris(pentafluorophenyl)borane [B(C6F5)3], have emerged as metal-free catalysts for carbene transfer reactions of α-diazocarbonyl compounds in a variety of functionalization reactions. The established mechanism for how borane facilitates carbene generation for these compounds in the scientific community is based on the formation of a B–O (C=O) intermediate (path O). Herein, we report an extensive DFT study that challenges the notion of a ubiquitous path O, revealing that B–C(=N=N) bond formation (path C) for certain diazocarbonyl substrates proves to be the preferred pathway. This study elucidates, through the introduction of 22 various substituents on each side of the α-diazocarbonyl backbone, how the electron-donating and -withdrawing properties of substituents influence the competition between these B–O and B–C pathways. To elucidate the impact of the electronic features of diazo substrates on the competition between the O and C pathways in the studied dataset, we employed a machine learning approach based on the Random Forest model. This analysis revealed that substrates with higher electron density on the diazo-attached carbon, lower electron density on the carbonyl carbon, and more stable HOMO orbitals tend to proceed via pathC. Furthermore, this study not only demonstrates that borane efficiency in facilitating N2 release is greatly affected by the nature of substituents on both sides of the α-diazocarbonyl functionality but also shows that for some substrates, borane is incapable of catalyzing the release of molecular nitrogen.
Keywords: α-diazocarbonyl, carbene transfer, tris(pentafluorophenyl)borane, boron, catalysis, DFT, machine learning
1. Introduction
Trivalent boron compounds, possessing a vacant p-orbital that makes them effective Lewis acid catalysts, have long served as powerful tools in organic synthesis.1,2 Over the past decade, tris(pentafluorophenyl)borane, B(C6F5)3, has garnered significant attention for its catalytic function in activating α-diazocarbonyl compounds in carbene transfer reactions, enabling their broad application in cyclization, alkenylation, or X-H insertion reactions.3−17
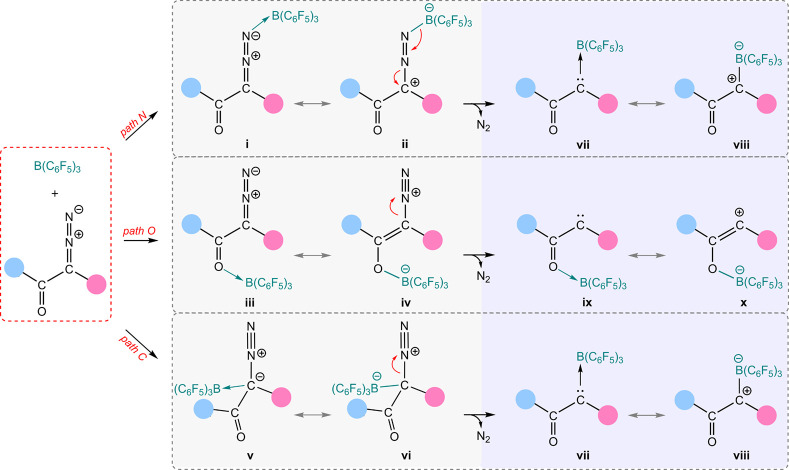
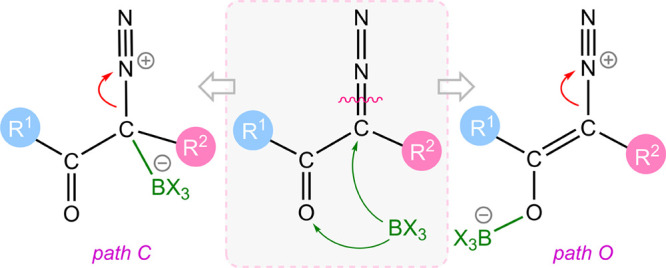
Three plausible pathways can be envisioned for B(C6F5)3-catalyzed N2 release from α-diazocarbonyl compounds.18 As depicted in Scheme 1, borane may facilitate N2 release via the formation of B–N adduct, (path N), B–O adduct (path O), and B–C adduct (path C). The contribution of resonance structures ii, iv, and vi, which feature a weakened C–N bond, is expected to contribute to a decrease in the activation energy for N2 release. Notably, borane can also stabilize the resulting carbenes by delocalizing the electron density (Scheme 1). Density functional theory (DFT) studies have revealed that path N is not the preferred pathway for these borane-catalyzed transformations.7,18 The weak electron donation (from the sp orbital) of the nascent N2 molecule to the boron atom appears to be the underlying reason, preventing the stabilization of transition structures for N2 elimination as well as the ensuing N → B intermediates.
Scheme 1. Possible Pathways for Activation of α-Diazocarbonyl Precursors for N2 Release Using B(C6F5)3.
Red arrows indicate the direction of electron transfer leading to the subsequent structures.
Recently, Melen and their co-workers19 conducted a DFT study to demonstrate that B(C6F5)3 can promote the release of N2 from α-diazocarbonyl compounds via B–O adduct formation in a series of carbene transfer reactions. According to their proposed mechanism, the borane-stabilized carbene intermediate ix (Scheme 1), which also exhibits carbocationic characteristics as evidenced by resonance contributor x, is poised for nucleophilic attack at the carbon atom. Consequently, this intermediate undergoes C–H insertion, cyclopropanation, and ring-opening reactions (Scheme 2). This proposed mechanism has been extensively cited in subsequent studies by them20−23 as well as by other research groups.8−10,12,22−28 Noteworthy that this pathway (path O) had also been proposed by Zhang et al. in a separate study.18 Nevertheless, our preliminary computations have indicated that path O may not invariably represent the preferred catalytic route for borane-catalyzed N2 elimination from α-diazocarbonyl precursors; instead, path C poses a potentially competitive alternative. Indeed, substituents on either side of the α-diazocarbonyl moiety exert distinct effects on the activation energies associated with these competing pathways.
Scheme 2. B(C6F5)3-Catalyzed Carbene Transfer Reactions Reported by Melen and Co-Workers.
Therefore, to establish the energy barriers for borane-catalyzed carbene formation from α-diazocarbonyl compounds via both path O and path C, we undertook comprehensive DFT studies at the SMD/M06-2X/def2-TZVP//SMD/M06-2X/6-31G(d) level of theory. Additionally, a machine learning (ML) approach was employed to analyze the DFT results and identify relevant chemical descriptors. This integrated approach has the potential to uncover previously unseen correlations and provide a deeper understanding of chemical transformations.
2. Results and Discussion
2.1. Scrutinous Look at the Mechanism of Carbene Generation from Phenyldiazoacetate
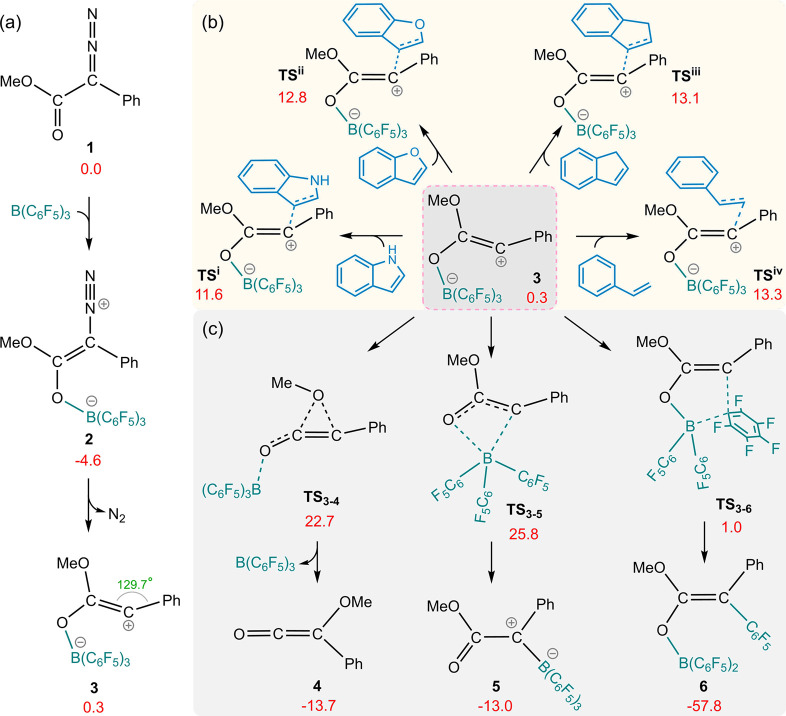
We undertook a scrutinizing investigation of the mechanistic aspects of the B(C6F5)3-catalyzed reaction of methyl phenyldiazoacetate (1) with nucleophiles indole, benzofuran, indene, and styrene, as reported by Ariafard and co-workers.19 The relative free energies for the B–C adduct (2) and borane-stabilized carbene (3) were calculated to be −4.6 and 0.3 kcal/mol, respectively (Figure 1a). Both the carbocation and carbene resonance forms of intermediate 3 possess a vacant p orbital perpendicular to the molecular plane, rendering it susceptible to nucleophilic attack.
Figure 1.
Calculated free energy for (a) N2 elimination of phenyldiazoacetate (1) in the presence of B(C6F5)3 via path O, (b) nucleophilic attack transition structures of indole, benzofuran, indene, and styrene, on the carbon center of 3, and (c) plausible rearrangement of intermediate 3. The relative free energies are given in kcal/mol, and the angle is annotated in green.
Our DFT calculations show that the relative free energy barriers for the addition of indole, benzofuran, indene, and styrene to 3 are 11.6, 12.8, 13.1, and 13.3 kcal/mol, respectively (Figure 1b). However, the inherent carbenic-carbocationic character of intermediate 3 renders it highly reactive, potentially leading to intramolecular rearrangement before nucleophilic attack. The methoxy group might undergo migration to the formally positively charged carbon in a Wolff rearrangement. Although DFT calculations for the 3 → 4 rearrangement show that this migration is exergonic, it exhibits a high free energy barrier of 27.3 (22.7 – (−4.6)) kcal/mol. Similarly, B(C6F5)3 migration from oxygen to carbon to form zwitterion 5, through TS3–5, requires an activation energy of 30.4 (25.8 – (−4.6)) kcal/mol. However, our calculations indicate that intermediate 3 readily undergoes C6F5 migration to the positively charged carbon atom via TS3–6 (ΔG‡ = 1 – (−4.6) = 5.6 kcal/mol). The generated intermediate (6) is thermodynamically highly stable, suggesting that this step is not reversible. This essentially renders the experimental product unattainable, leading us to consider the possibility that the transformation does not proceed via the proposed mechanism.
The borane-catalytic mechanism, initiated by the addition of borane to carbon possessing diazo functionality (Scheme 1—path C), has rarely been considered. This mechanism was explored by Zhang et al.18 as a possible pathway for borane-catalyzed carbene transfer reactions. However, their calculations did not identify it as the preferred pathway. Nonetheless, in 2023, Nemoto and co-workers7 demonstrated the functional potential of path C in facilitating N2 release from specific α-diazocarbonyl compounds.
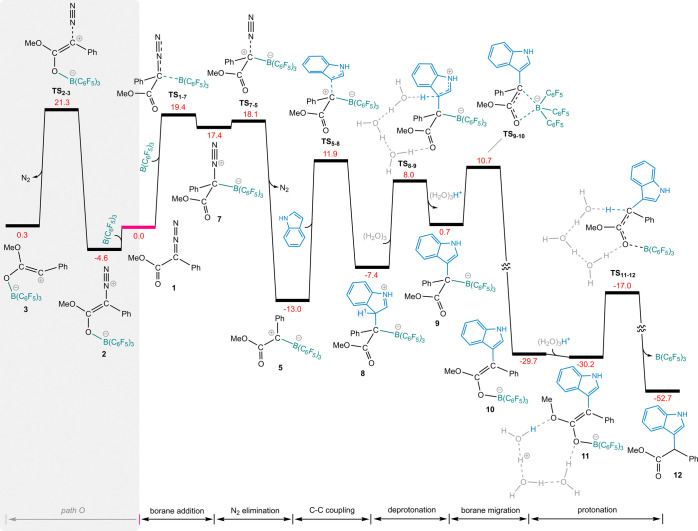
We therefore calculated the free energy profile for path C of the aforementioned reaction, starting with the binding of B(C6F5)3 to the carbon atom bearing the diazo functionality. Figure 2 depicts the results of our DFT calculations for this pathway. Following the formation of the B–C adduct (7), N2 is released via transition state TS7–5, generating borane-stabilized carbene 5. Both transition structures TS1–7 and TS7–5 lie at lower free energy levels compared to transition structure TS2–3, making path C more favorable in competition with path O. Subsequently, to explore nucleophilic reactions arising from intermediate 5 (Scheme 2), we calculated the free energy profile for its reaction with indole as a representative nucleophile. Intermediate 5 can adopt a zwitterionic resonance structure featuring a positively charged carbon atom and a negatively charged boron atom. The carbon atom in this resonance contributor, as well as in the carbenic resonance structure (vii - Scheme 1), is susceptible to nucleophilic attack. The addition of indole to intermediate 5 proceeds via transition structure TS5–8, requiring an activation energy of 24.9 kcal/mol (the free energy difference between TS5–8 and 5) and leads to the formation of species 8 in an endergonic manner. Hydrogen atom 1 in intermediate 8 is remarkably acidic, readily undergoing deprotonation, even with mild bases such as indole or adventitious water. Adventitious water present in solvents such as dichloromethane can act as a proton shuttle. Instances of water functioning as a proton shuttle in nonaqueous solvents have been documented.29−32 Proton transfer was considered to be mediated by water molecules in this step. In both aqueous and nonaqueous solvents, water molecules can form clusters through hydrogen bonding, and it is well-documented that clusters of three water molecules (H2O)3 can participate in chemical transformations.33−36 The calculated free energy barrier for water-assisted proton elimination from 8 to yield 9 in an uphill process via the transition structure TS8–9 is 21.0 kcal/mol relative to 5. Intermediate 9 undergoes B(C6F5)3 migration from carbon to oxygen, leading to a substantial stabilization of 30.4 kcal/mol stabilization. The resulting species 10 can form ion-pair adduct 11 by establishing hydrogen bonds with (H2O)3H+. Proton transfer from (H2O)3H+ to the carbon atom, overcoming an energy barrier of 13.2 kcal/mol, yields the final product 12.
Figure 2.
DFT-computed pathways for B(C6F5)3-catalyzed N2 release of phenyldiazoacetate (1), followed by reaction with the indole substrate. The relative free energies are given in kcal/mol.
2.2. Does Path C Always Take Priority over Path O?
To address whether all carbene transfer reactions from α-diazocarbonyl precursors occur through path C or not, we investigated pathways O and C for a nonester α-diazocarbonyl compound. Stephan and co-workers recently described a B(C6F5)3-catalyzed Wolff rearrangement (Scheme 3).5
Scheme 3. B(C6F5)3-Catalyzed Carbene Transfer Reactions Reported by Stephan and Co-Workers.

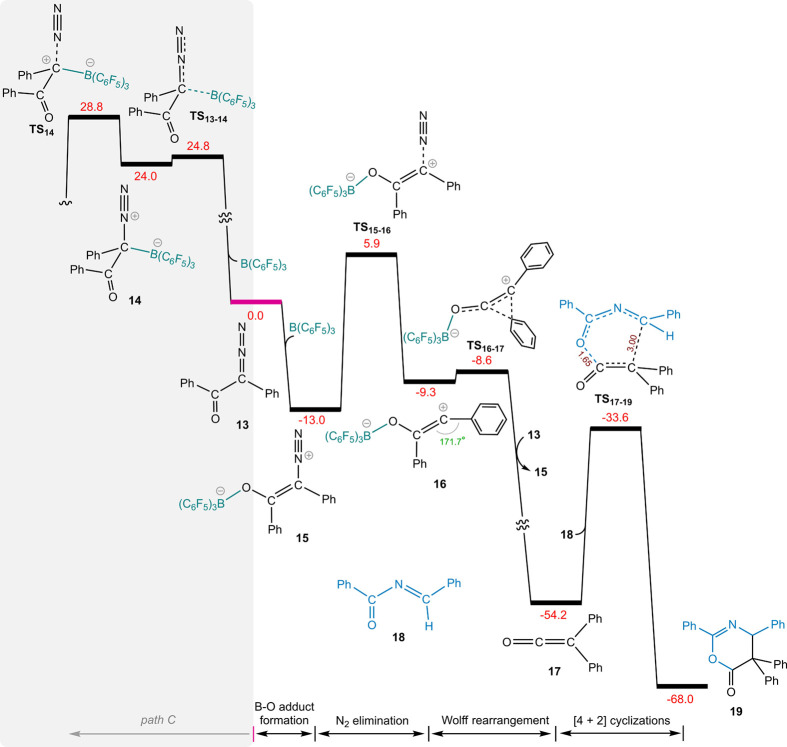
Figure 3 illustrates the calculated energy profile for the formation of ketene from 2-diazo-1,2-diphenylethan-1-one (13). Interestingly, the initial B–O adduct (15) for this diazo substrate is significantly more stable compared to that of adduct 2. This heightened stability makes it difficult for path C to proceed. Our results reveal a striking difference in the N2 dissociation pathways for α-diazoester versus α-diazoketones. While path C is preferred for the former (Figure 2), path O emerges as the favorable route for the latter, as evidenced by TS15–16 being 22.9 (5.9–28.8) kcal/mol more stable than TS14 (Figure 3). The B(C6F5)3-stabilized carbene 16 undergoes facile phenyl migration, affording ketene 17 in a highly exergonic fashion. The [4 + 2] cycloaddition of 18 and ketene proceeds through transition structure TS17–19 to yield the final product (19), requiring a moderate activation energy of 20.6 kcal/mol.
Figure 3.
DFT-computed pathways for B(C6F5)3-catalyzed N2 release of 2-diazo-1,2-diphenylmethane-1-one (12), followed by Wolff rearrangement and [4 + 2] cyclization. The relative free energies are given in kcal/mol. The selected distances (Å) are annotated in brown, and the angle is shown in green.
To further validate our findings, we recalculated the key structures of the two reaction pathways illustrated in Figures 2 and 3 using additional DFT methods, including the M06, M06-D3, and wB97XD functionals. These computed energies are summarized in Table S1 of the Supporting Information.
2.2.1. Path C vs Path O
To elucidate the influence of substituent positioning on α-diazocarbonyl precursors, we investigated their preference for path O or path C in the dissociation of N2. To this end, we opted for cost-effective computations using the smaller molecule BCl3 instead of B(C6F5)3. BCl3 is a slightly stronger Lewis acid than B(C6F5)3.37 Although neither of these boranes protects the boron atom with their substitution, the effects of steric hindrance may vary depending on the substrates. Additionally, interactions such as CH−π and π–π stacking may occur in certain cases involving B(C6F5)3. Comparative energy profiles for the two different N2 elimination pathways for the two substrates discussed above (1 and 13), in the presence of BCl3, are provided in Figure S1. This analysis indicates that while changing the borane leads to somewhat different energy barriers, it does not affect the pathway preferences for these substrates. Nevertheless, in cases where the energy barrier difference between two pathways is small, the type of borane might be determinative. Additionally, employing BCl3 in this study could potentially draw more attention to this borane from the synthetic chemistry community.
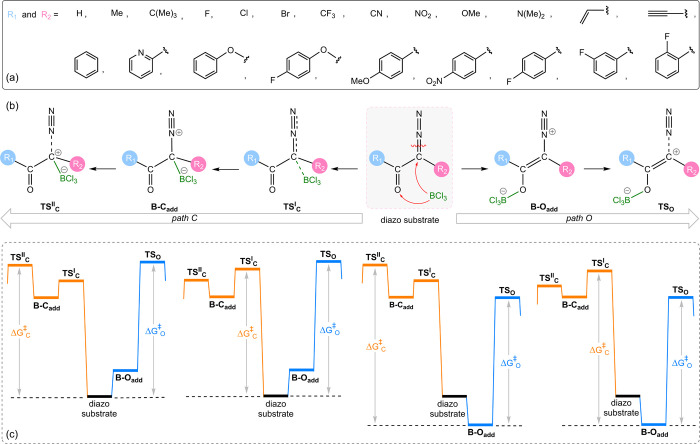
Accordingly, we introduced 22 different substituents on both sides of the α-diazocarbonyl backbone (Scheme 4a). The substitutions encompassed a wide range of electron-donating and -withdrawing groups. This resulted in 484 distinct samples. Notably, the substrate in which both R1 and R2 are substituted with H underwent rearrangement during N2 release via path O and was therefore excluded from the dataset. For each sample, key structures involved in the two potential mechanisms for N2 elimination via pathways O and C were identified. These structures include the B–O adduct (B–Oadd), the transition state for N2 release via path O (TSO), and two transition states for C–O adduct formation (TSIC) and subsequent N2 release (TSIIC) via path C (Scheme 4b). We also identified transition structures in the absence of BCl3 to assess the catalyst efficiency for each substrate. The activation energy for each pathway was obtained by calculating the difference in free energy between the most stable species (either the initial diazo compound or the B–O adduct) and the transition state energy for that pathway (Scheme 4c). It is worth noting that for path C, some substrates exhibit a higher energy barrier for TSIIC (N2 elimination) compared to TSIC (B–O bond formation), while others demonstrate a higher barrier for TSIC. Moreover, for a subset of diazo substrates, N2 elimination occurs concomitantly with B–C bond formation, thus circumventing the formation of a B–C adduct as a stationary point.
Scheme 4. (a) R1 and R2 Substituents Employed To Generate Our α-Diazocarbonyl Dataset, (b) Two Catalytic Pathways O and C, (c) Schematic Illustrating the Four Possible Scenarios for Calculating ΔG‡O and ΔG‡C for Each Diazo Substrate.
Figures S2 and S3 illustrate the catalytic efficacy of BCl3 in pathways O and C for each sample, and Figure S4 complements this analysis by depicting the overall catalytic efficiency of BCl3. Our findings suggest that in certain samples the involvement of BCl3 results in an elevation of the activation energy required for N2 elimination, causing it to fail to function as a catalyst in either of the two pathways. Our entire dataset is presented in Table S3, and a graphical representation of the preferred reaction pathway for each substrate is provided in Figure 4.
Figure 4.
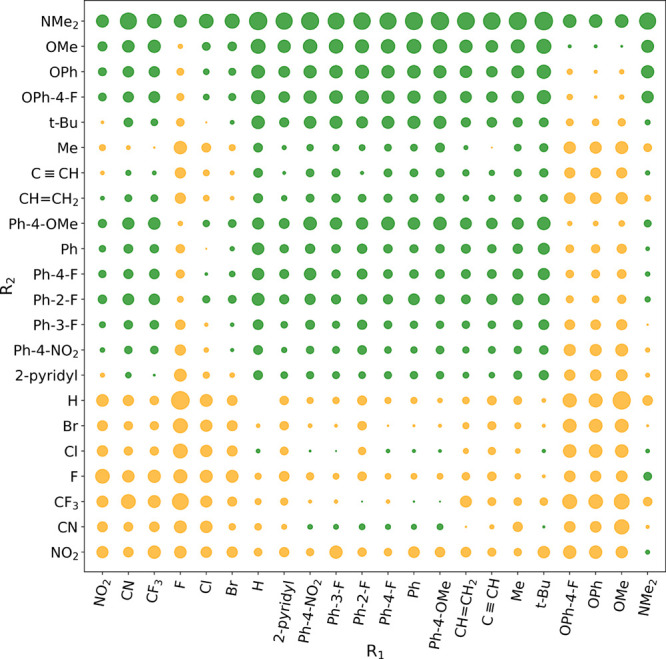
Effect of the R1 and R2 substituents on ΔΔG (ΔG‡C – ΔG‡O). Positive ΔΔG values indicate the superiority of path O (represented by green circles), while negative ΔΔG values suggest greater favorability for path C (represented by orange circles). The diameter of each circle is proportional to the magnitude of ΔΔG. Small circles denote a minor energy difference in the activation barrier values between the two pathways.
The results (Figure 4 and Tables S2 and S3) indicate that methoxy and phenoxy functional groups at the R1 position favor path C, but the electron-donating ability of R2 modulates this preference. Accordingly, when the R2 group is NO2, CF3, or CN (with R1 being OMe, OPh, or OPh-4-F), path C is more favored compared to path O. However, as the electron-donating strength of R2 increases, the difference between ΔG‡O and ΔG‡C diminishes, and for a strong R2 electron-donor like NMe2, path O becomes preferred. Supporting this trend, the preference for path C for this class of samples follows the order: 4-methoxyphenyl < phenyl < 4-nitrophenyl for R2. Furthermore, weaker π-donating groups such as aromatic rings, vinyl groups, and ethynyl groups at the R1 position generally favor path O when R2 is a group of the same type or a strong σ-donor like tert-butyl. It is also worth noting that halogens and strong electron-withdrawing groups such as NO2, CF3, and CN at the R2 position, combined with a set of R1 groups including halogens, NO2, CF3, CN, methoxy, and phenoxy, favor path C. However, in most cases, π-donors at the R2 position select path C unless R1 is methoxy, phenoxy, or fluorine.
2.2.2. Most Important Parameters
2.2.2.1. B–O Adduct Stability
Some examples of data derived from our calculations, with more details, are showcased in Table 1 along with additional examples in Table S2. The significance of the stability of the B–O adduct emerges as a pivotal determinant of pathway selectivity. When the B–O adduct exhibits high thermodynamic stability, the reaction path C becomes challenging, even if there is a small energy difference between its transition structures and the starting materials due to the elevated energy difference between the transition structures and the resting state of the catalyst (Figure S5).
Table 1. Dataset Examples: i.e., Free Energy Barrier (in kcal/mol) of N2 Release (without BCl3, Pathways C and O), ΔG‡C – ΔG‡O, Relative Stability of the B–O Adduct (in kcal/mol), NPA Charge on Backbone Carbons, and HOMO Energy Level (in eV) for Each Diazo Substrate.
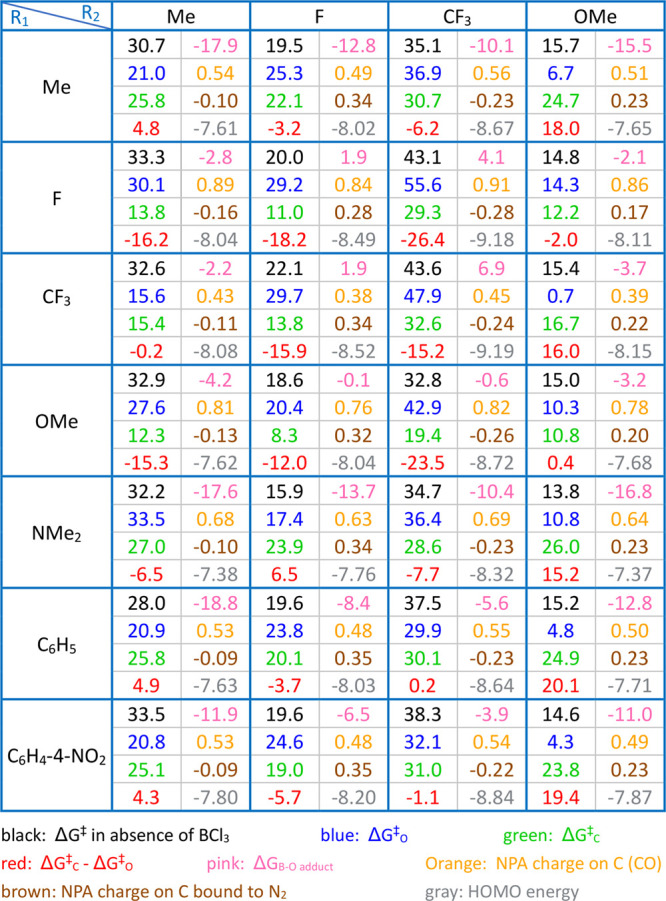
R1 electron-donating substituents augment the basicity of the carbonyl oxygen, thereby strengthening the B–O bond. This effect is exemplified by methyl, amine, and phenyl substituents. For instance, when R1 and R2 are methyl groups, the highest transition structure for path C displays an energy difference of merely 8.9 kcal/mol relative to the starting materials. Nevertheless, due to the B–O adduct’s relative free energy of −17.9 kcal/mol, the free energy barrier for path C amounts to 25.8 (8.9 + 17.9) kcal/mol.
Our findings indicate a notable correlation between the energy levels of the highest occupied molecular orbital (HOMO) and the stability of the B–O adducts (Figure 5). The HOMO energy level can serve as an indicator of the electron-withdrawing and -donating properties of the substituents on either side of the diazo functionality. On the other hand, although the px lone pair electrons on oxygen, which interact with the vacant boron orbital, are located at different underlying layers in HOMO-n for various diazo molecules, a correlation exists between the energy levels of the HOMO and those of oxygen’s px orbital (for further details, see the Supporting Information.). The elevated energy of the px orbital of oxygen, which is predominantly reflected in the higher-energy HOMO, leads to a stronger interaction with the vacant boron orbital, resulting in a more stable B–O adduct.
Figure 5.
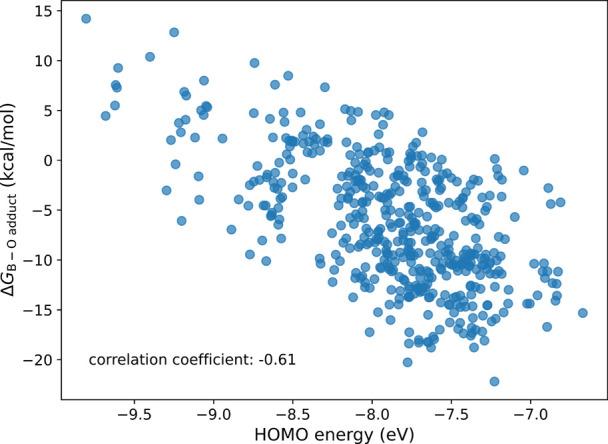
Scatter plot of the HOMO energy levels versus the stability of the B–O adducts.
Overall, the electron-donating properties of both substituents elevate the HOMO energy level, which increases the interaction between borane and the diazo substrate, thereby facilitating path O.
2.2.2.2. B–C Adduct Stability
Samples with R1 and R2 substituents exhibiting σ-donating (tBu), σ-withdrawing (CF3), and π-donating (OMe) characteristics were selected to investigate the stability of the B–C adducts and the ease of their formation. It should be noted that the free energy values for TSIC, B–Oadd, and TSIIC were calculated relative to the starting materials (the corresponding diazo substrate and BCl3).
As shown in Figure 6, greater electron donation by R2 leads to a more stable B–C adduct as carbon can more effectively donate electron density to the boron center. For structures in which R2 is OMe, no local minimum for the B–C adduct was found. In these cases, the N2 molecule is eliminated during the formation of the boron–carbon bond, facilitated by electron donation from OMe to the nascent carbene pz orbital. For these compounds, the relative energy of TSIC is significantly lower compared to those with R2 = tBu or CF3. However, in a sample such as 22, the lower energy of the B–O adduct ultimately leads to a higher ΔG‡C. These results indicate that in addition to R2, the electron-donating ability of R1 also contributes to the stability of the B–C adduct, with this effect being more pronounced for π-donating properties compared to σ-donating properties.
Figure 6.
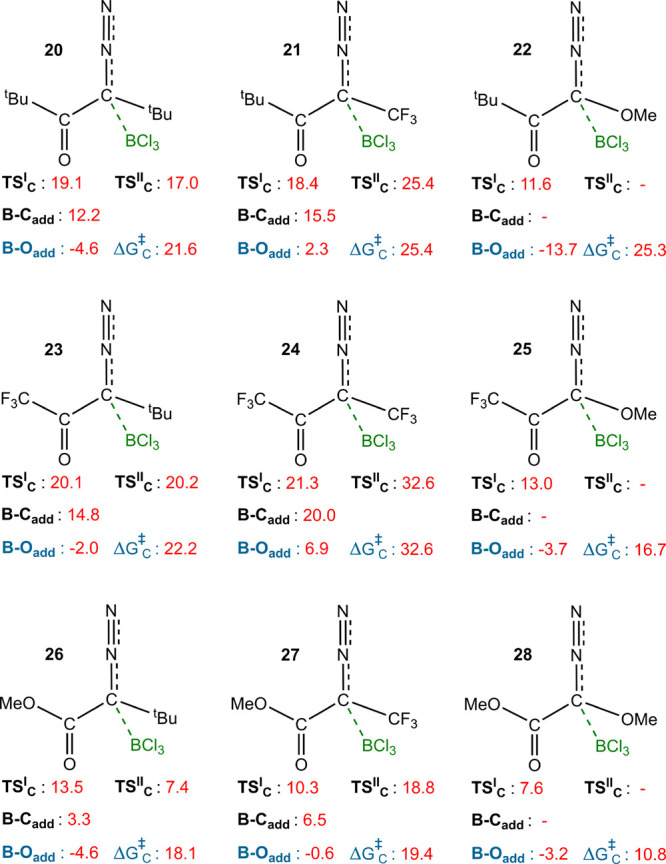
Effect of changing R1 and R2 from tBu to CF3 and OMe on TSIC and ΔG‡C.
2.2.2.3. Thermodynamic Stability of the Borane-Stabilized Carbenes
For an α-diazocarbonyl compound possessing R1 = CF3 and R2 = Me, the activation energy for N2 elimination in path O is 15.6 kcal/mol, whereas when R2 is substituted with F, the activation energy increases to 29.7 kcal/mol (Table 1). This is likely caused by the thermodynamic stability of the ensuing species after N2 release, which, to some extent, is reflected in the transition structures. The relative free energy for species 29 is 9.7 kcal/mol, while for species 30, it is calculated to be 24.7 kcal/mol (Figure 7a). The instability of the ensuing intermediate is attributable to the destabilizing effect of fluorine on zwitterion 30, which reduces the contribution of resonance structure x (Scheme 1). Substitution of the F moiety with a CF3 group further accentuates this effect, resulting in a significant elevation of the energy barrier to 47.9 kcal/mol (Table 1).
Figure 7.
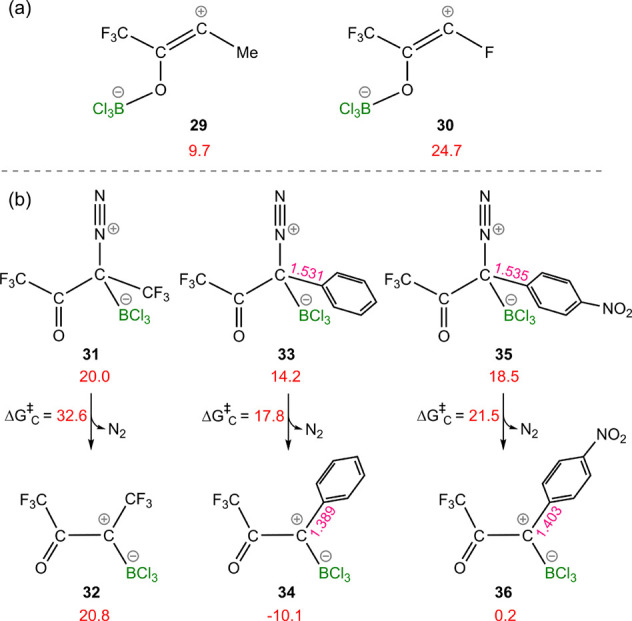
(a) Impact of borane-stabilized carbene stability on the energy barrier of path C. (b) Comparison of the effect of substituents on the thermodynamic stability of borane-stabilized carbenes on path O. The relative free energies are given in kcal/mol, and selected bond lengths are given in Å.
While the stability of the B–C adduct undeniably affects the activation barrier for path C, the stability of the ensuing intermediate after N2 release also exerts a substantial impact on the magnitude of TSIIC. A better π-donor R2 can interact with the antibonding orbital of the N–C bond, thus lowering the activation energy for N2 elimination (TSIIC). The magnitude of this stabilization can be reflected by the intermediate. This is exemplified by B–C adduct 35 (Figure 7b), which exhibits a relative free energy close to that of 31 but has a considerably lower ΔG‡C. This discrepancy can be seen in the stability of their subsequent intermediates. Species 36 was found to be 20.6 kcal/mol lower in energy than 32. This enhanced stability is clearly reflected in the activation energy for N2 elimination, differing by 11.1 kcal/mol. The 4-nitrophenyl substituent, acting as a π-donor by delocalizing the positive charge in 36, stabilizes it. As depicted in Figure 7b, the phenyl group exerts a more pronounced stabilizing effect than the 4-nitrophenyl group, evidenced by the shorter carbon–carbon bond distance in 34 compared to 36.
2.2.2.4. π-Donating Capability of R1 Substituents
Another noteworthy observation requiring elucidation is an upward shift in activation energy for path O, rising from 15.6 to 30.1 kcal/mol, where R2 = Me, upon substituting R1 from CF3 (39) to F (37), with closely relative energy levels for the B–O adducts (Table 1, Figure 8a). This can be attributed to the π-donating capability of the fluorine atom, which increases the contribution of resonance structure xi (Figure 8b), wherein the carbon-diazo bond is reinforced, necessitating higher energy for dissociation. A similar effect is also evident for the NMe2 group (41), which diminishes the efficacy of the Lewis acid catalyst for path O. Comparison of the R1-carbonyl carbon bond lengths in the substrates and B–O adducts, as depicted in Figure 8a, reveals a more pronounced shortening of C–F and C–N bonds for F and NMe2 substituents in their corresponding adducts (38 and 42). This indicates the higher π-donating ability of these substitutions in the adduct compared to the substrate, supporting the participation of resonance structure xi (Figure 8b).
Figure 8.
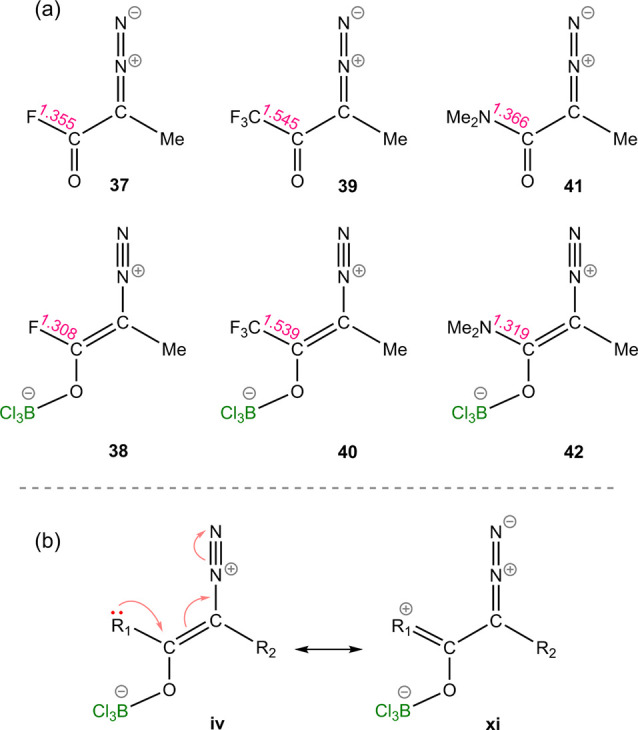
(a) Comparison of the R1-carbonyl carbon bond lengths in diazo substrates and B–O adducts. (b) Resonance contributor xi as a result of π-donation from R1. Interatomic distances are given in Å.
Overall, R1 π-donating groups, such as alkoxy, phenoxy, and amine, disfavor path O by pushing electron density into the π-orbital of C=N. It is noteworthy that diazo substrates with strong π-donating R1 groups, such as NMe2 and OMe, exhibit low activation energies for N2 release even in the absence of a catalyst.38 These results suggest that in the presence of borane path O is often favored for these substrates.
2.2.2.5. Differential Effects of σ- vs π-Donating Properties of R1 on Reaction Pathways
By comparison of samples with different electronic characteristics for R1, distinct effects of σ-donating and π-donating properties can be discerned. For example, where R1 and R2 = CF3, ΔG‡O and ΔG‡C are calculated to be 47.9 and 32.6 kcal/mol, respectively (Table 1). Changing R1 to F, a substituent exhibiting σ-withdrawing and π-donating properties, leads to an increase in ΔG‡O to 55.6 kcal/mol and a decrease in ΔG‡C to 29.3 kcal/mol. Replacing R1 with Me, a purely σ-donating group, results in a decrease in ΔG‡O to 36.9 kcal/mol, while ΔG‡C (30.7 kcal/mol) even increases slightly compared to when fluorine is in the R1 position. Introducing OMe, a strong π-donor but σ-withdrawing group, at the R1 position yields energy barriers of 42.9 and 19.4 kcal/mol for ΔG‡O and ΔG‡C, respectively. These observations highlight the contrasting effects of σ- and π-donations on the two pathways. While the trend is somewhat influenced by R2 variation, which is primarily driven by changes in the catalyst’s resting state energy, the overall conclusion remains that the σ-donating property of R1 is more effective in decreasing ΔG‡O, whereas the π-donating characteristic of R1 is particularly efficient at diminishing ΔG‡C.
2.2.3. Correlation Analysis of Descriptors and ΔΔGG
To gain data-driven insights into this transformation, we investigated the relationship between a list of electronic properties of α-diazocarbonyl molecules and the activation energy difference between pathways O and C (ΔΔG = ΔG‡C – ΔG‡O) for each sample. We initially employed natural population analysis (NPA) charges on the atoms of the α-diazo functionality (i.e., the carbonyl carbon (C1), carbonyl oxygen (O), the two diazo nitrogen atoms (N1: nitrogen bonded to carbon, N2: terminal nitrogen) and the carbon bonded to the diazo group (C2)), along with the HOMO energy level (in eV), px orbital occupancy (Occ) of oxygen, and pz orbital occupancy of C1. It is noteworthy that in the B–O adduct, the boron atom lies in the plane of the diazocarbonyl moiety, receiving electrons from the oxygen’s px orbital. In contrast, the boron center in the B–C adduct interacts with the carbon’s pz orbital.
A multiple linear regression analysis was performed to explore the relationship between the proposed descriptors and the computed ΔΔG (in kcal/mol). The resulting equation is as follows:
 |
1 |
The model’s coefficient of determination (R2) is 0.67, with a mean absolute error (MAE) of 4.62 kcal/mol. These metrics indicate a suboptimal linear correlation between the chosen descriptors and ΔΔG. To address this limitation and potentially uncover more complex (nonlinear) relationships, we opted to employ a machine learning approach.
2.2.4. Machine Learning Approach
The aforementioned properties were used in the feature space to train a random forest39 regression model (see the Supporting Information for the model selection rationale and model details.). Subsequently, to optimize the model’s performance, we excluded features that did not significantly contribute to its predictive ability. This resulted in the following final input features: NPA charges on the carbon bound to N2 and the carbonyl carbon along with the HOMO energy level. Figure 9a illustrates the predictability of the trained model. The model attained average R2 scores of 0.98 on the training set, 0.85 on the validation set, and 0.86 for the out-of-bag samples after 256 model iterations, with corresponding MAEs of 1.03 2.79, and 2.81 kcal/mol, respectively. These results underscore the effectiveness of the input variables provided in our ML model in detecting patterns and learning trends. The SHapley Additive exPlanations (SHAP) analysis40 was utilized to decode the importance of features and interpret the ML model. The SHAP analysis aims to dissect a model’s prediction by assessing the contribution of each feature to its predictions. This breakdown highlights the significance of each feature in shaping the model’s prediction. By quantifying the influence of each feature, the SHAP analysis provides a comprehensive and intuitive understanding of the model’s behavior. Figure 9b depicts the impact of the features on the trained model. Accordingly, a more negative partial charge on the carbon atom attached to the diazo group favors path C. This is likely due to the strengthening of the boron–carbon bond in the B–C adduct, leading to its enhanced stability. Conversely, a more negative partial charge on the carbonyl carbon enhances the stability of the B–O adduct, resulting in a preference for path O.
Figure 9.
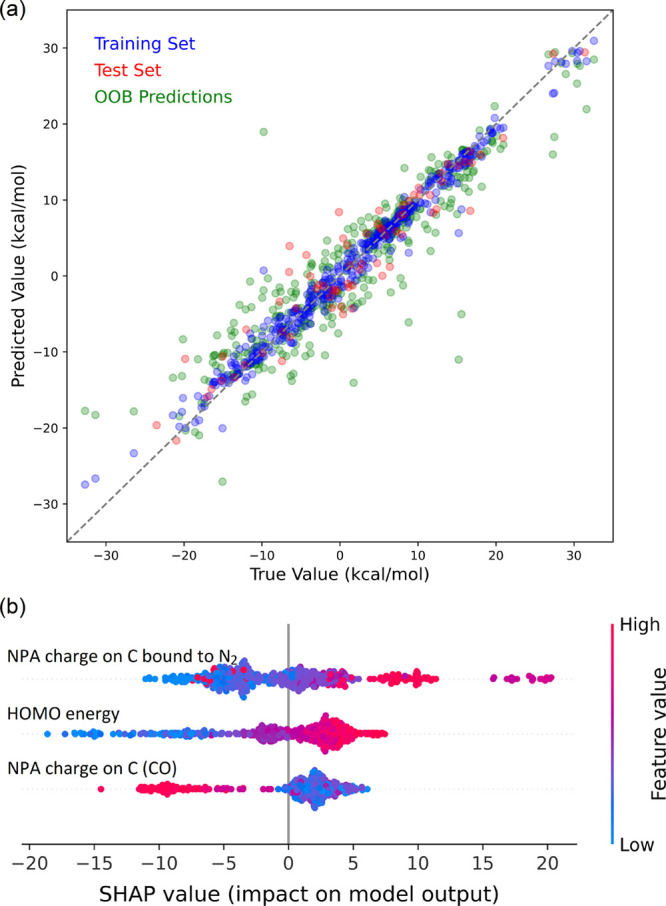
(a) Scatter plots of the DFT values for ΔΔG vs the predicted values from the trained ML model, based on attribute features, for the training, test, and out-of-bag sets. (b) SHAP values for different features across various samples. Colors indicate the feature values, ranging from low (blue) to high (red).
The machine learning results indicate that a higher HOMO energy level makes path C less favorable, which aligns with the DFT-based analysis for the formation of a more stable B–O adduct and ultimately widening of the energy gap between the transition structures for path C and the energy reference point (the B–O adduct in such cases). Additionally, according to the ML results, a more negative partial charge on the carbon atom attached to N2 facilitates path C, suggesting an increased propensity of borane as a Lewis acid to bind to this carbon, leading to a more stable B–C adduct. Conversely, a higher negative partial charge on the carbonyl carbon, based on the ML results, favors path O. This is in line with the DFT results, as it leads to a more stable B–O adduct, which is located on path O.
Overall, in the presence of BCl3, α-diazocarbonyl compounds that possess lower HOMO energy levels and less electron density on the carbonyl carbon (C1) are more likely to proceed via path C. Conversely, compounds with higher HOMO energy levels and a more negative partial charge on C1 tend to react via the path O.
3. Conclusions
In conclusion, through DFT calculations, we have demonstrated that in carbene transfer reactions catalyzed by borane the prevalent mechanism, which involves the formation of B–O adducts, is not necessarily the preferred pathway. An alternative pathway entails the attachment of borane to carbon bearing the diazo group (path C). We evaluated the catalytic pathway favorability by introducing 22 different substituents on both sides of α-diazocarbonyl precursors while utilizing BCl3 as a Lewis acid. The activation energies for N2 elimination were computed for each sample through three scenarios: via the B–O path, via the B–C path, and without borane.
Our findings demonstrate that σ-donating R1 groups (attached to the carbonyl) and σ- or π-donating R2 groups (attached to the diazo-bearing carbon) facilitate path O (Scheme 1), while π-donating R1 substituents favor the path C unless R2 is a strong π-donor. Indeed, these features influence the stability of the initial adducts (B–O adduct or B–C adduct) and the boron-stabilized carbenes, and the stability of the transition structures is significantly affected by the thermodynamic stability of these species. Additionally, this study depicts the variable catalytic efficiency of borane depending on substrate substitution, suggesting that even in some cases, borane cannot play a catalytic role in the formation of carbene intermediates in either of the two pathways.
Machine learning study revealed that lower electron density on the carbonyl carbon (C1) and higher electron density on the diazo-attached carbon (C2) facilitate path C. This study also demonstrates the variable catalytic performance of boron, depending on substrate substitution, with boron failing to catalyze the formation of a carbene intermediate in a few instances.
The information supplied in this research challenges the conventional understanding of borane-catalyzed carbene transfer reactions and provides valuable insights into the factors governing pathway selection and catalyst performance. The presented findings have implications for the rational design of efficient catalysts for borane-catalyzed carbene transfer reactions.
3.1. Computational Details
Gaussian 1641 was used to fully optimize all the structures reported in this paper at the M06-2X level of theory.42 For all the calculations, solvent effects were considered using the SMD solvation model43 with dichloromethane as the solvent. To fully optimize the geometry of structures and subsequently Frequency calculations, the 6-31G(d) basis set44 was employed. Transition structures were located using the Berny algorithm. To further refine the energies obtained from the SMD/M06-2X/6-31G(d) calculations, we carried out single-point energy calculations using a more accurate def2-TZVP basis set.45 Tight convergence criterion and an ultrafine integral grid were also employed to increase the accuracy of the calculations. IRC calculations were used to confirm the connectivity between transition structures and minima.46,47
The free energy for each species in solution was calculated by using the following formula:
| 2 |
We used the random forest regression machine learning model as implemented in the Scikit-learn package48 of Python.
Acknowledgments
This project has received funding from the European Union-NextGenerationEU instrument and is funded by the Academy of Finland under grant number 348327. The authors thank Finland CSC-IT Center for generous grants of computer time.
Data Availability Statement
Scripts and dataset available at: https://github.com/KavehFarshadfar/Borane-Diazocarbonyl.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscatal.4c03368.
Computational results; Cartesian coordinates of the calculated species; and machine learning details (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- De Vries T. S.; Prokofjevs A.; Vedejs E. Cationic tricoordinate boron intermediates: borenium chemistry from the organic perspective. Chem. Rev. 2012, 112, 4246–4282. 10.1021/cr200133c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deloux L.; Srebnik M. Asymmetric boron-catalyzed reactions. Chem. Rev. 1993, 93, 763–784. 10.1021/cr00018a007. [DOI] [Google Scholar]
- Xiao L.; Jin L.; Zhao Y.; Guo J.; Stephan D. W. B(C6F5)3-catalyzed cyclopropanation of 3-alkenyl-oxindoles with diazomethanes. Chem. Commun. 2023, 59, 1833–1836. 10.1039/D2CC06744G. [DOI] [PubMed] [Google Scholar]
- Stefkova K.; Guerzoni M. G.; Van Ingen Y.; Richards E.; Melen R. L. B(C6F5)3-catalyzed diastereoselective and divergent reactions of vinyldiazo esters with nitrones: Synthesis of highly functionalized diazo compounds. Org. Lett. 2023, 25, 500–505. 10.1021/acs.orglett.2c04198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song W.; Guo J.; Stephan D. W. B(C6F5)3-catalyzed Wolff rearrangement/[2+2] and [4+2] cascade cyclization of α-diazoketones with imines. Org. Chem. Front. 2023, 10, 1754–1758. 10.1039/D3QO00054K. [DOI] [Google Scholar]
- Yan M.; Xiao L.; Xiong J.; Jin L.; Stephan D. W.; Guo J. Borane catalyzed transesterification of tert-butyl esters using α-aryl α-diazoesters. Org. Biomol. Chem. 2023, 21, 8279–8283. 10.1039/D3OB01548C. [DOI] [PubMed] [Google Scholar]
- Ito T.; Harada S.; Homma H.; Okabe A.; Nemoto T. Mechanistic Investigation on Dearomative Spirocyclization of Arenes with α-Diazoamide under Boron Catalysis. ACS Catal. 2023, 13, 147–157. 10.1021/acscatal.2c04504. [DOI] [Google Scholar]
- Chen C.-Y.; Zhao J.-H.; Xiong L.-X.; Wang F.; Yang G.; Ma C. Borane-catalyzed arylation of aryldiazoacetates with N, N-dialkylanilines. Org. Biomol. Chem. 2022, 20, 4101–4104. 10.1039/D2OB00447J. [DOI] [PubMed] [Google Scholar]
- Dong K.; Liu X.-S.; Wei X.; Zhao Y.; Liu L. Borane-catalysed S–H insertion reaction of thiophenols and thiols with α-aryl-α -diazoesters. Green Synth. Catal. 2021, 2, 385–388. 10.1016/j.gresc.2021.10.001. [DOI] [Google Scholar]
- He F.; Koenigs R. M. Borane-Catalyzed Carbazolation Reactions of Aryldiazoacetates. Org. Lett. 2021, 23, 5831–5835. 10.1021/acs.orglett.1c01982. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Mandal D.; Guo J.; Wu Y.; Stephan D. W. B(C6F5)3-Catalyzed site-selective N1-alkylation of benzotriazoles with diazoalkanes. Chem. Commun. 2021, 57, 7758–7761. 10.1039/D1CC03048E. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Zhang X.; Zhao J.; Jiang J. B(C6F5)3-catalyzed O–H insertion reactions of diazoalkanes with phosphinic acids. Org. Biomol. Chem. 2021, 19, 5772–5776. 10.1039/D1OB01035B. [DOI] [PubMed] [Google Scholar]
- San H. H.; Wang C.-Y.; Zeng H.-P.; Fu S.-T.; Jiang M.; Tang X.-Y. Boron-catalyzed azide insertion of α-aryl α-diazoesters. J. Org. Chem. 2019, 84, 4478–4485. 10.1021/acs.joc.8b03278. [DOI] [PubMed] [Google Scholar]
- Rao S.; Kapanaiah R.; Prabhu K. R. Boron-Catalyzed C- C Functionalization of Allyl Alcohols. Adv. Synth. Catal. 2019, 361, 1301–1306. 10.1002/adsc.201801389. [DOI] [Google Scholar]
- Rao S.; Ashwathappa P. K. S.; Prabhu K. R. Boron-Catalyzed Carbonate Functionality Transfer Reaction. Asian J. Org. Chem. 2019, 8, 320–323. 10.1002/ajoc.201800751. [DOI] [Google Scholar]
- San H. H.; Wang S.-J.; Jiang M.; Tang X.-Y. Boron-catalyzed O–H bond insertion of α-aryl α-diazoesters in water. Org. Lett. 2018, 20, 4672–4676. 10.1021/acs.orglett.8b01988. [DOI] [PubMed] [Google Scholar]
- Yu Z.; Li Y.; Shi J.; Ma B.; Liu L.; Zhang J. (C6F5)3BCatalyzed Chemoselective and ortho-Selective Substitution of Phenols with α-Aryl α-Diazoesters. Angew. Chem., Int. Ed. 2016, 55, 14807–14811. 10.1002/anie.201608937. [DOI] [PubMed] [Google Scholar]
- Zhang Q.; Zhang X.-F.; Li M.; Li C.; Liu J.-Q.; Jiang Y.-Y.; Ji X.; Liu L.; Wu Y.-C. Mechanistic insights into the chemo-and regio-selective B(C6F5)3catalyzed C–H functionalization of phenols with diazoesters. J. Org. Chem. 2019, 84, 14508–14519. 10.1021/acs.joc.9b02035. [DOI] [PubMed] [Google Scholar]
- Dasgupta A.; Babaahmadi R.; Slater B.; Yates B. F.; Ariafard A.; Melen R. L. Borane-catalyzed stereoselective C–H insertion, cyclopropanation, and ring-opening reactions. Chem. 2020, 6, 2364–2381. 10.1016/j.chempr.2020.06.035. [DOI] [Google Scholar]
- Pramanik M.; Melen R. L. Activation of Diazo Compounds by Fluorinated Triarylborane Catalysts. Synthesis 2023, 55, 3906. 10.1055/a-2118-3046. [DOI] [Google Scholar]
- Babaahmadi R.; Dasgupta A.; Hyland C. J.; Yates B. F.; Melen R. L.; Ariafard A. Understanding the Influence of Donor-Acceptor Diazo Compounds on the Catalyst Efficiency of B(C6F5)3Towards Carbene Formation. Chem.—Eur. J. 2022, 28, e202104376 10.1002/chem.202104376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dasgupta A.; Richards E.; Melen R. L. Triarylborane catalyzed carbene transfer reactions using diazo precursors. ACS Catal. 2022, 12, 442–452. 10.1021/acscatal.1c04746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefkova K.; Heard M. J.; Dasgupta A.; Melen R. L. Borane catalysed cyclopropenation of arylacetylenes. Chem. Commun. 2021, 57, 6736–6739. 10.1039/D1CC01856F. [DOI] [PubMed] [Google Scholar]
- Wang P.; Gong Y.; Wang X.; Ren Y.; Wang L.; Zhai L.; Li H.; She X. Solvent-free, B(C6F5)3-Catalyzed S- H Insertion of Thiophenols and Thiols with α-Diazoesters. Chem.—Asian J. 2022, 17, e202200465 10.1002/asia.202200465. [DOI] [PubMed] [Google Scholar]
- Wen X.; Lu P.; Shen Y.; Peng H.; Ke Z.; Zhao C. DFT Mechanistic Study of the Cyclopropanation of Styrene and Aryldiazodiacetate Catalyzed by Tris(pentafluorophenyl)borane. ACS Omega 2022, 7, 12900–12909. 10.1021/acsomega.2c00200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X.-Y.; Gao W.-X.; Zhou Y.-B.; Liu M.-C.; Wu H.-Y. Tris(pentafluorophenyl)borane-Catalyzed Oxygen Insertion Reaction of α-Diazoesters (α -Diazoamides) with Dimethyl Sulfoxide. Adv. Synth. Catal. 2022, 364, 750–754. 10.1002/adsc.202101336. [DOI] [Google Scholar]
- Cao T.; Gao C.; Kirillov A. M.; Fang R.; Yang L. DFT quest for mechanism and stereoselectivity in B(C6F5)3-catalyzed cyclopropanation of alkenes with aryldiazoacetates. Mol. Catal. 2021, 516, 111980 10.1016/j.mcat.2021.111980. [DOI] [Google Scholar]
- Mancinelli J. P.; Wilkerson-Hill S. M. Tris(pentafluorophenyl)borane-Catalyzed Cyclopropanation of Styrenes with Aryldiazoacetates. ACS Catal. 2020, 10, 11171–11176. 10.1021/acscatal.0c03218. [DOI] [Google Scholar]
- Henneveld J. S.; Shiri F.; Ariafard A.; Lucas N. T.; Bissember A. C.; Hawkins B. C. Dipole-Transmissive 1, 3-Dipolar Cycloadditions for the Rapid Construction of Polycyclic N-Heterocycles: Synthetic and Mechanistic Investigations. Chem.—Eur. J. 2023, 29, e202301254 10.1002/chem.202301254. [DOI] [PubMed] [Google Scholar]
- Farshadfar K.; Tague A. J.; Talebi M.; Yates B. F.; Hyland C. J. T.; Ariafard A. Discovery of Redox-Promoted Bro̷nsted Acid Catalysis in the Gold(III)-Catalyzed Annulation of Phenol and Cyclohexadiene. ACS Catal. 2022, 12, 7918–7925. 10.1021/acscatal.2c01194. [DOI] [Google Scholar]
- Hu C.; Farshadfar K.; Dietl M. C.; Cervantes-Reyes A.; Wang T.; Adak T.; Rudolph M.; Rominger F.; Li J.; Ariafard A.; et al. Gold-catalyzed [5, 5]-rearrangement. ACS Catal. 2021, 11, 6510–6518. 10.1021/acscatal.1c01108. [DOI] [Google Scholar]
- Wang X.-N.; Krenske E. H.; Johnston R. C.; Houk K.; Hsung R. P. Torquoselective ring opening of fused cyclobutenamides: evidence for a cis, trans-cyclooctadienone intermediate. J. Am. Chem. Soc. 2014, 136, 9802–9805. 10.1021/ja502252t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farshadfar K.; Laasonen K. DFT Mechanistic Investigation into Ni(II)-Catalyzed Hydroxylation of Benzene to Phenol by H2O2. Inorg. Chem. 2024, 63, 5509–5519. 10.1021/acs.inorgchem.3c04461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song L.; Tian X.; Farshadfar K.; Shiri F.; Rominger F.; Ariafard A.; Hashmi A. S. K. An unexpected synthesis of azepinone derivatives through a metal-free photochemical cascade reaction. Nat. Commun. 2023, 14, 831. 10.1038/s41467-023-36190-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farshadfar K.; Bird M. J.; Olivier W. J.; Hyland C. J.; Smith J. A.; Ariafard A. Computational investigation into the mechanistic features of bromide-catalyzed alcohol oxidation by PhIO in water. J. Org. Chem. 2021, 86, 2998–3007. 10.1021/acs.joc.0c02903. [DOI] [PubMed] [Google Scholar]
- Chipman A.; Gouranourimi A.; Farshadfar K.; Olding A.; Yates B. F.; Ariafard A. A computational mechanistic investigation into reduction of gold(III) complexes by amino acid glycine: A new variant for amine oxidation. Chem.—Eur. J. 2018, 24, 8361–8368. 10.1002/chem.201800403. [DOI] [PubMed] [Google Scholar]
- Lawson J. R.; Melen R. L. Tris(pentafluorophenyl)borane and beyond: modern advances in borylation chemistry. Inorg. Chem. 2017, 56, 8627–8643. 10.1021/acs.inorgchem.6b02911. [DOI] [PubMed] [Google Scholar]
- Farshadfar K.; Hashemi A.; Khakpour R.; Laasonen K. Kinetics of N2Release from Diazo Compounds: A Combined Machine Learning-Density Functional Theory Study. ACS Omega 2024, 9, 1106–1112. 10.1021/acsomega.3c07367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Random forests. Mach. Learn. 2001, 45, 5–32. 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Lundberg S. M.; Lee S.-I.. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems; Curran Associates Inc., 2017; Vol. 30. [Google Scholar]
- Frisch M. J.et al. Gaussian 16, Version 16, Revision A.03; Gaussian, Inc.: Wallingford CT, 2016; https://gaussian.com/gaussian16/. [Google Scholar]
- Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Hariharan P. C.; Pople J. A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta. 1973, 28, 213–222. 10.1007/BF00533485. [DOI] [Google Scholar]
- Weigend F.; Furche F.; Ahlrichs R. Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr. J. Chem. Phys. 2003, 119, 12753–12762. 10.1063/1.1627293. [DOI] [Google Scholar]
- Fukui K. The path of chemical reactions-the IRC approach. Acc. Chem. Res. 1981, 14, 363–368. 10.1021/ar00072a001. [DOI] [Google Scholar]
- Fukui K. Formulation of the reaction coordinate. J. Phys. Chem. 1970, 74, 4161–4163. 10.1021/j100717a029. [DOI] [Google Scholar]
- Pedregosa F.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. 10.5555/1953048.2078195. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Scripts and dataset available at: https://github.com/KavehFarshadfar/Borane-Diazocarbonyl.