Abstract
Conventional approaches for establishing bioequivalence (BE) between test and reference formulations using non‐compartmental analysis (NCA) may demonstrate low power in pharmacokinetic (PK) studies with sparse sampling. In this case, model‐integrated evidence (MIE) approaches for BE assessment have been shown to increase power, but may suffer from selection bias problems if models are built on the same data used for BE assessment. This work presents model averaging methods for BE evaluation and compares the power and type I error of these methods to conventional BE approaches for simulated studies of oral and ophthalmic formulations. Two model averaging methods were examined: bootstrap model selection and weight‐based model averaging with parameter uncertainty from three different sources, either from a sandwich covariance matrix, a bootstrap, or from sampling importance resampling (SIR). The proposed approaches increased power compared with conventional NCA‐based BE approaches, especially for the ophthalmic formulation scenarios, and were simultaneously able to adequately control type I error. In the rich sampling scenario considered for oral formulation, the weight‐based model averaging method with SIR uncertainty provided controlled type I error, that was closest to the target of 5%. In sparse‐sampling designs, especially the single sample ophthalmic scenarios, the type I error was best controlled by the bootstrap model selection method.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
Non‐compartmental analysis (NCA) is the conventional method used in bioequivalence (BE) analysis for oral drug products, while bootstrap NCA serves as the conventional approach in the BE analysis for ophthalmic drug products. Both of these suffer from low power in many cases. Model‐integrated evidence (MIE) approaches exist, but may suffer from inflated type I error.
WHAT QUESTION DID THIS STUDY ADDRESS?
Can model averaging be leveraged to improve the type I error control and achieve high power in MIE approaches for BE analysis of oral and ophthalmic formulations?
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
Model averaging MIE BE methods can adequately control type I error and achieve high power in oral and ophthalmic studies. Accurately estimating and integrating parameter uncertainty is crucial to MIE BE methods. Bootstrap model selection and weight‐based model averaging with sampling importance resampling (SIR) uncertainty are promising methods for MIE BE analysis.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
Our novel MIE approach may provide an alternative to traditional BE approaches, especially in studies where only sparse sampling is possible, such as studies of ophthalmic formulations.
INTRODUCTION
To receive approval for marketing a generic product, applicants must demonstrate the absence of a significant difference in the rate and extent of absorption of the active ingredient compared with a reference listed drug (RLD). For drug products that are systemically absorbed, bioequivalence (BE) of a test product to the RLD is traditionally determined by comparing geometric means of maximum concentration (C max) and area under the concentration–time curve (AUC) between the two formulations, as calculated by non‐compartmental analysis (NCA). 1 , 2 However, conventional BE approaches using NCA typically require rich pharmacokinetic (PK) sampling and demonstrate low power in situations of sparse PK sampling. 3 Model‐integrated evidence (MIE) approaches for BE evaluation proposed by Hu et al. 3 and Dubois et al. 4 , 5 show promise, especially in PK studies with sparse sampling, but have shown inflated type I error. 5 Using methods with inflated type I error will cause non‐bioequivalent formulations to be accepted as bioequivalent at higher‐than‐expected rates. 3
In these previously proposed MIE BE methods, a single population PK model that contains treatment effects, and period and sequence effects for crossover designs, is fitted to the data. The estimated treatment effects on primary PK parameters (and their uncertainty) are converted into treatment effects for the secondary PK parameters (and their uncertainty) used for BE determination (AUC, C max) by means of a bootstrap 3 or the delta method. 5 A conclusion on whether the test product is BE to the RLD can then be reached with two one‐sided t‐tests (TOST). 1
There has recently been progress made in controlling the type I error of MIE methods 6 , 7 , 8 through improvement in testing methods and improvement in parameter uncertainty estimation. However, all of the MIE methods referenced above rely on a single model to describe the system and assume that model to be true. Methods based on a single model are subject to model misspecifications and model selection bias and may significantly underrepresent the uncertainty. Model averaging can alleviate some of these problems by allowing multiple alternative descriptions of the system. 9 , 10
Model averaging has been used to alleviate problems caused by the selection of a single model. 9 , 10 , 11 Any pharmacometric model has misspecifications compared with the biological system and population that it intends to describe, and any predictions from a single model assume that the model is true. Traditional model building examines different models and selects the best model for the data at hand, estimating the parameter values and parameter uncertainty under that model. Using a single model in this fashion carries the misspecifications of that model into the model predictions and onward to any downstream analyses. This can be counteracted by model averaging, whereby several models in a (predefined) model pool contribute to predictions, which are weighted based on their respective goodness‐of‐fit. 9 The misspecifications in one feature of an otherwise good model can thus be balanced by complementary features in other models. This can be thought of as accounting for the uncertainty of the model structure within the scope of the model pool.
Since MIE BE shows particular promise in sparse data situations, 4 , 8 it is interesting to examine BE testing using model averaging approaches in these situations. In this work, we examine two simulated scenarios with sparse PK data: (1) oral formulations with sparse sampling; and (2) ophthalmic drug formulations with extremely sparse sampling (1–2 samples per subject). With such sparse data, complex (and perhaps more mechanistic) models may not fit the data, but model averaging enables different models in a model pool to capture different features that are not simultaneously identifiable in a single model.
Ophthalmic formulations present particular challenges as they often do not cause quantifiable systemic concentrations of the drug. Current FDA guidance on studies to determining BE through PK studies for generic ophthalmic products, outlined by Shen and Machado, 12 uses PK samples from the aqueous humor of the eye at different timepoints after administration. These studies use either parallel designs with a single sample in each subject, or crossover designs with one sample from each eye. The single‐sample nature of these trials excludes traditional NCA methods. Instead, a bootstrapped NCA method 12 , 13 , 14 is employed, where NCA is performed on a mean concentration curve of bootstrapped datasets. Our hypothesis is that the model averaging approaches presented in this paper may be significantly better than the bootstrapped NCA method for BE assessment of this type of data.
This work presents MIE BE analysis procedures that use model averaging and parameter uncertainty estimates to control type I error while maintaining high power. It evaluates them through simulation experiment of BE studies for ophthalmic and oral formulations simulated under bioequivalent and non‐bioequivalent scenarios, respectively, and compares the power and type I error behavior of these methods to conventional BE methods recommended by the FDA.
METHODS
We have developed MIE BE analysis procedures that employ two of the model averaging approaches described by Aoki et al. 9 These procedures produce estimates of model parameters and uncertainty, which in turn produce predictions of metrics of interest for BE. In weight‐based model averaging, we examined three different methods for estimating parameter uncertainty: (1) sandwich covariance matrix, (2) bootstrap, and (3) sampling importance resampling (SIR). Bootstrap model selection captures parameter uncertainty and sampling uncertainty in the bootstrap step of the procedure.
Model averaging methods
In the presented work, we explored two approaches of model averaging: (1) bootstrap selection, and (2) relative weights.
Model averaging by bootstrap selection
In bootstrap model selection, 9 visualized in Figure 1, the study subject level data of each BE study were bootstrapped with replacement into N Boot datasets stratified to maintain the same proportions of treatments, sampling schedules, and treatment sequences (for crossover studies) as the original study (N Boot = 500 in the presented simulation experiments). All eligible models in the model pool were fitted to each of the bootstrapped datasets. For each bootstrapped dataset, the model with the lowest AIC was selected (subject to each model passing a practical identifiability test, see below), producing N Boot selected models with associated parameter estimates. These were used for simulations, presented in section “Model‐averaged simulations” below. See Data S1 for code examples.
FIGURE 1.
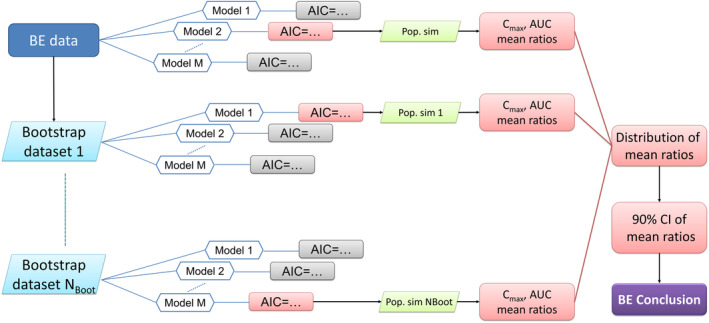
Overview of the model averaging by bootstrap selection bioequivalence procedure.
Model averaging by relative weights
In model averaging by relative weights, visualized in Figure 2, all models in the model pool were fitted to the BE study data. Each model was then assigned a weight based on its AIC according to Equation 1, 17
| (1) |
where w m is the relative weight for model m, AICm is the AIC for model m, AICi is the AIC for the ith candidate model, and M is the number of models in the model pool. Parameter uncertainty was estimated using either the sandwich covariance matrix from a NONMEM covariance step, SIR, 18 or nonparametric bootstrap. See Data S1 for code examples. For each model that passed a practical identifiability test (see section “Model validation for model averaging,” below), sets of parameter values from these uncertainty distributions were used for simulations to determine BE (see section “Model‐averaged simulations” below). Due to extensive runtimes and relatively poor performance, the weight‐based model averaging with bootstrap uncertainty was excluded from the two ophthalmic scenarios for type I error evaluation and the parallel design ophthalmic scenario for power evaluation.
FIGURE 2.
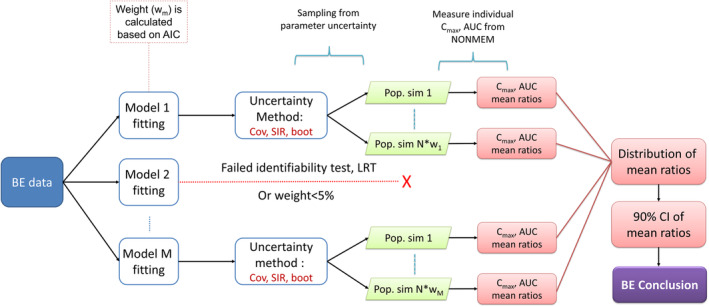
Overview of the model averaging by relative weights procedure for bioequivalence evaluation.
Model validation for model averaging
To be included in model‐averaged simulations, each model had to pass a practical identifiability test using saddle‐reset. 19 The estimation was deemed acceptable if the difference in objective function value (OFV) before and after saddle‐reset was less than 1, and no parameter estimate changed by more than 10%. For nested candidate models, the larger model was excluded unless a likelihood‐ratio test indicated a significant improvement (p = 0.05) in model fit. The smaller model was included regardless of inclusion or exclusion of the larger model. In weight‐based model averaging, models that receive a relative weight of less than 5% were excluded from the BE determination in order to reduce the number of models.
Model‐averaged simulations
In order to produce test‐to‐reference geometric mean ratios of the PK metrics, each included model was used for population simulation (for a total of N = 500 simulations per dataset, for this work). In weight‐based model averaging, this corresponded to using the model to produce a number of simulations proportional to its relative weight (w m × N simulations for model m). Parameter uncertainty distributions were then generated for each included model by the respective uncertainty method (sandwich covariance matrix, bootstrap, or SIR), and parameter vectors for simulation were sampled from these distributions. In bootstrap model selection, each included model was used to simulate a portion of populations corresponding to the number of times out of 500 that the model was selected for each bootstrapped dataset. The selected model for each bootstrap sample, and the respective final parameter values from the estimation of that model in that bootstrap sample were used to simulate a population of n = 1000 subjects. Individual values of AUClast, AUC∞, and C max were calculated for both formulations using closed‐form model‐based solutions (since such solutions exist for all models in the investigated model sets). The simulation design was a single‐dose, two‐way crossover design with one sequence. In order to isolate the formulation effects, the period and sequence effects were disregarded in the simulation for BE determination. Inter‐occasion variability was also ignored, but the inter‐individual variance was increased by the inter‐occasion variance.
Model‐averaged bioequivalence test
BE parameters in a population of n = 1000 subjects were simulated. The individual test‐to‐reference ratios, and then the geometric means of these ratios across the population were calculated. Uncertainty distributions of the geometric means were generated as described in the previous section. The nonparametric 90% confidence intervals of these AUClast, AUC∞, and C max geometric mean ratios, across the N = 500 population simulations, were then computed. The 5th and 95th percentiles were compared with the pre‐determined ratio limits for BE, that is, 80% and 125%. The BE assessment was performed using the TOST method with the null hypothesis that the test product is not bioequivalent, that is, , where was AUC∞, AUClast, or C max. The two products were deemed bioequivalent If the 90% confidence intervals of the geometric mean ratios for all examined parameters fell entirely within the allowed confidence interval as outlined by regulatory guidance, 20 .
Simulation experiments
Simulation models (“True” models)
A one‐compartment model with first‐order absorption and first‐order elimination was adapted from the theophylline PK model implementation in Dubois et al. 5 The model predicts concentration y for individual i at observation j and occasion k:
| (2) |
where F is relative bioavailability, D is dose, k a is the absorption rate constant, V is the volume of distribution, CL is clearance, and is time after dose. The proportional residual error, , is assumed to be normally distributed around zero, with a variance of σ 2:
| (3) |
Parameter values for Individual i and occasion k were given by:
| (4) |
| (5) |
| (6) |
| (7) |
where is the population parameter, is the individual deviation from the typical subject with variance , is the occasion deviation from the individual value with variance , and is the treatment effect on bioavailability and set as 1 for the reference product.
The population parameter values used to simulate the BE data were bioavailability, , absorption rate constant, , volume of distribution, , and clearance, . Variance for inter‐occasion variability in any parameter was (~15% CV), variance for inter‐individual variability in any parameter was set to (approximately 50% CV) and the variance of residual error is set to σ2 = 0.01 (10% CV). The true model was altered in the oral and parallel ophthalmic scenarios by removing the inter‐individual and inter‐occasion variability on some parameters (setting their variances to zero). The true model in the oral scenarios included inter‐individual variability on k a, V, and CL, and inter‐occasion variability on F ( = = = = 0). The true model in the parallel ophthalmic scenario included inter‐individual variability on all parameters, but no inter‐occasion variability ( = 0).
Scenarios
Single‐dose BE studies of oral and ophthalmic formulations were simulated under different study designs, detailed in Table 1. For oral formulation scenarios, BE data were simulated using a single‐dose, two‐treatment, two‐period crossover design, simply referred to as a crossover design in this work, with either a rich sampling design (24 subjects, 10 samples/subject), or a sparse‐sampling design (40 subjects, 3 samples/subject), the intermediate and sparse designs used by Dubois et al. 5 For ophthalmic formulation scenarios, sample(s) were collected once for each subject and each period and simulations were performed for both a parallel design with 480 subjects (a single sample collected from one eye for each subject) and a crossover design with 120 subjects (two samples collected from each subject, one from each eye).
TABLE 1.
Overview of studied simulation scenarios.
| Description | True mean‐ratio a (%) | Subjects | Sampling times (hours after dose) |
|---|---|---|---|
| Oral formulation | |||
| Power analysis | |||
| Crossover design with rich sampling | 90 | 24 | 0.25, 0.5, 1, 2, 3.5, 5, 7, 9, 12, 24 |
| Crossover design with sparse sampling | 90 | 40 | 0.25, 3.35, 24 |
| Type I error analysis | |||
| Crossover design with rich sampling | 125 | 24 | 0.25, 0.5, 1, 2, 3.5, 5, 7, 9, 12, 24 |
| Crossover design with sparse sampling | 125 | 40 | 0.25, 3.35, 24 |
| Ophthalmic formulation | |||
| Power analysis | |||
| Parallel design | 90 | 480 | 0.25, 1.5, 5, 15, 24 b |
| Crossover design | 90 | 120 | 0.25, 1.5, 5, 15, 24 b |
| Type I error analysis | |||
| Parallel design | 125 | 480 | 0.25, 1.5, 5, 15, 24 b |
| Crossover design | 125 | 120 | 0.25, 1.5, 5, 15, 24 b |
β TRT,F value used for test formulation in simulations.
For ophthalmic formulations: In parallel trials, each subject is sampled once, in crossover trials, each subject is sampled twice at the same time after the dose, once per study period. Subjects are assigned evenly across timepoints.
For each study design, simulations with different expected BE outcomes were carried out to evaluate type I error and the power of the studied methods. The expected BE outcome was imposed by simulating with a proportional test treatment effect on bioavailability (β TRT,F , relative bioavailability, see Equation 4). The power of the compared methods was examined under bioequivalent scenarios, with a relative bioavailability of 90% (β TRT,F = 0.9) used to simulate BE datasets. The type I error rates were examined using non‐bioequivalent scenarios with a treatment effect on the relative bioavailability of 125% (β TRT,F = 1.25). This change in relative bioavailability is equivalent to a change of 125% in AUC∞ (where applicable), AUClast, and C max between test and reference formulations for the simulation models described above. Additional type I error scenarios with a treatment effect of 80% were excluded due to long runtimes. Power and type I error was calculated for each method and each BE metric. In addition, an overall power or type I error was also obtained where BE was concluded when all required metrics approved bioequivalence (AUC∞, AUClast, and C max for oral formulations, and AUClast and C max for ophthalmic formulations). For each scenario, 500 BE study datasets were simulated and the applicable BE methods for the scenario were applied to each simulated BE study. Type I error was considered controlled if it fell within 3.2%–7.0%, which is the 95% binomial proportion confidence interval around the expected 5% type I error rate for 500 trials (calculated using the Cornish‐Fisher expansion 21 implementation in R 22 ). Type I error rates above 7.0% were considered not adequately controlled, and below 3.2% were considered overly conservative.
Model pools
The pools of candidate models for the model averaging approach were different for the three different BE study design scenarios (see Table 2). The three model pools were based on the simulation (“true”) model, and thus made up of one‐compartment models with first‐order absorption, first‐order elimination, and proportional residual error. The study designs did not enable the estimation of all simulation model parameters. For example, the simulated study designs assumed an oral dose of the studied drug products, and therefore total bioavailability () could not be estimated in any of the designs and was fixed to a value of 1. All relative changes in bioavailability based on treatment can be estimated in the standard BE study designs investigated in this work.
TABLE 2.
Overview of the model pools used in the simulation experiments.
| Ophthalmic formulation parallel design model pool | Ophthalmic formulation crossover design model pool | Oral formulation model pool | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model number | Inter‐individual variability | Treatment effects | Model number | Inter‐individual variability | Treatment effects | Model number | Inter‐individual variability | Treatment effects | Inter‐occasion var. | Sequence effects | Period effects | ||||||||||||||
| F | Ka | V | CL | F | Ka | F | Ka | V | CL | F | Ka | F | Ka | V | CL | F | Ka | F | F | Ka | F | Ka | |||
| 1 | ✓ | ✓ | ✓ | ✓ | 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| 2 | ✓ | ✓ | ✓ | ✓ | 2 | ✓ | ✓ | ✓ | ✓ | ✓ | 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| 3 | ✓ | ✓ | ✓ | ✓ | 3 | ✓ | ✓ | ✓ | ✓ | ✓ | 3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| 4 | ✓ | ✓ | ✓ | 4 | ✓ | ✓ | ✓ | ✓ | ✓ | 4 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| 5 | ✓ | ✓ | ✓ | 5 | ✓ | ✓ | ✓ | ✓ | ✓ | 5 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| 6 | ✓ | ✓ | ✓ | 6 | ✓ | ✓ | ✓ | ✓ | 6 | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| 7 | ✓ | ✓ | ✓ | 7 | ✓ | ✓ | ✓ | ✓ | 7 | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| 8 | ✓ | ✓ | 8 | ✓ | ✓ | ✓ | ✓ | 8 | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| 9 | ✓ | ✓ | ✓ | 9 | ✓ | ✓ | ✓ | 9 | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| 10 | ✓ | ✓ | ✓ | 10 | ✓ | ✓ | ✓ | 10 | ✓ | ✓ | ✓ | ||||||||||||||
| 11 | ✓ | ✓ | ✓ | 11 | ✓ | ✓ | ✓ | 11 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| 12 | ✓ | ✓ | 12 | ✓ | ✓ | ✓ | ✓ | ✓ | 12 | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| 13 | ✓ | ✓ | 13 | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| 14 | ✓ | ✓ | 14 | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| 15 | ✓ | ✓ | 15 | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| 16 | ✓ | 16 | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||
| 17 | ✓ | ✓ | ✓ | ||||||||||||||||||||||
| 18 | ✓ | ✓ | ✓ | ||||||||||||||||||||||
| 19 | ✓ | ✓ | ✓ | ||||||||||||||||||||||
| 20 | ✓ | ✓ | |||||||||||||||||||||||
| 21 | ✓ | ✓ | |||||||||||||||||||||||
| 22 | ✓ | ✓ | |||||||||||||||||||||||
Note: Rows indicate numbered models, and the features of each model are indicated by checkmarks in the applicable columns. All models used were one‐compartment models with first‐order absorption, first‐order elimination, and proportional error. Shaded rows indicate that the model was excluded from model averaging by bootstrap model selection to reduce runtimes.
Treatment effects were added to all absorption parameters of the simulation model ( and ), and for crossover scenarios sequence and period effects were also added to the absorption parameters. Based on the resultant full model evaluating those design elements, a series of reduced candidate models were generated that included different combinations of features: covariate effect (treatment, sequence, and period effects on absorption parameters) and random effects (inter‐individual variability and inter‐occasion variability). The selection of candidate models was determined based on model identifiability, which was investigated using PopED, 16 or based on estimation success rate in a preliminary simulation experiment. For example, models estimating >2 random effect parameters were not identifiable and excluded for the ophthalmic parallel study scenario. Since there is only a single observation per individual in the ophthalmic parallel scenario, inter‐individual variability is essentially an extension of the residual error in those models, and the two may not be independently identifiable. Inter‐occasion variability cannot be estimated in ophthalmic scenarios, and it was not included in either of the ophthalmic scenario model pools.
To reduce runtimes of simulation experiments, certain models that were expected to have little chance to impact the final model averaging results were removed. For example, the models without treatment effect on F were not included in ophthalmic BE studies. The model pool for bootstrap model selection, the method with the longest runtime, was further reduced to the 10 models with the highest average weights in weight‐based model averaging based on preliminary simulation results. The features of the models in each model pool are detailed in Table 2.
Standard NCA‐based BE evaluation
For the oral product formulations, the model averaging approaches were compared with the NCA‐based method outlined for BE studies using a single‐dose, two‐way crossover design in the FDA guidance. 20 In this method, individual AUC∞, AUClast, and C max were calculated on log scale (using NCA in the NCAPPC package 15 ) and fitted to a linear mixed‐effects model according to Equation 8.
| (8) |
where is the value of metric m (AUC∞, AUClast, or C max) of subject i during period p, is the expected value of the metric at the reference levels of all design covariates. TRT i,p , SEQ i , and PER p are the treatment, sequence, and period indicators, and , , and are the corresponding coefficients for metric . The random effects are η m,i , for inter‐individual variability in metric m, and ε m,i,p is the residual error. The 90% parametric confidence interval of the treatment effect coefficient for each metric, , was then calculated, and if it fell entirely within the 80%–125% range the test treatment was accepted as bioequivalent.
For the ophthalmic product formulations, the model averaging approaches were compared with a nonparametric bootstrapped NCA method for aqueous humor PK data described by Shen and Machado, 12 which is currently recommended by the FDA in relevant product‐specific guidances. 14 In the simulated scenario, the drug was administered at a set time before cataract surgery, with a single sample of aqueous humor taken during the surgery. Crossover designs are possible, where two samples are taken at the same sample time after administration, one from each eye in two surgeries on separate occasions. At each sampling time, all individuals measured at that time were bootstrapped with replacement 105 times. In parallel studies, this was done separately for the two treatments, while for crossover studies both test and reference measurements were included when a subject was selected by the bootstrap. Values for C max and AUClast were calculated using NCA for each treatment in each bootstrapped dataset from the geometric mean concentrations at each sampling time, obtaining 105 test‐to‐reference ratios of C max and AUClast. AUC∞ is not calculated in this method. 12 Nonparametric confidence intervals for each metric ratio were formed from the 5th and 95th percentiles of the ratios from all bootstraps, and the test formulation passed the BE test if that interval fell within 80%–125%, see Figure S1 in Data S1.
Software
Estimation, including parameter uncertainty estimation, was performed using NONMEM 7.4, 23 facilitated by Perl speaks NONMEM (PsN). 24 Run management and statistical calculations were performed in R. 22 The NCA metrics were calculated using the NCAPPC package. 15
RESULTS
Type I error
Type I error results for each PK metric and the overall BE determination are visualized in Figure 3. Several model averaging approaches displayed inflated type I errors. This behavior was apparent for weight‐based model averaging with bootstrap and covariance matrix uncertainty in all crossover scenarios, for model averaging by bootstrap model selection in the crossover design with rich sampling for oral formulations, and for weight‐based model averaging with SIR uncertainty in the parallel design for ophthalmic formulations. In scenarios with sparse sampling and higher numbers of subjects, that is, the ophthalmic scenarios and the sparse crossover oral scenario, the type I error remained best controlled with the bootstrap model selection method. In the oral scenario with sparse sampling, the bootstrap model selection method had exactly 7.0% type I error, which is the upper limit of the acceptable interval. Where this method failed to adequately control type I error, however, was in the oral scenario with rich crossover design and few subjects. Weight‐based model averaging with SIR uncertainty successfully controlled type I error in both oral formulation scenarios.
FIGURE 3.
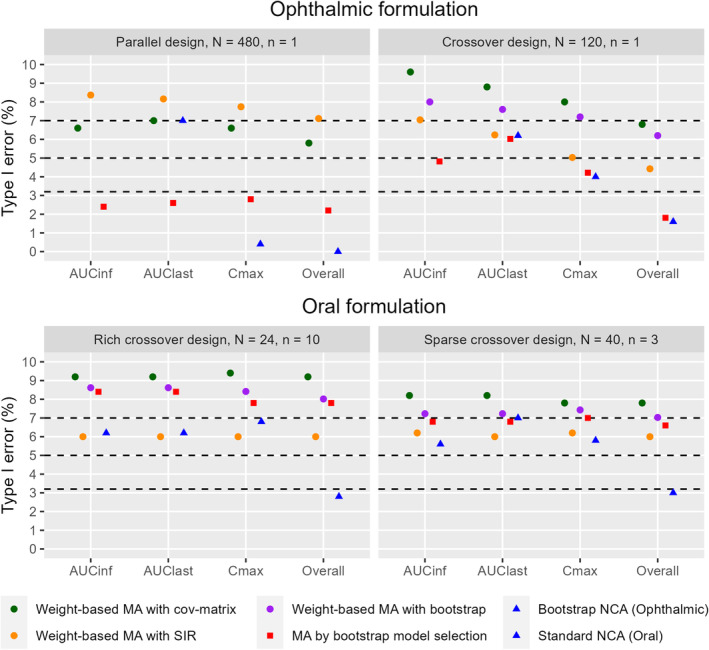
Method comparison of type I error for bioequivalence tests of AUC∞, AUClast, C max, and all metrics combined (overall) in the ophthalmic product scenarios (top) and oral product scenarios (bottom). Type I error results within the 95% binomial proportion confidence interval (top and bottom dashed lines) are not statistically significantly different from the expected 5% (middle dashed line). Please note that not every method was examined in every scenario. The bootstrapped NCA method does not produce AUCinf. N represents the number of subjects and n represents the number of samples per subject and period in each scenario.
The type I errors of NCA‐based methods fell within the expected range for all individual metrics in all scenarios except the parallel ophthalmic scenario, where C max was overly conservative. However, the NCA BE result was not consistent across metrics within each simulated study, meaning that different metrics failed different studies. This led to the overall NCA BE result being overly conservative in all scenarios (0.0%–3.0%). See Figure S2 in Data S1 for a density plot of the GMR and its 5th and 95th percentiles to visualize how the GMR is distributed in the different methods of the oral formulation, rich sampling, and crossover design scenario.
Power
Power results for each PK metric and the overall BE determination are visualized in Figure 4. Model averaging approaches demonstrated considerably higher power over NCA methods when the BE data were simulated with 90% test‐to‐reference relative bioavailability (bioequivalence). The improvement in power is strongest in AUC∞ and C max. In the parallel ophthalmic scenario, C max power for model averaging methods ranged between 33.6% and 50.8%, compared with the 4.2% power of the bootstrap NCA method. In the oral scenarios, AUC∞ power for model averaging methods was 8.6%–18.0% higher than the standard NCA method.
FIGURE 4.
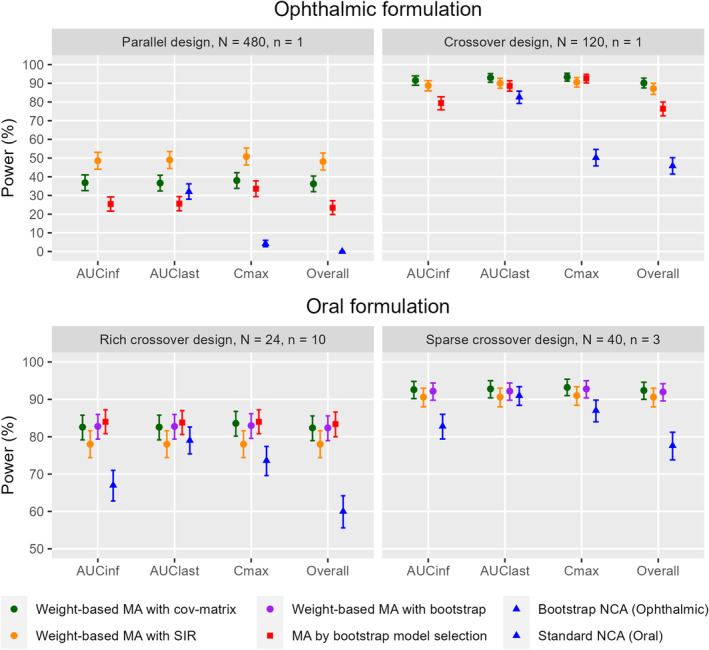
Method comparison of power for bioequivalence tests of AUC∞, AUClast, C max, and all metrics combined (overall) in the ophthalmic product scenarios (top) and oral product scenarios (bottom). Error bars represent the 95% binomial proportion confidence interval of the power. Please note that not every method was examined in every scenario. The bootstrapped NCA method does not produce AUCinf. N represents the number of subjects and n represents the number of samples per subject and period in each scenario.
For ophthalmic formulations, the crossover design with 120 subjects enabled all methods to achieve higher power than in the parallel design with 480 subjects. Similar to the type I error results, the power of model averaging methods was more consistent across metrics, leading to overall BE results close to the results of the individual metrics, while NCA‐based methods had lower overall power. The parallel ophthalmic scenario was severely underpowered for the bootstrap NCA method, with an overall power near 0%.
Model weights and selection frequency in model averaging approaches
To provide additional context for the comparison between model averaging approaches, we compared the weights assigned to each model in weight‐based model averaging (Equation 1) and the weights, or rather the relative selection frequencies, for each model in bootstrap model selection. The weights for the 16 models (listed in Table 2) and 500 simulated BE studies in the parallel ophthalmic simulation experiment are shown in Figure 5. This comparison reveals that the weight‐based model averaging method favored assigning high weight to one model in each study, while bootstrap model selection selected a wider range of models with lower frequencies to describe each dataset.
FIGURE 5.
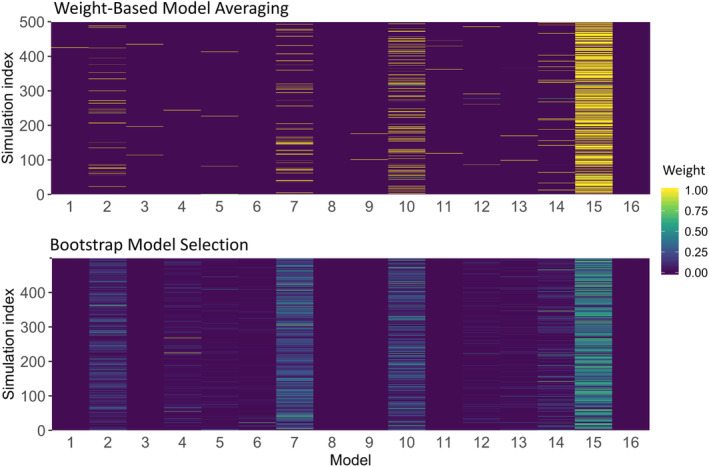
Weights of the weight‐based model averaging method (top) and relative selection frequencies of the bootstrap model selection method (bottom) for the 16 models and 500 simulated BE studies in the parallel ophthalmic BE study example.
DISCUSSION
The model averaging methods presented here vastly outperformed the power characteristics of the NCA‐based methods for BE assessment, while two of the methods, model averaging by bootstrap model selection and weight‐based model averaging with SIR uncertainty, maintained acceptable type I error in respective designs.
MIE approaches can account for the variability and uncertainty of different sources (statistical model, parameter uncertainty, etc.), which leads to more precise estimation of BE metrics. More precise BE metrics produce narrower geometric mean ratio confidence intervals than those from NCA methods. Narrower confidence intervals are more likely to fit within the BE limits, and thus the MIE methods have higher power. However, the uncertainty must be accurately estimated and accounted for in MIE methods, as they may not adequately control type I error otherwise.
MIE approaches can evaluate C max at any timepoint, while NCA methods are restricted to the observed timepoints based on the study design. MIE approaches also have a more elaborate and constrained time‐dependency, providing more accurate AUC extrapolation to infinity. 25 , 26 This gives MIE methods C max and AUC∞ power advantages, especially striking for C max in the ophthalmic scenarios, and for AUC∞ in the oral scenarios (see Figure 4). The MIE methods also produced more consistent BE results across the three PK metrics in each dataset. The inconsistency across metrics in the NCA methods can be seen in Figures 3 and 4 as the overall BE results were lower than the individual results for each PK metric. It is worth noting that the MIE approaches allow AUC∞ comparisons for ophthalmic formulations, which is not performed in the currently used bootstrapped NCA method. For AUClast the different BE methods produced much more similar results, with the NCA methods displaying higher power and higher type I error in AUClast compared with the other metrics. The designs studied here are not ideal for performing NCA analyses, and NCA would achieve higher power in designs with richer and longer sampling. They are, however, still relevant designs that enable method comparisons.
Two methods stood out as the best performers in the studied scenarios: model averaging by bootstrap model selection and weight‐based model averaging with SIR uncertainty. Weight‐based model averaging with SIR uncertainty controlled the type I error in the oral formulation scenarios but failed to adequately control type I error in the ophthalmic formulation scenarios. Model averaging by bootstrap model selection best controlled the type I error in the ophthalmic formulation scenarios, with a slightly overly conservative type I error and a slight reduction in power compared with the weight‐based model averaging methods, but it failed to control the type I error rate in the oral formulation scenario with rich sampling in a study with relatively few subjects (24 subjects). These results reflect the strengths and weaknesses of the respective uncertainty methods. The bootstrap is robust even in sparse‐sampling scenarios but requires enough subjects to provide an adequate representation of the population. The SIR method is robust with fewer subjects but struggles to accurately estimate parameter uncertainty in very sparse data.
It is worth noting that the bootstrap model selection method is much more time‐consuming than the weight‐based model averaging methods. We observed overly conservative type I error rates for the bootstrapped NCA and model averaging by bootstrap model selection methods in the parallel design ophthalmic scenario (Figure 3 top left). This behavior is the result of the nature of performing two one‐sided tests when the variability is large due to extremely sparse data, and other factors such as an inadequate sample size, or using a parallel design. The high variation can produce cases in the type I error scenarios where the 95th percentile is within the 80%–125% range, but the 5th percentile falls below 80%, which leads to the observed low type I error, that is, the type I error (or more precisely the type I error of the upper limit test minus the type II error of the lower limit test) is overly conservative compared with the expected 5%. It can even lead to a result where none of the 500 cases have both the 5th and the 95th percentiles within 80%–125%. In addition, the high variation caused low power (Figure 4 top left), with bootstrap NCA having 0% overall power (AUClast and C max combined) in the parallel design ophthalmic scenario. Improved properties may be observed with an adequately powered study.
Compared with single‐model MIE approaches, model averaging approaches allow for fewer model assumptions. For example, several plausible formulation effects and statistical models can be tested within the scope of a single analysis. The inevitable misspecifications of any single model, compared with the biological system it describes, may cause uncontrolled type I error. 4 , 9 Taking multiple models into consideration will mitigate that risk. 9 , 10
Another interesting note regarding the traditional single‐model MIE methods is that even if it would be possible to find a model close to the true model, that model may not be practically identifiable with the available data. This is particularly relevant for ophthalmic formulations, where the extremely sparse data is unlikely to support the estimation of the true model. The proposed model averaging methods include a check for practical identifiability with saddle‐reset to reduce the risk of using a non‐identifiable model in the analysis. They can then average over practically identifiable models that cover different features of a more accurate, but non‐identifiable, model. MIE approaches also open the door for multiple ways of examining the final treatment effect. For example, in a linear system with a proportional treatment effect on bioavailability, BE can be tested directly on the parameter estimates. In the proposed method, we have chosen to simulate concentration–time profiles, which means that any PK model can be included in the model pool, including nonlinear models and models with complex treatment effects.
The main question that remains for the model averaging methods is how the model pool should be compiled. It seems that bootstrap model selection can handle a larger model pool because one model is selected for each bootstrapped dataset, rather than assigning a weight to each model in the pool. Using different strategies for compiling and validating a model pool can undoubtedly have a major impact on the results. In this work, we have employed PopED optimal design investigations to qualify models for inclusion in the model pool, and then likelihood‐ratio tests for nested models and saddle‐reset to qualify each estimation. It is recommended to constrain the model pool to a relatively small number of plausible models, but the strategies for selecting these model pools should be further investigated. One approach that we have identified as promising is to test the ability of each model to describe the study dataset. For this purpose, the posterior predictive check (PPC) of the R package NCAPPC 15 can be used, excluding any model that cannot predict the observed data. However, no models were excluded when the method was applied in this study.
We also acknowledge that this work is based on simulated data, which generally allows for a much more thorough examination and comparison than using real‐world data. The presented BE analysis methods using model averaging will be further evaluated on clinical trial data in future efforts.
CONCLUSION
The model averaging approaches presented here showed high power while maintaining controlled type I error rates for BE analysis. They should be further evaluated as potential alternative BE approaches in scenarios where NCA‐based methods are not expected to perform well (e.g., sparse sampling, few individuals, high variability, incomplete washout, etc.). In this work, model‐informed approaches seemed to perform especially well in the extremely sparse data scenarios of ophthalmic formulations. Model averaging by bootstrap model selection performed best in scenarios with sparse sampling in large numbers of subjects, such as those for ophthalmic products, while the weight‐based model averaging with SIR uncertainty performed best in the rich sampling scenario with fewer subjects.
AUTHOR CONTRIBUTIONS
H.B.N., X.C., M.D., L.F., L.Z., M.O.K., and A.C.H. wrote the manuscript. H.B.N., X.C., M.D., L.F., L.Z., M.O.K., and A.C.H. designed the research. H.B.N. and X.C. performed the research. H.B.N. and X.C. analyzed the data.
FUNDING INFORMATION
No funding was received for this work.
CONFLICT OF INTEREST STATEMENT
M.D., L.Z., and L.F. are employed by the U.S. Food and Drug Administration. H.B.N. is a former employee of Uppsala University and is currently employed with Pharmetheus AB. A.C.H. and M.O.K. have received consultancy fees from, and own stock in Pharmetheus AB, all unrelated to this manuscript. The opinions expressed in this manuscript are those of the authors and should not be interpreted as the position of the U.S. Food and Drug Administration. All other authors declared no competing interests for this work. As an Associate Editor for CPT: Pharmacometrics & Systems Pharmacology, Andrew Hooker was not involved in the review or decision process for this paper.
Supporting information
Data S1.
ACKNOWLEDGMENTS
The authors would like to acknowledge the research funding by the FDA and the collaborators on the project “Evaluation and development of model‐based bioequivalence analysis strategies” under the FDA contract HHSF223201710015C.
Bjugård Nyberg H, Chen X, Donnelly M, et al. Evaluation of model‐integrated evidence approaches for pharmacokinetic bioequivalence studies using model averaging methods. CPT Pharmacometrics Syst Pharmacol. 2024;13:1748‐1761. doi: 10.1002/psp4.13217
REFERENCES
- 1. U.S. Department of Health and Human Services Centre for Drug Evaluation and Research (CDER), and FDA . FDA Guidance for industry, statistical approaches to establishing bioequivalence. https://www.fda.gov/media/163638/download 2022.
- 2. U.S. Department of Health and Human Services Centre for Drug Evaluation and Research (CDER), and FDA . FDA guidance for industry, bioequivalence studies with pharmacokinetic endpoints for drugs submitted under an ANDA. https://www.fda.gov/media/87219/download 2021.
- 3. Hu C, Moore KHP, Kim YH, Sale ME. Statistical issues in a modeling approach to assessing bioequivalence or PK similarity with presence of sparsely sampled subjects. J Pharmacokinet Pharmacodyn. 2004;31:321‐339. [DOI] [PubMed] [Google Scholar]
- 4. Dubois A, Gsteiger S, Pigeolet E, Mentré F. Bioequivalence tests based on individual estimates using non‐compartmental or model‐based analyses: evaluation of estimates of sample means and type I error for different designs. Pharm Res. 2010;27:92‐104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Dubois A, Lavielle M, Gsteiger S, Pigeolet E, Mentré F. Model‐based analyses of bioequivalence crossover trials using the stochastic approximation expectation maximisation algorithm. Stat Med. 2011;30:2582‐2600. [DOI] [PubMed] [Google Scholar]
- 6. Möllenhoff K, Loingeville F, Bertrand J, et al. Efficient model‐based bioequivalence testing. Biostatistics. 2022;23:314‐327. [DOI] [PubMed] [Google Scholar]
- 7. Loingeville F, Bertrand J, Nguyen TT, et al. New model‐based bioequivalence statistical approaches for pharmacokinetic studies with sparse sampling. AAPS J. 2020;22:141. [DOI] [PubMed] [Google Scholar]
- 8. Chen X, Bjugård Nyberg H, Karlsson MO, Hooker AC. Model‐based bioequivalence evaluation for ophthalmic products using model averaging approaches. in ACoP (ISOP) 2019.
- 9. Aoki Y, Röshammar D, Hamrén B, Hooker AC. Model selection and averaging of nonlinear mixed‐effect models for robust phase III dose selection. J Pharmacokinet Pharmacodyn. 2017;44:581‐597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Buatois S, Ueckert S, Frey N, Retout S, Mentré F. Comparison of model averaging and model selection in dose finding trials analyzed by nonlinear mixed effect models. AAPS J. 2018;20:1‐9. [DOI] [PubMed] [Google Scholar]
- 11. Dosne AG, Bergstrand M, Karlsson MO, Renard D, Heimann G. Model averaging for robust assessment of QT prolongation by concentration‐response analysis. Stat Med. 2017;36:3844‐3857. [DOI] [PubMed] [Google Scholar]
- 12. Shen M, Machado SG. Bioequivalence evaluation of sparse sampling pharmacokinetics data using bootstrap resampling method. J Biopharm Stat. 2017;27:257‐264. [DOI] [PubMed] [Google Scholar]
- 13. Tardivon C, Loingeville F, Donnelly M, et al. Evaluation of model‐based bioequivalence approach for single sample pharmacokinetic studies. CPT Pharmacometrics Syst Pharmacol. 2023;12:904‐915. doi: 10.1002/psp4.12960 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. FDA Office of Generic Drugs . Draft guidance on loteprednol etabonate. https://www.accessdata.fda.gov/drugsatfda_docs/psg/PSG_050804.pdf 2019.
- 15. Acharya C, Hooker AC, Turkyilmaz GY, Jonsson S, Karlsson MO. A diagnostic tool for population models using non‐compartmental analysis: the ncappc package for R. Comput Methods Prog Biomed. 2016;127:83‐93. [DOI] [PubMed] [Google Scholar]
- 16. Nyberg J, Ueckert S, Strömberg EA, Hennig S, Karlsson MO, Hooker AC. PopED: an extended, parallelized, nonlinear mixed effects models optimal design tool. Comput Methods Prog Biomed. 2012;108:789‐805. [DOI] [PubMed] [Google Scholar]
- 17. Kim SB, Sanders N. Model averaging with AIC weights for hypothesis testing of Hormesis at low doses. Dose‐Response. 2017;15:1559325817715314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Dosne A‐G, Bergstrand M, Karlsson MO. An automated sampling importance resampling procedure for estimating parameter uncertainty. J Pharmacokinet Pharmacodyn. 2017;44:509‐520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bjugård Nyberg H, Hooker AC, Bauer RJ, Aoki Y. Saddle‐reset for robust parameter estimation and Identifiability analysis of nonlinear mixed effects models. AAPS J. 2020;22:90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. U.S. Department of Health and Human Services Centre for Drug Evaluation and Research (CDER), F. and D. A . FDA guidance for industry, statistical approaches to establishing bioequivalence. https://www.fda.gov/media/70958/download 2001.
- 21. Cornish EA, Fisher RA. Moments and Cumulants in the specification of distributions. Revue de l'Institut International de Statistique / Review of the International Statistical Institute. 1938;5:307‐320. [Google Scholar]
- 22. R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Preprint at; 2017. [Google Scholar]
- 23. Beal S, Sheiner LB, Boeckmann A, Bauer RJ. NONMEM 7.4 user's guides. (1989‐2018), Icon development solutions, Ellicott City, MD, USA. Preprint at 2017.
- 24. Keizer RJ, Karlsson MO, Hooker AC. Modeling and simulation workbench for NONMEM: tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst Pharmacol. 2013;2:e50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Busse D, Schaeftlein A, Solms A, et al. Which analysis approach is adequate to leverage clinical microdialysis data? A quantitative comparison to investigate exposure and response exemplified by levofloxacin. Pharm Res. 2021;38:381‐395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Collins JW, Heyward Hull J, Dumond JB, Bjugård Nyberg H. Comparison of tenofovir plasma and tissue exposure using a population pharmacokinetic model and bootstrap: a simulation study from observed data. J Pharmacokinet Pharmacodyn. 2017;44:631‐640. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1.


