Material properties in regenerating axolotl limbs using inverse finite element analysis

Abstract

Background:

The extracellular mechanical environment plays an important role in the skeletal development process. Characterization of the material properties of regenerating tissues that recapitulate development, provides insights into the mechanical environment experienced by the cells and the maturation of the matrix. In this study, we estimated the viscoelastic material properties of regenerating forelimbs in the axolotl (Ambystoma mexicanum) at three different regeneration stages: 27 days post-amputation (mid-late bud) and 41 days post-amputation (palette stage), and fully-grown time points. A stress-relaxation indentation test followed by two-term Prony series viscoelastic inverse finite element analysis was used to obtain material parameters. Glycosaminoglycan (GAG) content was estimated using a 1,9- dimethyl methylene blue assay.

Results:

The instantaneous and equilibrium shear moduli significantly increased with regeneration while the short-term stress relaxation time significantly decreased with limb regeneration. The long-term stress relaxation time in the fully-grown time point was significantly lower than 27 and 41 DPA groups. The GAG content was not significantly different between 27 and 41 DPA but the GAG content of cartilage in the fully-grown group was significantly greater than in 27 and 41 DPA.

Conclusions:

The mechanical environment of the proliferating cells changes drastically during limb regeneration. Understanding how the tissue’s mechanical properties change during limb regeneration is critical for linking molecular-level matrix production of the cells to tissue-level behavior and mechanical signals.

1. Introduction

Limb growth is a highly complex process involving an interplay of a variety of biochemical and biomechanical signals (Sermeus et al., 2022). Vertebrate limb growth involves multiple tissue types that change in composition and mechanics. Mesenchymal cells in the limb bud condense and differentiate into cartilage. As the cartilage matures, the extracellular matrix undergoes significant changes in composition with mineralized bone replacing hypertrophic chondrocytes leaving cartilage only at the end of long bones (Shea et al., 2015). Mechanics are thought to influence every stage of limb growth both in development and regeneration.

Physiological loading of growing musculoskeletal tissues can induce mechanical, chemical, and electrical signals within the loaded tissue. Cells in embryonic tissues are mechanosensitive; they can sense the changes in the environment and translate the mechanical signal into a molecular response. Chai et al. showed that directional mechanical compression of the zebrafish embryo can realign the anterior-posterior axis (Chai et al., 2015). Similarly, proximodistal limb pattering in urodeles (newts and salamanders) is influenced by the differential stiffness gradient along the limb during regeneration (Steinberg, 1978). Disruption of the mechanical stimuli or the mechano-sensing pathway in growing tissues leads to dysfunctional growth and disease. Rodriguez et al. showed that lack of in-utero movement of the embryo leads to poor bone mineralization in human fetuses (Rodríguez et al., 1988). Similarly, studies in immobilized chicks, salamanders, and muscle-less murine models showed altered joint morphology, limb patterning, and material composition caused by lack of mechanical loading (Nowlan et al., 2010; Comellas et al., 2022; Mikic et al., 2004; Hu et al., 2022). Identification of mechanosensitive genes through in-vitro and in-vivo experiments further illustrates the importance of mechanical forces in limb growth (Roddy et al., 2011; Nowlan et al., 2008). There is little understanding, however, of how tissue-level loading is transduced to cellular-level signals in-vivo, especially during the different stages of limb growth (Nowlan et al., 2007).

Computational models are often used to study how tissue-level physiological load manifests as a stimulus at the cellular level by combining in-silico and in-vivo studies (Comellas et al., 2022). A finite element (FE) model is a mathematical representation of the geometry, material properties, and loading conditions of a structure that allows the mechanical environment within the structure to be determined. Characterization of the material properties of developing musculoskeletal tissues provides insights into the mechanical environment experienced by the cells (Thompson et al., 2000).

The stiffness in growing skeletal tissues comes from a combination of the solid matrix (collagen and proteoglycans) and fluid (water) components (Berteau et al., 2016; Humphrey, 2003). Proteoglycan side chains glycosaminoglycans (GAGs), trap water and influence fluid flow in the tissues (Samosky et al., 2005; Williamson et al., 2001). Several studies have shown the importance of GAGs on the mechanical behavior of mature cartilage (Samosky et al., 2005; Kempson et al., 1970; Allen, 1996). By estimating GAG content in the growing skeletal tissues, we can correlate the mechanical properties to the composition thereby better elucidating the role of extra-cellular matrix components in defining the mechanical behavior.

Previous studies in growing rabbits, (Julkunen et al., 2009) mice, (Berteau et al., 2016) and rats (Hamann et al., 2014) examined the material properties of cartilage in the limbs during post-natal stages of development. These studies determined the relationship between age and material parameters of the cartilage such as stiffness and permeability. A few studies have analyzed fetal murine, bovine, and equine cartilage specimens but the cartilage was immature articular cartilage and cartilage undergoing endochondral ossification (Xu et al., 2016). Studies on limb development in chick embryos showed an increasing trend of GAG content over time. However, a correlation between GAG content and elastic moduli could not be established due to the difficulty in sample acquisition (Mikic et al., 2004; Forgacs et al., 1998). Estimation of mechanical properties in the early stages of development (in utero in mammals, in ovo in birds) remains challenging. One challenge is the size of the samples. Difficulty in acquiring sufficiently sized samples which represent the bulk properties of the developing tissues leads to unreliable mechanical testing measurements (Mikic et al., 2004; Berteau et al., 2016).

Regenerative capabilities of Axolotls (Ambystoma mexicanum), animals that can regrow limbs, provide a unique opportunity to measure mechanical properties during limb growth. The skeletal regeneration process in axolotls is easily accessible for manipulation and experimentation. The regeneration process is also similar to the development process in mammals, including typical gene expression (Lee and Gardiner, 2012; Fröbisch and Shubin, 2011; Monaghan et al., 2012; Lovely et al., 2022). By studying the material properties of regenerating axolotl limbs, we can characterize the mechanical environment in developing skeletal tissues. Riquelme-Guzmán et al. used confocal Brillouin microscopy to estimate the material parameters of cartilage during digit regeneration in axolotls. They showed that the material elastic contrast (a function of the longitudinal modulus) increases with regeneration and development time (Riquelme-Guzmán et al., 2022). The “longitudinal modulus” (M) estimated by Brillouin microscopy is highly dependent on the water content and insensitive to the changes in the stiffness (resistance to deformation, which is classically measured by Young’s modulus, E, of the matrix) (Wu et al., 2018). Since growing tissues have high-water content, M is an incomplete measure for matrix stiffness.

The time-dependent stress relaxation behavior of hydrated biological tissues is a function of matrix deformation, interstitial fluid flow and the inherent molecular rearrangement of the proteins in the matrix (Han et al., 2011). A Prony series viscoelastic FE material model can capture this behavior since the parameters in the model are empirical relations and not specifically associated with properties like viscosity and permeability (Mattice et al., 2006). Through inverse finite element analysis, the parameters in the model can be tuned until the finite element model stress relaxation matches experimental stress relaxation data (Valluru et al., 2022).

Indentation is commonly used to estimate time-dependent material properties of biological tissues, probing tissues on the length scale of nanometers-millimeters (Pei et al., 2022; Islam et al., 2020; Moghaddam et al., 2020; Wahlquist et al., 2017). Micro-indentation involves indenter diameters of the order 0.1–1 mm with maximum indentation depths of 1–200 μm. Nanoindentation uses indenters of diameters in the range of 0.1–100 μm with a max depth of 0.5–100 μm. AFM-assisted indentation typically uses tip diameters of 1 nm- 5 μm with max indentation depths of 1 μm (Pei et al., 2022). The indentation technique employed depends on the research question. AFM-assisted indentation is used to study submicron to nanoscale structures like protein molecules and cells, such as adhesion between cells (B. et al., 2019). Cells within tissues have diameters in the range of 10–40 μm and nanoindentation is used for characterizing the stiffness of the cell’s immediate local environment (Oyen, 2013). Micro-indentation testing allows for the measurement of bulk microscale tissue-level material properties of hydrated tissues (Jacot et al., 2006).

Cell morphology, sample thickness, and surface roughness also affect the choice of indentation technique. Nanoindentation and AFM are especially sensitive to sample pore size and surface roughness and require elaborate sample preparation (Pei et al., 2022). Micro-indentation requires very little sample preparation and can be adapted to a variety of sample shapes (Gilbert and Merkhan, 2004). Given the size of cells in axolotl limbs (nuclei diameter ~20 μm), (Comellas et al., 2022) micro-indentation is a suitable choice to measure the bulk tissue properties in regenerating axolotl limbs.

By combining experimental load-displacement data and inverse finite element analysis of a viscoelastic model, we can estimate the time-dependent material properties of biological tissues. In this study, a regenerating axolotl limb was used as a model to study cartilage development. The objective of the study was to estimate the viscoelastic material properties and GAG content of cartilaginous tissues in regenerating axolotl forelimbs at different regeneration stages.

2. Methods

2.1. Animal care and handling

All animals were bred at Northeastern University, and all procedures and surgeries were approved by the Northeastern University Institutional Animal Care and Use Committee. Surgeries were performed while axolotls were anesthetized in 0.01% benzocaine.

2.2. Animal model and sample generation

Both forelimbs of 16 fully developed axolotls (total snout to tail (ST) length: 16 ± 1 cm) were amputated at the proximal humerus. Amputated, fully grown limbs served as the fully-grown time point. Blastemas from regenerating forelimbs were harvested at 27- and 41-days post-amputation (DPA), (n = 8 animals, 16 limbs at each time point). Full regeneration happens around 90 DPA in 16 cm axolotls. 27 DPA samples represented the mid to late bud stage of regeneration while the 41 DPA samples represented palette stage of regeneration. One blastema from each axolotl was used for mechanical testing and the contralateral blastema was used for sulfated GAG quantification at every time point. The snout-to-tail length of the animals was measured at every time point before amputation. A representative sample from each time point was scanned using microcomputed tomography in the scout view (10 μm resolution, 55 kVp, 71 mA, 400 ms integration time, Scanco Medical μCT35) to illustrate the amputation plane within the blastema.

2.3. Initial sample preparation

Epithelium from the samples was carefully removed using forceps. Fully-grown limb samples were further dissected to remove connective tissues and isolate the humerus with the cartilaginous epiphysis. Indentation samples were frozen in Optimal Cutting Temperature (OCT) compound, (Gupta et al., 2009) and GAG quantification samples were frozen in 80% PBS at −20°C until used (Qu et al., 2014).

2.4. Indentation sample preparation

Further sample preparation of 27 DPA samples was not necessary due to the homogenous nature of the blastema as well as limited sample thickness. 41 DPA samples have differentiated chondrocytes within the extracellular matrix (Tank et al., 1976). To expose the cartilaginous extracellular matrix, the samples were sectioned on a cryostat to remove 100 μm of soft and connective tissue from the posterior surface of the blastema. Fully-grown samples did not undergo any further preparation as the cartilage was easily accessible after removing the soft tissue (Fig. 1). All samples were washed with 1× PBS (Sigma-Aldrich) to dissolve OCT. The samples were then glued on the anterior side to a glass side using a cyanoacrylate adhesive (Liquid Skin^®, Chemence Medical Products). (Keenan et al., 2013).

Fig. 1.

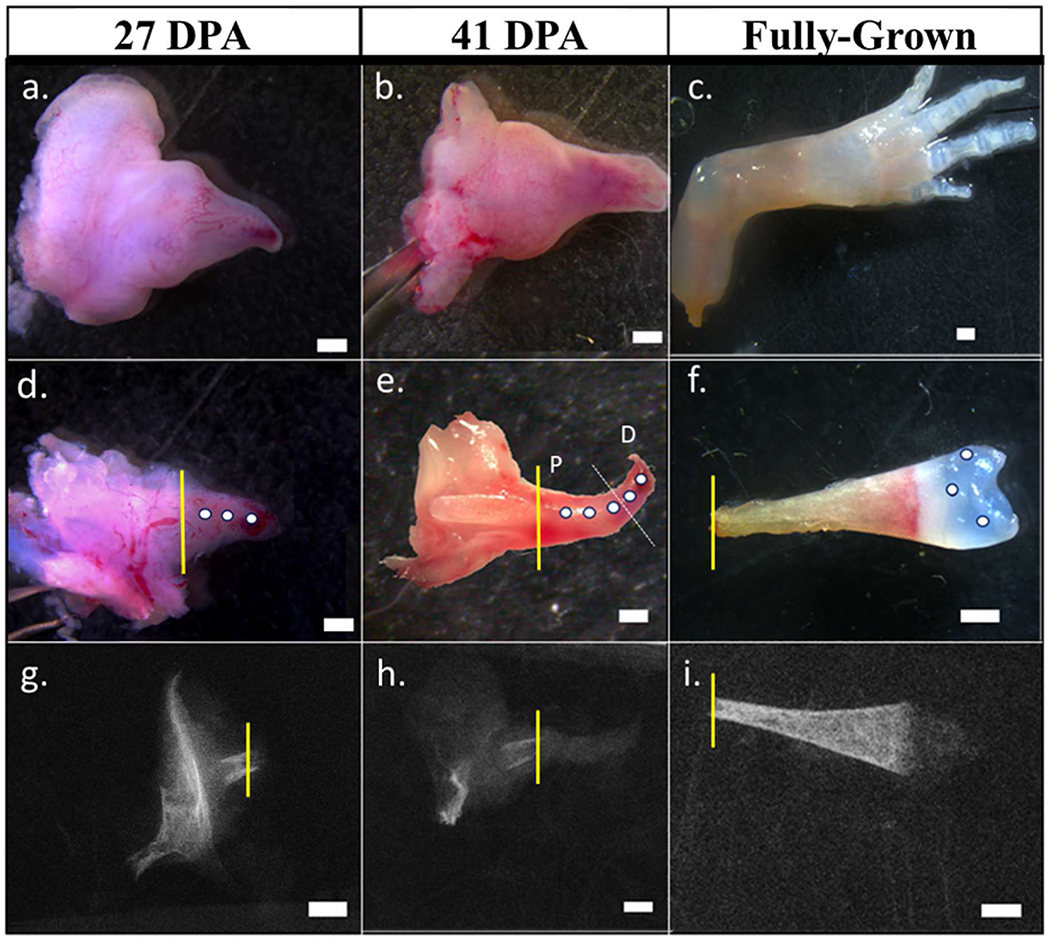
(a–c): Amputated limb at different stages of development. (d): Epithelium of 27 DPA blastema was removed to prepare the specimen for indentation. (e): 41 DPA blastema was embedded in OCT and sectioned on cryostat until the amputated bone was exposed. The demarcation between proximal (P) and distal (D) indentation points are shown in white (f): The epithelium and underlying soft tissues were carefully dissected to isolate the humerus with the cartilaginous epiphysis in the fully-grown limb samples. (g–i): micro-CT scans of representative specimens with amputation plane illustrated in yellow. All scale bars are 1 mm in length.

2.5. Micro-indentation

Stress relaxation indentation experiments were conducted on the samples using Mach-1 Micromechanical System (V500C, Biomomentum LLC). The system consisted of a linear actuator, a load cell (range: 0–245 mN), A 2-axis stage controller, and a sample holder. The glass slides were glued to the sample holder and kept hydrated by submerging them in 1X PBS throughout the experiment. A ruby spherical indenter (diameter = 300 μm) was used to perform a displacement-controlled indentation experiment.

The samples were positioned under the indenter. The indenter descended slowly toward the sample until a contact force of 0.01 mN was detected. The sample was allowed to equilibrate, and the load was zeroed (tare). Following the tare step, the indenter was ramped at a speed of 50 μm/s to reach a peak displacement of 50 μm in 1 s. The displacement was held constant for 60 s in the hold step to obtain equilibrium in the force. Refer to Fig. 2 for representative force-displacement and force-time curves. The indentation depth was chosen to ensure that the peak force was within a reliable measurable range.

Fig. 2.

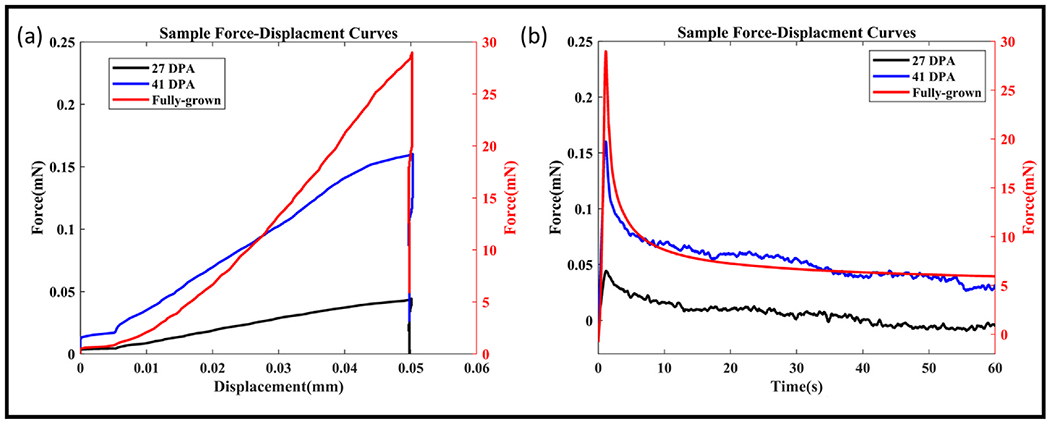
(a) Representative experimental force-displacement curves of samples from different time points (b) Representative experimental force-time curves of samples from different time points. 27 and 41 DPA time points are plotted on the left axis while the fully-grown time point is plotted on the right.

Three measurements were made on the 27 DPA limbs, 5 measurements were made on the 41 DPA limbs from proximal to distal, and 3 measurements were made on the epiphyseal cartilage of the fully-grown limb.

2.6. Inverse finite element modeling

A viscoelastic finite element model was used to fit the force-displacement data and obtain the mechanical properties from the standard linear spring model (Keenan et al., 2013). Since, the depth of indentation was much greater than 15% of indenter radius, to avoid bias due to geometric assumptions in the analytical model, an inverse finite element approach was used (Toohey et al., 2016). Displacement-controlled indentation experiments were simulated in ABAQUS© (Simulia, Providence, RI, USA). The tissue sample was modeled as a 2D rectangle with dimensions of 1 mm X 1 mm and an axis-symmetric boundary condition on the left edge. The bottom edge was defined as fixed support. The spherical indenter (radius 150 μm was modeled as a rigid body with frictionless contact (Fig. 3). The mesh was strategically seeded along the edge to have finer mesh under the indenter and a thorough mesh sensitivity analysis was conducted. The mesh density of 700 elements and 2217 nodes was chosen when further refinement yielded less than 1% change in the reaction force. The mesh is shown in Fig. 3b. The tissue material was modeled as a viscoelastic material with E, ν, g₁, g₂, τ₁, and τ₂ as independent material parameters (Table 1).

Fig. 3.

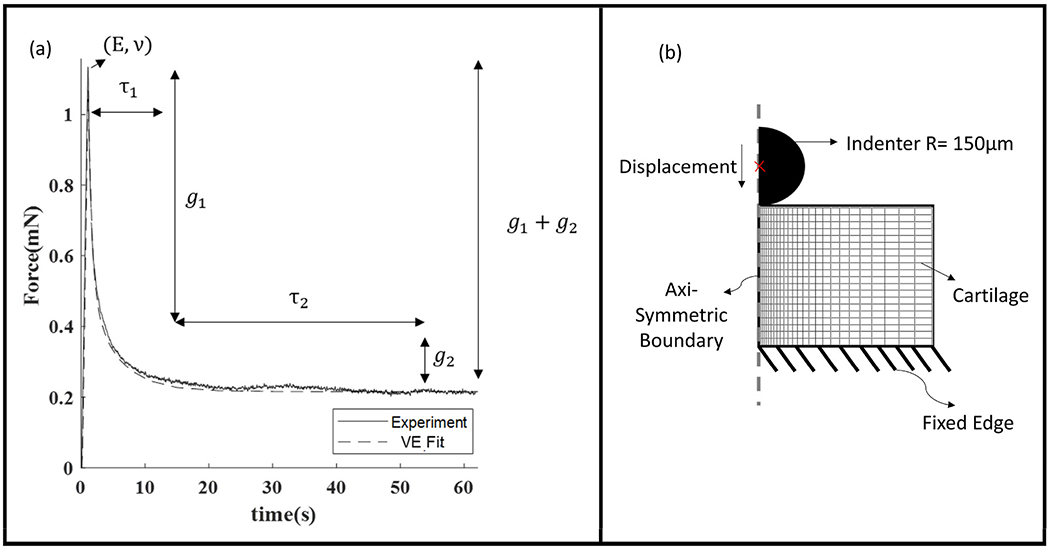
(a)Representative stress relaxation curve with fitting parameters annotated against the region that is sensitive to them (b) FE model setup.

Table 1.

Description of two-term prony series viscoelastic parameters.

Parameter	Description
E	Young’s modulus
N	Poisson’s ratio
τ1, τ2	Relaxation Time Constants
g1,g2	Dimensionless viscoelastic loss parameters
	$G(t)=G_O(1-\sum _{i=1}^2{g}_i(1-e^{\frac{-t}{{\tau }_i}}))$
${\text{K}}_1^{\text{vol}}$,${\text{K}}_2^{\text{vol}}$	Bulk relaxation moduli

Elastic modulus, E, and Poisson’s ratio, ν, represent the elastic behavior and determine the instantaneous (peak) force. The instantaneous shear modulus Go represents the initial peak stiffness and is calculated from E and ν (see equation (1)). Poisson’s ratio ν was set to be 0.25 based on average equilibrium values reported in earlier studies and its small influence on curve fitting (Valluru et al., 2022; Korhonen et al., 2002; Mow et al., 1989).

$$G_O=\frac{E}{2(1+\nu )}$$ (1)

The terms g₁, g₂, τ₁, and τ₂ represent the viscous time-dependent behavior. We used two viscous terms (called a two-term Prony series), to represent the two stages of the stress relaxation curve (Fig. 3). Prony series representation of the time dependent viscoelastic material behavior is commonly available in FE softwares like ABAQUS^®. In the first stage, the force drops quickly, which is represented by g₁ with a time period of τ₁. In the second stage the force continues to decline but at a slower rate, represented by g₂ with a time period of τ₂. The higher the values of τ₁ and τ₂, the longer it takes for the stress to relax. Similarly, the higher the values of g₁ and g₂, the more the peak force decreases over time (viscoelastic loss).

The stiffness of the matrix after it has relaxed and the force is constant, is the equilibrium shear modulus, G_eq and is a function of G_O and viscoelastic loss parameters (see equation (2)). (Note: we assumed bulk modulus ${\text{K}}_1^{\text{vol}}$ and ${\text{K}}_2^{\text{vol}}$ to be zero because they have little influence on the stress relaxation behavior curve (Valluru et al., 2022)).

$$G_{eq}=G_O\left(1-g_1-g_2\right)$$ (2)

CAX8R: 8-node axisymmetric, biquadratic, quadrilateral, and reduced integration elements were used in ABAQUS^®. The ramp and the hold phases were solved using a non-linear visco-type procedure.

Time-displacement values from the experimental ramp phase were used to move the indenter into the sample. The displacement was held at the peak value for 60 s. The force-time values were extracted and compared to experimental data using a custom-built code in MATLAB. The fitting parameters were iterated through until the errors between the experimental and simulated peak force and equilibrium force values were minimized.

2.7. Glycosamineglycans quantification assay

Frozen samples of the contralateral limbs were defrosted and the blastemas were carefully separated from the 27- and 41-DPA samples. The cartilage from the distal end of the humeri was collected from the fully-grown samples. The collected samples were weighed (XSE105, Metler Toledo) and digested in proteinase-K (conc: 1 mg/mL, Sigma-Aldrich) at 57°C until all the samples were completely digested. GAG content in the digested samples was quantified using the 1,9-dimethyl methylene blue (DMMB) assay following the procedure described in Farndale et al. (1986) The GAG content per unit weight of the tissue was compared across time points.

2.8. Statistical analysis

MATLAB (R2019b) Statistical Toolbox was used to perform all statistical analyses. The data were checked for normal distribution. A Kruskal-Wallis test followed by a post-hoc test with Bonferroni correction was used to compare the material properties between the groups with an alpha threshold for all tests set at p < 0.05. A Pearson correlation was used to estimate the correlation coefficient (r) between G_O and GAG content, and τ₁ and GAG content.

3. Results

The average ST length of the animals between different time points was not significantly different (p > 0.05) (see Supplemental Information). Fig. 2a shows the raw load-displacement data from indentation testing while Fig. 2b shows the stress-relaxation behavior of the samples.

3.1. Instantaneous and equilibrium shear modulus

The instantaneous shear modulus (G_o), which is a measure of the instantaneous stiffness or peak stiffness of the material, significantly increased between time points during regeneration (Fig. 4a). Similarly, the equilibrium modulus (G_eq), which characterizes the stiffness after relaxation, increased between the time points (Fig 4b). The instantaneous modulus of the distal end of the rudiment was lower than the proximal end in 41 DPA samples (p < 0.01). However, there was no significant difference between the equilibrium shear modulus of proximal and distal points in the 41 DPA timepoint (p > 0.05) (see supplemental).

Fig. 4.

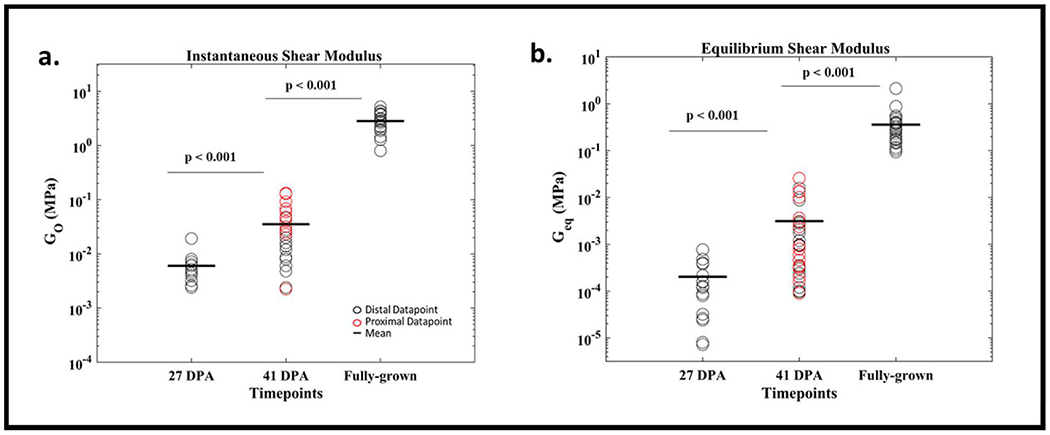
(a) Instantaneous and (b) Equilibrium Shear Moduli increase during regeneration time points.

3.2. Prony series parameters

The sum of the viscoelastic loss parameters, g₁+g₂, which represent the total drop in the instantaneous shear modulus during relaxation, is lower in fully-grown samples compared to 27- and 41-DPA group (Fig. 5a). The loss parameters are not significantly different between 27- and 41-DPA groups. Similarly, no significant difference was found in the viscoelastic loss parameters between the proximal and distal indentation points in the 41 DPA group (see Supplementary Information). The time constant τ₁ significantly decreased (Fig. 5b) during regeneration between time points. τ₂ values of fully grown time point was significantly lower than 27- and 41-DPA time points while no difference was found between 27- and 41-DPA groups (p > 0.05) (Fig. 5c). τ₂ was significantly greater than τ₁ at every time point (p < 0.05). Time constant τ₁ of proximal points was higher than distal points in the 41 DPA group (p < 0.05) while no such difference was found in time constant τ₂ (see supplemental).

Fig. 5.

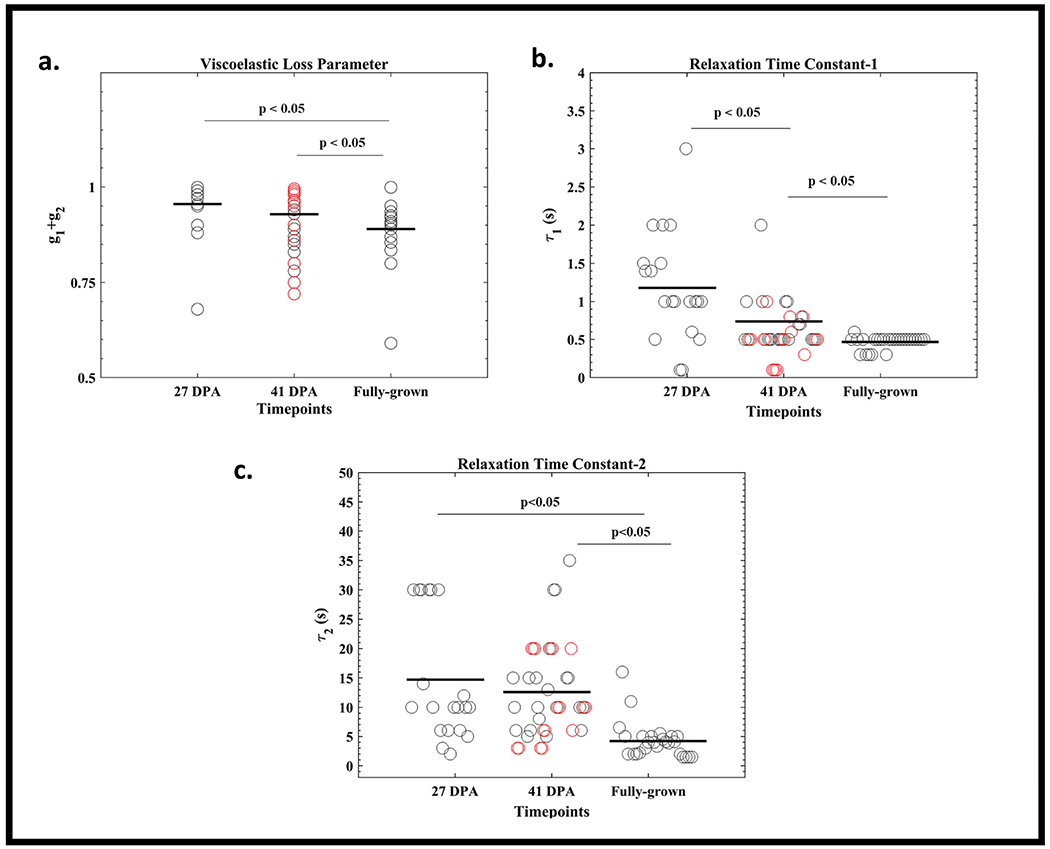
(a–c) Prony Series Material Parameters at different regeneration time points. (a) The viscoelastic loss parameter and (b and c) the relaxation time constants decrease during regeneration.

3.3. Glycosaminoglycan quantification

The GAG content per unit weight of the tissue was not different between 27- and 41- DPA-time groups (p = 0.9). However, there was a significant difference in the GAG content per unit weight between 41 DPA and fully-grown samples (p < 0.05) (Fig 6a).

Fig. 6.

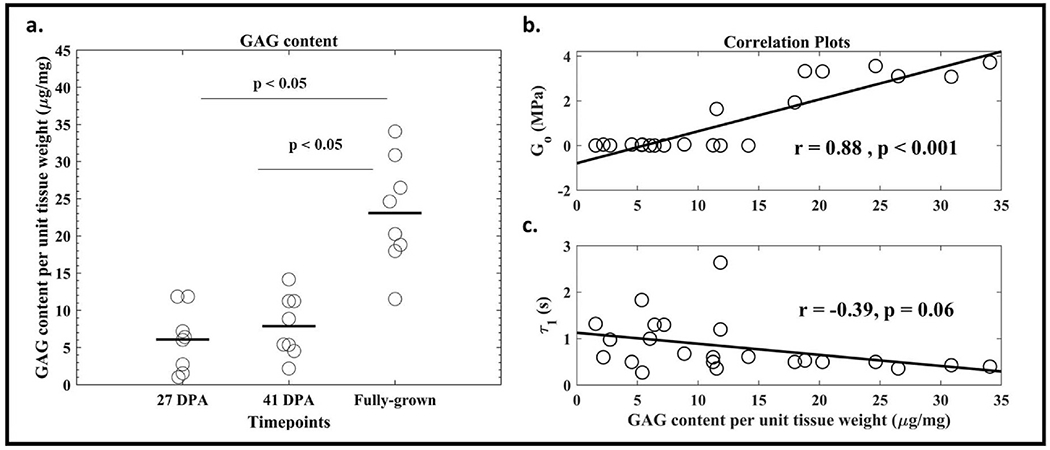
(a) GAG content of regenerating limbs increases during regeneration (b) There is a positive correlation between Instantaneous modulus and GAG content per unit weight (c) There is a non-significant negative correlation between Time Constant (τ₁) and GAG content per unit weight.

A positive correlation was found between the average instantaneous modulus (G_o) and GAG content. No statistically significant correlation was found between the average time constant (τ₁) and GAG content between the samples (Fig. 6b).

4. Discussion

In this study, we estimated the viscoelastic material properties and GAG content of regenerating axolotl limbs at three different time points of regeneration. We found that the stiffness of the matrix increases while the relaxation time decreases with regeneration time. Further, there is a correlation between increasing stiffness and GAG content.

Previous studies on developing articular cartilage showed that the instantaneous modulus increases with developmental age (Williamson et al., 2001; Brommer et al., 2005; Xu et al., 2016). Similarly, Riquelme-Guzmán et al. showed that the elastic contrast of limb (a function of longitudinal modulus and water content) increases with developmental age and digit regeneration (Riquelme-Guzmán et al., 2022). In our viscoelastic model, G_o represents the instantaneous shear modulus and reflects the stiffness of the matrix and fluid content together while G_eq reflects the matrix stiffness at equilibrium. At 27 DPA, the blastema is composed of dedifferentiated cells with little to no cartilaginous extracellular matrix leading to low values of ${\text{G}}_{\text{O}}^{44}$ Forgacs et al. showed that the shear modulus of limb bud in ~3.5 days old chick embryo was in the order of 1 kPa which is close to the lower range measured in this study for 27 DPA samples (2 kPa). (Forgacs et al., 1998).

The G_o of 41 DPA samples (0.002 MPa–0.13Mpa) is in the same range as the shear modulus of day 3.5 (~0.001 MPa) and day 14 (~0.1 MPa) chick embryo limb specimens (Mikic et al., 2004; Forgacs et al., 1998). Bone collar begins to form by day 6.5 in chick embryos (Nowlan et al., 2007) while the 41 DPA limb samples in the current study represent palette-stage blastema (Tank et al., 1976). The animals in the 41 DPA group showed varied rates of regeneration with some blastema samples having cartilaginous elements in the proximal part of the blastema while others were just beginning to condense. This resulted in a wide distribution of mechanical properties between the samples and within a blastema, with proximal regions having higher G_o values than distal regions.

The increase in G_o between the first two time points is not associated with an increase in GAG content suggesting that collagen content might play a significant role in the increase of matrix stiffness. In fully developed axolotl limbs, the cartilage has significantly higher values of G₀ and G_eq compared to the earlier time points and the increase is correlated with the increase in GAG content. This result is consistent with previous findings on the relationship between local GAG content and shear modulus in articular cartilage (Williamson et al., 2001).

Previous studies on developing cartilage have modeled cartilage as viscoelastic (Forgacs et al., 1998; Keenan et al., 2013) (matrix reorganization causes stress relaxation), poroelastic (Berteau et al., 2016) (fluid flow causes stress relaxation), and poro-viscoelastic (Valluru et al., 2022) (both fluid flow and matrix reorganization). Both viscoelastic and poroelastic materials have similar stress relaxation curves (decrease in force over time for a given displacement). Poroelastic behavior is characterized by matrix permeability (k), which is the ability of water to move through a matrix. With a high permeability, the water flows easily in the matrix. In order to assess poroelastic behavior, indentation must move sufficient water. With a small indenter (radius ~100 μm), there is insufficient fluid movement to decouple poroelastic and viscoelastic behavior (Valluru et al., 2022). (Viscoelastic behavior is not dependent on indenter size (Strange et al., 2013).) Because our indenter was near the limit of being able to move sufficient fluid, a two-term viscoelastic model was chosen in this study, and the material parameters determined are influenced by both fluid movement and matrix viscoelasticity (see supplemental). A two-term viscoelastic elastic model can fit the entire stress relaxation curve to estimate the short-term and long-term mechanical properties of the tissues while the poroelastic model can either fit the initial loading part of the curve (Valluru et al., 2022) or the long-term relaxation (Keenan et al., 2013) depending on the use of inverse finite element methods or analytical methods. To decouple the effect of fluid flow and inherent relaxation of tissue matrix, future experiments will use different size indenters and a poro-viscoelastic model. We could have used an analytical model to fit the data. However, we found that assumptions made about contact area significantly influence the results; FE simulates the contact area, likely rendering the results to be more accurate of the experimental conditions.

We believe that g₁ and τ₁ are likely dominated by fluid movement; while g₂ and τ₂ likely reflect the behavior of the viscous matrix. Previous studies on the poroelasticity of cartilaginous tissues have shown a negative correlation between GAG content and permeability (k) (more negatively charged GAG holds in the water resulting in lower permeability). There is also a negative correlation between permeability and viscoelastic relaxation time (the lower permeability, the slower the fluid moves and the longer it takes to relax) (Keenan et al., 2013; Valluru et al., 2022). Poroelastic relaxation time (τ_PE) is inversely proportional to G_o and k for a given Poisson’s ratio and radius of contact (see equation (3)). (Berteau et al., 2016; Wang et al., 2020; Hu et al., 2010)

$${\tau }_{PE}\propto \frac{r^2}{G_{o}k},$$ (3)

We found GAG content increased during limb regeneration, indicating decreasing permeability (k). However, the decrease in permeability (k) was likely smaller than the increase in G_o, causing an overall decrease in τ₁. τ₂ might be more influenced by the inherent relaxation of the extracellular matrix molecules.

One caveat to our study is that we did not measure the changes in collagen content during limb development but previous studies have shown collagen content has a high correlation to the increase in matrix stiffness and cell proliferation in embryonic tissues (Williamson et al., 2001; Prein et al., 2016).

Decoupling the influence of GAG and collagen content on matrix viscoelastic behavior in experiments using a standard linear spring viscoelastic model poses challenges. The study by Thomas et al. (2009) advocates for more sophisticated models, featuring a constituent-based nonlinear viscoelastic model with a GAG-collagen stress balance (Thomas et al., 2009). Furthermore, future studies can employ artificial neural networks as a novel approach to rapidly and accurately estimate the mechanical properties of cartilage. Unlike traditional computational methods that involve repetitive finite element simulations for each experiment, this method utilizes finite element models to simulate indentation tests, with the obtained force–time curves used to train a neural network. The trained network demonstrated the ability to predict cartilage properties swiftly and robustly within the trained range, eliminating the need for additional finite element modeling in the estimation process (Arbabi et al., 2016). Nevertheless, reliance on challenging-to-obtain experimental force-displacement datasets persists in these intricate models. While acknowledging its simplistic assumptions, our study provides crucial insights into evolving tissue-level matrix stiffness in growing limb tissues, correlating with dynamic changes in glycosaminoglycan (GAG) content.

Axolotl regeneration provides a unique template for studying chondrogenesis in limbs in a size that can be studied at the tissue level. Although the timing of chondrogenesis may differ in mammalian systems, we anticipate the trends of limb morphogenesis and genetic expression are similar (Comellas et al., 2022; Lee and Gardiner, 2012; Fröbisch and Shubin, 2011). Moreover, the observations on how the mechanical environment affects limb development can still provide valuable insights (Shea et al., 2015).

5. Conclusions

In this study, we estimated the viscoelastic material properties of regenerating axolotl limbs. The results from this study could inform future computational models that can account for the changes in mechanical properties during cartilage growth. Computer simulations could then inform experimental design for isolating the specific mechanical stimuli at the tissue level responsible for molecular-level metabolic activities.

Data availability

Data will be made available on request.