Border-ownership tuning determines the connectivity between V4 and V1 in the macaque visual system

Abstract

Cortical feedback connections are extremely numerous but the logic of connectivity between higher and lower areas remains poorly understood. Feedback from higher visual areas to primary visual cortex (V1) has been shown to enhance responses on perceptual figures compared to backgrounds, an effect known as figure-background modulation (FBM). A likely source of this feedback are border-ownership (BO) selective cells in mid-tier visual areas (e.g. V4) which represent the location of figures. We examined the connectivity between V4 cells and V1 cells using noise-correlations and micro-stimulation to estimate connectivity strength. We show that connectivity is consistent with a model in which BO-tuned V4 cells send positive feedback in the direction of their preferred figure and negative feedback in the opposite direction. This connectivity scheme can recreate patterns of FBM observed in previous studies. These results provide insights into the cortical connectivity underlying figure-background perception and establish a link between FBM and BO-tuning.

The logic of feedback connectivity in the visual system is largely unknown. Here the authors show that border-ownership tuned cells in V4 have stronger feedback connectivity with V1 cells located in their preferred figure location.

Introduction

Our visual perception does not resemble a pixel-by-pixel pattern of luminances and colors, but is organized into perceptual objects that are well segregated from their background. The underlying neural processes are recurrent in nature. Feedforward connections from the retina to the primary visual cortex and onward to areas that are higher in the visual hierarchy extract increasingly complex features from the visual scene. Feedback connections carry inferences about the structure of the environment back to early visual areas^1–3. At the neural level it is well established that activity in the primary visual cortex (V1) is enhanced on perceptual objects (‘figures’) and suppressed on backgrounds^4–7. Converging evidence indicates that cortical feedback from higher visual areas back to V1 is responsible for this figure-background modulation (FBM)^8–12, but the underlying logic of this connectivity is unknown. A likely source of these feedback signals are the numerous cells in higher visual areas which respond to borders in visual images and are tuned for the side-of-ownership of the border^13,14. These cells, known as border-ownership tuned (BO) cells, can indicate the location of a figure (and therefore also the background) relative to their RF making them well-suited to send feedback to modulate neural activity in lower-level visual areas. Until now border-ownership and figure-background segregation have been studied separately by different researchers who used distinct paradigms so that the relationship between these effects has remained unclear.

Here we aim to integrate FBM and BO into a common framework. We propose that BO-tuned cells in higher visual areas, including areas V2, V3, and V4, feed back to V1 to generate FBM (Fig. 1A). The hypothesis is that BO-tuned cells in higher areas send feedback to V1 in a direction that is orthogonal to their preferred orientation¹⁵, with an excitatory or inhibitory influence reflecting their preferred figure position. Specifically, they should send excitatory feedback in the direction of their preferred figure location (red lines in Fig. 1A) and inhibitory feedback in their non-preferred direction (blue lines in Fig. 1A). As a proof-of-principle, we used this connection scheme to model the FBM pattern observed in a recent study using complex objects⁷. We then examined the functional connectivity pattern using simultaneous recordings of neural activity in area V1 and V4 of macaque monkeys to measure noise correlations, which are correlated fluctuations of activity across trials. We found a clear relation between the strength of the inter-areal noise-correlations, the configuration of RFs in the two brain regions, and the BO-tuning of V4 neurons. Furthermore, activation of V4 neurons with electrical micro-stimulation increased the activity of V1 neurons with RFs at the figure location preferred by the V4 neurons relative to that of V1 neurons with RFs at the preferred background location of the cells. The results support the hypothesis that feedback connections from BO-tuned cells are anatomically arranged to produce FBM in lower visual areas.

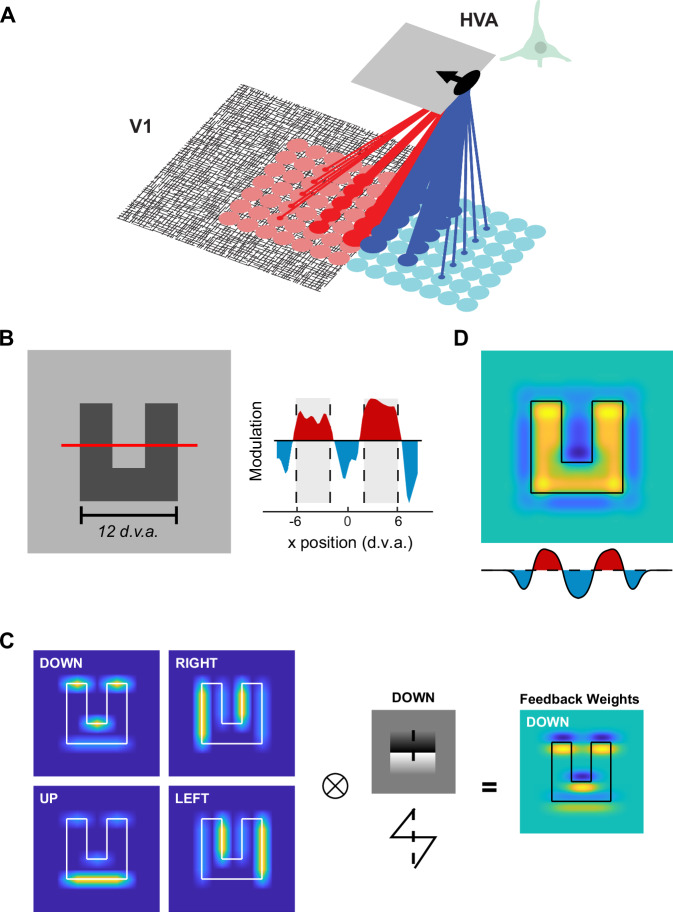
Fig. 1. Feedback from border-ownership neurons can explain patterns of figure-background modulation observed in V1.

A The proposed logic of the feedback connections. An example BO-tuned cell in a higher visual area (HVA; e.g. V2, V3 or V4) is depicted which prefers a figure located to the left of its RF (indicated by the black arrow). We hypothesized that the cell sends excitatory feedback back to V1 in the direction of its preferred side-of-ownership (red lines) and inhibitory feedback in the non-preferred direction (blue lines). The strength of the feedback is depicted as the thickness of the lines, with the strongest feedback to V1 cells with RFs that are nearby and aligned with the RF of the HVA cell. B Left, In a previous study⁷ of FBM in V1 in response to complex shapes, we used texture-defined ‘n’ and ‘u’ shaped objects. We measured the V1 response along a cross-section depicted by the red line. Right, V1 activity elicited by the figure was enhanced (red regions and gray shading) and that elicited by the background was suppressed (blue regions). The scale bar is 12 degrees of visual angle d.v.a. C Left, The modelled activity of four sub-populations of HVA cells with different side-of-ownership preferences (warmer colors = higher activity). Border-ownership modulated the orientation-tuned responses of the model cells, e.g. HVA neurons tuned to ‘Down’ preferred horizontal borders and their activity was stronger if the figure was situated downwards relative to the RF. We convolved the activity pattern of each HVA sub-population with its connectivity kernel (black-white pattern illustrates the kernel of the ‘Down’ preferring population) with a ‘saw-tooth’ shape (cross-section shows the kernel) representing the weights of feedback connections to V1. Right, Influence of the ‘Down’ preferring population on V1 activity. D The overall feedback influence on V1 summed across the four HVA sub-populations. Yellow and blue colors indicate positively and negatively modulated V1 responses, respectively (arbitrary units). The graph underneath shows a cross-section through the model’s V1 activity profile (red line in B). Note the similarity to the spatial profile of V1 activity in (B).

Results

Connectivity scheme

In a previous study⁷ we found that complex ‘n’ and ‘u’ forms lead to a precise pattern of V1 modulation, with an enhanced representation of the figure and suppressed representation of background regions (Fig. 1B). We constructed a simple model using the proposed connection scheme outlined in Fig. 1A. We included four sub-populations of BO-tuned cells in higher visual areas (HVA), which preferred figures in different directions relative to the center of their RF (up, down, left, and right; Fig. 1C, see Methods). These HVA cells send feedback to V1 according to the connectivity scheme outlined in Fig. 1C, i.e. excitation to V1 in the direction in which they prefer to have the figure and inhibition in the opposite direction (see Methods for model details). The strength of the excitatory and inhibitory modulation fell off linearly with increasing distance between the RFs in V1 and HVA. In this simple model, the combined influence of the four HVA BO-subpopulations on V1 activity closely resembled the patterns of FBM of the previous study (Fig. 1B). Interestingly, the model replicated the enhanced figure responses as well as the suppressed responses on the nearby background regions (Fig. 1D). So far, there has been no experimental evidence in favor or against the proposed connectivity pattern. In what follows, we report on BO-tuning in a mid-level visual area (V4) of macaque monkeys, on the correlated variability in neuronal firing rates in areas V1 and V4 and on the influence of electrical micro-stimulation in V4 on V1 activity. We used the pattern of these so-called noise correlations to estimate the connectivity between V1 and V4, and use the connectivity estimates to update our initial modeling results (Fig. 1) in a later section.

Border-ownership tuning in area V4

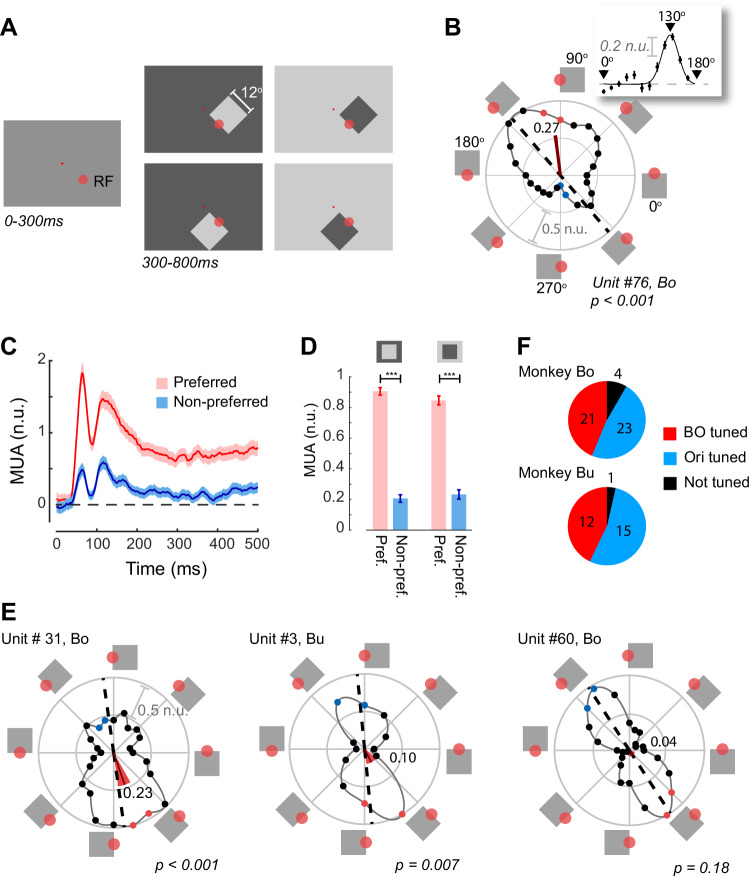
Single cells in visual area V4 have been shown to be tuned for the side-of-ownership of borders¹³. Recent studies have suggested that BO-tuning in V4 is organized into columns of cells preferring similar orientations of ownership¹⁶ and that cells are clustered by BO-preference¹⁷ so that it can be measured with multi-unit recording techniques. Multi-unit activity (MUA) reflects the spiking of neurons within 100–150 μm of the electrode and MUA population responses are very similar to those obtained by pooling across single units^18–21. We recorded MUA from two monkeys (Monkey Bo and Monkey Bu) who were chronically implanted with Utah arrays (Blackrock Neurotech) in areas V4 and V1. We measured BO-tuning using square stimuli similar to those previously used to demonstrate BO-preference¹³. We presented luminance defined squares with edges of 12° to the animals, who were passively fixating on a central dot at two contrast polarities, i.e. a bright square on a dark background and a dark square on a bright background. Across trials, one edge of the square was rotated around the aggregate RF centers of each recording array to measure the orientation and BO-tuning of neurons at each recording site (Fig. 2A). The corners of the square fell well outside the RF of the V4 cells and only the border fell within the RF. A classical BO-tuned cell responds more strongly when the border in the RF is at its preferred orientation, and when the square is on the preferred side of the edge in the RF. Figure 2B shows an example BO-tuned V4 recording site from Monkey Bo. Neurons at this site responded strongly to a border oriented at 130° (inset in Fig. 2B) and the response was considerably stronger when the figure was positioned on the upper-right of the RF compared to when it was located on the lower-left. The classical border-ownership angle for this cell was therefore 130°. A recent study has proposed that BO-tuned cells may also show preferences for side-of-ownership when the orientation of the border present in the RF differs from the preferred orientation¹⁶. The example recording site in Fig. 2B illustrates this effect, because the neurons’ preferred orientation was 130°, but the cells also gave strong responses when the figure was oriented to the right of the RF, at orientations around 90°. As a measure for the direction of BO-tuning that also takes responses away from the preferred orientation into account, we treated the response at each border-orientation as a vector from the origin and determined the length and angle of the average vector (Methods and Fig. 2B).

Fig. 2. Border-ownership tuning in V4.

A The stimuli used to measure BO-tuning. The monkey fixated on the small red fixation dot throughout the trial. The larger red circle indicates the approximate size of the V4 RF (not visible to the monkey). Luminance-defined squares were shown at one of 12 or 24 orientations and one of two luminances (dark or light grey) on a background with the opposite luminance. B Normalized responses at an example recording site, n = 38 (min) to 45 (max) trials per border-orientation. The squares around the edge of the plot depict the position of the figure relative to the RF. 0° is the condition in which the RF is situated on the upper border of the square. The solid line shows a polynomial fit to the data. The dashed black line indicates the fitted preferred orientation. The angle of the red line indicates the preferred border-ownership BO_pref. Its length represents 1-CircVar, which is a measure of border-ownership strength (here 0.27) and the width of the red-segment indicates the 95% confidence interval of BO_pref (here 6°). The filled red and blue dots indicate the border-orientations closest (red) and furthest (blue) from BO_pref used to test border-ownership. Scale bar, 0.5 normalized units (n.u.). Inset, orientation tuning, calculated by combining responses across borders with the same orientation. The fitted curve is a circular Gaussian. Error bars, s.e.m. across trials. C Time course of MUA activity at the site of panel B, elicited by a border with the preferred (red) and non-preferred ownership (blue) (borders correspond to colored dots in B). Shaded regions, ± s.e.m. D Average activity at the example recording site in B and C, in a time-window from 0 to 500 ms, for the two contrast polarities. Error-bars, s.e.m. ***p < 0.001 (weighted t-test). E Activity at three other recording sites. The leftmost two example recording sites were significantly BO-tuned (weighted t-test at the red/blue border-orientations), whereas the site at the right was orientation-tuned (p < 0.001), but not BO-tuned. Conventions as in B. F Pie-charts showing the number of BO-tuned, orientation-tuned (and not BO-tuned) and non-tuned recording sites in the two monkeys. Source data are provided as a Source Data file.

The mean vector angle (BO_pref) of the example recording site was 97.1° (red wedge in Fig. 2B) and it was not parallel to the neurons’ preferred orientation, as has been reported by Franken & Reynolds¹⁶. These deviations were not unusual in our sample of V4 recording sites, because the average absolute difference between the preferred orientation and BO_pref was 36° ( ± 28°) (Figure S1). Here we used BO_pref as our estimate of preferred border-orientation but the results were very similar if we used the BO at the preferred orientation in our analysis (Figure S2). To examine the time-course of BO-tuning, we compared the weighted average (see Methods) of the two border-orientations that were closest to BO_pref (red dots in Fig. 2B) and the responses at the opposite border-orientations (blue dots in Fig. 2B). At the example recording site, multi-unit responses at the preferred and non-preferred border-orientations diverged rapidly (Fig. 2C) and remained elevated at the preferred border-orientation for the duration of the stimulus presentation. The elevated activity for the preferred border-orientation occurred for stimuli with both contrast polarities (dark-on-light and light-on-dark; Fig. 2D). We considered cells at a recording site to be border-ownership tuned if they gave a significantly stronger response to a border at their preferred border-orientation compared to one at the opposite orientation, according to a weighted t-test (see Methods). Neurons at the site in Fig. 2B, C were significantly tuned (p < 0.001) and further examples of BO-tuning can be seen in Fig. 2E. We also found sites with significant orientation tuning (weighted t-test, see Methods) but without BO-tuning. Across all V4 recording sites with sufficient SNR (Monkey Bo: n = 48, Monkey Bu: n = 28), 33 were BO tuned (21 in Bo, 12 in Bu), 38 were only tuned for orientation (23 in Bo, 15 in Bu), and 5 showed neither tuning (4 in Bo and 1 in Bu) (Fig. 2F).

Border-ownership agreement angle

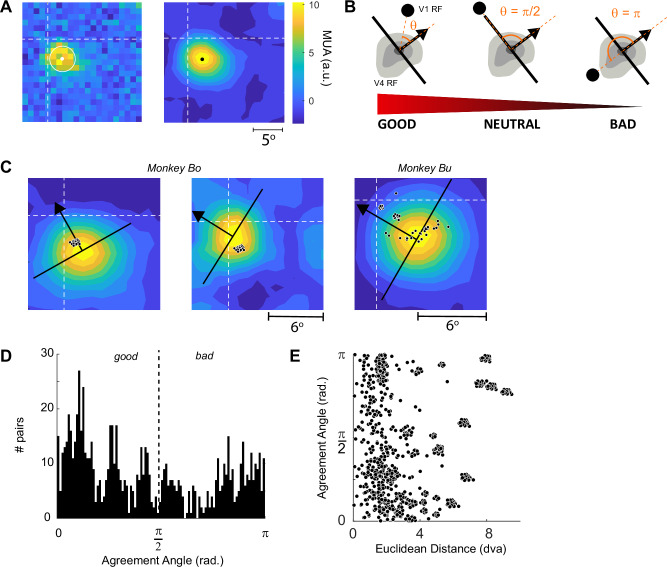
The model presented above predicts that the connectivity between neurons in V4 and V1 depends on the relationship between the RF position and BO-tuning of neurons at the V4 site and the RF position of neurons at the V1 site. We mapped the V4 RFs with luminance-defined square stimuli and determined the RF centers by fitting contours to the map of responsiveness and taking the center-of-mass of the highest contour ( > 90% of maximal activity, see Methods) (Fig. 3A). V1 RFs were mapped using a drifting bar stimulus as described previously²² (Methods). To quantify the relationship between the position of the V1 and V4 RFs and the BO-tuning of the V4 neurons, we defined a property that we refer to as BO agreement angle, θ_BO. We calculated the angle in radians between a line drawn in the direction of the V4 site’s preferred figure-location, orthogonal to the preferred border-orientation and the location of the V1 RF (Fig. 3B). Agreement angle, θ_BO, is the absolute value of this angle after it has been mapped onto the interval [-π, π] so that values close to 0 arise when the preferred figure location of the V4 neurons points towards the V1 RF. We refer to this arrangement as ‘good’ agreement. In contrast, values close to π arise when the V4 neurons’ preferred figure location points away from the V1 RF, an arrangement that we will refer to as ‘bad’ agreement. The example in the left panel of Fig. 3C illustrates good agreement. Neurons at a V4 site prefer a figure to the upper left of their RF and the RFs of all the V1 cells (small black dots show the RF centers) were located in this region of space. In contrast, the example pairs of V1 and V4 recording sites in the middle panel of Fig. 3C have a high θ_BO, close to π radians, indicating that the RFs are in ‘bad’ agreement. The right-hand panel of Fig. 3C shows an example from monkey Bu with multiple V1 arrays and the agreement value varied across the V1-V4 pairs. According to the model outlined above, the interactions should be excitatory between cells in good agreement and inhibitory for cells in bad agreement.

Fig. 3. Agreement angle, θ_BO.

A V4 RFs were estimated using a grid of luminance -defined square stimuli. Left, The response of neurons at a typical V4 recording site. Dashed lines: horizontal and vertical meridians. White dot and circle, center position and standard deviation of the best-fitting 2D Gaussian. Right, Contour-fit to the same data. The black dot indicates the center-of-mass of the highest-level contour and was our estimate of the center of the RF (see Methods). B The agreement angle (θ, orange segment) is the angle in radians between the line of preferred figure-location of the V4 neurons (black arrow) and the position of the V1 RF (black dot). Low values of θ indicate that the V1–V4 pair are in good agreement and high values indicate bad agreement. C Contour-maps from three example V4 sites, the preferred figure-location is shown by the black arrow. Black dots, centers of V1 RFs. The leftmost example shows a V4 cell that is in good agreement with all V1 sites, the middle example shows only bad agreement pairs and the rightmost shows an example from monkey Bu (for which we could include more V1 arrays) with a variety of agreement values. D The distribution of agreement angle across all V1–V4 pairs in monkeys Bo and Bu. E The joint distribution of agreement angle and the distance between the RF centers of all V1–V4 pairs in these two monkeys in degrees of visual angle (dva). The clustering of the data arises because V1 units recorded from the same Utah array have clustered RFs. Source data are provided as a Source Data file.

Spontaneous noise correlations

There are currently no methods that permit the in vivo measurement of anatomical connections at the resolution of cortical columns. However, the correlations between the spontaneous activity levels between neurons in brain areas that are connected is, on average, stronger than that between neurons without a direct connection²³. Noise-correlations are stronger between neurons with nearby RFs²⁴ and with similar tuning^24–26, as they are linked by stronger connections^27–31. Here, we measured interareal noise correlations with the Pearson’s correlation of the z-scored spontaneous activity of pairs of V4 and V1 recording sites. As spontaneous activity we used the baseline activity prior to the onset of the visual response (from -0.1 to 0.02 s relative to stimulus onset) in the BO-tuning sessions described above and we used a dataset recorded several weeks later for cross-validation (Methods). We included 306 V1–V4 pairs in Monkey Bo and 501 pairs in Bu with well-defined RFs, and significant BO-tuning of the V4 recording site.

To examine the influence of the agreement angle, θ_BO, and RF-distance (in dva) on the interareal noise correlation, we defined a general linear model that included an interaction term. We first examined the distributions of these variables across recording sites. There was a variety of agreement-angles, slightly biased toward good agreement pairs (Fig. 3D) and the joint distribution of RF-distance and agreement angle gave reasonable coverage of the parameter space, up to distances of 8 dva (Fig. 3E). Furthermore, RF distance and agreement angle were not strongly correlated (Pearson’s r = 0.17).

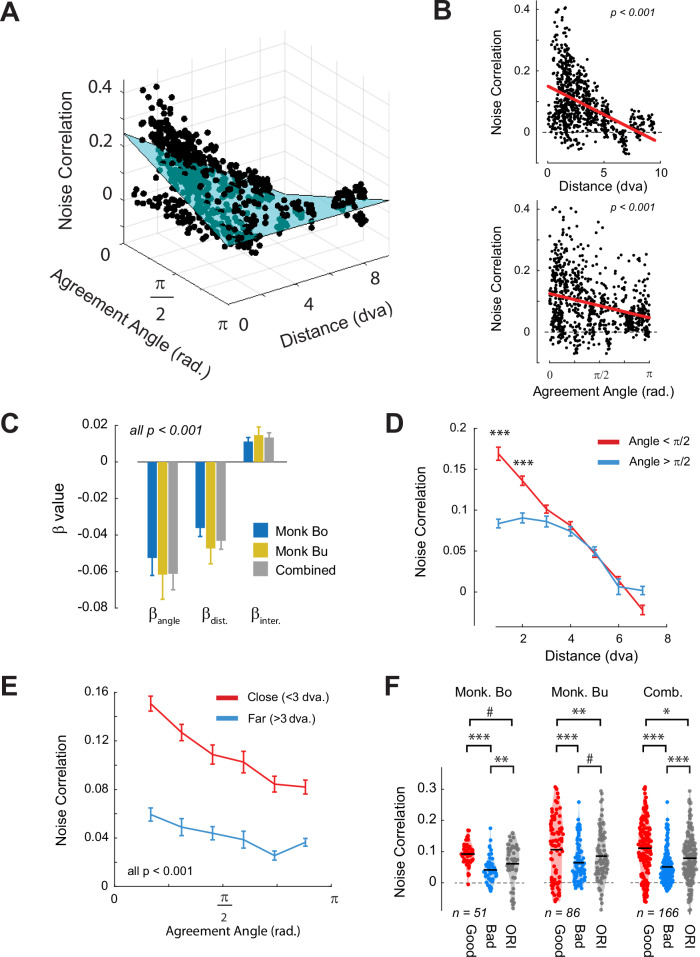
The general linear model provided an excellent fit to the pattern of noise correlations in both animals (Monkey Bo: r² = 0.58, p < 0.001; Monkey Bu: r² = 0.24, p < 0.001) as well as to the combined dataset (Combined: r² = 0.36, p < 0.001) (Fig. 4A). Importantly, the beta coefficients were consistent across both animals and showed the predicted significant negative correlations between both agreement angle and distance with noise correlation (beta-values, significance and marginal relationships are shown in Fig. 4B, C, regression results of individual animals are shown in Figure S3A, B). The interaction term was positive and significant in both animals because the influence of the agreement angle on the noise correlation decreased with RF-distance (Supplementary Movie 1, Fig. 4A). To examine the interaction in more detail, we grouped the pairs into good (< π/2) and bad (> π/2) agreement pairs. The noise correlations were larger for good agreement than for bad agreement pairs if the distance between the RFs was smaller than 3 degrees (Fig. 4D). When we split the data into V1–V4 pairs with nearby (distance <3 dva) and far (> 3 dva) RFs, the noise correlation depended on agreement angle, for nearby but not for far pairs (Fig. 4E), in accordance with the significant interaction. The fitted regression parameters also generalized to a dataset (see Methods) that was held back when fitting the regression model (Monkey Bo: cross-validated r² = 0.46, p < 0.001. Monkey Bu: r² = 0.17, p < 0.001) and we obtained similar regression coefficients with a Linear Mixed Effects models in which the hierarchical grouping of electrodes within arrays was taken into account (Figure S3C). The results were relatively insensitive to the precision of the RF estimates, because they did not change when we jittered the position of the V4 RFs relative to the V1 RFs up to ±2 dva (Figure S4).

Fig. 4. Noise correlations depend on agreement angle and the distance between RFs.

A Results from a general linear model in which the strength of V1–V4 noise correlations (z-axis) were predicted from the agreement angle (x-axis), the distance between the RF centers (y-axis) and their interaction. The best-fitting regression surface is depicted in blue. A video showing rotation of this graph is shown in Supplementary Video 1. B The marginal distributions for distance (upper) and agreement angle (lower). The red line shows a linear regression on the marginal distribution. C The best-fitting beta coefficients for each animal separately and the combined data. D Noise-correlations for good (< π/2, red) and bad (> π/2, blue) agreement angle, binned according to the RF distance. *** = p < 0.001, independent samples t-test with Bonferroni correction. E Noise-correlations for V1–V4 pairs with nearby (< 3 dva, red) and far (> 3 dva, blue) RFs, binned according to agreement angle. All comparisons were significant at the p < 0.001 corrected level. F The average noise correlations for nearby pairs separated into good, bad agreement and for V4 sites that were tuned to orientation but not to BO. The black lines indicate the means of the populations. The n value indicates the number of V1–V4 pairs after stratification to equalize the RF distance between populations. Error-bars in C–E denote s.e.m. ***:p < 0.001, **:p < 0.01, *:p < 0.05, #:p < 0.1 independent samples t-test. Source data are provided as a Source Data file.

The model outlined in Fig. 1 predicts that connectivity is positive between cells in good agreement and negative between cells in bad agreement. We note, however, that noise correlations between cortical cells tend to be positive even for cells that are not connected^25,28,32, presumably due to changes in activity levels caused by variations in the activity of neuro-modulatory systems that are related to the animal’s alertness^33,34. We therefore estimated the component of the V1–V4 noise correlation that is independent from border -ownership by examining the V4 recording sites that were tuned to orientation but not to BO. The baseline correlation for pairs of V1 sites and V4 sites without BO-tuning at a distance smaller than 3 dva was 0.11 ± 0.008 (grey bars in Fig. 4F), which was weaker than the value of 0.16 ± 0.008 for pairs in good agreement and stronger than the value of 0.08 ± 0.005 for pairs in bad agreement (we stratified the data to ensure a similar distribution of RF-distance values; see Methods). This result suggests that V4 BO-tuned neurons engage in excitatory interactions with V1 neurons that are in good agreement and suppressive interactions with V1 neurons that are in bad agreement, against a baseline of moderately positive, but non-specific inter-areal correlations. These interactions would be explained by excitatory and inhibitory feedback from V4 to V1 neurons for good and bad agreement, respectively, in accordance with the model of Fig. 1. We note, however, that noise correlations provide an indirect measure of connectivity and that our results would also support connectivity schemes with weaker excitation between neurons with RFs in bad agreement than between those with RFs in good agreement.

Relationship between border-ownership and figure-background modulation

The differential pattern of noise correlations places V4 BO-tuned cells in an ideal position to generate both figure-enhancement and background suppression in V1. So far, we focused on the noise-correlations during spontaneous activity. We next measured whether the strength of BO-tuned activity of V4 cells predicts the strength of FBM in V1, on a trial-by-trial basis, in the epoch when the monkey saw the luminance defined square (Fig. 2A).

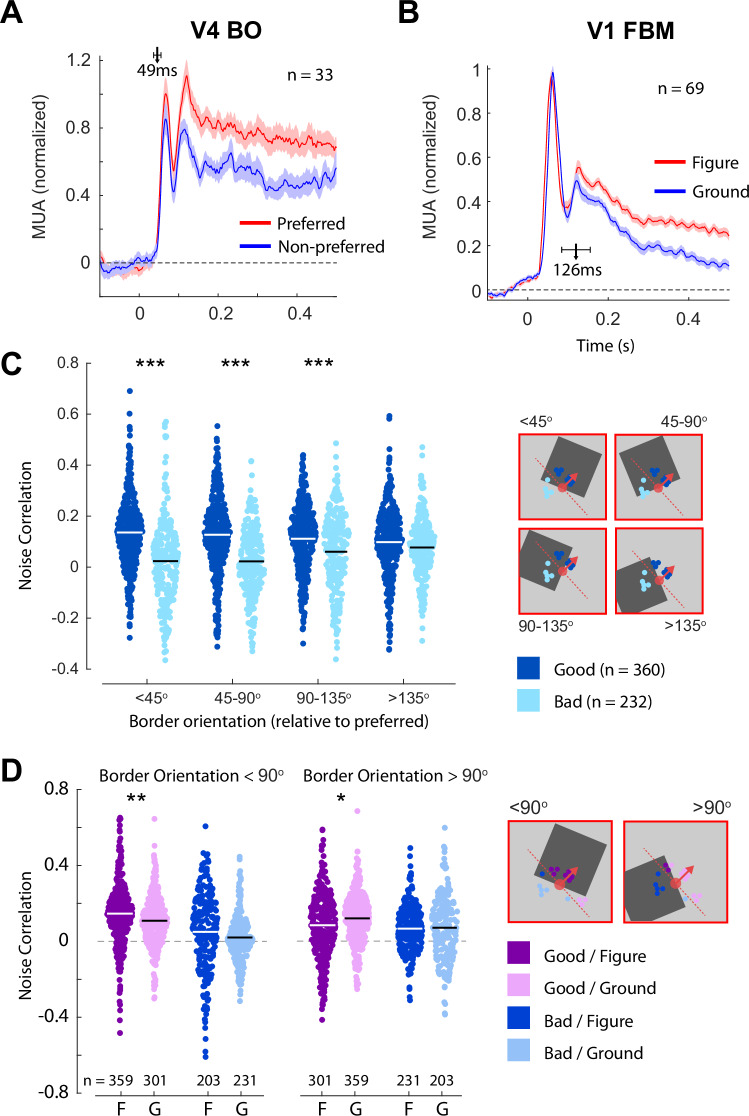
We first examined the mean population responses to the preferred and non-preferred border-orientations in V4 (Fig. 5A). By definition, the responses were higher for preferred border-orientations (t₃₂ = 6.1, p < 0.001) and the latency at which BO influenced the firing rate was short (49 ms ± 14 ms), in line with previous studies¹³. We also determined whether the RF of every V1 recording site fell on the figure or background for each of the stimuli, averaging across the two different contrast conditions so that the average luminance in the RF was the same for figure and background (Fig. 5B). In line with previous work^5,35, V1 responses were stronger when their RFs fell on the figure region (t₆₈ = 10, p < 0.001) and the latency of the effect (126 ms ± 44 ms) was significantly longer than that of BO (p = 0.049, bootstrap test, see Methods), suggesting that BO-tuned cells in V4 could play a causal role in generating FBM in V1.

Fig. 5. Noise correlations between neurons in V1 and V4 during responses to visual stimuli.

A Mean responses across 33 BO-tuned V4 recording sites elicited by their preferred and non-preferred border-orientations. The shaded region is ±1 s.e.m. The arrow marks the estimated latency of BO modulation, error-bars indicate the 95% confidence interval. B Mean response across 69 V1 recording sites to the luminance-defined squares used to determine BO-tuning. We sorted trials according to whether the RF fell on the square figure (red) or on the background (blue). The shaded region is ± 1 s.e.m. The arrow marks the estimated latency of FBM, error-bars indicate the 95% confidence interval. C Noise correlations between V4 and V1 recording sites in the sustained period of firing (100–500 ms). Correlations were calculated separately for pairs in good (dark blue) or bad (light blue) agreement in bins reflecting the difference in the orientation of the border inside the V4 RF relative to the preferred border-orientation. The white/black lines indicate the means of the distributions. The inset on the right shows the preferred border-orientation (red-dashed line) and preferred figure-location (red arrow) of a V4 recording site, example figure locations, and V1 recording sites that were in good (dark blue) and bad (light blue) agreement. *** = p < 0.001, ** = p < 0.01 independent samples t-test, Bonferroni corrected. Error-bars are ±1 sem. D Noise-correlations in the sustained period split according to whether the V4 neurons responded to their preferred border or not, the agreement angle of the V4–V1 pair and whether the V1 RF fell on the figure or the background. ** = p < 0.01, * = p < 0.05 paired t-test, Bonferroni corrected. Source data are provided as a Source Data file.

To examine the relation between the activity of V4 BO-tuned cells and that of V1 cells we measured the influence of the agreement angle θ_BO on the noise correlations during the sustained period of the response (100–500 ms after stimulus onset). The general pattern of noise-correlations during the sustained period of the response showed a similar relationship to agreement angle and RF distance as observed for spontaneous correlations (Figure S5A). However, noise correlations during stimulus presentation will depend on both the underlying connectivity and the activity caused by the stimulus. We therefore examined the strength of the V1–V4 noise correlations when the border in the V4 RF matched the cells’ BO-tuning and when it did not. We predicted that a strong visual drive of V4 neurons by their preferred border-orientation might accentuate the pattern of correlations with V1 cells during spontaneous activity and increase the difference between good-agreement and bad-agreement pairs. These interactions are predicted to be weaker when a non-preferred border falls in the V4 RF, because the neurons are less active and are likely to have a reduced influence on V1 activity.

Noise correlation indeed depended on the agreement angle and the match between the border in the V4 RF and the BO -preference (Fig. 5C). When V4 neurons were driven by their preferred border-orientation (border-orientation was within 45 degrees of BO_pref), we observed a significant difference in correlation between good and bad pairs. Good pairs (n = 360) showed a noise correlation of 0.14 ± 0.02 whereas the correlation for bad pairs (n = 232) was -0.008 ± 0.01. As the border-orientation rotated away from the preferred orientation, the difference in correlation between good and bad pairs decreased monotonically (Mixed ANOVA; interaction between agreement and border-orientation category: F_3,1770 = 19.10, p < 10^-10). This pattern of results is consistent with the hypothesis that V4 neurons that respond to their preferred border excite V1 neurons with RFs in good agreement that respond to the figure while inhibiting V1 neurons with RFs in bad agreement that overlie the background. The relative strength of noise correlations between V1 and V4 pairs in good and bad agreement changed over time relative to the presentation of the visual stimulus (Figure S5B). The onset of the visual stimulus reduced noise correlations, particularly for good agreement pairs, but after the onset of FBM in V1 the difference between good and bad pairs increased again.

If a V4 cell is driven by its preferred border, then the RFs of V1 cells which are in good agreement are more likely to fall on the figure than on the background (Fig. 5C). Previous studies indicate that noise correlations between neurons with higher firing rates are stronger. We therefore asked if the pattern of noise correlations is caused by differences in firing rates. However, we observed little effect of whether the V1 RF was on the figure, where firing-rates were higher, or the background, where firing-rates were lower (Mixed ANOVA, main-effect of figure-background, F_1,500 = 0.70, p = 0.4, Fig. 5D). Hence, the strength of the noise-correlations in our experiment were not solely determined by the V1 firing rates. Interestingly, if the V4 neurons responded to their preferred border, their noise correlations were stronger with V1 neurons with RFs on the figure than with those with RFs on the background. This influence of the V1 RF position on the strength of the V1–V4 correlation suggests that V4 cells that respond to their preferred border engage in recurrent interactions with V1 cells that represent the same perceptual object.

Causal investigation of connectivity

Noise correlations provide an indirect estimate of connectivity between neurons, but do not provide information about directionality. We proposed that V4 neurons provide feedback based on border ownership tuning, but our results might also be compatible with a connection scheme in which V1 neurons with RFs in good and bad agreement have a different feedforward influence on V4 neurons that are tuned to BO. We obtained some evidence against the feedforward account when we examined the time-course of the noise-correlation upon the appearance of a visual stimulus (Figure S5). During the initial responses in V1 and V4, which are dominated by feedforward processing, the difference in noise correlation between good and bad agreement pairs decreased.

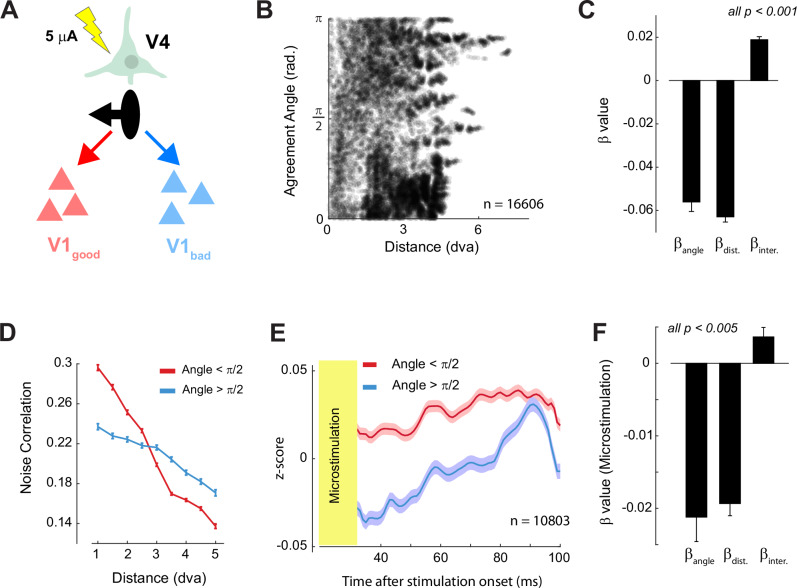
To gain more insight into the directionality we carried out an electrical micro-stimulation experiment in a third monkey (monkey N). We hypothesized that stimulation of V4 neurons should specifically enhance the activity of V1 cells with RFs in good agreement (Fig. 6A). Monkey N was implanted with many electrodes in V1 (n = 448) and V4 (n = 256) and the distribution of RF distance and agreement angle was more uniform than in monkeys Bo and Bu (Fig. 6B). We first examined the relationship between agreement angle, RF distance and the V1-V4 noise-correlation. The regression coefficients and the interaction between the factors in monkey N were similar to those in the other two monkeys (Fig. 6B-D, Figure S3C).

Fig. 6. Micro-stimulation of V4 drives V1 responses in accordance to the Agreement Angle.

A We used micro-stimulation to activate neurons at individual V4 recording sites. The pictured V4 site prefers figures to the left of its RF (black arrow). We hypothesized that weak V4 stimulation would cause increased activity in V1 sites with RFs situated to the left of the V4 cell’s RF (red cells, good agreement) compared to sites in bad agreement (blue cells). B Distribution of agreement angle and RF distance of V1–V4 pairs in monkey N. C Beta coefficients a linear model relating noise correlations to agreement angle and RF distance in monkey N (conventions as in Fig. 4C). D The V1–V4 noise correlation in monkey N as function of RF distance for good (red) and bad agreement pairs (blue). Comparisons were significant in every RF-distance bin (p < 0.05, independent samples t-test with Bonferroni correction). Error bars indicate ± 1 s.e.m. E Average responses in V1 aligned on the onset of micro-stimulation in V4. V1 sites were split into sites that were in good (red) and bad (blue) agreement with the stimulated V4 site. The shaded region indicates ± 1 s.e.m. F Beta coefficients from a linear model, identical to that in panel C, except that the V1 MUA response after micro-stimulation (35−100 ms) was the dependent variable. Error-bars indicate ±Source data are provided as a Source Data file.

We selected 62 V4 electrodes with well-defined RFs (R² > 0.6 for Gaussian fit to the RF) and applied weak electrical currents to each electrode (5 μA, 200 Hz, 5 biphasic pulses, train duration of 20 ms). We measured the activity of V1 cells in a time-window shortly after cessation of the micro-stimulation to avoid contamination of the responses by stimulation artifacts (35–100 ms after the start of stimulation). The effect of V4 micro-stimulation on V1 neurons with RFs in good agreement was more excitatory than the effect on V1 neurons with RFs in bad agreement (linear mixed effects: t₅₄₉₁ = 4.2, p = 0.00002). We also ran the linear model described above with the V1 activity after micro-stimulation as the dependent variable. The beta coefficients strongly resembled those of the noise correlation analyses with significant main effects of agreement angle, RF distance and their interaction (all ps <0.001). We obtained similar regression coefficients with a linear mixed effects model in which the hierarchical grouping of electrodes within arrays was taken into account (all ps <0.001). The consistency across the micro-stimulation and noise correlation results within and across animals strongly supports the proposed feedback connectivity scheme.

Revisiting the Computational Model

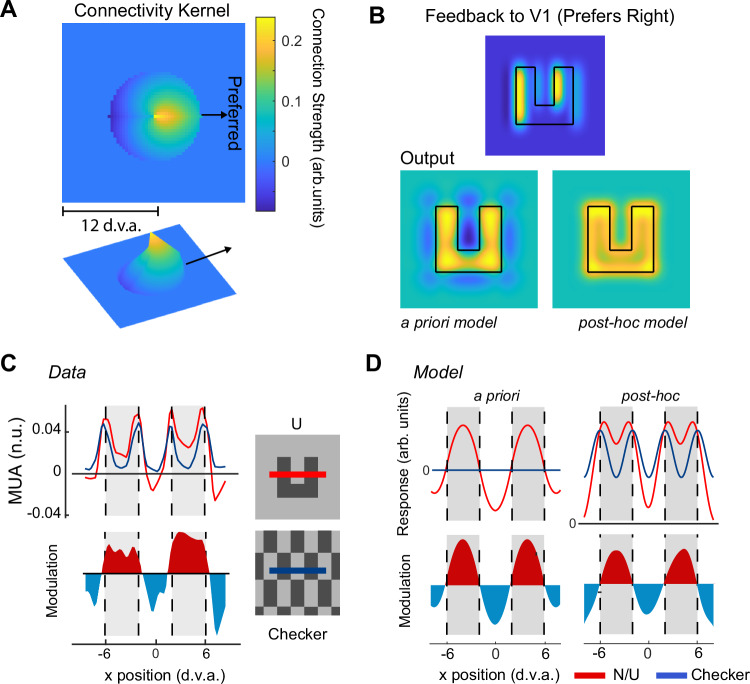
We will now revisit the model in which feedback from V4 neurons with BO -tuning determines figure-background modulation in V1. We generated a refined post-hoc model based on the regression plane of Fig. 4A, which estimates the feedback connectivity weights between areas V4 and V1 (Fig. 7A). The feedback connections were predominantly excitatory and their profile was ‘cardioid’ rather than the saw-tooth profile of our initial a priori model. The pattern of FBM differed between the a priori and post hoc models, because FBM was stronger near borders in the post hoc model (Fig. 7B). To discriminate between these models, we compared the model output to the patterns of V1 activity observed in the previous study (Fig. 7C), in which we compared the activity elicited in V1 by ‘n’ and ‘u’ shaped figures to the activity evoked by a textured checkerboard pattern⁷. Checkerboards are a good baseline stimulus for this comparison, because they contain the same local borders as the n/u shapes but do not perceptually segregate into figure and background. Hence, the subtraction of V1 activity elicited by checkerboards from that elicited by n/u shapes isolates the FBM and removes the border responses. We measured the response of the a priori and post-hoc models to the checkerboard and ‘u’ shape and calculated the difference between them (Fig. 7D).

Fig. 7. Refined model of figure-background modulation.

A We revised the a priori model from Fig. 1 by using the best-fitting regression plane shown in Fig. 4A as the connectivity matrix between V4 and V1, which is shown in 2 and 3 dimensions. The preferred figure-location for this example kernel is to the right. Other preferences were achieved by rotating the kernel. B upper panel, The overall feedback signal to V1 from V4 units preferring surfaces to the right obtained by convolving the kernel with a ‘u’ shaped figure. Lower panels, predictions of V1 activity for the a priori and post hoc model (using the kernel of A). C Neuronal data in area V1 of monkeys elicited by a textured-defined ‘u’ shape (red trace) and checkerboard pattern (blue trace) along a cross-section indicated by the red/blue line of the inset (from Self et al.⁷). The lower panel shows the difference between the conditions (identical to Fig. 1B). Red regions are regions with V1 excitation, blue regions signal V1 inhibition. D left, V1 activity according to the a priori model. Note that this dataset was not used to fit the refined model.

Both models exhibited FBM (colored profile in the lower panels of Fig. 7D) but only the refined post hoc model replicated the activity elicited by both the n/u shape and the checkerboard. The a priori model does not respond to the checkerboard, because excitatory influences from one population of BO-tuned cells are cancelled out by inhibitory influences from cells with the opposite border-preference (saw tooth profile in Fig. 1C). The refined model connectivity kernel is unbalanced, with stronger excitatory influences (Fig. 7A) so that responses from populations with opposite BO-tuning do not cancel out. Furthermore, the refined model captures the enhanced response at the borders of the n/u and the on-average weaker suppression of the central background region compared to that elicited by the background regions outside the n/u. We conclude that the refined model provides a good estimate of the putative feedback influences onto V1 that cause FBM for complex shapes (Figure S6).

Discussion

In area V1, the responses elicited by figures are stronger than those elicited by the background⁴. The enhanced representation of figures is believed to be important for perceptual segregation of figure and background³⁶, perception of the finer details of visual objects³⁷ and selection of objects for behavior^1,38. Indeed, a recent study in mice demonstrated that optogenetic silencing of the delayed response phase of V1 neurons, during which they exhibit FBM, impairs the perception of figure-background structure¹². So far, the studies examining FBM remained disconnected from the pioneering work from the von der Heydt group who described neurons tuned to border-ownership^13,14,39. We set out to link together these disparate research fields through a model in which figure-background modulation in V1 arises through feedback from BO-tuned neurons in higher visual areas. In our model the strength of connectivity between a higher visual area neuron and a V1 neuron is determined by two factors—the distance between the RFs of the V4 and V1 cells in retinotopic space and the relationship between the preferred border-ownership angle of the V4 cell and the relative location of the V1 cell’s RF (quantified by the ‘agreement angle’ metric). Our model predicted that connectivity should go from excitation to inhibition when the agreement angle goes from good to bad and that the strength of the connections should decrease for neurons with RFs at a larger separation. We verified these predictions by measuring the spontaneous noise correlations between V1 and V4, reproduced them in a held-back dataset and verified the causality of the effects with a V4-microstimulation experiment. BO-tuned V4 neurons that responded to their preferred border correlated strongly with V1 neurons in good agreement and weakly with V1 neurons in bad agreement and this difference disappeared when the border in the V4 RF was non-preferred. V4-microstimulation increased the activity of V1 neurons with RFs in good agreement more than the activity of neurons with RFs in bad agreement, in accordance with the proposed role for V4 cells in shaping V1 activity to reflect figure-ground relationships. Indeed, a model constructed with the estimated connectivity from HVA to V1 reproduced the patterns of FBM that we had previously measured in area V1 of monkeys.

Border-ownership tuning is commonly observed in areas V2, V3 and V4 where approximately half of the neurons exhibit BO-tuning¹³. BO-tuning also occurs for complex, overlapping objects^13,14,39,40 and natural images⁴¹. The initial studies of the von der Heydt group described BO-tuning of single units, but more recent studies reported that neurons tuned to BO are clustered in patches in areas V2, V3, V3A and V4¹⁷. V4 neurons in the same cortical column are more likely to prefer the same side-of-ownership¹⁶. However, Hesse and Tsao¹⁷ found that the degree to which neighboring cells prefer the same border-ownership direction varies, with heterogeneous BO-tuning in some clusters and homogeneous tuning in others. We recorded MUA using chronically implanted electrode arrays and observed BO-tuning at more than 60% of the V4 recording sites, in accordance with the hypothesis that this property is clustered. This multi-unit BO-tuning enabled us to study the relation between BO-tuning in V4 and FBM in V1.

Previous studies demonstrated that FBM in V1 likely arises through cortical feedback^8,12 that enhances the representation of the figure and suppresses the background representation^6,7,42. We hypothesized that BO-tuned cells in higher visual areas are an important source of FBM in V1, for a number of reasons. First, BO-tuned cells signal the spatial location of the figure relative to their RF within 70 ms after stimulus onset¹³, and this signal precedes FBM in V1, which typically arises at around 100 ms after stimulus onset^5,8 (reproduced in Fig. 5A, B). Second, BO-tuning is relatively robust to changes in the spatial position of the border¹³ and many V2, V3 and V4 cells are tuned to BO^13,40. Third, areas with BO-tuning such as V2, V3 and V4 send feedback to V1^43–46. We observed that a model in which BO-tuned cells in higher areas send excitatory feedback to V1 in the direction of their preferred side-of-ownership, and inhibitory feedback in the opposite direction, explains patterns of FBM in V1. Future work may further explore the generation of BO-tuning itself (see Craft et al.⁴⁷; Jehee et al.⁴⁸ for possible mechanisms).

The proposed connection scheme is consistent with previous findings on feedback connectivity, although detailed knowledge about the specificity of feedback connections is still lacking. First, feedback from V2 to V1 interconnects retinotopically matched regions^43,49,50. Second, in mice feedback projections from LM, which is equivalent to mid-level visual cortex in primates, to V1 can have excitatory and suppressive effects⁵¹ that are strongest in a direction orthogonal to the LM cell’s preferred orientation¹⁵. In our model, BO-tuned neurons in HVA also exerted the most prominent excitatory and inhibitory influences onto V1 in directions orthogonal to their preferred orientation. The suppressive influence in the non-preferred direction requires that feedback connections of V2/V3/V4 cells, which are almost entirely glutamatergic, target inhibitory interneurons in V1. In mice, there is considerable evidence that feedback connections target GABA-ergic cells, including SST and PV interneurons, to cause inhibition. In our model, feedback connections in the preferred direction could directly excite pyramidal cells in V1 or they could relieve inhibition via a VIP - > SST -> Pyr circuit^52,53. A recent study demonstrated that the suppression of VIP neurons decreases FBM in V1 of mice¹², which is in accordance with a role for this disinhibitory feedback pathway. However, the precise connectivity of feedback to V1 in monkeys and its relation to BO-tuning remains to be investigated.

Noise-correlations to estimate connectivity

In monkeys, there are currently no methods that permit studying the relation between long range connectivity and the tuning of the neurons from which the connections originate at the level of neural populations. We used noise correlations to estimate the functional strength of the connectivity between neurons in V1 and V4. Noise-correlations measure the correlated fluctuations in activity between a pair of recording sites across trials²⁵ and feedback connections contribute significantly to their magnitude^24,54,55. However, positive noise correlations do not imply direct connections⁵⁶, because they can also be caused by common input from different brain regions⁵⁷. It is possible that the correlations between neurons in V1 and V4 are in part mediated via neurons in area V2 and V3 and loops through the pulvinar nucleus of the thalamus^58,59. Furthermore, the noise correlations include global neuro-modulatory influences, and the resulting global excitability variations will cause slightly positive noise correlations for unconnected cells^28,29. Irrespective of the precise circuits that cause the noise correlations between V1 and V4 neurons, we found that they are stronger when the V4 neurons have a border-ownership tuning pointing toward the location of the V1 neurons’ RF (good agreement pairs) than when it points away (bad agreement pairs).

We hypothesized that feedback connections in the preferred and non-preferred direction of ownership would have excitatory and suppressive effects on V1 activity, respectively. In support of this idea, the spontaneous noise correlations between non-BO tuned V4 neurons and V1 neurons were lower than those of good-agreement pairs and higher than those of bad-agreement pairs. This pattern is consistent with a mix of excitatory^9,12,53,60 and suppressive^61–65 feedback effects. However, we cannot rule out the possibility that both effects are excitatory, with stronger connectivity for good-agreement pairs causing higher noise correlations. The difference in the magnitude of the noise correlation between good- and bad-agreement pairs was limited to V1 cells with RF centers closer to the V4 RF center than approximately 3 dva. This region matches the typical RF size of V4 cells at the eccentricities we recorded from (Fig. 3A) and is consistent with the feedback projection zone of a V4 cell⁶⁶. Furthermore, the strength of the correlation fell-off approximately linearly with increases in agreement angle.

The presentation of a visual stimulus influenced the magnitude of the noise correlation. If neurons at V4 sites responded to their preferred border-orientation, their correlation with V1 neurons strongly differentiated between good and bad agreement and were strongest with V1 neurons that responded to the figure. In contrast, correlation did not depend strongly on agreement when the V4 cell was weakly driven by non-preferred border-orientations and the correlations of bad agreement pairs did not depend on whether the V1 neurons were driven by the figure of background.

In accordance with previous studies, the pattern of noise correlations changed over time relative to the presentation of the visual stimulus. Stimulus onset caused an initial reduction in noise correlations, which was most pronounced for the V1-V4 pairs that were in good agreement, so that the influence of agreement angle became weaker. It seems likely that during this phase, activity was dominated by feedforward information from the LGN (Churchland et al., 2010; Semedo et al., 2022; Smith and Kohn, 2008). However, during a later phase of the response, coinciding with FBM in V1, the difference in noise correlation between good and bad pairs was reestablished. We hypothesize that V4 and V1 now engaged in recurrent interactions, in accordance with the influence of agreement angle and figure-ground segregation on the noise correlations.

Noise-correlations do not provide information about the directionality of the connectivity, from V1 to V4 or vice-versa. Our results are, however, most parsimoniously explained by a feedback influence from V4 to V1. First, BO-tuning emerged in V4 before we observed FBM in V1. Second, the influence of BO-tuning on the noise-correlation decreased during the early visual response, during which feedforward interactions dominate (Figure S5). Finally, we tested the causal influence from V4 onto V1 using electrical micro-stimulation. Stimulating V4 with weak currents caused more excitation of V1 cells with RFs in good agreement with the stimulated V4 neurons than of V1 cells with RFs in bad agreement. The relationship of the V4 stimulation effect on V1 with agreement angle and RF distance resembled the relationship of the V1-V4 noise-correlations (Fig. 6C,F), supporting the proposed feedback connectivity scheme.

Our highly organized visual percept is the result of recurrent interactions between low- and high-level visual areas. The results presented here suggest that cells in mid-tier visual areas encode the location of perceptual objects relative to their RF and send this information back to early visual areas to label this objects’ representation with enhanced firing and suppress background information. These findings connect studies on border-ownership and figure-background segregation, indicating that these phenomena, which had so far not been studied in the same experiment, are manifestations of a single computational process. Future studies can build on this connection between the processes that help parsing of visual scenes into objects and the background.

Methods

Experimental model and subject details

All procedures complied with the NIH Guide for Care and Use of Laboratory Animals, and were approved by the institutional animal care and use committee of the Royal Netherlands Academy of Arts and Sciences. Three male macaque monkeys participated in the experiment. The monkeys were socially housed in stable pairs in a specialized primate facility with natural daylight, controlled humidity and temperature. The home-cage was a large floor-to-ceiling cage that allowed natural climbing and swinging behavior. The cage had a solid floor, covered with sawdust and was enriched with toys and foraging items. Their diet consisted of monkey chow supplemented with fresh fruit. Their access to fluid was controlled, according to a carefully designed regime for fluid uptake. During weekdays, the animals received water or diluted fruit juice in the experimental set-up upon correctly performed trials. We ensured that the animals drank sufficient fluid in the set-up and supplemented extra fluid after the recording session if the animals did not drink enough. In the weekend, the animals received at least 700 ml of water in the home-cage supplied in a drinking bottle. The animals were regularly checked by veterinary staff and animal caretakers, and their weight and general appearance were recorded in an electronic logbook on a daily basis during fluid-control periods.

Computational model

We generated a model of V1’s response to a ‘u’ shaped stimulus. The ‘u’ shape was constructed as a 12 × 12 dva square with a central 8 × 4 dva (height × width) rectangle removed. V1 was modelled as a 500 × 500 matrix representing 25 × 25 dva of visual space (Fig. 1B). The V4 population response to the figure was modelled as a combination of an orientation tuned component, which was not sensitive to figure direction, and a border-ownership tuned component that was sensitive. Both components were generated with 80×80 kernels representing 10 dva. We first defined four base kernels,$K_{\left(i,j,s\right)}$, with different border-ownership tuning preferences: left, right, up and down. The sub-scripts i,j refer to horizontal and vertical spatial coordinates, respectively, and s refers to the BO-tuning direction. Each kernel had a value of 1 in the direction of preferred ownership and -1 in the non-preferred direction. For example, an ‘upwards’ tuned kernel would have a 40 × 80 region filled with 1 s above a 40 × 80 region filled with -1s. The border-ownership tuned V4 response was generated by convolving each base kernel with an input matrix, F (500 × 500), which was 1 on the figure and 0 on the background and the orientation -tuned component was the absolute value of the same kernel. The V4 response, $R_{V4\left(x,y,s\right)}$, for a given border-ownership tuning direction, s, was the sum of the orientation-selective and BO-tuned components. The BO-tuned component was weighted by a factor w (0.5 in the simulation of Fig. 1B):

$$R_{V4\left(x,y,s\right)}=w\left(F\left(x,y\right)\otimes K_{\left(i,j,s\right)}\right)+\mathrm{abs}\left(F\left(x,y\right)\otimes K_{\left(i,j,s\right)}\right)$$ 1

The V1 response depends on the connectivity matrix between V4 and V1. For our initial a priori model the connectivity matrix was unknown and we used a ‘sawtooth’ connection scheme, $C_{V4V1\left(i,j,s\right)},$ in which V4 cells have excitatory connections in the direction of preferred ownership and inhibitory weights in the opposite direction. The magnitude of the weights linearly decreased towards zero with distance from the preferred border location of the cell (D_i,j). For example, the connectivity matrix for a ‘prefers down’ cell was given by:

$$\begin{array}{c}\hfill C_{V4V1\left(i,j,1\right)}=\max \left(0,1-{\mathrm{mD}}_{\mathrm{ij}}\right),\mathrm{where}\mathrm{j}\ge 0\hfill \\ \hfill C_{V4V1\left(i,j,1\right)}=\min \left(0,-1+{\mathrm{mD}}_{\mathrm{ij}}\right),\mathrm{where}\mathrm{j}\le 0\hfill \end{array}$$ 2

where m was the slope of the ‘ramp’ in degrees of visual angle. We used a value of 0.2 for m in these simulations so that the connectivity strength reached 0 at a distance of 5 dva. The connectivity matrix of the refined post-hoc model was based on the measured pattern of noise correlations between V4 and V1. We used the best-fitting regression plane across monkeys (Figs. 4A and 6A) as the connectivity matrix. For simplicity, we did not include the interaction term. We set all connectivity weights further than 4 dva from the RF center to zero, because we observed no difference between good and bad agreement pairs beyond this distance (Fig. 4D). The feedback strength FB_V4V1(x,y,s), of feedback connections from V4 to V1 were modelled as:

$${FB}_{V4V1\left(x,y,s\right)}={\mathrm{R}}_{V4\left(s\right)}\otimes C_{V4V1\left(i,j,s\right)}$$ 3

Where R_V4(x,y,s) was the response of the V4 population with the border-ownership tuning s, C_V4V1(i,j,s) was the connectivity matrix for s^th sub-population as described above. The modulated output of V1, $R_{V1\left(x,y\right)}$, was then calculated as the sum across all sub-populations:

$$R_{V1\left(x,y,o\right)}={\sum }_{s=1}^4{W}_{V4V1\left(x,y,s\right)}$$ 4

We also modelled the response of the a priori and refined models to a checkerboard stimulus. This was constructed in an identical fashion to the ‘u’ shape with alternating checks of 8 ×4 dva. The V4 response to the checkerboard only contained the orientation-tuned component because checkerboards do not perceptually segregate into figure and background.

Training history and surgical details

We implanted the monkeys with a titanium head-post (Crist instruments) under aseptic conditions and general anesthesia as reported previously²². The monkeys were trained to fixate on a 0.5° diameter fixation dot and hold their eyes within a small fixation window (1.1° diameter). Monkeys Bu and N were implanted with a titanium baseplate containing fixation points for the array connectors, this was followed by a recovery period of several months to allow full bone integration of the implant. The monkeys underwent a final operation to implant arrays of micro-electrodes (Blackrock Microsystems) over opercular V1 and dorsal V4³⁸ and inferotemporal cortex (Monkey N only).

Electrophysiology

We recorded the envelope of multi-unit activity by digitizing the raw signal referenced to a subdural electrode at 24.4 kHz (monkey Bo and Bu, Tucker-Davis Technologies 96 channel ZIF-clip amplifier and PZ2 preamplifier) or 30 kHz (monkey N, Blackrock Microsystems Cereplex M headstage amplifier). The raw signal was then band-pass filtered (2^nd order Butterworth filter, 500Hz-5KHz) to isolate high-frequency (spiking) activity. This signal was full-wave rectified (negative becomes positive) and low-pass filtered (corner frequency = 200 Hz) to produce the envelope of the high-frequency activity, which we refer to as MUA. The MUA signal was down-sampled to 763 Hz (Monkey Bo and Bu) or 1000 Hz (Monkey N) for further analysis. The MUA signal reflects the population spiking of neurons within 100-150 µm of the electrode and the population responses are very similar to those obtained by pooling across single units^18–21.

Visual Stimuli

All stimuli were presented on a CRT monitor at a refresh rate of 85 Hz and with a resolution of 1024×768 pixels viewed from a distance of 52 cm. The monitor had a width of 40 cm, yielding a field-of-view of 41.6° × 31.2°. The background luminance, displayed during inter-trial intervals, was 21.2 cd m^-2. All stimuli were created using the COGENT graphics toolbox (developed by John Romaya at the LON at the Wellcome Department of Imaging Neuroscience) running in MATLAB (Mathworks Inc.).

Receptive field mapping

We mapped the RFs of each multi-unit site in V1 using a drifting luminance-defined bar that moved in one of four directions. The mean response to each direction was fit with a Gaussian function and the onset/offset of activity was calculated as the mean of the Gaussian ± 1.96 standard deviations. The borders of the RF were then calculated by averaging onset/offset positions from bar-sweeps with opposite directions as described previously¹⁸. The signal-to-noise ratio (SNR_RF) of the response was estimated as the peak of the Gaussian divided by the standard deviation of the pre-trial baseline response. Only RFs for which the responses to all four bar directions had an SNR_RF of over 1 were included in the analyses. Of 56 recording sites in Bo, 8 sites were excluded due to a lower SNR and in Bu 20 out of 48 sites were excluded. In monkey N 26 sites out of 448 were excluded. In Monkey Bo the median V1 RF size was 1.25° (range 1.1° to 1.7°) and the median eccentricity of the RFs was 3.1° (range = 2.9° to 3.5°), in monkey Bu the median V1 RF size was 2.4° (range 0.4° to 4.9°) and the median eccentricity was 2.4° (range 0.6° to 6.6°). In monkey N the median RF size was 1.6° (range 0.1° to 3.3°) and the median eccentricity was 1.8° (range 0.14° to 5.0°).

To map the V4 multi-unit RFs, we used a single luminance defined square (1.0° on each side), which was flashed for 150 ms at each position of a 21° × 21° grid. To construct the RF map, we took the average response, R_xy, to each square (with coordinates x and y) in a time-window from 0 to 250 ms. V4 cells often have a ‘hotspot’, which is not necessarily in the center of a circular RF. We took the location of the hotspot to be the preferred border location of the unit. We estimated the location of the hotspot with a contour plot. The responses R_xy were divided into 11 equally spaced levels from the minimum to the maximum response and contours were drawn around each of these levels (using the MATLAB contour.m function). We took the center-of-mass of the highest level contour as an estimate of the hotspot location.

Border-ownership mapping stimuli

Border-ownership preferences were measured using luminance-defined squares of varying size (6° or 12° on each side) and orientation. Border-ownership preferences were generally consistent across the different stimuli and we therefore chose one stimulus (the 12° luminance-defined squares) to estimate BO -tuning. The monkey initiated the trial by fixating on a red fixation point of 0.33° diameter on a mean luminance grey of 51.7 cd m^-2. The stimulus appeared After 300 ms of fixation. We presented dark squares (31.7 cd m^-2) on a uniform bright background (71.7 cd m^-2) and also the opposite configuration on interleaved trials. In the 0° configuration, the upper border of the square was centered in the aggregate RF of a recording array. On different trials, the square was presented rotated through θ degrees relative to this configuration and was targeted to different aggregate RFs. In monkeys Bo and N we used 24 equally spaced BO-angles (θ = 0, 15, 30, etc.) whereas in monkey Bu we used 12 equally spaced angles (θ = 0, 30, 60, etc.).

Quantification and Statistical Analysis

Preprocessing

A component of the MUA in area V1 of Monkey Bo tracked the monitor refresh frequency⁶⁷, which was removed in the analysis with a band-stop filter (2^nd order Butterworth filter, stopband centered on 85, 170 and 255 Hz ±1 Hz). The raw MUA data from each recording site was normalized on each session by subtracting the baseline activity and dividing by the maximum response. We used a running estimate of the baseline (-100 to 20 ms relative to stimulus onset in each trial) to remove slow drifts, which might contaminate the measurement of noise correlations. These values were smoothed using robust loess regression (‘smooth.m’ function in MATLAB) with one third of the trials as the span, but the exact choice of smoothing window did not affect the results (Figure S3D). We subtracted these values to estimate the baseline activity on each trial. We normalized all responses to the maximum of the smoothed (20 sample moving window) response (40-150 ms after stimulus onset), averaging across all conditions. The data are therefore expressed in normalized units, i.e. a value of 0.1 indicates 10% of the difference in MUA between the peak and the baseline.

Trials with extreme values were removed using an iterative procedure as the Pearson correlation is sensitive to outliers. We first calculated the mean response across all trials and smoothed the resulting trace with a 20 sample rectangular moving window. Individual samples were z-scored with reference to the smoothed mean response. Trials with samples with an absolute z-score higher than 10 were removed. This procedure was repeated twice. On average 2% of trials were removed using this approach. Occasionally recording sites would show poor or noisy signals on individual days. To exclude these days, we measured the signal-to-noise ratio (SNR_DAY) of each recording site on every day. SNR_DAY was estimated as the reciprocal of the standard deviation of the normalized baseline activity across trials. Recording sites on which SNR_DAY < 1.5 were removed from the analysis.

BO-tuning analysis

To estimate the strength of border-ownership tuning, we measured the response of each V4 site to square stimuli with different rotation angles and contrast-polarities (Fig. 2A) in a window of 40–500 ms after stimulus onset. We used two approaches to measure border-ownership preferences. In the classical approach we first determined the preferred orientation of each unit by collapsing across opposite BO -angles and contrast polarities (Fig. 2B, inset) and fitting the resulting response with a circular Gaussian function, using nonlinear least-squares fitting in MATLAB:

$$R\left(\theta \right)=C+R_p\bullet \exp \left(-\frac{{{ang}_{ori}\left(\theta -{ORI}_{pref}\right)}^2}{{2\sigma }^2}\right)$$ 5

where R(θ) is the response for orientation θ, C is the offset, R_p is the response to the preferred orientation $\left({ORI}_{pref}\right)$, ang_ori(x) = min(abs(x),abs(x-180),abs(x + 180)) wraps angular differences to the interval 0° to 90°, and σ is the standard deviation of the Gaussian. The classically preferred border-ownership tuning (BO_classic) was then calculated based on the activity elicited by ORI_pref and ORI_pref + 180⁰. We determined whether the cell was significantly border-ownership tuned using a weighted General Linear Model (GLM). As the preferred border-orientation of the unit was not guaranteed to fall exactly at one of the tested orientations, we weighted responses at the two tested border-orientations closest to the preferred border-orientation so that responses at an orientation closer to the preferred border-orientation carried stronger weights in the regression. Specifically, weights were given by:

$$w_1=\frac{\mathrm{\Delta }-\mathrm{abs}\left({ORI}_{pref}-{\theta }_1\right)}{\mathrm{\Delta }}$$ 6

$$w_2=1-w_1$$

Where w₁ was the weight for data from the closest tested orientation ${\theta }_1$ to the preferred orientation, w₂ was the weight for the second closest orientation ${\theta }_2$ and $\mathrm{\Delta }$ was the difference in orientation between ${\theta }_1$ and ${\theta }_2$. Responses from opposite border-orientations were weighted by these terms and entered into the GLM to test for a difference in mean response. If w₁ = w₂ = 0.5 this procedure is equivalent to an independent samples t-test. Neurons at the recording sites were considered border-ownership tuned if p < 0.05.

In the second vector-sum approach we calculated the preferred border-orientation by treating the response at each tested border-orientation as a complex valued vector and taking the sum of these vectors to derive a complex-valued grand-vector (V):

$$\mathrm{V}={\sum }_k\mathrm{R}\left({\theta }_k\right)e^{i{\theta }_k}$$ 7

where R(θ_k) is the response to the square with border-orientation θ_k (in radians). The preferred border-orientation, BO_pref, was defined as the angle of this vector V relative to the origin.

$${BO}_{pref}={\tan }^{-1}\left(\frac{\mathfrak{I}\left(V\right)}{\mathfrak{R}\left(V\right)}\right),$$ 8

where ℑ(V) and ℜ(V) are the imaginary and real parts. We determined whether units were significantly border-ownership tuned under this approach using a weighted GLM approach as described above, but using BO_pref derived from Eq. 8 to calculate the weighting factors. In the regression analyses of noise correlations described below, we only included V4 sites with significant border-ownership tuning using this approach. We used BO_pref for the main analyses and replicated our main results with BO_classic (Figure S2).

Analysis of spontaneous noise correlations

We estimated the noise correlation between each pair of V4 and V1 recording sites. To determine the spontaneous noise correlation, we took the baseline activity of each recording site (in a window from -100  ms to 20  ms relative to stimulus onset) on each trial of the BO-tuning sessions described above. The baseline values from each recording day were z-scored before being concatenated across days to account for any changes in noise level that can vary across recording days. We used the Pearson’s correlation between the z-scored baseline values. The relationship between BO_pref, RF distance and noise correlation was estimated using multiple linear regression. We also included the interaction of BO_pref and RF distance as a predictor in the model. Regression weights were estimated using ordinary least squares. We cross-validated the regression model by fixing the beta-weights for the three predictors and calculating the R² value using a held-back dataset recorded several weeks later. The held-back data came from a session in which the monkeys were passively fixating and we used the baseline activity period (-100–20 ms) while a grey screen was shown to measure the noise -correlations. To compare the strength of noise correlations between good, bad and orientation-tuned pairs, we included only pairs with an RF separation of less than 3 degrees. We then stratified the dataset to ensure a similar distribution of RF distance values between the three groups. This was achieved by binning the distribution of RF distance values into quintiles comparing the number of recording site pairs per bin. Pairs were removed until the bin numbers were equal for all three groups.

Analysis of stimulus-driven noise correlations

Stimulus-driven noise correlations were derived from the border-ownership tuning stimuli (luminance-defined squares). We took the average activity on each trial in a time-window from 100 ms to 500 ms after stimulus onset when neural activity had reached a stable level. We calculated noise correlations between each V4 unit and each V1 unit separately for each border-orientation (grouping across contrast-polarity) and only used stimuli that were well-centered on the V4 RF. We then binned the noise correlations into four groups depending on the difference in orientation between the preferred border-orientation of the V4 unit and the tested border-orientation. Means were then taken for each bin separately for V4/V1 pairs that were in good and bad agreement. To analyze the effect of figure-background assignment on noise correlations (Fig. 5D), we separated trials according to whether the V1 RF fell on the figure or background. We further split the trials according to whether the V4 cell was responding to its preferred (border-orientation <90° from preferred) or non-preferred ( > 90°) border-orientation. We then averaged noise correlations separately for V1–V4 pairs that were in good or bad agreement. For both analyses we only included V4 recording sites with significant BO-tuning (as described above) and V4/V1-pairs with RFs separated by less than 3 degrees. Analyses were performed using a mixed ANOVA with within subject factors being border-orientation (split into 4 bins for Fig. 5C or preferred/non-preferred for 5D), or figure-ground compartment (5D only) and the between subjects factor was the agreement angle (good or bad). Post-hoc t-tests were two-sided and corrected for multiple comparisons using Bonferroni corrections.

Latency of FBM and BO

Latencies of FBM and BO were measured by fitting a cumulative Gaussian function with two free parameters (mean and standard-deviation) to the mean difference between the figure and background or the preferred/non-preferred border-orientation using non-linear least-squares (fit.m in MATLAB 2021b). The latency was then taken as the time-point at which the fitted curve reached 33% of its maximum. To estimate the variability of the latency we bootstrapped the population of recording sites 2000 times and regenerated the FBM and BO difference for each iteration. The same curve-fitting approach was used to generate bootstrapped estimates of latency and the standard deviation across the 1000 iterations was taken as the estimate of the standard error of the mean. To test the significance of the latency difference between FBM and BO we used the same bootstrapping approach. For each iteration of the bootstrap we calculated the latency for FBM and BO. We only included iterations for which the quality of the fit was good (r² > 0.5) and redrew 1000 latency estimates from the included iterations separately for each condition. Under the assumptions of the null hypothesis, the mean difference between the two conditions is zero. We subtracted each condition’s mean across the 1000 iterations before calculating their difference to render a distribution consistent with the null-hypothesis. The observed difference in latency between FBM and BO was then compared to the null distribution and the p-value was calculated as the proportion of differences from the null distribution that were greater than, or equal to, the observed difference.

Micro-stimulation of V4

In monkey N we applied micro-stimulation to a subset of V4 recording sites and measured the effects on MUA in V1 (n = 448 sites) in a single recording session. We first measured the RFs of V1 and V4 and the border-ownership tunings as described above. We then selected 62 V4 sites with RFs that were well fit by the Gaussian function described above (R² > 0.6) to be micro-stimulated. We connected a stimulation device (Cerestim - Blackrock microsystems) to one bank of V4 electrodes (32 recording sites) and then randomly selected on each trial which site was stimulated from the pre-selected sites, while recording from V1. After a total of 50 trials at each selected site, we switched the stimulator to a different bank of V4 sites and repeated the experiment. We applied 5 bipolar pulses of 5 μA at a frequency of 200 Hz (pulse-width = 170 μS, interphase-delay = 60 μS). The return electrode was a subdural wire. The procedure was divided into trials, the monkey initiated the trial by fixating on a red circle of 0.3° radius on an otherwise uniform grey screen. After 200 ms the micro-stimulation train was triggered and the monkey had to carry on fixating for a further 200 ms to receive a juice reward. The micro-stimulation pulses caused large artifacts in the recorded signal and we therefore focused on V1 activity 35–100 ms after the onset of the stimulation train. We removed trials containing outlying values in this time period using the iterative procedure described above. We then z-scored the V1 data of each channel in the time period 35–100 ms by subtracting the mean activity of the recording site across all trials and samples and then dividing by the standard deviation. We examined the difference between good and bad agreement pairs use a linear mixed effects model with random intercept terms for the V1 and V4 channel IDs, this is because each recording site appeared multiple times in the dataset due to the pairing with other sites. The mean z-scored data on each trial was also entered into a linear model as described above with the agreement angle and distance between the V1 and V4 RFs as predictors. Linear mixed effects models were also run using the array identity of the V4 and V1 electrodes as random intercept terms.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

D.J. and M.W.S. conceived of the research. D.J., A.F.v.H., A.G., P.P. and M.W.S. recorded the data. D.J., P.R.R., and M.W.S. conceived of the analysis approach and D.J. and M.W.S. analyzed the data. M.W.S. supervised the project and wrote the initial manuscript. All authors edited and approved of the final manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The electrophysiological data reported in this manuscript and custom MATLAB analysis scripts are available from OSF at the following 10.17605/OSF.IO/FJ7AV. Source data are provided with this paper.

Code availability

The script⁶⁸ used to calculate the model results in Figs. 1 and 7 is available at: https://github.com/fattsmellf/BorderOwnership.

Competing interests

P.R.R. is a co-founder and shareholder of a neurotechnology start-up, Phosphoenix BV (Netherlands) (https://phosphoenix.nl). The remaining authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53256-8.