Abstract
Tuberculosis (TB) is a highly contagious disease that remains a global concern affecting numerous countries. Kazakhstan has been facing considerable challenges in TB prevention and treatment for decades. This study aims to understand TB transmission dynamics by developing and comparing statistical and deterministic models: Seasonal Autoregressive Integrated Moving Average (SARIMA) and the basic Susceptible-Infected-Recovered (SIR). TB data from 2014 to 2019 were collected from the Unified National Electronic Health System (UNEHS) using retrospective quantitative analysis. SARIMA models were able to capture seasonal variations, with Model 2 exhibiting superior predictive accuracy. Both models showed declining TB incidence and revealed a notable predictive performance evaluated by statistical metrics. In addition, the SIR model calculated the basic reproduction number ( ) below 1, indicating a receding epidemic. Models proved the capability of each to accurately capture trends (SARIMA) and provide mathematical insights (SIR) into TB transmission dynamics. This study contributes to the general knowledge of TB transmission dynamics in Kazakhstan thus laying the foundation for more comprehensive studies on TB and control strategies.
) below 1, indicating a receding epidemic. Models proved the capability of each to accurately capture trends (SARIMA) and provide mathematical insights (SIR) into TB transmission dynamics. This study contributes to the general knowledge of TB transmission dynamics in Kazakhstan thus laying the foundation for more comprehensive studies on TB and control strategies.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-76721-2.
Keywords: SIR, SARIMA, Forecasting, Tuberculosis, Statistical modeling, Kazakhstan
Subject terms: Tuberculosis, Epidemiology, Applied mathematics, Scientific data, Statistics, Software
Introduction
TB is an infectious disease with high fatality rates and stands among the top ten causes of death worldwide. It poses a significant burden, affecting approximately one-third of the global population, particularly in underdeveloped regions1. Humanity witnessed a staggering count of nearly 10 million new TB cases worldwide in 2016, with children under 15 years of age constituting approximately 7% of those cases2. Furthermore, most of these new cases, exceeding 85%, were reported in developing nations. Specifically, Asian and African countries contributed 61% and 25% of the total cases, respectively, while only seven countries accounted for nearly 65% of the global TB burden2. In the year 2018, there were more than 230,000 deaths attributed to TB, and over 1 million cases of TB were reported in children below the age of 15. It is worth noting that around 55% of these reported cases remained undiagnosed or unreported3. Furthermore, a mere eight countries were responsible for nearly 67% of all new TB cases reported in 2019, while 30 countries with a high burden of TB accounted for approximately 87% of the total number of new TB cases globally4.
In Kazakhstan, the occurrence of multidrug-resistant tuberculosis (MDR-TB) is notably high, with 26% of patients being diagnosed for the first time and 44% having previously undergone treatment5. Through their analysis of Kazakhstan’s national surveillance data from 2006 to 2010, Terlikbayeva et al. identified several significant characteristics associated with new TB cases. These included being a registered contact of a TB case, having experienced detention within the past two years, and being unemployed6. Sakko et al. studied significant parameters of TB dynamics in Kazakhstan: incidence, mortality, and survival rates and its risk factors using large-scale health data from 2014 to 2019. The study revealed a downward trend in incidence cases from 2014, 227 cases per 100,000 population to 2019, 15.2 cases per 100,000 population, and the increase in all-cause mortality rate: 8.4–15.2 per 100,000 population. In addition, the authors recommend putting more emphasis on older adults, men, urban residents, and HIV/diabetes patients when implementing control strategies7. However, the existing research on TB in Kazakhstan is limited, with a lack of comprehensive examination of the disease’s risk factors. Previous studies have predominantly focused on populations such as injectable drug users and incarcerated individuals8,9. Few studies have specifically investigated TB in the general population of Kazakhstan or explored other risk factors, such as chronic illnesses, associated with TB.
Official reports indicate that implementing the Comprehensive Plan has led to a stable epidemiological situation for TB in Kazakhstan. Over the past decade, the incidence of TB has decreased by 2.3 times, with a rate of 35.7 per 100,000 population in 2020 compared to 105.3 per 100,000 in 2009. The prevalence of TB in 2020 stood at 49.3 per 100,000 population. Additionally, the mortality rate has decreased sixfold, reaching 1.9 per 100,000 population in 2020. Notably, in 2020, 71.2% of TB patients commenced treatment on an outpatient basis, indicating an improvement from 61.1% in the previous year. In Kazakhstan, the prevention, diagnosis, and treatment of TB are provided free of charge. The country has achieved high effectiveness in treating TB patients, surpassing global standards. In 2020, the treatment success rate for newly diagnosed patients with susceptible TB reached 87.5% (exceeding the WHO standard of 85%), while for multidrug-resistant TB (MDR-TB), it was 82.5% (above the WHO standard of 75%)10.
Extensive discussions have centered around the use of mathematical models to simulate epidemic dynamics and relationships within populations, highlighting the need for leveraging such modeling approaches to enhance understanding, develop more effective policies, and address resource limitations in TB control interventions. Such strategies would positively impact both public health and the economy11. The specific application of new machine learning techniques, including SARIMA and SIR models, in modeling disease occurrence within Kazakhstan remains relatively unknown. However, various versions of the former model were employed to predict short-term and long-term trends in non-infectious diseases such as cancer and malaria12–14. At the same time, numerous modifications of the latter were used to understand the dynamics of highly infectious diseases such as COVID-19, measles, and pertussis15,16. The studies indicate that while SARIMA models can predict occurrences, their forecast accuracy is not guaranteed, particularly over longer forecast horizons12. These models perform best when applied to stable data or data with a consistent trend over time and minimal outliers13. Consequently, in the absence of a defined strategy for handling outliers and in cases of insufficient data, SARIMA models would be unsuitable and prone to underfitting or overfitting issues17. SIR, a classic mathematical model in epidemiology, is known for its ease of use and ability to describe the general trend of the disease using few parameters and states16. Its simplicity may be an obstacle if one desires to observe the demographic and strategic effects on the population since these are not considered in the model18.
To gain a comprehensive understanding of TB infection in Kazakhstan and develop effective interventions, assessing the trend and forecasting the incidence using existing surveillance data and innovative models is essential. This approach enables the identification of specific conditions and parameters for accurate modeling and forecasting. The present study compares TB occurrences among patients in Kazakhstan using linear-based SARIMA and deterministic SIR models, aiming to enhance understanding and devise creative measures to curb the spread of TB in the country.
Materials and methods
Study type and location
This retrospective quantitative study was conducted in the Republic of Kazakhstan, which benefits from a strategically favorable geographical location in the central part of the Eurasian continent. The country is equidistant from the Atlantic and Pacific oceans, positioning it in a unique and advantageous position. Regarding the indicator under investigation, Kazakhstan ranks ninth globally and fourth among the countries in Eurasia19.
Information source and data analysis
Daily TB case data were abstracted and aggregated for each month between January 2014 and December 2019. It utilized aggregated monthly TB cases of outpatient and inpatient hospital records retrieved from the Unified National Electronic Health System (UNEHS)20. Only patients diagnosed with TB according to the International Classification of Diseases-10 (ICD-10), specifically those classified under A15 (respiratory tuberculosis confirmed bacteriologically and histologically) and A16 (respiratory tuberculosis, not confirmed bacteriologically or histologically), were included.
UNEHS was launched in 2005 as a strategic investment project aimed at improving the efficiency of the healthcare system by digitalizing data related to health services and medical billing. The establishment of UNEHS has emerged as a credible and reliable data repository for population health research in Kazakhstan due to its ability to offer comprehensive nationwide administrative data on patient hospitalization and medical services20. The present study did not collect of utilize individual patient data. Since it involved secondary data derived from the UNEHS, the requirement for informed consent from study participants was waived by the Nazarbayev University Institutional Review Ethics Committee (NU-IREC 315/21092020). All methods were conducted in accordance with the “Reporting of studies conducted using observational routinely-collected health data” (RECORD) guideline.
The primary objective of conducting time-series analysis is to utilize the available observed time series data to make predictions regarding future observations. When new empirical data for prediction is unavailable, the cross-validation technique is applied to estimate the future predictive accuracy of a model and reduce errors. Additionally, when training and evaluating a model on the same datasets, particularly in situations with limited data availability there is a risk of overfitting. Consequently, the dataset underwent partitioning into training and validation sets, facilitating effective model evaluation. The results were then synthesized via the utilization of tables and figures.
Statistical analysis
Seasonal autoregressive integrated moving average models (SARIMA) models
Smoothing techniques were initially applied to the time series data to identify underlying patterns and address high-frequency fluctuations. The monthly TB notification rate from 2014 to 2018 served as the dataset for modeling purposes, while data from 2019 were reserved for forecasting. The SARIMA model, specified as SARIMA (p, d, q) (P, D, Q) S, was utilized for analysis. In this notation, the parameters p, d, and q indicate the autoregressive order, the number of differences, and the moving average order, respectively. Likewise, P, D, and Q represent the seasonal autoregressive order, the number of seasonal differences, and the seasonal moving average order, respectively. The parameter S signifies the length of the seasonal period. The modeling process adhered to the Box and Jenkins methodology21, consisting of four main stages. Initially, the Augmented Dickey-Fuller (ADF) test was applied to assess the stationarity of the time series. If the series demonstrated non-stationarity, differencing techniques were implemented.
Furthermore, the Ljung-Box portmanteau test was utilized to ensure that the resulting stationary series did not exhibit characteristics resembling white noise. In the second stage, the autocorrelation coefficient (ACF) and partial autocorrelation coefficient (PACF) of the stationary sequence were examined to identify appropriate model parameters (p, d, q, P, D, Q) and establish potential alternative models. Subsequently, the third stage involved applying goodness-of-fit tests based on the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) to select the optimal SARIMA model from competing alternatives. The chosen model had to pass both parametric tests and the Ljung-Box portmanteau test, indicating that its residual series resembled white noise. Finally, the performance of the selected model was assessed using metrics such as Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percent Error (MAPE), and determination coefficient (R-squared)15.
The classic susceptible-infected-recovered (SIR) model
SIR is the basic compartmental model to analyze the spread of infectious diseases, first proposed by Kermack and McKendrick in 192722. It is a convenient and apprehensible method to describe the flow of the disease and how it can be affected by various factors such as control strategies, the inclusion additional compartments, or a seasonality of a particular disease.
Each letter in the name of the model stands for a certain compartment—a group of the population: 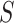 —susceptible,
—susceptible, 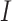 —infected, and
—infected, and 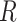 —recovered people. In the current model, initially, the whole population is considered to be in the susceptible group
—recovered people. In the current model, initially, the whole population is considered to be in the susceptible group  : to have the same level of immunity and to be at risk of infection. As soon as an infectious person enters this community and infects its representative, a newly infected person is moved to compartment
: to have the same level of immunity and to be at risk of infection. As soon as an infectious person enters this community and infects its representative, a newly infected person is moved to compartment  . If the patient has recovered, they are moved to the group of recovered people
. If the patient has recovered, they are moved to the group of recovered people  . The flow between compartments is described using parameters and rates of changes. Figure 1 illustrates this process.
. The flow between compartments is described using parameters and rates of changes. Figure 1 illustrates this process.
Fig. 1.
SIR flow diagram.
Mathematically, this model is represented as the system of ordinary differential Eq.
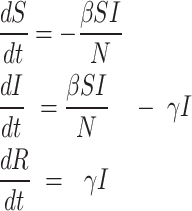 |
1 |
Derivatives on the left-hand side of the system above describe the rate of change in the number of individuals in each compartment. Meanwhile, the right-hand side represents the flow of individuals between compartments. The number of new infections per unit of time, first proposed by ReVelle et al.23, is given as  , where the contact rate
, where the contact rate  is the rate at which one gets infected as he/she meets an infectious person. It is assumed that the recovery from the disease is guaranteed and confers immunity, which is denoted as
is the rate at which one gets infected as he/she meets an infectious person. It is assumed that the recovery from the disease is guaranteed and confers immunity, which is denoted as 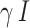 . The total population
. The total population 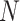 is held constant.
is held constant.
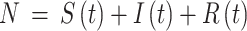 |
2 |
In our case, monthly data from 2014 to 2017 was used to train the model and get the optimal values for parameters  and
and 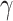 , while the data from 2018 to 2019 served as test data for forecasting purposes.
, while the data from 2018 to 2019 served as test data for forecasting purposes.
To gain further insights into the disease transmission dynamics, one of the key parameters, the basic reproduction number  , was calculated using optimal
, was calculated using optimal 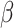 and
and 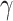 24:
24:
 |
3 |
where  is the average infectious period.
is the average infectious period. 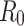 gives the average number of secondary infections: the number of people infected by an infectious person during an infectious period. It serves as a threshold value determining if the disease becomes epidemic (
gives the average number of secondary infections: the number of people infected by an infectious person during an infectious period. It serves as a threshold value determining if the disease becomes epidemic ( ) or dies out (
) or dies out ( 24.
24.
The model was fitted to the selected portion of data, with initial values obtained from reported data and the official information source of the Prime Minister of the Republic of Kazakhstan. As optimal 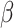 and
and  values were estimated, the number of infected people in 2018 and 2019 was forecasted, and the basic reproduction number was calculated using these parameters. The accuracy of predictions was evaluated using common statistical metrics such as Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and the determination coefficient (R-squared). These metrics were imported from the scikit-learn library and implemented using Python.
values were estimated, the number of infected people in 2018 and 2019 was forecasted, and the basic reproduction number was calculated using these parameters. The accuracy of predictions was evaluated using common statistical metrics such as Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and the determination coefficient (R-squared). These metrics were imported from the scikit-learn library and implemented using Python.
Time-series forecasting was performed using Python, version 4.1.2 with relevant packages designed for time-series data analysis, while for the SIR model Python version 3.9.18 with packages for data fitting and optimization was used. To be more precise, a powerful function curve_fit from the SciPy library, which fits data using the nonlinear least squares method, was employed for the SIR model.
Ethical approval and considerations
The study was approved by the Institutional Review and Ethics Committee of the Nazarbayev University (NU-IREC 315/21092020 on 23/09/2020) with an exemption from informed consent.
Results
Model fitting and estimation of model parameters
SARIMA model
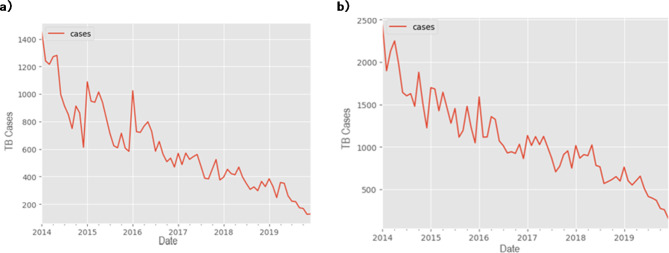
A decreasing trend and seasonal variation in TB notification rate were found from 2014 to 2019 in Kazakhstan (Fig. 2). The seasonal trend indicated that the peak occurred during the initial six months of the year (Fig. 2, Supplementary Figure S1). The time series was stationary (ADF test: t = − 3.05 and ADF test: t = − 6.52, P < 0.001) after the first-order regular difference and the first seasonal difference. In addition, the stationary sequence was not a white noise (P < 0.01).
Fig. 2.
Monthly notification rate of TB cases, (a) ICD-10 code A15 and (b) ICD-10 code A16.
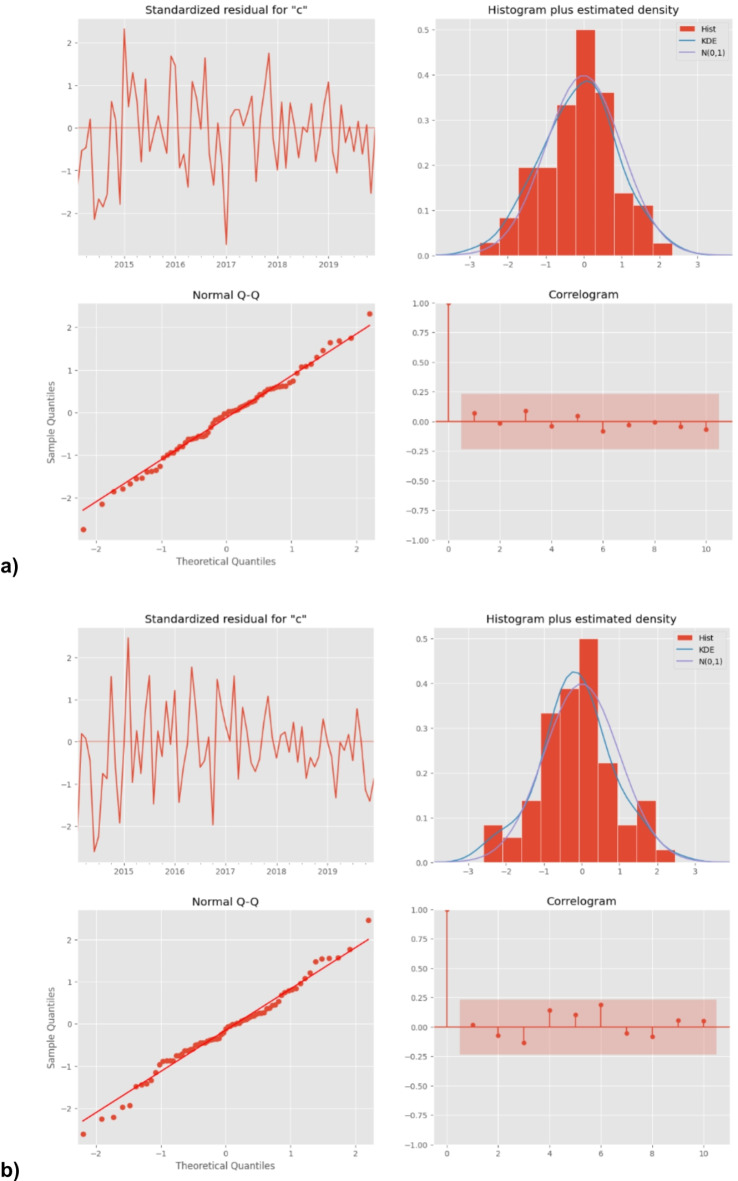
The ACF and PACF graphs (Supplementary Figure S2) were used to explore the parameters of the ARIMA model, and several candidate models were identified accordingly. As described above, the most preferred model must show the minimum values of AIC and BIC and should comply with the parametric and residual tests. Finally, SARIMA model 1 (2,1,0) (1,0,0)12 and SARIMA model 2 (2,1,0) (2,0,0)12 were identified as the most appropriate forecasting model, and the monthly TB notification rates in 2019 were then forecasted. Diagnostics for residual series are shown in Fig. 3.
Fig. 3.
Diagnostics for TB after differencing for (a) ICD-10 code A15 and (b) ICD-10 code A16. Standardized residuals, histogram, qqplot and correlogram (from the top left to the right).
SIR model
The model was fitted using nonlinear curves and the initial values listed in Table 1. Since the analysis covered the years 2014–2019 and the population size was held constant,  was set to the population size of Kazakhstan in 2014 which was recorded as 17.29 million25. Initial state values for the model were chosen as follows:
was set to the population size of Kazakhstan in 2014 which was recorded as 17.29 million25. Initial state values for the model were chosen as follows:  , since the whole population was considered susceptible, with the same level of immunity except for those already infected;
, since the whole population was considered susceptible, with the same level of immunity except for those already infected; 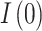 is the number of cases confirmed in the first month of 2014, and
is the number of cases confirmed in the first month of 2014, and 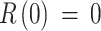 , since we assumed the disease first entered the population in January 2014. As a result of the fitting and optimization process, the best values for parameters
, since we assumed the disease first entered the population in January 2014. As a result of the fitting and optimization process, the best values for parameters  and
and  were determined for each of the datasets. Using these values,
were determined for each of the datasets. Using these values, 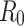 was calculated as in Eq. (2). The results are presented in Table 1 below.
was calculated as in Eq. (2). The results are presented in Table 1 below.
Table 1.
SIR model parameters and states.
| Parameter/initial state | Description | Value (A15) | Value (A16) | Source |
|---|---|---|---|---|
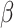
|
The rate of infection | 0.0127 | 0.0096 | Calculated |
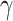
|
The rate of recovery | 0.0431 | 0.0375 | Calculated |
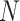
|
Population size | 17.2900  106 106
|
17.2900  106 106
|
Data26 |

|
Initial number of susceptible people | 17.2885  106 106
|
17.2876  106 106
|
Calculated |

|
Initial number of infected people | 1450 | 2434 | Data |

|
Initial number of recovered people | 0 | 0 | Assumed |

|
The basic reproduction number | 0.2960 | 0.2574 | Calculated |
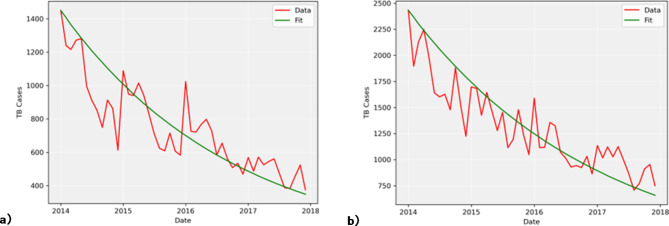
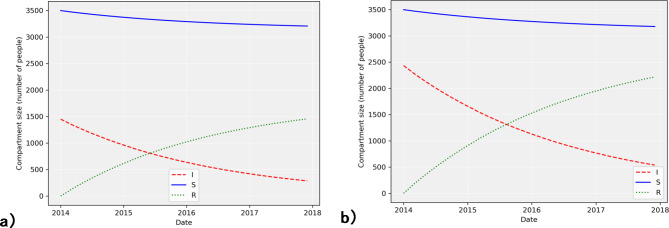
One of the key processes in this model is the change in  . Using the parameters described earlier, the model was simulated with training data from 2014 to 2017 (Fig. 4) and the disease transmission was forecasted with test data from 2018 to 2019 (Fig. 5), allowing us to evaluate the performance of the model.
. Using the parameters described earlier, the model was simulated with training data from 2014 to 2017 (Fig. 4) and the disease transmission was forecasted with test data from 2018 to 2019 (Fig. 5), allowing us to evaluate the performance of the model.
Fig. 4.
Model fitting using 2014–2017 training data for (a) ICD-10 code A15 and (b) ICD-10 code A16.
Fig. 5.
Model simulation using 2014–2017 training data for (a) ICD-10 code A15 and (b) ICD-10 code A16.
As shown in Fig. 4, the estimated number of infected people is compared to real data. A closer look at the dynamics of the infected compartment 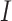 is necessary to fully understand the disease transmission. Simulations including all three compartments are presented in Fig. 5. It should be noted that values for the susceptible group
is necessary to fully understand the disease transmission. Simulations including all three compartments are presented in Fig. 5. It should be noted that values for the susceptible group  were scaled due to the large disparity between the numbers of
were scaled due to the large disparity between the numbers of  and
and 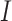 . The basic reproduction number for both datasets was calculated, resulting in
. The basic reproduction number for both datasets was calculated, resulting in 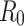 values of 0.2960 and 0.2574 for A15 and A16 categories, respectively.
values of 0.2960 and 0.2574 for A15 and A16 categories, respectively.
Models’ predictive accuracy
The accuracy of the model was evaluated using common statistical metrics such as RMSE, R-squared, MAE and MAPE. The results of the evaluation are presented in Table 2 below.
Table 2.
Results of the models’ predictive accuracy test.
| Model | R-squared | RMSE | MAE | MAPE | |
|---|---|---|---|---|---|
| SARIMA | A15 | 0.76 | 46.97 | 37.8 | 0.14 |
| A16 | 0.89 | 68.96 | 56.74 | 0.14 | |
| SIR | A15 | 0.61 | 60.60 | 48.85 | 0.18 |
| A16 | 0.42 | 174.56 | 146.11 | 0.38 | |
Juxtaposing the two models’ predictive accuracy, SARIMA demonstrates clear superiority over the basic SIR model in predicting the transmission dynamics of TB (Table 2). To illustrate, SARIMA attained an R-squared value of 0.76 for A15 class and 0.89 for A16 class data, meaning that 76% and 89% of variance in the data are explained by the model. In contrast, SIR showed a lower R-squared values of 0.61 and 0.42 for A15 and A16 classes, respectively. Moreover, SARIMA reached lower RMSE and MAE values for both patient classes: 46.97 and 37.8 for A15, and 68.96 and 56.74 for A16, indicating fewer errors when predicting in comparison with SIR model with higher RMSE and MAE. It is worth noting that SIR reached the record values of RMSE, MAE and MAPE when predicting A16 class data. While the MAPE for SARIMA remains at 0.14 for both classes, it is considerably high for SIR model, especially for the A16 class of. Overall, SARIMA surpasses SIR across both classes of patient data, with higher R-squared values and lower errors.
SARIMA model
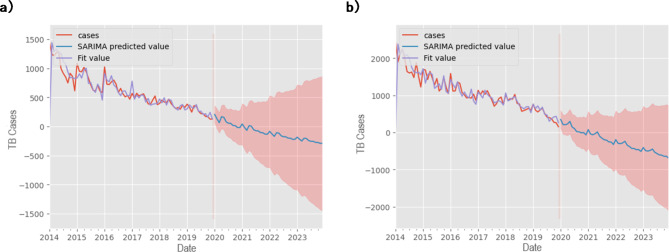
In assessing the accuracy of parameters and measures within the Seasonal ARIMA model, two distinct models were analyzed: Model 1, denoted by (2,1,0)(1,0,0)12, and Model 2, represented as (2,1,0)(2,0,0)12. Both models were fitted to actual TB case data to gauge their performance. The evaluation revealed significant findings: Model 1 demonstrated an R-squared value of 0.76, accompanied by MAE, RMSE, and MAPE values of 37.87, 46.97, and 0.14, respectively. In contrast, Model 2 exhibited higher accuracy metrics, with an R-squared value of 0.89 and corresponding MAE, RMSE, and MAPE values of 56.74, 68.96, and 0.14, respectively. These comparisons highlighted the superior predictive capability of Model 2. Moreover, an analysis of monthly median plots juxtaposing fitted and actual median TB cases provided visual confirmation of the model’s ability to capture the seasonal patterns inherent in the data (Fig. 6). In addition to the main prediction curve, the model provides a range of possible cases shown in red on Fig. 6. This observation reinforces the models’ utility in forecasting TB cases while emphasizing their capacity to discern temporal fluctuations accurately. Furthermore, the seasonal parameter, denoted as  , was adopted in this study to accommodate the monthly nature of TB case data, aligning with the established convention of analyzing monthly trends in epidemiological studies.
, was adopted in this study to accommodate the monthly nature of TB case data, aligning with the established convention of analyzing monthly trends in epidemiological studies.
Fig. 6.
Monthly notification rate of TB cases and results of the SARIMA model, (a) ICD-10 code A15 and (b) ICD-10 code A16.
SIR model
To evaluate the performance of the model, error estimates were calculated during the forecasting and testing phases. Monthly data on TB cases for 2018 and 2019 were used to test the model. First, the fitted parameters  and
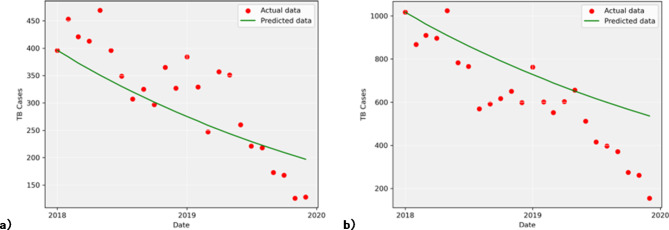
and 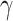 were utilized to simulate the behavior of the infection during this period. To assess the model’s predictive accuracy, already known data for A15 and A16 classes was compared to the predicted values. The plots of simulated and actual data points are presented in Fig. 7. The reported data is scattered in dots, while the predicted data is represented by a line. As shown in Fig. 7, the SIR model, using estimated parameters, was able to predict approximately half of the actual TB cases for the A15 class and less than half for the A16 class.
were utilized to simulate the behavior of the infection during this period. To assess the model’s predictive accuracy, already known data for A15 and A16 classes was compared to the predicted values. The plots of simulated and actual data points are presented in Fig. 7. The reported data is scattered in dots, while the predicted data is represented by a line. As shown in Fig. 7, the SIR model, using estimated parameters, was able to predict approximately half of the actual TB cases for the A15 class and less than half for the A16 class.
Fig. 7.
Model prediction using 2018–2019 test data for (a) ICD-10 code A15 and (b) ICD-10 code A16.
A comparison of the model’s prediction and the actual reported cases of TB was done using MAPE and R-squared. Error analysis revealed MAPE values of 0.175 for bacteriologically and histologically confirmed TB data (A15) and 0.383 for bacteriologically and histologically not confirmed TB data (A16). The R-squared values were 0.612 and 0.416 for A15 and A16 classes, respectively.
Discussion
To the best of our knowledge, this study is the first to examine the trend of TB notification rates over recent years in Kazakhstan using SARIMA and SIR models. Our analysis revealed a decreasing trend in TB notification rates and identified seasonal fluctuations from 2014 to 2019, with a notable peak occurring in the first half of the year. The SARIMA model exhibited superior performance over the SIR model in forecasting TB notification rates within the country.
Similar results are reached in many works dedicated to TB modeling. Some of these studies incorporate demographic effects such as birth and death rates to create more realistic scenarios27–29. Others compare the performance of two or more models27,30, seeking the most descriptive and efficient ones. This work juxtaposes a deterministic model with a statistical model and evaluates the ability of each to describe the disease transmission dynamics and forecast them.
This section elaborates on the results presented in the previous one. To begin with, consider Fig. 4a,b which explains the behavior of the infected group. The fitted curve starts at the initial point 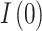 (Table 1) and decreases in line with the actual data throughout the specified period for both classes A15 and A16. Although the difference between the two classes can be observed in the contact and the recovery rates (Table 1), their respective values differ only for
(Table 1) and decreases in line with the actual data throughout the specified period for both classes A15 and A16. Although the difference between the two classes can be observed in the contact and the recovery rates (Table 1), their respective values differ only for  , hence showing that whatever the class is, the disease is receding. Most of the previous works on TB modeling discover disease peaks (maximum number of cases) at some point in the considered period16,28,29, which was also captured by SARIMA. However, Figs. 4, 5 and 7 reveal that SIR could only observe an always decreasing number of infected people. This is explained by
, hence showing that whatever the class is, the disease is receding. Most of the previous works on TB modeling discover disease peaks (maximum number of cases) at some point in the considered period16,28,29, which was also captured by SARIMA. However, Figs. 4, 5 and 7 reveal that SIR could only observe an always decreasing number of infected people. This is explained by  being much less than 1. A very small value of the contact rate over the whole period results in a decrease in
being much less than 1. A very small value of the contact rate over the whole period results in a decrease in  from the beginning27,31,32. Such a trend in infection spread dynamics can also be explained using the basic reproduction number calculated using fitted
from the beginning27,31,32. Such a trend in infection spread dynamics can also be explained using the basic reproduction number calculated using fitted 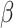 and
and 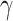 . As described in the previous section,
. As described in the previous section, 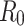 is 0.2960 and 0.2574 for A15 and A16 categories. It is less than one for each class, meaning that a single representative of an infected compartment could infect on average less than 1 person, which means that incidence cases would go down33. Considering that the fitting was performed using a nonlinear curve, the fit described the spread of the infection relatively well, although it did not cover the fluctuations.
is 0.2960 and 0.2574 for A15 and A16 categories. It is less than one for each class, meaning that a single representative of an infected compartment could infect on average less than 1 person, which means that incidence cases would go down33. Considering that the fitting was performed using a nonlinear curve, the fit described the spread of the infection relatively well, although it did not cover the fluctuations.
As model parameters were fitted, it became possible to simulate the whole model (1) to see how compartments relate to each other. Figure 5a,b illustrates this simulation. It shows that as the number of active cases decreases, the number of recovered people increases. Moreover, despite the decline in 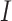 , there are still new cases of infection, which lead to a slight decrease in the number of susceptible people. Overall, this suggests that measures to control the spread of tuberculosis are efficient27. Such a result was also reached by scientists from Turkey and Malaysia, who used local patient data on TB cases. The scientists fitted the model and evaluated its predictive ability27.
, there are still new cases of infection, which lead to a slight decrease in the number of susceptible people. Overall, this suggests that measures to control the spread of tuberculosis are efficient27. Such a result was also reached by scientists from Turkey and Malaysia, who used local patient data on TB cases. The scientists fitted the model and evaluated its predictive ability27.
It can also be observed that the SIR model is not able to capture the seasonality which starts in 2017 (Figs. 4 and 5), due to the constant parameters used in the model. In various works, since seasonality is a common property of disease transmission dynamics, researchers used more complex models such as SEIR ( - compartment of exposed individuals) or periodic and statistical models to explain and forecast such a pattern34–36. Although the SIR model was not able to use such a pattern to forecast the TB transmission dynamics, the SARIMA model filled this gap and outperformed SIR in forecasting.
- compartment of exposed individuals) or periodic and statistical models to explain and forecast such a pattern34–36. Although the SIR model was not able to use such a pattern to forecast the TB transmission dynamics, the SARIMA model filled this gap and outperformed SIR in forecasting.
With fitted models and estimated parameters in hand, the models were tested for their predictive properties. Given the data for 2018–2019, the SIR model predictions and reported data were plotted and compared (Fig. 7). The plot shows tolerable gaps between SIR predicted and actual values. The distribution of the points around the predicting line is not uniform, leading to the conclusion that the model has some limitations. This conclusion is supported by the results of the error analysis. First, MAPE was significantly lower for SARIMA compared to SIR, meaning that SARIMA offers more reliable predictions in the context of public health forecasting37. In addition, SARIMA achieved an R-squared of 0.89, indicating that 89% of the variance in TB cases is explained by the model. In contrast, SIR, with an R-squared of 0.61, explains only 61% of the variance. At the same time, the SARIMA model’s prediction (Fig. 6) followed the seasonality pattern of the disease dynamics and showed the possible peaks at the beginning of each year. The combination of these metrics demonstrates that SARIMA, particularly Model 2, is more accurate in forecasting short-term TB trends, which is critical for timely interventions. In addition, the prediction complies with the recent data on TB incidence by the World Health Organization. According to the reports, the number of TB cases in Kazakhstan had been experiencing a decline until 2019 followed by a notable growth38. Figure 6 shows that SARIMA can foresee such an upward trend by giving a wide range of confidence interval even though it was given only decreasing data for previous years.
This study compared the performance of two SARIMA models in forecasting TB incidence. Model 2, characterized by parameters (2,1,0)(2,0,0)12, demonstrated superior accuracy metrics, including an R-squared value of 0.89 and lower MAE, RMSE, and MAPE values compared to Model 1 (parameters: (2,1,0)(1,0,0)12). These results align with previous research assessing SARIMA((2),0,(2))(0,1,0)12 models, which also exhibited strong predictive capabilities with low error metrics39. Our findings emphasize the effectiveness of SARIMA models in TB incidence forecasting, particularly models with more refined specifications. Additionally, regarding the accuracy measurements, the MAPE results closely align with previous research indicating that a MAPE value below 10% is deemed highly accurate for forecasting40.
These results lay the foundation for further, more detailed research on TB transmission. Various studies have focused on public awareness regarding TB, measures to take in case of infection, and have reviewed the effectiveness of anti-TB measures implemented under the state program for healthcare development of the Republic of Kazakhstan “Salamatty Kazakhstan (Healthy Kazakhstan)”41,42. Although these studies enhance the level of knowledge of the local population, the current research enables public health representatives to use simulations and forecasting tools to evaluate specific control measures. The basic SIR model can be improved to consider such measures as patient treatment, vaccination, and rapid case identification (diagnosis). To illustrate, it can be shown that diagnosing correctly and vaccinating the population is more efficient than treating already infectious individuals43. Public health decisions can be based on such research outcomes. In this work, by comparing the two models, we highlight the practical implications for public health: SARIMA’s ability to accurately predict seasonal peaks makes it a more reliable tool for planning resource allocation and intervention strategies, while SIR may be better suited for studying long-term disease behavior in conjunction with other models.
Limitations
While the SARIMA model is effective for analyzing time series data, it may oversimplify the dynamics of complex systems such as disease epidemics like HIV. Unlike more sophisticated models such as the SIR model, which can incorporate multiple compartments representing demographic factors like age, gender, ethnicity, and regional variations, SARIMA’s inability to account for such nuances may limit its ability to accurately capture disease dynamics. Although the SIR model offers a simpler representation with only three compartments and lacks demographic effects or control strategies crucial for realistic scenarios and accurate analysis, increasing model complexity does not always result in improved forecasting accuracy. Moreover, due to the lack of necessary data, it was not feasible to conduct a more complex analysis. For instance, the model could have included the disease-induced death rate if sufficient data on such cases were available. While these models perform well in short-term predictions, long-term forecasts may require hybrid methods. In addition, both SARIMA and SIR models assume the time independence of epidemiological parameters, an assumption that may not hold in reality and could lead to inaccuracies in predictions.
Conclusion
In conclusion, our study contributes to the general knowledge of TB transmission dynamics in Kazakhstan. The SARIMA model proved effective in capturing trends and forecasting TB occurrences, while the SIR model provided insights into the underlying dynamics of infection spread. Although further refinements are required, this analysis lays the foundation for more complex and crucial studies on TB transmission in Kazakhstan, thus developing public health strategies in the region.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
We express our gratitude to the entire staff at the Republican Center of Electronic Healthcare for their assistance in providing data and valuable consultancy throughout this study.
Author contributions
All authors have endorsed the finalized manuscript for submission and have collectively agreed to take personal responsibility for their contributions. A.Kal., S.Y. and Y.S.: conceptualization and methodology. A.Kal., S.Y. and Y.S.: software. Y.S., A.T., Sh.K., A.G. and A.Kash.: validation. A.Kal. and S.Y.: formal analysis. A.Kal. and S.Y.: resources and writing— original draft preparation. A.Kal., S.Y. and Y.S.: data curation. A.Kal., S.Y., Sh.K., A.G. and A.Kash.: writing—review and editing. A.Kash.: supervision, project administration, and funding acquisition.
Funding
This research is funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. BR24993094).
Data availability
The secondary data used for the study are available from the Republican Center for Electronic Health of the Ministry of Health of the Republic of Kazakhstan with restrictions applied. These data were used under license for this study and are not publicly available. Although, the data will be made available upon reasonable request from the corresponding author and with the permission of the Ministry of Health of the Republic of Kazakhstan.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Liao, C. M., Lin, Y. J. & Cheng, Y. H. Modeling the impact of control measures on tuberculosis infection in senior care facilities. Build. Environ. 59, 66–75 (2013). [Google Scholar]
- 2.World Health Organization. Global Tuberculosis Report 2017. (2017).
- 3.Floyd, K., Glaziou, P., Zumla, A. & Raviglione, M. The global tuberculosis epidemic and progress in care, prevention, and research: an overview in year 3 of the end TB era. Lancet Respir Med. 6, 299–314 (2018). [DOI] [PubMed] [Google Scholar]
- 4.World Health Organization. Global Tuberculosis Report 2020. (2020).
- 5.World Health Organization. WHO Global Lists of High Burden Countries for Tuberculosis (TB), TB/HIV and Multidrug/Rifampicin-Resistant TB (MDR/RR-TB), 2021–2025 Background Document. (2021).
- 6.Terlikbayeva, A. et al. Tuberculosis in Kazakhstan: analysis of risk determinants in national surveillance data. BMC Infect. Dis. 12 (2012). [DOI] [PMC free article] [PubMed]
- 7.Sakko, Y. et al. Epidemiology of tuberculosis in Kazakhstan: data from the Unified National Electronic Healthcare System 2014–2019. BMJ Open. 13 (2023). [DOI] [PMC free article] [PubMed]
- 8.Hermosilla, S. et al. Tuberculosis report among injection drug users and their partners in Kazakhstan. Public. Health 129, 569–575 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Stuckler, D., Basu, S., McKee, M. & King, L. Mass incarceration can explain population increases in TB and multidrug-resistant TB in European and central Asian countries. Proc. Natl. Acad. Sci. U S A 105, 13280–13285 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Unified platform of Internet resources of state bodies. The incidence of tuberculosis decreased by 2.3 times [Zabolevayemost’ tuberkulezom snizilas’ v 2,3 raza]. (2021). https://www.gov.kz/memleket/entities/almaty/press/news/details/164520?lang=ru
- 11.Houben, R. M. G. J. et al. How can mathematical models advance tuberculosis control in high HIV prevalence settings? Int. J. Tuberc. Lung Dis. 18, 509–514 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alfred, R. & Obit, J. H. The roles of machine learning methods in limiting the spread of deadly diseases: a systematic review. Heliyon 7 (2021). [DOI] [PMC free article] [PubMed]
- 13.Langat, A. K., Orwa, G. O. & Koima, J. Cancer cases in Kenya; forecasting incidents using Box & Jenkins Arima model. Biomedical Stat. Inf. 2, 37 (2017). [Google Scholar]
- 14.Anokye, R., Acheampong, E., Owusu, I. K. & Obeng, E. I. Time series analysis of malaria in Kumasi: using ARIMA models to forecast future incidence. Cogent Soc. Sci. 4, 1461544 (2018). [Google Scholar]
- 15.Anwar, M. Y., Lewnard, J. A., Parikh, S. & Pitzer, V. E. Time series analysis of malaria in Afghanistan: using ARIMA models to predict future trends in incidence. Malar. J. 15, (2016). [DOI] [PMC free article] [PubMed]
- 16.Cooper, I., Mondal, A. & Antonopoulos, C. G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals. 139, 110057 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ebhuoma, O., Gebreslasie, M. & Magubane, L. A. Seasonal Autoregressive Integrated moving average (SARIMA) forecasting model to predict monthly malaria cases in KwaZulu-Natal, South Africa. SAMJ South. Afr. Med. J. 108, 573 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Hethcote, H. W. The mathematics of Infectious diseases. Siam Rev. 42, 599–653 (2000). [Google Scholar]
- 19.About Kazakhstan. (2024). https://www.gov.kz/article/19305?lang=en
- 20.Gusmanov, A. et al. Review of the research databases on population-based registries of unified electronic Healthcare system of Kazakhstan (UNEHS): possibilities and limitations for epidemiological research and real-world evidence. Int. J. Med. Inf. 170, 104950 (2023). [DOI] [PubMed] [Google Scholar]
- 21.Box, G. E. P. & Jenkins, G. M. Time Series Analysis: Forecasting and Control. Revised Edition. Oakland: Holden-Day (1976).
- 22.Kermack, W. O. A. G. M. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 115, 1 (1927).
- 23.ReVelle, C., Lynn, W. R. & Feldmann, F. M. Mathematical models for the economic allocation of tuberculosis control activities in developing nations. PubMed. 96, 893–909 (1967). [DOI] [PubMed] [Google Scholar]
- 24.van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2, 288–303 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.In January-March. the population of the Republic of Kazakhstan increased by 1.5% - Statistics Agency [Za yanvar’-mart 2014 goda chislennost’ naseleniya RK uvelichilas’ na 1,5% - statagentstvo]. (2014). https://primeminister.kz/ru/news/za-janvar-mart-2014-goda-chislennost-naselenija-rk-uvelichilas-na-15-statagentstvo (2014).
- 26.Harjule, P., Tiwari, V. & Kumar, A. Mathematical models to predict COVID-19 outbreak: an interim review. J. Interdiscip. Math. 24, 259–284 (2021). [Google Scholar]
- 27.Ucakan, Y., Gulen, S. & Koklu, K. Analysing of Tuberculosis in Turkey through SIR, SEIR and BSEIR Mathematical models. Math. Comput. Model. Dyn. Syst. 27, 179–202 (2021). [Google Scholar]
- 28.Azizan, F. L., Sathasivam, S., Khan, M. & Ali, M. Study of transmission of tuberculosis by sir model using Runge-Kutta method (Kajian Transmisi Tuberkulosis Oleh Model SIR Menggunakan Kaedah Runge-Kutta). J. Qual. Meas. Anal. JQMA. 18, 13–28 (2022). [Google Scholar]
- 29.Side, S., Utami, A., Sukarna, S. & Pratama, M. I. Numerical solution of SIR model for transmission of tuberculosis by Runge-Kutta method. J. Phys. Conf. Ser. 1040, 12021 (2018). [Google Scholar]
- 30.Colijn, C., Cohen, T. & Murray, M. Mathematical models of tuberculosis: accomplishments and future challenges. BIOMAT. 1, 123–148. 10.1142/9789812708779_0008 (2006). [Google Scholar]
- 31.Garcia, D. A. Simple mathematics on COVID-19 expansion. medRxiv (Cold Spring Harbor Laboratory). 10.1101/2020.03.17.20037663 (2020). [Google Scholar]
- 32.Pei, H., Yan, G. & Huang, Y. N. Impact of contact rate on epidemic spreading in complex networks. Eur. Phys. J. B Condens. Matter Phys. (Print). 96, 1 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hethcote, H. W. Qualitative analyses of communicable disease models. Math. Biosci. 28, 335–356 (1976). [Google Scholar]
- 34.Aron, J. L. & Schwartz, I. B. Seasonality and period-doubling bifurcations in an epidemic model. J. Theor. Biol. 110, 1 (1984). [DOI] [PubMed] [Google Scholar]
- 35.Soetens, L. C., Boshuizen, H. C. & Korthals Altes, H. Contribution of seasonality in transmission of mycobacterium tuberculosis to seasonality in Tuberculosis disease: a simulation study. Am. J. Epidemiol. 178, 1 (2013). [DOI] [PubMed] [Google Scholar]
- 36.Augeraud-Véron, E. & Sari, N. Seasonal dynamics in an SIR epidemic system. J. Math. Biol. 68, 701–725 (2014). [DOI] [PubMed] [Google Scholar]
- 37.sklearn.metrics.mean_absolute_percentage_error. https://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_absolute_percentage_error.html
- 38.World Health Organization. Global Tuberculosis reports. https://www.who.int/teams/global-tuberculosis-programme/tb-reports.
- 39.Zheng, Y., Zhang, L., Wang, L. & Rifhat, R. Statistical methods for predicting tuberculosis incidence based on data from Guangxi, China. BMC Infect. Dis. 20, 1 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang, Y. et al. Temporal trends analysis of tuberculosis morbidity in mainland China from 1997 to 2025 using a new SARIMA-NARNNX hybrid model. BMJ Open. 9, 1 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Abildayev, T. S., Berikova, E. A., Baimukhanova, K. K. & Ismailova, A. T. Results of the implementation of anti-tuberculosis measures within the framework of the state program for the development of healthcare of the Republic of Kazakhstan Salamatty Kazakhstan[Rezul’taty realizatsii protivotuberkuleznykh meropriyatiy v ramkakh gosudarstvennoy programmy razvitiya zdravookhraneniya Respubliki Kazakhstan Salamatty Kazakstan]. Vestnik AGIUV[ASIPME Bulletin ] 4, 1 (2013).
- 42.Aringazina, A. et al. Awareness level of the population and key groups of the Republic of Kazakhstan in matters of tuberculosis. Nauka i Zdravookhranenie [Science Healthcare]. 23, 67–77 (2021). [Google Scholar]
- 43.Ayinla, A. Y., Othman, W. A. M. & Rabiu, M. A Mathematical Model of the tuberculosis epidemic. Acta Biotheor. 69 (2021). [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The secondary data used for the study are available from the Republican Center for Electronic Health of the Ministry of Health of the Republic of Kazakhstan with restrictions applied. These data were used under license for this study and are not publicly available. Although, the data will be made available upon reasonable request from the corresponding author and with the permission of the Ministry of Health of the Republic of Kazakhstan.