Abstract
The mechanical rock-crushing efficiency is directly influenced by rock properties and joint structure. Tipped-hob is widely used in the construction of shafts. By analyzing the motion of tipped-hob and the mechanical properties of granite and sandstone, numerical rock samples with different mechanical properties were built to investigate the influences of rock properties and joint structure on rock-crushing efficiency using a single ring of tipped cutter. The results revealed correlations between compressive strength, tensile strength, hardness, brittleness, specific energy consumption, and the vibration of thrusting forces. It was suggested that the spacing, dip angle, and continuity of joints have a significant impact on the failure patterns and crack propagation in the process of rock fragmentation, as well as on the vibration frequency and amplitude of breaking-force of cutter and the specific energy consumption. This research is crucial for controlling the stability of drilling machine during shaft sinking by drilling method.
Keywords: Tipped-hob of shaft drilling machine, Shaft sinking by drilling method, Motion characteristics of inserted teeth, Rock fragmentation, Discrete element method
Subject terms: Civil engineering, Computational methods
Introduction
With the increase in energy demand and the exhaustion of shallow resources, the construction of shafts has encountered an extremely complex deep geological environment with a yearly increase in the depth of mining1. In the exploitation of deep resources, mechanical drilling can not only significantly reduce the cost, but also prevent the occurrence of geologic disasters. Therefore, efficient mechanical drilling has become the primary problem in the exploitation of deep resources. Many scholars have suggested that rock properties are the most direct factors affecting drilling efficiency2,3. The tipped-hob is widely used in vertical drilling, because the discontinuous contact line can suffer a larger thrusting force, and the grooves between inserted teeth can facilitate the flow of rock chips for air flush drilling, as shown in Fig. 1.
Fig. 1.
The arrangement of tipped hobs.
Gong4 provided an overview of TBM tunnelling under adverse geological conditions and summarized tunnelling studies in mixed ground, fractured rock mass, highly stressed rock mass and limited boreability conditions. According to the literature, sufficient research has been conducted on rock fragmentation with a TBM disc cutter. However, there are few studies on the performance prediction of drilling machines using tipped-hob based on rock cutting tests5. Gong’s overview paper declares that TBM tunneling depends on the interaction between the cutter head and rock mass, and the rock mass properties are directly related to the rock breakage process by the cutters and excavation efficiency. Xue6 studied the influence of joint parameters (e.g., joint inclination, orientation, spacing, etc.) on the cutting force and rock fragmentation. This suggested that the influence of the joint orientation and spacing on the cutting force and rock fragmentation volume is obvious, and the propagation mode of cracks varies with respect to the joint orientation. The rock-breaking mechanism of tipped-hob is quite different from that of disc cutter. Therefore, more attention should be given to investigating the influences of rock properties and joints on the rock-crushing efficiency of tipped-hob.
Full-scale linear cutting tests, such as the studies of Pan7, Xu8, Li9, Ma10, Peng11, etc., have been proven to be reliable approaches for mechanical rock fragmentation investigations. Zhang12 proposed a design scheme for a disc cutter with surface grooves that has a discontinuous contact line with rock. It suggests that at the same penetration depth, the cutting force required by the grooved cutters is lower than that required by the conventional flat-top cutter, and the decrease in the rock chip volume is not significant. Thus, the rock-cutting specific energy is reduced. This is why the tipped-hob can withstand a greater thrusting force. Related research has irreplaceable importance in the performance estimation and optimization of mining machines, which makes it possible to realistically and reliably simulate cutting actions applied under different cutting conditions. Due to several difficulties, such as obtaining large blocks of rock samples, costly jobs, and laboratory facilities, it is sometimes not possible to perform physical cutting tests. Nevertheless, with the development of numerical methods, simulations have been introduced to model the rock fragmentation process, which can not only reduce the experimental cost, but also save time. The rock fragmentation mechanism and rock-breaking pattern between tipped-hob and disc cutter are certainly very different. The rock-breaking mechanism of tipped-hob is mainly impact breaking, while that of disc cutter is mainly cutting1.
Geng13 reported that the traditional finite element method (FEM) has some shortcomings in simulating the rock cutting process, and provided a new rock material definition strategy for FEM simulation of the rock breaking process by disc cutters. In recent years, the discrete element method (DEM) has been widely used in rock fragmentation research, such as in the studies of Li2, Xue6, Zou3 and Zhang14. Gong15,16 studied the effects of joint orientation and spacing on rock fragmentation by UDEC, and showed that the properties of joints have a conspicuous influence on crack propagation and debris morphology. Moon17 used the particle flow code (PFC) to simulate indentation experiments and investigated the optimal configuration of cutter spacing and penetration. The above papers not only prove the importance of numerical studies in rock fragmentation research, but also prove their feasibility. The process of rock fragmentation is characterized by discontinuous failure, and only discrete elements can accurately depict the fracture state of rock. The numerical study of this paper is aimed at the rock fragmentation process of the tipped-hob using the discrete element method.
Investigating the effects of mechanical properties on rock fragmentation
The compressive strength and elastic modulus of rock are considered to be most closely related to the drillability of rocks18, but the indentation hardness, fracture toughness and brittleness have not been deeply researched in rock fragmentation3,19. This is because there is no unified standard for their definition20,21, and on the other hand, it is difficult to obtain rock samples with specific indexes in physical experiment analysis. Liu22 suggested a close relationship between the brittleness and failure patterns of rock. Therefore, studying the correlation between the hardness, fracture toughness, and brittleness of rocks and rock-breaking effects using tipped-hob is highly important. To obtain rock with different indexes, the numerical samples generated by the DEM are very convenient. Xu23, Liu24 and Yang25 studied the process of rock-breaking using DEM, and the correlation between the micro-parameters of numerical samples and macro-structures was also investigated. Their research suggested that the micro-parameters, namely, the elasticity modulus and stiffness ratio, have a marked impact on the elasticity modulus of rock samples, the micro-parameter stiffness ratio has a marked impact on Poisson’s ratio, and the micro-parameters, namely, the compressive strength, cohesion strength, elasticity modulus and stiffness ratio, have a marked impact on the uniaxial compressive strength (UCS) and Brazilian tensile strength (BTS) of rock samples. Moreover, the change in the stiffness ratio can be modelled numerically with different tensile-to-compressive strength ratios.
Calculation of rock models with different rock properties
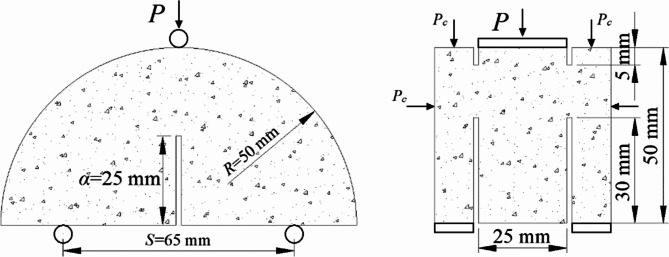
Among the mechanical properties of rocks, tensile strength and compressive strength are the most widely used variables and are often used as the calculation variables of other indexes. In accordance with Deere and Miller’s engineering rock classification19,26, numerical models of granite and sandstone rocks with different macro-parameters were obtained by changing the ratio of cohesion to compressive strength of discrete elements. In this paper, for indentation hardness testing, a spherical indenter with a radius of 2.5 mm was used. The different brittleness levels of rocks can be calculated according to Liu’s research22, as shown in Table 1.  is the UCS,
is the UCS,  is the BTS. The suggested testing models of the Type I and Type II fracture toughness of the International Society for Rock Mechanics (ISRM) are shown in Fig. 227,28. In the calculation of the fracture toughness KII, the servo pressure is set to 5 MPa, the unit of force P is kN, the unit of pressure Pc is MPa, and the unit of fracture toughness is MPa m0.5 according to the suggestions of the ISRM.
is the BTS. The suggested testing models of the Type I and Type II fracture toughness of the International Society for Rock Mechanics (ISRM) are shown in Fig. 227,28. In the calculation of the fracture toughness KII, the servo pressure is set to 5 MPa, the unit of force P is kN, the unit of pressure Pc is MPa, and the unit of fracture toughness is MPa m0.5 according to the suggestions of the ISRM.
Table 1.
The calculation formula for the brittleness, toughness and hardness of rock.
| Brittleness indexes | Fracture toughness indexes | Hardness index |
|---|---|---|

|

|
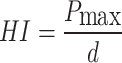
|

|

|
|

|

|
Fig. 2.
The testing models of KIC and KIIC in ISRM.
After a series of common mechanical tests of granite and sandstone were conducted, the micro-parameters of granite and sandstone were calculated according to their mechanical parameters using the trial and error method (Fig. 3), as shown in Table 2. The difference ratio is controlled by ± 5.9%, as shown in Table 3. In the study of micro-parameter calculations, the ratios of the element bond cohesion strength to the element bond tensile strength clearly influence the ratio of the tensile strength to the compressive strength of the numerical rock models. Therefore, different rock models were tested built by changing the ratio coefficients  and
and  of cohesion to the tensile strength of the discrete element model. In addition to the original model parameters of 2.37 and 3.46, the ratios of the other numerical models are set to 1.5 and 4.0. On the basis of the numerical models, the UCS, BTS, HI, KIC, and KIIC are calculated.
of cohesion to the tensile strength of the discrete element model. In addition to the original model parameters of 2.37 and 3.46, the ratios of the other numerical models are set to 1.5 and 4.0. On the basis of the numerical models, the UCS, BTS, HI, KIC, and KIIC are calculated.
Fig. 3.
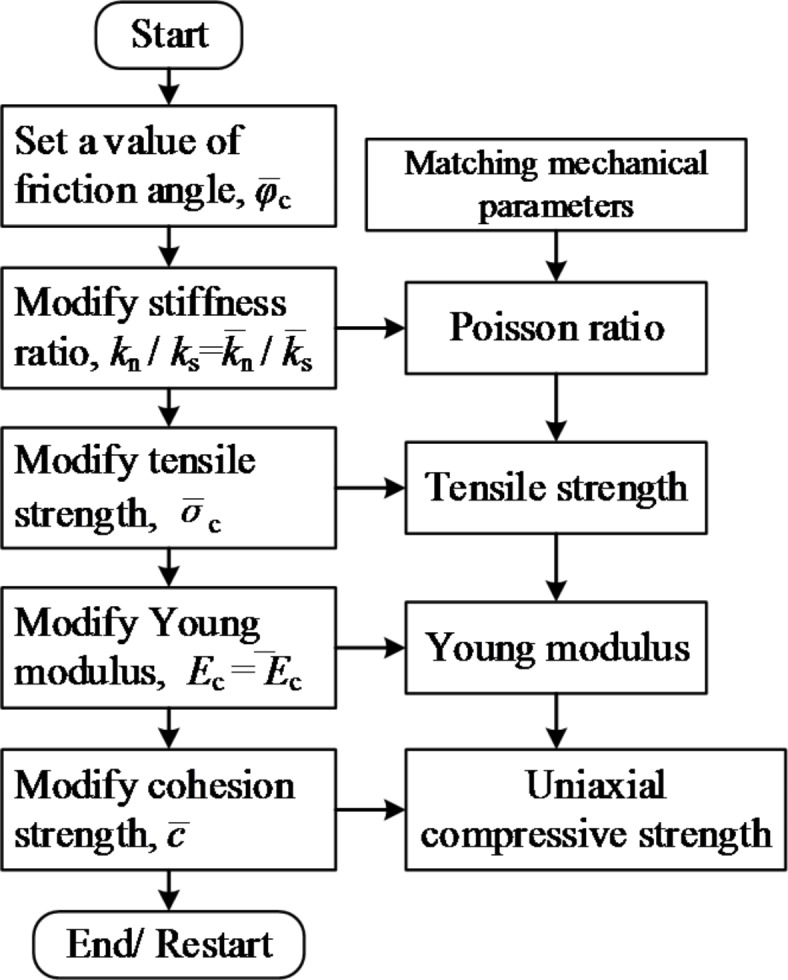
Trial and error tests to match the mechanical parameters.
Table 2.
The micro-parameters of the numerical models of granite and red sandstone.
| Micro-Parameters | Granite | Sandstone |
|---|---|---|
Minimum particle size,  /mm /mm |
0.60 | 0.60 |
Ratio of maximum particle size to minimum particle size, 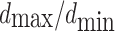
|
1.66 | 1.66 |
Porosity ratio 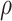
|
0.06 | 0.06 |
| Coordination number, N | 4.00 | 4.00 |
Effective modulus of particle and bond, 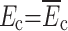 / GPa / GPa |
53.20 | 15.70 |
Ratio of normal to shear stiffness of particle and bond, 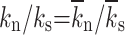
|
2.26 | 2.77 |
Element bond tensile strength,  /MPa /MPa |
22.15 | 8.57 |
Element bond cohesion strength,  /MPa /MPa |
52.40 | 29.65 |
Local friction angle,  /° /° |
15.00 | 25.00 |
| Residual friction coefficient, µ | 0.30 | 0.30 |
Table 3.
Comparison of results obtained from numerical and experimental tests.
| Classification | E/ GPa | v | UCS/ MPa | BTS/ MPa | c/ MPa | φ/ ° |
|---|---|---|---|---|---|---|
| Experiment | 49.42 | 0.189 | 101.35 | 10.27 | 25.42 | 36.7 |
| Modelling | 49.5 | 0.19 | 101.0 | 10.5 | 24.1 | 39 |
| Difference | -0.16 | -0.53% | 0.35 | -2.19% | 5.48 | -5.90% |
| Experiment | 13.69 | 0.216 | 52.98 | 3.35 | 12.07 | 41.2 |
| Modelling | 13.8 | 0.22 | 52.4 | 3.4 | 11.9 | 41 |
| Difference | -0.80 | -1.82% | 1.11 | -1.47% | 1.43% | 0.49% |
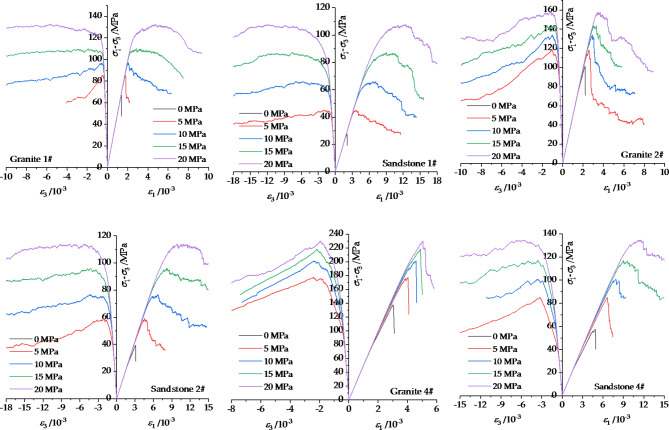
The compressive stress-strain curves of each model are shown in Fig. 4. With increasing ratio coefficients  and
and  , the UCS and Type II fracture toughness increase. The BTS, hardness and Type I fracture toughness remain approximately the same because the tensile strength of the element does not change. Moreover, with increasing confining pressure, the brittleness increased, especially for granite. As shown in Figs. 5, 6 and 7. This suggested that there is a good linear relationship between the UCS and KIIC, and the correlation between BTS and KIC is very high. With the increase in the ratio coefficients
, the UCS and Type II fracture toughness increase. The BTS, hardness and Type I fracture toughness remain approximately the same because the tensile strength of the element does not change. Moreover, with increasing confining pressure, the brittleness increased, especially for granite. As shown in Figs. 5, 6 and 7. This suggested that there is a good linear relationship between the UCS and KIIC, and the correlation between BTS and KIC is very high. With the increase in the ratio coefficients  and
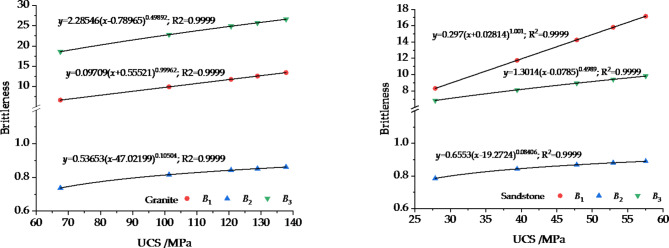
and  , all the brittleness indexes increase. Figures 8 and 9 indicated that parameters B1 and B3 change in a relatively large range, which can directly reflect the degree of brittleness. For the sandstone model, the sensitivity of B1 is greater than that of B3. Therefore, in the follow-up brittleness correlation analysis, the corresponding brittleness index B1 is considered.
, all the brittleness indexes increase. Figures 8 and 9 indicated that parameters B1 and B3 change in a relatively large range, which can directly reflect the degree of brittleness. For the sandstone model, the sensitivity of B1 is greater than that of B3. Therefore, in the follow-up brittleness correlation analysis, the corresponding brittleness index B1 is considered.
Fig. 4.
Some compression tests of rock models with different micro-parameters.
Fig. 5.

The relationship between UCS and ratio  and
and 
Fig. 6.
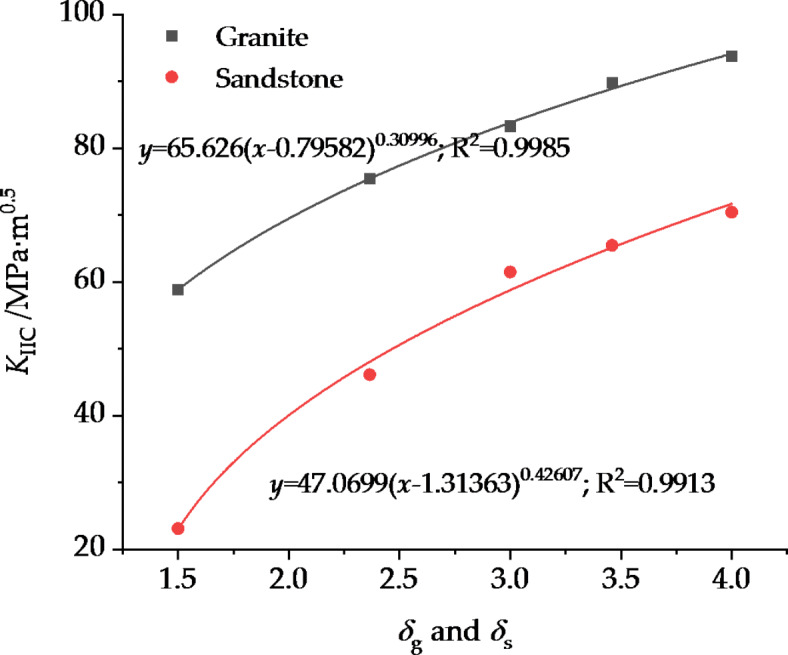
The relationship between KIIC and  and
and 
Fig. 7.
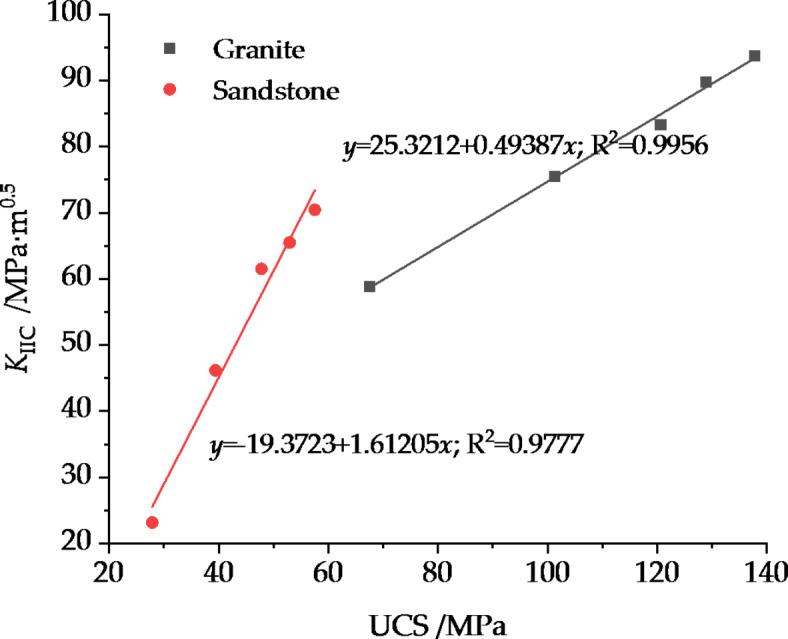
The relationship between UCS and KIIC
Fig. 8.
The relationship between brittleness and UCS.
Fig. 9.
The relationship between brittleness and KIIC
The strength theory of rock has always been a hot topic and foundation problem in the study of rock failure, and the strength criterion without considering the middle principal stress is in favour of safety. A biaxial numerical compression test is carried out to analyse the strength criterion to which the numerical model conforms. The confining pressure conditions of biaxial compression numerical tests are set to 5, 10, 15 and 20 MPa. The common rule of rock strength mainly includes the M-C strength criterion ( ), H-B strength criterion (
), H-B strength criterion ( ), generalized H-B strength criterion (
), generalized H-B strength criterion (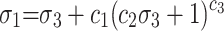 ), exponential strength criterion (
), exponential strength criterion (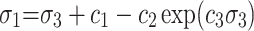 ) and Rocker strength criterion (
) and Rocker strength criterion ( ). The parameters of ci are constant coefficients. The strength fitting curves of several models are shown in Fig. 10, which indicate that the generalized Hawke-Brown strength criterion has the best applicability in this group of models.
). The parameters of ci are constant coefficients. The strength fitting curves of several models are shown in Fig. 10, which indicate that the generalized Hawke-Brown strength criterion has the best applicability in this group of models.
Fig. 10.
The fitting results of rock models with different strength criterion.
Analysis of the mechanical parameters and fragmentation parameters
According to the above numerical models of granite and sandstone, a pure rolling crushing model of multi-tooth hob is established to study the correlation between different lithologies and rock crushing behavior. In this group of numerical studies, to eliminate the influence of crushing parameters and other factors, a single-ring of 15-inch hob with 30 teeth is selected, the linear speed is set to 1.0 m/s, the corresponding coupling rotation speed in the pure rolling mode is 5 rad/s, and the crushing depth is 3 mm. In addition to the abovementioned thrusting load and the fracture development state of the rock models, the pixel ratio method was proposed to calculate the equivalent particle size and cumulative gradation curve of broken cuttings29. The formula for calculating the equivalent particle size 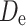 is calculated by
is calculated by  , where n is the number of particles in each cutting,
, where n is the number of particles in each cutting,  is the average particle size (0.798 mm), and ρ is the mesoscale void ratio of the model. To meet the basic model size requirements and not reduce the computational efficiency, a numerical model was built with a width of 240 mm and a height of 160 mm, and the model boundary size with a thickness of 80 mm was increased.
is the average particle size (0.798 mm), and ρ is the mesoscale void ratio of the model. To meet the basic model size requirements and not reduce the computational efficiency, a numerical model was built with a width of 240 mm and a height of 160 mm, and the model boundary size with a thickness of 80 mm was increased.
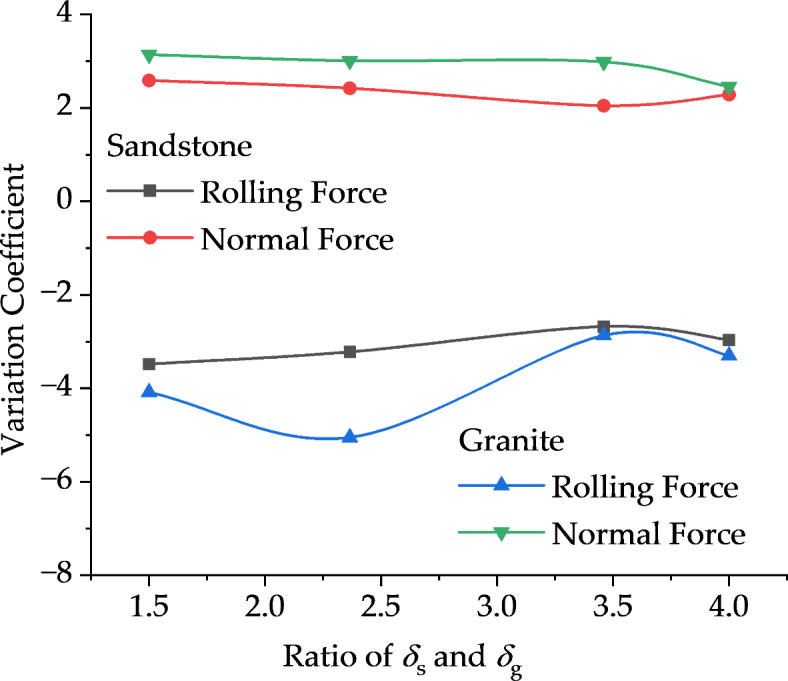
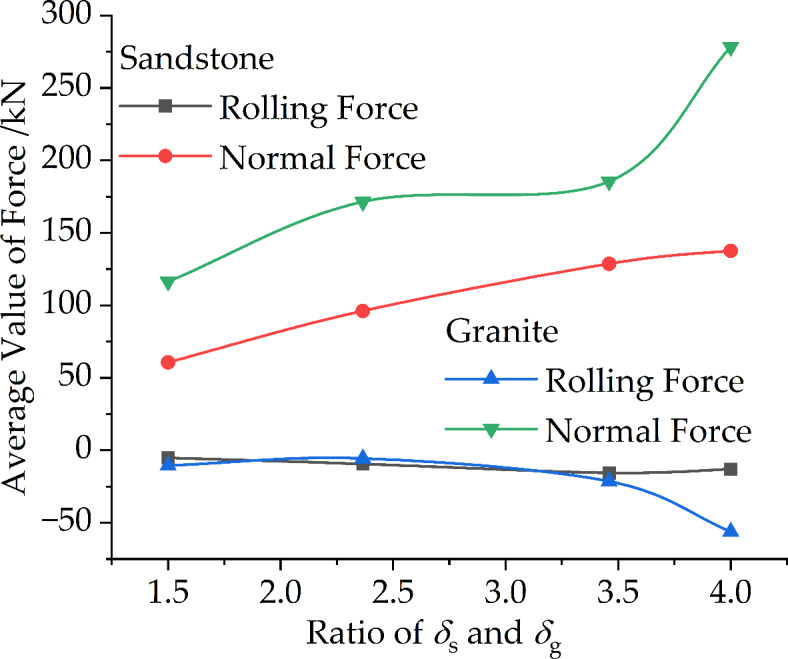
Some simulation results of rolling impact rock-breaking of models with a single ring inserted tooth cutter are shown in Table 4. Figure 11 shows that the variation coefficients of the breaking-force have no obvious change trend. The specific energy consumption (SE) of sandstone initially increases and then decreases with increasing strength proportional coefficient, while the SE of granite increases monotonically, as shown in Fig. 12. Figure 13 shows that the average value of the normal force increases with increasing strength ratio coefficient, while the rolling force has no obvious change trend. In the process of rolling rock-breaking, the response steps of the rolling force and normal force are the same. The number of tensile failure microcracks is generally greater than that of shear failure microcracks, indicating that the failure is mainly tensile failure, and the ratio of the number of tensile failure cracks to shear failure cracks tends to increase. This suggests that the average value and variation coefficient of the rolling force are closely related to the tensile strength, while the normal force is closely related to the compressive strength. Figure 14 shows that there is no obvious change in the maximum equivalent particle size, but regardless of which model is used, the equivalent particle size of most of the broken particles is between 1.25 and 7.5 mm.
Table 4.
Some fragmentation results of sandstone and granite using a single-ring tipped-hob.
Fig. 11.
The variation coefficient of rolling force and normal force.
Fig. 12.

The relationship between SE and strength ratio coefficient.
Fig. 13.
The mean of rolling force and normal force of cutter.
Fig. 14.
The cumulative distribution curve rock fragment of sandstone rocks.
The analysis of Figs. 15, 16, 17 and 18 shows the correlation between the lithology parameters and crushing parameters of the above rock numerical models. In summary, the analysis shows that the dimensionless specific energy consumption SE/UCS is positively correlated with the brittleness parameter B1 and fracture toughness KIIC, and in the case of similar fracture toughness KIIC, the specific energy consumption of the sandstone model is greater than that of granite model. With increasing brittleness parameter B1, the variation coefficient of the normal force decreases, while the variation coefficient of rolling force increases. Moreover, the average rolling load does not change when the fracture toughness KIIC is less than 85, but the normal load increases significantly. The average value of the normal force is more sensitive to the change in KIIC than the change in the rolling force and increases exponentially. The crushing behavior of rock is affected by rock physical and mechanical properties, geological environmental conditions and rock breaking parameters of the rock, but these parameters do not respond independently, and a certain or a group of parameters cannot completely describe the crushing behavior of rock.
Fig. 15.

The relationship between  and dimensionless SE.
and dimensionless SE.
Fig. 16.
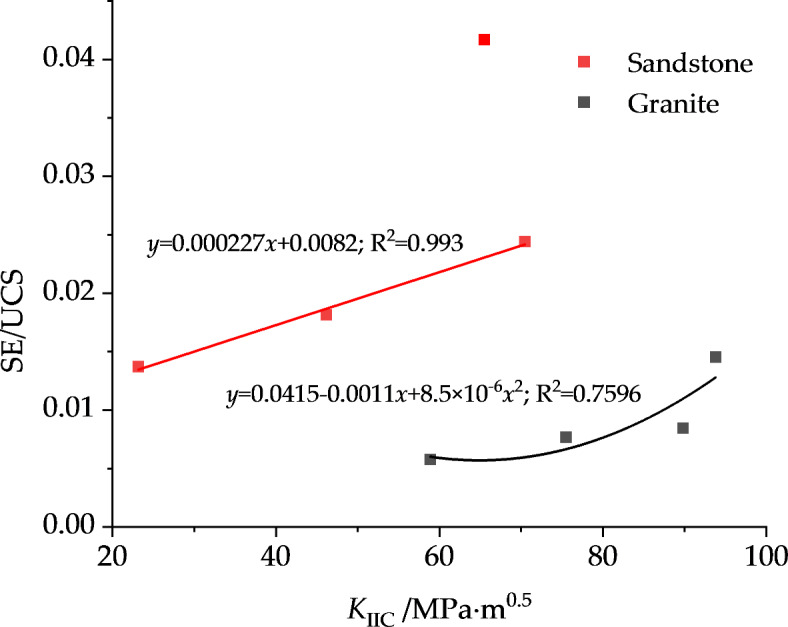
The relationship between  and dimensionless SE.
and dimensionless SE.
Fig. 17.

The relationship between 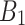 and the variation coefficient of breaking forces
and the variation coefficient of breaking forces
Fig. 18.

The relationship between 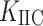 and the mean of breaking forces
and the mean of breaking forces
Investigating the effects of joints on rock fragmentation
Engineering practices suggest that joints in rock are important factors affecting the physical and mechanical properties of rock, and they cannot be ignored in engineering practice. The characteristics of joints mainly include joint spacing, dip angle, roughness, flatness, filler, opening, extension distance, continuity and occurrence, among which spacing and dip angle are the most significant factors affecting rock breaking behavior25. This section studies the influence of the dip angle and spacing of joints and the rock-bridge ratio on the rock breaking behavior of a single-ring hob. To define the above joint factors, a rock model of discontinuous joints with rock-bridges is built, in which the parameters lq and lc are the length of the discontinuous fracture and the length of the rock bridge between the fractures, respectively; the parameter lj is the distance between the joints; and θ is the dip angle of the fracture. The numerical rock samples are established with the original model parameters in Table 2, and the friction coefficient of the joints is set to 0.35. The designs of the orthogonal tests are shown in Table 5.
Table 5.
Design of the orthogonal experimental scheme for the investigation of joint parameters.
| NO. | lj/mm | θ/° | lc/lq | The graphic description |
|---|---|---|---|---|
| T1 | 40 | 15 | 0.5 |

|
| T2 | 40 | 45 | 2 | |
| T3 | 40 | 75 | 1 | |
| T4 | 60 | 15 | 2 | |
| T5 | 60 | 45 | 1 | |
| T6 | 60 | 75 | 0.5 | |
| T7 | 80 | 15 | 1 | |
| T8 | 80 | 45 | 0.5 | |
| T9 | 80 | 75 | 2 |
Influence of joints on granite rock breaking behavior
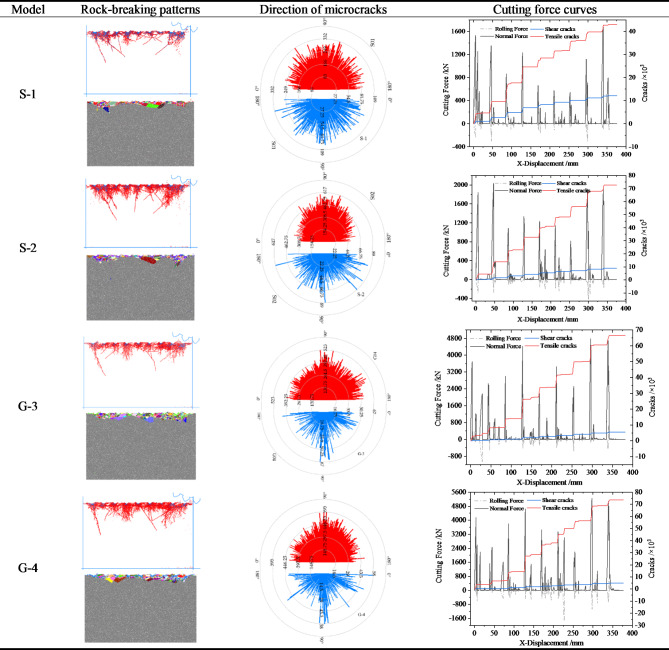
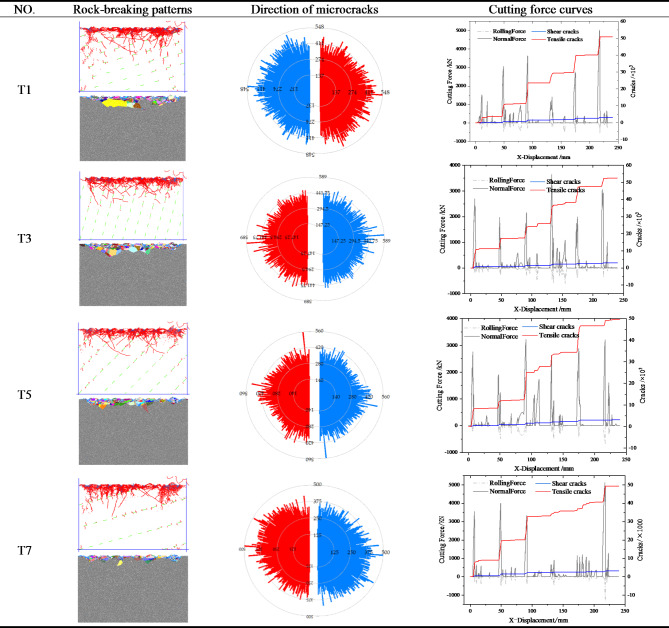
Some numerical results of granite rock crushing are shown in Table 6. The crushing crack tends to propagate to the tip of the joint, most of the cracks are truncated when they extend to the position of the joint, and wing cracks appear at the tip of the intermittent joint. According to the image of the broken mode, the formation of the broken rock block will be truncated to the joint position, and the azimuth distribution of the shear crack will be greatly affected by the joint. The dip angle of the joint has a great influence on the path of the fracture extending to the depth of the rock model, and its extension to the joint position will be truncated, and then further extended to the depth from the end of the discontinuous joint; however, the direction of expansion is related to the dip angle of the joint.
Table 6.
The results of the granite rock models with joints.
According to the results in Tables 7 and 8, the influence sequence of the joint characteristics on the variation coefficient of the breaking-force is θ > lc/lq > lj, and that on the special energy consumption is lj > θ > lc/lq. The dynamic response of the normal breaking-force to the joint characteristics is not significant, while the variation coefficient of the rolling breaking-force is positively correlated with lc/lq, negatively correlated with lj, and first increases and then decreases with θ, as shown in Fig. 19. The special energy consumption is positively correlated with lj and has an extreme value with increasing lc/lq and θ, as shown in Fig. 20.
Table 7.
The variation coefficient of the rock-breaking force in the cutting tests.
| Type | NO. | lj/ mm | θ/ ° | lc / lq |

|
|
|---|---|---|---|---|---|---|
| Normal rock-breaking force | Rolling rock-breaking force | |||||
| Design of the orthogonal experimental scheme | 1 | 40 | 15 | 0.5 | 2.8107 | 2.9462 |
| 2 | 40 | 45 | 2 | 1.9061 | 22.4013 | |
| 3 | 40 | 75 | 1 | 2.4470 | 2.5792 | |
| 4 | 60 | 15 | 2 | 2.6184 | 5.5525 | |
| 5 | 60 | 45 | 1 | 2.3556 | 3.9159 | |
| 6 | 60 | 75 | 0.5 | 2.7480 | 3.4356 | |
| 7 | 80 | 15 | 1 | 2.8904 | 4.5466 | |
| 8 | 80 | 45 | 0.5 | 2.2041 | 4.1702 | |
| 9 | 80 | 75 | 2 | 2.2108 | 2.9227 | |
| normal rock-breaking force |

|
2.3879 | 2.7732 | 2.5876 | 22.1911 | / |

|
2.5740 | 2.1553 | 2.5643 | |||

|
2.4351 | 2.4686 | 2.2415 | |||
| R | 0.1861 | 0.6179 | 0.3425 | / | / | |
| Optimal level | 40 | 45 | 2 | / | / | |
| rolling rock-breaking force |

|
9.3089 | 4.3484 | 3.5173 | / | 52.4702 |

|
4.3013 | 10.1625 | 3.6806 | |||
|
3.8798 | 2.9792 | 10.2922 | |||
| R | 5.4291 | 7.1833 | 6.7748 | / | / | |
| Optimal level | 80 | 75 | 0.5 | / | / | |
Table 8.
The energy analysis of the rolling breaking-force in the cutting tests.
| NO. | lj/ mm | θ/ ° | lc / lq | SE/ 105N·m |
|---|---|---|---|---|
| 1 | 40 | 15 | 0.5 | 21.5175 |
| 2 | 40 | 45 | 2 | 20.8915 |
| 3 | 40 | 75 | 1 | 25.2405 |
| 4 | 60 | 15 | 2 | 30.8208 |
| 5 | 60 | 45 | 1 | 39.4526 |
| 6 | 60 | 75 | 0.5 | 22.1559 |
| 7 | 80 | 15 | 1 | 45.6146 |
| 8 | 80 | 45 | 0.5 | 66.0607 |
| 9 | 80 | 75 | 2 | 48.3156 |

|
22.5498 | 32.6510 | 36.5780 | 320.0697 |

|
30.8110 | 42.1349 | 36.7692 | |
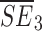
|
53.3303 | 31.9040 | 33.3426 | |
| R | 30.7805 | 10.2309 | 3.4266 | / |
| Optimal level | 40 | 75 | 2 | / |
Fig. 19.
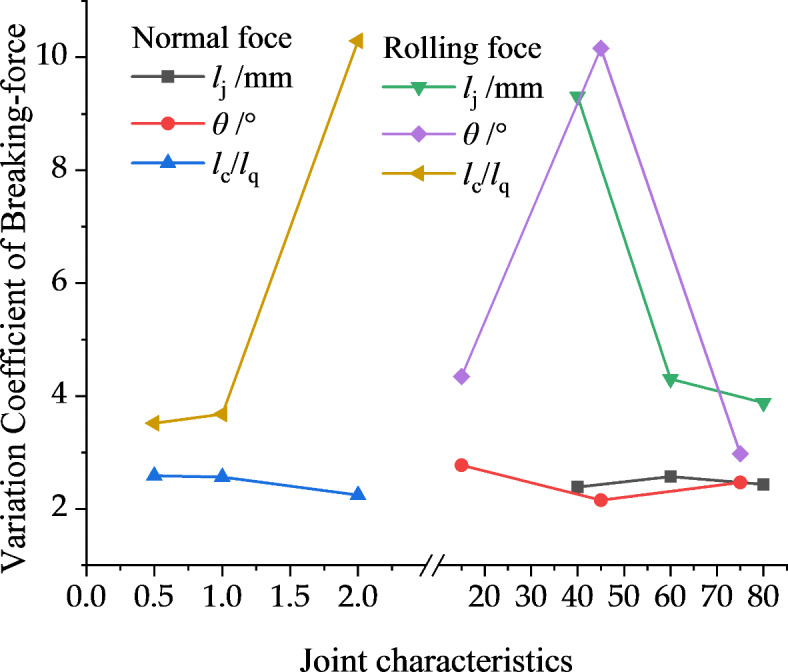
The relationship between joint characteristics and variation coefficient of breaking-force.
Fig. 20.
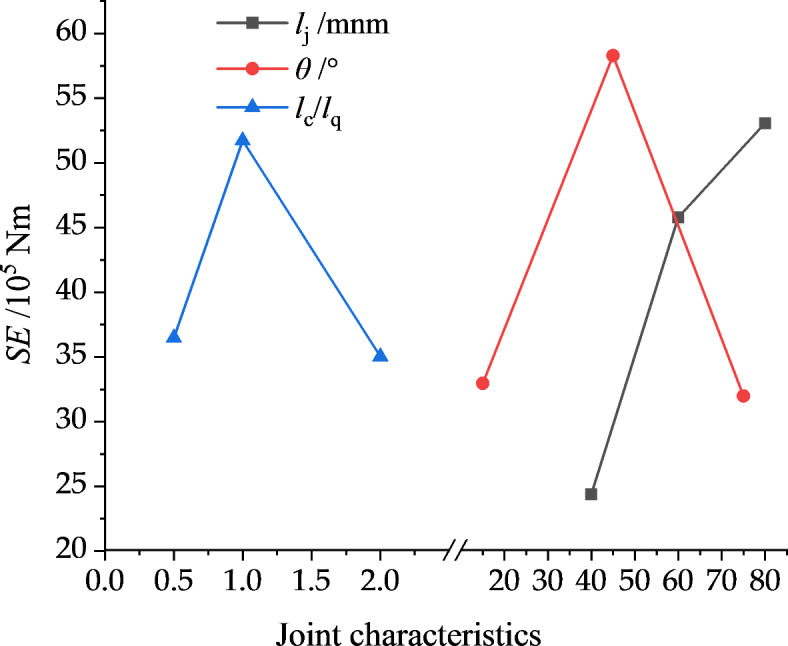
The relationship between joint characteristics and specific energy consumption.
Influence of joints on sandrock breaking behavior
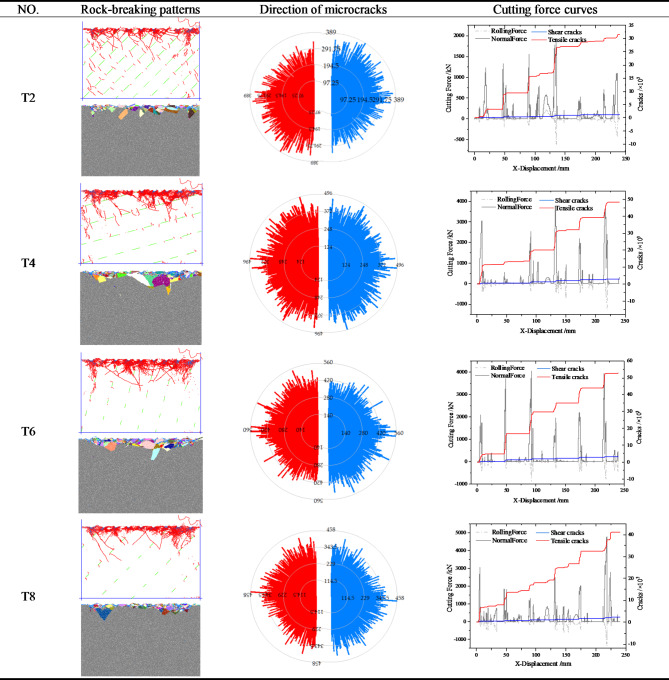
Some numerical results of sandstone crushing are shown in Table 9. The promoting effect of joints on rock fragmentation becomes weaker with the increasing joint spacing. The fracture extending to the deep part of the surrounding rock is mainly divided into two parts: one is nearly parallel to the joint direction between the joints, and the other extends across the joint in the direction nearly perpendicular to the joint. The cumulative number growth law of microcracks shows the same frequency characteristics as the fluctuation law of the breaking-force. The simulation results of the granite models show the same variation pattern, and the special energy consumption increases with increasing lj, and has extreme values for both θ and lc/lq.
Table 9.
The results of rock models with continuous joints.
According to the results in Tables 10 and 11, the influence sequence of the joint characteristics on the variation coefficient of the breaking-force is θ > lc/lq > lj, and that on the special energy consumption is lj > θ > lc/lq. The dynamic response of the normal breaking-force to the joint characteristics is not significant, while the variation coefficient of the rolling breaking-force is positively correlated with lc/lq, negatively correlated with lj, and first increases and then decreases with θ, as shown in Fig. 21. The special energy consumption is positively correlated with lj and has an extreme value with increasing lc/lq and θ, as shown in Fig. 22. The results show that the calculation results of granite and sandstone are the same.
Table 10.
The variation coefficient of the normal rock-breaking force in the cutting tests.
| Type | NO. | lj/ mm | θ/ ° | lc / lq |

|
|
|---|---|---|---|---|---|---|
| Normal rock-breaking force | Rolling rock-breaking force | |||||
| Design of the orthogonal experimental scheme | 1 | 40 | 15 | 0.5 | 2.8105 | 2.9461 |
| 2 | 40 | 45 | 2 | 1.9061 | 22.4014 | |
| 3 | 40 | 75 | 1 | 2.4470 | 2.5792 | |
| 4 | 60 | 15 | 2 | 2.6184 | 5.5525 | |
| 5 | 60 | 45 | 1 | 2.3556 | 3.9159 | |
| 6 | 60 | 75 | 0.5 | 2.7481 | 3.4356 | |
| 7 | 80 | 15 | 1 | 2.8904 | 4.5466 | |
| 8 | 80 | 45 | 0.5 | 2.2041 | 4.1703 | |
| 9 | 80 | 75 | 2 | 2.2108 | 2.9227 | |
| Normal rock-breaking force |

|
2.3879 | 2.7731 | 2.5876 | 22.1910 | / |

|
2.5740 | 2.1553 | 2.5643 | |||
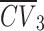
|
2.4351 | 2.4686 | 2.2451 | |||
| R | 0.1862 | 0.6178 | 0.3425 | / | / | |
| Optimal level | 40 | 45 | 2 | / | / | |
| Rolling rock-breaking force |

|
9.3089 | 4.3484 | 3.5173 | / | 52.4703 |

|
4.3013 | 10.1625 | 3.6806 | |||
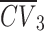
|
3.8799 | 2.9792 | 10.2922 | |||
| R | 5.4290 | 7.1834 | 6.7749 | / | / | |
| Optimal level | 80 | 75 | 0.5 | / | / | |
Table 11.
The energy analysis of the rolling force in the cutting tests.
| NO. | lj/ mm | θ/ ° | lc / lq | SE /105N·m |
|---|---|---|---|---|
| 1 | 40 | 15 | 0.5 | 21.5189 |
| 2 | 40 | 45 | 2 | 26.3473 |
| 3 | 40 | 75 | 1 | 25.2871 |
| 4 | 60 | 15 | 2 | 30.9557 |
| 5 | 60 | 45 | 1 | 83.4827 |
| 6 | 60 | 75 | 0.5 | 22.9102 |
| 7 | 80 | 15 | 1 | 46.4217 |
| 8 | 80 | 45 | 0.5 | 65.0329 |
| 9 | 80 | 75 | 2 | 47.7773 |

|
24.3844 | 32.9654 | 36.4873 | 369.7338 |
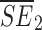
|
45.7829 | 58.2876 | 51.7305 | |

|
53.0773 | 31.9915 | 35.0268 | |
| R | 28.6929 | 26.2961 | 16.7037 | |
| Optimal level | 40 | 75 | 2 |
Fig. 21.
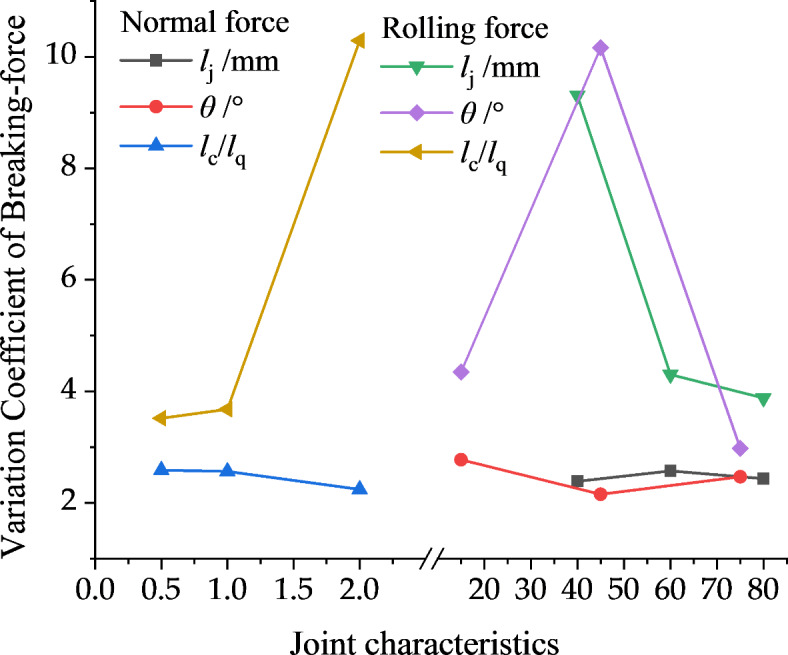
The relationship between joint characteristics and variation coefficient of breaking-force.
Fig. 22.

The relationship between joint characteristics and specific energy consumption.
Conclusions
Several sets of numerical rock models with different properties are obtained through the calibrated macro-parameters of granite and sandstone prototypes. This approach provides an effective method for analysing the correlation between the above indexes and the rock breaking effect of an inserted tooth hob. The main conclusions are as follows:
The analysis of the lithologic parameters of the model reveals a strong correlation between UCS and type II fracture toughness, as well as between BTS and type I fracture toughness. Among various brittleness indexes, the brittleness description parameters B1 and B3 are more suitable for brittleness analysis. In comparison with the fitting results, the generalized Hawke-Brown strength criterion demonstrates the best applicability in this group of models.
The average normal force increases with an increasing strength ratio coefficient. The vibration response steps of the rolling and normal force are identical. The number of tensile-failure microcracks exceeds that of shear-failure microcracks, indicating predominant tensile failure. Additionally, the ratio of tensile failure cracks to shear failure cracks increases with an increasing strength ratio coefficient. While the variation coefficient of sandstone model’s breaking force remains relatively stable with an increasing strength ratio coefficient, high-strength granite exhibits clear fluctuations in rolling breaking-force, highlighting its sensitivity to lithology in hard rock breaking scenarios.
The SE increases as UCS and brittleness B3 increase, the dimensionless SE/UCS is positively correlated with the brittleness B1 and fracture toughness KIIC. When the fracture toughness approaches KIIC, the SE of sandstone exceeds that of granite. Increasing B1 leads to a slight decrease in the variation coefficient of normal force, while it slightly increases for rolling force. The average rolling force remains relatively unchanged, while the normal force increases slightly. The average normal force is more sensitive to changes in KIIC, and exhibits an exponential growth pattern. Additionally, the difference coefficient is relatively constant.
The analysis results of the discontinuous joints indicate that the proportion of discontinuous in the joints significantly influences crack propagation. The crack propagation to the joint position will be limited, making wing cracks more likely to occur at the tips of the joints. Additionally, the azimuth distribution of the shear failure microcrack is greatly affected by the joint. Both the maximum load for crack initiation and the corresponding invasion are heavily influenced by joint characteristics.
Acknowledgements
The authors gratefully acknowledge the financial support from the Engineering Research Center of Underground Mine Construction, Ministry of Education (Anhui University of Science and Technology) (JYBGCZX2022102), the Anhui Key Laboratory of Mining Construction Engineering (Anhui University of Science and Technology) (GXZDSYS2022105) and the Scientific Research Foundation for High-level Talents of Anhui University of Science and Technology (2020136).
Author contributions
P.P.X. and J.Q.Z. wrote the main manuscript text. X.H. and J.Q.Z. carried out formal analysis and supervision. P.P.X. and J.H.H. prepared all figures. All authors reviewed the manuscript.
Data availability
All data generated or analysed during this study are included in this published article.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Zou, J., Yang, W., Zhang, T., Wang, X. & Gao, M. Experimental investigation on hard rock fragmentation of inserted tooth cutter using a newly designed indentation testing apparatus. Int. J. Min. Sci. Technol. 10.1016/j.ijmst.2022.02.002 (2022). [Google Scholar]
- 2.Xuefeng, L., Shibo, W., Shirong, G., Malekian, R. & Zhixiong, L. Investigation on the influence mechanism of rock brittleness on rock fragmentation and cutting performance by discrete element method. Meas. J. Int. Meas. Confed 113, 120–130 (2018). [Google Scholar]
- 3.Zou, J., Yang, W. & Han, J. Discrete element modeling of the effects of cutting parameters and Rock properties on Rock Fragmentation. IEEE Access. 8, 136393–136408 (2020). [Google Scholar]
- 4.Gong, Q., Yin, L., Ma, H. & Zhao, J. TBM tunnelling under adverse geological conditions: an overview. Tunn. Undergr. Sp Technol. 57, 4–17 (2016). [Google Scholar]
- 5.Shaterpour-Mamaghani, A. et al. Full-scale linear cutting tests using a button cutter and deterministic performance prediction modeling for raise boring machines. Tunn. Undergr. Sp Technol. 127, 104609 (2022). [Google Scholar]
- 6.Xue, Y., Zhou, J., Liu, C., Shadabfar, M. & Zhang, J. Rock fragmentation induced by a TBM disc-cutter considering the effects of joints: a numerical simulation by DEM. Comput. Geotech. 136, 104230 (2021). [Google Scholar]
- 7.Pan, Y., Liu, Q., Liu, J., Liu, Q. & Kong, X. Full-scale linear cutting tests in Chongqing Sandstone to study the influence of confining stress on rock cutting efficiency by TBM disc cutter. Tunn. Undergr. Sp Technol. 80, 197–210 (2018). [Google Scholar]
- 8.Xu, H., Geng, Q., Sun, Z. & Qi, Z. Full-scale granite cutting experiments using tunnel boring machine disc cutters at different free-face conditions. Tunn. Undergr. Sp Technol. 108, 103719 (2021). [Google Scholar]
- 9.Li, B. et al. Full-scale linear cutting tests to study the influence of pre-groove depth on rock-cutting performance by TBM disc cutter. Tunn. Undergr. Sp Technol. 122, 104366 (2022). [Google Scholar]
- 10.Ma, H., Gong, Q., Wang, J., Yin, L. & Zhao, X. Study on the influence of confining stress on TBM performance in granite rock by linear cutting test. Tunn. Undergr. Sp Technol. 57, 145–150 (2016). [Google Scholar]
- 11.Peng, X. et al. Study on the influence of different control modes on TBM Disc Cutter performance by Rotary cutting tests. Rock. Mech. Rock. Eng. 51, 961–967 (2018). [Google Scholar]
- 12.Zhang, M., Gou, B., Mo, J., Duan, W. & Zhou, Z. Rock-cutting and wear performance of a novel TBM disc cutter with spiral grooves. Tunn. Undergr. Sp Technol. 129, 104660 (2022). [Google Scholar]
- 13.Geng, Q., Wei, Z. & Ren, J. New rock material definition strategy for FEM simulation of the rock cutting process by TBM disc cutters. Tunn. Undergr. Sp Technol. 65, 179–186 (2017). [Google Scholar]
- 14.Zhang, X. P., Ji, P. Q., Zhang, Q., Liu, Q. S. & Wu, S. C. Study of contact pressure distribution between cutter and rock surface using the discrete element method. Int. J. Rock. Mech. Min. Sci. 146, 104875 (2021). [Google Scholar]
- 15.Gong, Q. M., Zhao, J. & Jiao, Y. Y. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters. Tunn. Undergr. Sp Technol. 20, 183–191 (2005). [Google Scholar]
- 16.Gong, Q. M., Jiao, Y. Y. & Zhao, J. Numerical modelling of the effects of joint spacing on rock fragmentation by TBM cutters. Tunn. Undergr. Sp Technol. 21, 46–55 (2006). [Google Scholar]
- 17.Moon, T. & Oh, J. A study of optimal rock-cutting conditions for hard rock TBM using the discrete element method. Rock. Mech. Rock. Eng. 45, 837–849 (2012). [Google Scholar]
- 18.Özşen, H., Dursun, A. E. & Aras, A. Estimation of specific energy and evaluation of roadheader performance using rock properties and bond work index. Min. Metall. Explor. 38, 1923–1932 (2021). [Google Scholar]
- 19.Xuefeng, L., Shibo, W., Shirong, G., Malekian, R. & Zhixiong, L. Investigation on the influence mechanism of rock brittleness on rock fragmentation and cutting performance by discrete element method. Measurement 113, 120–130 (2018). [Google Scholar]
- 20.Yagiz, S. Assessment of brittleness using rock strength and density with punch penetration test. Tunn. Undergr. Sp Technol. 24, 66–74 (2009). [Google Scholar]
- 21.Yagiz, S. & Gokceoglu, C. Application of fuzzy inference system and nonlinear regression models for predicting rock brittleness. Expert Syst. Appl. 37, 2265–2272 (2010). [Google Scholar]
- 22.Liu, Q. et al. Evaluation of rock brittleness indexes on rock fragmentation efficiency by disc cutter. Yanshilixue Yu Gongcheng Xuebao/Chinese J. Rock. Mech. Eng. 35, 498–510 (2016). [Google Scholar]
- 23.Xu, X., Wu, S., Gao, Y. & Xu, M. Effects of micro-structure and micro-parameters on Brazilian Tensile Strength using flat-joint model. Rock. Mech. Rock. Eng. 49, 3575–3595 (2016). [Google Scholar]
- 24.Liu, J. & Wang, J. The effect of indentation sequence on rock breakages: a study based on laboratory and numerical tests. Comptes Rendus Mécanique 346, 26–38 (2018). [Google Scholar]
- 25.Yang, X. X. & Qiao, W. G. Numerical investigation of the shear behavior of granite materials containing discontinuous joints by utilizing the flat-joint model. Comput. Geotech. 104, 69–80 (2018). [Google Scholar]
- 26.Zhang, L. Chapter 7 - Strength. in (ed. Zhang, L. B. T.-E. P. of R. (Second E.) 251–338 (Butterworth-Heinemann, doi: (2017). 10.1016/B978-0-12-802833-9.00007-9
- 27.Backers, T. & Stephansson, O. ISRM suggested method for the determination of mode II fracture toughness. Rock. Mech. Rock. Eng. 45, 1011–1022 (2012). [Google Scholar]
- 28.Kuruppu, M. D., Obara, Y., Ayatollahi, M. R., Chong, K. P. & Funatsu, T. ISRM-suggested method for determining the mode i static fracture toughness using semi-circular bend specimen. Rock. Mech. Rock. Eng. 47, 267–274 (2014). [Google Scholar]
- 29.Jeong, H. & Jeon, S. Characteristic of size distribution of rock chip produced by rock cutting with a pick cutter. Geomech. Eng. 15, 811–822 (2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analysed during this study are included in this published article.