Abstract
The increasing complexity and high-dimensional nature of real-world optimization problems necessitate the development of advanced optimization algorithms. Traditional Particle Swarm Optimization (PSO) often faces challenges such as local optima entrapment and slow convergence, limiting its effectiveness in complex tasks. This paper introduces a novel Hybrid Strategy Particle Swarm Optimization (HSPSO) algorithm, which integrates adaptive weight adjustment, reverse learning, Cauchy mutation, and the Hook-Jeeves strategy to enhance both global and local search capabilities. HSPSO is evaluated using CEC-2005 and CEC-2014 benchmark functions, demonstrating superior performance over standard PSO, Dynamic Adaptive Inertia Weight PSO (DAIW-PSO), Hummingbird Flight patterns PSO (HBF-PSO), Butterfly Optimization Algorithm (BOA), Ant Colony Optimization (ACO), and Firefly Algorithm (FA). Experimental results show that HSPSO achieves optimal results in terms of best fitness, average fitness, and stability. Additionally, HSPSO is applied to feature selection for the UCI Arrhythmia dataset, resulting in a high-accuracy classification model that outperforms traditional methods. These findings establish HSPSO as an effective solution for complex optimization and feature selection tasks.
Keywords: Particle Swarm Optimization algorithm, Hybrid strategy, Adaptive weight adjustment, Reverse learning strategy, Cauchy mutation mechanism, Hook-Jeeves strategy, Feature selection
Subject terms: Applied mathematics, Computational science, Computer science, Information technology
Introduction
In the real world, the development of new phenomena often follows a spiral upward trend, a pattern equally observed in nature. The continuous emergence of new entities has spurred extensive interest in utilizing swarm intelligence optimization algorithms to address various optimization challenges associated with these phenomena. Optimization, as a crucial aspect of the design process, ultimately aims to minimize or maximize the objective function.
Background
Model optimization is a cornerstone in computational fields and is generally categorized into constrained and unconstrained optimization. These approaches are integral to various domains, including computer science1, artificial intelligence2, and engineering3. Despite substantial advances in machine learning algorithms, notable limitations persist, especially in addressing complex and non-convex optimization problems. Traditional machine learning methods often struggle to find global optima, tending instead to become trapped in local optima. This challenge has driven researchers to explore novel optimization methods, with a significant focus on swarm intelligence algorithms known for their global search capabilities and avoidance of local optima.
Swarm intelligence algorithms, such as Genetic Algorithm (GA)4, Particle Swarm Optimization (PSO)5, Cuckoo Search (CS)6, Differential Evolution (DE)7, Artificial Bee Colony (ABC)8, Ant Colony Optimization (ACO)9, Dwarf Mongoose Optimization (DMO)10, Firefly Algorithm (FA)11, and Butterfly Optimization Algorithm (BOA)12, have garnered extensive research interest due to their efficiency in global search and optimization. These algorithms are also adept at optimizing dataset feature selection problems. For instance, integrating DMO with chaos theory enhances the global search capability, facilitating the discovery of optimal feature subsets13. Additionally, combining evolutionary algorithms with genetic algorithms enables the selection of suitable feature subsets from high-dimensional datasets, improving model training efficiency and classification performance14,15.
The development and optimization of evolutionary algorithms are well-documented in the literature. For instance, Akbari et al.16 introduced the Cheetah Optimizer, a nature-inspired metaheuristic for large-scale optimization problems, demonstrating significant advancements in solving complex optimization challenges. Similarly, Ghasemi et al.17 proposed the Geyser Inspired Algorithm, a new geological-inspired meta-heuristic tailored for real-parameter and constrained engineering optimization. Another notable contribution is the Lungs Performance-based Optimization (LPO) algorithm18, which draws inspiration from the functional performance of lungs and offers innovative solutions for optimization. Additionally, the Ivy Algorithm19, inspired by the smart behavior of plants, provides an efficient approach to tackling engineering optimization problems. These works collectively contribute to a deeper understanding of evolutionary optimization and inspire further exploration into hybrid strategies like HS-PSO.
Particle Swarm Optimization (PSO) stands out for its versatile applications. It has been employed to optimize the trajectory planning of serial manipulators15, to simulate average daily global solar radiation values20, and to enhance Support Vector Machine (SVM) classification accuracy in fault diagnosis of rotating machinery21. Demir et al.22 studied the combination of PSO with gradient boosting algorithms for predicting earthquake-induced liquefaction lateral spread. Li et al.23 proposed an improved Criminisi algorithm based on PSO for image inpainting. Zhang et al.24 introduced a regional scheduling method based on PSO and differential evolution (PSO-DE) to reduce the scheduling cost of shared vehicles.
Li et al.25 proposed a novel Simulated Assisted Multi-Cluster Optimization (SAMSO) method, which divides the population into two groups. The first group employs the learner stage of the Teaching–Learning-Based Optimization (TLBO) algorithm to enhance exploration, while the second group utilizes Particle Swarm Optimization (PSO) to accelerate convergence. These groups interact to form a dynamic population size adjustment scheme that controls the evolutionary process. In reference26, a variant of the PSO algorithm incorporating heterogeneous behavior and dynamic multi-group topology is presented. This variant significantly improves algorithm performance through a dual-group mechanism and guidance by heterogeneous behavior, demonstrating superior results in CEC benchmark tests. Reference27 introduces the Random Drift Particle Swarm Optimization (RDPSO) algorithm for solving the economic dispatch problem in power systems. RDPSO enhances global search by simulating the random drift of particles and considers the nonlinear characteristics of generators. Experimental results indicate that RDPSO outperforms other optimization techniques in solving economic dispatch problems.
Reference28 presents an adaptive granularity learning distributed PSO (AGLDPSO), employing two machine learning techniques: Location-Sensitive Hashing (LSH) for clustering analysis and adaptive granularity control based on Logistic Regression (LR). The literature29 introduces the Vector Coevolving PSO (VCPSO), a novel algorithm that partitions particles and applies diverse operators to enhance diversity and search capability. Experimental results show that VCPSO exhibits superior or comparable performance on benchmark tests. Reference30 describes an enhanced PSO algorithm based on Hummingbird Flight (HBF), which improves search quality and diversity. Comprehensive benchmark evaluations demonstrate that HBF-PSO outperforms other methods, particularly in economic dispatch problems, confirming its effectiveness.
However, the original PSO algorithm has inherent weaknesses such as susceptibility to local optima, slow search speeds, poor search capabilities, and low local search precision. These limitations necessitate the development of advanced variants of PSO.
Motivation
The increasing complexity and high-dimensional nature of real-world problems underscore the critical need for efficient optimization algorithms. Despite the widespread application and advantages of traditional Particle Swarm Optimization (PSO), it often faces challenges such as entrapment in local optima, slow convergence rates, and inadequate local search precision. These limitations diminish its effectiveness in tackling intricate optimization tasks, especially within high-dimensional search spaces. Consequently, there is a strong motivation to develop an advanced optimization algorithm that integrates multiple strategies to overcome these shortcomings.
Hybrid Strategy Particle Swarm Optimization (HSPSO) aims to address these challenges through the incorporation of several innovative mechanisms. These include adaptive weight adjustment to avoid entrapment in local optima, a reverse learning strategy to enhance particle adjustment within the search space, a Cauchy mutation mechanism to diversify the search and enhance global search capabilities, and the Hook-Jeeves strategy for iterative fine-tuning of particle positions to improve local search accuracy. The development of HSPSO seeks to provide a robust solution that not only mitigates the inherent weaknesses of traditional PSO but also excels in both global and local optimization tasks.
Contributions
This paper introduces the Hybrid Strategy Particle Swarm Optimization (HS-PSO) algorithm, which incorporates several novel strategies to enhance traditional PSO performance. The key contributions of this paper include:
Adaptive Weight Adjustment Mechanism: To prevent local optima entrapment and improve optimization in high-dimensional functions.
Reverse Learning Strategy: To enhance intelligent particle adjustment and accelerate the search process.
Cauchy Mutation Mechanism: To increase search diversity and global search capability.
Hook-Jeeves Strategy: For iterative fine-tuning of particle positions, improving local search accuracy.
Comprehensive Evaluation: Validation of HS-PSO through comparative analysis on CEC-2005 and CEC-2014 benchmark functions, demonstrating its superiority over standard PSO, Dynamic Adaptive Inertia Weight PSO (DAIW-PSO), BOA, ACO, and FA.
Practical Application: Application of HS-PSO to the arrhythmia dataset from the UCI repository for feature selection, establishing the effectiveness of the HS-PSO-FS model in real-world scenarios.
Organization of the paper
The organization of this paper is as follows: the “Hybrid Strategy Particle Swarm Optimization Algorithm” section introduces the original particle swarm algorithm and the hybrid strategy particle swarm optimization algorithm. Subsequently, in the “Function Optimization” section, comparative results of HS-PSO, PSO, DAIW-PSO, BOA, ACO, and FA across CEC-2005 and CEC-2014 benchmark functions are presented. In the “Applications” section, HSPSO is applied to feature selection on the arrhythmia dataset from the UCI public repository, establishing the HSPSO-FS feature selection model. Relevant conclusions and discussions are provided in the “Conclusions and Discussion” section.
Particle Swarm Optimization
Particle Swarm Optimization (PSO) is an optimization algorithm introduced by Kennedy et al.5, which simulates the foraging behavior of bird flocks. This algorithm emulates the collaborative cooperation and information exchange among birds, enabling the entire population to locate food more effectively. In nature, bird flocks explore randomly for food without precise knowledge of its exact location, but they can sense the general direction. Each bird searches based on this perceived direction, records the locations and quantities of discovered food, and shares this information with the flock. During the search process, each bird dynamically adjusts its search direction based on its own recorded positions of the most food (local optimal solutions) and the shared information about the flock’s best food positions. Eventually, after a period of searching, the flock locates the most abundant food source in the forest, representing the global optimal solution. The simulation steps for this search behavior in PSO are as follows:
Define the initial bird flock, including their positions and velocities.
Calculate the amount of food each individual bird has found.
Update each individual’s best-known food position and the flock’s best-known food position.
Check if the search termination condition is met. If satisfied, output the optimal solution; otherwise, continue searching.
In the PSO algorithm, each individual in the bird flock is treated as a particle in a D-dimensional space, without volume or mass. Each particle, analogous to a bird, has velocity and position, and it dynamically tracks the search progress in real-time through its recording function. Using a fitness evaluation function, particles continuously converge towards their own historical best positions (Pbest) and the population’s historical best position (Gbest), dynamically adjusting their search strategies to achieve the goal of finding the optimal solution.
Assuming a population size of N in a D-dimensional space, the process of updating positions and velocities can be represented by Eq. (1)31:
| 1 |
Here, and represent the j-th dimensional velocity and position components of the i-th particle at iteration t. i = 1, 2, 3,…, N denotes the particle index, with N being the population size, j = 1, 2, …, D denotes the dimension index. c1 and c2 are acceleration coefficients, rand1 and rand2 are random numbers uniformly distributed in the interval [0,1], and ω is the inertia weight that controls the inertia of particle velocity.
To balance convergence speed and local search ability, Shi et al.32,33 proposed a strategy of dynamically decreasing inertia weight linearly over time. The inertia weight factor is represented by Eq. (2):
| 2 |
where ωMax and ωMin are the maximum and minimum values of the inertia weight, typically set to 0.8 and 0.4, respectively. t represents the current iteration number, and Tmax denotes the maximum number of iterations.
Thus, the original Particle Swarm Optimization (PSO) algorithm is established, offering a novel approach to tackling various complex optimization problems through its unique search mechanism and efficient information-sharing methods.
Hybrid strategy Particle Swarm Optimization algorithm
To further enhance the optimization effectiveness of the original Particle Swarm Optimization (PSO) algorithm, this paper proposes a Hybrid Strategy Particle Swarm Optimization (HS-PSO) algorithm. This algorithm integrates several advanced mechanisms to address the challenges associated with high-dimensional function optimization.
First, an adaptive weight adjustment mechanism is introduced to prevent the algorithm from easily becoming trapped in local optima when dealing with complex high-dimensional functions. This mechanism dynamically adjusts the inertia weight to balance exploration and exploitation during the search process.
Second, a reverse learning strategy is incorporated to enhance the intelligent adjustment capability of particles within the search space. This strategy optimizes particle search speed by improving their ability to navigate through the search space.
Third, to enhance the diversity and global search capability, a Cauchy mutation mechanism is introduced. This mechanism helps in diversifying particle positions and improving their global search performance.
Fourth, the Hook-Jeeves strategy is applied to iteratively fine-tune particle positions, further enhancing the algorithm’s local search accuracy. This strategy allows particles to explore their neighborhoods more effectively, leading to better local optimization results.
The pseudo code of the HSPSO algorithm is presented in Fig. 1.
Fig. 1.
The pseudo code of HS-PSO algorithm.
Dynamic adaptation of inertia weight
In the early stages of the PSO algorithm, the update of individual particle velocities is closely related to the inertia weight ω and velocity. When the inertia weight ω is low, particles may find it difficult to explore the search space. In the later stages of the PSO algorithm, particles tend to converge towards high-fitness areas, resulting in a rapid decrease in particle velocities. If a low inertia weight is maintained for an extended period, the algorithm may converge prematurely.
Standard Deviation of the Population Fitness (STF) is used to measure the dispersion of fitness values across the population. STF provides a statistical metric for evaluating population diversity. It is calculated as follows:
| 3 |
where N is the population size, fi is the fitness of the i-th particle, and s the mean fitness of the population. This metric aids in adjusting the inertia weight adaptively to balance exploration and exploitation during the optimization process. By utilizing STF, the algorithm can dynamically modulate the search behavior based on the current state of the population fitness distribution, enhancing its capability to escape local optima and improving overall optimization performance.
To prevent the algorithm from getting trapped in local optima during complex high-dimensional function optimization, we introduce a nonlinear dynamic adaptive weight adjustment mechanism34. As the fitness values obtained during the particle search are discrete, we describe this change using Eq. (4), where Hi represents the adaptability discreteness of the i-th particle.
| 4 |
In machine learning, the Sigmoid function is commonly used to construct neuron activation functions, as it provides a balance between linearity and non-linearity, with smooth upper and lower boundaries, resulting in output values ranging between 0 and 1. Its expression is given by35:
| 5 |
Combining Eqs. (4) and (5) yields the Non-linear Dynamic Adaptive Inertia Weight (DAIW)34, which enhances both the initial search capability and the later exploitation ability of particles. Its expression is given by Eq. (6):
| 6 |
where b is the damping factor, typically ranging from 0 to 1.
Enhancing search efficiency with reverse learning strategy
Reverse learning is a method for adjusting particle velocity by comparing the current individual’s fitness with its historical best fitness. The core idea is that when particles are trapped in a local optimum, moving in the opposite direction can help them escape the local optimum area, thereby increasing the efficiency of finding the global optimum. Let F represent the fitness evaluation function, and the process can be described by Eq. (7):
| 7 |
If the current individual’s fitness is lower than its historical individual fitness, it indicates that the current individual’s fitness value is better than the historical one, suggesting that the current position may represent a more promising search direction. Therefore, the particle moves towards the global best position while incorporating the current position information to execute the reverse learning strategy, thereby exploring the solution space more efficiently. If the current position’s performance is inferior to the historical best position, the particle follows the traditional PSO velocity update method, maintaining focus on local search to balance global and local search strategies and avoid premature convergence.
Boosting population diversity with Cauchy mutation
To enhance the diversity of particle search and increase population diversity, this paper employs individual mutation perturbation methods to promote the generality of global search. Typically, two perturbation methods are used: Gaussian mutation and Cauchy mutation. Figure 2 illustrates the density function comparison between these two mutation methods.
Fig. 2.

Comparison of Gaussian and Cauchy.
By observing Fig. 2, it can be concluded that the tails of the Cauchy mutation function are much longer, indicating a significantly higher probability for individual particles to escape local optima. This characteristic amplifies the differences between offspring and parents, making Cauchy mutation exhibit stronger perturbative characteristics. In the later stages of the PSO algorithm, particles tend to converge rapidly towards regions of higher fitness, which results in a deceleration of their velocities and may lead to premature convergence. To counteract premature convergence, this paper employs the Cauchy mutation method to enhance population diversity and help particles escape local optima. The perturbation applied to particles is expressed as follows36:
| 8 |
where γ is the scale parameter, “random” represents a random number uniformly distributed in the interval [0, 1], and “Cauchy” denotes the standard Cauchy perturbation random value.
Enhancing local search precision with the Hook-Jeeves algorithm
To enhance the precision of local search in the PSO algorithm, the Hook-Jeeves algorithm is introduced to fine-tune each particle. The Hook-Jeeves algorithm37, an iterative method for nonlinear optimization, progressively improves solutions by refining them around the current point and demonstrates excellent performance in unconstrained optimization problems. It conducts small step-size probes in various directions around the current solution to find new positions that reduce the objective function value. Superior solutions discovered during the probing process are adopted as new starting points, with the step size appropriately reduced for subsequent iterations. This integration significantly enhances the accuracy and efficiency of the local search phase in the PSO algorithm. The pseudo-code for the Hook-Jeeves algorithm is presented by Fig. 3:
Fig. 3.
The pseudo code of Hook-Jeeves algorithm.
By combining the above strategies, this paper aims to enhance the accuracy of local search while maintaining the global search capability of the particle swarm algorithm, thereby achieving faster convergence to the optimal solution.
Function optimization
In this section, the performance of the proposed Hybrid Strategy Particle Swarm Optimization (HS-PSO) algorithm is evaluated using benchmark functions from CEC-200515 and CEC-201438.
Benchmark functions
Fifteen benchmark functions from CEC-2005 are utilized to compare HS-PSO with PSO, DAIW-PSO, BOA, ACO, and FA. Additionally, thirty benchmark functions from CEC-2014 are employed to compare HS-PSO with PSO, DAIW-PSO, and Hummingbird Flight PSO (HBF-PSO), a modified PSO algorithm that enhances search quality and population diversity using hummingbird flight patterns.
Table 1 lists the 15 n-dimensional benchmark functions from CEC-2005 along with their ranges and dimensions. Functions F1(x) to F7(x) in Table 1 are unimodal functions, F8(x) to F13(x) are multimodal functions, and F14(x) and F15(x) are fixed-dimensional functions. Figure 4 illustrates the three-dimensional representations of the benchmark functions F1(x), F3(x), F7(x), F8(x), F9(x), and F10(x).
Table 1.
Benchmark functions F1(x) ~ F15(x) of CEC-200515.
| The function expression | Dim | Range | Min |
|---|---|---|---|
| 30 | [− 100,100] | 0 | |
| 30 | [− 10,10] | 0 | |
| 30 | [− 100,100] | 0 | |
| 30 | [− 100,100] | 0 | |
| 30 | [− 10,10] | 0 | |
| 30 | [− 100,100] | 0 | |
| 30 | [− 1.28,1.28] | 0 | |
| 30 | [− 500,500] | − 418.93E+5 | |
| 30 | [− 5.12,5.12] | 0 | |
| 30 | [− 600,600] | 0 | |
| 30 | [− 50,50] | 0 | |
| 30 | [− 50,50] | 0 | |
| 30 | [− 10,10] | 0 | |
| 2 | [− 5,5] | − 1.0316 | |
| 2 | [− 5,5] | 0.398 |
Fig. 4.
Presents the 3D versions of benchmark functions F1(x), F3(x), F7(x), F8(x), F9(x), and F10(x) in CEC-2005. (Functions F3(x) and F7(x) were generated using MATLAB R2018a, while the rest were generated using PyCharm Community Edition).
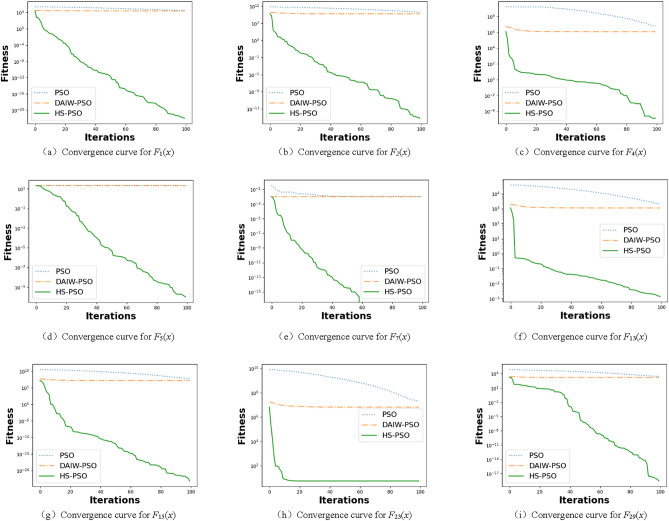
Table 2 provides the best fitness values, means, and standard deviations of the 15 benchmark functions of CEC-2005 for the six algorithms. The bold values represent the optimal performance for each benchmark function. Figure 5 also shows the convergence curves of these algorithms on selected functions.
Table 2.
The best fitness value, mean, and standard deviation of the 15 benchmark functions of CEC-2005 across the 6 algorithms.
| Fun | Algorithm | Best fitness | Mean | Std | Fun | Algorithm | Best fitness | Mean | Std |
|---|---|---|---|---|---|---|---|---|---|
| F1 | PSO5 | 3900.756 | 1.998 | 11.226 | F9 | PSO5 | 100.272 | 0.298 | 0.990 |
| ACO9 | 2138.513 | 7.920e−13 | 2.688e−12 | ACO9 | 99.489 | − 9.769e−12 | 6.422e−10 | ||
| FA11 | 2153.832 | 7.920e−13 | 2.688e−12 | FA11 | 98.003 | − 9.769e−12 | 6.422e−10 | ||
| BOA12 | 581.290 | 0.581 | 23.898 | BOA12 | 49.309 | 0.001 | 0.511 | ||
| DAIW-PSO34 | 2138.650 | 1.891 | 8.229 | DAIW-PSO34 | 100.262 | 0.298 | 0.990 | ||
| HS-PSO | 1.854e−22 | 2.227e−13 | 2.476e−12 | HS-PSO | 0.00e+00 | 9.077e−12 | 5.246e−10 | ||
| F2 | PSO5 | 11.7842 | 0.014 | 0.580 | F10 | PSO5 | 511.864 | 43.507 | 257.337 |
| ACO9 | 11.7841 | 2.567e−15 | 2.828e−15 | ACO9 | 381.367 | 2.293e−09 | 4.322e−08 | ||
| FA11 | 4.905e+19 | − 0.235 | 6.054 | FA11 | 386.955 | 2.293e−09 | 4.322e−08 | ||
| BOA12 | 76001877.206 | 0.440 | 16.403 | BOA12 | 118.920 | 11.025 | 684.131 | ||
| DAIW-PSO34 | 11.784 | 0.014 | 0.580 | DAIW-PSO34 | 380.645 | 43.370 | 220.768 | ||
| HS-PSO | 1.114e−14 | − 2.322e−16 | 3.567e−16 | HS-PSO | 0.00E+00 | 1.667e−09 | 8.642e−09 | ||
| F3 | PSO5 | 33779.437 | − 1.295 | 35.923 | F11 | PSO5 | 3.075 | − 0.938 | 4.339 |
| ACO9 | 21422.058 | 2.286e−08 | 7.893e−07 | ACO9 | 0.078 | 0.078 | 0.356 | ||
| FA11 | 21363.828 | 2.286e−08 | 7.893e−07 | FA11 | 1050073320.173 | 6.057 | 25.655 | ||
| BOA12 | 55131.719 | 1.826 | 185.528 | BOA12 | 5.087e+08 | 2.744 | 117.038 | ||
| DAIW-PSO34 | 21461.451 | − 0.054 | 30.561 | DAIW-PSO34 | 3.075 | − 0.937 | 4.340 | ||
| HS-PSO | 7.88e-15 | − 2.015e−10 | 2.569e−08 | HS-PSO | − 1.022 | 0.078 | 0.356 | ||
| F4 | PSO5 | 21.258 | − 0.384 | 12.412 | F12 | PSO5 | 48.609 | 0.539 | 3.493 |
| ACO9 | 16.712 | 3.303e−07 | 3.334e−06 | ACO9 | 47.483 | 1.013 | 0.030 | ||
| FA11 | 98.569 | 10.388 | 51.512 | FA11 | 49.184 | 1.013 | 0.030 | ||
| BOA12 | 87.680 | 10.393 | 287.585 | BOA12 | 1.360e+09 | 1.008 | 143.213 | ||
| DAIW-PSO34 | 16.713 | 0.388 | 9.536 | DAIW-PSO34 | 48.342 | 0.539 | 3.495 | ||
| HS-PSO | 1.153e−07 | 1.123e−08 | 5.682e−08 | HS-PSO | − 0.096 | 1.006 | 0.030 | ||
| F5 | PSO5 | 3730.416 | 0.314 | 0.984 | F13 | PSO5 | 15.512 | 0.145 | 1.621 |
| ACO9 | 4728.786 | 0.044 | 0.130 | ACO9 | 15.511 | − 1.466e−13 | 1.273e−13 | ||
| FA11 | 4589.090 | 0.044 | 0.130 | FA11 | 72.774 | − 0.126 | 4.851 | ||
| BOA12 | 3082143.498 | 1.610 | 24.552 | BOA12 | 3.707e−06 | 5.253e−07 | 7.838e−06 | ||
| DAIW-PSO34 | 3719.717 | 0.308 | 0.980 | DAIW-PSO34 | 15.511 | 0.145 | 1.621 | ||
| HS-PSO | 27.057 | 0.046 | 0.136 | HS-PSO | 1.147e−15 | − 3.824e−16 | 2.044e−16 | ||
| F6 | PSO5 | 2143.357 | − 0.346 | 8.451 | F14 | PSO5 | − 1.032 | 0.311 | 0.401 |
| ACO9 | 1102.599 | − 0.485 | 0.021 | ACO9 | − 1.032 | − 0.285 | 0.415 | ||
| FA11 | 1113.206 | − 0.485 | 0.021 | FA11 | 69.492 | − 0.486 | 2.232 | ||
| BOA12 | 75814.068 | − 13.174 | 266.449 | BOA12 | − 0.845 | 0.240 | 0.763 | ||
| DAIW-PSO34 | 1103.467 | − 1.597 | 5.965 | DAIW-PSO34 | − 1.032 | 0.311 | 0.401 | ||
| HS-PSO | 2.260e−08 | − 0.500 | 1.865e−05 | HS-PSO | − 1.032 | − 0.311 | 0.401 | ||
| F7 | PSO5 | 13.699 | 0.008 | 0.257 | F15 | PSO5 | 14.889 | 5.319 | 4.680 |
| ACO9 | 40.118 | 0.025 | 0.112 | ACO9 | 14.889 | 64.228 | 61.085 | ||
| FA11 | 38.703 | 0.025 | 0.112 | FA11 | 8088.353 | 64.171 | 61.029 | ||
| BOA12 | 12.015 | 0.022 | 0.816 | BOA12 | 15.073 | 5.304 | 6.640 | ||
| DAIW-PSO34 | 13.388 | 0.008 | 0.257 | DAIW-PSO34 | 14.889 | 5.320 | 4.680 | ||
| HS-PSO | 10.539 | 0.014 | 0.096 | HS-PSO | 3.927 | 1.715 | 0.943 | ||
| F8 | PSO5 | − 2366.845 | − 77.871 | 253.180 | – | – | – | – | – |
| ACO9 | 77.858 | 156.620 | 281.447 | ||||||
| FA11 | − 1398.593 | − 9.178 | 430.151 | ||||||
| BOA12 | − 2407.616 | − 134.117 | 2420.034 | ||||||
| DAIW-PSO34 | − 2366.845 | − 77.871 | 253.180 | ||||||
| HS-PSO | − 10792.911 | 59.223 | 361.747 |
The bold values represent the optimal value for each benchmark function.
Fig. 5.
Convergence curves for benchmark functions F1(x)–F4(x), F6(x), F7(x), F9(x), F10(x), and F13(x) of CEC-2005.
Table 3 further details the average values and standard deviations of the experimental results from independent runs of PSO, DAIW-PSO, HS-PSO, and HBF-PSO on 30 benchmark test functions according to the CEC-2014 standard. Figure 6 presents the convergence curves of the algorithms on these functions.
Table 3.
The mean and standard deviation of the 30 benchmark functions of CEC-2014 across the 4 algorithms.
| Fun | Algorithm | Mean | Std | Fun | Algorithm | Mean | Std |
|---|---|---|---|---|---|---|---|
| F1 | PSO30 | 3.90E+07 | 2.70E+07 | F16 | PSO30 | 1.39E+01 | 1.77E−01 |
| DAIW-PSO34 | 1.788 | 15.735 | DAIW-PSO34 | 7.168 | 18.856 | ||
| HBF-PSO30 | 3.18E+05 | 2.69E+05 | HBF-PSO30 | 1.06E+01 | 5.19E−01 | ||
| HS-PSO | 5.26E−13 | 1.09E−12 | HS-PSO | 3.26E−10 | 1.19E−09 | ||
| F2 | PSO30 | 8.08E+07 | 3.04E+07 | F17 | PSO30 | 3.49E+06 | 3.30E+06 |
| DAIW-PSO34 | 1.075 | 7.227 | DAIW-PSO34 | 2.85E+01 | 2.68E+01 | ||
| HBF-PSO30 | 3.55E−05 | 1.51E−04 | HBF-PSO30 | 2.25E+04 | 1.99E+04 | ||
| HS-PSO | 1.18E−09 | 2.98E−09 | HS-PSO | 2.04E+04 | 1.87E+04 | ||
| F3 | PSO30 | 1.01E+05 | 2.64E+04 | F18 | PSO30 | 5.38E+03 | 8.95E+03 |
| DAIW-PSO34 | 5.121 | 23.7 | DAIW-PSO34 | 4.33E+03 | 6.12E+03 | ||
| HBF-PSO30 | 6.80E−08 | 1.78E−07 | HBF-PSO30 | 2.88E+02 | 4.26E+02 | ||
| HS-PSO | 0.003 | 0.152 | HS-PSO | 2.96E+02 | 4.42E+02 | ||
| F4 | PSO30 | 2.05E+02 | 6.66E+01 | F19 | PSO30 | 3.53E+01 | 3.01E+01 |
| DAIW-PSO34 | 1.074 | 9.916 | DAIW-PSO34 | 2.88E+01 | 2.69E+01 | ||
| HBF-PSO30 | 4.73E+01 | 5.74E+01 | HBF-PSO30 | 1.96E+01 | 2.25E+01 | ||
| HS-PSO | 0.033 | 0.400 | HS-PSO | 1.93E+01 | 2.10E+01 | ||
| F5 | PSO30 | 2.12E+01 | 5.49E−02 | F20 | PSO30 | 1.19E+05 | 1.26E+05 |
| DAIW-PSO34 | 7.899 | 30.106 | DAIW-PSO34 | 0.459 | 7.966 | ||
| HBF-PSO30 | 2.00E+01 | 5.64E−05 | HBF-PSO30 | 7.08E+01 | 2.87E+01 | ||
| HS-PSO | 3.26E−12 | 2.50E−11 | HS-PSO | 1.907E−10 | 1.29E−09 | ||
| F6 | PSO30 | 4.36E+01 | 3.91E+00 | F21 | PSO30 | 8.22E+05 | 8.49E+05 |
| DAIW-PSO34 | 2.83E+01 | 3.41E+01 | DAIW-PSO34 | 0.631 | 8.717 | ||
| HBF-PSO30 | 2.04E+01 | 2.48E+00 | HBF-PSO30 | 7.29E+03 | 7.34E+03 | ||
| HS-PSO | 1.98E+02 | 2.32E+02 | HS-PSO | 0.000 | 0.003 | ||
| F7 | PSO30 | 1.65E+00 | 2.56E−01 | F22 | PSO30 | 1.02E+03 | 3.31E+02 |
| DAIW-PSO34 | 0.005 | 0.108 | DAIW-PSO34 | 3.453 | 8.896 | ||
| HBF-PSO30 | 1.01E−02 | 2.37E−02 | HBF-PSO30 | 6.75E+02 | 2.23E+02 | ||
| HS-PSO | 3.79E−09 | 1.24E−08 | HS-PSO | 0.000 | 0.002 | ||
| F8 | PSO30 | 3.99E+02 | 4.60E+01 | F23 | PSO30 | 3.38E+02 | 1.64E+01 |
| DAIW-PSO34 | 1.833 | 6.561 | DAIW-PSO34 | 5.208 | 11.848 | ||
| HBF-PSO30 | 7.63E+00 | 2.85E+00 | HBF-PSO30 | 3.15E+02 | 2.72E−12 | ||
| HS-PSO | 1.25E−10 | 7.58E−10 | HS-PSO | 0.000 | 0.001 | ||
| F9 | PSO30 | 4.21E+02 | 3.61E+01 | F24 | PSO30 | 2.41E+02 | 7.08E+00 |
| DAIW-PSO34 | 0.096 | 1.068 | DAIW-PSO34 | 1.722 | 6.804 | ||
| HBF-PSO30 | 1.17E+02 | 2.59E+01 | HBF-PSO30 | 2.33E+02 | 9.27E+00 | ||
| HS-PSO | 5.385E−10 | 2.01E−09 | HS-PSO | 0.000 | 0.003 | ||
| F10 | PSO30 | 8.87E+03 | 4.80E+02 | F25 | PSO30 | 2.20E+02 | 6.34E+00 |
| DAIW-PSO34 | 7.53E+02 | 3.65E+03 | DAIW-PSO34 | 0.274 | 9.397 | ||
| HBF-PSO30 | 4.18E+01 | 5.38E+01 | HBF-PSO30 | 2.16E+02 | 5.29E+00 | ||
| HS-PSO | 3.14E+02 | 4.21E+02 | HS-PSO | 3.126E−10 | 6.79E−10 | ||
| F11 | PSO30 | 9.21E+03 | 6.08E+02 | F26 | PSO30 | 1.77E+02 | 4.29E+01 |
| DAIW-PSO34 | 7.18E+05 | 4.88E+02 | DAIW-PSO34 | 1.963 | 8.457 | ||
| HBF-PSO30 | 2.87E+03 | 6.50E+02 | HBF-PSO30 | 1.35E+02 | 5.07E+01 | ||
| HS-PSO | 2.67E+03 | 5.33E+02 | HS-PSO | 0.000 | 0.003 | ||
| F12 | PSO30 | 5.51E+00 | 9.09E−01 | F27 | PSO30 | 1.22E+03 | 4.27E+02 |
| DAIW-PSO34 | 10.728 | 47.323 | DAIW-PSO34 | 4.691 | 9.931 | ||
| HBF-PSO30 | 1.91E−01 | 5.39E−02 | HBF-PSO30 | 7.63E+02 | 2.48E+02 | ||
| HS-PSO | 17.708 | 76.511 | HS-PSO | 0.000 | 0.001 | ||
| F13 | PSO30 | 5.88E−01 | 1.45E−01 | F28 | PSO30 | 9.26E+03 | 1.15E+03 |
| DAIW-PSO34 | 0.051 | 11.868 | DAIW-PSO34 | 2.927 | 7.048 | ||
| HBF-PSO30 | 2.99E−01 | 7.18E−02 | HBF-PSO30 | 2.33E+03 | 6.18E+02 | ||
| HS-PSO | 2.38E−14 | 9.41E−14 | HS-PSO | 0.001 | 0.005 | ||
| F14 | PSO30 | 2.90E−01 | 1.22E−01 | F29 | PSO30 | 1.36E+08 | 2.83E+08 |
| DAIW-PSO34 | 2.507 | 6.15 | DAIW-PSO34 | 0.353 | 7.058 | ||
| HBF-PSO30 | 1.18E−01 | 5.65E−02 | HBF-PSO30 | 2.90E+05 | 1.58E+06 | ||
| HS-PSO | 0.078 | 0.165 | HS-PSO | 1.788E−11 | 1.62E−10 | ||
| F15 | PSO30 | 5.40E+01 | 2.61E+01 | F30 | PSO30 | 1.59E+05 | 1.56E+05 |
| DAIW-PSO34 | 0.246 | 8.148 | DAIW-PSO34 | 3.53 | 11.204 | ||
| HBF-PSO30 | 1.29E+01 | 4.31E+00 | HBF-PSO30 | 2.37E+03 | 9.61E+02 | ||
| HS-PSO | 3.78E−14 | 1.24E−13 | HS-PSO | 0.000 | 0.003 |
The bold values represent the optimal value for each benchmark function.
Fig. 6.
Convergence curves for benchmark functions F1(x), F2(x), F4(x), F5(x), F7(x), F13(x), F15(x), F23(x), and F29(x) of CEC-2014.
Experimental setup
To ensure the fairness and objectivity of the experimental results, all algorithms are configured with the same parameters: population size N = 20, maximum iteration count T = 100, and maximum fitness evaluation count MFE = N × T = 2000. The learning factors are set to c1 = c2 = 1.5, the inertia weight ranges from to , and the velocity limits are and .
Evaluation metrics
The evaluation metrics include the best fitness, average fitness, standard deviation, and the P-value from the rank sum test of fitness scores. These metrics provide insights into the peak performance, overall search efficiency, stability of the algorithm, and statistical significance of performance differences among the algorithms.
Experimental results
To ensure the accuracy and reliability of our experimental results, each algorithm underwent 30 independent runs on every test function in this study. The experimental environment utilized the Windows 10 operating system, powered by an Intel Core i7-9750H processor running at 2.6 GHz, and equipped with 16 GB of memory to ensure efficient computational capabilities. Algorithm development was carried out on the PyCharm 2021 platform using Python as the programming language, which facilitated implementation and debugging processes.
Performance on CEC-2005 benchmark functions
The performance of HS-PSO was analyzed using 15 benchmark functions from CEC-2005. The key findings are summarized as follows:
In the testing of unimodal functions F1(x) to F7(x), the HS-PSO algorithm demonstrated exceptional performance, particularly on F1(x), achieving optimal results in terms of global best fitness value, average fitness value, and stability (standard deviation). For F2(x) to F4(x), although all algorithms performed similarly on certain metrics, HS-PSO consistently achieved the best outcomes with the smallest global best fitness value, average fitness value close to zero, and lower standard deviation, showcasing its superior optimization capability and stability. Even on functions F5(x) and F6(x), where ACO and FA demonstrated notable stability, HS-PSO maintained its lead with the smallest fitness values and standard deviations, underscoring its robustness.
For multimodal functions F8(x) to F13(x), HS-PSO’s performance was generally strong but varied across different functions. Although HS-PSO’s best fitness value on F8(x) did not surpass PSO and DAIW-PSO, it effectively found the global optimal solution on other multimodal functions such as F9(x) and F10(x), with low average fitness values and standard deviations, highlighting its robust search capability in complex environments. On F10(x), HS-PSO performed comparably well with ACO and FA, standing out with its minimal best fitness value and standard deviation.
Throughout the entire experimental process, HS-PSO consistently exhibited superior performance across most functions. Despite certain instances, such as F8(x), where its best fitness value was not optimal, this does not detract from the overall effectiveness and versatility of the HS-PSO algorithm. It continues to outperform or match other algorithms in various scenarios, addressing optimization problems with diverse complexities and characteristics effectively. Table 2 summarizes the experimental results on the CEC-2005 benchmark functions, providing the best fitness values, means, and standard deviations for the six algorithms. Figure 5 presents the convergence curves of HS-PSO and other algorithms, demonstrating HS-PSO’s rapid convergence and robust performance.
Performance on CEC-2014 benchmark functions
The performance of HS-PSO was further assessed using 30 benchmark functions from CEC-2014, comparing it with PSO, DAIW-PSO, and HBF-PSO. The analysis revealed the following key insights:
Unimodal Functions F1(x) to F3(x): HS-PSO consistently achieved the best mean and standard deviation values for F1(x) and F2(x), demonstrating its superior performance in simple optimization landscapes. Although HS-PSO did not achieve the lowest mean value for F3(x), it still had an advantage in performance.
Simple Multimodal Functions F4(x) to F16(x): HS-PSO excelled in most simple multimodal functions, achieving the lowest mean values and standard deviations in the majority of these functions. It is worth noting that the performance of HS-PSO is slightly weaker on F6(x), F10(x), F12(x), and F14(x), and further improvement is needed.
Hybrid Functions F17(x) to F22(x): HS-PSO performed exceptionally well on hybrid functions such as F19(x), F21(x) and F22(x), achieving the lowest mean values and standard deviations, reflecting its robustness in combining various optimization characteristics.
To evaluate the significance of differences between the algorithms, the team conducted a rank-sum test on PSO, DAIW-PSO, and HS-PSO. The results indicated that the P-values of the rank-sum tests among the three algorithms on the CEC-2014 benchmark functions were all less than 0.05, suggesting statistically significant differences between them.
Composition Functions F23(x) to F30(x): In the more challenging composition functions, HS-PSO demonstrated superior performance with the smallest mean values and standard deviations across most functions. However, its stability could be further improved on F23(x). These results highlight HS-PSO’s capability to effectively handle complex, multimodal landscapes.
Overall, HS-PSO consistently outperformed or matched other algorithms in terms of mean fitness and stability across most CEC-2014 benchmark functions, showcasing its effectiveness and adaptability to a wide range of optimization problems.
Table 3 presents the detailed performance metrics for the 30 benchmark functions, including mean values and standard deviations across the four algorithms. The bold values represent the optimal performance for each benchmark function. Figure 6 shows the convergence curves of the algorithms on these functions, illustrating the fast and stable convergence of HS-PSO compared to the other algorithms.
Applications
Classification of Arrhythmia dataset
In high-dimensional datasets, large data volumes can lead to extended runtime for model analysis, consequently decreasing model performance. To mitigate the impact of noise and irrelevant features on the model, prevent potential overfitting, and reduce training time and computational resource demands, feature selection methods are often employed. This paper applies HS-PSO for feature selection, constructing an HS-PSO-FS model, and evaluates its performance on the UCI Arrhythmia dataset.
The UCI Arrhythmia dataset, available at UCI Arrhythmia Dataset, contains 279 features and 1 class label, including variables such as age, gender, weight, QRS duration, and various test results. Although the dataset originally includes 16 classes, this study consolidates them into two categories: normal and abnormal, encompassing 452 instances in total. Detailed experimental data is presented in Table 4. The effectiveness of the improved algorithm is demonstrated when a smaller number of selected features achieves high classification accuracy. To balance the relationship between the number of selected features and accuracy, the fitness evaluation function for HSPSO-FS is defined as follows39:
| 9 |
where Accuracy represents the accuracy rate, is the weight coefficient of accuracy, is the weight coefficient of the feature subset, and it satisfies . Here, FS denotes the number of features in the selected subset, and N is the total number of features.
Table 4.
UCI Arrhythmia dataset information.
| Dataset | Instances | Features size | Classes size |
|---|---|---|---|
| Arrhythmia | 457 | 279 | 16 |
In the experiments, both PSO-FS and HS-PSO-FS were set with a population size of 20 and a dimensionality equivalent to the total number of features in the dataset. Each algorithm was run for 100 iterations and independently executed 20 times. The comparison focused on the highest accuracy and the optimal number of feature subsets for the Arrhythmia dataset, with results shown in Table 5.
Table 5.
Comparison of experimental results between PSO-FS and HSPSO-FS on the Arrhythmia dataset.
| Model | Length of feature subset | Accuracy (%) |
|---|---|---|
| PSO-FS (best) | 143.0 | 0.791 |
| HSPSO-FS (best) | 6.0 | 0.802 |
As shown in Table 5, the experimental results indicate that HSPSO-FS offers advantages in both the length of the feature subset and accuracy. Specifically, HSPSO-FS achieves a feature subset length of only 6.0, significantly smaller than the 143.0 achieved by PSO-FS, while also attaining higher classification accuracy. This underscores HSPSO-FS’s superior performance in feature selection and classification tasks on the Arrhythmia dataset. Additionally, Table 6 compares the average feature subset length and classification accuracy across various PSO-based optimization algorithms on the Arrhythmia dataset, as reported in the literature39, against both the best and average results achieved by HSPSO-FS. The data confirms that HSPSO-FS not only reduces the feature subset size but also enhances classification accuracy, demonstrating its effectiveness and efficiency in optimizing feature selection.
Table 6.
The comparison results table of various algorithms with HSPSO-FS on dataset Arrhythmia.
According to the data in Table 6, we conducted a comparative analysis of various feature selection algorithms. Among these algorithms, HSPSO-FS stands out in both feature selection and accuracy in the best-performing trial. However, on average, ISBIPSO still performs excellently. HSPSO-FS (Best) and HSPSO-FS (Average) demonstrate outstanding performance in feature selection tasks, with average accuracies reaching 80.21% and 81.31%, respectively, significantly higher than other methods. In contrast, other algorithms such as ISBIPSO, SBPSO, UBPSO, QBPSO, CSO(C), and CSO(A) generally exhibit lower average accuracies, ranging only from 62 to 64%. Taking all factors into consideration, the HSPSO-FS algorithm demonstrates a significant advantage in feature selection tasks and can be considered the preferred method for feature selection, enhancing both the accuracy and efficiency of feature selection and providing robust support for data analysis and model construction.
Conclusions and discussion
This paper introduces an improved PSO called HSPSO, which incorporates adaptive weight adjustment mechanism, Cauchy particle mutation mechanism, fusion of reverse learning strategy, and utilizes the Hook-Jeeves strategy. The effectiveness of HSPSO is validated using CEC-2005 and CEC-2014 benchmark functions, and experimental results demonstrate that HSPSO outperforms PSO, DAIWPSO, BOA, ACO, and FA. Finally, HSPSO is combined with Support Vector Machine (SVM) for feature selection and classification on the Arrhythmia dataset. The results indicate that HSPSO-FS surpasses PSO-FS, thus confirming the feasibility of HSPSO once again.
Acknowledgements
This research was supported by the Guangxi Science and Technology Project (Grant No. Guike AB23026031, Grant No. Guike AD2302300).
Author contributions
J.Y. conceived and conducted the experiments, and participated in writing and revising the manuscript. J.D. conceptualized the flowchart and participated in manuscript revisions. H.L. generated the 3D visualization of benchmark functions. X.L., F.L. and J.L reviewed the paper and provided revision suggestions. Siyuan Yuan was responsible for proofreading the final version of the paper. All authors reviewed the manuscript.
Data availability
Data will be made available on request, and the public data of the Applications section in this article is provided within the manuscript. Requests for data can be directed to the first author, Jicheng Yao, via email at yjc_jeff@163.com.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Xiaonan Luo, Email: luoxn@guet.edu.cn.
Fang Li, Email: lifang@guet.edu.cn.
References
- 1.Simaiya, S. et al. A hybrid cloud load balancing and host utilization prediction method using deep learning and optimization techniques. Sci. Rep. 14, 1337 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rahimi, I. et al. Efficient implicit constraint handling approaches for constrained optimization problems. Sci. Rep. 14, 4816 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Abdelhameed, E. H. et al. Effective hybrid search technique based constraint mixed-integer programming for smart home residential load scheduling. Sci. Rep. 13, 21870 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Holland, J. H. Genetic algorithms. Sci. Am. 267(1), 66–72 (1992).1411454 [Google Scholar]
- 5.Eberhart, R. & Kennedy, J. Particle Swarm Optimization. In Proc. IEEE Inter Conf. Neural Netw. 4, 1942–1948 (IEEE, 1995).
- 6.Yang, X. S. & Deb, S. Cuckoo search via Lévy flights. In 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). 210–214 (IEEE, 2009).
- 7.Pant, M. et al. Differential evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 90, 103479 (2020). [Google Scholar]
- 8.Karaboga, D. An idea based on honey bee swarm for numerical optimization. Technical Report 06, Erciyes University, Engineering Faculty, Computer Engineering Department (2005).
- 9.Dorigo, M., Birattari, M. & Thomas, S. Ant colony optimization. IEEE Comput. Intell. Mag. 1(04), 28–39 (2006). [Google Scholar]
- 10.Agushaka, J. O., Ezugwu, A. E. & Abualigah, L. Dwarf mongoose optimization algorithm. Comput. Methods Appl. Mech. Eng. 391, 114570 (2022). [Google Scholar]
- 11.Yang, X. S. Nature-Inspired Metaheuristic Algorithm 81–96 (Luniver Press, 2008). [Google Scholar]
- 12.Arora, S. & Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 23(3), 715–734 (2019). [Google Scholar]
- 13.Abdelrazek, M., Abd Elaziz, M. & El-Baz, A. H. Chaotic dwarf mongoose optimization algorithm for feature selection. Sci. Rep. 14, 701 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brahim Belhaouari, S. et al. Bird’s eye view feature selection for high-dimensional data. Sci. Rep. 13, 13303 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhao, J., Zhu, X. & Song, T. Serial manipulator Time-Jerk optimal trajectory planning based on hybrid IWOA-PSO algorithm. IEEE Access 10, 6592–6604 (2022). [Google Scholar]
- 16.Akbari, M. A. et al. The cheetah optimizer: A nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci. Rep. 12(1), 10953 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghasemi, M. et al. Geyser inspired algorithm: a new geological-inspired meta-heuristic for real-parameter and constrained engineering optimization. J. Bionic Eng. 21(1), 374–408 (2024). [Google Scholar]
- 18.Ghasemi, M. et al. Optimization based on performance of lungs in body: Lungs performance-based optimization (LPO). Comput. Methods Appl. Mech. Eng. 419, 116582 (2024). [Google Scholar]
- 19.Ghasemi, M. et al. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 295, 111850 (2024). [Google Scholar]
- 20.Mohandes, M. A. Modeling global solar radiation using Particle Swarm Optimization (PSO). Solar Energy 86(11), 3137–3145 (2012). [Google Scholar]
- 21.Deng, W. et al. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 23, 2445–2462 (2019). [Google Scholar]
- 22.Demir, S. & Sahin, E. K. Predicting occurrence of liquefaction-induced lateral spreading using gradient boosting algorithms integrated with Particle Swarm Optimization: PSO-XGBoost, PSO-LightGBM, and PSO-CatBoost. Acta Geotech. 18(6), 3403–3419 (2023). [Google Scholar]
- 23.Li, F. F. et al. A developed Criminisi algorithm based on Particle Swarm Optimization (PSO-CA) for image inpainting. J. Supercomput. 80, 1–19 (2024). [Google Scholar]
- 24.Zhang, B., Song, J. & Wang, Y. PSO-DE-based regional scheduling method for shared vehicles. Autom. Control Comput. Sci. 57(2), 167–176 (2023). [Google Scholar]
- 25.Li, F. et al. A surrogate-assisted multiswarm optimization algorithm for high-dimensional computationally expensive problems. IEEE Trans. Cybern. 51(3), 1390–1402 (2020). [DOI] [PubMed] [Google Scholar]
- 26.Varna, F. T, & Husbands, P. HIDMS-PSO: A new heterogeneous improved dynamic multi-swarm PSO algorithm. In 2020 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE, 473–480 (2020).
- 27.Sun, J. et al. Solving the power economic dispatch problem with generator constraints by random drift Particle Swarm Optimization. IEEE Trans. Ind. Inf. 10(1), 222–232 (2013). [Google Scholar]
- 28.Wang, Z. J. et al. Adaptive granularity learning distributed Particle Swarm Optimization for large-scale optimization. IEEE Trans. Cybern. 51(3), 1175–1188 (2020). [DOI] [PubMed] [Google Scholar]
- 29.Zhang, Q. et al. Vector coevolving Particle Swarm Optimization algorithm. Inf. Sci. 394, 273–298 (2017). [Google Scholar]
- 30.Zare, M. et al. A modified Particle Swarm Optimization algorithm with enhanced search quality and population using hummingbird flight patterns. Decis. Anal. J. 7, 100251 (2023). [Google Scholar]
- 31.Eberhart, R. C., Shi, Y. & Kennedy, J. Swarm Intelligence (Elsevier, 2001). [Google Scholar]
- 32.Shi, Y. & Eberhart, R. C. A modified particle swarm optimizer. In Proceedings of IEEE International Conference on Evolutionary Computation. 69–73 (IEEE Press, 1998).
- 33.Shi, Y. & Eberhart, R. C. Empirical study of Particle Swarm Optimization. In Proceedings of IEEE Congress on Evolutionary Computation. 945–1950 (IEEE Press, 1999).
- 34.Wang, S. & Liu, G. A nonlinear dynamic adaptive inertia weight PSO algorithm. Comput. Simul. 38(4), 249–253 (2021). [Google Scholar]
- 35.Zhou, Z. Machine Learning (Tsinghua University Press, 2016). [Google Scholar]
- 36.Fuqing, Su. et al. Reactive power optimization based on Cauchy mutation improved Particle Swarm Optimization. J. Electr. Eng. 16(1), 55–61 (2021). [Google Scholar]
- 37.Chen, B. Optimization Theory and Algorithm (Tsinghua University Press Co., 2005). [Google Scholar]
- 38.Liang, J. J., Qu, B. Y. & Suganthan, P. N. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. Comput. Intell. Lab., Zhengzhou Univ., Zhengzhou China Tech. Rep., Nanyang Technol. Univ., Singapore 635(2), 2014 (2013). [Google Scholar]
- 39.Li, A. D., Xue, B. & Zhang, M. Improved binary Particle Swarm Optimization for feature selection with new initialization and search space reduction strategies. Appl. Soft Comput. 106, 107302 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request, and the public data of the Applications section in this article is provided within the manuscript. Requests for data can be directed to the first author, Jicheng Yao, via email at yjc_jeff@163.com.