Understanding and mitigating the impact of race with adversarial autoencoders

Abstract

Background

Artificial intelligence carries the risk of exacerbating some of our most challenging societal problems, but it also has the potential of mitigating and addressing these problems. The confounding effects of race on machine learning is an ongoing subject of research. This study aims to mitigate the impact of race on data-derived models, using an adversarial variational autoencoder (AVAE). In this study, race is a self-reported feature. Race is often excluded as an input variable, however, due to the high correlation between race and several other variables, race is still implicitly encoded in the data.

Methods

We propose building a model that (1) learns a low dimensionality latent spaces, (2) employs an adversarial training procedure that ensure its latent space does not encode race, and (3) contains necessary information for reconstructing the data. We train the autoencoder to ensure the latent space does not indirectly encode race.

Results

In this study, AVAE successfully removes information about race from the latent space (AUC ROC = 0.5). In contrast, latent spaces constructed using other approaches still allow the reconstruction of race with high fidelity. The AVAE’s latent space does not encode race but conveys important information required to reconstruct the dataset. Furthermore, the AVAE’s latent space does not predict variables related to race (R² = 0.003), while a model that includes race does (R² = 0.08).

Conclusions

Though we constructed a race-independent latent space, any variable could be similarly controlled. We expect AVAEs are one of many approaches that will be required to effectively manage and understand bias in ML.

Plain Language Summary

Computer models used in healthcare can sometimes be biased based on race, leading to unfair outcomes. Our study focuses on understanding and reducing the impact of self-reported race in computer models that learn from data. We use a model called an Adversarial Variational Autoencoder (AVAE), which helps ensure that the models don’t accidentally use race in their calculations. The AVAE technique creates a simplified version of the data, called a latent space, that leaves out race information but keeps other important details needed for accurate predictions. Our results show that this approach successfully removes race information from the models while still allowing them to work well. This method is one of many steps needed to address bias in computer learning and ensure fairer outcomes. Our findings highlight the importance of developing tools that can manage and understand bias, contributing to more equitable and trustworthy technology.

Sarullo and Swamidass use an adversarial variational autoencoder (AVAE) to remove race information from computer models while retaining essential data for accurate predictions, effectively reducing bias. This approach highlights the importance of developing tools to manage bias, ensuring fairer and more trustworthy technology.

Introduction

Artificial intelligence (AI) carries the risk of exacerbating some of our most challenging societal problems, but it also has the potential of mitigating and addressing these problems. As a relatively new area of research, AI for social good, aims to apply AI to address current social, environmental, and public health challenges^1,2. One chief concern is understanding and mitigating the impact of race on machine learning (ML)^3–6.

This study aims to mitigate the impact of race on data-derived models. In this study, race is represented as a binary variable, where patients self-identify as either Black or non-Black. Race is often highly correlated with the target variable. Consequently, predictive models often rely heavily on race in making predictions. Race is also highly correlated with other input variables. So models that do not include race explicitly as an input variable might still rely on proxies of race, thereby implicitly relying on a high-fidelity estimate of race.

To overcome the challenges of training a race-independent model, we propose using an adversarial variational autoencoder (AVAE) to ensure the information used for building ML models is independent of race. The AVAE (1) learns a low dimensionality latent spaces, (2) employs an adversarial training procedure that ensure its latent space does not, even implicitly, encode race, and (3) contains necessary information for reconstructing the data. While training the autoencoder, a race predictor uses the latent space as an input. The autoencoder’s weights are tuned to maximize the loss of this predictor, while the predictor’s weights are tuned to minimize its loss. This study benchmarks and studies this approach in a clinical dataset that relates birthweight, race, and several other clinical variables.

Autoencoders (AE) are a widely used technique, applicable to tasks such as disentangling information, anomaly detection, data generation, classification, clustering, dimensionality reduction, and data visualization. Autoencoders are also used for representation learning, often to encode electronic healthcare records (EHRs) for prediction tasks⁷. Common tools used in representation learning include stacked spare autoencoders⁸, deep belief networks⁹, variational autoencoders^10,11, weighted autoencoders¹², and adversarial autoencoders (AAE)¹³. The results of a comparative study state that a variational autoencoder worked well in capturing and summarizing information from EHRs.

In addition to the wide use of AAEs, there are several bodies of work attempting to disentangle race from related factors in machine learning models¹⁴. This related work uses a very similar dataset to disentangle and identify sources of effects for socioeconomic status and other psychosocial factors stating race is often used as a proxy. However, there is no use of latent spaces to predict these infant outcomes. This analysis will also use these latent spaces for prediction on a real-world clinical problem to see how each latent space performs.

Autoencoders are already widely used to separate and disentangle variables. One study, for example, uses an AE to separate style and content from images, demonstrating that the digit displayed in an image can be separated from the style of the digit¹³. Though termed an adversarial AE, this study does not include adversarial training or loss. Instead, it includes the class labels in the latent space, essentially controlling the style latent space for the digit class. As we will see, while the learned latent vector can, in principle, be independent of the control variable, there are still correlations between the latent vector and the controlled variable. As a point of comparison, this approach is included as a Race-Control variational autoencoder (VAE) and latent space.

Another approach to adversarially predicting variables is called adversarial debiasing¹⁵. Adversarial debiasing has also been used with latent space applications¹⁶. This work is very similar, however, our method employs an adversarial training procedure that ensures its latent space does not, even implicitly, encode race. Specifically, race has a confounding effect in clinical studies therefore mitigating any effect of race is crucial to determine underlying relationships where race acts as a proxy.

In contrast, we propose building ML models based on a latent space with stronger separation, by minimizing the performance of a strong predictor trained to reconstruct race from the latent space. This study addresses this issue by using an adversarial variational autoencoder (AVAE) to mitigate the impact of race, which, although often excluded as an input variable, is still implicitly encoded due to correlations with other variables. This approach is truly adversarial, in that the autoencoder network is trained with one loss function, while a predictor network is trained with an oppositely directed loss. We develop a model that learns low-dimensional latent spaces, employs adversarial training to ensure these spaces do not encode race, and retains necessary information for data reconstruction. The AVAE effectively removes race information from the latent space (AUC ROC = 0.5), unlike other approaches which allow high-fidelity reconstruction of race. The AVAE’s latent space does not predict race-related variables (R² = 0.003), whereas models including race do (R² = 0.08). Although this study focuses on creating a race-independent latent space, the approach can be adapted to control for other variables. AVAEs represent one of many necessary strategies to effectively manage and understand bias in machine learning.

Methods

The dataset for this research is provided through the Early Life Adversity and Biological Embedding of Risk for Psychopathology (eLABE) study, a multi-wave multi-method NIMH-funded investigation designed to study the mechanisms by which prenatal and early life adversity impact infant neurodevelopment. Other methods have struggled to include race in their models due to the high collinearity race has to several other variables¹⁷. Machine learning methods have been shown to handle highly collinear data more gracefully than common statistical techniques like structural equation modeling (SEM).

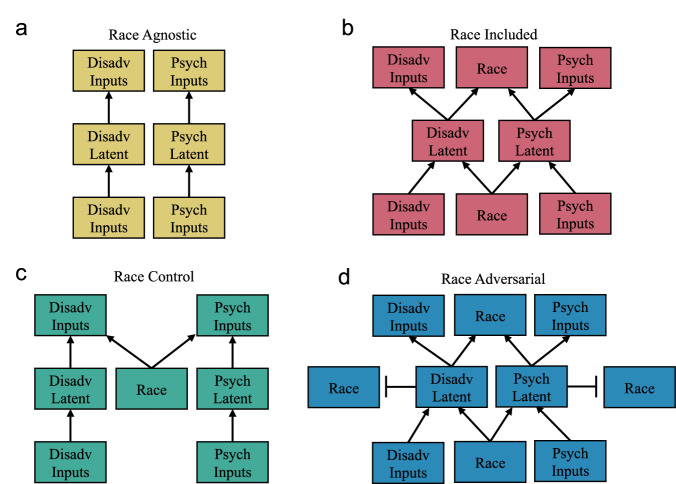
To address these challenges, we develop four distinct autoencoders that generate different latent spaces from the same dataset: (1) a Race-Agnostic version that does not include race as an input variable, (2) a Race-Included version that does include race, (3) a Race-Control version that includes race in the latent space to enable separation of race and non-race components of the latent space, and (4) a Race-Adversarial version that minimizes the correlation between race and the latent space (Fig. 1).

Fig. 1. Variational AutoEncoder model architectures used to disentangle race from other factors.

Each Variational AutoEncoder (VAE) trains two named latent spaces, disadvantage and psychological stress, where the inputs are separated into categories. a The Race-Agnostic VAE has no overlap in inputs. There are two separate encoders and decoders for the different inputs. b The Race-Included VAE inputs races to both latent spaces and reconstructs race. c The Race-Control VAE concatenates race to both latent spaces. d The Race-Adversarial Adversarial Variational AutoEncoder (AVAE) inputs race to both latent spaces and reconstructs race. This model is adversarial due to the adversarially-trained race predictor added to the model (depicted with a t-shaped connector).

Autoencoders

Autoencoders (AE) have two components, an encoder network, and a decoder network. The encoder compresses knowledge of the original input to a smaller dimensionality, creating a latent space, and the decoder reconstructs the original data. The latent space can in turn decrease the complexity of future modeling tasks. Both, the encoder and decoder, tasks minimize a reconstruction loss function (Equation (1)), such as

$$L_R=\mid \mid x-\widehat{x}\mid {\mid }_2.$$ 1

This loss function is the mean squared error between the encoder input (x) and decoder output ($\widehat{x}$). Other reconstruction losses are possible, but largely independent of this inquiry.

Variational autoencoders (VAE) are an improvement on the simplest formulations of an autoencoder, and the focus of this study. Instead of computing a point estimate of the latent space from the encoder, the encoder network (e) outputs a mean (μ_x) and standard deviation (σ_x) for each component of the latent space. A sample from this latent space distribution is sent to the decoder network (d) with added noise (ϵ),

$$\widehat{x}=d\left({\mu }_x+{\sigma }_xϵ\right).$$ 2

The total loss is the sum of the reconstruction loss and the Kullback–Leibler (KL) loss¹⁸,

$$L=L_R+L_{KL}.$$ 3

The KL loss regularizes the latent space to be normally distributed. It is defined as the KL divergence between the latent space and the standard distribution,

$$L_{KL}=D_{kl}\left(\mathcal{N}\left({\mu }_x,{\sigma }_x\right)\mid \mid \mathcal{N}\left(\mathbf{0},\mathbf{I}\right)\right).$$ 4

In this study, the Race-Agnostic, Race-Included, and Race-Control latent spaces all use this loss (Fig. 1). The encoder and decoder tasks for each of the above models contains five hidden layers to train the disadvantage and psychological stress latent space. Each hidden layer uses an Exponential Linear Unit (ELU) activation function while the output layers use an activation function specific to type of data. Continuous data use a linear activation function and categorical and binary variables use a sigmoid activation function. To fit the models, the Root Mean Square Propagation (RMSProp) optimizer uses a validation split of 0.2, a learning rate of 0.001, shuffling enabled, and 100 epochs.

Adversarial variational autoencoders

The autoencoder we develop for this study is an adversarial variational autoencoder (AVAE). This AVAE has one extra term subtracted from the VAE’s total loss: the predictor loss (Equation (5)).

$$L=L_R+L_{KL}-L_P.$$ 5

This final term is defined as the cross entropy loss between the race variable and the prediction of a network that is trained to predict race based on the latent space (Equation (6)).

$$L_P=-\frac{1}{n}{\sum }_{i=1}^n{y}_i\cdot \log {\widehat{y}}_i+\left(1-y_i\right)\cdot \log \left(1-{\widehat{y}}_i\right).$$ 6

The weights of the predictor minimize the predictor loss, while the weights of the autoencoder train in the opposite direction, to maximize the predictor loss. This model is referred to as the Race-Adversarial VAE (Fig. 1d). The only difference in setup for this model is the use of 500 epochs and a batch size of 128.

Race predictor

The latent space of each AE attempt to predict race. In the case of the AVAE, this was an added predictor distinct from the predictor trained alongside the autoencoder. This predictor contains a single hidden layer of width two with the Exponential Linear Unit (ELU) activation function. To fit the models, RMSProp optimizer uses a learning rate of 0.001, a random uniform initializer for the weights, L2 regularization, and 50 epochs. The output layer uses a sigmoid activation function. We compare results both with and without 5-fold cross-validation, and they were not sensitive to adjustments to the predictor’s architecture.

Child birthweight predictor

Additionally, we investigate the utility of the latent space by building a predictor of child birthweight, a target that is highly correlated with several adverse medical outcomes. We consider two types of birthweight prediction models, a linear regressor (LR) and a neural network (NN). Each model type then has two input options, a stand-alone latent space, or the latent space with a concatenated race variable. The linear regressor trained directly from the inputs to child birthweight while the neural network contained a hidden layer of width two with the Exponential Linear Unit (ELU) activation function. The output layer uses a linear activation function. To fit the models, RMSProp optimizer uses a learning rate of 0.001, a random uniform initializer for the weights, L2 regularization, and 100 epochs with 5 restarts The results were computed with 5-fold cross-validation.

Comparison metrics

Throughout this analysis, we make use of several comparison metrics. To compare the performance of the latent spaces in the autoencoders, we compare reconstruction loss, defined above. To compare the performance of the latent space predicting race, we use the Area Under The Curve (AUC) Receiver Operating Characteristics (ROC) curve. The higher the curve, the better the model is at classifying the outcome. To compare the performance of the latent spaces predicting birthweight, we use the coefficient of determination or R² value. The higher the R² value, the better the model is at predicting the outcome. All p values provided are performed with a two-sided p-test.

Data

Early Life Adversity Biological Embedding and Risk for Developmental Precursors of Mental Disorders (eLABE), is a multi-wave, multi-method NIMH-funded study designed to investigate the mechanisms by which prenatal and early life adversity impact infant neurodevelopment. All study procedures were previously approved by the Washington University School of Medicine Institutional Review Board (WUSM IRB). Pregnant women who were participants in a large-scale study of preterm birth within the Prematurity Research Center at Washington University in St. Louis with negative drug screens (other than cannabis) and without known pregnancy complications or known fetal congenital problems, were invited for eLABE participation. Written informed consent was obtained for each participant, with written parental informed consent for each infant. The study recruited N = 395 women during pregnancy (N = 268 eligible subjects declined participation) and their N = 399 singleton offspring (N = 4 mothers had 2 singleton births during the recruitment period). Out of those originally invited and interested in participation, N = 26 were deemed ineligible (N = 13 screened out prior to consent and N = 13 consented subjects were deemed ineligible due to later discovery of substance abuse or the finding of a congenital anomalies). Women facing social disadvantage were over-sampled by increased recruitment from a clinic serving low-income women. The sample was also enriched for preterm infants with N = 51 born preterm (<37 weeks gestation). Of the 399 pregnancies, 50 reported tobacco use during pregnancy, and 49 reported cannabis use (of which 20 reported both).

A variety of variables describing maternal social disadvantage and maternal psychosocial stress were collected and used for analyses throughout this study (Table 1). Social disadvantage is described by income to needs, Area Deprivation Index (ADI)^19,20, maternal nutrition, (through the Healthy Eating Index (HEI))^21–24, self-reported race, insurance status, mother’s education, and discrimination²⁵. Psychosocial stress is described by the Edinburgh Postnatal Depression Scale (EPDS)²⁶, Perceived Stress Scale (PSS)²⁷, and lifetime stressful and traumatic life events (STRAIN)^28,29. A confirmatory factor analysis was used to derive these variables as a two latent construct¹⁷. Since missing data poses a challenge when working with clinical data, we employ a straightforward imputation method. Continuous missing variables are substituted with the mean value of the respective column while binary or categorical variables are substituted with the median value of the respective column.

Table 1.

Descriptions of variables used in analysis

Variable	N	Mean (SD) or N (%)	Blacks Mean (SD) or N (%)	Non-Blacks Mean (SD) or N (%)	R2 to Race
Social Disadvantage
Log10 Income to Needs
1st Trimester	385	0.24 (0.40)	0.009 (0.23)	0.61 (0.33)	0.509
2nd Trimester	305	0.28 (0.41)	0.015 (0.235)	0.63 (0.31)	0.447
3rd Trimester	330	0.26 (0.41)	0.004 (0.233)	0.62 (0.32)	0.469
Area Deprivation Index	376	69.09 (24.84)	81.08 (16.84)	51.21 (24.49)	0.342
Healthy Eating Index 2016	308	58.45 (9.90)	55.72 (9.08)	62.32 (9.75)	0.086
Race	399
Black		249 (62%)
Not Black		150 (38%)
Health Insurance	399
Individual/Group		200 (50%)	74 (30%)	126 (84%)	0.190
Medicaid		145 (36%)	131 (53%)	14 (9%)	0.000
Medicare		7 (2%)	4 (1%)	3 (2%)	0.277
Uninsured		45 (11%)	39 (15%)	6 (4%)	0.000
VA/Military		2 (1%)	1 (1%)	1 (1%)	0.032
Education	356
Less than high school		26 (7%)	21 (10%)	5 (3%)	0.010
High school grad		196 (55%)	169 (79%)	27 (19%)	0.237
College grad		56 (16%)	19 (9%)	37 (26%)	0.056
Post-grad degree		77 (22%)	3 (2%)	74 (52%)	0.349
Discrimination Survey	364	1.62 (0.88)	1.66 (0.97)	1.20 (0.60)	0.054
Psychosocial Stress
Edinburgh Postpartum Depression Scale
1st Trimester	396	5.25 (4.88)	5.83 (5.08)	4.29 (4.37)	0.024
2nd Trimester	331	5.00 (4.94)	5.49 (5.19)	4.25 (4.45)	0.013
3rd Trimester	332	4.38 (4.70)	4.63 (5.04)	4.02 (4.16)	0.004
Perceived Stress Survey
1st Trimester	394	13.69 (7.39)	14.68 (7.30)	12.08 (7.26)	0.029
2nd Trimester	304	13.81 (7.68)	15.23 (7.97)	11.89 (6.84)	0.037
3rd Trimester	325	13.25 (7.36)	13.74 (7.50)	12.55 (7.12)	0.005
STRAIN (Life Events)	372
STRAIN-CT (count)		6.70 (5.31)	7.84 (6.39)	7.25 (5.50)	0.002
STRAIN-WTSEV (weighted severity)		22.67 (19.91)	23.86 (21.49)	20.93 (17.21)	0.005
Outcomes
Birthweight	399	3134 (599)	3008 (582)	3343 (568)	0.074

This table includes statistical information on each variable used within this study analysis.

Social disadvantage and psychosocial stress latent spaces

In this particular case, there is a semantic partition between variables (Table 1). There are 8 variables associated with social disadvantage and 8 variables associated with psychosocial stress, not including race. If race is included, social disadvantage and psychosocial stress would have a dimensionality of 9. Both the social disadvantage latent space and the psychosocial stress latent space have a reduced dimensionality of 1.

The structure of each VAE and AVAE was modified to use each partition of inputs to construct a corresponding latent space (Fig. 1). The Race-Agnostic VAE has the disadvantage inputs encoded into a disadvantage latent space which reconstructs the disadvantage inputs. Separately the psychosocial stress inputs are encoded into a psychosocial stress latent space which reconstructs the psychosocial stress inputs. (Fig. 1a). The Race-Included VAE works similarly, however, race is fed into the encoder to both latent spaces and reconstructed (Fig. 1b). The Race-Control VAE concatenates race to both latent spaces before the decoder runs (Fig. 1c). The Race-Adversarial AVAE has race as an input to both latent spaces and each latent space is connected to a separate race predictor (Fig. 1d).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Results and discussion

Reconstruction loss

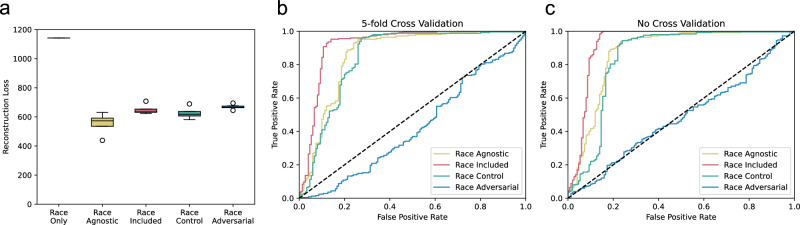
The first assessment of each approach is the reconstruction loss (Fig. 2a). The lower the reconstruction loss the more accurately the latent space (alongside the race variable, when noted) encodes the input data. We find that the reconstruction loss of all four VAEs is statistically indistinguishable (loss of 553, 650, 626, and 668, respectively). As a control, a model trained to predict all variables from only race is substantially worse, with a reconstruction loss close to twice that of the autoencoders (loss of 1142), indicating approximately 50% of variation in this dataset is independent of race. We conclude that the four autoencoders enable essentially equivalent reconstructions of the data, and that their latent spaces all encode the information necessary for the reconstruction of the data.

Fig. 2. The Race-Adversarial VAE effectively obscures race while maintaining reconstruction accuracy.

We compare different performance metrics for the latent spaces. a The reconstruction loss is the combined reconstruction loss for both disadvantage and psychosocial stress. The lower the reconstruction loss, the more accurately the latent space encodes the input data. We find that the reconstruction loss of all four Varational AutoEncoders (VAEs) are statistically indistinguishable (loss of 553, 650, 626, and 668, respectively). b The Race-Agnostic, Race-Included, and Race-Control VAEs all compute latent spaces from which race could be reconstructed with high fidelity (5-fold cross-validated Area Under the Curve (AUC) = 0.85, 0.92, and 0.83, respectively). The Race-Adversarial VAE's latent space predictor yields a cross-validated AUC substantially worse than a random predictor (AUC = 0.41). Race can still be accurately modeled by flipping the sign of the predictions. c The AUC of a trained predictor on its training set (without cross-validation), however, is indistinguishable from a random predictor (AUC = 0.49, p value = 0.3385), indicating that the predictor was trained appropriately and the AUC was artificially lowered below a random as an artifact of cross-validation.

Reconstructing race from the latent

We next systematically quantify the relationship between race and the latent spaces (Fig. 2). While correlation is one way of assessing this relationship, it might miss more complicated non-linear and multivariate relationships that would still enable a flexible ML model to reconstruct race. Consequently, we focused instead on a more stringent test: the performance of a predictor of race, trained on the concatenated latent spaces of each VAE.

We aim to build a latent space that is independent of race and from which race cannot be reconstructed. Perhaps unsurprisingly, the Race-Agnostic, Race-Included, and Race-Control VAEs all compute latent spaces from which race could be reconstructed with high fidelity (5-fold cross-validated AUC = 0.85, 0.92, and 0.83, respectively). This indicates that models built using latent spaces of all three of these approaches can still, implicitly or explicitly, rely on race.

In contrast, the Race-Adversarial VAE’s latent space predictor yields a cross-validated AUC substantially worse than a random predictor (AUC = 0.41) (Fig. 2b). This result raises concern that race is indeed possible to reconstruct from the predictor, by flipping the sign of the predictions. This also may be a sign of overfitting. We can quantify how much we are over-correcting by comparing the results with and without cross-validation. The AUC of a trained predictor on its training set, without cross-validation is indistinguishable from a random predictor (AUC = 0.49, p value = 0.3385), indicating that the predictor was trained appropriately with no substantial overfitting. The AUC was artificially lowered below a random as an artifact of cross-validation (Fig. 2c). We conclude, therefore, that race has been entirely disentangled from the AVAE’s latent space, and a model built using this latent space will be independent of race.

Distribution of race in latent space

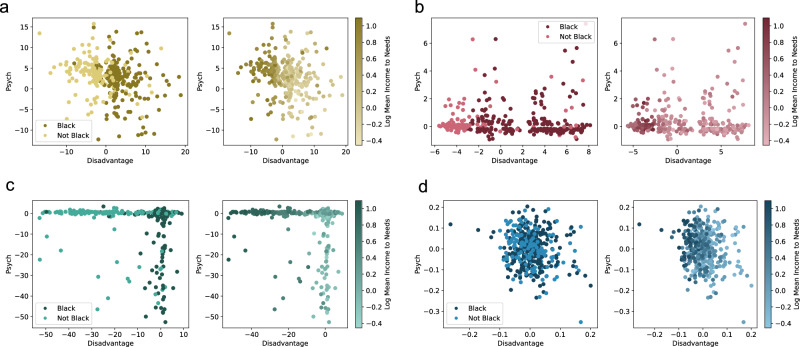
Of particular interest to our inquiry is the relationship between each latent space and the race variable. Our first approach to assessing this relationship is an examination of the distribution of race in the latent space. Particularly, race should not be visually separable within the latent space (Fig. 3).

Fig. 3. The Race-Adversarial VAE cannot be easily separability by race and maintains a monotonic relationship with income-to-needs.

Of particular interest is the relationship between each latent space and the race variable. Race should not be visually separable within the latent space. In addition, domain experts expect income-to-needs to be monotonically related to the latent space, at least within each race subgroup. a The latent space of the Race-Agnostic Variational AutoEncoder (VAE) was obviously separable by race and there is a clear relationship between disadvantage and income to needs. b The latent space of the Race-Included VAE exhibited similar results. c The latent space of the Race-Control VAE also exhibited similar results which is a surprising result. Controlling for race in this manner is not enough for race to be inseparable. d The latent space of the Race-Adversarial AVAE was completely inseparable making predicting race a difficult task. As a result, it becomes difficult to see whether the latent space is also monotonically related to the latent space within each race subgroup, however, this is easily solved by plotting each race subgroup individually.

Black and non-Black patients are clearly separable in the latent space of the Race-Agnostic VAE (Fig. 3a), consistent with the high AUC performance of a classifier trained on this latent space (Fig. 2). Similar results follow with the latent space of the Race-Included VAE (Fig. 3b) and the latent space of the Race-Control VAE (Fig. 3c). This is, perhaps, a surprising result for the latent space of the Race-Control VAE. How this model controls for race is not sufficient to disentangle race from its latent space. However, the latent space of the Race-Adversarial AVAE is completely inseparable by race (Fig. 3d). The adversarial component of the AVAE was able to mask the impact of race and related psychosocial factors.

Distribution of Income-to-Needs Ratio in Latent Space

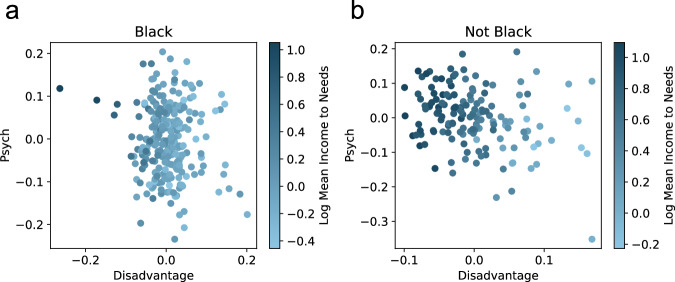
Though race is not encoded, other variables, such as the income-to-needs ratio, are encoded in the latent spaces. Domain experts expect income-to-needs to be monotonically related to the latent space, at least within each race subgroup. The latent spaces of the Race-Agnostic VAE (Fig. 3a), the Race-Included VAE (Fig. 3b), and the Race-Control VAE (Fig. 3c) are consistent with this constraint. Although not perfectly monotonic, there is a clear relationship between disadvantage and income to needs. Future work can address this limitation by adding monotonicity constraints to the VAE. At first glance, it is not clear that the latent space of the Race-Adversarial AVAE is monotonically related to the latent space within each race subgroup (Fig. 3d). This is easily resolved by observing each racial subgroup individually (Fig. 4). Within each race subgroup, patients are monotonically related to the latent space, consistent with expectations.

Fig. 4. The race-adversarial VAE maintains income-to-needs correlation within race subgroups.

Domain knowledge anticipated income-to-needs to be monotonically related to the latent space, within each race subgroup. The latent space of the Race-Adversarial Adversarial Variational AutoEncoder (AVAE) was unclear because it was inseparable by race. a When plotting only Black participants, the log mean income to needs is clearly correlated with the latent space, disadvantage. b When plotting only non-Black participants, a similar result follows, hence the latent space of the Race-Adversarial AVAE is also consistent with domain knowledge.

Modeling birthweight with latent spaces

The four latent spaces were applied to the task of modeling child birthweight (Fig. 5). Two types of models were implemented for this task, a linear regressor (LR) (Fig. 5a) and a neural network (NN) (Fig. 5b). Similar to previous work¹⁴, all NN models outperformed the LR models. A neural network can uncover additional relationships otherwise missed by a linear model due to the lack of a non-linear component, and the NN results are therefore where we focus, though are conclusions from the LR data alone are unaltered (Fig. 5c).

Fig. 5. The Race-Adversarial VAE was unable to predict birthweight without race included while all other models showed minimal improvement with the inclusion of race, confirming that race is encoded in all latent spaces except the Race-Adversarial VAE.

The four latent spaces were applied to the task of modeling child birthweight. The inputs are greyed out because they have been trained. The question mark indicates race either is or is not concatenated to the latent space. a A linear regressor (LR) and (b) a neural network (NN) were used to predict child birthweight. c The LR and (d) NN R² performances were recorded for each latent space predicting child birthweight without race. As a baseline, we use all data describing both social disadvantage and psychosocial stress to model child birthweight with LR and NN (R² = 0.038 and R² = 0.072, respectively). The NN trained on the Race-Agnostic, Race-Included, and Race-Control latent spaces can all predict birthweight (R² = 0.051 p value  < 5.12e-06, R² = 0.088 p value  < 1.63e-09, and R² = 0.056 p value  < 1.9e-06, respectively), but the Race-Adversarial Variational AutoEncoders (VAEs) performance was indistinguishable from zero (R² = 0.003, p value = 0.31). e The LR and (f) NN R² performances were recorded for each latent space, concatenated with race, predicting child birthweight. The performance of each model is approximately the same, with the exception of the Race-Adversarial VAE. When its latent space is concatenated with race, the performance is essentially identical to the other predictors. All predictors performed better than a model trained only on race, indicating that useful information was encoded in their latent spaces.

As a baseline, we use all data describing both social disadvantage and psychosocial stress to model child birthweight with LR and NN (R² = 0.038 and R² = 0.072, respectively). NN trained on the Race-Agnostic, Race-Included, and Race-Control latent spaces can all predict birthweight (R² = 0.051 p value  < 5.12e-06, R² = 0.088 p value  < 1.63e-09, and R² = 0.056 p value  < 1.9e-06, respectively), but the Race-Adversarial VAE’s performance was indistinguishable from zero (R² = 0.003, p value = 0.31) (Fig. 5d). The first three performances are low, by the standards of ML, but still on par with the performance of models in this domain¹⁴. Much of the variability in this dataset is not accounted for by the measured factors. Notably, the more race was encoded within each latent space, the higher the R² value. The latent space of the Race-Included VAE modeled child birthweight with the highest performance, followed by the latent space of the Race-Control VAE, the latent space of the Race-Agnostic VAE, and finally the latent space of the Race-Adversarial AVAE.

As a control, we model child birthweight by training a predictor based on each latent space concatenated with the race variable. Notably, the performance of each model is approximately the same, with the exception of the Race-Adversarial VAE (Fig. 5e). When its latent space is concatenated with race, the performance is essentially identical to the other predictors. All predictors performed better than a model trained only on race, indicating that useful information was encoded in their latent spaces (Fig. 5f). Moreover, using latent spaces performed similarly, if not better than, using all data available.

These results demonstrate how important race is for modeling child birthweight. In fact, all the information predictive of birthweight, in this dataset, is entirely correlated with race. The information in the dataset independent of race is not predictive of birthweight. Consequently, building a birthweight predictor independent of race may not be possible. Consequently, the low performance of the Race-Adversarial latent space is not a deficiency, but reflective of the structure of this dataset, giving us important insight into the relationship between race and birthweight in this dataset.

To build race-independent models, we need to identify different variables that provide information independent of race, and are correlated with birthweight. Our Race-Adversarial approach provides a stringent approach to quantifying the value of different variables to this end, and thereby can guide research in this area. Although this work focuses on creating a race-blind model, a reviewer has suggested it could possibly be applied to gender as well.

Conclusion

We develop an autoencoder that constructs an adversarially-controlled latent space, from which race cannot be reconstructed. In contrast, race is reconstructed with high fidelity from the latent space of more widely used approaches, causing models built on these latent spaces to implicitly rely on race. The adversarially-controlled latent space encodes the information in the dataset that is independent of race, enabling the construction of models that are independent of race, and quantifying how important race is to particular tasks.

Though this study focuses on race, our approach is trivially generalizable to build latent spaces that do not encode any particular variable. So this approach may be useful in several domains. For example, adversarial VAEs can construct latent spaces for public disclosure and sharing, adversarially trained not to encode information about particular columns of the dataset. In this way, the latent space might be shareable with strong security and privacy guarantees.

In the case of race, however, this study also highlights the high correlation of race with key target variables, and the difficulty of disentangling race from ML. We expect AVAEs are one of many approaches that will be required to effectively manage and understand bias in ML.

Author contributions

The authors confirm contribution to the paper as follows: study conception, design, and data collection: K.S., S.J.S.; We would like to acknowledge Deanna M. Barch, Christopher D. Smyser, Cynthia Rogers, Barbara B. Warner, J. Philip Miller, and Joan Luby for their contributions to the Early Life Adversity and Biological Embedding of Risk for Psychopathology (eLABE) study and access to the data; analysis and interpretation of results: K.S., S.J.S.; draft manuscript preparation: K.S.; All authors reviewed the results and approved the final version of the manuscript.

Peer review

Peer review information

Communications Medicine thanks Oguz Akbilgic and Tian Xia for their contribution to the peer review of this work. Peer reviewer reports are available.

Data availability

All data that support the findings of this study are included within this paper and its Supplementary Data. Source data for the figures are available as Supplementary Data 1.

Code availability

All code is available on the GitHub repository³⁰.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s43856-024-00627-3.