Low-Ohmic Resistance Comparison: Measurement Capabilities and Resistor Traveling Behavior

Abstract

The low-ohmic resistance measurement capabilities of the Van Swinden Laboratorium, National Institute of Standards and Technology, and the Federal Office of Metrology (METAS) were compared using a set of resistors with values 100 mΩ, 10 mΩ,1 mΩ, and 100 μΩ, respectively. The measurement results of the three laboratories agree extremely well within the respective measurement uncertainties with the comparison reference value. Careful transport of the resistors was crucial for achieving this result. Still, some of the resistors showed steps in value at each transport which likely relates to the construction of the resistance elements of these resistors.

I. Introduction

Low-ohmic resistors are important for the power industry, where shunts are, for example, used for the measurement of large direct and alternating currents. For the best uncertainties, shunts are required with good long-term stability and both a small temperature and power coefficient. The latter is particularly relevant for resistance values of 1 mΩ and lower, since shunts at these very low levels are typically used in industry at dissipations above 1 W in order to have a sufficient voltage signal. This 1-W dissipation is much larger than the 10-mW dissipation usual in precision resistance measurements.

The traceability of industrial shunt measurements worldwide is provided by national metrology institutes (NMIs). Given the economic importance of these measurements, it is useful to compare low-ohmic resistance measurement capabilities at the best uncertainty level between NMIs. Still, in the past decades, very few efforts have been performed at NMI level in this resistance range.

In 1998–2000, a bilateral comparison between the Swedish National Testing and Research Institute (SP, Sweden) and Justervesenet (JV, Norway) was performed, containing, among others, 1- and 10-mΩ resistance standards. The differences in measurement values of the two laboratories at these resistance levels were (1.9 ± 4.0) and (−0.3 ± 1.8) μΩ/Ω, respectively [1]. In order to reduce problems with the transport behavior of the standards, they were transported by car between SP and JV. Still, the 10-mΩ resistor suffered once from a 6-μΩ/Ω change in value, during the first transport. Since the two laboratories measured each resistor twice, the first measurement point could be discarded for this particular resistor [2].

During 2005–2007, a similar bilateral comparison was organized between the Van Swinden Laboratorium (VSL, the Netherlands) and the National Physical Laboratory (NPL, U.K.) for resistance values from 100 mΩ down to 100 μΩ. Here, the resistors (one at each resistance value) were not hand carried between the two laboratories, and the traveling behavior of the resistance standards limited the uncertainties achieved in the comparison to not better than a few parts in 10⁶ [3], well above the claimed calibration measurement capabilities of VSL and NPL.

In 2011–2012, an exercise was performed, aiming to evaluate the low-ohmic measurement capabilities of the National Institute of Standards and Technology (NIST, U.S.), the Van Swinden Laboratorium (VSL, NL), and the Federal Office of Metrology (METAS, CH). Resistors with values between 100 mΩ and 100 μΩ were measured by each institute. Following the lessons learned from the previous two comparisons described earlier, at least two resistors were available for each resistance value, and furthermore, extra attention was paid to the transport of the resistors. The initial results of the NIST and VSL measurements have already been reported [4]. This paper describes the final results of this exercise, including the measurements of METAS. First, a short description is given of the respective measurement setups at the three NMIs, as well as of the resistors used in the comparison. This is followed by the presentation and discussion of the measurement results of the comparison.

II. Low-Ohmic Measurement Systems

A. VSL

A schematic overview of the VSL low-ohmic measurement setup is shown in Fig. 1. It is a dedicated home-built system, based on a commercial current comparator [5]. In most measurement laboratories, as, e.g., NIST and METAS, this instrument is used as range extender in conjunction with a direct current comparator (DCC) resistance measurement bridge (see Fig. 2). In the VSL system, the current extender is used as stand-alone current comparator. A high-current source drives a large current $I_x$ through $R_x$, and the internal current source $I_s$ in the current comparator is adjusted by an internal feedback system such that the current ratio in the two arms of the bridge is equal to the reciprocal of the winding ratio of the comparator:$N_s·I_s=N_x·I_x$. The comparator has three winding ratios, 1 : 10, 1 : 100, and 1 : 1000, respectively. The applied current is measured with a current meter in the low-current arm of the bridge. A nanovoltmeter measures the voltage resulting from any deviation of the resistance ratio from the current ratio (i.e., the comparator winding ratio). The main difference with commonly used DCC resistance bridges is that, in the VSL system, the reading of the nanovoltmeter is not zeroed by a voltage feedback system. Thus, the gain of the nanovoltmeter needs to be stable and known, which is not a problem with the high-quality nanovoltmeters that are presently commercially available, such as the Agilent 34420A used in this setup.¹

Fig. 1.

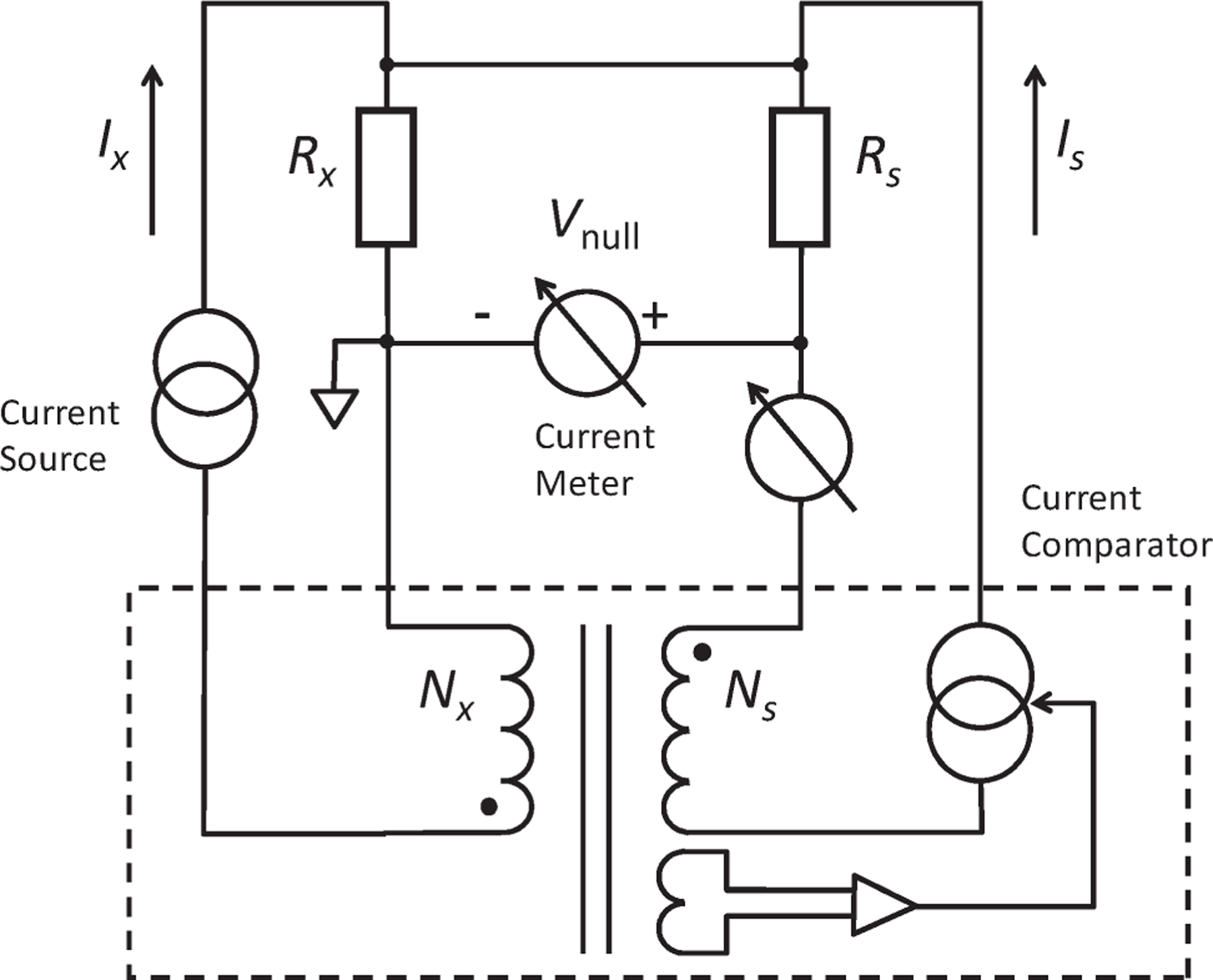
Schematic overview of the low-ohmic measurement bridge at VSL. The dashed box indicates the current comparator for balancing the currents in the two arms of the bridge. The dc high-current source can generate $I_x$ currents up to 100 A.

Fig. 2.

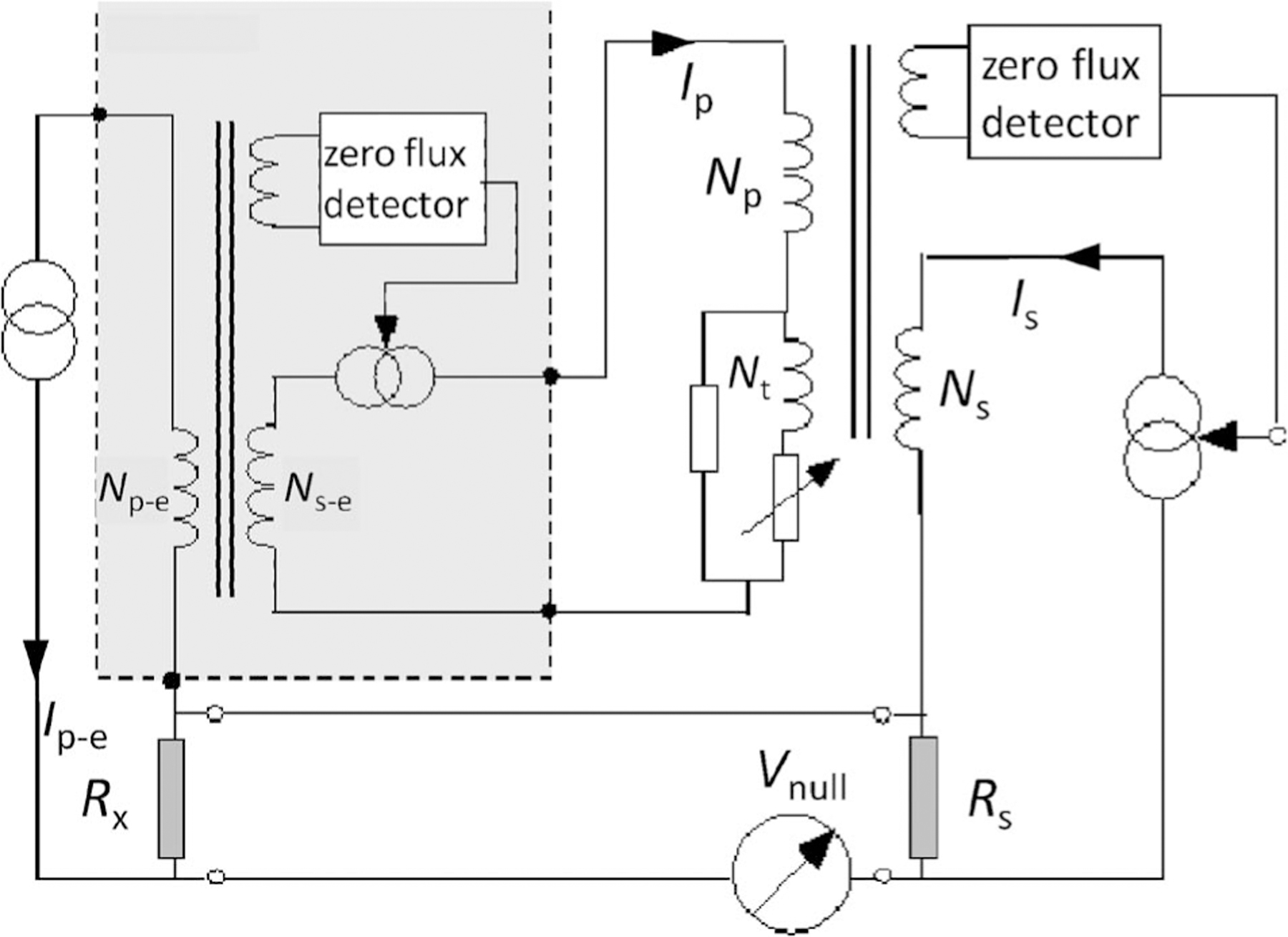
Schematic overview of the low-ohmic measurement system used at METAS and NIST based on a (top right) commercial room-temperature current comparator bridge, together with a (gray area) range extender and (left) dc current source capable of driving maximally 100 A.

The setup is completely automated and includes a scanner, with low-thermal voltage switches and capable of switching currents up to 30 A, so that all resistors can be repeatedly measured without any operator action. A typical measurement on a single resistor contains 13 current reversals, and the results of the last ten reversals are used to calculate a resistance value. For none of the resistors, a significant drift caused by the 10-mW measurement power could be seen during the measurements.

Dominant uncertainty sources in the setup are the noise in the measurements, the calibration of the nanovoltmeter, and the accuracy of the current comparator ratios. The latter is checked via an extensive series of cross-checks as follows:

$$1\mathrm{\Omega }\to 100\text{m}\mathrm{\Omega }\to 10\text{m}\mathrm{\Omega }\to 1\mathrm{\Omega }$$

$$1\mathrm{\Omega }\to 100\text{m}\mathrm{\Omega }\to 1\text{m}\mathrm{\Omega }\to 1\mathrm{\Omega }$$

$$100\text{m}\mathrm{\Omega }\to 10\text{m}\mathrm{\Omega }\to 100\mu \mathrm{\Omega }\to 100\text{m}\mathrm{\Omega }.$$

In the first check, two consecutive 10 : 1 resistance measurement steps are compared to a single 100 : 1 step. In the second and third checks, the combined result of a 10 : 1 and 100 : 1 resistance measurement step is compared to a 1000 : 1 step. This verification is considered a quite thorough check of the ratio accuracy of the current comparator. The agreement of the three cross-checks as performed just before the comparison measurements with only 10-mW dissipation in the lowest resistance values was (−0.03 ± 0.02), (−0.16 ± 0.06), and (−0.04 ± 0.12) μΩ/Ω, respectively ($k=1$ uncertainties).

B. METAS

The low-ohmic measurement system at METAS consists of a series of reference standards and a commercially available current comparator bridge coupled to a current-comparator-based range extender. The measurement setup is shown in Fig. 2.

Similar to the VSL setup, a current source drives a large current through $R_x$. This current is scaled to a lower value with a range extender (gray area in Fig. 2) to a level that can be measured with a regular DCC resistance bridge (top right part in Fig. 2). This DCC bridge has an adjustable number of turns $N_t$ in series with the primary windings $N_p$, so that a null condition on the nanovolt detector can be achieved by varying $N_t$. In this way, the value of the unknown resistor $R_x$ can be determined in terms of the standard resistor $R_s$ and the small relative difference in turn ratio [6].

The approach of the METAS calibration of the range extender is based on the following observation: The nonlinearity of the device is assumed to be essentially dependent on the flux distribution inside the iron cores and on the response of the electronics. Both characteristics are mostly related to the secondary rather than the primary current value. Hence, it is assumed that the nonlinearity of the range extender is completely known by characterizing it on the most convenient ratio, i.e., ten. In this range, it is possible to span secondary currents $I_s$ up to 100 mA using a pair of resistors that have been fully characterized using a cryogenic current comparator (CCC): 100 mΩ and 1 Ω. The extender ratios of 100 and 1000 can then only be characterized in their turn ratio error, independent of the current level, using low currents and a pair of CCC-characterized resistors of 100 mΩ and 10 Ω and 100 mΩ and 100 Ω, respectively.

The main influence factors of the measurement are the winding ratio error of the range extender (independent of current), the range extender’s detector gain and offset (nonlinearity), the main bridge error in computing a resistance ratio, the uncertainty on the reference resistor value, the temperature dependence of the resistor under test, the type-A uncertainty on the measurement results, and any uncompensated offsets. The latter two effects dominate the uncertainty budget for measurements at 10 mΩ and lower resistance values, whereas for 100 mΩ, almost all influence factors contribute to the measurement uncertainty.

C. NIST

The NIST low-ohmic measurement system is based on an automated commercial current comparator resistance bridge, combined with a high-current range extender, similar to that of METAS, as given in Fig. 2 [7].

The accuracy of the NIST system was verified by the measurement of the same resistor by different scaling paths, using different ratios of a certain range extender [8]. For example, the 10-mΩ resistor was measured at a 1-A current with the 1 : 10, 1 : 100, and 1 : 1000 ratios, respectively. The agreement of the resulting values in this and similar tests was well within the NIST published measurement uncertainties, being 0.5, 0.8, 1.2, and 4 μΩ/Ω for resistance values of 100 mΩ, 10 mΩ,1 mΩ, and 100 μΩ, respectively. Similar agreement was achieved between the results of measurements performed with the automated bridge used in this comparison and those obtained with an older manual bridge from a different manufacturer. Finally, measurements were made with three copies of the same type of range extender, to verify the firmware and hardware specifications of the automated bridge.

III. Traveling Standards

The resistors used in the comparison were carefully selected by NIST. It was decided to use two resistors at each resistance value of 100, 10, and 1 mΩ and three resistors of 100 μΩ. The resistors are all of the Reichsanstalt design and constructed of manganin wire. From the available resistors at NIST, the ones with long-term drifts of better than 1.5 μΩ/Ω/year and power coefficients of less than 10 μΩ/Ω/W were chosen, except for one of the three 100-μΩ resistors, where, intentionally, a resistor with a significant temperature and power coefficient was selected (resistor number 8; see data in Table I).

TABLE I.

Overview of the Properties of the Nine Resistance Standards Used in the Comparison. Here, α₂₅ and β₂₅ Are the Linear and Quadratic Temperature Coefficients at 25 °C, Respectively, and δ₂₅ Is the Power Coefficient at 25 °C. The Manufacturers Are Leeds and Northrup (L&N), National Bureau of Standards (NBS; Now NIST), and Otto Wolff

No	Nominal value [mΩ]	Manufacturer	α25 [μΩ/Ω/K]	β25 [μΩ/Ω/K2]	δ25 [μΩ/Ω/W]
1	100	NBS	3.3	−0.53	6
2	100	NBS	0.9	−0.53	5
3	10	NBS	4.9	−0.55	2
4	10	NBS	5.1	−0.55	5
5	1	L&N	3.9	−0.51	2.5
6	1	L&N	1.6	−0.49	2
7	0.1	L&N	−5.7	−0.43	−2
8	0.1	L&N	10.4	−0.35	24
9	0.1	Otto Wolff	3.6	−0.49	2

All measurements at the three NMIs were performed with the resistors placed in stirred oil at (25.000 ± 0.010) °C and with a 10-mW dissipation in the resistors.

Table I gives an overview of the properties of the resistors. The fact that all resistors are constructed from a similar material is reflected in the very similar values of the second-order temperature coefficient $\beta$. There is a clear physical correlation between the value of the linear temperature coefficient $\alpha$ and the power coefficient $\delta$, since the latter is in first order caused by heating of the resistor due to dissipation of the applied measurement current [7], [9]. The exact amount of heating and, thus, the value of $\delta$ are influenced by the cooling power of the environment, in this case, stirred oil. Even though this cooling power slightly differs from institute to institute, it has no significant effect at the low 10-mW dissipation used for the measurements in this comparison. The values of δ₂₅ obtained at NIST and VSL agree within 1–3 μΩ/Ω/W with each other; Table I gives the average of the values obtained at both institutes.

Fig. 3 shows an example for a power dependence measurement of the L&N 100-μΩ resistor number 7, where the small difference in VSL and NIST data at higher power levels probably is caused by the different cooling powers in the respective oil baths. Using the value of the temperature coefficients as given in Table I, the resistance change at a 1-W power as measured by NIST would correspond to a heating of around 0.5 °C. The few parts in 10⁷ rise in resistance value at low power levels is smaller than the standard deviation in the measurements. If it still is a real effect, it must be due to an effect other than temperature, since the resistor has a negative temperature coefficient.

Fig. 3.

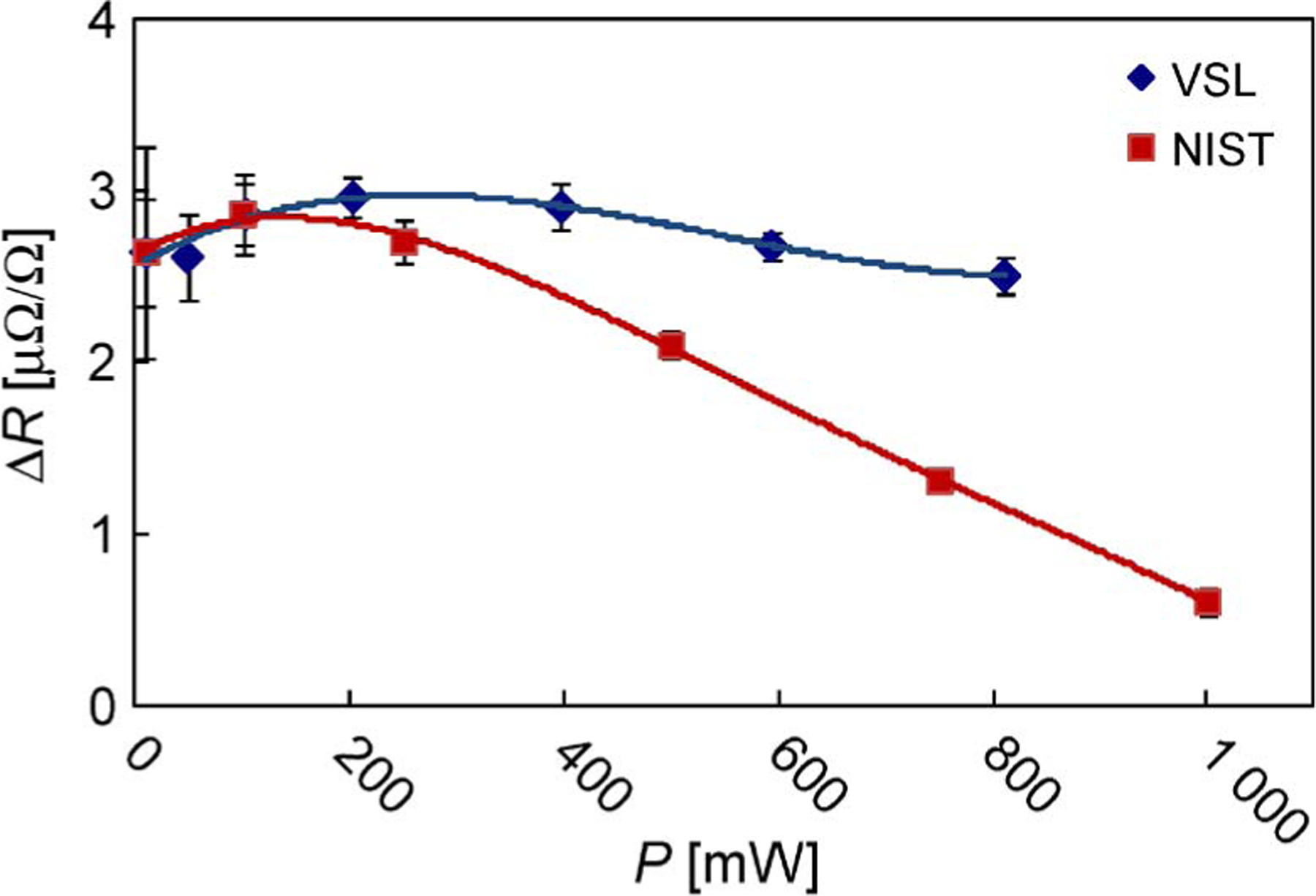
Effect of measurement power P on the resistance value ΔR, expressed as relative deviation from nominal value, of the L&N 100-μΩ standard resistor number 7. Uncertainty bars give the experimental standard deviation (type A; k = 1) only; lines are a guide to the eye through the data.

Given the experience in previous low-ohmic comparisons that low-ohmic resistance standards are sensitive to both shocks and large temperature variations during transport, it was decided to carefully pack the resistors in a large transport case, and in addition, special attention was paid to the transport between the laboratories. For the transatlantic air flight between the U.S. and The Netherlands, the transport case was part of the cargo luggage. However, since the case was too heavy, one 10-mΩ resistor (number 4) had to be taken out of the case and put in a separate smaller case. For the transport between The Netherlands and Switzerland, a special courier service was used that personally picked up the resistors and delivered them within 24 h to the destination laboratory without exposing them to large temperature excursions.

IV. Measurement Results

A. Traveling Behavior

Even though special attention was paid to the packaging and transport of the resistors, not all resistors appeared to travel well. First of all, the 10-mΩ resistor (number 4) that had not traveled in the large transport case between the U.S. and The Netherlands showed a 65-μΩ/Ω step change in value due to the transport. After an initial exponential decay over the first four months after arrival at VSL, the decay started to become approximately linear with a drift rate of −1 μΩ/Ω/year. This made the resistor still useful for comparing VSL and METAS measurement capabilities at this resistance level.

Second, two more resistors (number 2 and number 3) showed irregular behavior caused by the transport, as shown in Fig. 4. Since the effects are on the order of the measurement uncertainties of the NMIs, or even significantly larger in the case of the 10-mΩ resistor, it was decided not to use the measurement values of these resistors in the comparison. In the earlier evaluation made of the NIST and VSL measurements [4], the difference in NIST and VSL measurements for the 10-mΩ resistor number 3 was around the combined measurement uncertainties of both laboratories. With the present additional data on this resistor, it has become clear that this difference is caused by the traveling behavior of this resistor and not by a discrepancy in the measurement capabilities of NIST and VSL.

Fig. 4.

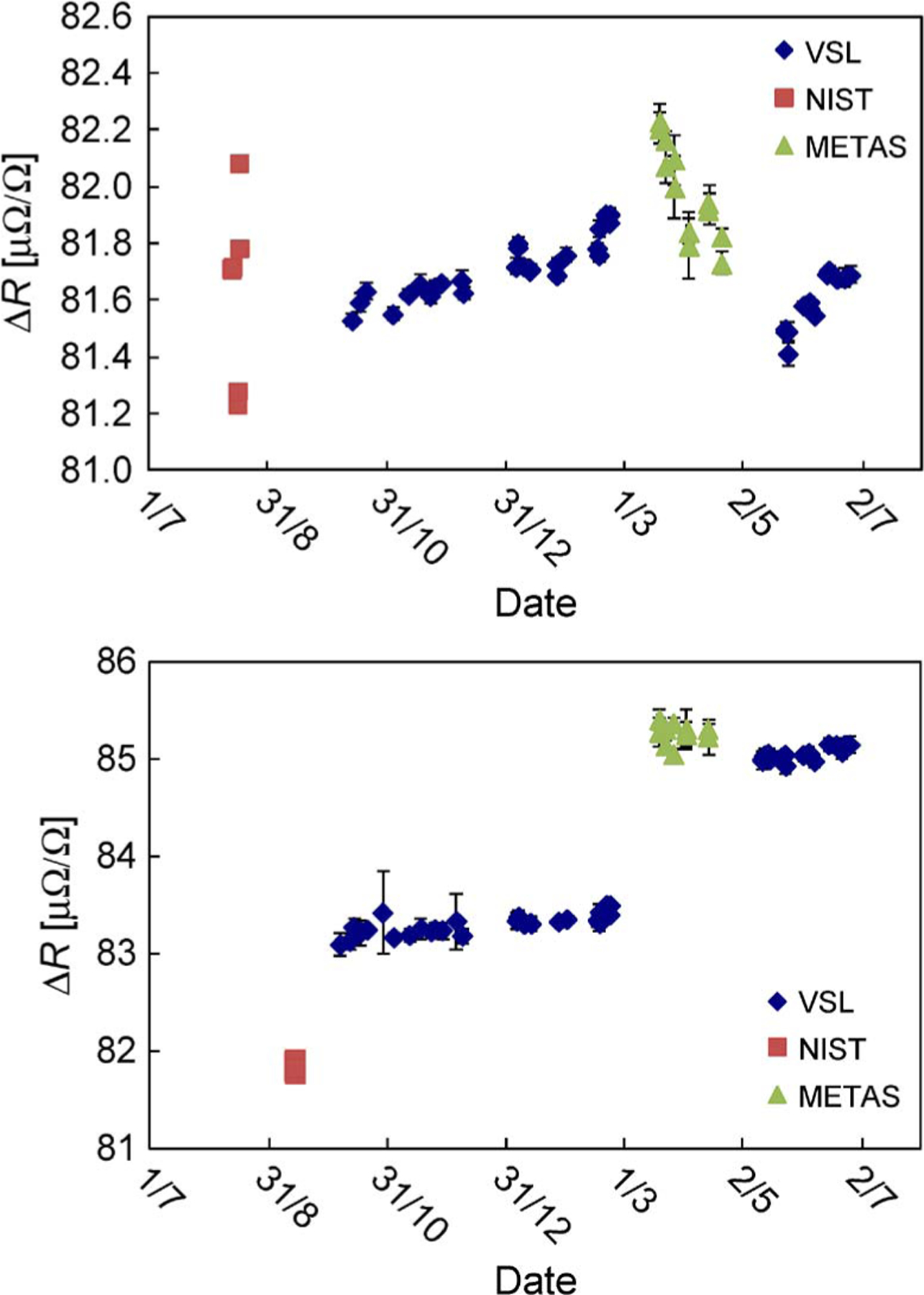
Comparison resistance values ΔR, expressed as relative deviation from nominal value, of the (top) NBS 100-mΩ number-2 resistor and (bottom) NBS 10-mΩ number-3 resistor indicating their nonideal traveling behavior. The VSL, NIST, and METAS experimental standard deviations (type A; k = 1) as given in the figure typically are 0.02, 0.02, and 0.06 μΩ/Ω for the 100-mΩ resistor and 0.04, 0.08, and 0.10 μΩ/Ω for the 10-mΩ resistor, respectively.

Since all NBS resistance standards were suffering from nonideal traveling behavior, a closer look was taken at the construction of these standards. All low-ohmic resistance standards used in this comparison are of the Reichsanstalt design, i.e., a resistor with a perforated can where the resistance element, either a coil or a ribbon, is exposed to circulating oil. However, there are some clear differences in the construction of the NBS and L&N resistance standards. At 100 mΩ, the L&N resistor has a six-turn bifilar free hanging coil made from a 2.5-mm-diameter resistance wire as the resistance element, whereas the NBS resistor is made from a similar wire but wound around a cylinder for mechanical support (see upper part of Fig. 5). This mechanical support apparently does not lead to good stability of the resistor during transport, possibly related to mechanical stresses it induces in the resistance element. At 10 mΩ, the NBS resistors are also coil-type with a special construction, consisting of a single coil making up five parallel resistance sections. This clearly is less mechanically stable than the very rigid foil construction used in 10-mΩ L&N resistors (see bottom part of Fig. 5).

Fig. 5.

Resistance elements of (top and bottom) 100- and 10-mΩ standard resistors. The L&N resistors are on the left (top resistor number 1; bottom resistor not used in the comparison), and NBS resistors are on the right side, respectively (top resistor number 2; bottom resistor number 3 of the comparison).

B. Comparison Results

The NBS resistors numbers 2 (100 mΩ) and 3 (10 mΩ) were completely excluded from the comparison evaluation because of their traveling behavior as described in the previous section. For the other NBS 10-mΩ resistor (number 4), only the VSL and METAS data were used, because of the 65-μΩ/Ω step change in value during the NIST–VSL transport.

The data analysis was performed as indicated in Fig. 6. First, a linear fit was made through the VSL data in order to determine the drift of the resistance during the complete comparison. The maximum drift observed for the resistors was only 0.3 μΩ/Ω/year in the almost-one-year period of the VSL measurements. Subsequently, the fit value was compared to the measurement values of NIST and METAS at their respective mean date of measurement. The comparison reference value (CRV) for each resistor was calculated using the weighted mean values of each laboratory. Finally, for each laboratory, the degree of equivalence (DoE) with the CRV was calculated for all resistors. The uncertainty in each DoE U_DoE is calculated as the root-sum-squared value of the uncertainty in the CRV and the correctly weighted uncertainties of the laboratories, taking into account the correlation of each DoE with the CRV [10]. Table II shows the results.

Fig. 6.

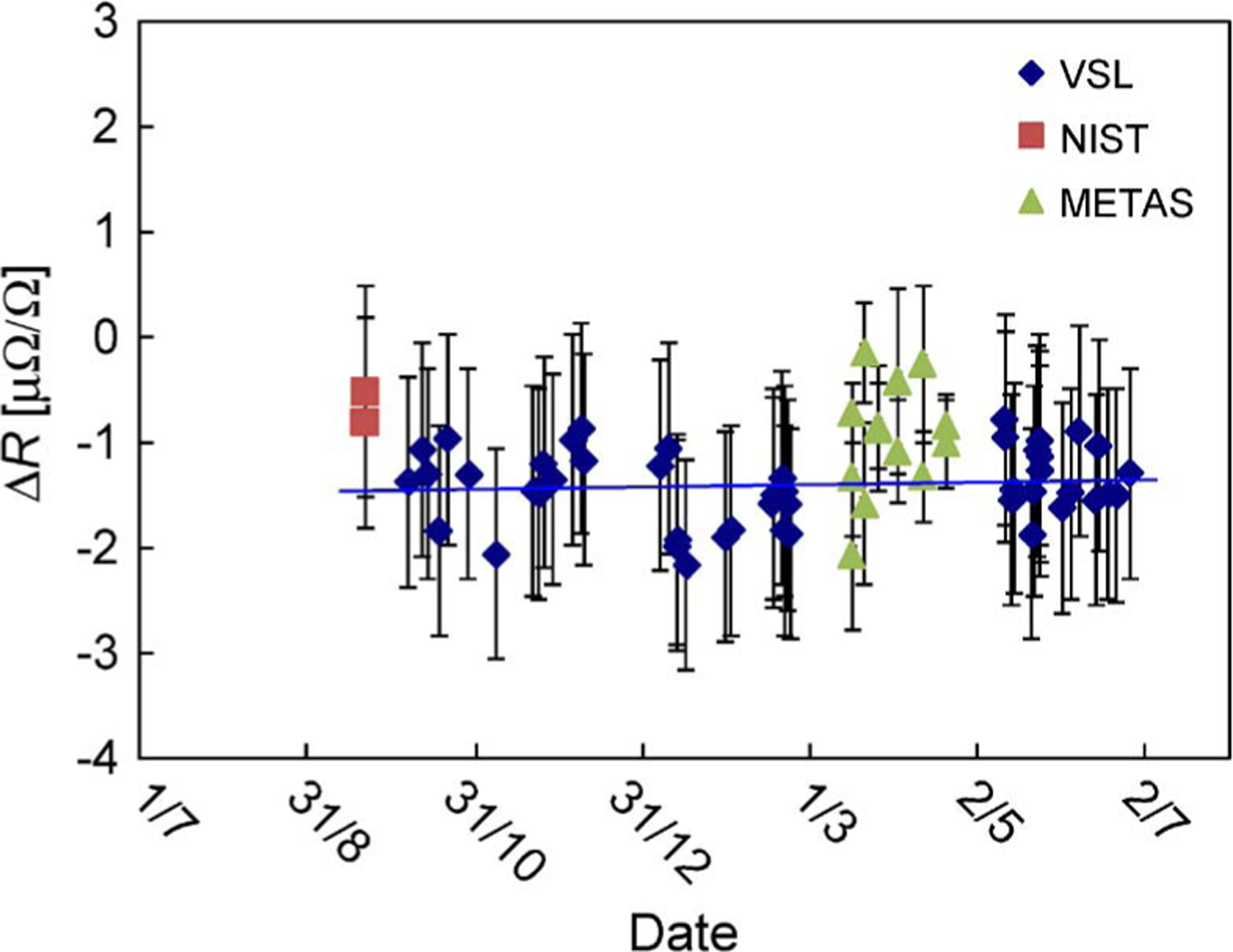
Comparison resistance values ΔR, expressed as relative deviation from nominal value, of L&N 100-μΩ resistor number 8. The measurement values have been given an arbitrary offset value. Uncertainty bars give the experimental standard deviation (type A; k = 1) only. The solid line is a fit through the VSL data, showing a drift rate of the resistor of only (0.15 ± 0.20) μΩ/Ω/year.

TABLE II.

DoEs With k = 2 Uncertainties U_DoE for Each Resistor for the Three Laboratories Participating in the Low-Ohmic Comparison

No	Nominal Resistance [mΩ]	VSL		NIST		METAS
		DoE [μΩ/Ω]	UDoE [μΩ/Ω]	DoE [μΩ/Ω]	UDoE [μΩ/Ω]	DoE [μΩ/Ω]	UDoE [μΩ/Ω]
1	100	0.01	0.19	0.05	0.50	−0.10	0.40
4	10	0.02	0.34			−0.03	0.42
5	1	0.10	0.70	−0.15	1.20	−0.11	1.00
6	1	0.10	0.70	−0.25	1.20	−0.04	1.00
7	0.1	0.35	1.32	−0.16	4.00	−0.63	1.82
8	0.1	0.19	1.32	−0.62	4.00	−0.25	1.82
9	0.1	−0.16	1.44	2.05	4.01	−0.27	2.42

For NIST, no DoE can be calculated at the 10-mΩ level, since both 10-mΩ resistors did not travel well between NIST and VSL. Still, it is highly unlikely that there is a significant difference between the NIST 10-mΩ measurement results and those of the other two NMIs given the operation principle of the range extender (see Section II-B) and the good DoE values for all other resistance values.

Since for the 1-mΩ and 100-μΩ resistance values multiple resistors showed good traveling behavior, the overall DoE of the NMIs at these resistance values was calculated as the average of the DoEs obtained for each individual resistor. This averaging was justified since the DoEs obtained for different resistors of the same resistance value as given in Table II were in good agreement with each other. This particularly was verified for the 100-μΩ resistor number 8 which had a significant temperature and power coefficient (see Table I and Fig. 6). The resulting average DoE values are presented in Fig. 7.

Fig. 7.

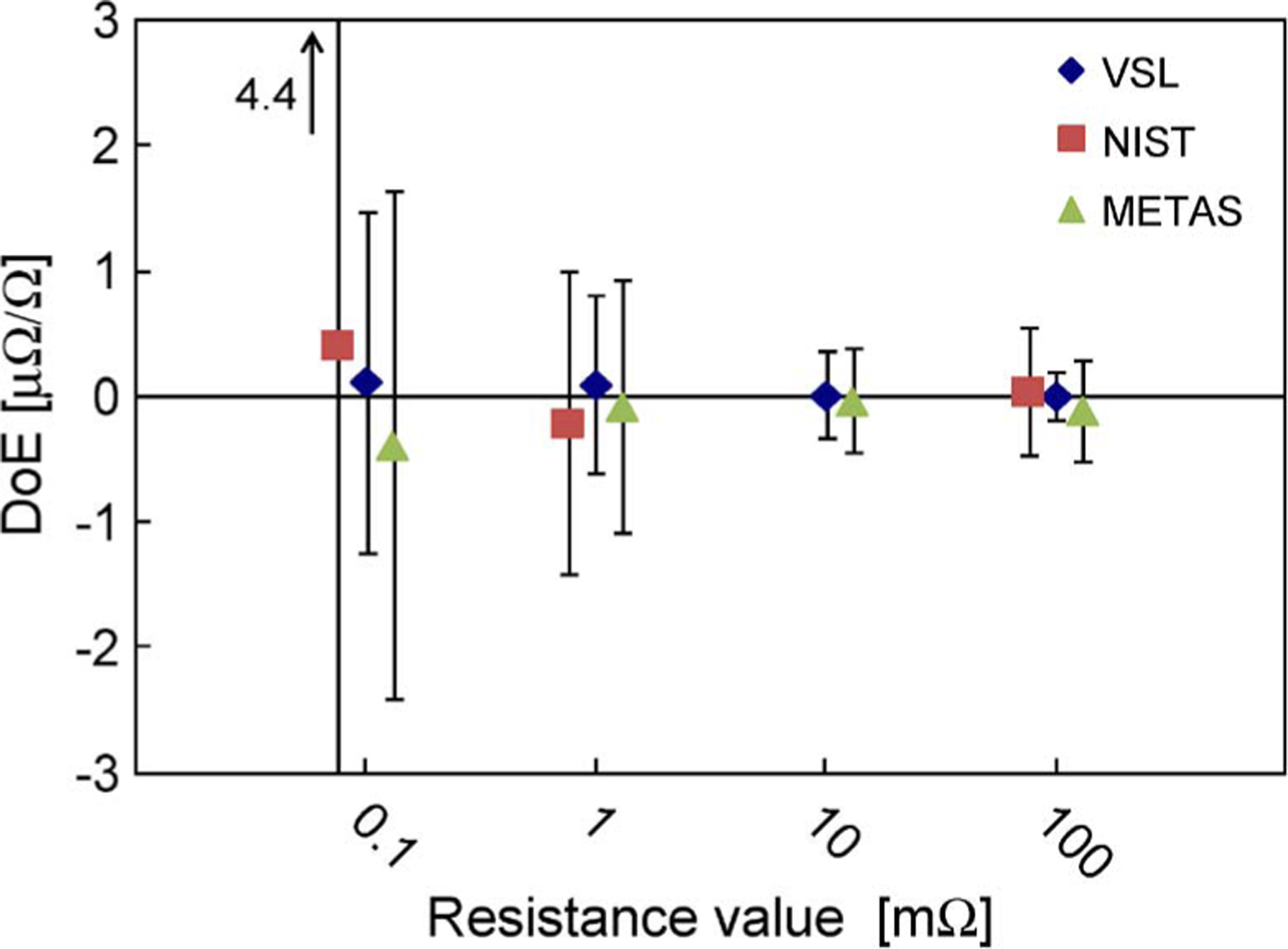
DoEs with k = 2 uncertainties for each of the three laboratories participating in the low-ohmic comparison.

V. Conclusion

A set of nine low-ohmic resistors with values in the range of 100 mΩ down to 100 μΩ have been used to compare the resistance measurement capabilities of NIST, VSL, and METAS. Even though special attention was paid to careful hand-carried transport, still, three of the nine resistors showed irregular traveling behavior. All five resistors of 1 mΩ and 100 μΩ showed excellent traveling behavior.

The DoEs calculated for the three NMIs at the four resistance levels show excellent agreement of the respective measurement values: The value of the DoEs is never more than 25% of the k = 2 uncertainty in the DoE.

The measurement data confirm earlier experiences that low-ohmic resistors are very sensitive to mechanical and thermal shocks and thus preferably should be hand carried between laboratories in a comparison. In the present comparison, even hand carrying appeared not sufficient to guarantee good traveling behavior of the resistors made by NBS, where the resistance elements are coil-type. This nonideal traveling behavior is a serious limitation for possible future organization of a low-ohmic measurement comparison involving many laboratories, particularly if the resistors have to be transported by plane.

Biographies

Gert Rietveld (M’10–SM’12) was born in The Netherlands, in 1965. He received the M.Sc. (cum laude) and Ph.D. degrees in low-temperature and solid-state physics from Delft University of Technology, Delft, The Netherlands, in 1988 and 1993, respectively.

Since 1993, he has been with the Van Swinden Laboratorium (VSL), the National Metrology Institute of The Netherlands, Delft, where he is a Senior Scientist with the dc/LF group of the Research and Development Department. He is involved in the development of power measurement systems and electrical quantum standards, particularly the quantum Hall resistance standard. Other scientific work concerns the measurement of very small electrical currents and evaluation of “self-calibrating” instruments. In addition, he has been a Program Manager, coordinating the scientific work of all technological areas within VSL. He currently is coordinating a 22-partner joint research project on smart grid metrology.

Dr. Rietveld is a member of the Consultative Committee for Electricity and Magnetism (CCEM) of the International Bureau of Weights and Measures (BIPM), the contact person for VSL in the Technical Committee of Electricity and Magnetism of the European Association of National Metrology Institutes (EURAMET), the Chair of the EURAMET subcommittee on “Power and Energy,” and a member of several CCEM and EURAMET working groups.

Jan H. N. van der Beek was born in Rijswijk, The Netherlands, in 1960. He received the B.S. degree (cum laude) in electronics from the Middelbare Technische School Leyweg, The Hague, The Netherlands, in 1989.

After his studies, he joined the Van Swinden Laboratorium, the National Metrology Institute of The Netherlands, Delft, in 1989, where he specialized in impedance measurements, multifunction and dc voltage measurements, and high ohmic dc resistance. As from 2008, his main working area is in dc voltage and dc resistance. Other areas of expertise include quantum voltage standards.

Marlin Kraft was born in Ransom, KS, in 1951. He received the A.S. degree in electronic technology from Kansas State University, Manhattan, in 1980.

From 1980 to 2001, he was with Primary Standards Laboratory, Sandia National Laboratories. He specialized in all areas of dc metrology and was the Associate Project Leader. Since 2002, he has been with the U.S. National Institute of Standards and Technology (NIST), Gaithersburg, MD, for the metrology of the ohm in the Fundamental Electrical Measurements group. His work with NIST has been dc current, high and low dc resistance, and dc high voltage.

Randolph E. Elmquist (M’90–SM’98) received the Ph.D. degree in physics from the University of Virginia, Charlottesville.

Since 1986, he has worked with the National Institute of Standards and Technology, Gaithersburg, MD, in the field of electrical and quantum metrology, contributing to the experimental design and measurement of the electronic kilogram, the quantum Hall effect, the fine structure constant, and ac-dc coaxial calculable impedance standards. He is currently the leader of the dc resistance calibration service and leads efforts on cryogenic current comparator systems and graphene electronic devices for metrology.

Dr. Elmquist is a member of the American Physical Society.

Alessandro Mortara (M’95) was born in Rome, Italy, in 1963. He received the Laurea degree in electronic engineering from the University of Rome “La Sapienza”, Rome, Italy, in 1988, the M.Sc. degree from Massachusetts Institute of Technology, Cambridge, in 1991, and the Ph.D. degree in analog IC design from the Federal Institute of Technology (EPFL), Lausanne, Switzerland, in 1995.

He was with the Centre Suisse d’Electronique et de Microtechnique, Neuchâtel, Switzerland, and Heuer Mikro Technik Microelectronics Ltd., Biel, Switzerland, developing mixed-signal application-specific integrated circuits for industrial applications. Since 2005, he has been with the Federal Office of Metrology (METAS), Bern, Switzerland, where he is currently in charge of the Current, Voltage, and Impedance Laboratory. His research interests include ac/dc transfer, measurements, low-level current and charge measurements, and fundamental accuracy ac voltage generation.

Beat Jeckelmann received the Ph.D. degree in experimental particle physics from the University of Fribourg, Fribourg, Switzerland, in 1986.

He continued research work as a Visiting Scientist with Massachusetts Institute of Technology, Cambridge, in the field of high-energy particle physics. Since 1989, he has been with the Federal Office of Metrology (METAS), Bern, Switzerland, where he became the Section Head of the Electricity, Acoustics, and Time Section in 1997 and is currently Chief Science Officer and Head of the Electricity Sector. His research work is focused on the development of electrical quantum standards.