Unified Scaling Law for flux pinning in practical superconductors: III. Minimum datasets, core parameters, and application of the Extrapolative Scaling Expression

Abstract

In Part 2 of these articles, an extensive analysis of pinning-force curves and raw scaling data was used to derive the Extrapolative Scaling Expression (ESE). This is a parameterization of the Unified Scaling Law (USL) that has the extrapolation capability of fundamental unified scaling, coupled with the application ease of a simple fitting equation. Here in Part 3, the accuracy of the ESE relation to interpolate and extrapolate limited critical-current data to obtain complete $I_{\text{c}}(B,T,\epsilon )$ datasets is evaluated and compared with present fitting equations. Accuracy is analyzed in terms of root mean square (RMS) error and fractional deviation statistics. Highlights from 92 test cases are condensed and summarized, covering most fitting protocols and proposed parameterizations of the USL. The results show that ESE reliably extrapolates critical currents at fields $B$, temperatures $T$, and strains $\epsilon$ that are remarkably different from the fitted minimum dataset. Depending on whether the conductor is moderate-$J_{\text{c}}$ or high-$J_{\text{c}}$, effective RMS extrapolation errors for ESE are in the range 2–5 A at 12 T, which approaches the $I_{\text{c}}$ measurement error (1–2%).

The minimum dataset for extrapolating full $I_{\text{c}}(B,T,\epsilon )$ characteristics is also determined from raw scaling data. It consists of one set of $I_{\text{c}}(B,\epsilon )$ data at a fixed temperature (e.g., liquid helium temperature), and one set of $I_{\text{c}}(B,T)$ data at a fixed strain (e.g., zero applied strain). Error analysis of extrapolations from the minimum dataset with different fitting equations shows that ESE reduces the percentage extrapolation errors at individual data points at high fields, temperatures, and compressive strains down to 1/10th to 1/40th the size of those for extrapolations with present fitting equations. Depending on the conductor, percentage fitting errors for interpolations are also reduced to as little as 1/15th the size.

The extrapolation accuracy of the ESE relation offers the prospect of straightforward implementation of the USL in several new areas: (l) A five-fold reduction in the measurement space for unified temperature-strain apparatuses through extrapolation of minimum datasets; (2) Combination of data from separate temperature and strain apparatuses, which provides flexibility and productive use of more limited data; and (3) Full conductor characterization from as little as a single $I_{\text{c}}(B)$ curve when a few core parameters have been measured in a similar conductor. Default core scaling parameter values are also given, based on analysis of a wide range of practical Nb₃Sn conductors.

1. Introduction to extrapolations

Different parameterizations of the Unified Scaling Law (USL) have been proposed since its inception (Ekin 1980, 1981). In the early years, unified scaling was carried out by the registration of flux pinning curves into a master scaling curve. This normalization process provides values of the maximum pinning force $F_{\text{Pmax}}(T,\epsilon )$ and effective upper critical field ${B_{\text{c}2}}^{\ast }(T,\epsilon )$ (denoted here as raw scaling data), which determine the individual parameters in the USL. More recently, the emphasis has shifted from this fundamental scaling process (i.e. the formation of master scaling curves) to postulating fitting equations that contain varying numbers of empirical or semi-empirical constants and parameters. The parameter values are determined by a simultaneous global fit to three-dimensional $I_c(B,T,\epsilon )$ data, where $B$ is the magnetic field, $T$ temperature, and $\epsilon$ mechanical strain. However, these global fitting equations are interpolative in nature and do not retain the broad-based extrapolation capability of fundamental scaling.

In Part 1 of this series (Ekin 2010), the different global fitting equations are compared and organized into separable parts. The resulting table 3 in Part 1 forms the starting point for Parts 2 and 3. In Part 2 (previous article, Ekin et al 2016a), a different approach is undertaken wherein each parameter of the general USL parameterization is evaluated, either individually or in small groups, from analysis of hundreds of raw scaling data measured in a broad range of Nb₃Sn conductors. This very extensive analysis, based on raw scaling data, determines which parameters are conductor specific, and which retain the same constant value over the wide range of Nb₃Sn conductors studied. The scaling constants obtained by this fundamental process are stable with respect to conductor configuration, magnetic self-field correction, and the factors used in the raw-scaling-data analysis of the pinning-force curves.

Table 3.

Limited datasets and the scaling parameters that can be determined from theme.

	Types of datasets	Parameters determined
				Core parameters
		$C$ a	${B_{\text{c}2}}^{\ast }(0,0)$	${T_{\text{c}}}^{\ast }(0)$	$\eta$	$s$	$b_{\text{c}2}(\epsilon )$	$p$	$q$
1	$I_{\text{c}}(B,T,\epsilon )$ (unified $T-\epsilon$ apparatus)	✓	✓	✓	✓	✓	✓	✓	✓
2	$I_{\text{c}}(B,T)$) fixed $\epsilon$ (dedicated $T$ rig)	✓	✓	✓	✓			✓	✓
3	$I_{\text{c}}(B,\epsilon )$ fixed $T$ (dedicated $\epsilon$ rig)	✓	✓			✓	✓	(✓)	✓
4	$I_{\text{c}}(T)$ fixed $B,\epsilon$ (dedicated $T$ rig)	✓		✓	✓
5	$I_{\text{c}}(\epsilon )$ fixed $B,T$ (dedicated $\epsilon$ rig)	✓					✓
6	$I_{\text{c}}(B)$ fixed $T,\epsilon$ (routine $I_{\text{c}}$ testing)	✓	✓					(✓)	✓
7	$I_{\text{c}}$ fixed $B,T,\epsilon$ (routine $I_{\text{c}}$ testing)	✓

Notes: ✓ Indicates parameters that can be accurately determined from the indicated dataset.

Blank: Indicates parameters that must be supplied, either with values from other datasets, or with default values (from section 5.5).

(✓) Indicates there is often insufficient data at low magnetic fields and temperatures to determine $p$, in which case it must be assigned a default value. This is particularly the case for high-$J_{\text{c}}$ conductors if data are available only at liquid helium temperatures where transport current heating effects usually prevent measurements at low enough fields to determine $p$ (examples of the lack of sufficient low-field data are seen in the master pinning-force curves illustrated in Part 2, both in section 5 and in the master scaling curves in appendix A). Fortunately, tests show that the precise default values for $p$ (and $q$) do not effectively change the RMS error ($\text{ΔRMSE}=\sim 0.02\text{\%}$), as long as $p$ and $q$ are fixed in a reasonable range $p=\sim 0.4$ to 0.5, or $q=1.5$ to 2.5, and used with corresponding core parameter values.

^aDefinition: $C\equiv K(0,0)$.

The results of this analysis determine the Extrapolative Scaling Expression, or ESE (‘easy’). Despite the initial comprehensive evaluation of raw scaling data required for its derivation, the ESE relation can be applied with the ease of a simple fitting equation (without the analysis of raw scaling data). It should also, in principle, retain the intrinsic general extrapolation capability of fundamental scaling.

Here in Part 3, we evaluate the extrapolation (and interpolation) accuracy of the ESE equation compared with present global-fitting equations. The results show that ESE accurately extrapolates $I_{\text{c}}(B,T,\epsilon )$ at fields, temperatures, and strains that are remarkably different from the fitted minimum dataset. Depending on whether the conductor is moderate-$J_{\text{c}}$ or high-$J_{\text{c}}$, effective root mean square (RMS) extrapolation errors for ESE are in the range 2–5 A at 12 T, which approaches the $I_{\text{c}}$ measurement error (1–2%).

This capability offers flexibility and the prospect for extrapolation of more limited data in several new areas:

• The ESE relation can be used to reduce the measurement space for unified $T-\epsilon$ apparatuses for full $I_{\text{c}}(B,T,\epsilon )$ conductor characterization to about 1/5th the size, by removing the need to measure all the $T-\epsilon$ cross terms (sections 2 and 3). Also, with the ESE fitting equation, there is no requirement for orthogonal $B-T-\epsilon$ measurement grids (needed for fundamental scaling with raw scaling data).

• The relation makes possible the combination of data from separate apparatuses, measured at different times in different laboratories (e.g., one apparatus dedicated to strain measurement and another to temperature measurement).

• In special situations, such as qualifying production quantities of wire, the determination of a few core parameters in one of the conductors can serve to accurately give full $I_{\text{c}}(B,T,\epsilon )$ characterizations for similar billets, by a simple fit of ESE to a single $I_{\text{c}}(B)$ curve measured for each billet (section 5.10).

• ESE can also significantly increase the accuracy for interpolations (section 5.1), and, if desired, the parameter set generated by the interpolative fit can provide reliable extrapolations to the neighboring $B-T-\epsilon$ space through the use of default values for a few core parameters.

Default values for the core parameters are described in section 5.5 and in item 7 of the Part 3 summary (section 6.3).

1.1. Organization of the article

A comprehensive synthesis of the main results of both Parts 2 and 3 is given in the combined summary at the end of this article in section 6. The summary is combined, to make Part 3 more self-contained (without extensive referencing back to Part 2), as well as to provide a cohesive summary for these two highly integrated articles. A short paper condensing these results and supplying additional analysis of concatenated errors will also be published (Ekin et al 2016b).

Part 3 is organized as follows:

1. Introduction to extrapolations

2. Minimum datasets

3. Extrapolation testing from minimum datasets

4. Discussion: ‘Everything should be made as simple as possible, but not simpler’

5. Application of the ESE relation

6. Summary and conclusions, Parts 2 and 3

Appendix A gives typical values of the ESE parameter set for a number of practical Nb₃Sn conductors, and provides default scaling parameter values.

A supplemental website, www.ResearchMeasurements.com, contains Excel^™ files of the original source data, as well as an ESE scaling spreadsheet tool for application to practical Nb₃Sn conductor characterization and magnet design.

2. Minimum datasets

The use of minimum datasets can save considerable measurement time compared with measurements of the full $I_{\text{c}}(B,T,\epsilon )$ matrix. For this purpose, we define the minimum dataset as the smallest set of $I_{\text{c}}$ data needed to accurately extrapolate a full $I_{\text{c}}(B,T,\epsilon )$ characteristic. Various minimum datasets have been suggested, including Godeke (2005), Godeke et al (2006), and Ilyin et al (2007). These have been mainly based on the parameters needed for a particular fitting equation. In this section, we instead use the pinning-force analysis of Part 2 to determine the smallest practical minimum dataset.

2.1. $T-\epsilon$measurement map

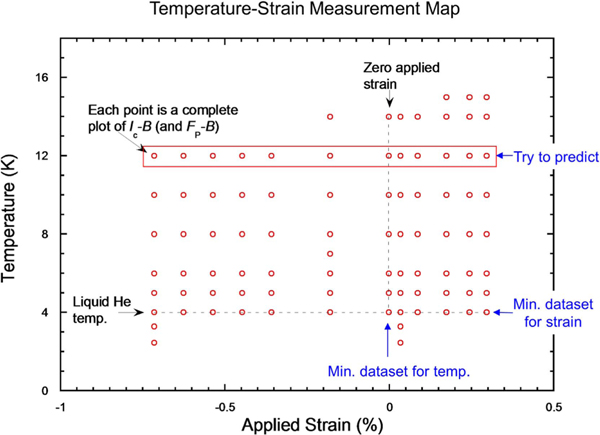
Minimum datasets are relatively easy to visualize through the introduction of a temperature-strain ($T-\epsilon$) map. Figure 1 shows an example of such a map for the OST-RRP^® dataset fabricated for the high luminosity large hadron collider (HL-LHC) magnets, as well as for nuclear magnetic resonance (NMR) magnets. Each location in this plot represents a set of $I_{\text{c}}-B$ measurements, all taken at the strain and temperature corresponding to that point in the map (about a thousand $I_{\text{c}}$ measurements for the whole plot). A similar measurement map (not shown) can be constructed for the extensive WST-ITER dataset for the ITER toroidal-field magnets (containing $I_{\text{c}}-B$ data at 91 such $T-\epsilon$ combinations), or any of the other conductors considered here. (Further conductor information for the conductors in this study is given in appendix A of Part 2, and complete data tabulations are given online in a supplemental website accompanying these articles, www.ResearchMeasurements.com. An $I_c$ criterion of $0.1\mu \text{V}$ cm⁻¹ is used throughout these datasets, unless stated otherwise.)

Figure 1.

Temperature-strain ($T-\epsilon$) map of $I_{\text{c}}-B$ measurements for the very large dataset for the RRP^® high-$J_{\text{c}}$ conductor (the complete data file is given online at www.ResearchMeasurements.com). Each point in the figure represents an $I_{\text{c}}-B$ curve measured at the indicated temperature-strain pair (nearly a thousand $I_{\text{c}}$ measurements in total). The map graphically displays the minimum dataset, a simple cross cut through the $T-\epsilon$ map (in this case, at liquid helium temperature and at an applied strain of near zero, indicated in the figure by the two orthogonal dashed lines). Extrapolations from this minimum dataset were carried out to predict the critical current measured at all the other strains, temperatures, and magnetic fields in the map. An example of extrapolations to strains and magnetic fields at 12 K is indicated by a red box in the figure.

This map results naturally from the best protocol for taking $I_{\text{c}}(B,T,\epsilon )$ data: the sample is strained to a maximum (tensile) value below the irreversible strain limit, and then temperature is stepped through all values of interest (a vertical column in the map, for example at even temperatures between 4 and 12 K). At each temperature point in the column, $I_{\text{c}}$ is measured as a function of magnetic field, and then the whole process is repeated for the next lower strain column. This protocol ensures a constant strain as magnetic field and temperature are varied, since the strain state of the conductor is the most difficult to replicate.

2.2. Minimum dataset derived from raw scaling data

The smallest practical minimum dataset is determined by the parameters that need to be fitted for a full $I_{\text{c}}(B,T,\epsilon )$ characteristic. The results are given here in terms of the notation for the general parameterization of the USL developed in Part 1:

General separable parameterization of the USL (Ekin 2010)

$$F_{\text{P}}(B,T,\epsilon )=I_{\text{c}}(B,T,\epsilon )B=K(T,\epsilon )f(b)=C\boxed{g(\epsilon )}\boxed{h(t)}\boxed{f(b)},$$ (1a)

$$=C\boxed{{[b_{\text{c}2}(\epsilon )]}^{\mathit{s}}}\boxed{{(1-t^v)}^{\mathit{\eta }-\mathit{\mu }}{(1-t^2)}^{\mathit{\mu }}}\boxed{b^p{(1-b)}^q}$$ (1b)

with reduced magnetic field $b\equiv B/{B_{\text{c}2}}^{\ast }(T,\epsilon )$ and reduced temperature $t\equiv T/T_{\text{c}}^{\ast }(\epsilon )$, where:

$$\begin{gathered} {B_{\text{c}2}}^{\ast }(T,\epsilon )={B_{\text{c}2}}^{\ast }(0,0)\boxed{b_{\text{c}2}(t)}\boxed{b_{\text{c}2}(\epsilon )} \\ ={B_{\text{c}2}}^{\ast }(0,0)\boxed{(1-t^v)}\boxed{b_{\text{c}2}(\epsilon )} \end{gathered}$$ (1c)

$$T_{\text{c}}^{\ast }(\epsilon )=T_{\text{c}}^{\ast }(0){\left[b_{\text{c}2}(\epsilon )\right]}^{1/w}$$ (1d)

with ten scaling parameters: $C,{B_{\text{c}2}}^{\ast }(0,0),T_{\text{c}}^{\ast }(0),s,v,\eta ,\mu ,w,p,q$, plus the various strain parameters modeling $b_{\text{c}2}(\epsilon )$.

The raw scaling data analysis of Part 2 showed which of the parameters in this equation-set are constant and which need to be fitted for each conductor. The results break down by measurement variable as follows:

• The temperature parameters $T_{\text{c}}^{\ast }(0),v$, and the co-joined parameters $\eta$ and $\mu$. These parameters characterize the temperature part of: the upper critical field $b_{\text{c}2}(t)$ in equation (1c) and the USL prefactor $h(t)$ in equation (1a). The parameter $v$ is a scaling constant ($v=1.5$), but $T_{\text{c}}^{\ast }(0)$, as well as either $\eta$ or $\mu$, need to be fitted for each conductor. (The star indicates an effective scaling critical temperature determined by $I_c$ measurements, as distinct from the limiting $T_c$ where all superconductivity disappears.) For their determination, source $I_c(B)$ data are needed along one variable-temperature, vertical cut through the $T-\epsilon$ map at constant $\epsilon$. (Note that this cut contains the variable $B$ data embedded at each point in the map.) The easiest to measure is a variable-temperature cut without applied strain (other than thermal contraction strain introduced by the sample holder on cooldown). This is indicated by the vertical dashed line near zero applied strain in figure 1. These $I_{\text{c}}-B$ data can be obtained in a unified $T-\epsilon$ apparatus, or with a dedicated variable-temperature measurement apparatus that has no variable-strain capability (examples of such apparatus are given in Goodrich et al 2013).

• The strain parameters $s$ and those in $b_{\text{c}2}(\epsilon )$. These characterize the strain parts of the USL prefactor $g(\epsilon )$ in equation (1a) and the upper critical field $b_{\text{c}2}(\epsilon )$ in equation (1c) and need to be fitted. (The various parameterizations for $b_{\text{c}2}(\epsilon )$ are summarized in section 4.5 and appendix B of Part 2.) In addition to these fitted strain parameters, there is a strain constant, the moderate-strain curvature parameter $u=1.7$, which appears explicitly or implicitly in some of the $b_{\text{c}2}(\epsilon )$ models (table 5 in Part 2). To determine the fitted strain parameters, $\text{s}$ and $b_{\text{c}2}(\epsilon )$, source $I_c(B)$ data are needed along one variable-strain, horizontal cut through the $T-\epsilon$ map at constant $T$. (Again, note that this cut also contains the variable $B$ data embedded at each point in the map.) The easiest to measure is a variable-strain cut at liquid helium temperature, indicated by the horizontal dashed line near 4 K in figure 1.³ This temperature is far away from the limiting $T_{\text{c}}$, and thus the effects of flux creep are also minimized. These strain measurements can be supplied by a unified $T-\epsilon$ apparatus, or with a simpler dedicated variable-strain apparatus, operating as a liquid helium dip probe, without variable-temperature capability.

• The magnetic field parameters $p,q,{B_{\text{c}2}}^{\ast }(0,0)$, and $C$. These characterize the pinning-force shape function $f(b)$. (Again, the star indicates an effective scaling upper critical magnetic field determined by $I_c$ measurements, as distinct from the limiting upper critical magnetic field where all superconductivity disappears.) These parameters vary significantly and need to be fitted for each conductor. They are determined by the $I_c$ versus $B$ data at any point in the $T-\epsilon$ map of figure 1, provided the data cover sufficient magnetic fields below and above the peak pinning force to determine the parameter values. Otherwise default values are used (see comments on $p$ and $q$ in sections 3.8.2 and 5.5.1).

• Finally, the cross-link parameter $w$. This connects the strain and temperature functions $T_{\text{c}}^{\ast }(\epsilon )$ and ${B_{\text{c}2}}^{\ast }(0,\epsilon )$. Fortunately, we saw from the extensive raw-scaling-data analysis in section 4.3 of Part 2 that $w$ is a scaling constant ($\text{w}=3$) and therefore no measurements are needed for this parameter. This is serendipitous, because if it were a fitted parameter, the only way to determine its value precisely would be from extensive raw scaling data for ${B_{\text{c}2}}^{\ast }(T,\epsilon )$ and $K(T,\epsilon )$⁴ calculated from large, orthogonal datasets of combined variable temperature and strain measurements. This would have precluded the concept of the simple global fitting equation approach.

Table 5.

ESE parameter values for combining minimum datasets for $I_{\text{c}}(B,T)$ and $I_{\text{c}}(\epsilon )$ from two different measurement apparatuses. These were obtained with equation-set (11) evaluated with the Invariant $b_{\text{c}2}(\epsilon )$ model. For the iterative procedure, red italic type indicates those parameters that can be determined by each limited dataset. These values are then used to fix parameter values in the next step (indicated in bold). Same source data and fitting conditions as table 4.

				Core scaling parameters
Parameters:		$C$ (AT)	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	${T_{\text{c}}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_m$ (%)	$c_2$	$c_3$	$c_4$	$p$	$q$
Simultaneous fit, $I_{\text{c}}$ criterion = 0.1 μV cm−1 for both datasets
		14,166	28.60	16.21	1.966	1.4	0.323	0.660	0.669	1.136	0.562	1.709
Three-step iterative fit (temp-strain-temp), strain data $I_{\text{c}}$ criterion = 1 μV cm−1, temp data $I_{\text{c}}$ criterion = 0.1 μV cm−1
1	$I_{\text{c}}(B,T)$ 0.1μV cm−1	14 087	28.49	16.19	1.966	1.4	$b_{\text{c}2}(\mathit{\epsilon })=1$				0.562	1.710
2	$I_{\text{c}}(\epsilon )$ 1μV cm−1	16 277	28.49	16.19	1.966	1.4	0.319	0.641	0.519	0.803	0.562	1.710
3	$I_{\text{c}}(B,T)$ 0.1μV cm−1	14160	28.60	16.21	1.966	1.4	0.319	0.641	0.519	0.803	0.562	1.710

Because both temperature and strain parameters need to be fitted, we find from the separable parts of equation-set (1) that the smallest practical minimum dataset is the combination of one temperature cut and one strain cut through the $T-\epsilon$ map, as illustrated by the two dashed lines in figure 1.

Thus, the minimum dataset derived from the analysis of raw scaling data in Part 2 consists of one measurement of $I_c(B,T)$ (at fixed strain) with one of $I_c(B,\epsilon )$ (at fixed temperature).

2.2.1. Effect of extrapolating from larger datasets.

Additional extrapolation tests were also conducted with three cuts through the $T-\epsilon$ map to see if extrapolating from additional source data beyond the two-cut minimum dataset leads to a continuum of reduced extrapolation errors. Extrapolations from such an expanded set of data showed no significant reduction in error (details given in section 3.1.1). This result indicates that the errors evaluated in section 3 are systemic for each fitting equation, and not significantly reduced by the addition of more source data. This also verified that the minimum dataset is indeed optimum. That is, datasets larger than two cuts through the $T-\epsilon$ map made negligible difference in reducing extrapolation errors.

2.2.2. Earlier work.

The minimum dataset derived here from raw scaling data is also consistent with a minimum dataset described earlier by Ilyin et al (2007). The earlier dataset is actually included in the raw-scaling-data minimum dataset as a subset. The earlier subset consists of one measurement of $I_c(B,T)$ and one of $I_c(\epsilon )$. The difference from the present finding [that is, $I_{\text{c}}(B,\epsilon )$ versus $I_{\text{c}}(\epsilon )$], is that the earlier work was based on a specific empirical equation, the G/ITER model, where the parameter $s$ is fixed at $s=1$. However, the raw scaling data analysis of Part 2 shows the parameter $s$ varies for different conductors (figure 9 in Part 2). For example, in the ITER conductors, $s=\sim 1.4$ as determined by the extensive studies of Cheggour et al (2014). For the minimum dataset to be generally applicable, a variable field measurement of $I_c(B,\epsilon )$, rather than $I_c(\epsilon )$, is needed to determine all the strain parameters: $s$ and those in $b_{\text{c}2}(\epsilon )$.

Figure 9.

Pinning-force fitting versus critical-current fitting. (a) Fitting the minimum dataset in terms of the critical current results in considerable errors between the extrapolated curves and the measured data points. (b) Fitting in terms of the pinning force ($F_{\text{P}}=I_{\text{c}}B$) reduces extrapolation error at individual data points to as little as 1/5th the size, particularly at higher strains and temperatures. The large improvement given by $F_{\text{P}}$ fitting was consistently observed for all test cases where high extrapolation accuracy was observed.

However, for the specialized case where the value of s is already known for a similar conductor, only an $I_{\text{c}}(\epsilon )$ measurement at fixed magnetic field is needed, and then the minimum dataset derived from raw scaling data reduces to that of Ilyin et al. An example of this case is shown later in sections 5.7–5.9, where an $I_{\text{c}}(B,T)$ dataset is combined with an $I_{\text{c}}(\epsilon )$ dataset to give a full $I_{\text{c}}(B,T,\epsilon )$ description. This is made possible because a reliable value $s=1.4$ had already been measured in similar conductors.

The examples in sections 5.7–5.9 also illustrate that the minimum dataset can indeed be constructed from separate variable temperature and strain apparatuses. This is a significant result, because the data can be acquired more economically with specialized equipment, at different times, and in different laboratories.

The extrapolation tests carried out next (section 3) utilize the complete minimum dataset derived from raw scaling data, consisting of one measurement of $I_{\text{c}}(B,T)$ and one of $I_{\text{c}}(B,\epsilon )$. Such extrapolations provide an effective general test of the different fitting equations that also encompasses the more specialized minimum dataset of Ilyin et al.

2.3. Illustration of the two types of extrapolations

The $T-\epsilon$ map of figure 1 also provides a convenient way to illustrate the two types of extrapolations noted at the end of Part 2.

1. In the first type, the ESE relation is used to extrapolate the complete $I_{\text{c}}(B,T,\epsilon )$ dataset from one temperature measurement $I_{\text{c}}(B,T)$ and one strain measurement $I_{\text{c}}(B,\epsilon )$, as just described. With this type of extrapolation, the temperature and strain axes of the $T-\epsilon$ map are extrapolated to fill-in the rest of the $T-\epsilon$ box in figure 1. Again, the main advantage of this type of extrapolation is that it has a great multiplier effect—it speeds up data acquisition in a unified $T-\epsilon$ apparatus by removing the need to measure all the $T-\epsilon$ cross terms with orthogonal grids of $B-T-\epsilon$ data. As noted above, it also offers the flexibility of combining measurements from two different apparatus (one dedicated to strain measurement and the other to temperature measurement). But, in general, ESE does not extrapolate beyond the strain or temperature limits of the given data along the temperature and strain axes in the $T-\epsilon$ map. This first type of extrapolation is obtained by use of ESE with almost any of the $h(t)$ and $b_{\text{c}2}(\epsilon )$ models described in Part 2.

2. In the second type of extrapolation, the Exponential $b_{\text{c}2}(\epsilon )$ model can be used to extrapolate data along the strain axis of figure 1 from moderate strains to higher compressive strains (figure 13 in Part 2). Similarly, the Hybrid1 or Hybrid2 $h(t)$ models can be used to extrapolate data along the temperature axis of figure 1 from measurements above 4 K to lower temperatures (figures 16(a) and (b) in Part 2). This is particularly useful to avoid the difficulties of transport-current heating and instabilities at temperatures $\ll 4\text{K}$.

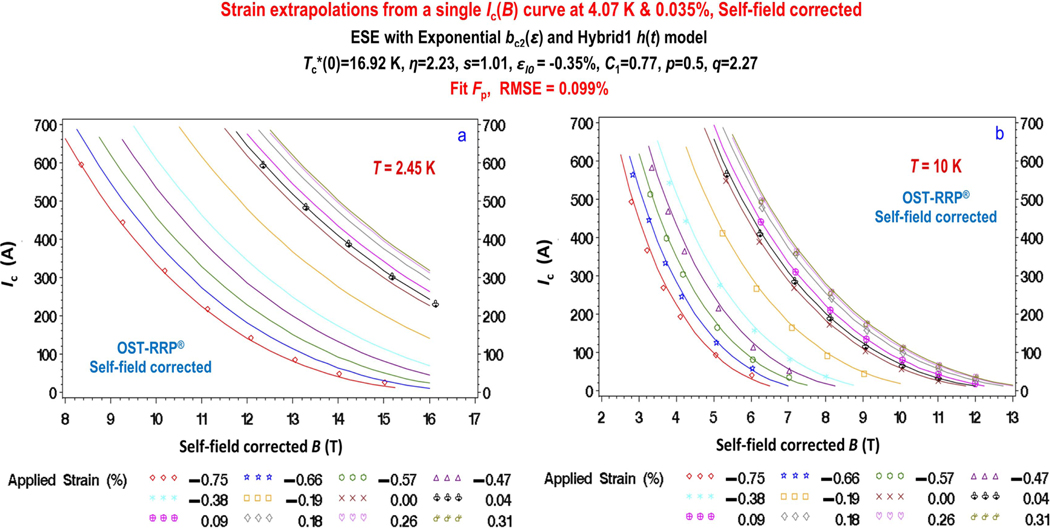
Figure 13.

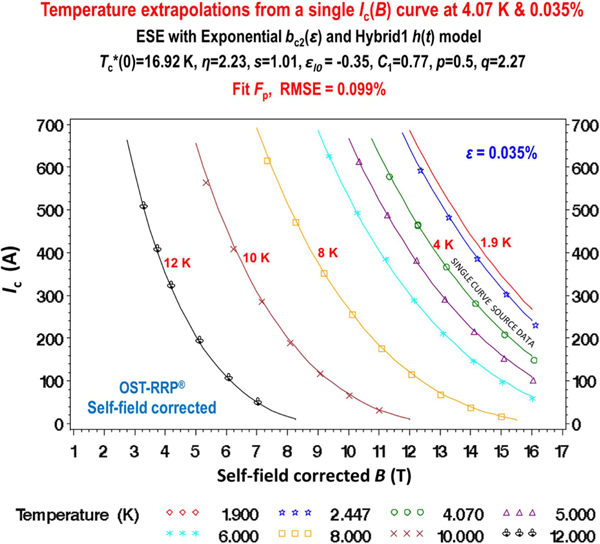
Strain extrapolations from a single $I_{\text{c}}(B)$ curve at 4.07 K and an applied strain of 0.35% (same conditions as figure 12). (a) Extrapolations to 2.45 K and applied strains from −0.75% to +0.31% (corresponding to intrinsic strains of −1.05% to 0.01%). (b) Extrapolations to 10 K and the same range of strains. The RMS $F_{\text{P}}$ extrapolation error is only ∼0.10%.

In brief, the specific combination of ESE with the Exponential and the Hybrid1 or Hybrid2 parameterizations not only fills in the $T-\epsilon$ box, but expands its overall size as well (by making extrapolations along the stain and temperature axes of the $T-\epsilon$ measurement map beyond the given data).

In the rest of this article we focus mainly on evaluating the accuracy of the various fitting equations for the first type of extrapolation (i.e., extrapolating all the $T-\epsilon$ cross terms from the minimum dataset). A few examples are also described of extrapolation accuracies of the second type (extrapolating beyond the limits of the given minimum dataset with the Exponential and Hybrid parameterizations).

3. Extrapolation testing from minimum datasets

In this section we test the extrapolation capability of the ESE relation compared with the present fitting equations. This is done by a simultaneous global fit of the parameters in each model equation to the minimum dataset shown by the crosscut dashed lines in the example of figure 1. The extrapolation accuracies of each equation are then evaluated by comparison of the extrapolated curves with the entire set of measured $I_{\text{c}}$ data. (The critical current criterion is $0.1\mu \text{V/cm}$ throughout this article unless otherwise stated.)

The present fitting equations are evaluated with the constants and fitting parameters usually used for each equation (defined for each model later in this section). Notation is that given by the general equation-set (1).

The ESE fitting equation is evaluated with parameters defined by:

ESE, the ‘easy’ fit

$$I_{\text{c}}(B,T,\epsilon )B=C{\left[b_{\text{c}2}(\epsilon )\right]}^s{(1-t^{1.5})}^{\eta -\mu }{(1-t^2)}^{\mu }{b}^p{(1-b)}^q$$ (2a)

with reduced magnetic field $b\equiv B/{B_{\text{c}2}}^{\ast }(T,\epsilon )$ and reduced temperature $t\equiv T/T_{\text{c}}^{\ast }(\epsilon )$, where:

$${B_{\text{c}2}}^{\ast }(T,\epsilon )={B_{\text{c}2}}^{\ast }(0,0)(1-t^{1.5})b_{\text{c}2}(\epsilon )$$ (2b)

$$T_{\text{c}}^{\ast }(\epsilon )=T_{\text{c}}^{\ast }(0){[b_{\text{c}2}(\epsilon )]}^{1/3}$$ (2c)

with five fitting parameters: $C,{B_{\text{c}2}}^{\ast }(0,0),T_{\text{c}}^{\ast }(0),s$, either $\eta$ or $\mu$ (but not both), plus the parameters in $b_{\text{c}2}(\epsilon )$.

The pinning-force shape parameters, $p$ and $q$, are also preferably fitted (simultaneously with the other parameters), but not necessarily, because the increase in overall RMS fitting error shown later in Tables A3–A5 is less than ∼0.02% if default values $p=0.5$ and $q=2.0$ are used instead. For these extrapolation tests, $p$ and $q$ for all the models were fixed at the same values (determined from master scaling curves) to insure consistency for the comparisons presented. The uniaxial parameterizations used for the different $b_{\text{c}2}(\epsilon )$ models are defined in appendix B of Part 2.

Fitting procedure

Both pinning-force fitting and critical-current fitting were carried out. In all cases the percentage errors at individual data points were about 5 times greater for $I_{\text{c}}$ fitting compared with $F_{\text{P}}$ fitting. This is because $I_{\text{c}}$ fitting unduly weights high $I_{\text{c}}$ data at low magnetic fields, where magnets are usually not designed. This is discussed in more detail in section 3.8 and shown later in figure 9.

Because of the large difference is error, only the results for $F_{\text{P}}$ fitting are shown here. The fitting procedure is as follows:

1. Pinning force data $F_{\text{P}}(B,T,\epsilon )=I_{\text{c}}(B,T,\epsilon )$ $B$ are calculated from the $I_{\text{c}}$ measurements.

2. If magnetic self-field corrections are applied, both $B$ and $F_{\text{P}}\left(=I_{\text{c}}B\right)$ are corrected (Garber et al 1989, Bordini 2010, Cheggour et al 2017).

3. A nonlinear regression program is used to simultaneously fit the parameters of a given fitting equation to the minimum dataset described in section 2: that is $F_{\text{P}}(B,T)$ measured at a strain near zero applied strain, and $F_{\text{P}}(B,\epsilon )$ measured at $\sim 4\text{K}$. Regression analysis is carried out by minimizing the sum of the squared pinning-force residuals $\text{Σ}{(F_{\text{P}}-F_{\text{P}}^{\text{fit}})}^2$.

4. The RMS error and RMS fractional deviation are calculated in terms of percentage $F_{\text{P}}$ residuals, as described below.

5. The absolute $I_{\text{c}}$ extrapolation accuracy is shown by semi-logarithmic graphs of the measured critical currents compared with the predicted critical current curves $I_{\text{c}}(B,T,\epsilon )=F_{\text{P}}(B,T,\epsilon )/B$.

Error analysis

Comparisons are expressed by the percentage RMS $F_{\text{P}}$ errors, and the root mean squared fractional deviations (RMSFD) averaged over all temperatures, magnetic fields, and strains in the complete measured dataset.

The root mean square error (RMSE) is defined as the sum of the squared residuals between the observed $F_{\text{P}}$ values ($y_i$) and the calculated results (${\widehat{y}}_i$),

$$\text{RMSE}\equiv \sqrt{\sum _{i=1}^n\frac{{(y_i-\widehat{y_i})}^2}{n-p}}.$$ (3a)

Here $p$ is the number of parameters in the fit, and $n$ is the number of observations. RMS errors are expressed as percentages to facilitate comparisons between different conductors. Percentage RMSE is calculated by normalizing the absolute RMS $F_{\text{P}}$ error by the lead fitting constant $C[=K(0,0)]$ in the USL parameterization, equation-set (1). (Typical parameter values of $C$ are tabulated in appendix tables A1–A5.)

The emphasis in this article is on the relative performance of the different fitting equations, and so the percentage RMS $F_{\text{P}}$ errors serve this purpose. The percentage RMS $F_{\text{P}}$ errors are also representative of the percentage RMS $I_{\text{c}}$ errors, because the measurement error contributed by the magnetic field to $F_{\text{P}}(=I_{\text{c}}B)$ is negligible compared to that of $I_{\text{c}}$. An effective RMS $I_{\text{c}}$ error can be obtained at any specific field by multiplying the percentage RMS $F_{\text{P}}$ error by lead constant $C$ and dividing by $B$. However, absolute $I_{\text{c}}$ errors are best shown by comparisons of individual data curves in the many $I_{\text{c}}$ graphs in the rest of this article.

The RMS fractional deviation (RMSFD) is defined as the root mean square fractional deviation of the $F_{\text{P}}$ residuals summed over the whole dataset

$$\text{RMSFD}\equiv \sqrt{\sum _{i=1}^n\frac{{\left(\frac{y_i-{\widehat{y}}_i}{y_i}\right)}^2}{n-p}}.$$ (3b)

The RMSFD is included as a quality-of-fit metric, because it focuses on the percentage errors at individual data points, especially at the high magnetic fields and strains of interest for many magnet applications.

3.1. Summary tables of minimum-dataset extrapolation errors

We have run minimum-dataset extrapolation tests for nearly all commonly used parameter combinations, as well as for different methods of fitting the minimum dataset. All totaled, 92 test cases were conducted. Despite the large number of tests, the results are surprising simple.

3.1.1. Three-cut extrapolations.

As noted in section 2.2, we also ran additional extrapolation tests from datasets larger than the minimum two cuts through the $T-\epsilon$ measurement map, to see if this leads to further reduction of extrapolation errors. For these additional tests, the source data were expanded to include: (1) two sets of $I_{\text{c}}(B,T)$ data at two different strains, plus (2) an $I_{\text{c}}(B,\epsilon )$ dataset near 4 K. This is actually a practical measurement combination, because the additional data could be fairly easily integrated into the typical measurement sequence with a unified $T-\epsilon$ apparatus, by running an extra temperature series at a new strain setting (i.e., another column of points in the $T-\epsilon$ map of figure 1). Tests were made with the Durham, G/ITER, and MAG fitting equations (defined in sections 3.3 and 3.4), and with the ESE relation defined by equation-set (2).

Extrapolations from this expanded three-cut set of source data showed no significant reduction in error.

In all tests, the RMS $F_{\text{P}}$ errors were reduced by only 0.003%. This confirmed that the minimum two-cut dataset derived in section 2.2 is indeed optimum. These additional tests also show that the extrapolation errors for each fitting equation are systemic, and not reduced by additional source data.

3.1.2. Summary tables.

Tables 1 and 2 summarize some of the many tests conducted for extrapolations from the (two-cut) minimum dataset. Testing was carried out for both high-$J_{\text{c}}$ (table 1) and moderate-$J_{\text{c}}$ (table 2) conductors. (Conductor descriptions are given in appendix A of Part 2.) Only the highlights are tabulated in these two tables. Many more cases were also run to test less commonly used combinations of fitting parameters, and the results were similar. Details for each tested equation are given in the sections that follow. Unless stated otherwise, the ESE fitting equation (2) was evaluated with the Hybrid1 $h(t)$ model ($\mu =1$ and $\eta$ fitted), but the same ESE results were obtained within experimental error for the Hybrid2 model ($\mu =\eta /2$ and $\eta$ fitted). (The different $h(t)$ models are summarized in section 4.2 of Part 2.)

Table 1.

Summary of results for extrapolations from the minimum dataset for the high-$J_{\text{c}}$ OST-RRP^® conductor, showing the reductions in minimum-dataset extrapolation errors for the ESE relation given by equation-set (2) (indicated as red-italic RMSE and RMSFD values in the last two columns). Small differences in the overall RMSFD and RMS percentage errors indicate a considerable difference in the quality of the fit, as shown by comparing the relative RMSFD and RMSE values for cases 2–7 with the percentage errors at individual $I_{\text{c}}$ data points in the semi-logarithmic figures 3–5 that follow. Differences in parameters between corresponding cases are highlighted in red (‘var’ denotes ‘variable’).

Case #		OST Dataset (high-$J_{\text{c}}$ RRP® conductor): Extrapolation test cases	RMSFD (%)	RMSE (%)
Test case with all free parameters
1	All parameters simultaneously fitted (to show the large extrapolation errors when fitting all the scaling parameters)		58.1
Polynomial ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })$, Taylor (2005)
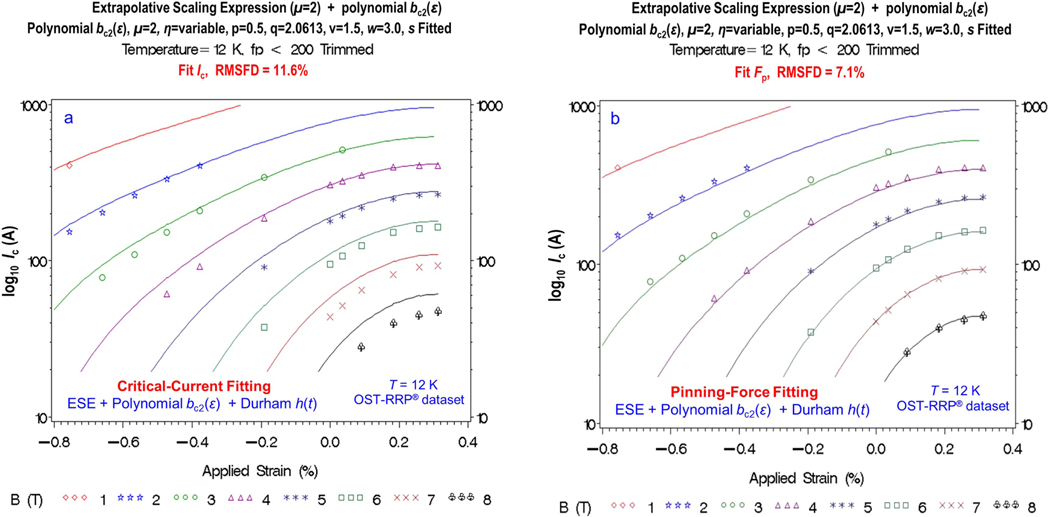
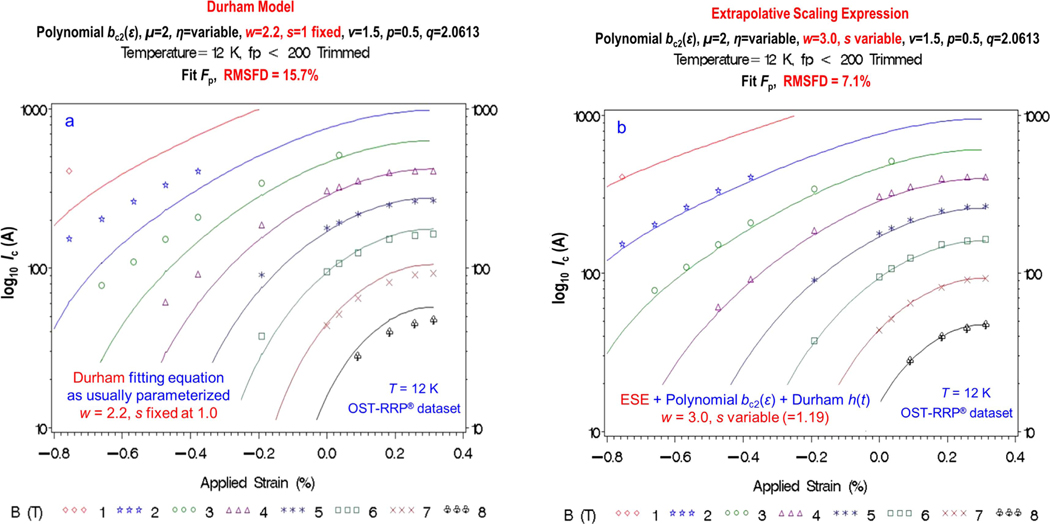
2	Durham:	polynomial ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =2,\eta =\mathrm{var},w=2.2,s=1,v=1.5,p=0.5,q=2.0613$	15.7	0.200
3	ESE:	polynomial ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =2,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	7.1	0.115
Deviatoric $b_{\text{c}2}(\epsilon )$, ten Haken (1994), Godeke et al (2006), Arbelaez et al (2009), Mentink (2008,2014)
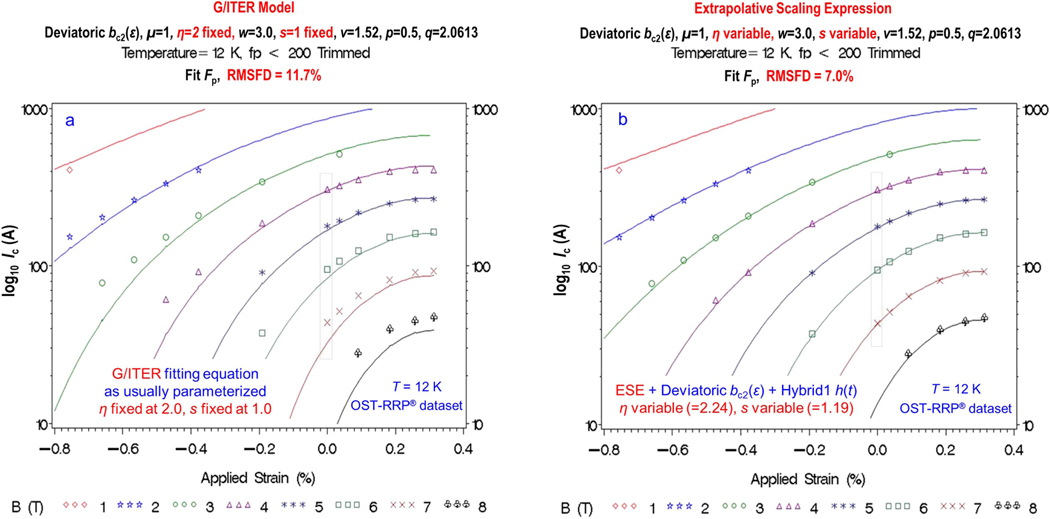
4	G/ITER:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =1,\eta =2,w=3.0,s=1,v=1.52,p=0.5,q=2.0613$	11.7	0.156
5	ESE:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	7.0	0.114
6	MAG:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\eta -\mu =1,\mu =\mathrm{var},w=3.0,s=1,v=1.52,p=0.5,q=2.0613$	9.5	0.130
7	ESE:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\eta -\mu =1,\mu =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	7.7	0.114
Extended Power Law $b_{\text{c}2}(\epsilon )$, NIST (Ekin 2006)
8	ESE:	extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =0,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	7.3	0.126
9	ESE:	extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	6.8	0.110
10	ESE:	extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =2,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	7.0	0.114
Invariant Strain Function $b_{\text{c}2}(\epsilon )$, Markiewicz (2006)
11	ESE:	invariant strain ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	6.9	0.112
Exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon )$, CERN (Bordini et al 2013)
12	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =0,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	8.7	0.131
13	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	8.3	0.121
14	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$, $\text{fit only}{\mathbf{\epsilon }}_0\ge -0.48\text{\%}$	15.6	0.189
15	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\epsilon ),\mu =2,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	8.5	0.128

$F_{\text{P}}$ was trimmed below 200 AT for table 1 and below 125 AT for table 2 to minimize flux creep effects at the lowest $F_{\text{P}}$ levels (near ${T_{\text{c}}}^{\ast }$ and ${B_{\text{c2}}}^{\ast }$). The specific trim level (discussed further in section 3.8) had negligible effect on the RMSE, but did affect the RMSFD results. Therefore, the RMSE results are general, whereas the RMSFD results are restricted to comparisons within each table. [The difference in table-to-table RMSFD levels depends on the $F_{\text{P}}$ trim level set relative to the conductor’s $F_{\text{Pmax}}$ or $K(0,0)$ value. That is, the relative trim level was lower (not as restrictive) for the OST-RRP^® conductor because it is normalized by significantly higher $J_{\text{c}}$ and $K(0,0)$ values, compared to the WST-ITER conductor ($F_{\text{Ptrim}}/K(0,0)=0.4\%$ for the OST-RRP^® dataset, versus 0.7% for the WST-ITER dataset). This resulted in the inclusion of more outlier data points for the OST-RRP^® dataset at the extremes.]

Table 2.

Summary of results for extrapolations from the minimum dataset for the moderate-$J_{\text{c}}$ WST-ITER conductor, showing reductions in RMSE and RMSFD values for the ESE equation-set (2) similar to those in table 1 (red-italic values). These results are for voltage tap 1 on the WST-ITER conductor, located at the center of the magnet. Essentially the same results were obtained for taps 2 and 3 located just above and below the magnet center (not shown), which contribute statistical significance to the results. Differences in parameters between corresponding cases are highlighted in red (‘var’ denotes ‘variable’).

Case #	WST Dataset (moderate-$J_{\text{c}}$ ITER conductor): Extrapolation test cases		RMSFD (%)	RMSE (%)
Test case with all free parameters
1	All parameters simultaneously fitted		116.0	2.194
Polynomial ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })$, Taylor (2005)
2	Durham:	polynomial ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =2,\eta =\mathrm{var},w=2.2,s=1,v=1.5,p=0.5665,q=1.8111$	13.6	0.340
3	ESE:	polynomial ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =2,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.0	0.168
Deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })$, ten Haken (1994), Godeke et al (2006), Arbelaez et al (2009), Mentink (2008,2014)
4	G/ITER:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =1,\eta =2,w=3.0,s=1,v=1.52,p=0.5665,q=1.8111$	8.8	0.268
5	ESE:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.5	0.144
6	MAG:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\eta -\mu =1,\mu =\mathrm{var},w=3.0,s=1,v=1.52,p=0.5665,q=1.8111$	8.8	0.268
7	ESE:	deviatoric ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\eta -\mu =1,\mu =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.5	0.145
Extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })$, NIST (Ekin 2006)
8	ESE:	extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =0,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	6.3	0.150
9	ESE:	extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.4	0.139
10	ESE:	extended power law ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =2,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.4	0.172
Invariant strain function ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })$, Markiewicz (2006)
11	ESE:	invariant strain ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5,q=2.0613$	5.3	0.135
Exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon })$, CERN (Bordini et al 2013)
12	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =0,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	6.7	0.148
13	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.7	0.134
14	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =1,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$, $\text{fit only}{\mathbf{\text{ε}}}_0\ge -0.57\text{\%}$	6.4	0.181
15	ESE:	exponential ${\mathit{b}}_{\mathbf{\text{c}}\mathbf{2}}(\mathit{\epsilon }),\mu =2,\eta =\mathrm{var},w=3.0,s=\mathrm{var},v=1.5,p=0.5665,q=1.8111$	5.4	0.163

Tables 1 and 2 serve to compare at a glance the many different combinations of scaling constants and parameters in use for parameterizing the general USL equation-set (1). The net result is that all cases show large relative improvement in extrapolation errors for ESE compared with the present fitting equations, when evaluated under comparable conditions [i.e., with the same $b_{\text{c}2}(\epsilon )$ and the same or similar $h(t)$]. The ESE results are indicated by the red-italic RMSFD and RMSE numbers in the last two columns of tables 1 and 2. The overall RMS $F_{\text{P}}$ errors obtained for ESE correspond to very low effective RMS $I_{\text{c}}$ errors, in the range 2–5 A at 12 T (depending on whether the conductor is moderate $J_{\text{c}}$ or high $J_{\text{c}}$). These extrapolation errors approach typical $I_{\text{c}}$ measurement errors.

We emphasize that small differences in the overall RMS error in tables 1 and 2 make a very large difference in the percentage errors at individual data points, especially those further away from the source minimum dataset. This is shown more sensitively by the RMSFD results, and most clearly by the graphs of individual $I_c$ data curves in figures 2–9 in the following subsections, which are correlated with the case results in tables 1 and 2.

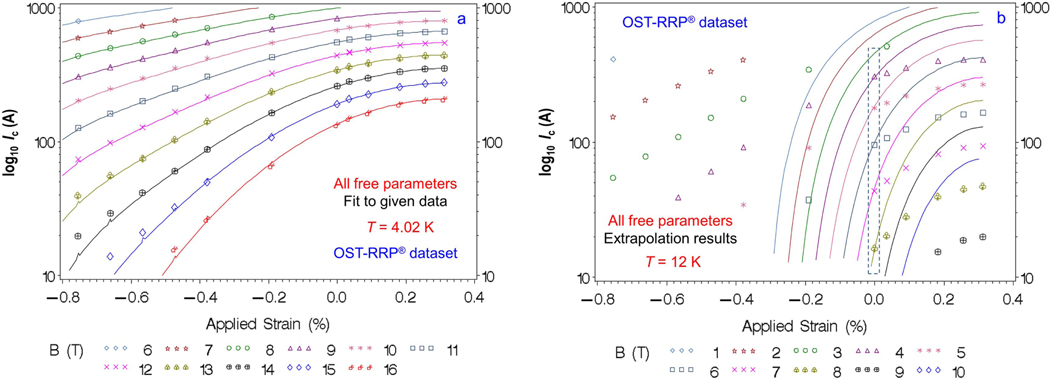
Figure 2.

Effect of fitting all parameters in the general parameterization of the USL to the minimum dataset at 0.0% strain and 4.02 K (i.e., the dashed crosscut in figure 1). (a) High accuracy interpolative fit to the given minimum dataset at 4.02 K when fitting all parameters in the general parameterization of the USL (i.e., no constants). Solid curves show the fitting results, whereas symbols show the measured data. (b) Results extrapolated from the minimum dataset to 12 K, showing the extremely poor extrapolation capability when simultaneously fitting all the scaling parameters to the minimum dataset. Despite the large general errors, note that the fit in figure (b) to the given data at 0.0% strain is highly accurate (dashed box).

3.2. Examples of minimum-dataset extrapolation error

Sections 3.2–3.7 show examples of minimum-dataset extrapolation errors for the different fitting equations.

• Results are usually plotted at 12 K because of the larger extrapolation errors at this temperature compared with lower temperatures. However, in some cases considerable interpolation errors also occurred. In such cases, results are also shown at ∼4 K to display errors to the fitted source data.

• The extrapolation test results are plotted as $I_{\text{c}}-\epsilon$ curves at different magnetic fields, rather than in the more usual form of $I_{\text{c}}-B$ curves at different strains or temperatures. This is done because $I_{\text{c}}-\epsilon$ curves are flatter, thus making it easier to visualize errors. Later, in section 5 on the practical application of ESE, we plot the results in the more usual way as $I_{\text{c}}-B$ curves for application to magnet design.

• Testing was carried out on critical-current data that were not corrected for magnetic self-field, but the fitting results should be applicable to either corrected or uncorrected data because of the near identity of the scaling constants for both types of data, as shown in section 5 of Part 2. This is also verified here in Part 3 by the extrapolations carried out with self-field corrected data in section 5.

As a first example, figures 2(a) and (b) show, for perspective, the problem of fitting too many parameters simultaneously. Here all the parameters in the general parameterization of the USL [equation-set (1)] are fitted, without any constant parameters. As might be expected with so many fitting parameters, figure 2(a) shows that the interpolation of the given $I_{\text{c}}$ data at 4.02 K is excellent over the entire strain and magnetic-field range.

However, figure 2(b) shows that extrapolation of the 4 K minimum dataset to off-axis $I_{\text{c}}$ values at 12 K (the red-boxed data in the $T-\epsilon$ measurement map of figure 1) leads to relative errors of 400% or more at high compressive strains. Note, by way of contrast, that the fit to the given data at 0.0% strain and 12 K [dashed box in figure 2(b)] is spot on, as we would expect. This illustrates the importance of not trying to determine too many scaling parameters simultaneously for extrapolation accuracy.

With this case we also show that plotting the residuals at 12 K in the following figures gives a high-leverage extrapolation test, because it is difficult to extrapolate so far away from the on-axis minimum dataset at 4 K. When extrapolating to temperatures closer to the given data, the extrapolation errors are less, approximately proportional to the temperature difference from 4 K.

3.3. Durham global-fitting equation (cases 2 and 3 in tables 1 and 2)

The Durham global-fitting equation (Taylor and Hampshire 2005, Lu et al 2008) is given by the following equation-set:

Durham interpolative equation:

$$\begin{array}{c}{I}_{\text{c}}(B,T,\epsilon )B=C{b}_{\text{c}2}(\epsilon ){(1-t^{1.5})}^{\eta -2}{(1-t^2)}^2{b}^p{(1-b)}^q,\\ (s=1,\mu =2)\end{array}$$ (4a)

$$T_{\text{c}}^{\ast }(\epsilon )=T_{\text{c}}^{\ast }(0){[b_{\text{c}2}(\epsilon )]}^{1/2.2}(w=2.2).$$ (4b)

Polynomial uniaxial model

$$b_{\text{c}2}(\epsilon )=1+c_2{{\epsilon }_0}^2+c_3{{\epsilon }_0}^3+c_4{{\epsilon }_0}^4$$ (4c)

Here, ${\epsilon }_0$ is the intrinsic strain defined as ${\epsilon }_0\equiv \epsilon -{\epsilon }_{\text{m}}$, where, for the uniaxial strain case, $\text{ε}$ is the longitudinal applied strain and ${\epsilon }_{\text{m}}$ is the longitudinal strain at the maximum $I_{\text{c}}(\epsilon )$. The model has four fixed constants $s=1,v=1.5,\mu =2,w=2.2$; and fitted parameters $C,{B_{\text{c}2}}^{\ast }(0,0),T_{\text{c}}^{\ast }(0),\eta ,p,q,c_2,c_3,c_4$, and ${\epsilon }_{\text{m}}$. Sometimes the parameter $w$ is also included as a fitted parameter.

This is a very precise parameterization of the USL for interpolating data, and, in fact, it is named an ‘interpolative’ model. As listed above, the strain exponent in this model is fixed at $s=1$, and the cross-link exponent is usually set to the constant value $w=2.2$.

Figure 3(a) shows the results for this model, extrapolation tested with the minimum dataset for the extensive OST-RRP^® Nb₃Sn dataset (i.e., curves were extrapolated from the $I_{\text{c}}-B$ data along the crossed dashed lines in figure 1 to the rest of the $T-\epsilon$ map.) Of course, this model was not designed to be an extrapolative equation, but for illustration purposes, the extrapolation errors at individual data points are seen to be as large as 200% in the high compressive strain range on the left side of the figure (note that the ordinate in these figures is a logarithmic scale). Results similar to the 12 K results in figure 3(a) were also obtained at 10, 8, and 6 K, with proportionately smaller errors as the temperature approached the given minimum dataset at 4.02 K.

Figure 3.

Minimum-dataset extrapolation tests for the Durham fitting equation, utilizing the very large OST-RRP^® Nb₃Sn dataset. Solid curves show the 12 K results extrapolated from the minimum dataset at 0.0% strain and 4.07 K (i.e., the dashed crosscut in figure 1)., Data points show the measured $I_{\text{c}}$ values. (a) Extrapolation results for the Durham fitting equation parameterized with the Durham $h(t)$ model (i.e., $\mu =2$) and Polynomial $b_{\text{c}2}(\epsilon )$ (appendix B.3 of Part 2), (b) Extrapolation results for ESE, also applied with the same Durham $h(t)$ and Polynomial $b_{\text{c}2}(\epsilon )$. In figure (b) the percentage extrapolation errors at individual data points at high compressive strains are reduced to as little as 1/30th to 1/40th the size of those in figure 3(a) (note the vertical scales are logarithmic). The main differences between the two figures is that in 3(b): (1) the cross-link parameter is set to the constant $w=3.0$, instead of the Durham default value $w=2.2$; and (2) the strain exponent $s$ is freed to be a fitted parameter, instead of fixed at $s=1.0$.

Tests were also run with $w$ allowed to be a free parameter. RMS extrapolation errors increasing by an order of magnitude, and errors at individual data points were almost as extreme as those in figure 2(b). From the standpoint of scaling, $w$ is a very sensitive parameter wherein small errors have a considerable effect on the other parameter values and the extrapolation error.

Figure 3(b) shows the extrapolation curves for the ESE relation applied with the same Durham $h(t)$ model and polynomial $b_{\text{c}2}(\epsilon )$ parameterizations as in the Durham global-fitting equation results of figure 3(a). The ESE relation reduces the percentage extrapolation errors at individual data points to as little as 1/30th to 1/40th the size of those in figure 3(a) at 12 K and high compressive strains. The corresponding large reduction in overall RMSFD error is shown by comparing cases 2 and 3 in table 1 (15.7% reduced to 7.1%) and table 2 (13.6% reduced to 5.0%).

3.4. Godeke, ITER, and MAG global-fitting equations (cases 4–7 in tables 1 and 2)

The Godeke (Godeke et al 2006, 2009, 2013) global-fitting equation is given by equation-set (5):

Godeke fitting equation:

$$\begin{gathered} I_{\text{c}}(B,T,\epsilon )B=C{b}_{\text{c}2}(\epsilon )(1-t^{1.52})(1-t^2)b^{0.5}{(1-b)}^{2.0} \\ (s=1,\eta =2,\mu =1,p=0.5,q=2.0), \end{gathered}$$ (5a)

Deviatoric uniaxial model

$$b_{\text{c}2}(\epsilon )=\frac{1-C_{a,1}\sqrt{{{\epsilon }_0}^2+{{\epsilon }_{0,a}}^2}-C_{a,2}\left({{\epsilon }_0}^3-3{{\epsilon }_{0,a}}^2{\epsilon }_0\right)}{1-C_{a,1}{\epsilon }_{0,a}}.$$ (5b)

where ${\epsilon }_0$ is the intrinsic strain defined as ${\epsilon }_0\equiv \epsilon -{\epsilon }_{\text{m}}$, and ${\epsilon }_{\text{m}}$ is the longitudinal strain at the maximum $I_{\text{c}}(\epsilon )$. The model has seven fixed constants $s=1,v=1.52,\eta =2,\mu =1,w=3,p=0.5,q=2.0$; and fitted parameters $C$, ${B_{\text{c}2}}^{\ast }(0,0),T_{\text{c}}^{\ast }(0)$, $C_{a,1},C_{a,2},{\epsilon }_{0,a}$, and ${\epsilon }_{\text{m}}$.

The ITER fitting equation (Bottura and Bordini 2009) is the same as the Godeke equation-set (5), except that the shape exponents of the pinning-force curve, $p$ and $q$, are fitted parameters rather than fixed at constant values $p=0.5$ and $q=2.0$ as in the Godeke equation, so that the $f(b)$ term in equation (5a) becomes $b^p{(1-b)}^q$. That is,

ITER fitting equation:

$$\begin{gathered} I_{\text{c}}(B,T,\epsilon )B=C{b}_{\text{c}2}(\epsilon )\left(1-t^{1.52}\right)\left(1-t^2\right)b^p{(1-b)}^q \\ (s=1,\eta =2,\mu =1), \end{gathered}$$ (6a)

Deviatoric uniaxial model.

$$b_{\text{c}2}(\epsilon )=\frac{1-C_{a,1}\sqrt{{{\epsilon }_0}^2+{{\epsilon }_{0,a}}^2}-C_{a,2}({{\epsilon }_0}^3-3{{\epsilon }_{0,a}}^2{\epsilon }_0)}{1-C_{a,1}{\epsilon }_{0,a}}$$ (6b)

The model has five constants $s=1,v=1.52,\eta =2,\mu =1,w=3$; and fitted parameters $C,B_{\text{c}2}\ast (0,0),T_{\text{c}}^{\ast }(0),p,q,C_{a,1},C_{a,2},{\epsilon }_{0,a}$, and ${\epsilon }_{\text{m}}$.

The Godeke and ITER models served their purpose reasonably well for many of the moderate-$J_{\text{c}}$ ITER conductors (but not all, e.g., the EM-LMI results of section 4.2 in Part 2). They can also be quite accurate for interpolations for some Nb₃Sn conductors.

However, figure 4(a) for a high-$J_{\text{c}}$ conductor shows that extrapolation errors at individual data points for the ITER model [equation-set (6)] can be up to 50% of the measured $I_{\text{c}}$ data, especially at high compressive strains (again, note the logarithmic vertical scale). If we focus on just the fit to the given minimum-dataset measurements at zero applied strain [boxed data in figure 4(a)], we see that there are also significant interpolation errors for the given data (up to 30% at higher fields).

Figure 4.

Minimum-dataset extrapolation tests for the G/ITER fitting equation, evaluated utilizing the high-$J_{\text{c}}$ OST-RRP^® dataset. Solid curves show the predicted 12 K results extrapolated from the minimum dataset at 0.0% strain and 4.07 K (i.e., the dashed crosscut in figure 1). Individual data points show the measured $I_{\text{c}}$ values. (a) The ITER fitting equation shows relatively large extrapolation errors, including considerable interpolation errors in fitting the given data at 0.0% applied strain (shown by a light box in the two figures); the Godeke model (fixed $p=0.5$ and $q=2.0$) gives larger extrapolation errors, up to 80% higher (not shown). (b) The ESE relation applied with the Deviatoric $b_{\text{c}2}(\epsilon )$ and Hybrid1 $h(t)$ gives a reduction in percentage extrapolation and interpolation errors at individual data points at high compressive strains and fields to as little as 1/15th the size of those in figure 4(a), for both extrapolated and interpolated data.

For the Godeke equation-set (5) (i.e., $p=0.5$ and $q=2.0$), the test results (not shown) gave both interpolation and extrapolation errors greater than those in figure 4(a), particularly at high magnetic fields where the extrapolation errors were up to 80% of the measured $I_{\text{c}}$ data.

Figure 4(b) shows the ESE fitting equation applied with the same Deviatoric $b_{\text{c}2}(\epsilon )$ as for the Godeke model (appendix B.4 of Part 2), but with the Hybrid1 $h(t)$ temperature parameterization instead of fixing both temperature exponents ($\eta =2$ and $\mu =1$) and setting the strain parameter $s$ to a constant ($s=1$). A comparison of figure 4(a) with 4(b) shows reduction of the percentage extrapolation errors in figure 4(b) at individual data points to as little as 1/15th the size of those in figure 4(a) at high magnetic fields and compressive strains. Significant improvement also occurs for the fit to the given data (boxed data points in figure 4(b) at applied strain = 0.0%). The overall RMSFD percentage error was reduced by more than a third, shown by comparing cases 4 and 5 in table 1 (11.7% reduced to 7.0%). A similar reduction in overall RMS error was also observed for the moderate-$J_{\text{c}}$ WST-ITER conductor, where the RMS error was almost halved (cases 4 versus 5 in table 2).

3.4.1. Simplified expressions.

Mathematically simplified re-expressions of the G/ITER parameterizations have also been made (Mentink 2008), wherein two of the separable parts, $g(\epsilon )$ and $b_{\text{c}2}(t)$, are combined. That is, from the general separable USL parameterization [equation-set (1)]

$$\begin{gathered} I_{\text{c}}(B,T,\epsilon )B=Cg(\epsilon )h(t)f(b) \\ =C\boxed{{[b_{\text{c}2}(\epsilon )]}^{\mathit{s}}}\boxed{{(1-t^{\text{v}})}^{\mathit{\eta }-\mathit{\mu }}{(1-t^2)}^{\mathit{\mu }}}\boxed{b^p{(1-b)}^q}, \end{gathered}$$ (7)

the separate strain and temperature parts (left and middle boxed parts above) are combined with the $B$ variable on the left side and rearranged to give a mixed term (boxed below) that is a combination of reduced temperature, strain, and (non-reduced) magnetic field

$$I_{\text{c}}(B,T,\epsilon )=C\boxed{[b_{\text{c}2}{(\epsilon )}^{\mathit{s}}{(1-t^{\text{v}})}^{\mathit{\eta }-\mathit{\mu }}/B]}{\left(1-t^2\right)}^{\mathit{\mu }}{b}^p{(1-b)}^q.$$ (8)

Now if the exponents are fixed to constant values $s=1$, $\eta =2$, and $\mu =1$, the boxed term in equation (8) reduces to $B_{\text{c}2}\ast {(0,0)}^{-1}{b}^{-1}$, since $b^{-1}\equiv {B_{\text{c}2}}^{\ast }(T,\epsilon )/B\equiv {B_{\text{c}2}}^{\ast }(0,0)b_{\text{c}2}(\epsilon )(1-t^{\nu })/B$ [from equation (1c)]. This gives the Mentink fitting equation (Mentink 2008, Godeke et al 2009, 2013):

Mentink fitting equation:

$$\begin{gathered} I_c(H,T,\epsilon )={\text{C}}_1(1-t^2)h^{p-1}{(1-h)}^q, \\ (s=1,\eta =2,\text{μ}=1) \end{gathered}$$ (9)

where ${\text{C}}_1\equiv C{B_{\text{c}2}}^{\ast }{(0,0)}^{-1}$, and the notation $H$ and $h\equiv H/H_{\text{c}2}(t,\epsilon )$ are equivalent to $B$ and $b\equiv B/B_{\text{c}2}(t,\epsilon )$ as defined in this article (i.e., $B\equiv {\mu }_{0}H$, which gives the practical units of tesla). The form of $h^{p-1}{(1-h)}^q$, on the right hand side of equation (9) was used earlier by Hampshire et al (1985). Since equation (9) is mathematically equivalent to the G/ITER fitting equation (6) (where the scaling exponents are also fixed at constant values $s=1$, $\eta =2$, and $\mu =1$), the extrapolation and interpolation errors are identical to those shown in figure 4(a).

The need for a fitted temperature parameter in $h(t)$ was described earlier (Keys and Hampshire 2003, Taylor and Hampshire 2005, Ekin 2006, Lu et al 2008, and Bottura and Bordini 2009), and recently more specifically for the Godeke/ITER $h(t)$ (Ekin 2010 and Ekin et al 2013). Accordingly, a modification of equation (9) was subsequently introduced by Mentink (2014) (labeled the MAG relation, for Mentink, Arbelaez, and Godeke)

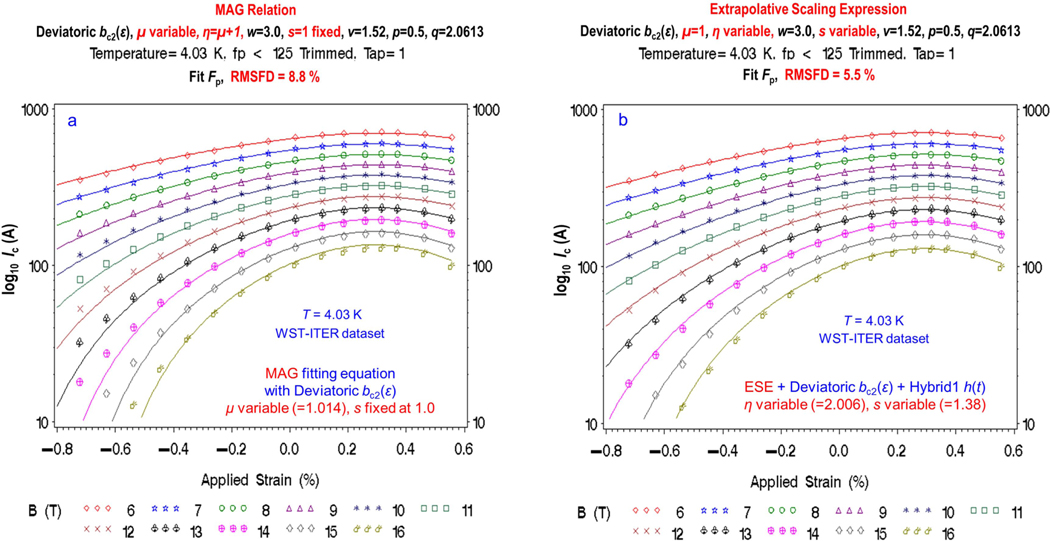
MAG fitting equation:

$$\begin{gathered} I_{\text{c}}(H,T,\epsilon )=C_{\text{l}}{(1-t^2)}^{\mu }{h}^{p-1}{(1-h)}^q. \\ (s=1,\eta =\mu +1) \end{gathered}$$ (10)

In this parameterization, the temperature exponent $\mu$ in equation (8) is made a fitting parameter (with the other exponent $\eta$ fixed by $\eta =\mu +1$). This improves the fitting accuracy of this relation. However, the simplified mathematical form [equation (10)] results only if the strain parameter s is still fixed at the constant value $s=1$. The MAG model thus has significant extrapolation errors, as well as relatively large interpolation errors for the given data at 4.03 K shown in figure 5(a) (up to 50% of the measured $I_{\text{c}}$ data at high compressive strains and magnetic fields). By comparison, the ESE results in figure 5(b) similarly evaluated with the Deviatoric $b_{\text{c}2}(\epsilon )$ strain function, but with a fitted strain parameter $s$, shows reduction in percentage interpolation errors down to as little as 1/15th the size of those in figure 5(a) at higher compressive strains. The overall reduction in RMSE and RMSFD extrapolation errors with ESE was also significant, whether the Hybrid1 $h(t)$ or Mentink $h(t)$ function was used with ESE (e.g., in table 2, RMSFD = 8.8% for the MAG equation in case 6, reduced to 5.5% for the ESE equation with either fitted $\eta$ in case 5 or fitted $\mu$ in case 7). Similar error reductions were also measured for the OST-RRP^® dataset (same case numbers in table 1).

Figure 5.

Interpolation errors for the MAG equation for fitting all the given data at 4.03 K (figures 3 and 4 were at the extrapolated temperature of 12 K). Solid curves show the fitted interpolation curves, and symbols indicate the given 4.03 K data for the moderate-$J_{\text{c}}$ WST-ITER conductor. (a) The MAG equation shows relatively large interpolation errors (up to 50% of the measured $I_{\text{c}}$ data at high compressive strains and magnetic fields; note the semi-logarithmic scale). (b) The ESE equation, where $s$ is freed to be a fitted parameter, shows reductions in interpolation errors down to as little as 1/15th the size at high magnetic fields and compressive strains. The particular temperature parameterization used for $h(t)$ in ESE for figure 5(b) made only a small difference, as shown by the comparably low RMSFD and RMS errors for fitting either $\mu$ or $\eta$ with the ESE relation parameterized with the same Deviatoric $b_{\text{c}2}(\epsilon )$ as the MAG relation (cases 5 and 7 in tables 1 and 2). The main difference in fitting errors between the MAG and ESE relations is a result of the fixed exponent $s=1$ in the MAG model. For the example shown in figure (b), the globally fitted value of $s$ in the ESE equation was $s=1.38$, consistent with the values obtained for the ITER conductors ($s=1.4\pm 0.1$) from analysis of raw scaling data (section 4.4 in Part 2).

Thus, the simplicity of the Mentink expressions is attractive, but the extrapolation and interpolation errors are significant. There are also a couple structural issues:

• The parameters are no longer separated: The separable parts $g(\epsilon )$ and $h(t)$ [boxed in equation (7)] are comingled with the pinning-force curve function $f(b)$ to give the extra $h^{-1}$ term in equations (9) and (10). This makes it difficult to determine the parameters of this expression from raw scaling data for ${B_{\text{c}2}}^{\ast }(T,\epsilon )$ and $K(T,\epsilon )$ without re-separating the parts. No testing with raw scaling data was done in the formulation of the MAG fitting equation.

• Reintroduction of $B$ is needed for $F_{\text{P}}$ fitting: The emphasis of the expressions is on $I_{\text{c}}$, isolated on the left-hand side of equations (9) and (10), rather than $F_{\text{P}}$. However, what scales is not $I_{\text{c}}$, but $F_{\text{P}}$. This is not a major issue like extrapolation and interpolation accuracy, but a $B$ term needs to be reintroduced into the relation to explicitly give $F_{\text{P}}$ to carry out the more-accurate $F_{\text{P}}$ fitting (section 3.8).

3.5. NIST global-fitting equation (cases 8–10 in tables 1 and 2)

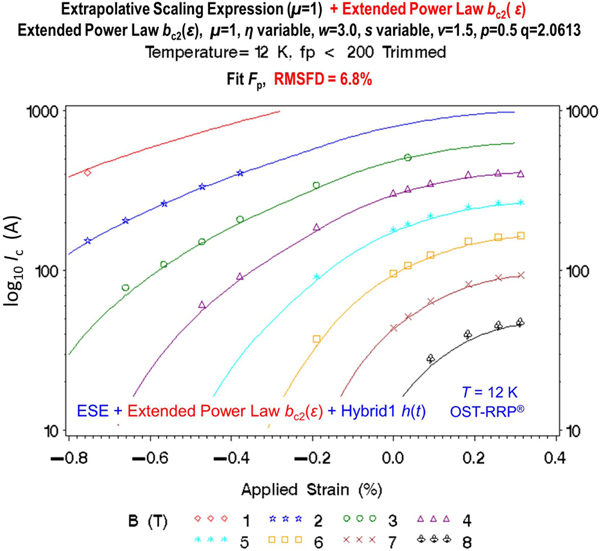
The Extended Power Law for $b_{\text{c}2}(\epsilon )$ (appendix equation (B.2) in Part 2), expands the Power Law parameterization to high compressive strains ${\epsilon }_0\ll -0.5\text{\%}$, while preserving the curvature constant $u=1.7$ for moderate strains (Ekin 1980, 1981, 2006 and 2010). Figure 6 shows the minimum-dataset extrapolation results for ESE when used in combination with the Extended Power Law $b_{\text{c}2}(\epsilon )$ parameterization and the Hybrid1 $h(t)$ parameterization. Extrapolation errors are comparable to those in figures 3(b), 4(b), and 5(b) where ESE is fitted with other $b_{\text{c}2}(\epsilon )$ functions. The RMSFD errors for the Extended Power Law case were among the lowest of any of the cases studied (case 9 in tables 1 and 2: RMSFD = 6.8% for the OST-RRP^® dataset, and 5.4% for the WST-ITER dataset). Remarkably, when the ESE relation is used with the Extended Power Law, plus the Fietz and Webb parameterization for $h(t)$ [equation (15) in Part 2], this gives the original USL parameterization proposed in 1980 for the moderate strain regime [updated here with the recently measured parameterization for $b_{\text{c}2}(t)(=1-t^{1.5})$]. This original combination also had very low RMSFD extrapolation errors (case 8 in tables 1 and 2: RMSFD = 7.3% for OST-RRP^® dataset, and 6.3% for WST-ITER dataset).

Figure 6.

Minimum-dataset extrapolation results for ESE with the Extended Power Law $b_{\text{c}2}(t)$ and the Hybrid1 $h(t)$ parameterizations (OST-RRP^® dataset). RMSFD errors were among the lowest for the cases studied. Solid curves show the 12 K results extrapolated from the minimum dataset at 0.0% strain and 4.07 K (i.e., the dashed crosscut in figure 1). Symbols show the measured $I_{\text{c}}$ data.

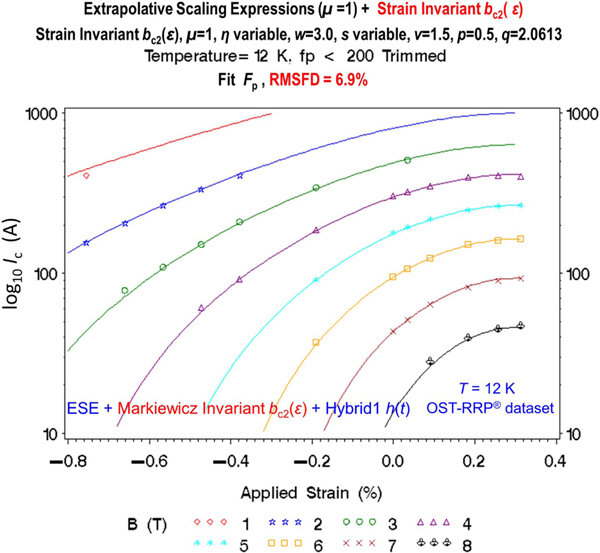
3.6. Invariant ${\text{b}}_{\text{c}2}(\text{ε})$ used with the ESE fitting equation (case 11 in tables 1 and 2)

The numerically integrated strain-invariant model of Markiewicz was the first that utilized three-dimensional (3-D) strain invariants (Markiewicz 2004). Subsequently, others have also expressed their empirical parameterizations of $b_{\text{c}2}(\epsilon )$ in terms of strain invariants. The original Markiewicz model is based on a first-principles calculation, but it is not convenient to use. So the features of this fundamental calculation were formulated into the more user-friendly, but empirical, Invariant Strain Function given by appendix equations (B.9) and (B.10) in Part 2 (Markiewicz 2006). This model gives precise fitting results as shown in figure 7 (case 11 in tables 1 and 2), plus it has the capability to extend one dimensional strain measurements to 3-D design applications.

Figure 7.

Minimum-dataset extrapolation tests for the Invariant strain function. This parameterization of $b_{\text{c}2}(\epsilon )$ was also among the most accurate when used with ESE, shown here with the Hybrid1 $h(t)$ parameterization. Solid curves present the 12 K results extrapolated from the minimum dataset at 0.0% strain and 4.07 K; symbols indicate measured $I_{\text{c}}$ values.

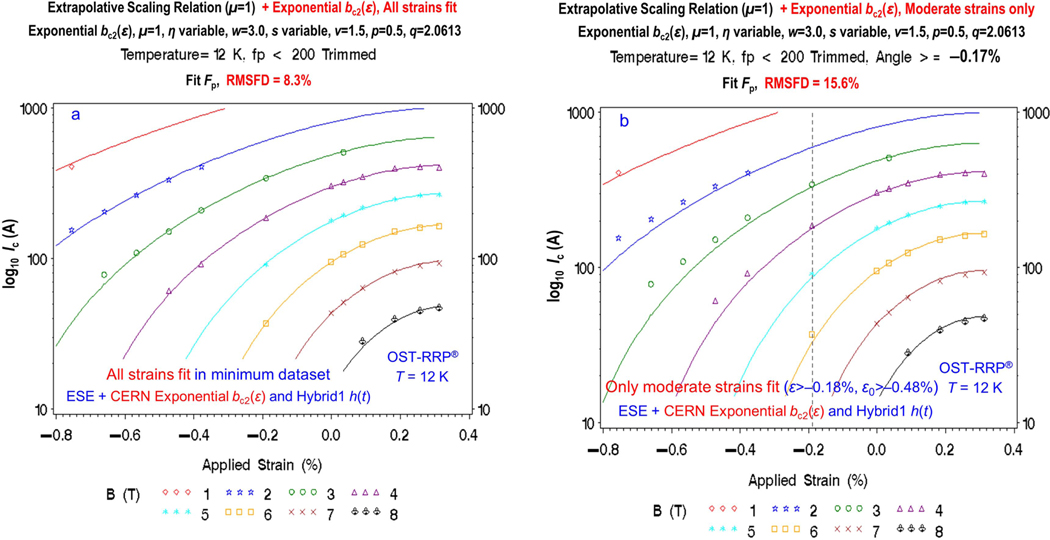
3.7. Exponential ${\text{b}}_{\text{c}2}(\text{ε})$ used with the ESE fitting equation (cases 12 and 13 in tables 1 and 2)

The Exponential strain model for $b_{\text{c}2}(\epsilon )$, given by appendix equations (B.11) and (B.12) in Part 2 (Bordini et al 2013), has the unique capability to extrapolate moderate strain data ($-0.5\text{\%}<{\epsilon }_0<{\epsilon }_{0,\text{irr}}$) to extended compressive strains (${\epsilon }_0\ll -0.5\text{\%}$). (This is the second type of extrapolation described in section 2.3). A fit to just the moderate strain data for the WST-ITER dataset gives remarkably low extrapolation errors even though the fitted data are extrapolated out to intrinsic strains of –1.03% (RMSFD = 6.4%, case 14, table 2; which is nearly the same error as for a fit to the complete strain range, RMSFD = 5.7%, case 13, table 2).

Of course, when high compressive strain data are available, it is preferable to fit the entire strain range because random errors in the fitted moderate-strain data can otherwise extrapolate to larger errors. Figure 8 shows an example of this for the more-difficult-to-fit OST-RRP^® dataset (which has an irreversible intrinsic strain limit ${\epsilon }_{0,\text{irr}}$ near 0%, whereas the WST-ITER conductor has a more normal ${\epsilon }_{0,\text{irr}}=\sim +0.3\text{\%}$ that permits data to be measured on the tensile side of the strain peak). When all strains are fitted for the OST-RRP^® dataset, the RMSFD is relatively low (8.3%, which is comparable to the results for the other $b_{\text{c}2}(\epsilon )$ models even though they have many more fitting parameters). But when only moderate strains are fitted (to the right of the dashed vertical line in figure 8(b)) and extrapolated to extended compressive strains, the RMSFD increases to 15.6%. This example also shows the importance of having a relatively fine measurement grid when extrapolating limited data to higher compressive strains (compare the measurement grid in figure 8 with the finer measurement grid for the WST-ITER dataset in figure 5).

Figure 8.

Minimum-dataset strain extrapolation tests for the Exponential $b_{\text{c}2}(\epsilon )$ model with ESE, shown for the more difficult-to-fit OST-RRP^® conductor where ${\epsilon }_{0,\text{irr}}$ was near 0% (cases 13 and 14 in table 1). (a) Results for fitting all strains in the minimum dataset. (b) Results for fitting strains only over the limited range of moderate strains ($\epsilon >-0.18\%$, to the right of the dashed line), and then extrapolating to compressive strains of −0.72% (intrinsic strains of −1.03%). Accuracy is lower for figure 8b, but still reasonable considering the curves in figure (b) are extrapolated to an extended strain range well beyond the given data. For the WST-ITER conductor where ${\epsilon }_{0,\text{irr}}$ is ∼0.3%, RMSFD errors are significantly lower when extrapolating moderate strain data to extended compressive strains with the Exponential model (RMSFD errors are only 5.7% and 6.4% for the same two cases, 13 and 14 in table 2).

Nevertheless, the capability of the Exponential $b_{\text{c}2}(\epsilon )$ parameterization to extrapolate limited strain data to higher compressive strains can be very useful, a capability not shared by the other models. Furthermore, the single fitted parameter in this model, $C_1$, can be used as a strain sensitivity index, as well as provide consistency and noise rejection over the dominant peak $I_{\text{c}}$ stain range (detailed in item 5 of the summary section 6.2).

3.8. Factors for achieving extrapolation and interpolation accuracy with global-fitting equations

Several factors are needed to achieve the exceptional accuracy of the ESE relation in sections 3.3–3.7 for interpolations and extrapolations from minimum datasets.

3.8.1. Pinning-force fitting versus critical-current fitting.

The accuracies reported here are obtained by converting the critical-current data to pinning-force data ($F_{\text{P}}=I_{\text{c}}B$) before fitting (procedural steps are listed at the beginning of section 3). Fitting $F_{\text{P}}$ places emphasis on the mid-magnetic field region (where $F_{\text{P}}$ peaks) and avoids unduly weighting the lower magnetic fields dominated by the highest critical currents. Fitting $F_{\text{P}}$, rather than $I_{\text{c}}$, reduces percentage extrapolation errors at individual data points down to as little 1/5th the size, as shown by comparing figure 9(a) for $I_{\text{c}}$ fitting, with figure 9(b) for $F_{\text{P}}$ fitting. This considerable difference in extrapolation accuracy was consistently seen in all test cases where high extrapolation accuracy was observed (i.e., the ESE cases shown by the red italic RMSFD values in tables 1 and 2).

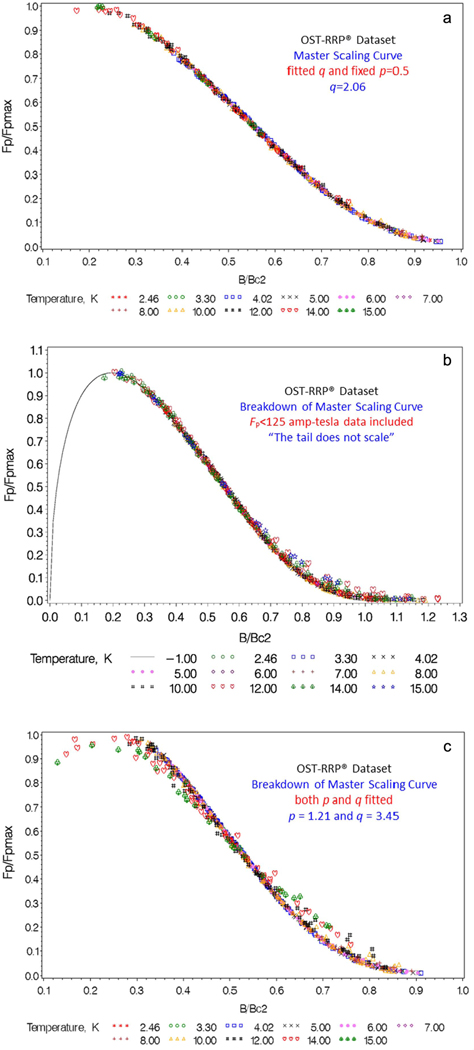
3.8.2. Insufficient data to determine values of $p$ and $q$.

When data on the low-field side of the pinning-force peak are insufficient to determine the shape parameter $p$, erroneous $p$ values result, and then $p$ needs to be set to a default value such as $p=0.5$.⁵ This was the case for the OST-RRP^® conductor, where heating effects at very high $I_{\text{c}}$ levels prevented the measurement of sufficient data at low fields, < ∼5 T at 4.2 K). This situation will become more common as Nb₃Sn conductors are developed with further increases in $J_{\text{c}}$. A comparison of figures 10(a) with (c) shows the lack of curve registration in this case, which, if great enough, can result in the loss of the extrapolation accuracy provided by unified scaling.

Figure 10.

Master scaling curves for the OST-RRP^® dataset (not corrected for magnetic self field). (a) An example of a precise master scaling curve that results from registering $F_{\text{P}}-B$ curves (for this example, $p$ is fixed at 0.5, $q$ is fitted, and data are trimmed below $F_{\text{P}}<125$ AT). (b) The tail of the master curve does not scale well when low-$F_{\text{P}}$ data (<125 AT) are not trimmed, although the presence of such a low pinning-force tail does not have much effect on overall extrapolation errors (see text). (c) Loss of scaling when $p$ is fitted when there is insufficient data below the pinning-force peak (note the high fitted value of $p=1.21$ in this case).

Likewise, the parameter $q$ will be accurately determined only if a sufficient range at higher magnetic fields is available above the pinning-force peak, usually from ∼10 T to ≥15 T at 4.2 K. (However, the needed relative magnetic field range becomes easier to measure at higher temperatures; see below.) Erroneous fitted values are avoided in this situation by also setting $q$ to a default value, typically $q=2.0$.⁵

When data over a sufficient magnetic field range are available, $p$ and $q$ can be determined by several different methods: from master scaling curves, by globally fitting the entire dataset, or by averaging the results for a few selected $F_{\text{P}}-B$ data curves. In the last case, the curves are best selected at moderate strain levels and at higher temperatures where a greater range of relative magnetic fields $B/{B_{\text{c}2}}^{\ast }$ is usually available. This is seen in the master-scaling-curve examples of appendix A of Part 2, particularly that shown by the Vacuumschmelze master scaling curve in appendix figure A7 in Part 2. There, we see that data on the low-magnetic-field side of the pinning-force peak are available only at 12 K (blue data points), and not at 8 or 4 K. (The extrapolation tests in section 3 uses values of $p$ and $q$ determined from master scaling curves, mainly to ensure consistency for the comparisons presented.)

Fortunately, the precise values used for $p$ and $q$ have little effect on the extrapolation accuracy of the ESE fitting equation over the magnetic field ranges tested here, as long as the default values used for $p$ and $q$ are not too extreme. The RMSE results in appendix tables A3–A5 show this more explicitly. This flexibility is because the scaling constants and the core scaling parameters (sections 5.3 and 5.5) depend only on the ratios of the raw scaling data ${B_{\text{c}2}}^{\ast }(T,\epsilon )/{B_{\text{c}2}}^{\ast }(0,0)$ and $K(T,\epsilon )/K(0,0)$.

3.8.3. Trimming data at high temperatures and low pinning forces.

Although not essential, trimming data is useful to minimize the effects of flux creep and facilitate convergence of non-linear regression programs.⁶ An example of the noise from flux creep is given in figure 10(b), which shows the lack of scaling at low $F_{\text{P}}$ levels. Generally, good cut-off levels are to trim data at temperatures above ∼12 K, and at pinning forces $F_{\text{P}}$ below ∼100–200 AT. From a practical standpoint, such trimming is not a problem, because magnets are usually not designed at such low pinning-force levels.

The scaling constants and core parameter values are affected very little ($\text{Δ}<\sim 2\text{\%}$) by the specific trim levels used for temperature and $F_P$. RMS fitting errors are also effectively unchanged. For example, if trim levels are relaxed to half of the values used in tables 1 and 2, the RMSE values increase by only a few hundredths of a percent.

4. Discussion: ‘Everything should be made as simple as possible, but not simpler.’ –Albert Einstein

This epigraph summarizes one of main points of this article regarding ‘optimum simplicity’. The shortcut of global-fitting equations (rather than registering pinning-force curves into a single master scaling curve) foregoes the most powerful and beautiful aspect of scaling—extrapolation. The usual labeling in the literature of the fitting equations as ‘scaling laws’ is a misnomer. They are either empirical parameterizations of the USL or based on limited raw scaling data, but they are not fundamental scaling and they lack extrapolation capability.

The number of fitting parameters used can also be an issue, as we saw in figure 2. Too many gives good accuracy for interpolation, but not extrapolation. In figures 3–5 we saw the opposite problem—fitting too few or fixing parameters with values that are not scaling constant values; this compromises both extrapolation and interpolation capabilities. The solution goes back to the basics of scaling and to individually determining each parameter (or small group of parameters) with extensive raw scaling data. This takes a considerable one-time effort, but the end result is a raw-scaling-data based fitting equation that provides extrapolation capability for practical engineering design and conductor characterization, but can be easily applied with the simplicity of a global-fitting equation.

Another question—What minimum dataset is the right minimum? This is also a question of optimum simplicity. A number of proposals have been made, but the answer lies in determining which parameters are not fundamental scaling constants, as determined in the extensive analysis of section 4 in Part 2. Fundamental scaling analysis shows that the minimum data set consists of one measurement of $I_{\text{c}}(B,T)$ at a fixed strain, and one measurement of $I_{\text{c}}(B,\epsilon )$ at a fixed temperature (depicted by the two dashed lines in the $T-\epsilon$ measurement plot of figure 1). This is the minimum dataset, and it is quite powerful, because $I_{\text{c}}-B$ curves at all other points in the $T-\epsilon$ map can be filled in by extrapolations from this simple crosscut through the $T-\epsilon$ measurement space.

Again, it is a case of making things as simple as possible, but not simpler.

5. Application of the ESE relation

Section 5 is the payoff for the extensive raw scaling data analysis of Part 2 and the extrapolation testing of section 3 in the present article. Here we illustrate the practical application of ESE in several new areas:

• Interpolations (section 5.1). Such interpolations also provide the option for reliable extrapolations to the nearby measurement space through the use of default values for the core scaling parameters [$T_{\text{c}}^{\ast }(0),\eta ,\text{s}$, and $b_{\text{c}2}(\epsilon )$, described in sections 5.3 and 5.5].

• Shortened data-acquisition time for unified $T-\epsilon$ apparatuses (section 5.2). A five-fold reduction in measurement space for full $I_{\text{c}}(B,T,\epsilon )$ characterization can be obtained by extrapolation from minimum datasets.

• Combining measurements from separate dedicated temperature and strain apparatuses (sections 5.6–5.9). The use of separate, simpler apparatuses offers flexibility and savings compared with the construction and commissioning of a complex unified $T-\epsilon$ apparatus. For example, full $I_{\text{c}}(B,T,\epsilon )$ datasets can be obtained by combining strain data from a standard liquid helium immersion apparatus, with separately measured temperature data from a variable temperature apparatus.

• Extrapolations of full $I_{\text{c}}(B,T,\epsilon )$ datasets from only a single $I_{\text{c}}(B)$ curve in special situations (section 5.10). Such minimal measurements are typically made on conductorswhen qualifying production wire for large magnet applications. Such extrapolations are possible because of the stability of a few core parameters.

In the following application illustrations, we use the two most effective extrapolative forms of the ESE relation with the Hybrid1 and Hybrid2 temperature paramterizations.

Extrapolative Scaling Expression with Hybrid1 temperature parameterization

$$\begin{gathered} F_{\text{c}}(B,T,\epsilon )=I_{\text{c}}(B,T,\epsilon )B \\ =C{\left[b_{\text{c}2}(\epsilon )\right]}^{\mathit{s}}{\left(1-t^{1.5}\right)}^{\mathit{\eta }-1}\left(1-t^2\right)b^p{(1-b)}^q, \end{gathered}$$ (11a)

where $b\equiv B/{B_{\text{c}2}}^{\ast }(T,\epsilon )$ is the reduced magnetic field and $t\equiv T/T_{\text{c}}^{\ast }(\epsilon )$ is the reduced temperature, and:

$${B_{\text{c}2}}^{\ast }(T,\epsilon )={B_{\text{c}2}}^{\ast }(0,0)(1-t^{1.5})b_{\text{c}2}(\epsilon ),$$ (11b)

$$T_{\text{c}}^{\ast }(\epsilon )=T_{\text{c}}^{\ast }(0){\left[b_{\text{c}2}(\epsilon )\right]}^{1/3}$$ (11c)

with five scaling parameters: $C,{B_{\text{c}2}}^{\ast }(0,0),T_{\text{c}}^{\ast }(0),s,\eta$, plus the parameters in $b_{\text{c}2}(\epsilon )$.

Essentially the same results are obtained within experimental error with ESE parameterized with the Hybrid2 temperature function.

Extrapolative Scaling Expression with Hybrid2 temperature parameterization

$$\begin{gathered} F_{\text{c}}(B,T,\epsilon )=I_{\text{c}}(B,T,\epsilon )B \\ =C{[b_{\text{c}2}(\epsilon )]}^{\mathit{s}}{[(1-t^{1.5})(1-t^2)]}^{\eta /2}{b}^p{(1-b)}^q, \end{gathered}$$ (12a)

where the rest of the equation set is the same as equation set (11).

In these examples, the $b_{\text{c}2}(\epsilon )$ strain function is parameterized with either the Exponential or Invariant models because of the practical advantages these strain parameterizations offer, as outlined in the conclusions to Part 2. (Parameterizations for each strain model are defined in item (5) of section 6.2 of this article.) Although results for both $b_{\text{c}2}(\epsilon )$ parameterizations are presented for perspective, the Exponential model would generally be preferred because of its single fitting parameter and strain extrapolation capability. The Invariant model is used when additional strain interpolation accuracy is needed.

All fitting in these application examples is carried out in terms of the pinning force $F_{\text{P}}$, not $I_{\text{c}}$, to increase extrapolation accuracy and avoid overweighting low fields where $I_{\text{c}}$ is the highest (see figure 9 and the accompanying discussion). (If very low regions of magnetic field are of primary design interest, then $I_{\text{c}}$ fitting is preferable. However, this is usually not the case for most conductor characterizations.)

5.1. Interpolation

The results of interpolating extensive datasets with the ESE relation are given in appendix tables A1–A5. (Specific fitting steps are given at the beginning of section 3 and summarized in appendix A.1) The RMS $F_{\text{P}}$ errors in the last column of tables A1–A5 show that interpolation errors are exceptionally small, between about 0.1% and 0.2%, depending on the particular dataset. These correspond, for example, to RMS $I_{\text{c}}$ errors of only 1–5 A at 12 T, depending on the $J_{\text{c}}$ of the conductor.

Interpolations with ESE give parameter sets that can be used not only to interpolate the source data, but also to reliably extrapolate more limited data to the nearby parameter space. This can be done even when data are insufficient to accurately determine all of the ESE parameter values, through the use of default values for the core parameters. (Default values are given in section 5.5 and listed in item 7 of the Part 3 summary in section 6.3.)

5.2. Unified $\text{T}-\text{ε}$ apparatus—saving measurement time with the minimum dataset

For unified $T-\epsilon$ apparatuses, ESE can significantly reduce the number of measurements needed for full conductor characterization, through the use of minimum datasets. Section 3 shows that fitting data along just two axes in the $T-\epsilon$ map (dashed cross-cut lines in figure 1) allows the rest of the $T-\epsilon$ cross terms to be accurately extrapolated. (Note that each point in the $T-\epsilon$ map corresponds to an $I_{\text{c}}-B$ data curve; see section 2.1). From figure 1 we see this decreases the measurement space to about 1/5th the size, compared with measuring an $I_{\text{c}}-B$ curve at every point in the $T-\epsilon$ map. Measurement times for full $I_{\text{c}}(B,T,\epsilon )$ characterization are typically shortened from several weeks to a few days, especially when making fine-grid measurements such as those presented here for the WST-ITER and OST-RRP^®conductors. Also, by fitting the minimum dataset, there is no requirement for orthogonal $B-T-\epsilon$ measurement grids to register pinning-force curves into a master scaling curve, as there is with fundamental scaling.

The accuracy of such minimum-dataset extrapolations is extensively demonstrated by the many examples with the ESE relation in sections 3.3–3.7. The RMS $F_{\text{P}}$ errors are typically between 0.11% and 0.15% for ESE with both the Hybrid1 and Hybrid2 temperature parameterizations (see the red highlighted cases in tables 1 and 2). Extrapolation errors from minimum datasets are comparable to interpolation errors for the full dataset. The increase in RMS $F_{\text{P}}$ error between whole dataset fitting (appendix tables A1 and A2) and extrapolations from minimum datasets (tables 1 and 2) is less than 0.03%, which corresponds to an increase in effective RMS $I_{\text{c}}$ error of less than ∼1 A at 12 T. Thus, the accuracy of such minimum-dataset extrapolations is more than enough to provide a considerable reduction in data acquisition time for full conductor characterization.

5.3. Core scaling parameters: ${{\text{T}}_{\text{c}}}^{\ast }(0)\text{η},\text{s}$, and ${\text{b}}_{\text{c}2}(\text{ε})$

Tables A3–A5 also show the variability of the ESE parameter values:

• The lead constant $C$ and the parameter ${B_{\text{c}2}}^{\ast }(0,0)$ have the greatest variability. They change by about 5% to 10% for different values of $p$ and $q$, and by about ±10% for the magnetic self-field correction.

• However, values of the core parameters $T_{\text{c}}^{\ast }(0),\eta ,s$, and $b_{c2}(\epsilon )$ in these tables are more stable and consistent:

  1. For different values of $p$ and $q$, the changes in core parameter values are less than ±2%; the changes in the temperature core parameters $T_{\text{c}}^{\ast }(0)$ and $\eta$ are even smaller, less than ±0.5%.
  2. When the magnetic self-field correction is applied, the changes in core parameter values are less than ±3%, although the decreases in $s$ can be somewhat greater, up to ∼10%.

The greater stability of the core parameters is a result of them being dependent only on ratios of the raw scaling data ${B_{\text{c}2}}^{\ast }(T,\epsilon )/{B_{\text{c}2}}^{\ast }(0,0)$ and $K(T,\epsilon )/K(0,0)$, unlike the non-core parameters $C$, ${B_{\text{c}2}}^{\ast }(0,0)$, $p$ and $p$.

Although the core parameters are quite stable, the many tests we have made show that the highest extrapolation accuracy is obtained by carrying out extrapolations with the same $p$ and $p$ values that were used to measure the core parameters employed in the extrapolation. Likewise, when extrapolating data corrected for magnetic self field, accuracy is increased by use of core parameter values that were also measured from self-field corrected data (appendix tables A3–A5).

(Note that the scaling constants are essentially unaffected by either changes in the values of $p$ and $q$, or by magnetic self-field corrections, as shown earlier in the analysis of Part 2.)

5.4. Combining limited datasets measured in separate apparatus

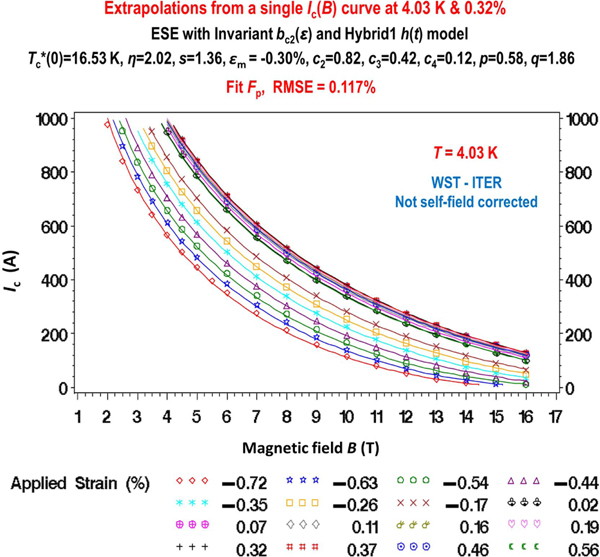
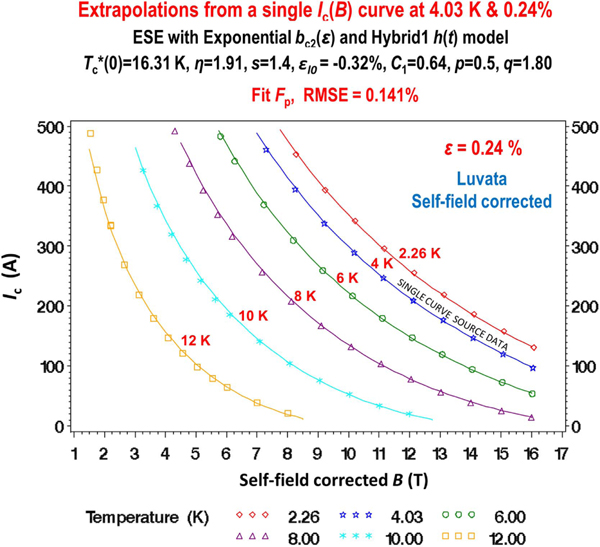
The stability of the ESE core parameter values also makes it possible to combine limited data from separate apparatus (examples are given in sections 5.6–5.9). Combining separately measured datasets avoids the cost of the design, construction, and commissioning of a complex unified $T-\epsilon$ apparatus. Their stability also opens the possibility to utilize data more limited than the minimum dataset, by joining various combinations of measurements into a complete dataset. Extrapolations can even be carried out from as little as a single $I_{\text{c}}(B)$ measurement (section 5.10) if the core parameter values have been measured in a similar conductor.

Examination of the ESE equation-set (11) shows which parameters can be reliably determined when only limited data are available. The results are shown for some of the more common limited datasets in table 3, arranged in order of descending complexity.

Row 1 in table 3 indicates all the parameters needed for full $I_{\text{c}}(B,T,\epsilon )$ characterization, typically obtained with a unified $T-\epsilon$ apparatus.

Rows 2–5 show the parameters that can be obtained from more limited datasets measured with separate strain and temperature apparatuses. Although none of these more limited datasets alone is enough to provide a full $I_{\text{c}}(B,T,\epsilon )$ dataset, combining them works quite well to supply complete conductor characterization. For example:

• Separate measurements of $I_{\text{c}}(B,T)$ and $I_{\text{c}}(B,\epsilon )$ combine to give a complete minimum dataset.

• A complete parameter set is also given by combining separate measurements of $I_{\text{c}}(B,\epsilon )$ and $I_{\text{c}}(T)$ (i.e. temperature measurements carried out at only a constant magnetic field), if the magnetic field range for the strain measurements is great enough to accurately determine $p$ and $q$ (otherwise default $p=0.5$ and $q=2$ values can be also used).

• In special situations, a complete minimum dataset can be obtained from $I_{\text{c}}(B,T)$ combined with a relatively quick $I_{\text{c}}(\epsilon )$ measurement (at constant $B$ and $T$). This works only if s is known from measurements on a similar conductor. Examples of this case are given in sections 5.8 and 5.9.

Combinations other than those illustrated also blend well, but at least these show the flexibility and usefulness of the ESE relation for some common measurement situations.

Several combinations are also more practical than others. For example, the second bullet above, $I_{\text{c}}(B,\epsilon )$ plus $I_{\text{c}}(T)$, works mathematically, but if $I_{\text{c}}(T)$ is being measured in a variable temperature apparatus anyway, it makes sense to measure the magnetic field dependence $I_{\text{c}}(B,T)$ as well. In practice, $I_{\text{c}}(B,T)$ is one of the most useful measurements to make, at least for one sample of a given conductor type, because it provides the range of data needed to accurately determine many of the core parameters that will transfer to other conductors of that type. This is especially the case for the stable temperature core parameters.

For any of these limited-data cases, if some of the parameters needed for a full $I_{\text{c}}(B,T,\epsilon )$ dataset are not available, default core parameter values can be used to fill in missing core parameters in table 3. This gives adequate accuracy, at least for limited extrapolations, and the results are easily updated later if additional core-parameter data become available.

5.5. Default values for the core parameters

When data are insufficient or unavailable, there is too much freedom in the fitting process to fit all the parameters. Erroneous or indeterminant parameter values result. In such a case, default parameter values give significantly improved extrapolation accuracy. Their use also gives flexibility to the types of data that can be combined by filling in the blanks in table 3.

Default values for the core parameters are preferably obtained from more complete datasets, such as $I_{\text{c}}(B,T)$, $I_c(B,\epsilon )$, or complete $I_{\text{c}}(B,T,\epsilon )$ datasets, measured in a conductor similar to the one being extrapolated. Representative values of core parameters are listed in the middle columns of tables A1–A5. With additional measurements, it may be possible over time to develop a more complete compilation of core parameter values to use for different types of conductors.

For the present, the core parameters listed in the appendix tables can be useful as default parameter values, especially for extrapolations into the neighboring measurement space not too distant from the source data.

5.5.1. Measurement ranges needed to determine parameter values; when to use default values.

When should default values be used, and when are they not needed? Guidelines for adequate measurement ranges to accurately determine the scaling parameters are listed below, along with default parameter values to use when the data are insufficient. In general, a fine measurement grid over the suggested ranges is desirable, with preferably a minimum number of four or five data points. Also, if multiple measurements are made at the same $B-T-\epsilon$ point, it is best to average them as a single value before fitting, to prevent unintentional weighting.

• $\eta$ and ${T_{\text{c}}}^{\ast }(0)$: For these core temperature parameters, high temperature data $I_{\text{c}}(B,T)$ above ∼4 K are generally needed to determine their values (for example, at even temperature values preferably up to ∼12 K). The data in tables A1–A5 cluster around a default average value of about 16.7 K for ${T_{\text{c}}}^{\ast }(0)$. Similarly, default values for $\eta$ group around values of 2.0 (ITER conductors) or 2.2 (RRP^®-Ta), where the higher number is possibly correlated with conductors having compositional inhomogeneities (figure 6 in Part 2).

• $s$ and $b_{\text{c}2}(\epsilon )$: For these core strain parameters, $I_{\text{c}}(B,\epsilon )$ data are needed, usually obtained from liquid helium dip tests. As far as the measurement sequence, in the NIST data sets given here, the sample was initially strained up to a maximum strain less than the irreversible strain limit and then magnetic field data were obtained at each strain as strain was decreased in steps of ∼0.1% (preferably down to about −1% intrinsic strain, which is the approximate elastic strain limit of the beryllium-copper Walters spring). This sequence gives consistent data and avoids multiple loadings of the sample, which can result in irreversible three-dimensional strain effects. A fairly complete set of $I_{\text{c}}(B,\epsilon )$ data is needed to determine $s$. However, for the parameters in $b_{\text{c}2}(\epsilon )$, if a good estimate for $s$ is available for a similar conductor, $b_{\text{c}2}(\epsilon )$ can be obtained by measuring $I_{\text{c}}(\epsilon )$ alone (i.e., at constant $B$ and $T$). An average default value for $s$ from tables A1–A5 is about $s=\sim 1.1$ for the high-$J_{\text{c}}$ RRP^®-Ta conductor. A higher default value of $s=\sim 1.4$ is measured for the moderate-$J_c$ ITER conductors.

• $p$ and $q$: At 4.2 K, multiple tests have shown that magnetic field measurements are needed over the range from ∼10 T to $⩾\sim 15\text{T}$ to accurately determine $q$, and at fields below ∼5 T to determine. $p$ It is usually much easier to determine $p$ and $q$ accurately from $I_{\text{c}}(B,T)$ data above ∼4 K. Lacking such data, it is better to use the default Nb₃Sn values $p=0.5$ and $q=2.0$. The precise values of $p$ and $q$ have little effect on the extrapolation accuracy of the ESE relation, if the same p and q values are used in the extrapolations as those used to determine the default core parameters. The results in the tables A3–A5 show that use of default values $p=0.5$ and $q=2.0$ increases the overall RMS $F_{\text{P}}$ error by less than ∼0.02%, compared with fitting values for $p$ and $q$.

• The lead parameters $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ are quite variable between conductors, and depend on values of $p$ and $q$, so they are best measured on an individual conductor basis. Fortunately, they can be accurately determined from just a single $I_{\text{c}}(B)$ curve for a particular conductor, as illustrated in section 5.10.

5.6. Combining separately measured ${\text{I}}_{\text{c}}(\text{B},\text{T})$ and ${\text{I}}_{\text{c}}(\text{B},\text{ε})$ datasets into a minimum dataset

Mathematically, it makes no difference whether the minimum dataset illustrated by the cross-cut in figure 1 is obtained from a unified measurement apparatus or from two different test apparatuses, one dedicated to measuring strain $I_{\text{c}}(B,\epsilon )$ and the other to measuring temperature $I_{\text{c}}(B,T)$. The intrinsic accuracy of the ESE relation to combine such separate datasets has already been demonstrated through the extensive minimum-dataset extrapolation testing summarized in tables 1 and 2.

In practice, of course, there are extrinsic errors resulting from differences between the test samples used in different measurement apparatuses. Samples need to have similar filament architecture, composition, doping, and heat treatment. Also, the $I_c$ values need to match reasonably well where the two datasets overlap. When they mismatch, techniques can be used to correct for differences, as described in the next section.

5.7. Practical considerations for combining separate datasets: extrinsic corrections for matching ${\text{I}}_{\text{c}}$ criteria, prestrain, and magnetic self field

If the apparatus conditions for the two measurements are different (sample length, mounting technique, sample holder material and diameter), these differences can often be corrected, at least to first order. A good indicator of the quality of the corrections is the mismatch in the (corrected) critical currents at the temperature and strain where the two datasets overlap.

1. $I_{\text{c}}$ criterion dependence: Data can be matched to a common $I_{\text{c}}$ criterion with the ‘$n$’ value method (i.e., $V-I$ curves are modeled as $V=C{I}^n$). The correction is illustrated, for example, in section 10.1 of Ekin [2006, equation (10.6)].

2. Prestrain from differential thermal contraction of the sample holder: Different holder materials introduce different amounts of thermal-contraction strains into the samples during cooldown from the sample soldering temperature to cryogenic temperatures. The differences in strain introduced by different sample holders can be approximately corrected with the thermal-contraction data recently compiled in an international benchmarking study (Cheggour et al 2017).

3. Self-field: If the sample holders have substantially different shapes, the difference in magnetic self-field effects can be a factor. Self-field correction factors have been calculated with finite element analysis for many of the sample holder geometries in present use (Bordini 2010, tabulated in Cheggour et al 2017).

These extrinsic corrections are illustrated in the following examples.

5.8. Combining separate ${\text{I}}_{\text{c}}(\text{B},\text{T})$ and ${\text{I}}_{\text{c}}(\text{ε})$ datasets—example of simultaneous fitting for combining well-matched datasets

In this and the following section we illustrate two procedures for combining separately measured datasets. The first, simultaneous fitting, applies to the case where the (corrected) datasets match well where they overlap, usually at liquid helium temperature and the as-cooled strain state of the conductor.

The second procedure, iterative fitting (presented in the section 5.9), is preferable when:

1. The two datasets do not match well (for example, because of significant differences in $I_{\text{c}}$ criteria that cannot be accurately corrected because of the lack of accurate $n$ values).

2. One dataset is more reliable than the other.

3. One dataset better matches the temperature range or $I_{\text{c}}$ criterion for the intended use of the data.

The first procedure of simultaneous fitting is essentially the same as that used for all the minimum dataset extrapolations in section 3. It is simply a simultaneous fit of the ESE equation to both datasets. We illustrate the procedure by combining two limited datasets, one a variable temperature $I_{\text{c}}(B,T)$ measurement, the other a strain measurement of $I_{\text{c}}(\epsilon )$ at only a single magnetic field, 12 T.

5.8.1. Data.

These separate datasets were measured on two samples of the same conductor, both reacted with the same heat treatment. These data are for a Luvata ITER toroidal-field (TF) internal-tin Nb₃Sn conductor, billet #NT8404 (conductor crossection shown in appendix figure A5 of Part 2). Complete source data for both datasets are given online in the supplemental website accompanying these articles, www.ResearchMeasurements.com.

• The temperature $I_{\text{c}}(B,T)$ dataset was measured in a variable-temperature apparatus in flowing helium gas (Goodrich et al 2013). The coil-shaped sample was carefully threaded onto a cylindrical sample holder made of Ti-6%Al-4%V (ITER-type barrel). The ends of the sample were soldered to copper current rings at the ends of the holder. However, the middle of the sample was not soldered, but wound without slack. Also, the Lorentz force was directed inward, so the sample holder provided support. Data were obtained at an $I_{\text{c}}$ criterion of $0.1\mu \text{V}{\text{cm}}^{-1}$.

• The strain $I_{\text{c}}(\epsilon )$ dataset was measured in a separate apparatus at ∼4 K at a fixed magnetic field of 12 T. The sample was soldered along its entire length to a Walters spring sample holder (Walters et al 1986) made of Cu-2%Be (Cheggour et al 2014). Because the measurements were carried out in liquid helium (unlike the flowing gas environment of the variable-temperature apparatus), heating effects were smaller and so $I_{\text{c}}$ could be analyzed at three widely different $I_{\text{c}}$ criteria: $1\mu \text{V}{\text{cm}}^{-1}$, $0.1\mu \text{V}{\text{cm}}^{-1}$, and $0.01\mu \text{V}{\text{cm}}^{-1}$. We use the $0.1\text{V}{\text{cm}}^{-1}$ strain data to match the $I_{\text{c}}$ criterion of the temperature data. (We will use a mismatched $I_{\text{c}}$ criterion to demonstrate the iterative fitting process in the next example in section 5.9.)

5.8.2. Procedure.

The two sample-holder materials and mounting conditions were different (Cu–Be versus Ti–Al–V, and soldered versus unsoldered), so the samples experienced different cooldown strain introduced by the sample holders. An inspection of the data shows that the $I_{\text{c}}$ values for the two datasets matched at the overlap point (12 T and 4 K) for an applied strain of 0.24% in the $I_{\text{c}}(\epsilon )$ dataset. Analysis of the expected differential thermal contraction for these two sample-holder materials (using thermal contraction data from Cheggour et al 2017), also gave an effective matching strain within 0.01% to 0.02% of this value.

Both datasets were trimmed at $F_{\text{P}}<100$ AT and at temperatures >12 K, although the specific trim levels had less than a 2% effect on the resulting core parameter values, and negligible effect on the RMS fitting errors (section 3.8).

Finally, since there are no variable magnetic-field data accompanying the $I_{\text{c}}(\epsilon )$ dataset, it is not possible to simultaneously determine both $b_{\text{c}2}(\epsilon )$ and the strain parameter $s$ (for that we need strain data at variable fields, $I_{\text{c}}(B,\epsilon )$; i.e., row 3 in table 3). Fortunately, $s$ has been determined from extensive raw scaling data by Cheggour et al (2017) to be consistently $s=1.4\pm 0.02$, independent of strain, for a series of internal-tin (and bronze-route) ITER-TF conductors, similar to this conductor. We take 1.4 as a reliable value for $s$ in this ITER conductor, which enables the limited fixed-field $I_{\text{c}}(\epsilon )$ measurement to determine the parameters in $b_{\text{c}2}(\epsilon )$ [and therefore the complete parameter set when combined with the $I_{\text{c}}(B,T)$ data; i.e., rows 2 and 5 combined in table 3].

5.8.3. Results.

The upper part of tables 4 and 5 labeled ‘Simultaneous fit’ show the results for a simultaneous fit to both datasets (after matching strain) for the Exponential and Invariant $b_{\text{c}2}(\epsilon )$ models, respectively. Although not shown in the tables, the fitting errors for both strain models were about the same, and quite low, RMSE = 0.08% and RMSFD = 2.0%. Note that the core parameter values in the two tables are nearly the same [except for the parameters in $b_{\text{c}2}(\epsilon )$], which shows the stability of the core values with respect to the $b_{\text{c}2}(\epsilon )$ model used. The shape parameters $p$ and $q$ obtained from this simultaneous fit are also consistent with those obtained from the master scaling curve $f(b)$ shown in appendix figure A6 of Part 2 (where $p=0.564$ for the master curve versus 0.562 in both tables 4 and 5, and $q=1.74$ in the master curve versus 1.70 and 1.71 in tables 4 and 5 respectively). (The slightly higher $q$ value for the master curve is due to the smaller trim value $F_{\text{P}}<25$ AT used in appendix A.3 of Part 2, whereas data for the simultaneous fits shown here were trimmed at $F_{\text{P}}<100$ AT to minimize the effect of outlier points on the RMSFD for comparative purposes).

Table 4.

ESE parameter values for combining minimum datasets for $I_{\text{c}}(B,T)$ and $I_{\text{c}}(\epsilon )$ from two different measurement apparatuses. These were obtained with equation-set (11) and the Exponential model for $b_{\text{c}2}(\epsilon )$. Two fitting procedures were used: a simultaneous fit for well-matched datasets (top part of the table) and a three-step iterative procedure for mismatched datasets (lower part). Red italic type indicates the parameters that can be determined by each limited dataset (as listed in table 3). By iterating, these values are then used to fix parameter values in the next step (indicated in bold type). Data are for a Nb₃Sn conductor made by Luvata, billet #NT8404 ITER-TF conductor, trimmed at $F_{\text{P}}<100$ AT, $T>12\text{K}$. Source data for both datasets are given as Excel^™ files online in the supplemental website.

				Core scaling parameters
Parameters:		$C$	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	${T_{\text{c}}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_{l0}$ (%)	$C_1$	$p$	$q$
Simultaneous fit, $I_{\text{c}}$ criterion = 0.1 μV cm−1 for both datasets
		14 955	29.74	16.43	1.966	1.4	−0.321	0.657	0.562	1.703
Three-step iterative fit (temp-strain-temp), strain data $I_{\text{c}}$ crit = 1 μV cm−1, temp data $I_{\text{c}}$ crit = 0.1 μV cm−1
1	$I_{\text{c}}(B,T)$ 0.1μV cm−1	14 087	28.49	16.19	1.966	1.4	$b_{\text{c}2}(\mathit{\epsilon })$		0.562	1.710
2	$I_{\text{c}}(\epsilon )$ 1μV cm−1	18 050	28.49	16.19	1.966	1.4	−0.318	0.616	0.562	1.710
3	$I_{\text{c}}(B,T)$ 0.1μV cm−1	14 930	29.70	16.41	1.966	1.4	−0.318	0.616	0.562	1.710

Thus, the use of a simultaneous fit of ESE to combine strain and temperature datasets that match reasonably well (at the point where field, temperature, and strain overlap) gives a full $I_{\text{c}}(B,T,\epsilon )$ characterization that otherwise would not have been possible because of the limited, separately measured datasets (which was all that were available for this conductor). We take these parameter values and their use with the ESE relation to give a reliable full characterization of this conductor for the following reasons: (1) the extrapolation procedure is mathematically equivalent to the extensive testing carried out in section 3; (2) both test samples were similar (same billet) and reacted with the same heat treatment; (3) the value of $s$, which is needed because $I_{\text{c}}(\epsilon )$ data are available at only a fixed magnetic field, was consistently measured to have the same value in a series of similar conductors in the ITER benchmarking article by Cheggour et al (2017); and (4) the corrections for the difference in strain introduced by the different samples holders give an effective strain that agrees within 0.01%–0.02% with the strain where the $I_{\text{c}}$ of the two datasets matched.

5.9. Example of iterative fitting for combining mismatched datasets

We now consider an example for two datasets that do not match well where they overlap. In this case, an iterative fitting procedure of the ESE equation is more reliable for extrapolating a full $I_{\text{c}}(B,T,\epsilon )$ dataset. In fact, a simultaneous fit of the data usually does not converge for this situation, due to the large mismatch in $I_{\text{c}}$ at the temperature and strain where the two datasets should coincide.

5.9.1. Data.

To illustrate the procedure for this case, we combined the same two separate Luvata datasets from section 5.8, but this time with $I_{\text{c}}$ criteria that mismatch by an order of magnitude: $1\mu \text{V}{\text{cm}}^{-1}$ for the strain data and $0.1\mu \text{V}{\text{cm}}^{-1}$ for the temperature data. The order of magnitude difference in criteria results in more than a 14% difference in $I_{\text{c}}$ values at 12 T and 0.24% strain, where the two datasets should overlap. [The $n$-value correction method would have worked in this case, because the strain measurements were in liquid helium and reliable $n$-value measurements were available over a wide electric-field range. However, this would not typically be the case for measurements in gaseous helium, or if the sample were conduction cooled in a cryocooler. Nevertheless, this example serves our purpose to illustrate the fitting procedure when there is a significant mismatch in the two datasets.]

5.9.2. Procedure and results.

The procedure is illustrated in tables 4 and 5 by the last three rows under the heading ‘Three-step iterative fit’.

• Step 1 of this sequence shows the results of fitting only the temperature data $I_{\text{c}}(B,T)$ at $0.1\mu \text{V}{\text{cm}}^{-1}$, with the strain parameters represented by simply setting $b_{\text{c}2}(\epsilon )=1$. Again, the parameter $s$ is set to $s=1.4$ (from measurements on similar conductors by Cheggour et al 2017).

• Step 2 is a fit of only the strain data $I_{\text{c}}(\epsilon )$, measured at an $I_{\text{c}}$ criterion of $1\mu \text{V}{\text{cm}}^{-1}$ (ten times greater). In this step, the temperature and magnetic-field parameters are fixed by the results of step 1 [that is, ${T_{\text{c}}}^{\ast }(0),{B_{\text{c}2}}^{\ast }(0,0),\eta ,p$, and $q$, shown with bold values in the tables]. Step 2 results in a very different value of the lead constant $C$ than obtained in step 1, to accommodate the significantly higher $I_{\text{c}}$ criterion of the strain data.

• Step 3, the fit to $I_{\text{c}}(B,T)$ is repeated, but with the parameters for $b_{\text{c}2}(\epsilon )$ fixed by the results obtained in step 2.

Although the lead constant changes significantly between the different steps, the values obtained for the core temperature parameters in step 3 are changed very little from those in step 1, where the absence of strain data was accommodated by assigning $b_{\text{c}2}(\epsilon )=1$. This shows the relative independence of the temperature and strain core parameters when making such iterative calculations.

The quality of the resulting extrapolation is shown in figure 11 by comparing the $I_{\text{c}}$ at 12 T resulting from the $1\mu \text{V}{\text{cm}}^{-1}$ source data (pink curve) with the strain data actually measured at an $I_{\text{c}}$ criterion of $0.1\mu \text{V}{\text{cm}}^{-1}$ (blue star symbols). The agreement in $I_{\text{c}}$ over the span of strain data is within about ±1%. Furthermore, as seen in tables 4 and 5, the scaling parameter values in the final step of the three-step iterative fit are almost identical with those obtained by the previous simultaneous fit, where all the data were at a $0.1\mu \text{V}{\text{cm}}^{-1}$ criterion. The main difference was a slightly decreased value of the strain sensitivity parameter $C_1$ in the Exponential $b_{\text{c}2}(\epsilon )$ model (table 4), which reflects the slightly smaller strain sensitivity for the higher $I_{\text{c}}$ criterion of $1\mu \text{V}{\text{cm}}^{-1}$ (used in the three-step procedure), than for the $0.1\mu \text{V}{\text{cm}}^{-1}$ criterion (used in the simultaneous fit). This can also be seen in figure 11 where the $1\mu \text{V}{\text{cm}}^{-1}$ curve at 12 T (pink curve) resulting from the iterative process is slightly flatter than the actual $0.1\mu \text{V}{\text{cm}}^{-1}$ strain data (blue stars). All in all, this iterative procedure gives acceptably close agreement for situations where there is such a significant mismatch in the data where they overlap.

Figure 11.

Illustration of the use of the ESE equation with the three-step iterative fitting procedure to combine two separate, mismatched datasets: $I_{\text{c}}(B,T)$ measured at an $I_{\text{c}}$ criterion of $0.1\mu \text{V}{\text{cm}}^{-1}$ in a variable-temperature apparatus, and $I_{\text{c}}(\epsilon )$ measured at 1 $\mu \text{V}{\text{cm}}^{-1}$ in a separate strain apparatus. The 12 T $I_{\text{c}}(\epsilon )$ pink curve obtained by an iterative process from $1\mu \text{V}{\text{cm}}^{-1}$ source data (light grey diamond symbols) agrees with the actual $0.1\mu \text{V}{\text{cm}}^{-1}$ data (blue star symbols) to within about ±1%. The variable-temperature $I_{\text{c}}(B,T)$ data are shown at 4.03 K by the orange star symbols at 0.24% strain, near the peak of each strain curve.

Thus, the iterative process allows separately measured data to be combined rather precisely, even when mismatched. If one dataset is more reliable than the other, or one dataset better matches the temperature range or $I_{\text{c}}$ criterion for the intended use of the data, then the three-step iteration is carried out with the favored dataset fit last, either temperature-strain-temperature, or strain-temperature-strain.

Again, the purpose of these examples is to show the procedures for combining separate datasets, and how values of the core parameter set can be built up from limited data.

5.10. Extrapolations of full ${\text{I}}_{\text{c}}(\text{B},\text{T},\text{ε})$ datasets from a single ${\text{I}}_{\text{c}}(\text{B})$ curve

In this final section on applications, accuracy testing is conducted for extrapolating full $I_{\text{c}}(B,T,\epsilon )$ characteristics from a single $I_{\text{c}}(B)$ curve. This type of extrapolation enables the efficient characterization of large production quantities of wire from routine measurements of a single $I_{\text{c}}(B)$ curve for each billet at zero applied strain and 4.2 K. Extrapolation testing has been carried out with ESE parameterized with the Hybrid1 and Hybrid2 temperature models, and the Exponential and Invariant strain models. All combinations give essentially the same results within experimental error. Illustrations are shown for conductor characterization over a wide range: from 1.9 K (for applications such as the High Luminosity LHC magnets), to 10 K (for applications such as cryo-cooled NMR magnets).

5.10.1. Core scaling parameters required.

Extrapolations of this type require values of the core parameters [$T_{\text{c}}^{\ast }(0),\eta ,s$, and $b_{\text{c}2}(\epsilon )$; table 3] measured in similar conductors with a similar heat treatment. The non-core parameters $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ in the ESE parameter set vary from wire to wire, but the core parameters are stable enough that they transfer well between similar conductors. As discussed in sections 5.4–5.9, they can be measured either all at once in a unified apparatus, or combined from measurements in separate temperature and strain apparatuses.

The core temperature parameters, ${T_{\text{c}}}^{\ast }(0)$ and $\eta$, are particularly useful for extrapolating production conductor measurements made at ∼4.2 K to other temperatures. These parameters can be effectively obtained from one $I_{\text{c}}(B,T)$ measurement on one production conductor. Lacking such a measurement, default values can be used, as listed in section 5.5. Default values still give reliable extrapolations for 4.2 K data, but over a more limited temperature range.

5.10.2. Extrinsic errors.

Extrinsic errors depend on reasonably matching the sample used for the core parameter measurement to the production samples. This includes heat treatment, $I_{\text{c}}$ criterion, strain introduced by differential thermal contraction with the sample holder, and differences in magnetic self-field arising from different sample holder shapes (section 5.7). Strain mismatches can be the most difficult to correct if the sample holder materials and mounting conditions are mismatched. The greatest strain uncertainty usually arises from Lorentz forces that can strain unsoldered conductors, e.g., as the conductor is forced to settle into the grooves of a Ti-alloy holder. When the opportunity is available to plan the design of separate apparatuses, the best control of sample-holder strain is to use the same holder material, with the sample soldered continuously along its length to eliminate variability in strain. This is readily done with beryllium-copper holders. (Melted paraffin wax is also used to reduce disturbance-induced quenches; however, it is mechanically weaker than soldering for controlling strain.) The most reliable assessment of such extrinsic errors is given by a comparison of the single $I_{\text{c}}(B)$ curves of the production samples with the core-parameter source data, at the temperature and strain where they should overlap.

5.10.3. Intrinsic errors.

Intrinsic errors are those introduced by extrapolating the entire dataset from only a single ${\text{I}}_{\text{c}}(B)$ curve with core parameters from a matched or similar conductor. In this section, we evaluate such errors over a wide range of temperatures and strains for a number of large datasets.

Fitting is carried out with equation-sets (11) or (12), following the steps given at the beginning of section 3:

• Core parameter values are obtained from the whole-dataset fits in tables A1–A5 [${T_{\text{c}}}^{\ast }(0),\eta ,s$, plus those in $b_{\text{c}2}(\epsilon )$]. The core parameters could also have been obtained from minimum-dataset extrapolations, instead of whole-dataset fits (examples are given in Ekin et al 2016b). The core values are chosen to be either self-field corrected (tables A3–A5) or not (tables A1 and A2), to be consistent with the $I_{\text{c}}(B)$ data being extrapolated. If magnetic self-field corrections are applied to the data, both $B$ and $F_{\text{P}}(=I_{\text{c}}B)$ are corrected before fitting. (Magnetic self-field corrections, which depend on both wire diameter and sample holder geometry, were determined from the finite element analysis of Bordini 2010, also tabulated in Cheggour et al 2017).

• The remaining parameters [$C,{B_{\text{c}2}}^{\ast }(0,0)$, $p$ and $q$] are fit from a single $I_{\text{c}}(B)$ curve chosen near 4.2 K and zero applied strain, since this is usually the most convenient for routine production measurements. The fit is carried out by minimizing the sum of the squared pinning-force residuals $\text{Σ}{(F_{\text{P}}-F_{\text{P}}^{\text{fit}})}^2$.

• Values of $p$ and $q$ are either fit from the single $I_{\text{c}}(B)$ curve along with $C,{B_{\text{c}2}}^{\ast }(0,0)$, or they are fixed with the same $p$ and $q$ values used to determine the core parameters, listed in tables A1–A5. The accuracy of both procedures is assessed.

• RMS $F_{\text{P}}$ errors are determined by analysis of the differences between the single-curve extrapolations and the complete dataset measurements.

Extrapolation accuracy is evaluated for fourteen cases. Three examples are given below. The first example is a comparison of the complete OST-RRP^® dataset with extrapolations from fitting one $I_{\text{c}}(B)$ curve at 4.07 K and 0.35% strain. In this example, data are corrected for magnetic self field, and the extrapolated curves are calculated with $p$ and $q$ fixed at the same values used to determine the core parameters (second row of table A3).

Figure 12 shows the temperature results for this first example. Utilizing the ESE-Hybrid1 equation-set (11) and the Exponential strain model [equations (19)–(22)], the entire dataset was extrapolated from a single $I_{\text{c}}(B)$ curve at 4.07 K (green circle symbols). Extrapolations were carried out to a low temperature of 1.9 K and a high temperature of 12 K. This temperature range includes a wide variety of applications, from HL-LHC (1.9 K) to cryo-cooled NMR magnets (5 and 10 K). The resulting overall RMS $F_{\text{P}}$ error is ∼0.10%, which is remarkably low, considering the wide span of temperatures and strains extrapolated from this single $I_{\text{c}}(B)$ measurement. From the accuracy of the extrapolation shown at 2.45 K in figure 12 (blue star symbols), the short additional extrapolation to 1.9 K should be reliable for the HL-LHC magnets (where it is difficult to obtain short-sample transport measurements because of high-current heating effects).

Figure 12.

Temperature extrapolations from a single $I_{\text{c}}(B)$ curve at 4.07 K and an applied strain of 0.35% (green circle symbols). Data are for the OST-RRP^® conductor, corrected for magnetic self field: symbols show measured data, and curves the extrapolated $I_{\text{c}}(B)$ results. The RMS $F_{\text{P}}$ error is 0.099%, only 0.005% higher than fitting the entire measured dataset (second row of table A3). Extrapolations are carried out with the ESE-Hybrid1 equation-set (11) and the Exponential strain model [equations (19)–(22)]. The same results were obtained with the ESE-Hybrid2 equation-set (12) to within an RMSE of 0.01%. Extrapolations to the higher temperatures of 5 K and 10 K shown in the figure are relevant to Nb₃Sn cryo-cooled NMR magnets. The extrapolation to lower temperatures of 1.9 K are included to show the usefulness of the ESE-Hybrid1 or Hybrid2 models for HL-LHC conductors. In this example, values of $p$ and $q$ are fixed to match those used in determining the core parameters (second row of table A3).

Figures 13(a) and (b) show strain extrapolations for the same example. Strain extrapolation results are shown only near the extreme ends of the temperature range: at 2.45 K in figure 13(a) (the lowest temperature where data are available), and at 10 K in figure 13(b). Again, the overall RMS error is surprisingly low, about 0.10%, especially considering the wide range of extrapolated strains: from –0.75% to +0.31% (corresponding to intrinsic strains of –1.05% to +0.01%).

Figure 14 shows the single-curve strain extrapolations for a second example: the WST-ITER conductor, with data not corrected for magnetic self field. The $I_{\text{c}}(B)$ curves are extrapolated from a single $I_{\text{c}}(B)$ curve measured at 4.03 K and 0.32% strain (shown by cross symbols, embedded in the upper group of curves). Extrapolations were carried out with the ESE-Hybrid1 equation-set (11) and the Invariant strain function [equations (17)–(18)]. Results are shown at 4.03 K for a relatively wide range of applied strains from –0.72% to +0.56% (corresponding to intrinsic strains of –1.02% to 0.26%). The RMS extrapolation error was only ∼0.12% for the full range of available temperatures and strains. In this example, extrapolations were carried with the same $p$ and $q$ values used to determine the core parameters (second row of table A2).

Figure 14.

Strain extrapolations from a single $I_{\text{c}}(B)$ curve at 4.03 K and an applied strain of 0.32% (cross symbols, nested in the upper grouping of curves). Data are for the WST-ITER conductor, uncorrected for self field: symbols show measured data, and curves the calculated $I_{\text{c}}(B)$ results. The RMS extrapolation error is 0.117%, only 0.01% higher than fitting the entire dataset (second row of table A2). Extrapolated curves are shown at 4.03 K for a wide range of applied strains (–0.72% to +0.56%) (intrinsic strains of –1.02% to +0.26%). $I_{\text{c}}(B)$ curves are extrapolated with equation-set (11) and the Invariant strain function [equations (17)–(18)]. Values of $p$ and $q$ are fixed to those used for the core parameters (second row of table A2).

In the final example, figure 15 shows the results for extrapolating a single $I_{\text{c}}(B)$ curve at 4.03 K (blue star symbols) to a wide temperature range for the Luvata ITER conductor. Again, extrapolations were carried out with the ESE-Hybrid1 equation-set (11) and the Exponential strain model [equations (19)–(22)]. As in figures 12–14, a small RMS error of 0.14% is obtained, which includes extrapolations to an even lower temperature of 2.26 K than in figure 12 (red diamond symbols in figure 15).

Figure 15.

Temperature extrapolations from a single $I_{\text{c}}(B)$ curve at 4.03 K (blue star symbols), showing high accuracy down to 2.26 K and up to 12 K. Data are for the Luvata conductor, corrected for magnetic self field: symbols show measured data, and curves the calculated $I_{\text{c}}(B)$ results. Fitting is carried out with the ESE-Hybrid1 equation (11), applied with the Exponential strain model [equations (19)–(22)]. Values of $p$ and $q$ are fixed to those used for the core parameters (second last row of table A3).

Other single-curve extrapolations were also carried out with different sets of core data, and either fixed or fitted values of $p$ and $q$. The differences that values of $p$ and $q$ make are summarized as follows:

• Extrapolations carried out with default values $p=0.5$ and $q=2.0$, and core parameters determined with the same default $p$ and $q$ values, give RMS $F_{\text{P}}$ errors that are only slightly higher than for core parameters determined with fitted $p$ and $q$ values. For example, RMSE = 0.10% for the OST-RRP^® data (listed in the heading to figure 12) with fitted $p$ and $q$, versus 0.12% with default values of $p=0.5$ and $q=2.0$. This is an increase in error of only 0.02%. Also, these single-curve extrapolation errors are less than 0.01% higher than the interpolation errors for fitting the entire data set (tabulated in the last column of the appendix tables A3 and A5).

• When $p$ and $q$ values are determined as part of the fit to the single $I_{\text{c}}(B)$ curve (i.e., not matched to those used for the core parameters), the overall RMSE increases more (RMSE = 0.10% matched, versus RMSE = 0.17% unmatched).

Thus, the highest single-curve extrapolation accuracy is obtained when extrapolations are carried out with $p$ and $q$ values that match those used to determine the core parameters, whether they are fitted or default values (just as long as they are the same as those used for the core parameters).

5.10.4. Summary: single ${\text{I}}_{\text{c}}(\text{B})$ curve extrapolations.

1. Intrinsic error testing shows that RMS $F_{\text{P}}$ errors are only 0.10% to 0.14% when extrapolating full $I_{\text{c}}(B,T,\epsilon )$ datasets from a single $I_{\text{c}}(B)$ curve measured at a convenient temperature and strain (such as ∼4 K and the initial strain state). Fourteen test cases were run, covering: (1) moderate-$J_{\text{c}}$ and high-$J_{\text{c}}$ conductors, (2) magnetic self-field corrected and uncorrected data, and (3) the Hybrid1 and Hybrid2 temperature models, and Exponential and Invariant strain models. All had comparably low errors. The best accuracies were obtained with values of $p$ and $q$ corresponding to those used to determine the core parameters employed to carry out the extrapolations.

2. The core scaling parameters (section 5.3) are quite stable, and thus can be obtained from measurements on similar conductors with the same architecture and heat treatment. Because of the stability of the core parameters, the samples do not need to be exactly matched. The stability of the core parameters is essential to the extrapolation capability for single $I_{\text{c}}(B)$ curves.

3. The non-core scaling parameters, $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$, have a variability that is 2 to 5 times higher than that of the core parameters (appendix tables A3–A5). Fortunately, $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ are the very parameters that can be most effectively determined by a single $I_{\text{c}}(B)$ curve. The results show that $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ values fit from a single $I_{\text{c}}(B)$ curve give RMS $F_{\text{P}}$ errors within a few hundredths of a percent of those obtained from interpolating the entire dataset.

4. Extrinsic errors introduced by apparatus differences between the core-parameter measurements and the $I_{\text{c}}(B)$ curve measurement can be corrected, at least to first order, with the techniques in section 5.7. Of particular importance is the care used to match sample strain, which can be done most conveniently by matching sample-holder materials and mounting conditions for the different apparatuses.

6. Synthesis and summary of Parts 2 and 3

Parts 2 and 3 of this series are highly integrated. A combined summary is provided to give a self-contained overview of both parts.

6.1. Overview

The ESE relation is derived in Part 2 from analysis of hundreds of pinning-force curves and raw scaling data in a wide range of Nb₃Sn conductors. This new parameterization of the USL is fundamentally different from present non-extrapolative fitting equations, where the parameters are empirically postulated or determined from limited pinning-force data. The basis of the ESE relation lies in its derivation from extensive raw scaling data, which gives the relation extrapolation capability similar to fundamental scaling. However, unlike fundamental scaling, it can be applied with the convenience of a global-fitting equation, where all the parameters are determined in a quick straightforward manner by simultaneous fitting, without analysis of raw scaling data.

The relation enables useful extrapolations in several new areas:

• Unified $T-\epsilon$ apparatuses: ESE can be used to extrapolate minimum datasets, thereby reducing the measurement space required to obtain full $I_{\text{c}}(B,T,\epsilon )$ datasets to about 1/5th the size. Depending on whether the conductor is moderate-$J_{\text{c}}$ or high-$J_{\text{c}}$, effective RMS extrapolation errors for ESE are in the range 2–5 A at 12 T, which approaches the $I_{\text{c}}$ measurement error (1–2%). Also, there is no requirement for orthogonal $B-T-\epsilon$ measurement grids to register pinning-force curves into a master scaling curve, as with fundamental scaling. (Sections 2, 3 and 5.2.)

• Combination of data from separate temperature and strain apparatuses: With the ESE relation, it is possible to combine data from different apparatuses, measured at different times, and in different laboratories (e.g., one apparatus dedicated to strain measurements and the other to temperature measurements). This provides flexibility and productive use of more limited data. (Table 3 and sections 5.4–5.9.)

• Extrapolation of $I_{\text{c}}(B,T,\epsilon )$ datasets from single $I_{\text{c}}(B)$ curves: Intrinsic error testing shows that full $I_{\text{c}}(B,T,\epsilon )$ datasets can be extrapolated from single $I_{\text{c}}(B)$ curves, with RMS pinning-force errors of only 0.10%–0.14%. These errors are only a few hundredths of a percent higher than those for whole dataset interpolations (appendix tables A1–A5). The source data for the single $I_{\text{c}}(B)$ curve can be measured at a convenient temperature and strain (such as 4.2 K and the initial strain state), which makes it particularly useful for characterizing production quantities of wire for large magnet applications. (Section 5.10.)

6.2. Summary of Part 2: Derivation of the ESE relation

1. An extensive analysis was made of each separable part of the general parameterization of the USL, equation-set (1), which contains ten parameters plus those in $b_{\text{c}2}(\epsilon )$. The parameters were determined either individually or in small groups with extensive raw scaling data from a number of large Nb₃Sn datasets, including two new, very complete datasets (tabulated online in their entirety in the supplemental website accompanying these articles, www.ResearchMeasurements.com).

   The analysis showed the existence of three scaling constants for practical Nb₃Sn conductors:

   $v=1.50\pm 0.04$	upper-critical-field temperature parameter [equation (4), Part 2];
   $w=3.0\pm 0.3$	cross-link parameter, which can be precisely determined only from large sets of raw scaling data [equation (9), Part 2];
   $u=1.7\pm 0.1$	moderate-strain curvature para meter [equation (26), Part 2].

   These constants have the same values for both high-$J_{\text{c}}$ and moderate-$J_{\text{c}}$ conductors. They are also independent of the factors used in their analysis: (1) they change by only $\text{Δ}<1\text{\%}$ for magnetic self-field corrections; (2) $\text{Δ}<2\text{\%}$ for a five-fold adjustment the trim levels used to determine raw scaling data); and (3) $\text{Δ}<~1\text{\%}$ for different values of $p$ and $q$ (including the default values $p=0.5$ and $q=2$). Their stability derives in part from the fact they depend only on the ratios of the raw scaling data ${B_{\text{c}2}}^{\ast }(T,\epsilon )/{B_{\text{c}2}}^{\ast }(0,0)$ and $K(T,\epsilon )/K(0,0)$.

   The raw scaling data analysis also shows that the rest of the parameters are conductor specific and thus need to be fitted for each conductor, rather than fixed (as is often the case).

2. When these parameter results are combined with the general parameterization of the USL, they determine the ESE relation, which reduces the number of fitting parameters in the general parameterization to five plus those in $b_{\text{c}2}(\epsilon )$.

   Extrapolative scaling expression (ESE)

   $$I_{\text{c}}(B,T,\epsilon )B=C{[b_{\text{c}2}(\epsilon )]}^s{(1-t^{1.5})}^{\eta -\mu }{(1-t^2)}^{\mu }{b}^p{(1-b)}^q$$ (13a)

   with reduced magnetic field $b\equiv B/{B_{\text{c}2}}^{\ast }(T,\epsilon )$ and reduced temperature $t\equiv T/T_{\text{c}}^{\ast }(\epsilon )$, where:

   $${B_{\text{c}2}}^{\ast }(T,\epsilon )={B_{\text{c}2}}^{\ast }(0,0)(1-t^{1.5})b_{\text{c}2}(\epsilon )$$ (13b)

   $$T_{\text{c}}^{\ast }(\epsilon )=T_{\text{c}}^{\ast }(0){[b_{\text{c}2}(\epsilon )]}^{1/3}$$ (13c)

   with five scaling parameters: $C,{B_{\text{c}2}}^{\ast }(0,0),T_{\text{c}}^{\ast }(0),s$, either $\eta$ or $\mu$ (but not both), plus the parameters in $b_{\text{c}2}(\epsilon )$.
3. The parameterization of the ESE equation is flexible to the extent that:

   • $p$ and $q$, the shape parameters of the pinning force curve, are preferably fit (simultaneously with the other parameters) to minimize errors in the magnetic field dependence. However, the analysis in tables A3–A5 shows that overall RMS pinning-force error is increased by less than ∼0.02% if default values $p=0.5$ and $q=2.0$ are used instead, especially when the range of relative field b is not extensive. Such default values become essential if the magnetic-field range of the available data is insufficient to determine their values (necessary data ranges are summarized in section 5.5.1 of Part 3).
   • $\eta$ or $\mu$, the parameters for the temperature part of the prefactor $h(t)$, can be prescribed according to any of the temperature models summarized in section 4.2 of Part 2, but for general applicability, both parameters should not be fixed (as in the G/ITER model). The need for a fitted temperature parameter may rise from composition inhomogeneities (figure 6 in Part 2). Also, although interpolation accuracies are similar for most of the $h(t)$ models, there are significant practical and extrapolation differences (described in item 4 below).
   • $b_{\text{c}2}(\epsilon )$ [aka $S(\epsilon )$], the strain part of the upper critical field, can be parameterized effectively with any of the $b_{\text{c}2}(\epsilon )$ models summarized in appendix B of Part 2. However, there are also practical differences between $b_{\text{c}2}(\epsilon )$ models (item 5 below).

4. Preferred parameterization for $\eta$ and $\mu$: Although most of the temperature $h(t)$ parameterizations give nearly the same fitting accuracy, the Hybrid1 model (with $\mu =1$ and $\eta$ fitted) and Hybrid 2 model (with $\mu =\eta /2$ and $\eta$ fitted) offer advantages in parameter consistency and overall fitting accuracy. Most important, these two models have consistently demonstrated extrapolation errors of only ∼1% when data above 4 K are extrapolated down to 2.26 K, as shown for raw scaling data in figures 16(a) and (b) in Part 2, and for $I_{\text{c}}$ data in figures 12, 13, and 15 in this article. This temperature extrapolation capability is especially useful for transport data, where the very low temperature regime is difficult to access because of heating effects and instabilities. Such factors do not have the same effect on magnetization measurements, but magnetization data do not always represent transport data because of inhomogeneity effects (item 9 below).

   Use of the Hybrid1 $h(t)$ parameterization with the ESE relation gives the extrapolative form:

   ESE, with Hybrid1

   $$I_c(B,T,\epsilon )B=C{[b_{c2}(\epsilon )]}^s{(1-t^{1.5})}^{\eta -1}(1-t^2)b^p{(1-b)}^q,$$ (14)
   ESE, with Hybrid2

   $$I_c(B,T,\epsilon )B=C{[b_{c2}(\epsilon )]}^s{\left[(1-t^{1.5})(1-t^2)\right]}^{\eta /2}{b}^p{(1-b)}^q,$$ (15)

   where the rest of the equation sets (14) and (15) are given by equations (13b) and (13c). Fitted scaling parameter values for these two models are nearly the same. Representative values are given for several practical conductors in appendix tables A1.3 and A1.5.
5. Preferred parameterizations for $b_{\text{c}2}(\epsilon )$: Again, there is little difference in fitting accuracy for ESE with any of the strain functions, but there are considerable convenience and functional differences between the $b_{\text{c}2}(\epsilon )$ strain models (details summarized in Part 2: section 6.4 and appendix B). For small magnet design at moderate strains, the Power Law model is preferred because of its simplicity and single strain-sensitivity parameter. For large magnet systems, where high-compressive three-dimensional (3-D) strains become important, the following two models have significant advantages:

   • The Invariant strain function is noteworthy in that uniaxial strain measurements can be extended to three dimensions through the use of strain invariants. Also, this model intrinsically incorporates the moderate strain curvature parameter $u=1.7$ in its lowest order term, the second strain invariant $J_2$. This gives this strain function consistency and extrapolation capability over the dominant peak strain range (figure 11 in Part 2). The Invariant model is preferred when high interpolation accuracy is needed. The parameterization is given by (Markiewicz 2006):

     $$b_{\text{c}2}(\epsilon )={\left(1-a_1{I}_1\right)}^{-1}{\left(1+a_2{J}_2+a_3{J}_3+a_4{J_2}^2\right)}^{-1}$$ (16)

     with strain invariants:

     $$I_1={\epsilon }_1+{\epsilon }_2+{\epsilon }_3,$$ (17a)

     $$J_2=1/6[{({\epsilon }_1-{\epsilon }_2)}^2+{({\epsilon }_2-{\epsilon }_3)}^2+{({\epsilon }_3-{\epsilon }_1)}^2],$$ (17b)

     $$J_3=({\epsilon }_1-I_1/3)({\epsilon }_2-I_1/3)({\epsilon }_3-I_1/3).$$ (17c)

     For uniaxial strain (without the hydrostatic parameter $a_1$), the Invariant parameterization reduces to:

     $$b_{\text{c}2}(\epsilon )={[1+c_2{{\epsilon }_0}^2+c_3{{\epsilon }_0}^3+c_4{{\epsilon }_0}^4]}^{-1},$$ (18)

     where in this case, $\epsilon$ is the axial (longitudinal) strain, ${\epsilon }_0$ is the intrinsic axial strain defined as ${\epsilon }_0\equiv \epsilon -{\epsilon }_{\text{m}}$, and ${\epsilon }_{\text{m}}$ is the axial strain at the maximum $I_{\text{c}}(\epsilon )$. The relation of the uniaxial fitting parameters $c_{\text{i}}$ to the 3-D parameters ${\text{a}}_i$ is given in Markiewicz (2006).
   • The Exponential model has a combination of useful features. It: (1) treats 3-D strains, (2) provides a single strain-sensitivity index $C_1$, (3) implicitly incorporates the moderate strain curvature constant $u=1.7$ in its lowest order term $J_2$ (figure 12 in Part 2), and (4) can extrapolate moderate strain data to high compressive strains (figure 13 in Part 2). This parameterization is given in terms of the total 3-D strain by (Bordini et al 2013):

     $$b_{c2}(\epsilon )=\frac{{\text{e}}^{-C_1\frac{J_2+3}{J_2+1}{J}_2}+{\text{e}}^{-C_1\frac{{I_1}^2+3}{{I_1}^2+1}{I_1}^2}}{2}.$$ (19)

     For the case of strain applied along the axis of a single round wire, the strain invariants $I_1$ and $J_2$ reduce to

     $$I_1=(1-2\nu ){\epsilon }_{\text{a}}+{\epsilon }_{l0}+2{\epsilon }_{t0},$$ (20a)

     $$J_2=\frac{1}{3}{\left({\epsilon }_{l0}-{\epsilon }_{t0}+(1+\nu ){\epsilon }_{\text{a}}\right)}^2$$ (20b)

     with the empirical relationship

     $${\epsilon }_{t0}=-\nu {\epsilon }_{l0}+\mathrm{0.1.}$$ (21)

     In equations (20a) and (20b), ${\epsilon }_{\text{a}}$ denotes the applied longitudinal (axial) strain [to distinguish it from the total 3-D strain in equation (19)], ${\epsilon }_{l0}$ and ${\epsilon }_{t0}$ are the longitudinal and transverse residual strains (expressed in percent), and $\nu$ is the effective Poissonʼs ratio, measured to be about $\nu =0.36$ for Nb₃Sn. The longitudinal residual strain is given approximately by ${\epsilon }_{l0}\approx -{\epsilon }_{\text{m}}$, where ${\epsilon }_{\text{m}}$ is the longitudinal (axial) strain at the maximum $I_{\text{c}}({\epsilon }_{\text{a}})$. In terms of intrinsic axial strain, ${\epsilon }_0\equiv {\epsilon }_{\text{a}}+{\epsilon }_{l0}$, the strain invariants for the case of uniaxial applied stain simplify to

     $$I_1=(1-2\nu ){\epsilon }_0+0.2$$ (22a)

     $$J_2=\frac{1}{3}{\left[(1+\nu ){\epsilon }_0-0.1\right]}^2$$ (22b)

   On balance, the Exponential model is generally preferred among the different strain models because of its combination of features and single fitting parameter $C_1$.

6. The unique combination of the ESE relation with the Hybrid and Exponential parameterizations offers an additional type of extrapolation capability. It not only provides for the extrapolation of $T-\epsilon$ cross terms from minimum datasets (figure 1 in Part 3), but can also extrapolate both temperature and strain data along the two axes in figure 1 to greater range limits (i.e., the type-two extrapolations described in section 2.3 of Part 3).

   The ESE relation with the Hybrid2 and Exponential parameterizations is being implemented by EuroCirCol and the Future Circular Collider design studies, and by CERN for HL-LHC magnet margin calculations.

7. Differences between the ESE relation and present non-extrapolative fitting equations:

   Durham fitting equation: $w$ is fixed at $w=2.2$ instead of the scaling constant value $w=3.0$, and $s$ is fixed at $s=1$ instead of being a free fitting parameter as in the ESE relation (section 3.3).

   G/ITER fitting equations: The temperature parameters $\eta$ and $\mu$ are fixed at $\eta =2$ and $\mu =1$, and the strain scaling parameter $s$ is fixed at $s=1$, instead of allowing these parameters to be fitted as in the ESE equation (section 3.4).

   MAG fitting equation: This simplified mathematical form results only if $s$ is fixed at $s=1$, instead of a free parameter as in the ESE relation (raw scaling values for $s$ are usually significantly higher than 1, between $s=1.1$ and 1.4) (section 3.4).

8. Magnetic self-field correction: The data in these articles have been analyzed both without and with correcting for magnetic self field (sections 4 and 5 in Part 2, respectively). Self-field correction factors for a number of sample holder geometries have been calculated by Bordini (2010), and tabulated in Cheggour et al (2017).

   • The self-field correction shifts data to higher fields (figure 14 in Part 2), but the pinning-force curves at different temperatures and strains still register into a master scaling curve. Thus, unified scaling holds for both corrected and uncorrected data.
   • Values of the scaling constants are the same for either self-field corrected or uncorrected data to within 1%. This is consistent with scaling being an intrinsic pinning property of the Nb₃Sn grains, independent of conductor twist pitch or test holder geometry.
   • Magnetic self-field corrections are suggested for large magnet applications, because they facilitate comparison of data between short-sample predictions and magnet performance, between data measured on different sample holders in different laboratories, and between magnetization and transport measurements.

9. Magnetization versus transport critical currents: An initial comparison is made between these two types of measurements with matched Ta-doped RRP^® samples from the same billet, and reacted with the same heat treatment. The temperature dependence of the upper critical field ${B_{\text{c}2}}^{\ast }(T,\epsilon )$ is notably altered [figure 15(b) in Part 2], which may be a result of inhomogeneous shielding currents from the decrease in dopant levels in the outer shell region of each of the sub-elements (observed with energy-dispersive x-ray spectroscopy by Tarantini et al 2016). The temperature dependence of the $K(T,\epsilon )$ term, on the other hand, has a more similar curvature between the two types of measurements, although the overall temperature slope for magnetization is somewhat lower (figure 17 in Part 2).

6.3. Summary of Part 3: Application of the ESE relation

1. Minimum dataset extrapolations: The minimum dataset for extrapolating full $I_{\text{c}}(B,T,\epsilon )$ characteristics is determined from raw scaling data to consist of two reduced datasets: a variable-temperature measurement $I_{\text{c}}(B,T)$, plus a variable-strain measurement $I_{\text{c}}(B,\epsilon )$ (i.e., a ‘2-cut’ fit along the two perpendicular axes of the $T-\epsilon$ measurement map in figure 1). Extrapolations from a ‘3-cut’ fit through the measurement map provided no significant improvement in extrapolation accuracy (section 3.1), verifying that the minimum dataset is indeed optimum. Extrapolating from the minimum dataset gives a five-fold reduction in the number of measurements needed for full $I_{\text{c}}(B,T,\epsilon )$ characterization by eliminating the need to measure the many $T-\epsilon$ cross terms in the measurement map. Also, such extrapolations with the ESE fitting equation remove the requirement for orthogonal $B-T-\epsilon$ measurement grids to register pinning-force curves into a master scaling curve (needed for the fundamental scaling approach).

2. $F_{\text{P}}$ fitting versus $I_c$ fitting: Higher accuracy is obtained by fitting the pinning force $F_{\text{P}}=I_{\text{c}}B$, rather than fitting $I_{\text{c}}$. Errors at individual data points are reduced to about 1/5th the size (figure 9). Error reduction is especially significant at moderate-to-high magnetic fields, because fitting $F_{\text{P}}$ avoids unduly weighting the high $I_{\text{c}}$ values at low fields. Note also that $F_{\text{P}}$ is the physical quantity that scales, not $I_{\text{c}}$.

3. Accuracy of minimum-datasets extrapolations: Test results are obtained from 92 case studies covering most possible parameterizations and fitting protocols. Compared with present global-fitting equations, the ESE relation improves the percentage extrapolation accuracy at individual data points by up to 10–40 times, especially at high magnetic fields, temperatures, and strains (shown by the $I_{\text{c}}$ comparisons in figures 3–5). RMS $F_{\text{P}}$ extrapolation errors for ESE are reduced to about 0.11% and 0.15% (tables 1 and 2, respectively). Depending on whether the conductor is moderate-$J_{\text{c}}$ or high-$J_{\text{c}}$, this corresponds to an effective RMS $I_{\text{c}}$ error of about 2–5 A at 12 T, which approaches the $I_{\text{c}}$ measurement error.

4. Interpolation errors: The interpolation errors for ESE are also reduced to as little as 1/15th the size of those for present fitting equations at high temperatures, strains, and magnetic fields (shown by the $I_{\text{c}}$ comparisons in figures 4 and 5). When ESE is used for interpolations, it also enables extrapolations to be made to the neighboring measurement space through the use of default core parameters (item 7 below).

5. Core parameters: $T_{\text{c}}^{\ast }(0),\eta ,s$, and $b_{\text{c}2}(\epsilon )$: These parameters are more stable than the other scaling parameters because they depend only on ratios of the raw scaling data $K(T,\epsilon )/K(0,0)$ and ${B_{\text{c}2}}^{\ast }(T,\epsilon )/{B_{\text{c}2}}^{\ast }(0,0)$. Thus, they can be reliably transferred between similar conductors to carry out full $I_{\text{c}}(B,T,\epsilon )$ extrapolations with RMS pinning-force errors of only 0.10%–0.14% (sections 5.3–5.10). This is especially cost effective when characterizing large quantities of production wire, because, with core parameters, extrapolations can be made to a full range of temperatures and strains from only a single $I_{\text{c}}(B)$ measurement on individual wire samples at an easy-to-measure temperature (4.2 K) and no applied strain (section 5.10; item 10 below).

   • For different values of $p$ and $q$, including default values $p=0.5$ and $q=2.0$, the core parameters changed by less than ±2% (appendix tables A3–A5). The change for the temperature core parameters $T_{\text{c}}^{\ast }(0)$ and $\eta$ is particularly low, only ±0.5%. Magnetic self-field corrections also do not have much effect on the core parameters, less than ±3%, although s can decrease as much as 10%.
   • In contrast to the core parameters, the parameters $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ have a variability that is 2–5 times higher. Their values also change considerably with the values of $p$ and $q$ (up to 10%–20%) (tables A3–A5). Fortunately, these parameters are precisely the parameters most effectively determined by extrapolating a single $I_{\text{c}}(B)$ curve.
   • Note that the scaling constants $v$, $w$, and $u$ are essentially unaffected by either the self-field correction or $p-q$ values (Part 2).
6. Core parameter measurement: Measurements of the core parameters ${T_{\text{c}}}^{\ast }(0),\eta ,s$, and $b_{\text{c}2}(\epsilon )$ can be determined in two ways:

   1. Preferable they are determined by fitting the ESE relation to a minimum-dataset measurement in a conductor with the same architecture, and reacted with the same heat treatment.
   2. Lacking such data, default values can be used for the core parameters, obtained from minimum dataset measurements in similar conductors (item 7 below). An initial ‘catalogue’ of such default values is given in tables A1–A5.

   The strain core parameters, $s$ and $b_{\text{c}2}(\epsilon )$, are usually more quickly measured than the temperature core parameters, because they can be determined from an $I_{\text{c}}(B,\epsilon )$ dip test in liquid helium. If a reasonable value of $s$ is known, the strain function $b_{\text{c}2}(\epsilon )$ can be obtained from just a liquid helium $I_{\text{c}}(\epsilon )$ measurement at a fixed magnetic field (illustrated by the examples in sections 5.8 and 5.9).

   The temperature core parameters ${T_{\text{c}}}^{\ast }(0)$ and $\eta$, on the other hand, generally require higher temperature $I_{\text{c}}(B,T)$ data from about 4 K to 12 K to determine their values accurately (lower-temperature data have little leverage in setting their values). If these two temperature parameters are known, the ESE-Hybrid equation-sets (14) or (15) can extrapolate transport $I_{\text{c}}$ data at 4 K down to ∼2.2 K with $I_{\text{c}}$ errors of only ∼1% (figure 16 in Part 2, and figures 12 and 15 in Part 3). In practice, $I_{\text{c}}(B,T)$ is one of the most useful measurements to make, at least for one sample of a given conductor type, because it provides the range of data needed to accurately determine many of the core parameters that will transfer to other conductors of that type (row 2 of table 3).

7. Default values for core parameters: When core parameter measurements are unavailable, or data cover a range too small to accurately determine them, default values can still provide reliable extrapolations into the neighboring measurement space (section 5.5). From the survey of values in the appendix tables A1–A5, we find the parameters for fully optimized, ternary, strong-pinning Nb₃Sn conductors cluster around the following common default average values:

   $$\begin{gathered} T_{\text{c}}^{\ast }(0)\approx 16.7\text{K} \\ \eta =2.0\text{(ITER)}-2.2\left({\text{RRP}}^{\circledR }\text{-Ta doped}\right);\text{[the higher number may correlate with compositional inhomogeneities and/or distributed diffusion barriers]} \end{gathered}$$

   $$\begin{gathered} s=1.1\left({\text{RRP}}^{\circledR }\text{-Ta}\right)-1.4\text{(ITER)} \\ p=0.5\text{and}q=\mathrm{2.0.} \end{gathered}$$

   • Temperature core parameters $T_{\text{c}}^{\ast }(0)$ and $\eta$: Default values provide reasonable extrapolation accuracy with equations (14) or (15) at temperatures $T\ll T_{\text{c}}^{\ast }(0)$.
   • Strain core parameters $s$ and the function $b_{\text{c}2}(\epsilon )$ [aka $S(\epsilon )$]: Default values for $b_{\text{c}2}(\epsilon )$ can be readily characterized with the Exponential strain function, which has only a single fitting parameter $C_1$. This parameter gives a useful index of strain sensitivity that facilitates intercomparison of conductors (e.g., see comparative values of $C_1$ in tables A1, A3 and A5).
   • Default values for the pinning-force shape parameters $p$ and $q$: At liquid helium temperature, multiple fitting tests have shown that magnetic fields over the range ∼10 T to ⩾∼ 15 T are needed to accurately determine $q$, and at fields below ∼5 T to determine $p$. Usually, it is easier to determine $p$ and $q$ from higher temperature data, above ∼4 K. When there is ambiguity, it is better to use the default Nb₃Sn values $p=0.5$ and $q=2.0$. Little accuracy is lost if extrapolations are consistently carried out with the same $p$ and $q$ values that were used to determine the core parameters $T_{\text{c}}^{\ast }(0)$, $\eta$, $s$, and $b_{\text{c}2}(\epsilon )$. (This is shown by the comparable RMS errors for different sets of $p-q$ parameters in tables A3–A5.)

8. Combining measurements from separate temperature and strain apparatuses: The $I_{\text{c}}(B,T)$ and $I_{\text{c}}(B,\epsilon )$ data, which comprise the minimum dataset, do not need to be measured in a unified $T-\epsilon$ apparatus. They can be obtained separately from less complex strain and temperature apparatuses, and then combined utilizing ESE to provide full three-dimensional $I_{\text{c}}(B,T,\epsilon )$ datasets. Combinations of datasets more limited than the minimum dataset also work. Table 3 gives a guide for which parameters are accurately determined from more limited data. Default values for the missing core parameters can be substituted when data are limited, and updated later if more complete core parameter measurements become available. Two protocols for combining data from different apparatuses are illustrated in sections 5.8 and 5.9 (simultaneous fitting and iterative fitting). The intrinsic errors of such combined data are quite low, about RMSE = 0.11%–0.14%.

9. Extrinsic errors for combining measurements from different samples and apparatuses: Extrinsic errors depend on: (1) matching the basic filament configuration, composition, doping, and heat treatment of the samples, and (2) the care used when correcting any differences in $I_{\text{c}}$ criteria, self-field effects from different sample holder geometries, and, in particular, mismatches in strain introduced by differential thermal contraction between the sample and the sample holder. Correction techniques are referenced in section 5.7. Uncertainties in the strain correction can be minimized when the opportunity is available to plan the design of different apparatuses, by using the same sample-holder material and soldering the samples continuously along their length (such as with beryllium-copper holders). The agreement in $I_{\text{c}}$ values where the strains and temperatures overlap is a good indicator of such extrinsic errors.

10. Extrapolations from single $I_{\text{c}}(B)$ curves for characterizing production samples (section 5.10): When the core parameters plus $b_{\text{c}2}(\epsilon )$ have been measured in one of the production conductors (reacted with similar heat treatment), full $I_{\text{c}}(B,T,\epsilon )$ datasets can be effectively extrapolated from only a single $I_c(B)$ measurement on individual wire samples. Because of the stability in the core parameters, the samples do not need to be matched exactly. The highest accuracies are obtained when the same $p$ and $q$ values originally used to determine the core parameters are used to carry out the extrapolations. Intrinsic RMS $F_P$ errors of only 0.10%–0.14% (corresponding to effective RMS $I_{\text{c}}$ errors of 1–5A at 12 T) are obtained in 14 test cases with the ESE-Hybrid equations (14) or (15) and the Exponential strain model. These low errors were obtained, for both moderate-$J_{\text{c}}$ and high-${\text{J}}_c$ conductors, for magnetic self-field corrected and uncorrected data, and for core parameter values determined either with fitted $p$ and $q$ values, or with default values $p=0.5$ and $q=2.0$. Such extrapolations are particularly useful for determining transport critical currents at temperatures $\ll 4\text{K}$ or $\gg 4\text{K}$, or at extended strains, from a single $I_{\text{c}}(B)$ curve measured at ∼ 4K and no applied strain.

6.4. Future research

Suggested research areas for future scaling studies include:

• Measurements of the four core parameters $T_{\text{c}}^{\ast }(0),\eta ,s$, and $C_1$ in additional types of Nb₃Sn conductors. Measurement of a minimum dataset is suggested for at least a single production sample to accurately determine the core scaling parameters for large magnet systems, such as HL-LHC, FCC, and fusion prototype magnets. [An immediate need is for the measurement of the temperature dependence $I_{\text{c}}(B,T)$ from $\le \sim 4\text{K}$ to ∼12 K on a single sample of the Ti-doped RRP^® and PIT production wires for HL-LHC to determine $T_{\text{c}}^{\ast }(0)$ and $\eta$. This would provide for accurate extrapolation of production billet transport $I_{\text{c}}$ measurements at ∼4.2 K down to 1.9 K, the operating temperature of HL-LHC.] Over time, measurements of the four core parameters in a wide range of Nb₃Sn conductors (including different wire architectures, dopant levels, and a check for parameter constancy in strands extracted from Rutherford cables) would also provide a useful compilation of default values for different conductor types (i.e., expansion of tables A1–A5).

• Assessment of whether the USL, scaling constants, and the ESE relation hold for Nb₃Sn conductors with artificial-pinning-center (APC) architectures. Even though the pinning force peak is shifted for APC conductors, the constants and core scaling parameters depend only on ratios of the raw scaling data ${B_{\text{c}2}}^{\ast }(T,\epsilon )/{B_{\text{c}2}}^{\ast }(0,0)$ and $K(T,\epsilon )/K(0,0)$. Such shifts in the pinning force curves were also observed for magnetic self-field corrections (section 5 of Part 2), but ESE was still applicable. So ESE or a variant expression may apply to APC conductors as well. However, it is emphasized that to be accurate and provide extrapolation capability for APC conductors, the initial analysis of the scaling parameter values needs to be done with raw scaling data (as in sections 4 and 5 of Part 2). The sequence also needs to follow that outlined at the beginning of section 4 in Part 2.

• Assessment of the extrapolation accuracy and limits of ESE in extreme regions of $B-T-\epsilon$ parameter space for magnet modeling where routine measurements are difficult (e.g., at very low magnetic field for determining losses in fusion and other large magnet applications).

• Evaluation of the relationship between magnetization and transport data in different types of practical Nb₃Sn conductors, beyond the initial matched-sample comparison made in sections 5.3 and 5.5 of Part 2. Significant differences between the two types of measurements can arise from inhomogeneous screening currents in commercial Nb₃Sn wires.

• Measurement and analysis of raw scaling data in superconducting materials other than Nb₃Sn. Fitting equations with extrapolation capability similar to the ESE relation may exist for other practical materials that exhibit scaling (including MgB₂, BSCCO, Nb₃Al, and YBCO). Again, any time a master scaling curve can be formed, one flux-pinning curve can predict them all, if the scaling parameters have been determined with raw scaling data.

Appendix

A.1. The ESE parameter set for several practical Nb₃Sn conductors

In this appendix, we give examples of the ESE parameter set obtained from fitting several large Nb₃Sn datasets, both uncorrected and corrected for magnetic self field (tables A1–A2, and A3–A5 respectively). These relatively large datasets (described in appendix A of Part 2) cover a wide range of magnetic fields $B$, temperatures $T$, and strains $\epsilon$.

The parameter values in tables A1–A5 were obtained by simultaneously fitting the whole datasets with the ESE relation, applied with the Hybrid1 $h(t)$ parameterizations [equation (14)], and either the Invariant or Exponential parameterizations of $b_{\text{c}2}(\epsilon )$ [equations (18) and (19), respectively]. Table A5 gives corresponding parameter values for ESE applied with the Hybrid2 $h(t)$ parameterization [equation (15)]. Fitting was carried out in terms of the pinning force $F_{\text{P}}$, not $I_{\text{c}}$, to avoid overweighting low fields (where magnets are generally not designed).

The fitting steps are as follows:

1. Critical-current data are converted to pinning-force data, $F_{\text{P}}(B,T,\epsilon )=I_{\text{c}}(B,T,\epsilon )B$.

2. If magnetic self-field corrections are applied, both $B$ and $F_{\text{P}}\left(=I_{\text{c}}B\right)$ are consistently corrected (Garber et al 1989, Bordini 2010, Cheggour et al 2017).

3. The fit is performed with a non-linear regression program, minimizing the sum of the squared pinning-force residuals $\text{Σ}{(F_{\text{P}}-F_{\text{P}}^{\text{fit}})}^2$.

4. The RMS errors and RMS fraction deviations listed in the last columns of tables A1–A5 are calculated in terms of percentage pinning-force error [equations (3a) and (3b)], which is also representative of the percentage critical-current RMS error (section 3), because the measurement error contributed by the magnetic field is negligible in comparison to that of $I_{\text{c}}$.

Trimming is used to facilitate convergence with the nonlinear regression program, although the scaling constants and core parameter values are effectively insensitive to the trim levels (changes of less than ∼2%). Trim levels for the temperature were set at $T>12\text{K}$ (for all the conductors); and for the pinning force, $F_{\text{P}}<200$ AT for OST-RRP^®, $F_{\text{P}}<125$ AT for WST-ITER, $F_{\text{P}}<100$ AT for Luvata, and $F_{\text{P}}<25$ AT for the more moderate-$J_{\text{c}}$ VAC and EM-LMI conductors.

Source $I_{\text{c}}(B,T,\epsilon )$ datasets used in these fits are published online for the NIST measurements of the OST-RRP^® and WST-ITER conductors at www.ResearchMeasurements.com. Source $I_{\text{c}}(B,T,\epsilon )$ datasets for the VAC and EM-LMI conductors were measured by the Durham group (Taylor and Hampshire 2005) and were obtained online at http://dur.ac.uk/superconductivity.durham/. Micrographs for many of the conductor crossections are shown in appendix A of Part 2.

A.2. The ESE parameter set for data not corrected for magnetic self field

Tables A1 and A2 give values of the ESE parameter set for the Exponential and Invariant parameterizations of $b_{\text{c}2}(\epsilon )$, respectively.

These results can be used to set default values for the core parameters ${T_{\text{c}}}^{\ast }(0),\eta ,s$, and $b_{\text{c}2}(\epsilon )$ in similar wires (values listed in item 7 of the summary section 6.3; and discussed in section 5.5). When these values are used to carry out extrapolations with ESE, the highest accuracy is obtained if the $p$ and $q$ values that are used in the extrapolations match those used in determining the core parameters.

A.3. The ESE parameter set for data corrected for magnetic self field

Tables A3–A5 give corresponding parameter values for the same wires as in tables A1 and A2, except the data are corrected for magnetic self field. (Self-field correction information was not available for the Durham measurements, so these wires are not included in tables A3–A5). Such corrections are particularly suggested for magnet applications to relate short-sample data to magnet performance. Also, such corrections facilitate comparison between short-sample data measured with different sample holders in different laboratories, and between transport and magnetization measurements.

The effect of different values of $p$ and $q$ is also compared in tables A3–A5. The assignment of a default value for $p$ usually becomes necessary when data are corrected for magnetic self field because the low field data are insufficient to determine $p$. RMS errors are slightly lower for the case of setting $p=0.5$ compared with $p=0.4$. The high-field shape parameter $q$ was fixed at $q=2$ for the last case for all three conductors in tables A3–A5 ($p-q$ values are shown as bold type in all three tables). Comparisons within each table show that the values assigned to $p$ and $q$ have very little effect on the RMSE $F_{\text{P}}$ fitting error (<∼0.02%).

The data also show that the non-core parameters $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ are more variable than the other parameters. Changes of ±5% to ±10% occurred over the range of values of $p$ and $q$. Also, the effect of applying magnetic self-field corrections resulted in differences of about ±10% between values of $C$ and ${B_{\text{c}2}}^{\ast }(0,0)$ in tables A3 and A4, versus the corresponding uncorrected data in tables A1 and A2.

The core parameters [$T_{\text{c}}^{\ast }(0),\eta ,s$, and $C_1$], on the other hand, are relatively stable with respect to these two effects:

1. $\text{Δ}<\pm 2\text{\%}$ for the range of $p$ and $q$ values tested, with even smaller changes ($\text{Δ}<\pm 0.5\text{\%}$) for the temperature core parameters $T_{\text{c}}^{\ast }(0)$ and $\eta$ (tabulated in the middle of tables A3–A5). (The greater variability of the core parameters for the Luvata conductor was not included because the available source data were very limited for this conductor, allowing greater scatter in the fitting parameter values.)

2. $\text{Δ}<\pm 3\text{\%}$ for magnetic self-field corrections, although $s$ decreased about 10% for the corrected data in tables A3 and A4, compared with tables A1 and A2. As noted for tables A1 and A2, when these core data are used to carry out extrapolations from limited data, the highest accuracy is obtained if the $p$ and $q$ values used in the extrapolations match those used in determining the core parameters.

Table A1.

The ESE parameter set, with the Hybrid1 parameterization of $h(t)$ and the Exponential parameterization of $b_{\text{c}2}(\epsilon )$ for data not corrected for magnetic self field.

			Core scaling parameters
Nb3Sn conductor	$C$ (AT)	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	${T_{\text{c}}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_{l0}$a (%)	$C_1$ b	$p$ c	$q$ c	RMSFDd (%)	RMSEd (%)
OST-RRP®	50 510	29.09	16.94	2.25	1.15	−0.355	0.75	0.50	2.06	9.0	0.120
WST-ITER	21 020	31.02	16.81	2.02	1.39	−0.302	0.82	0.57	1.83	4.8	0.114
LUVATA	14 960	29.70	16.43	1.97	1.40	−0.321	0.66	0.56	1.70	2.0	0.078
VAC	7 630	29.91	16.84	2.00	1.10	−0.313	0.92	0.48	1.44	4.6	0.247
EM-LMI	11 920	30.79	17.02	2.38	0.87	−0.271	1.14	0.50	1.84	3.6	0.170

Notes:

^aThe compressive prestrain values ${\epsilon }_{l0}(=-{\epsilon }_m)$ are dependent on the strain introduced by the sample holder on cooldown, and therefore are not strictly part of the core parameter set. All these samples were soldered with Pb–Sn solder to Cu–Be sample holders.

^bThe $C_1$ values for the Exponential $b_{\text{c}2}(\epsilon )$ model in the last core-parameter column of table A1 give a strain sensitivity index for comparing the different conductors (because the strain parameter $C_1$ is a not interdependent on other strain parameters). A comparison of the $C_1$ values in this column shows immediately that the EM-LMI conductor has the greatest strain sensitivity ($C_1=1.14$), followed by VAC, WST-ITER, and OST-RRP^® conductors. This is not the case for the Invariant Strain Function parameters in table A2, or for any of the other $b_{\text{c}2}(\epsilon )$ models (except the Extended Power Law model), because these other models have multiple parameters that compensate each other and thus require the $b_{\text{c}2}(\epsilon )$ function to be plotted before a conductor’s relative strain sensitivity is known.

Due to the very low value of ${\epsilon }_{0,\text{irr}}$ for the OST-RRP^® conductor (Cheggour et al 2010), there were not enough data on the tensile side of the strain peak to determine the value of ${\epsilon }_{l0}(=-{\epsilon }_{\text{m}})$ independently of $C_1$. Thus, for this particular situation, $C_1$ is not truly an independent strain sensitivity index, since the scarcity of tensile data gives it freedom to interact with ${\epsilon }_{l0}$ to some degree to improve the fit. For example, note the difference between the ${\epsilon }_{l0}$ and $-{\epsilon }_{\text{m}}$ values for this conductor in tables A1 and A2, whereas the correspondence in the values of these two parameters was close for all the other conductors. Although the value of $C_1$ may not be as precise an index of strain sensitivity for this particular conductor, a detailed inspection of the data showed that the $C_1$ ranking shown in the tables A1 was nevertheless correct.

^cPinning-force shape parameters $p$ and $q$ were determined as part of the simultaneous global-fitting process for all the datasets, except the high-$J_{\text{c}}$ OST-RRP^® dataset. It lacked sufficient low-magnetic field data to determine $p$, so $p$ was fixed at $p=0.5$ for this particular conductor. (The parameter $q$ was determined from the master scaling curve, but it would also have worked well to fix $p=0.5$ and fit $q$ as part of the simultaneous fitting process.)

^dThe RMSFD and RMS $F_{\text{P}}$ errors in the last two columns are defined by equations (3a) and (3b) in the text. Errors are expressed as percentages to facilitate comparisons between conductors. The percentage RMSE $F_{\text{P}}$ errors in these tables correspond to effective RMS $I_{\text{c}}$ errors of 1–5 A at 12 T, depending on the $J_{\text{c}}$ of the conductor (section 3).

Table A2.

The ESE parameter set, with the Hybrid1 parameterization of $h(t)$ and the Invariant parameterization of $b_{\text{c}2}(\epsilon )$ for data not corrected for magnetic self field.

			Core scaling parameters
Nb3Sn conductor	$C$ (AT)	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	$T_{\text{c}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_m$a (%)	$c_2$	$c_3$	$c_4$	$p$ b	$q$ b	RMSFDc (%)	RMSEc (%)
OST-RRP®	47 950	27.58	16.65	2.25	1.21	0.302	1.02	0.72	0.18	0.50	2.06	7.3	0.104
WST-ITER	19 770	29.62	16.53	2.02	1.36	0.305	0.82	0.42	0.12	0.58	1.86	4.5	0.106
LUVATA	14 170	28.60	16.21	1.97	1.40	0.323	0.66	0.67	1.14	0.56	1.71	2.0	0.082
VAC	7 650	28.92	16.45	1.97	1.04	0.311	0.89	0.38	0.05	0.51	1.55	4.5	0.219
EM-LMI	11 420	28.81	16.71	2.40	0.85	0.273	1.05	0.61	0.26	0.50	1.88	3.6	0.156

Notes:

^aThe compressive prestrain values ${\epsilon }_{\text{m}}$ are dependent on the strain introduced by the sample holder on cooldown, and therefore are not strictly part of the core parameter set. All these samples were soldered with Pb–Sn solder to Cu–Be sample holders.

^bPinning-force shape parameters $p$ and $q$ were determined as part of the simultaneous global-fitting process for all the datasets, except the high-$J_{\text{c}}$ OST-RRP^® dataset. It lacked sufficient low-magnetic field data to determine $p$, so, for this particular conductor, $p$ was fixed at $p=0.5$. (The parameter $q$ was determined from the master scaling curve, but it would also have worked well to fix $p=0.5$ and fit $q$ as part of the simultaneous fitting process.)

^cThe RMSFD and RMS $F_{\text{P}}$ errors in the last two columns are defined by equations (3a) and (3b) in the text. Errors are expressed as percentages to facilitate comparisons between conductors. The percentage RMSE $F_{\text{P}}$ errors in these tables correspond to effective RMS $I_{\text{c}}$ errors of 1–5 A at 12 T, depending on the $J_{\text{c}}$ of the conductor (section 3).

Table A3.

The ESE parameter set with the Hybrid1 parameterization of $h(t)$ and the Exponential parameterization of $b_{\text{c}2}(\epsilon )$ for data corrected for magnetic self field. The data show minimal variation of the core parameter values with changes in $p$ and $q$ (bold type).

			Core scaling parameters
Nb3Sn Conductor	$C$ (AT)	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	$T_{\text{c}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_{l0}$a (%)	$C_1$ b	$\mathit{p}$ c	$\mathit{q}$ c	RMSFDf (%)	RMSEf (%)
OST-RRP®	51 640	29.31	16.93	2.24	1.02	−0.352	0.77	0.4	2.12 d	9.6	0.114
OST-RRP®	59 990	29.73	16.92	2.23	1.01	−0.351	0.77	0.5	2.27 d	9.2	0.094
OST-RRP®	54 230	28.21	16.94	2.24	1.07	−0.355	0.75	0.5	2.00	12.9	0.113
WST-ITER	16 480	30.17	16.76	1.98	1.31	−0.302	0.83	0.4	1.58 d	6.0	0.166
WST-ITER	20 700	32.08	16.73	1.97	1.29	−0.302	0.84	0.5	1.93 d	4.8	0.144
WST-ITER	21 080	32.75	16.70	1.96	1.29	−0.302	0.85	0.5	2.00	5.0	0.144
$\sim \text{Δ}$ from $p$, $q$	±7–11%	±2–4%	±0.2%	±0.5%	±2%	±0.5%	±1.5%		OST-RRP® and WST-ITER
LUVATA	12 310	28.76	16.40	1.94	1.4	–0.321	0.65	0.426 e	1.48 e	3.3	0.146
LUVATA	14 880	30.77	16.31	1.91	1.4	–0.322	0.64	0.5	1.80 e	2.1	0.143
LUVATA	15 570	32.71	16.18	1.88	1.4	–0.327	0.61	0.5	2.00	3.2	0.160

Notes:

^aThe compressive prestrain values ${\epsilon }_{l0}(=-{\epsilon }_m)$ are dependent on the strain introduced by the sample holder on cooldown, and therefore are not strictly part of the core parameter set. The samples were soldered with Pb–Sn solder to Cu–Be sample holders for these measurements.

^bThe $C_1$ values for the Exponential $b_{\text{c}2}(\epsilon )$ model in the last core-parameter column of table A3 give a strain sensitivity index, because $C_1$ is not interdependent on other strain parameters. Due to the very low value of ${\epsilon }_{0,\text{irr}}$ for the OST- RRP^® (Cheggour et al 2010), there were not enough data on the tensile side of the strain peak to determine the value of ${\epsilon }_{l0}(=-{\epsilon }_m)$ independently of C₁. This results in a difference between the ${\epsilon }_{l0}$ and $-{\epsilon }_{\text{m}}$ values between tables A3 and A4 for this conductor, whereas the correspondence was close for all other conductors.

^cThe pinning-force shape parameter $p$ was fixed to a constant value ($p=0.4$ or 0.5) because the magnetic self-field correction shifted all the data to higher fields, which resulted in insufficient low-magnetic field data to determine $p$. The high-field shape parameter $q$ was kept as a fitting parameter for two cases for each wire and fixed at the default value $q=2$ for the third case.

^dFixed from a fit to the master scaling curve.

^eFitted simultaneously with the other parameters.

^fThe RMSFD and RMS $F_{\text{P}}$ errors in the last two columns are defined by equations (3a) and (3b) in the text. Errors are expressed as percentages to facilitate comparisons between conductors. The percentage RMSE $F_{\text{P}}$ errors in these tables correspond to effective RMS $I_{\text{c}}$ errors of 1 A to 5 A at 12 T, depending on the $J_{\text{c}}$ of the conductor (section 3).

Table A4.

The ESE parameter set with the Hybrid1 parameterization of $h(t)$ and the Invariant parameterization of $b_{\text{c}2}(\epsilon )$ for data corrected for magnetic field. The data show minimal variation of the core parameter values with changes in $p$ and $q$ (bold type).

			Core scaling parameters
Nb3Sn Conductor	$C$ (AT)	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	$T_{\text{c}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_m$a (%)	$c_2$	$c_3$	$c_4$	$\mathit{p}$ b	$\mathit{q}$ b	RMSFDe (%)	RMSEe (%)
OST-RRP®	49 320	27.76	16.63	2.23	1.08	0.303	1.03	0.73	0.19	0.4	2.12 c	8.0	0.097
OST-RRP®	57 300	28.16	16.62	2.22	1.07	0.303	1.03	0.72	0.19	0.5	2.27 c	7.5	0.079
OST-RRP®	51 690	26.77	16.66	2.24	1.12	0.306	0.99	0.68	0.17	0.5	2.00	11.9	0.099
WST-ITER	15 370	28.71	16.47	1.98	1.275	0.305	0.84	0.43	0.12	0.4	1.59 c	5.8	0.156
WST-ITER	19 300	30.52	16.44	1.97	1.248	0.305	0.85	0.43	0.12	0.5	1.93 c	4.5	0.135
WST-ITER	19 610	31.10	16.41	1.96	1.243	0.305	0.85	0.43	0.12	0.5	2.00	4.6	0.136
$\sim \text{Δ}$ from $p$, $q$	±7–11%	±2–4%	±0.2%	±0.5%	±2%	±0.5%	±2%	±4%	±5%		OST-RRP® and WST-ITER
LUVATA	11 660	27.67	16.18	1.94	1.4	0.325	0.66	0.74	1.32	0.426 d	1.49 d	3.2	0.154
LUVATA	14 110	29.64	16.09	1.91	1.4	0.327	0.64	0.84	1.57	0.5	1.81 d	2.1	0.150
LUVATA	14 800	31.52	15.99	1.88	1.4	0.339	0.65	1.37	2.72	0.5	2.00	3.2	0.166

Notes:

^aThe compressive prestrain values ${\epsilon }_m$ are dependent on the strain introduced by the sample holder on cooldown, and therefore are not strictly part of the core parameter set. The samples were soldered with Pb–Sn solder to Cu–Be sample holders for these measurements.

^bThe pinning-force shape parameter $p$ was fixed to a constant value ($p=0.4$ or 0.5) because the magnetic self-field correction shifted all the data to higher fields, which resulted in insufficient low-magnetic field data to determine $p$. The high-field shape parameter $q$ was kept as a fitting parameter for two cases for each wire and fixed at the default value $q=2$ for the third case.

^cFixed from a fit to the master scaling curve.

^dFitted simultaneously with the other parameters.

^eThe RMSFD and RMS $F_{\text{P}}$ errors in the last two columns are defined by equations (3a) and (3b) in the text. Errors are expressed as percentages to facilitate comparisons between conductors. The percentage RMSE $F_{\text{P}}$ errors in these tables correspond to effective RMS $I_{\text{c}}$ errors of 1–5 A at 12 T, depending on the $J_{\text{c}}$ of the conductor (section 3).

Table A5.

The ESE parameter set with the Hybrid2 parameterization of $h(t)$ and the Exponential parameterization of $b_{\text{c}2}(\epsilon )$ data corrected for magnetic self field. A comparison with table A3, shows that the Hybrid1 and Hybrid2 parameterizations of ESE have nearly the same parameter values ($\text{Δ}<\sim 1\text{\%}$).

			Core scaling parameters
Nb3Sn Conductor	$C$ (AT)	${B_{\text{c}2}}^{\ast }(0,0)$ (T)	$T_{\text{c}}^{\ast }(0)$ (K)	$\eta$	$s$	${\epsilon }_{l0}$a (%)	$C_1$ b	$\mathit{p}$ c	$\mathit{q}$ c	RMSFDd (%)	RMSEd (%)
OST-RRP®	59,700	29.72	16.93	2.26	1.01	−0.351a	0.77	0.5	2.27 e	9.2	0.095
OST-RRP®	53,950	28.20	16.95	2.27	1.07	−0.355a	0.75	0.5	2.00	12.9	0.114
WST-ITER	20,710	32.09	16.72	1.96	1.29	−0.302	0.84	0.5	1.93 e	4.8	0.143
WST-ITER	21,080	32.76	16.69	1.95	1.28	−0.302	0.85	0.5	2.00	5.0	0.143
$\sim \text{Δ}$ from $p$, $q$	±2–6%	±2–4%	±0.2%	±0.5%	±2%	±0.5%	±1.5%	OST-RRP® and WST-ITER
LUVATA	14,920	30.84	16.27	1.89	1.4	–0.322	0.67	0.5	1.81 f	2.2	0.140
LUVATA	15,590	32.74	16.14	1.85	1.4	–0.327	0.61	0.5	2.00	3.1	0.156

Notes:

^aThe compressive prestrain values ${\epsilon }_{l0}(=-{\epsilon }_m)$ are dependent on the strain introduced by the sample holder on cooldown, and therefore are not strictly part of the core parameter set. The samples were soldered with Pb-Sn solder to Cu-Be sample holders for these measurements.

^bThe $C_1$ values for the Exponential $b_{\text{c}2}(\epsilon )$ model in the last core-parameter column of tables A3 and A5 give a strain sensitivity index, because $C_1$ is not interdependent on other strain parameters. Due to the very low value of ${\epsilon }_{0,\text{irr}}$ for the OST- RRP^® (Cheggour et al 2010), there were not enough data on the tensile side of the strain peak to determine the value of ${\epsilon }_{l0}(=-{\epsilon }_m)$ independently of $C_1$ in this particular case. This results in a difference between the ${\epsilon }_{l0}$ and $-{\epsilon }_{\text{m}}$ values between table A3 and tables A4 or A5 for this conductor, whereas the correspondence was close for all other conductors.

^cThe pinning-force shape parameter $p$ was fixed to a constant value (p = 0.4 or 0.5) because the magnetic self-field correction shifted all the data to higher fields, which resulted in insufficient low-magnetic field data to determine $p$. The high-field shape parameter $q$ was kept as a fitting parameter for the first case for each wire and fixed at the default value $q=2$ for the second case.

^dThe RMSFD and RMS $F_{\text{P}}$ errors in the last two columns are defined by equations (3a) and (3b) in the text. Errors are expressed as percentages to facilitate comparisons between conductors. The percentage RMSE $F_{\text{P}}$ errors in these tables correspond to effective RMS $I_{\text{c}}$ errors of 1 A to 5 A at 12 T, depending on the $J_{\text{c}}$ of the conductor (section 3).

^eFixed from a fit to the master scaling curve.

^fFitted simultaneously with the other parameters.