Cross-sectional and Longitudinal Age-related Disintegration in Functional Connectivity: Reference Ability Neural Network Cohort

Abstract

Some theories of aging have linked age-related cognitive decline to a reduction in distinctiveness of neural processing. Observed age-related correlation increases among disparate cognitive tasks have supported the dedifferentiation hypothesis. We previously showed cross-sectional evidence for age-related correlation decreases instead, supporting an alternative disintegration hypothesis. In the current study, we extended our previous research to a longitudinal sample. We tested 135 participants (20–80 years) at two time points—baseline and 5-year follow-up—on a battery of 12 in-scanner tests, each tapping one of four reference abilities. We performed between-tasks correlations within domain (convergent) and between domain (discriminant) at both the behavioral and neural level, calculating a single measure of construct validity (convergent - discriminant). Cross-sectionally, behavioral construct validity was significantly different from chance at each time point, but longitudinal change was not significant. Analysis by median age split revealed that older adults showed higher behavioral validity, driven by higher discriminant validity (lower between-tasks correlations). Participant-level neural validity decreased over time, with convergent validity consistently greater than discriminant validity; this finding was also observed at the cross-sectional level. In addition, a disproportionate decrease in neural validity with age remained significant after controlling for demographic factors. Factors predicting longitudinal changes in global cognition (mean performance across all 12 tasks) included age, change in neural validity, education, and National Adult Reading Test (premorbid intelligence). Change in neural validity partially mediated the effect of age on change in global cognition. Our findings support the theory of age-related disintegration, linking cognitive decline to changes in neural representations over time.

INTRODUCTION

Age-related cognitive decline has been reported in several cognitive abilities, both cross-sectionally (Ebaid, Crewther, MacCalman, Brown, & Crewther, 2017; Kaufman, Salthouse, Scheiber, & Chen, 2016; Hartshorne et al., 2015; Dore, Elias, Robbins, Elias, & Brennan, 2007; Salthouse & Ferrer-Caja, 2003) and longitudinally (Hughes, Agrigoroaei, Jeon, Bruzzese, & Lachman, 2018; Zaninotto, Batty, Allerhand, & Deary, 2018; Whitley et al., 2016). However, discrepancies do exist between longitudinal and cross-sectional findings regarding the trajectories of cognitive change across the breadth of adulthood (see Salthouse, 2016; Salthouse, 2010; Rönnlund, Nyberg, Bäckman, & Nilsson, 2005). Although the relative contribution of cohort effects toward the stability of findings has been a point of debate (see Salthouse, 2009; c.f. Schaie, 2009), longitudinal designs are arguably essential to considering dynamic lifespan changes in addition to specific biopsychosocial characteristics that might account for these changes.

One possible hypothesis to explain age-related cognitive declines across multiple domains has been dedifferentiation, or the loss of specificity among distinct abilities and the neural resources dedicated to those abilities. In support of this claim at the cognitive level, some studies, both cross-sectionally and longitudinally, have reported age-associated links in performance levels across disparate cognitive tasks such as fluid intelligence, sensory functioning, semantic knowledge, visuospatial ability, episodic memory (MEM), and processing speed (SPEED; Hülür et al., 2015; Lindenberger & Ghisletta, 2009; de Frias, Lövdén, Lindenberger, & Nilsson, 2007; Li et al., 2004; Ghisletta & Lindenberger, 2003; Baltes & Lindenberger, 1997), whereas others have found no such relationship between tasks (Molenaar, Kő, Rózsa, & Mészáros, 2017; Batterham, Christensen, & Mackinnon, 2011; Tucker-Drob & Salthouse, 2008; Anstey, Hofer, & Luszcz, 2003; Zelinski & Lewis, 2003). Conversely, some research has supported age-related differentiation, or disintegration (c.f. Salthouse, 2012), where cognitive tasks become more independent with advancing age, resulting in correlation decreases (Blum & Holling, 2017; Tucker-Drob & Salthouse, 2008; Anstey et al., 2003; Deary & Pagliari, 1991).

At the neural level, evidence in favor of dedifferentiation has shown age-related reductions in the distinctiveness of neural response elicited by different stimuli such as category membership (for a review, see Koen & Rugg, 2019), across several processing regions including visual, auditory, motor, and pFCs (Simmonite & Polk, 2022; Carp, Park, Hebrank, Park, & Polk, 2011; Carp, Park, Polk, & Park, 2011; Voss et al., 2008; Park et al., 2004). In addition, age-related increases in the functional covariance during multiple memory task performance has been found across prefronto-parietal-occipital networks (Sambataro et al., 2012), with the specificity of neural activation linked to long-term memory recall (St-Laurent, Abdi, Bondad, & Buchsbaum, 2014). Other studies, however, have found limited or no evidence for age-related neural dedifferentiation in category-selective regions (Zheng et al., 2018; Chee et al., 2006), with results suggesting that task demands may be an important contributing factor to theses discrepancies. In addition, among recent brain activation studies that have supported dedifferentiation, some have not found age-related associations (Seider, Porges, Woods, & Cohen, 2021).

Neural dedifferentiation can be and has been operationalized in different ways. Although most studies have targeted selectivity of fMRI BOLD activity elicited by different visual categories, other modes of investigation have been covariance patterns among structural brain factors (e.g., de Mooji et al., 2018), which has supported a hypothesis of disintegration, and correlations between large-scale brain networks (e.g., Damoiseaux, 2017), which has arguably lent itself to differing conceptual interpretations. Dedifferentiation from a network connectivity perspective has largely been supported on grounds of age-related declines in functional segregation, or decreases in within-network connectivity coupled with increases in between-networks connectivity, suggesting diffuse and less specialized patterns of functional connections (Damoiseaux, 2017; Antonenko & Flöel, 2013). However, age-related reductions not only in within-network connectivity but also between-networks connectivity have also been interpreted as theoretically consistent with dedifferentiation accounts (Zhang, Gertel, Cosgrove, & Diaz, 2021). Longitudinal evidence for age-related declines in functional specialization has also largely been instantiated in terms of the relative ratio of within- to between-networks connectivity, where aging is associated with both declines in segregation and increases in global integration among subnetworks (Malagurski, Liem, Oschwald, Mérillat, & Jäncke, 2020; Rakesh, Fernando, & Mansour, 2020; Wig, 2017). In addition, recent work has demonstrated the impact of white matter integrity on segregation, specifically in large-scale associative networks, which is also linked with global cognitive ability (Pedersen et al., 2021). One potential drawback to these metric calculations is the reliance on network parcellation schemes that may be affected by atlas selection.

In a prior work, we investigated the relationship between tasks belonging to the same or different cognitive domain, at both the cognitive and neural level, to evaluate support for the dedifferentiation hypothesis in a cross-sectional lifespan sample (see Argiris, Stern, & Habeck, 2021). We represented task correlations in terms of convergent (within-domain) and discriminant (between-domain) validity, calculating a single measure of construct validity (CV; convergent - discriminant). We reasoned that tasks belonging to domains derived from latent variable modeling should express high behavioral and neural similarity within their respective domain (i.e., convergent validity) and low similarity when compared with other domains (i.e., discriminant validity). We hypothesized that CV would decrease with age because of a loss of specificity of processing. However, we additionally hypothesized that this process could be driven by correlation (r) increases among unrelated tasks, pertaining to discriminant (D) validity (higher correlation = lower discriminant validity), or correlation decreases among related tasks, pertaining to convergent (C) validity (lower correlation = lower convergent validity):

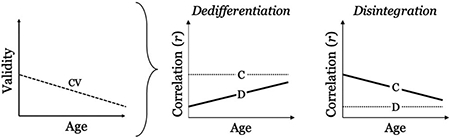
Admittedly, it is also feasible that age-related declines in CV could be observed in the case of both higher correlations in D and lower correlations in C; in such a scenario, distinguishing between the two theories would pose a challenge. We therefore additionally investigated the effect of age on each validity measure separately. We observed a negative age effect on CV, which was driven by a decrease in convergent validity. We interpreted these findings as favoring a theory of disintegration in task-elicited functional connectivity as opposed to the proponent theory of dedifferentiation. In the current work, we aimed to test the reproducibility of our findings in a longitudinal sample as well as investigate the relationship between within-participant change in validity and its relationship to both age and change in cognition. A comparison between cross-sectional and longitudinal findings is essential, particularly in the context of the dedifferentiation hypothesis, as meta-analytic work has suggested little evidence for age-dependent increases in the cross-sectional correlations between the task themselves (i.e., static dedifferentiation) but an age-dependent increase in the shared variance of change across cognitive abilities (i.e., dynamic dedifferentiation Tucker-Drob, Brandmaier, & Lindenberger, 2019).

METHODS

Participants

One hundred thirty-five native English-speaking, right-handed (Edinburgh Handedness Inventory; Oldfield, 1971) adults (age = 52.3 ± 16.71; range = 20–80 years) were tested at two time points—baseline and 5-year follow-up. Participants were recruited via random-market-mailing and part of the Reference Ability Neural Network cohort, which is a community-based cohort from the greater New York area. As we wished to maximize participant inclusion, we did not restrict our sample to participants who completed all 12 tasks of our design. However, no participant had less than 9 of the 12 tasks available (M = 11.41, SD = 0.81). All participants were screened for serious psychiatric or medical conditions, poor hearing and vision, and any other impediments that could hinder MRI acquisition using the Patient Health Questionnaire and medical screening questionnaire. This preliminary screening was performed over the phone via structured interview by trained research assistants. In addition, participants were screened for dementia and mild cognitive impairment using the Dementia Rating Scale (Mattis, 1988; exclusion cutoff: < 125) and other neuropsychological testing. Participants who had more than 50% of their data “scrubbed,” as explained in the fMRI Data Preprocessing section, were eliminated from the analysis. A list of sample demographics and neuropsychological performance can be found in Table 1.

Table 1.

Participant Demographics (Upper Panel), Scrubbing Percentages (Middle Panel), and Descriptive Statistics for Neuropsychological Performance (Lower Panel), Divided by Age Group

	Younger (F =37)		Older (F = 35)
Demographics	Mean	SD	Mean	SD
Age	0.30	1.03	0.27	0.99
Education	−0.32	0.95	−0.23	1.02
NART	0.08	1.00	0.14	0.98
	Baseline (BL)		Follow-up (FU)
Scrubbing	Mean	SD	Mean	SD
Younger
Memory	3.03	3.87	3.98	6.44
FLUID	3.94	4.17	5.24	5.69
SPEED	2.76	3.25	4.08	4.76
VOCAB	6.81	6.89	6.10	6.42
Older
Memory	4.42	5.39	5.91	5.23
FLUID	7.02	6.78	8.94	6.57
SPEED	5.76	4.97	6.99	5.39
VOCAB	11.26	8.33	11.66	8.37
	Baseline (BL)		Follow-up (FU)		FU – BL
Behavior	Mean	SD	Mean	SD	Mean	SD
Younger
Memory	0.18	1.02	0.27	0.91	0.07	0.92
FLUID	0.16	0.98	0.26	0.98	0.09	0.91
SPEED	0.30	1.03	0.27	0.99	−0.03	0.82
VOCAB	−0.32	0.95	−0.23	1.02	0.04	0.73
Global cognition	0.08	1.00	0.14	0.98	0.04	0.84
Older
Memory	−0.17	0.94	−0.01	1.01	0.11	1.03
FLUID	−0.15	0.99	−0.31	0.99	−0.16	0.83
SPEED	−0.28	0.87	−0.60	0.84	−0.28	0.70
VOCAB	0.30	0.93	0.32	0.93	0.03	0.73
Global cognition	−0.08	0.93	−0.15	0.94	−0.08	0.82

Age groups were defined by median split (older group: ≥ 52 years). Only baseline values were considered for age, education, and NART. The number of female participants in each group is provided. Scrubbing is provided as mean, and standard deviation of percentage for volumes was replaced because of motion artifacts in each domain for each group. For the four domain behavioral outcomes and global cognition, the mean and standard deviation are presented as z scores averaged across participants and within domain. As a reminder, memory, FLUID, and VOCAB performance were based on accuracy; SPEED performance was based on RT and was sign-inverted to align with accuracy, where higher scores denote better performance.

Procedure

fMRI data were acquired from participants as they performed 12 computerized cognitive tasks in scanner, each relating to one of four reference abilities (RAs; Stern et al., 2014). Participants completed the battery of tasks over two sessions, each lasting for approximately 2 hr and containing six of the 12 tasks belonging to two of the four RAs. Tasks within each reference domain were presented in a fixed order, but the order of the two sessions was counter-balanced across participants. Before each scanning session, participants were familiarized with the six tasks relevant to the current session during an out-of-scanner training session, which was performed on a laptop computer. For all but one task, a keyboard button was pressed in response; the picture-naming task used an oral response. Training sessions were self-paced such that breaks could be taken when needed and participants were given the option of repeating the training session if desired. Participants also completed a neuropsychological battery in a separate session, but results from this battery will not be addressed in the current article.

Stimulus Presentation

Stimuli were back-projected onto an LCD monitor positioned at the end of the scanner bore. Participants viewed the screen via a tilted mirror system that was mounted on the head coil. When needed, vision was corrected-to-normal using MR-compatible glasses (manufactured by SafeVision, LLC). Responses were made on a LUMItouch response system (Photon Control Company). E-Prime v2.08, operating on PC platform, was used for stimulus delivery and data collection. Task onset was electronically synchronized with the MRI acquisition device.

RA Tasks

Twelve cognitive tasks, each belonging to one of four reference domains, were presented in-scanner. A brief description of each task, divided by domain, is provided below (for a more thorough description, see Stern et al., 2014). For all tasks, with the exception of picture naming, responses were made via button press; picture naming, instead, required a vocal response. For MEM, fluid reasoning (FLUID), and vocabulary (VOCAB) domains, accuracy—measured as the proportion of correct trials to total trials included—was used as the behavior endpoint. For the SPEED domain, RT data were chosen for each task. For all tasks, anticipatory responses, with a RT greater than 200 msec, were considered as incorrect and eliminated from further analysis. For the remainder of the document, an abbreviated version for each RA will be used: MEM, FLUID, SPEED, and VOCAB. We also will interchangeably use the terms “domain” and “reference ability” to refer to our RAs.

MEM.

For all three MEM tasks, both study and test phases were scanned together and were not separated in the analysis. The percentage of correct trials served as the dependent variable. Three tasks were used to assess MEM. Logical memory: Participants were required to read a story scenario on a screen and answer multiple-choice questions regarding the content, choosing from four possible answers. Word order recognition: Participants were presented with a list of 12 words in a specific order in a study phase; during the test phase, they were presented with a probe word and four choice words below and asked to indicate which of the four choice words was presented subsequent to the probe. Paired associates: Participants were presented with a list of 12 word-pairs in a study phase; during the test phase, they were presented with a probe word and four choice words below and asked to select which word was previously paired with the probe word.

FLUID.

The percentage of correct trials served as the dependent variable. Three tasks were used to assess FLUID. Matrix reasoning (adapted from Raven, 1962): Participants were presented with a nine cell (3 × 3) matrix reflecting a particular pattern given by an unspecified rule, with the bottom right cell empty; participants had to choose between eight figures, selecting the figure that best completes the pattern. Letter sets (Ekstrom et al., 1976): Participants were presented with five sets of letters, four of which expressed a common rule; participants were asked to infer the rule and identify the letter set that deviates from it. Paper folding (Ekstrom et al., 1976): Participants were presented with a folded paper with a sequence of holes punched through it and had to choose between six options the configuration of holes on the paper when unfolded.

SPEED.

RT served as the dependent variable. Three tasks were used to assess SPEED. Digit symbol (adapted from Salthouse, 1998): Participants were presented with a code key of nine number–symbol pairs and asked to indicate if a probe number–symbol pair presented below it was present in the code key. Letter comparison (Salthouse & Babcock, 1991): Participants were presented with two strings of three to five letters each and asked to indicate whether the strings were the same or different. Pattern comparison (Salthouse & Babcock, 1991): Participants were presented with two figures, each containing lines connected in different configurations, and were asked to indicate whether the figures were the same or different.

VOCAB.

The percentage of correct trials served as the dependent variable. Three tasks were used to assess VOCAB: antonyms (Salthouse & Kersten, 1993): Participants were asked to indicate which of four choice words was most dissimilar to a probe word. Picture naming (images selected from the WJ-R Psycho-Educational battery; Salthouse, 1998; Woodcock, Johnson, & Mather, 1989): Participants were asked to identify a picture by vocal response. Synonyms (Salthouse & Kersten, 1993): Participants were asked to indicate which of four choice words was most similar to a probe word.

fMRI Data Acquisition

Image acquisition was performed using a 3 T Philips Achieva Magnet. The full 12 fMRI task battery was conducted over two, 2-hr MR imaging sessions. At each session, a scout, T1-weighted image was acquired to determine participant position. Participants underwent a T1-weighted magnetization prepared rapid gradient echo scan to determine brain structure, with a echo time/repetition time (TR) of 3/6.5 msec and flip angle of 8°, in-plane resolution of 256 × 256, field of view of 25.4 × 25.4 cm, and 165–180 slices in axial direction with slice-thickness/gap of 1/0 mm. All scans used a 240-mm field of view. T1 image segmentation was performed using FreeSurfer (Fischl et al., 2002; Dale, Fischl, & Sereno, 1999). Each image was visually inspected to identify potential errors. For the EPI acquisition, the parameters were: echo time/TR (msec) = 20/2000; flip angle = 72°; in-plane resolution (voxels) = 112 × 112; slice thickness/gap (mm) = 3/0; slices = 41. Each participant’s scan was reviewed by a neuroradiologist; any observed abnormality was communicated to the participant’s primary care physician.

fMRI Data Processing and Functional Connectivity

Images were preprocessed using an in-house developed native space method implemented in FMRIB Software Library (Razlighi et al., 2014). In brief, the preprocessing pipeline included: slice-timing correction and motion correction (MCFLIRT; Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012; Jenkinson, Bannister, Brady, & Smith, 2002); frame-wise displacement (FWD), as described in Power et al. (2012), calculated from the six motion parameters; contaminated volume identification (FWD > 0.5 mm and root mean square difference > 0.3%) and replacement by linear interpolation, before temporal filtering (Carp, 2013); temporal band-pass filtering (0.01 < f < 0.09 Hz) of the motion-corrected signal using Flsmaths–bptf (Jenkinson et al., 2002); residualization of the processed data by regressing out the FWD; root mean square difference; left and right hemisphere white matter; and lateral ventricular signals (Birn, Diamond, Smith, & Bandettini, 2006). T1 image segmentation was performed using FreeSurfer (Fischl, van der Kouwe et al., 2004; Fischl, Salat, et al., 2002; Dale et al., 1999). The coordinates of 264 putative functional nodes derived by Power et al. (2011) were transferred to each participant’s space via nonlinear registration of the participant’s structural scan to the Montreal Neurological Institute template using the ANTS software package. Next, a 10-mm radius spherical mask, centered at each transferred coordinate, was generated and intersected with the FreeSurfer gray matter mask to obtain the ROI mask for the 264 functional nodes. An intermodal, intraparticipant, rigid-body registration of fMRI reference image and T1 scan was performed with FLIRT with 6 degrees of freedom, normalized mutual information as the cost function (Jenkinson & Smith, 2001), and used to transfer all ROI masks from T1 space to fMRI space. These transferred ROI masks were then used to average all the voxels within each mask to obtain a single fMRI time-series for each node. Pearson correlations were then performed for all pairwise combinations. This resulted in 264 × 263/2 = 34,716 fMRI connectivity pairs, or the upper triangle of the 264 × 264 node correlation matrix.

The length of the time-series, concatenated across TRs (1 TR = 2000 msec), varied for each task because of task constraints. The number of TRs per task was as follows: MEM: Log_Mem—210, Word_Order—208, Pair_Assoc—99; FLUID: Mat_Reason—430, Letter_Sets—430, Paper_Fold—430; SPEED: Digit_Sym—210, Letter_Comp—195, Pattern_Comp—190; VOCAB: Antonyms—194, Pic_Name—190, Synonyms—194.

Analytical Approach

Data were analyzed using custom-written MATLAB codes (MathWorks). FC correlation values (r) between nodes were converted to Z coefficients using Fisher’s transformation (i.e., inverse tangent of r).

To standardize comparisons between tasks and time points, behavioral scores at each time point were z-transformed using the mean and standard deviation calculated across all participants, for each task separately, at baseline. Given that speed tasks were measured as RT, z-score values were sign-inverted to correspond with accuracy scores, with higher scores always indicating better performance. When treating regressions of longitudinal change, both behavioral and neural factors with measurements considered at both time points were residualized with respect to baseline values.

CV

CV calculation.

We employed a measure of CV that was previously described in Argiris et al. (2021) and followed a procedure similar to that of Habeck et al. (2015). For the detailed analytic procedure, see Argiris et al. (2021). In brief, we reasoned that when both behavioral and neural data reliably pertains to a specific underlying cognitive construct, they should display both high convergent and discriminant validity; that is, tasks belonging to the same domain should be more similar than tasks belonging to different domains, respectively. To test this assumption, we calculated the within-domain (convergent) and between-domains (discriminant) task correlations for each task pairing for both the behavioral and neural data, averaging correlation values across all convergent versus discriminant validity task pairings. Both high convergent validity (i.e., high correlation across within-domain tasks) and high discriminant validity (i.e., low correlation across between-domains tasks) should be present when evaluating the relatability of measures to a given underlying construct (see schematic above). To clarify, the precise quantification of discriminant validity is the negative sign of the between-domains task correlations, but taking its absolute value achieves the same computation and renders the true correlation among tasks more interpretable. We then computed the overall CV as the difference between the mean Fisher’s $Z$ correlation (i.e., ${\widehat{Z}}_{\text{within}}$) for all within-domain task pairings and the mean Fisher’s $Z$ correlation for all between-domains task pairings (i.e., ${\widehat{Z}}_{\text{between}}$), where $CV={\widehat{Z}}_{\text{within}}-{\widehat{Z}}_{\text{between}}$. We only considered between-domains task pairings belonging to the same testing sessions to eliminate the possibility of session effects inflating differences between validity measures. It also rendered a comparison between ${\widehat{Z}}_{\text{within}}$ (= 12 task pairings) and ${\widehat{Z}}_{\text{between}}$ (= 18 same session task pairings) more commensurate.

CV can be computed across participants or within participants. For across-participant calculations, CV was first calculated across the entire sample to compare results with the findings previously reported in Argiris et al. (2021). To test for potential age effects, we then repeated the analyses using a median age split (median age = 52 years), dividing our sample into two groups, younger (> 52 years) and older (≥ 52 years) adults. As a sensitivity analysis, we also repeated this procedure using two additional cutoffs around the median (i.e., 50 years and 55 years of age). In anticipation of our findings, the results withheld in both cases.

For behavioral CV, convergent and discriminant validity were limited to across participant calculations. For neural CV, convergent and discriminant validity were computed at both the individual participant level (i.e., correlations between each task pairing were performed across the FC connectome, then averaged within validity type) and across participants (i.e., the mean across all participants for each task pairing, then averaged within validity type). More specifically, for each participant, correlations were performed across all connectivity pairs (= 34,716) that formed the upper triangle of the 264 × 264 nodal correlation matrix, between each task pairing. Convergent validity was then computed as the mean correlation across within-domain task pairings (= 12) and discriminant validity as the mean correlation across same session between-domains task pairings (= 18), yielding two values per participant on which to compute CV. For across participant calculations, the mean across all participants for each task pairing were first calculated; then, the within- versus same-session between-domains means were calculated. Finally, CV was computed as the difference between the two. For longitudinal CV, the difference between follow-up (FU) and baseline (BL) was defined as CV_FU − CV_BL = ΔCV.

CV significance testing.

Across-participant CV significance was assessed via permutation testing. For across participant correlation where only a single value of CV was possible cross-sectionally, within- and between-tasks correlation values were permuted to disrupt label assignment and a null distribution created based on this randomized computation of CV values from the permuted “convergent” and “discriminant” validity vectors. For longitudinal CV significance, convergent and divergent validity values were first randomly shuffled across time points, maintaining validity label assignment but disrupting the time label assignment. CV at each time point was then calculated and subsequently, ΔCV as defined above. Significance was assessed as the ratio between the number of times the absolute value of the null distribution (to account for both tails) generated a difference (i.e., cross-sectionally: convergent – divergent; longitudinally: CV_FU − CV_BL) greater than the one observed in the data divided by the number of permutations (= 10,000). We additionally investigated the correlation between behavioral and neural validity measures, looking at convergent validity and discriminant validity separately. This was motivated by an interest to see which measure could be driving potential differences in CV (see schematic above). We assessed significance by randomly permuting the neural validity vector and testing its correlation with the behavioral validity vector, where we calculated the number of times the absolute value of the null distribution was greater than the real correlation value, divided by the number of permutations (= 10,000). Given the repeated nature of the longitudinal design, we additionally tested for behavioral repetition effects by comparing a subsample of age-matched participants at follow-up to baseline-replacement individuals, tested at the follow-up period, without prior exposure to the testing battery. We computed within- and between-tasks correlation values independently for each group then conducted permutation testing (= 10,000 permutations) by randomly swapping correlation values to disrupt group affiliation over 10,000 permutations. We observed no statistically significant difference in CV between individuals exposed to the task only at follow-up versus at both time points (p = .585).

For neural CV calculated within participant, a one-way t test was performed for both cross-sectional and longitudinal analyses to test the likelihood of observed data occurring by chance alone. For cross-sectional analysis, permutation testing was employed by randomly swapping the mean convergent and divergent validity scores within participants, calculating the difference (CV measure), and performing a one-way t test to generate a null distribution of t-statistic. For longitudinal analysis, permutation testing was employed by randomly swapping the calculated CV values between time points, disrupting time label assignment, and regressing out the “baseline” vector from the difference calculation. Significance was assessed as the ratio between the number of times the absolute value of the null t-distribution generated a t-statistic greater than the one observed from the data, divided by the number of permutations (= 10,000).

Linear Regression

Neural CV.

We first explored the simple relationship between age and neural CV, both cross-sectionally and longitudinally, without controlling for other baseline factors. We then created a full longitudinal model, regressing longitudinal change in neural CV (Δneural CV) on baseline factors—age, the National Adult Reading Test (NART), a widely used measure of premorbid intelligence, sex, and education.

Global cognition.

A composite variable—global cognition (i.e., G) —was created from the z-transformed behavioral performance measures across all tasks. Global cognition was calculated as the mean difference in behavioral performance across all 12 tasks at each time point. In the case of longitudinal change in global cognition (i.e., ΔG), a change score was calculated by first subtracting baseline from follow-up for each task and then residualizing out task-level baseline performance before calculating the mean change. A linear regression model was then used to explore potential factors explaining change in global cognition. We analyzed the effect of baseline factors in addition to Δneural CV on ΔG.

Mediation Model

We additionally wanted to examine a potential longitudinal mediating role of Δneural CV on the relationship between age and ΔG using regression analysis (Baron & Kenny, 1986). We implemented a three-step bootstrapping process following the percentile method (Preacher & Kelley, 2011). Sex, education, and NART were included as covariates in each model. First, we regressed age on Δneural CV to ensure a significant main effect was present; second, we regressed age on ΔG, while controlling for the effect of Δneural CV; third, we simulated a comparison between these two regression models over multiple iterations (= 10,000) using a nonparametric bootstrapping of random samples (with replacement) approach to test the significance of the indirect effect of Δneural CV on the relationship between age and ΔG. The results yielded point estimates for indirect, direct, and total effects in addition to the proportion of mediation, along with confidence intervals to ascertain significance.

RESULTS

Behavioral CV

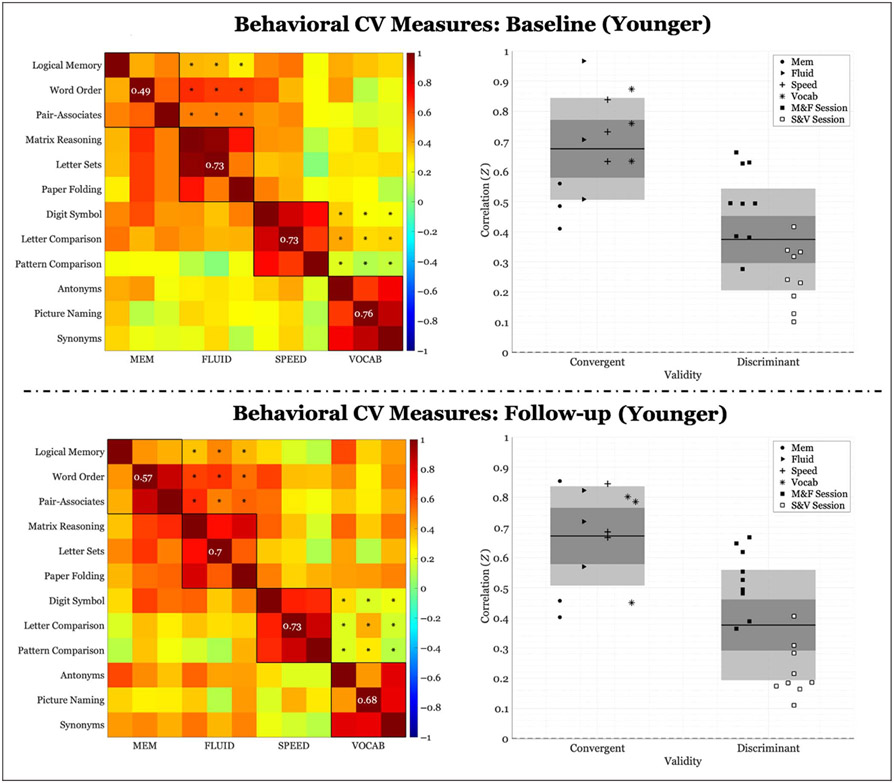
Both cross-sectional and longitudinal results are presented for the behavioral CV measure. Even in the more restrictive longitudinal sample, our results mirrored cross-sectional findings from our previous article. Cross-sectional behavioral CV at baseline was .418 (convergent validity: .664 ± .167; discriminant validity: .246 ± .209). Cross-sectional behavioral CV at follow-up was .423 (convergent validity: .66 ± .194; discriminant validity: .246 ± .225). Permutation testing revealed that behavioral CV was significantly different from chance (p < .001) at both time points. Longitudinal change in behavioral CV was.004 (Δconvergent validity: −.004 ± .1; Δdiscriminant validity: −.008 ± .11) and was not significant (p = .907).

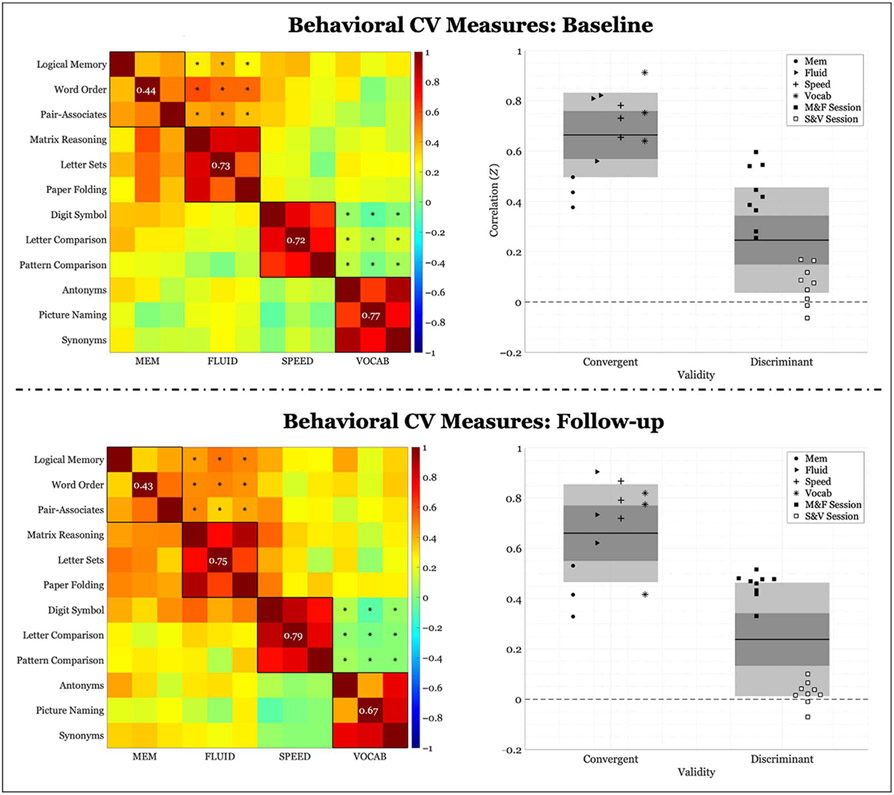
Cross-sectional correlation block matrices for the full sample and corresponding scatter plots are presented in Figure 1. As can be observed from the figure, FLUID, SPEED, and VOCAB displayed notably higher within-domain correlation than between-domains correlation, whereas MEM displayed convergent validity not appreciably different from discriminant validity.

Figure 1.

Behavioral correlations of within-domain (convergent) versus between-domains (discriminant) task performance. Left column: Fisher’s Z correlation matrix of all behavioral task pairings. Black outlined boxes indicate within-domain tasks. Centered values within each square indicate the average within-task correlation not considering a task’s perfect correlation with itself. Asterisks represent the between-tasks correlations used to compute discriminant validity, where only same session tasks were considered. Right column: scatter plots of Fisher’s Z coefficients divided by task pairing. For convergent validity, correlation coefficients are organized by domain; for discriminant validity, correlation coefficients are organized by the session from which they were calculated (see legend). “M&F” indicates between-domains correlations for memory and FLUID, and “S&V” indicates between-domains correlations for speed and VOCAB. The expanse of the box represents 1 SD, the shaded middle region represents the SEM for the 95% confidence interval, and the black line represents the mean.

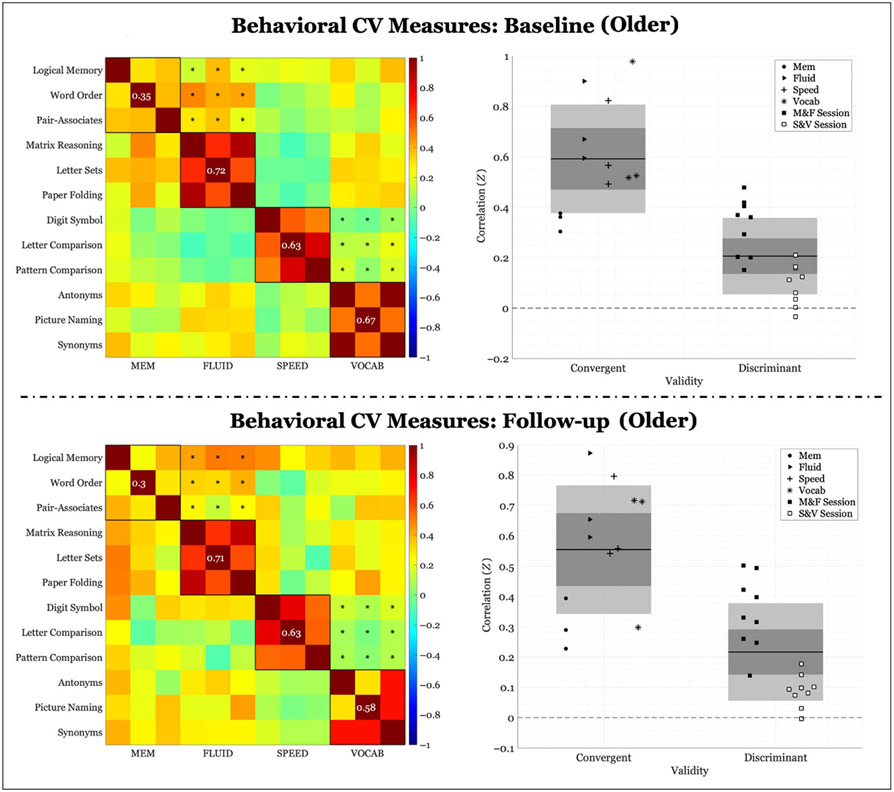
When looking at the median age split, we observed a similar pattern at both time points, irrespective of age group. Cross-sectional behavioral CV for the younger group was .301 at baseline (convergent validity: .676 ± .169; discriminant validity: .375 ± .168) and .295 at follow-up (convergent validity: .672 ± .164; discriminant validity: .376 ± .182). Cross-sectional behavioral CV for the older group was.386 at baseline (convergent validity: .592 ± .215; discriminant validity: .206 ± .151) and .338 at follow-up (convergent validity: .555 ± .211; discriminant validity: .217 ± .160). Permutation testing revealed that behavioral CV was significantly different from chance at both time points, for both age groups (p < .001). In addition, when we compared the CV in the younger group to that of the older group, the older group displayed significantly higher CV than the younger group at both time points (baseline: p < .001; follow-up: p = .005).

Longitudinal change in behavioral CV was insignificant for both the younger group (ΔCV: −.005, p = .918; Δconvergent validity: −.004 ± .162; Δdiscriminant validity: .002 ± .108) as well as the older group (ΔCV: −.005, p = .396; Δconvergent validity: −.037 ± .158; Δdiscriminant validity: .011 ± .143). Plots of results for the age group division are presented in Appendices A and B. In addition, the relative change in CV between groups was not significant (p = .613).

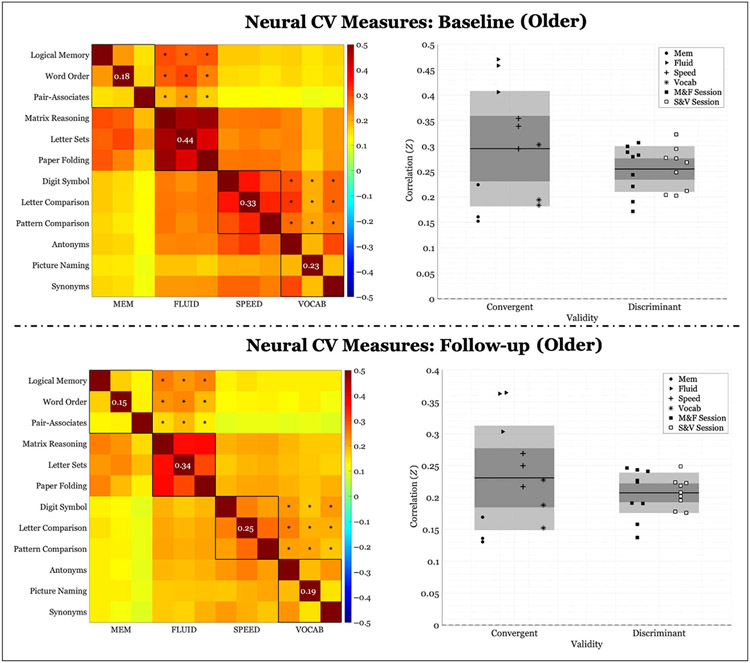
Neural CV

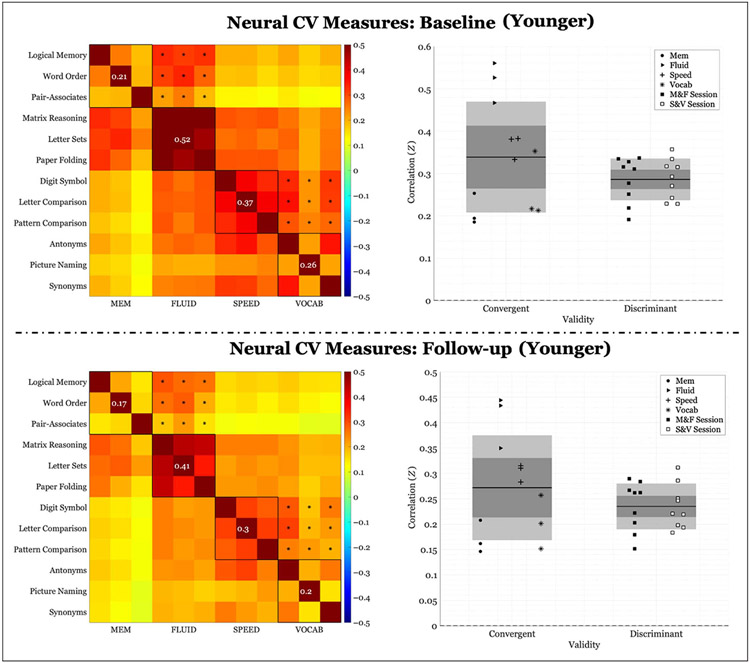
Across-participant Measurement

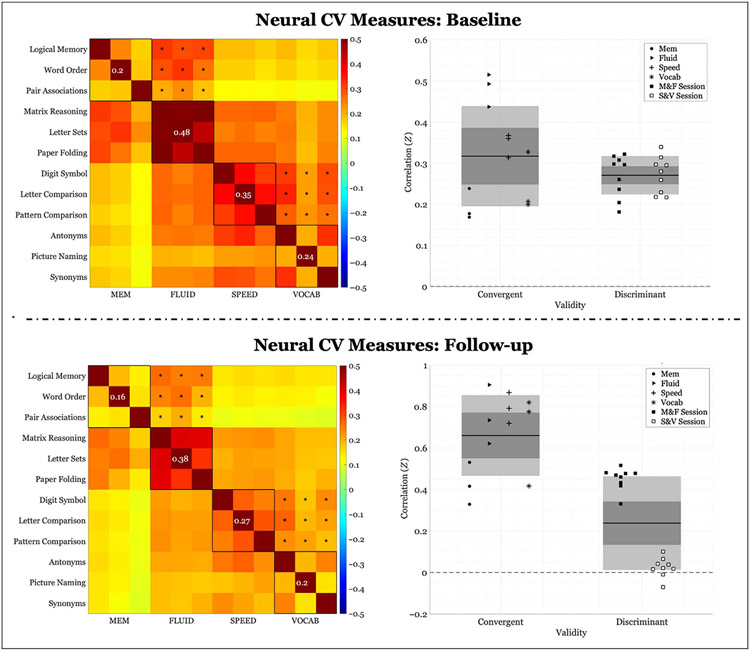
Both cross-sectional and longitudinal results are also presented for the neural CV measure. Cross-sectional neural CV, calculated across participant, at baseline was .046 (convergent validity: .317 ± .122; discriminant validity: .271 ± .047). Permutation testing revealed a CV measure that was not significantly different from chance (p = .149). Cross-sectional neural CV at follow-up was.03 (convergent validity: .251 ± .092; discriminant validity: .221 ± .038). Permutation testing revealed that neural CV was not significantly different from chance (baseline: p = .149; follow-up: p = .223) at neither time point. Correlation block matrices of all correlations and corresponding scatter plots can be found in Figure 2. Convergent validity was notably lower for the neural compared with the behavioral data, resulting in reductions in CV at both time points. The FLUID domain demonstrated the highest convergent validity of all domains, along with a comparably lower discriminant validity. Longitudinal change in neural CV was −.016 (Δconvergent validity: −.066 ± .033; Δdiscriminant validity: −.05 ± .017) and was not significant (p = .509); however, permutation testing revealed that convergent and discriminant validity, independently, significantly decreased over time (p < .001).

Figure 2.

Neural correlations of within-domain (convergent) versus between-domains (discriminant) task performance averaged across participants. Left column: Fisher’s Z correlation matrix of all task pairings of FC values. Black outlined boxes indicate within-domain tasks. Centered values within each square indicate the average within-task correlation not considering a task’s perfect correlation with itself. Asterisks represent the between-tasks correlations used to compute discriminant validity, where only same session tasks were considered. Right column: scatter plots of Fisher’s Z coefficients divided by task pairing. For convergent validity, correlation coefficients are organized by domain; for discriminant validity, correlation coefficients are organized by the session from which they were calculated (see legend). “M&F” indicates between-domains correlations for memory and FLUID, and “S&V” indicates between-domains correlations for speed and VOCAB. The expanse of the box represents 1 SD, the shaded middle region represents the SEM for the 95% confidence interval, and the black line represents the mean.

Again, when looking at the median age split, we observed a similar pattern at both time points for both age groups. Cross-sectional neural CV for the younger group was .053 at baseline (convergent validity: .339 ± .131; discriminant validity: .286 ± .049) and .037 at follow-up (convergent validity: .272 ± .103; discriminant validity: .235 ± .045). Permutation test indicated that it was insignificant at both baseline (p = .129) and follow-up (p = .190). Cross-sectional neural CV for the older group was .040 at baseline (convergent validity: .295 ± .113; discriminant validity: .255 ± .045) and.023 at follow-up (convergent validity: .231 ± .082; discriminant validity: .207 ± .031). Again, neural CV was insignificant at both baseline (p = .182) and follow-up (p = .278). In addition, when we compared the neural CV between groups, there was no significant difference (baseline: p = .435; follow-up: p = .409).

Longitudinal change in neural CV was insignificant for both the younger group (ΔCV: −.016, p = .535; Δconvergent validity: −.067 ± .034; Δdiscriminant validity: −.051 ± .018) as well as the older group (ΔCV: −.012, p = .495; Δconvergent validity: −.064 ± .035; Δdiscriminant validity: −.047 ± .021). Plots of results for the age group division are presented in Appendices C and D. Moreover, the relative longitudinal change between groups was not significant (p = .904).

Within-participant Measurement

For neural CV calculated at the within-participant level, we also tested whether the CV measure calculated per participant was significantly different from chance, both cross-sectionally and longitudinally.

Cross-sectional validity.

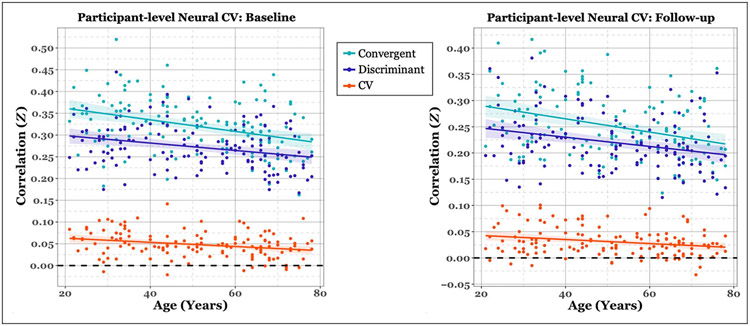
Cross-sectional permutation testing revealed that this was indeed the case at both time points (baseline: p < .001; follow-up: p = .002). Of the 135 participants in our sample, 127 demonstrated convergent validity that was higher than discriminant validity at baseline and 122 at follow-up. Importantly, we were also interested in testing the relationship between neural CV and age. Permutation testing of the Fisher z-transformed Pearson’s correlation revealed significant negative correlations with age at both time points (baseline: Z = −.36, p = .001; follow-up: Z = −.24, p = .005). Figure 3 illustrates the participant-level validity measures plotted against age for each time point. We can observe from the figure that convergent validity displayed a stronger age-related decline compared with discriminant validity in contributing to age-related decreases in CV, although a z test to assess significance between the two correlations was not significant (baseline: Z_diff = .75, p = .45; follow-up: Z_diff = .64, p = .52).

Figure 3.

Scatter plot of cross-sectional neural validity measures for each time point. Validity measures are plotted per participant as a function of baseline age. Colored lines represent the least-squares fit per measure. Colored ribbons represent the standard error around the mean. As can be observed, there is a negative relationship between validity measures and age.

Longitudinal validity.

Critically, we investigated whether neural CV significantly changes over time and potential age-related associations. To do this, we regressed out baseline validity measures from each difference calculation (FU – BL). Longitudinal permutation testing indicated that Δconvergent (p < .001), Δdiscriminant (p < .001), and ΔCV (p < .001) all displayed a significant decrease over time.

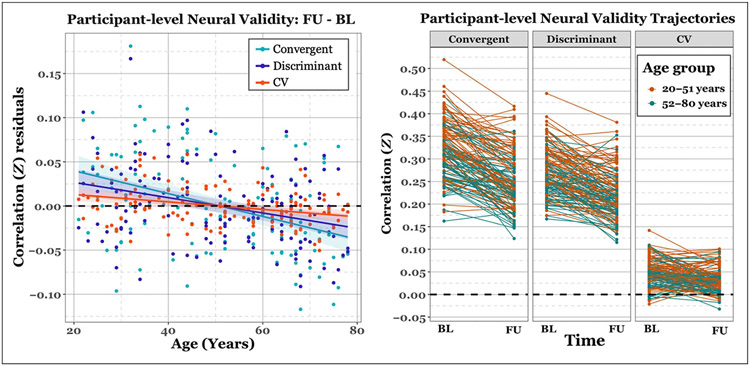
Permutation testing of the Pearson’s correlation revealed a significant negative correlation between age and Δconvergent (p = .001), Δdiscriminant (p < .001), and ΔCV (p = .001), where age-related differences in the linear rate of change over time indicated a disproportionate decrease in validity with advancing age. Figure 4 demonstrates the participant-level changes in neural convergent, discriminant, and CV measures and their negative relationship with age.

Figure 4.

Plots of longitudinal neural validity measures. Left column: Scatter plot of the difference in validity measures (FU – BL) per participant as a function of baseline age and reflect the residuals after adjusting for baseline values. Colored lines represent the least-squares fit per measure. Colored ribbons represent the standard error around the mean. As can be observed, there is a negative relationship between age and longitudinal change in each validity measure. Right panel: spaghetti plot of participant-level trajectories between each time point. Plots are divided by validity type. Colored lines and dots represent the age group to which each participant belongs based on median age split.

Longitudinal Multiple Linear Regression of Change

We employed multiple linear regression analysis to test which variables best predict longitudinal change in participant-level neural CV and global cognition.

Longitudinal Neural CV

Linear regression analysis revealed a significant regression, F(4, 123) = 5.192, p < .001, f² = .132 with an adjusted R² of .117 (see Table 2 for a list of model parameters). Age significantly predicted Δneural CV, and there was a marginal effect of NART IQ.

Table 2.

Model Parameters for Linear Regression Analysis

Outcome Variable	Independent Variable	β	P	CI	${\eta }_{\mathrm{p}}^2$
ΔNeural CV
	Age***	−.387	<.001	[−0.012, 0.005]	.130
	Sex	−.127	.145	[−0.013, 0.002]	.017
	NART†	.193	.058	[−0.0001, 0.009]	.029
	Edu	−.024	.793	[−0.002, 0.002]	.001
ΔG
	Age***	−.420	<.001	[−0.021, 0.009]	.186
	ΔNeural CV*	.158	.035	[0.312, 8.151]	.036
	NART***	.432	<.001	[0.020, 0.042]	.179
	Sex	−.048	.504	[−0.223, 0.110]	.004
	Education*	.190	.014	[0.010, 0.088]	.048

Sex was coded as 0 for male and 1 for female participant. ΔG represents global cognition, or the average z scores across the 12 cognitive tasks. β = Standardized coefficient beta; p = p value (uncorrected); CI = 95% confidence interval; ${\eta }_{\mathrm{p}}^2$ = partial eta-squared effect size.

^†p < .1.

^*p < .05.

^**p < .01.

^***p < .001.

Longitudinal Global Cognition

Linear regression analysis revealed a significant regression, F(5, 122) = 5.192, p < .001, f² = .682 with an adjusted R² of .405 (see Table 2 for a list of model parameters). Age, Δneural CV, NART IQ, and education significantly predicted ΔG. Figure 5 provides a scatter plot of the relationship between ΔG, Δneural CV, and age.

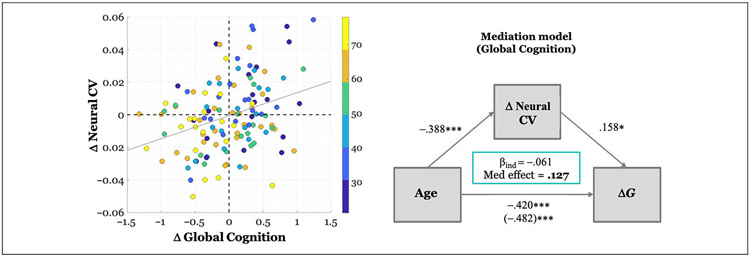
Figure 5.

Relationship between baseline age, ΔNeural CV, and change in Global Cognition (ΔG). Left column: scatter plot where each dot represents participant’s Δneural CV and ΔG value. The color of the dot depicts the age band to which the participant belongs. ΔG values have been adjusted for baseline behavior, NART, education, and sex and thus represent the raw residuals after this adjustment. Δ neural CV values have been adjusted for baseline CV. The gray line represents the least-squares fit (β = .242). Right column: Mediation model illustrating model parameters. The model has been adjusted for NART, education, and sex. Values along arrows represent standardized beta coefficients for the indirect and direct effects. The total effect of age on ΔG, after covariate adjustment and with or without mediator inclusion, respectively, is represented in parentheses. The beta coefficient for the indirect mediating effect of ΔG (i.e., β_ind) as well as the proportion of the effect that is mediated is reported in the green box.

Longitudinal ΔNeural CV as Mediator

As a final analysis, prompted by the observed negative association between ΔCV and age, coupled with the positive association between Δneural CV and ΔG, we explored a post hoc potential mediating role of Δneural CV in the age–cognition relationship. We observed a significant indirect mediation effect of Δneural CV (average causal mediation effects = −.0022, CI = [−.0048, −.0002], p = .028) with a significant direct effect of age on ΔG (average direct effects = −.015, CI = [−.021, −.009], p < .001), indicating a negative partial mediation of Δneural CV on the effect of age on ΔG. This finding indicates that advancing age leads to a disproportionate decrease in neural CV over time, which, in turn, leads to a greater reduction in global cognition. The proportion of mediation relative to the total effect was 0.127 (C1 = [0.012, 0.294], p = .028). Figure 5 provides a schematic of the mediation model parameters.

DISCUSSION

In the present study, we tested a lifespan cohort on in-scanner fMRI tasks tapping into four cognitive domains, at both baseline and 5-year follow-up. We sought to investigate both cross-sectional consistency in behavioral and neural CV measures, as previously reported in Argiris et al. (2021), in addition to longitudinal associations in neural CV. Specifically, we examined age-related changes in task-based neural specificity using whole-brain connectivity, assessing how individual-level change in neural correlations impact the change in cognition over time.

Behavioral CV, calculated cross-sectionally across participants, was significant at both time points, displaying a high level of consistency even over a 5-year interval. This finding confirms the high interrelatedness between tasks that tap into the same underlying cognitive ability (Habeck et al., 2015; Salthouse & Ferrer-Caja, 2003). Notably, when we split participants by median age, both younger and older participants displayed a similar pattern of results, contrary to the notion of dedifferentiation, or higher interability correlation, that accompanies the aging process (cf. de Frias et al., 2007; Li et al., 2004). Although several behavioral studies have supported such a hypothesis, others have indeed challenged its reliability. Some research has reported stability, from childhood into old age, in correlation across cognitive tests (Bickley, Keith, & Wolfle, 1995), a finding supported by both cross-sectional and longitudinal analysis (Anstey et al., 2003). Moreover, Tucker-Drob and Salthouse (2008) reported even greater distinctiveness, or reduction in correlation, among older adults. Our study has shown that older adults maintain significantly high levels of CV, indicated by lower interability task correlations and relatively higher intra-ability task correlations, corroborating findings that contrast a dedifferentiation hypothesis. This was further supported by a relative comparison of CV between groups, which indicated that older adults displayed higher CV—driven by higher discriminant validity—suggesting age-related reductions in interability correlations. Longitudinal analysis, however, did not reveal significant changes in CV itself over time, neither across the whole sample nor at the group level.

Although neural CV was not significant neither when calculated across the sample nor at the age-group level, FLUID appeared to consistently display the highest convergent validity. One reason for this finding could be the distributed nature of the networks underlying intelligence (Colom, Karama, Jung, & Haier, 2010), with FLUID tasks tapping into a general mental ability. Given that fluid ability has been mapped to distributed functional architectures across frontoparietal, temporal, and limbic systems (Barbey et al., 2014), and that neural CV was calculated in an omnibus manner utilizing the whole brain connectome, it perhaps makes sense that is should display the strongest within-domain connectivity. The memory domain, on the other hand, displayed the lowest within-domain task correlations at both the behavioral and neural levels, irrespective of age group. One explanation for low validity could be that memory can be fractionated into sub-processes such as encoding, maintenance, and retrieval, which were not partitioned out in our task design; in this case, the interaction between these subsystems could have been differentially impacted by the task, resulting in low whole-brain coherence across tasks. Furthermore, recent work in precision fMRI has argued for individual-specific network configurations for memory-related brain systems (Gilmore, Nelson, & McDermott, 2021), which may have been diluted in across-participant calculations.

When we calculated neural CV at the individual-participant level, however, we observed significant age-related reductions at both baseline and follow-up, again mirroring cross-sectional findings at baseline in the full sample (see Argiris et al., 2021). As can be observed in Figure 3, this decrease in CV with increasing age manifested as a greater decline in convergent validity, or a decrease in within-domain task correlations. Integrally, longitudinal analysis of age-related change over time indicated a disproportionate decrease in CV with advancing age that was driven by steeper declines in convergent validity (see Figure 4). These findings strongly support a hypothesis alternative to that of dedifferentiation, whereby cognitive and brain variables become more, and not less, independent with age, because of decreases in structural or functional connectivity (i.e., St. Jacques, Dolcos, & Cabeza, 2009; O’Sullivan et al., 2001), potentially producing weaker interrelations among tasks. Linear regression analysis revealed that age yielded the strongest effect on longitudinal change in neural CV; NART IQ displayed a marginal positive effect, with higher baseline IQ related to higher values of CV over time. This higher integrity at the latent construct level, as represented here by higher CV, tentatively associated with both higher IQ and better global cognition, potentially suggesting that higher IQ might facilitate the link between better cognition and domain-related neural specificity; moreover, high CV was largely driven by the FLUID domain. Much debate has surrounded the associations between crystallized intelligence (e.g., NART IQ) and fluid intelligence, for example, when considering the moderating factors of age and general ability level (e.g., Hartung et al., 2018); it is thus necessary to further explore how these factors interact with neural substrates.

The dedifferentiation hypothesis has been tackled from various analytic points. From the conventional massunivariate task activation perspective, dedifferentiation has manifested as age-related reductions in the distinctiveness of distributed cortical patterns of activation to specific categorical stimuli (Goh, Suzuki, & Park, 2010; Voss et al., 2008; Park et al., 2004). From the functional connectivity perspective, some have argued that dedifferentiation presents itself as a loss of functional network specialization, defined by a decrease in within-network connectivity and simultaneous increase in between-networks connectivity (e.g., Malagurski et al., 2020). Zhang et al. (2021) found higher between-networks resting-state functional connectivity in older adults, which was additionally linked to poorer language ability. On the other hand, lower within-network connectivity alone is denoted by a decrease in correlation between regions once engaged in synchronized activity, which itself has additionally been linked to lower cognition (Chan, Park, Savalia, Petersen, & Wig, 2014). In the present study, we utilized whole-brain connectivity, irrespective of network affiliation, to analyze the fidelity of the functional neural response to domain-specific tasks. Rather than observe an age-related increase in whole-brain connectivity because of reduced neural specialization, we observed an age-related decrease in connectivity, both cross-sectionally and longitudinally, with reductions in CV being driven primarily by disproportionate decrease with advancing age of within-domain task correlations. We argue that these whole-brain correlation reductions better fit a disintegration hypothesis of cognitive aging (Salthouse, 2012), where weakened connectivity may contribute to disruptions in information processing and communication within the brain. Disintegration has been characterized as a breakdown in the intrinsic connectivity within networks (Warren, Rohrer, & Hardy, 2012) observed in resting-state functional connectivity and linked to pathology such as neurodegeneration (Zhou et al., 2010).

Few studies have investigated dedifferentiation in a longitudinal cohort and relate network activation to cognition. Malagurski et al. (2020) utilized longitudinal resting state to test for network-level segregation effects and its relationship to cognition in healthy older adults. They observed age-related declines in functional segregation that was linked to reduced cognition in SPEED, verbal learning, and verbal memory, arguing for functional dedifferentiation of associative resting state networks. Other longitudinal studies have focused on network-level integration, observing age-related global declines in both segregation and integration of functional networks, with cross-sectional links to poorer cognitive performance (Chong et al., 2019). Other research has observed a non-linear trajectory of within-network functional connectivity, where both network-specific (i.e., default mode network) and whole-brain functional connectivity may actually increase early in the aging process, which is then followed by rapid declines in old age; in addition, intraindividual change in within-default mode network connectivity was positively linked to change in MEM (Staffaroni et al., 2018). Here, we observed that longitudinal reductions in neural CV was also linked to longitudinal declines in global cognition. Linear regression analysis revealed that longitudinal change in global cognition was best predicted by age, change in neural CV, NART IQ, and education. Moreover, longitudinal mediation analysis further revealed that age-related change in global cognition was partially negatively mediated by change in neural CV, where greater age-related reductions in neural CV were linked to greater declines in global cognition. This finding emphasizes a potential mechanistic pathway that underlies age-related changes in cognition and underscores a potential causal link in the aging process. Notably, this negative mediation was also mirrored in the cross-sectional sample reported in prior work (i.e., Argiris et al., 2021), not only signifying a robustness in the stability of the pattern, but extends beyond static associations to capturing a dynamic relationship between rates of change in both brain and behavior. Cross-sectional mediation analysis has typically come under scrutiny for generating biased estimates of longitudinal parameters, with advocacy for longitudinal designs to capture within-person processes in age-related outcomes (Hofer & Piccinin, 2010; Maxwell & Cole, 2007).

Our study is not without limitations. First, the sample size of our longitudinal sample is modest. However, the fact that cross-sectional analyses in the more restricted longitudinal sample mirrored those of the more inclusive cross-sectional sample utilized in our prior study mitigates this concern. Furthermore, our number of comparisons was relatively small, and we used permutation testing to assess significance. Another limitation is that the derivation of our CV measure is metric-specific. Here, we used Pearson’s correlation as our metric of similarity; however, it is conceivable that a different metric selection could have yielded a different validity outcome. Finally, our CV metric was derived at the whole-brain level and not localized to any specific region where specialization of function in task engagement might be considered. Our aim was to circumvent network affiliation of our parcellation scheme and to consider whole-brain “coherence” among tasks pertaining to the same versus different cognitive domain. However, we acknowledge that neural specificity of function has oftentimes been examined in terms of activation in differentiated brain areas or orchestrated connectivity within specific brain networks. Here, we began from the premise that discerning between hypotheses of dedifferentiation/disintegration at the latent construct level would involve looking at the way in which whole-brain similarity between within-domain and between-domains tasks changes with age. If correlations among between-domains tasks were to have increased because of loss of neural specificity, resulting in lower CV, we would have taken this to align more with a hypothesis of dedifferentiation; if correlations among within-domain tasks were to have decreased because of loss of specificity, we would have considered this a breakdown in the once orchestrated neural activity pertinent to domain-specific processing, and thus reflecting disintegration. Dedifferentiation has been investigated from a number of different perspectives (see Koen & Rugg, 2019), so we feel it is both necessary and sufficient to have laid out the rationale, definitions, and analytic decisions taken here.

In the current work, we replicated findings from our prior work investigating the dedifferentiation hypothesis in a cross-sectional sample, extending those findings to the longitudinal domain. We found consistently high behavioral CV, particularly among older adults, with no evidence for longitudinal age-related decline. We did observe though individual-level differences in neural CV both cross-sectionally and longitudinally, where age-related declines were linked to declines in global cognition; moreover, neural CV mediated the effect of age on cognitive decline. In summary, cross-sectional replication at two time points and longitudinal declines in neural CV support a theory of disintegration with age and provide an important link between cognitive functioning and underlying neural representations.

APPENDIX A

Figure A1.

Behavioral correlations of within-domain (convergent) versus between-domains (discriminant) task performance for the younger group (< 52 years). Left panel: Fisher’s Z correlation matrix of all behavioral task pairings. Black outlined boxes indicate within-domain tasks. Centered values within each square indicate the average within-task correlation not considering a task’s perfect correlation with itself. Asterisks represent the between-tasks correlations used to compute discriminant validity. Right panel: scatter plots of Fisher’s Z coefficients divided by task pairing. For convergent validity, correlation coefficients are organized by domain; for discriminant validity, correlation coefficients are organized by session (see legend). “M&F” indicates between-domains correlations for memory and FLUID, and “S&V” indicates between-domains correlations for speed and VOCAB. The expanse of the box represents 1 SD, the shaded middle region represents the SEM for the 95% confidence interval, and the black line represents the mean.

APPENDIX B

Figure B1.

Behavioral correlations of within-domain (convergent) versus between-domains (discriminant) task performance for the older group (> = 52 years). Left panel: Fisher’s Z correlation matrix of all behavioral task pairings. Black outlined boxes indicate within-domain tasks. Centered values within each square indicate the average within-task correlation not considering a task’s perfect correlation with itself. Asterisks represent the between-tasks correlations used to compute discriminant validity. Right panel: scatter plots of Fisher’s Z coefficients divided by task pairing. For convergent validity, correlation coefficients are organized by domain; for discriminant validity, correlation coefficients are organized by session (see legend). “M&F” indicates between-domains correlations for memory and FLUID, and “S&V” indicates between-domains correlations for speed and VOCAB. The expanse of the box represents 1 SD, the shaded middle region represents the SEM for the 95% confidence interval, and the black line represents the mean.

APPENDIX C

Figure C1.

Neural correlations of within-domain (convergent) versus between-domains (discriminant) task performance averaged across participants belonging to the younger group (< 52 years). Left panel: Fisher’s Z correlation matrix of all task pairings of FC values. Black outlined boxes indicate within-domain tasks. Centered values within each square indicate the average within-task correlation not considering a task’s perfect correlation with itself. Asterisks represent the between-tasks correlations used to compute discriminant validity. Right panel: scatter plots of Fisher’s Z coefficients divided by task pairing. For convergent validity, correlation coefficients are organized by domain; for discriminant validity, correlation coefficients are organized by session (see legend). “M&F” indicates between-domains correlations for memory and FLUID, and “S&V” indicates between-domains correlations for speed and VOCAB. The expanse of the box represents 1 SD, the shaded middle region represents the SEM for the 95% confidence interval, and the black line represents the mean.

APPENDIX D

Figure D1.

Neural correlations of within-domain (convergent) versus between-domains (discriminant) task performance averaged across participants belonging to the older group (> = 52 years). Left panel: Fisher’s Z correlation matrix of all task pairings of FC values. Black outlined boxes indicate within-domain tasks. Centered values within each square indicate the average within-task correlation not considering a task’s perfect correlation with itself. Asterisks represent the between-tasks correlations used to compute discriminant validity. Right panel: scatter plots of Fisher’s Z coefficients divided by task pairing. For convergent validity, correlation coefficients are organized by domain; for discriminant validity, correlation coefficients are organized by session (see legend). “M&F” indicates between-domains correlations for memory and FLUID, and “S&V” indicates between-domains correlations for speed and VOCAB. The expanse of the box represents 1 SD, the shaded middle region represents the SEM for the 95% confidence interval, and the black line represents the mean.

Diversity in Citation Practices

Retrospective analysis of the citations in every article published in this journal from 2010 to 2021 reveals a persistent pattern of gender imbalance: Although the proportions of authorship teams (categorized by estimated gender identification of first author/last author) publishing in the Journal of Cognitive Neuroscience (JoCN) during this period were M(an)/M = .407, W(oman)/M = .32, M/W = .115, and W/W = .159, the comparable proportions for the articles that these authorship teams cited were M/M = .549, W/M = .257, M/W = .109, and W/W = .085 (Postle and Fulvio, JoCN, 34:1, pp. 1–3). Consequently, JoCN encourages all authors to consider gender balance explicitly when selecting which articles to cite and gives them the opportunity to report their article’s gender citation balance.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.